Correlated decision making across multiple phases of olfactory-guided search in Drosophila improves search efficiency

ABSTRACT

Nearly all motile organisms must search for food, often requiring multiple phases of exploration across heterogeneous environments. The fruit fly, Drosophila, has emerged as an effective model system for studying this behavior; however, little is known about the extent to which experiences at one point in their search might influence decisions in another. To investigate whether prior experiences impact flies’ search behavior after landing, I tracked individually labelled fruit flies as they explored three odor-emitting but food-barren objects. I found two features of their behavior that are correlated with the distance they travel on foot. First, flies walked larger distances when they approached the odor source, which they were almost twice as likely to do when landing on the patch farthest downwind. Computational fluid dynamics simulations suggest this patch may have had a stronger baseline odor, but only ∼15% higher than the other two patches. This small increase, together with flies’ high olfactory sensitivity, suggests that their flight trajectory used to approach the patches plays a role. Second, flies also walked larger distances when the time elapsed since their last visit was longer. However, the correlation is subtle and subject to a large degree of variability. Using agent-based models, I show that this small correlation can increase search efficiency by 25–50% across many scenarios. Furthermore, my models provide mechanistic hypotheses explaining the variability through either a noisy or stochastic decision-making process. Surprisingly, these stochastic decision-making algorithms enhance search efficiency in challenging but realistic search scenarios compared with deterministic strategies.

Summary: Fruit flies spend more time searching for food near attractive odors when the time since their last visit to a similar odor source is longer, which increases efficiency, as does stochasticity in the decision-making process.

INTRODUCTION

All moving organisms spend a significant amount of their time and energy searching for food, mates, or oviposition and nesting sites. Improving our knowledge of the algorithms that animals use during these search efforts represents a critical step towards understanding how organisms function by connecting neuroscience, behavior, ecology and evolution (Hein et al., 2016). On the behavior and ecology fronts, countless field studies have helped shape our understanding of the search behavior exhibited by mammals, birds and fish in the context of optimal foraging theory and satisficing (Carmel and Ben-Haim, 2005; Charnov, 1976). In laboratory environments designed to discover the neural basis underlying these decisions, many efforts have focused on olfactory search of organisms including mice (Findley et al., 2021), insects (van Breugel et al., 2018) and crustaceans (Michaelis et al., 2020; for a review, see Baker et al., 2018). To move the field forward, there is a growing push to connect laboratory and field experiments.

Most natural environments consist of a patchwork of potential resources, demanding multiple scales of search: long-range, intermediate, local and nutrient driven. Perhaps surprisingly, the unassuming fruit fly, Drosophila melanogaster, has emerged as a prime model to bridge the investigation of behaviors in patchy environments among disparate size scales. Long-range search for a Drosophila consists of flights of up to 10 km across food-barren areas in search of a resource cluster (Coyne et al., 1982; Jones et al., 1981), initially relying on celestial cues (Warren et al., 2019; Weir and Dickinson, 2012), as well as vision and wind (Leitch et al., 2021) until it catches an odor plume to follow (Budick and Dickinson, 2006; van Breugel and Dickinson, 2014). Within a resource cluster, a fly begins its intermediate search phase: tracking odor plumes (Becher et al., 2012; Dweck et al., 2013; Mansourian et al., 2018; van Breugel et al., 2018) and approaching visual cues (Saxena et al., 2018; van Breugel and Dickinson, 2014), often relying on the integration of the two (Cheng et al., 2019; van Breugel et al., 2015) in addition to wind information (Suver et al., 2019; van Breugel and Dickinson, 2014) to find fermenting fruit. After landing (van Breugel and Dickinson, 2012), the fly enters its third phase, local search. Now travelling on foot, the fly continues using odors to navigate the patchiness (Álvarez-Salvado et al., 2018; Demir et al., 2020; Gaudry et al., 2013; Jung et al., 2015; Tao et al., 2020), as cracks in the fruits’ skin serve as entry points, whereas mold renders portions too toxic (Stensmyr et al., 2012). After tasting some nutrients, the fly enters its final nutrient-driven search phase, characterized by a so-called ‘dance’ that is driven mainly by idiothetic cues (Corfas et al., 2019; Dethier, 1957; Kim and Dickinson, 2017). Regardless of whether the fly finds the nutrients it needs, eventually it will decide to take flight and leave, only to start the process all over again.

Whereas each phase of flies’ search has been subject to recent research efforts aimed at understanding both the behavior and neurobiology, little is known about how individual experiences from one encounter with an odor or food patch might influence the next. Building an understanding of this process has important implications for interpreting their neurobiology, ecology and behavior (Hein et al., 2016).

In this paper, I simulate a patchy environment in the lab by placing three ethanol-emitting objects in a wind tunnel. Individually marked fruit flies are allowed to freely explore these objects for 18 h. My results indicate that their local search behavior on each individual patch is correlated with (1) whether they approach the odor source and (2) the time interval since their prior visit. Although the relationship is subtle, agent-based models indicate that both this interval correlation and the variability in their decision-making process can increase search efficiency for certain environmental scenarios. These small improvements could easily add up over the timescale of a flies’ lifespan or over a population as a whole.

MATERIALS AND METHODS

Animals and experiments

To discover the relationship between decisions that Drosophila melanogaster Meigen 1830 make during local and intermediate search behaviors in patchy landscapes, I placed three food-barren odorous patches (10.8 cm diameter) in a wind tunnel (61×61×150 cm) with 40 cm s⁻¹ wind (Fig. 1A–C; van Breugel et al., 2018). Each patch constantly emitted the attractive odorant ethanol from the center of the patch by bubbling 60 ml min⁻¹ of air through a 50% ethanol/water solution. The acrylic patches had a perforated area in the center for emitting the odor and were all identical in size, shape, color, odor type and concentration. Although I did not characterize the spatial distribution of odor on the patch, it was likely most concentrated at the perforated holes, with a plume extending downwind near the surface of the platform (see fig. 2B in van Breugel et al., 2018). The edge was coated in fluon (byFormica, byformica.com) to prevent the flies from crawling out of view.

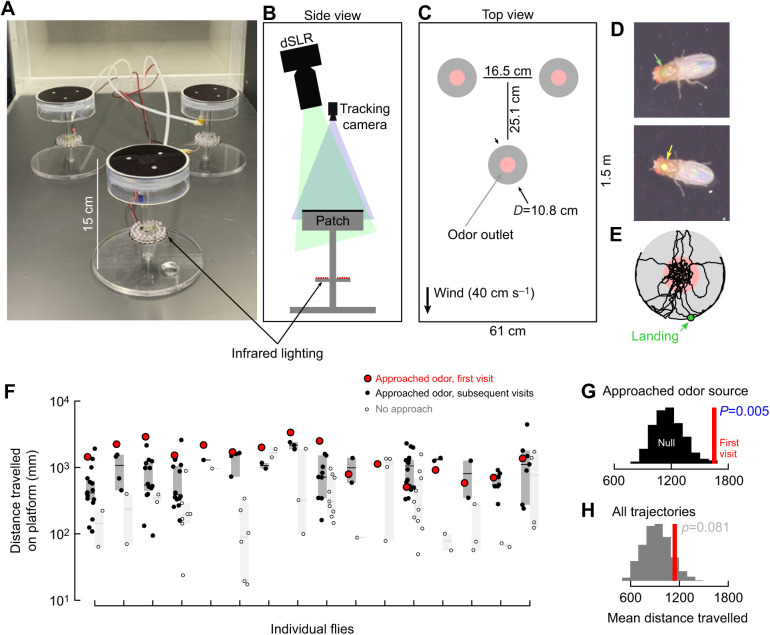
Fig. 1.

Flies explore odorous objects longer on their first encounter. (A) Photograph of experimental arrangement of three odor emitting patches inside a 60×60×120 cm wind tunnel (ELD, Lake City, MN, USA). (B) Above each patch was a machine vision camera to track the flies’ walking trajectories, and a digital SLR to image their markings. All six cameras were positioned to maximize the size of the patch in the field of view. (C) Top view diagram of experimental arrangement, red shading indicates approximate region where ethanol odor was emitted (see van Breugel et al., 2018). (D) Representative photographs of flies indicating their identifying color spots painted on with nail polish. (E) Representative trajectory on one patch. (F) Distance travelled on the patch by individual flies that approached the odor (black) or did not (white). Red: first approach. Shading indicates 95% confidence interval about the median. (G,H) Histograms show bootstrapped distributions of the expected mean distance flies should travel if each visit is identical and independent. Red line shows the actual mean distance travelled only the first visit. In G, only trajectories where the flies approached the odor were considered. In H, all trajectories were considered.

Above each patch there was both a 400×600 pixel monochrome machine vision camera (acA720-520um, Basler, Exton, PA) equipped with a Tamron 4-12 mm IR lens (Tamron USA, Commack, NY, USA) and an 18 megapixel color dSLR camera (Canon Rebel SL2; Canon USA, Huntington, NY, USA) equipped with Tokina 100 mm macro lenses (Tokina, Tokyo, Japan) (Fig. 1B). The optics and camera positions for both the machine vision and dSLR cameras were set to fill their field of view with the platform. When the flies landed on a patch, the machine vision camera tracked them at 30 frames s⁻¹ using the software described previously (van Breugel et al., 2018), with one modification. As soon as a fly landed, and every 10 s thereafter, the dSLR photographed the flies in higher resolution. This tracking system did not allow me to track flies in three dimensions between patch visits. The analysis presented here focuses only on the trajectories while flies were on one of the three patches.

To keep track of individual flies across all three patches, I painted a dot of colored nail polish on their thorax (Fig. 1D). The flies were cold-anesthetized for the painting and allowed to recover while being deprived of food, but not water, for 8 h before the experiment started. For each experiment, I used six female flies (Heisenberg Canton-S background). They were placed in the wind tunnel 6 h prior to their entrained dusk (relative to a 16 h:8 h light:dark cycle) and allowed to move freely throughout the wind tunnel for 18 h. In some experiments, nearly all flies visited the patch at least once, but typically only 2–3 of the flies made an appearance.

All trajectories were hand-corrected for tracking errors to guarantee their completeness and manually associated with the correct color identity from the dSLR images. This approach allowed for the clear identification of 194 out of the 201 total trajectories recorded. The seven unidentifiable trajectories ranged in length between 0.23 and 360 s (mean 135 s) and were omitted from my analysis. They could have contributed to some of the unexplained variance seen in the results. I limited the analysis to individuals who made at least three landings, as a critical component of their search behavior was the time interval between their visits. After this filtering, 178 trajectories remained, contributed by 16 individual flies. Except for the analysis presented in Fig. 1, I had to omit the first visit from the analysis since the interval before that visit is undefined. In a few cases, two flies interacted with one another on the patches, sometimes exhibiting aggressive behavior such as wing threats. These encounters were rare (<5% of trajectories), and their potential effects were ignored in the analysis.

Statistics: comparing first encounters with subsequent encounters

To determine if the distance flies travelled on their first visit to a patch was significantly larger than on their subsequent visits, I compared the mean distance that the 16 flies travelled on their first visits to a bootstrapped null distribution. To create the null distribution, which represents the expected distribution of mean distance travelled assuming that all the visits were independent and identical, I randomly selected one visit for each fly, calculated the mean of these 16 values, and repeated this operation for 1000 iterations. I then compared the mean of the distance travelled only on the first visits to this bootstrapped distribution. I ran this analysis for two scenarios: (1) including only visits where the flies approached the odor source, and (2) all the visits that flies made.

Statistics: mixed-effects model

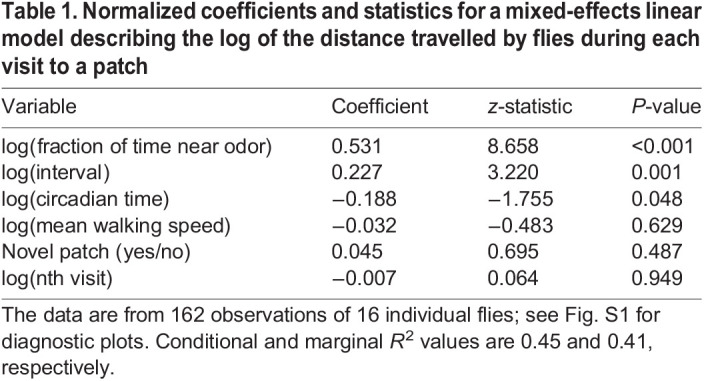
To analyze which of six potential inputs might be correlated with the distance flies travelled on the platform while also accounting for the potential differences across individual flies, I ran a mixed linear model on the data with random intercepts for each individual fly. I first log-transformed the distance travelled and all but one of the inputs (Table 1) to ensure that they were relatively symmetrically distributed about the mean. I also normalized each input to the standard deviation to allow the coefficients of the model to serve as a measure of effect size. See Fig. S1 for a summary of goodness-of-fit metrics. For these goodness-of-fit metrics, as well as the R² values, I report both marginal and conditional results, where the marginal only takes into account the fixed effects. The conditional considers both the fixed and random effects due to each individual fly (Nakagawa and Schielzeth, 2013). There is some heteroskedasticity in the residuals for the mixed-effects model (Breusch–Pagan test P=0.002). By replacing the fraction of time spent near the odor with a related metric, regardless of whether flies approached the odor source (i.e. spent more than 1% of their time near the odor), and applying a Box–Cox transformation to the output and inputs, this heteroskedasticity can be removed (Breusch–Pagan test P=0.078), without having any meaningful impact on the mixed-effects model results. To improve the interpretation of the data, I use the log-transformed data as opposed to the Box–Cox transformed data throughout the paper. All analyses, modeling and statistics were performed in Python, statistics were calculated using SciPy (Virtanen et al., 2020) and StatsModels (Seabold and Perktold, 2010), and the code is provided online at https://github.com/florisvb/correlated_decision_making_jeb.

Table 1.

Normalized coefficients and statistics for a mixed-effects linear model describing the log of the distance travelled by flies during each visit to a patch

Computational fluid dynamics

To analyze the flow patterns of the odor plumes, a two-dimensional (2D) quasi-DNS (direct numerical simulation) was performed using OpenFOAM. A 2D computational domain mimicking the geometry of the wind tunnel but having a length of 3 m was used. The cylinders were positioned according to the wind tunnel setup (see Fig. 1). However, they were shifted 0.01 m from center to avoid numerical instabilities. No-slip boundary conditions were enforced on the walls and each cylinder. A zero-pressure (gauge) outlet was used. The inlet velocity was ramped from 0 to 0.4 m s⁻¹ over the first half-second of simulation time to avoid divergence.

After the flow had settled to its transient base flow, a constant concentration of passive scalars was introduced at each node of the cylinder walls. Note that this differs from the actual odor release site, which was restricted to the center of the cylinders. This simplification was needed to run the simulation in 2D and provides a more conservative result. The simulation was then run for an additional 21 convective lengths. The transport equation for the scalar was solved at each time step according to:

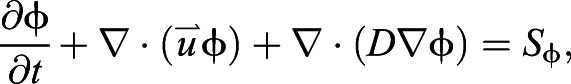(1)

where 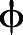is the scalar quantity, D is the diffusivity coefficient (10⁻⁴ m s⁻¹), 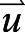is the velocity vector and 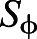is the source term (Maric et al., 2014). During each convective cycle, 32 snapshots of the flow were stored for analysis.

Agent-based modelling of decision-making strategies and goodness-of-fit

To understand the impact of my results on hypothetical food search scenarios, I ran a series of agent-based models. I primarily consider four decision-making strategies (TGUD, ITGUD, GPL, IGPL) guiding when flies should leave a patch in search of a new one in my agent-based models. These strategies can be described by probability density functions of distance travelled. In addition to these four primary strategies, I also discuss four other strategies, including stochastic renditions of TGUD and ITGUD, a slight modification of the IGPL strategy, and a fixed probability of leaving strategy. Descriptions and mathematical equations of these strategies are given below. Parameter values and implementation are available online at https://github.com/florisvb/correlated_decision_making_jeb and their discretized 2D probability mass functions are shown in Fig. S3.

TGUD (threshold giving-up distance)

In this deterministic strategy, agents always leave after travelling a constant distance (i.e. d=a, where a is a constant).

ITGUD (interval threshold giving-up distance)

In this deterministic strategy, agents always leave after travelling a distance that is log-linearly correlated with the time interval (i) since their last visit to a patch. Mathematically the distance travelled (d) is given by:

(2)

where a and b are both constants.

GPL (gamma probability of leaving)

In this stochastic strategy, agents leave after travelling a distance that has a gamma-distributed probability density function regardless of the time interval. Mathematically, the probability density function (PDF) of distance travelled (d) given the interval (i) is described by:

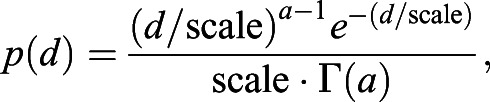(3)

where both a and ‘scale’ are constants, and Γ is the gamma function.

IGPL (interval gamma probability of leaving)

In this stochastic strategy, agents leave after travelling a distance that has a gamma-distributed probability density function with parameters that depend on the time interval. Mathematically, the PDF of distance travelled (d) given the interval (i) is:

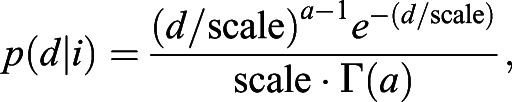(4)

where a and ‘scale’ are defined by the following equations with a₁, a₂, s₁, s₂ being constants:

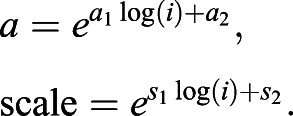(5)

STGUD (stochastic threshold giving-up distance)

In this stochastic strategy, agents leave after travelling a distance that has a log-normally distributed probability density function:

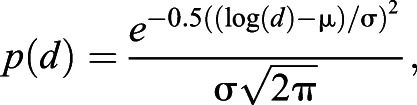(6)

where μ and σ are constants.

SITGUD (stochastic interval threshold giving-up distance)

In this stochastic strategy, agents leave after travelling a distance that has a log-normally distributed probability density function with parameters that are functions of the interval since the last visit:

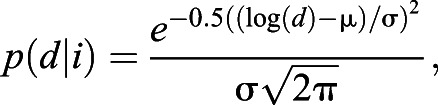(7)

where σ is a constant, but 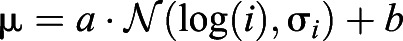, and a, b, σ_i are constants. This strategy models the assumption that the agent has a noisy measurement of the interval (i).

IGPLO (interval gamma probability of leaving offset)

This strategy is almost identical to the IGPL strategy, except that the gamma distribution has an offset parameter, which can be thought of as a minimal distance travelled threshold. Mathematically, the PDF of distance travelled (d) given the interval (i) is:

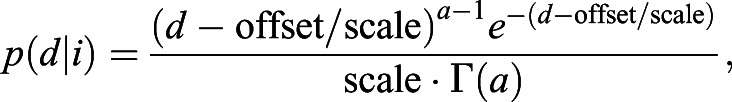(8)

where ‘offset’ is a constant, but a and ‘scale’ are defined as in the IGPL strategy.

FPL (fixed probability of leaving)

In this stochastic strategy the agent has an equal probability of leaving at each step, resulting in the following distance-travelled probability density function:

(9)

where 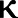is a constant.

For each strategy, I chose values for the parameters that maximize the log-likelihood of the data. To evaluate the goodness-of-fit for each strategy, I compared the log-likelihood of the data to a bootstrapped distribution of log-likelihoods for simulated datasets derived from the model (Fig. S4).

Agent-based modelling: relative search efficiency

To compare the efficiency of two decision-making strategies such as those highlighted in the previous section, I calculated the relative difference in the mean metabolic costs for an agent in my simulations to find food across 50,000 trials in a given environment scenario. I define the mean metabolic cost (MC) for a strategy as:

(10)

where t_p is the total time spent searching on patch, t_i is the total time spent during intervals between patch visits (i.e. the quantity of patch visits minus one multiplied by the mean time interval elapsed between visits), MR is the metabolic ratio describing the relationship between the metabolic cost to travel between patches and to search a patch, and k is energy cost per unit time for time spent on the patch. I then define the relative search efficiency between two strategies as the difference in these metabolic costs as:

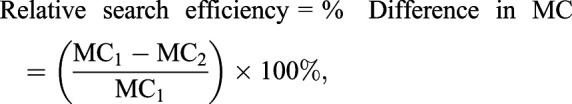(11)

which eliminates the factor k. Since the decision strategies I consider rely on the agent estimating distance travelled on a patch, I first convert these distances to time t_p using the log–log relationship given by the data (Fig. S3A, R²=0.7). For a fruit fly, the metabolic cost of flight is approximately 10–15 times greater than the basal metabolic rate (Chadwick, 1947; Lehmann and Dickinson, 1997), so if the agents spent all of their time between patch visits flying MR should be 10–15. However, just like the flies in my experiments, the agents may spend some of this time resting, so I considered a range of values for MR from 1 to 10.

RESULTS

After landing, many of the flies performed a stereotypical search bout during which they spent a significant amount of time near the odor source in the center of the patch, while also making periodic forays towards the edge, often circling the perimeter of the object (Fig. 1E, see also Movie 1). This complex search phase has been described in great detail previously by several authors (Álvarez-Salvado et al., 2018; Demir et al., 2020; Gaudry et al., 2013; Jung et al., 2015; Tao et al., 2020). Here, I set out to quantify how behavior varied across subsequent visits to the odorous objects. I focused on the distance the flies travelled during their search, which provides a measure of how much surface area they explored before giving up and leaving, and is likely measurable for an insect (Kim and Dickinson, 2017; Wittlinger et al., 2006). There is a large degree of variability in the distance each fly travelled on a patch before giving up and leaving (Fig. 1F). Although a substantial amount of this variability is likely due to unobservable factors such as the internal behavioral state of the flies, as is the case with any complex behavior, the goal of this paper is to understand how much of that variability can be explained by observable features of the flies’ behavior and environment.

First visits are longer than subsequent visits

For the majority of flies (10 of 16), the first time they visited the patch and also approached the odor source (i.e. entered the red region shown in Fig. 1C and spent at least 1% of their time there) they travelled farther than the average of their subsequent visits in which they also approached the odor source (compare the red dot with black dots in Fig. 1F). To understand if the distance travelled on these first visits was statistically longer than expected if all visits were independent and identical, I compared the average distance travelled on these first visits to a null distribution bootstrapped from all of the flies’ visits (see the Materials and Methods for detail). When only considering visits during which flies approached the odor source, flies did indeed walk significantly farther on their first visit compared with the average of all their visits (resampling test one-tailed P-value=0.005, Fig. 1G). However, when considering all the trajectories, not just those where the flies approached the odor source, flies did not walk significantly farther on their first visits (Fig. 1H). These observations suggest that both approaching the odor source and prior experiences play an important factor in flies’ decision-making process for how long they search the patch before leaving. To address these two hypotheses in more rigorous detail while also considering four other potential factors, I next built a mixed-effects linear model with all the visits after the first one.

Approaching the odor source and the interval between visits are key correlates with distance travelled

What potential factors might influence the distance flies travelled while searching? I considered six potential factors as hypotheses, as follows (Fig. 2A). First, flies might become habituated to the odor with multiple successive encounters or learn a negative association with the odor because of their failure to locate food nearby (nth visit). Second, if there is such a memory, perhaps it fades with time, suggesting that the time between visits might be important (interval). Note that in my experiments, it was not possible to track the flies during these intervals, so this time likely includes periods of flying, walking and resting. Third, perhaps flies that approach the odor source (i.e. entered the red region shown in Fig. 1C) or spend a larger fraction of their time near it are more likely to continue searching for longer (fraction of time near odor). Fourth, previous experiments indicate that the overall activity is correlated with attraction (van Breugel et al., 2018) and that might explain some of the variability (mean walking speed). As an alternative to mean walking speed, I also considered the fraction of time that flies were moving faster than 1 mm s⁻¹, which produced qualitatively similar results. Fifth, perhaps flies can visually remember the spatial location of the patch they visit (Ofstad et al., 2011) and search more on novel patches (novel patch). And sixth, the timing of their landing relative to their circadian rhythm might play a role (van Breugel et al., 2018) (circadian time). Hunger is also likely to play a role in modulating the local search behavior (Root et al., 2011). In my experiments, the flies were all starved before the experiment began, and subsequent increases in hunger were correlated with the circadian time. Finally, each fly may have its own behavioral idiosyncrasies owing to genetics (Ayroles et al., 2015) or perhaps the hunger state for each individual is variable despite all being taken off of food at the same time. To determine which of the six potential features as well as the individual variability can explain the distance flies travelled, I built a mixed-effects (random intercept) linear model (Table 1, Fig. 2B) from all the visits, excluding the first visit contributed by 16 individual flies, resulting in a total of 162 visits.

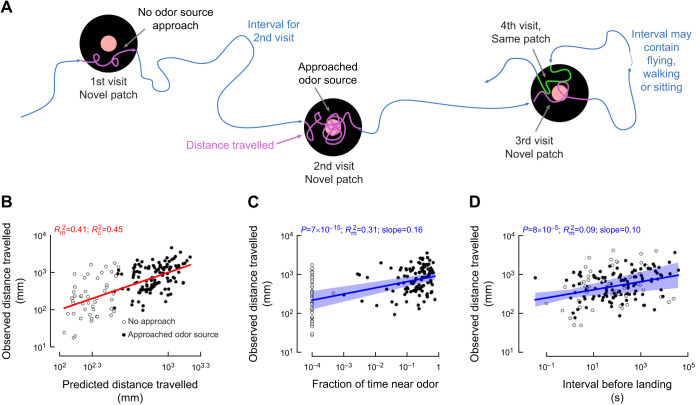
Fig. 2.

When flies explore an odorous, but food-barren, patch, the distance they travel on the object is larger when they approach the odor, and when the time since their last visit to a similar object is longer. (A) Cartoon of a hypothetical sequence of four visits to three odor-emitting patches. (B) Observed versus predicted distance travelled for a mixed effects linear model (Table 1). Filled and open circles indicate trajectories during which flies approached, or did not approach, the odor, respectively. Marginal (m) and conditional (c) R² values are given for the model. Red line indicates a slope of 1. (C) Observed distance travelled after controlling for all relationships in the mixed linear model except for the fraction of time flies spent near the odor. (D) Observed distance travelled after controlling for all relationships in the mixed linear model except for the interval before landing. Shading around the blue lines in C,D indicates the 95% confidence interval for the slope and intercept for the relationship.

Only two of the six features I considered were significantly correlated with distance travelled: the fraction of time spent near the odor and the time interval elapsed since the last visit to one of the odorous patches (Table 1). Note that these two correlations are consistent with the independent conclusions drawn from the flies’ first visits to the patches. Although the mixed-effects linear model serves as an efficient means for testing the six hypotheses under consideration, it is not intended to offer an accurate prediction of the flies’ behavior. Approximately 45% of the variance in the distance travelled is explained if fly individuality is taken into account (conditional R²=0.45). In contrast, without the random fly effect, 41% of the variance is explained (marginal R²=0.41). The similarity between these R² values suggests that although some differences may be attributed to individual flies, the effect is relatively small. The next two subsections consider these two significant features in greater depth in conjunction with theoretical modeling to understand: (1) why some flies might approach the odor source and others not, (2) how the relatively small effect size of the interval between visits could impact search efficiency in a meaningful way over the course of multiple visits, and (3) what mechanisms might underlie the variability in behavior and the impact of such variability on search efficiency.

The likelihood of approaching the odor source is correlated with patch location

Flies that spend even just a small fraction of their time near the odor source travelled a significantly larger distance during their search bout compared with flies that did not (Fig. 2C). The distance they travel, however, is not correlated with the fraction of time that the flies spent in a ±45 deg wedge downwind of the odor source (Fig. S2). To better understand the potential mechanisms underlying this behavior, I split the data into two groups: flies that approached the odor source (i.e. spent at least 1% of their time in the red region shown in Fig. 1C) and those that did not. Flies that approached the odor source travelled significantly farther (Fig. 3A). One trivial explanation could be that finding the odor source is difficult, and simply by covering more ground, flies may be more likely to encounter the odor source. If this were true, we would expect to see flies that take a long time approaching the odor source to also travel significantly farther. There is, however, no such correlation (Fig. 3B). In fact, the majority of flies that approached the odor source did so early in their trajectory: in the first ∼100 mm travelled compared with their average distance travelled of ∼1000 mm (Fig. 3C). Since most approaches happen early in the search, it is likely that encountering the odor triggers flies to pursue a longer search bout rather than the other way around. The flies that did not approach the odor source also generally travelled close to ∼100 mm or more, so should have had ample opportunity to approach the odor source (Fig. 3D).

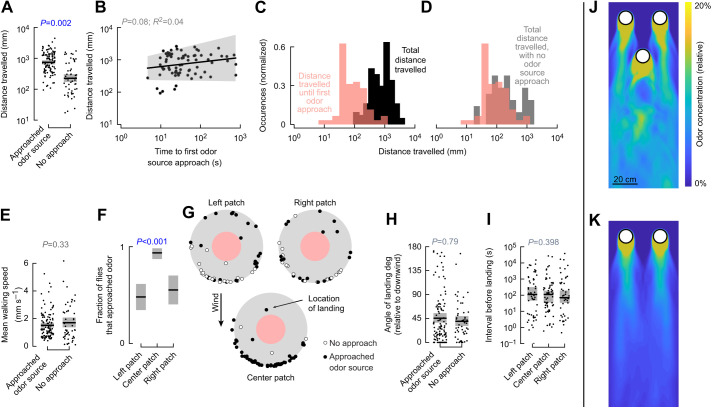
Fig. 3.

Flies are more likely to approach odor source when landing on the downwind patch. (A) Flies that approach the odor also travel farther on the patch. (B) Distance travelled is not correlated with the time elapsed between landing and the first odor approach. Shading indicates 95% confidence interval of the relationship. (C) The total distance flies travel on the patch is much larger than the distance they travel before first approaching the odor, whereas (D) the distributions are similar for flies that do not approach the odor. (E) The main walking speed is no different for flies that do or do not approach the odor. (F) Flies are more likely to approach the odor on the center-downwind patch. (G) Location of landings for each trajectory on the three patches (see Fig. 1). (H) Angle of landing is uncorrelated with approaching the odor. (I) The interval between patch visits is not different for the three patches. (J,K) Average relative odor concentration for a 2-dimensional computational fluid dynamics simulation of the three patches (J) or just the two upwind patches to provide a point of comparison (K). All non-regression statistics calculated with a resampling test. Shading in panels A,E,F and H,I: 95% confidence interval around the median.

Why might some flies approach the odor source and others not? Perhaps the flies were in different behavioral states that made them less motivated to search. Although this cannot be discounted entirely, prior experiments have found that flies are unlikely to land on an object in the presence of wind unless they first detect an odor (Budick and Dickinson, 2006; van Breugel and Dickinson, 2014), suggesting that the majority of the flies landing on the patches in my experiment had already detected some amount of odor prior to landing. Furthermore, the mean walking speeds of flies that approached and did not approach the odor source were no different (Fig. 3E), suggesting that their activity states were similar.

Flies were, however, significantly more likely to approach the odor source when searching the center patch (93% of 68 landings) compared with the other two patches that were positioned upwind of the center patch (left: 49% of 59 landings; right: 52% of 52 landings) (Fig. 3F). Perhaps the flies land on different locations on each patch, thereby resulting in different initial olfactory experiences? This is unlikely because flies predominantly landed roughly downwind from the odor source on all three patches (Fig. 3G). There were no differences in the mean angle at which flies landed, regardless of whether they approached the odor source (Fig. 3H), or in how far they travelled after landing. Finally, since flies landed at roughly similar frequencies on the three patches (68, 59, 52), it is not surprising that the time interval between landings was no different for the three patches (Fig. 3I).

Why are flies more likely to approach the odor source when landing on the downwind patch? One possibility is that odors advected downwind from the two upwind patches increase the odor concentration near the downwind patch. To explore this possibility, a colleague performed a 2D computational fluid dynamics simulation with passive tracers for my experimental arrangement. We ran the simulation for two scenarios: with all three patches as arranged in the wind tunnel (Fig. 3J, Movie 1) and just the two upwind patches (Fig. 3K, Movie 2). Although simplified compared with the full 3D flow, these 2D simulations together offer a rough estimate of how much odor from the upwind patches may have come close to the downwind patch. Comparing the two simulations suggests that, on average, there may have been a slight (∼15%) increase in odor concentration at the downwind patch due to the advected odor emanating from the upwind patches.

Agent-based modeling suggests that both interval correlation and behavioral variance improve search efficiency

Of the variables I tested, the only other correlate with distance travelled was the interval between patch visits (Table 1). Unlike odor source approaches, there was no correlation between which patch the flies landed on and the interval between visits (Fig. 3I). After accounting for the effect of approaching the odor source, there is still a significant but subtle positive correlation relating the interval between visits with the distance travelled (Fig. 2D). This correlation could be due to a variety of factors that I could not measure in this experiment. However, one possibility that can be explored with this dataset is whether it is possible that such a correlation could provide an advantage to the overall food search efficiency. The data show that when the time interval between visits was large, flies tended to search farther and longer before giving up and leaving. From an efficiency standpoint this makes sense: if it will take a long time to find a new candidate patch, it might pay off to be absolutely certain there is no food on the patch where the fly is presently searching. On the other hand, if the interval between visits is very short, the cost of leaving and finding a fresh patch may be small enough that it is worth leaving early, especially if it is generally easy to localize food on a patch. This section carefully explores this hypothesis by answering three questions: (1) could the subtle positive correlation I observed have a meaningful effect on search efficiency, (2) could the unexplained variance from my statistical model be the result of a simple underlying stochastic decision-making process, and (3) might such a stochastic process actually improve the search efficiency?

To understand how the relationship of the time between patch visits and the distance travelled on each patch might impact the search behavior of flies, I ran a series of agent-based models of a simple search paradigm (Fig. 4A). In my models, after landing on a patch with P_f probability of having food, the agents travelled for some distance before giving up and leaving. I modelled the decision to leave using a probability density function that describes the outcome of several decision-making strategies (see the Materials and Methods for mathematical details). During their search, I modeled the likelihood of finding food (when not on a barren patch) as identical for each step they took. This corresponds to a cumulative distribution function of an exponential distribution with parameter λ (CDF=1−e^−λd, where d is the distance travelled). This modeling decision is based on previously published data for walking flies searching a 170 mm arena for a small dab of yeast (Fig. 4B; Kim and Dickinson, 2017). In this model, larger values of λ⁻¹ correspond to patches where it is more difficult to localize food. At each step, agents who did not find food decided according to one of several decision-making strategies to either continue searching or leave. If the agent left, there was a time interval before encountering a new patch, which models the x-axis of the data shown in figures such as Fig. 2D. As in my experiments, this interval could include active travel time as well as resting time. To compare the efficiency of the two strategies, I calculated a mean metabolic cost, effectively a weighted sum of the total search time (see the Materials and Methods).

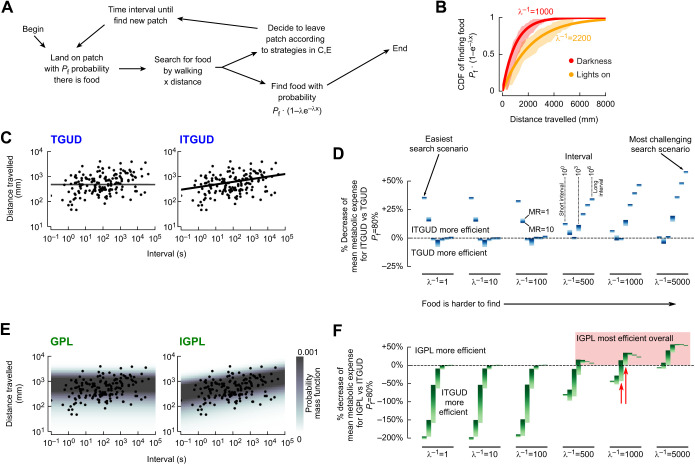
Fig. 4.

Correlating the decision to leave with the interval between visits and introducing variance into the decision both improve efficiency during challenging searches. (A) Decision sequence for agent-based models with three environmental parameters: interval (time between visits); P_f (probability there is food on patch); λ (probability of finding food each mm travelled). (B) Empirical cumulative distribution functions (CDFs) of exponential distributions for the given values of λ for when flies searching a 170 mm arena for a ∼2 mm dab of yeast first located the food (Kim and Dickinson, 2017) in darkness (red) or with lights on (orange). Shading: 95% confidence intervals. (C) Comparison of data from Fig. 2D with two deterministic strategies, with or without the interval dependence. The ITGUD (interval threshold giving-up distance) strategy is derived from the relationship in Fig. 2D. (D) Relative increase in metabolic efficiency of the ITGUD versus TGUD strategies for 42 environment scenarios consisting of 7 time interval values and 6 values of λ (see Fig. S3 for P_f=20%). For each scenario, 50,000 trials of a search sequence were run until the agent found food, and average relative change in metabolic cost for a range of metabolic ratios (MR) of 1 to 10 (see text for details) is shown. MR=10 (dark blue) corresponds to cases where the agent is flying 100% of its time between patch visits and walking 100% of its time on a patch. (E) Comparison of data from Fig. 2D with the probability mass functions of two stochastic strategies, with or without interval dependence. See the Materials and Methods for mathematical descriptions. (F) Comparison of IGPL (interval gamma probability of leaving) and ITGUD strategies to isolate the effect of stochasticity in the decision-making process. Red shading indicates the environment parameter space where IGPL is always the most efficient strategy; red arrows indicate environment scenarios that best match the data shown in Figs 2D and 4B. Strategy descriptions: TGUD, flies leave after a fixed threshold distance travelled; ITGUD, flies leave after a threshold distance travelled that is larger for larger intervals between patch visits; GPL, flies leave with some probability at each step, where the probability is drawn from a constant gamma distribution; IGPL, flies leave with some probability at each step, where the probability is drawn from a constant gamma distribution with parameters that depend on the time interval.

In ecology, the process of search has been dominated by the field of optimal foraging theory, namely, the marginal value theorem (Charnov, 1976; Schoener, 1971; Nonacs, 2001) and satisficing (Carmel and Ben-Haim, 2005). Neither model, however, provides an explanation for how these strategies could be implemented by a simple neural mechanism. However, several ‘rules of thumb’ that could be easily implemented have been proposed (Green, 1984; Iwasa et al., 1981). I considered two variations each of previously described deterministic and stochastic rules of thumb, resulting in four decision-making strategies.

One example of a deterministic search strategy is ‘threshold giving-up time’ (TGUT) (Croze, 1970; McNair, 1982), which states that an animal should continue searching for food in a patch for an amount of time proportional to the quality of the patch (i.e. the likelihood of finding food). However, because maintaining an accurate sense of time elapsed is challenging, a more likely strategy for insects is to leave after some ‘threshold giving-up distance travelled’ (TGUD) has been reached, given the behavioral and neural evidence for insects’ ability to count steps (Kim and Dickinson, 2017; Wittlinger et al., 2006). In my experiments, where everything is identical for each patch, the TGUD strategy is equivalent to traveling the same threshold distance on each patch until giving up and leaving, regardless of the travel time between patches. When the time interval between patch visits is large, either due to large travel times or the difficulty of finding patches, it might make sense for the animal to commit more effort (i.e. distance travelled) searching for food when they do get to a patch before giving up and leaving. I call this extension of the TGUD strategy the ‘interval threshold giving up distance-travelled’ (ITGUD). For both the TGUD and ITGUD strategies, I chose thresholds and a slope that best matched my data (Fig. 4C). The addition of the subtle interval dependence found in my data improves the mean search efficiency across all scenarios I considered with only slight losses in efficiency for the intermediate intervals (Fig. 4D, Fig. S3B). These results are not strongly dependent on the choice of metabolic ratio, nor do they depend on the value of P_f (Fig. S3B). In challenging search scenarios, corresponding to environments where it is difficult to localize food on a patch (large values of λ⁻¹) and where time intervals between patch visits are large, the ITGUD strategy is as much as 25–50% more efficient compared with TGUD. Meanwhile in easy search scenarios, corresponding to environments with small values of λ⁻¹ and where time intervals between patch visits are short, the ITGUD strategy also prevails. Overall the ITGUD strategy is consistently more efficient because it tunes the decision to leave based on the time interval between patch visits, whereas the TGUD strategy relies on a fixed decision to leave that is tuned for the average across all intervals.

The distances that flies travelled in my experiments exhibit substantial variability that is not explained by the deterministic strategies. This variability could arise from a number of different sources, including: (1) general behavioral variability due to unobservable states of the fly such as their overall motivation and their activities between visits; (2) flies having poor estimates of distance travelled, though some walking insects exhibit remarkable accuracy in their distance estimates (Wittlinger et al., 2006); and (3) poor estimates of the time interval between visits given the challenge of accurately estimating time. The latter two of these scenarios are discussed later, after considering another intriguing possibility: the variability may result from a stochastic decision-making process. Furthermore, regardless of the source, variability in the decision-making process might improve the average search efficiency across a population of flies.

In contrast to deterministic threshold-based strategies, the search behavior of some animals like jumping spiders has been described by a simple stochastic heuristic: the fixed probability of leaving (FPL) (Kareiva et al., 1989). With the FPL strategy, the animal does not need to remember time elapsed (or distance travelled) and instead leaves with a fixed probability at each time step (or physical step), resulting in an exponential distribution. By its very nature, the exponential distribution has a peak probability density function at zero with a long tail, resulting in more short visits than long ones, which may lead to visiting an unnecessarily large number of patches (Fig. S4). To avoid these short visits without the addition of any memory, it is possible to use a sum of FPL processes, corresponding to a sum of exponential distributions, which is equivalent to an Erlang distribution, a special case of the gamma distribution. With the right choice of parameters, an Erlang or gamma distribution allows for an entirely stochastic process to have a peak probability density at a non-zero value. By implementing a decision to leave based on such a gamma distribution, a fly could, on average, approximate a noisy TGUD decision-making process without the need for any memory or step counting. I call this strategy the ‘gamma probability of leaving’ (GPL), and implementation-wise it is the most straightforward decision-making strategy I consider. Finally, since my experiment suggests that there is a positive correlation between the distance travelled and the interval since the last visit, I considered an extension of the GPL strategy where the parameters of the gamma distribution are a function of the time interval since the last visit, which I call ‘interval gamma probability of leaving’ (IGPL). I chose parameters for both the GPL and IGPL strategies to maximize the log-likelihood of my data concerning the 2D probability mass functions (Fig. 4E, Fig. S3). To understand the impact of stochasticity in the decision-making process, I compared the efficiency of the IGPL and ITGUD strategies (Fig. 4F, Fig. S3B) and find that for more challenging scenarios (large values of λ⁻¹ and large intervals), the IGPL strategy is the most efficient.

Which search strategy is most consistent with my data? To address this question, I reconsider the possibility that flies may utilize a stochastic TGUD strategy (STGUD) with log-normal variability in their measurements of distance travelled, or a stochastic ITGUD strategy (SITGUD) with log-normal variability in their measurements of the time interval between visits as well as distance travelled. The SITGUD and IGPL strategies both offer more explanatory power than their non-interval dependent counterparts, as seen by the lower Akaike information criterion (AIC) values (Fig. S4). Comparing the SITGUD and IGPL strategies, there are subtle differences. Still, overall, they both offer a similar fit with the data (Fig. S4). In summary, the data from my experiments are most consistent with a strategy that has a subtle correlation with the time interval between visits and high variance. However, the source of this variance could be either a simple stochastic mechanism, a noisy measurements process, or a combination thereof. Critically, the correlation and variance both offer improved efficiency in the more challenging search scenarios.

DISCUSSION

My results indicate that flies’ travel farther on odorous but food-barren objects before giving up and leaving when (a) they approach the odor source, and (b) the time interval between patch visits is large. Flies search behavior is, however, quite variable across visits. Using an agent-based modeling framework, I show that both the time interval correlation as well as the variance in their behavior could be the result of a simple stochastic decision-making process that actually improves the average search efficiency for some environmental scenarios.

Significance of which patch flies land on

Despite all three patches being identical in size, shape, color, and odor emitted, flies were more likely to approach the odor source when landing on the downwind patch. Computational fluid dynamics simulations suggest that although the downwind patch may have a slightly higher baseline odor landscape compared to the two upwind patches, the effect is relatively small: a ∼15% increase. This slight increase in concentration would have resulted in a slightly higher baseline odor distribution across the top of the patch, potentially increasing the motivation of flies to search the patch more thoroughly, leading them to discover the odor source in the center of the patch. Alternatively, the flies landing on the downwind patch may have experienced a higher or different olfactory experience prior to landing based on their flight trajectories, resulting in a different internal state. Future experiments that simultaneously track walking and flying flies will be needed to test the hypothesis that flies are more likely to approach an odor source depending on their olfactory experience during flight.

Significance of interval-correlation and variability in the decision to leave

The time interval between visits had a significant but subtle impact on how far flies walked on the patches before giving up and leaving. It is possible that the correlation I observed could be due to other unmeasured factors that cannot be addressed in this manuscript. However, to understand whether a subtle interval correlation might have a meaningful impact on search efficiency I developed a series of general purpose agent-based search strategies. My models demonstrate that incorporating an interval correlation in the decision to leave improves the search efficiency in nearly all search scenarios because it tailors the search behavior to parameters of the environment (i.e. the time to travel between patches). When these models are applied to the specific correlation that I observed in my experiments with flies, this increase in efficiency was in some cases 25–50% -- a surprisingly large increase for the subtlety of the correlation. It is possible that other organisms may exhibit even stronger correlations. Future field experiments with a variety of animals will be needed to test the validity of my models in a broader context. Furthermore, my models suggest that flies’ behavior is consistent with a stochastic decision-making process, which requires less memory and is more efficient on average than a deterministic strategy in some realistic search scenarios. Over the course of a fly's life, these improvements in efficiency could add up to thousands of fewer fruitless landings, and across an entire population, this may represent a significant evolutionary advantage.

Although my agent-based modelling suggests that the observed variability in behavior may be expected if flies utilize a stochastic decision-making process, there are many other possible causes of the underlying variance. These other factors include: (a) their motivation for landing in the first place, (b) whether there are social interactions on the patch and (c) what exactly the flies are doing in between their visits [they are almost certainly not flying that whole time, as insects spend most of the time sitting in these wind tunnel experiments (van Breugel et al., 2015)]. Finally, although all the flies were starved for the same amount of time before starting each experiment, it is possible that some became hungrier than others over the course of the experiment, which would change how persistent they would be during their search bouts on the patches (Root et al., 2011; Sayin et al., 2019) and thus introduce additional variability. Future experiments that monitor fly behavior throughout the chamber will be needed to address these hypotheses.

Which of the environmental scenarios that I consider are the best match for real-world conditions? This is, unfortunately, impossible to answer without data from flies behaving in their natural habitat. However, it is possible to make some rough estimates. The red arrows in Fig. 4F indicate scenarios that best match the values of λ⁻¹ from Fig. 4B and the range of intervals seen in Fig. 2D. Note that these values of λ⁻¹ are for when the fly first encountered the food. After this point, flies typically initiate a new local nutrient-driven search (Corfas et al., 2019; Kim and Dickinson, 2017), so the real value of λ⁻¹ may actually be much higher. Together, these results suggest that flies’ decision-making strategy for when to leave an odorous patch may be optimally tuned for challenging search scenarios. One limitation of my simulations is that I did not consider heterogeneous environments that might have patches with different values of P_f, different intervals, or different values of λ on each patch. Future experiments will be needed to determine the real-world heterogeneity of such patches for wild flies and how much time flies spend on natural odor sources before finding a suitable food source or giving up and leaving.

How might flies keep track of the interval between visits?

Although a number of models for neural encoding of interval-timing have been proposed (Tallot and Doyère, 2020), there is little experimental evidence for minute to hour scale interval-timing. In rats, extended time sense is encoded in the hippocampus (Mankin et al., 2012, 2015; Rubin et al., 2015). However, the accuracy is modulated by drugs, hormones, and context (Meck, 1983; Penney et al., 1998). For insects, the ability to measure time intervals on the scale of seconds to minutes is open for debate. Parasitoid wasps can learn time intervals (Parent et al., 2016, 2017). Honeybees, however, can not (Grossmann, 1973; Philip et al., 2014). Although their cousins, bumblebees, have been shown to learn fixed time intervals (Boisvert and Sherry, 2006), the analysis has been called into question (Philip et al., 2014). Instead, their behavior suggests that they may have learned a different strategy that approximates interval timing. An alternative to keeping track of true time elapsed could be through habituation, sensory adaptation, or novelty detection.

In my experiments, although the time interval since the last visit was significantly correlated with distance travelled on the patch (Fig. 2D), the quantity of repeated prior visits was not (Table 1), suggesting that long-term habituation is unlikely. I further confirmed this by re-analyzing previously published data of walking flies encountering an ethanol stimulus every 40 min over the course of 18 h (van Breugel et al., 2018) (see supplemental code for detail: https://github.com/florisvb/correlated_decision_making_jeb). In these experiments, the preference index for flies towards ethanol was primarily determined by their mean walking speed (mixed linear model R²=0.552), rather than a combination of speed and the number of prior encounters (mixed linear model R²=0.592, P=0.267 for prior encounters). Sensory adaptation is unlikely to be the sole contributing factor given that peripheral olfactory receptor level adaptation occurs on much faster time scales [∼0.5 s (Bell and Wilson, 2016) to 10s of seconds (Martelli and Fiala, 2019)] compared with the behavior observed in my experiments, which occurs on the scale of minutes to hours. A likely explanation consistent with my data is that flies rely on some form of one-shot novelty detection mediated by the mushroom bodies, which has a time scale of up to 1 h (Hattori et al., 2017), which corresponds surprisingly well with the ∼3600 s mean interval (on the log scale) in my experiments. Future experiments will leverage genetic tools to manipulate this system to see how it changes their search behavior.

Conclusion

My results suggest that the search behavior exhibited by fruit flies likely depends on the recency of prior experiences. These results, along with recent innovations in genetic tools, optogenetics, imaging etc., suggest that flies may serve as a powerful model system for studying multi-scale complex search behavior in heterogeneous environments. Finally, the research approach and results presented here offer possible paths to uncover the neural basis of these behaviors.