Abstract
Vision-correcting displays are key to achieving physical and physiological comforts to the users with refractive errors. Among such displays are holographic displays, which can provide a high-resolution vision-adaptive solution with complex wavefront modulation. However, none of the existing hologram rendering techniques have considered the optical properties of the human eye nor evaluated the significance of vision correction. Here, we introduce vision-correcting holographic display and hologram acquisition that integrates user-dependent prescriptions and a physical model of the optics, enabling the correction of on-axis and off-axis aberrations. Experimental and empirical evaluations of the vision-correcting holographic displays show the competence of holographic corrections over the conventional vision correction solutions.
1. Introduction
The emergence of virtual reality (VR) devices has brought unprecedented public attention to near-eye display technologies. Numerous approaches have been proposed to improve the visual experience by miniaturizing the form factors [1,2] and alleviating visual discomfort [3] with a support of focus cues [4–8]. Despite the numerous approaches aimed at physical and physiological comforts, these displays lack the flexibility to provide optimal visual experience to various users. Vision is a factor that largely differs among individuals, and near-eye displays ought to provide a user-adaptive vision solution to encourage mass adoption.
In reality, hundreds of millions suffer from various visual imperfections worldwide, and the affected population continues to increase in number [9]. These people experience blurry images even when viewing an ideal display, mainly due to the presence of monochromatic ocular aberrations. Monochromatic aberrations often occur due to abnormal refraction in the eye, which results in common refractive errors such as myopia (near-sightedness), hyperopia (far-sightedness), and astigmatism. Monochromatic ocular aberration correction, also known as vision correction, and its impact on acuity [10] has been actively studied in the field of adaptive optics [11,12]. Recent refractive surgeries [13,14] benefit from the adaptive technologies. Nevertheless, the users prefer to wear eyeglasses because these surgical treatments are invasive.
One of the most overlooked, but possibly most crucial, challenges in the near-eye display industry is that numerous users with refractive errors need to wear the devices with their optical corrections. Various vision-correcting displays are introduced by adopting additional optics [15–18], adopting retinal projection scheme [19], or tailoring light field [20–22]. Yet, employing additional optics is less versatile since they utilize optics customized to a specific prescription or cannot deal with astigmatism, which is one of the common refractive errors. Retinal projection displays hardly support focus cues since the exit-pupil of the display is narrow. Moreover, light field displays are less feasible due to the inherent trade-off relationship between spatial and angular resolution, and additional optimization requirements.
Among the potential displays, holographic displays can correct various types of refractive errors [23], provide high-resolution images and support focus cues [24] by modulating complex wavefront of coherent light using a spatial light modulator (SLM). Recent holographic near-eye displays [7,8,25] have sought improvements in image quality by hologram manipulation to handle the undesirable aberrations in the optical structures. However, these are often carried out using manual calibrations [7,26], iterative search algorithms [8,27] and iterative optimization procedure [28,29]. These approaches have the disadvantage of low practicality due to lengthy procedures, and this aspect gets more prominent in terms of obtaining a vision-correcting hologram. Moreover, the acquisition of a vision-correcting hologram by assuming the human eye as a thin lens is not sufficiently accurate and can hardly be performed if the viewing condition deviates from a specific case. Therefore, a hologram rendering that can be utilized in arbitrary conditions through fast and accurate calculations is required. Although the potential application of holographic display as a mean of vision correction is introduced before [7], implementation of vision-correcting holographic display has neither been performed and the significance of vision correction is nor evaluated with user experiments.
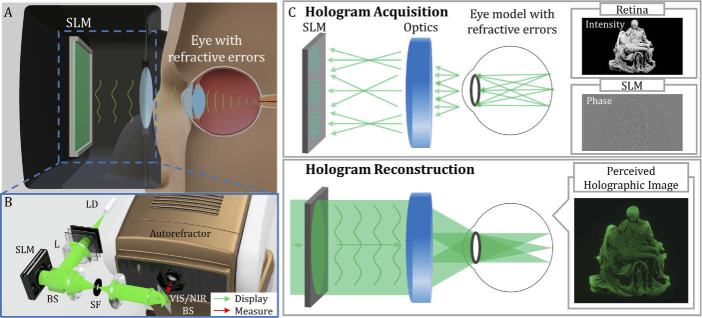
Here, we introduce a vision-correcting holographic display shown as Fig. 1(A) with hologram acquisition based on a physical model of the optics as well as a human eye, and assess the proposed work experimentally and empirically. The proposed approach enables the correction of on-axis and off-axis monochromatic ocular aberrations along with the aberrations of the optical system. Then, we evaluate the holographic corrections with other conventional vision correction modes, and investigate its impact on visual acuity with user experiments. To realize, we built a prototype of holographic near-eye display incorporating a light engine and an autorefractor described as Fig. 1(B), and accelerated the entire hologram calculation to reflect the user’s prescription measured on-site. The results obtained through user studies demonstrate potential uses of holographic displays to users with refractive errors and provide guidance for improving user experience through holographic displays.
Fig. 1.
(A) Concept of vision-correcting holographic display. (B) Bench-top prototype of vision-correcting holographic display integrated with the autorefractor measuring the prescription data (SPH (spherical requirement), CYL (cylindrical requirement) and AXIS (axis of astigmatism)). (LD: laser diode, L: lens, BS: beam splitter, SF: spatial filter, and VIS/NIR BS: visible and near-infrared beam splitter) (C) Principle of hologram acquisition (1st row) and reconstruction (2nd row) to perceive aberration and vision-corrected holographic image. (Pieta: purchased 3D model from CGTrader.)
2. Vision-correcting holographic display
2.1. Principle of aberration-corrected hologram acquisition
We introduce and elaborate on the aberration-corrected hologram acquisition based on ray tracing. It is known that if the overall optical system is free from aberrations, the exit-pupil is filled with spherical waves forming a set of ideal points and vice versa [30]. Therefore, we begin hologram generation by assuming the sensor as an array of point emitters emanating coherent spherical waves, as shown in Fig. 1(C). Then, a spherical wave can be approximated to a set of ray bundles when ignoring diffraction: the direction perpendicular to wavefront matches the direction of the ray, and the phase of a plane wave is a result of the accumulated optical path that the ray experiences. As a result, each spherical wave heading towards the pupil can be substituted by a set of rays with uniform distribution in diverging direction.
A ray can be characterized with the present position and direction, further containing five-dimensional information. Based on the parameters, we can represent additional information, complex amplitude, acquired through propagation. The complex amplitude of k-th ray emanated from the point in the sensor (or retina) can be expressed as
| (1) |
where, is the wavelength of coherent light, is the accumulated optical path, is a real-valued initial amplitude as a square root of intensity, and is an initial phase, respectively. The accumulated optical path, of a single ray, can be described as
| (2) |
where, denotes the refractive index of -th material in wavelength of , and refers to the Euclidean distance of two intersection points being determined by ray with an index of and -th material. Here, the wavelength-dependent refractive indices of the materials consisting the conventional optics, are well-defined with the Abbe number.
The rays originated from the retina pass through the entire optical system and eventually reach the SLM plane. Departed from a single point , the estimated wavefront function, , can be acquired in a discrete form as
| (3) |
where, is a set of rays departed from a single point and simultaneously incident to SLM plane within the diffraction angle, (: pixel pitch of SLM). The lateral placement that the ray with an index of can be represented in coordinates of SLM plane as . If rays reach the SLM plane within the cut-off frequency, are sporadically distributed, the wavefront function can be reconstructed by interpolation. Then, the resultant impulse response function that corresponds to the SLM coordinate of can be acquired as
| (4) |
Here, is a real-valued window function with the size determined by cut-off frequency; we use a Gaussian window function considering the Stiles-Crawford effect [31]. is a coordinate of window function. Equation (4) can be precisely determined with a consideration of other optical parameters. Thus, we employ a schematic eye model to acquire vision-correcting holograms. However, studies on schematic eye models involving the different types of refractive errors are scarce since the ocular parameters vary in individuals, especially in case of the eye of refractive errors. Therefore, we bypass this issue by utilizing the integrated version of the eye model that combines a robust schematic eye model of normal vision and an additional error-inducing complementary phase plate applying the prescription data.
2.2. Extension to vision-correcting hologram
For a physical model of the eye, we adopt the Arizona eye model [31] as it satisfies major requirements. Above all, it is constructed with several statistical and clinical studies matching the eye structure of a large population leading to highly accurate prediction of both on-axis aberrations and off-axis aberrations. In addition, the parameters of the eye model are adjusted with a single input of accommodation state that allows accommodation-dependent modeling of residual aberrations.
Prescription data that vary individual can be applied at the mid of ray tracing by placing a complementary phase plate in front of the schematic eye. This phase plate allows to shape the wavefront in a desirable shape since a ray can be interpreted as a local gradient of the wavefront. Here, we denote the grating vector of the prescription phase plate as . When a ray with a grating vector of is incident to the phase plate, the first-order solution of diffraction is given as
| (5) |
where is a -vector of an outgoing ray. If the prescription data is given as , each and component of the corresponding phase plate is given as
| (6) |
in a system after transformations to match the -axis of the local coordinate to . Here, represents the local coordinate of the intersection point between the ray and the phase plate. Since , the direction of the outgoing rays can be determined with Eq. (5). Likewise, the additional optical path can be calculated in a simple relation as
| (7) |
where, and denote the accumulated optical path of the rays incoming to the phase plate and outgoing from the phase plate, respectively.
2.3. Hologram encoding
It can be observed that the impulse response function is a four-dimensional function as Eq. (4). Therefore, it is necessary to perform ray tracing for every single point on the retina to generate the individual wavefront function. However, since ray tracing requires a large number of rays to eliminate the noise from ray sampling, the computation time is huge. Therefore, we only employed ray tracing for the acquisition of the wavefront function, and the generation of the entire hologram is performed by the look-up-table (LUT) based method [32].
In our method, the spatially varying wavefront function, is represented in Zernike polynomials and its coefficients are stored in the LUT. The relation between Zernike basis and the wavefront function is expressed as
| (8) |
where, is an index of Zernike polynomial, is Zernike coefficient corresponding to the index, and is a -th Zernike polynomial. Note that the aberration of the optical system is spatially varying, so the wavefront function and its Zernike coefficients differ spatially. The obtained Zernike coefficients, are stored into LUT. The number of LUTs equals the number of Zernike polynomial and the size of LUTs is determined by hologram resolution. We assume that the aberration of the optical system is spatially slow-varying. Thus, the Zernike coefficient maps that span the entire field are obtained by interpolation of the Zernike coefficients acquired at the sample points. The interpolation is conducted adopting triangulation-based cubic interpolation with continuity. The impulse response function is reconstructed from the LUT of Zernike coefficients and convolved with the target complex amplitude to generate complex field as
| (9) |
The amplitude component of the target retinal image is given as a square root of intensity profile extracted from a single RGB-D image. The phase component of retinal complex target is initialized with a randomized pattern ranging from 0 to , and phase-only SLM () can be encoded as,
| (10) |
where, the stands for a phase extraction operator from a complex matrix. Here, the phase patterns are encoded by adopting the amplitude discarding method since the high spatial frequency region is well-preserved without additional phase encoding procedure such as double phase method [7]. Finally, the user can perceive aberration-corrected holographic image as shown in the bottom row of Fig. 1(C).
2.4. Simulation on spatially varying aberration correction
In this subsection, we adopt the proposed holographic correction in the conventional optical system with the disclosed parameters and demonstrate the feasibility of the proposed approach. The simulation is conducted on the 4-f system that consists of two off-the-shelf lenses (Thorlabs, AC508-075-A-ML). There are likely explanations for choosing the specific optical structure. First, 4-f system is commonly utilized in near-field holographic displays. In addition, the structure is comparably free from on-axis aberrations but inherently suffers from field curvature.
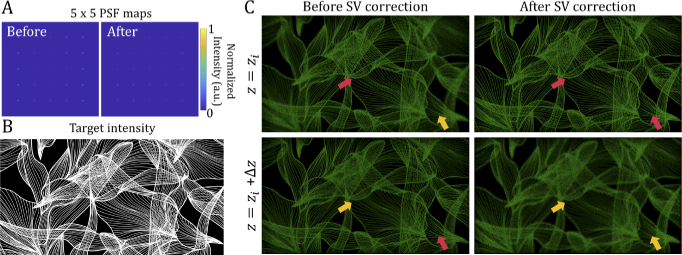
As observed from the point spread function (PSF) maps in Fig. 2(A), the optical structure suffers from field curvature which is one of spatially varying aberrations. The points located away from the optical axis suffers from the undesirable blur at the target depth. Likewise, although the near-field hologram is reconstructed to form a planar holographic image of target intensity provided as Fig. 2(B), the optically relayed field reconstructs the field with undesirable curvature as Fig. 2(C). The holographic images of Fig. 2(C) are reconstructed in two different depth planes and ) with slight deviation in axial location of sensor. If SV correction is not adopted, the peripheral sections of the holographic image is not sharply focused at but the sectional image rather gets clear at ). However, if the hologram is constructed based on proposed approach, the field can be tailored to form a planar holographic image at . Without losing generality, this physical model driven hologram acquisition realizes the reconstruction of aberration-corrected holographic image.
Fig. 2.
Simulation results of spatially varying (SV) holographic correction with the specified optical structure. The (A) 5×5 point spread function (PSF) maps are simulated at the original image depth. In addition, the examples of SV aberration-corrected single-frame holographic images with the (B) target intensity (purchased imagery from Shutterstock) are demonstrated. The SV correction realizes to flatten the pixel-wise depth mismatch in the reconstructed holographic image as provided in (C). The red arrows in the holographic images point the in-focus regions while the orange arrows point the out of focus regions. For better viewing, the brightness of reconstructed holographic images has been increased by six times.
3. Implementation
3.1. Software
3.1.1. Ray tracing
Prior to ray tracing, the optical configuration of the entire system has to be defined. The sag profiles of lenses serve as refractive boundaries. Then, we solve the quadratic equation consisted of the sag profile of each refractive surface and line equation representing a ray. Refraction is simulated by Snell’s law. The physical parameters (radius of curvature, thickness, the refractive index at target wavelength, semi-diameter, conic constant, etc.) that define individual optics have been identified in the Zemax Optic studio library [33]. The distances between optics are determined by the imaging condition.
We performed ray tracing based on the designated configuration. In ray tracing, 500×500 rays within a diverging angle of 20 degrees are generated from a single point towards the SLM plane. We have heuristically determined the number of rays according to the interpolation errors within the tolerance level. Here, we ignore the rays that are blocked by the physical apertures of the optics. Ray tracing has been conducted in Python rather than commercial ray tracing tool, Zemax Optic studio to boost the speed. We conducted ray tracing with parallel computation with PyCUDA [34], one of the representative parallel computation APIs from Python. It only took 0.004 seconds to propagate a quarter-million rays through twelve consecutive layers with an Nvidia GeForce GTX 1070 GPU. Increasing the computational speed of the ray tracing itself can potentially play a significant role in interactive hologram rendering that considers focus adjustment or pupil movement.
3.1.2. Hologram rendering
A hologram is then acquired by a different set of Zernike coefficients since the aberration is intrinsically spatially varying. Thus, the hologram, with a target of a single RGB-D image [35], is processed with the look-up table (LUT) method [32]. The LUT matrix size is equal to the resolution of the field as 3840×2160, and the number of LUT corresponds to the number of Zernike polynomials considered in the hologram rendering. However, point-wise integration of Zernike coefficient maps suffers from intensive computation, although it has been accelerated with compute unified device architecture (CUDA). In the experimental evaluation, we rendered SV corrected hologram with six 3840×2160 Zernike cofficient LUTs corresponding to piston (), -tilt (), -tilt (), vertical astigmatism (), defocus () and oblique astigmatism (), with the individual window size of 601×325. The window size can be adjusted with the prescription data. It took 20 minutes per each hologram frame with graphic card of Nvidia Titan RTX.
In the user experiments, we assumed that the aberration is spatially invariant and the hologram is processed with a single zernike coefficient set acquired at the center index. We used CUDA for the GPU programming and cuFFT library to perform a discrete Fourier transform on the GPU for acceleration. The calculation time of a single-color hologram with a resolution of 3840×2160 and window size of 1001×1001 was 0.19 seconds, achieving an interactive rate with an Nvidia Geforce RTX 3070 graphic card. The overall procedure only took a minute to render holograms of various acuity targets employed in the user experiments.
3.2. Hardware
The proposed approach has been assessed with a bench-top prototype of a holographic near-eye display fully constructed with the off-the-shelf lenses. The experimental setup of the prototype is provided in Fig. 3(A)-(B). The coherent laser beam with the wavelength of 532 nm is spatially filtered and collimated with a lens (Thorlabs, AC-508-200-A-ML). The collimated beam passes through a linear polarizer to match the desired polarization state of the phase-only SLM. The reflective-type phase-only liquid crystal on silicon (LCoS) SLM, a product of Holoeye (GAEA-2), was utilized as a displaying device. It contains a resolution of 3840×2160 pixels, a pitch of , and an active area of 1.53 cm×0.92 cm. High-order noises due to the pixelated structure of SLM are eliminated by placing a low-pass filter in the middle of 4- optics. In addition, a small portion of the filter’s central region is blocked to rule out the noise of direct reflection from SLM. The 4- optics consisted of two lenses (Thorlabs, AC-508-75-A-ML) that optically relay the SLM plane to the counterpart. However, relay optics constructed with off-the-shelf lenses cause undesirable aberration, such as field curvature. A 2-inch lens with a focal length of 75 mm (Thorlabs, AC-508-75-A-ML) is utilized as an eyepiece lens to virtually float the reconstructed holographic image. With this setting, 10.7 mm× 10.7 mm of eye-box is guaranteed with 532 nm illumination to fill the pupil over 6 mm. A charge-coupled device (CCD) with resolution of 4096×3000, and pixel pitch of is utilized to capture the experimental results.
Fig. 3.
(A-B) Bench-top prototype of holographic near-eye display for the experimental evaluation. The green arrow indicates the beam path. We implemented the setup with off-the-shelf lenses with the disclosed physical parameters and examined the feasibility of aberration correcting hologram. The enlarged views of the (C) red box and the (D) orange box show a series of lenses equipped to match the prescription data (). (E) Another type of bench-top prototype of vision-correcting holographic near-eye display utilized in user experiments.
As shown in Fig. 3(C)-(D), a series of a cylindrical lens and a spherical lens is consecutively placed with the minimal distance between them to generate a refractive error in front of an offset spherical lens. A 1-inch cylindrical lens (Thorlabs, LJ1653RM-A) with a focal length of 200 mm and a 1-inch spherical lens (Thorlabs, LA1908-A) with a focal length of 500 mm are consecutively placed to mimic the eye with prescription of (). Individual additional placement of lenses denote refractive errors; spherical power (SPH) of −2.0 D and cylindrical power (CYL) of −5.0 D. A 1-inch spherical doublet lens (Thorlabs, AC254-030-A) is utilized to serve as an ideal lens. As the effective dioptric power of the eye is known to be 60 D, we equipped the lens having the greatest dioptric power among the possible candidates. This stack of lenses represents an imitated eye optics with ocular refractive errors.
We built another prototype of holographic near-eye display to perform user experiments as shown in Fig. 3(E). To secure eye safety, the light source was modified to a laser diode (Green: OSRAM PL520B) that is capable of intensity modulation with a light engine (Wikistars) and additional neutral density filter (NDF) is placed. The wavelength of laser diode was 520 nm. A LP and a half wave plate (HWP) is consecutively placed to match the polarization angle of the laser diode and the phase-only LCoS SLM. The phase-only LCoS SLM, a product of MAY, having identical specifications with those of Holoeye GAEA-2, was utilized. In order to reduce the systematic aberration, the 4-f relay optics are substituted with two camera lenses (Canon, f=50 mm, F/1.8) that optically relay the SLM plane to the counterpart without a minimal error. A 1-inch lens with a focal length of 75 mm (Thorlabs, AC254-075-A-ML) is utilized as an EL to float the reconstructed holographic image virtually. The virtual holographic image was directed by a visible/near-infrared beam splitter (VIS/NIR BS, Thorlabs BSW20R) to the user’s eye while his/her head was constrained to the chin rest of the autorefractor.
4. Experiments
4.1. Experimental evaluation
We present monochromatic results consisting of holographic images processed with various hologram correction methods as shown in Fig. 4. SPH correction, a conventional depth-tuning solution, provides a low-contrast image to the users with additional astigmatism. SPH&CYL correction demonstrates high-contrast imagery to the users with target prescription. Yet, since the display system is intentionally built to have spatially varying aberrations, the holographic image at the peripheral area is captured blurry. SPH&CYL + spatially varying (SV) correction visualizes a holographic image with correction in peripheral area. Therefore, if the aberration is noticeably spatially varying, the proposed approach provides a significant improvement in the reconstructed holographic content without additional calibration procedures. In addition, prediction of aberration map as a function of lateral position can be employed in hologram rendering that corrects pupil swim effects that will be discussed in discussion section.
Fig. 4.
Captured photographs of holographic images processed with various holographic correction modes are demonstrated. From the first column, the target intensity, the photographs of holographic images after SPH correction, SPH&CYL correction, and SPH&CYL + SV correction are provided sequentially. The captured results are digitally combined with 25 different hologram frames to reduce speckle noise and emphasize the degradation in image quality in the presence of undesirable aberrations. We ruled out the demonstration of uncorrected holographic image as the content can hardly be recognized.
In the next subsection, we describe the user experiments conducted to evaluate the feasibility of the proposed framework and the vision correction performance of holographic display. In the tests conducted, we implemented another type of holographic near-eye display prototype that contains minimal aberrations induced by optical structures as Fig. 3(E). Then, we evaluated the performance of on-axis ocular aberration-correcting hologram due to three reasons. First, the prescription is measured in an on-axis condition. Next, people perceive a high-resolution image near the fovea region [36]. Finally, the computation of hologram that corrects both central and peripheral vision is hardly applicable for on-site measurement and evaluation.
4.2. User experiments
Acuity is the most intuitive metric that indicates the performance of vision correction. A user experiment was conducted that compared acuity of the holographic images after various corrections. The detailed conditions, experimental procedures and results will be introduced in the subsequent subsections.
4.2.1. Apparatus
In the bench-top prototype for the user experiments, the emission spectra of the green color primary through the NIR/VIS BS were measured. The emission spectra of the light source were calculated from the radiant flux measured by the optical power detector (Newport, 818-SL/DB) at the eye-box. Radiance () and luminance () can be estimated as
| (11) |
where, is the radiant flux, is the solid angle, is the projected area, is the wavelength of the light source, and is the standard luminosity function. In our apparatus, the projected area was , and the solid angle was 0.043. The radiant flux was measured as . Then, the radiance and the luminance can be estimated as and , respectively. Although the low luminance level undesirably enlarges the pupil diameter, the luminance level should be kept far below the permissible level [37] to secure eye safety.
4.2.2. Subjects
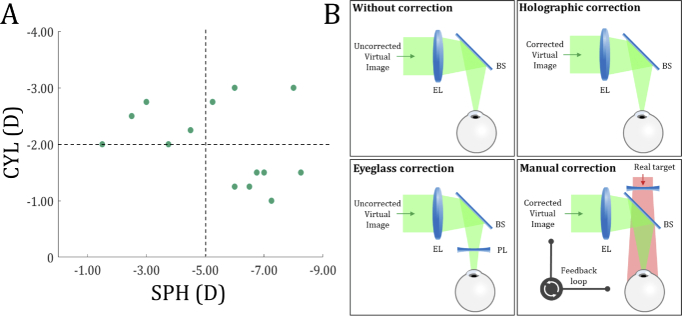
For this test, we gathered users with CYL below −1.0 D (diopter, metric of focal power), which is slightly greater in value than the reported value of the minimum CYL [38] that requires correction. Fifteen adults (ages 20 to 34, two females) were recruited for the test. We confirmed the current prescriptions of their left eye with the autorefractor, Grand Seiko WAM-5500. Before the full-scale experiment, we measured the best-corrected visual acuity (BCVA) of the subjects with trial lenses under laboratory lighting and examined whether it was above 20/30 (0.176 logMAR (logarithm of the minimum angle of resolution)). One of 15 subjects was screened out for failing to meet the criterion of the BCVA being above 20/30. The distribution of 14 subjects’ prescription data (SPH and CYL) is provided as Fig. 5(A). All subjects experience either high myopia (SPH≤−5.0 D) [39] or severe astigmatism (CYL≤−2.0 D), or both.
Fig. 5.
(A) The prescription data (SPH and CYL) distribution participated in the user experiments. (B) The illustrations that describe each of the corrective modes.
4.2.3. Procedure
After fine-tuning the prescription data, an acuity test was conducted with a bench-top prototype of the holographic near-eye display, which provided an early treatment diabetic retinopathy study (ETDRS) chart [40] as a target intensity floated at the distance of 1.0 m. Holograms with various modes were calculated based on the Arizona eye model [31], prescription data, and displayed with monochromatic illumination. The acuities of holographic images that have undergone various corrective modes were compared to evaluate the proposed hologram rendering approach and simultaneously examine the vision correction performance of the holographic display. The illustrations shown in Fig. 5(B) demonstrate each case’s schemes (without correction, holographic correction, eyeglass correction, and manual correction). Without correction stands for the case when neither hologram nor optics are compensated for user’s refractive errors. Holographic correction stands for manipulation of hologram. Eyeglass correction refers to the case when viewing an uncorrected holographic image through the prescribed glasses. Manual correction refers to modification of the impulse response function by tuning the low-order Zernike coefficients as the user simultaneously watches the real target. This method has been suggested by Maimone et al. [7] as an interactive mode of vision correction in holographic display.
In detail, in case of hologram rendering modes that correspond to the case of without correction and eyeglass correction, is assumed. On the other hand, SPH correction and SPH&CYL correction are initialized with and respectively. Except the manual correction mode, the eye model is assumed with correspondence to the individual corrective mode. The target is then updated with an ETDRS chart with smaller letters until the subject does not correctly respond to more than half of the letters in a line.
4.2.4. Eyeglass correction mode
In the evaluation of holographic image acuity, the comparison between holographic correction and eyeglass correction is conducted. Yet, we measure the prescription data with the autorefractor assuming a contact lens. In reality, the distance between the eye and the prescription lens cannot be neglected, especially to those with severe refractive errors. The prescription conversion relations based on the distance from the eye and the prescription lens are presented as
| (12) |
where, stands for the distance between the eye and the prescribed lens, and is the prescription data of the prescribed lens. Note that the axis of astigmatism () is the angle between the power meridian and the horizontal axis of the pupil. Thus, it can be managed by axially rotating the cylindrical lens. In the case of eyeglass correction mode, was assumed to be 12 mm based on the specification of a commercialized phoropter.
4.2.5. Manual correction mode
In manual correction mode, wavefront shaping is conducted prior to the acuity measurement by manually updating Zernike coefficients that correspond to the low-order aberrations, and the hologram is generated with the set of the Zernike coefficient . Here, we utilize a 5×5 grid image with a line width of a single pixel as an image utilized in the calibration process. The residual procedure measuring the acuity in manual correction mode begins after the hologram calibration process.
To elaborate the manual correction procedure, we placed the proper set of the prescribed lenses beyond the VIS/NIR BS, allowing the user to view a clear image of a real target during the whole procedure of holographic calibration. The virtual holographic image of a grid image is provided at 1.0 D from the user’s eye as an initial state. Obviously, the subject has difficulty in clearly perceiving an uncorrected holographic image due to his/her eye’s refractive errors. The instructor then adjusts the wavefront function by modifying the three second-order Zernike coefficients, each indicating vertical astigmatism(), defocus(), and oblique astigmatism(), respectively.
We performed a two alternative forced choices (2AFC) test with the stimuli presented temporally and asked each subject which of two cases provided a sharper image. In addition, the subject is asked to respond to two questions: 1) How does the grid image look like? 2) Does the depth of the virtual image match with that of the real target? Based on the subject’s responses, the instructor manipulated the hologram to sharpen the image by pushing the buttons in a keypad to increment or decrement each coefficient. If the user says that the grid image looks sharp and is located on the same plane with the real object as well, the instructor saves the set of Zernike coefficients and finishes the procedure. With the acquired set of Zernike coefficients, we calculated holograms with a target image of the ETDRS chart.
4.2.6. Acuity measurement
Acuity tests are usually performed with a physical chart designed with a strict protocol. Some researches have performed the acuity measurements with a conventional LCD [41] and a head-mounted display [42], and the results show minimal differences. We conducted the acuity tests with a VR holographic image of the ETDRS chart. To do so, we calibrated the size of the ETDRS chart image to match with the actual size. We confirmed that the image covers a constant portion of the visual field as the depth is shifted. In the acuity test, the ETDRS chart is cropped by three lines, each of which contains five Sloan letters, and is displayed at the center because the impact of aberrations becomes noticeable at the periphery. The cropped image of the ETDRS chart is superimposed with a sparse grid to rule out the background noise. Here, each subsequent line in the chart gets smaller by 0.1 logMAR. If the user successfully identifies the letters in a single line, the user was asked to read the next line. This procedure stopped when the user failed to identify the letters, and the acuity was finally recorded by deducting 0.02 logMAR per letter that the user failed to identify. We conducted these tests three times, and five different sets of images were provided to rule out dependency on the content. For some participants who failed to read a minimum acuity (1.2 logMAR), the acuity was reported as 1.2 logMAR.
4.2.7. Institutional review board
The studies adhered to the Declaration of Helsinki. All the subjects gave voluntary written and informed consent. The Institutional Review Board at Seoul National University approved the research.
4.2.8. Results
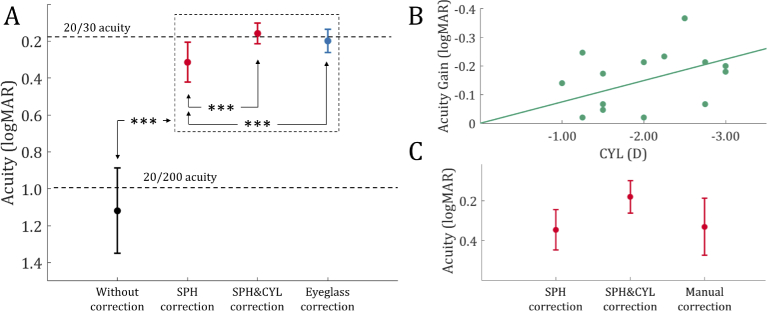
Figure 6(A) shows the average acuities measured depending on several corrective modes. The figure shows that the holographic correction improves the acuity of a holographic image by applying individual prescriptions in hologram rendering. The subjects with uncorrected visual acuity (UCVA) under 20/200 achieved above 20/30 acuity with SPH&CYL correction, on average. The acuity gains are plotted in logMAR units, as shown in Fig. 6(B) to illustrate improvements in acuity with additional astigmatism correction (CYL correction). The participants with CYL requirements (−2.02±0.70 D, mean±standard deviation (SD)), on average, gained the acuity to read one or two lines more in the ETDRS chart. The acuity gain and CYL show a positive correlation.
Fig. 6.
Monochromatic ocular aberration correction result. Acuities of holographic images that have undergone various corrective modes were measured on the subjects with compound myopic astigmatism. (A) The average acuities measured with (black) an uncorrected holographic image, (red) a holographic image with two different holographic correction modes, and (blue) a holographic image viewed through the prescribed eyeglasses. The inset shows the distribution of the subjects’ prescriptions (SPH and CYL). (B) The acuity gains of individuals comparing SPH correction and SPH&CYL correction are plotted depending on the CYL of subjects’ prescription. It shows significance of holographic correction compared to the depth-tuning solution. (C) The average acuities are partially compared with the measurements of the subjects who completed the manual calibration. The asterisks indicate significance at the *** level. The error bars indicate the standard error (SE) across the participants.
We analyzed the acuities of holographic images with a one-way repeated measures analysis of variance (ANOVA), using these corrective modes: without correction, SPH correction, SPH&CYL correction, and eyeglass correction. We conducted a post-hoc analysis with pairwise tests between the corrective modes, and Bonferroni correction was applied to the resultant values. Both holographic and optical corrections undoubtedly show a significant gain () of acuity compared to the case when none of the corrections were performed. In particular, the SPH correction showed a mean acuity gain of −0.805 logMAR () over the mean acuity value in the condition when none of the corrections were applied. Furthermore, the SPH&CYL correction produced a significantly greater acuity over the SPH correction with a mean acuity gain of −0.156 logMAR (). Although, the SPH&CYL correction does not significantly enhance acuity more than optical correction through eyeglasses (, one-tailed binomial test), the SPH&CYL correction (0.159±0.053 logMAR) showed high fidelity results with a smaller error than the eyeglass correction (0.200±0.062 logMAR).
With the subjects (4 out of 14) who completed the manual correction, we partially compared the acuities as shown in Fig. 6(C). The average acuity after SPH correction, SPH&CYL correction and manual correction as 0.347±0.051 logMAR (mean±standard error (SE)), 0.180±0.041 logMAR and 0.331±0.072 logMAR, respectively. Although statistical significance is not derived due to a lack of sample sizes, all subjects who have completed the manual correction showed the best acuity when the SPH&CYL correction was performed. One subject even reported the worst acuity in the manually corrected case. It implies that interactive mode of holographic vision correction suggested by Maimone et al. [7] may require lengthy training procedures, and it can hardly be a feasible option of vision correction.
Overall, all holographic corrective modes show a significantly greater acuity than the acuity measured under the uncorrected mode. The acuity comparison confirmed that holographic display offers a significantly improved performance in astigmatism correction, which other vision-correcting displays with depth modulation can hardly achieve. Moreover, holographic vision correction is comparable to optical correction in experiencing a high-resolution holographic VR image.
5. Discussion
In this work, we have focused on the acquisition of vision-corrected hologram incorporating with the optical aberration of holographic near-eye display. However, there are some limitations that require to be discussed for further improvements.
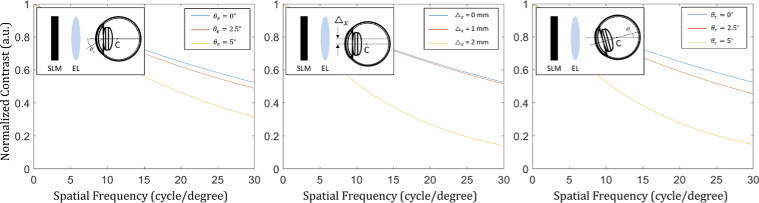
First of all, the user experiments evaluated the feasibility of the proposed approach with on-axis vision-corrected hologram. Although the hologram computation time for rendering full-resolution SV aberration-corrected hologram is a critical bottleneck, the peripheral holographic image suffers comparably a little image quality degradation when hologram is rendered on the basis of line-of-sight. Figure 7 describes the contrast curves of the reconstructed holographic images assuming three representative cases that require holographic correction; (left) peripheral vision with an eccentricity of , (middle) lateral movement of the eye with in the eye-box, and (right) pupil rotation of based on the center of rotation(), which is located 13 mm from the retina. The simulation environments are identical to those of the experimental prototype employed in the user experiment. The pupil diameter is assumed to be 6 mm. The system has a cut-off frequency far exceeding 30 cycle per degree (cpd), a field of view of 10.5∘(H)×5.94∘(V), and an eye-box of 10.8 mm×10.8 mm in wavelength of 520 nm.
Fig. 7.
Contrast curves of the reconstructed holographic images assuming three representative cases that require hologram modification; (left) peripheral vision with an eccentricity of , (middle) lateral displacement of the eye with , and (right) pupil rotation of based on the center of rotation(). The simulation environments are identical to those of the experimental prototype employed in the user study. Here, Michelson contrast is computed as where are the maximum and minimum intensity in the reconstructed holographic image, respectively.
Among three cases described in Fig. 7, correction of peripheral image is not highly efficient since the eye itself contains constant image quality in a decent field of view, and the high-resolution image is dominantly perceived by the small region near the fovea. Thus, holographic correction for a full field of view in on-axis configuration implemented with precisely designed optics is hardly distinguishable with a fixed gaze at the center. However, when the pupil swim effects (lateral displacement and rotation of the eye) are present, contrast degradation can be noticeable without an update of hologram. Thus, the proposed work on holographic correction can efficiently correct aberration caused by pupil swim effects and this technology can be adopted with a minimal cost since the recent VR devices are equipped with eye-trackers. In addition, holographic correction of pupil swim can be highly emphasized with expanded étendue displays. Moreover, we can estimate how the image contrast gets affected when misaligned optics and displays are present with the proposed approach.
In addition, the holographic correction resulted the mean acuity as 0.159 logMAR, which is below than 20/20 acuity. The resolution of the bench-top prototype utilized in user experiments is tested with two different targets (ETDRS chart and USAF-1951 resolution chart), as shown in Fig. 8. The prototype ensures the resolution limit beyond 30 cpd with simulation shown in Fig. 7 and temporally multiplexed holographic images in Fig. 8. Yet, the Sloan letters in those regions are hardly distinguishable when only a single frame is displayed without temporal multiplexing due to speckle noise. As the number of hologram increases for temporal multiplexing, the speckle noise dims and it makes the user distinguish high-frequency regions. Our prototype is only capable of updating a single hologram frame within a time interval of 1/60 seconds. The speckle noise diminishes the perceived acuity. LED-based holographic display is relatively free from such a speckle noise but has the disadvantage of a decreased resolution due to low coherent characteristics [43]. In detail, the illumination of beam with the wavelength deviated from the wavelength employed in hologram rendering results in axial distance error of the reconstructed hologram. The degradation in acuity through the existence of speckle noise can be resolved by adopting high-speed display devices [26,44] or an engineered light engine [45].
Fig. 8.
Photographs of holographic images displayed with the prototype for user evaluation. The intensity targets (ETDRS chart and USAF-1951 resolution chart) are provided with five-times enlarged views. The white bar represents one degree of visual angle. The Sloan letters in the ETDRS chart correspond to 0.1, 0.0, −0.1 logMAR from the top row to the bottom, respectively. The captured results of the holographic images depending on the number of hologram frames utilized for temporal multiplexing are provided.
One of the potential reasons that the display could not reach target 20/20 acuity may lay in the unexpected enlargement in pupil size. Although the average pupil diameter is 3.7 mm in a typical VR environment [46], the pupil diameter is expected to be above 6.0 mm [47] with the luminance level measured in our apparatus. High-order aberrations can undesirably be present in the enlarged pupil. This issue can be resolved by precise measurement of one’s ocular aberrations through the advanced measurement devices [48]. Further, high-order aberration correction can help the low-vision patients with severe refractive disorders that cannot be corrected with eyeglasses.
6. Conclusion
Computational vision correction, which was considered as a minor application only appealing to a particular group of people, can be attractive to numerous people as a fundamental daily-use near-eye display application. Among potential displays, holographic displays have exhibited a promising performance in the correction of aberrations. More specifically, holographic vision correction has significantly improved holographic image acuity, especially for those with astigmatism, and showed comparable results with the eyeglass correction. In this study, the proposed acquisition of aberration-corrected hologram has been validated with experimental and empirical evaluations. Finally, the experimental results are analyzed and discussed.
Despite the remnant challenges of holographic displays, the vision-correcting holographic display exhibited significant improvements in acuity to the observers. Vision correction application will soon be accepted as a considerable advantage, thereby accelerating the commercialization of holographic displays. We believe our study on the aberration and vision-correcting hologram rendering and the user experiments on holographic displays are significant steps forward, interconnecting the field of computational displays and vision, thus allowing a user-adaptive virtual reality experience with utmost comfort.
Acknowledgments
This work is supported by the Institute for Information and Communications Technology Promotion Grant funded by the Korea Government (MSIT) (development of vision assistant HMD and contents for the legally blind and low vision).
Funding
Institute for Information and Communications Technology Promotion10.13039/501100010418 Planning and Evaluation Grant funded by the Korean Government (MSIT) (2017-0-00787).
Disclosures
The authors declare no conflicts of interest.
Data availability
The raw data supporting this article’s conclusions will be made available by the authors without undue reservation.
References
- 1.Lanman D., Luebke D., “Near-eye light field displays,” ACM Trans. Graph. 32(6), 220 (2013). 10.1145/2508363.2508366 [DOI] [Google Scholar]
- 2.Maimone A., Wang J., “Holographic optics for thin and lightweight virtual reality,” ACM Trans. Graph. 39(4), 67 (2020). 10.1145/3386569.3392416 [DOI] [Google Scholar]
- 3.Hoffman D. M., Girshick A. R., Akeley K., Banks M. S., “Vergence–accommodation conflicts hinder visual performance and cause visual fatigue,” J. Vis. 8(3), 33 (2008). 10.1167/8.3.33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Huang F.-C., Luebke D. P., Wetzstein G., “The light field stereoscope,” in SIGGRAPH Emerging Technologies (2015), p. 24.
- 5.Kim D., Lee S., Moon S., Cho J., Jo Y., Lee B., “Hybrid multi-layer displays providing accommodation cues,” Opt. Express 26(13), 17170–17184 (2018). 10.1364/OE.26.017170 [DOI] [PubMed] [Google Scholar]
- 6.Lee S., Jo Y., Yoo D., Cho J., Lee D., Lee B., “Tomographic near-eye displays,” Nat. Commun. 10(1), 2497 (2019). 10.1038/s41467-019-10451-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Maimone A., Georgiou A., Kollin J. S., “Holographic near-eye displays for virtual and augmented reality,” ACM Trans. Graph. 36(4), 85 (2017). 10.1145/3072959.3073624 [DOI] [Google Scholar]
- 8.Jang C., Bang K., Li G., Lee B., “Holographic near-eye display with expanded eye-box,” ACM Trans. Graph. 37(6), 195 (2019). 10.1145/3272127.3275069 [DOI] [Google Scholar]
- 9.Holden B. A., Fricke T. R., Wilson D. A., Jong M., Naidoo K. S., Sankaridurg P., Wong T. Y., Naduvilath T. J., Resnikoff S., “Global prevalence of myopia and high myopia and temporal trends from 2000 through 2050,” Ophthalmology 123(5), 1036–1042 (2016). 10.1016/j.ophtha.2016.01.006 [DOI] [PubMed] [Google Scholar]
- 10.Yoon G.-Y., Williams D. R., “Visual performance after correcting the monochromatic and chromatic aberrations of the eye,” J. Opt. Soc. Am. A 19(2), 266–275 (2002). 10.1364/JOSAA.19.000266 [DOI] [PubMed] [Google Scholar]
- 11.Fernández E. J., Iglesias I., Artal P., “Closed-loop adaptive optics in the human eye,” Opt. Lett. 26(10), 746–748 (2001). 10.1364/OL.26.000746 [DOI] [PubMed] [Google Scholar]
- 12.Porter J., Queener H., Lin J., Thorn K., Awwal A. A., Adaptive Optics for Vision Science: Principles, Practices, Design, and Applications, vol. 171 (John Wiley & Sons, 2006). [Google Scholar]
- 13.Moreno-Barriuso E., Lloves J. M., Marcos S., Navarro R., Llorente L., Barbero S., “Ocular aberrations before and after myopic corneal refractive surgery: Lasik-induced changes measured with laser ray tracing,” Investigative Ophthalmology & Visual Science 42(6), 1396–1403 (2001). [PubMed] [Google Scholar]
- 14.Wang L., Koch D. D., “Ocular higher-order aberrations in individuals screened for refractive surgery,” J. Cataract. Refract. Surg. 29(10), 1896–1903 (2003). 10.1016/S0886-3350(03)00643-6 [DOI] [PubMed] [Google Scholar]
- 15.Zhou L., Chen C. P., Wu Y., Zhang Z., Wang K., Yu B., Li Y., “See-through near-eye displays enabling vision correction,” Opt. Express 25(3), 2130–2142 (2017). 10.1364/OE.25.002130 [DOI] [PubMed] [Google Scholar]
- 16.Wu J.-Y., Kim J., “Prescription AR: a fully-customized prescription-embedded augmented reality display,” Opt. Express 28(5), 6225–6241 (2020). 10.1364/OE.380945 [DOI] [PubMed] [Google Scholar]
- 17.Padmanaban N., Konrad R., Stramer T., Cooper E. A., Wetzstein G., “Optimizing virtual reality for all users through gaze-contingent and adaptive focus displays,” Proc. Natl. Acad. Sci. 114(9), 2183–2188 (2017). 10.1073/pnas.1617251114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chakravarthula P., Dunn D., Akşit K., Fuchs H., “Focusar: Auto-focus augmented reality eyeglasses for both real world and virtual imagery,” IEEE Trans. Vis. Comput. Graph. 24(11), 2906–2916 (2018). 10.1109/TVCG.2018.2868532 [DOI] [PubMed] [Google Scholar]
- 19.Chen C. P., Zhou L., Ge J., Wu Y., Mi L., Wu Y., Yu B., Li Y., “Design of retinal projection displays enabling vision correction,” Opt. Express 25(23), 28223–28235 (2017). 10.1364/OE.25.028223 [DOI] [PubMed] [Google Scholar]
- 20.Pamplona V. F., Oliveira M. M., Aliaga D. G., Raskar R., “Tailored displays to compensate for visual aberrations,” ACM Trans. Graph. 31(4), 81 (2012). 10.1145/2185520.2185577 [DOI] [Google Scholar]
- 21.Huang F.-C., Lanman D., Barsky B. A., Raskar R., “Correcting for optical aberrations using multilayer displays,” ACM Trans. Graph. 31(6), 185 (2012). 10.1145/2366145.2366204 [DOI] [Google Scholar]
- 22.Huang F.-C., Wetzstein G., Barsky B. A., Raskar R., “Eyeglasses-free display: towards correcting visual aberrations with computational light field displays,” ACM Trans. Graph. 33(4), 59 (2014). 10.1145/2601097.2601122 [DOI] [Google Scholar]
- 23.Upatnieks J., Vander Lugt A., Leith E., “Correction of lens aberrations by means of holograms,” Appl. Opt. 5(4), 589–593 (1966). 10.1364/AO.5.000589 [DOI] [PubMed] [Google Scholar]
- 24.Takaki Y., Yokouchi M., “Accommodation measurements of horizontally scanning holographic display,” Opt. Express 20(4), 3918–3931 (2012). 10.1364/OE.20.003918 [DOI] [PubMed] [Google Scholar]
- 25.Nam S.-W., Moon S., Lee B., Kim D., Lee S., Lee C.-K., Lee B., “Aberration-corrected full-color holographic augmented reality near-eye display using a pancharatnam-berry phase lens,” Opt. Express 28(21), 30836–30850 (2020). 10.1364/OE.405131 [DOI] [PubMed] [Google Scholar]
- 26.Lee B., Yoo D., Jeong J., Lee S., Lee D., Lee B., “Wide-angle speckleless DMD holographic display using structured illumination with temporal multiplexing,” Opt. Lett. 45(8), 2148–2151 (2020). 10.1364/OL.390552 [DOI] [PubMed] [Google Scholar]
- 27.Kaczorowski A., Gordon G. S., Wilkinson T. D., “Adaptive, spatially-varying aberration correction for real-time holographic projectors,” Opt. Express 24(14), 15742–15756 (2016). 10.1364/OE.24.015742 [DOI] [PubMed] [Google Scholar]
- 28.Peng Y., Choi S., Padmanaban N., Wetzstein G., “Neural holography with camera-in-the-loop training,” ACM Trans. Graph. 39(6), 1–14 (2020). 10.1145/3414685.3417802 [DOI] [Google Scholar]
- 29.Choi S., Kim J., Peng Y., Wetzstein G., “Optimizing image quality for holographic near-eye displays with michelson holography,” Optica 8(2), 143–146 (2021). 10.1364/OPTICA.410622 [DOI] [Google Scholar]
- 30.Goodman J. W., Introduction to Fourier Optics (Roberts and Company Publishers, 2005). [Google Scholar]
- 31.Schwiegerling J., Field Guide to Visual and Ophthalmic Optics (SPIE Bellingham, 2004). [Google Scholar]
- 32.Lucente M. E., “Interactive computation of holograms using a look-up table,” J. Electron. Imaging 2(1), 28–35 (1993). 10.1117/12.133376 [DOI] [Google Scholar]
- 33.“Zemax optic studio,” http://www.zemax.com, Accessed: 2021-02-21.
- 34.Klöckner A., Pinto N., Lee Y., Catanzaro B., Ivanov P., Fasih A., “Pycuda and pyopencl: a scripting-based approach to gpu run-time code generation,” Parallel Comput. 38(3), 157–174 (2012). 10.1016/j.parco.2011.09.001 [DOI] [Google Scholar]
- 35.Chen J.-S., Chu D., “Improved layer-based method for rapid hologram generation and real-time interactive holographic display applications,” Opt. Express 23(14), 18143–18155 (2015). 10.1364/OE.23.018143 [DOI] [PubMed] [Google Scholar]
- 36.Navarro R., Artal P., Williams D. R., “Modulation transfer of the human eye as a function of retinal eccentricity,” J. Opt. Soc. Am. A 10(2), 201–212 (1993). 10.1364/JOSAA.10.000201 [DOI] [PubMed] [Google Scholar]
- 37.International Committee on Non-Ionizing Radiation Protection , “Icnirp guidelines on limits of exposure to laser radiation of wavelengths between 180 nm and 1, 000 μm,” Health Phys. 105(3), 271–295 (2013). 10.1097/HP.0b013e3182983fd4 [DOI] [PubMed] [Google Scholar]
- 38.Villegas E. A., Alcón E., Artal P., “Minimum amount of astigmatism that should be corrected,” J. Cataract. Refract. Surg. 40(1), 13–19 (2014). 10.1016/j.jcrs.2013.09.010 [DOI] [PubMed] [Google Scholar]
- 39.W. H. Organization , International Statistical Classification of Diseases and Related Health Problems: Tabular List, vol. 1 (World Health Organization, 2004). [Google Scholar]
- 40.Ferris F. L., III, Kassoff A., Bresnick G. H., Bailey I., “New visual acuity charts for clinical research,” Am. J. Ophthalmol. 94(1), 91–96 (1982). 10.1016/0002-9394(82)90197-0 [DOI] [PubMed] [Google Scholar]
- 41.Calabrèse A., To L., He Y., Berkholtz E., Rafian P., Legge G. E., “Comparing performance on the mnread ipad application with the mnread acuity chart,” J. Vis. 18(1), 8 (2018). 10.1167/18.1.8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ong S. C., Pek I. L. C., Chiang C. T. L., Soon H. W., Chua K. C., Sassman C., Koh V. T., “A novel automated visual acuity test using a portable augmented reality headset,” Investigative Ophthalmology & Visual Science 60, 5911 (2019). [Google Scholar]
- 43.Deng Y., Chu D., “Coherence properties of different light sources and their effect on the image sharpness and speckle of holographic displays,” Sci. Rep. 7(1), 5893 (2017). 10.1038/s41598-017-06215-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Collings N., Crossland W., Ayliffe P., Vass D., Underwood I., “Evolutionary development of advanced liquid crystal spatial light modulators,” Appl. Opt. 28(22), 4740–4747 (1989). 10.1364/AO.28.004740 [DOI] [PubMed] [Google Scholar]
- 45.Lee S., Kim D., Nam S.-W., Lee B., Cho J., Lee B., “Light source optimization for partially coherent holographic displays with consideration of speckle contrast, resolution, and depth of field,” Sci. Rep. 10(1), 18832 (2020). 10.1038/s41598-020-75947-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Privitera C. M., Renninger L. W., Carney T., Klein S., Aguilar M., “Pupil dilation during visual target detection,” J. Vis. 10(10), 3 (2010). 10.1167/10.10.3 [DOI] [PubMed] [Google Scholar]
- 47.Mathur A., Gehrmann J., Atchison D. A., “Influences of luminance and accommodation stimuli on pupil size and pupil center location,” Invest. Ophthalmol. Vis. Sci. 55(4), 2166–2172 (2014). 10.1167/iovs.13-13492 [DOI] [PubMed] [Google Scholar]
- 48.Sabesan R., Yoon G., “Visual performance after correcting higher order aberrations in keratoconic eyes,” J. Vis. 9(5), 6 (2009). 10.1167/9.5.6 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The raw data supporting this article’s conclusions will be made available by the authors without undue reservation.