Estimation of core body temperature by near-infrared imaging of vein diameter change in the dorsal hand

Abstract

Core body temperature (T_core) is a key indicator of personal thermal comfort and serves as a monitor of thermal strain. Multi-parametric sensors are not practical for estimating core temperature because they require long data collection times and a wide variety of settings. This study introduces dorsal hand vein dynamics as a novel indicator along with heart rate (HR) and dorsal hand skin temperature (T_hand) for predicting T_core during rest following T_core elevation. Twelve healthy males aged 27 ± 9 years old participated in the experiment. The experimental procedure consisted of a 10-min rest followed by 60 min of passive heat stress induced by leg immersion in hot water at 42°C and a 40-min thermal relaxation period after the legs were removed from the water. A near-infrared (NIR) imaging system was configured to monitor the dorsal hand veins during the entire experimental session. The values of HR, T_hand, and T_core were continuously monitored while the ambient temperature and relative humidity (RH) were maintained in a climate chamber at 20°C and 50%, respectively. Our selected predictor parameters demonstrated similar patterns in the T_core such that the value increased as a result of passive heat stress and decreased in the thermal relaxation phase. The experimental data were divided into two phases: thermal stress and relaxation. At the resting condition, inclusion of the hand vein diameter (VD) improved the multiple linear regression value (R²) about 26%. At the relaxation phase, however, training regressions R² = 0.68 and R² = 0.94 were observed in the regression model with and without considering VD, respectively. The test regression value of R² = 0.88 and the root mean square error (RMSE) of 0.18°C showed good agreement with the predicted values. These findings demonstrate acceptable validity of the non-invasive T_core estimation at the resting condition. In particular, the inclusion of VD as a predictor in the regression analysis increases the prediction accuracy with a lower RMSE value.

1. Introduction

Core temperature (T_core), also known as body core temperature, refers to the temperatures of human internal organs such as the liver, stomach, bladder, and rectum. That is, T_core does not necessarily represent the temperature at a specific location; rather, it reflects the temperature of inner tissue that does not change significantly by circulatory adjustment and environmental effects [1]. The human body tends to maintain its T_core within a very narrow range of 36.5°C–38.5°C (or 97.7°F–101.3°F).

T_core is central to quantification of heat strain. However, regular measurement procedures for obtaining rectal, esophageal, or gastrointestinal temperatures have low practicality outside of a dedicated laboratory environment, particularly during long periods. Therefore, non-invasive measures for monitoring heat strain are necessary. Previous studies using mathematical models to predict T_core have employed non-invasive physiological parameters including skin temperature (T_skin), heat fluxes at various body sites, heart rate (HR), breathing frequency, accelerometer data, and environmental climatic variables such as air temperature, radiant temperature, relative humidity (RH), and wind speed [2–5]. However, further research is warranted to identify the most relevant predictor variables and to examine the general validity of these models.

Measurement of T_core can be a critical indicator of individual heat strain assessment during field work or other movement [6,7]. It is impractical to use a multi-parametric sensing system in a field setting because it requires extended measurement periods and a variety of settings. Traditionally used laboratory rectal and esophageal probes are not practical for use in ambulatory conditions. Several non-invasive methods used for estimating T_core such as ingesting thermometer pills [8] have shown great success in field settings. However, some patients with certain medical conditions are advised to not ingest thermometer pills owing to contraindications, and the results might be inaccurate if the patient consumes hot or cold fluids prior to measurement. Alternatively, zero heat flux (ZHF) [9,10] and thermoregulatory [11–13] methods have gained attention for their accuracy in measuring T_core. However, these methods are more effective in laboratory settings than in ambulatory or field conditions owing to the inconvenience of preparing the required apparatus. Further, many researchers have developed techniques for estimating T_core from HR measurement. In particular, some studies employ various methods such as the Kalman filter (KF) [14–16] model to estimate T_core based on HR signals.

In addition, many medical researchers have studied the relationship between T_skin and T_core to develop a new approach for measuring T_core using non-invasive methods [17,18]. In particular, Niedermann et al. [4] developed an algorithm for predicting T_core using T_skin measured at the chest although. However, they used only highly professional instruments that are not suitable for long-term continuous monitoring of subjects in natural habitats or in daily environments. Therefore, this resource is limited because it is impractical to develop a complete algorithm for predicting T_core. Hand vein diameter (VD) is a potential predictor of T_core, although little research has focused on its relationship with T_core.

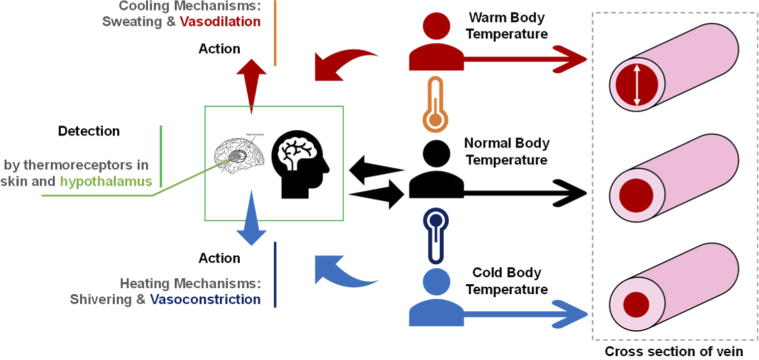
It is widely accepted that efferent responses cause natural changes in the body’s self-protection mechanism against extreme changes in temperature, resulting in sweating, vessel dilation, vessel constriction, shivering, and other involuntary responses [19,20] as shown schematically in Fig. 1. Considering that vessel dynamics, specifically VD, have a role in estimating T_core, the combination of VD, the temperature of a peripheral organ such as hand skin temperature (T_hand), and HR data can increase the accuracy of T_core measurement in ambulatory or field conditions. Accordingly, HR measurement based on a wearable apparatus and non-invasive techniques has been the focus of recent relevant studies [4,21,22].

Fig. 1.

Schematic diagram describing the role of vein dynamics in thermoregulation.

Considering the mobility and simplicity of the system used for personal and ambulatory applications, near-infrared (NIR) imaging is a promising approach. Several potential applications for VD measurement systems include driver monitoring in vehicles and user monitoring for bicycles employed in physical training. In these approaches, it is important to monitor the HR and T_core of the drivers and trainees. By determining these values, the thermal comfort level of an individual can be monitored, and safety systems installed in vehicles or exercise equipment can be adjusted accordingly. Although such systems can be used as personal monitoring devices, they can also be used to monitor the thermal state of a field worker in hot weather conditions. The aim of this study is to observe that whether T_core elevation is a driving force of peripheral vein dilation such as dorsal metacarpal veins in a controlled room temperature. We performed a multiple regression analysis to predict T_core with physiological parameters such as HR, T_hand, and VD that can be measured non-invasively. We hypothesize that T_core would be a driving force to dilate the peripheral veins for dissipating the heat from the skin as an action of thermoregulation.

2. Materials and methods

2.1. Subjects

Twelve male subjects between the ages of 24 and 41 with no diagnosed metabolic or cardiovascular diseases were recruited for this study. The mean values for age, height, mass, and body mass index (BMI) are shown in Table 1 as demographic characteristics. None of the subjects were athletes, and any potential subject having cardiovascular, respiratory, or heat-related illnesses or symptoms were excluded in the recruiting process. Each subject was instructed to refrain from strenuous exercise and from consuming alcohol or caffeine prior 12 hours on the day of the experiment [23,24] as well as to fast at least for 6 hours before arriving at the laboratory. The objectives, procedures, potential discomfort, and risks of the present study were explained to the subjects prior to the experiments, and all subjects signed informed consent documents. The current study was performed in compliance with the guidelines and regulations issued by the Institutional Review Board of Kookmin University.

Table 1. Demographic characteristics of the subjects participating in this study.

No. of Subjects	Age (years)	Height (m)	Weight (kg)	BMI (kg/m2)
12	27 ± 9	1.74 ± 0.1	72.5 ± 12.2	23.8 ± 2.8

2.2. Experimental design

The participants arrived at a laboratory at Seoul National University between 09:00 and 12:00 KST during November and December 2020 for the experimental session. The environmental conditions of the laboratory were 20°C and 50% RH. Prior to the experiment, the subjects were familiarized with the experimental protocol, devices, and objectives of the study, and basic data of the general clinical parameters were collected such as age, height, weight, recent diseases, and abnormal health conditions while the subjects were resting at the lab facility. In the second step, after remaining for about 30 min in the testing climate chamber, sensors for data collection were attached to each subject’s body. A non-invasive chest strap bearing an electrocardiogram (ECG) sensor (RS400, Polar Electro Oy, Kempele, Finland) was attached to the chest of each subject to monitor HR and ECG waveforms in real time at a data collection rate of 128 Hz. In addition, a non-invasive skin temperature sensor (LT ST08-12, Gram, Tokyo, Japan) was attached by adhesive tape to the skin of the dorsal part of each subject’s hand. Invasive core temperature measurement was conducted using a rectal temperature sensor (LT ST08-11, Gram, Tokyo, Japan). To assess the T_core based on rectal temperature, each participant was instructed to self-insert the sensor at least 15 cm beyond the anal sphincter [25].

The subjects immersed their lower legs up to the calf in water at a constant temperature 42°C ± 2°C. The temperature of the hot water bath used for leg immersion (LH-300, Limho Industry, Seoul, South Korea) was controlled to maintain temperature stability throughout the experiment. A water bath [26] is commonly used for passively increasing T_core and to relieve physiological symptoms such as fatigue and insomnia. We selected the temperature of 42°C for three reasons. First, the T_core increases significantly with leg immersion in water bath [27]. Second, the reported pain threshold for skin (T_skin) is 45°C ± 1.7°C [28]. Third, the probability of burning porcine skin is low at temperatures below 44°C; no significant quantitative differences have been noted between human and porcine skin regarding susceptibility to thermal injury [29].

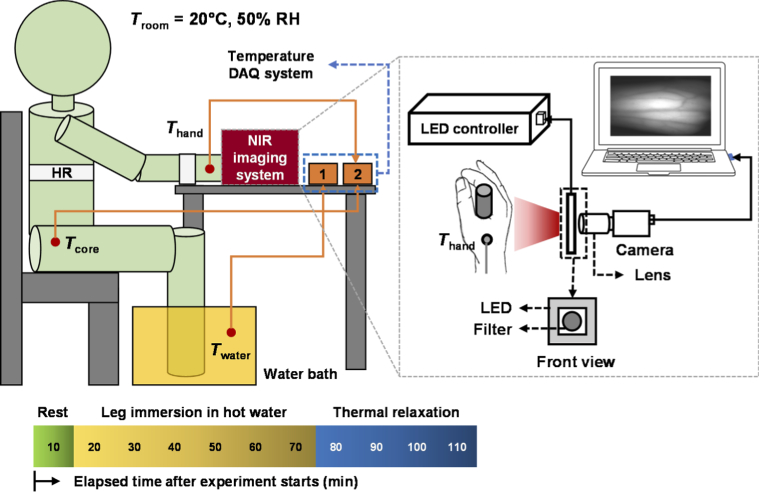
We selected the leg immersion technique for our experiment owing to its stable setting and T_core elevation capability. In this method, the subject can remain in the resting condition, and the physiological dynamics are not strongly considered. A leg immersion period of 1 h was needed to increase the T_core about 0.6°C–1°C depending on the subject; the experiment was terminated when the T_core reached 39°C. Figure 2 shows a schematic diagram of the experimental setup for T_core elevation in the climate chamber. An NIR imaging system containing several components was placed over the subject’s hand to capture sequential images of superficial veins before and after thermal stimulation. We used an NIR charge-coupled device (CCD) camera (Grasshopper3 GS3-U3-41C6NIR-C, FLIR, Wilsonville, Oregon, USA) and a high-resolution lens (LYM1614, Tuss Vision Inc., Tokyo, Japan) with a bandpass filter (BP850, Midwest Optical Systems, Palatine, Illinois, USA) to measure the VD. An NIR light-emitting diode light source (LV-ILA-94SF-IR-850, LVS, Incheon, South Korea) was used for illuminating the veins on the dorsal side of the hand. A schematic diagram of the NIR imaging setup is shown in the inset in Fig. 2.

Fig. 2.

Schematic diagram of the experimental setup for elevating core temperature (T_core) by hot water leg immersion and for near-infrared (NIR) imaging of the dorsal hand veins. Thermocouple temperature sensors were connected to a data logger for recording T_core and the skin temperature in dorsal hand (T_hand). Another temperature sensor was placed in the water bath to monitor the water temperature (T_water). For data collection, a heart rate (HR) measurement sensor was attached to the subject’s chest, and a monitor was secured around the wrist.

Finally, physiological data such as temperature and HR were recorded simultaneously according to the acquisition rate for NIR imaging of the dorsal part of the hand.

2.3. Vein diameter

The raw images required further preprocessing prior to analysis to observe the sharp contrast of the vein edges. Several techniques were used to enhance the images for digital analysis. The target site of the blood vessel was geometrically corrected for reducing the shaking effect of the subject’s hand, as described in our previous report [30]. The sequential images were first cropped to a specific region of interest (ROI) based on the position in the image, as shown in Fig. 3(a) and (b). We selected the convolutional neural network (CNN) for all image processing in the VD analysis. Once the CNN was trained, no further processing was needed for the analysis. Before programing input/output data in the machine learning model, the image frame data were preprocessed in two steps. The images were first down-sampled to 256 × 256 pixels to compensate for the computer’s limited graphics processing unit (GPU) memory allocation.

Fig. 3.

(a) Region of interest (ROI) set in the sequential images based on the visibility and existence of the vein. (b) Cropped image focusing on the vein pattern in the ROI. (c) The cropped images were further processed to enhance the veins using the convolutional neural network (CNN). Scale bar = 10 mm.

In the second step, the scaled images were enhanced after image down-sampling to improve the contrast and details before the scaled images were applied to the input/output in the machine learning model. The processes included the following algorithms. (1) Grayscale conversion: The input patch images were first converted into grayscale format to train and predict the model efficiently. Because the NIR images had no color channel, converting them into grayscale images increased the model performance. (2) Dataset normalization: Each image was normalized across the dataset whereby the minimum of each pixel value in the dataset was subtracted, and the result was divided by the difference between the maximum and minimum pixel values of the dataset. This result was then multiplied by 255 to match the image data format widely supported by MATLAB (MathWorks, Natick, Massachusetts, USA). (3) Contrast limited adaptive histogram equalization (CLAHE): Each image was tiled in an 8 × 8 pixel image before the histogram was equalized. (4) Gamma adjustment: The gamma values were adjusted in each image to obtain better contrast. (5) Normalization to 0–1: The number of pixels in each image was divided by 255 to match the image data format widely supported by MATLAB. (6) Training dataset generation: Thirty-three full-sized images of 970 × 970 pixels were used to generate the training and validation datasets. Thirteen full-sized images were included in the test dataset and were downscaled to 256 × 256 pixels. To build the training–validation and test datasets, the images were first used to manually generate the binary masks of the vein images. GNU Image Manipulation Program (GIMP) image processing software was used to generate the vein masks of the corresponding vein images, which were used as ground truth data for training the model. In addition, the mask images for the test dataset were used for evaluating the training model. An example of a CNN processed image is shown in Fig. 3(c). (7) Model architecture: The image processing was based on the deep neural network following the procedure proposed by Ronneberger et al. [31] as described in our previous study [30].

The NIR images were recorded at 1 min intervals for the core thermal elevation studies. The images were post-processed using CNN to mask the vein images in a binary format. The processed images were further analyzed through MATLAB using a custom-made algorithm. The outputs of the MATLAB algorithm were stored in a Microsoft Excel document for further analysis. The data were stored as pixel units and were later converted to actual units based on the necessity.

2.4. Data processing

To analyze T_core elevation, the data were recorded under thermoneutral conditions (20°C, 50% RH) in a climate chamber (FLC-5000S, Fuji Medical Science, Kashiwa, Japan). The T_hand, chest temperature, forehead temperature, and T_core were recorded every 5 s, and the data were transferred from the data logger to the computer for storage in a text file for further analysis. A non-invasive polar ECG strap was attached to the subject’s chest to record HR at an acquisition rate of 1 Hz. These recorded data were transferred to a text file and stored at an interval of 1 min for further processing in accordance with the image acquisition rate.

Microsoft Excel and SPSS software were used to process data for all statistical analyses. All temperature readings were analyzed using Excel. The data were expressed as mean and standard deviation values. The coefficient of variance (CV) was calculated to determine the accuracy of measurement:

$$CV=\frac{\sigma }{u},$$ (1)

where σ and u are the standard deviation and mean, respectively.

2.5. Effects of elevated core temperature

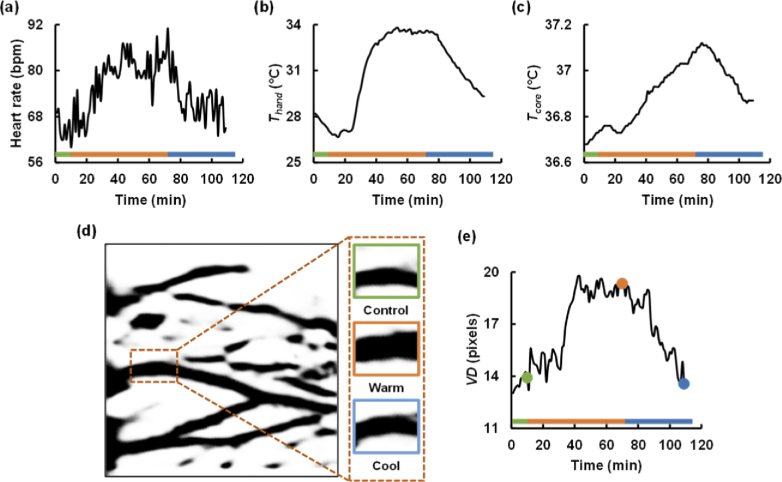
We observed several physiological responses including those of T_hand, VD, and HR during the T_core elevation. The responses of one subject are shown in Fig. 4. After undergoing passive heat stress for 60 min, the participants rested for 40 min to stabilize the increased T_core.

Fig. 4.

Thermal response of one subject to core temperature (T_core) elevation. The green, orange, and blue bars in the panels indicate the resting, heat stress, and relaxation phases, respectively. Heart rate (HR), hand skin temperature (T_hand), and T_core increased at the thermal stress phase and decreased at the relaxation phase, as shown in (a), (b), and (c), respectively. (d) Processed images of dorsal metacarpal vein in a region of interest (ROI) under control, warm, and cool conditions. The insets are cropped images of the veins in the ROI at different time points indicated in (e). (e) Vein diameter (VD) versus time plot, showing that the VD variation follows the trend of T_core change.

2.6. Estimation of T_core

The experimental data were divided into two phase groups for predicting T_core in our model: thermal elevation and relaxation time. In the relaxation phase, we observed a linear decreasing trend. In our analysis, T_core was considered as output or prediction values; other measured variables were considered as predictors. A multiple linear regression (MLR) model was built to predict T_core, in which T_hand, HR, and VD were considered as predictors. The predictors showed linear change with T_core, as shown in Fig. 4. The obtained data were made dimensionless by dividing the observed value by the initial value. These fractionated values were used in MLR model for building the prediction model:

$$\frac{T_{core}}{T_{core,rest}}-1=A\left(\frac{VD}{V{D}_{rest}}-1\right)+B\left(\frac{HR}{H{R}_{rest}}-1\right)+C\left(\frac{T_{hand}}{T_{hand,rest}}-1\right).$$ (2)

2.7. Validation of prediction model

To validate the newly generated prediction model, we applied the datasets contained in the stored computer documents. After training, the differences of the fractionated T_core and predicted T_core were used to create a Bland–Altman plot, and the mean of the difference was measured. The difference was later subtracted from the test fractionated prediction value.

3. Results and discussion

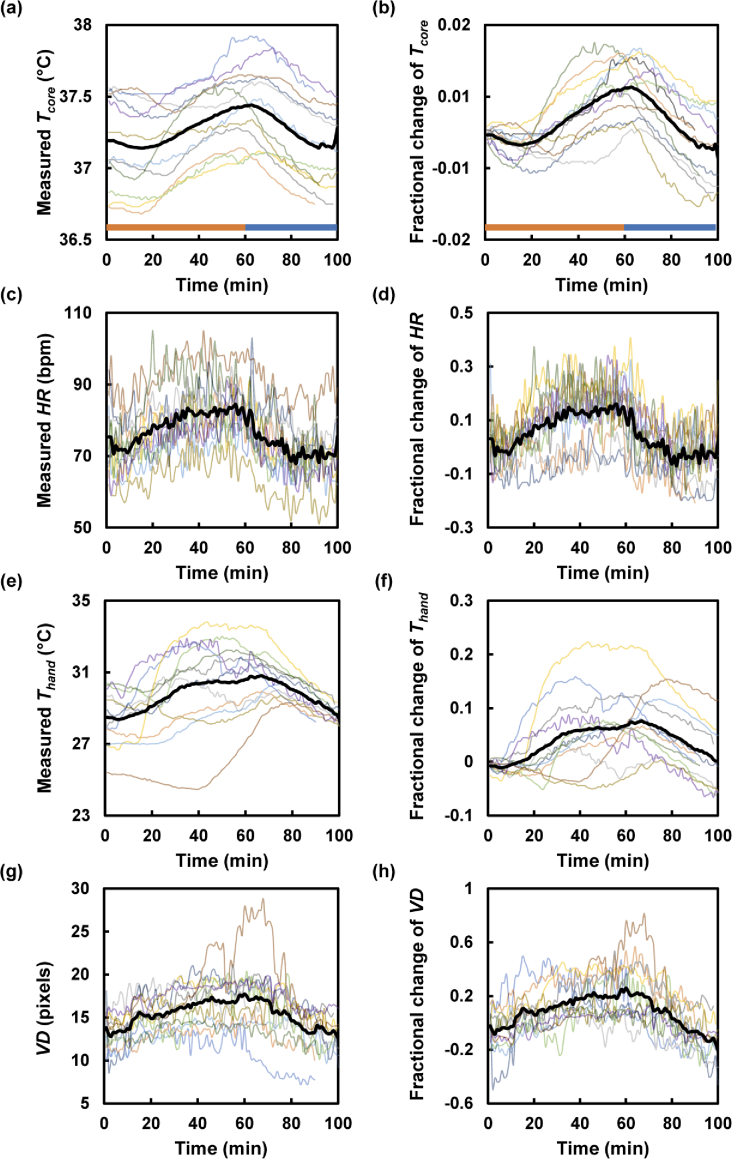
The thermal protocol was successful in eliciting the desired manipulations of whole-body temperature, as shown in Fig. 4. We observed several physiological responses such as T_hand, VD, and HR during the T_core elevation. The responses of all subjects are shown in Fig. 5(a), (c), (e), and (g). After undergoing passive heat stress for 60 min, the participants rested for 40 min to stabilize the increased T_core. Further, we generated non-dimensional data from the raw data by measuring the corresponding fractional change and normalizing the result by subtracting 1 from the fraction. The non-dimensional data are shown in Fig. 5(b), (d), (f), and (h). The average minimum, maximum, and elevated temperatures recorded for all the participants were 37.1°C, 37.4°C, and 0.3°C, respectively.

Fig. 5.

Thermal responses of all subjects (n = 12) after leg immersion in hot water for 60 min. The plots in (a), (c), (e), and (g) include raw data for T_core, HR, T_hand, and VD response measured every 1 min, respectively. The plots in (b), (d), (f), and (h) show fractional changes in T_core, HR, T_hand, and VD, respectively. The orange and blue bars in (a) and (b) indicate the thermal stress and relaxation phases, respectively. The black solid lines show the average of the thermal responses of all subjects.

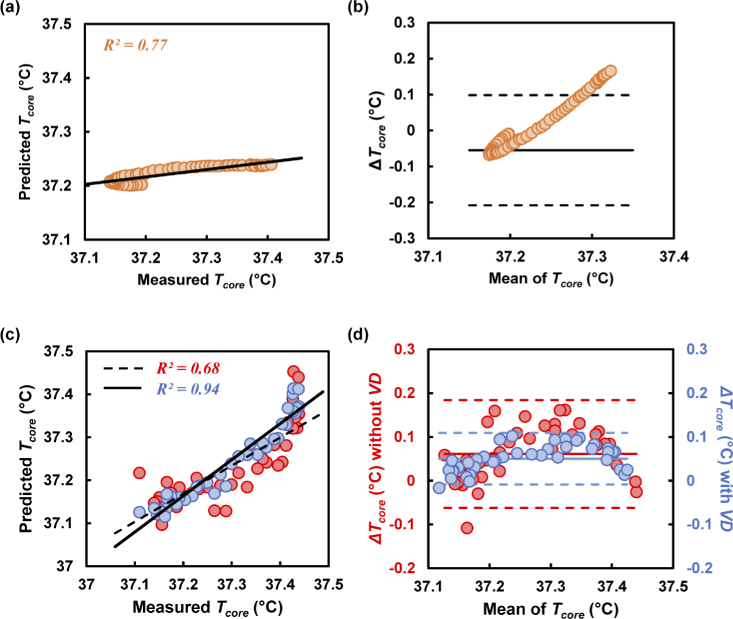
Scatter plots of the measured T_core predictions at the thermal stress phase and the following relaxing phase are presented in Fig. 6(a) and (c) respectively. In the development of the MLR-based prediction model for T_core at the thermal phase, the contribution of T_hand was more significant than that of HR and VD. The corresponding coefficient was measured to be 0.014, shown as C in Eq. (2). The prediction difference was calculated as shown in Fig. 6(b). The bias of this measurement was found to be −0.05°C, and the lower and upper limits of agreement (LOA) were −0.2°C and +0.09°C, respectively.

Fig. 6.

(a) T_core prediction at the thermal phase. (b) Difference between predicted and measured T_core (ΔT_core) plotted against the mean T_core. (c) Scatter plot between measured and predicted T_core at the relaxing phase. The red and blue circles represent the predicted values excluding and including VD, respectively. The black straight and dashed lines in the scatter plot represent agreement between the measured and predicted values including and excluding VD. (d) Bland–Altman plot showing the limit of agreement for predicting T_core including and excluding VD in the MLR model.

In the cooling phase, the coefficient of determination (R²) was higher, at R² = 0.94, when VD was considered in the model as a predictor, as shown in Fig. 6(c). However, the value was lower, at R² = 0.68, when VD was not introduced in Eq. (2). An increment of 26% was observed between these two measurements. The Bland–Altman plot shown in Fig. 6(d) demonstrates the deviation of prediction from the measured value of T_core. Specifically, the measurement bias was observed to be 0.06°C (0.05°C) when VD was (was not) included in the prediction model. The coefficients were measured for the MLR model as 0.043 and 0.008 for B and C, respectively, in Eq. (2) when predicted without using VD. In addition, the R² was 0.68 (0.94) for the average cooling phase when excluding (including) VD, as shown in Fig. 6(c). In this case, the coefficients were found to be 0.013, 0.02, and zero for A, B, and C, respectively in Eq. (2). The T_hand did not contribute when VD was introduced in the MLR prediction model.

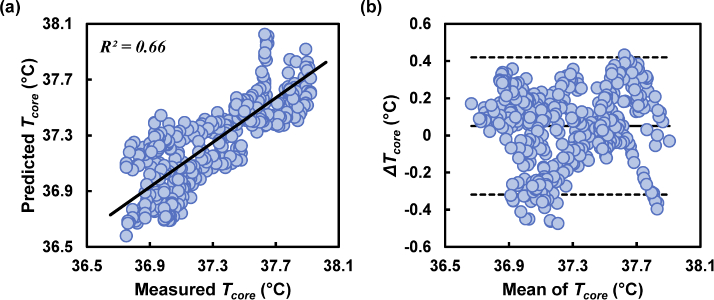
The MLR model was trained using the averages of all physiological parameters of the participants; the validation results showed good agreement in the predicted T_core during the relaxation phase, as shown in Fig. 7. The data of each subject were then evaluated according to the obtained coefficients and the regression model, as shown in Fig. 7(a) and (b). The linearity between the measured and predicted value was determined by the R² value to be 0.66. The Bland–Altman plot used for demonstrating the difference (ΔT_core) between the measured and predicted values is shown in Fig. 7(b).

Fig. 7.

Multiple linear regression analysis and prediction accuracy according to Bland–Altman analysis. (a) Accuracy of R² prediction by considering VD in the MLR prediction model. (b) Bland–Altman plot showing the maximum possible difference from the measured values.

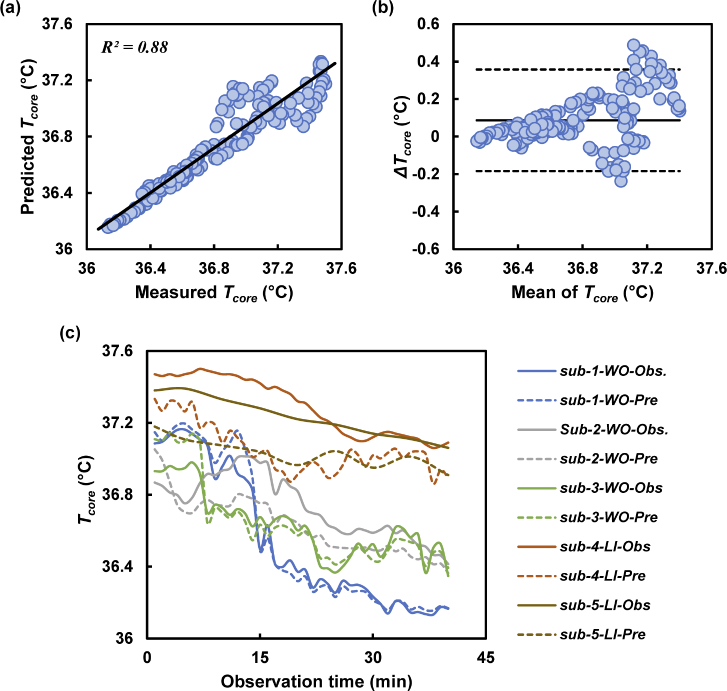
Although we obtained good agreement in predicting T_core, as shown in Fig. 7, we further tested the model with data obtained from five subjects. The fractionated T_core showed good agreement between the measured and predicted T_core. The fractionated T_core values were further converted to dimensional T_core values for comparison with the original T_core values. The linearity between the measured and predicted values yielded R² = 0.88, as shown in Fig. 8(a). The original deviation of T_core was measured by the Bland–Altman plot shown in Fig. 8(b).

Fig. 8.

Prediction model validated using the test data. (a) Good linearity (R² = 0.88) shown with the test sets of data for predicting T_core. (b) The error was measured within an acceptable range. (c) Time course of T_core measurement plotted to observe similar trends between the measured (solid line) and predicted (dotted line) values.

The test subject results are shown in Fig. 8(c), which also plots the 40 min time sequence for the measured and predicted T_core. In the plot, the predicted temperature showed trends of decrease with time, which is similar to that of the measured value. The predicted T_core showed good agreement with the measured values, as shown by R² = 0.87. The maximum and minimum deviations were +0.48°C and −0.23°C, respectively. The bias was calculated to be 0.08, and the lower and upper LOA were −0.18°C and +0.35°C, respectively. The plot shown in Fig. 8(c) includes the data of the five subjects validated using the MLR model. The predicted T_core maintained similar decrease trends with time as that of the measured value.

This study aimed to define the validity of a novel parameter for predicting T_core under two different conditions: during T_core elevation and relaxation under controlled room temperature and humidity. However, the thermal phase was not validated by testing in this study owing to a narrow temperature range and a lower estimation, as shown in Fig. 6(a). Moreover, during the thermal phase, T_core elevation varied among the subjects, as shown in Fig. 5(a). Although all subjects showed a similar pattern of T_core throughout the experiment, their T_core elevation occurred at different times during leg immersion. Thus, for validation of the MLR model, we included only the resting phase analysis.

We demonstrated that a small number of parameters can be used to predict T_core using a simple MLR model. The present findings confirmed that during relaxation of T_core, the agreement (R² = 0.64) between the predicted and measured values was low, as shown in Fig. 6(c). However, the R² was 0.94 for the relaxation phase when VD was introduced in the model. The test R² value was 0.88, and the difference between the measured and predicted T_core was within −0.18 to +0.35°C, which is <0.5°C and thus considered to be within the acceptance criteria [5,32].

It is worth mentioning that traditional T_core prediction models are generally determined on the basis of many collected non-invasive parametric data, and a set of suitable parameters is determined for the final prediction model construction. However, our study included a limited choice of predictor parameters. Considering that this prediction model is designed to be used for peripheral parts of the body only, all of the data can be collected from a non-contact source such as an imaging system. The NIR imaging system can visualize the hand vein and is thus highly efficient for biometric authentication [33]. A popular and accurate method is HR measurement using an NIR light source [34]. In addition, a non-contact infrared temperature sensor such as MLX90614 [35] is gaining popularity for measuring T_hand. A future direction of this work is to integrate these devices to build a prediction model for T_core estimation. In addition to personal health monitoring, this technique can be implemented in houses or electric vehicles for suggesting helpful techniques for managing energy-efficient thermal comfort.

The current study has several limitations. The sample size was relatively small, and only male volunteers were included. Women were not included to avoid bias owing to differences in hormonal status between measurement sessions, which could affect both the static and dynamic superficial veins. To validate the NIR imaging method proposed in our study, the rectal temperature range should be ∼39.2°C, indicating a 2°C increase. The present study, however, was originally planned with increases of 1°C to ensure safety in experiments involving human subjects. To expand the range in rectal temperature, endogenous heating (e.g., exercise) under thermal stress is required. Passive heating (e.g., leg immersion) alone is insufficient for inducing an increase of 2.0°C. Thus, further studies are planned to cover 1.5°C−2.0°C increase in rectal temperature.

4. Conclusions

The current study evaluated the contribution of VD as a novel parameter for predicting T_core. This parameter along with other predictors such as T_hand and HR increased the agreement of the linear regression model, which was validated under a controlled climate. The observed level of agreement, at 95% LoA, −0.18 to +0.35°C, was within the criteria set for monitoring deep body temperature. Vasodilation during T_core elevation was demonstrated through NIR imaging. This study can be replicated to determine the subject’s thermal comfort based on knowledge of the T_core. Moreover, this T_core prediction method can be integrated in many facilities for enhancing quality of life. For example, the present imaging technique can be used in indoor fitness facilities as well as in personal vehicles to obtain T_core information of the user.

Funding

Korea Evaluation Institute of Industrial Technology10.13039/501100003662 (20011377); National Research Foundation of Korea10.13039/501100003725 (NRF-2019R1A2C2006961, NRF-2019R1A2C2088973).

Disclosures

The authors declare no conflicts of interest.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.