Graphical abstract
Keywords: Fractional order impedance model, Lung function, Mimicked tumor, Forced oscillations technique, Lung properties, Viscoelasticity
Abstract
Introduction
As pulmonary dysfunctions are prospective factors for developing cancer, efforts are needed to solve the limitations regarding applications in lung cancer. Fractional order respiratory impedance models can be indicative of lung cancer dynamics and tissue heterogeneity.
Objective
The purpose of this study is to investigate how the existence of a tumorous tissue in the lung modifies the parameters of the proposed models. The first use of a prototype forced oscillations technique (FOT) device in a mimicked lung tumor setup is investigated by comparing and interpreting the experimental findings.
Methods
The fractional order model parameters are determined for the mechanical properties of the healthy and tumorous lung. Two protocols have been performed for a mimicked lung tumor setup in a laboratory environment. A low frequency evaluation of respiratory impedance model and nonlinearity index were assessed using the forced oscillations technique.
Results
The viscoelastic properties of the lung tissue change, results being mirrored in the respiratory impedance assessment via FOT. The results demonstrate significant differences among the mimicked healthy and tumor measurements, (p-values 0.05) for impedance values and also for heterogeneity index. However, there was no significant difference in lung function before and after immersing the mimicked lung in water or saline solution, denoting no structural changes.
Conclusion
Simulation tests comparing the changes in impedance support the research hypothesis. The impedance frequency response is effective in non-invasive identification of respiratory tissue abnormalities in tumorous lung, analyzed with appropriate fractional models.
Introduction
Fractional calculus models allow understanding the physiological processes that occur in biological tissues as the effect of dynamic events caused by diseases [1]. Such that, cell and tissue environment have been typically described with complex models in order to predict the behavior of the experimental observations with real applicability in various subdivisions of science and engineering [2], [3]. Recently, predictive mathematics methods through numerical simulations based on fractional derivatives are used in many applications [4], [5], [6], [7] and control problems [8], [9], and also for natural phenomena [10], [11].
Tumor growth models have been able to allow the simulation and evaluation of treatment protocols and tumor behavior by using fractional (FDEs), ordinary (ODEs) and partial differential equations (PDEs). The mutual conclusion among researchers is that fractional models have better performance for decision-making process and provide future new characteristics for exploration [12]. A fractional mathematical model was proposed in [13] for evaluating the interactions between tumor cells and immune response, being included into a control strategy together with the effect of applied chemotherapy. For radiotherapy, another model for cancer treatment using Caputo-Fabrizio fractional derivative was presented in [14]. Tumor growth models that incorporate the fundamental physiological processes encountered during tumor evolution are presented in [15], [16]. Novel evidence proven that combining radiotherapy, immuno- and targeted therapy in early stage lung cancer results in synergistic effects, enhancing the efficacy of treatments [17], [18], [19]. Similarly, a modified model that includes the dose–effect synergy among all three anti-cancer therapies is the pharmacokinetic-pharmacodynamic (PKPD) model developed in [17], studying the drug interactions effects on tumor volume.
A lung tumor can be classified among pulmonary obstructive disease, with airway blockage that occurs due to abnormal tissue growth in the respiratory tree levels. Hence, the fractal structure of the lungs changes into a heterogeneous morphometry, influencing its functional capacity. Different airway structure, elasticity, or more pathologies, disrupt the fractal process leading to the need of remodeling the branching tree [20]. Ladder network mathematical model is available in this paper for simulating the respiratory tree of 24 levels in case of normal and tumorous lung. A bronchial obstruction in the peripheral bifurcations assumes specific pulmonary abnormalities. The lung structure is divided in two bronchial generations: levels 1–16 for gas transport and levels 17–24 for gas exchange. The information is provided by existing literature, where the lung morphometry and its fractal geometry have been studied to provide the link between lung structure and lung physiology [21]. This motivates the usefulness for fractional calculus in yielding insights into the mechanism of tumor growth for quantification of molecular processes in cancer [22].
The fractional order circuit element, i.e., impedance, is capable to reproduce bio-mechanical properties, by analogy with the electric circuit elements. Different fractional impedance models have been addressed in recent years for biomedical applications in [1], [23], [24], [25], [26], [27].
Motivated by the above discussion, this work aims to use mathematical modeling and a forced oscillations technique device (FOT) in the clinical decision-making process of choosing the optimal lung cancer management. This paper proposes and applies a fractional order model for a tumorous lung hypothesis. Simulations were validated with input impedance data measured in a laboratory setup that imitates the lung tumor. The results of the measured and modeled impedance demonstrate the variation of the mechanical parameters between the normal (healthy) and abnormal setups. To the best of our knowledge, this is the first attempt which investigates the use of FOT device and fractional order impedance model (FOIM) in a lung cancer application. This original work enables the initial steps toward introducing FOT as a non-invasive assessment of lung respiratory properties in lung cancer patients. Furthermore, using a prototype FOT device at lower frequencies has particular interest from clinical point of view, where viscoelastic properties are assessed during airway remodeling due to illnesses. Introducing the ladder model for the case of lung cancer is a first time occurrence in literature. Randomly chosen ratios for obstructed airways were used in numerical simulations, notwithstanding the respiratory system as a recurrent tree in the case of disease incidence.
The remainder of this paper is structured as follows. The second section contains an overview of the proposed modeling approaches for the respiratory tree and respiratory impedance, by means of fractional calculus. The third section describes the materials and methods used for performing the measurements, consisting of: the mimicked lung tumor setup, the measurement device, and the design of the study. Next, experimental and simulation results are provided for the proposed methodology in the fourth section. The discussion section presents the complete correlation of this research with tumor dynamics, in a clinical practice overview for modeling and predicting patient-specific response to cancer therapy. The last section concludes this work, summarizing its content.
Modeling approaches
Developing a quantitative understanding of lung mechanics requires a systematic construction of fractional order mathematical models. A set of equations provides a precise statement of lung structure and function described from the mechanical and viscoelastic assumptions. With an anatomically accurate forward model of the lung, we can simulate pressure-flow relationships when only the distal airways are narrowed and modified [28]. Hence, it allows to analyze if this modified structure reproduces the relationships that are measured experimentally for the mimicked tumor.
Ladder network model of the respiratory tree
Modeling the respiratory tract by means of electrical analogy implies the simplification of the lung morphology and structure. For reporting the pulmonary function, a symmetrical structure of the lung is assumed in healthy tissue. An asymmetrical representation of the airways in the respiratory tree can be considered for a diseased lung parenchyma, introducing tissue heterogeneity. Both modeling approaches are implemented for measurements obtained in mimicked setups for normal and tumorous lungs.
Hence, making an electrical analogy, the equivalence for the lung pressure P and air flow Q can be considered the voltage and the current, respectively [29], [30]. In case of viscoelastic airway walls, the functions for the mechanical properties (resistance , compliance , and inertance ) can be given by:
| (1) |
| (2) |
| (3) |
where the electrical resistances represent the resistance inside the lungs caused by the airflow friction, the electrical capacitors are correlated with pulmonary compliance which describes the lung distensibility (stretch/ expand), and electrical inductors represent the inertia of the air. For each of these parameters, the geometrical () and mechanical () characteristics of the air tube and the air properties () are taken into consideration for the mentioned definitions. Furthermore, the equations consider also the following parameters: viscosity [], density [], Poisson coefficient , initial tube radius R [m], wall thickness h [m], effective modulus of elasticity [kPa], length of an airway tube [m], modulus of the Bessel function of order 1 , phase angle of the complex Bessel function (order 1) , and Womersley parameter .
Referring to Eqs. (1), (2), (3) and to the respiratory system as a recurrent tree with 24 levels, a mathematical model of RL-C parallel configuration enables identification of the input impedance in the ladder network. For each level, the mechanical parameters vary, being calculated based on specific ratios between the consecutive levels, as follows:
| (4) |
| (5) |
| (6) |
where m is the level in the respiratory system tree from 1 to 24.
With the parameters given by the above described equations, it is possible to consider variations in viscoelasticity with morphology and with pathology depending on the levels of the respiratory tree.
Because of the recurrent geometry, the respiratory system is considered as having a fractal structure, leading to a recurrent ladder network, with the admittance calculated as follows:
| (7) |
By reducing the ladder network from (7) to an analogue representation, the admittance is obtained as:
| (8) |
and the impedance:
| (9) |
Notice that the effects produced by the parameter are insignificant at lower frequencies due to the fact that its values are very small compared with parameter . In Eqs. (7), (8), (9), denotes the resistance and the compliance, both in the first airway level, represents the ratio of resistances per total N levels and the ratio of compliances per total levels, s is the Laplace operator, and a scale factor with the fractional order .
This paper implements the ladder model for the case of lung cancer, using different ratios for the conducting zone of the respiratory system. The difference can be explained by the fact that lung cancer leads to the rupture of the walls and the blockage of the airways once a new abnormal formation grows along them. Usually, the respiratory levels are function of power 2, described by a recurrent dichotomous respiratory tree with 24 levels, approximately alveolar ducts. Because the obstructive tumor growth starts in the lower airways (i.e., 16–24), the ratios are specifically changed for these conducting airway levels. Then, the asymmetry appears and the model is randomly recalculated (using randn Matlab function). For each iteration, the same new ratios are kept (using seed Matlab function) by initializing the random number generator to a certain status. Hence, seeding inside the loop keeps the same random numbers created inside that loop in each iteration, from the 16th level to the 24th one.
Fractional order respiratory impedance model
Ladder network models allow more significant variations of model parameters with frequency, being useful for characterizing broad ranges of frequencies. Such models lead to multiple fractional-order lumped parametric models, necessary to describe the complexity of the natural respiratory system. The behavior origins for fractional order models are the viscoelastic properties of the lung tissue and the fractal structure of the respiratory tree. Usually, both viscoelasticity and diffusion phenomena alter airway mechanics at low frequencies. These variations are physiologically explained and correlated to airway modeling in pathology, leading to different values for the model parameters. These parameters can change, depending on different structural changes in lungs (e.g., rupture of alveolar walls, tissue inflammation, decreased density of the lungs or various degrees of obstruction). The modification leads to different fractional order terms within respiratory zones. Consequently, measuring the respiratory impedance of the human respiratory system allows the detection of changes in tissue properties, as well as the impairment level of the lungs by a certain disease [31].
A fractional order model was implemented to represent the resistance and reactance at low frequencies, influenced by the fact that frequency-dependent impedance values variations are difficult to be captured. The lumped form of the fractional order impedance model (FOIM) is proposed to estimate the respiratory impedance, as follows:
| (10) |
where in analogy with the electrical equivalent model, P is the air-pressure [kPa], Q the air-flow [], the respiratory impedance [], the peripheral resistance [], the the total inertance (electric: inductance) [], the respiratory compliance (electric: capacitance) [], s the Laplace parameter, and fractional orders and , 01, 01.
The last term can be correlated with changes in tissue damping (viscoelasticity) [] and tissue elastance [], their ratio denoting the degree of heterogeneity present in the tissue (hysteresivity coefficient-dimensionless):
| (11) |
| (12) |
| (13) |
Changes in represent changes in parenchyma or in very small airways (if there are small changes in ) and changes in reflect changes in the intrinsic mechanical properties of the parenchyma. Hysteresivity (lung compliance) is a dimensionless property of tissues with viscoelastic properties. This ratio also characterizes the sources for nonlinear distortions in the respiratory dynamical properties. For the evaluation of the non-linear contributions existing in the respiratory system, the following index of heterogeneity is used (dimensionless):
| (14) |
The index expresses the relative ratio of the contributions at non-excited frequencies (even and odd) with respect to the contributions at the excited frequencies (odd), as reported in [32]. Each variable represents the sum of the absolute values of all the contributions in the pressure and flow signals. Respiratory impedance at low frequencies indicates the mechanical properties of the lung: resistance, inertance and compliance, which further estimate the viscoelastic properties of airways and tissue: damping and elastance. Hence, a method for quantifying the non-linear effects coming from the airways and lung tissue is introduced for validating the hypothesis that T index is increased in patients diagnosed with respiratory disease [28]. These are successful tools for analyzing the frequency-dependence in human respiratory impedance for various pathologies. Diseases affect the structure and morphology of the airways and tissue, changing air-flow dynamics and, hence introducing non-linear effects (quantified with T index). From clinical insight, asthma, COPD and cancer patients have increased values of the proposed index compared to healthy subjects.
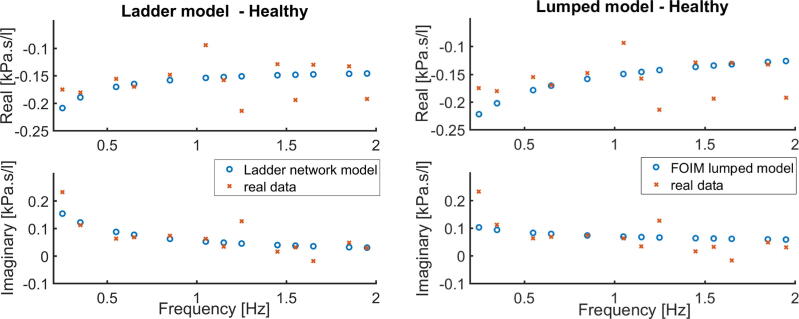
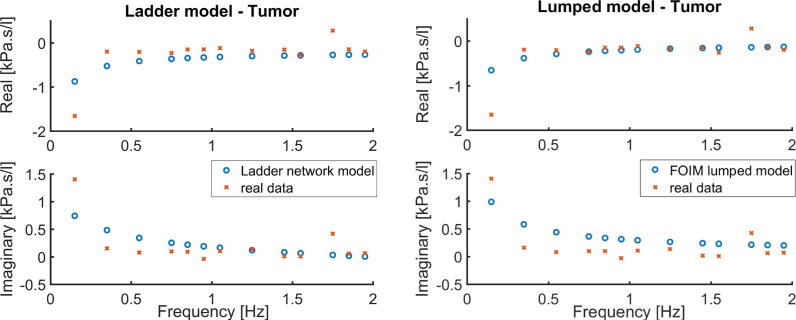
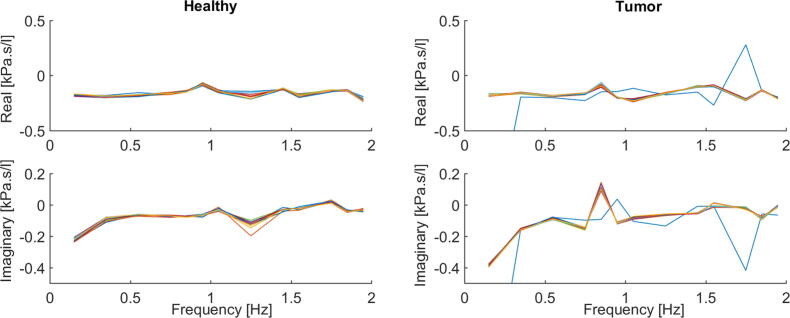
The identification procedure is employed for both presented models in order to obtain the complex impedance by means of its real and imaginary parts as a function of frequency. The results are depicted in Fig. 1 for the experiment performed with healthy mimicked setup and in Fig. 2 for the tumor mimicked setup. Prediction error method and least squares minimization are used to fit the model parameters to measured data assessed with FOT. The proposed models are nonlinear in the parameters (fractional orders). The nonlinear least square technique with iterative procedure is used.
Fig. 1.
Healthy mimicked setup data and identified models: Ladder Network Model (left figure) and Lumped model (right figure). Impedance in complex representation.
Fig. 2.
Tumor mimicked setup data and identified models: Ladder Network Model (left figure) and Lumped model (right figure). Impedance in complex representation.
Materials and methods
In order to test the usefulness and validity of presented models in lung cancer, experimental measurements are performed on a laboratory setup to assess the mechanical function of a mimicked lung. The study of lung mechanics has been realized throughout the measurement of impedance at the device opening during forced oscillations. Two scenarios were tested, using a laboratory setup to mimic a healthy and a tumorous lung, as presented hereafter. The performed experiments have the purpose of characterizing the changes in the pulmonary impedance as an effect of tumor incidence. The existence of a tumor produces modifications in tissue and airways properties.
Experimental setup
For the measurement of lung impedance, it was employed an experimental setup available to mimic a normal lung and a tumorous lung, by using rubber balloons, with different viscoelastic degrees. A normal lung lobe has been assumed to be mimicked by a single regular rubber balloon. The lung cancer tissue within a lung lobe has been simulated by inserting an inner aired balloon (stiffer) into the normal one (more elastic). The lung model setup was built in order to observe the dynamical effects caused by the changes in:
-
•
micro-environment formed by the second balloon;
-
•
tissue composition changing determined by the introduction of the balloon in water or a physiological saline solution.
The research hypothesis is that a significant difference occurs in the respiratory impedance model coefficients for tumor respiratory tissue.
FOT measurements
A FOT device was used to detect the changes in damping resistance and viscous or elastic reactance. An excitation signal was optimized to better reflect the airway obstruction during simulation of tidal breathing [28]. The use and purpose of FOT is explained with respect to the respiratory measurement taken under different conditions and manoeuvres. The driving signals are forced oscillations applied to the respiratory system, in our setup represented by the balloons. For clinical extrapolation, the impedance (spectral relationship between pressure and airflow) is measured in a frequency range from 0.15 to 2 Hz, closer to the frequency of human respiration. The respiratory impedance at these frequencies is dominated by the viscoelastic properties of the lungs, significantly changed with pathology. To use linear models, one needs to use low amplitude oscillations, which overcome important nonlinear dynamics at frequencies close to breathing [33].
The impedance is determined knowing the pressure and the airflow, parameters that are different in various conditions of the respiratory function. From the pathological viewpoint, the tumor will invade the lung tissue which automatically will lead to obstructions and blockages in the respiratory branches and finally to the respiratory function modifications [34], [35]. Having changes in the respiratory function, the nonlinear distortions caused by the breathing of the patient are captured by the device. The aim of the experiments is to offer a statistical analysis of these pathological changes that occur in cancer lung and to evaluate the changes in respiratory function.
Study design
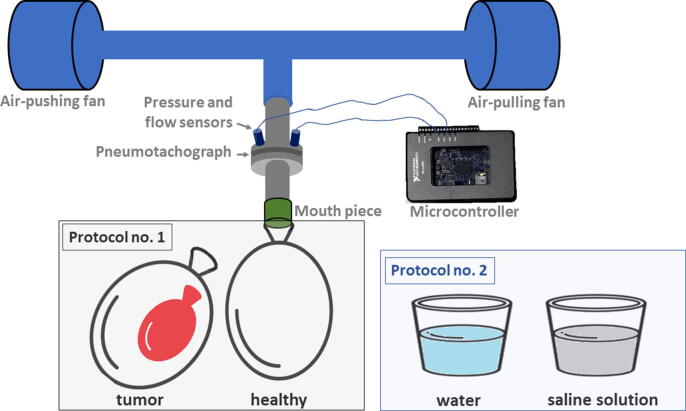
The measurement scenario is depicted in Fig. 3. For the purposes of this study, the impedance assessment at low frequencies has been done using a prototype FOT device. The primary construction of the device consists of two fans located at each extreme of a tube (one brings the air inside the tube and the other one outside the tube). The tube is filled with plastic straws to enable laminar flow conditions. Other components are one mouth piece attached to a pneumotachograph and two pressure sensors. An embedded platform (National Instruments CompactRIO) was programmed with LabVIEW tools to allow the control of the estimated pressure signal applied. The structure of the device and the development process are described in [36], [37], [38], the device being custom-made for the specific frequency range (0.15–2 Hz).
Fig. 3.
Measurements scenario for the proposed protocols.
Given the difference in structure and viscoelastic properties introduced by the two protocols, differences are expected between each set of measurements. The measurements have been taken using the FOT prototype device, in sets of 10 measurements per protocol. As the lung tumor is considered an obstructive disease, implying a reduced total lung capacity because of the existence of excess air in the lungs, it is expected that the impedance has the same behavior as in obstructive diseases (COPD) [34], [35], [39], [40]. Several calibration methods were performed as described in [32], [37], [38].
Protocol No. 1. Starting with the single balloon measurement, the pressure and flow signals are registered for 140 s each, the device stopping automatically afterwards. The device records the signals which are superimposed over the excitatory signal (the pressure) maintained at a peak-to-peak variation of 0.2 kPa. The measurements were performed 10 times continuously without switching on/off the FOT device or changing the input signal. The second set of 10 measurements was executed with double dry balloons. The larger balloon represents the lung, having an inserted smaller balloon inside which characterizes the lung cancer tissue within a lung lobe.
During the simulations, the lung is mimicked in the two mentioned conditions: healthy and tumorous tissue. In clinical onset, a significant difference is observed between the model parameters when the airways are obstructed, narrowed or blocked due to an abnormal formation of tissue. The model parameters offer the possibility to evaluate the respiratory impedance for all the morphological changes in relation to the lung disease.
Protocol No. 2. Taking the case with double balloons, the inner one was immersed before the measurements in one of the two solutions: normal water for the first set of measurements and high concentration saline solution for the second set. Protocol No. 2 consisted of 10 measurements per each case.
The complexity of cancer includes the heterogeneity of the tumorous tissue, together with its interaction with the micro-environment affected by the tissue composition changing and weight. Using a weighing scale, it was measured the mass of the inner balloon. While a normal dry balloon had 2 grams, a wet balloon (in salted and unsalted water) doubled its weight, meaning 4 grams. The analysis becomes even more difficult when tissue properties change, such as in obstructive disease, and the differentiation between the myriad of different influencing factors is not yet possible. The solution of salt concentration could influence the dynamics inside the lungs mostly if it is in the context of an affected respiratory system [41]. In lung injuries, the lung water content rises interests among clinicians, regarding the effect of fluid balance on changes in respiratory impedance of human lung.
All measurements were done in the absence of disturbances, i.e., in absence of mimicked respiration.
Results
The software was used for data processing and iterative analysis of impedance measurements.
For statistics, boxplots and one-way analysis of variance (ANOVA) were used to compare the two sets of samples.
Protocol No. 1. To analyze the response per excited frequency, the impedance has been plotted for both cases, tumor and healthy tissue, by means of real and imaginary parts. The impedance is depicted as a function of frequency in Fig. 4. In the case of mimicked airway obstruction, resistance (“real part”) is slightly increased at the lower applied frequencies, but falls with increasing applied frequencies. Concomitant, reactance (“imaginary part”) at low frequencies is more negative and increases as frequencies increase. It can be observed that in healthy tissue the has the tendency of being constant with increases in frequency. The trend for is similar with the one for tumor, albeit shifted larger values.
Fig. 4.
Frequency-dependent impedance for healthy tissue lobe (left) and for the lobe with tumorous tissue (right), within Protocol 1. Ten measurements per each case are displayed.
Hence, the results showed in Fig. 4 demonstrate the hypothesis specified, as a tumorous tissue implies indeed higher impedance values, due to increased tissue resistance. By analogy to lung physiology, if a tumor grows in a specific part of the bronchial tree, the air flow will automatically decrease and the pressure increase, resulting in increased impedance values.
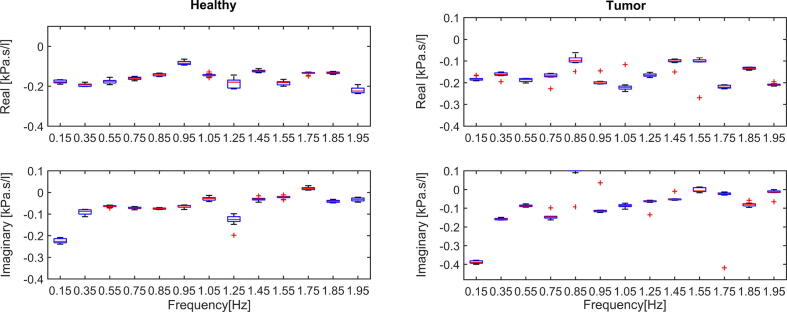
The graphics displayed for Boxplot analysis in Fig. 5 indicate that the tests are consistent within groups and the quartiles respect the trends of the variation in samples of each statistical population.
Fig. 5.
Boxplot for healthy case (left) and tumor case (right) for various frequency points and tests, within Protocol 1.
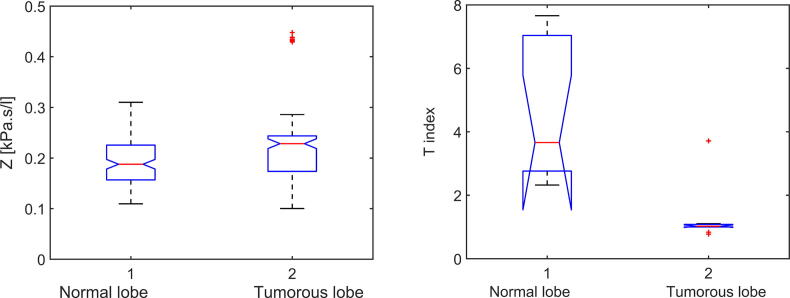
The differences among the healthy and tumor groups of measurements have been evaluated using Anova. The p-values for impedance Z and T index have been compared for both cases. For impedance, the p-value resulted is 0.0117. The T index values were calculated with (14), resulting a p-value of 0.0089 (as depicted in Fig. 6). The results indicate a difference statistically significant for both impedance and T index among healthy and tumor cases. These results confirm the original hypothesis of this research, that the presence of tumor in lungs affects the frequency-dependent respiratory impedance and tissue heterogeneity expressed by T index.
Fig. 6.
Anova for healthy and tumor cases (Protocol 1), in terms of impedance Z (left figure) and T index (right figure).
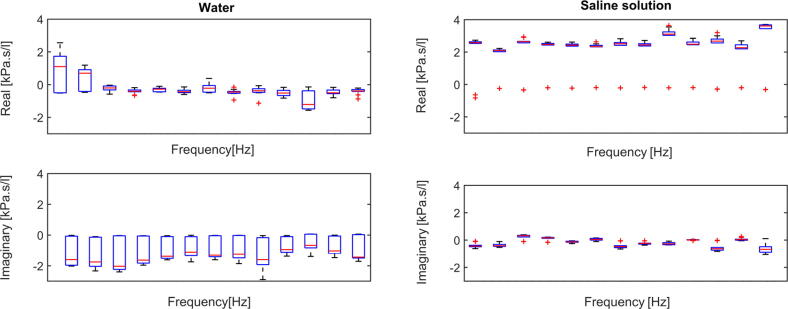
Protocol No. 2. From the graphical model of the frequency dependent impedance obtained from the signals (air pressure and airflow) registered by the device, it can be noticed that the impedance values change from the dry lobe to the ones immersed in both water or saline solution. Nonlinearities can be studied because the changes were linked to the material properties and there are no structural changes for the normal lobe. The composition and the weight of the measured systems influence their behavior, despite their tissue structure.
The impedance is plotted in its complex representation for the water case and for saline case in Fig. 7. Compared with the water impedance data, resistance is higher and positively frequency-dependent in saline solution, whereas reactance has also higher values, but constant with frequency. The equivalent boxplots are given in Fig. 8.
Fig. 7.
Frequency-dependent impedance for the lobe immersed in water (left) and for the lobe immersed in saline solution (right), within Protocol 2. Ten measurements per each case are displayed.
Fig. 8.
Boxplot for water case (left) and saline soultion case (right) for various frequency points and tests, within Protocol 2. The columns represent data for each frequency [0.15, 0.35, 0.55, 0.75, 0.85, 0.95, 1.05, 1.25, 1.45, 1.55, 1.75, 1.85, 1.95 Hz].
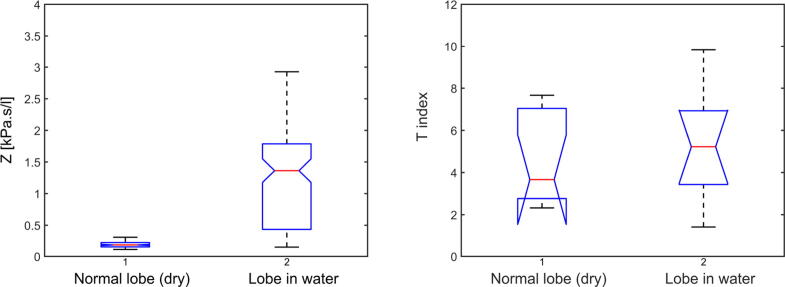
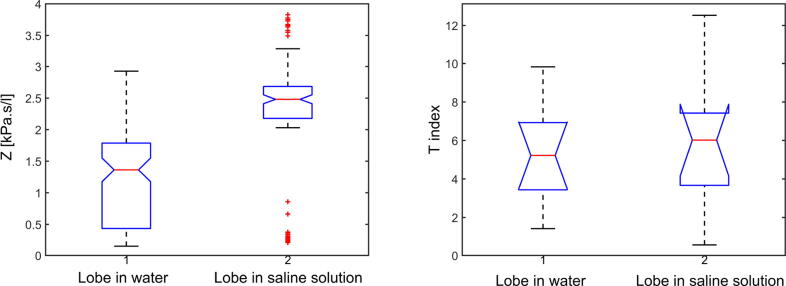
The p-value for both impedance and T index have been calculated for each of the 10 measurements per case. Fig. 9 did not reveal significant differences at baseline for Z or T index between the dry normal lobe and the normal lobe immersed in water. The same result can be depicted for the comparison between the lobe immersed in water and the one immersed in saline solution from Fig. 10. The results suggest that a water and a high sodium concentration solutions are not influencing the heterogeneity response of the tissue.
Fig. 9.
Anova for normal tissue lobe (dry) and high water concentration lobe (Protocol 2), in terms of impedance Z (left figure) and T index (right figure).
Fig. 10.
Anova for high water concentration lobe and lobe in saline solution (Protocol 2), in terms of impedance Z (left figure) and T index (right figure).
Discussion
In a pandemic context, to control the health outcomes of individual patients with underlying chronic diseases represent a major concern. The prioritization of health resources in clinical practice for patients diagnosed with both COVID-19 and lung cancer is not yet established. The medical oncology team has to decide stopping or continuing anticancer treatment, while treating the COVID-19 pneumonia [42]. Most potential interactions between anticancer and coronavirus therapies are unknown. Hence, the comprehensive therapeutic management of patients with lung cancer increases in complexity during a pulmonary pandemic. Furthermore, the transmission and persistence of epidemic need to be studied in order to understand and predict the spread of viruses [43].
Recent studies have emphasized the usefulness and uniqueness of developing epidemic models. In the current pandemic of COVID-19, numerical simulations have been performed with: a fractional-order model with two different operators (classical Caputo operator and Atangana-Baleanu-Caputo operator) for the transmission of COVID-19 epidemic [44] and a continuous time Markov Chain through stochastic model approach for the persistence and extinction of coronavirous [45]. Other epidemic models were developed for different diseases: a mathematical model with fractional-order Caputo derivative for Zika virus transmission [46], model with fractal fractional Caputo derivative operator for transmission dynamics of an infectious disease [47], and a fractional model approach in the sense of ABC model (a new derivative operator with Mittag–Leffler kernel in the Caputo sense) for human respiratory syncytial virus (HRSV) [48]. Recently, many researchers have developed different control strategies for disease transmission, diagnosis and treatment, while addressing mathematical models containing fractional and integer order differential equations [13], [49], [50].
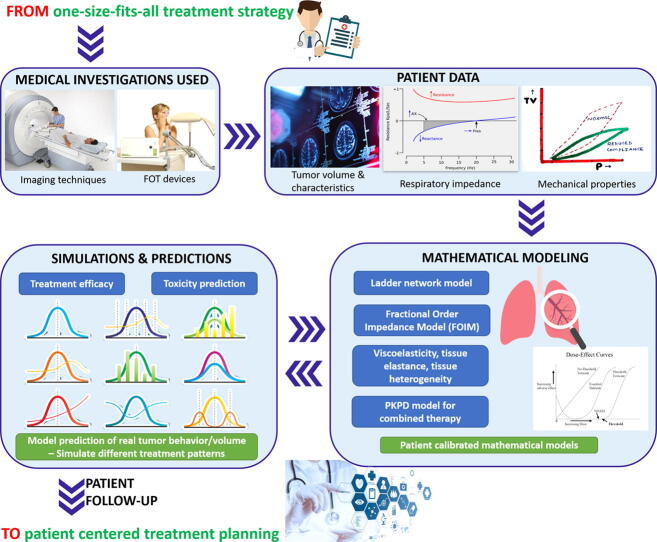
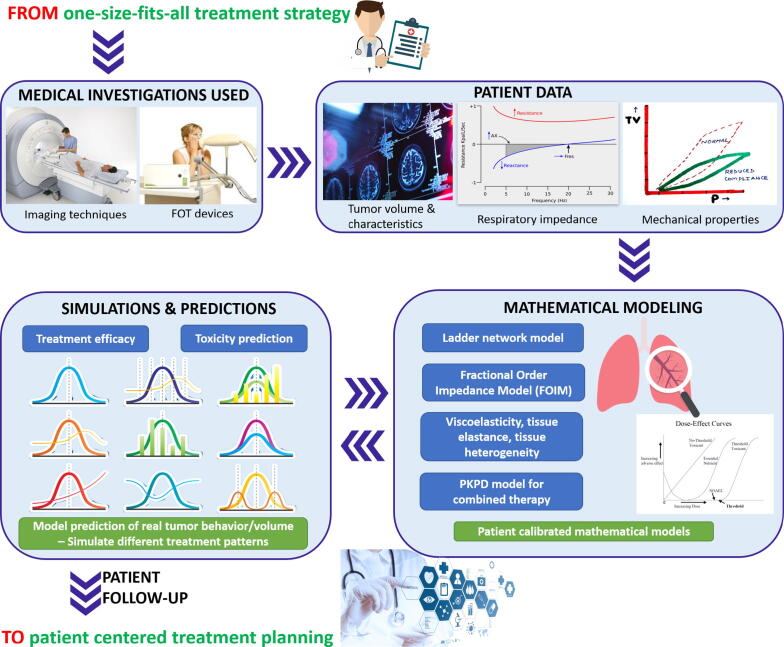
Rapid progress in oncology requires personalized therapies for cancer able to replace the traditional medicine, where a one-size-fits-all treatment approach is exceeded. The clinical decision making process should not be based only on best practices, but also on integration of clinical data and high-precision tools, as illustrated in Fig. 11.
Fig. 11.
Personalization of treatment planning by integration of mathematics, modeling and simulation tools.
Personalizing medicine by modeling and predicting patient-specific responses to cancer therapy is the best way towards prospective clinical trials. To provide optimal treatment for the individual patient, clinical and engineering tools are used to forecast tumor dynamics. Primary investigations include the assessment of lung function with FOT device and tumor characteristics with imaging techniques for diagnosis of lung properties in lung cancer. All patient data is integrated in mathematical models for identifying parameters predictive of treatment outcome in lung cancer. Simulation for prediction of tumor evolution will be made with lung mechanical properties, kinetics and dynamics interactions, time-varying tissue heterogeneity, and drug resistance. Using these tools, it becomes feasible to simulate time-dependent effects during treatment and to compare different time-dose patterns in terms of their tumor management. All the above techniques (imaging, pulmonary function tests, mathematical models) used in a congruent manner will ensure better guidance for physicians in managing each treatment outcome while minimizing its toxicities.
To address the raised challenges and to maximize the success of a treatment in an individual, clinicians need to be aware of both tumor characteristics and lung tissue properties (enabled here by forced oscillations lung function test data).
We established that changes in tissue heterogeneity can be acquired and described with a FOT device. Modifications of viscoelastic properties of respiratory tissue can be captured from time-based data by fractional order models of respiratory impedance [28], [29].
To gain insight into the behavior of a drug in situations not yet studied, extended numerical simulations are required. The application of physiologically based pharmacokinetic (PK) and pharmacodynamic (PD) principles has been shown to enhance the selection of optimum doses and treatment designs, without human exposure [51]. A minimal PKPD interaction model has been proposed by our team in [17] for estimating therapy doses and dosing intervals to provide specific synergy degree among drugs and patient response in simulated non-small cell lung cancer (NSCLC) therapies. This model can be used to determine the drug response in humans, by predicting steady-state responses and optimum dosing regimens to achieve desired responses in tumor regression. Efficient numerical procedures for prediction of interaction between tumor cell populations and various therapies, with direct effect on tumor growth or regression has been also addressed in [12], [13], [15].
The final use of the simulation analysis presented in this paper is to evaluate changes in the respiratory impedance as a function of time, as to identify the effects of treatment on tumor volume. Tumor and patient response to drug therapy can be simulated for different anti-cancer therapies by means of PKPD model. Both mathematical models form a decision-making platform to assist the healthcare team plan, the next dose treatment as a function of periodically evaluated lung function tests and the updated tumor/lung model parameters.
Conclusions
Mathematical modeling of the respiratory function as a response of heterogeneous tissue represents an attractive avenue towards narrowing the set of possibilities that should be tested prior to clinical trials. Feature extraction from modeling a respiratory function through a specific fractional order impedance model can be transposed to lung tumor dynamics. Furthermore, changes in the lung geometry along the levels of the respiratory tree are simulated, replacing the recurrent lung geometry for a tumorous lung with random asymmetry.
A mimicked lung tumor setup has been employed in experimental analysis with a FOT device during two protocols. By analysis of different induced abnormalities, upon impedance model parameters, the results have shown the changes in viscoelastic properties of respiratory tissue. Non-linear effects coming from the airways and lung tissue validated our hypothesis that T index is increasing with changes in viscoelasticity (i.e., various rubber balloons).
Future research investigations involve using tools such as FOT in clinical trials for assessing the respiratory function in lung cancer patients. Through correlation of the respiratory function with the tumor volume provided by imaging techniques, FOT can be used as a useful ally for auxiliary treatment planning and toxicity prediction. Using real clinical data in mathematical formulations based on fractional calculus and compartmental PKPD models enables a smoother decision making process for treatment synergy [17], highly relevant in a challenging pandemic context [44], [45], [47], [48].
Declaration of Competing Interest
The authors declare that there is no conflict of interests regarding the publication of this manuscript.
Compliance with Ethics Requirements
This manuscript does not contain any studies performed on human or animal subjects.
Acknowledgements
This research was supported by the Special Research Fund of Ghent University, doctoral scholarship No. 01D15919 (Maria Ghita), grant No. 01J01619 and by the Flanders Research Foundation (FWO) post-doctoral grant fellowship No. 12X6819N (Dana Copot).
Biographies

Maria Ghita received the M.Sc. degree in medical informatics from the Politechnica University in Bucharest, Romania in 2018, and her work was awarded the 2018 IEEE Systems Man and Cybernetics MSc Thesis Grant Initiative for the contributions on non-invasive and objective pain level assessment methods. She is recipient of the doctoral scholarship from Special Research Funds of Ghent University, Belgium. Her research interests are on modeling biological tissues and developing optimal control therapies for fighting cancer.

Dana Copot received the M.Sc. degree in chemical engineering from the Gh. Asachi Politechnica University in Iasi, Romania in 2012. She obtained her PhD degree at Ghent University in 2018 on modeling diffusion mechanisms in biological tissues. Currently she is the recipient of the prestigious Flanders Research Foundation grant for post-doctoral fellows at the same university. Her main research topic is predictive control of drug delivery systems.

Clara Ionescu received the M.Sc. degree in industrial informatics and automation from the Dunarea de Jos University of Galati, Romania, in 2003, and the Ph.D. degree from Ghent University, Belgium, in 2009 on modeling the human respiratory system with fractional order models for diagnosis purposes. Between 2011-2016 she was the recipient of the prestigious Flanders Research Fund grant for postdoctoral fellows at the same university. Since October 2016 she is professor at Ghent University, teaching Computer Control of Industrial Processes within the Control and Automation Master Program. She is working on the application of generic control algorithms (fractional, predictive and PID-type) to dynamic processes in various application fields.
Footnotes
Peer review under responsibility of Cairo University.
References
- 1.Magin R. Fractional calculus models of complex dynamics in biological tissues. Comput Math Appl. 2010;59(5):1586–1593. doi: 10.1016/j.camwa.2009.08.039. [DOI] [Google Scholar]
- 2.Ionescu C., Lopes A., Copot D., Machado J., Bates J. The role of fractional calculus in modeling biological phenomena: A review. Commun Nonlinear Sci Numer Simulat. 2017;51:141–159. doi: 10.1016/j.cnsns.2017.04.001. [DOI] [Google Scholar]
- 3.Sun H., Zhang Y., Baleanu D., Chen W., Chen Y. A new collection of real world applications of fractional calculus in science and engineering. Commun Nonlinear Sci Numer Simulat. 2018;64:213–231. doi: 10.1016/j.cnsns.2018.04.019. [DOI] [Google Scholar]
- 4.Qureshi S., Chang M., Shaikh A.A. Analysis of series RL and RC circuits with time-invariant source using truncated M, atangana beta and conformable derivatives. J Ocean Eng Sci. 2020 doi: 10.1016/j.joes.2020.11.006. 2468–0133. [DOI] [Google Scholar]
- 5.Baleanu D., Jajarmi A., Sajjadi S.S., Asad J.H. The fractional features of a harmonic oscillator with position-dependent mass. Commun Theor Phys. 2020;72(5):055002. doi: 10.1088/1572-9494/ab7700. [DOI] [Google Scholar]
- 6.Jajarmi A., Baleanu D. A new iterative method for the numerical solution of high-order non-linear fractional boundary value problems. Front Phys. 2020;8:220. doi: 10.3389/fphy.2020.00220. [DOI] [Google Scholar]
- 7.Baskonus H.M., Bulut H. On the numerical solutions of some fractional ordinary differential equations by fractional Adams-Bashforth-Moulton method. Open Mathemat. 2015;13:547–556. doi: 10.1515/math-2015-0052. [DOI] [Google Scholar]
- 8.Jajarmi A., Baleanu D. On the fractional optimal control problems with a general derivative operator. Asian J Control. 2019:1–10. doi: 10.1002/asjc.2282. [DOI] [Google Scholar]
- 9.Baleanu D., Ghanbari B., Asad J.H., Jajarmi A., Pirouz H.M. Planar system-masses in an equilateral triangle: Numerical study within fractional calculus. CMES-Comput Model Eng Sci. 2020;124(3):953–968. doi: 10.32604/cmes.2020.010236. [DOI] [Google Scholar]
- 10.Shiri B., Wu G.-C., Baleanu D. Collocation methods for terminal value problems of tempered fractional differential equations. Appl Num Mathe. 2020;156:385–395. doi: 10.1016/j.apnum.2020.05.007. [DOI] [Google Scholar]
- 11.Sajjadi S.S., Baleanu D., Jajarmi A., Pirouz H.M. A new adaptive synchronization and hyperchaos control of a biological snap oscillator. Chaos Solitons Fractals. 2020;138:109919. doi: 10.1016/j.chaos.2020.109919. [DOI] [Google Scholar]
- 12.Valentim C.A., Oliveira N.A., Rabi J.A., David S.A. Can fractional calculus help improve tumor growth models? J Comput Appl Math. 2020;379:112964. doi: 10.1016/j.cam.2020.112964. [DOI] [Google Scholar]
- 13.Baleanu D., Jajarmi A., Sajjadi S., Mozyrska D. A new fractional model and optimal control of a tumor-immune surveillance with non-singular derivative operator. Chaos. 2019;29(8):083127. doi: 10.1063/1.5096159. [DOI] [PubMed] [Google Scholar]
- 14.Dokuyucu M.A., Celik E., Bulut H., Baskonus H.M. Cancer treatment model with the Caputo-Fabrizio fractional derivative. Eur Phys J Plus. 2018;133(92):1–6. doi: 10.1140/epjp/i2018-11950-y. [DOI] [Google Scholar]
- 15.Drexler D.A., Sapi J., Kovacs L. Modeling of tumor growth incorporating the effects of necrosis and the effect of bevacizumab. Complexity. 2017;3:1–10. doi: 10.1155/2017/5985031. [DOI] [Google Scholar]
- 16.Ghita M., Drexler D.A., Kovacs L., Copot D., Muresan C.I., Ionescu C.M. 21st IFAC World Congress, Berlin, Germany. 2020. Model-based management of lung cancer radiation therapy; pp. 16149–16154. [Google Scholar]
- 17.Ionescu C.M., Ghita M., Copot D., Derom E., Verellen D. A minimal PKPD interaction model for evaluating synergy effects of combined NSCLC therapies. J Clin Med. 2020;9(6):1832. doi: 10.3390/jcm9061832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lin A.J., Roach M., Bradley J., Robinson C. Combining stereotactic body radiation therapy with immunotherapy: current data and future directions. Transl Lung Cancer Res. 2019;8(1):107–115. doi: 10.21037/tlcr.2018.08.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Manegold C., Dingemans A.-M.C., Gray J.E., Nakagawa K., Nicolson M., Peters S. The potential of combined immunotherapy and antiangiogenesis for the synergistic treatment of advanced NSCLC. J Thorac Oncol. 2017;12(2):194–207. doi: 10.1016/j.jtho.2016.10.003. [DOI] [PubMed] [Google Scholar]
- 20.Lennon F., Cianci G., Cipriani N., Hensing T., Zhang H., Chen C., Murgu S., Vokes E., Vannier M., Salgia R. Lung cancer–a fractal viewpoint. Nat Rev Clin Oncol. 2015;12(11):664–675. doi: 10.1038/nrclinonc.2015.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Weibel E. Lung morphometry: the link between structure and function. Cell Tissue Res. 2017;367:413–426. doi: 10.1007/s00441-016-2541-4. [DOI] [PubMed] [Google Scholar]
- 22.Iomin A. Fractional kinetics under external forcing. Nonlinear Dyn. 2015;80:1853–1860. doi: 10.1007/s11071-014-1561-4. [DOI] [Google Scholar]
- 23.Fu B., Freeborn T. Cole-impedance parameters representing biceps tissue bioimpedance in healthy adults and their alterations following eccentric exercise. J Adv Res. 2020;25:285–293. doi: 10.1016/j.jare.2020.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Grimnes S, Martinsen G. Bioimpedance and bioelectricity basics, T3rd ed. Oxford: Academic Press; 2015. doi:https://doi.org/10.1016/B978-0-12-411470-8.00010-6.
- 25.Ghita M., Neckebroek M., Juchem J., Copot D., Muresan C., Ionescu C. Bioimpedance sensor and methodology for acute pain monitoring. Sensors. 2020;20(23):6765. doi: 10.3390/s20236765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Copot D., De Keyser R., Derom E., Ortigueira M., Ionescu C. Reducing bias in fractional order impedance estimation for lung function evaluation. Biomed Signal Process Control. 2018;39:74–80. doi: 10.1016/j.bspc.2017.07.009. [DOI] [Google Scholar]
- 27.Magin R., Ortigueira M., Podlubny I., Trujillo J. On the fractional signals and systems. Signal Process. 2011;91(3):350–371. doi: 10.1016/j.sigpro.2010.08.003. [DOI] [Google Scholar]
- 28.Ghita M., Copot D., Ghita M., Derom E., Ionescu C. Low frequency forced oscillation lung function test can distinguish dynamic tissue non-linearity in COPD patients. Front Physiol. 2019;10:1390. doi: 10.3389/fphys.2019.01390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Copot D., De Keyser R., Derom E., Ionescu C. Structural changes in the COPD lung and related heterogeneity. Plos One. 2017;12(5):e0177969. doi: 10.1371/journal.pone.0177969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ala G., Di Paola M., Francomano E., Li Y., Pinnola F. Electrical analogous in viscoelasticity. Commun Nonlinear Sci Numer Simulat. 2014;19(7):2513–2527. doi: 10.1016/j.cnsns.2013.11.007. [DOI] [Google Scholar]
- 31.Ionescu C., Segers P., De Keyser R. Mechanical properties of the respiratory system derived from morphologic insight. IEEE Trans Biomed Eng. 2009;56(4):949–959. doi: 10.1109/TBME.2008.2007807. [DOI] [PubMed] [Google Scholar]
- 32.Ionescu C.M., Vandersteen G., Schoukens J., Desager K., Keyser R.D. Measuring nonlinear effects in respiratory mechanics: A proof of concept for prototype device and method. IEEE Trans Instrum Meas. 2014;63(1):124–134. doi: 10.1109/TIM.2013.2277519. [DOI] [Google Scholar]
- 33.King G.G., Bates J., Berger K.I., Calverley P., de Melo P.L., Dellacà R.L., Farré R. Technical standards for respiratory oscillometry. Eur Respir J. 2020;55:1900753. doi: 10.1183/13993003.00753-2019. [DOI] [PubMed] [Google Scholar]
- 34.Ribeiro C., Faria A., Lopes A., de Melo P. Forced oscillation technique for early detection of the effects of smoking and COPD: contribution of fractional-order modeling. Int J Chron Obstruct Pulmon Dis. 2018;13:3281–3295. doi: 10.2147/COPD.S173686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Faria A., Veiga J., Lopes A., Melo P. Forced oscillation, integer and fractional-order modelling in asthma. Comput Methods Programs Biomed. 2016;128:12–26. doi: 10.1016/j.cmpb.2016.02.010. [DOI] [PubMed] [Google Scholar]
- 36.Lonescu C. The human respiratory system: an analysis of the interplay between anatomy, structure, breathing and fractal dynamics. Series BioEng, Springer, London, 2013. doi:10.1007/978-1-4471-5388-7.
- 37.Olarte O., De Keyser R., Ionescu C. Fan-based device for non-invasive measurement of respiratory impedance: Identification, calibration and analysis. Biomed Signal Process Control. 2016;30:127–133. doi: 10.1016/j.bspc.2016.06.004. [DOI] [Google Scholar]
- 38.Maes H., Vandersteen G., Muehlebach M., Ionescu C. A fan-based, low-frequent, forced oscillation technique apparatus. IEEE Trans Instrum Meas. 2014;63(3):603–611. doi: 10.1109/TIM.2013.2282188. [DOI] [Google Scholar]
- 39.Soares M., Richardson M., Thorpe J., Owers-Bradley J., Siddiqui S. Comparison of forced and impulse oscillometry measurements: A clinical population and printed airway model study. Sci Rep. 2019;9(1):2130. doi: 10.1038/s41598-019-38513-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sokai R., Ito S., Iwano S., Uchida A., Aso H., Kondo M. Respiratory mechanics measured by forced oscillation technique in rheumatoid arthritis-related pulmonary abnormalities: frequency-dependence, heterogeneity and effects of smoking. Springerplus. 2016;5:335. doi: 10.1186/s40064-016-1952-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sobota V., Muller M., Roubik K. Intravenous administration of normal saline may be misinterpreted as a change of end-expiratory lung volume when using electrical impedance tomography. Sci Rep. 2019;9:5775. doi: 10.1038/s41598-019-42241-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Calabrò L., Peters S., Soria J.-C., Giacomo A.D., Barlesi F., Covre A. Challenges in lung cancer therapy during the COVID-19 pandemic. Lancet Respir Med. 2020;8(6):542–544. doi: 10.1016/S2213-2600(20)30170-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jafari H. A new general integral transform for solving integral equations. J Adv Res. 2020 doi: 10.1016/j.jare.2020.08.016. 2090–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Naik P.A., Yavuz M., Qureshi S., Zu J., Townley S. Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan. Eur Phys J Plus. 2020;135(795):1–42. doi: 10.1140/epjp/s13360-020-00819-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Din A., Khan A., Baleanu D. Stationary distribution and extinction of stochastic coronavirus (COVID-19) epidemic model. Chaos, Solitons and Fractals. 2020;139:110036. doi: 10.1016/j.chaos.2020.110036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rezapour S., Mohammadi H., Jajarmi A. A new mathematical model for Zika virus transmission. Adv Diff Eqs. 2020;2020:589. doi: 10.1186/s13662-020-03044-7. [DOI] [Google Scholar]
- 47.Qureshi S., Atangana A. Fractal-fractional differentiation for the modeling and mathematical analysis of nonlinear diarrhea transmission dynamics under the use of real data. Chaos, Solitons Fractals. 2020;136:109812. doi: 10.1016/j.chaos.2020.109812. [DOI] [Google Scholar]
- 48.Jajarmi A., Yusuf A., Baleanu D., Inc M. A new fractional HRSV model and its optimal control: A non-singular operator approach. Phys A. 2020;547:123860. doi: 10.1016/j.physa.2019.123860. [DOI] [Google Scholar]
- 49.Ameen I., Baleanu D., Ali H.M. An efficient algorithm for solving the fractional optimal control of SIRV epidemic model with a combination of vaccination and treatment. Chaos, Solitons Fractals. 2020;137:109892. doi: 10.1016/j.chaos.2020.109892. [DOI] [Google Scholar]
- 50.Czakó B., Kovács L. Nonlinear model predictive control using robust fixed point transformation-based phenomena for controlling tumor growth. Machines. 2018;6(49) doi: 10.3390/machines6040049. [DOI] [Google Scholar]
- 51.Rosenbaum SE. Basic pharmacokinetics and pharmacodynamics: an integrated textbook and computer simulations. 2nd ed. New Jersey, United States of America: John Wiley &; Sons Inc; 2017. doi:10.1007/978-1-4471-5388-7.