Interindividual Signatures of fMRI Temporal Fluctuations

Abstract

The complexity and variability of human brain activity, such as quantified from Functional Magnetic Resonance Imaging (fMRI) time series, have been widely studied as potential markers of healthy and pathological states. However, the extent to which fMRI temporal features exhibit stable markers of inter-individual differences in brain function across healthy young adults is currently an open question. In this study, we draw upon two widely used time-series measures—a nonlinear complexity measure (sample entropy; SampEn) and a spectral measure of low-frequency content (fALFF)—to capture dynamic properties of resting-state fMRI in a large sample of young adults from the Human Connectome Project. We observe that these two measures are closely related, and that both generate reproducible patterns across brain regions over four different fMRI runs, with intra-class correlations of up to 0.8. Moreover, we find that both metrics can uniquely differentiate subjects with high identification rates (ca. 89%). Canonical correlation analysis revealed a significant relationship between multivariate brain temporal features and behavioral measures. Overall, these findings suggest that regional profiles of fMRI temporal characteristics may provide stable markers of individual differences, and motivate future studies to further probe relationships between fMRI time series metrics and behavior.

Introduction

In recent years, the temporal variability and complexity of neural time series have gained increasing attention as potential markers of brain function. Theoretical work has linked neural complexity with information processing, and with the brain’s capacity to flexibly transition between a range of states (Bassett and Gazzaniga 2011; Deco et al. 2011; Li et al. 2019; Kang et al. 2019a). Metrics such as Sample Entropy (SampEn) (Richman and Moorman 2000) and Multiscale Entropy (Costa et al. 2002) may be calculated upon electrophysiological or fMRI time series measured from the human brain, where alterations have been found in disorders such as Autism Spectrum Disorder (Easson and McIntosh 2019; Kang et al. 2019b; Zhang et al. 2020b), Alzheimer’s Disease (Mizuno et al. 2010; Wang et al. 2017; Grieder et al. 2018), and Attention-Deficit/Hyperactivity Disorder (Sokunbi et al. 2013; Chenxi et al. 2016), as well as in normal aging (Sokunbi 2014; Jia et al. 2017).

Although most often studied in the context of pathological states and aging, there is growing evidence that the dynamic properties of fMRI time series may also provide an indicator of healthy cognitive function. For example, brain signal complexity, as captured by multiscale entropy of electroencephalogram (EEG) signals, has been suggested to increase in the process of learning unfamiliar faces and may play a role in memory processing (Heisz et al. 2012), and was linked with creativity in healthy elderly subjects (Ueno et al. 2015). The sample entropy of resting-state fMRI signals has been shown to exhibit stable and organized spatial patterns that aligned with functional subdivisions (Wang et al. 2014), and multi-scale entropy was found to reliably differentiate between four resting-state functional networks implicated in higher-order cognition (McDonough and Nashiro 2014). Resting-state fMRI signal entropy has also been found to correlate to measures of intelligence (Saxe et al. 2018) and to be modulated with repetitive transcranial magnetic stimulation (Song et al. 2019a). Indeed, the characteristics of moment-to-moment brain signal fluctuations is an emerging research area in the human neuroimaging field (Garrett et al. 2013; Nomi et al. 2017; Uddin 2020).

Yet, while fMRI studies typically aggregate data across groups of participants to draw inferences about brain function, understanding individual behaviors and phenotypes requires investigating individuals’ unique brain activity profiles. The possibility of uniquely identifying an individual subject within a group has previously been demonstrated using profiles constructed from whole-brain functional connectivity (pairwise correlations) (Finn et al. 2015); however, it is not clear whether the dynamic properties of regions’ fMRI time series themselves differ robustly across subjects and reflect between-subject variations in cognition/behavior. Prior studies have suggested that the temporal complexity and low-frequency amplitude of fMRI fluctuations exhibit high test–retest reliability (Zuo et al. 2010; Zhang et al. 2020a) and may correspond with gene expression (Wang et al. 2015), motivating their examination as stable markers of inter-individual differences.

Here, we examine whether the characteristics of time-varying activity encode information that can sensitively differentiate between healthy young individuals and their behavioral profiles. For this investigation, we quantified and compared both the within-subject stability and inter-individual discriminability of two widely used temporal metrics: sample entropy (SampEn) and Fractional Amplitude of Low-frequency Fluctuation (fALFF) (Zou et al. 2008). Using resting-state data from 410 subjects from the Human Connectome Project (HCP) (Van Essen et al. 2012), we first establish that both SampEn and fALFF are consistent over four scans collected over 2 days, supporting their promise as stable markers of individual traits. Second, although much fMRI research treats SampEn (a nonlinear complexity measure) and fALFF (a spectral measure) separately, here we observe that under the selected parameter ranges, these features are strongly (negatively) related to each other (Song et al. 2019b). Next, we demonstrate that these regional temporal features are not only stable within each individual, but are also distinct enough from other individuals to allow for fingerprinting with high accuracy. Finally, we show that there is a significant relationship between these temporal features and individual differences in behavioral traits.

Materials and Methods

Imaging Data

Resting-state fMRI data were downloaded from the S500 release of the HCP database. In the HCP, each subject underwent four resting-state fMRI scans, acquired with a simultaneous multi-slice EPI sequence with the following parameters: TR = 720 ms, duration = 864 s (14.4 min), spatial resolution = 2 mm isotropic, 72 slices, multi-band factor = 8 (Van Essen et al. 2012; Van Essen et al. 2013). During these scans, subjects were instructed to keep their eyes open and maintain fixation on a cross-hair. We used the FIX-denoised version of the data (Salimi-Khorshidi et al. 2014), and further excluded subjects that did not pass our quality check for head motion or had incomplete behavioral measures, resulting in 410 subjects in total. For head motion, subjects were excluded if the average frame-to-frame motion value was above 0.14 (Finn et al. 2015) for at least one of the four resting-state scans. All procedures were conducted according to the HCP data use guidelines.

Behavioral Measures

The behavioral measures selected for this study include 15 frequently-used measures that tap into human cognition, emotion, and quality of life (Liegeois et al. 2019), which we collectively refer to as “behavioral measures” for simplicity: (1) Attention, (2) CardSort—Cognitive Flexibility, (3) Dexterity, (4) ER40_CRT—Emotion Recognition, (5) Flanker—Inhibition (Flanker Task), (6) ListSort—Working Memory (List Sorting), (7) PMAT24_A_CR—Fluid Intelligence, (8) PSQI_Score—Sleep Quality, (9) PicSeq—Visual Episodic Memory, (10) ProcSpeed—Processing Speed, (11) Relational Task Acc—Relational Processing, (12) SCPT SEN—Sustained Attention (Sens.), (13) SCPT SPEC—Sustained Attention (Spec.), (14) VSPLOT TC—Spatial Orientation, and (15) WM Task Acc—Working Memory (N-back).

Calculation of SampEn

SampEn quantifies dynamic properties of physiological signals. It can be calculated using the following steps (Sokunbi et al. 2013; Sokunbi 2014; Jia et al. 2017).

First, given a time series (a row vector), 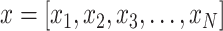, and an embedding dimension, m, an embedding vector with m consecutive data points can be extracted from 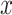: 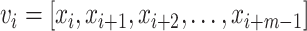. Second, for each 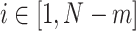, we have

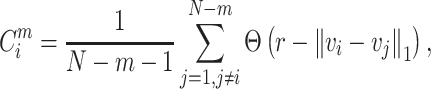(1)

r indicates a tolerance distance (value), which can be calculated as 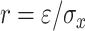, where 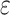is a scaling parameter and 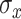is the standard deviation of input signal vector. 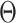() is the Heaviside function:

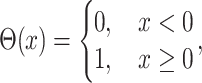(2)

and 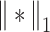represents the Chebyshev distance, which can be expressed as:

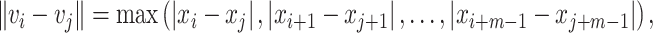(3)

Therefore, 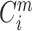indicates the proportion of 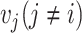whose distances to 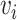are less than r. In same rationale, for each 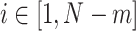we further define:

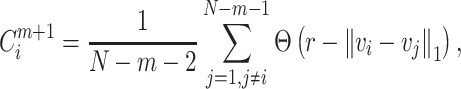(4)

where 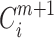indicates the proportion corresponding to the dimension of m + 1; 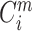and 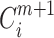have the same form, but embedding vectors in the two cases are defined in different phase spaces.

Next, we average across all embedding vectors to obtain:

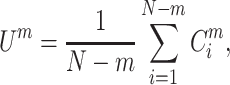(5)

and

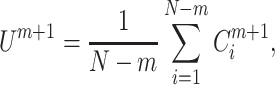(6)

Finally, the SampEn of x is computed as

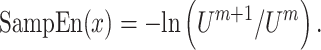(7)

There is no rigorous guidance for the choice of r and m, and it is usually application-specific (Sokunbi et al. 2013; Sokunbi 2014; Jia et al. 2017). To our knowledge, frequently-used ranges for r and m in the biomedical signal processing literature are 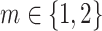and 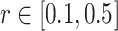. For this work, we chose m = 2 and r = 0.5 for as the parameters for calculating SampEn. It has been shown that m = 2 may enable more detailed reconstruction of the joint probabilistic dynamics compared to m = 1 (Sokunbi 2014).

Fractional Amplitude of Low-Frequency Fluctuations (fALFF)

fALFF quantifies the ratio of the power spectrum in a low-frequency band to that of the entire frequency range (i.e., up to the Nyquist frequency). The time series for each ROI was transformed to the frequency domain using Fast Fourier Transform (FFT), and the corresponding power spectrum was obtained as the square of the magnitude. The low-frequency cut-off was chosen as 0.1 Hz.

Calculation of Intraclass Correlation

Intraclass correlation (ICC) was used to quantify the across-scan reliability of SampEn and fALFF. Within a given ROI or network, we can treat each subject’s regional SampEn and fALFF features across four scans as four “judgments/ratings,” whose reliability can be measured using ICC. There are three steps for selecting the most appropriate ICC calculation among 10 different possible forms defined by McGraw et al. (McGraw and Wong 1996) and Koo et al. (Koo and Li 2016). First, we chose “Two-Way Random-Effects Model,” to consider those scans/ratings (which differ by acquisition time) as random draws from a population of scans acquired at different times. Second, we used “single measurement/rater” type, because we are interested in the repeatability of values across individual scans (i.e., the reliability of a single rater, as opposed to the mean value of multiple raters). Finally, there are two ICC definitions: “absolute agreement” and “consistency.” We choose the “absolute agreement” because we are interested in the reliability of the exact values across the four scans, without allowing for the possibility of systematic differences. Therefore, the form we used to calculate ICC is ICC(2, 1): “Two-Way Random-Effects, absolute agreement, single rater/measurement.”

Other Relevant Brain Complexity Features

While fALFF and SampEn were the main metrics considered here, we also considered two alternate, complementary metrics to ensure that our results were robust across various measures of temporal complexity. The amplitude of low-frequency fluctuations (ALFF) (Zang et al. 2007) measures the integral of the power spectrum of the entire frequency range. The calculation corresponds to the numerator of the fALFF metric. Percent amplitude of fluctuation (PerAF) (Jia et al. 2020) quantifies the percentage of BOLD fluctuations relative to the mean BOLD signal intensity for each time point, which was further averaged across the whole time series. PerAF can be calculated as follows:

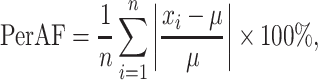(8)

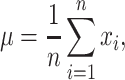(9)

where 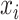is the signal intensity of the ith time point, n is the total number of time points of the time series, and 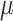is the mean value of the time series.

Canonical Correlation Analysis

We employed canonical correlation analysis (CCA) as an approach for probing relationships between fMRI temporal complexity and cognitive measures. The two sets of variables input to CCA consisted of a neuroimaging feature matrix (410 subjects 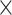90 ROI matrix, where the (i, j) entry corresponds to either SampEn or fALFF for the ith subject in the jth ROI) and a behavioral measures matrix (410 subjects 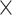15 behavioral measures). The neuroimaging feature matrix was averaged across all 4 resting-state scans. Prior to CCA, we applied Principal Component Analysis (PCA) to reduce the dimensionality of both matrices, where the number of selected PCA components was based on preserving 75% of the variance.

Two statistical analyses were conducted. In the first, we fit CCA model between these two sets of variables for all 410 subjects, and applied a permutation test to assess the significance of the first mode (i.e., the mode with the highest correlation between linear combinations of neuroimaging features and behavioral measures). The permutation test was conducted by shuffling the rows of the neuroimaging feature matrix at each iteration. To visualize the contributions of each ROI and behavioral measure, the resulting CCA coefficients were used to project the first mode back to the original brain and behavior space. As a more stringent test of generalization, we also conducted a split-halves “out-of-sample” test. Here, we applied CCA to the first half of the subjects (205 subjects; “training set”), resulting in trained CCA coefficients. These coefficients were then applied to the second half of the subjects (205 subjects; “test set”). Prior to CCA, the PCA step was applied to training set (again, preserving 75% of the variance), and the resulting loadings were applied to the test set.

Identification Rate Associated with Different fALFF/ALFF Frequency Bands

Given that fALFF requires the selection of a particular frequency band, we also investigated the effects of different frequency bands on the fingerprinting identification rate. Based upon a previous study (Gong et al. 2021), we also examined fALFF and ALFF for the following 5 frequency bands features: 0.607–0.694 Hz, 0.223–0.607 Hz, 0.082–0.223 Hz, 0.03–0.082 Hz, and 0.012–0.03 Hz.

Results

Stability of fMRI Temporal Features Across Repeated Scans

In the HCP database, each subject has two resting-state fMRI scans (denoted “LR,” “RL”) in each of two different sessions collected on different days (denoted “REST1,” “REST2”). From each scan, we extracted the SampEn and fALFF of the average time course in each of 90 ROIs (Shirer et al. 2012), resulting in a 410 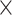 90 matrix for each of the four scans and for each of the two temporal measures. The four corresponding SampEn matrices and fALFF matrices (Fig. 1) were qualitatively consistent with one another, indicating that both of these temporal features are largely stable across repeated measurements. The clear vertical patterns in these matrices also indicate that certain regions tended to have consistently higher or lower SampEn/fALFF features across all subjects, which we further investigate below (see the section “Dependence of temporal complexity on ROI size and data processing methods”). To examine whether these results were specific to the selected parameters, we repeated the analysis with a different choice of embedding dimension (m = 5) for SampEn, obtaining similar results (Supplementary Fig S1). Intraclass correlation (ICC) values, calculated for each ROI, were found to have a wide range across the 90 ROIs, from 0.006–0.788 for SampEn and 0.059–0.803 for fALFF (Fig. 2). Since the present study focuses on region-level measures, all ICC analyses were based on region-level (ROIs) rather than voxel-wise time series.

Figure 1 .

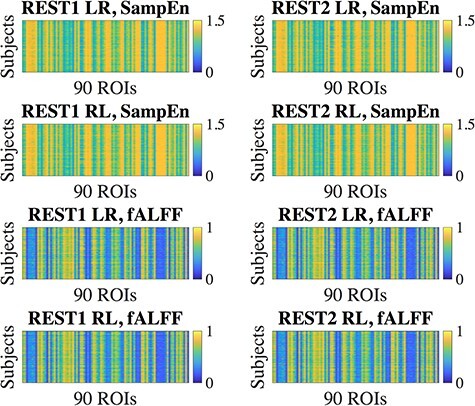
Regional SampEn and fALFF, calculated over 410 subjects for each run. Both of these features exhibited consistent patterns over the four runs. “REST1” and “REST2” indicate the two different sessions (days) over which the scans were collected, where each session contains two different scans that differed by phase-encoding direction (“LR” and “RL”).

Figure 2 .

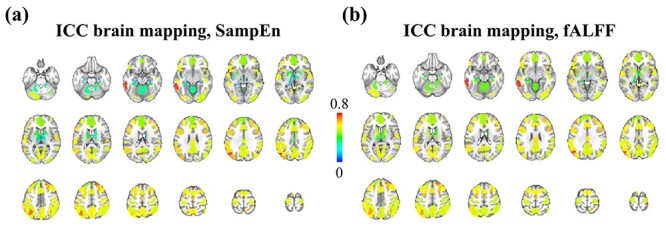
Intraclass correlation of SampEn and fALFF across 90 ROIs. (a) ICC within each ROI, quantifying the consistency of each region’s SampEn across four resting-state fMRI runs. (b) Similar to (a), the ICC brain mapping for fALFF.

We also observed that the SampEn- and fALFF-based features yielded similar anatomic trends across resting-state networks. As our 90-ROI atlas is composed of 14 core resting-state networks (RSNs), we examined these network-level trends by averaging SampEn and fALFF values, respectively, within each of the 14 networks (Supplementary Fig S2a,b).

Figure 3 indicates that, under the parameter settings used here, SampEn and fALFF themselves exhibit a clear inverse relationship. SampEn quantifies the amount of irregularity and unpredictability of fluctuations in a time series, and fALFF represents the proportion of low-frequency components, relating to the smoothness of the signals, which may be expected to be related inversely to SampEn. Figure 3 also indicates that the strength of this relationship varies with the embedding dimension m, with m = 2 yielding a closer match between SampEn and the low-frequency fluctuation amplitude (in the <0.1 Hz band) compared with m = 5. Spearman’s correlation was used because the relationship between SampEn and fALFF appears monotonic but not linear. A table listing the Spearman correlations between fALFF and SampEn (m = 2, 5) for each ROI is shown in (Supplementary Table S1).

Figure 3 .

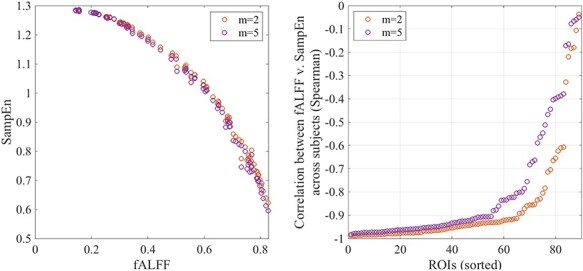
(Left) The relationship between regional SampEn and fALFF. Each dot represents one ROI, whose SampEn or fALFF is averaged across all subjects as well as across all four runs. The orange and purple dots correspond to SampEn calculated with two different embedding dimensions (m = 2, 5). (Right) Relationship between SampEn and fALFF within each ROI, calculated as the Spearman correlation between SampEn and fALFF values across subjects. Regions are shown ranked according to the Spearman correlation magnitude, from strongest to weakest negative correlation.

Inter-individual Differentiation of Regional Temporal Profiles

Given that SampEn and fALFF may constitute stable features of brain activity, we also investigated their ability to uniquely differentiate between subjects. To examine this possibility, an individual’s temporal variability profile (constructed as the 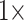90 vector of SampEn or fALFF calculated in 90 ROIs) from a given scan was compared to that of all individuals’ profiles from a different scan using Pearson correlation. If such a profile is indeed unique to an individual, then we would expect that the correlation of subject k’s profile during one scan would be highest with that of subject k’s profile in a different scan, compared to that of all other subjects.

We observed that these SampEn and fALFF profiles are indeed able to identify subjects across different scans with high identification (ID) rate, defined by the fraction of total subjects where the best correlation of the profile from another scan is with itself (Fig. 4). Given that each subject’s four fMRI scans were collected within two sessions, we also consider the case of averaging the profiles from the two scans acquired in one day (REST1) and the two scans acquired on a different day (REST2). Comparing the average of scans in REST1 with that of REST2 (Figs. 4a,d) proved to yield the strongest identification power, for both SampEn (Fig. 4b, 86%) and fALFF (Fig. 4e, 89%). Here, the blue-colored diagonal elements indicate that each subject’s profiles have stronger correlation with itself than any other subjects from another session. Fig. 4b and e further indicate that the within-session ID rate is always higher than between-session ID rate.

Figure 4 .

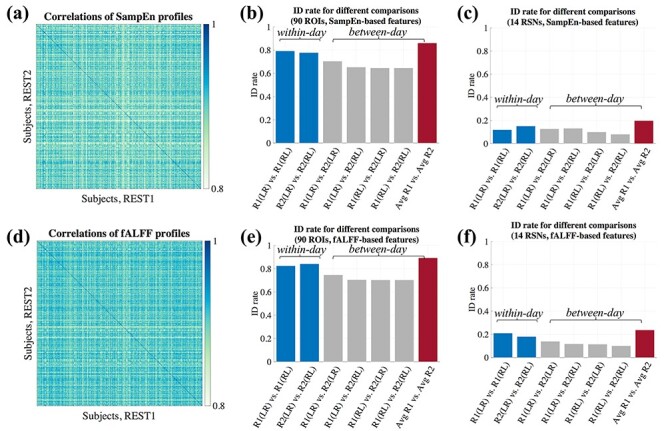
Between-subject differentiation of SampEn (first row) and fALFF-based profiles (second row). In this figure, we use ‘R1’ and ‘R2’ to denote REST1 (session 1) and REST2 (session 2), for brevity. (a,d) Pairwise similarity (Pearson correlation) between profiles of different subjects across two different sessions. Here, the average profiles across the two scans acquired within the first session (REST1) were compared to the average of those acquired in the second session (REST2). The diagonal elements indicate the correlation of profiles for same subjects across different scans. These profiles were calculated using 90 ROIs. (b,e) The identification rate for different pairwise combinations of scans. The blue and gray bars indicate within-session and between-session comparisons, respectively. The red bars denote the between-session comparison where the average of the two scans in REST1 is compared with the average of the two scans in REST2. Panels (c) and (f) show the corresponding results for (b) and (e) based on the profiles constructed from 14 core resting-state networks, respectively. The ID rate drops drastically for all situations in comparison to (b) and (e).

To probe whether a more condensed, network-level profile can also successfully identify the subjects across different scans, we collapsed the original profiles by averaging the original SampEn and fALFF vectors within each core RSN, resulting in a 1 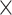 14 profile. Compared to the ID rate when using 90 ROIs, this network-based profile was not nearly as high (Figs. 4c and f).

Since the group of 410 subjects may contain some subjects who are genetically related to one another, we also conducted an identical analysis on a subset of unrelated subjects, hypothesizing that these subjects may be more distinct from one another in their temporal variability profiles. From the HCP 100 Unrelated Subjects release, we used 87 subjects who passed the head-motion threshold and had FIX-corrected data available. These subjects indeed showed higher ID rates, reaching 88.5% for SampEn and 93% for fALFF based on profiles with 90 ROIs. For these subjects, network-level performances were also better than those based on 410 subjects for both the SampEn comparisoxns and the fALFF comparisons. Results for SampEn are shown in Fig. 5.

Figure 5 .

Between-subject differentiation of SampEn for 87 unrelated subjects, with ID rates based on 90 ROIs (b) or 14 core RSNs (c). Panel (a) shows the pairwise similarity (Pearson correlation) between profiles of different subjects across two different sessions. Here, the average of profiles across the two scans acquired within the first session (REST1) was compared to the average of those acquired in the second session (REST2).

Linking fMRI Temporal Signatures with Behavioral Measures: CCA Analysis

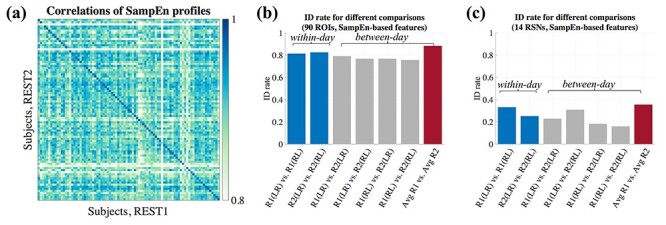
Since SampEn and fALFF may indeed carry reliable inter-individual signatures, we further investigate their ability to characterize individual behavioral phenotypes. Here, we apply Canonical Correlation Analysis (CCA) to examine the relationship between SampEn- and fALFF-based profiles (here, averaged over all 4 scans) and 15 selected behavioral/self-report measures available in the HCP (see Methods). CCA is a widely used method for investigating the underlying relationships between two sets of variables, seeking to find linear combinations of two sources of data (“modes”) that maximize the correlation (r) between them. Given the similarity between fALFF and SampEn, we only report the results based on SampEn in this section, and the fALFF-based results are reported in SI (Supplementary Fig S3). Prior to CCA, we applied Principal Component Analysis (PCA) to reduce the dimensionality of data (Smith et al. 2015), where the number of selected PCA components is based on preserving 75% of the variance in both sets of variables. As shown in Fig. 6a, the first mode generated a significant r value (r   0.44, P = 0.003; permutation testing, 5000 iterations). We projected the first mode back to the original brain and behavior space to visualize the contributions of each ROI and behavioral measure (Fig. 6c,d). One observation is that some regions, such as those falling within Ventral Default Mode Network (DMN) and Dorsal Anterior Salience Network, have high canonical coefficients, as do Dexterity and Relational Processing in behavioral measure space, indicating these ROIs and measures strongly contribute to the first CCA mode. Note that the way we projected the first behavioral measure mode back to original space was to multiply the loadings of PCA, applied to behavioral measures matrix prior to CCA, with the corresponding CCA coefficients. Therefore, the final result included negative values, which we call “negative contribution”.

Figure 6 .

Canonical correlation analysis indicates a multivariate association between SampEn and behavioral traits. (a) The first CCA mode reveals significant relationship between brain canonical variate and behavioral variate (dash line indicates the unity line—perfect fitting). (b) Split-halves validation: the canonical coefficients of the first mode were calculated on the first half of the subjects (205 subjects) as a training set, and applied to the remaining 205 subjects as a testing set. The panel indicates the resulting brain-behavior mode on testing set. (c) The projection of first brain mode back to original space, indicating different contribution of ROIs to the mode. (d) The first behavioral measure mode projected back to original space.

To further investigate the predictive power of CCA, we also examined the extent to which these canonical coefficients produced a significant brain-behavior mode in an independent sample of participants. Here, the first half of the subjects (training set) was used to calculate the canonical coefficients, which were then applied to the second half (test set) (Helmer et al. 2020). The first mode of brain-behavior correlation on the test set, using those predetermined CCA coefficients, is shown in Fig. 6b, where r  0.22, P = 0.002. In addition, since the 410 subjects may include twins/siblings, we also repeated the split-halves validation after randomly selecting one subject from any set of twins or siblings. This analysis yielded positive correlations (Supplementary Fig. S4), though they did not reach significance in this sample (P = 0.056 for SampEn, P = 0.2 for fALFF; see Discussion for further details).

Finally, we note that sleep quality measure is not strictly a measure of cognition/behavior, and it is also a self-report rather than an objective measure. Given that sleep quality represents the largest load in the behavioral mode (Fig. 6d), we also carried out experiments after removing sleep quality from the CCA analysis. As shown in Supplementary Fig S5, the correlation values of the first mode decreased slightly, although these were still significant. We discuss this point in detail in the Discussion.

Correlations of Regional Temporal Features with Behavioral Measures

We then more closely investigated the links between both SampEn- and fALFF-based features and behavioral traits in individual brain regions. To do this, we calculated one (410 subjects  90 regions) matrix for SampEn and one matrix for fALFF features, where we averaged over all four scans. We then correlated the columns of each matrix against the columns of a 410  15 matrix of cognitive measures, thereby generating two correlation matrices that capture the association between each ROI and each behavioral measure. Here, we use (1-fALFF) instead of fALFF to facilitate visual comparison with SampEn, due to their inverse relationship. As shown in Fig. 7, SampEn– and fALFF–behavior correlations are also similar to each other, which is consistent with their strong relationship (Fig. 3). Some of the behavioral measures, such as Fluid Intelligence, tend to anti-correlate with the temporal complexity across a large number of brain regions in both sessions and for both SampEn and fALFF profiles, while some other measures, such as Processing Speed, showed more positive correlations with the features in multiple regions. Finally, we note that although the individual entries of these matrices may not be significant if corrected for multiple comparisons, this analysis was conducted to examine the qualitative patterns and their similarities across runs.

Figure 7 .

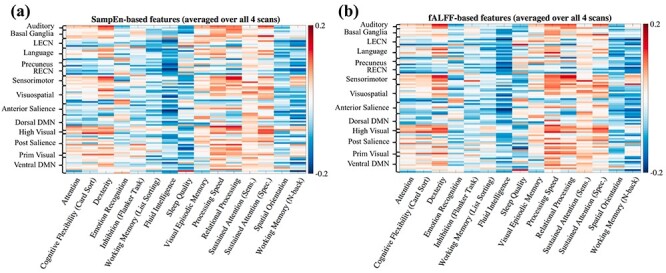
Correlations between regional temporal complexity features and individual cognitive measures. For all panels, color of the (i,j) element indicates the correlation between the SampEn- or fALFF-based features in the ith ROI and the jth cognitive measure, taken across 410 subjects. Both types of features were averaged over all four scans.

Dependence of Temporal Complexity on ROI Size and Data Processing Methods

While SampEn and fALFF were found to be consistent over different fMRI sessions, we also observed strong global trends wherein certain regions tended to have consistently high or low complexity measures across all subjects (Fig. 1). We hypothesized that one factor may relate to the size of the ROI (number of voxels it contains), where larger ROIs may have smaller SampEn, that is, larger fALFF, since averaging over a larger spatial extent tends to result in smoother time courses. The first row in Fig. 8 indeed points to a general anti-correlated relationship between the size of each ROI and the SampEn (where the latter is averaged over all subjects and within the two scans acquired within REST1 and REST2, respectively), and the second row reveals a positive correlation between fALFF and ROI size. However, we observe a large spread of values for both SampEn and fALFF for ROIs with small numbers of voxels. For each panel in Fig. 8, Spearman (rank) correlations of ROI size with each subject’s brain features in 90 ROIs (averaged across four scans), and their associated P-values, were as follows: (r, P): (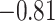, 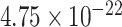) for SampEn REST1, (−0.81, 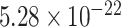) for SampEn REST2, (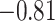, 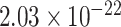) for fALFF REST1, (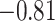, 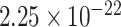) for fALFF REST2. The sign of Spearman correlation values for fALFF was inverted to maintain consistency between SampEn and fALFF. However, while there is a strong relationship between ROI size and SampEn/fALFF, the successful discrimination of individual subjects (Figs. 4 and 5) suggests that there are important subject-to-subject differences.

Figure 8 .

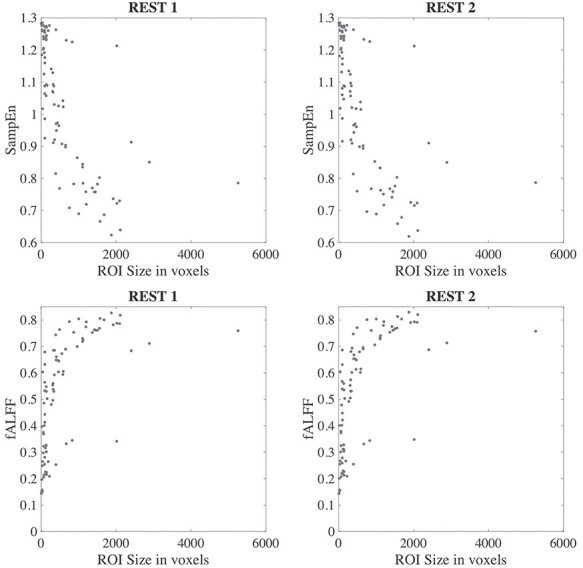
Relationship between SampEn and fALFF versus ROI size, for SampEn (top row) and fALFF (bottom row).

Nonetheless, this result motivates examining an alternate way of calculating SampEn or fALFF profiles. Specifically, rather than calculating SampEn or fALFF on time courses that had been averaged within an ROI, one could first calculate SampEn or fALFF within each individual voxel, and then average over the voxels contained within each ROI. We tested this alternate procedure in an 87-subject subset of the 100 Unrelated Subjects release (Van Essen et al. 2012; Van Essen et al. 2013). Consistent with the above results, this procedure was found to yield consistent temporal complexity values across scans (Supplementary Fig. S6) as well as high identification rates (Supplementary Fig. S7), comparable with the results of Fig. 5. This result was calculated using a different preprocessing pipeline (HCP minimally preprocessed data (Glasser et al. 2013), followed by removal of linear and quadratic trends and band-pass filtering in the 0.01–0.5 Hz range), suggesting the relative insensitivity of the main results to processing methodology.

Identification Rate Associated with Different fALFF/ALFF Frequency Bands

As shown in Supplementary Fig. 8a, fALFF yielded different ID rates across different frequency bands. Specifically, among the higher frequency bands considered, the 0.223–0.607 Hz band had the strongest identification power. This may be explained, in part, by the fact that the fractional power in this wide band conveys nearly the same information as original fALFF band (i.e., is complementary to the original band of 0.01–0.1 Hz). Due to this ambiguity in interpretation when using the (fALFF) metric, we repeated the analysis for ALFF. As shown in Supplementary Fig S8b, the best-performing bands were in the low frequencies (spanning 0.012–0.082 Hz; close to the low-frequency band used in our original analysis).

Identification Rate for Alternate Brain Temporal Features

Several studies have shown that the fALFF has lower test–retest reliability than ALFF (Somandepalli et al. 2015), and that PerAF has similar intra-scanner test–retest reliability but better inter-scanner reliability than ALFF (Zhao et al. 2018). Motivated by these studies, we conducted a fingerprinting analysis for these two additional features to complement our above analysis of SampEn and fALFF. Further, as other publications have suggested that global standardization (i.e., subtracting and dividing by the spatial mean of these values) may enhance test–retest reliability of certain metrics (Yan et al. 2013) we also carried out a corresponding analysis with standardization.

As shown in Fig. 9, PerAF-based brain features generated higher ID rates than those for ALFF-based features, which is consistent with to the claim that perAF has better inter-scanner reliability than ALFF. However, overall, both PerAF- and ALFF-based features did not yield identification power as high as that of fALFF-based features (Fig. 9c,d). The corresponding ICC analyses indicate that PerAF is more stable than ALFF (see Supplementary Fig. S10). Finally, although standardized features generated almost same identification power as for the non-standardized features, the corresponding ICC was generally higher for standardized features (Supplementary Fig. S10).

Figure 9 .

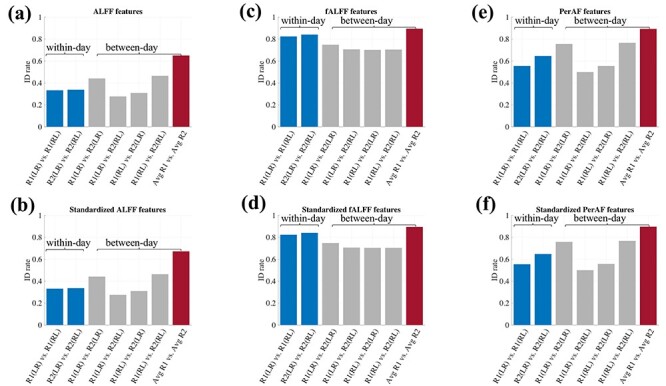
Inter-individual identification analysis for ALFF and PerAF features, with and without global standardization. The results for fALFF-based features are shown in panels (c) and (d) for comparison.

Discussion

Overall, the present results indicate that fMRI temporal features—here, captured by SampEn and fALFF—are stable across sessions and days, uniquely distinguish between individuals with high accuracy, and exhibit a significant relationship to behavioral measures. This study extends prior studies on the neurobiological relevance of fMRI temporal complexity and variability features, suggesting that regional fMRI signal variability may provide stable markers of individual differences and behavior in healthy young adults. It also extends the growing literature on the search for sensitive neuro-markers of individual brain function, which to date has focused most heavily on pairwise functional connectivity (e.g., Miranda-Dominguez et al. 2014; Finn et al. 2015; Gordon et al. 2017; Dubois et al. 2018; Jalbrzikowski et al. 2020). Another main observation of this work is that sample entropy (nonlinear complexity) and fALFF (a spectral measure), which are often considered separately in the fMRI literature, have a close relationship with one another in HCP fMRI data under certain parameter ranges examined here, which is consistent with a recent study (Song et al. 2019a) as well as computational simulations and observations in electrophysiological data (Kosciessa et al. 2020). This observation helps to bridge between studies that have considered either of the two measures (further discussed below).

We observed that both SampEn and fALFF features exhibit high stability across different resting-state fMRI scans (Fig. 1), which is further corroborated by the fact that their correlations with behavioral measures were also reproducible across different runs (Fig. 7). The consistency of SampEn over scans also held with a different choice of embedding dimension (m = 5;  Supplementary Fig. S1). Along similar lines, it was recently demonstrated that regional brain complexity, captured by multiscale entropy, was reproducible across individuals over four rs-fMRI runs (Omidvarnia et al. 2021). Our findings of network-based differences in entropy are also consistent with those of (McDonough and Nashiro 2014); including high temporal complexity in default model network and lower complexity in high-visual networks (Supplementary Fig. S2).

Motivated by the question of which brain areas are more consistent than others, we used ICC to quantify the within-subject consistency of SampEn and fALFF for each ROI (Fig. 2). We found that subcortical brain regions have lower ICC compared to cortical regions, and that some of the cortical regions with the highest ICC are small areas in parietal lobe. We also calculated the ICC within 14 functional networks, finding values of 0.57–0.71 for SampEn, and 0.56–0.68 for fALFF. Although the mean values of ICC across 14 RSNs are higher than those across 90 ROIs, it appears that stronger consistency (higher ICC) does not always manifest in better differentiation between subjects, as the ID rate dropped drastically for both SampEn- and fALFF-based brain features (Figs. 4 and 5). These observations motivate future studies on resolving why cortical brain regions (even small ones) have higher ICC in comparison to subcortical regions.

Aside from their consistency across scans, we further observed that these temporal features appeared to be unique across individuals, such that they could successfully identify a given subject out of 409 other subjects. Note that compared to the widely used connectome-based fingerprinting (Finn et al. 2015; Amico and Goni 2018), the regional temporal features examined here present a much more concise representation for each subject (a 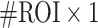vector, as compared to the upper-triangle of a #ROI 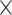#ROI correlation matrix), yet still generate high ID rates (~90% for fALFF, in the case where the average of the two REST1 scans is compared to the average of the two REST2 scans). However, further compression of the features along pre-defined network boundaries (to a 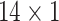vector) led to much lower performance, suggesting that this within-network averaging removed features that were necessary to capture individuals’ physiological signatures. We also note that the functional connectivity features (Ma et al. 2013; Plitt et al. 2015; Jia et al. 2017; Cui and Gong 2018; Yoo et al. 2018; Mu et al. 2020; Wang et al. 2020) more commonly used in the literature are calculated based on pairwise correlations of individual brain regions’ time series, from which regional temporal complexity features are built. Therefore, our study may pave the way for future investigations of how regional times series-based fingerprinting relates to connectivity-based fingerprinting.

The empirical results from this study and others have indicated a close qualitative relationship between SampEn and fALFF, and it makes intuitive sense that spectral properties and entropy are related. However, the link between fALFF and SampEn, as well as the performance of these metrics for individual identification, may be dependent on parameters of the acquisition as well as the choice of frequency band. HCP data used a fast TR (0.72 s), which is not typical of most datasets. Therefore, we probed the impact of different fMRI acquisition parameters by under-sampling the time series in each voxel by factor of 3 (i.e., TR = 2.16 s), and then re-analyzed the fingerprinting results and ICC maps. There are several key observations for this new analysis (Supplementary Figs S12–S14). First, compared to left panel in Fig. 3, Supplementary Fig S12 shows that SampEn and fALFF measures do not have as clean a relationship at this new sampling rate. This effect may stem from the fact that SampEn depends on a parameter m that governs the length of the sequence (in samples) used for pattern-matching. When m is kept fixed but the underlying sampling rate changes, a sequence of length m samples now captures a different time scale of the data. However, fALFF—which quantifies the fractional low frequency content of a signal—should be relatively stable (over a range of sampling rates that avoid aliasing the power spectrum of the BOLD hemodynamic response or shifting aliased cardiac and respiratory peaks in or out of the low-frequency band). Consistent with this observation, the corresponding identification rate (Supplementary Fig. S13) and ICC (Supplementary Fig. S14) analysis demonstrated that fALFF-based brain features were more stable than SampEn after undersampling the time series. In addition to the sampling rate, we also examined the dependence of fALFF across different frequency bands (Results section: “Identification rate associated with different fALFF/ALFF frequency bands”). The reliability of these features was indeed affected by the choice of frequency band (Supplementary Fig S8a), motivating the future analysis to investigate if there is a “golden frequency range” for achieving the best individual identifiability or test–retest reliability.

In the HCP dataset, resting-state runs that differed by phase-encoding direction (LR and RL) were acquired, which also motivates the question of whether SampEn or fALFF patterns could differ across these phase-encoding directions. First, we note that our analysis used 90 regions of interest derived from a functional atlas spanning core resting-state networks rather than the whole brain, and that most of these atlas regions did not cover areas that tend to be prominently affected by difference in RL/LR phase encoding direction. Difference maps (calculated within each parcel) did, however, indicate some differences between RL and LR (Supplementary Fig. S11). Therefore, together with the ICC maps (Fig. 2), we might conclude that while both SampEn and fALFF generated reproducible patterns on average, the reproducibility was higher in some ROIs than others and may be impacted by acquisition parameters.

All of the brain complexity features involved in this study can be employed either with or without standardization, and previous studies have suggested that test–retest reliability based on standardized features would be higher. Supplementary Fig S10 and S15 and Fig. 8 indicate that, compared to the fingerprinting results without standardization, the standardized brain complexity features did not seem to improve the ID rates for most comparisons, but did increase the test–retest reliability, which was supported by the corresponding ICC analysis.

The CCA analysis employed in this study revealed a relationship between brain temporal features and behavioral measures. Our CCA analysis was inspired by the study of Smith et al. (Smith et al. 2015), which investigated the relationship, in a holistic manner, between subjects’ functional connectivity and behavioral and demographic measures. This link between temporal complexity features and behavioral measures lends further support to the notion that resting-state complexity may indeed represent neurobiologically relevant properties of individual subjects. Further, the split-halves validation (Fig. 6b) provides additional evidence that the relationship is generalizable, and indicates the extent to which CCA was overfitted in-sample (Fig. 6a). It is known that association strengths using metrics like CCA can be over-estimated (Helmer et al. 2020), even by permutation testing (Winkler et al. 2020), motivating us to carry out the additional out-of-sample validation. We also conducted an extra analysis for the split-halves validation after removal of twins and siblings from the original 410 subjects. Although it is a limitation that our analysis is not significant for out-of-sample testing when siblings are removed, this result may also suggest that SampEn and fALFF metrics are capturing family structure, since including twins/sibling relationships boosted this result. Further investigation of the relationship between SampEn or fALFF and family structure may be an interesting avenue of future work.

One of the strongest weights in the CCA was sleep quality, and removing the sleep quality from original CCA analysis generated lower correlation in the first mode. This finding is consistent with previous literature suggesting that sleep and brain complexity are closely related. For example, the descent into sleep has been shown to be accompanied by a dynamic increase in the amplitude and low-frequency content of fMRI signals (Horovitz et al. 2008; Larson-Prior et al. 2009). If the sleep quality index is inversely correlated with the drowsiness level of a subject during the fMRI scan, then one possibility is that the relationships with SampEn and fALFF is capturing state-related differences in brain activity.

In addition, this CCA result also indicates that the temporal complexity of resting-state networks may be functionally relevant across multiple demographic factors and assessments. Projecting the first CCA mode back to the original brain and behavior space yielded several results that resemble previous findings: for example, relational processing and working memory are typically associated with the frontal and superior parietal cortices (Barch et al. 2013), and these behavioral and brain regions all had strong negative canonical coefficients. Dexterity was another strongly negative canonical coefficient, which may relate to the large negative coefficients in motor-related brain areas such as the precentral and postcentral gyri or the right caudate (Kuhtz-Buschbeck et al. 2001). While these previous studies examined BOLD activity during these behaviors, the present study suggests that the resting-state temporal complexity of these regions may also be linked to the performance in these tasks. Yet, the multivariate nature of this analysis limits the conclusions we can draw about individual brain regions or behaviors, and so we hope this analysis may motivate future studies to examine these relationships more comprehensively.

Probing the relationships between dynamic brain features and behavioral or cognitive measures has been of recent interest to the fMRI community (Takahashi 2013; Finn et al. 2015; Cohen 2018; Qian et al. 2018; Wang et al. 2018; Kashyap et al. 2019; Liegeois et al. 2019; Lin et al. 2019; Gao et al. 2020), and our study may motivate further studies that generate stronger predictive power and for a broader range of cognitive measures. As the current behavioral measures in HCP were only collected only once, we also expect that future studies may examine the stability of these measures over time, and in relation to the stability of fMRI temporal complexity measurements.

As might be expected, SampEn and fALFF were found to relate to the number of voxels in each ROI. The anti-correlations between SampEn and ROI size likely stems from the increased smoothing that arises when averaging larger numbers of voxels, resulting in lower entropy values. Similarly, smoother signals generate a higher proportion of low-frequency content, producing lower SampEn (and higher fALFF) values, leading to positive correlations between fALFF and ROI size. Yet, while ROI size may have led to strong commonalities in SampEn and fALFF across subjects, as evident in both Fig. 1 and Fig. 7, we found that individual subjects also maintained unique enough profiles to enable fingerprinting with a high degree of accuracy (Figs 4 and 5). Furthermore, calculating SampEn and fALFF on a voxel-wise basis within each ROI, rather than on the average time course, also led to high ID rate and across-scan consistency (Supplementary Fig. S7).

Recent publications have emphasized the importance of understanding the reliability and validity in fMRI data analysis (Zuo et al. 2019; Bridgeford et al. 2020). In present study, the features examined in this work (fALFF, SampEn) showed both high ID rates and high ICC using the 90-ROI parcellation; further, Supplementary Fig. S13 shows that undersampling the fMRI time course leads to a decrease in both the ID rate (“validity”) and ICC (“reliability”) of SampEn (but not fALFF). Interestingly, however, we also observed that high ICC did not always imply a higher fingerprinting accuracy: our 14-network-level analysis showed higher ICC than with the 90 ROIs, but lower fingerprinting accuracy (Fig. 4c,f). This observation may demonstrate that, while high fingerprinting may come with higher ICC, perhaps the converse is not true. The limitations of fingerprinting and ICC for assessing validity and reliability should also be considered (Bridgeford et al. 2020).

While the present work does not address the underpinnings of inter-individual differences in temporal profiles, other potential factors that may shape individual-subject differences in SampEn/fALFF include subject-specific anatomical boundaries, low-frequency cardiorespiratory activity, vascular variations, and signal-to-noise ratio. Another limitation of our study lies in the limited power of the current temporal complexity features for predicting behavioral measures, as out-of-sample prediction rates were significant but of moderate effect size, and just below significance when twins/siblings were not included. It is possible that greater accuracy could be achieved using different brain atlases. We expect that further information about brain function, based on temporal complexity and variability, may be extracted in future studies.

Funding

The National Institute of Neurological Disorders and Stroke of the National Institutes of Health (grant numbers R01 NS112252 (to C.C.), R01 NS108445 (to V.L.M.), and R01 NS11030 (to V.L.M.)).