Objective pain stimulation intensity and pain sensation assessment using machine learning classification and regression based on electrodermal activity

Abstract

An objective measure of pain remains an unmet need of people with chronic pain, estimated to be 1/3 of the adult population in the United States. The current gold standard to quantify pain is highly subjective, based upon self-reporting with numerical or visual analog scale (VAS). This subjectivity complicates pain management and exacerbates the epidemic of opioid abuse. We have tested classification and regression machine learning models to objectively estimate pain sensation in healthy subjects using electrodermal activity (EDA). Twenty-three volunteers underwent pain stimulation using thermal grills. Three different “pain stimulation intensities” were induced for each subject, who reported the “pain sensation” right after each stimulus using a VAS (0–10). EDA data were collected throughout the experiment. For machine learning, we computed validated features of EDA based on time-domain decomposition, spectral analysis, and differential features. Models for estimation of pain stimulation intensity and pain sensation achieved maximum macroaveraged geometric mean scores of 69.7% and 69.2%, respectively, when three classes were considered (“No,” “Low,” and “High”). Regression of levels of stimulation intensity and pain sensation achieved R² values of 0.357 and 0.47, respectively. Overall, the high variance and inconsistency of VAS scores led to lower performance of pain sensation classification, but regression was better for pain sensation than stimulation intensity. Our results provide that three levels of pain can be quantified with good accuracy and physiological evidence that sympathetic responses recorded by EDA are more correlated to the applied stimuli’s intensity than to the pain sensation reported by the subject.

INTRODUCTION

Pain is an unpleasant sensory and emotional experience associated with actual or potential tissue damage (1). Currently, clinicians and researchers use self-rating tools based on either numerical or visual scales as the gold standard for pain sensation assessment (2). These methods work for alert and cooperative patients; however, they are highly subjective in nature. An objective and accurate assessment of pain sensation level is of increased interest, as it would facilitate the delivery of appropriate doses of medications especially for those cases when the self-reported pain intensity cannot be either communicated or trusted. In our attempt to overcome this limitation, we tested the feasibility of an objective biomarker of pain sensation based on electrodermal activity (EDA).

Chronic pain is considered a disease (3). It affects one in three adults in the United States (4, 5) and represents a huge economic burden, costing $560–$635 billion annually, which is more than heart disease, cancer, and diabetes (6). Treatment for chronic pain is often conducted by prescribing opioids; however, the abuse of opioid prescriptions has become a national epidemic as they are highly addictive (7, 8), with a cost of about $500 billion per year including medical, economic, social, and criminal costs (9). A reliable biomarker of pain that does not rely on a subjective report for pain assessment will enable the objective quantification of pain levels and detection of attenuation (or not) of pain after treatment. The development of an effective treatment for chronic pain has been hampered by the lack of such an objective measure.

The autonomic nervous system (ANS) is the primary pathway for brain-gut communication and controls the body’s emotional and psychological states (10). This makes it particularly relevant to pain, which also has a strong emotional component. The ANS includes the sympathetic and parasympathetic nervous systems, and chronic pain reportedly correlates with an unchecked predominance of sympathetic and desensitized parasympathetic activity (11). Thus, assessing the dynamics of the ANS, especially the sympathetic branch, is a promising target for developing sensitive and robust biomarkers for chronic pain. Electrodermal activity (EDA) is a marker of sympathetic autonomic control (12). The EDA is a simple measure and has shown to be highly sensitive to sympathetic arousal (13–15). EDA has been recently used to assess subjects’ response to pain stimulation (12, 16–21).

We hypothesize that indices that exhibit differences in response to different pain stimulation intensities can be used to develop a quantitative pain diagnosis via a machine learning model. In this study, we collected EDA recordings from healthy volunteers undergoing pain-evoking stimuli delivered to their skin but without any tissue damage using thermal grills and documented subject-reported pain scores. We used statistical analysis and machine learning algorithms to evaluate the feasibility of indices of EDA to estimate both the pain sensation reported by subjects and the pain stimulation intensity delivered using thermal grills.

MATERIALS AND METHODS

Subjects

All human study protocols were approved by the University of Connecticut Institutional Review Board. Twenty-three healthy volunteers (11 males and 12 females) of ages ranging from 19 to 34 yr old (24.5 ± 4.8; means ± SD) were enrolled in this study. All volunteers provided written informed consent to participate in the study. Participants were asked to avoid caffeine and alcohol during the 24 h preceding the test and instructed to fast for at least 3 h before the test. The study was conducted in a quiet and dimly lit room (ambient temperature, 26–27°C) to avoid any external stimuli. Throughout the stimulus protocols, EDA data were collected from each subject’s left-hand fingers and data were processed post hoc in both time and frequency domains to assess and quantify different levels of sympathetic activities.

Devices

A galvanic skin response device was used to collect EDA (FE116, ADInstruments) using reusable stainless-steel electrodes placed on subjects’ left index and middle fingers. The skin of the subject was cleaned with alcohol before placing the EDA electrodes. The EDA signals were recorded at 500 Hz.

Protocol

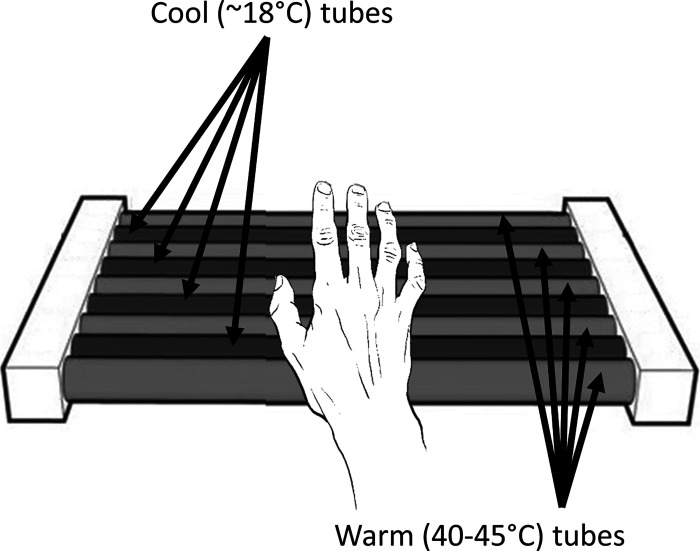
To ensure hemodynamic stabilization, subjects were asked to stay still before the test, resting in a chair for 5 min. Stimulation of the hand’s glabrous skin was delivered by a set of three customized thermal grills (Fig. 1), labeled TG1, TG2, and TG3. Each thermal grill consists of interlaced tubes that are set at a warm (40–50°C) or cool (18°C) temperature. By creating an illusion of pain in the brain by presenting the warm and cold stimuli collectively (22–25), the thermal grill provokes a sensation of pain commensurate with higher temperatures in the warm tubes without causing tissue injury (18). We perfused the cool tubes of all grills with ice water flowing through a controlled coil to maintain a temperature of 18°C in the grill bars and the warm tubes with water from a temperature-controlled water bath. For each subject, we adjusted the temperature in the warm tubing in TG2 until the subject reported a pain score of 5 to 6 out of 10 on visual analog scale (VAS). This temperature was labeled as Tm. The temperature of water in the warm tubing of TG1 and TG3 was adjusted to Tm − 2°C and Tm + 2°C, respectively. Thermal grills (TGs) TG1, TG2, and TG3 were used to deliver “Level 1,” “Level 2,” and “Level 3” pain stimulation intensities, respectively (Table 1). For safety reasons, we confirmed that the temperature of all tubes was always below 50°C. Each individual stimulus consisted of asking the subject to put their right hand on a specific TG and maintain it there for as long as the subject could bear the pain (<10 s). We generated a train of 21 stimuli, consisting of 7 stimuli for each TG, with randomized sequence and interstimulus interval of 1 min.

Figure 1.

Thermal grill used to induce heat sensation pain on each subject’s right hand; the left hand was used to collect EDA data. EDA, electrodermal activity. n = 23 subjects.

Table 1.

Categorization for pain level and VAS

	Pain Stimulation Intensity
	Level 0 (Pre-TG)	Level 1 (TG1)	Level 2 (TG2)	Level 3 (TG3)
Three-class classification	No	Low		High
Four-class classification	No	Low	Medium	High

	Pain Sensation Level (VAS)
	0 (Pre-TG)	1–3	4–6	7–10
Three-class classification	No	Low		High
Four-class classification	No	Low	Medium	High

TG, thermal grill stimulation; VAS, visual analog scale.

Subjects reported pain levels using a VAS ranging from 0 (no pain) to 10 (worst pain possible) immediately after each stimulus (18). For the classification of pain sensation, we defined the following ranges based on VAS scores: 0 ≤ VAS < 1 as “No pain”; 1 ≤ VAS < 4 as “Low”; 4 ≤ VAS ≤ 6 as “Medium”; and 6 ≤ VAS ≤ 10 as “High.”

EDA Signal Processing

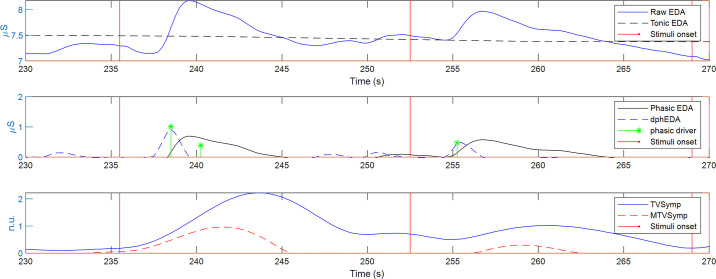
The raw EDA signals were decomposed into tonic and phasic components (13) as indicated in Fig. 2 (top and middle). The tonic component reflects the slow transients in the skin conductance amplitude. The phasic component is the rapid transient visible in the raw EDA signal, i.e., the skin conductance responses (SCRs) that are caused by the rapid reaction of the sympathetic nervous system to a certain external or internal triggering event (26). Several methods have been implemented for obtaining tonic EDA and phasic EDA (14), including the convex optimization approach (cvxEDA) (27) and the sparse deconvolution approach (sparsEDA) (28). cvxEDA and sparsEDA also provide an estimation of the phasic drivers that elicit the individual SCR. Note that in Fig. 2, sparsEDA was used to obtain the tonic EDA, phasic EDA, and the estimation of the phasic drivers for illustration purposes.

Figure 2.

Decomposition of EDA. Tonic EDA, phasic EDA, phasic driver, dphEDA, TVSymp, and MTVSymp. dphEDA, derivative of the phasic component of electrodermal activity; EDA, electrodermal activity; MTVSymp, modified TVSymp; TVSymp, time-varying index of electrodermal activity.

From the phasic EDA obtained from each approach, we computed the derivative of the phasic component of EDA (dphEDA) as an index of pain (Fig. 2, middle), which has been reported as an EDA feature that is sensitive to pain (29). The dphEDA for each of the five approaches was computed by using the 5-point stencil central finite differences equation (30), for each sample n, as follows:

$$\mathrm{d}\mathrm{p}\mathrm{h}\mathrm{E}\mathrm{D}\mathrm{A}\mathrm{ }\left(n\right)=\frac{P\left(n-2\right)\mathrm{ }-\mathrm{ }8·P\left(n-1\right)\mathrm{ }+\mathrm{ }8·P\left(n+1\right)\mathrm{ }-\mathrm{ }P(n+2)}{12\mathrm{ }·(1/fs)}$$ (1)

where f_s is the sampling frequency (4 Hz) and P is the phasic component of EDA.

As illustrated by the red trace in Fig. 2 (bottom), we implemented a novel EDA index in this study, the time-varying index of EDA (TVSymp) (31), which has been shown by our previous studies to be more sensitive and consistent than time-domain measures of EDA derived from counting SCRs and computing the mean value (level) of the signal for a given period of time (15). We computed the TVSymp using variable frequency complex demodulation, an algorithm that we developed in characterizing dynamics of biosignals (32). To optimize the calculation of TVSymp, we extracted the frequency powers from 0.08 to 0.24 Hz from the EDA signal, following a protocol we recently reported (31). Amplitudes of the time-varying components in this band are summed together to obtain an estimated reconstruction of the EDA signal while suppressing other frequencies that are not part of the sympathetic responses. The reconstructed signal is then univarianced and the instantaneous amplitudes of the resulting signal are computed using the Hilbert transform (33). The modified TVSymp (MTVSymp) was obtained by computing the difference in value of TVSymp with respect to the mean value of TVSymp of the previous 5-s window. Negative values of MTVSymp were set to 0. MTVSymp enhances the changes in the sensitivity of the TVSymp signal to pain, by removing other possible sources of arousal (e.g., underlying stress) (29).

The mean levels of the phasic EDA, tonic EDA, dphEDA, TVSymp, and MTVSymp in a time window of 5 s were measured before and after each stimulus. The subject-reported pain sensation was considered to be pain sensation level 0, “no pain,” for prestimulus signal segments. The prestimulus values are meant to capture any changes in EDA, slow and fast (SCRs), expected to be spontaneously elicited by other stimuli-like anticipation and underlying stress. Incorporating these changes in the EDA not produced by pain act in the model as a control response to improve the accuracy of pain assessment. The signal segments right after each stimulus were associated to the VAS score reported by the subject.

Statistics

Normality of the VAS and measures of EDA were tested for the different pain stimulation intensities and pain sensation levels using the Kolmogorov–Smirnov test (34–36). Repeated-measures analysis was performed to test the difference in the VAS and measures of the EDA at different stimulation intensities and sensation levels. In normally distributed data, two-way analysis of variance (ANOVA) was performed to test for significant differences between measures. If nonnormality was found in a specific index, we used the Dunn’s test (37). The Bonferroni method was used for correction of multiple comparisons.

Machine Learning Modeling

We used classification and regression machine learning algorithms to evaluate the feasibility of indices of EDA to estimate both the pain sensation reported by subjects and the pain stimulation intensity delivered using thermal grills. In machine learning, classification algorithms are used when the outputs are limited to certain categorical values (classes), whereas regression algorithms are used when the outputs to be predicted are continuous and may have a numerical value within a range. For instance, a classification algorithm that detects a given disease based on physiological parameters, the input would be the set of physiological features, and the output would be the diagnosis of each subject (positive or negative) (38).

In general, in regression algorithms, the estimation target (dependent variable) is modeled a function of the independent variables called the regression function. Many techniques for carrying out regression analysis have been developed. The most common form of regression is the linear regression, where the dependent variable is specified as a linear combination of the independent variables and the best fit is defined according to a mathematical criterion such as least squares. Linear regression is considered parametric, as the regression function is defined in terms of a finite number of unknown parameters that are estimated from the input data. In contrast, techniques that allow the regression function to lie in a specified set of functions (which may be infinite-dimensional) are referred as nonparametric regression. Nonparametric regression includes regression trees, support vector regression, neural networks, among others.

Both pain stimulation intensity and pain sensation based on VAS scores are ordinal targets and integers, respectively. If the levels are defined as “No pain,” “Low,” “Medium,” and “High,” the labels can be considered classes and the estimation is a classification problem. If levels are defined as ordinal numerical targets, that is, “No pain” corresponding to 0, “Low” corresponding to 1, “Medium” corresponding to 2, and “High” corresponding to 3, the estimation can be seen as a regression problem. As seen, our prediction can be approached as an ordinal regression or classification problem. Therefore, to study objective pain estimation in more detail, we tested both approaches machine learning classification and regression.

Classification.

First, to test the feasibility of the detection of pain stimulation intensity and pain sensation with a resolution of 3 and 4 levels, we performed classification with two different target associations: 1) three-class (“No,” “Low,” and “High”) and 2) four-class (“No,” “Low,” “Medium,” and “High”), as shown in Table 1. All segments before each stimulus were set as class 1 (class “No”). For three-level classification, segments from the low and medium pain-inducing thermal grills or with VAS 1–6 were considered as class 2 (low pain), and from the high pain thermal grill or with VAS ≥ 7 was set as class 3 (high pain). For the four-class approach, segments from the low pain thermal grill or with VAS 1–3 were set as class 2 (low pain), from the medium pain thermal grill or with VAS 4–6 as class 3 (medium pain), and from the high pain thermal grill or with VAS ≥ 7 as class 4 (high pain).

We tested four machine learning classifiers using the leave-one-subject-out cross-validation strategy, including support vector machine with linear kernel (SVML), support vector machine with radial basis function kernel (SVMR), multilayer perceptron (MLP), and random forest (RF). We selected the maximum and mean values of the following EDA features: phasic, TVSymp, MTVSymp, and dPhEDA (29). Random forest classifiers were configured with 100 as the number of estimators and Gini criterion. MLP classifiers were set with a rectified linear unit activation function, Adam optimizer (39), and 0.001 for the learning rate. Moreover, parameters C of SVML, C and gamma of SVMR, and hidden unit and layer structures of MLP were selected using a grid-search cross-validation technique with group fourfold cross validation. C parameters for SVML and SVMR were chosen among 0.01, 0.1, 1, 10, 100, and 1,000. Gamma parameter for SVMR was selected among 10, 1, 0.1, 0.01, 0.001, and 0.0001. The hidden unit and layer structure were chosen among the three candidates: 1 layer and 100 units, 2 layers and 50 units, and 3 layers and 20 units. Data were normalized with zero mean and unit variance. We applied class weights, as the data set is not balanced. We used Python 3.6 with Scikit-learn library (40).

To evaluate the performance of each classifier, we calculated macroaveraged geometric mean scores, which is a metric that penalizes misclassifications. Each class of geometric mean scores is calculated by the root mean square of the multiplication of sensitivity and specificity. As our data set is not balanced, we averaged each class of geometric mean scores (i.e., macroaveraged), as follows:

$$\mathrm{M}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{d}\mathrm{ }\mathrm{g}\mathrm{e}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{ }\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{ }\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=\frac{{\sum }_i^{N_{class}}\sqrt{\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{t}{\mathrm{y}}_i\mathrm{ }\times \mathrm{ }\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}{\mathrm{y}}_i}}{N_{class}}$$ (2)

Regression.

We also conducted regression for both pain stimulation intensity and pain sensation. We used the same designations of the four-class classification approach described in Table 1 to have the scales with the same number of elements, which is necessary for a fair comparison of different regressors of pain stimulation intensity and pain sensation. We tested several regressors and found that MLP and SVMR outperformed others. We obtained features by computing the maximum and mean values of EDA features: phasic driver, TVSymp, MTVSymp, and dPhEDA (29). We used the same parameters for both SVMR and MLP for classifications. We handled the imbalance of the data set using SVM-Synthetic Minority Oversampling Technique (SMOTE) (41–43). To evaluate the performance of regressors, we calculated three indices: coefficient of determination (R²), macroaveraged root mean square error (M-RMSE), and macroaveraged mean absolute error (M-MAE). M-RMSE and M-MAE were calculated by averaging RMSE and MAE of each class, as they provide better evaluation for imbalanced ordinal regression datasets (44, 45).

RESULTS

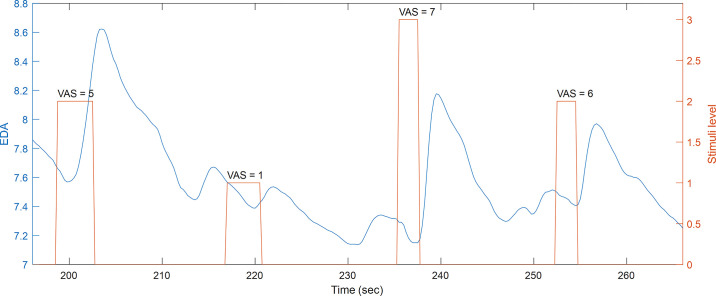
Figure 3 shows a segment of raw EDA data for a subject undergoing pain stimulation using thermal grills. Notice the three stimulation intensities and the VAS reported by the subject after each stimulus. The width of each bar in the stimuli trace represents the time the subject held their right hand to the thermal grill. EDA typically exhibits an SCR right after the onset of the pain stimulus. Nevertheless, other SCRs are also observed before stimuli.

Figure 3.

Segment of raw EDA and stimuli for a given subject. EDA, electrodermal activity.

Statistical Analysis

Tables 2 and 3 include the values for phasic and tonic EDA, dphEDA, phasic driver, TVSymp, and MTVSymp for the different levels of thermal grill stimulation and pain sensation levels reported by the subjects, respectively. Also, the values of VAS for different stimulation intensities and the values of level intensity for the different pain sensation levels are reported in Table 2. Pain stimulation “Level 0” and pain sensation “No” correspond to the segments before stimulation. We observed significant differences in VAS between all stimulation intensity levels in Table 2, and in stimulation level between all pain sensation levels, shown in Table 3. Significant differences are marked as superscript numbers. As for the indices of EDA, tonic EDA did not exhibit significant differences between stimulation intensity levels. The tonic component obtained with cvxEDA exhibited significant differences only between “Medium” and “No pain” sensation levels. All other indices that are associated with the higher-frequency dynamics of EDA (phasic EDA, dphEDA, TVSymp, and MTVSymp) exhibited more differences between levels of stimulation intensity and pain sensation than the tonic component. The indices that exhibited more differences than the others between levels of stimulation intensity were dphEDA from sparsEDA, phasic driver from cvxEDA and sparsEDA, and MTVSymp. None of the indices exhibited significant differences between level 2 and level 3 of stimulation intensity.

Table 2.

Indices for different levels of thermal grill stimulation intensity

	Level 0	Level 1	Level 2	Level 3
VAS	0 ± 0	3.5 ± 1.90	5.9 ± 1.3 0,1	7 ± 1.30,1,2
cvxEDA
Phasic, µS	1.3 ± 2.8	1.4 ± 2.6	1.7 ± 3.60	1.7 ± 2.50,1
Tonic, µS	7.8 ± 8.4	8.1 ± 8.3	8 ± 8.9	7.6 ± 8.2
dphEDA	− 0.066 ± 0.18	0.15 ± 0.250	0.23 ± 0.280	0.29 ± 0.320,1
Phasic driver (a.u.)	2.4 ± 5.2	3.4 ± 3.80	4.4 ± 4.20, 1	5 ± 4.70, 1
sparsEDA
Phasic, µS	0.31 ± 0.97	0.57 ± 2.3	0.77 ± 1.1 0, 1	0.58 ± 1 0
Tonic, µS	8.8 ± 7.3	8.9 ± 7.1	8.8 ± 7.3	8.7 ± 7.4
dphEDA	− 0.082 ± 0.17	0.17 ± 0.520	0.23 ± 0.27 0,1	0.3 ± 0.30,1
Phasic driver (a.u.)	0.094 ± 0.53	0.54 ± 1.60	1 ± 1.6 0,1	1.2 ± 1.60,1
Spectral
TVSymp	0.79 ± 0.62	0.98 ± 0.76	1.3 ± 0.8 0,1	1.4 ± 0.910,1
MTVSymp	0.13 ± 0.18	0.26 ± 0.290	0.34 ± 0.3 0,1	0.39 ± 0.380,1

Superscript numbers denote significant differences to the given levels of stimulation intensity. cvxEDA, convex optimization of electrodermal activity; dphEDA, derivative of the phasic component of electrodermal activity; MTVSymp, modified time-varying index of electrodermal activity; sparsEDA, sparse deconvolution of electrodermal activity; TVSymp, time-varying index of electrodermal activity; VAS, visual analog scale. Repeated-measures analysis using ANOVA or Dunn’s test for normal or non-normal distributed data, respectively.

Table 3.

Indices for different levels of subject pain sensation after thermal grill stimulation based on VAS

	No	Low	Medium	High
Level	0.0085 ± 0.092	1.1 ± 0.340	1.9 ± 0.750,1	2.6 ± 0.530,1,2
cvxEDA
Phasic, µS	1.2 ± 2.8	1.3 ± 2.5	2 ± 3.60	1.2 ± 22
Tonic, µS	7.8 ± 8.4	9.9 ± 9.7	6.8 ± 8.51	8.3 ± 7.6
dphEDA	−0.065 ± 0.18	0.14 ± 0.240	0.22 ± 0.30	0.27 ± 0.30,1
Phasic driver (a.u.)	2.4 ± 5.2	3.3 ± 3.7	4.9 ± 4.70	4 ± 40
sparsEDA
Phasic, µS	0.31 ± 0.96	0.67 ± 3.1	0.66 ± 1.20	0.6 ± 0.89
Tonic, µS	8.8 ± 7.3	11 ± 8.7	8.2 ± 6.7	8.9 ± 7.1
dphEDA	−0.081 ± 0.17	0.19 ± 0.680	0.22 ± 0.270	0.27 ± 0.290
Phasic driver (a.u.)	0.1 ± 0.59	0.57 ± 2.10	0.94 ± 1.60	1.1 ± 1.40,1
Spectral
TVSymp	0.78 ± 0.62	0.88 ± 0.67	1.2 ± 0.890,1	1.4 ± 0.820,1
MTVSymp	0.13 ± 0.18	0.21 ± 0.25	0.33 ± 0.330,1	0.4 ± 0.340,1

“No”: 0 ≤ VAS < 1; “low”: 1 ≤ VAS < 4; “medium”: 4 ≤ VAS < 7; “high”: 7 ≤ VAS ≤ 10. Superscript numbers denote significant differences to the given pain sensation levels. cvxEDA, convex optimization of electrodermal activity; dphEDA, derivative of the phasic component of electrodermal activity; MTVSymp, modified time-varying index of electrodermal activity; sparsEDA, sparse deconvolution of electrodermal activity; TVSymp, time-varying index of electrodermal activity; VAS, visual analog scale. Repeated-measures analysis using ANOVA or Dunn’s test for normal or non-normal distributed data, respectively.

As for the levels of pain sensation (Table 3), the indices that exhibited more differences than the other measures were dphEDA from cvxEDA, phasic driver from sparsEDA, TVSymp, and MTVSymp. dphEDA for cvxEDA and sparsEDA, and phasic driver from sparsEDA were the only indices significantly different between “Low” and “No pain” levels of pain sensation. Similar to the case of the stimulation intensity, none of the indices of EDA exhibited significant differences between “High” and “Medium” levels of pain sensation.

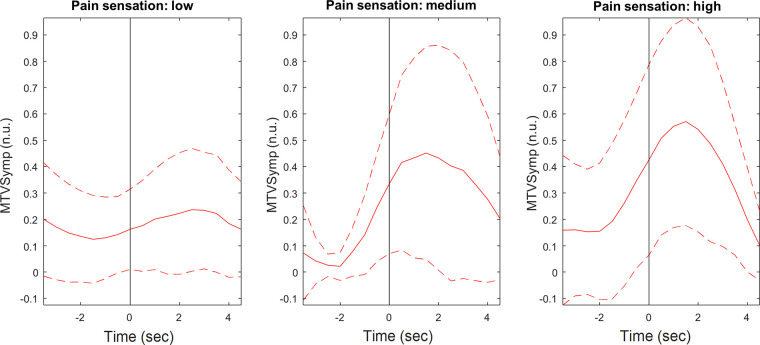
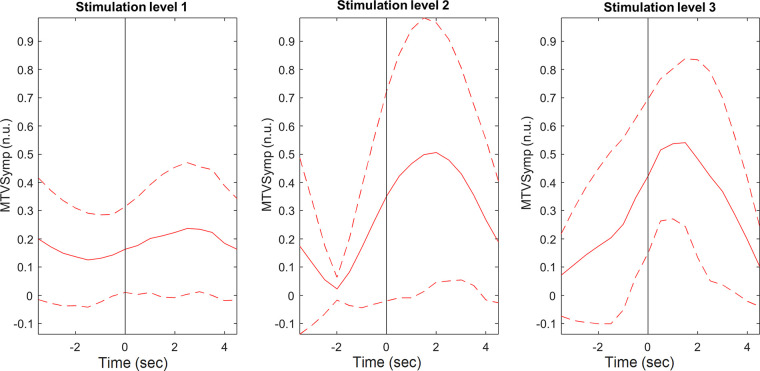
As shown, compared with the indices of EDA, MTVSymp is one of the indices that exhibits more significant differences between levels of pain stimulation intensity and pain sensation. For illustration purposes, Figs. 4 and 5 present the ensemble average of MTVSymp for different levels of pain stimulation intensity and pain sensation, respectively, for a given subject. The solid and dashed lines indicate the mean and its standard deviation bounds, respectively. The onset of stimulation is marked with a vertical line. It is apparent that MTVSymp slightly increases with ascending stimulus intensity and pain sensation. However, for this specific subject, it is apparent that a slight increase between “high” and “medium” levels of pain sensation (although not significant) is seen, but not as much can be observed between level 3 and level 2. This is in agreement with results exhibited in Tables 2 and 3.

Figure 4.

Ensemble average of MTVSymp for a given subject, for the different levels of pain stimulation. Solid and dashed lines represent the mean and standard deviation, respectively. MTVSymp, modified time-varying index of electrodermal activity.

Figure 5.

Ensemble average of MTVSymp for a given subject, for the different levels of pain sensation based on VAS. Solid and dashed lines represent the mean and standard deviation, respectively. MTVSymp, modified time-varying index of electrodermal activity; VAS, visual analog scale.

Classification

Table 4 shows comparison of classifiers for the three-class and four-class approaches, for pain stimulation intensity and pain sensation. For the three-level classification, the highest macroaveraged geometric mean scores for pain stimulation intensity and pain sensation were 69.7% and 69.2%, respectively, with features of TVSymp, MTVSymp, phasic and driver components obtained with sparsEDA, and MLP classifier. For the four-class classification, except for the SVML classifier with features of TVSymp, MTVSymp, and cvxEDA components of EDA, which showed poorer performance than the others, pain stimulation intensity classification showed higher macroaveraged geometric mean scores than for pain sensation. The highest macroaveraged geometric scores were 56.9% and 51.6%, respectively, with sparsEDA and MLP.

Table 4.

Comparison of classifiers for three-class and four-class approaches using macroaveraged geometric mean scores for pain stimulation intensity and pain sensation

Features	Classifier	Three-Class Classification		Four-Class Classification
		Pain stimulation Intensity	Pain sensation (VAS)	Pain stimulation intensity	Pain sensation (VAS)
cvxEDA components, TVSymp, MTVSymp	SVML	0.605	0.598	0.331	0.346
	SVMR	0.649	0.664	0.541	0.511
	MLP	0.665	0.674	0.529	0.501
	RF	0.658	0.658	0.523	0.490
sparsEDA components, TVSymp, MTVSymp	SVML	0.632	0.594	0.381	0.341
	SVMR	0.664	0.686	0.549	0.447
	MLP	0.697	0.692	0.569	0.516
	RF	0.689	0.681	0.526	0.511

cvxEDA, convex optimization of electrodermal activity; MLP, multilayer perceptron; MTVSymp, modified time-varying index of electrodermal activity; RF, random forest; sparsEDA, sparse deconvolution of electrodermal activity; SVML, support vector machine linear kernel; SVMR, support vector machine with radial basis function kernel; TVSymp, time-varying index of electrodermal activity; VAS, visual analog scale. The classifier with the highest macroaveraged geometric mean scores is boldface.

Table 5 shows the confusion matrices of the classifiers that showed the highest macroaveraged geometric mean scores for each category. No stimulation/pain segments were classified with higher accuracy than the other classes in all classifiers. In the four-class approach, the number of correctly classified instances was higher than the number of instances incorrectly assigned to other individual classes; however, this was not the case for four-class pain sensation classification, in which sometimes the number of instances incorrectly assigned to other classes was higher than for the correct class.

Table 5.

Confusion matrices for three-class and four-class classification approaches for pain stimulation intensity and pain sensation

		Three-Class Classification						Four-Class Classification
		Estimated Intensity			Estimated Sensation			Estimated Intensity				Estimated Sensation
		0	1	2	0	1	2	0	1	2	3	0	1	2	3
Trueclass	0	0.83	0.14	0.03	0.83	0.13	0.04	0.77	0.15	0.07	0.02	0.75	0.17	0.05	0.03
	1	0.21	0.52	0.27	0.21	0.42	0.37	0.20	0.39	0.25	0.17	0.27	0.26	0.24	0.23
	2	0.15	0.40	0.45	0.14	0.33	0.53	0.13	0.25	0.38	0.24	0.13	0.27	0.26	0.34
	3	N/A			N/A			0.09	0.24	0.31	0.36	0.10	0.17	0.23	0.50

Regression

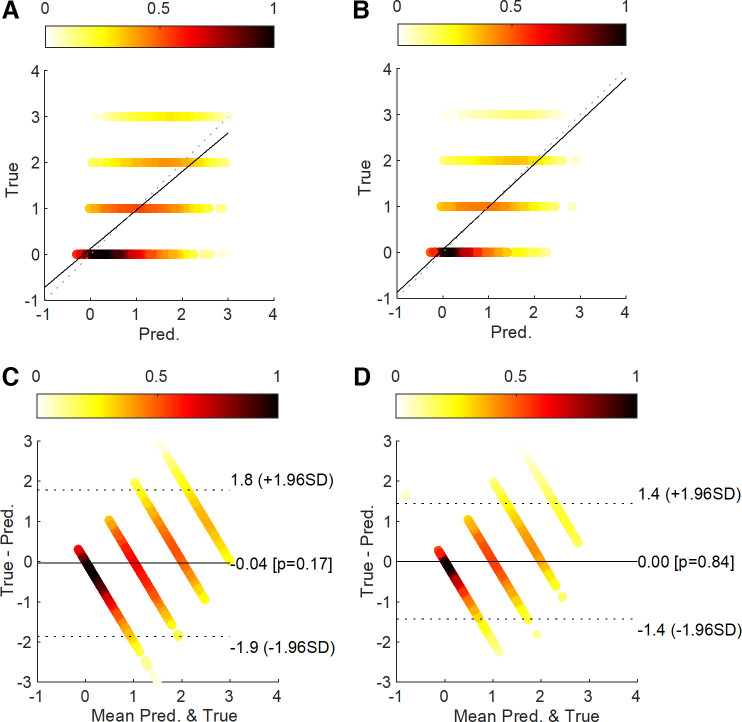
Table 6 shows a comparison of regression models for pain stimulation intensity and pain sensation. Regressors showed higher R² and lower M-RMSE and M-MAE for pain sensation than for pain stimulation intensity. For regressors of pain stimulation intensity, SparsEDA with SVMR showed the highest R² of 0.357 with the lowest M-RMSE and M-MAE of 0.936 and 0.762. For regressors of pain sensation, SparsEDA with MLP showed the highest R² of 0.470 with the lowest M-RMSE and M-MAE of 0.853 and 0.705. Figure 6 illustrates the correlation analysis and Bland–Altman density plots of the regressors that showed the highest R² for each category. Each true value group for pain sensation showed denser distribution than for pain stimulation intensity.

Table 6.

Comparison of regressions of pain stimulation intensity and pain sensation

		Pain Stimulation Intensity			Pain Sensation (VAS)
Features	Regressor	R 2	M-RMSE	M-MAE	R 2	M-RMSE	M-MAE
cvxEDA components, TVSymp, MTVSymp	MLP	0.146	1.071	0.850	0.378	0.937	0.765
	SVMR	0.297	0.983	0.827	0.419	0.906	0.756
sparsEDA components, TVSymp, MTVSymp	MLP	0.333	0.957	0.770	0.470	0.853	0.705
	SVMR	0.357	0.936	0.762	0.429	0.897	0.749

The 0–3 scale for regression was defined the same way as for the four-class classification approach. cvxEDA, convex optimization of electrodermal activity; M-MAE, macroaveraged mean absolute error; MLP, multilayer perceptron; M-RMSE, macroaveraged root mean square error; MTVSymp, modified time-varying index of electrodermal activity; sparsEDA, sparse deconvolution; SVMR, support vector machine with radial basis function kernel; TVSymp, time-varying index of electrodermal activity; VAS, visual analog scale.

Figure 6.

Correlation density plots for pain stimulation intensity (A) and pain sensation (B). Bland–Altman density plots for pain stimulation intensity (C) and pain sensation (D).

DISCUSSION

We have trained and tested machine learning models on EDA features for the objective measure of stimulation pain intensity and pain sensation. Overall, good classifications of different levels of pain stimulation and pain sensation were found to be feasible using features derived from EDA. In addition, classification of pain stimulation intensities had better performance than classification of pain sensation levels based on features obtained from EDA. This is in agreement with previous studies that found a higher correlation of sympathetic function to stimulus intensity as compared with perceived pain intensity (46, 47). However, the regression of pain sensation levels achieved an apparently better fit, as a higher R², and lower M-RMSE and M-MAE were achieved than the regression of stimulus intensity. A possible reason for this better fit is that the pain stimulation intensities 0 and 1 do not cause significant difference in EDA, whereas the difference between pain sensation associated to VAS = 0 (segments of no stimulation previous to every stimulus) and VAS={1,2} is more prominent. For this reason, the regression of VAS 0 does a better job than the regression of “No” in the regression of pain stimulation intensity (Fig. 6). Adaptation is another possible reason for the lower performance in regression for stimulation intensities, as low stimulation levels that initially caused some reaction in the subjects were perceived as less or not painful as the experiments progressed.

Furthermore, the estimation of pain sensation is hampered by the subjectiveness and variation of pain reported by the subjects using VAS or other similar scale. For example, assigning a VAS value of 5, 6, or 7 to a given perceived pain sensation is a fuzzy decision and these scores vary among subjects due to their different pain tolerance.

For pain stimulation, we have delivered different levels of pain intensity, and evoked pain sensations reported to be as high as VAS = 10 (e.g., subjectively perceived as the “worst pain possible”) without causing tissue damage (temperature was maintained below 45°C, insufficient to burn the glabrous skin) using an array of thermal grills. The differences in VAS scores between the levels of stimulation support the effectiveness of thermal grills to elicit different levels of pain. Previous studies have suggested that thermal grills evoke more consistent pain stimulation across subjects, as compared with traditional methods for pain stimulation like electric shocks (18).

A significant correlation between pain sensation and the elevation of the dynamics of the autonomic nervous system (ANS) has been reported before (48). In the brain, the periaqueductal gray, amygdala, hypothalamus, anterior cingulate, and insular cortex intervene in both autonomic responses and pain (49, 50). Although an understanding of the multiple mechanisms of interplay between ANS and pain is not fully elucidated, a noxious painful stimulus is known to cause autonomic reactions and autonomic activity affecting pain responses (51, 52). Although multiple studies have looked into the relationship between ANS reactions and stimulus intensity (53–56), some years ago, researchers were able to determine a hierarchy in the relationship between ANS and pain and determine that ANS sympathetic responses are more correlated to the intensity of the stimulus applied than to the subjective sensation of pain elicited by the stimulus (46, 47). Another study found that the response observed in the skin sympathetic nerve activity was irrespective of the difference in sensation elicited by stimulating either the muscle or the skin (57). In that study, muscle pain induced by hypertonic saline injections was reported to have a deep, dull poorly localized quality, whereas skin pain was sharp, burning, and highly localized. Despite the differences in sensation, both types of pain elicited seemingly identical responses. In agreement with such findings, we also observed that stimulation intensity is easier to classify than pain sensation.

The statistical analysis indicated than indices of EDA associated with higher frequencies (phasic EDA, dphEDA, phasic drivers, TVSymp, and MTVSymp) showed more significant differences between stimulation levels than did the other indices of EDA. This suggests that the elicited pain also evoked a concomitant sympathetic physiological reaction. Also, the differences between stimulation and no stimulation on dphEDA, TVSymp, and MTVSymp are in agreement with previous studies that validated the sensitivity of the index to sympathetic arousal and pain stimulation (18, 29, 31, 58).

Describing the fundamental grounds of pain perception is a centuries-old field of study (59). Several pain theories have been proposed to explain individuals’ pain sensation, why and how (60). Although none of those theories completely accounts for all aspects of pain perception, the model that comprehensively considers the interactions among the biological, psychological, and social components unique to each individual (biopsychosocial), and the issues embedded in such interactions, is considered to provide the most successful explanation of the etiology of pain (61). Another widely accepted theory is the intensity theory of pain (62). This theory defines pain as an emotion that occurs when a stimulus is stronger than usual, rather than as a unique sensory experience. In other words, pain occurs when sufficient intensity is reached rather than being a stimulus modality. In this study, we have found evidence supporting that when a stimulus intensity reached certain threshold, it produced an objective and measurable reaction in the body and the summation effect produced by the increased intensity can be used to assess the level of pain perceived by human subjects.

Perspectives and Significance

We have tested the feasibility of objective pain assessment using machine learning models trained on EDA features. We evaluated the classification and regression of pain stimulation intensity and pain sensation in healthy subjects. We computed features of EDA previously reported to be sensitive to sympathetic tone and pain, based on time-domain decomposition, spectral analysis, and differential analyses. Overall, classification of pain stimulation intensity achieved better results than pain sensation, possibly the latter due to the high variance and inconsistency of VAS scores reported by the subjects. Models for classification of pain stimulation intensity and pain sensation achieved maximum macroaveraged geometric mean scores of 69.7% and 69.2%, respectively, when three classes were considered (“No,” “Low,” and “High”). Regression of stimulation intensity and pain sensation achieved maximum values. Interestingly, regression of pain sensation achieved lower error compared with pain stimulation intensity (R² values of 0.47 and 0.357, respectively). Our results constitute additional physiological evidence that autonomic responses are more correlated to the applied stimuli’s intensity than to the pain sensation reported by the subject.

GRANT

This work was funded by National Institutes of Health Grant R21 DE029563-01.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

H.F.P-Q. and K.H.C. conceived and designed research; H.F.P-Q. and Y.K. performed experiments; H.F.P-Q. and Y.K. analyzed data; H.F.P-Q., Y.K., and K.H.C. interpreted results of experiments; H.F.P-Q. and Y.K. prepared figures; H.F.P-Q. drafted manuscript; H.F.P-Q., Y.K., and K.H.C. edited and revised manuscript; H.F.P-Q., Y.K., and K.H.C. approved final version of manuscript.