Estimation of general time-varying single particle tracking linear models using local likelihood

Abstract

In this work, we study a general approach to the estimation of single particle tracking models with time-varying parameters. The main idea is to use local Maximum Likelihood (ML), applying a sliding window over the data and estimating the model parameters in each window. We combine local ML with Expectation Maximization to iteratively find the ML estimate in each window, an approach that is amenable to generalization to nonlinear models. Results using controlled-experimental data generated in our lab show that our proposed algorithm is able to track changes in the parameters as they evolve during a trajectory under real-world experimental conditions, outperforming other algorithms of similar nature.

I. INTRODUCTION

Single Particle Tracking (SPT) refers to a class of experimental techniques and mathematical algorithms for following small particles (less than 100 nm) moving inside living cells, including viruses, proteins, and strands of RNA [1]. By labeling the particles with a fluorescent reporter such as a fluorescent protein or quantum dot, the motion of the tag and, by extension, the motion of the particle can be observed. While there are many different schemes, the general paradigm in SPT involves capturing a series of widefield fluorescence images, localizing the fluorescent particle in each frame to form a trajectory, and then analyzing the trajectory to estimate motion model parameters. Knowing these parameters provides vital information to understanding the underlying biological processes and has been used to understand processes from viral infection [2], intracellular communication between neurons [3], and other applications.

There are many models that are relevant to the biophysical application domain including (among others) free diffusion, confined diffusion, directed motion, and combinations of these, such as joint diffusion and directed motion [4]. Among the variety of motion models, diffusion is arguably the simplest and one of the most commonly used models when describing biomolecular motion. Because it is a fairly straightforward model, it is amenable to analysis and the use of optimal estimation. This was recognized and developed in [5]–[8]. Using optimal techniques such as Maximum Likelihood (ML) estimation places the problem on firm theoretical grounding, ensures that the analysis method is both consistent and asymptotically efficient, and provides a rigorous understanding of the accuracy and performance of the estimator. A similar approach has also been developed for the analysis of confined diffusion [9].

Existing ML schemes in SPT assume that model parameters, while unknown, are fixed (time invariant). There have been efforts on extending the analysis to determine the most likely model among a given set [4] but these also assumed fixed parameters [10]. One of the authors has considered time-varying parameters using a jump Markov model [11] but such models do not allow for continuously varying parameters, assume that the number of levels to which the parameter can jump is known, and impose a probabilistic structure on the changing parameter values that may be non-physical. In [12], the authors considered for the first time a windowed approach for the pure diffusion setting, combined with a strategy of change detection to refine the estimation of the diffusion constants after initial estimates were generated.

In this work, we develop an alternative estimation algorithm based on local likelihood estimation, extending beyond simple diffusion to general linear models typically found in SPT with time-varying parameters. The main idea is to take a window of data and fit a time-invariant parameter model in the window. Then the window is moved along by a fixed amount and the process repeated to trace out time-varying parameters. One of the fundamental insights from the statistical literature [13], [14] is that rectangular windows induce a kind of Gibbs-ringing (familiar from Fourier analysis) which can produce bias in the estimates. Thus, only smooth windows should be used. Unfortunately, in a lot of the applied literature this basic insight is unknown and rectangular windows are still very common.

The problem of estimating diffusion constants can be translated to one of estimating the process noise covariance matrix. This is a well-studied problem with a variety of approaches in the literature, e.g., maximum likelihood [15], [16], Bayesian estimation [17], covariance matching [15], and correlation techniques [18]. Some of these works are designed for adaptive filtering, including [15], [19]–[21]. A fair comparison against these adaptive innovation-based algorithms is carried out in [22] where it is shown that the algorithm introduced in that paper outperforms the others. In the present work, then, we compare our method to that of [22]. It is important to note, however, that our method is more general than that of [22], allowing for estimation of any of the model parameters and not just the process covariance.

II. SPT model

SPT refers to a broad collection of experimental techniques and data analysis algorithms for studying the motion of single, labeled biological macromolecules moving in their native environments, including inside living cells. The basic paradigm is to collect a series of images from a CCD camera, localize the particle in each of the images, link these positions into a trajectory, and then analyze the trajectory for motion model parameters using, typically, a curve fit to an MSD curve. Localization can be done using a variety of different algorithms, ranging from simple centroid calculations through full ML estimation [23]–[25]. One of the most common techniques is a fit of the intensity in the image to a simple Gaussian profile, yielding an accuracy on the order of 10 nm, well below the diffraction limit of light.

Given a trajectory, analysis typically proceeds by selecting a parameterized model and using the trajectory to identify those parameters. In this work we consider the following quite general model (expressed here in the x-axis only with similar models holding in the other axes):

$$\begin{gathered} x_{k+1}=a_t{x}_k+b_t+w_k,w_k~\mathcal{N}\left(0,q_t\right), \\ {y}_k=x_k+v_k,v_k~\mathcal{N}\left(0,r_t\right), \end{gathered}$$ (1)

where $x_k,y_k,w_k,v_k\in ℝ,q_t=2D_t\mathrm{\Delta }t$ is the variance of the process noise defined by the diffusion coefficient D_t and the sampling time Δt, and r_t is the variance of the measurement noise as generated by a variety of processes, including shot noise due to the physics of photon generation in fluorescence and read-out noise in the camera. System (1) can be used to represent several models important in the SPT application. For example, setting a_t = 1, b_t = 0 describes pure diffusion; if we choose a_t < 1, b_t = 0, we have the Ornstein-Uhlenbeck model that can capture tethered motion of a biomolecule or be used to approximate confined diffusion [9], [26]. We note that the restriction to one dimension in (1) is for simplicity of presentation only. The extension to the multi-dimensional setting is straightforward since motion in the different axes is generally considered to be independent.

The model in (1) also allows for time-varying parameters. For example, the process noise q_t can vary as the particles move into different regions of the cells with different local environments, interact with different species in their surroundings, or go through biochemical changes due to the natural activity in the cell. This insight will set up the conditions for the examples given in Sec. IV-B. For notation purposes, we add subindex t to a parameter to indicate that it is time-varying, and remove the subindex t when it is presumed to be time-invariant.

Despite the complex reality of measurement noise, it is often modeled as a simple Gaussian white noise process. The Gaussian approximation works well at high signal-to-noise levels but does break down at low intensities, necessitating a more complex description of the data [27]. In general, the measurement noise r_t has reasonably static statistics as it is driven primarily by the experimental equipment. However, r_t may also due to non-uniform background or changes in illumination intensity during the measurements.

Our goal, then, is to develop an algorithm based on local ML estimation that can track the time-varying parameters of motion in (1), namely, a_t, b_t, q_t and r_t. (Of course, if some parameters in the model are known a priori or can be independently measured, one should use that value instead of trying to estimate it from the data; the approach below is easily modified for estimating a subset of these parameters.)

III. Inference problem

Our goal is to use a local likelihood approach to handle time-varying estimation. We begin with a single window where the problem reduces to the time-invariant case.

A. Time-invariant parameter estimation via EM

Consider model (1). We define β, the parameter vector containing all the unknowns, that is, β = [Γ q r]^T, where Γ = [a b]. The ML estimation problem (for a particular window) is then given by

$$\widehat{\beta }=\arg \underset{\beta }{\max }l(\beta ),$$ (2)

where l(β) is the log-likelihood function defined as l(β) = log p(Y_N|β) and Y_N is the observed data defined as Y_N = y₁,...,y_N. For convenience and future reference, we also define X_N = {x₁,...,x_N}.

Many authors have worked on problem (2) for model (1) (or on variations) using the EM algorithm, see, e.g., [28]–[32] and references therein. The EM algorithm produces a sequence of estimates ${\widehat{\beta }}^{(i)},i=1,2,\cdots ,$ of the unknown parameter β, which is guaranteed to converge to a local maximum of the log-likelihood function l(β) [32]. The basic idea is to use a hidden¹ variable, which in our case is taken to be the underlying particle trajectory X_N, to create an auxiliary function $\mathcal{Q},$ which approximates the log-likelihood function. The EM algorithm is summarized in Algorithm 1.

Algorithm 1:

Time invariant EM

It turns out that, under quite general conditions, if the estimate ${\widehat{\beta }}^{(i+1)}$ is chosen as in (4), then the sequence of numbers $l({\widehat{\beta }}^{(i)}),i=1,2,\cdots$ is monotonically increasing, and therefore the parameter sequence ${\widehat{\beta }}^{(i)}$ converges to a local maximum of the log-likelihood function l(β) [32].

It is well-known, see e.g. [33, p.343], that for the system in (1), with time-invariant parameters (a_t = a, b_t = b, q_t = q, r_t = r), the associated E-step (ignoring constant terms and the parameters of the initial condition) is given by

$$\begin{gathered} \mathcal{Q}\left(\beta ,{\widehat{\beta }}^{(i)}\right)=\mathbb{E}\left\{-2l(\beta )\mid Y_N,{\widehat{\beta }}^{(i)}\right\}=-N\log q^{-1} \\ -N\log r^{-1}+\sum _{k=1}^N\mathbb{E}\left\{{\left(y_k-x_k\right)}^2{r}^{-1}\mid Y_N,{\widehat{\beta }}^{(i)}\right\}+ \\ \sum _{k=1}^N\mathbb{E}\left\{{\left(x_{k+1}-\mathrm{\Gamma }{z}_k\right)}^2{q}^{-1}\mid Y_N,{\widehat{\beta }}^{(i)}\right\} \end{gathered}$$ (5)

where, for convenience, we have defined $z_k={\left[\begin{array}{ll}{x}_k\hfill & u_k\hfill \end{array}\right]}^T.$ Notice that we have included an input u_k with enough energy (different to the constant 1) that does not exist in the original model (1), with the purpose of improving the estimation of b_t (or b for the time-invariant case). $\mathbb{E}\left\{\cdot \mid Y_N,{\widehat{\beta }}^{(i)}\right\}$ refers to the expected value given the incomplete data Y_N, see e.g. [28], [29]. For details about the optimization of the auxiliary function $\mathcal{Q}$ (the M-step), we refer to [29], where a general robust numerical implementation can be found.

B. Time-varying estimation using local likelihood

In this section, we describe an algorithm to trace time-varying parameters associated with (1). We pose a time-varying likelihood, which is time-invariant in a window of a nominated length h, optimize in this window, and continue the process by leaving one sample out and taking a new one in order to keep the same window size. The process finishes when we have included the last available sample. There are alternative ways to local modeling. For example, there is much literature on how to model data using a global polynomial fit. However, this method can potentially have the drawback of needing a large number of components to have a reasonably low bias [14], and, as a consequence, may lead to over-parametrization, which has an effect on the variance of the estimate. The local approximation approach, in general, only requires a small number of parameters.

The local likelihood is defined as:

$$l_t\left({\beta }_t\right)=\sum _{k=1}^N{K}_{k,t}l\left(y_k\mid {\beta }_t\right),$$ (6)

where $K_{k,t}:=K\left(\frac{k-t}{h}\right)$ is the kernel, h is the window length², t is a point within the window, usually the middle point, k indicates any point within the window, and l(y_k|β_t) is the likelihood of y_k|β_t. Different values for h can be used, as well as different kernels, and appropriate selection of them is a nontrivial issue, see e.g. [14]. However, it is important to use smooth windows to minimize the effects caused by the Gibbs ringing phenomenon, which is achieved by using K_k,t to create a window with rounded edges, see e.g. [34]. Examples of such kernels can be found from the following expression

$$K(v)=\{\begin{array}{ll}\frac{1}{\beta (1/2,\gamma +1)}\left(1-v^2\right),\hfill & \text{if}\left|v\right|\le 1,\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (7)

where K(v) ≥ 0 and ${\int }_{-\infty }^{\infty }K(v)dv=1.$ For γ = {0, 1, 2}, we obtain the uniform, Epanechnikov, and biweight kernels, respectively. The kernel progressively downweights data points far from the kernel centre. In this way, data points are introduced smoothly into the windowed neighbourhood.

If we now multiply (6) by −2, consider (5), take $\mathbb{E}\left\{\cdot \mid Y_N,{\widehat{\beta }}_t^{(i)}\right\}$ on both sides, then we can find that the time-varying auxiliary function is given by

$${\mathcal{Q}}_t\left({\beta }_t,{\widehat{\beta }}_t^{(i)}\right)=E\left\{-2l\left({\beta }_t\right)\mid Y_N,{\widehat{\beta }}_t^{(i)}\right\}$$ (8)

where the log-likelihood l(β_t) is given by (ignoring constant terms and the initial condition)

$$-2l\left({\beta }_t\right)=\sum _{k=1}^N{K}_{k,t}l\left(y_k\mid {\beta }_t\right),$$ (9)

with l defined as

$$l\left(y_k\mid {\beta }_t\right):={\left(x_{k+1}-{\mathrm{\Gamma }}_t{z}_k\right)}^2{q}_t^{-1}+{\left(y_k-x_k\right)}^2{r}_t^{-1}.$$ (10)

Remark 1:

Notice that the difference of ${\mathcal{Q}}_t$ with respect to the $\mathcal{Q}$ (found in the time-invariant EM) is the inclusion of the kernel function K(v), where v := (k − t)/h, and the time dependancy of the parameters of interest. We have added the sub-index t in this function to denote that it depends on the time-varying parameter β_t.

For our scalar case, and discarding the constant terms and the parameters for the initial conditions, we can obtain the following auxiliary function ${\mathcal{Q}}_t$

$$\begin{gathered} {\mathcal{Q}}_t\left({\beta }_t,{\widehat{\beta }}_t^{(i)}\right)=-\left(\log q_t^{-1}+\log r_t^{-1}\right)\sum _{k=1}^N{K}_{k,t}+ \\ {q}_t^{-1}\left[{\tilde{S}}_{11}-{\tilde{S}}_{01}^T{\mathrm{\Gamma }}_t^T-{\mathrm{\Gamma }}_t{\tilde{S}}_{01}+{\mathrm{\Gamma }}_t{\tilde{S}}_{00}{\mathrm{\Gamma }}_t^T\right]+ \\ {r}_t^{-1}\sum _{k=1}^N{K}_{k,t}\left[{\left(y_k-{\widehat{x}}_{k\mid h}\right)}^2+P_{k\mid h}\right],\text{with} \end{gathered}$$ (11)

$$\begin{gathered} {\tilde{S}}_{11}=\sum _{k=1}^{N}E\left\{K_{k,t}{x}_{k+1}^2\mid Y_N,{\widehat{\beta }}_t^{(i)}\right\} \\ =\sum _{k=1}^N{K}_{k,t}\left[{\widehat{x}}_{k+1\mid h}^2+P_{k+1\mid h}\right], \end{gathered}$$ (12)

$$\begin{gathered} {\tilde{S}}_{01}=\sum _{k=1}^{N}E\left\{K_{k,t}\left[\begin{array}{l}{x}_k{x}_{k+1}\hfill \\ u_k{x}_{k+1}\hfill \end{array}\right]\mid Y_N,{\widehat{\beta }}_t^{(i)}\right\} \\ =\sum _{k=1}^N\left[\begin{array}{c}{K}_{k,t}{\left[{\widehat{x}}_{k+1\mid h}{\widehat{x}}_{k\mid h}+P_{k+1,k\mid h}\right]}^T\\ K_{k,t}{u}_k{\widehat{x}}_{k+1\mid h}\end{array}\right], \end{gathered}$$ (13)

$$\begin{gathered} {\tilde{S}}_{00}=\sum _{k=1}^{N}E\left\{K_{k,t}\left[\begin{array}{cc}{x}_k^2& x_k{u}_k\\ u_k{x}_k& u_k^2\end{array}\right]\mid Y_N,{\widehat{\beta }}_t^{(i)}\right\} \\ =\sum _{k=1}^N\left[\begin{array}{cc}{K}_{k,t}\left[{\widehat{x}}_{k\mid h}^2+P_{k\mid h}\right]& K_{k,t}{u}_k{\widehat{x}}_{k\mid h}\\ K_{k,t}{\widehat{x}}_{k\mid h}{u}_k& K_{k,t}{u}_k^2\end{array}\right] \end{gathered}$$ (14)

and where the values of ${\widehat{x}}_{k\mid h},P_{k,k-1\mid h},$ and P_k|h are defined by the smoothed distributions within the appropriate window. In our setting, these can be calculated from the Kalman smoother equations within the window h, see e.g. [35]. K_k,t is taken out of the expected values since it is deterministic.

The algorithm also depends upon choosing a window length h = h_oN where h_o << 1. The choice of h_o affects the rate of change of the parameters that can be followed as well as the accuracy and robustness to noise. Typically some trial and error, as well as experience, is needed to select an appropriate window size. However, there are data-based methods that can be used based on the Steins Unbiased Risk Estimator (SURE) [36].

C. Optimization of the time-varying E-step

We now optimize the time-varying E-step. Taking the derivatives of ${\mathcal{Q}}_t$ with respect to ${\mathrm{\Gamma }}_t,Q_t^{-1}\text{and}{R}_t^{-1}$ and setting them to zero yields:

$$\begin{gathered} {\widehat{\mathrm{\Gamma }}}^{(i+1)}={\tilde{S}}_{01}{\tilde{S}}_{00}^{-1}, \\ {\widehat{Q}}_t^{(i+1)}=\frac{1}{n}({\tilde{S}}_{11}-{\tilde{S}}_{01}^T{\left({\mathrm{\Gamma }}_t^{(i+1)}\right)}^T-{\mathrm{\Gamma }}_t^{(i+1)}{\tilde{S}}_{01}- \\ {\mathrm{\Gamma }}_t^{(i+1)}{\tilde{S}}_{00}{\left({\mathrm{\Gamma }}_t^{(i+1)}\right)}^T), \\ {\widehat{R}}_t^{(i+1)}=\frac{1}{n}\sum _{k=1}^N{K}_{k,t}\left[\left(y_k-{\widehat{x}}_{k\mid h}\right){\left(y_k-{\widehat{x}}_{k\mid h}\right)}^T+P_{k\mid h}^T\right], \end{gathered}$$ (15)

where $n={\sum }_{k=1}^N{K}_{k,t}$.

The time-varying estimation algorithm is summarized in Algorithm 2.

Algorithm 2:

Time-varying EM

While not applied here, we note that there are several approaches to improve the numerical robustness of the Kalman filtering and smoothing algorithms such as extending the work in [29] or using an SVD decomposition, see e.g. [37].

D. Convergence

It is well-known that the only requirement needed in the EM algorithm to converge to a stationary point of the likelihood function (which is not necessarily the global maximum) is that $\mathcal{Q}\left({\widehat{\beta }}^{(i+1)},{\widehat{\beta }}^{(i)}\right)>\mathcal{Q}\left({\widehat{\beta }}^{(i)},{\widehat{\beta }}^{(i)}\right).$ In fact, this is assured to occur when another auxiliary function found in the EM algorithm, known as $\mathcal{H}\left(\beta ,{\widehat{\beta }}^{(i)}\right),$ is proven to be non-increasing; for details see e.g. [38].

The next lemma shows that the local likelihood does increase at each step of the EM iteration. Since our algorithm is based on EM, it inherits these same convergence properties. Of course, this also implies we cannot guarantee convergence to the true value because the EM algorithm itself only yields the global maximum under certain special cases [38, ch.3].

Lemma 1:

In our scheme, the proposed l_t(β_t) defined in (6) has the following property:

$$l_t\left({\widehat{\beta }}_t^{(i+1)}\right)>l_t\left({\widehat{\beta }}_t^{(i)}\right).$$

Proof. Following the reasoning in [38], we show that the inclusion of the kernel K_k,t does not affect the non-decreasing nature of the function $\mathcal{H}\left({\beta }_t,{\widehat{\beta }}_t^{(i)}\right):=\mathbb{E}\left\{{\sum }_{k=1}^N{K}_{k,t}\log p_{\beta }\left(x_k\mid y_k\right)\mid Y_N,{\widehat{\beta }}_t^{(i)}\right\}.$ We have for any β_t

$$\begin{gathered} \mathcal{H}\left({\beta }_t,{\widehat{\beta }}_t^{(i)}\right)-\mathcal{H}\left({\widehat{\beta }}_t^{(i)},{\widehat{\beta }}_t^{(i)}\right)= \\ \mathbb{E}\left\{\sum _{k=1}^N{K}_{k,t}\log p_{{\beta }_t}\left(x_k\mid y_k\right)\mid Y_N,{\beta }_t^{(i)}\right\}-\mathbb{E}\{\sum _{k=1}^N{K}_{k,t} \\ \log p_{{\widehat{\beta }}_t^{(i)}}\left(x_k\mid y_k\right)\mid Y_N,{\widehat{\beta }}_t^{(i)}\} \\ =\mathbb{E}\left\{\sum _{k=1}^N{K}_{k,t}\log \frac{p_{{\beta }_t}\left(x_k\mid y_k\right)}{p_{{\widehat{\beta }}_t^{(i)}}\left(x_k\mid y_k\right)}\mid Y_N,{\widehat{\beta }}_t^{(i)}\right\} \\ =\sum _{k=1}^N{K}_{k,t}\mathbb{E}\left\{\log \frac{p_{{\beta }_t}\left(x_k\mid y_k\right)}{p_{\widehat{\beta }(i)}\left(x_k\mid y_k\right)}\mid Y_N,{\widehat{\beta }}_t^{(i)}\right\} \\ \le \sum _{k=1}^N{K}_{k,t}\log \left[\mathbb{E}\left\{\frac{p_{{\beta }_t}\left(x_k\mid y_k\right)}{p_{{\widehat{\beta }}_t^{(i)}}\left(x_k\mid y_k\right)}\mid Y_N,{\widehat{\beta }}_t^{(i)}\right\}\right]=0. \end{gathered}$$ (16)

Using Jenssen’s inequality in (16) yields that the expected value is 1, since the expectation is taken with respect to (x_k|y_k). This completes the proof that $\mathcal{H}\left({\beta }_t,{\widehat{\beta }}_t^{(i)}\right)$ is a non-decreasing function, thus guaranteeing that the likelihood in (6) increases at each iteration of the EM algorithm. □

E. Comparison with other approaches

Adaptive filtering techniques have been used for a long time for the estimation of covariances matrices Q and R using the Kalman filter. Literature goes back to the late 60s and early 70s, see e.g. [15], [39]. Here, we make a comparison with [22]. This method uses a retrospective optimization to update the process noise covariance at each time and is based on the minimization of a quadratic function based on the innovations. We take this paper for reference as it claims to have better accuracy than other methods regarded as innovations-based adaptive Kalman filter [15], [19]–[21].

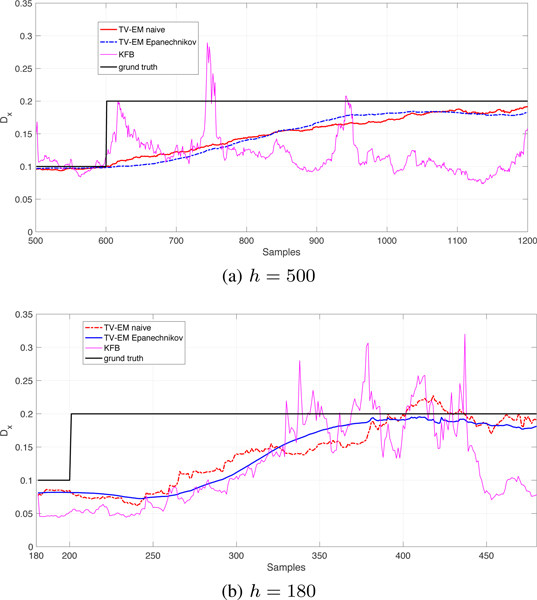
In simulation, we generated trajectories with a change in the diffusion constant from D_x = 0.1 μm²/s to D_x = 0.2 μm²/s, holding the parameters a_t = 1, b_t = 0, and r_t = 0.1 constant and known. In Fig. 2, we show the comparison between our method using K(v) = 1 (naive approach), K(v) as the Epanechnikov kernel, and the method in [22] for the mean of 5 repetitions, considering two window sizes h = 180, 500. We observe that our proposed method outperforms both the method of [22] and the naive EM scheme. The inclusion of the kernel plays an important role in smoothing out the estimate, specially when the window size is smaller.

Fig. 2.

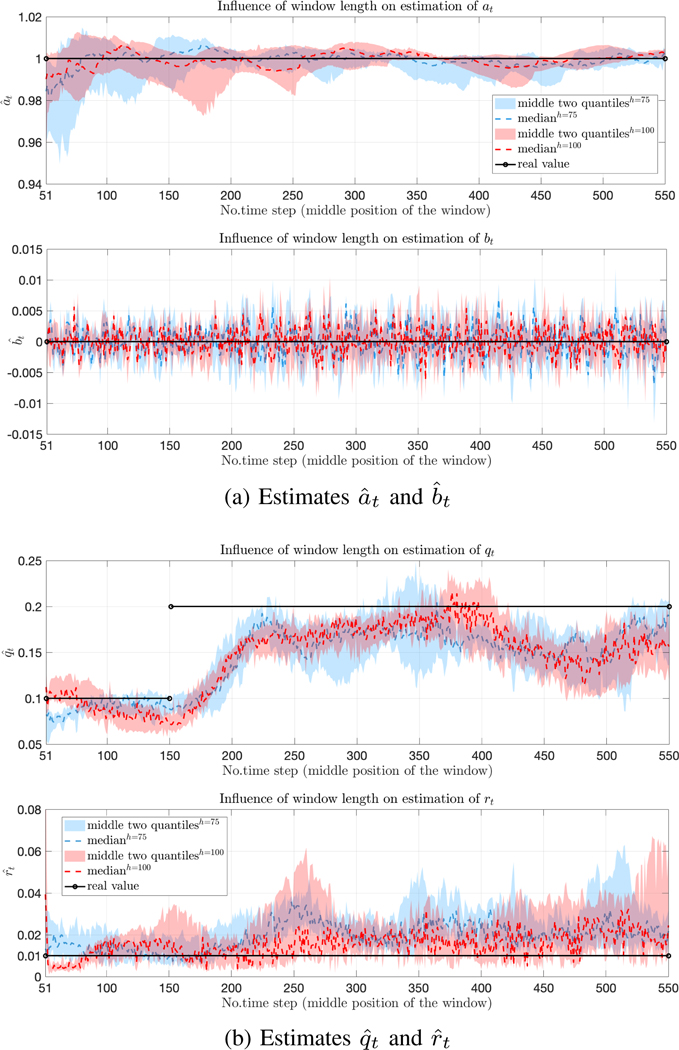
Comparison of estimates ${\widehat{a}}_t,{\widehat{b}}_t,{\widehat{q}}_t,{\widehat{r}}_t$ using two different window sizes h = 75 (blue) and h = 100 (red).

F. Effect of window sizes

There is a clear trade-off between the length of the window size with more sensitivity coming with shorter windows but at the cost of higher variance. To explore this, we performed simulations using the ground-truth values a_t = 1, β_t = 0, and r_t = 0.01, with q_t taking two values (0.1 and 0.2) during the run. We applied our method using short windows (h = 75, 100). (Note that even for estimating only q_t, the method in [22] fails to produce an estimate for such short windows.) In Fig. 2, we show the estimate for all the unknowns, and for two different window sizes. The statistics are taken over 20 runs of the same experiment. As expected, we see that shorter windows (blue) the estimates have greater variance longer ones(red) while reacting somewhat faster.

IV. Controlled experiments

A. Generation of data

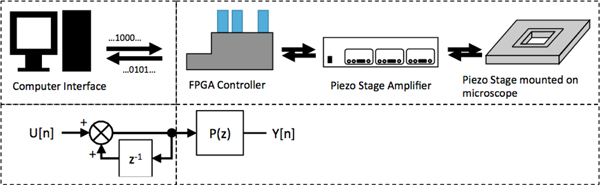
Here, we test our algorithm with a more realistic situation based on controlled experiments with known ground truth information to generate data sets. The experimental procedure, described in detail in [40], consists of four steps: 1) generate numerical sample paths using the motion model in (1); 2) control the position of a fluorescent microsphere with a nano-positioning stage to follow the sample paths; 3) observe the motion using a widefield fluorescent microscope; 4) do image processing to extract position information from the resulting stack of images. This method effectively provides data sets that exhibit the phenomenon of interest with motions that are accurate, precise, and repeatable while also being subject to real-world effects. Our specific implementation of the controlled experiment, diagrammed in Fig. 3, uses a typical single particle tracking microscope. Realizations using (1) were generated for specific values of a, b, and q_t. The value of r_t was a result of the experimental conditions that include fluorophore brightness, illumination intensity, integration time of the camera and the amount of background light collected by the microscope. These trajectories were then sent to the amplifier of the microscope stage via a National Instruments compact reconfigurable input-output system (NI 9076 cRIO) programmed through the LabView interface. To observe the particle motion, a Zeiss Axiovert 200 equipped with a 63x 1.2 NA water immersion objective and a photometrics 95B sCMOS camera was used to acquire diffraction-limited images at 10 frames per second with an integration time of 50 ms. The microscope stage would move and settle during the time when the camera was off-loading the previous image and the next image would be taken after the stage settled. This yielded a single position per image period. The single particles were then localized using a least squares fitting of the image data to a Gaussian profile with background to the image data. The time series of localizations were then analyzed with local ML.

Fig. 3.

A block diagram showing the signal flow. (Upper left) computer generated realizations of our model (bottom) is sent to the controller and is translated to an analog control voltage. This control voltage is sent to the stage amplifier which then generates the high voltage needed to generate motion in the stage.

B. Results

In this section, we demonstrate the performance of our algorithm using experimental data generated using the procedure described in section IV-A. Two dimensional trajectories were generated, modeled as two independent systems of the form (1). The true values of a_t and b_t for both cases were fixed to a_t = 1 and b_t = 0. The diffusion coefficients began at 0.9 μm²/s, then switched to 0.1 μm²/s at time 25 s, and then again back to 0.9 μm²/s at time 50 s.

The ground truth value used for the creation of the trajectories are shown in Fig. 4 (solid-thin line), as well as the results of the estimation window length h = 100 samples. In Fig. 4 (upper-left plot), we show the estimation of a_t which, as expected, moves around the true value of 1; the upper-right plot shows the estimation of b_t, which is around 0; Fig. 4 (lower plot) shows the estimation of the diffusion constant D_t. Plots include the estimation for both x and y-axes.

Fig. 4.

Estimation of the unknown parameters in x (blue-solid) and y (red-dashed) axis of controlled experiments.

We also calculate the Mean Square Error (MSE) for each parameter using different window lengths h = 75, 100, 125. The rationale behind the selection of these window lengths is that in SPT one typically has a limited number of images due to photobleaching and biological effects, leading to the choice of relatively short windows. In Table I, we can observe that for the fixed parameters MSE values decrease as the window h increases for a and b, which is expected. However, the estimation of the time-varying diffusion coefficient actually gets worse as the window length increases. This is because the change is abrupt and the longer windows imply a longer time for the old data to move out of the window. Thus, there is a clear trade-off between accuracy and capacity to follow the change, having several possibilities for addressing this, such as adaptive windows or combining a forward and a backward pass. Resolving this is left to future work.

TABLE I.

MSE versus window length h

	h = 75		h = 100		h = 125
parameter	x-axis	y-axis	x-axis	y-axis	x-axis	y-axis
at	.0197	.0297	.0157	.0157	.0133	.0100
bt	.0048	.0044	.0043	.0042	.0036	.0033
$D_t=\frac{q_t}{2\mathrm{\Delta }t}$	.0526	.0507	.0633	.0617	.0703	.0789

V. CONCLUSIONS

In this paper, we have developed a local likelihood estimation algorithm to track time-varying parameters in a general model that captures several common motion paradigms used in SPT. Our approach uses local likelihood in a sliding window, which is well-known in the statistics literature. We generated data using a controlled real experimental setup, and our approach was demonstrated using this generated data.

While focused on pure linear systems with additive Gaussian noise on the trajectory, the basic scheme can represent a wide variety of useful models found in SPT. One way to extend our work is by considering more complex models by replacing the underlying linear filtering and smoothing with nonlinear techniques such as sequential Monte Carlo filtering. There are also clear questions about the optimal way to select window sizes, and the effect of measurements noise and modelling errors.

Fig. 1.

Comparison of our method with Epanechnikov kernel, no kernel, and innovation-based method [22] (KFB). Measurement noise r_t = 0.1