Abstract
Single-particle electron cryomicroscopy (cryo-EM) is an increasingly popular technique for elucidating the three-dimensional structure of proteins and other biologically significant complexes at near-atomic resolution. It is an imaging method that does not require crystallization and can capture molecules in their native states.
In single-particle cryo-EM, the three-dimensional molecular structure needs to be determined from many noisy two-dimensional tomographic projections of individual molecules, whose orientations and positions are unknown. The high level of noise and the unknown pose parameters are two key elements that make reconstruction a challenging computational problem. Even more challenging is the inference of structural variability and flexible motions when the individual molecules being imaged are in different conformational states.
This review discusses computational methods for structure determination by single-particle cryo-EM and their guiding principles from statistical inference, machine learning, and signal processing that also play a significant role in many other data science applications.
Keywords: Electron cryomicroscopy, three-dimensional tomographic reconstruction, statistical estimation, conformational heterogeneity, image alignment and classification, contrast transfer function
1. INTRODUCTION
In the past few years, electron microscopy of cryogenically-cooled specimens (cryo-EM) has become a major technique in structural biology (1). Electrons interact strongly with matter, and they can be focused by magnetic lenses to yield magnified images in which individual macromolecules are visible (2). Noise obscures high-resolution details in such micrographs, so information must be combined and averaged from images of multiple copies of the macromolecules (3).
There are two main approaches in cryo-EM. In electron tomography multiple images are taken from the same field of a frozen specimen as it is tilted to various angles. A 3-D tomogram is constructed, from which are excised small 3-D subtomograms, each representing one macromolecule. The subtomograms are averaged to yield a 3-D structure. The other approach, single-particle reconstruction (SPR), starts with a single image taken from each field of the specimen. In the field are randomly-oriented and positioned macromolecules or “particles”. Through subsequent image analysis the orientations of the particles are determined. Given the orientations, particle images can be grouped and averaged, and subsequent tomographic reconstruction yields a three-dimensional density map. SPR is the subject of this review.
A very important advantage of Cryo-EM SPR is that ordered arrays (crystals) of macromolecules are not required to allow the averaging of particle images. Sets of 105 to 106 particle images are typically used to obtain maps with near-atomic resolution, and in favorable cases datasets of this size can be acquired in a few hours of microscope time.
Because in SPR crystallization of the protein is not required, structure determination is greatly simplified especially for membrane proteins for which crystallization has been extremely difficult. This advantage has led to a surge in the number of protein structures deposited in the Protein Data Bank. This number has nearly doubled each year for the past five years. In the past year some 1300 cryo-EM structures were determined, representing about 10% of all depositions (see http://www.ebi.ac.uk/pdbe/emdb/).
The process of extracting information from the images for SPR structure determination is completely computational. This review focuses on the primary computational methods and their underlying theory, as well as on important remaining computational challenges. The computational methods are implemented in one form or another in a variety of software packages that keep evolving. A list EM software is available at https://www.emdataresource.org/emsoftware.html. This review does not attempt to be a user manual and deliberately avoids mentioning specific software. Another useful online source closely related to this review is http://3demmethods.i2pc.es where readers can find a more complete list of publications related to computational methods.
1.1. Overview of Structural Biology
Molecular machines perform functions in living cells that include copying the DNA, transducing chemical and electrical signals, catalyzing reactions, causing mechanical movements, and transporting molecules into and out of cells. Molecular machines are macromolecules or macromolecular assemblies that can contain hundreds of thousands of atoms, and the goal of structural biology is to determine their three-dimensional structure–that is, the position of each atom in the machine–to try to understand the way in which the machine works. Machines such as a molecular motor or a solute transporter pass through various distinct conformations in the course of their reaction cycles. Thus a complete understanding of its operation requires the determination of multiple structures, one for each conformation.
Macromolecules are composed of polymers of small component parts. Nucleic acids (DNA and RNA) are composed of individual nucleotides, each conveying one of the four “letters” of the genetic code. Proteins are polymers of amino acids, of which there are 20 varieties. Coding sequences of DNA dictate the particular order of amino acids in the protein’s polypeptide chain, and this sequence specifies in turn the particular three-dimensional shape into which the chain folds. Because of hydrogen-bonding patterns, portions of the chain often curl up into alpha helices or lie in extended, parallel strands of beta sheets. Nevertheless, the folding process has many degrees of freedom and may also be dependent on the presence of other macromolecules such as molecular chaperones. Thus, the prediction of the 3D structure of a protein from its sequence–called the “protein folding problem”–has been successful only for some small proteins. The experimental determination of 3D structures of macromolecules is therefore a key step in understanding the fundamental processes in cells.
The size of a macromolecule is typically described as its molecular mass (or “weight”) in daltons, where 1 Da is about the mass of a hydrogen atom. A typical amino acid residue is about 120 Da in mass; a large molecular machine might be a complex of multiple subunits totalling 1MDa in molecular weight, and have physical dimensions on the order of 200 angstroms.
The atomic structure of a macromolecule is obtained by fitting an atomic model into a 3D density map. The resolution of such a map is typically specified by the period of the highest-frequency Fourier component that can be faithfully estimated. The resolution needs to be about 1.5Å if individual atoms of carbon, nitrogen etc. are to be located directly; however a map of 3 – 4 Å resolution is sufficient to produce an informative atomic model. Chemical constraints allow such lower-resolution, “near-atomic resolution” maps to be interpreted. Constraints come from the prior knowledge that proteins are composed of polypeptide chains, that the order of the amino-acid subunits in a chain is determined by the corresponding DNA sequence, and from knowledge of the geometric constraints of covalent bonds on the local arrangements of atoms.
1.2. X-ray crystallography, NMR, and cryo-EM
The first and most widely used method for determining macromolecular structures is X-ray crystallography. Development started in the 1960s, when it was found that macromolecules, especially small proteins, can be coaxed into forming highly-ordered crystals. When exposed to an X-ray beam and rotated through many angles, a crystal produces diffracted beams that are recorded as spots on film or an electronic detector. X-ray wavelengths near 1Å are used. More and better data can be collected from crystals that are cooled to cryogenic temperatures, where effects of radiation damage to the crystal are mitigated. Radiation damage limits the allowable X-ray dose. The recorded spot intensities represent the magnitude-squared coefficients of a Fourier-series expansion of the 3D density of a single unit cell of the crystal. The phases of the coefficients can be determined by various other means, so that solving an X-ray structure is, in principle, simply the inversion of a discrete Fourier transform. The most difficult part of obtaining a structure is the process of purifying and crystallizing a sample of the macromolecule in question.
A second method for protein structure determination is based on nuclear magnetic resonance (NMR). The spin of an atomic nucleus produces a small magnetic dipole. In the presence of a strong background magnetic field the nuclear dipoles can be flipped to a higher-energy state by exposure to a radio-frequency (hundreds of megahertz) field. In decaying to the ground state, there is a distance-dependent probability of exciting nearby nuclear dipoles, and it is the measurement of this coupling that provides an estimate of the pairwise distance between atoms. In small proteins (fewer than about 200 amino acid residues) it is possible to distinguish the signals from individual residues and thereby assign distances to many specific atom pairs in the protein. The 3D structure is then obtained computationally by determining the global structure from the local distance estimates.
Cryo-EM is transmission microscopy using electrons, which like X-rays allow angstrom-scale features to be detected. Also like X-ray crystallography, radiation damage is a limitation, even when mitigated by keeping the sample at low temperature. As it turns out, the amount of damage per useful scattering event is orders of magnitude smaller with electrons, which allows more information to be obtained from each copy of a macromolecular particle. Because of this, cryo-EM allows structures to be determined from relatively few particles, theoretically as few as 104 (2, 4), as compared to ~ 108 macromolecules in a minimal-sized crystal (5) for X-ray structure determination at a similar resolution.
A striking advantage of single-particle cryo-EM is its ability to work with heterogeneous ensembles of particles. In the same way that image analysis allows orientations of particles to be estimated, it also allows, within limits, the discrimination of distinct classes of particles. It is therefore possible to obtain structures of multiple conformations of a macromolecular machine from a single dataset. In some cases it is also possible to obtain 3D density maps of multiple proteins in a mixture.
1.3. Example of a cryo-EM study
Throughout this review we use a recent cryo-EM study by Sathyanarayanan et al.(6) to illustrate the steps in structure determination by cryo-EM. The object was the bacterial enzyme PaaZ which is important in the breakdown of environmental pollutants. PaaZ has two catalytic activities, a hydratase and a dehydrogenase, each having a distinct active site. Very efficient transfer of the small substrate molecule from one active site to the other had been measured, and now with the solved structure it is clear that the substrate pivots in a short “tunnel” connecting the active sites. The PaaZ complex is composed of six identical polypeptide chains totaling 500kDa in mass.
Cryo-EM specimens typically consist of a film of solution 200–600Å in thickness, containing the macromolecules of interest and frozen very rapidly by plunging into liquid ethane. The specimen is kept at cryogenic temperature throughout storage and imaging. In the PaaZ study the film of solution was formed over a graphene oxide substrate. A micrograph (Figure 1) taken with a high-end microscope and electron-counting camera, shows hundreds of dark particles on a noisy background. From 502 such micrographs 118,000 particle images were extracted, of which 86,400 were used in computing the final 3D density map. This map has 2.9Å resolution and was used to build an atomic model of the protein complex, illustrated at the end of this article.
Figure 1.
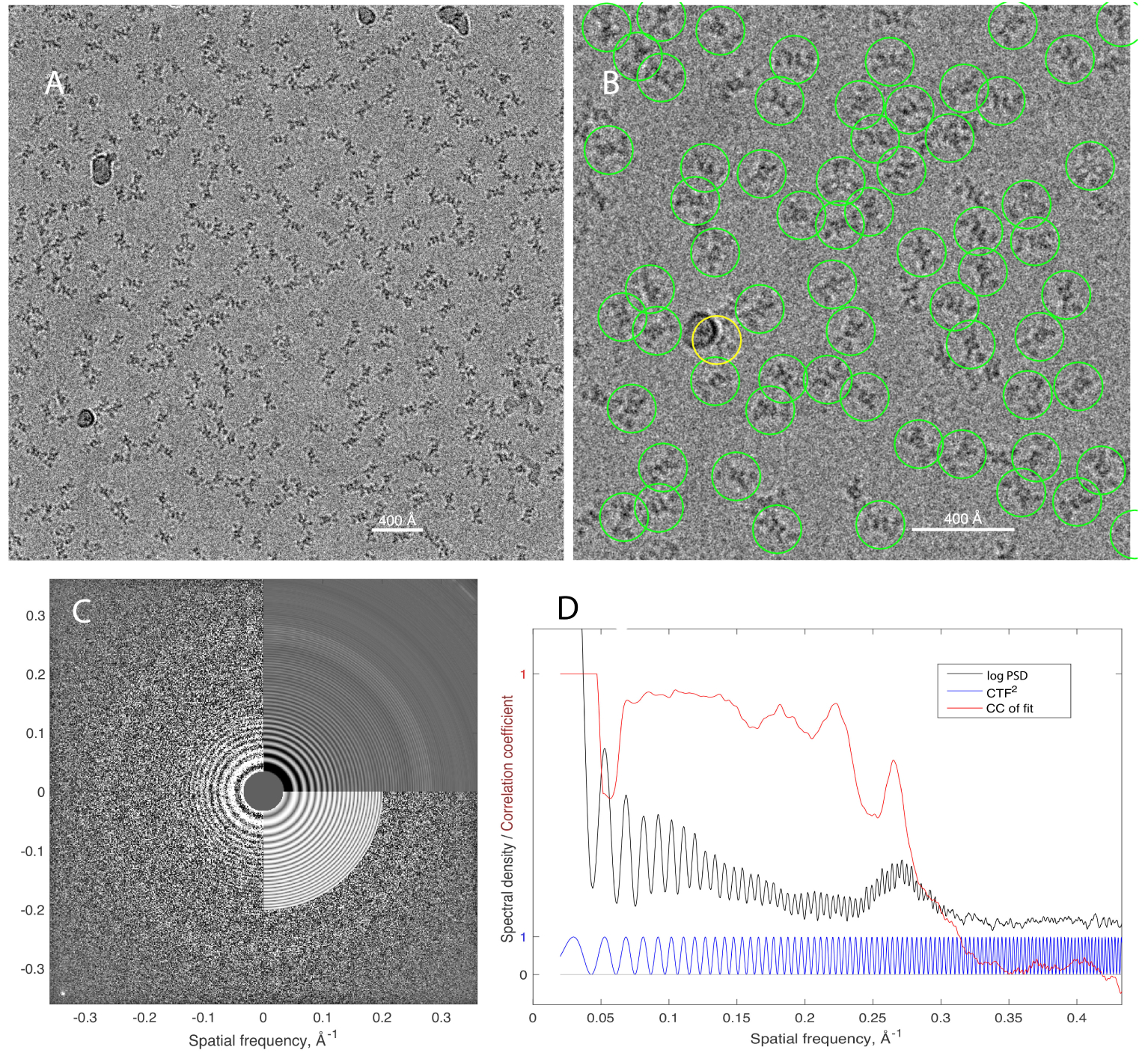
A cryo-EM micrograph of PaaZ protein particles. A, the entire micrograph, depicting a specimen area of 434 × 434 nm with a pixel size of 1.06Å. The field contains about 220 PaaZ particles along with a few contaminating “ice balls”. The image was obtained on a Titan Krios microscope at 300kV, and is displayed after low-pass filtering for clarity. B, a close-up of the micrograph with particles, selected automatically by template-matching, indicated by circles. One particle image selected in error (yellow circle) has an ice ball superimposed. C, Fit of the CTF to the 2D power spectrum of the micrograph. The left half of the image shows the experimental power spectrum of the micrograph; the upper right quadrant shows the circularly-averaged power spectrum; the lower right quadrant shows the fitted CTF2(|k|). The fitted parameters included defocus = 2.66μm and astigmatism 49 nm. The bright spot in the lower-left corner comes from a 2.1Å periodicity of the underlying crystalline graphene oxide substrate. D, a 1D representation of the power spectrum (black curve), obtained, after rough prewhitening, by approximately-circular averaging that takes into account astigmatism. Also shown is the theoretical contrast-transfer function H2 (Eq. 7; blue curve) and a plot of the cycle-by-cycle correlation coefficient between the two (red curve) showing that information is present for spatial frequencies |k| ≲ 0.3Å−1. The broad peak near |k| = 0.27Å−1 comes from the amorphous ice itself; although not in a crystal lattice, water molecules have correlated positions with a nearest-neighbor distance of about 3.7Å. Experimental data in this and subsequent figures are from (6).
2. IMAGE FORMATION MODEL
2.1. The electron microscope
The first electron microscope was built in 1933 by Ernst Ruska, an invention for which he won the Nobel Prize in Physics in 1986. The electron microscope is based on the fundamental quantum mechanical principle of the wave-particle duality of electrons. The wavelength λ of electrons with velocity v is , where h is Planck’s constant and me is the relativistic electron mass. Modern microscopes accelerate electrons to energies between 100 to 300 keV for which the associated wavelengths range from approximately 0.037 Å to 0.020 Å. Although, theoretically, sub-angstrom resolutions could be obtained, in practice, the resolution is limited to about 1 Å due to aberrations in the magnetic objective lens.
For the purpose of imaging, the molecules are frozen in fixed positions. The solution of molecules is cooled so rapidly that water molecules do not have time to crystallize, forming a vitreous ice layer (7). This rapid cooling process, known as vitrification, is critical for otherwise the high contrast contribution of crystallized ice to the image would overwhelm the faint signal coming from the molecules. Another important aspect of rapid cooling is that molecules do not have sufficient time to deform their structure from that in room temperature.
Images are formed by exposing the specimen to the electron beam. A majority of electrons recorded by the detector are those that pass through without any interaction, thus leading only to shot noise. The remaining electrons are scattered, either elastically or inelastically. Inelastic scattering damages the molecules (ionization, etc.), a process often referred to as radiation damage. Radiation damage imposes severe limitations on the total electron dose and exposure time. Inelastically-scattered electrons do not contribute to image contrast; they can be removed by an energy filter or otherwise they contribute to shot noise. The amount of inelastic scattering with ice increases with the thickness of ice, and it is therefore helpful to have a thin ice layer. Also, the thinner the ice layer is the more likely it is that the electron beam would pass through no more than a single molecule at each location.
Elastic scattering is the physical phenomenon that gives rise to tomographic projections. For cryo-EM imaging of biological molecules the most important imaging mode is phase contrast. The phase of an electron wave is shifted by its passage near the nucleus of each atom and it is elastically scattered (its energy is not changed). The positive potential it experiences (a few tens of volts over a path length on the order of an angstrom) results in a small phase advance on the order of a milliradian. The average inner potential of water (or vitreous ice) is about 5 V; for lipid bilayers, about 6.5 V; for protein, about 7.5 V. It is the contrast between protein and ice that we are usually imaging. “Phase-contrast” and “interference-contrast” devices are used in light microscopy to see cultured cells (Zernike, Nobel Prize 1953). The primitive way to get contrast by an electron microscope is to defocus the objective lens. The process by which this phase-contrast image is formed is a bit complicated. One way do derive it is by use of the Fresnel propagator, the integral that shows how wavefronts develop in free space. The Fourier transform of the Fresnel propagator yields the contrast transfer function (CTF) directly. Another way to derive it is based on diffracted electron waves, which we use here.
2.2. Phase contrast imaging and the contrast transfer function
In elastic scattering, electrons are scattered by the molecule in an angle that depends on the spatial frequency k of the electrostatic potential the molecule creates. An ideal microscope would then focus the scattered electrons on the back focal plane, where the Fourier transform of the image is formed. At the image plane, scatterings at different angles are recombined, performing Fourier synthesis, that is, the inverse Fourier transform. Because waves scattered at different angles traverse different distances, they undergo different phase shifts. Classical diffraction theory implies that to first approximation this phase shift equals πzλ|k|2, where z is the defocus distance (the distance from the specimen to the plane where the lens is focused) and |k| is the radial frequency. In addition, the weak phase approximation models the phase shift as the creation of a diffracted wave with a phase shift (with respect to the unscattered wave) of . The overall phase shift is . The total wave function ψ is the interference of the scattered wave ψs with the unscattered wave ψu, with their superposition being ψ = ψs + ψu. The probability of an electron being detected by the detector is proportional to |ψ|2. Suppose ϵ(k) is the frequency content of the sample, satisfying ϵ ⪡ 1. Then,
| 1. |
The CTF H is the deviation from 1, given by
| 2. |
Notice that the contrast is vanishing for an in-focus microscope (z = 0). The point spread function (PSF) h is the inverse Fourier transform of the CTF.
Let f by the electrostatic potential of the sample. Ignoring noise and other modeling effects that are later discussed, the micrograph I is given by
| 3. |
where P is the tomographic projection operator defined by
| 4. |
where z is the direction of the beaming electrons and 2 ⋆ denotes convolution: (h⋆g)(x, y) = ∫ h(x − u, y −v)g(u, v) du dv. The Fourier transform takes a convolution into a regular product, thus
| 5. |
where denotes the Fourier transform.
The CTF oscillates between positive and negative values: some frequency bands get positive contrast, while others are negated. The CTF starts negative, therefore particle images in micrographs look dark rather than bright. Crucially, the CTF vanishes at certain frequencies (known as “zero crossings”) and information in the original projection images is completely lost at such frequencies. As a result, images at multiple defocus levels are needed for either 2D or 3D image recovery. Notice that CTF oscillations are more frequent at high frequencies as the phase grows as |k|2. Larger defocus gives more contrast at low frequencies, but high frequency features are affected by the more frequent oscillations.
The power spectrum of the image is given by the squared magnitudes
| 6. |
(notice that H is real-valued and it is therefore not required to take absolute value before squaring.) It follows that the power spectrum vanishes on rings of radial frequencies that correspond to zero crossings of the CTF. The pattern of dark and bright rings in the power spectrum image is known as Thon rings, and facilitates the identification of the CTF (see (Figure 1C)
A more accurate model for the CTF is slightly more involved and takes the form (8, 9)
| 7. |
where Cs is the spherical aberration, w is the amplitude contrast, and E(|k|) is an envelope function.
The defocus z is modeled by the three unknown parameters z1, z2, αz as , where is the average defocus, is the astigmatism of the objective lens, and αz is the astigmatism angle (here, αk is the angle of the frequency k in polar coordinates). The astigmatism is typically small so that the CTF is approximately circularly symmetric. Notice that the spherical aberration term depends on |k|4 and becomes important only at high resolutions with k ≳ 0.25Å−1.
The envelope function is often assumed to be Gaussian of the form where B is the so-called “B-factor” or “envelope-factor”. B has units of nm2 or Å2. The envelope function has the effect of blurring the image. Good cryo-EM images have B values of 60 – 100 Å2, but even these values are not so good. At 60 Å2 spatial frequencies of 4 Å are attenuated to 1/e of their original amplitude, and the power in the signal (the square of the amplitude) is reduced to about 1/10 of the original value. Higher spatial frequencies are attenuated even more.
The envelope function is the result of several factors. A typical defocus of 1 μm is about 500,000 wavelengths away from the specimen. Now suppose that the effective electron source size is such that some of the incident electrons follow a slightly different path than others. A typical situation in a microscope with a tungsten filament source would be that the incident electrons follow paths that differ in angle by 10−3 radians. These different paths can blur out the image of high-resolution features at large distances from the specimen. The variation in electron path is called spatial incoherence. For example, suppose the specimen has a periodicity d = 1 nm. At defocus of 1 μm these results in differences in intensity with this same periodicity. But the periodic pattern imaged by electrons 10−3 radians will be shifted by 10−3 × 1 μm = 1 nm compared to the pattern imaged with zero angle (traveling along the z-axis). Thus if the paths of the incident electrons have random angles in this range, the 1 nm pattern will be completely washed out. This is why the field-emission electron gun is so important: it allows the effective electron source size to be so small that angular spreads of 10−5 or 10−6 radians are attainable, which in turn should allow high resolution at high defocus values.
There is another process that increases angular spread and therefore decreases spatial coherence, called “charging”. When an incident electron is inelastically scattered, it transfers some of its energy to an electron of one of the atoms in the specimen, typically causing it to be ejected from the specimen. The result is that the specimen starts to take on a positive charge. This charge, if it is inhomogeneous or if the sample is tilted, causes a deflection of other incident electrons. This deflection has the same effect as a large source size: it causes a variation in the electron path angle, and washes out fine details in the image.
Charging and spatial incoherence both have the effect of blurring the image. Beam induced motion and misalignment in video recording mode can contribute even more to image blur. More on that in the next subsection.
2.3. Direct electron detectors and beam induced motion
Images are acquired by a detector. In the old days, experimentalists would use photographic film, which would then be scanned for digitization. Film was mostly replaced in the early 2000s by CCD cameras, but the resolution obtained using these detectors was almost always worse than 6Å, unless using very large datasets for highly symmetric molecules like a virus for which a 3Å resolution was the state-of-the-art in 2012. This was rather disappointing, because theoretical studies predicted that cryo-EM should achieve much better resolution with significantly fewer particles. Cryo-EM was often referred to by the unflattering term “blob-ology” as it could only produce low-resolution structures that demonstrated the overall shape without important finer structural detail (10).
The situation changed dramatically around 2012 with the introduction of direct electron detector (DED) cameras (11, 12). Unlike CCD cameras, where electrons are first converted to photons and photons are converted again to an electric signal, DED cameras detect electrons directly and can even detect a single electron hit. This gives them higher detective quantum efficiency (DQE) and therefore better SNR compared with CCD cameras. Moreover, DED cameras have a high frame rate and can operate in a video mode, for example, recording 40 frames during 2 seconds of exposure time.
Recording a video of static molecules that are maintained at liquid nitrogen temperature may seem pointless: If particles do not move during the imaging process, then individual frames can simply be averaged to produce an equivalent still image. Surprisingly, early experiments using DED cameras showed that there is typically significant movement of the specimen between individual movie frames, with particles exhibiting movements as large as 20Å (13). The largest displacements are often associated with the first few frames of the movie. This movement of particles due to exposure is referred to as “beam induced motion”. Although there is no consensus on the physical origin of the motion and its modeling, one plausible explanation is that the motion is the result of energy transfer from the electron beam to the specimen: the molecules are irradiated by inelastic scattering which in turn may induce mechanical pressure on the supporting ice layer that wiggles and buckles as a result.
The image blur associated with beam induced motion can be corrected by alignment of individual movie frames, therefore significantly enhancing image quality and the overall resolution. Motion-corrected images enjoy a smaller B-factor, Thon rings are visible at higher radial frequencies (indicating better resolution), and the contrast is better. Consequently, the introduction of DED cameras has entered the cryo-EM field into a new era, because it has enabled structure determination at significantly better resolutions and from smaller macromolecules. Resolutions of 3 – 4Å were first reported (14, 15) and structures have recently been determined to about 1.5Å resolution (16). This transformative change in the power of cryo-EM is known as the “Resolution Revolution” (17).
3. PROCESSING MICROGRAPHS
The computational pipeline in single-particle cryo-EM can be roughly split into two stages. The first stage consists of methods that operate at the level of entire micrographs such as motion correction, CTF estimation, and particle picking. The second stage involves methods that operate on individual particle images such as 2D classification, 3D reconstruction, and 3D heterogeneity analysis. The two stages are also distinguished by the type of approaches. Methods in the first stage mainly rely on classical image and signal processing, whereas those in the second stage are mostly based on statistical estimation and optimization. In this section we focus on micrograph processing.
3.1. Motion correction
Motion correction refers to translational alignment and averaging of movie frames. Early methods for motion correction find the relative motion between any pair of individual frames and then estimate the frame shifts by solving a least squares problem. However, the movement is not homogeneous across the field of view, with particles in different regions moving in different velocities (in terms of both direction and speed). The local motion can be estimated by cross-correlating smaller image patches. Assuming that the velocity field is smooth with respect to both location and time, the initial estimates are further fitted and interpolated using local low-degree polynomials. After estimation of the velocity field, the frames are aligned and averaged (18, 19). It is also possible to compute dose weighted averaging, where the weights are derived from a radiation damage analysis (20).
3.2. CTF estimation and correction
Although the CTF may vary across the micrograph due to a slight tilt or due to particles at different heights within the ice layer, in most cases those possible variations are ignored to first approximation. The three defocus parameters of the CTF are then estimated from the power spectrum of the whole micrograph, utilizing the following relationship between the power spectral density (PSD) of the micrograph PSDI with the CTF H, the average PSD of the particles, carbon support and other contaminants PSDf, and the PSD of the background noise PSDb, given by
| 8. |
In principle, estimating the parameters of H from Eq.(8) is an ill-posed problem, because both PSDf and PSDb are unknown. In practice, the estimation is tractable due to the fact that PSDf and PSDb are slowly varying functions (and usually monotonically decreasing in the radial frequency), while H2 is a rapidly oscillating function.
The CTF H is approximately circularly symmetric, because astigmatism is typically small. Circularly averaging the estimated PSDI produces a cleaner radial profile which is a superposition of the slowly varying background term and the rapidly oscillating CTF-dependent term. The background term can be estimated by local averaging of the radial profile, by fitting a low-degree polynomial, or by linear programming methods. The local minima of the background subtracted PSD correspond to the zero crossings of the CTF from which the defocus value can be estimated. For noisier and more challenging micrographs for which finding local minima is too sensitive, the defocus can be determined using cross-correlation of the background subtracted PSD with the CTF (see Figure 1D). The two other defocus parameters related to astigmatism are determined in a similar fashion by cross-correlating the CTF with the background subtracted PSD in two-dimensions (21, 22).
After estimating the CTF, it is sometimes desirable to perform CTF correction of the images, that is, to undo the effect of the CTF on the images. This is useful, for example, for obtaining a better visual sense of how projection images really look like without CTF distortion. The CTF distorts the images in several ways, including delocalizing images and increasing their support size.
CTF correction requires deconvolution by the PSF h (see Eq.(3)), or equivalently, in the Fourier domain, inversion by the CTF H (see Eq.(5)). This is an ill-posed problem due to the zero crossings of the CTF and the decay of the envelope function at high frequencies. A popular approach for CTF correction is “phase flipping”, by which the filter sign(H) (which takes the values 1 and −1, depending on the sign of H) is applied to the images. Phase flipping corrects for the phase of H, but not for its varying amplitude. It is impossible to fully correct for the CTF of an individual micrograph, because there is information missing at certain frequencies where the CTF is zero; and near the zeroes and at high frequencies, where there is information, it is nevertheless often unusable because its amplitude is so low. Beyond its simplicity, another advantage of phase flipping is that it preserves the noise statistics.
Another frequently used method for CTF correction is Wiener filtering (23), which also attempts to correct for the amplitude of H. The Wiener filter minimizes the mean squared error among all linear filters and employs the spectral signal-to-noise ratio (SSNR), which is the function of the radial frequency given by (notice that PSDf and PSDb are byproducts of the CTF estimation procedure). Compared with “phase flipping”, amplitude correction is better accounted for in Wiener filtering, but information missing at zero crossings cannot be recovered.
In more advanced stages of the computational pipeline, such as 2D classification and 3D reconstruction, the problem of information loss at the zero crossings is overcome by combining data taken at various defocus values. This way the zeros from one image are filled in by data from others. Wiener filtering can be used to combine information from multiple defoci, as well as invert the effects of the CTF. Such information aggregation happens when 2D class averages are formed following the step of 2D classification, and when 3D reconstruction is performed from images with varying CTFs.
3.3. Particle picking
Current 3D reconstruction procedures require as input individual particle images rather than entire micrographs. Therefore, particle images need to be selected from the micrographs while discarding regions that contain noise or contaminants. “Particle picking” is the computational step of segmenting and boxing out particle images from micrographs. The reliability of particle detection depends on the particle size: the smaller the molecule, the lower the SNR and the image contrast. Therefore, particles of samples with small molecular mass cannot be reliably detected and oriented due to poor SNR (24). The detection threshold was recognized early on as a crucial limiting factor in SPR (2, 4). To date, the biological macromolecules whose structures have been determined using cryo-EM usually have molecular weights greater than 100 kDa. Cryo-EM using defocus contrast cannot be applied to map molecules with molecular mass below a certain threshold (~ 40 kDa at present), because particles of samples with small molecular mass cannot be reliably detected and oriented.
Image contrast depends crucially on the CTF. Large defocus increases low-frequency content and improves image contrast, making detection of particles easier. On the other hand, high-frequency features are mitigated at large defocus, and it is therefore required to use images taken at low defocus for which particle picking is more challenging.
Image contrast can be significantly improved using a Volta phase plate (VPP) that effectively shifts the phase of the CTF, thus boosting information content at low frequencies (25, 26). However, VPP are often unstable and suffer from phase drift. There is an ongoing debate regarding the added value of VPP, and other physical mechanisms for phase shift are being actively explored.
Hundreds of thousands of particle images are often required for heterogeneity analysis and high resolution reconstruction. Manual selection of such a large number of particles is tedious and time consuming. Semi-manual and automatic approaches for particle picking are therefore becoming more common.
Many procedures for particle picking are based on template matching (27, 28, 29), where a small number of template images are cross-correlated with all possible micrograph windows, and windows with high correlation values are selected. The templates can be predefined, such as Gaussian blobs or their difference (30), or they can be determined by other means. For instance, low resolution (e.g., at ~ 40Å) projection images obtained by negative staining can be used as templates. Another alternative is to manually select a relatively small number of particles, e.g., 1000 or 10000 particles, and compute from those a smaller number of 2D class averages (say, between 10 to 100) to be used as templates.
Although template matching is simple and fast, it has the potential risk of model bias in the sense that the particular choice of templates dictates which windows are selected as particles and may bias the final reconstruction towards having projections similar to the templates. In cryo-EM folklore this risk is referred to as “Einstein from noise” (31, 32): when an image of Einstein is used as template to select particles from pure noise micrographs, the average of selected particles mimics the original image of Einstein. To address this issue, an automated template-free procedure was recently proposed (33).
Following the success of deep neural networks in image recognition and natural language processing, among others, their application to particle picking has also been considered recently (34, 35). The hope is that a deep net architecture can be trained with a small number of samples to match the quality of manual selection but faster. Deep nets are also prone to model bias and the training stage is often time consuming. This is an active area of research with room for improvement in terms of automation, speed, and quality of detection. Eliminating the step of particle picking altogether by reconstructing directly from the micrographs is another exciting research avenue.
4. THREE-DIMENSIONAL RECONSTRUCTION
Three-dimensional reconstruction is the focal point of the computational pipeline of SPR, as in this step the three-dimensional electrostatic potential of the molecule needs to be estimated from the picked particle images. We therefore devote to this computational step the most attention. This section provides the mathematical, statistical, and computational aspects of 3D reconstruction.
Particle images are noisy two-dimensional tomographic projection images of the molecules taken at unknown viewing angles. Moreover, the projections are slightly off-centered, distorted by the CTF, and may be affected by other sources of variability such as variations in the ice thickness, all of which further complicate the reconstruction. Another difficulty is that the stack of images often contains a significant number of outliers that were falsely identified as particles. Such non-particle images might be images with more than one particle, images with only a part of a particle, or images of pure noise.
Related to 3D reconstruction in SPR is the reconstruction problem in classical computerized tomography (CT) that arises in medical imaging. In both cases the 3D structure needs to be determined from tomographic projection images. There are, however, some key differences between the two problems. First, the pose parameters (i.e., the viewing angles and centers) of projection images are known in CT, but they are unknown in SPR. CT reconstruction from projection images with known pose parameters is a linear inverse problem for which there exist mature solvers (36). The missing pose parameters in SPR makes it a much more challenging nonlinear inverse problem. Second, the level of noise in SPR is significantly higher compared with CT. As a result, a large number of images is required in order to average out the noise. This lends itself into computational challenges that are associated with processing large datasets.
4.1. Maximum likelihood estimation
At its core, 3D reconstruction is a statistical estimation problem. The electrostatic potential ϕ of the molecule needs to be estimated from n noisy, CTF-affected projection images I1,I2,…,In with unknown viewing angles, modeled as
| 9. |
Here, hi is the PSF of the i’th image (the inverse Fourier transform of the CTF Hi), P is the tomographic projection operator (defined in Eq. (4)), Ri is an unknown 3 × 3 rotation matrix (i.e., an element of the rotation group SO(3)) representing the unknown orientation of the i’th particle, and R ∘ ϕ denotes rotation of ϕ by R, that is, (R ∘ ϕ)(r) = ϕ(R−1r) for r = (x, y, z). The noise is represented by ϵi and assumptions on the noise statistics are discussed later. Other effects, such as varying image contrast, varying noise power spectrum, uncertainties in CTF (e.g., defocus value), and non-perfect centering can be included in the forward model (9) as well, but we leave them out for simplicity of exposition. Figure 2 is an illustration of the image-formation model.
Figure 2.
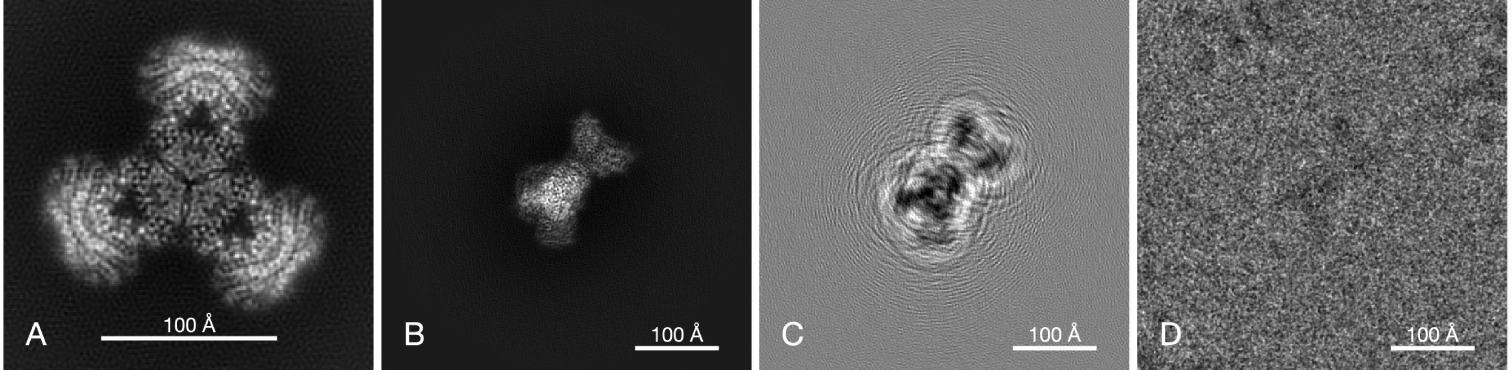
Model of image formation by defocus contrast. A, a projection of the experimental density map of PaaZ. B, projection of the map at the best-match orientation determined from a particle image. C, the same projection, but filtered by the CTF. The substantial defocus (2.6μm) results in considerable delocalization of information, resulting in fringes surrounding the particle. D, the corresponding experimental image of a particle. The large size of the particle image (440 × 440Å) is necessary to include the delocalized information up to a spatial frequency of about 0.4Å−1.
From a structural biologist’s standpoint, the 3D structure ϕ is the only parameter of interest; the rotations R1,…,Rn are nuisance parameters. While the actual values of rotations definitely impact the quality of the reconstruction, they do not carry any added value about the molecular structure. In fact, all other model parameters besides ϕ such as image shifts, per-image defocus value, noise power spectrum, and image normalizations are considered nuisance parameters.
Maximum likelihood estimation is a cornerstone of statistical estimation theory as it enjoys several appealing theoretical properties (37). Under certain mild technical conditions the maximum likelihood estimator (MLE) is a consistent estimator and it is asymptotically efficient in the sense that it achieves the Cramér-Rao bound (in other words, it has the smallest possible variance in the limit of large sample size). At first glance it seems as if there are two alternative ways of defining the MLE. One way would be to find ϕ and R1,…,Rn that maximize the likelihood function. The other way would be to find ϕ that maximizes the marginalized likelihood function, where marginalization is over all nuisance parameters (such as R1,…,Rn). The latter is the “correct” way in the sense that the technical conditions that guarantee consistency and efficiency of the MLE are satisfied. Indeed, the number of parameters must be fixed and independent of the size of the data to ensure consistency and efficiency. But if rotations are also estimated, then the number of model parameters grows indefinitely with the number of images. The failure of MLE in this case is sometimes regarded as overfitting due to the large number of model parameters. A famous example of the inconsistency of the MLE in the case of increasingly many parameters is the Neyman-Scott “paradox” (38).
Assuming white Gaussian noise with pixel variance σ2 (again, this restrictive assumption is only made for exposition purposes), the likelihood function is
| 10. |
where p is the number of pixels in an image. The marginalized likelihood function Ln(ϕ) is obtained by integrating Ln(ϕ, R1,…,Rn) over the nuisance parameters as
| 11. |
| 12. |
| 13. |
The marginalized log-likelihood is given by
| 14. |
Since the first term is independent of ϕ, the maximum marginalized likelihood estimator is defined as
| 15. |
Finding therefore requires solving a high-dimensional, nonlinear, and non-convex optimization problem. For example, for a 3D structure represented by 100 × 100 × 100 grid points, the optimization is over a space of 106 parameters. For such high-dimensional optimization problems, classical second-order algorithms such as Newton’s method may be ill suited, because executing even a single iteration may be too costly. This leaves us with first-order methods (where only the gradient is computed or approximated) and the expectation-maximization (EM) algorithm. To avoid any acronym confusion, we use ML-EM to refer to maximum-likelihood expectation-maximization. Due to its iterative nature, ML-EM is also widely referred to as iterative refinement. Both ML-EM and first-order methods are popular workhorses for 3D reconstruction.
4.2. Expectation-Maximization
ML-EM is tailored to missing data problems such as the cryo-EM reconstruction problem in which the rotations are latent variables (39, 40). ML-EM starts with some initial guess and then iterates between two steps until convergence: the expectation (E) step, and the maximization (M) step. In the E-step of iteration t, a conditional distribution of the latent variables is computed given the current estimate of the parameter of interest . That is, for each latent variable Ri, the parameter space SO(3) is discretized with S fixed rotations U1,…,US ∈ SO(3), and a vector of responsibilities (also known as weights or probabilities) of length S is computed as
| 16. |
Note that the denominator is simply a normalization to ensure the responsibilities sum to one. In the M-step, a new estimate is defined as the maximizer of the log-likelihood of the images with the given responsibilities
| 17. |
This is a linear least squares problem for which the solution can be obtained by any of the existing methods for CT reconstruction, such as the Fourier gridding method (41), non-uniform fast Fourier transform (NUFFT) methods (42, 43), or algebraic reconstruction techniques (ART) (44).
ML-EM is guaranteed to increase (more precisely, not decrease) the marginal likelihood in each iteration, and to converge to a critical point. However, it does not necessarily converge to the global optimum. In practice, either one needs to have a good initial guess, or run ML-EM multiple times with different initializations, and pick the solution with the largest likelihood value.
4.2.1. Computational complexity of ML-EM.
The E-step requires the computation of the responsibility vectors . For images of size L × L, the latent variable space of SO(3) is discretized with S = O(L3) rotations. The discretization is taken as O(L2) different viewing directions on the unit sphere, each of which is in-plane rotated O(L) times.
To compute tomographic projections of the current estimate one employs the Fourier projection slice theorem (45): For sampling O(L2) slices of size L×L, the Fourier transform of needs to be evaluated on O(L4) off-grid points. This is computed efficiently using NUFFT in O(L4) (46).
The cost of projection-matching a single noisy image Ii with a single projection image and all its in-plane rotations is O(L2 log L). This is achieved by resampling the images on a polar grid (e.g., using NUFFT) and computing the correlations over concentric rings by employing the convolution theorem and using the standard 1-D FFT. Thus, the cost of computing all responsibility vectors for n images is O(nL4 log L). This step clearly dominates the cost of generating the projection images.
The M-step involves a weighted tomographic reconstruction from the noisy images. The solution to the least squares problem Eq.(17) can be formally written as
| 18. |
where PT is the back-projection operator. In words, the least squares solution involves back-projecting all images in all possible directions followed by a matrix inversion. For computing the back-projection of an image for all possible rotations, it is more efficient to fix a viewing direction and first compute a weighted average (with respect to the latent probabilities) of the image and its in-plane rotations in O(L2 log L). The cost for repeating for all images and all viewing directions is O(nL4 log L). The matrix to be inverted can be shown to be a convolution kernel and its computation also takes O(nL4 log L) using NUFFT (43). The linear system can be solved iteratively using conjugate gradient (CG). The convolution kernel has a Toeplitz structure as a matrix and it can therefore be applied fast using FFT. Each iteration of CG costs O(L3 log L), and the overall cost of CG iterations is negligible compared to that of previous steps.
We conclude that the cost of projection-matching (E-step) is comparable to the cost of tomographic reconstruction (M-step), both given by O(nL4 log L). Typical sizes of n = 105 and L = 200 give nL4 = 1.6 × 1014. Keeping in mind that images are off-centered, another factor of 100 can easily be included to account for searching in a 10×10 square of possible translations, and a factor of at least 10 for the logarithmic factors and constants of the NUFFT. The number of flops can easily top 1017. The main factor responsible for the ballooning computational cost is the grid size L, or equivalently the resolution, due to the L4 scaling.
4.2.2. Accelerated ML-EM.
Given the high computational cost of ML-EM it is no surprise that considerable effort was invested in modifying the basic approach in order to reduce the overall computational cost. The most common way to cut the cost of the tomographic reconstruction step is by sparsification of the responsibility vectors (i.e., by setting small weights to zero). This thresholding is justified whenever the conditional distribution of the rotations is peaky around its mode (47). That is, whenever there is a high confidence in rotation assignment. In such cases, hard assignment of rotations (i.e., assigning the entire weight to the best-match rotation, and zero weight to all other rotations) is much cheaper compared to soft assignment and still provides a similar output. It should be noted that hard assignment of rotations was in fact proposed and applied for SPR long before ML-EM (48, 49). Another way to cut down the cost of the M-step is by using the gridding technique or a crude interpolation instead of the more accurate NUFFT. Given the noise in the data, the approximation error of the gridding method is often tolerable.
Computational savings of both the E and M steps are obtained by limiting the search space of the hidden variables. For example, the previous ML-EM iteration provides a good idea of the latent variable probabilities and one can set a lower bound to cut the search space. This is the basis of the branch and bound method (50).
The latent variable space can also be discretized at different levels of granularity. In adaptive EM (51, 52) several grids are used for latent variable space of rotations and shifts. After a first swap over the coarse grid, only grid points that account for 99.9% (or some other fixed threshold) of the overall probability are kept, and then the search proceeds to the finer level that corresponds to these points. Adaptive EM does not help so much in initial iterations when the latent distributions are flat, but can produce an order of magnitude acceleration near convergence when the probabilities become more “spiky”.
Subspace-EM (53) accelerates ML-EM by reducing the dimensionality of the images using principal component analysis (PCA). Correlations between the projection images and the eigen-images (principal components) are pre-computed. Then, correlations between projection images and the noisy experimental images are quickly evaluated as linear combinations of the pre-computed correlations.
Even with all these modifications and heuristics, iterative refinement is often a computationally expensive step, especially if a high resolution reconstruction or heterogeneity analysis are performed on large datasets (54, 55). It is also becoming more common for the reconstruction procedure to be applied to individual movie frames and to introduce more latent variables such as per-image defocus (47, 16) in order to reach higher resolution and squeeze out as much as possible out of the data (56). To accelerate such large-scale computations, specialized GPU implementations have been recently developed (50, 57, 58).
4.3. Bayesian Inference
The problem of tomographic reconstruction (even with known pose parameters) can be ill-posed, due to poor coverage of slices in the Fourier space and small values of the CTF at certain frequencies. The MLE can therefore have a large mean squared error (MSE), even though it is consistent and asymptotically efficient. This is a well-known problem of the maximum likelihood framework which is not specific to SPR.
A classic solution to counter the bad conditioning is using regularization which can significantly reduce the MSE. In effect, regularization incorporates a prior on the parameters of interest and the prior information is weighted accordingly with the observed data.
Without regularization, the ML-EM procedure for reconstruction was empirically observed to often produce 3D structure with artificial content at high frequencies. This is a clear indication of over-fitting. A prior on the model parameters may help mitigate these problems. This is the basic idea behind Bayesian inference and it has proven to be quite powerful in SPR (59, 52).
An important concept in Bayesian inference is that of the posterior distribution. Suppose Pr(ϕ) is a prior distribution on the parameter ϕ. Using Bayes’ law, the posterior probability of the parameters given the data X is
| 19. |
The denominator Pr(X) is called the evidence, and is independent of ϕ. Thus, maximizing the posterior probability is equivalent to maximizing Pr(X|ϕ)Pr(ϕ). Recall that Pr(X|ϕ) is the likelihood. So, the maximum a-posteriori probability (MAP) estimate is obtained by maximizing the likelihood times the prior.
The posterior distribution Pr(ϕ|X) can in fact be very powerful: If it can be somehow computed, then the mean, variance, and any statistic of interest of ϕ can be derived. This might be very useful for 3D reconstruction — as we can obtain not just the mean volume, but also confidence intervals which can prove useful for model validation. The posterior can be used to define the minimum mean square error (MMSE) estimator, given by
| 20. |
the derivation of which is analogous to the Wiener filter.
However, except for some specialized low-dimensional problems, calculating the posterior distribution is out of reach. There are clever techniques for sampling from the posterior distribution (e.g., Markov Chain Monte-Carlo methods), but they are currently not widely used in SPR.
The MAP estimate is obtained by maximizing the sum of the log-likelihood with the log-prior
| 21. |
MAP estimation is often regarded as the “poor man’s version of Bayseian inference”, since the only information obtained about the posterior distribution is its mode. The MAP estimate is a solution to an optimization problem. Sometimes it is the only practical choice for large-scale problems, for which it is too expensive to get more information about the posterior.
The expectation-maximization algorithm can also be applied to MAP estimation, and we refer to it as MAP-EM. It enjoys from similar theoretical guarantees, namely, the posterior probability increases in each iteration, and iterations converge to a critical point of the posterior. MAP-EM iterations consist of an E-step and an M-step. The E-step is the same as for MP-EM, and a soft projection-matching step is performed to compute conditional probabilities of the latent variables. In the M-step a new structure is reconstructed that maximizes the posterior (rather than the likelihood) given the conditional probabilities of the latent variables. Here is where the prior is kicking in by regularizing the tomographic reconstruction step.
A popular prior in SPR is to assume (59) that each frequency voxel of Φ (the Fourier transform of ϕ) is an independent zero-mean complex Gaussian, with variance τ2:
| 22. |
The variance function τ2 is unknown and is treated as a model parameter, that is, it is refined during EM iterations via
| 23. |
In practice, τ is assumed to be a 1-D radial function, so its new value is obtained by averaging over concentric frequency shells. The value of τ is actually multiplied by an ad-hoc constant T, recommended to be set to values between 2 and 4. The intuition is that the prior does not account for correlations between the Fourier coefficients, hence the diagonal part of the covariance matrix needs to be artificially inflated (59).
The Gaussian prior implies that the MAP 3D reconstruction update step effectively includes a Tikhonov regularization parameter inversely proportional to in the Fourier domain; equivalently, τ2 can be regarded as the SNR in the Wiener filtering framework. If the initial guess ϕ(0) for the 3D structure is of low resolution, then Eq. (23) suggests that would be large only at low-frequencies, hence high frequencies would be severely regularized. As a result, the MAP-EM iterates would gradually increase the effective resolution of the 3D map. This behavior is often referred to as frequency marching, in which the resolution gradually increases as iterative refinement proceeds.
Masking is another popular prior in SPR. In masking, the support of molecule in real space is specified and values of ϕ outside the support are masked out and set to zero. Masking can push the resolution higher by effectively decreasing the parameter space and diminishing the noise. However, this comes at risk of introducing manual bias into the reconstruction. In principle, the mask should be provided before iterative refinement (for example, if the molecule is known to be confined to a geometrical shape that deviates considerably from a ball, e.g., a cigar-like shape). In practice, however, it is common to determine the mask after a first run of iterative refinement, and provide that mask to a second run of iterative refinement. This practice is an example of a mathematical “inverse crime” (60) and is known to lead to overoptimistic results.
4.4. ML-EM 2D classification
If images corresponding to similar viewing directions can be identified, they can then be rotationally (and translationally) aligned and averaged to produce “2D class averages” that enjoy a higher SNR (see Figure 3). The 2D class averages can be used as input to ab initio structure estimation, as templates in semi-automatic procedures for particle picking, for symmetry detection, and to provide a quick assessment of the particles and the quality of the collected data.
Figure 3.

Particle images and 2D class averages. Left, a gallery of particle images extracted from micrographs. The experimental images are shown cropped to boxes of 256 pixels of 1.06Å per pixel, and contrast has been reversed to make protein “white”. Right, a complete set of 2D class averages computed from 118,000 particles using ML-EM in Relion 2.0. Numbers give the percentage of the total particle set contributing to each average image. Of the eight smallest classes, five come from small numbers of artifact images, and three converged to zero in the ML-EM iterations.
A popular way for 2D classification and averaging is using a maximum likelihood framework similar to that of 3D reconstruction and classification (61). Specifically, each experimental image is assumed to be formed from one of K fixed images followed by in-plane rotation, translation, corruption by CTF and noise. The in-plane rotations, translations, and class assignments are treated as latent variables, and expectation-maximization is used to find the maximum likelihood estimator of the K class averages. Note that since viewing directions are arbitrarily distributed over the sphere, the statistical model with a finite K is inaccurate. A large value of K leads however to high computational complexity and to low-quality results because few images are assigned to each class. ML-EM also suffers from the “rich getting richer” phenomenon: most experimental images would correlate well with, and thus be assigned to the class averages that enjoy higher SNR. As a result, ML-EM tends to output only a few, low-resolution classes. This phenomenon was recognized in (62) and is also present for ML-EM based 3D classification and refinement.
Beside the ML-EM approach there are several other methods for 2D classification which are discussed in Supplemental Appendix B,
4.5. Stochastic gradient descent
Computing the MLE or the MAP estimate requires large-scale optimization for which second-order methods are not suitable. Instead, expectation-maximization and first-order gradient methods are natural candidates for optimization. Classical gradient methods are likely however to get trapped in bad local optima. Moreover, the computation of the exact gradient is expensive as it requires processing all images at once. In stochastic gradient descent (SGD) only a single image or a few randomly selected images are used to compute an approximate gradient in each iteration (50).
SGD exploits the fact that the objective function is decoupled into individual terms, each of which depends on a single image. Indeed, the MAP estimate is the solution of the optimization problem
| 24. |
The log-posterior objective f can be written as
| 25. |
Gradient based algorithms (often called “batch”) are of the form ϕ(t+1) = ϕ(t) + αt∇f(ϕ(t)), where αt is the step size (also known as the learning rate). For SGD, the gradient is approximated by a random subset (drawn uniformly) (mini-batch) of fi’s:
| 26. |
Only images in the batch are needed to compute the approximate gradient. There are several variants of SGD that can be more suitable in practice, such SAG and SAGA, among others (63).
It is commonly believed that the inherent randomness of SGD helps to escape local minima in some non-convex problems. Note that due to its stochastic nature, SGD iterations never converge to the global optimum but rather fluctuate randomly. Hence, SGD is not useful for high-resolution 3D reconstruction. Instead, the main application of SGD is for low-resolution ab-initio modeling, and resolutions up to 10Å have been successfully obtained using this method. Although strictly speaking SGD is not a fully ab-initio method because it also requires an initial guess ϕ(0), it has been empirically observed to have little dependence on the initialization, and even random initializations perform well. There are various ab initio methods for obtaining a structure directly from particle images, which are described in Supplemental Appendix A.
5. HETEROGENEITY ANALYSIS
Unlike X-ray crystallography and NMR that measure ensembles of particles, single particle cryo-EM produces images of individual particles. Cryo-EM therefore has the potential to analyze compositionally and conformationally heterogeneous mixtures and, consequently, can be used to determine the structures of complexes in different functional states.
The heterogeneity problem of mapping the structural variability of macromolecules is widely recognized nowadays as the main computational challenge in cryo-EM (1, 64, 65, 66). Much progress has been made in distinguishing between a small number of distinct conformations, but the reconstruction of highly similar states and “3D movies” of the continuum of states remain an elusive unfulfilled promise.
Indeed, current software packages offer tools for 3D classification (or 3D sorting) and reconstruction of a small number of distinct conformations that are typically based on the maximum likelihood and Bayesian inference frameworks used for 3D reconstruction (67, 52, 55, 50, 68, 69, 70, 71). Specifically, the parameter of interest in this case are K different structures ϕ1,…,ϕK (with K > 1), and for each image the latent variables now also include the class assignment. These methods for 3D classification are quite powerful when K is small. However, the quality of their output deteriorates significantly as K increases, because for large K each class is assigned a small number of images and class assignment therefore becomes more challenging. Moreover, the computational complexity of 3D classification increases linearly with K. A common practice is to run 3D classification with a small K, discard bad classes and their corresponding images, and perform hierarchical classification on the good classes (typically using masking). There is a great deal of manual tweaking that puts in question the reliability and reproducibility of the analysis. There is a wide consensus that more computational tools are needed for analyzing highly mobile biomolecules with many, in particular, continuous spectrum of conformational changes, and method development for analyzing continuous variability is a very active field of research (72).
One useful approach for characterizing the structural variability is by estimating the variance-covariance matrix of the 3D structures in the sample. The basic theory of (73, 74) has been considerably developed over the years (75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87). The covariance matrix of the population of 3D structures can be estimated using the Fourier slice theorem for covariance. Specifically, for every pair of non-collinear frequencies, together with the origin they uniquely define a central slice; therefore, the covariance can be computed for any pair of frequencies given a full coverage of viewing directions. In contrast to classical 3D reconstruction which is well-posed even with partial coverage of viewing directions (as long as each frequency is covered by a slice), covariance estimation requires full coverage which is a far more stringent requirement. Moreover, the covariance matrix is of size L3 × L3, and storing O(L6) entries increases quickly with L. The computational complexity and the number of images required for accurate estimation also grow quickly as a function of L. As a result, the covariance matrix is usually estimated only at low-resolution. Still, the variance map indicates flexible regions of the molecule, and the leading principal components of the covariance matrix offer considerable dimension reduction.
Methods based on normal mode analysis of the 3D reconstruction (88, 89, 90) or of the multiple 3D classes (91) have also been applied. However, extrapolating the harmonic oscillator approximation underlying normal mode analysis to complex elastic deformations is questionable.
Methods based on manifold learning, specifically, diffusion maps, have also been proposed to analyze continuous variability. Similar to the covariance matrix approach, also here the rotations are assumed to be known. One approach performs manifold learning on disjoint subsets of 2D images corresponding to similar viewing directions (92, 93, 94). In this way, the heterogeneity at the level of 2D images can be characterized, and insight into energy landscapes can be obtained. However, the nature of 3D variability is not fully resolved because stitching the manifolds resulting from different viewing directions does not have an adequate solution at present. An alternative diffusion map approach that performs directly at the 3D level has been recently developed, but its evaluation on experimental datasets in still ongoing (95).
Methods for continuous heterogeneity analysis that do not require known rotations have also been recently introduced. Multi-body refinement (96, 97) takes a segmentation of a 3D molecular reconstruction and attempts to refine each part separately from a static base model, with independent viewing directions and shift parameters for each part. Multi-body refinement, however, may fail to accurately reconstruct the interface between moving parts and it cannot capture non-rigid movements typical of complex macromolecules. Other recent approaches that are still under development and aim to recover continuous heterogeneity jointly with rotations are based on representing the 3D movie of molecules as a higher dimensional function (98) and using deep neural nets (99).
6. EVALUATION OF THE MAP AND FITTING THE MODEL
Given the 3D reconstruction in the form of a density map, the final step in structure determination is to fit an atomic model, as illustrated in Figure 4 for the PaaZ macromolecule. The validity of the model is however dependent on the resolution of the map, and the process of determining this resolution is quite different from methods employed in other forms of microscopy. There are also techniques to test for errors in the creation of the map and in the estimation of its resolution. These methods are described in Supplemental Appendix C.
Figure 4.
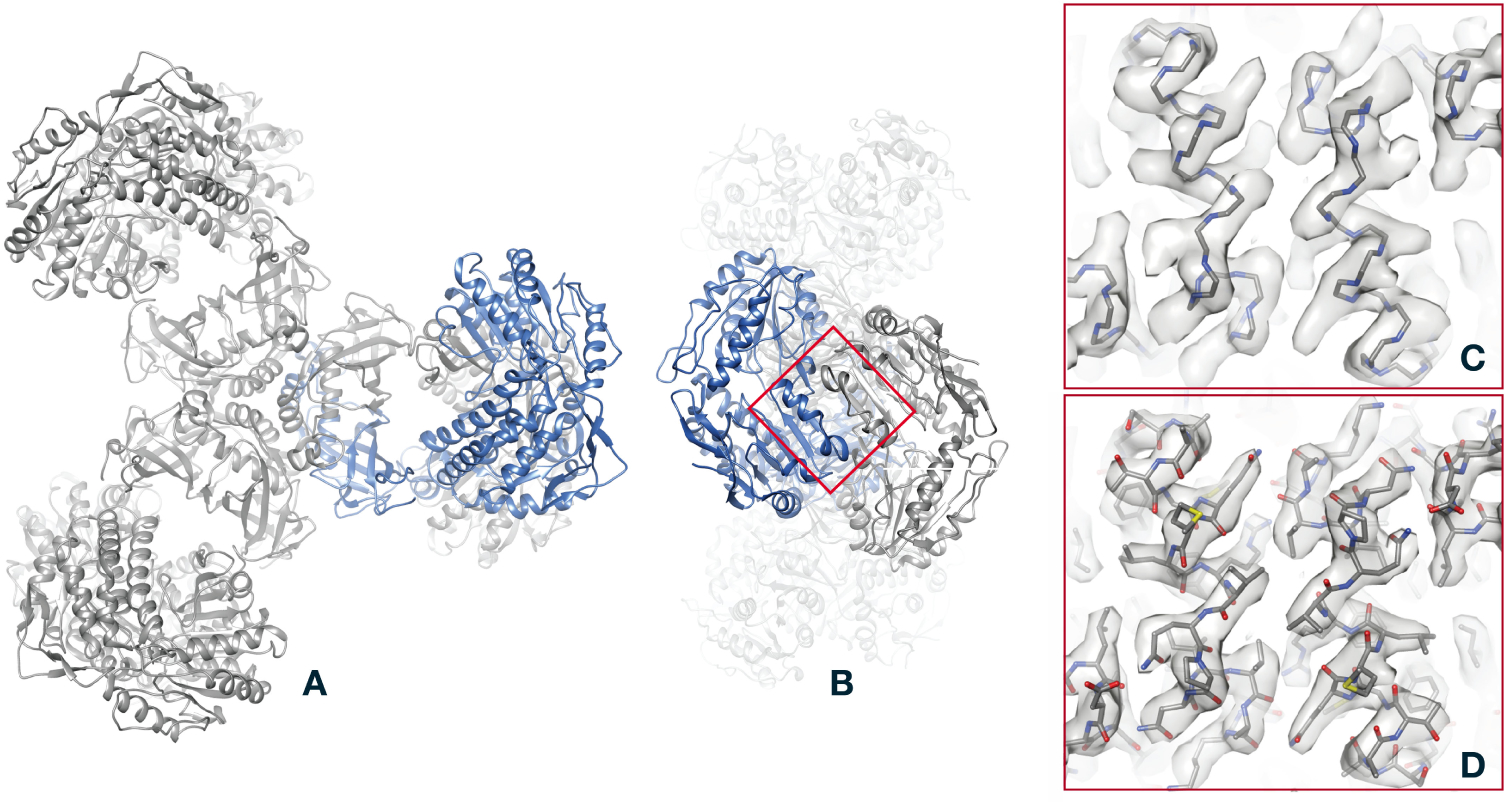
The last step in structure determination: fit of an atomic model to the PaaZ reconstruction. A, overview of the PaaZ model, with ribbons denoting the folding of the polypeptide chain. To give an idea of the physical scale of the model, the helical structures (alpha helices) have a pitch of 5.4Å. One of the six identical subunits in the PaaZ macromolecule is colored blue. B, an “end” view of the model, obtained by a 90° rotation. C, superposition of the polypeptide backbone on the density map (gray surface rendering), shown for the region of two alpha helices marked by the red square in B. D, comparison of the map and model, this time with all non-hydrogen atoms shown. Although individual atoms are not resolved in the 2.9Å map, bulges in the helical features of the map constrain the angles of flexible bonds in the amino-acid side chains, so that atom positions are well determined.
7. FUTURE CHALLENGES
7.1. Specimen preparation and protein denaturation
A protein macromolecule is a linear polymer of amino acids that folds into a particular shape due to various non-covalent interactions. The surface of a protein has many polar and charged groups that interact strongly with the surrounding water molecules, while the interior is hydrophobic, with essentially all polar groups stabilized by fixed hydrogen bonds. When exposed to a hydrophobic environment or an air-water interface most proteins unfold–that is, denature–bringing the hydrophobic interior residues to the surface. Exposed hydrophobic regions in neighboring proteins coalesce, yielding amorphous aggregates of misfolded proteins.
Recall that a cryo-EM specimen consists of a film of protein solution only a few hundred angstroms thick which is quickly frozen to produce an amorphous ice layer. During the time before freezing, typically several seconds, a protein molecule diffuses rapidly (diffusion constant ~ 1013 Å2/s) and has many opportunities to diffuse up to the edge of the film. Some proteins appear to remain as intact single particles in cryo-EM specimens, while others form large aggregates that are useless for structure determination. The best remedy appears to be the provision of solid substrate to anchor proteins within the aqueous layer. Such an aggregation problem was encountered in the PaaZ study (6) and was solved by the provision of a layer of graphene oxide bounding the aqueous film. The protein adsorbs to the graphene oxide and is thereby protected from the air-water interface. Graphene and its derivatives form an ideal support film because graphene is a two-dimensional crystal only one carbon-atom thick, and so introduces very little electron scattering to the specimen. The fabrication of EM grids with graphene derivatives of good surface properties is unfortunately still an art form, such that a general substrate for single particle work remains to be developed.
Another problem that arises in specimen preparation is preferred orientation of particles. Many proteins orient with one surface preferentially interacting with the air-water interface, or preferentially interacting with a supporting film. The result is an uneven distribution of projection angles, resulting in poor 3D reconstructions. Sometimes the introduction of surfactants, changes in pH or other measures can mitigate the preferred orientations. If necessary, data are collected from tilted specimens (100) because this provides a larger range of orientations. However, tilting the sample is disadvantageous for high-resolution work because the effects of beam-induced specimen motion are increased. This is because the largest motions are normal to the specimen plane. New computational approaches for datasets with preferred orientations would be very welcome in the field.
One solution to both of these issues in cryo-EM sample preparation would be to image the macromolecules without removing them from their native cellular environment. This is commonly done (but with low-resolution results) in cryo-EM tomography. Might this also be possible for SPR, given better computational tools? The very crowded environment inside cells results in greatly increased background noise, but promising results in the detection and orientation of large macromolecules (ribosomes) have been reported from cellular imaging (101).
7.2. The B factor and resolution limitation
The envelope function of the CTF, summarized by the B factor, is the ultimate limitation in high-resolution cryo-EM projects. At present the B-factor from a high-quality dataset is roughly 100, which as we saw in Section 2.2 represents an attenuation of signal to 1/e already at 5Å resolution, or 1/e2 at 2.5Å. Physical contributions to this limitation in resolution have been described in a recent review (102) and are summarized here.
Current high-end microscopes have highly coherent electron beams and extremely stable stages, so they make little contribution to the blurring represented by the B-factor. Charging of the specimen also makes little contribution if proper imaging conditions are used (103). There is however unavoidable particle movement due to beam-induced rearrangement of water molecules in the vitreous ice (104). Water molecules move with a diffusion constant of about 1Å2 per electron dose of 1e/Å2 and so produce Brownian motion of particles. This motion may become substantial for smaller particles, and per-particle motion correction has been implemented (56).
The largest contribution to the B-factor seems to be uncorrected beam-induced specimen movement. Motion correction during exposure has greatly improved cryo-EM imaging, but it is during the initial dose of 1 – 2e/Å2, typically captured in the first frame of an acquired movie, that the largest specimen movements occur. Even if a faster movie frame rate is employed it is not clear that there is sufficient signal to allow these movements to be adequately tracked and compensated, but improvements from novel computational approaches would have a large effect. Radiation damage is typically characterized as a loss of high-resolution signal, and after 2e/Å of exposure the radiation damage corresponds to more than half of the B-factor value that is observed.
7.3. Autonomous data processing
Traditionally there is user intervention in two parts of the data processing pipeline. At the stage of particle picking, the user checks the particle selection and tunes parameters, such as the selection threshold, to ensure a low number of false-positives. Farther along the processing pipeline, users perform 2D classification or reconstruct multiple 3D volumes (3D classification) to further select a subset of the particle images that produce the “best” reconstruction. It often occurs that a majority of particle images are rejected at this stage.
Researchers are often happy to reject large portions of their datasets in order to achieve higher-resolution reconstructions. The rejected particles are sometimes contaminating macromolecules, or complexes missing one or more subunits. Rejected particles may be partially denatured or are aggregated. Improvements in biochemical purity and in specimen preparation may reduce these populations in the future, but meanwhile improved outlier-rejection algorithms would help greatly. However there is also the possibility that rejected particles represent alternative conformations of the complex, or states in which there is more flexibility; in these cases a more objective process of evaluating particle images through an entirely automated pipeline would be very desirable.
Another reason for automation of the processing pipeline has to do with quality control of data acquisition. In a cryo-EM structure project traditionally one spends some hours or days collecting micrographs, and then carries out the image processing offline over some days or weeks afterward. Unfortunately only after creation of the final 3D map does one know for sure that a dataset yields a high-resolution structure. Some hints of data quality can be obtained along the way: correlations to high resolution in power spectrum fits (Figure 1D) and the visibility of fine structure in 2D classes provide some confidence that a high-resolution structure will result. Automatic data processing, concurrent with acquisition, is currently being implemented at cryo-EM centers. This is beginning to allow experimenters to evaluate quickly the data quality at the 2D classification stage and even with 3D maps. Such real-time evaluation can greatly increase the throughput of cryo-EM structure determination. Most importantly it accelerates the tedious process of specimen optimization. Further, it allows for much better use of time on expensive microscopes for high-resolution data collection.
Supplementary Material
ACKNOWLEDGMENTS
A.S. was partially supported by NSF BIGDATA Award IIS-1837992, award FA9550-17-1-0291 from AFOSR, the Simons Foundation Math+X Investigator Award, and the Moore Foundation Data-Driven Discovery Investigator Award. F.J.S. was supported by NIH grants R25 EY029125 and R01NS021501. The authors are grateful to G. Cannone (MRC Laboratory of Molecular Biology, Cambridge, U.K.) and K.R. Vinothkumar (National Center for Biological Sciences, Bangalore, India) for sharing the raw images and intermediate data underlying their published study (6). The authors thank Philip Baldwin, Alberto Bartesaghi, Tamir Bendory, Nicolas Boumal, Ayelet Heimowitz, Ti-Yen Lan, and Amit Moscovich for commenting on an earlier version of this review.
Footnotes
DISCLOSURE STATEMENT
The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
LITERATURE CITED
- 1.Nogales E 2016. The development of cryo-EM into a mainstream structural biology technique. Nature Methods 13:24–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Henderson R 1995. The potential and limitations of neutrons, electrons and X-rays for atomic resolution microscopy of unstained biological molecules. Quarterly reviews of biophysics 28:171–193 [DOI] [PubMed] [Google Scholar]
- 3.Frank J 2006. Three-dimensional electron microscopy of macromolecular assemblies. Academic Press [Google Scholar]
- 4.Glaeser RM. 1999. Electron crystallography: present excitement, a nod to the past, anticipating the future. Journal of structural biology 128:3–14 [DOI] [PubMed] [Google Scholar]
- 5.Holton JM, Frankel KA. 2010. The minimum crystal size needed for a complete diffraction data set. Acta Crystallographica Section D: Biological Crystallography 66:393–408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sathyanarayanan N, Cannone G, Gakhar L, Katagihallimath N, Sowdhamini R, et al. 2019. Molecular basis for metabolite channeling in a ring opening enzyme of the phenylacetate degradation pathway. Nature communications 10:1–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dubochet J, Lepault J, Freeman R, Berriman J, Homo JC. 1982. Electron microscopy of frozen water and aqueous solutions. Journal of Microscopy 128:219–237 [Google Scholar]
- 8.Erickson H, Klug A. 1971. Measurement and compensation of defocusing and aberrations by Fourier processing of electron micrographs. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences: 105–118 [Google Scholar]
- 9.Wade R 1992. A brief look at imaging and contrast transfer. Ultramicroscopy 46:145–156 [Google Scholar]
- 10.Smith MT, Rubinstein JL. 2014. Beyond blob-ology. Science 345:617–619 [DOI] [PubMed] [Google Scholar]
- 11.Li X, Mooney P, Zheng S, Booth CR, Braunfeld MB, et al. 2013. Electron counting and beam-induced motion correction enable near-atomic-resolution single-particle cryo-EM. Nature Methods 10:584–590 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.McMullan G, Faruqi A, Henderson R. 2016. Direct electron detectors. In The Resolution Revolution: Recent Advances In cryoEM, ed. Crowther R, vol. 579of Methods in Enzymology. Academic Press, 1–17 [DOI] [PubMed] [Google Scholar]
- 13.Brilot AF, Chen JZ, Cheng A, Pan J, Harrison SC, et al. 2012. Beam-induced motion of vitrified specimen on holey carbon film. Journal of structural biology 177:630–637 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liao M, Cao E, Julius D, Cheng Y. 2013. Structure of the TRPV1 ion channel determined by electron cryo-microscopy. Nature 504:107–112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Amunts A, Brown A, Bai Xc, Llácer JL, Hussain T, et al. 2014. Structure of the yeast mitochondrial large ribosomal subunit. Science 343:1485–1489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bartesaghi A, Aguerrebere C, Falconieri V, Banerjee S, Earl LA, et al. 2018. Atomic resolution cryo-EM structure of β-galactosidase. Structure 26:848–856 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kühlbrandt W 2014. The resolution revolution. Science 343:1443–1444 [DOI] [PubMed] [Google Scholar]
- 18.Ripstein Z, Rubinstein J. 2016. Processing of Cryo-EM movie data. Methods in Enzymology 579:103–124 [DOI] [PubMed] [Google Scholar]
- 19.Zheng SQ, Palovcak E, Armache JP, Verba KA, Cheng Y, Agard DA. 2017. MotionCor2: anisotropic correction of beam-induced motion for improved cryo-electron microscopy. Nature Methods [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Grant T, Grigorieff N. 2015. Measuring the optimal exposure for single particle cryo-EM using a 2.6 å reconstruction of rotavirus VP6. Elife 4:e06980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rohou A, Grigorieff N. 2015. Ctffind4: Fast and accurate defocus estimation from electron micrographs. Journal of structural biology 192:216–221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhang K 2016. Gctf: Real-time ctf determination and correction. Journal of structural biology 193:1–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sindelar CV, Grigorieff N. 2011. An adaptation of the wiener filter suitable for analyzing images of isolated single particles. Journal of structural biology 176:60–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sigworth FJ. 2004. Classical detection theory and the cryo-em particle selection problem. Journal of structural biology 145:111–122 [DOI] [PubMed] [Google Scholar]
- 25.Danev R, Baumeister W. 2016. Cryo-EM single particle analysis with the Volta phase plate. Elife 5:e13046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Khoshouei M, Radjainia M, Baumeister W, Danev R. 2017. Cryo-EM structure of haemoglobin at 3.2 Å determined with the Volta phase plate. Nature communications 8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Frank J, Wagenknecht T. 1983. Automatic selection of molecular images from electron micrographs. Ultramicroscopy 12:169–175 [DOI] [PubMed] [Google Scholar]
- 28.Chen JZ, Grigorieff N. 2007. SIGNATURE: a single-particle selection system for molecular electron microscopy. Journal of structural biology 157:168–173 [DOI] [PubMed] [Google Scholar]
- 29.Scheres SH. 2015. Semi-automated selection of cryo-EM particles in RELION-1.3. Journal of structural biology 189:114–122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Voss N, Yoshioka C, Radermacher M, Potter C, Carragher B. 2009. DoG picker and TiltPicker: software tools to facilitate particle selection in single particle electron microscopy. Journal of structural biology 166:205–213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shatsky M, Hall RJ, Brenner SE, Glaeser RM. 2009. A method for the alignment of heterogeneous macromolecules from electron microscopy. Journal of structural biology 166:67–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Henderson R 2013. Avoiding the pitfalls of single particle cryo-electron microscopy: Einstein from noise. Proceedings of the National Academy of Sciences 110:18037–18041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Heimowitz A, Andén J, Singer A. 2018. APPLE picker: Automatic particle picking, a low-effort cryo-EM framework. Journal of structural biology 204:215–227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang F, Gong H, Liu G, Li M, Yan C, et al. 2016. DeepPicker: A deep learning approach for fully automated particle picking in cryo-EM. Journal of structural biology 195:325–336 [DOI] [PubMed] [Google Scholar]
- 35.Bepler T, Morin A, Rapp M, Brasch J, Shapiro L, et al. 2019. Positive-unlabeled convolutional neural networks for particle picking in cryo-electron micrographs. Nature Methods: 1–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Herman GT. 2009. Fundamentals of computerized tomography: Image reconstruction from projections. Springer Science & Business Media [Google Scholar]
- 37.Wasserman L 2013. All of statistics: a concise course in statistical inference. Springer Science & Business Media [Google Scholar]
- 38.Neyman J, Scott EL, et al. 1948. Consistent estimates based on partially consistent observations. Econometrica 16:1–32 [Google Scholar]
- 39.Dempster A, Laird N, Rubin D. 1977. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological): 1–38 [Google Scholar]
- 40.Sigworth F 1998. A maximum-likelihood approach to single-particle image refinement. Journal of structural biology 122:328–339 [DOI] [PubMed] [Google Scholar]
- 41.Penczek PA, Renka R, Schomberg H. 2004. Gridding-based direct fourier inversion of the three-dimensional ray transform. JOSA A 21:499–509 [DOI] [PubMed] [Google Scholar]
- 42.Dutt A, Rokhlin V. 1993. Fast Fourier transforms for nonequispaced data. SIAM Journal on Scientific computing 14:1368–1393 [Google Scholar]
- 43.Wang L, Shkolnisky Y, Singer A. 2013. A Fourier-based approach for iterative 3D reconstruction from cryo-EM images. arXiv preprint arXiv:1307.5824 [Google Scholar]
- 44.Marabini R, Herman GT, Carazo JM. 1998. 3D reconstruction in electron microscopy using ART with smooth spherically symmetric volume elements (blobs). Ultramicroscopy 72:53–65 [DOI] [PubMed] [Google Scholar]
- 45.Natterer F 1986. The mathematics of computerized tomography. Springer [Google Scholar]
- 46.Barnett AH, Magland J, af Klinteberg L. 2019. A parallel nonuniform fast fourier transform library based on an exponential of semicircle” kernel. SIAM Journal on Scientific Computing 41:C479–C504 [Google Scholar]
- 47.Grigorieff N 2007. FREALIGN: High-resolution refinement of single particle structures. Journal of structural biology 157:117–125 [DOI] [PubMed] [Google Scholar]
- 48.Harauz G, Ottensmeyer F. 1983. Direct three-dimensional reconstruction for macromolecular complexes from electron micrographs. Ultramicroscopy 12:309–319 [Google Scholar]
- 49.Harauz G, Ottensmeyer F. 1984. Nucleosome reconstruction via phosphorous mapping. Science 226:936–941 [DOI] [PubMed] [Google Scholar]
- 50.Punjani A, Rubinstein JL, Fleet DJ, Brubaker MA. 2017. cryoSPARC: algorithms for rapid unsupervised cryo-EM structure determination. Nature Methods 14:290–296 [DOI] [PubMed] [Google Scholar]
- 51.Tagare HD, Barthel A, Sigworth FJ. 2010. An adaptive expectation–maximization algorithm with GPU implementation for electron cryomicroscopy. Journal of structural biology 171:256–265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Scheres S 2012. RELION: implementation of a Bayesian approach to cryo-EM structure determination. Journal of structural biology 180:519–530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Dvornek NC, Sigworth FJ, Tagare HD. 2015. SubspaceEM: A fast maximum-a-posteriori algorithm for cryo-EM single particle reconstruction. Journal of structural biology 190:200–214 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Scheres SH, Valle M, Grob P, Nogales E, Carazo JM. 2009. Maximum likelihood refinement of electron microscopy data with normalization errors. Journal of structural biology 166:234–240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Scheres SH. 2016. Processing of structurally heterogeneous cryo-EM data in RELION. In Methods in enzymology, vol. 579. Elsevier, 125–157 [DOI] [PubMed] [Google Scholar]
- 56.Zivanov J, Nakane T, Scheres SH. 2019. A Bayesian approach to beam-induced motion correction in cryo-EM single-particle analysis. IUCrJ 6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kimanius D, Forsberg BO, Scheres SH, Lindahl E. 2016. Accelerated cryo-EM structure determination with parallelisation using GPUs in RELION-2. eLife 5:e18722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zivanov J, Nakane T, Forsberg BO, Kimanius D, Hagen WJ, et al. 2018. New tools for automated high-resolution cryo-EM structure determination in RELION-3. Elife 7:e42166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Scheres SH. 2012. A Bayesian view on cryo-EM structure determination. Journal of molecular biology 415:406–418 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kaipio J, Somersalo E. 2006. Statistical and computational inverse problems, vol. 160. Springer Science & Business Media [Google Scholar]
- 61.Scheres SH, Valle M, Nuñez R, Sorzano CO, Marabini R, et al. 2005. Maximum-likelihood multi-reference refinement for electron microscopy images. Journal of molecular biology 348:139–149 [DOI] [PubMed] [Google Scholar]
- 62.Sorzano C, Bilbao-Castro J, Shkolnisky Y, Alcorlo M, Melero R, et al. 2010. A clustering approach to multireference alignment of single-particle projections in electron microscopy. Journal of structural biology 171:197–206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bottou L, Curtis FE, Nocedal J. 2018. Optimization methods for large-scale machine learning. Siam Review 60:223–311 [Google Scholar]
- 64.Glaeser RM. 2016. How good can cryo-EM become? Nature Methods 13:28–32 [DOI] [PubMed] [Google Scholar]
- 65.Subramaniam S, Kühlbrandt W, Henderson R. 2016. CryoEM at IUCrJ: a new era. IUCrJ 3:3–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Sorzano COS, Carazo JM. 2017. Challenges ahead electron microscopy for structural biology from the image processing point of view. arXiv preprint arXiv:1701.00326 [Google Scholar]
- 67.Scheres SH, Gao H, Valle M, Herman GT, Eggermont PP, et al. 2007. Disentangling conformational states of macromolecules in 3D-EM through likelihood optimization. Nature Methods 4:27–29 [DOI] [PubMed] [Google Scholar]
- 68.Ludtke SJ. 2016. Single-particle refinement and variability analysis in EMAN2.1. In Methods in enzymology, vol. 579. Elsevier, 159–189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.De la Rosa-Trevín J, Otón J, Marabini R, Zaldivar A, Vargas J, et al. 2013. Xmipp 3.0: an improved software suite for image processing in electron microscopy. Journal of structural biology 184:321–328 [DOI] [PubMed] [Google Scholar]
- 70.Lyumkis D, Brilot AF, Theobald DL, Grigorieff N. 2013. Likelihood-based classification of cryo-EM images using FREALIGN. Journal of structural biology 183:377–388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Grant T, Rohou A, Grigorieff N. 2018. cisTEM, user-friendly software for single-particle image processing. Elife 7:e35383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Sorzano C, Jiménez A, Mota J, Vilas J, Maluenda D, et al. 2019. Survey of the analysis of continuous conformational variability of biological macromolecules by electron microscopy. Acta Crystallographica Section F: Structural Biology Communications 75:19–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Liu W, Frank J. 1995. Estimation of variance distribution in three-dimensional reconstruction. I. Theory. JOSA A 12:2615–2627 [DOI] [PubMed] [Google Scholar]
- 74.Liu W, Boisset N, Frank J. 1995. Estimation of variance distribution in three-dimensional reconstruction. II. Applications. JOSA A 12:2628–2635 [DOI] [PubMed] [Google Scholar]
- 75.Penczek PA. 2002. Variance in three-dimensional reconstructions from projections. In Biomedical Imaging, 2002. Proceedings. 2002 IEEE International Symposium on. IEEE [Google Scholar]
- 76.Penczek PA, Yang C, Frank J, Spahn CM. 2006. Estimation of variance in single-particle reconstruction using the bootstrap technique. Journal of structural biology 154:168–183 [DOI] [PubMed] [Google Scholar]
- 77.Zhang W, Kimmel M, Spahn CM, Penczek PA. 2008. Heterogeneity of large macromolecular complexes revealed by 3D cryo-EM variance analysis. Structure 16:1770–1776 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Penczek P, Kimmel M, Spahn C. 2011. Identifying conformational states of macromolecules by eigen-analysis of resampled cryo-EM images. Structure 19:1582–1590 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Liao H, Frank J. 2010. Classification by bootstrapping in single particle methods. In 2010 IEEE International Symposium on Biomedical Imaging (ISBI). IEEE [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Zheng Y, Wang Q, Doerschuk PC. 2012. Three-dimensional reconstruction of the statistics of heterogeneous objects from a collection of one projection image of each object. JOSA A 29:959–970 [DOI] [PubMed] [Google Scholar]
- 81.Wang Q, Matsui T, Domitrovic T, Zheng Y, Doerschuk PC, Johnson JE. 2013. Dynamics in cryo EM reconstructions visualized with maximum-likelihood derived variance maps. Journal of structural biology 181:195–206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Xu N, Veesler D, Doerschuk PC, Johnson JE. 2018. Allosteric effects in bacteriophage HK97 procapsids revealed directly from covariance analysis of cryo EM data. Journal of structural biology 202:129–141 [DOI] [PubMed] [Google Scholar]
- 83.Tagare HD, Kucukelbir A, Sigworth FJ, Wang H, Rao M. 2015. Directly reconstructing principal components of heterogeneous particles from cryo-EM images. Journal of structural biology 191:245–262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Klaholz BP. 2015. Structure sorting of multiple macromolecular states in heterogeneous cryo-EM samples by 3D multivariate statistical analysis. Open Journal of Statistics 5:820 [Google Scholar]
- 85.Katsevich E, Katsevich A, Singer A. 2015. Covariance matrix estimation for the cryo-EM heterogeneity problem. SIAM Journal on Imaging Sciences 8:126–185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Andén J, Katsevich E, Singer A. 2015. Covariance estimation using conjugate gradient for 3D classification in cryo-EM. In 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI). IEEE [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Andén J, Singer A. 2018. Structural variability from noisy tomographic projections. SIAM Journal on Imaging Sciences 11:1441–1492 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Jin Q, Sorzano COS, De La Rosa-Trevín JM, Bilbao-Castro JR, Nunez-Ramirez R, et al. 2014. Iterative elastic 3D-to-2D alignment method using normal modes for studying structural dynamics of large macromolecular complexes. Structure 22:496–506 [DOI] [PubMed] [Google Scholar]
- 89.Sorzano COS, De La Rosa-Trevín JM, Tama F, Jonić S. 2014. Hybrid electron microscopy normal mode analysis graphical interface and protocol. Journal of structural biology 188:134–141 [DOI] [PubMed] [Google Scholar]
- 90.Jonić S 2017. Computational methods for analyzing conformational variability of macromolecular complexes from cryo-electron microscopy images. Current opinion in structural biology 43:114–121 [DOI] [PubMed] [Google Scholar]
- 91.Schilbach S, Hantsche M, Tegunov D, Dienemann C, Wigge C, et al. 2017. Structures of transcription pre-initiation complex with TFIIH and Mediator. Nature 551:204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Dashti A, Schwander P, Langlois R, Fung R, Li W, et al. 2014. Trajectories of the ribosome as a Brownian nanomachine. Proceedings of the National Academy of Sciences 111:17492–17497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Frank J, Ourmazd A. 2016. Continuous changes in structure mapped by manifold embedding of single-particle data in cryo-EM. Methods 100:61–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Dashti A, Hail DB, Mashayekhi G, Schwander P, des Georges A, et al. 2018. Functional pathways of biomolecules retrieved from single-particle snapshots. bioRxiv: 291922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Moscovich A, Halevi A, Andén J, Singer A. 2019. Cryo-EM reconstruction of continuous heterogeneity by Laplacian spectral volumes. Inverse Problems Accepted [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Shan H, Wang Z, Zhang F, Xiong Y, Yin CC, Sun F. 2016. A local-optimization refinement algorithm in single particle analysis for macromolecular complex with multiple rigid modules. Protein & cell 7:46–62 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Nakane T, Kimanius D, Lindahl E, Scheres SH. 2018. Characterisation of molecular motions in cryo-EM single-particle data by multi-body refinement in RELION. eLife 7:e36861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Lederman RR, Andén J, Singer A. 2019. Hyper-molecules: on the representation and recovery of dynamical structures, with application to flexible macro-molecular structures in cryo-EM. arXiv preprint arXiv:1907.01589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Zhong ED, Bepler T, Davis JH, Berger B. 2019. Reconstructing continuously heterogeneous structures from single particle cryo-EM with deep generative models. arXiv preprint arXiv:1909.05215 [Google Scholar]
- 100.Tan YZ, Baldwin PR, Davis JH, Williamson JR, Potter CS, et al. 2017. Addressing preferred specimen orientation in single-particle cryo-EM through tilting. Nature methods 14:793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Rickgauer JP, Grigorieff N, Denk W. 2017. Single-protein detection in crowded molecular environments in cryo-EM images. Elife 6:e25648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Glaeser RM. 2019. How good can single-particle cryo-EM become? What remains before it approaches its physical limits? Annual review of biophysics 48:45–61 [DOI] [PubMed] [Google Scholar]
- 103.Russo CJ, Henderson R. 2018. Microscopic charge fluctuations cause minimal contrast loss in cryoEM. Ultramicroscopy 187:56–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.McMullan G, Vinothkumar K, Henderson R. 2015. Thon rings from amorphous ice and implications of beam-induced brownian motion in single particle electron cryo-microscopy. Ultramicroscopy 158:26–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


