Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Sep 2.
Published in final edited form as: Neuroimage. 2020 Aug 14;223:117242. doi: 10.1016/j.neuroimage.2020.117242

Intensity warping for multisite MRI harmonization

J Wrobel a, ML Martin c, R Bakshi d,e, PA Calabresi f, M Elliot g, D Roalf h, RC Gur g,h,i, RE Gur g,h,i, RG Henry j, G Nair k, J Oh f,l, N Papinutto j, D Pelletier j, DS Reich f,k, WD Rooney m, TD Satterthwaite h, W Stern j, K Prabhakaran h, NL Sicotte n, RT Shinohara c, J Goldsmith b, NAIMS Cooperative
PMCID: PMC8412236  NIHMSID: NIHMS1734328  PMID: 32798678

Abstract

In multisite neuroimaging studies there is often unwanted technical variation across scanners and sites. These “scanner effects” can hinder detection of biological features of interest, produce inconsistent results, and lead to spurious associations. We propose mica (multisite image harmonization by cumulative distribution function alignment), a tool to harmonize images taken on different scanners by identifying and removing within-subject scanner effects. Our goals in the present study were to (1) establish a method that removes scanner effects by leveraging multiple scans collected on the same subject, and, building on this, (2) develop a technique to quantify scanner effects in large multisite studies so these can be reduced as a preprocessing step. We illustrate scanner effects in a brain MRI study in which the same subject was measured twice on seven scanners, and assess our method’s performance in a second study in which ten subjects were scanned on two machines. We found that unharmonized images were highly variable across site and scanner type, and our method effectively removed this variability by aligning intensity distributions. We further studied the ability to predict image harmonization results for a scan taken on an existing subject at a new site using cross-validation.

Keywords: elsarticle.cls, image harmonization, intensity normalization, warping, multisite imaging

1. Introduction

Medical imaging has become an established practice in clinical studies and medical research, leading to situations where images must be compared across site locations, scanners, or scanner types. Upgrades in scanner technology within a site may render old data incomparable to data collected on a newer machine, and this presents challenges in studies where acquisition techniques change over time. Multisite studies have become common as well; examples include large neuroimaging studies such as the Alzheimer’s Disease Neuroimaging Initiative [1] and the Human Connectome Project [2], as well as targeted clinical trials studying interventions for neurological diseases such as multiple sclerosis [3, 4].

Measurement across multiple sites and scanners introduces unwanted technical variability in the images [5]. Going forward we will refer to technical artifacts introduced across either sites or scanners as “scanner effects.” Scanner effects in imaging studies can reduce power to detect true differences across images and distort downstream measurements of regional volumes, brain lesions, and other biological features of interest [6, 7, 8, 9, 10]. In structural magnetic resonance imaging (MRI) studies, detection of scanner effects is particularly challenging because images are collected in arbitrary units of intensity; as a result, raw MRI intensities are often not comparable across study visits even within the same subject and scanner. We refer to unwanted technical variability within the same scanner and subject that are due to arbitrary unit intensity values as “intensity unit effects.” Though often conflated, intensity unit effects and scanner effects are distinct sources of unwanted technical variation and should be treated separately.

We refer to methods intended to address intensity unit effects as “intensity normalization” methods to distinguish them from methods intended to reduce scanner effects, which we term “image harmonization” methods. Both scanner effects and unit effects are present in multisite MRI studies, and in practice they can be challenging to separate. Specifically, intensity normalization methods are applied to each scan in a study separately, without an integrated analysis or dependence on additional variables. In contrast, image harmonization methods target unwanted variation attributable to some additional variable; that is, they harmonize images with respect to a covariate.

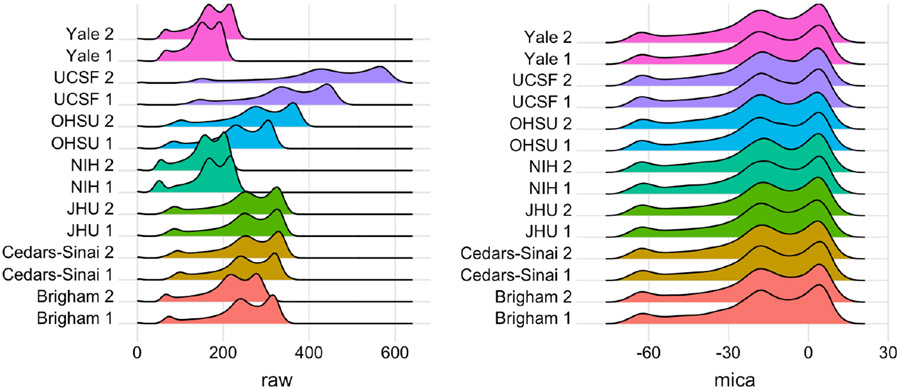
Scanner effects can be due to differences in scanner hardware, scanner software, scan acquisition protocol, or other unknown sources. Examples include head and body coil effects, imaging gradient effects, pulse sequence implementation effects, and image scaling factor effects. Coil effects and pulse sequence implementation effects can be mitigated through the use of inhomogeneity correction algorithms such as N4 [11] and well-calibrated scanner protocols, respectively, but residual scanner effects remain. When present, images collected at different sites may have systematically different distributions of intensity values. For example, [12] showed substantial differences in volumetries across sites and scanner types even for a single, biologically stable subject measured under standardized protocols at the same held strength on platforms produced by the same vendor. The left panel of Figure 1 shows histograms of intensity values for this single subject, who was scanned twice at each of seven sites across the U.S. Large scanner effects are evident; smaller but visible differences within site show that intensity unit effects are present as well. In subsequent analyses, scanner effects produced inconsistent measurements of MS lesion volume both when lesions were segmented manually or by a variety of automated software pipelines [12].

Figure 1:

Figure 1:

Open in a new tab

Histograms of voxel intensities for scan-rescan data on a single subject with MS across seven sites in the NAIMS pilot study: Brigham and Women’s Hospital (Brigham), Cedars-Sinai, Johns Hopkins University (JHU), National Institutes of Health (NIH), Oregon Health & Sciences University (OHSU), University of California San Francisco (UCSF), and Yale University (Yale). Left panel shows raw voxel intensities; right panel shows densities after mica harmonization and White Stripe normalization. At each site two scans were collected; a 1 or 2 after site name indicates the first or second scan, respectively.

The issue of arbitrary units has long been recognized and is the subject of a large literature on intensity normalization [13, 14, 15, 16]. Intensity normalization methods facilitate comparability across subjects measured on the same scanner and standardize voxel intensity values; for a review of several methods see [17]. Histogram matching is an early approach that aligns densities of voxel intensities to quantiles of an image template constructed from several control subjects. Though popular, histogram matching often fails to preserve biological characteristics of individual scans and removes useful information regarding variation among subjects. [15] formalized the principles of image normalization and introduced the White Stripe method. White Stripe normalizes images using patches of normal appearing white matter (NAWM), so that rescaled intensity values are biologically interpretable as units of NAWM. White Stripe can effectively normalize white matter across subjects and is a useful preprocessing step for automated lesion segmentation in MS [18, 19, 20], but technical variability can remain in the gray matter. Additionally, many studies have shown alterations in NAWM for subjects with MS, and this caveat should be considered when using this method [21, 22].

Unlike intensity normalization methods, which target intensity unit effects, harmonization methods aim to reduce scanner effects so that downstream analyses are more comparable across sites and scanners [23, 24]. [25] and [26] focused on diffusion MRI data, harmonizing these data across sites and scanners, and scans collected with different acquisition parameters, respectively. [27] described a voxel-wise regression method, based on tools from genomics, that harmonizes cortical thickness measurements from MRI scans. This method succeeds in removing scanner effects for measurements extracted from each image; in contrast, our goal in the present study was to develop an effective harmonization method that can be applied to the entire brain. Similar tools from genomics are used to correct for scanner effects in multisite diffusion tensor imaging data [23] and multisite functional MRI data [24]. However, these harmonization methods require spatial registration to a population template, which can lower image resolution and make it challenging to detect important disease features such as MS lesions. Ideally, an all-purpose harmonization method would remove scanner effects from the whole brain without requiring that all subjects be spatially registered to the same template image.

In the past, “normalization” has been used to simultaneously address the problems we characterize as unit and scanner effects, although these are more correctly viewed as distinct problems. As a result, intensity normalization techniques such as histogram matching and White Stripe are often used to address harmonization issues [5, 15, 28]. Unlike harmonization techniques mentioned previously, these normalization techniques can be applied to the whole brain, do not require spatial registration, and reduce intensity unit effects. When scanner effects are due to the same voxel intensity transformations used to reduce unit effects, the normalization techniques will reduce scanner effects as well. However, often they fail to reduce much of the variability across sites, especially when large nonlinear scanner effects are present. Additionally, histogram matching normalizes voxel intensities across images at the cost of removing biological variability across subjects which can distort structures and mask inter-subject differences of interest.

Here, we introduce a new image harmonization framework for multisite studies. We use data in which a subject was scanned on multiple scanners closely enough in time that any image differences can be attributed to differences across acquisition platforms (scanner effects) rather than biological effects. Our objectives in this study were to (1) establish a method that removes scanner effects by leveraging multiple scans collected on the same subject, and, building on this, (2) develop a technique to estimate scanner effects in large multisite studies so these can be reduced with preprocessing steps. The first objective establishes a framework for understanding harmonization, and the second relates to the practical use of this framework in multisite studies.

We propose multisite image harmonization by CDF alignment (mica), which harmonizes images by aligning cumulative distribution functions (CDFs) of voxel intensities. Our approach estimates nonlinear, monotonically increasing transformations of the voxel intensity values in one scan such that the resulting intensity CDF perfectly matches the intensity CDF from a second (“target”) scan. CDFs can be perfectly aligned using standard approaches to curve registration, a problem with an extensive history in the functional data analysis literature, see, for example, [29] and references therein. These intensity transformations, called warping functions, define a one-to-one mapping between intensity values from an initial scan and corresponding intensity values from the target scanner. This transformation is then applied to intensity values at each voxel in the initial scan to produce a harmonized image. For a subject measured on different scanners in close succession, this allows us to identify and remove scanner effects; CDF mappings established in this way can be used to reduce the impact of scanner effects in multisite studies.

We motivate and assess our harmonization approach using two data sets with distinct but related problems. The North American Imaging in Multiple Sclerosis (NAIMS) pilot study [12, 30, 31, 32, 10] found large scanner effects in a single subject with biologically stable MS. We use these data to highlight differences between intensity units and scanner effects and show that mica reduces technical variability across sites while preserving the ability to detect MS lesions. A second study, which we refer to as the trio2prisma study, scanned ten healthy subjects on two different machines and found systematic nonlinear differences between the scanners. We used mica to harmonize images from the first scanner so that they are comparable to images collected on the second scanner; this demonstrates how our method can be used to create a mapping between scanners, and that scanner effects can be removed when data are available from both scanners for all subjects. Since scan-rescan data are often only available for a subset of study subjects, we also employed a leave-one-scan-out cross-validation approach to assess the utility of our harmonization method in this common setting. For both studies, we used mica to understand and, to the extent possible, remove scanner variability.

In the next section, we describe our data and the mica methodology. We then present the results of our technique in different settings, followed by a discussion.

2. Materials and Methods

2.1. Data and processing

2.1.1. NAIMS dataset

The NAIMS steering committee developed a brain MRI protocol relevant to MS lesion quantification [12]. Using this protocol, two scans were collected at each of seven sites across the United States on a 45-year-old man with clinically stable relapsing-remitting MS. All scans were performed on 3T Siemens scanners (four Skyra, two TimTrio, and one Verio). At each site, scan-rescan imaging was performed on the same day, with the subject exiting the machine between scans. The participant was also assessed at the beginning and end of the study on the same scanner to confirm disease stability by clinical and MRI assessments.

Each image was bias-corrected using the N4 inhomogeneity correction algorithm [11], including the --rescale-intensities option to correct for intensity drift, then brain extraction was performed using the FSL BET skull-stripping algorithm [33]. T1-weighted (T1-w) and fluid attenuated inversion recovery (FLAIR) images were White Stripe normalized [34] to remove intensity unit effects, mica harmonization was then performed on the White Stripe normalized images as described in Section (2.2). We paired our method with White Stripe to remove intensity unit effects and enable automated MS lesion detection using the MIMoSA [20] software pipeline, though in principle other intensity normalization methods could be used instead.

2.1.2. trio2prisma dataset

The trio2prisma data were collected from ten healthy subjects ages 19 to 29 at the University of Pennsylvania. For each subject, brain MRI scans were obtained on both a Siemens Trio machine and a Prisma scanner. Scans were performed between 2 and 11 days apart for each subject (mean 4.2 days), a time window in which we expect only minor structural changes in the brain. We focused on T1-w images for the trio2prisma data, though our method can easily be applied to other modalities as well. Images were bias-corrected and skull-stripped using the same algorithms described for the NAIMS data. Because normalization methods have often been used for harmonization in the past, we compared mica to White Stripe and histogram matching normalization. To assess method performance on this data, we compared white and gray matter segmentations for mica-harmonized images to White Stripe and histogram matching normalized images. All white and gray matter segmentations were obtained using a combination of multi-atlas Joint Label Fusion [35] and FSL FAST [36].

While spatial registration is not required for our harmonization method in general, for the purpose of validating our method in this paper we spatially registered the Prisma scan to the Trio scan for each subject in the trio2prisma dataset. This was performed using ANTsR software [37], and enables a voxel-wise comparison of mica to methods and raw images.

2.2. Methodology

Our framework for image harmonization uses non-linear transformations of image intensity values to remove scanner effects. The transformations were calculated by aligning distribution functions of intensity values. For a particular imaging modality (for example, T1-w), Yijk(v) represents the intensity at a given voxel v for scan j of subject i measured at site k. Then fijk(x) and Fijk(x) represent the probability density function (PDF) and CDF, respectively, for the voxel intensities of image Yijk measured over intensities x. Within each subject we assumed variability in voxel intensities across visits j and sites k is due to scanner and intensity unit effects rather than biological change, and that non-biological differences could be removed by aligning all CDFs for the ith subject to a subject-specific “template CDF,” Fit(x), for template t; template choices for our motivating studies are described below.

For image Yijk we estimate the nonlinear monotonic transformation of the intensity values, or warping function, hijk−1(x)=x~, which aligns the CDF Fijk(x) to its template via

Fijk{hijk−1(x)}=Fijk(x~)=Fit(x). (1)

After alignment, the CDF of the original images becomes identical to the CDF of the template. For this reason, we use the notation Fit(x) to represent the mica-harmonized CDF as well as the template for alignment. We further denote fijk{hijk−1(x)}=fit(x) and Yit(v) to be the mica-harmonized PDFs and images, respectively. The aligned PDFs, fit(x), can be recovered from CDFs differentiation.

The warping functions hijk−1(x)=x~ define a new intensity value, x~, for each original intensity value in x. The novelty of our approach lies in the use of warping functions to achieve image harmonization; many techniques to estimate these warping functions exist, and we implemented a warping approach that is straightforward and computationally efficient. Specifically, our approach takes a large (1000 or more) number of equally spaced intensity values along the range of x for the target and template images, aligns the target and template CDF at these values, and uses linear interpolation to estimate hijk−1(x) at values between sampled intensities.

Since each Yijk(v) is a voxel intensity in x, harmonized images Yit take values in x~ and are obtained by hijk−1{Yijk(v)}=Yit(v). Wed Appendix Figure (A.1) shows a high-level schematic of this process: images were bias corrected and skull-stripped, CDFs were computed from voxel-intensities, CDFs were aligned, and warping functions from CDF alignment were used to generate harmonized images.

Given this framework for quantifying scanner effects, we now address objectives (1) and (2) stated in Section (1). Our first objective, to establish a method that removes scanner effects, is illustrated using both the NAIMS and the trio2prisma data. For NAIMS data, we obtained empirical CDFs of T1-w and FLAIR images from the NAIMS dataset. Within an imaging modality, each CDF is given by Fijk(x), i = 1, j ∈ {1, 2}, k ∈ {1, …, 7}. We used the baseline taken taken at the NIH site, referred to as NIH scan 1, as the common template Fit(x) to which all CDFs within a modality are aligned, though in principle other templates could be used. For the trio2prisma data, we obtained empirical CDFs of T1-w images. Each CDF is given by Fijk(x), i ∈ {1, …, 10}, j = 1, k ∈ {Trio, Prisma}. For each subject, we used the CDF from the Prisma image, FiPrisma(x), as the template to which we align the CDF from the Trio image, FiTrio(x).

Our second objective was to develop a technique to mitigate scanner effects in large multisite studies. In such studies, most subjects are only measured on a single scanner; at best, only a subset of subjects will have scans collected at all locations in the study. In order to harmonize scans for all subjects in this real-world setting, we propose to White Stripe scans to remove intensity unit effects and then use mica to estimate warping functions for the subset of subjects who have multiple scans. The average of these warping functions across subjects can be used to harmonize images for subjects with only a single available scan. We assessed the performance of this approach using leave-one-scan-out cross validation in the trio2prisma data. Specifically, we removed the Prisma scan for one subject and computed the mica warping functions {hi−1(x)} for the remaining subjects. We then computed the pointwise mean of these warping functions; using this as the warping function for the removed subject, we obtained a predicted Prisma scan from the known Trio scan. This process was repeated for each of the ten subjects. In subsequent sections, scans harmonized using this leave-one-scan-out (mica-loso) approach will be referred to below as mica-loso-harmonized images and Trio scans harmonized using the full data will be referred to as mica-harmonized scans.

2.3. Statistical performance

All analyses were performed in the R software environment.

2.3.1. NAIMS data

To assess the performance of our method on the NAIMS data we quantified T2-hyperintense lesion volume from the 3D FLAIR and T1-w images in both the White Stripe normalized images and images that had been both White Stripe normalized and mica-harmonized. MIMoSA [20] was used for automated lesion segmentation. Because the number and volume of lesions are important metrics for monitoring MS disease progression [38] and the evaluation of therapeutic efficacy [39], eliminating non-biological variability in detected lesion volumes will help clinicians deliver the best possible care to their patients.

We quantified mean and variance of lesion volumes within and across sites after applying White Stripe alone and after applying White Stripe followed by mica.

2.3.2. trio2prisma data

For the trio2prisma data, we compared mica and mica-loso to the histogram matching algorithm proposed by [13], as implemented in [28]. For better performance we first removed background voxels before running the histogram matching algorithm. To quantify performance of the methods we computed Hellinger distance of images before and after normalization, both within and across subjects. The Hellinger distance operates on PDFs of intensities, and its square is given by

h2(fl,fk)=12∫(fl(x)−fk(x))2dx (2)

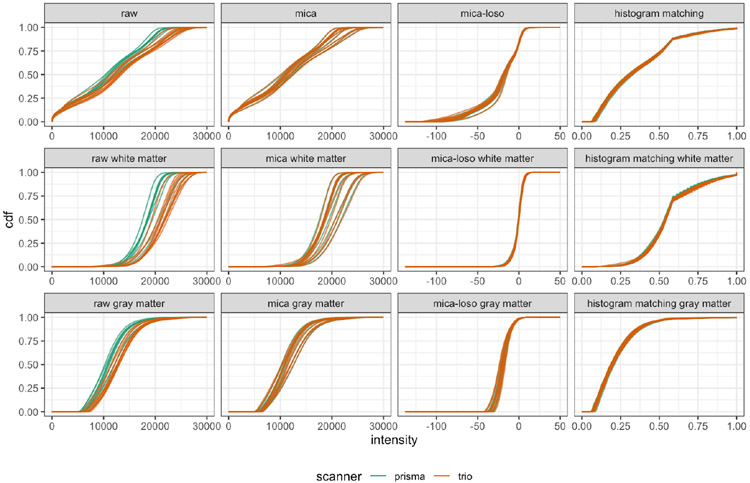
for PDFs fl(x) and fk(x). We visualized CDFs and calculated Hellinger distances (Figures 3 and 4, respectively) using images that had been mica or mica-loso-harmonized but not yet White Stripe normalized or spatially registered. This is to identify and visualize the effects of our method.

Figure 3:

Figure 3:

Open in a new tab

CDFs of intensities before and after harmonization by tissue type in the trio2prisma study. Rows indicate tissue type, with whole brain, white matter, and gray matter shown in rows 1, 2, and 3, respectively. Columns correspond to different harmonization methods.

Figure 4:

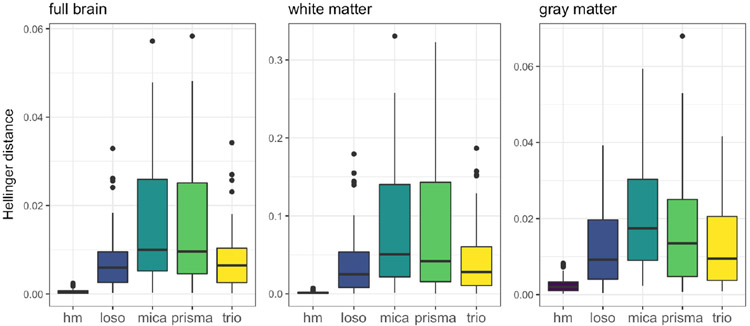
Figure 4:

Open in a new tab

Boxplots of pairwise Hellinger distances across all subjects, shaded by method. Columns show results for full brain (left), white matter (middle), and gray matter (right). Pairwise distances for Prisma and Trio scans are included for reference.

Finally, to quantify the difference between Trio and Prisma images at each voxel, we calculated the normalized root mean square voxel-wise error (NRMSE) for raw image pairs, histogram matched pairs, White Stripe processed pairs, mica aligned pairs, and mica-loso aligned pairs. The NRMSE was calculated for trio2prisma brain volumes in which the Trio scan was spatially registered to the Prisma scan for each subject. To statistically compare performance of White Stripe and mica with respect to NRMSE, we performed a two-sided paired t-test.

3. Results

For the NAIMS pilot data, we compared White Stripe normalized images to images processed using the mica approach outlined in Section (2). For the trio2prisma data, we compared four harmonization strategies: no harmonization, histogram matching, mica, and mica-loso. The main findings from these comparisons are summarized in the following two sections.

3.1. mica reduces variation in lesion volumes across sites in the NAIMS study

We White Stripe normalized then mica-harmonized the NAIMS scans, and then quantified MS lesion volume to assess the effect of scanner variability on a common downstream analysis before and after mica harmonization. The left panel of Figure 1 shows PDFs of raw voxel intensities from the NAIMS study images, and the right panel shows PDFs of images that have been White Stripe normalized then mica-harmonized. The raw PDFs show small differences within site, which are attributable to intensity unit effects, and larger differences across site, which are attributable to scanner effects. Scanner effects are particularly large between the UCSF site and other sites. After mica harmonization, the images across and within site have the same distributions of voxel intensities. An extension of this Figure showing PDFs after White Stripe alone and mica alone is available in the Appendix.

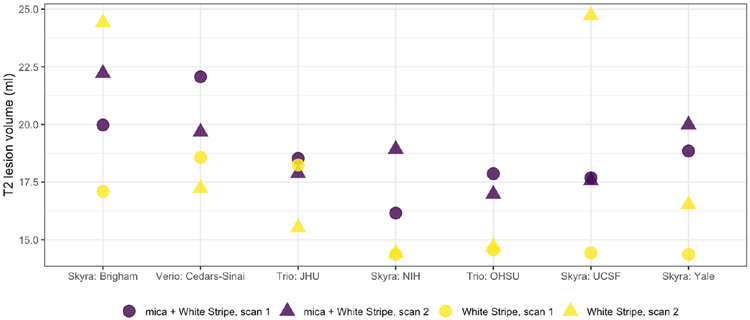
Figure 2 shows estimated T2-hyperintense lesion volume across sites for both White Stripe alone and White Stripe in conjunction with mica for scan-rescan pairs across the seven NAIMS sites. Compared to White Stripe alone, mica in conjunction with White Stripe yielded less variable lesion volume measurements across sites (variance 3.37 ml2 [mica] vs. 11.8 ml2 [White Stripe]) and within sites (variance 1.5 ml2 [mica] vs. 12.4 ml2 [White Stripe]). The reduction in variability across sites suggests that our method, together with White Stripe, decreases site-to-site variance as expected. On average, our method performs better than White Stripe alone for within-site variance as well, though it is worth noting that at some sites the intra-site variability is lower for White Stripe alone.

Figure 2:

Figure 2:

Open in a new tab

Estimated T2 lesion volumes for scan-rescan pairs at each of 7 sites in the NAIMS study. Circles indicate scan 1 and triangles indicate scan 2. Light and dark colors are volumes for White Stripe normalized images and mica normalized images, respectively.

3.2. mica preserves variation across subjects in the trio2prisma study

An appropriate harmonization method for multisite studies should reduce variability across scanners within the same subject but preserve biological differences across subjects. Here, we evaluate results from the trio2prisma data with these goals in mind. We compared mica and mica-loso-harmonized images to images processed by histogram matching.

Figure 3 shows CDFs under different harmonization scenarios. A similar figure showing PDFs is given in the Web Appendix. Visual inspection of intensity CDFs in untransformed images suggests differences across scanners: the Prisma scans tend to have lower intensity values and higher peaks than the Trio scans. For both mica and histogram matching, within-subject technical variability is reduced because CDFs of Trio scans and Prisma scans are aligned. mica accomplishes this by mapping the CDF of the Trio scan to the CDF of the original Prisma scan, thus preserving the original features of the Prisma scans including variability across subjects. Histogram matching must be applied to scans from both the Trio and Prisma scanners, and reduces within-subject variability at the expense of eliminating desired differences across subjects. mica-loso provides reasonable harmonization in that it maps Trio scans into the same range of intensity values as Prisma scans, but has less accuracy in reducing within-subject variability than mica or histogram matching. However, much of the desired across-subject variability is retained. Figure 3 provides visual confirmation that mica retains biological variability across subjects while histogram matching removes much of it, and these observations are directly quantified next.

We quantified the variability across subjects using the Hellinger distance from equation (2) on PDFs of voxel intensities. Figure 4 displays boxplots of these pairwise distances for the original Trio scans, original Prisma scans, and scans processed by histogram matching, mica-loso, and mica. Figure 4 is divided into distances calculated on the full skull-stripped images (left column), white matter (middle column), and gray matter (right column). The mica-harmonized Trio scans have similar across-subject variability to the Prisma scans. The mica-loso scans have variability comparable to the original Trio scans but smaller than the Prisma scans. After histogram matching, pairwise distances across subjects are nearly zero. Together, these results suggest that mica can harmonize images while preserving differences across subjects, as can mica-loso to a somewhat lesser extent; histogram matching, in contrast virtually eliminates inter-subject variability, including that which is presumably biological.

The left panel and top row of Figure 5 shows an axial slice of an image for one subject from the trio2prisma dataset. The slice is shown for raw intensity values collected on the Prisma and Trio scanners (left and top right, respectively), intensity values after applying mica harmonization to the Trio scan, and intensity values after applying histogram matching to the Trio scan. Here, mica-harmonization brightens the contrast between white and gray matter but does not distort the shape of biological features in the tissue. Histogram matching, however, drastically changes the appearance of the image, converting some gray matter to CSF and some white matter to gray matter. The bottom row of Figure 5 shows image residuals indicating the voxelwise differences between the Prisma image and the Trio, mica harmonized, and histogram matching normalized images, respectively. The smallest residuals are seen in the mica image, while the largest are in the F1M image. Overall, Figure 5 indicates that the mica-harmonized image retains biologically relevant features better than histogram matching.

Figure 5:

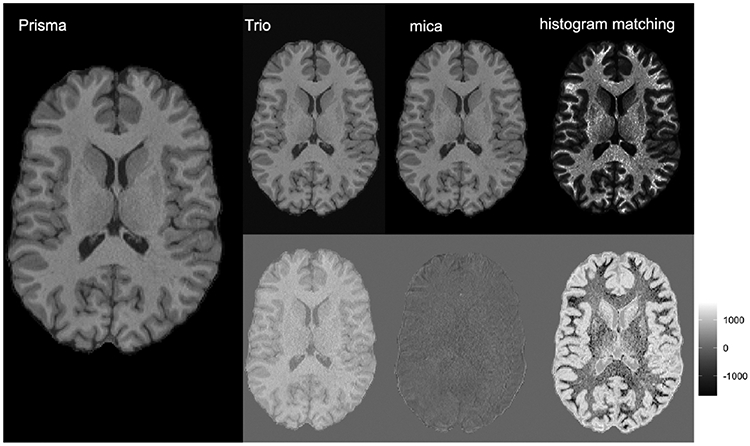
Figure 5:

Open in a new tab

Axial slice of skull-stripped, T1-weighted images from a single subject in the trio2prisma dataset. At left is an image collected on the Prisma scanner. The top row from left to right show an image collected on the Trio scanner that has been spatially registered to the Prisma image, the Trio image after mica harmonization, and the Trio image after histogram matching, respectively. The bottom row shows image residuals indicating the voxelwise differences between the Prisma image and the Trio, mica harmonized, and histogram matching normalized images, respectively.

The left panel of Figure 6 shows boxplots across methods of normalized root mean square voxel-wise error (NRMSE) for (Trio, Prisma) image within-subject pairs. The NRMSE comparison allows us to directly compare how well corrected intensities match on a voxel-wise level. Histogram matching and White Stripe transform data to a different scale because they are normalization rather than harmonization methods, and thus normalized RMSE is needed to compare across methods.

Figure 6:

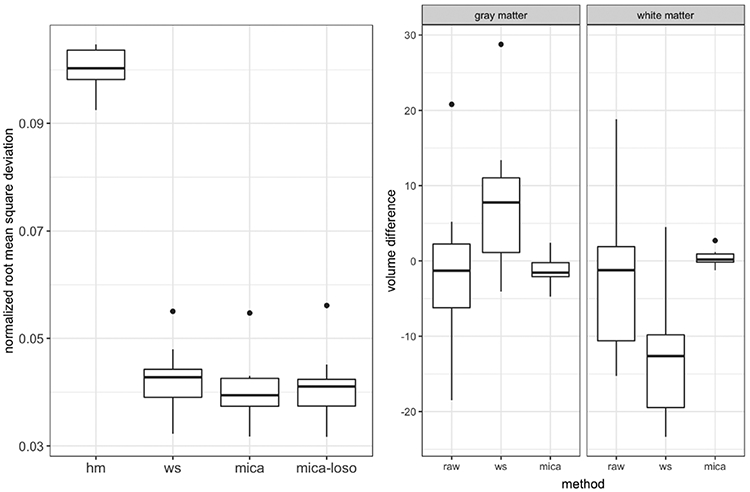
Figure 6:

Open in a new tab

Left Panel: boxplots of normalized root mean square voxel-wise error for trio2prisma image pairs across methods. Shown are raw image pairs (raw: median interquartile range = 0.3998 {0.0545}), histogram matched pairs (hm: 0.1003 {0.0055}), White Stripe normalized pairs (ws: 0.0428 {0.0052}), mica harmonized pairs (mica: 0.0394 {0.0051}), and pairs harmonized using the leave-one-scan-out approach (mica-loso: 0.0410 {0.0049}). Center and Right Panels: boxplots of difference in Trio and Prisma volumes of white matter (WM) and gray matter (GM), where WM/GM segmentation was performed after normalization/harmonization for White Stripe and mica, respectively.

There are several important features here, which relate both to the relative performance of methods and to the separability of intensity unit effects and scanner effects. First, we note that mica performs best among these methods, suggesting that mica successfully harmonizes images across sites; White Stripe also performs well, particularly in comparison to histogram matching, though the difference between White Stripe and mica is statistically significant (p = 0.0062). The difference between the performance of mica and White Stripe reflects the degree to which the scanner effect is non-linear: White Stripe implements linear transformations of intensity values on both the trio and prisma images, which implies a linear intensity CDF mapping from the Trio scan to the Prisma scan, while mica explicitly defines a non-linear intensity CDF mapping for each subject. mica-loso, which mitigates both intensity unit effects and scanner effects, performs somewhat less well than mica but better than White Stripe alone. Overall, Figure 6 suggests that mica and mica-loso outperform competing methods in terms of NRMSE, and the degree to which they are superior will depend on the amount of non-linearity in the transformation that underlies scanner effects.

We obtained white matter/gray matter segmentations on the trio2prisma images both before and after White Stripe normalization and mica harmonization. Our aim was to show that white matter and gray matter volumes within a subject comparing Trio to Prisma are more similar after mica than before normalization or harmonization. The center and right panels of Figure 6 show boxplots of the difference in these white and gray matter volumes across methods. In Figure 6, Trio and Prisma volumes for both white matter and gray matter are more comparable within a subject for mica harmonized image pairs than for White Stripe normalized or raw image pairs, and the variability in volume difference is smallest for mica. Along with Figure 2, Figure 6 provides evidence that mica harmonization reduces unwanted variation in downstream analyses.

4. Discussion

Unwanted technical variability due to scanner effects in multisite clinical trials and observational studies is an increasingly common problem; to mitigate these scanner effects we introdce mica, a method that harmonizes structural MRI images by defining nonlinear transformations between CDFs of voxel intensities. To specifically target scanner effects, we developed a paradigm for understanding scanner effects and intensity unit effects as related but distinct sources of technical variability in MRI scans. Intensity unit effects are due to arbitrary MRI unit intensities within a single scanner, and scanner effects are unwanted technical artifacts introduced across scanners or sites. We also distinguish between approaches targeting these sources of variability: normalization methods address intensity unit effects, and harmonization methods, the focus of our study, address scanner effects. Though we focus on across-scanner harmonization, within-scanner variability across software upgrades or protocol changes is also a major problem, and the harmonization technique we pose will likely apply directly in these scenarios.

In the statistical harmonization literature, there are two fundamental approaches: the first aims to reduce inter-scanner variation in derived measures which are extracted from imaging data. These approaches, including [28], benefit from the ability to focus on the features under study for the harmonization process and thus can be more transparent and low-dimensional in their modeling strategies. The second approach, which is under study in this work, aims to reduce inter-scanner differences in the acquired images directly. This approach, if successful, will lead to more comparable extracted features. Benefits of this approach continue to be explored, but could potentially include the use of nuisance information for inter-scanner harmonization as well as the ability to assess harmonization performance in subsequently extracted features. In addition, by reducing biases in images as opposed to extracted features, modeling of coherent patterns of variation that are due to technical factors and are present in the acquired image space may be conducted more parsimoniously than in the context of subsequently extracted features.

Our data came from two small studies, the NAIMS pilot study and the trio2prisma study, with multiple images per subject taken on multiple scanners, and nonlinear scanner effects. We found that mica reduced within-subject variability in whole brain scans as well as white and gray matter while preserving biological variability across subjects. We also found that mica, paired with White Stripe, enhanced reproducibility of measurements of MS lesion volume across sites.

Normalization methods such as histogram matching and White Stripe are sometimes used for harmonization, but they are inadequate in cases where across-site differences are much larger than those within site. Additionally, histogram matching can reduce biological variability across subjects and White Stripe can leave residual technical variability in the gray matter. While we differentiate conceptually between intensity unit effects and scanner effects, we also acknowledge that in reality these artifacts can be challenging to separate. As a result, mica is likely to remove some intensity unit effects and intensity normalization methods are likely to remove some scanner effects when applied separately. In particular, White Stripe alone will likely perform well as a harmonization method when scanner effects are small, linear transformations. Histogram matching, however, is likely to remove desired variability across subjects and bias results.

Because our method is flexible and operates on the full brain, we can map images from one scanner to another. This mapping is only exact for a particular subject when images are available from both scanners, which is not realistic for most studies. That said, our leave-one-scan-out analysis suggests that when systematic site differences are present, mica can help understand scanner effects and mitigate those differences. Before conducting multisite studies, we recommend obtaining a baseline measurement of scanner variability by having a subset of patients measured at all sites, and using standardized scanner protocols to mitigate sensitivity to adjustable scanner parameters. Our method can then be applied to all images collected to remove average scanner variability. We acknowledge that this solution is imperfect in the sense that average scanner variability collected from a subset of patients in a trial will not always capture the true scanner variability for each subject. However, our simple and easy-to-apply methodology is an important step forward for an increasingly prevalent problem. Scanner effects may vary across covariates such as gender and age, so extensions to mica that incorporate covariates may address some of the issues outlined above. One question we do not directly address in our paper is the optimal number of scan-rescan subjects required to estimate a stable scanner effect. Due to limited available data, the optimal allocation of participants in our pilot studies across multiple sites is unclear, and is the subject of future work.

5. Software

To enable use of mica we have written an R software package which is available for download at https://github.com/julia-wrobel/mica.

Supplementary Material

supplementary materials

Acknowledgements

This work was supported by the National Institutes of Health R01NS085211, R21NS093349, R01MH112847, R01MH119185, R01MH120174, R01NS060910, R01EB017255, R01HL123407, R01NS097423, S10OD016356, and the National Multiple Sclerosis Society RG-1707-28586, and the Race to Erase MS Foundation. This work was also partially supported by the Intramural Research Program of NINDS. The NIH funded the RF coil used to collect data through its shared instrument program. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.

References

  • [1].Mueller SG, Weiner MW, Thai LJ, Petersen RC, Jack CR, Jagust W, Trojanowski JQ, Toga AW, Beckett L, Ways toward an early diagnosis in alzheimer’s disease: the alzheimer’s disease neuroimaging initiative (adni), Alzheimer’s & Dementia 1 (1) (2005) 55–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [2].Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium W-MH, et al. , The wu-minn human connectome project: an overview, Neuroimage 80 (2013) 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [3].Kappos L, Antel J, Comi G, Montalban X, O’Connor P, Polman CH, Haas T, Korn AA, Karlsson G, Radue EW, Oral fingolimod (fty720) for relapsing multiple sclerosis, New England Journal of Medicine 355 (11) (2006) 1124–1140, pMID: 16971719. doi: 10.1056/NEJMoa052643. [DOI] [PubMed] [Google Scholar]
  • [4].Hauser SL, Bar-Or A, Comi G, Giovannoni G, Hartung H-P, Hemmer B, Lublin F, Montalban X, Rammohan KW, Selmaj K, Traboulsee A, Wolinsky JS, Arnold DL, Klingelschmitt G, Masterman D, Fontoura P, Belachew S, Chin P, Mairon N, Garren H, Kappos L, Ocrelizumab versus interferon beta-1a in relapsing multiple sclerosis, New England Journal of Medicine 376 (3) (2017) 221–234, pMID: 28002679. doi: 10.1056/NEJMoa1601277. [DOI] [PubMed] [Google Scholar]
  • [5].Schnack HG, van Haren NE, Hulshoff Pol ME, Picchioni M, Weisbrod M, Sauer H, Cannon T, Huttunen M, Murray R, Kahn RS, Reliability of brain volumes from multicenter mri acquisition: a calibration study, Human brain mapping 22 (4) (2004) 312–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [6].Schnack HG, van Haren NE, Brouwer RM, van Baal GCM, Picchioni M, Weisbrod M, Sauer H, Cannon TD, Huttunen M, Lepage C, et al. , Mapping reliability in multicenter mri: Voxel-based morphometry and cortical thickness, Human brain mapping 31 (12) (2010) 1967–1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [7].Jovicich J, Marizzoni M, Sala-Llonch R, Bosch B, Bartrés-Faz D, Arnold J, Benninghoff J, Wiltfang J, Roccatagliata L, Nobili F, et al. , Brain morphometry reproducibility in multi-center 3 t mri studies: a comparison of cross-sectional and longitudinal segmentations, Neuroimage 83 (2013) 472–484. [DOI] [PubMed] [Google Scholar]
  • [8].Cannon TD, Sun F, McEwen SJ, Papademetris X, He G, van Erp TG, Jacobson A, Bearden CE, Walker E, Hu X, et al. , Reliability of neuroanatomical measurements in a multisite longitudinal study of youth at risk for psychosis, Human brain mapping 35 (5) (2014) 2424–2434. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [9].Keshavan A, Paul F, Beyer MK, Zhu AH, Papinutto N, Shinohara RT, Stern W, Amann M, Bakshi R, Bischof A, et al. , Power estimation for non-standardized multisite studies, NeuroImage 134 (2016) 281–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [10].Schwartz DL, Tagge I, Powers K, Ahn S, Bakshi R, Calabresi PA, Todd Constable R, Grinstead J, Henry RG, Nair G, et al. , Multisite reliability and repeatability of an advanced brain mri protocol, Journal of Magnetic Resonance Imaging. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [11].Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC, N4itk: improved n3 bias correction, IEEE transactions on medical imaging 29 (6) (2010) 1310–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [12].Shinohara RT, Oh J, Nair G, Calabresi PA, Davatzikos C, Doshi J, Henry RG, Kim G, Linn KA, Papinutto N, et al. , Volumetric analysis from a harmonized multisite brain mri study of a single subject with multiple sclerosis, American Journal of Neuroradiology 38 (8) (2017) 1501–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [13].Nyúl LG, Udupa JK, et al. , On standardizing the mr image intensity scale, image 1081. [DOI] [PubMed] [Google Scholar]
  • [14].Shinohara RT, Crainiceanu CM, Caffo BS, Gaitán MI, Reich DS, Population-wide principal component-based quantification of blood–brain-barrier dynamics in multiple sclerosis, NeuroImage 57 (4) (2011) 1430–1446. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [15].Shinohara RT, Sweeney EM, Goldsmith J, Shiee N, Mateen FJ, Calabresi PA, Jarso S, Pham DL, Reich DS, Crainiceanu CM, et al. , Statistical normalization techniques for magnetic resonance imaging, NeuroImage: Clinical 6 (2014) 9–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [16].Ghassemi R, Brown R, Narayanan S, Banwell B, Nakamura K, Arnold DL, Normalization of white matter intensity on t1-weighted images of patients with acquired central nervous system demyelination, Journal of Neuroimaging 25 (2) (2015) 184–190. [DOI] [PubMed] [Google Scholar]
  • [17].Shah M, Xiao Y, Subbanna N, Francis S, Arnold DL, Collins DL, Arbel T, Evaluating intensity normalization on mris of human brain with multiple sclerosis, Medical image analysis 15 (2) (2011) 267–282. [DOI] [PubMed] [Google Scholar]
  • [18].Sweeney E, Shinohara R, Shea C, Reich D, Crainiceanu C, Automatic lesion incidence estimation and detection in multiple sclerosis using multisequence longitudinal mri, American Journal of Neuroradiology 34 (1) (2013) 68–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [19].Sweeney EM, Shinohara RT, Shiee N, Mateen FJ, Chudgar AA, Cuzzocreo JL, Calabresi PA, Pham DL, Reich DS, Crainiceanu CM, Oasis is automated statistical inference for segmentation, with applications to multiple sclerosis lesion segmentation in mri, NeuroImage: clinical 2 (2013) 402–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [20].Valcarcel A. m., Linn KA, Vandekar SN, Satterthwaite TD, Muschelli J, Calabresi PA, Pham DL, Martin ML, Shinohara RT, Mimosa: An automated method for intermodal segmentation analysis of multiple sclerosis brain lesions, Journal of Neuroimaging. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [21].Zeis T, Graumann U, Reynolds R, Schaeren-Wiemers N, Normal-appearing white matter in multiple sclerosis is in a subtle balance between inflammation and neuroprotection, Brain 131 (1) (2008) 288–303. [DOI] [PubMed] [Google Scholar]
  • [22].Moll NM, Rietsch AM, Thomas S, Ransohoff AJ, Lee J-C, Fox R, Chang A, Ransohoff RM, Fisher E, Multiple sclerosis normal-appearing white matter: Pathology-imaging correlations, Annals of neurology 70 (5) (2011) 764–773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [23].Fortin J-P, Parker D, Tunc B, Watanabe T, Elliott MA, Ruparel K, Roalf DR, Satterthwaite TD, Gur RC, Gur RE, et al. , Harmonization of multi-site diffusion tensor imaging data, Neuroimage 161 (2017) 149–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [24].Yu M, Linn KA, Cook PA, Phillips ML, McInnis M, Fava M, Trivedi MH, Weissman MM, Shinohara RT, Sheline YI, Statistical harmonization corrects site effects in functional connectivity measurements from multi-site fmri data, Human brain mapping 39 (11) (2018) 4213–4227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [25].Mirzaalian H, Ning L, Savadjiev P, Pasternak O, Bouix S, Michailovich O, Grant G, Marx C, Morey RA, Flashman L, et al. , Inter-site and inter-scanner diffusion mri data harmonization, NeuroImage 135 (2016) 311–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [26].Karayumak SC, Bouix S, Ning L, James A, Crow T, Shenton M, Kubicki M, Rathi Y, Retrospective harmonization of multi-site diffusion mri data acquired with different acquisition parameters, NeuroImage 184 (2019) 180–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [27].Fortin J-P, Cullen N, Sheline YI, Taylor WD, Aselcioglu I, Cook PA, Adams P, Cooper C, Fava M, McGrath PJ, et al. , Harmonization of cortical thickness measurements across scanners and sites, NeuroImage 167 (2018) 104–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [28].Fortin J-P, Sweeney EM, Muschelli J, Crainiceanu CM, Shinohara RT, Initiative ADN, et al. , Removing inter-subject technical variability in magnetic resonance imaging studies, NeuroImage 132 (2016) 198–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [29].Wrobel J, Zipunnikov V, Schrack J, Goldsmith J, Registration for exponential family functional data, Biometrics 75 (1) (2019) 48–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [30].Dworkin J, Sati P, Solomon A, Pham D, Watts R, Martin M, Ontaneda D, Schindler M, Reich D, Shinohara R, Automated integration of multimodal mri for the probabilistic detection of the central vein sign in white matter lesions, American Journal of Neuroradiology 39 (10) (2018) 1806–1813. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [31].Oh J, Bakshi R, Calabresi PA, Crainiceanu C, Henry RG, Nair G, Papinutto N, Constable RT, Reich DS, Pelletier D, et al. , The naims cooperative pilot project: Design, implementation and future directions, Multiple Sclerosis Journal 24 (13) (2018) 1770–1772. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [32].Papinutto N, Bakshi R, Bischof A, Calabresi PA, Caverzasi E, Constable RT, Datta E, Kirkish G, Nair G, Oh J, et al. , Gradient non-linearity effects on upper cervical spinal cord area measurement from 3d t1-weighted brain mri acquisitions, Magnetic resonance in medicine 79 (3) (2018) 1595–1601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [33].Smith SM, Fast robust automated brain extraction, Human brain mapping 17 (3) (2002) 143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [34].Shinohara RT and Muschelli J, WhiteStripe: White Matter Normalization for Magnetic Resonance Images using WhiteStripe, r package version 2.3.1 (2018). URL http://CRAN.R-project.org/package=WhiteStripe [Google Scholar]
  • [35].Wang H, Suh JW, Das SR, Pluta JB, Craige C, Yushkevich PA, Multi-atlas segmentation with joint label fusion, IEEE transactions on pattern analysis and machine intelligence 35 (3) (2013) 611–623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [36].Zhang Y, Brady M, Smith S, Segmentation of brain mr images through a hidden markov random held model and the expectation-maximization algorithm, IEEE Transactions on Medical Imaging 20 (1) (2001) 45–57. [DOI] [PubMed] [Google Scholar]
  • [37].Avants BB, Tustison NJ, Stauffer M, Song G, Wu B, Gee JC, The insight toolkit image registration framework, Frontiers in neuroinformatics 8 (2014) 44. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [38].Bakshi R, Neema M, Healy BC, Liptak Z, Betensky RA, Buckle GJ, Gauthier SA, Stankiewicz J, Meier D, Egorova S, Arora A, Guss ZD, Glanz B, Khoury SJ, Guttmann CRG, Weiner HL, Predicting Clinical Progression in Multiple Sclerosis With the Magnetic Resonance Disease Severity Scale, Archives of Neurology 65 (11) (2008) 1449–1453. arXiv:https://jamanetwork.com/journals/jamaneurology/articlepdf/1107511/noc80053\_1449\_1453.pdf, doi: 10.1001/archneur.65.11.1449. URL 10.1001/archneur.65.11.1449 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [39].Filippi M, Wolinsky JS, Comi G, Group CS, et al. , Effects of oral glatiramer acetate on clinical and mri-monitored disease activity in patients with relapsing multiple sclerosis: a multicentre, double-blind, randomised, placebo-controlled study, The Lancet Neurology 5 (3) (2006) 213–220. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

supplementary materials
NIHMS1734328-supplement-supplementary_materials.pdf (1.1MB, pdf)

RESOURCES