Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 Aug 19;6(34):21952–21959. doi: 10.1021/acsomega.1c02310

Theoretical Study of O-CH3 Bond Dissociation Enthalpy in Anisole Systems

Rui Li †, Tianshu Du †, Jingxing Liu †, Adelia J A Aquino †,‡,§,*, Jianyu Zhang †,*
PMCID: PMC8412933  PMID: 34497890

Abstract

graphic file with name ao1c02310_0006.jpg

Understanding ubiquitous methyl transfer reactions requires a systematic study of thermodynamical parameters that could reveal valuable information about the nature of the chemical bond and the feasibility of those processes. In the present study, the O-CH3 bond dissociation enthalpies (BDEs) of 67 compounds belonging to phenol/anisole systems were calculated employing the Gaussian-4 (G4) method. Those compounds contain different substituents including alkyl groups, electron-donating groups (EDGs), and electron-withdrawing groups (EWGs). The results show that the bigger branched alkyl groups and EDGs will destabilize the O-CH3 bond, while EWGs have the opposite effect. A combination of different effects including steric effects, hydrogen bonds, and substituents and their position can achieve around 20 kcal/mol difference compared to the basic phenyl frame. Also, the linear correlation between σp+ and O-CH3 BDE can provide a reference for the O-CH3 BDE prediction. The present study represents a step forward to establish a comprehensive O-CH3 BDE database to understand the substituent effect and make its contribution to the rational design of inhibitors and drugs.

1. Introduction

Methylation, a ubiquitous transformation in nature, is one of the most basic and important reactions in organic chemistry and biological organic chemistry.1−4 Phenols were intensively studied because of their involvement in many chemical, electrochemical, and biochemical reactions5 and the important role they play in chemical synthesis, industrial production, pesticides, spices, dyes, and especially drugs.6 Catechols, including adrenaline, noradrenaline, and dopamine, are closely associated with several neurological diseases such as Parkinson’s disease.7−9 Scientists have designed hundreds of related drug precursors, several of which, like Entacapone and Tolcapone, are already on the market to treat neurological diseases.7 Phenols are common substrates for methyl transfer reactions, and thus the factors that affect the stability of the O-CH3 bond of the anisole products have a direct impact on the methyl transfer reaction.10 There is limited thermodynamic information available for a full understanding of the methylation process. BDE (bond dissociation enthalpy) is a thermodynamic parameter that could reveal valuable information about the nature of the chemical bond. Thus, it is desirable to study the O-CH3 BDE of anisoles, which is the enthalpy change for the dissociation of the anisole O-CH3 bond to corresponding radical products, in a systematic and comprehensive manner. This could provide insights into factors that affect the stability of the O-CH3 bond. As measuring BDEs for every molecule experimentally is challenging,11 using reliable theoretical approaches to predict BDEs is an ideal alternative.

In the past few years, the development of computational methods, which can accurately and economically calculate BDEs, make it possible to systematically predict the O-CH3 BDE in phenol/ anisole systems. Several studies have been reported to calculate the BDE in different systems.12,13 However, few of them are involved in the O-CH3 bond, which is indispensable to the mechanistic understanding of the methyl transfer reaction. Pratt et al.12 used a combination of experiment and theory to examine the influence of Y substituents on the O-CH3 bond dissociation enthalpies of 4-YC6H4O-CH3. They found that both electron-withdrawing (EW) and electron-donating (ED) groups of Y substituents reduce C–X bond dissociation enthalpies relative to the parent compound. Wu et al.13 calculated substituent effects on O-CH3 and O–H bond dissociation energies for a series of 11 para-substituted anisoles and 18 para-substituted phenols using JMW/DN and BLYP/6-31G*. It showed that the density functional method can give satisfactory results for analyzing substituent effects on the anisole O-CH3 BDEs and the phenol O–H BDEs. Also, the substituent effects on phenol O–H BDE and anisole O-CH3 BDE are nearly identical. Though those research studies did not give a comprehensive analysis about the substituent effect, they expanded on the findings of related aspects and laid a certain theoretical foundation. Recently, the G4 approach was selected as the preferred method for the accurate theoretical estimation of the O-CH3 bond.11 Based on this study, the G4 method was applied in the present work to predict the O-CH3 BDEs of anisole systems to study the factors, including but not limited to steric effects, electronic effects, and H-bonding effects, that influence the magnitude of O-CH3 BDEs. The present investigation is the first important step to establish a comprehensive O-CH3 BDE database, which could facilitate the understanding of the mechanism of methylation and providing guidance for designing corresponding inhibitors and drugs.

2. Results and Discussion

Using the G4 simulation method, the BDEs of more than 50 target molecules (Figure 1) were calculated, as shown in Tables 1–3. The range of BDEs varies from 50.1 kcal/mol (Compound 6) to 74.8 kcal/mol (Compound 26e). To fully understand the intrinsic element that controls the size of the BDE, factors including steric and electronic effects were systematically investigated by appropriate theoretical simulation for more than 50 well-designed anisoles.

Figure 1.

Figure 1

Open in a new tab

Structures of target molecules.

Table 1. Bond Dissociation Enthalpy (BDE) of O-CH3 for Molecules with Various Substituted Alkyl Groups in Group I and the Corresponding Different Types of Steric Effect Parameters.

substituent compound# BDE (kcal/mol) –ESa Vxb ΔDFc (104 J/mol)
H 1 65.3 –1.24 0  
Me 2 57.9 0 0.52 0
Et 3 58.23 0.07 0.56 0.86
n-Bu 4 58.21 0.39 0.68 0.86
i-Pr 5 56.8 0.47 0.76 2.29
t-Bu 6 50.1 1.54 1.24 3.82
Open in a new tab
a

ES, gross steric effect constants, belongs to kinetic and thermodynamic parameters derived from reaction rate constants of substituents and the reference bases in hydrolytic reactions (data from ref (16)).

b

Vx, steric parameter, is based on the calculation from volumes and bond lengths defined by van der Waals radii (data from ref (17)).

c

ΔDF, steric substituent constant for alkyl groups, is a set of parameters from computational calculation based on molecular mechanics taking into account the tension energy of a molecule including bond length deformation, bond angle tension, bond torsion tension, and nonbond interaction (data from ref (18)).

Table 3. Bond Dissociation Enthalpy (BDE) of Molecules in Group III with Mono-, Di-, and Tri-substituents.

substituent compound# BDE (kcal/mol) type
NH2 22 53.7 mono
47.8 di
43.4 tri
       
OCH3 23 59.0 mono
55.5 di
52.1 tri
       
F 24 62.0 mono
61.3 di
60.5 tri
       
Cl 25 62.4 mono
62.2 di
61.1 tri
       
Br 26 62.5 mono
62.7 di
61.9 tri
       
CHO 27 67.7 mono
73.3 di
71.9 tri
       
NO2 28 66.7 mono
67.4 di
74.8 tri
       
CN 29 67.7 mono
67.2 di
69.1 tri
Open in a new tab

2.1. BDE of O-CH3 with Steric Effects

When dealing with steric effects, chemists are always faced with the dilemma of which methods and parameters are used to correlate or predict results. Steric effects encounter difficulty in finding reference reactions in which they can operate independently of the substituent electronic effects. One possibility is to employ a series of groups with different sizes but almost constant electronic effects such as alkyl groups. Thus, a series of aromatic compounds (Compounds 2–5 in Group I, Figure 1) with different alkyl substituents including methyl, ethyl, isopropyl, n-butyl, and t-butyl were designed to explore the steric effect on the O-CH3 BDEs (Table 1). The alkyl groups are at the 2,6-positions. The O-CH3 BDEs are all within a range of 50–60 kcal/mol with the tertiary butyl substituent having the smallest one (50.1 kcal/mol). Compounds 2–4, whose substituents contain methyl, ethyl, and n-butyl belonging to the chain alkyl group, show a very similar size of O-CH3 BDE at around 58 kcal/mol within a 0.5 kcal/mol difference. This similarity suggested that the length of the straight chain in the alkyl group did not alter the size of O-CH3 BDE. When turning to the branched alkyl groups, it is obvious that there is a significant drop of O-CH3 BDEs to 56.8 and 50.1 kcal/mol when the substituents are isopropyl (i-Pr, 5) and tertiary butyl (t-Bu, 6), respectively. As it is known that the steric hindrance of the isopropyl and tertiary butyl group is larger than that of the straight chain alkyl group (methyl, ethyl, and n-butyl herein), the corresponding O-CH3 BDE on benzene becomes smaller. The order of the steric hindrance effect (t-Bu > i-Pr > n-Bu ≈ Et ≈ Me) of the alkyl substituent on the benzene ring is just the opposite of the trend of the corresponding O-CH3 BDEs (t-Bu < i-Pr < n-Bu ≈ Et ≈ Me). We could conclude that the bigger the alkyl group, the smaller the value of O-CH3 BDE. This fact suggested that the more crowded region around the O-CH3 functional group could facilitate the carbon–oxygen cleavage, that is, the C–O bond is easier to break with lower O-CH3 BDE.

The steric effect comes from the fact that every atom in a molecule takes up a certain amount of space.14 This effect mainly arises from three kinds of steric tensions including a repulsive force (crowding of large atoms or groups), the tension (the bond angle deformation), and the torsional deformation (the rotation of the sigma bond). The decreasing BDE herein for the case of O-CH3, R–H, and R-CH3 with bulky substituents came from the crowding and deformation of the alkyls, the stability of the resulting radicals and the hyperconjugation of the adjacent alkyl groups stabilizing the resulting radical center. In fact, the steric effect could be quantified to a certain extent. More than a century ago, Hofmann first reported the steric effect when methyl iodide could not react with methylated anilines under normal conditions.15 Various methods have been proposed to estimate the importance of steric factors in reaction. The first consistent scale used for quantifying this structure–activity property was proposed by Taft16 who defined ES as the gross steric effect. The significant contribution of Taft was to propose a general scale of the steric effect and choose a model hydrolytic reaction in which only steric effects were involved without any other electronic effects. After that, other parameters such as steric parameters Vx(17) and steric substituent constants ΔDF19 derived from different methods and standards were proposed, as shown in Table 1. Compared to ES, the scale Vx is a different method based on the calculation from volumes and bond lengths defined by van der Waals radii. This is a scale proposed by Charton,17 which is generally accepted at present. ΔDF is a set of parameters based on molecular mechanics that takes into account the tension energy of a molecule including bond length deformation, bond angle tension, bond torsion tension, and nonbonding interactions. The plots of −ES, Vx, and ΔDF against O-CH3 BDEs are displayed in Figure S1. All the negative slopes shown in Figure S1 could reflect the decline of O-CH3 BDE with crowdedness around the methyl group. Interestingly, regardless of which steric parameter was considered, there is a general trend where with increasing parameter size, the BDE decreases. This trend consists of the steric effect influence on R–H BDE and R-CH3 BDE18 (Table S1). When referring to R-OH, the bond strength with the corresponding substituent increase in the order of CH3 < Et < i-Pr < t-Bu while the O-CH3 (anisole), R–H, and R-CH3 bond strength with the corresponding substituent decrease in that order.

It is indicated that other than the steric repulsion, the intramolecular charge-induced dipole in R–X should be considered (X = H, CH3, and OH). Our result is also supported by the view of the aspect that intramolecular charge-induced dipole and germinal repulsion could alter the trends of R–X BDE.20 Simulation of benzylic p-YC6H4G-X molecules also supports the dipole argument21 where the effect of substituents on benzylic C–H bonds would be opposite of the effect on C-halogen bonds. It is clear that the larger the bulkiness of the R group with a more repulsive effect between the R and CH3, the smaller the BDEs of R-CH3.

2.2. Mono-substituted Anisole Compounds

When the substituents are extended from the alkyl group to the other functional group with different electronic effects, the steric effect is not the main factor controlling the size of O-CH3 BDE. A series of 45 substituted anisoles (Group II in Figure 1) have been studied in this work to understand the direction and magnitude of the electronic effect. All of the calculated O-CH3 BDEs are arranged in ascending order, as shown in Table 2. The span of BDEs ranges largely from 51.8 kcal/mol (o-OH, 8a) to 68.4 kcal/mol (p-NO2, 20c) with a range of 16.6 kcal/mol. In general, the electron-donating substituents including NH2, OH, OCH3, CONH2, and CH3 with halo substituents F, Cl, and Br weaken the O-CH3 bond, while electron-withdrawing groups COOCH3, CF3, COOH, CHO, NO2, and CN strengthen the O-CH3 bond at all ortho-, meta-, and para- positions. Furthermore, it is interesting to find that in the ortho-position, the substituent effect was the largest of all (−13.5 to 2.4 kcal/mol using anisole 1 as the standard). The meta-substituent effect distributes more evenly with a much narrower variation (−1.1 to 3.0 kcal/mol). The para-position is intermediate of the other two (−8.0 to 3.1 kcal/mol).

Table 2. Bond Dissociation Enthalpy (BDE) of O-CH3 for Molecules with Different Substituents in Group II (Units in kcal/mol).

substituent compound# o-position m-position p-position
NH2 7 53.7 64.2 57.3a
OH 8 51.8/57.0b 64.6 60.4a
OCH3 9 59.0 66.1a 59.6a
CONH2 10 57.8/61.9b 66.5 65.9
CH3 11 63.3 64.4 63.3a
F 12 62.0 66.2 63.6
Cl 13 62.4 66.4a 64.3
Br 14 62.5 66.5 64.7
CCl3 15 64.8 65.1 65.9
H 1 65.3b 65.3 65.3
COOCH3 16 65.0 65.7 65.8
CF3 17 66.1 66.0 66.9
COOH 18 66.5 66.4 66.8
CHO 19 67.7 67.4 66.6
NO2 20 66.7 67.8 68.4
CN 21 67.7 68.3a 67.5
Open in a new tab
a

Data from ref (11).

b

Two different structures (substituent group oriented toward the −OCH3 group of the ring favoring the hydrogen bond formation is shown in bold, see text).

If we take a detailed examination on each substituent in different o-, m-, and p- positions, it is shown that the size of the O-CH3 BDE took the order of o < p < m for all the electron-donating substituents and halo substituents (7–14). The trend of BDE values switched to o ≤ m < p when electron-withdrawing groups were induced to the system except with the −CHO and −CN substituents (15–18 and 20). This small BDE of the substituent o-position is most probably due to the radical resonance stabilization effect. Especially for 8a, it is clear that the O radical single electron is delocalized to the C atom next to the o-OH, which is stabilized by the OH group through the resonance effect and could enhance the stability of the phenoxy radical, which causes the O-CH3 bond to weaken. Aldehyde (−CHO, 19) and cyano (−CN, 21) groups belong to a special catalog with the order p < o < m for O-CH3 BDE. This modest difference between o-, m-, and p- and the re-order are presumably due to the possible intermolecular interaction provided by the aldehyde and cyano groups in para- and ortho-positions.

Compared to experimental data, the computational method tends to underestimate the BDE value with the standard error between 1.4 and 2.9 kcal/mol (Table S2) in most cases. For substituents including −NH2, −OH, and −OCH3, which belong to electron-donating groups, the computational method will overestimate the BDE value for both o- and p-positions. Another overestimation is for −CF3 substituents at the para-position. In the case of meta-position substituents, there is a narrow range of BDE values for both theoretical BDEs and experimental BDEs, suggesting that the change of the functional group at the m-position cannot alter the BDE value significantly.

For the −OH and CONH2 substituents, two structures with the substituents in the ortho-position were analyzed: (i) the −OH and −CONH2 groups oriented toward the −OCH3 group of the ring favoring the hydrogen bond formation; (ii) no consideration for the possible hydrogen bonding formation. From Table S2, it is noticed that the BDE for the ortho-hydroxyl substituent 8a with a value of 57.05 kcal/mol is in good agreement with the experiment. This is due to the formation of intramolecular hydrogen bonds of 2.074 and 1.968 Å between the oxygen atom from the −OCH3 group and the hydrogen atom from the OH group and from the radical oxygen and −OH hydrogen, respectively. The hydrogen bonding could stabilize both the radical and the parent molecule. The formation of CO-H intramolecular hydrogen bond as the key factor to stabilize the oxygen radicals has been reported by Alvareda et al., who demonstrated that the lower BDEs of the C-OH bond of some flavonoids present radicals stabilized by a hydrogen bond.22 The same effect is observed for CONH2 for which there is no experimental data available. The BDE value for the structure with hydrogen bonding formation is 61.87 kcal/mol. The intramolecular hydrogen bonding distances between the −CONH2 group and oxygen radical and the hydrogen atom from the −OH group are 1.937 and 1.916 Å, respectively. With the strong electron-withdrawing ability of the nitro substituent, it is not surprising to find the largest BDE (20c) with the nitro group at the para-position. Although the strength of the O-CH3 bond is limited with the involvement of the nitro group (1–3 kcal/mol), this small thermodynamical difference could be the key point for the design of the corresponding pharmaceutical inhibitor.

In fact, the effect of electron-donating groups (EDGs) and electron-withdrawing groups (EWGs) are a combination of conjugative and inductive effects.23Figure S2 shows the activity of different substituents divided into a strongly activating group, moderately activating group, weakly activating group, weakly deactivating group, moderately deactivating group, and strongly deactivating group based on the effects on the reactivity of benzene rings. In general, a good correlation between the activity of substituents and BDEs of O-CH3 could be observed by EDGs making the O-CH3 bond in phenols easier to break, while EWGs stabilize the oxygen–carbon bond. However, as a weakly deactivating group, F, Cl, and Br did not strengthen the O-CH3 bond but decreased the O-CH3 BDE value compared to H. There is controversy over the property of halo substituents: F, Cl, and Br are generally classified as electron-withdrawing groups, while it is also reported that they could stabilize the radical and destabilize the ground state, having the property of electron-donating substituents.14 This difference may come from where the parameters are derived, through either the kinetic model or thermodynamic method. Furthermore, strongly deactivating groups such as CF3 and CCl3 do not show the corresponding weakening ability as expected. The BDE of CCl3-substituted anisole is almost the same as the BDE value of anisole. In these cases, steric effects make a more obvious contribution to the decrease in the BDE value. Especially at the o-position, the O-CH3 BDE size of CCl3-substituted anisole is bigger than that of CF3, which has a more obvious steric effect to make the O-CH3 bond break easily.

For further quantitative analysis, the factor of electronegativity was taken into consideration. However, there is no obvious correlation between O-CH3 BDEs with the electronegativity of the functional group, regardless of which parameters were used from different groups (Table S3). It is believed that the electron demand (i.e., electron-donating or electron-withdrawing ability) rather than the electronegativity had a decisive role in the substituent effect on the bond dissociation enthalpy.24

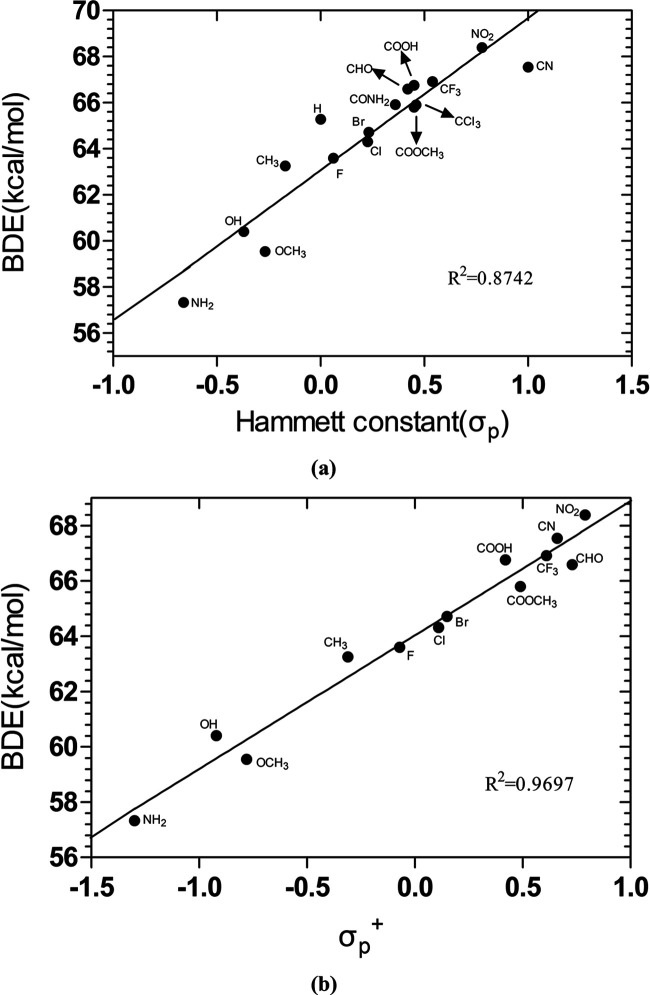
The Hammett equation with its extended forms is one of the most extensive means of studying and understanding organic reactions and the corresponding mechanisms.25 Panel a in Figure 2 and Figure S3 display the correlation plots between O-CH3 BDEs with Hammett constants σp and σm, respectively. The linear correlation is not good for σm with R2 = 0.7055, while for para-substituents, the correlation became better (R2 = 0.8742) but not satisfactory. In addition, the Hammett constants can be separated to field (induction) and resonance (conjugation) contributions, which could be represented by Swain and Lupton F and R values, respectively26 (Table S4). Figure S4 shows the correlation between calculated BDE values and these parameters (σp, F, and R). The poor correlation for F but good correlation for R suggested that the resonance effect plays a more important role than the field effect. This conclusion is also supported by the modified Hammett equation (eq 1) with the correlation of BDEs to both F and R simultaneously to access the sensitivity of resonance and field effects (indicated by f and r, respectively) (Figure S5).26 From Figure S5, it is clear that for meta-substituents, the field effect mainly controls the BDE value with some contribution from the resonance effect with f (4.2) > r (1.6). In the case of ortho-substituents, the resonance fully dominates the trend of BDEs with r = 14.8 much larger than f = −0.02. These totally different behaviors toward resonance and field effects upon different positions of substituents (ortho-, meta-, and para-) enables us to adjust the BDE values using the proper substituent group.

2.2. 1

Figure 2.

Figure 2

Open in a new tab

Correlation plots of calculated BDEs of O-CH3 in substituted anisoles with (a) Hammett constants (σp) and (b) Brown σp+ constants.

Furthermore, Brown27 and Okamoto came up with the idea of a σp+ constant for substituents conjugated to the center of the reaction and capable of delocalizing positive charges. The calculated O-CH3 BDEs can be correlated well with σp+ (R2 = 0.9697, Figure 2b). This good correlation suggested that the stability of the anisole radical is influenced by the polar effect provided by the para-substituent. The improvement of the linear correlation from σp to σp+ indicated the importance of the conjugation effect in BDEs. Figure 3 shows the correlation of calculated BDE (O-CH3) and available Creary’s radical substituent constants (c*)29 for the m-position with R2 equals to 0.8434. In addition, the other two positions’ parameters (o- and p-) gave a more discrete distribution with no significant correlation (Table S5 and Figures S6 and S7), illustrating that the spin delocalization plays a more important role when the substituents are on the m-position. Our results confirm that in many free-radical reactions, the correlation can be well obtained by using polar parameters. Jiang had also pointed out that in many reactions involving radicals, it is not necessary to use the radical parameter but the polarity parameter for correlation.30−33 This connection suggested that the polarity effect plays a more important role than spin delocalization.

Figure 3.

Figure 3

Open in a new tab

Bond dissociation enthalpies (BDE) of O-CH3 in substituted anisoles against Creary radical substituent constants (c*) for meta-substituted anisole. Substituents include CH3, F, Cl, H, CF3, NO2, and CN.

2.3. Multi-substituted Anisole Compounds

As is stated above, we mainly focus on the effect of the O-CH3 bond by a single substituent. It would be interesting to see how the number of substituents affects the BDEs of O-CH3. Eight typical substituents including NH2, OCH3, F, Cl, Br, CHO, NO2, and CN with mono-, di-, and tri-substituent (Group III, Figure 1) were selected to investigate the BDEs of O-CH3. The simulated results are shown in Table 3 and Figure 4. From Table 3 and Figure 4, it is clear that as the number of electron-donating (−NH2 and −OCH3) and halo (−F, −Cl, and −Br) substituents increases, the value of BDE of O-CH3 decreases. This additive effect is especially obvious for −NH2 (22) and −OCH3 (23) substituents where EDGs weaken the O-CH3 bond. For halo substituents (−F, −Cl, and −Br), the number of substituents has a neglectable effect on the size of BDEs. In the case of electron-withdrawing groups (EWGs), in general, BDE increases slightly as the number of substituents increases. One surprising finding is that the BDE of anisole with two aldehyde groups is considerably higher than those of mono- and tri-substituents. The BDE of anisole with two aldehyde groups is considerably bigger than that of the mono-substituent, which we did not expect. While the possible formation of weak hydrogen bonds between hydrogen on the methyl group and oxygen on the aldehyde group plays a more important role in making the C–O bond more stable. Indeed, the existence of C–H···O bonding and the form in the aromatic system have been systematically reported.34−37 It is hard to explain the smaller BDE value of the tri-substituent with one more CHO substituent on the p-position compared to the di-substituent. Furthermore, systematical research studies will be necessary to explore all these details.

Figure 4.

Figure 4

Open in a new tab

Coordinate effect of substituents on BDEs of O-CH3. The bars indicate the BDE value of O-CH3. Every suit represents a class of substituents and the number of substituents increases from left to right.

3. Conclusions

The importance of methyl transfer in both chemical and biological systems requires the systematic study of the thermodynamical parameters. The present study is the first important step to establish a comprehensive O-CH3 BDE theoretical database using the G4 method, which has been shown to be reliable for it.11 The BDE order (t-Bu < i-Pr < n-Bu ≈ Et ≈ Me) with the ortho-substitution on the benzyl ring suggested that bigger alkyl groups usually implied in greater steric hindrance could make the O-CH3 BDE smaller. The simulation results with different types of substituents suggested that the electron-donating groups (EDGs) make the O-CH3 bond on anisole easier to break while electron-withdrawing groups (EWGs) strengthen the O-CH3 bond. The position of the substitution would also be important to the bond strength. Furthermore, a linear correlation between σp+ and O-CH3 BDE indicates the importance of taking the conjugate effect into account. By considering the steric effect, hydrogen bond, and substituent and its position, a wide range spanning around 20 kcal/mol of BDEs could be achieved in the same basic molecular frame, providing a useful strategy to scale and select a candidate compound to achieve certain activity. Besides the prediction and estimation of BDEs, the present study provides more perspectives to help in analyzing the role of substituents through the establishment of O-CH3 BDE database, which would contribute to the rational design of inhibitors and drugs. The present study will be continued for the full establishment of the O-CH3 BDE database.

4. Computational Details

Bond dissociation enthalpy of O-CH3 corresponds to the enthalpy change shown in the following reaction (eq 2) in the gas phase, with a temperature of 298.15 K and pressure of 1 atm:

4. 2

The calculation of dissociation enthalpies at 298 K (DH) followed the equation below (eq 3)

4. 3

D0 is the dissociation enthalpy, which is the change in electronic energy, while dissociation (De) is the zero-point energy correction at 0 K. ΔHT is the difference between the radicals and the undissociated molecule.

The calculations cover more than 50 aromatic molecules shown in Figure 1. The Gaussian 09 program suite38 was used to calculate the BDE of O-CH3 in the gas phase at 298 K. Following a previous study,11 the G4 method was selected to compute the BDEs. The fourth Gaussian-n39−41 quantum chemical method is based on a battery of single-point energy calculations with different levels of accuracy and basis sets designed to approach the exact energy. The application of the G4 method has been shown to perform well on aromatic molecules.42 All molecules were previously optimized using the B3LYP functional43 and the def2-TZVP basis set.44 The D3 dispersion of Grimme correction45 was included in all calculations. Frequency calculations of all optimized structures were also performed, and no imaginary frequencies were found.

Acknowledgments

The authors acknowledge the financial support provided by the National Natural Science Foundation of China (NSFC 21772143 and 21927814) and the Natural Science Foundation of Tianjin (17JCYBJC42200). Generous computer time on the School of Pharmaceutical Science and Technology computer cluster Arran is gratefully acknowledged.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c02310.

  • Parameters of electronegativity, Hammett constants, Creary’s spin delocalization values and experimental BDEs, and figures of correlations between calculated BDE and corresponding parameters (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao1c02310_si_001.pdf (811.4KB, pdf)

References

  1. Christian T.; Sakaguchi R.; Perlinska A. P.; Lahoud G.; Ito T.; Taylor E. A.; Yokoyama S.; Sulkowska J. I.; Hou Y. M. Methyl Transfer by Substrate Signaling From a Knotted Protein Fold. Nat. Struct. Mol. Biol. 2016, 23, 941–948. 10.1038/nsmb.3282. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ho H. E.; Oniwa K.; Yamamoto Y.; Jin T. N-Methyl Transfer Induced Copper-Mediated Oxidative Diamination of Alkynes. Org. Lett. 2016, 18, 2487–2490. 10.1021/acs.orglett.6b01067. [DOI] [PubMed] [Google Scholar]
  3. Saez D. A.; Vogt-Geisse S.; Inostroza-Rivera R.; Kubař T.; Elstner M.; Toro-Labbé A.; Vöhringer-Martinez E. The Effect of the Environment on the Methyl Transfer Reaction Mechanism Between Trimethylsulfonium and Phenolate. Phys. Chem. Chem. Phys. 2016, 18, 24033–24042. 10.1039/C6CP02821G. [DOI] [PubMed] [Google Scholar]
  4. Schubeler D. Function and Information Content of DNA Methylation. Nature 2015, 517, 321–326. 10.1038/nature14192. [DOI] [PubMed] [Google Scholar]
  5. Weber M.Phenol. In Ullmann’s Encyclopedia of Industrial Chemistry, 5th ed.; Ley C., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, 2020; pp. 299–312 [Google Scholar]
  6. Huang W. Y.; Cai Y. Z.; Zhang Y. Natural Phenolic Compounds From Medicinal Herbs and Dietary Plants: Potential Use for Cancer Prevention. Nutr. Cancer 2009, 62, 1–20. 10.1080/01635580903191585. [DOI] [PubMed] [Google Scholar]
  7. Kiss L. E.; Soares-da-Silva P. Medicinal Chemistry of Catechol O-methyltransferase (COMT) Inhibitors and Their Therapeutic Utility. J. Med. Chem. 2014, 57, 8692–8717. 10.1021/jm500572b. [DOI] [PubMed] [Google Scholar]
  8. Sharman D. F. the Catabolism of Catecholamines Recent Studies. Br. Med. Bull. 1973, 29, 110–115. 10.1093/oxfordjournals.bmb.a070978. [DOI] [PubMed] [Google Scholar]
  9. Kopin I. J. Catecholamine Metabolism: Basic Aspects and Clinical Significance. Pharmacol. Rev. 1985, 37, 333–364. [PubMed] [Google Scholar]
  10. Männistö P. T.; Kaakkola S. Catechol-O-methyltransferase (COMT): Biochemistry, Molecular Biology, Pharmacology, and Clinical Efficacy of the New Selective COMT Inhibitors. Pharmacol. Rev. 1999, 51, 593–628. [PubMed] [Google Scholar]
  11. Du T.; Quina F. H.; Tunega D.; Zhang J.; Aquino A. J. A. Theoretical O–CH3 Bond Dissociation Enthalpies of Selected Aromatic and Non-aromatic Molecules. Theor. Chem. Acc. 2020, 139, 75. 10.1007/s00214-020-02592-1. [DOI] [Google Scholar]
  12. Pratt D. A.; DiLabio G. A.; Valgimigli L.; Pedulli G. F.; Ingold K. U. Substituent Effects on the Bond Dissociation Enthalpies of Aromatic Amines. J. Am. Chem. Soc. 2002, 124, 11085–11092. 10.1021/ja026289x. [DOI] [PubMed] [Google Scholar]
  13. Wu Y.-D.; Lai D. K. W. A Density Functional Study of Substituent Effects on the O–H and O–CH3 Bond Dissociation Energies in Phenol and Anisole. J. Org. Chem. 1996, 61, 7904–7910. 10.1021/jo960069i. [DOI] [PubMed] [Google Scholar]
  14. Liu S.; Hu H.; Pedersen L. G. Steric, Quantum, and Electrostatic Effects on SN2 Reaction Barriers in Gas Phase. J. Phys. Chem. A. 2010, 114, 5913–5918. 10.1021/jp101329f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Regan C. K.; Craig S. L.; Brauman J. I. Steric Effects and Solvent Effects in Ionic Reactions. Science 2002, 295, 2245–2247. 10.1126/science.1068849. [DOI] [PubMed] [Google Scholar]
  16. Pinter B.; Fievez T.; Bickelhaupt F. M.; Geerlings P.; De Proft F. On the Origin of the Steric Effect. Phys. Chem. Chem. Phys. 2012, 14, 9846–9854. 10.1039/c2cp41090g. [DOI] [PubMed] [Google Scholar]
  17. Charton M. Steric effects I. Esterification and Acid-Catalyzed Hydrolysis of Esters. J. Am. Chem. Soc. 1975, 97, 1552–1556. 10.1021/ja00839a047. [DOI] [Google Scholar]
  18. Beckhaus H.-D. Sf Parameters—A Measure of the Front Strain of Alkyl Groups. Angew. Chem., Int. Ed. Engl. 1978, 17, 593–594. 10.1002/anie.197805931. [DOI] [Google Scholar]
  19. Gronert S. An Alternative Interpretation of the C–H Bond Strengths of Alkanes. J. Org. Chem. 2006, 71, 1209–1219. 10.1021/jo052363t. [DOI] [PubMed] [Google Scholar]
  20. Cao C. Z. Influence of Steric and Intramolecular Inductive Effects on the Variable Trends in R-X (R=Alkyl) Bond Dissociation Energy. Sci. China, Ser. B: Chem. 2009, 52, 943–951. [Google Scholar]
  21. Zavitsas A. A.; Rogers D. W.; Matsunaga N. Remote Substituent Effects on Allylic and Benzylic Bond Dissociation Energies. Effects on Stabilization of Parent Molecules and Radicals. J. Org. Chem. 2007, 72, 7091–7101. 10.1021/jo0707129. [DOI] [PubMed] [Google Scholar]
  22. Alvareda E.; Denis P. A.; Iribarne F.; Paulino M. Bond dissociation energies and enthalpies of formation of flavonoids: A G4 and M06-2X investigation. Comput. Theor. Chem. 2016, 1019, 18–23. 10.1016/j.comptc.2016.06.021. [DOI] [Google Scholar]; In addition, during the pre-review process, one of the referees suggested that the formation of hydrogen bond shown here would be achieved through the resonance structures where the single electron on O radical delocalized to the neighboring benzene ring with stabilization by the -OH group. The -CONH2 case acts in a similar manner.
  23. Ouellette R. J.; Rawn J. D.. Electrophilic Aromatic Substitution. In Organic Chemistry, 2nd ed.; Weber M., Ed.; Academic Press: New York, 2018; pp. 375–407. [Google Scholar]
  24. Feng Y.; Huang H.; Liu L.; Guo Q. X. Homolytic Bond Dissociation Energies Associated with Acyl Radicals and Electron Demands of Acyl Groups. Phys. Chem. Chem. Phys. 2003, 5, 685–690. 10.1039/b211078d. [DOI] [Google Scholar]
  25. Hansch C.; Leo A.; Taft R. W. A survey of Hammett Substituent Constants and Resonance and Field Parameters. Chem. Rev. 1991, 91, 165–195. 10.1021/cr00002a004. [DOI] [Google Scholar]
  26. Frank H. Q.; Erick L. B.. Fundamental Aspects of Quantitative Structure-Reactivity Relationships. In Encyclopedia of Physical Organic Chemistry, 1st ed.; Wang Z., Ed.; Wiley: New Jersey, 2017; pp. 437–490. [Google Scholar]
  27. Brown H. C.; Okamoto Y. Electrophilic Substituent Constants. J. Am. Chem. Soc. 1958, 80, 4979–4987. 10.1021/ja01551a055. [DOI] [Google Scholar]
  28. Creary X. Super Radical Stabilizers. Acc. Chem. Res. 2006, 39, 761–771. 10.1021/ar0680724. [DOI] [PubMed] [Google Scholar]
  29. Jiang X. K. Establishment and Successful Application of the σJJ• Scale of Spin-Delocalization Substituent Constants. Acc. Chem. Res. 1997, 30, 283–289. 10.1021/ar950121h. [DOI] [Google Scholar]
  30. Ji G. Z.; Jiang X. K.; Zhang Y. H.; Yuan S. G.; Yu C. X.; Shi Y. Q.; Zhang X. L.; Shi W. T. The Spin Delocalization Substitutent Parameter σJJ. 5. Correlation Analysis of 19F Chemical Shifts of Substituted Trifluorostyrenes. The unresolved polar substituent parameter σmb. J. Phys. Org. Chem. 1990, 3, 643–650. 10.1002/poc.610031005. [DOI] [Google Scholar]
  31. Ding F. X. W.; Xie R. Y. J.; Ji G. Z.; Jiang X. K. Application of the Dual Parameter Equation to the Correlation Analysis of the Redox Potential Data of Five para-Substituted Phenyl Compounds. J. Chem. Res., Synop. 1998, 368–369. 10.1039/A708379C. [DOI] [Google Scholar]
  32. Jiang X. K.; Ding F. X. W.; Zhang Y. H. The Nucleophilic Silyl Radical: Dual-Parameter Correlation Analysis of the Relative Rates of Bromine-Atom Abstraction Reactions as Measured by a Rigorous Methodology. Tetrahedron 1997, 53, 8479–8490. 10.1016/S0040-4020(97)00527-9. [DOI] [Google Scholar]
  33. Huggins C. M.; Pimentel G. C.; Shoolery J. N. Proton Magnetic Resonance Studies of Chloroform in Solution: Evidence for Hydrogen Bonding. J. Chem. Phys. 1955, 23, 1244–1247. 10.1063/1.1742249. [DOI] [Google Scholar]
  34. Trotter J. A Three-Dimensional Analysis of the Crystal Structure of p-benzoquinone. Acta Cryst. 1960, 13, 86–95. 10.1107/S0365110X60000212. [DOI] [Google Scholar]
  35. Taylor R.; Kennard O. Crystallographic Evidence for the Existence of C-H···O, C-H···N and C-H···Cl Hydrogen Bonds. J. Am. Chem. Soc. 1982, 104, 5063–5070. 10.1021/ja00383a012. [DOI] [Google Scholar]
  36. Gilli G.; Gilli P.. The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory, Oxford University Press: Oxford, 2009. pp. 23–47. [Google Scholar]
  37. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A.; Peralta J. E. Jr.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J. (2016) in Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT [Google Scholar]
  38. Pople J. A.; Martin H. G. M.; Fox D. J.; Raghavachari K.; Curtiss L. A. Gaussian-1 Theory: A General Procedure for Prediction of Molecular Energies. J. Chem. Phys. 1989, 90, 5622–5629. [Google Scholar]
  39. Curtiss L. A.; Raghavachari K.; Trucks G. W.; Pople J. A. Gaussian-2 Theory for Molecular Energies of First- and Second-row Compounds. J. Chem. Phys. 1991, 94, 7221–7230. 10.1063/1.460205. [DOI] [Google Scholar]
  40. Curtiss L. A.; Redfern P. C.; Raghavachari K. Gaussian-3 Theory for Molecules Containing First and Second-row Atoms. J. Chem. Phys. 1998, 109, 084108. [Google Scholar]
  41. Curtiss L. A.; Redfern P. C.; Raghavachari K. Gaussian-4 Theory. J. Chem. Phys. 2007, 126, 084108 10.1063/1.2436888. [DOI] [PubMed] [Google Scholar]
  42. Becke A. D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  43. Weigend F.; Ahlrichs R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  44. Grimme S. Semiempirical GGA-type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c02310_si_001.pdf (811.4KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES