Abstract
We present a detailed theoretical investigation of the interaction of graphene with the SrO-terminated (001) surface of pristine and La-doped SrTiO3. The adsorption of graphene is thermodynamically favorable with interfacial adsorption energies of −0.08 and −0.32 J/m2 to pristine SrTiO3 and La-doped SrTiO3 surfaces, respectively. We find that graphene introduces C 2p states at the Fermi level, rendering the composite semimetallic, and thus the electrical properties are predicted to be highly sensitive to the amount and quality of the graphene. An investigation of the lattice dynamics predicts that graphene adsorption may lead to a 60–90% reduction in the thermal conductivity due to a reduction in the phonon group velocities, accounting for the reduced thermal conductivity of the composite materials observed experimentally. This effect is enhanced by La doping. We also find evidence that both La dopant ions and adsorbed graphene introduce low-frequency modes that may scatter heat-carrying acoustic phonons, and that, if present, these effects likely arise from stronger phonon–phonon interactions.
Keywords: thermoelectrics, graphene/strontium titanate composite materials, electronic structure, structural dynamics, thermal transport, graphene adsorption on perovskite oxides
Introduction
With continued growth in global energy consumption, greater importance must be placed on moving away from fossil fuels to clean energy solutions. An increase in renewable energy generation must also be delivered alongside technologies to improve the efficiency of existing energy-intensive systems such as internal combustion engines to mitigate the worst effects of climate change.1 Thermoelectric (TE) power generation is a promising method to reduce energy consumption and increase efficiencies by recycling waste heat back to electrical energy.2 TE devices have already found applications in the aerospace, automotive and heavy manufacturing industries, and in remote power generation, and further improvements to their performance would allow them to compete economically with traditional sources of primary energy generation.3−5
The performance of a TE material is determined by the dimensionless figure of merit ZT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, κ = κel + κlatt is the thermal conductivity, and T is the temperature. The thermal conductivity has contributions from the electrical thermal conductivity κel and the lattice (phonon) thermal conductivity κlatt. Methods for optimizing ZT include doping and dimensionality reduction6−9 through nanostructuring10−12 and nanocompositing.8,13,14 However, improving TE performance is a complex process due to the interdependence of the electrical properties—increasing σ by increasing the carrier concentration n improves the power factor S2σ but also increases κel and tends to decrease S.
Most TE materials currently on the market are alloys containing bismuth, antimony, and tellurium,15−18 which are rare, toxic, and/or expensive. While the highest ZT are currently obtained with chalcogenide TEs,19,20 recent work has shown that metal oxides20−22 such as CaMnO3,23 SrTiO3,24−27 M2CoO3,28 BaTiO3,29 tungsten bronze,30,31 Bi2Sr2Co1.8Oy,32 In2O3,33 and La1/3NbO334 may be promising alternatives to conventional TE materials while being made from cheaper, more earth-abundant, and less toxic materials.35,36 Among the potential oxide TEs, strontium titanate (SrTiO3; STO) shows promise due to its thermal stability at high temperature and tolerance to doping.26,27,37 Bulk SrTiO3 has a relatively poor ZT, and thus doping has been extensively explored as a possible route to improving its performance with examples including substituting Sr sites with rare-earth elements such as La38,39 and Ti sites with other transition metals such s Nb.40−42 La doping has been shown to promote the formation of A-site vacancies, which both increases the electrical conductivity and decreases the thermal conductivity through enhanced phonon scattering.43 Doping with La under reducing conditions further leads to the formation of oxygen vacancies, which decreases the thermal conductivity while having minimal impact on the electrical conductivity. Wang et al.38 showed that doping SrTiO3 with 12% Dy and 8% La increased the ZT from 0.05 to 0.36 at ∼800 °C.
As an alternative to doping, strain engineering,44,45 grain boundary engineering,10,11,46,47 and nanocompositing SrTiO3 with materials such as graphene also have the potential to improve the TE performance. In the latter case, whereas a graphene-based TE would perform poorly due to its large thermal conductivity, the addition of graphene to conventional-48,49 and oxide-based8,13,14,50,51 TEs has been shown to produce synergistic improvements in the ZT. Lin et al.13 investigated the addition of graphene to lanthanum-doped (LSTO) and noted a widening of the operating window to room temperature, a decrease in the thermal conductivity, and a significant increase in the electrical conductivity. The best results were obtained when 0.6 wt % of graphene was added, achieving a ZT of 0.42 at room temperature and 0.36 at 750 °C, amounting to a 280% improvement over pure LSTO. Bantawal et al.50 and Baran et al.52 investigated the electronic structure of graphene–SrTiO3 composites and found that carbon states were present at the Fermi level within the SrTiO3 band gap. The latter study52 also showed that by altering the SrTiO3 surface termination the electrical properties of the material could be tuned to optimize the electrical conductivity and to obtain both p and n-type transport.
In this work, we extend these previous studies by performing further detailed characterization of STO/LSTO–graphene composites, including modeling the structural dynamics and elucidating the impact of graphene adsorption on the thermal transport. We find that the nanocompositing produces surface interactions that impact both the electronic and thermal properties of the composite. Analysis of the electronic density of states displays characteristic fingerprints of graphene, which are reflected in the electrical properties of the composite, and analysis of the phonon spectra and group velocities indicates that the La doping and graphene adsorption are both likely to suppress the heat transport in the composite materials. These results provide further fundamental insight into how surfaces and interfaces can be exploited through nanocompositing, providing a firm foundation for the discovery and optimization of future high-performance TEs.
Methodology
Calculations were performed using pseudopotential plane-wave density functional theory (DFT) as implemented in the Vienna Abinitio Simulation Package (VASP) code.53−56 We employed the Perdew–Burke–Ernzerhof (PBE) generalized-gradient approximation (GGA) functional57,58 with the DFT-D3 dispersion correction59 to account for van der Waals interactions. The projector augmented-wave (PAW) method was used to describe interactions between the core and valence electrons, with the following valence configurations: O—2s22p4; C—2s22p2; Sr—4s24p65s2, Ti—3d24s2, and La—5s25p66s25d1.60,61 A kinetic energy cutoff of 520 eV was used to represent the Kohn–Sham orbitals, which was determined from explicit convergence testing. Γ-centered k-point grids with 6 × 6 × 6 and 4 × 4 × 1 subdivisions were used to integrate the Brillouin zones of bulk SrTiO3 and surface models, respectively. Surface models were generated with an initial vacuum spacing of 20 Å between periodic images, and a dipole correction was applied in the direction of the surface normal. The electronic energies were converged to 10–6 eV, and geometry optimizations were performed until the magnitude of the forces on the atoms were below 10–2 eV/Å. For the surface models, geometry optimizations were performed with the cell shapes and volumes fixed.
Transport coefficients were evaluated by solving the linearized Boltzmann transport equations within the constant relaxation-time approximation using the BoltzTraP code.62 The band energies of bulk SrTiO3 and the surface models were calculated non-self-consistently on dense 50 × 50 × 50 and 20 × 20 × 1 k-point meshes, respectively, and Fourier interpolation was used to increase these densities by a further 5×. The BoltzTraP results were compared to calculations using the BoltzWann code,63,64 details of which are given in the SI. To obtain the charge carrier concentration, we used Boltzmann transport analysis, where the chemical potential is directly related to the carrier concentration. As the chemical potential is shifted into the valence or conduction bands, the number of hole or electron carriers increases. By interpolating the density of states (DOS), the number of carriers at any given chemical potential can thus be determined. To validate the BoltzTrap and BoltzWann methods, we calculated the Seebeck coefficient of bulk SrTiO3 as a function of carrier concentration (Figure S5) and as a function of temperature at a fixed carrier concentration corresponding to the bottom of the conduction band (Figure S6).62,65 The calculations with the two methods give similar results (Figures S7 and S8). We also compared the band structures of bulk SrTiO3 and the surface models obtained from our DFT calculations and by Wannier interpolation using the Wannier functions employed in our transport calculations (Figures S2–S4).
Finally, we employed the Phonopy66 and Phono3py codes68 to compute for the slab models the harmonic force constants, phonon spectra, phonon group velocities, and quantities related to the lattice thermal conductivity. In these calculations, VASP was used as the force calculator to obtain the harmonic force constants using the supercell finite-displacement method.67 Atomic displacements were generated in 2 × 2 × 1 supercells, and accurate single-point force calculations were performed with a 500 eV cutoff energy and proportionally reduced 2 × 2 × 1 k-point meshes. For these calculations, the PAW projection was performed in reciprocal space, and an auxiliary charge–density grid with 8× the density of points was used when evaluating the forces.
Results and Discussion
Structure and Energetics
The optimized surface models investigated in this work are shown in Figure 1. Low-energy ion-scattering (LEIS) experiments have shown that perovskite surfaces display a dominant AO termination at elevated temperature,69−72 based on which we chose the SrO-terminated {001} surface of SrTiO3 as our starting point. An appropriate slab model was constructed from bulk cubic SrTiO3, consisting of 20 SrTiO3 and 5 SrO formula units (Figure 1). The additional 5 SrO units are required to form a complete monolayer, and the top and bottom surfaces of the slab models are therefore identical. A single-layer graphene model comprising 30 C atoms was then constructed and combined with the SrTiO3 surface, with the lattice vectors of both components redefined using the METADISE code73 to reduce the residual strain on the graphene sheet to ∼0.90%.52
Figure 1.
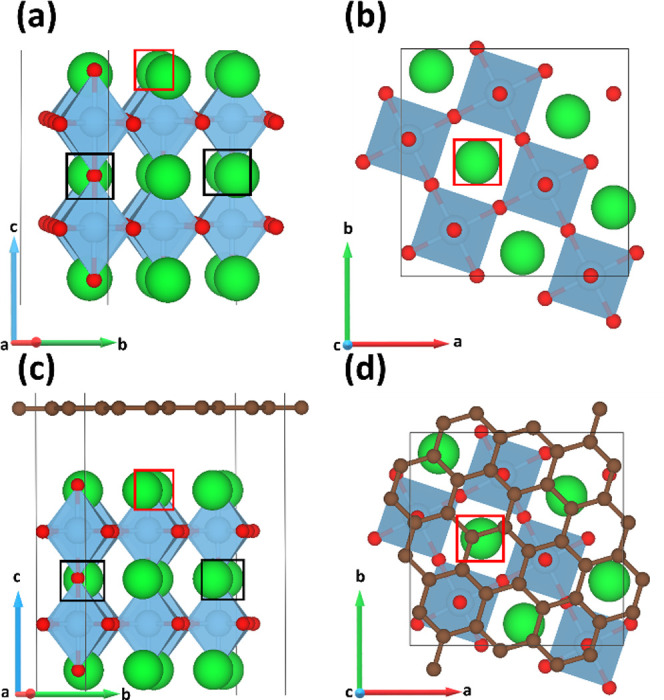
Surface structures investigated in this work. (a, b) SrTiO3 surface—(a) side and (b) top view. (c, d) graphene-decorated SrTiO3 surface—(c) side and (d) top view. The black and red squares mark the positions of La dopant atoms and charge-balancing Sr vacancies in the corresponding La-doped SrTiO3 surface models.
Models of La-doped SrTiO3 with and without adsorbed graphene were further generated by introducing two Sr vacancies on each side of the corresponding SrTiO3 slabs and substituting four subsurface Sr atoms with La to maintain overall charge neutrality, which we found to be the most stable arrangement.52
The surface energies of the SrTiO3 and La-doped SrTiO3 slab models were calculated according to
| 1 |
| 2 |
| 3 |
| 4 |
where the ES and EB are the energies of the surface and bulk models, respectively, and A is the surface area. We calculate a γS of 1.76 J/m2 for SrTiO3 and 1.86 J/m2 for La-doped SrTiO3.
The graphene layer adsorbs to the SrTiO3 surfaces at a distance of 3.23 Å, in good agreement with the 3.19 Å distance obtained in the calculations by Zou et al.74 The graphene adsorption and interfacial adsorption energies were calculated as
| 5 |
| 6 |
| 7 |
| 8 |
where Eg-surf and Esurf are the energies of the graphene-coated and pristine surfaces, respectively, and Egraph is the energy of the graphene sheet with nC = 30 carbon atoms. We note that our models of pristine graphene and the graphene-decorated surfaces have the same number of C atoms. We obtain EAds, graph = −0.01 and −0.05 eV per C atom for the SrTiO3 and La-doped SrTiO3 surfaces, respectively, which give the magnitude of the attachment energy for graphene to the oxide surfaces and indicate a small but energetically favorable adsorption. The interfacial adsorption energies were calculated to be −0.08 and −0.32 J/m2, respectively, for graphene adsorbed to pristine SrTiO3 and La-doped SrTiO3 surfaces. Such small energies are similar to the average binding energy of graphene onto the SrTiO3 (100) surfaces of 0.056 eV per C atom calculated by Zou et al.74 The difference in energy may be due to the lower level of strain in the graphene sheets in this work (0.9 vs 2.5% in the study in ref (74)).
Finally, the energies for La doping were calculated as
| 9 |
| 10 |
| 11 |
where the EB are the bulk energies of SrO and La2O3, ELa,surf and Esurf are the energies of the La-doped and pristine surfaces, respectively, and nLa is the number of La dopant atoms. We calculate an ED,La of 0.57 eV per La atom for the SrTiO3 surfaces and 0.28 eV per La for the graphene-coated SrTiO3 (g-SrTiO3) surfaces, indicating that the energetic penalty for La doping is substantially reduced in the presence of graphene.
Electronic Structure
We calculate direct and indirect band gaps of 2.0 and 1.65 eV for bulk SrTiO3 (Figure S2). The former may be compared to values of 2.74 eV using the LDA75 and 2.34 eV using the PBE GGA.76 Similarly, our calculated indirect gap can be compared to values of 2.1475,77 and 1.85 eV using the LDA78 and 1.99 eV using PBE.76 Our calculations deviate from the experimental values of 3.75 and 3.25 eV (direct/indirect) due to the well-known band gap underestimation inherent in (semi-)local DFT.79 The underestimation of our calculated band gaps compared to other computational literature is likely due to the inclusion of a van der Waals correction (DFT-D3); indeed, Holmström et al.80,81 calculated a band gap of 1.76–2.00 eV with PBE-D3, which is in keeping with our results. Despite the band gap underestimation, our calculations still correctly predict SrTiO3 to be a semiconductor and thus do not affect the qualitative analysis of the electronic structure, and, most importantly, the quantitative comparison between the slab models.
The electronic density of states (DOS) of SrTiO3 and La-doped SrTiO3 surface models indicate them to be semiconductors. As for bulk SrTiO3, the surfaces are predicted to have an indirect band gap (Figures S3 and S4). The orbital-projected partial density of states (Figure 2a,c) shows an asymmetric DOS with sharp peaks in the valence band. At the PBE-D3 level of theory, the calculated band gaps for SrTiO3 and La-doped SrTiO3 are 1.75 and 1.89 eV, respectively. These are in line with previous calculations on the SrO-terminated (001) surface, which estimated band gaps of 1.72–2.01 eV80 (PBE-D3) and 1.86 eV (LDA).78 In agreement with both theory and experiment, we find that the valence band maximum and conduction band minimum are dominated by O 2p and Ti 3d states, respectively.79 The addition of graphene to the surface introduces C 2p states into the SrTiO3 band gap (Figure 2b,d). However, the contribution of these states at the Fermi level is relatively small, and as such that the composite could be classified as a semimetal, that is, graphene does not induce metallic behavior in bulk SrTiO3, but rather introduces gap states that allow for metallic conduction with a small number of carriers. Previous studies using the (bare) PBE functional predicted a similar introduction of C 2p states at the Fermi level when SrTiO3 is composited with porous graphene (i.e., with carbon vacancies), irrespective of the concentration of pores.50
Figure 2.
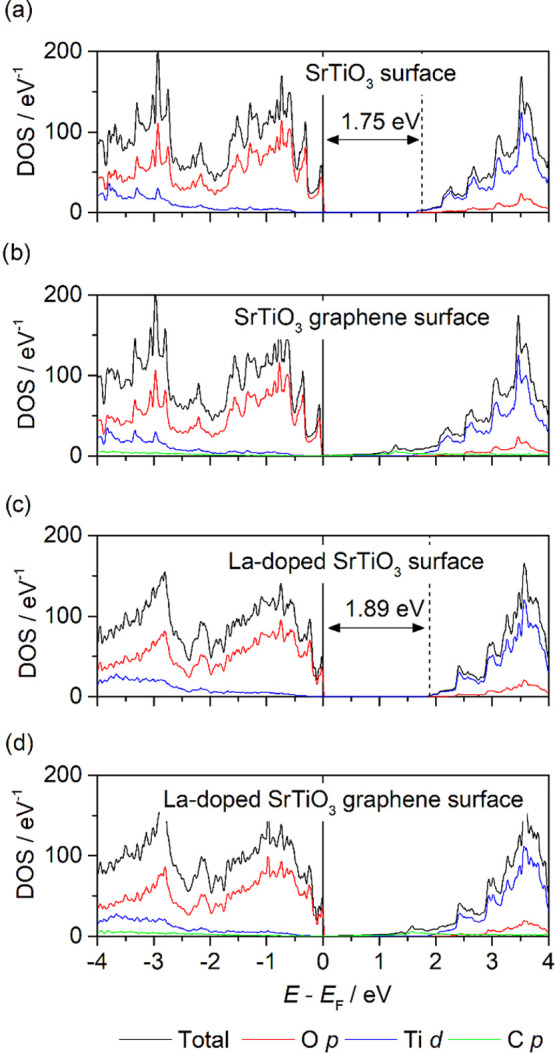
Total and orbital-projected electronic densities of states (DOS) from DFT calculations showing the composition of the valence and conduction bands in SrTiO3 and La-doped SrTiO3 surfaces with and without adsorbed graphene sheets.
Electronic Transport
It is clear from Figure 2 that the interaction of graphene with SrTiO3 surfaces intrinsically alters the electronic structure and as such is expected to impact upon the electronic transport and thermoelectric properties. The three crucial properties controlled by the electronic structure are the Seebeck coefficient S, the electrical conductivity σ, and the electronic part of the thermal conductivity κel.
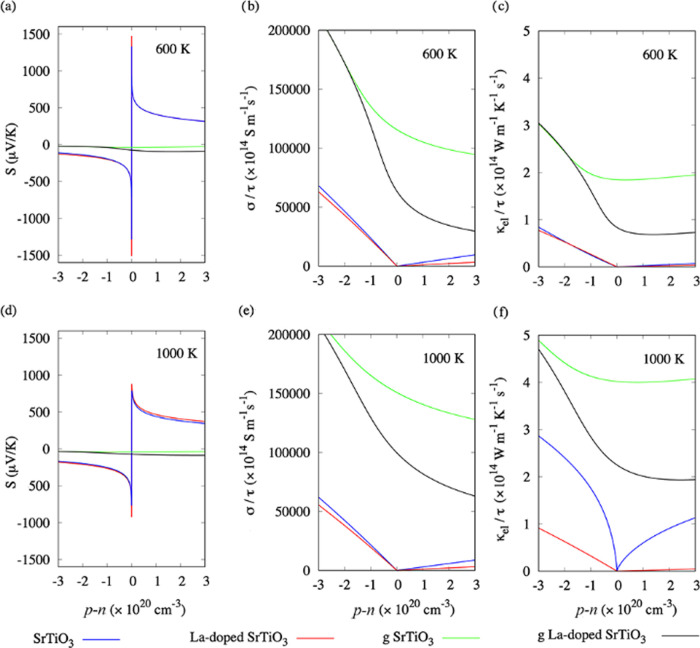
Figure 3 shows calculations of these three properties as a function of carrier concentration for the pristine and graphene-adsorbed surfaces. The same properties as a function of chemical potential are presented in Figure S10. Figure 3a compares the Seebeck coefficients of the pristine SrTiO3 and La-doped SrTiO3 surfaces as a function of carrier concentration. Within the constant relaxation-time approximation (CRTA) used by BoltzTraP, σ and κel are determined with respect to an unknown electron relaxation time τ, while S is independent of this parameter. Within this model, we obtain Seebeck coefficients of 1 333 and 1 475 μV/K at 600 K for the SrTiO3 and La-doped SrTiO3 surfaces, respectively (Figure 3a). Comparable values of 1342 and 1498 μV/K are obtained using BoltzWann (Figure S7). A general feature of the DOS of both models is an asymmetry arising from sharper features at valence band edges than at conduction band edges. For an intrinsic (undoped) semiconductor, where no charge carriers are present (p–n = 0), the Seebeck coefficient is governed solely by the gradient of the DOS at the band edges. In undoped SrTiO3, the larger gradient of the DOS at the valence band edge compared to the conduction band edge leads to a larger p-type contribution and a positive S (Figure S9). At higher temperatures, the smoothing out of the Fermi–Dirac distribution reduces the asymmetry in the DOS and S becomes negative, indicating n-type conductivity.82 The larger Seebeck coefficient of the La-doped SrTiO3 surface compared to the SrTiO3 surface is consistent with the steeper states in the DOS of the former (Figure 2).
Figure 3.
Seebeck coefficient S (a, d), electrical conductivity σ/τ (b, e), and electronic thermal conductivity κel/τ (c, f) as a function of carrier concentration p–n for pristine and graphene-adsorbed SrTiO3 and La-doped SrTiO3 surfaces at T = 600 (a–c) and 1000 K (d–f), calculated using the BoltzTraP code.
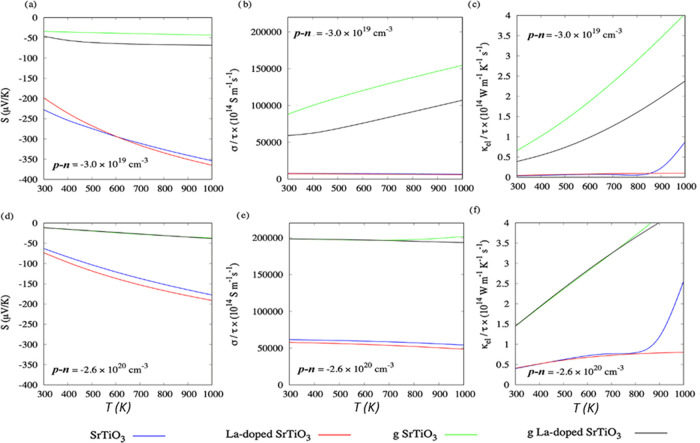
These values represent the maximum theoretical value that could be obtained for ideal, defect-free compositions. In reality, all materials contain defects that promote n or p-type conductivity, and the carrier concentrations are therefore heavily dependent on the material preparation. Both bulk and thin-film SrTiO3 show n-type conductivity,83,84 so we calculated the carrier concentrations relative to the bottom of the conduction band. This method is valid within the rigid-band approximation65 and has been used on similar perovskite systems. We obtain a carrier concentration of ∼1020 cm–3 for bulk SrTiO3 (Figure S6) and about 2.6 × 1020 cm–3 for the SrTiO3 surface model, which is in line with the ∼3.5 × 1020 cm–3 reported by Ravichandran et al. for undoped SrTiO3 thin films.84 Based on recent experiments,13 we also report values of S at carrier concentrations of 3 × 1019 cm–3. Figure 4a shows the Seebeck coefficients obtained for the surface models using BoltzTraP, and comparisons with BoltzWann are given in Figures S5–S7. The absolute value of the Seebeck coefficient increases with temperature, as is observed in bulk SrTiO3 at a fixed carrier concentration, and has previously been reported for bulk85 and thin-film samples.84
Figure 4.
Seebeck coefficient S (a,d), electrical conductivity σ/τ (b,e), and electronic thermal conductivity κel/τ (c,f) as a function of temperature for pristine and graphene-adsorbed SrTiO3 and La-doped SrTiO3 surfaces, with carrier concentrations of p–n = −3.0 × 1019 cm–3 (a–c) and −2.6 × 1020 cm–3 (d–f), calculated using the BoltzTraP code.
The electronic structures in Figure 2 show that the addition of graphene introduces C 2p states into the SrTiO3 band gap, resulting in a semimetallic electronic structure for both graphene-adsorbed surfaces. As shown in Figures S10a, 3a, and 4a, this results in an extremely low Seebeck coefficient at 600 K, with an order of magnitude difference in the maximum absolute values between the pristine and graphene-adsorbed surfaces. While inconsistent with the findings of Lin et al.,13 this is most likely due to the effective concentration of graphene in our models—whereas we have an effectively infinite graphene layer adsorbed onto the surfaces of the perovskite material, which would correspond to an ∼8 wt % composite, the highest concentration used in the experimental work is a much smaller 1 wt %. However, we can infer from the discrepancy that the electrical performance of these composite TEs is likely to be highly sensitive to the amount of graphene present and also its quality in terms of flake size and defect concentration, as these would strongly influence both the electrical properties of the graphene sheets and their interaction with the perovskite surfaces. Introducing high concentrations of graphene in graphene-oxide composites would lead to the thermoelectric properties being driven mostly by the graphene component, and from this perspective, our results are qualitatively in line with the Seebeck coefficients predicted for graphene from tight-binding models.86
At higher carrier concentrations, S decreases with temperature (Figure 4a,d), implying that the oxide component retains some influence on the properties of the composite. This is opposite to what is seen for carbon nanoribbons interacting with SrTiO3 surfaces, where S instead increases with temperature in the composite material.52
As noted above, solving the Boltzmann transport equations within the constant relaxation-time approximation yields the electrical conductivity σ and electronic thermal conductivity κel with respect to an unknown electron scattering time τ. τ incorporates complex physical phenomena including electron–phonon coupling and cannot, at present, practically be calculated from the first principles. For completeness, we plot these two properties as a function of carrier concentration (Figure 3), chemical potential (Figure S10), and temperature (Figure 4) and again observe substantially different behavior for the pristine and graphene-adsorbed systems. As noted above, the graphene-adsorbed systems have semimetallic character, since electronic states cross the Fermi level in graphene-adsorbed models, and we predict p-type conduction. The change from semiconducting to metallic behavior has a large effect on the transport properties, resulting in an increased σ and κel together with a reduced S, since the latter is inversely related to the number of free carriers.87
Lattice Dynamics and Thermal Transport
The lattice component of the thermal conductivity κlatt can be calculated using the second-order (harmonic) and third-order (anharmonic) force constants. However, obtaining the latter is computationally very expensive and is prohibitive for large systems such as our surface models. For this reason, we chose instead to examine the atom-projected phonon density of states (PDOS), the weighted two-phonon joint density of states (wJDOS), and the mode group velocities, all of which can be computed using the second-order force constants, to assess how changes in the phonon spectrum due to the doping and graphene adsorption are likely to impact the heat transport.13
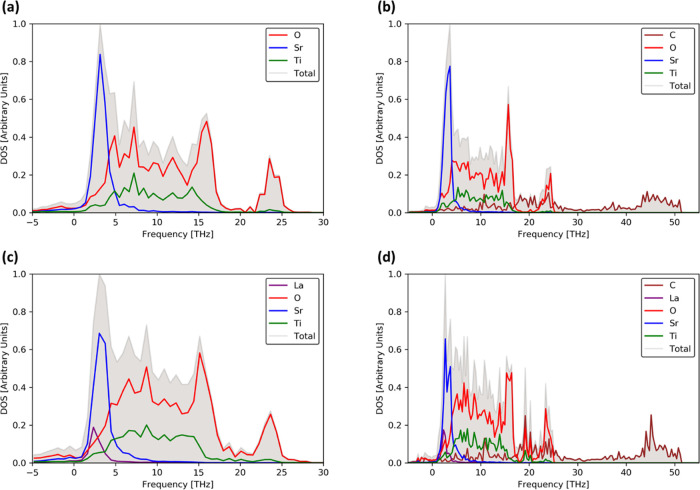
Figure 5 compares the atom-projected phonon DOS (PDOS) curves of the four surface models. The PDOS curves of La-doped surfaces show large contributions from La at low frequencies, suggesting that localized “rattling” modes involving La3+ cations could in principle couple strongly to low-frequency acoustic modes to suppress transport through the TiO6 octahedral framework. There is also a significant contribution from C to the low-frequency DOS in the graphene models, which likewise suggests that the graphene and SrTiO3 modes may also couple to suppress the thermal transport of both components.
Figure 5.
Atom-projected partial phonon density of states (PDOS) of the SrTiO3 surface model (a), the SrTiO3 surface with adsorbed graphene (b), the La-doped SrTiO3 surface model (c), and the La-doped SrTiO3 surface with adsorbed graphene (d).
Within the single-mode relaxation-time approximation (RTA) to the phonon Boltzmann transport equation, the lattice thermal conductivity tensors κlatt(T) can be written as a sum of contributions κλ(T) from the individual phonon modes λ as
| 12 |
where Cλ are the modal heat capacities, νλ are the group velocities, V0 is the volume of the unit cell, N is the number of reciprocal-space wavevectors (q) included in the sum over the Brillouin zone, and τλ are the phonon lifetimes given by
| 13 |
where Γλ are the phonon linewidths obtained as the self-energy from third-order perturbation theory. Cλ and νλ are calculated within the harmonic approximation as
| 14 |
| 15 |
where ωλ are the phonon frequencies, Wλ are the corresponding mode eigenvectors, and D(q) is the dynamical matrix for the wavevector q.
Although the calculation of τλ (T) in eq 13 is computationally prohibitive, we can follow the approach of Tang and Skelton88 and compute the sum over harmonic terms to obtain κlatt with respect to an unknown relaxation time τCRTA as
| 16 |
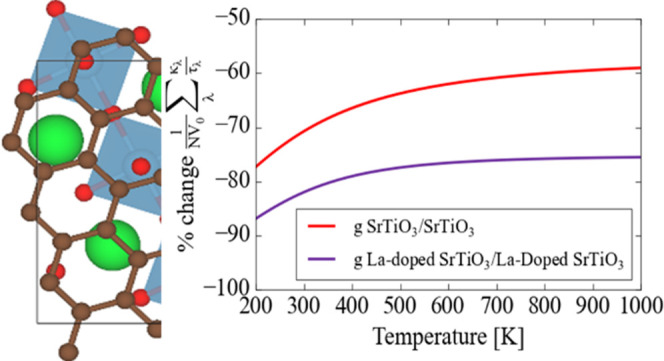
where the modal terms are the same as defined in eq 12. In the following, we consider the diagonal components of κlatt/τCRTA for in-plane transport 1/2 (xx + yy), after rotating the tensors to align with the equivalent directions in bulk STO (see Supporting Information). This analysis shows that one would expect a reduction in κlatt on the order of 60–90% by adsorbing graphene at the surface, based on the changes in the model heat capacities and group velocities (Figure 6). We note that we had difficulty converging the function in eq 16 with respect to the q-point sampling mesh (see the Supporting Information), although despite this, we still predict a reduction in the κlatt due to the graphene adsorption. This reduction is more pronounced in the case of lanthanum doping, with a predicted average reduction of 80% over the temperature range 400–1000 K compared to a 60–70% reduction without doping. This suggests a synergy between La doping and graphene addition in suppressing the thermal transport. A possible mechanism for this is that graphene increases the “effective mass” of the bulk STO modes and therefore reduces the frequency dispersion and “depresses” the mode group velocities. This would be consistent with the stronger graphene adsorption energies calculated for the La-doped surface. The predicted reduction in thermal conductivity supports the experimental work by Lin et al.,13 which demonstrated a widening of the operating temperature window for graphene/La-doped SrTiO3 samples to well below the standard operating temperature of the undoped material.
Figure 6.
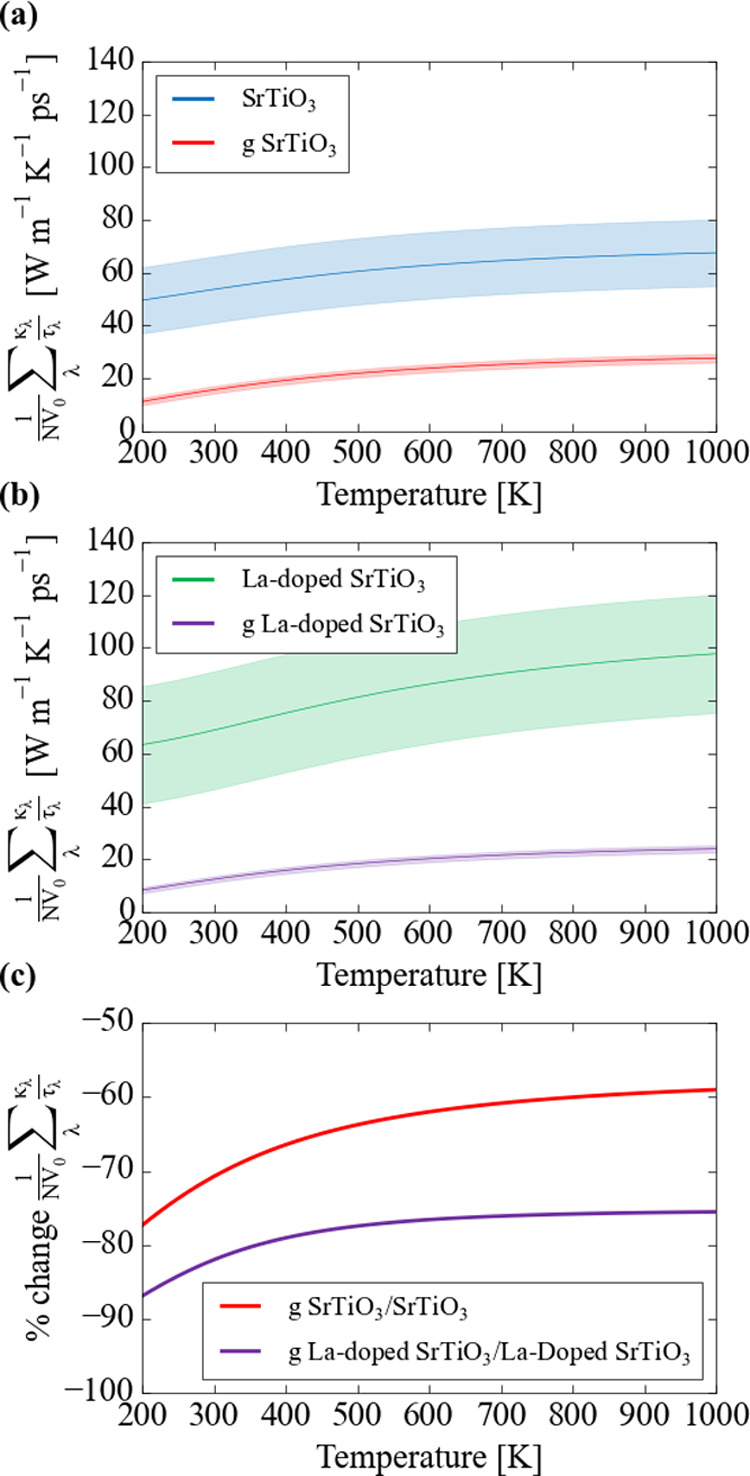
Calculated κlatt/τCRTA for in-plane transport in (a) pristine and graphene-adsorbed SrTiO3 and (b) La-doped SrTiO3 and graphene-adsorbed La-doped SrTiO3 surfaces. The shaded areas represent the calculated error due to erratic convergence of the function in eq 16 with respect to the Brillouin-zone sampling mesh (Figure S12). Plot (c) shows the calculated percentage change in the average κlatt/τCRTA due to the addition of graphene at the two surfaces.
We also note in passing that the average κlatt/τCRTA functions suggest that La doping would lead to changes in the harmonic terms in eq 15 that would increase κlatt. However, the poor convergence behavior means this finding may not be reliable. Moreover, as suggested by the phonon DOS, it is possible that “rattling” of the La ions would counteract the increase in the harmonic terms by reducing the phonon lifetimes, leading to an overall decrease in the thermal conductivity. We explore this point further in the following.
The Γλ in eq 13 are computed as a sum of contributions from energy- and momentum-conserving three-phonon scattering processes between phonon triplets consisting of a reference mode λ and two interacting modes λ′ and λ″. Computing the three-phonon interaction strengths Φλλ′ λ″, which capture the strength of the physical coupling between the modes, requires the third-order force constants, and obtaining these represents a substantial computational workload. If the coupling strength can be averaged over interacting modes λ′ and λ″, however, Γλ can be approximated as68
| 17 |
Pλ is the averaged phonon–phonon interaction strength defined as
| 18 |
where na is the number of atoms in the primitive cell, and hence 3na is the number of phonon bands at each wavevector q. N2 (q, ω) is the weighted two-phonon density of states (wJDOS) and is a sum of two functions for collision (Class 1) and decay processes (Class 2)
| 19 |
| 20 |
| 21 |
Here, the two functions Δ and δ enforce the conservation of (crystal) momentum and energy, respectively, and N2(1) and N2 count the number of energy- and momentum-conserving scattering processes for a reference mode with wavevector q and frequency ω. For making comparisons between systems, it is useful to further average the wJDOS functions over wavevectors to obtain functions of frequency only, i.e.,
| 22 |
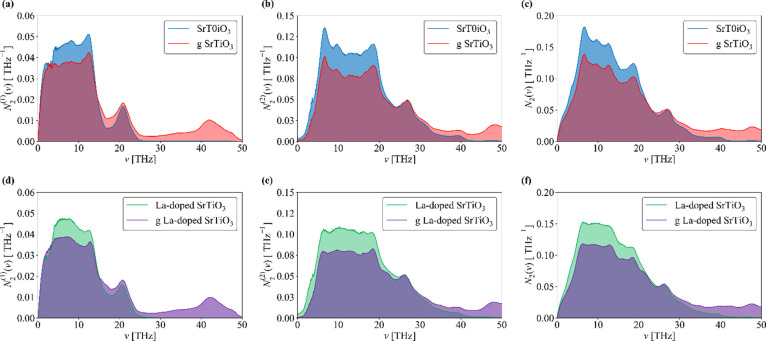
The phonon line widths (inverse lifetimes) can thus be separated into contributions from how strongly the modes interact, and contributions from the conservation of energy, due to the shape of the phonon spectrum, which are captured by the wJDOS.68,89 Unlike Pλ in eq 18, N̅2(ω) can be computed from the harmonic phonon frequencies. Figure 7 shows the calculated N̅2(1) and N̅2 for the SrTiO3 surface with and without La doping and adsorbed graphene, generated using a sampling mesh with 8 × 8 × 1 wavevectors (convergence tests are shown in Figure S13). To allow for comparison between systems, we have normalized the wJDOS functions by (3na)2, which is usually folded into the Pλ term in the expression for the approximate linewidth (cf. eq 18).
Figure 7.
Weighted joint two-phonon density of states (wJDOS) for (a, d) Class 1 events (N̅2(1)), (b, e) Class 2 events (N̅2), and (c, f) both types of event (N̅2) for pristine and graphene-coated SrTiO3 surfaces with and without La doping.
This method allows us to assess whether changes to the harmonic phonon spectrum are likely to increase/decrease the phonon linewidths and thereby decrease/increase the lifetimes. Since the thermal conductivity is proportional to the lifetimes, this can be a useful means to qualitatively compare how different dopants might affect the heat transport without the computational expense of a full third-order calculation. Peaks in N̅2(ω) at low frequencies are potentially indicative of enhanced acoustic-mode broadening; since these modes typically make the largest contributions to the thermal conductivity, this would suppress the overall heat transport.89 However, Figure 7 shows that adsorption of graphene tends to decrease the N̅2(ω) at low frequencies. Similarly, comparing between the pure SrTiO3 and La-doped systems suggests that the doping also has little effect on the wJDOS. This suggests that either the changes to the group velocities noted above are the dominant mechanism for the reduced thermal conductivity of the composites observed by Lin et al.13 or that changes to the frequency spectrum/wJDOS are secondary to changes in interaction strengths in reducing the phonon lifetimes in the composites and doped samples. In particular, our calculations do not indicate significant changes in the harmonic terms between the pristine and La-doped surface models without graphene, and the wJDOS functionals also seem to be generally smaller, so we might infer from this that any reduction in the thermal conductivity on doping may be attributed to stronger phonon–phonon interactions. To investigate this further would require explicit computation of the third-order force constants, which, as noted above, is presently not practical.
Conclusions
We have performed a detailed study of how the adsorption of graphene at the surface of SrTiO3 and La-doped SrTiO3 affects the electronic structure, transport properties, structural dynamics, and lattice thermal conductivity. Based on our results, we draw three main conclusions from our study.
First, there is a thermodynamic driving force for graphene to adsorb to the surfaces of SrTiO3 and La-doped SrTiO3, yielding favorable adsorption energies.
Second, we find that the adsorption of graphene introduces C 2p states into the SrTiO3 band gap, which would account for the reduced Seebeck coefficient observed by Lin et al.,13 but which is likely mitigated experimentally by using smaller amounts of graphene in the composites. This highlights the sensitivity of the electrical properties to the amount and quality of the graphene in the composite and indicates that controlling this may be a simple route to fine-tuning the thermoelectric properties. Our calculations predict that extended graphene layers will induce a change from semiconducting to semimetallic behavior. However, understanding whether this behavior is localized at interfaces or extends into the bulk will require input from both experiments and modeling to elucidate the impact of different graphene concentrations on the properties of the composite.
Finally, analysis of the phonon spectra shows a remarkable reduction in the phonon group velocities on graphene adsorption, which we predict to lead to decreases of 60–90% of the bulk lattice thermal conductivity. This effect appears to be enhanced by La doping. Furthermore, analysis of the phonon spectra suggests that both La doping and graphene adsorption introduce low-frequency modes into the density of states. The former, in particular, hints at low-frequency “rattling” modes in La-doped systems that could couple to acoustic modes and suppress the phonon lifetimes. While calculations of the two-phonon density of states do not suggest enhanced acoustic-mode broadening in La-doped or graphene-adsorbed systems, it is possible that a reduction in the mode lifetimes may instead be facilitated by stronger phonon–phonon interactions. This can potentially be investigated in the future by explicit calculation of the third-order force constants.
Acknowledgments
J.M.S. is grateful to UK Research and Innovation (UKRI) for the award of a Future Leaders Fellowship (MR/T043121/1), and to the University of Manchester for the previous support of a UoM Presidential Fellowship. S.C.P. thanks the EPSRC for funding (EP/P007821/1). Calculations were performed on the Balena HPC facility at the University of Bath, the Orion computing facility at the University of Huddersfield, the ARCHER UK National Supercomputing Service via our membership of the UK HEC Materials Chemistry Consortium (MCC; EPSRC EP/L000202, EP/R029431, EP/T022213), and the THOMAS facility at the UK Materials and Molecular Modelling Hub (MMM hub; EPSRC EP/P020194/1). The authors would also like to acknowledge computing time granted through the Spanish Supercomputing Network, RES, on the Tirant 3 supercomputer located at the University of Valencia (QS-2019-3-0025 and QS-2020-1-0021). Finally, this work also used the Isambard UK National Tier-2 HPC Service (http://gw4.ac.uk/isambard/) via the Resource Allocation Panel (RAP) Open Access to Tier-2 call, operated by the GW4 and the UK Met Office and funded by the EPSRC (EP/P020224/1).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.1c10865.
A detailed description of electronic transport calculations performed using the BoltzWann code and comparison to results obtained with BoltzTraP; additional data from BoltzTraP transport calculations; conversion of the in-plane thermal conductivity of the rotated slab model to the bulk SrTiO3 axes; and convergence of the harmonic CRTA function in eq 16 and wJDOS functions in eq 22 with respect to the q-point sampling mesh (PDF)
Author Contributions
⊥ J.T, A.A., and J.M.F. contributed equally to this work.
The authors declare no competing financial interest.
Notes
Raw data from this study is available from the authors on reasonable request.
Supplementary Material
References
- Freer R.; Powell A. V. Realising the Potential of Thermoelectric Technology: A Roadmap. J. Mater. Chem. C 2020, 8, 441–463. 10.1039/C9TC05710B. [DOI] [Google Scholar]
- Bell L. E. Cooling, Heating, Generating Power, and Recovering Waste Heat with Thermoelectric Systems. Science 2008, 321, 1457–1461. 10.1126/science.1158899. [DOI] [PubMed] [Google Scholar]
- Anatychuk L. I.; Rozver Y. Y.; Velichuk D. D. Thermoelectric Generator for a Stationary Diesel Plant. J. Electron. Mater. 2011, 40, 1206–1208. 10.1007/s11664-011-1600-6. [DOI] [Google Scholar]
- Yang J.; Stabler F. R. Automotive Applications of Thermoelectric Materials. J. Electron. Mater. 2009, 38, 1245–1251. 10.1007/s11664-009-0680-z. [DOI] [Google Scholar]
- Kim S. K.; Won B. C.; Rhi S. H.; Kim S. H.; Yoo J. H.; Jang J. C. Thermoelectric Power Generation System for Future Hybrid Vehicles Using Hot Exhaust Gas. J. Electron. Mater. 2011, 40, 778–783. 10.1007/s11664-011-1569-1. [DOI] [Google Scholar]
- Azough F.; Gholinia A.; Alvarez-Ruiz D. T.; Duran E.; Kepaptsoglou D. M.; Eggeman A. S.; Ramasse Q. M.; Freer R. Self-Nanostructuring in SrTiO3: A Novel Strategy for Enhancement of Thermoelectric Response in Oxides. ACS Appl. Mater. Interfaces 2019, 11, 32833–32843. 10.1021/acsami.9b06483. [DOI] [PubMed] [Google Scholar]
- Srivastava D.; Norman C.; Azough F.; Schäfer M. C.; Guilmeau E.; Freer R. Improving the Thermoelectric Properties of SrTiO3-Based Ceramics with Metallic Inclusions. J. Alloys Compd. 2018, 731, 723–730. 10.1016/j.jallcom.2017.10.033. [DOI] [Google Scholar]
- Srivastava D.; Norman C.; Azough F.; Ekren D.; Chen K.; Reece M. J.; Kinloch I. A.; Freer R. Anisotropy and Enhancement of Thermoelectric Performance of Sr0.8La0.067Ti0.8Nb0.2O3-δ Ceramics by Graphene Additions. J. Mater. Chem. A 2019, 7, 24602–24613. 10.1039/C9TA02883H. [DOI] [Google Scholar]
- Lin Y.; Dylla M. T.; Kuo J. J.; Male J. P.; Kinloch I. A.; Freer R.; Snyder G. J. Graphene/Strontium Titanate: Approaching Single Crystal–Like Charge Transport in Polycrystalline Oxide Perovskite Nanocomposites through Grain Boundary Engineering. Adv. Funct. Mater. 2020, 30, 1910079 10.1002/adfm.201910079. [DOI] [Google Scholar]
- Yeandel S. R.; Molinari M.; Parker S. C. The Impact of Tilt Grain Boundaries on the Thermal Transport in Perovskite SrTiO3 Layered Nanostructures. A Computational Study. Nanoscale 2018, 10, 15010–15022. 10.1039/C8NR02234H. [DOI] [PubMed] [Google Scholar]
- Yeandel S. R.; Molinari M.; Parker S. C. Nanostructuring Perovskite Oxides: The Impact of SrTiO3 Nanocube 3D Self-Assembly on Thermal Conductivity. RSC Adv. 2016, 6, 114069–114077. 10.1039/C6RA23887D. [DOI] [Google Scholar]
- Koumoto K.; Wang Y.; Zhang R.; Kosuga A.; Funahashi R. Oxide Thermoelectric Materials: A Nanostructuring Approach. Annu. Rev. Mater. Res. 2010, 40, 363–394. 10.1146/annurev-matsci-070909-104521. [DOI] [Google Scholar]
- Lin Y.; Norman C.; Srivastava D.; Azough F.; Wang L.; Robbins M.; Simpson K.; Freer R.; Kinloch I. A. Thermoelectric Power Generation from Lanthanum Strontium Titanium Oxide at Room Temperature through the Addition of Graphene. ACS Appl. Mater. Interfaces 2015, 7, 15898–15908. 10.1021/acsami.5b03522. [DOI] [PubMed] [Google Scholar]
- Okhay O.; Zlotnik S.; Xie W.; Orlinski K.; Hortiguela Gallo M. J.; Otero-Irurueta G.; Fernandes A. J. S.; Pawlak D. A.; Weidenkaff A.; Tkach A. Thermoelectric Performance of Nb-Doped SrTiO3 Enhanced by Reduced Graphene Oxide and Sr Deficiency Cooperation. Carbon 2019, 143, 215–222. 10.1016/j.carbon.2018.11.023. [DOI] [Google Scholar]
- Shen J. J.; Zhu T. J.; Zhao X. B.; Zhang S. N.; Yang S. H.; Yin Z. Z. Recrystallization Induced in Situ Nanostructures in Bulk Bismuth Antimony Tellurides: A Simple Top down Route and Improved Thermoelectric Properties. Energy Environ. Sci. 2010, 3, 1519–1523. 10.1039/c0ee00012d. [DOI] [Google Scholar]
- He W.; Wang D.; Wu H.; Xiao Y.; Zhang Y.; He D.; Feng Y.; Hao Y. J.; Dong J. F.; Chetty R.; Hao L.; Chen D.; Qin J.; Yang Q.; Li X.; Song J. M.; Zhu Y.; Xu W.; Niu C.; Li X.; Wang G.; Liu C.; Ohta M.; Pennycook S. J.; He J.; Li J. F.; Zhao L. D. High Thermoelectric Performance in Low-Cost SnS0.91Se0.09 Crystals. Science 2019, 365, 1418–1424. 10.1126/science.aax5123. [DOI] [PubMed] [Google Scholar]
- Shenoy U. S.; Bhat D. K. Electronic Structure Modulation of Pb0.6Sn0.4Te via Zinc Doping and Its Effect on the Thermoelectric Properties. J. Alloys Compd. 2021, 872, 159681 10.1016/j.jallcom.2021.159681. [DOI] [Google Scholar]
- Bhat D. K.; Shenoy U. S. SnTe Thermoelectrics: Dual Step Approach for Enhanced Performance. J. Alloys Compd. 2020, 834, 155181 10.1016/j.jallcom.2020.155181. [DOI] [Google Scholar]
- Tippireddy S.; Prem Kumar D. S.; Das S.; Mallik R. C.. Oxychalcogenides as Thermoelectric Materials: An Overview. ACS Applied Energy Materials; American Chemical Society, 2021. pp 2022–2040. [Google Scholar]
- Caballero-Calero O.; Ares J. R.; Martín-González M.. Environmentally Friendly Thermoelectric Materials: High Performance from Inorganic Components with Low Toxicity and Abundance in the Earth. In Advanced Sustainable Systems; John Wiley & Sons, Ltd., 2021; 2100095. [Google Scholar]
- Fergus J. W. Oxide Materials for High Temperature Thermoelectric Energy Conversion. J. Eur. Ceram. Soc. 2012, 32, 525–540. 10.1016/j.jeurceramsoc.2011.10.007. [DOI] [Google Scholar]
- Prasad R.; Bhame S. D.. Review on Texturization Effects in Thermoelectric Oxides. In Materials for Renewable and Sustainable Energy; Springer, 2020; pp 1–22. [Google Scholar]
- Srivastava D.; Azough F.; Freer R.; Combe E.; Funahashi R.; Kepaptsoglou D. M.; Ramasse Q. M.; Molinari M.; Yeandel S. R.; Baran J. D.; Parker S. C. Crystal Structure and Thermoelectric Properties of Sr-Mo Substituted CaMnO3: A Combined Experimental and Computational Study. J. Mater. Chem. C 2015, 3, 12245–12259. 10.1039/C5TC02318A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava D.; Azough F.; Molinari M.; Parker S. C.; Freer R. High-Temperature Thermoelectric Properties of (1 – x) SrTiO3 – (x) La1/3NbO3 Ceramic Solid Solution. J. Electron. Mater. 2015, 44, 1803–1808. 10.1007/s11664-014-3560-0. [DOI] [Google Scholar]
- Wang Y. F.; Lee K. H.; Ohta H.; Koumoto K. Fabrication and Thermoelectric Properties of Heavily Rare-Earth Metal-Doped SrO(SrTiO3)n (n = 1, 2) Ceramics. Ceram. Int. 2008, 34, 849–852. 10.1016/j.ceramint.2007.09.034. [DOI] [Google Scholar]
- Shenoy U. S.; Bhat D. K. Enhanced Thermoelectric Properties of Vanadium Doped SrTiO3: A Resonant Dopant Approach. J. Alloys Compd. 2020, 832, 154958 10.1016/j.jallcom.2020.154958. [DOI] [Google Scholar]
- Shenoy U. S.; Bhat D. K. Electronic Structure Engineering of SrTiO3 via Rhodium Doping: A DFT Study. J. Phys. Chem. Solids 2021, 148, 109708 10.1016/j.jpcs.2020.109708. [DOI] [Google Scholar]
- Baran J. D.; Molinari M.; Kulwongwit N.; Azough F.; Freer R.; Kepaptsoglou D.; Ramasse Q. M.; Parker S. C. Tuning Thermoelectric Properties of Misfit Layered Cobaltites by Chemically Induced Strain. J. Phys. Chem. C 2015, 119, 21818–21827. 10.1021/acs.jpcc.5b05583. [DOI] [Google Scholar]
- Shenoy U. S.; Bhat D. K. Vanadium-Doped BaTiO3 as High Performance Thermoelectric Material: Role of Electronic Structure Engineering. Mater. Today Chem. 2020, 18, 100384 10.1016/j.mtchem.2020.100384. [DOI] [Google Scholar]
- Azough F.; Cernik R. J.; Schaffer B.; Kepaptsoglou D.; Ramasse Q. M.; Bigatti M.; Ali A.; MacLaren I.; Barthel J.; Molinari M.; Baran J. D.; Parker S. C.; Freer R. Tungsten Bronze Barium Neodymium Titanate (Ba6–3nNd8+2nTi18O54): An Intrinsic Nanostructured Material and Its Defect Distribution. Inorg. Chem. 2016, 55, 3338–3350. 10.1021/acs.inorgchem.5b02594. [DOI] [PubMed] [Google Scholar]
- Azough F.; Freer R.; Yeandel S. R.; Baran J. D.; Molinari M.; Parker S. C.; Guilmeau E.; Kepaptsoglou D.; Ramasse Q.; Knox A.; Gregory D.; Paul D.; Paul M.; Montecucco A.; Siviter J.; Mullen P.; Li W.; Han G.; Man E. A.; Baig H.; Mallick T.; Sellami N.; Min G.; Sweet T. Ba6–3xNd8+2xTi18O54 Tungsten Bronze: A New High-Temperature n-Type Oxide Thermoelectric. J. Electron. Mater. 2016, 45, 1894–1899. 10.1007/s11664-015-4275-6. [DOI] [Google Scholar]
- Baran J. D.; Kepaptsoglou D.; Molinari M.; Kulwongwit N.; Azough F.; Freer R.; Ramasse Q. M.; Parker S. C. Role of Structure and Defect Chemistry in High-Performance Thermoelectric Bismuth Strontium Cobalt Oxides. Chem. Mater. 2016, 28, 7470–7478. 10.1021/acs.chemmater.6b03200. [DOI] [Google Scholar]
- Ahmad A.; Hussain M.; Zhou Z.; Liu R.; Lin Y. H.; Nan C. W. Thermoelectric Performance Enhancement of Vanadium Doped n-Type In2O3 Ceramics via Carrier Engineering and Phonon Suppression. ACS Appl. Energy Mater. 2020, 3, 1552–1558. 10.1021/acsaem.9b02011. [DOI] [Google Scholar]
- Kepaptsoglou D.; Baran J. D.; Azough F.; Ekren D.; Srivastava D.; Molinari M.; Parker S. C.; Ramasse Q. M.; Freer R. Prospects for Engineering Thermoelectric Properties in La1/3NbO3 Ceramics Revealed via Atomic-Level Characterization and Modeling. Inorg. Chem. 2018, 57, 45–55. 10.1021/acs.inorgchem.7b01584. [DOI] [PubMed] [Google Scholar]
- Pourkiaei S. M.; Ahmadi M. H.; Sadeghzadeh M.; Moosavi S.; Pourfayaz F.; Chen L.; Pour Yazdi M. A.; Kumar R. Thermoelectric Cooler and Thermoelectric Generator Devices: A Review of Present and Potential Applications, Modeling and Materials. Energy 2019, 186, 115849 10.1016/j.energy.2019.07.179. [DOI] [Google Scholar]
- Wei J.; Yang L.; Ma Z.; Song P.; Zhang M.; Ma J.; Yang F.; Wang X.. Review of Current High-ZT Thermoelectric Materials. Journal of Materials Science; Springer, 2020; pp 12642–12704. [Google Scholar]
- Kovalevsky A. V.; Yaremchenko A. A.; Populoh S.; Thiel P.; Fagg D. P.; Weidenkaff A.; Frade J. R. Towards a High Thermoelectric Performance in Rare-Earth Substituted SrTiO3: Effects Provided by Strongly-Reducing Sintering Conditions. Phys. Chem. Chem. Phys. 2014, 16, 26946–26954. 10.1039/C4CP04127E. [DOI] [PubMed] [Google Scholar]
- Wang H. C.; Wang C. L.; Su W. B.; Liu J.; Sun Y.; Peng H.; Mei L. M. Doping Effect of La and Dy on the Thermoelectric Properties of SrTiO3. J. Am. Ceram. Soc. 2011, 94, 838–842. 10.1111/j.1551-2916.2010.04185.x. [DOI] [Google Scholar]
- Azough F.; Jackson S. S.; Ekren D.; Freer R.; Molinari M.; Yeandel S. R.; Panchmatia P. M.; Parker S. C.; Maldonado D. H.; Kepaptsoglou D. M.; Ramasse Q. M. Concurrent La and A-Site Vacancy Doping Modulates the Thermoelectric Response of SrTiO3: Experimental and Computational Evidence. ACS Appl. Mater. Interfaces 2017, 9, 41988–42000. 10.1021/acsami.7b14231. [DOI] [PubMed] [Google Scholar]
- Ohta S.; Nomura T.; Ohta H.; Koumoto K. High-Temperature Carrier Transport and Thermoelectric Properties of Heavily La- Or Nb-Doped SrTiO3 Single Crystals. J. Appl. Phys. 2005, 97, 34106 10.1063/1.1847723. [DOI] [Google Scholar]
- Ohta S.; Nomura T.; Ohta H.; Hirano M.; Hosono H.; Koumoto K. Large Thermoelectric Performance of Heavily Nb-Doped SrTiO3 Epitaxial Film at High Temperature. Appl. Phys. Lett. 2005, 87, 092108 10.1063/1.2035889. [DOI] [Google Scholar]
- Ohta S.; Ohta H.; Koumoto K. Grain Size Dependence of Thermoelectric Performance of Nb-Doped SrTiO3 Polycrystals. J. Ceram. Soc. Japan 2006, 114, 102–105. 10.2109/jcersj.114.102. [DOI] [Google Scholar]
- Wan C.; Wang Y.; Wang N.; Norimatsu W.; Kusunoki M.; Koumoto K. Development of Novel Thermoelectric Materials by Reduction of Lattice Thermal Conductivity. Sci. Technol. Adv. Mater. 2010, 11, 044306 10.1088/1468-6996/11/4/044306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L.; Lü T. Y.; Wang H. Q.; Zhang W. X.; Yang S. W.; Zheng J. C. First Principles Studies on the Thermoelectric Properties of (SrO)m(SrTiO3)n Superlattice. RSC Adv. 2016, 6, 102172–102182. 10.1039/C6RA19661F. [DOI] [Google Scholar]
- Zou D.; Liu Y.; Xie S.; Lin J.; Li J. Effect of Strain on Thermoelectric Properties of SrTiO3: First-Principles Calculations. Chem. Phys. Lett. 2013, 586, 159–163. 10.1016/j.cplett.2013.09.036. [DOI] [Google Scholar]
- Dylla M. T.; Kuo J. J.; Witting I.; Snyder G. J.. Grain Boundary Engineering Nanostructured SrTiO3 for Thermoelectric Applications. InAdvanced Materials Interfaces; John Wiley & Sons, Ltd., 2019; 1900222. [Google Scholar]
- Huang J.; Yan P.; Liu Y.; Xing J.; Gu H.; Fan Y.; Jiang W. Simultaneously Breaking the Double Schottky Barrier and Phonon Transport in SrTiO3-Based Thermoelectric Ceramics via Two-Step Reduction. ACS Appl. Mater. Interfaces 2020, 12, 52721–52730. 10.1021/acsami.0c16084. [DOI] [PubMed] [Google Scholar]
- Dong J.; Liu W.; Li H.; Su X.; Tang X.; Uher C. In Situ Synthesis and Thermoelectric Properties of PbTe-Graphene Nanocomposites by Utilizing a Facile and Novel Wet Chemical Method. J. Mater. Chem. A 2013, 1, 12503–12511. 10.1039/c3ta12494k. [DOI] [Google Scholar]
- Ahmad K.; Wan C.; Al-Eshaikh M. A.; Kadachi A. N. Enhanced Thermoelectric Performance of Bi2Te3 Based Graphene Nanocomposites. Appl. Surf. Sci. 2019, 474, 2–8. 10.1016/j.apsusc.2018.10.163. [DOI] [Google Scholar]
- Bantawal H.; Sethi M.; Shenoy U. S.; Bhat D. K. Porous Graphene Wrapped SrTiO3 Nanocomposite: Sr-C Bond as an Effective Coadjutant for High Performance Photocatalytic Degradation of Methylene Blue. ACS Appl. Nano Mater. 2019, 2, 6629–6636. 10.1021/acsanm.9b01513. [DOI] [Google Scholar]
- Feng X.; Fan Y.; Nomura N.; Kikuchi K.; Wang L.; Jiang W.; Kawasaki A. Graphene Promoted Oxygen Vacancies in Perovskite for Enhanced Thermoelectric Properties. Carbon 2017, 112, 169–176. 10.1016/j.carbon.2016.11.012. [DOI] [Google Scholar]
- Baran J. D.; Eames C.; Takahashi K.; Molinari M.; Islam M. S.; Parker S. C. Structural, Electronic, and Transport Properties of Hybrid SrTiO3-Graphene and Carbon Nanoribbon Interfaces. Chem. Mater. 2017, 29, 7364–7370. 10.1021/acs.chemmater.7b02253. [DOI] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal-Amorphous- Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Erratum: Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.78.1396. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- Madsen G. K. H.; Singh D. J. BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comput. Phys. Commun. 2006, 175, 67–71. 10.1016/j.cpc.2006.03.007. [DOI] [Google Scholar]
- Pizzi G.; Volja D.; Kozinsky B.; Fornari M.; Marzari N. BoltzWann: A Code for the Evaluation of Thermoelectric and Electronic Transport Properties with a Maximally-Localized Wannier Functions Basis. Comput. Phys. Commun. 2014, 185, 422–429. 10.1016/j.cpc.2013.09.015. [DOI] [Google Scholar]
- Pizzi G.; Volja D.; Kozinsky B.; Fornari M.; Marzari N. An Updated Version of BOLTZWANN: A Code for the Evaluation of Thermoelectric and Electronic Transport Properties with a Maximally-Localized Wannier Functions Basis. Comput. Phys. Commun. 2014, 185, 2311–2312. 10.1016/j.cpc.2014.05.004. [DOI] [Google Scholar]
- Molinari M.; Tompsett D. A.; Parker S. C.; Azough F.; Freer R. Structural, Electronic and Thermoelectric Behaviour of CaMnO3 and CaMnO(3-δ). J. Mater. Chem. A 2014, 2, 14109–14117. 10.1039/C4TA01514B. [DOI] [Google Scholar]
- Togo A.; Tanaka I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
- Parlinski K.; Li Z. Q.; Kawazoe Y. First-Principles Determination of the Soft Mode in Cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063–4066. 10.1103/PhysRevLett.78.4063. [DOI] [Google Scholar]
- Togo A.; Chaput L.; Tanaka I. Distributions of Phonon Lifetimes in Brillouin Zones. Phys. Rev. B 2015, 91, 94306. 10.1103/PhysRevB.91.094306. [DOI] [Google Scholar]
- Staykov A.; Tellez H.; Druce J.; Wu J.; Ishihara T.; Kilner J. Electronic Properties and Surface Reactivity of SrO-Terminated SrTiO3 and SrO-Terminated Iron-Doped SrTiO3. Sci. Technol. Adv. Mater. 2018, 19, 221–230. 10.1080/14686996.2018.1440136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Druce J.; Téllez H.; Burriel M.; Sharp M. D.; Fawcett L. J.; Cook S. N.; McPhail D. S.; Ishihara T.; Brongersma H. H.; Kilner J. A. Surface Termination and Subsurface Restructuring of Perovskite-Based Solid Oxide Electrode Materials. Energy Environ. Sci. 2014, 7, 3593–3599. 10.1039/C4EE01497A. [DOI] [Google Scholar]
- Chen Y.; Téllez H.; Burriel M.; Yang F.; Tsvetkov N.; Cai Z.; McComb D. W.; Kilner J. A.; Yildiz B. Segregated Chemistry and Structure on (001) and (100) Surfaces of (La1-xSrx)2CoO4 Override the Crystal Anisotropy in Oxygen Exchange Kinetics. Chem. Mater. 2015, 27, 5436–5450. 10.1021/acs.chemmater.5b02292. [DOI] [Google Scholar]
- Burriel M.; Wilkins S.; Hill J. P.; Muñoz-Márquez M. A.; Brongersma H. H.; Kilner J. A.; Ryan M. P.; Skinner S. J. Absence of Ni on the Outer Surface of Sr Doped La2NiO4 Single Crystals. Energy Environ. Sci. 2014, 7, 311–316. 10.1039/C3EE41622D. [DOI] [Google Scholar]
- Watson G. W.; Kelsey E. T.; De Leeuw N. H.; Harris D. J.; Parker S. C. Atomistic Simulation of Dislocations, Surfaces and Interfaces in MgO. J. Chem. Soc., Faraday Trans. 1996, 92, 433–438. 10.1039/ft9969200433. [DOI] [Google Scholar]
- Zou B.; Walker C.; Wang K.; Tileli V.; Shaforost O.; Harrison N. M.; Klein N.; Alford N. M.; Petrov P. K. Growth of Epitaxial Oxide Thin Films on Graphene. Sci. Rep. 2016, 6, 31511 10.1038/srep31511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bantawal H.; Shenoy U. S.; Bhat D. K. Tuning the Photocatalytic Activity of SrTiO3 by Varying the Sr/Ti Ratio: Unusual Effect of Viscosity of the Synthesis Medium. J. Phys. Chem. C 2018, 122, 20027–20033. 10.1021/acs.jpcc.8b06514. [DOI] [Google Scholar]
- Jiao S.; Yan J.; Sun G.; Zhao Y. Electronic Structures and Optical Properties of Nb-Doped SrTiO3 from First Principles. J. Semicond. 2016, 37, 072001 10.1088/1674-4926/37/7/072001. [DOI] [Google Scholar]
- Shenoy U. S.; Bantawal H.; Bhat D. K. Band Engineering of SrTiO3: Effect of Synthetic Technique and Site Occupancy of Doped Rhodium. J. Phys. Chem. C 2018, 122, 27567–27574. 10.1021/acs.jpcc.8b10083. [DOI] [Google Scholar]
- Meyer B.; Padilla J.; Vanderbilt D. Theory of PbTiO3, BaTiO3, and SrTiO3 Surfaces. Faraday Discuss. 1999, 114, 395–405. 10.1039/a903029h. [DOI] [Google Scholar]
- Van Benthem K.; Elsässer C.; French R. H. Bulk Electronic Structure of SrTiO3: Experiment and Theory. J. Appl. Phys. 2001, 90, 6156–6164. 10.1063/1.1415766. [DOI] [Google Scholar]
- Holmström E.; Spijker P.; Foster A. S. The Interface of SrTiO3 and H2O from Density Functional Theory Molecular Dynamics. Proc. R. Soc. A 2016, 472, 20160293 10.1098/rspa.2016.0293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmström E.; Foster A. S. Adsorption of Water onto SrTiO3 from Periodic Møller-Plesset Second-Order Perturbation Theory. J. Chem. Theory Comput. 2017, 13, 6301–6307. 10.1021/acs.jctc.7b00549. [DOI] [PubMed] [Google Scholar]
- Scheidemantel T. J.; Ambrosch-Draxl C.; Thonhauser T.; Badding V.; Sofo O. Transport Coefficients from First-Principles Calculations. Phys. Rev. B 2003, 68, 125210 10.1103/PhysRevB.68.125210. [DOI] [Google Scholar]
- Okuda T.; Nakanishi K.; Miyasaka S.; Tokura Y. Large Thermoelectric Response of Metallic Perovskites: Sr1–xLaxTiO3 (0 ≤ x ≤ 0.1). Phys. Rev. B 2001, 63, 113104 10.1103/PhysRevB.63.113104. [DOI] [Google Scholar]
- Ravichandran J.; Siemons W.; Oh D. W.; Kardel J. T.; Chari A.; Heijmerikx H.; Scullin M. L.; Majumdar A.; Ramesh R.; Cahill D. G. High-Temperature Thermoelectric Response of Double-Doped SrTiO3 Epitaxial Films. Phys. Rev. B 2010, 82, 165126 10.1103/PhysRevB.82.165126. [DOI] [Google Scholar]
- Zhang R.-Z.; Wang C.-L.; Li J.-C.; Su W.-B.; Zhang J.-L.; Zhao M.-L.; Liu J.; Zhang Y.-F.; Mei L.-M. Determining Seebeck Coefficient of Heavily Doped La:SrTiO3 from Density Functional Calculations. Solid State Sci. 2010, 12, 1168–1172. 10.1016/j.solidstatesciences.2010.03.021. [DOI] [Google Scholar]
- Ouyang Y.; Guo J. A Theoretical Study on Thermoelectric Properties of Graphene Nanoribbons. Appl. Phys. Lett. 2009, 94, 263107 10.1063/1.3171933. [DOI] [Google Scholar]
- Wood C. Materials for Thermoelectric Energy Conversion. Rep. Prog. Phys. 1988, 51, 459–539. 10.1088/0034-4885/51/4/001. [DOI] [Google Scholar]
- Tang J.; Skelton J. M. Impact of Noble-Gas Filler Atoms on the Lattice Thermal Conductivity of CoSb3 Skutterudites: First-Principles Modelling. J. Phys.: Condens. Matter 2021, 33, 164002 10.1088/1361-648X/abd8b8. [DOI] [PubMed] [Google Scholar]
- Gold-Parker A.; Gehring P. M.; Skelton J. M.; Smith I. C.; Parshall D.; Frost J. M.; Karunadasa H. I.; Walsh A.; Toney M. F. Acoustic Phonon Lifetimes Limit Thermal Transport in Methylammonium Lead Iodide. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, 11905–11910. 10.1073/pnas.1812227115. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.