Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Aug 23;143(34):13944–13951. doi: 10.1021/jacs.1c06966

Substitution Pattern Controlled Quantum Interference in [2.2]Paracyclophane-Based Single-Molecule Junctions

Ksenia Reznikova †, Chunwei Hsu ‡, Werner M Schosser §, Almudena Gallego †, Katawoura Beltako §, Fabian Pauly §,*, Herre S J van der Zant ‡,*, Marcel Mayor †,∥,⊥,*
PMCID: PMC8414552  PMID: 34424713

Abstract

graphic file with name ja1c06966_0007.jpg

Quantum interference (QI) of electron waves passing through a single-molecule junction provides a powerful means to influence its electrical properties. Here, we investigate the correlation between substitution pattern, conductance, and mechanosensitivity in [2.2]paracyclophane (PCP)-based molecular wires in a mechanically controlled break junction experiment. The effect of the meta versus para connectivity in both the central PCP core and the phenyl ring connecting the terminal anchoring group is studied. We find that the meta-phenyl-anchored PCP yields such low conductance levels that molecular features cannot be resolved; in the case of para-phenyl-coupled anchoring, however, large variations in conductance values for modulations of the electrode separation occur for the pseudo-para-coupled PCP core, while this mechanosensitivity is absent for the pseudo-meta-PCP core. The experimental findings are interpreted in terms of QI effects between molecular frontier orbitals by theoretical calculations based on density functional theory and the Landauer formalism.

Introduction

In recent years, great advancements have been made in the field of molecular electronics toward single-molecule junction studies.1 The visionary idea of Aviram and Ratner2 to profit from single molecules as functional units in electronic devices led to the development of several proof-of-concept molecular devices, such as molecular wires,3,4 switches,5,6 rectifiers/diodes,7,8 and thermo-electronic devices.9,10 The design of molecules incorporated in such electrode–molecule–electrode junctions is guided by our understanding of charge transport through the molecules. Indeed, even small structural modifications such as substituent effects,11,12 conformational flexibility,13 and changes in the anchoring groups and their positions14−18 can result in large conductance variations. Particularly strong variations are predicted for quantum interference (QI) effects originating from the interplay between different transport pathways. Destructive QI (DQI) or constructive QI (CQI) between the pathways can occur, reflected in a low or high conductance, respectively.19 QI effects thus become essential molecular design elements, on the one hand enriching the variety of functionalities emerging from the molecular structure but on the other hand making a full comprehension of the molecule’s electronic transport behavior more challenging. A detailed understanding of these QI effects and of their origin in the molecule’s structure is thus crucial to realize their full potential in future electronic components and devices.

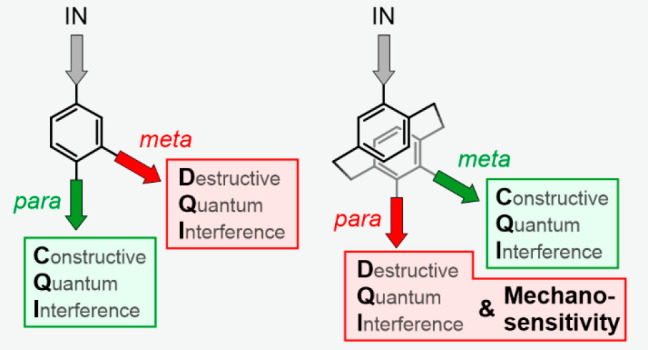
Relationships between substitution pattern and single-molecule conductance were already theoretically predicted and experimentally confirmed in a variety of examples, ranging from simple phenyl rings20 connected directly to the electrodes to more sophisticated oligo(phenylene vinylene) (OPV)21 and oligo(phenylene ethynylene) (OPE)-based molecular wires.15 Unanimously, these studies report a decrease in electronic transparency upon shifting the anchoring groups from the para to the meta position. This observation was rationalized by Yoshizawa and co-workers,22−24 who considered frontier orbital theory for simple organic molecules. Their set of rules predicts for benzene the para connection to be the symmetry-allowed one for charge transport, while charge transport involving the meta connection is symmetry-forbidden, resulting in high and low conductance, respectively.

Because the effects of substitution patterns in planar π-systems are well described and understood, our focus moved to three-dimensional structures like [2.2]paracyclophane (PCP), with two benzene systems facing each other interlinked by a pair of C2H4 bridges.25 Initially, we considered the structure as a model to investigate the through-space coupling of the stacked π-systems26,27 but realized quickly that their behavior is much richer. Already the first model compound28 (ps-para-para-OPE PCP in Figure 1) displayed a sharp destructive QI feature close to the Fermi level, but the phenomenon also depended substantially on the mechanical stress exposed to the molecule. It thus seemed that the rigid but squeezable PCP subunit provided mechanosensitivity to the molecular junction. Interestingly, Yoshizawa and co-workers29 already provided their orbital view of PCP subunits and predicted that the charge transport through the pseudo-para-substituted PCP should be suppressed due to DQI, while CQI would prevail for pseudo-meta-substituted PCP. It thus seems that the rule-of-thumb (para → good transport due to CQI; meta → bad transport due to DQI) is inverted for the PCP subunit.

Figure 1.

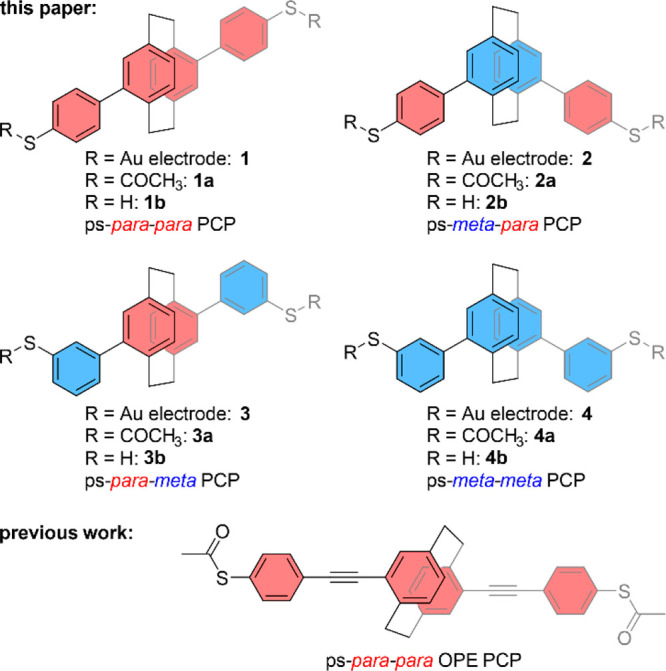
Figure 1

Open in a new tab

Schematic representation of target structures 1–4 together with the already reported model compound. The four molecules include either para or meta connection patterns in both the central PCP subunit and the peripheral phenyl subunits labeled in red and blue, respectively. For simplicity, the following text refers to the structures by their prefixes, with ps as an abbreviation for pseudo, followed by the prefix referring to the substitution pattern of the central PCP, and finally the prefix referring to the substitution pattern of the thiol anchor group in the phenyl subunits.

Excited by this hypothesis, we explored the effects of the substitution pattern in more detail and designed the four PCP model compounds 1–4 (see Figure 1) consisting of comparable subunits but with various substitution patterns. The oligo(phenylene)-type PCP structures combine the compactness favoring electronic transparency on a detectable level with straightforward synthetic accessibility. Terminal acetyl masked thiol anchor groups enable their immobilization in a mechanically controlled break junction (MCBJ) by covalent S–Au bonds, guaranteeing both electronic coupling and mechanical stability. The latter is of particular importance to enable subtle mechanical manipulation of the integrated single molecule. The investigation of their transport properties and the influence of mechanical manipulations are studied with MCBJ experiments. The findings are rationalized by QI effects emerging from the interplay of frontier molecular orbitals, discussed with a theoretical model based on density functional theory (DFT). The electronic transport is described in terms of the Landauer formalism,30 expressed through nonequilibrium Green’s function (NEGF) methods.

Results and Discussion

The PCP-based model compounds were assembled from the corresponding para/meta building blocks by Suzuki–Miyaura cross-coupling reactions. The literature known pseudo (ps)-para- or ps-meta-dibromo[2.2]paracyclophane31 and either 4- or 3-(tert-butylthio)phenyl boronic acid provided the PCP derivatives with four different combinations of substitution patterns. The adaption of a protocol from Jevric et al.32 enabled the subsequent transprotection and provided the target structures 1a–4a in reasonable isolated yields ranging from 63 to 85%. The identity of the new PCP derivatives was corroborated by 1H NMR, 13C{1H} NMR spectroscopy, and high-resolution mass spectrometry (HR-MS). A detailed description of the synthetic protocols and the analytical data of all new compounds are provided in the Supporting Information (section 1).

The single-molecule electronic transport properties of PCPs 1–4 were investigated by integrating them into an electronic circuit using an MCBJ setup operated at ambient conditions. Two types of measurements were performed: fast-breaking and modulation experiments (see below). Details of the technique providing a pair of mechanically adjustable electrodes with a distance resolution of atomic dimensions have been reported previously33,34 and are thus discussed in the Supporting Information (section 2.1).

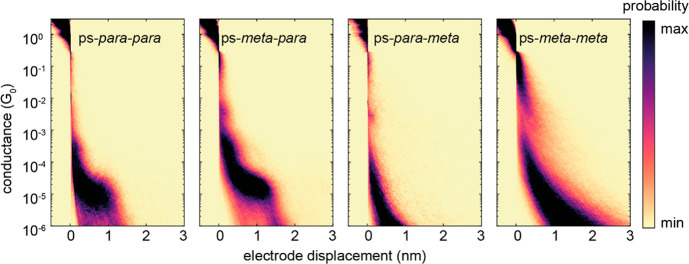
In the fast-breaking experiments, several thousand conductance traces for each investigated molecule were collected and plotted as two-dimensional (2D) histograms displayed in Figure 2. For the case of ps-para-para- and ps-meta-para-PCPs with a constant bias voltage of 100 mV, clear conductance plateaus with a length of ∼12.5 Å were observed. Through a reference-free clustering method35 on the unfiltered data, the pure gold-to-gold tunneling traces and the molecular traces were separated. The molecular conductances of ps-para-para- and ps-meta-para-PCPs were obtained through a log-normal fit distribution yielding values of 1.3 × 10–5G0 and 2.2 × 10–5G0, respectively, where G0 = 2e2/h is the quantum of conductance, as shown in the corresponding one-dimensional (1D) conductance histograms (see Supporting Information (section 2.2)).

Figure 2.

Figure 2

Open in a new tab

Two-dimensional conductance vs electrode displacement density histograms. The first (from the left) and second histograms are built up from 6 834 and 9 638 traces at 100 mV with ps-para-para- and ps-meta-para-PCP molecules, respectively. The third and fourth 2D histograms correspond to 3 780 and 10 000 traces at a bias voltage at 250 mV with ps-para-meta- and ps-meta-meta-PCP molecules, respectively.

For the molecules with the meta-phenyl anchoring (ps-para-meta-PCP and ps-meta-meta-PCP) the bias voltage in the transport experiment was increased to 250 mV in order to bring molecular levels closer to resonance, as the conductance of these PCPs was below the detection limit for a bias of 100 mV. However, even at this increased bias voltage, no clear conductance plateaus were detected, even when using the earlier-mentioned clustering method. Whether the lack of clear plateaus is due to molecular conductance below the detection threshold of the experimental setup of 10–6G0 or the molecules’ inability to form stable molecular junctions cannot be distinguished. The very short-breaking traces visible in Figure 2 at higher conductance values for both ps-para-meta- and ps-meta-meta-PCP are most likely due to direct electron injection into the molecules’ π-systems without controlled sulfur-to-sulfur immobilization.

Of particular interest are the distance-dependent single-molecule junction charge-transport studies of ps-para-para- and ps-meta-para-PCPs, as substantial differences in the transport behavior under mechanical stress are expected between the central ps-para- and ps-meta-PCP subunits. While the mechanosensitivity of the ps-para-PCP subunit was already evidenced in modulation experiments for the ps-para-para-OPE PCP (Figure 1)28 and rationalized as being due to a distance-dependent conductance dip close to the Fermi level originating from DQI, similar behavior is not expected for the ps-meta-PCP subunit, as CQI has been predicted.29

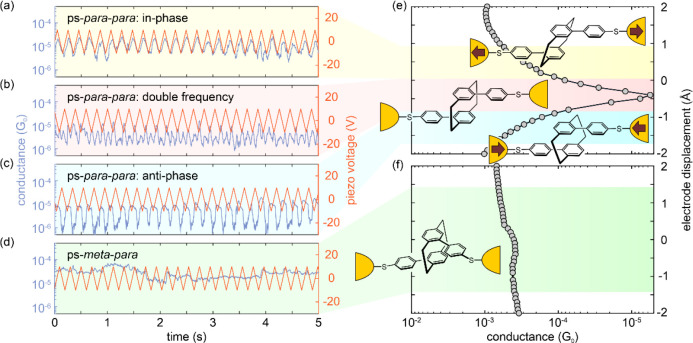
To study the presence of DQI in more detail, modulation experiments are useful. The modulation procedure consists of constricting the gold wire down to a conductance of 2 G0 with the piezo control.28 The junction will then break by itself due to its surface tension.36 The electrodes are then separated by 7.5 Å, and a pulse of a triangular waveform with an amplitude of 20 Vpeak-to-peak is applied to the piezoelectric element, which corresponds to a modulation amplitude of 5 Å between the electrodes. The conductance is continuously monitored, and the modulation is applied at a frequency of 5 Hz for 15 s. Hereafter, the junction is fused again, and a new modulation trace is recorded. The results of electrode-modulation experiments on PCPs 1 and 2 are summarized in Figure 3.

Figure 3.

Figure 3

Open in a new tab

(a–c) Conductance traces of modulation experiments with ps-para-para-PCP (1), displaying (a) in-phase, (b) double frequency, and (c) anti-phase modulations. (d) Conductance traces of the modulation experiments with ps-meta-para-PCP (2). The red line in the distance–modulation traces represents the voltage applied to the piezoelectric stack, whereas blue represents the measured conductance. The total modulation time of the experiments is 15 s; for better visibility, only 5 s are displayed. (e) Calculated conductance of the ps-para-para-PCP molecular junction during the gap opening. The conductance displacement data is extracted from Figure 5b by evaluating the transmission function at the Fermi energy. The sketches rationalize the variety of conductance vs electrode displacement modulation behaviors observed for ps-para-para-PCP in dependence of the position of the DQI dip with respect to the trapping state of the molecule in the individual junction; see panels a–c and e. In particular, light background colors (yellow, red, and blue) relate the different situations of junctions, including molecules in prestretched, relaxed, or precompressed states, respectively, to the behavior in modulation experiments. (f) Same plot as in panel e but for ps-meta-para-PCP, where mechanosensitivity is basically absent. The green background color connects the conductance that is rather insensitive to electrode displacements to the observations made in the modulation measurements in panel d.

Similar to ps-para-para-OPE PCP,28 a rich variety of distance-modulated conductance responses has been observed for ps-para-para-PCP (1). The periodic electrode displacement caused a substantial conductance modulation, which was either in-phase (Figure 3a), anti-phase (Figure 3c), or even two times the frequency (Figure 3b) of the voltage applied to the piezo stack. As sketched in Figure 3e, this observed mechanosensitivity is caused by the DQI dip in the conductance versus molecular length relation (insets in Figure 3e), with the variety of observed behaviors reflecting the exact position of the conductance dip in the particular molecular junction. We take the in-phase case as an example to explain the observed behavior. This corresponds to a starting position in which the molecule is prestretched, as depicted in Figure 3e (top, light yellow background). In this case, whenever the molecule is stretched by increasing the voltage applied to the piezoelectric element, the conductance goes up, and the conductance goes down when the piezo voltage decreases, i.e., the conduction follows the applied piezo-voltage modulation in-phase.

The striking similarity of the mechanosensitivity of ps-para-para-PCP (1) and ps-para-para-OPE PCP, both comprising a central para-PCP subunit, not only points at this structural motif as the origin of the phenomenon but also further corroborates its rationalization based on the presence of a DQI dip in proximity of the Fermi level. Equally interesting are the modulation experiments performed with the ps-meta-para-PCP (2). As displayed in parts d and f of Figure 3, single-molecule junctions with this structure do not feature significant conductance changes during the modulation experiments. Remarkably, the absence of mechanosensitivity of the ps-meta-para-PCP has not been reported experimentally before. Particularly, this behavior indicates the absence of a transmission dip as a function of electrode displacement (within the displacement window probed by the experiment), suggesting that DQI does not occur in the case of ps-meta-PCP cores. This is in agreement with previous predictions of π-stacked systems by the groups of Solomon26,27 and Yoshizawa.29

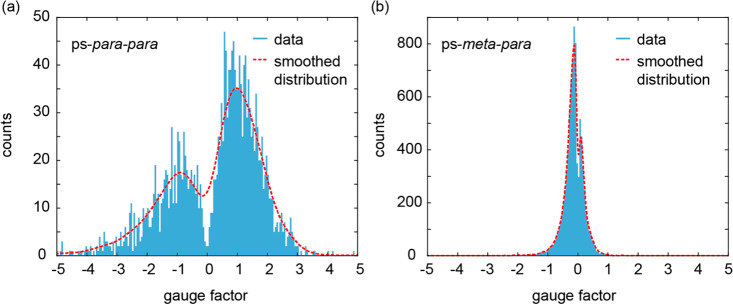
To quantify the mechanosensitivity of the molecule under investigation, the gauge factor (GF) was determined as the ratio between logarithmic conductance variation and linear electrode displacement (see the Supporting Information (section 2.4) for more information). Figure 4 displays the GFs for (a) ps-para-para-PCP and (b) ps-meta-para-PCP. Indeed, the GFs of the measurements of both structures visualize their difference. While the absence of mechanosensitivity of ps-meta-para-PCP results in a sharp peak close to zero (Figure 4b), the GF values recorded for ps-para-para-PCP (Figure 4a) display a broad distribution with a minimum at GF = 0, documenting its pronounced mechanosensitivity.

Figure 4.

Figure 4

Open in a new tab

Gauge factors obtained from (a) 1 442 ps-para-para-PCP traces and (b) 2 236 ps-meta-para-PCP traces in modulation experiments. The counts are collected from fast Fourier transform (FFT) spectra over 1 s intervals of the traces, which means that there are 15 counts, with different GFs for each recording, lasting 15 s.

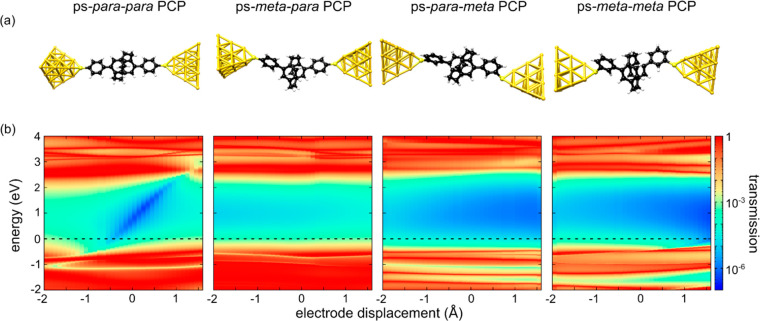
To rationalize the experimental observations described earlier, extensive DFT calculations were performed. First, the four model compounds ps-para-para-PCP (1b), ps-meta-para-PCP (2b), ps-para-meta-PCP (3b), and ps-meta-meta-PCP (4b) were optimized in the gas phase. The hydrogen atoms of the terminal thiol groups were removed, and the molecules were placed in model junctions, consisting of pairs of tetrahedral gold leads (Figure 5a). Optimizing the junction geometry, only the top three gold atoms in the first layer of each tip were allowed to relax, while the rest of the gold cluster remained fixed. Then, the systems were stretched in steps of 0.1 Å, and a geometry optimization was performed at every single step. A detailed description of the established approach37 and explanations of the calculations are provided in the Supporting Information (section 3.1).

Figure 5.

Figure 5

Open in a new tab

(a) Illustration of PCP derivatives 1–4 immobilized in junctions between two gold electrodes. (b) Transmission maps of the four types of PCP single-molecule junctions. The horizontal red resonances in the maps arise from molecular frontier orbitals. For the ps-para-para-PCP molecule, an antiresonance is observed inside the HOMO–LUMO gap that shifts in energy as the displacement is varied. Similar tunable DQI effects are absent for all other molecules, in particular for ps-meta-para-PCP junctions and ps-meta-meta-PCP junctions with central ps-meta-PCP systems. The position of the Fermi energy is indicated as a horizontal dashed line.

A closer look at the two-dimensional contour plots of transmission in dependence of energy and electrode displacement in Figure 5b reveals important information about the transmission behavior of the molecular junctions inside the electronic gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). In the case of the ps-para-para-PCP, a transmission valley (blue diagonal trace) with transmission values lower than 10–5 is observed between the molecular frontier orbitals (red horizontal traces). The transmission valley corresponds to the DQI conductance dip, as shown in Figure 3e. The energy position of the transmission minimum can be tuned by mechanical manipulation of the junction. It should be noted that the DQI crosses the complete HOMO–LUMO gap, making it a robust feature for experimental detection, because it does not depend on the precise position of the Fermi energy. A similar valley is not present for the ps-meta-para-PCP junction. Instead, the transmission stays rather constant in the range of ∼10–3–10–4 inside the molecule’s HOMO–LUMO gap. Rather uniform transmission values are furthermore predicted in the molecules’ electronic gap for both ps-para-meta- and ps-meta-meta-PCP. Interestingly, for this pair of model compounds with terminal meta-benzene linkers, ∼1 order of magnitude lower transmission values were calculated compared to the pair with terminal para-benzene linkers. This is also in line with the absence of measurable conductance plateaus for the meta-phenyl-connected PCPs in Figure 2.

The conductance that we compute within the DFT-NEGF formalism37 at the Fermi energy is plotted in parts e and f of Figure 3 for ps-para-para- and ps-meta-para-PCP derivatives, respectively. Considering the example of the ps-para-para-PCP single-molecule junction, the conductance features a dip that is shifted toward negative displacements and is ∼2 orders of magnitude lower than the base value. Molecular contacts constructed from ps-meta-para-PCP show instead a rather constant behavior in the studied displacement range without a DQI dip.

The behavior of another geometry that features a more complex stick–slip motion is discussed in the Supporting Information (section 3.2). In that case, remnants of transmission valleys are visible for the ps-para-meta-PCP molecular junction, further consolidating the hypothesis of the central ps-para-PCP subunit as the origin of the DQI phenomenon. Note, however, that we argue here on a qualitative level because we did not correct DFT quasiparticle energies and therefore expect uncertainties with respect to absolute conductance values,17,38−41 as a comparison of experimental and theoretical data in Figures 3 and 5 confirms.

While the calculated transmission plots perfectly support the hypothesis that mechanosensitivity can exclusively be observed for structures with a central ps-para-PCP subunit providing DQI, another qualitative argument is provided by considering orbital symmetry rules, as suggested by Yoshizawa and co-workers.29,42 The qualitative prediction of QI phenomena is based on the interplay of molecular frontier orbitals, especially the HOMO and LUMO, in transport models using Landauer–Büttiker scattering theory and Green’s function methods (details are provided in the Supporting Information (section 3.3)). Thus, the gas-phase frontier orbitals of the model compounds with terminal thiol groups were calculated and are displayed in Figure 6.

Figure 6.

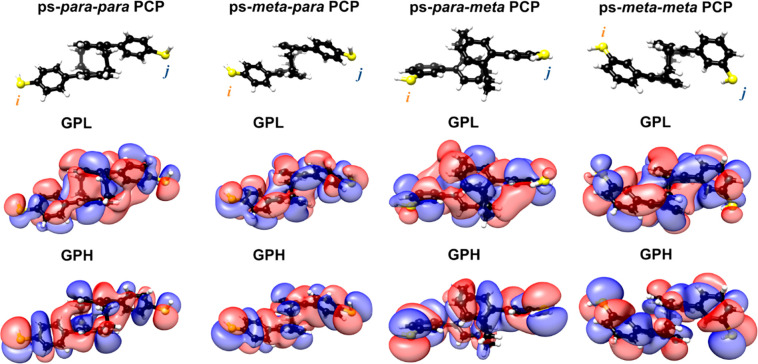
Figure 6

Open in a new tab

HOMO and LUMO molecular frontier orbitals of the ps-para-para-, ps-meta-para-, ps-para-meta-, and ps-meta-meta-PCPs. The anchoring sulfur atoms are marked i and j, respectively. Extended representations also including GPH–1 and GPL+1 for each molecule can be found in the Supporting Information (section 3.3).

Assuming that the Fermi energy of the electrodes lies between the molecule’s HOMO and LUMO energies due to charge neutrality, two orbital rules apply for the electronic transport properties.29,42 (1) The weights of the HOMO and LUMO wave functions on the anchoring atoms i and j (see Figure 6) need to be of decent size to yield a fair contribution to the transmission. (2) If the parities of the molecule’s HOMO and LUMO on the anchoring atoms are different in sign, transport is symmetry-supported through CQI, which is typically reflected in a high transmission inside the HOMO–LUMO gap. If HOMO and LUMO parities are the same instead, the related molecular orbital resonances cancel each other out at a certain energy inside the HOMO–LUMO gap. As a consequence, transport is symmetry-inhibited, resulting in a DQI dip in the energy-dependent transmission function, typically leading to a reduced conductance of the single-molecule junction. This argument assumes that HOMO and LUMO orbital wave functions are of similar character on the termini i and j.

The analysis of the molecules started by defining the terminal sulfur atoms as anchoring sites i and j (see Figure 6). Comparing orbital wave functions on the terminal sulfur atoms shows that gas-phase HOMO (GPH) and gas-phase LUMO (GPL) of both model compounds comprising a central para-PCP (ps-para-para- and ps-para-meta-PCP) are of similarly oriented π-character at the sulfur atoms and have the same parities; thus, these structures should show DQI. In contrast, both molecules with a ps-meta-PCP subunit have different parities in their GPH and GPL on the terminal sulfur atoms and thus exhibit CQI. The orbital symmetry rules thus rationalize the experimental observations and numerical computations reported earlier, which identify the central ps-para-PCP subunit as the origin of DQI.

Let us point out that ferrocene recently emerged as a related 3D system to the PCP, where the angle between two cyclopentadienyl decks can be tuned rather continuously around the central Fe core atom.43 The torsion can be compared to meta or para connection to the PCP. The mechanical distortion that explains the experimental results here is mainly the displacement of two benzene rings as compared to a rotation.

Conclusion

We have studied the electronic transport properties of single-molecule junctions based on π-stacked hydrocarbons. Our study confirms previous theoretical predictions for model compounds in terms of molecular orbital symmetry rules with regard to the suppression of electronic transport in PCP subunits when contacted in ps-para geometry as compared to ps-meta geometry. While the ps-meta subunit generally shows high conductance in comparison to the ps-para geometry (still relatively low compared to other conjugated molecular wires such as OPE3-dithiol44) and little sensitivity to mechanical manipulation, the ps-para subunit offers an exceptional mechanoelectric sensitivity. Notably, our theoretical calculations predict that the DQI can be tuned through the complete electronic gap region, explaining the experimental robustness of the feature, as observations should be largely independent of the precise location of the Fermi energy. Similar to an optical Fabry–Pérot interferometer, the DQI feature can be used to detect minute displacement changes and hence serves as a quantum sensor operating at ambient conditions, i.e., at room temperature.

Acknowledgments

This work was supported by a Horizon 2020 FET open project (QuIET; no. 767187). H.S.J.v.d.Z. and C.H. acknowledge support from The Netherlands Organisation for Scientific Research (NWO-Vrij program). M.M. acknowledges support from the Swiss National Science Foundation (SNF Grant no. 200020-178808) and the 111 project (90002-18011002).

Glossary

Abbreviations

QI

quantum interference

DQI

destructive quantum interference

CQI

constructive quantum interference

OPE

oligo(phenylene ethynylene)

PCP

[2.2]paracyclophane

MCBJ

mechanically controlled break junction

DFT

density functional theory

NEGF

nonequilibrium Green’s function

ps

pseudo

GF

gauge factor

FFT

fast Fourier transform

HOMO

highest occupied molecular orbital

LUMO

lowest unoccupied molecular orbital

GPH

gas-phase HOMO

GPL

gas-phase LUMO.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.1c06966.

  • Synthesis and characterization of all molecules, and details concerning transport measurements and calculations (PDF)

Author Contributions

# K.R., C.H., and W.M.S. contributed equally.

The authors declare no competing financial interest.

Supplementary Material

ja1c06966_si_001.pdf (8.3MB, pdf)

References

  1. van der Molen S. J.; Naaman R.; Scheer E.; Neaton J. B.; Nitzan A.; Natelson D.; Tao N. J.; van der Zant H. S. J.; Mayor M.; Ruben M.; Reed M.; Calame M. Visions for a Molecular Future. Nat. Nanotechnol. 2013, 8 (6), 385–389. 10.1038/nnano.2013.101. [DOI] [PubMed] [Google Scholar]
  2. Aviram A.; Ratner M. A. Molecular Rectifiers. Chem. Phys. Lett. 1974, 29 (2), 277–283. 10.1016/0009-2614(74)85031-1. [DOI] [Google Scholar]
  3. Luo L.; Choi S. H.; Frisbie C. D. Probing Hopping Conduction in Conjugated Molecular Wires Connected to Metal Electrodes. Chem. Mater. 2011, 23 (3), 631–645. 10.1021/cm102402t. [DOI] [Google Scholar]
  4. Huber R.; González M. T.; Wu S.; Langer M.; Grunder S.; Horhoiu V.; Mayor M.; Bryce M. R.; Wang C.; Jitchati R.; Schönenberger C.; Calame M. Electrical Conductance of Conjugated Oligomers at the Single Molecule Level. J. Am. Chem. Soc. 2008, 130 (3), 1080–1084. 10.1021/ja0767940. [DOI] [PubMed] [Google Scholar]
  5. Irie M.; Fukaminato T.; Sasaki T.; Tamai N.; Kawai T. A Digital Fluorescent Molecular Photoswitch. Nature 2002, 420 (6917), 759–760. 10.1038/420759a. [DOI] [PubMed] [Google Scholar]
  6. Liao J.; Agustsson J. S.; Wu S.; Schönenberger C.; Calame M.; Leroux Y.; Mayor M.; Jeannin O.; Ran Y.-F.; Liu S.-X.; Decurtins S. Cyclic Conductance Switching in Networks of Redox-Active Molecular Junctions. Nano Lett. 2010, 10 (3), 759–764. 10.1021/nl902000e. [DOI] [PubMed] [Google Scholar]
  7. Elbing M.; Ochs R.; Koentopp M.; Fischer M.; von Hanisch C.; Weigend F.; Evers F.; Weber H. B.; Mayor M. A Single-Molecule Diode. Proc. Natl. Acad. Sci. U. S. A. 2005, 102 (25), 8815–8820. 10.1073/pnas.0408888102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Lörtscher E.; Gotsmann B.; Lee Y.; Yu L.; Rettner C.; Riel H. Transport Properties of a Single-Molecule Diode. ACS Nano 2012, 6 (6), 4931–4939. 10.1021/nn300438h. [DOI] [PubMed] [Google Scholar]
  9. Naher M.; Milan D. C.; Al-Owaedi O. A.; Planje I. J.; Bock S.; Hurtado-Gallego J.; Bastante P.; Abd Dawood Z. M.; Rincón-García L.; Rubio-Bollinger G.; Higgins S. J.; Agraït N.; Lambert C. J.; Nichols R. J.; Low P. J. Molecular Structure–(Thermo)Electric Property Relationships in Single-Molecule Junctions and Comparisons with Single- and Multiple-Parameter Models. J. Am. Chem. Soc. 2021, 143 (10), 3817–3829. 10.1021/jacs.0c11605. [DOI] [PubMed] [Google Scholar]
  10. Stadler R.; Markussen T. Controlling the Transmission Line Shape of Molecular T-Stubs and Potential Thermoelectric Applications. J. Chem. Phys. 2011, 135 (15), 154109. 10.1063/1.3653790. [DOI] [PubMed] [Google Scholar]
  11. Markussen T.; Stadler R.; Thygesen K. S. The Relation between Structure and Quantum Interference in Single Molecule Junctions. Nano Lett. 2010, 10 (10), 4260–4265. 10.1021/nl101688a. [DOI] [PubMed] [Google Scholar]
  12. Jiang F.; Trupp D. I.; Algethami N.; Zheng H.; He W.; Alqorashi A.; Zhu C.; Tang C.; Li R.; Liu J.; Sadeghi H.; Shi J.; Davidson R.; Korb M.; Sobolev A. N.; Naher M.; Sangtarash S.; Low P. J.; Hong W.; Lambert C. J. Turning the Tap: Conformational Control of Quantum Interference to Modulate Single-Molecule Conductance. Angew. Chem., Int. Ed. 2019, 58 (52), 18987–18993. 10.1002/anie.201909461. [DOI] [PubMed] [Google Scholar]
  13. Venkataraman L.; Klare J. E.; Nuckolls C.; Hybertsen M. S.; Steigerwald M. L. Dependence of Single-Molecule Junction Conductance on Molecular Conformation. Nature 2006, 442 (7105), 904–907. 10.1038/nature05037. [DOI] [PubMed] [Google Scholar]
  14. Aradhya S. V.; Meisner J. S.; Krikorian M.; Ahn S.; Parameswaran R.; Steigerwald M. L.; Nuckolls C.; Venkataraman L. Dissecting Contact Mechanics from Quantum Interference in Single-Molecule Junctions of Stilbene Derivatives. Nano Lett. 2012, 12 (3), 1643–1647. 10.1021/nl2045815. [DOI] [PubMed] [Google Scholar]
  15. Mayor M.; Weber H. B.; Reichert J.; Elbing M.; von Hänisch C.; Beckmann D.; Fischer M. Electric Current through a Molecular Rod—Relevance of the Position of the Anchor Groups. Angew. Chem., Int. Ed. 2003, 42 (47), 5834–5838. 10.1002/anie.200352179. [DOI] [PubMed] [Google Scholar]
  16. Koga J.; Tsuji Y.; Yoshizawa K. Orbital Control of Single-Molecule Conductance Perturbed by π-Accepting Anchor Groups: Cyanide and Isocyanide. J. Phys. Chem. C 2012, 116 (38), 20607–20616. 10.1021/jp3068156. [DOI] [Google Scholar]
  17. Arroyo C. R.; Tarkuc S.; Frisenda R.; Seldenthuis J. S.; Woerde C. H. M.; Eelkema R.; Grozema F. C.; van der Zant H. S. J. Signatures of Quantum Interference Effects on Charge Transport Through a Single Benzene Ring. Angew. Chem., Int. Ed. 2013, 52 (11), 3152–3155. 10.1002/anie.201207667. [DOI] [PubMed] [Google Scholar]
  18. Kiguchi M.; Kaneko S. Single Molecule Bridging between Metal Electrodes. Phys. Chem. Chem. Phys. 2013, 15 (7), 2253–2267. 10.1039/C2CP43960C. [DOI] [PubMed] [Google Scholar]
  19. Lambert C. J. Basic Concepts of Quantum Interference and Electron Transport in Single-Molecule Electronics. Chem. Soc. Rev. 2015, 44 (4), 875–888. 10.1039/C4CS00203B. [DOI] [PubMed] [Google Scholar]
  20. Kiguchi M.; Nakamura H.; Takahashi Y.; Takahashi T.; Ohto T. Effect of Anchoring Group Position on Formation and Conductance of a Single Disubstituted Benzene Molecule Bridging Au Electrodes: Change of Conductive Molecular Orbital and Electron Pathway. J. Phys. Chem. C 2010, 114 (50), 22254–22261. 10.1021/jp1095079. [DOI] [Google Scholar]
  21. Arroyo C. R.; Frisenda R.; Moth-Poulsen K.; Seldenthuis J. S.; Bjørnholm T.; van der Zant H. S. Quantum Interference Effects at Room Temperature in OPV-Based Single-Molecule Junctions. Nanoscale Res. Lett. 2013, 8, 1. 10.1186/1556-276X-8-234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Li X.; Staykov A.; Yoshizawa K. Orbital Views of the Electron Transport through Polycyclic Aromatic Hydrocarbons with Different Molecular Sizes and Edge Type Structures. J. Phys. Chem. C 2010, 114 (21), 9997–10003. 10.1021/jp102280r. [DOI] [Google Scholar]
  23. Yoshizawa K.; Tada T.; Staykov A. Orbital Views of the Electron Transport in Molecular Devices. J. Am. Chem. Soc. 2008, 130 (29), 9406–9413. 10.1021/ja800638t. [DOI] [PubMed] [Google Scholar]
  24. Yoshizawa K. An Orbital Rule for Electron Transport in Molecules. Acc. Chem. Res. 2012, 45 (9), 1612–1621. 10.1021/ar300075f. [DOI] [PubMed] [Google Scholar]
  25. Brown C. J.; Farthing A. C. Preparation and Structure of Di- p -Xylylene. Nature 1949, 164 (4178), 915–916. 10.1038/164915b0.15407665 [DOI] [Google Scholar]
  26. Solomon G. C.; Vura-Weis J.; Herrmann C.; Wasielewski M. R.; Ratner M. A. Understanding Coherent Transport through π-Stacked Systems upon Spatial Dislocation. J. Phys. Chem. B 2010, 114 (45), 14735–14744. 10.1021/jp103110h. [DOI] [PubMed] [Google Scholar]
  27. Solomon G. C.; Herrmann C.; Vura-Weis J.; Wasielewski M. R.; Ratner M. A. The Chameleonic Nature of Electron Transport through π-Stacked Systems. J. Am. Chem. Soc. 2010, 132 (23), 7887–7889. 10.1021/ja102434m. [DOI] [PubMed] [Google Scholar]
  28. Stefani D.; Weiland K. J.; Skripnik M.; Hsu C.; Perrin M. L.; Mayor M.; Pauly F.; van der Zant H. S. J. Large Conductance Variations in a Mechanosensitive Single-Molecule Junction. Nano Lett. 2018, 18 (9), 5981–5988. 10.1021/acs.nanolett.8b02810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Li X.; Staykov A.; Yoshizawa K. Orbital Views on Electron-Transport Properties of Cyclophanes: Insight into Intermolecular Transport. Bull. Chem. Soc. Jpn. 2012, 85 (2), 181–188. 10.1246/bcsj.20110256. [DOI] [Google Scholar]
  30. Perdew J. P. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 33 (12), 8822–8824. 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]
  31. Vorontsova N. V.; Rozenberg V. I.; Sergeeva E. V.; Vorontsov E. V.; Starikova Z. A.; Lyssenko K. A.; Hopf H. Symmetrically Tetrasubstituted [2.2]Paracyclophanes: Their Systematization and Regioselective Synthesis of Several Types of Bis-Bifunctional Derivatives by Double Electrophilic Substitution. Chem. - Eur. J. 2008, 14 (15), 4600–4617. 10.1002/chem.200701683. [DOI] [PubMed] [Google Scholar]
  32. Jevric M.; Petersen A. U.; Mansø M.; Madsen A. Ø.; Nielsen M. B. Bismuth(III)-Promoted Acetylation of Thioethers into Thioacetates. Eur. J. Org. Chem. 2015, 2015, 4675–4688. 10.1002/ejoc.201500420. [DOI] [Google Scholar]
  33. Martin C. A.; Ding D.; van der Zant H. S. J.; van Ruitenbeek J. M. Lithographic Mechanical Break Junctions for Single-Molecule Measurements in Vacuum: Possibilities and Limitations. New J. Phys. 2008, 10 (6), 065008. 10.1088/1367-2630/10/6/065008. [DOI] [Google Scholar]
  34. Martin C. A.; Smit R. H. M.; van Egmond R.; van der Zant H. S. J.; van Ruitenbeek J. M. A Versatile Low-Temperature Setup for the Electrical Characterization of Single-Molecule Junctions. Rev. Sci. Instrum. 2011, 82 (5), 053907. 10.1063/1.3593100. [DOI] [PubMed] [Google Scholar]
  35. Cabosart D.; El Abbassi M.; Stefani D.; Frisenda R.; Calame M.; van der Zant H. S. J.; Perrin M. L. A Reference-Free Clustering Method for the Analysis of Molecular Break-Junction Measurements. Appl. Phys. Lett. 2019, 114 (14), 143102. 10.1063/1.5089198. [DOI] [Google Scholar]
  36. O’Neill K.; Osorio E. A.; van der Zant H. S. J. Self-Breaking in Planar Few-Atom Au Constrictions for Nanometer-Spaced Electrodes. Appl. Phys. Lett. 2007, 90 (13), 133109. 10.1063/1.2716989. [DOI] [Google Scholar]
  37. Pauly F.; Viljas J. K.; Huniar U.; Häfner M.; Wohlthat S.; Bürkle M.; Cuevas J. C.; Schön G. Cluster-Based Density-Functional Approach to Quantum Transport through Molecular and Atomic Contacts. New J. Phys. 2008, 10 (12), 125019. 10.1088/1367-2630/10/12/125019. [DOI] [Google Scholar]
  38. Quek S. Y.; Venkataraman L.; Choi H. J.; Louie S. G.; Hybertsen M. S.; Neaton J. B. Amine–Gold Linked Single-Molecule Circuits: Experiment and Theory. Nano Lett. 2007, 7 (11), 3477–3482. 10.1021/nl072058i. [DOI] [PubMed] [Google Scholar]
  39. Zotti L. A.; Bürkle M.; Pauly F.; Lee W.; Kim K.; Jeong W.; Asai Y.; Reddy P.; Cuevas J. C. Heat Dissipation and Its Relation to Thermopower in Single-Molecule Junctions. New J. Phys. 2014, 16 (1), 015004. 10.1088/1367-2630/16/1/015004. [DOI] [Google Scholar]
  40. Manrique D. Z.; Huang C.; Baghernejad M.; Zhao X.; Al-Owaedi O. A.; Sadeghi H.; Kaliginedi V.; Hong W.; Gulcur M.; Wandlowski T.; Bryce M. R.; Lambert C. J. A Quantum Circuit Rule for Interference Effects in Single-Molecule Electrical Junctions. Nat. Commun. 2015, 6 (1), 6389. 10.1038/ncomms7389. [DOI] [PubMed] [Google Scholar]
  41. Garner M. H.; Li H.; Chen Y.; Su T. A.; Shangguan Z.; Paley D. W.; Liu T.; Ng F.; Li H.; Xiao S.; Nuckolls C.; Venkataraman L.; Solomon G. C. Comprehensive Suppression of Single-Molecule Conductance Using Destructive σ-Interference. Nature 2018, 558 (7710), 415–419. 10.1038/s41586-018-0197-9. [DOI] [PubMed] [Google Scholar]
  42. Tsuji Y.; Yoshizawa K. Frontier Orbital Perspective for Quantum Interference in Alternant and Nonalternant Hydrocarbons. J. Phys. Chem. C 2017, 121 (17), 9621–9626. 10.1021/acs.jpcc.7b02274. [DOI] [Google Scholar]
  43. Camarasa-Gómez M.; Hernangómez-Pérez D.; Inkpen M. S.; Lovat G.; Fung E.-D.; Roy X.; Venkataraman L.; Evers F. Mechanically Tunable Quantum Interference in Ferrocene-Based Single-Molecule Junctions. Nano Lett. 2020, 20 (9), 6381–6386. 10.1021/acs.nanolett.0c01956. [DOI] [PubMed] [Google Scholar]
  44. Frisenda R.; Perrin M. L.; Valkenier H.; Hummelen J. C.; van der Zant H. S. J. Statistical Analysis of Single-Molecule Breaking Traces. Phys. Status Solidi B 2013, 250 (11), 2431–2436. 10.1002/pssb.201349236. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja1c06966_si_001.pdf (8.3MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES