A penalized regression framework for building polygenic risk models based on summary statistics from genome-wide association studies and incorporating external information

Abstract

Large-scale genome-wide association (GWAS) studies provide opportunities for developing genetic risk prediction models that have the potential to improve disease prevention, intervention or treatment. The key step is to develop polygenic risk score (PRS) models with high predictive performance for a given disease, which typically requires a large training data set for selecting truly associated single nucleotide polymorphisms (SNPs) and estimating effect sizes accurately. Here, we develop a comprehensive penalized regression for fitting l₁ regularized regression models to GWAS summary statistics. We propose incorporating Pleiotropy and ANnotation information into PRS (PANPRS) development through suitable formulation of penalty functions and associated tuning parameters. Extensive simulations show that PANPRS performs equally well or better than existing PRS methods when no functional annotation or pleiotropy is incorporated. When functional annotation data and pleiotropy are informative, PANPRS substantially outperforms existing PRS methods in simulations. Finally, we applied our methods to build PRS for type 2 diabetes and melanoma and found that incorporating relevant functional annotations and GWAS of genetically related traits improved prediction of these two complex diseases.

1. Introduction

One goal of genome-wide association studies (GWAS) is to develop accurate polygenic risk score (PRS) prediction models, which are fundamental for prevention, early detection and treatment of complex diseases. Although large-scale GWAS have identified dozens or even hundreds of single nucleotide polymorphisms (SNPs) associated with individual diseases, PRS models still have poor predictive performance, far away from the upper limit implicated by heritability analyses for most of diseases [1–3]. Theoretical analysis suggested that the performance of PRSs relies on both the genetic architecture of the disease and the sample size of the training data set [1, 3]. While PRSs can be improved by substantially increasing the sample sizes of the training data, efficient statistical method is also needed to improve PRS based on existing data.

PRS can be built with complex machine learning algorithms [4] or linear mixed models [5, 6] based on individual level genotypic and phenotypic data. However, developing PRS based on GWAS summary statistics (including the marginal regression coefficient ${\tilde{\beta }}_j$ and the p-value P_j based on single SNP analysis) may be preferred because of the easier access to large GWAS consortia. The simplest and most widely used PRS [7] incorporates independent SNPs achieving genome-wide significance in the form: $PR{S}_i={\sum }_{j=1}^K{\tilde{\beta }}_j{g}_{ij}$ where i indexes an individual and ${\tilde{\beta }}_j$ is the association coefficient for SNP j obtained from typical marginal association analysis of the SNPs. A more sophisticated PRS was proposed to include SNPs below genome-wide significance threshold in the form: $PR{S}_i\left(p_0\right)=\sum {\tilde{\beta }}_j{g}_{ij}I\left(P_j<p_0\right)$, where the optimal p-value threshold p₀ was selected based on the validation GWAS data [8]. This approach is typically implemented with linkage disequilibrium (LD)-based pruning to remove the noise due to correlated SNPs but may result in loss of underlying independent signals.

Recent work has shown that PRS can be improved by modelling LD explicitly [9], incorporating functional annotation data [10, 11] or modelling genetic pleiotropy [10, 12–14], i.e., leveraging information from traits that are genetically related with the primary trait. However, no unified statistical framework is available to incorporate functional annotation data and many secondary traits to maximize the predictive performance of PRS, particularly when only summary statistics are available.

Lasso and various other extensions based on L₁-regularization [15] is a powerful algorithm for building sparse prediction models when the number of predictors far exceeds the number of subjects. When individual genotypic and phenotypic data are available, these methods have been used for building PRS for complex diseases [16, 17]. The Bayesian interpretation of Lasso provides a natural way to incorporate functional annotation data by using SNP-specific regularization parameter. In addition, group Lasso type methods have been developed to regularize multiple predictors or the same predictor across many phenotypes [18]; thus, they have the potential to improve PRS performance by incorporating traits that are genetically related with the primary trait. Although the Lasso algorithm is powerful and flexible, it requires individual level data, which are difficult and often impossible to access.

Importantly, we and others have earlier shown that the sample size of the GWAS training data set is the most important factor for improving prediction accuracy [1, 3]. Often, the GWAS consortia for complex traits/diseases perform meta-analysis including most of the existing GWAS data sets. The GWAS summary statistics can be accessed from these consortia to build PRS models. Thus, it would be desirable to develop PRS methods using the GWAS summary statistics based on a large sample size to achieve a high predication accuracy.

Mat and colleagues [19] developed an algorithm lassosum for fitting a panelized linear regression model based on summary statistics that are derived based on linear regressions. It is not clear how to directly use the algorithm to summary statistics derived based on logistic regression for a binary trait. We herein develop a comprehensive statistical framework by incorporating Pleiotropy and ANnotation information into PRS (PANPRS) development through suitable formulation of penalty functions based on GWAS summary statistics with the flexibility to both quantitative and binary traits. We first develop a Lasso regression model for a single trait, either a quantitative trait or a binary trait, based on GWAS summary statistics. This approach uses local LD matrices estimated based on external genotypic data with relevant ancestry. We show that the Lasso model based on summary statistics and local LD information well approximates that based on raw genotypic data. Second, we modify regularization parameters to incorporate multiple functional annotation data, implicitly assuming that SNPs annotated with more functional categories are more likely to be associated with the trait/disease. Third, we adapt our recently developed penalty function [20] to jointly penalize multiple secondary traits/diseases that are genetically related with the primary trait. Finally, we present a unified framework to incorporate local LD pattern, multiple functional annotations and genetic pleiotropic information. The framework works for quantitative traits, binary traits or a combination of both. The R code is available at https://github.com/lsncibb/PANPRS.

The manuscript is organized as follows. Section 2 presents the statistical framework of PANPRS for quantitative traits. Section 3 extends the framework to binary traits. Simulation results are presented in Section 4. In Section 5, we exemplify PANPRS by building PRSs for type 2 diabetes and melanoma. Limitations and future directions are discussed in the final section.

2. PRS for quantitative traits using GWAS summary statistics

In this section, we propose methods for building PRSs for quantitative traits by fitting Lasso regression models using GWAS summary statistics. The parallel development of PRS for binary traits or a combination of quantitative and binary traits will be presented in Section 3.

2.1. Fitting the Lasso using GWAS summary statistics for a quantitative trait

Consider a GWAS for a quantitative trait with n unrelated subjects and M SNP markers. Let $\mathit{Y}={\left(y_1,\cdots ,y_n\right)}^{\prime }$ be the phenotypic values. Let $\mathit{X}=\left(x_{ij}\right)$ be the genotypic matrix, where $x_{ij}$ denotes the genotype for subject i and SNP j. Without loss of generality, we assume that the phenotype and the genotype for each SNP have been normalized to have mean zero and unit variance across subjects. When individual level data (X, Y) are available from a training GWAS data set, one can develop a linear, additive PRS by solving the following optimization problem:

$${\mathit{\beta }}_{Lasso}(\lambda )=argmi{n}_{\mathit{\beta }}\frac{1}{2n}{\sum }_{i=1}^n{\left(y_i-{\sum }_{j=1}^M{x}_{ij}{\beta }_j\right)}^2+{\sum }_{j=1}^M\lambda \left|{\beta }_j\right|,$$ (1)

where $\mathit{\beta }=\left({\beta }_1,\cdots ,{\beta }_M\right)$ are the effect sizes of M SNPs. The l₁ penalty shrinkages most of coefficients to zero and thus produces a sparse prediction model with an appropriately chosen λ.

The Lasso estimates can be obtained by the coordinate descent algorithm, which solves the single-variate Lasso problem sequentially and iteratively [21]. Assume that $\left({\widehat{\beta }}_1^{(t)},\cdots ,{\widehat{\beta }}_M^{(t)}\right)$ are the coefficients at iteration t. Define

$$z_j^{(t)}=\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}{y}_i-\frac{1}{n}{\sum }_{i=1}^n{\sum }_{l\ne j}{x}_{ij}{x}_{il}{\widehat{\beta }}_l^{(t)}=\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}{y}_i-{\sum }_{l\ne j}{\widehat{\beta }}_l^{(t)}\left(\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}{x}_{il}\right).$$ (2)

By solving the single-variate Lasso problem given current estimates, one can update ${\beta }_j$ as

$${\widehat{\beta }}_j^{(t+1)}=\{\begin{array}{ll}0& \text{if}\left|z_j^{(t)}\right|\le \lambda \\ \text{sign}\left(z_j^{(t)}\right)\left|\right|z_j^{(t)}|-\lambda |& \text{if}\left|z_j^{(t)}\right|>{\lambda }_1.\end{array}$$

This procedure continues until convergence is achieved.

Apparently, the key step of fitting the Lasso is to calculate $z_j^{(t)}$ in (2) for each iteration. Fortunately, $z_j^{(t)}$ can be approximated using GWAS summary statistics and local LD information. Remember that $x_{ij}$ and $y_i$ are normalized to have unit variance. For the first item in (2), we have $\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}{y}_i={\tilde{\beta }}_j$, the marginal coefficient of SNP j based on single SNP linear regression. For the second item, ${\widehat{\rho }}_{jl}:=\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}{x}_{il}$ is the empirical correlation between two SNPs (j, l). Ideally, ${\widehat{\rho }}_{jl}$ would be calculated based on the genotype of the training data set. As an approximation, we can calculate ${\widehat{\rho }}_{jl}$ based on the existing genotype data with relevant ancestry. For SNPs on different chromosomes or on the same chromosome but more than 5 mega base pairs (MB) away, we set ${\widehat{\rho }}_{jl}=0$. Thus, we only need to account for LD in local regions, which greatly simplifies the calculation of $z_j^{(t)}$. For SNP j, let $A_j$ denote the set of its neighboring SNPs less than 5 MB. We approximate $z_j^{(t)}$ as

$$z_j^{(t)}\approx \frac{1}{n}{\sum }_{i=1}^n{x}_{ij}{y}_i-{\sum }_{l\in A_j}{\widehat{\beta }}_l^{(t)}\left(\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}{x}_{il}\right)\approx {\tilde{\beta }}_j-{\sum }_{l\in A_j}{\widehat{\beta }}_l^{(t)}{\widehat{\rho }}_{jl}.$$ (3)

The framework of the algorithm proposed here is similar to lassosum [19]. The main difference is how to account for LD between SNPs. lassosum regularizes the estimated genotypic correlation matrix to achieve a stable solution to (1). We accounted for local LD while setting ${\widehat{\rho }}_{jl}=0$ for SNPs far away to make the algorithm computationally fast.

2.2. PANPRS with multiple functional annotations

Recent studies have reported that functional annotation data may improve accuracy of PRS [10, 11]. Intuitively, SNPs annotated with functional importance may be prioritized as truly associated SNPs and thus included in PRS with less stringent threshold [10]. Examples of functional annotations include expression quantitative trait loci (eQTL), methylation QTL (meQTL), cis-regulatory regions determined by Chromatin Immunoprecipitation Sequencing (ChIP-Seq) and genome conserved regions. It is biologically plausible that SNPs annotated with more functional categories are more likely to be causal. Existing methods (e.g., [10]) classify SNPs as functional or non-functional and do not fully leverage the information provided by multiple functional annotations. In this section, we extend PANPRS to incorporate multiple functional annotation data.

We assume r functional annotation categories. For SNP j and annotation s, we define a binary variable $R_{js}$, where $R_{js}=1$ if the SNP is not annotated for category s and $R_{js}=0$ otherwise. We can define $R_{js}$ based on a continuous annotation data after an appropriate transformation, e.g., sigmoid transformation. We propose to minimize the following cost function to derive regularized estimates of effect sizes:

$$\mathit{\beta }=argmi{n}_{\mathit{\beta }}\frac{1}{2n}{\sum }_{i=1}^n{\left(y_i-{\sum }_{j=1}^M{x}_{ij}{\beta }_j\right)}^2+{\sum }_{j=1}^M\left({\lambda }_0+{\sum }_{s=1}^r{\lambda }_s{R}_{js}\right)\left|{\beta }_j\right|.$$ (4)

Here, ${\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_r>0$. For SNP j, the total penalty is ${\text{Γ}}_j:={\lambda }_0+{\sum }_{s=1}^r{\lambda }_s{R}_{js}$, where ${\lambda }_0$ is the baseline penalty applying to all SNPs and the second term is SNP-specific penalty related with functional annotation information. Intuitively, if a SNP is annotated for more functional annotations, it is more likely to be causal for a trait and thus is less penalized in our framework.

Remark:

The annotation-specific regularization parameters $\left({\lambda }_1,\cdots ,{\lambda }_r\right)$ selected based on independent GWAS data may help identify annotation categories that are informative for prioritizing SNPs for PRS. In fact, ${\lambda }_s\gg 0$ indicates that the annotation category s is informative while the annotation is not informative if ${\lambda }_s\approx 0$.

Similarly, we can minimize the cost function (4) by the coordinate descent algorithm based on the GWAS summary statistics. Let $z_j^{(t)}$ in (3) be calculated at the t^th iteration. At the ${(t+1)}^{th}$ iteration, we update ${\beta }_j$ as

$${\widehat{\beta }}_j^{(t+1)}=\{\begin{array}{ll}0& \text{if}\left|z_j^{(t)}\right|\le {\text{Γ}}_j\\ \text{sign}\left(z_j^{(t)}\right)\left|\right|z_j^{(t)}\left|-{\text{Γ}}_j\right|& \text{if}\left|z_j^{(t)}\right|>{\text{Γ}}_j.\end{array}$$ (5)

2.3. PANPRS incorporating multiple traits

Genetic pleiotropy is the phenomenon by which individual genetic variants are associated with multiple traits. A variety of association tests have been proposed to identify SNPs that are modestly associated with multiple traits by modelling pleiotropy [22–24]. It has been recently reported that PRS performance can also be improved by modelling pleiotropy [12], i.e., incorporating GWAS data for traits that share genetic basis with the primary trait. In this section, we aim to extend PANPRS to model genetic pleiotropy by introducing a group-Lasso type penalty, which is more sensitive to select SNPs modestly associated with multiple traits.

Consider Q quantitative traits, each of which has $n_q$ subjects in GWAS. All studies are assumed to share the same set of M SNPs. For the q^th trait, let ${\mathit{Y}}_q=\left(y_{q1},\dots ,y_{q{n}_q}\right)$ be the phenotypic values and ${\mathit{X}}_q=\left(x_{qij}\right)$ for n_q subjects. Let ${\mathit{\beta }}_q={\left({\beta }_{q1},\cdots ,{\beta }_{qM}\right)}^{\prime }$ be the coefficients for M SNPs and for trait q. Let $\mathit{B}={\left({\mathit{\beta }}_1,\cdots ,{\mathit{\beta }}_Q\right)}^{\prime }$ be the coefficient matrix for all traits. We propose to obtain a sparse PRS by solving the following penalized least squares problem:

$$\mathit{B}=argmi{n}_{\mathit{B}}{\sum }_{q=1}^Q\frac{1}{2n_q}\Vert {\mathit{Y}}_q-{\mathit{X}}_q{\mathit{\beta }}_q{\Vert }_2^2+{\sum }_{q=1}^Q{\sum }_{j=1}^M{\lambda }_0\left|{\beta }_{qj}\right|+{\sum }_{j=1}^M{\lambda }_1\log ({\sum }_{q=1}^Q\left|{\beta }_{qj}\right|+\tau ),$$ (6)

where ${\lambda }_0(>0),{\lambda }_1(>0)$ and $\tau (>0)$ are tuning parameters. The group-wise log penalty was proposed in our previous work [25], which aims to select the variables that are associated with multiple traits with modest effects. Parameter τ > 0 is introduced to avoid indefinite values for $\log \left({\sum }_{q=1}^Q\left|{\widehat{\beta }}_{qj}^{(t)}\right|\right)$ when all $\left({\beta }_{1j},\cdots ,{\beta }_{Qj}\right)$ are penalized to 0 for SNP j. More discussions on the statistical properties of τ can be found in [25].

The solution to (6) can be obtained by applying a local linear approximation and the coordinate descent algorithm. Let ${\mathit{B}}^t=\left({\widehat{\beta }}_{qj}^{(t)}\right)$ denote the estimate at the t^th iteration. Define

$$u_{qj}^{(t)}={\tilde{\beta }}_{qj}-{\sum }_{\ell \in A_j}{\widehat{\rho }}_{j\ell }{\widehat{\beta }}_{q\ell }^{(t)},$$ (7)

where ${\tilde{\beta }}_{qj}$ is the marginal regression coefficient from the GWAS summary data, ${\widehat{\beta }}_{q\ell }^{(t)}$ is the updated coefficient at the t^th iteration and A_j is the neighboring SNP set for SNP j. Thus, $u_{qj}^{(t)}$ can be calculated using GWAS summary statistics ${\tilde{\beta }}_{qj}$ and the SNP correlation coefficients estimated based on external genotype data. In Supplementary Materials, we derive the following updating rule:

$${\widehat{\beta }}_{qj}^{(t+1)}=\{\begin{array}{ll}0& \text{if}\left|u_{qj}^{(t)}\right|\le T_{qj}\\ \mathrm{sgn}\left(u_{qj}^{(t)}\right)\left|\right|u_{qj}^{(t)}\left|-T_{qj}\right|& \text{if}\left|u_{qj}^{(t)}\right|>T_{qj}\end{array}.$$ (8)

Here, the threshold

$$T_{qj}={\lambda }_0+\frac{{\lambda }_1}{{\sum }_{q=1}^Q\left|{\widehat{\beta }}_{qj}^{(t)}\right|+\tau }$$ (9)

depends on the estimated total effects of the SNP across all Q traits. When the estimated total effects ${\sum }_{q=1}^Q\left|{\widehat{\beta }}_{qj}^{(t)}\right|$ is bigger, $T_{qj}$ is smaller and thus the SNP is more likely to be estimated as non-zero. Therefore, the SNP-specific and data-driven threshold $T_{qj}$ allow to select SNPs with modest individual effect but strong total effects across multiple traits.

2.4. PANPRS incorporating functional annotations and pleiotropic information

Finally, we extend PANPRS to incorporate both functional annotation data and multiple secondary traits that are genetically related with the primary trait. Based on the work in previous sections, we now derive the regularized estimates of effect sizes by minimizing the cost function:

$${\sum }_{q=1}^Q\frac{1}{2n_q}\Vert Y-{\mathit{X}}_q{\mathit{\beta }}_q{\Vert }_2^2+{\sum }_{q=1}^Q{\sum }_{j=1}^M\left({\lambda }_0+{\sum }_{s=1}^r{\lambda }_s{R}_{js}\right)\left|{\beta }_{qj}\right|+{\sum }_{j=1}^M\lambda \log \left({\sum }_{q=1}^Q\left|{\beta }_{qj}\right|+\tau \right).$$ (10)

For the ${(t+1)}^{th}$ iteration, we derive the update for ${\beta }_{qj}$ given the rest of parameters:

$${\widehat{\beta }}_{qj}^{(t+1)}=\{\begin{array}{ll}0& \text{if}\left|u_{qj}^{(t)}\right|\le T_{qj}^{\prime }\\ \mathrm{sgn}\left(u_{qj}^{(t)}\right)\left|\right|u_{qj}^{(t)}\left|-T_{qj}\right|& \text{if}\left|u_{qj}^{(t)}\right|>T_{qj}^{\prime }\end{array},$$ (11)

where $u_{qj}^{(t)}$ is given in (7) and

$$T_{qj}^{\prime }=\left({\lambda }_0+{\sum }_{s=1}^r{\lambda }_s{R}_{js}\right)+\frac{\lambda }{{\sum }_{q=1}^Q\left|{\widehat{\beta }}_{qj}^{(t)}\right|+\tau }.$$ (12)

Here, the first penalty is for multiple functional annotations and the second penalty is for multiple traits. Details are described in Supplemental Materials.

2.5. Selecting tuning parameters

For practical reasons, most of published PRS methods selected tuning parameters and reported performance of the corresponding PRS based on the same validation dataset, which makes assessment of predictive performance bias upward. Here, we select tuning parameters to make the assessment of PRS performance unbiased for both simulation studies and analyses of real data. For simulations, we simulated three data sets, one as the training data set, one for choosing tuning parameters and the third one for assessing PRS performance. For real data analysis, the independent “validation” data set was split into two data sets: one for selecting tuning parameters and the other for assessing PRS performance.

3. PRSs for binary traits using GWAS summary statistics

Let y_i be binary phenotypic value, where y_i = 1 represents a case and y_i = 0 represents a control. Let $\mathit{\beta }={\left({\beta }_0,{\beta }_1,\cdots ,{\beta }_M\right)}^T$ denote the intercept and the effect sizes for M SNPs. Define

$${\pi }_i(\mathit{\beta })=P\left(y_i=1\mid x_{i1},\cdots ,x_{iM}\right)=\frac{e^{{\beta }_0+{\sum }_{j=1}^M{x}_{ij}{\beta }_j}}{1+e^{{\beta }_0+{\sum }_{j=1}^M{x}_{ij}{\beta }_j}}.$$

When individual level data are available, one obtains a regularized estimate of β by minimizing

$$U_0(\mathit{\beta })=-{\sum }_{i=1}^n\left[y_i\log {\pi }_i+\left(1-y_i\right)\log \left(1-{\pi }_i\right)\right]+{\sum }_{j=1}^M\lambda \left|{\beta }_j\right|$$ (13)

using a similar coordinate descent algorithm proposed for non-convex penalty functions [27].

When only GWAS summary data, i.e., marginal coefficients ${\tilde{\beta }}_j$ estimated based on the single variant logistic regression, are available for M individual SNPs, we derive an updating rule in Appendix. Let $\left({\widehat{\beta }}_1^{(t)},\cdots ,{\widehat{\beta }}_M^{(t)}\right)$ be the coefficients at the t^th iteration. We calculate

$$z_j^{(t)}\approx {\tilde{\beta }}_j-{\sum }_{l\in A_j}{\widehat{\rho }}_{jl}{\widehat{\beta }}_l^{(t)},$$ (14)

where ${\widehat{\rho }}_{jl}$ is the correlation between a SNP pair (j, l) and A_j represents the set of SNPs in LD with SNP j. We update ${\widehat{\beta }}_j$ as

$${\widehat{\beta }}_j^{(t+1)}=\{\begin{array}{ll}0& \text{if}\left|z_j^{(t)}\right|\le \lambda \\ \mathrm{sgn}\left(z_j^{(t)}\right)\left|\right|z_j^{(t)}|-\lambda |& \text{if}\left|z_j^{(t)}\right|>\lambda \end{array}.$$

Note that formula (14) approximating $Z_j^{(t)}$ for a binary trait is identical to that for a quantitative trait (3) although the marginal coefficients ${\tilde{\beta }}_j$ are based on univariate logistic and linear regression, respectively. This observation makes the parallel extensions (i.e., incorporating functional data and modelling genetic pleiotropy) of the PANPRS framework straightforward for binary traits or for a combination of binary and quantitative traits.

As we will show in the Appendix, the algorithm works well when the resulting PRS explains a small fraction of phenotypic variance, which holds for most of complex diseases given the current sample sizes in the discovery sample set. Thus, we expect the algorithm to well approximate the true Lasso-based PRS in real situations.

4. Numerical studies

4.1. Genotypes for simulation studies

We conduct simulation studies by simulating phenotypic values conditioning on the genotypic data available from a GWAS of lung cancer [28]. This data set included 11,924 subjects of European ancestry after quality control.

4.2. Concordance between Lasso and PANPRS

For a set of M SNPs and a quantitative trait, we assume $y_i={\sum }_{k=1}^M{\beta }_k{g}_{ik}+{\epsilon }_i$. For a given λ, we assume $B^0(\lambda )=\left({\beta }_1^0,\cdots ,{\beta }_M^0\right)$ to be the estimates of the effect sizes based on the standard Lasso using individual level data. Similarly, we denote $B^1(\lambda )=\left({\beta }_1^1,\cdots ,{\beta }_M^1\right)$ as the estimates based on the PANPRS. We investigate the concordance between $B^0(\lambda )$ and $B^1(\lambda )$. Phenotypic values were simulated conditioning on the genotype data in the lung cancer GWAS.

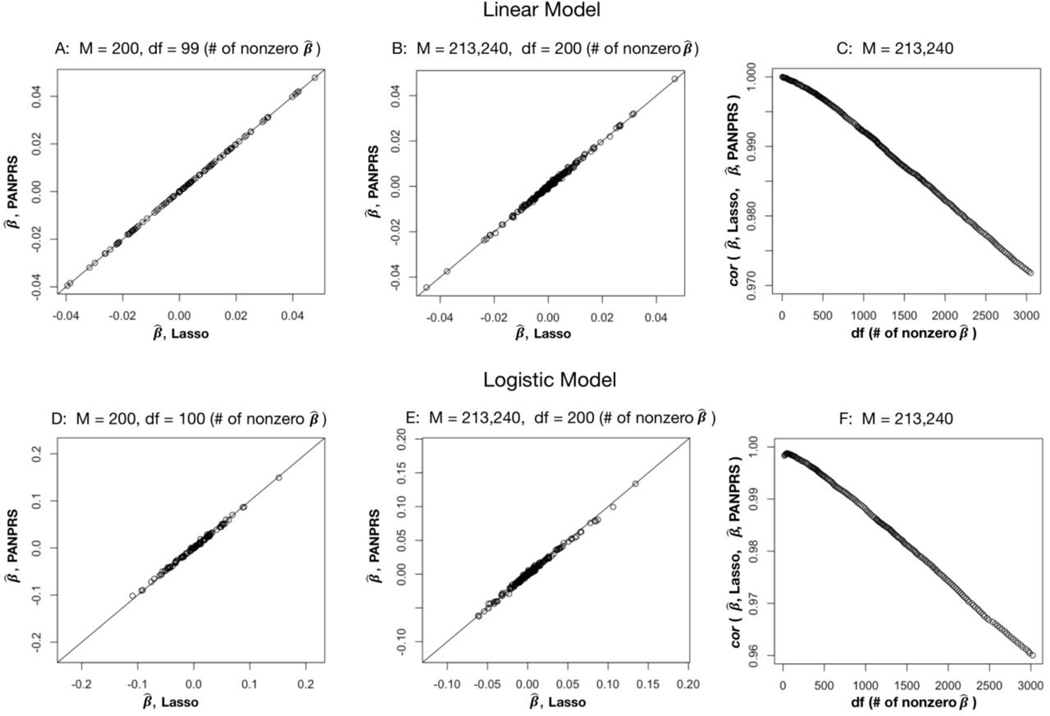
In the first numerical experiment, we generated data using M = 200 SNPs in a region selected from the first chromosome. Because of the small number of SNPs, the full LD matrix can be calculated and incorporated for PANPRS. In this scenario, $B^0(\lambda )$ and $B^1(\lambda )$ were nearly identical (Figure 1A). In the second experiment, we used M = 213,240 SNPs on the 22 autosomal chromosomes after LD-pruning with pairwise r² = 0.5. We randomly selected 500 causal SNPs to generate phenotypic values. For this experiment, we adjusted only the local LD for PANPRS. Results show that $B^0(\lambda )$ and $B^1(\lambda )$ were highly concordant for sparse models (Figures 1B and 1C) and reasonably concordant for dense models (Figure 1C). For PRS in real GWAS, the prediction models are typically sparse with several thousand SNPs at most; thus, we expect $B^0(\lambda )$ and $B^1(\lambda )$ to be highly concordant.

Figure 1.

Concordance between Lasso and PANPRS. Figures A, B and C are for a quantitative trait (linear regression). Figures D, E and F are for a binary trait (logistic regression). For Figures A, B, D and E, the x-coordinate is the β values based on Lasso with individual level data; the y-coordinate is the β values estimated based on PANPRS. For Figures C and F, the x-coordinate is the number of nonzero estimates of regression coefficients of Lasso model; the y-coordinate is the correlation between the β values estimated based on Lasso and PANPRS. Figure A and D: Numerical experiment for M = 200 SNPs on chromosome 1. Df denotes the number of non-zero coefficients in Lasso estimates. Figures B and E: Numerical experiment for M = 213,240 SNPs.

Next, we performed numerical experiments for binary traits. Because PANPRS only provides an approximation to Lasso for logistic regression (see Section 3), we do not expect $B^0(\lambda )$ and $B^1(\lambda )$ to be identical even when the full LD matrix is adjusted (when M = 200 SNPs were used; Figure 1D). In fact, results for binary traits are very similar to those for quantitative traits. In particular, for sparse models, $B^0(\lambda )$ and $B^1(\lambda )$ are highly concordant even when we only adjusted for local LD instead of the full LD matrix. Results are in Figures 1E and 1F.

4.3. Performance comparison of PRS methods for one phenotype

We partitioned the genome into segments of 1 Mb. Let M₁ be the number of causal SNPs. We randomly selected M₁/20 segments and selected 20 SNPs as causal SNPs for each segment. This procedure selected M₁ causal SNPs (denoted as V) to maintain modest LD. A quantitative trait was simulated as $y_i={\sum }_{k\in V}{\beta }_k{g}_{ik}+{\epsilon }_i$ with ${\beta }_k\sim N\left(0,{\sigma }^2\right)$. The heritability is calculated as $h^2={\sum }_{i,j\in V}{\beta }_i{\beta }_j{\rho }_{ij}$ with ${\rho }_{ij}$ being the correlation between two SNPs. In all simulations, we set the residue variance $Var\left({\epsilon }_i\right)=0.5$ and chose ${\sigma }^2$ numerically to have h² = 0.5. We performed two sets of simulations with either M₁ = 1250 or 2500 causal SNPs. Because of the fixed heritability 50%, the effect sizes are stronger with M₁ = 1250 causal SNPs compared to the setting with 2500 causal SNPs.

For each simulation, we randomly selected 8,424 (out of 11,924) subjects as the training data set to generate GWAS summary data, randomly selected 1750 subjects for choosing the tuning parameter and used the remaining 1750 subjects as the validation data set to calculate R², the fraction of phenotypic variance explained by the PRS.

We compared the performance of PANPRS to three previously published methods: p-value thresholding after LD-clumping [8] (denoted as PT), PT coupled with winner’s curse correction [10] (denoted as PTWC) and LD-Pred [9]. The PT method defines PRS as $PR{S}_i\left(p_0\right)=\sum {\tilde{\beta }}_j{g}_{ij}I\left(P_j<p_0\right)$, where ${\tilde{\beta }}_j$ is the marginal regression coefficient and P_j is the p-value for SNP j in the training data set. The threshold p₀ is chosen based on a validation data set. PTWC replaces ${\tilde{\beta }}_j$ with a version that reduces the bias due to the winner’s curse caused by the selection event $P_j<p_0$ LD-Pred uses summary statistics and external LD information to infer the posterior distribution of effect sizes to build PRS. For each setting, we performed 200 simulations. The simulation results are summarized in Table 1. Given heritability h² = 0.5, the number of causal SNPs has a huge impact on the predictive performance for all PRSs, which is concordant with our previous findings [1]. The PT method performed poorly compared to other methods. This is expected because all three other methods correct for winner’s curse implicitly or explicitly [10]. PTWC, LD-Pred and PANPRS performed similarly. Supplementary Tables 1 and 2 summarize the statistical significance of comparing each pair of methods.

Table 1:

Compare performance of four PRS methods. Reported are the prediction R² and the standard deviation in parenthesis. M₁ is the number of causal SNPs. Heritability h² = 50% in all simulations.

	M1 = 1250	M1 = 2500
PT	9.92% (0.08%)	3.60% (0.05%)
LD-Pred	11.69% (0.10%)	4.48% (0.06%)
PTWC	11.77% (0.08%)	4.56% (0.06%)
PANPRS	11.53% (0.08%)	4.89% (0.06%)

4.4. Improving risk prediction by incorporating functional annotation data

In simulations, 70% of SNPs are set not to belong to any annotation category; 15%, 10% and 5% of SNPs (randomly selected) are annotated with one, two and three functional categories, respectively. The motivation of the simulations is that functional SNPs are more likely to be enriched for truly associated SNPs. For the M₁ causal SNP to be selected, we denote p_j as the proportion of causal SNPs annotated with j functional categories. Here, ${\sum }_{i=0}^3{p}_i=1$ and $p_0$ is the proportion of causal SNPs not annotated with any functional category. In simulations, we set $\left(p_0,p_1,p_2,p_3\right)=(20\text{\%},30\text{\%},30\text{\%},20\text{\%})$. For example, 20% of simulated causal SNPs are annotated with three functional annotations. Comparing this distribution to (70%, 15%, 10%, 5%) suggests that SNPs annotated with functional annotations are enriched for causal SNPs, with enrichment fold change 2, 3 and 4, respectively. Thus, SNPs annotated with more functional categories are more likely to be associated with the trait. Simulation results are summarized in Table 2 and Supplementary Tables 1 and 2. Incorporating functional data improved R² from 11.53% to 13.10% for M₁ = 1250 and from 4.89% to 6.27% for M₁ = 2500.

Table 2:

Improve the performance of PANPRS by incorporating multiple functional annotation data and modelling secondary traits that are genetically related with the primary trait. Reported are the prediction R² and the standard deviation in parenthesis.

			M1 = 1250b		M1 = 2500b
			Incorporating multiple annotation data
		K a	NO	Yes	NO	Yes
No secondary traits		0	11.53%e	13.10%	4.89%	6.27%
			(0.08%f)	(0.08%)	(0.07%)	(0.07%)
With secondary traits	γ = 0.3c	2	12.69%	14.10%	5.31%	6.58%
			(0.08%)	(0.09%)	(0.07%)	(0.07%)
	ρ = 0.5d	4	13.71%	15.02%	5.56%	6.78%
			(0.09%)	(0.09%)	(0.07%)	(0.07%)
	γ = 0.3	2	13.63%	15.03%	5.42%	6.70%
			(0.09%)	(0.09%)	(0.07%)	(0.07%)
	ρ = 0.8	4	14.63%	15.88%	5.87%	7.16%
			(0.09%)	(0.09%)	(0.07%)	(0.07%)
	γ = 0.7	2	12.51%	13.58%	5.74%	7.07%
			(0.09%)	(0.10%)	(0.07%)	(0.07%)
	ρ = 0.5	4	14.18%	15.64%	6.16%	7.42%
			(0.09%)	(0.09%)	(0.07%)	(0.07%)
	γ = 0.7	2	13.31%	14.17%	6.38%	7.53%
			(0.09%)	(0.09%)	(0.07%)	(0.07%)
	ρ = 0.8	4	15.02%	16.26%	7.45%	8.41%
			(0.09%)	(0.09%)	(0.07%)	(0.07%)

^a:The number of secondary traits that are genetically related with the primary trait.

^b:The number of causal SNPs.

^c:The fraction of causal SNPs shared between the primary and the secondary traits

^d:The correlation between the effect sizes for the causal SNPs shared by the primary and the secondary traits

^ePrediction R² of PRS

^fEstimated standard deviation of R².

4.5. Improving risk prediction by modelling pleiotropy

We performed simulations for one quantitative trait (the primary trait) and K (K = 2, 4) secondary quantitative traits that share genetic component with the primary trait. The goal is to assess the efficiency gain by incorporating the information of secondary traits. We assumed the same number (M₁) of causal SNPs for all traits. For each secondary trait, we assumed that this trait and the primary trait shared $\gamma M_1$ causal SNPs. Two traits share no genetic component if γ = 0. We set γ = 0.3 and 0.7 in simulations. For a causal SNP shared by two traits, we let ρ as the correlation between the effect sizes. We set ρ = 0.6 and 0.8 in simulations. Results are based on 200 sets of simulations.

Simulation results are summarized in Table 2 and Supplementary Tables 3-10. As expected, modelling pleiotropy improves PRS prediction. The extent of improvement is positively associated with the number of secondary traits and the strength of shared genetic component characterized by γ and ρ. Furthermore, the method incorporating both functional annotation and pleiotropic information has the best performance. As a numerical example, when M₁ = 1250, γ = 0.7, ρ = 0.8 and K = 4 (the number of secondary traits), PANPRS improved R² from 11.53% to 15.02% when modelling pleiotropy and further improves R² to 16.26% when incorporating functional annotation data.

5. Real Data Analysis

5.1. Type-2 diabetes polygenic risk prediction

Type-2 diabetes (T2D) is a complex disease affecting about 8.5% population with age ≥ 18 worldwide. The heritability of T2D has estimated to range from 20% to 80% based on different populations and study designs. GWAS has identified and replicated more than 100 SNPs, that together explain a small fraction of the heritability [29, 30]. Even based on very large GWAS training datasets, the PRS based on established T2D SNPs typically can only explain approximately 2% of the phenotypic variance at the observational scale [30]. We analyzed a large scale T2D GWAS to compare the performance of different PRS methods. Our analyses were based on two T2D GWAS datasets: the DIAGRAM (DIAbetes Genetics Replication And Meta-analysis) consortium with 12,171 cases and 56,862 controls; the GERA (Genetic Epidemiology Research on Adult Health and Aging) study with 7131 cases and 49,747 controls. The training dataset included the DIAGRAM data and a randomly selected fraction of GERA samples (3631 cases and 46247 controls), which were meta-analyzed to create the summary statistics. For all methods, we randomly split the remaining 3500 cases and 3500 controls from GERA and used the first half to choose optimal tuning parameters and the second to assess model performance. The final R² for each method was the average of 500 random splits.

We used three functional annotation data sets to prioritize causal SNPs in the PRS: a blood cis-eQTL data combining two large-scale eQTL studies [31, 32], the histone mark H3K4me3 in the pancreatic islet cell line and methylation QTLs (meQTLs) based on adipose tissues [33]. A SNP was considered as functional if the SNP or its LD SNP (r² ≥ 80%) is a cis-QTL SNP, a meQTL SNP, or located in one of the H3K4me3 peak regions. We observed that SNPs annotated with these functional features are strongly enriched with T2D GWAS signals, suggesting the potential of improving PRS using these functional annotation features. More details can be found in our previous paper [10].

To further improve PRS prediction, we used the GWAS summary statistics from 16 T2D related traits as the secondary traits. The data for body mass index and waist circumference were downloaded from the GIANT consortium website. The data for glycaemic traits including Stumvoll Insulin Sensitivity Index, fasting glucose, fasting insulin, indices of β-cell function (HOMA-B) and insulin resistance (HOMA-IR), HbA1c, fasting proinsulin values, 2-hour glucose and 6 traits for insulin secretion were downloaded from the MAGIC (the Meta-Analyses of Glucose and Insulin-related traits Consortium) website. The quantile-quantile plot in Supplementary Figure S1 demonstrated that genetic signals of these traits were strongly enriched for T2D associations, suggesting the shared genetic component between these traits and T2D.

The overlapping SNPs with minor allele frequencies ≥ 5% for T2D and the 16 secondary traits were extracted for analysis. The set of the regression coefficients of each trait was standardized by the Z scores and sample sizes so that the coefficients are comparable across multiple traits. This step is important for modelling pleiotropic effects when studies have different sample sizes.

Prediction R², standard error and 95% confidence intervals (based on 100,000 bootstraps) are summarized in Table 3. Supplementary Table 11 reports the significance of comparing each pair of methods based on bootstrap sampling. The standard PT method had R² = 1.98%. When no functional data or pleiotropic information was used, PANPRS improved R² to 3.25%, similar to PTWC (R² = 3.22%) and LD-Pred (R² =3.18%). Modelling pleiotropy and incorporating multiple functional annotation data led to R² = 4.22%, which was significantly better compared to other methods.

Table 3:

Prediction performance of PRS methods on type 2 diabetes

PRS Methods		R 2	s.e.	95% C.I.
PT		1.98%	0.016%	(1.95%, 2.02%)
PTWC		3.22%	0.020%	(3.19%, 3.26%)
LD-Pred		3.18%	0.021%	(3.14%, 3.23%)
PANPRS	Neither	3.25%	0.020%	(3.21%, 3.29%)
	Pleiotropy	3.48%	0.021%	(3.44%, 3.53%)
	Functional annotation	3.93%	0.022%	(3.89%, 3.97%)
	Pleiotropy & Functional annotation	4.22%	0.024%	(4.17%, 4.27%)

5.2. Polygenic risk prediction for melanoma

We obtained the GWAS summary statistics as the training data set from the Melanoma Meta-Analysis Consortium that included 12,874 cases and 23,203 controls of European ancestry [34]. The individual-level GWAS data for melanoma from the MelaNorstrum consortium [35] were used for choosing tuning parameters and comparing performance. Next, we downloaded the GWAS summary statistics of seven traits (http://www.nealelab.is/uk-biobank) from the UK BioBank project. These traits are known to be genetically related with melanoma: skin color, ease of skin tanning, childhood sunburn occasions, other skin cancers, other malignant neoplasms of skin, carcinoma in situ of skin and other benign neoplasms of skin. In addition, we used two functional data sets related with melanoma biology: SNPs in the DNase I hypersensitive sites (DHSs) of a skin cell line from the ENCODE project and expression QTL SNPs for skin tissues [36].

Similar to the T2D analysis, we randomly partitioned the MelaNorstrum GWAS data 500 times; for each partitioning, we used one half for choosing tuning parameters and the other half to calculate R². Prediction R² (averaged across 500 partitions), standard error and 95% confidence intervals (based on 100,000 bootstraps) are summarized in Table 4. Supplementary Table 12 reports the significance of comparing each pair of methods. We observed similar performance for PANPRS and LD-Pred, which had a better performance than the PT and PTWC methods. Incorporating the information of seven secondary traits and two functional data sets into PANPRS significantly improved R2 from 4.87% to 5.50%.

Table 4:

Prediction performance of PRS methods on melanoma

PRS Methods		R 2	s.e.	95% C.I.
PT		3.88%	0.021%	(3.84%, 3.93%)
PTWC		3.94%	0.022%	(3.90%, 3.99%)
LD-Pred		4.88%	0.024%	(4.82%, 4.92%)
PANPRS	Neither	4.87%	0.025%	(4.84%, 4.93%)
	Pleiotropy	5.26%	0.025%	(5.19%, 5.28%)
	Functional annotation	5.04%	0.025%	(5.00%, 5.09%)
	Pleiotropy & Functional annotation	5.50%	0.032%	(5.41%, 5.54%)

6. Discussion

We developed PANPRS, a comprehensive and flexible statistical framework, for developing polygenic risk score (PRS) prediction models by fitting Lasso regression models using GWAS summary statistics, functional annotation data and genetic pleiotropic. By extensive simulations based on real genotypic data, we show that PANPRS without functional data or genetic pleiotropy performed similarly or better than existing PRS methods and substantially improved PRS prediction when incorporating informative functional annotation data and genetic pleiotropic information. We tested our method in large scale GWAS of T2D and melanoma. Encouragingly, incorporating functional annotation data and modeling pleiotropic information significantly improved prediction performance for both T2D (R² from 3.25% to 4.22%) and melanoma (R² from 4.87% to 5.50%). Notably, compared to the standard PT method that has been frequently used in genetic risk studies, PANPRS improved prediction from R² =1.98% to 4.22% for T2D and from R² =3.88% to 5.50% for melanoma.

Some features of PANPRS are summarized here. First, it applies to both quantitative and binary traits. Second, it produces PRS highly concordant to that based on individual level genotypic and phenotypic data. Third, it can incorporate multiple functional annotation data and multiple secondary traits to boost predictive performance. Fourth, it has the potential to maximize the predictive performance by using GWAS meta-analysis results based on large consortia because it is based on GWAS summary statistics.

Fitting penalized regression models based on GWAS summary statistics has received much attention recently. For example, Mat and colleagues [21] proposed to fit a Lasso regression to build PRS; Ning and collogues [37] proposed to fit a Lasso model to fine map a genomic region. However, both algorithms apply only to quantitative traits based on linear regression. When the marginal association coefficients are derived based on logistic regression analysis, our work provides theoretical justifications of using these algorithms.

In the current manuscript, we have evaluated the performance of PRS methods using criteria that reflect how much of the phenotypic variance can be explained by the PRS in the validation dataset. To apply PRS prediction models to clinical settings, it will be important to calibrate the model to produce an unbiased estimate of risk for individuals with different SNP profiles, which can be done by a simple regression analysis based on a relatively small validation sample. Moreover, even a modest improvement in prediction may be clinically meaningful by identifying more subjects at risk in a population. As an example, by incorporating functional annotation and GWAS of 16 traits that are genetically related with T2D, PANPRS improved R² from 3.25% to 4.22% for T2D. We calculated that 1.89% and 3.0%, respectively, of the population will be identified to have 2-fold risk for developing T2D compared to the general population. The difference is more prominent when screening for subjects with higher risk.

Finally, we point out some limitations and future directions. First, theoretical and empirical work are needed to automatically decide whether and how to best incorporate functional annotation data. Quantile-quantile plots are helpful for choosing informative functional annotation data [10]. Second, including many traits genetically unrelated with the primary trait may reduce PRS performance. Thus, additional work is needed to explicitly model shared genetic architecture between the primary trait and the multiple secondary traits, which may be useful to provide guidance to identify secondary traits and to best incorporate them into the PANPRS framework. Third, like most other methods, our method needs an independent GWAS data set to choose optimal tuning parameters. We have recently developed a method for accurately approximating the area under the ROC curve of a PRS model based on GWAS summary statistics [38] of an independent data set. Thus, we may choose tuning parameters using summary statistics that are publicly available (e.g., UK Biobank project and BioBank Japan project). In addition, we have r + 3 tuning parameters when there are r functional categories; thus, it is computationally expensive to run the grid search algorithm to search for the optimal tuning parameters. Finally, the performance of PANPRS depends on many factors, including the genetic architecture of the disease, the quality of the functional annotation data, the shared genetic architecture with secondary traits and the sample size of the training data set. To successfully apply PANPRS to other complex diseases, key steps will be to identify informative functional annotations and GWAS summary statistics of secondary traits that are genetically related with the primary trait.

Appendix: PANPRS for a binary trait

Fitting I₁ regularized logistic regression using individual level data

Let y_i be a binary phenotypic value with y_i = 1 representing a case. Let $\mathit{Y}={\left(y_1,\cdots ,y_n\right)}^T$ and X denote the genotype matrix for n subjects and M SNPs. Let $\mathit{\beta }={\left({\beta }_1,\cdots ,{\beta }_M\right)}^T$ denote the effect sizes for M SNPs and ${\beta }_0$ be intercept. Given β and β₀, we define

$${\pi }_i\left({\beta }_0,\mathit{\beta }\right)=P\left(y_i=1\mid x_{i1},\cdots ,x_{iM}\right)=\frac{e^{{\beta }_0+{\sum }_{j=1}^M{x}_{ij}{\beta }_j}}{1+e^{{\beta }_0+{\sum }_{j=1}^M{x}_{ij}{\beta }_j}}.$$ (A1)

When individual level data are available, one can obtain a regularized estimate of β by minimizing

$$U_0\left({\beta }_0,\mathit{\beta }\right)=-{\sum }_{i=1}^n\left[y_i\log {\pi }_i+\left(1-y_i\right)\log \left(1-{\pi }_i\right)\right]+{\sum }_{j=1}^M\lambda \left|{\beta }_j\right|$$ (A2)

using the coordinate descent algorithm proposed for non-convex penalty functions [27], which we describe here. Let $\left({\widehat{\beta }}_0^{(t)},{\widehat{\mathit{\beta }}}^{(t)}\right)$ be the coefficients at the t^th iteration. Let $\mathbf{1}={(1,\dots ,1)}^T$ be a vector of length n. Let ${\widehat{\pi }}_i^{(t)}$ denote the probability (13) calculated at $\left({\widehat{\beta }}_0^{(t)},{\widehat{\mathit{\beta }}}^{(t)}\right)$ and ${\widehat{\mathit{\pi }}}^{(t)}={\left({\widehat{\pi }}_1^{(t)},\cdots ,{\widehat{\pi }}_n^{(t)}\right)}^T$.

The iteratively reweighted least squares algorithm [39] is used based on a quadratic approximation of the likelihood function (A2) by the Taylor’s expansion at ${\widehat{\mathit{\beta }}}^{(t)}$:

$$U_1\left({\beta }_0,\mathit{\beta }\right)=\frac{1}{2n}{\left({\tilde{\mathit{Y}}}^{(t)}-\left(\mathbf{1}\cdot {\beta }_0+\mathit{X}\mathit{\beta }\right)\right)}^T{\widehat{\mathit{W}}}^{(t)}\left({\tilde{\mathit{Y}}}^{(t)}-\left(\mathbf{1}\cdot {\beta }_0+\mathit{X}\mathit{\beta }\right)\right)+{\sum }_{j=1}^M\lambda \left|{\beta }_j\right|.$$

Here, ${\widehat{\mathit{W}}}^{(t)}$ is an n × n diagonal matrix with element ${\widehat{w}}_i^{(t)}={\widehat{\pi }}_i^{(t)}\left(1-{\widehat{\pi }}_i^{(t)}\right)$ and ${\tilde{\mathit{Y}}}^{(t)}=\mathbf{1}$. ${\widehat{\beta }}_0^{(t)}+\mathit{X}{\widehat{\mathit{\beta }}}^{(t)}+{\left({\widehat{\mathit{W}}}^{(t)}\right)}^{-\mathbf{1}}\left(\mathit{Y}-{\widehat{\mathit{\pi }}}^{(t)}\right)$.

Let ${\mathit{X}}_j$ denote the j^th column of X and ${\mathit{X}}_{-j}$ be the submatrix of X without the j^th column. By letting

$$\frac{\partial }{\partial {\beta }_j}{U}_1\left({\beta }_j\mid {\widehat{\mathit{\beta }}}_{-j}^{(t)}\right)=\frac{1}{n}{\mathit{X}}_j^T{\widehat{\mathit{W}}}^{(t)}\left({\tilde{\mathit{Y}}}^{(t)}-\mathbf{1}\cdot {\widehat{\beta }}_0^{(t)}-{\mathit{X}}_{\mathbf{-}\mathit{j}}{\widehat{\mathit{\beta }}}_{-j}^{(t)}-X_j{\widehat{\beta }}_j^{(t)}\right)+\frac{\partial }{\partial {\beta }_j}\lambda \left|{\beta }_j\right|=0,$$

we can update ${\beta }_j$ as

$${\widehat{\beta }}_j^{(t+1)}=\{\begin{array}{ll}0& \text{if}\left|z_j^{(t)}\right|\le \lambda \\ \mathrm{sgn}\left(z_j^{(t)}\right)\left|\right|z_j^{(t)}|-\lambda |& \text{if}\left|z_j^{(t)}\right|>\lambda ,\end{array}$$ (A3)

where

$$z_j^{(t)}=\frac{{\mathit{X}}_j^T{\widehat{\mathit{W}}}^{(t)}\left({\tilde{\mathit{Y}}}^{(t)}-\mathbf{1}\cdot {\widehat{\beta }}_0^{(t)}\right)-{\mathit{X}}_j^T{\widehat{\mathit{W}}}^{(t)}{\mathit{X}}_{-\mathit{j}}{\widehat{\mathit{\beta }}}_{-\mathit{j}}^{(t)}}{{\mathit{X}}_j^T{\tilde{\mathit{W}}}^{(\mathit{t})}{\mathit{X}}_j}=a_j^{(t)}-b_j^{(t)}.$$ (A4)

Here,

$$a_j^{(t)}=\frac{{\mathit{X}}_j^T{\widehat{\mathit{W}}}^{(t)}\left({\tilde{\mathit{Y}}}^{(t)}-\mathbf{1}\cdot {\widehat{\beta }}_0^{(t)}\right)}{{\mathit{X}}_j^T{\widehat{\mathit{W}}}^{(t)}{\mathit{X}}_j}$$ (A5)

and

$$b_j^{(t)}=\frac{{\mathit{X}}_j^T{\widehat{\mathit{W}}}^{(t)}{\mathit{X}}_{-j}{\widehat{\mathit{\beta }}}_{-j}^{(t)}}{{\mathit{X}}_j^T{\widehat{\mathit{W}}}^{(\mathit{t})}{\mathit{X}}_j},$$ (A6)

Remark.

The intercept β₀ is not penalized. We can update β₀ using the rule in (A3) assuming λ = 0. More explicitly, we update β₀ as ${\mathbf{1}}^T{\widehat{\mathit{W}}}^{(t)}\left({\tilde{\mathit{Y}}}^{(t)}-\mathit{X}{\mathit{\beta }}^{(t)}\right)/{\mathbf{1}}^T{\widehat{\mathit{W}}}^{(t)}\mathbf{1}$.

Fitting I₁ regularized logistic regression using GWAS summary level data

The key step of fitting an l₁ regularized logistic regression model is to calculate $Z_j^{(t)}$ in (A4) for each iteration, which requires to approximate $a_j^{(t)}$ and $b_j^{(t)}$ using GWAS summary data.

We first approximate $b_j^{(t)}$ in (A6). Remember that ${\widehat{w}}_i^{(t)}={\widehat{\pi }}_i^{(t)}\left(1-{\widehat{\pi }}_i^{(t)}\right)$ for subject i in the t^th iteration, where ${\widehat{\pi }}_i^{(t)}$ is calculated based on (A1) at $\left({\beta }_0^{(t)},{\mathit{\beta }}^{(t)}\right)$. We here make an approximation that ${\widehat{w}}_i^{(t)}=w_0$ for all n subjects so that ${\widehat{\mathit{W}}}^{(t)}=w_0\mathit{I}$ with I being the identity matrix of n × n. This approximation is accurate when the resulting PRS is sparse and explains a small fraction of phenotypic variance, which is satisfied for most of complex diseases with current sample sizes. With this approximation, ${\mathit{X}}_j^T{\widehat{\mathit{W}}}^{(\mathit{t})}{\mathit{X}}_j=w_0{\mathit{X}}_j^T{\mathit{X}}_j=w_{0}n$ because X_j is standardized. Thus, $b_j^{(t)}$ in (A6) can be derived as

$$b_j^{(t)}\approx \frac{{\sum }_{i=1}^n{\sum }_{l\ne j}\left\{x_{ij}{\widehat{w}}_i^{(t)}{x}_{il}{\widehat{\beta }}_l^{(t)}\right\}}{w_{0}n}={\sum }_{l\ne j}\left(\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}{x}_{il}\right){\widehat{\beta }}_l^{(t)}={\sum }_{l\ne j}{\widehat{\rho }}_{jl}{\widehat{\beta }}_l^{(t)},$$ (A7)

where ${\widehat{\rho }}_{jl}=\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}{x}_{il}$ is the estimated correlation between SNP j and SNP l. Let A_j denote the set of neighboring SNPs for SNP j. For SNPs not in A_j, we set ${\widehat{\rho }}_{jl}=0$. Thus, (19) can be further approximated as

$$b_j^{(t)}\approx {\sum }_{l\in A_j}{\widehat{\rho }}_{jl}{\widehat{\beta }}_l^{(t)}.$$ (A8)

Now we process $a_j^{(t)}$ in (A5). Let ${\tilde{\beta }}_j$ be the univariate logistic regression coefficient for SNP j. To proceed, we review the algorithm to derive ${\tilde{\beta }}_j$ for SNP j using the iteratively reweighted least squares algorithm. We first introduce notations for the univariate model with SNP j only, denoted by $\cdot \mid j$. For the t^th iteration, let ${\tilde{\mathit{Y}}}_{\cdot \mid j}^{(t)}=\mathbf{1}\cdot {\widehat{\beta }}_0^{(t)}+{\mathit{X}}_j{\widehat{\beta }}_j^{(t)}+{\left({\widehat{\mathit{W}}}_{\cdot \mid j}^{(t)}\right)}^{-\mathbf{1}}\left(\mathit{Y}-{\widehat{\mathit{\pi }}}_{\cdot \mid j}^{(t)}\right)$, where ${\widehat{\mathit{W}}}_{\cdot \mid j}^{(t)}$ is a diagonal matrix with element ${\widehat{w}}_{i\mid j}^{(t)}={\widehat{\pi }}_{i\mid j}^{(t)}\left(1-{\widehat{\pi }}_{i\mid j}^{(t)}\right)$ and ${\widehat{\mathit{\pi }}}_{\cdot \mid j}^{(t)}={\left({\widehat{\pi }}_{1\mid j}^{(t)},\cdots ,{\widehat{\pi }}_{n\mid j}^{(t)}\right)}^T$. With these notations, the cost function at the t^th iteration is given as

$$L\left({\beta }_0,{\beta }_j\right)=\frac{1}{2n}{\left({\tilde{\mathit{Y}}}_{\cdot \mid j}^{(t)}-\left(\mathbf{1}\cdot {\beta }_0+{\mathit{X}}_j{\beta }_j\right)\right)}^T{\widehat{\mathit{W}}}_{\cdot \mid j}^{(t)}\left({\tilde{\mathit{Y}}}_{\cdot \mid j}^{(t)}-\left(\mathbf{1}\cdot {\beta }_0+{\mathit{X}}_j{\beta }_j\right)\right).$$

By letting $\frac{\partial }{\partial {\beta }_j}{L}_n\left({\beta }_0,{\beta }_j\right)=0$, we can update ${\beta }_j$ by

$${\widehat{\beta }}_j^{(t+1)}=\frac{{\mathit{X}}_j^T{\widehat{\mathit{W}}}_{\cdot \mid j}^{(t)}\left({\tilde{\mathit{Y}}}_{\cdot \mid j}^{(t)}-\mathbf{1}\cdot {\widehat{\beta }}_0^{(t)}\right)}{{\mathit{X}}_j^T{\widehat{\mathit{W}}}_{\cdot \mid j}^{(t)}{\mathit{X}}_j}$$ (A9)

until convergence to obtain ${\tilde{\beta }}_j$.

Note that $a_j^{(t+1)}$ in (A5) for the full model and the updating rule (A9) for univariate model have similar expression except for the difference between the diagonal weight matrices ${\widehat{\mathit{W}}}^{(\mathit{t})}$ and ${\widehat{\mathit{W}}}_{\cdot \mid j}^{(t)}$ and that between residues ${\tilde{\mathit{Y}}}^{(t)}$ and ${\tilde{\mathit{Y}}}_{\cdot \mid j}^{(t)}$. When other SNPs have small effects on y_i, we expect the difference between ${\widehat{\mathit{W}}}^{(t)}$ and ${\widehat{\mathit{W}}}_{\cdot \mid j}^{(t)}$ and the difference between ${\tilde{\mathit{Y}}}^{(t)}$ and ${\tilde{\mathit{Y}}}_{\cdot \mid j}^{(t)}$ to be small, which suggests using ${\beta }_j^{(t+1)}$ in (A9) to approximate $a_j^{(t+1)}$. Because ${\beta }_j^{(t+1)}$ in univariate logistic regression is unavailable, we propose to use ${\tilde{\beta }}_j$ (the converged value of ${\beta }_j^{(t+1)}$ to approximate $a_j^{(t+1)}$. This proposal may not be accurate in the beginning of the algorithm but may provide a reasonable approximation when the algorithm is near convergence. Combining this argument together with the approximation in (A8), we calculate $Z_j^{(t)}$ in (A4) as

$$z_j^{(t)}\approx {\tilde{\beta }}_j-{\sum }_{l\in A_j}{\widehat{\rho }}_{jl}{\widehat{\beta }}_l^{(t)}.$$ (A10)