Leaf size estimation based on leaf length, width and shape

Abstract

Background and Aims

Leaf size has considerable ecological relevance, making it desirable to obtain leaf size estimations for as many species worldwide as possible. Current global databases, such as TRY, contain leaf size data for ~30 000 species, which is only ~8% of known species worldwide. Yet, taxonomic descriptions exist for the large majority of the remainder. Here we propose a simple method to exploit information on leaf length, width and shape from species descriptions to robustly estimate leaf areas, thus closing this considerable knowledge gap for this important plant functional trait.

Methods

Using a global dataset of all major leaf shapes measured on 3125 leaves from 780 taxa, we quantified scaling functions that estimate leaf size as a product of leaf length, width and a leaf shape-specific correction factor. We validated our method by comparing leaf size estimates with those obtained from image recognition software and compared our approach with the widely used correction factor of 2/3.

Key Results

Correction factors ranged from 0.39 for highly dissected, lobed leaves to 0.79 for oblate leaves. Leaf size estimation using leaf shape-specific correction factors was more accurate and precise than estimates obtained from the correction factor of 2/3.

Conclusion

Our method presents a tractable solution to accurately estimate leaf size when only information on leaf length, width and shape is available or when labour and time constraints prevent usage of image recognition software. We see promise in applying our method to data from species descriptions (including from fossils), databases, field work and on herbarium vouchers, especially when non-destructive in situ measurements are needed.

INTRODUCTION

Leaf functional traits, such as leaf size, mass and longevity, link to variation in plant ecological strategies and connect to ecosystem functioning (Westoby et al., 2002). Among leaf traits, the size of a leaf has special significance. There is around 10⁶ variation among species in average leaf size, from ~1 mm² to 1 m², with many large-leaved species found in the tropics and many small-leaved species found in deserts and at high elevation and high latitudes (Wright et al., 2017; Baird et al., 2021). In general, species with larger leaves have longer internodes, larger flowers and thicker twigs (Westoby and Wright 2003), and deploy a larger total leaf area per branch (Preston and Ackerly 2003) – and thus have visual and physical properties distinct from small-leaved species. Leaf size also affects leaf temperature and thus photosynthesis, transpiration and respiration (Leigh et al., 2017). A variety of advantages and disadvantages of larger leaves have been proposed. For example, larger leaves may be more efficient in light capture under deep shade (Lusk et al., 2019), and achieve higher lifetime economic profitability (Villar et al., 2021). However, larger leaves may be more susceptible to herbivory and have higher within-leaf support costs (Niinemets et al., 2006). A number of leaf venation properties also vary predictably with leaf size (Sack et al., 2012; Baird et al., 2021). For all these reasons, leaf size is a key element of numerous studies on plant functional ecology. Its considerable ecological relevance makes it desirable to obtain leaf size estimations for as many species worldwide as possible.

Obtaining accurate and precise measures of leaf size across large cohorts of species is often time- and labour-intensive. Standard methods are based on image recognition software that require scans or images of (nearly) complete leaves (Pérez-Harguindeguy et al., 2013). While these methods are highly accurate and precise, in situ measurements can be challenging (Schrader et al., 2017). In addition, for most species, no high-quality images of leaves exist, rendering image-based methods unfeasible for large-scale gap fillings. Even as more digital imagery of leaves becomes available from large-scale digitization efforts in herbaria globally, a robust approach to estimating leaf size based on leaf dimensions remains overdue.

Allometric scaling functions using leaf dimensions provide an alternative method to image recognition software for leaf size estimation (Shi et al., 2019a). Allometric scaling functions are based on the observation that other leaf dimensions scale with leaf size, such as leaf length, width or mass (Bartelink, 1997; Pandey and Singh, 2011; Yu et al., 2020). Allometric scaling functions have the advantage of allowing us to deduce leaf size from easily measured leaf dimensions – which are often available from pre-existing species descriptions – without use of image recognition software.

Among different leaf allometric relationships, functions involving the product of leaf length and width are superior estimators for leaf size estimation to functions considering just one linear dimension (Shi et al., 2019a; Yu et al., 2020). Thus, the product of leaf length (L) and width (W) defines the area of a rectangle enclosing the leaf. Consequently, as most leaves are not rectangular in shape, the product of leaf length and width alone leads to an overestimation of leaf size, and the extent of overestimation depends on leaf shape (Cain and De Oliveira Castro, 1959).

Cain and De Oliveira Castro (1959) showed that L × W × 2/3 provided a robust estimate of leaf size for ovate leaves in Brazilian rainforest, describing the 2/3 value as the correction factor (CF, hereafter). Depending on leaf shape, they showed that the CF differed between 0.61 and 0.78. Dolph (1977) continued this line of research, calculating a CF for 18 species with different leaf shapes and reported CF values ranging from 0.51 for a pinnatisect leaf to 0.87 for an obovate leaf and noted that small leaves had a higher CF because they were more often rectangular in shape. Applying a CF of 2/3 resulted in significant bias in both leaf size over- and underestimation for 12 out of 18 leaves, with leaf size overestimated for dissected, lobed and dentate leaves and underestimated for rounded, cordate and small leaves (Dolph, 1977).

Leaf shapes are unevenly distributed globally. Leaves from wet and tropical climates are less dissected and more elliptical in shape, whereas leaves in cold climates are more dissected (Royer et al., 2005; Peppe et al., 2011). This implies that, especially in temperate regions, using a CF of 2/3 would result in biased leaf size estimation for many species. In addition, leaf shape can also be taxonomically constrained, meaning that closely related species share similar leaf morphologies (Givnish, 1987; Peppe et al., 2011). This would lead to an over- or underestimation for certain taxa using a CF of 2/3. In contrast, knowing whether and how the CF differs with leaf shape would enable accurate predictions of leaf size based on leaf length and width (Shi et al., 2019a). Despite the strong dependency of CF on leaf shape, the CF of 2/3 proposed by Cain and De Oliveira Castro (1959) to estimate leaf size is still used as a rule-of-thumb in many studies today (e.g. Cristofori et al., 2007; Merkhofer et al., 2015; Wright et al., 2017; Li et al., 2020). However, a unifying framework to estimate leaf size based on leaf shape, length and width regardless of species identity has not been developed.

Here, we tested whether leaf shape-specific CFs are suitable to accurately estimate leaf size. We assembled a globally representative dataset including all major leaf shapes, as well as a variety of other leaf morphologies. First, we measured leaf size, length and width using image recognition software and then calculated a CF for each leaf. Second, we developed a definition for different leaf shapes based on three distinct classification schemes that hierarchically build on each other. Third, we grouped all leaves according to their shape and estimated a CF for each shape, resulting in a leaf shape-specific CF. Fourth, as leaf shape may also be taxonomically constrained, we tested whether taxonomic relatedness affected the CF. Fifth, we compared the accuracy and precision of leaf shape- and family-specific CF and tested them against the CF of 2/3 using a test dataset with leaves of known size. Finally, we tested whether leaf base, dentition, symmetry and size class affected the CF.

MATERIAL AND METHODS

We assembled a globally representative dataset of 3125 leaf images from 144 families and 780 species and subspecies covering more than five orders of magnitude in leaf size. We defined leaf size as the one-sided projected area of single leaves or leaflets (Pérez-Harguindeguy et al., 2013). As leaf size and shape differ with climate and biogeographical region (Peppe et al., 2011; Wright et al., 2017), we included leaf samples from 26 countries from all major biomes. For leaf size estimation, we only considered the leaf blade (i.e. petioles and stipules were removed). For compound leaves, single leaflets were treated as analogous to simple leaves with the exception of highly dissected pinnae and fern fronds for which we measured the entire frond (for simplicity we hereafter refer to leaf for both leaves of angiosperms and fern fronds).

We used high-quality images – either as photographs or as scans – of all leaves. Leaf images were compiled from published journal articles (data from journal articles were taken from Royer et al., 2005; Peppe et al., 2011; Shi et al., 2019a, b, 2020, 2021; Schrader et al., 2020; Yu et al., 2020; Huang et al., 2021), or taken by the authors. Images were recorded with different equipment and resolutions for image recording. However, to be included to our final dataset images needed to meet the following criteria: (1) leaves were flattened out on white or black background, (2) no shadows at leaf edges occurred and (3) images were spatially referenced by a scanner or scale. When necessary, the images were manipulated digitally to restore damaged leaf margins and remove shadows (see methods in Peppe et al., 2011; Baumgartner et al., 2020). We calculated leaf size, length and width using the method described by Shi et al. (2019a). That is, we extracted the leaf profile from the photographs using matlab (v.R2009a) and then used the packages spatstat (Baddeley et al., 2015) to adjust leaf profiles and splancs (Bivand et al., 2021) to calculate leaf size, length and width in R (v.4.0.2; R Core Team, 2020).

We defined the leaf length (L) as the longest extension from leaf apex to base (i.e. connection point of leaf blade and petiole). Leaf width (W) corresponds to the longest extension of any two points on the blade edge perpendicular to the leaf length axis, that is the axes connecting leaf apex and base (Shi et al., 2019a; see Fig. 1 for examples).

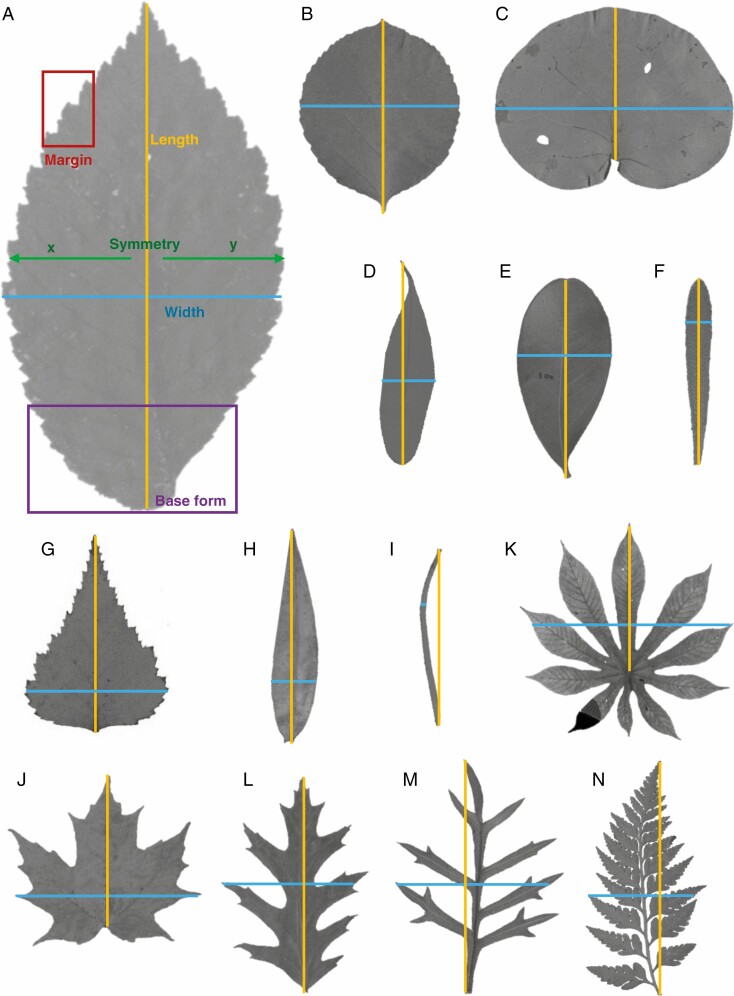
Fig. 1.

Leaves of different shapes. For defintions of leaf shapes see Table 1 and for leaf length, width, base form, medial symmtery and margin type see Material and Methods. Leaf shape names in brackets follow definitions for shape scheme 3. (A) Examples for leaf width (blue), length (orange), base form (pruple), margin type (red) and medial symmtery (green). Species: Ulmus americana (shape: elliptic; base form: complex; margin type: toothed; medial symmetry: asymmeric); (B) Celastrus orbiculatus (orbicular; cuneate; toothed; symmetrical); (C) Coccoloba univera (oblate; protruding; entire; symmetrical); (D) Salix lascandia (oblong; rounded; entire; symmertical); (E) Exocarpos latifolius (obovate; cuneate; entire; symmertical); (F) Suriana maritima (oblanceolate; cunneate; entire; symmetrical); )G) Betula populifolia (ovate; truncate; toothed; symmetrical); (H) Veronica salicifolia (lanceolate; convex; entire; symmetrical); (I) Hakea epiglottis (linear; decurrent; entire; symmetrical); (J) Acer saccharum (palmately lobed; truncate; entire; symmetrical); (K) Cecropia obtusifolia (panatisect; protruding; entire; symmetrical); (L) Quercus palustris (pinnately lobed; concanve; toothed; symmterical); (M) Lomatia silaifolia (pinnatisect; decurrent; entire; symmertical); (N) Davallia solida (fern; complex; entire; symetrical).

We grouped all leaves into five morphological categories described in detail below: leaf shape, leaf base form, margin type, leaf symmetry and size class following Ellis et al. (2009). Examples of leaf shape, base form, margin type and leaf symmetry are provided in Fig. 1.

Leaf shapes

In their influential Manual of Leaf ArchitectureEllis et al. (2009) reduced different leaf shapes to first principles based on laminar shape and lobe type. Here, we used a combination of laminar shape and lobe type, and developed a leaf shape definition based on three distinct shape classification schemes that hierarchically build on each other. This allowed us to also include different and commonly used definitions of leaf shapes (e.g. Stearn, 1966; Zhao et al., 2015) not considered by Ellis et al. (2009). Definitions for all three shape schemes are provided in Table 1, with examples provided in Fig. 1. The three hierarchical shape schemes, from the broadest to the finest, are:

Table 1.

Leaf shapes, definitions, correction factors (CF) and interquartile range (IQR) of CF for three schemes of leaf shapes. Examples correspond to panels in Fig. 1. Leaf shapes and definitions are based on Ellis et al. (2009) (except for highly dissected fern fronds categorized as fern)

Shape scheme 1	CF (IQR)	Definition shape scheme 1	Shape scheme 2	CF (IQR)	Definition shape scheme 2	Shape scheme 3	CF (IQR)	Definition shape scheme 3	Examples
Unlobed	0.69 (0.08)	Leaf has no lobes	Elliptic (sensu lato)	0.70 (0.08)	Unlobed leaf with widest part in the middle one-fifth and L : W < 10 : 1.	Elliptic (sensu stricto)	0.69 (0.07)	Elliptic leaf with L : W between 10 : 1 and 1 : 1.	A
						Orbicular	0.71 (0.09)	Elliptic leaf with L : W from 1.2 : 1.	B
						Oblate	0.79 (0.09)	Elliptic leaf with L : W between 1 : 1 and 1.2 : 1.	C
						Oblong	0.73 (0.06)	Elliptic leaf with opposite margins roughly parallel for at least the middle one-third of leaf.	D
			Obovate (sensu lato)	0.66 (0.07)	Unlobed leaf with widest part in the distal two-fifths.	Obovate (sensu stricto)	0.67 (0.07)	Obovate leaf with the widest part in the distal two-fifths and L : W < 3 : 1.	E
						Oblanceolate	0.64 (0.05)	Obovate leaf with L : W between 3 : 1 and 10 : 1.	F
			Ovate (sensu lato)	0.68 (0.08)	Unlobed leaf with widest part in the proximal two-fifths.	Ovate (sensu stricto)	0.67 (0.06)	Ovate leaf with proximal two-fifths with L : W < 3 : 1.	G
						Lanceolate	0.70 (0.08)	Ovate leaf with L : W between 3 : 1 and 10 : 1.	H
			Linear	0.71 (0.17)	Unlobed leaf with L : W > 10 : 1, regardless of position of widest part of leaf.	Linear	0.71 (0.17)	Same as for shape scheme 2.	I
Lobed	0.53 (0.20)	Leaf has lobes	Palmately lobed (sensu lato)	0.58 (0.17)	Lobed leaf where major veins of lobes are primary veins that arise from leaf base.	Palmately lobed (sensu stricto)	0.61 (0.16)	Palmately lobed leaf with veins reaching to ~2/3 to the petiole.	J
						Palmatisect	0.47 (0.13)	Palmately lobed leaf with incision reaching almost to the petiole but without resulting in distinct leaflets. Includes hastate and deltoid.	K
			Pinnately lobed (sensu lato)	0.53 (0.20)	Lobed leaf where major veins of lobes are formed by costal secondaries.	Pinnately lobed (sensu stricto)	0.55 (0.19)	Pinnately lobed leaf with veins reacching to ~2/3 to the petiole.	L
						Pinnatisect	0.39 (0.19)	Pinnately lobed leaf with incision reaching almost to the midvein but without resulting in distinct leaflets.	M
			Fern	0.41 (0.11)	Highly dissected fern fronds.	Fern	0.41 (0.11)	Same as for shape scheme 2.	N

• •Scheme 1: We grouped all leaves into unlobed or lobed. A lobe is a marginal projection whose apical sinus is incised by >25 % of the distance from the projection apex to the midvein (Ellis et al., 2009). Lobed leaves include highly dissected fern fronds.
• •Scheme 2: We grouped all unlobed leaves into elliptic sensu lato, ovate sensu lato, obovate sensu lato or linear, and all lobed leaves into palmately lobed, pinnately lobed or fern. Deltoid or hastate are often used terms for distinct leaf shapes (e.g. Stearn, 1966), but are categorized as palmately lobed here. Fern summarizes highly dissected fern fronds.
• •Scheme 3: This scheme follows specific definitions provided by Ellis et al. (2009), including ratios of leaf length and width or venation patterns. We grouped all elliptic sensu lato leaves to elliptic sensu stricto, orbicular or oblate; all ovate sensu lato leaves to ovate sensu stricto or lanceolate; all obovate sensu lato leaves to obovate sensu stricto or oblanceolate; all palmately lobed sensu lato leaves to palmately lobed sensu stricto or palmatisect; and all pinnately lobed sensu lato to pinnately lobed sensu stricto or pinnatisect. Highly dissected fronds of ferns were categorized as fern.

Leaf base form

Leaf base forms describe the proximal 25 % of the leaf blade. Ellis et al. (2009) suggested ten leaf base forms that can be difficult to define and probably have no or similar effect on CF estimation (Yu et al., 2020). Therefore, we only defined two categories that divided all leaves into non-protruding and protruding leaf bases. Non-protruding leaf bases had no basal extension (i.e. the leaf blade does not extend below the base). For protruding leaf bases, the leaf blade extended below the base.

Leaf margins

To test whether different leaf margins had an effect on CF estimation, we categorized all leaf margins as either toothed or entire. Leaf margins were toothed when their vascular projection is separated by apical sinuses incised <25 %. Leaf margins without incisions were categorized as entire (Ellis et al., 2009).

Leaf medial leaf symmetry

We visually determined whether a leaf blade was symmetrical or asymmetrical. When a leaf was either medially or basally asymmetrical according to Ellis et al. (2009) we considered them asymmetrical. The medial symmetry is determined by the width ratio from the mid-vein of the leaf. The basal symmetry is determined by the width ratio of the leaf base starting from the connection point of petiole and leaf blade (Ellis et al., 2009).

Leaf size class

Dolph (1977) noted that small leaves often had higher CF than larger leaves. To test this hypothesis, we grouped all leaves into seven size classes according to the Raunkiær–Webb classification (Webb, 1959). These were leptophyll (leaf size <25 mm²), nanophyll (25−225 mm²), microphyll (225−2025 mm²), notophyll (2025−4500 mm²), mesophyll (4500−18 225 mm²) and macrophyll (18 225−164 025 mm²).

Analyses

We randomly divided the dataset into two subsets. The first subset (75 % of all leaves) was used to estimate leaf shape- and family-specific CF. The second subset (25 % of all leaves) was used to compare the accuracy and precision of leaf size estimates using the leaf shape-specific CF, family-specific CF and the CF of 2/3 against leaf size obtained from image recognition software.

To estimate a CF for each individual leaf, we used the formula:

$$CF=\frac{\mathit{\text{leaf size}}}{\mathit{\text{leaf length}}*\mathit{\text{leaf width}}}.$$

Next, we grouped all leaves into the three shape schemes respectively (Table 1). For each leaf shape scheme, we calculated the median (represents the CF) and interquartile range (IQR; measure of the precision) of the CF from the individual leaves. To test whether CF values can be improved by incorporating taxonomic group (i.e. assuming species of the same family have a similar CF), we calculated the median CF as described above for all families in our dataset represented by at least six taxa and ten leaves.

We also calculated the CF for leaf groupings into base form, margin type, medial symmetry and size class following the same procedure. As CF values were normally distributed, we used one sided t-tests to examine whether the leaf shape- and family-specific CF differed significantly compared to the CF of 2/3, which we included as a reference value of the mean.

Using the second subset of data, we estimated leaf size of each leaf applying the CF calculated in the previous step. We then compared the leaf size estimated using the leaf shape- and family-specific CF and the CF of 2/3 respectively against the true leaf size obtained from image recognition software using the formula:

$$\mathit{\text{leaf size}}\left(\mathit{\text{difference}}\right)=\frac{\mathit{\text{leaf size }}(CF)-\mathit{\text{leaf size }}(\mathit{\text{true}})}{\mathit{\text{leaf size }}(\mathit{\text{true}})}.$$

This yielded a ratio indicating the magnitude of deviation between leaf sizes estimated from the CF and from image recognition software (the accuracy). Values <0 indicate underestimation of leaf size using the CF, and values >0 indicate overestimation of leaf size. Next, we calculated the IQR of the differences in leaf size for each shape. We applied t-tests to test whether leaf size estimated by the leaf shape-specific CF and the CF of 2/3 differed significantly from zero (used as the reference value of the mean).

RESULTS

Leaf shape-specific correction factors

Leaf size obtained from image recognition software ranged from 0.010 cm² (Eutaxia microphylla) to 1038 cm² (Piper sp.2) with a median of 22.13 cm² (all data can be found in Supplementary Data Table S1).

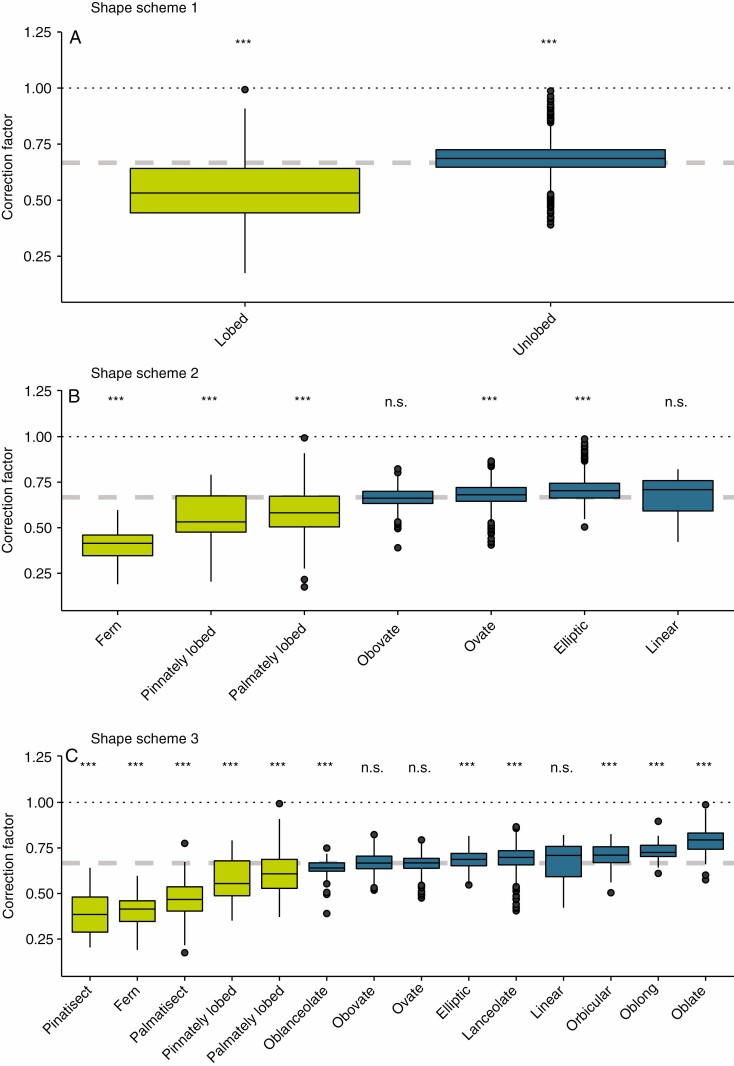
CF values calculated for all individual leaves ranged from 0.16 for a fern leaf (Diplopterygium bancroftii) to 1.22 for a palmately lobed leaf (Rubus parviflorus). The median CF for all leaves was 0.68 and remarkably close to the CF of 2/3. All unlobed leaves combined (shape scheme 1) had a median CF of 0.69 and all lobed leaves a CF of 0.53. For shape scheme 2, CF values differed from 0.53 for pinnately lobed leaves to 0.71 for linear leaves. CF values of shape scheme 3 ranged from 0.39 for pinnatisect leaves to 0.79 for oblate leaves. The IQR of the CF values was highest for pinnatisect and pinnately lobed leaves (IQR = 0.19), and lowest for oblanceolate leaves (0.05; see Table 1 for CF and IQRs for all leaf shapes). CF differed significantly from the CF of 2/3 for all leaf shapes over all shape schemes, except for obovate and linear leaves of shape scheme 2 and for ovate, obovate and linear laves of shape scheme 3 (Fig. 2).

Fig. 2.

Correction factors (CF) for three leaf shape schemes. Leaf shape definitions are provided in Table 1. Dotted black line indicates a CF of 1, for which the product of leaf length and width corresponds to the size of a rectangle. Dashed grey line indicates the CF of 2/3. Significant differences of the leaf shape-specific CF to the CF of 2/3 are indicated (***P ≤ 0.001; n.s., P > 0.05). Green boxplots indicate lobed leaves and blue boxplots indicate unlobed leaves.

Correction factors for leaf base form, margin type, medial symmetry and size class

Other leaf morphological characteristics had no or only minor effects on CF. Even though some leaf morphologies caused significant differences of the CF compared to the CF of 0.68 (median CF over all leaves), the total differences were always small. For the non-protruding leaf base form, the CF was 0.67, and for protruding leaves 0.68 (Supplementary Data Fig. S1a). CF calculated for toothed (CF = 0.62) and entire leaf margins (CF = 0.69) produced similar results (Fig. S1b). Leaf medial symmetry had no strong effect on CF, with asymmetrical leaves having a CF of 0.65 and symmetrical leaves a CF of 0.68 (Fig. S1c). The same pattern emerged for the CF calculated for the six leaf size classes, which ranged from 0.66 for microphyll leaves to 0.73 for macrophyll leaves (Fig. S1d).

Comparison of correction factors and image recognition software

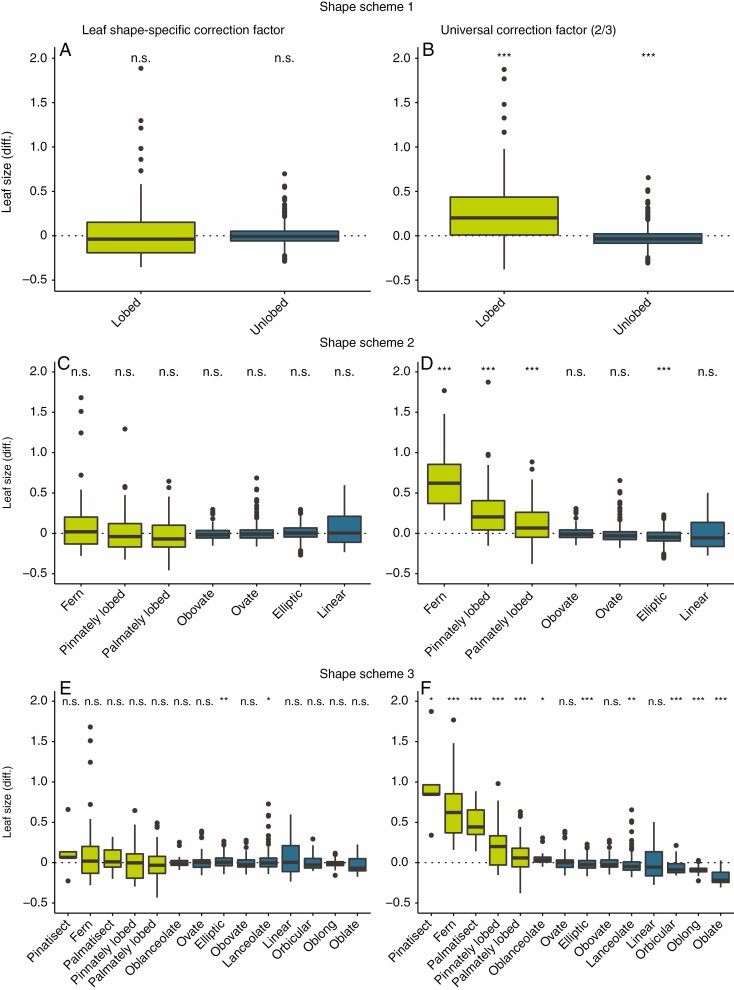
In general, leaf size estimated with leaf shape-specific CF was more accurate and precise than leaf size estimated using the CF of 2/3 (Fig. 3; Supplementary Data Table S2). Comparing leaf size estimates of leaf shape-specific CF against leaf size obtained from image recognition software yielded high congruence (Fig. 3). Only leaf size estimates for elliptic and lanceolate leaves of shape scheme 3 were significantly different from leaf size obtained from image recognition software. However, these differences were very small, with a relative difference of leaf size of +0.005 (0.5 %) for elliptic and −0.003 (−0.3 %) for lanceolate leaves.

Fig. 3.

Leaf size estimates using a leaf shape-specific correction factor (CF; left side) and the CF of 2/3 for all leaves (right side) compared against leaf size obtained from image recognition software. The y-axis indicates relative difference of estimated leaf size using the respective CF to leaf size from image recognition software. Values >0 indicate overestimation of leaf size applying the respective CF and values <0 indicate underestimation. Dotted black line (y = 0) indicates no difference between leaf size estimated using CF and leaf size from image recognition software. Leaf shape definitions are provided in Table 1. Green boxplots indicate lobed leaves and blue boxplots indicate unlobed leaves. Significant differences of the leaf shape-specific CF to leaf size from image recognition software are indicated (***P ≤ 0.001; **P ≤ 0.01; *P ≤ 0.05; n.s., P > 0.05).

Leaf size estimated using the CF of 2/3 yielded contrasting results and was, especially for lobed leaves, highly biased (Fig. 3). Across all leaf shapes only leaf size estimated for obovate, ovate and linear leaves of shape scheme 2 and for ovate, obovate and linear leaves of shape scheme 3 did not differ significantly from leaf size estimated from image recognition software. Leaf sizes of lobed leaves of shape scheme 1 were on average larger (+0.20; 20 %) than true leaf size whereas unlobed leaves were smaller (−0.04; 4 %) than true leaf size. For shape scheme 2, leaf size using the CF of 2/3 for ferns was on average overestimated by 64 % (0.64) and for linear leaves underestimated by 6 % (−0.06). Leaf size estimation for leaves of shape scheme 3 was even more biased. Pinnatisect leaves were on average overestimated by 85 % (0.85) and oblate leaves underestimated by 22 % (−0.22).

Family-specific correction factors

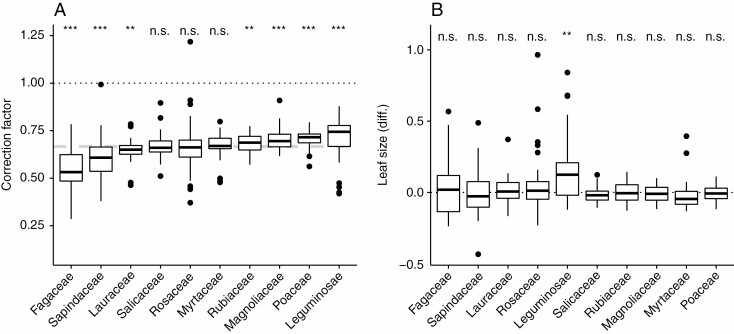
CF values for the ten most common families in our dataset ranged from 0.53 for Fagaceae to 0.74 for Leguminosae (Fig. 4A; Supplementary Data Table S3). For three families (Salicaceae, Rosaceae and Myrtaceae) the family-specific CF did not differ significantly from the CF of 2/3. For all other families the median CF was significantly different from the CF of 2/3 (Fig. 4B). The IQR was highest for Fagaceae (IQR = 0.14) and lowest for Lauraceae, Poaceae and Myrtaceae (IQR = 0.05). The CF and IQR for all families in our dataset represented by at least six taxa and ten leaves can be found in Table S3 (only results for the ten most common families are reported and shown in Fig. 4). Family-specific CF did not differ significantly from the true leaf size for nine out of ten families (expect Leguminosae; Fig. 4B).

Fig. 4.

Correction factors (CF) for the ten most common families in our dataset and leaf size estimates using a family-specific CF compared against leaf size obtained from image recognition software. (A) Dotted black line indicates CF = 1, for which the product of leaf length and width corresponds to the size of a rectangle. Dashed grey line indicates the CF of 2/3. Significant differences of the family-specific CF to the CF of 2/3 are indicated. (B) The y-axis indicates relative difference of estimated leaf size using the respective CF to leaf size from image recognition software. Values >0 indicate overestimation of leaf size applying the respective CF and values <0 indicate underestimation. Dotted black line (y = 0) indicates no difference between leaf size estimated using CF and leaf size from image recognition software. Significant differences of the leaf shape-specific CF to leaf size from image recognition software are indicated (***P ≤ 0.001; **P ≤ 0.01; n.s., P > 0.05).

DISCUSSION

We found that leaf size can be accurately estimated as the product of leaf length, width and a leaf shape-specific CF. Leaf size estimated using a family-specific CF yielded similar results. Among other leaf morphological characteristics, differences in leaf size estimation were small. Leaf shape-specific CF performed better in both accuracy and precision than the CF of 2/3 for nearly all leaves regardless of their shape, which was, especially for lobed leaves, highly biased. We see great potential in applying our approach to data obtained from species descriptions or large databases. In addition, this method can be used for fieldwork or on sensitive herbarium vouchers, especially when non-destructive in situ measurements are needed. When only taxonomic information is available, family-specific CF can be used as an alternative to leaf shape. As such, leaf size estimation based on the product of leaf length, width and a leaf shape- or taxon-specific CF can fill gaps in leaf sizes for many plant species worldwide with confidence.

Leaf shape-specific correction factors

We found that lobed leaves had a lower CF than unlobed leaves (see also Dolph, 1977; Yu et al., 2020). Lobed leaves are defined by incisions that can go as far as to the leaf midvein (Table 1), resulting in a reduced leaf size compared to unlobed leaves of the same dimensions. The incision is especially pronounced in highly dissected fern fronds and pinnatisect and palmatisect angiosperm leaves, which, unsurprisingly, had the lowest CF estimates (see also Shi et al., 2019a; Yu et al., 2020).

Oblong and oblate leaves had the highest CF. Oblong leaves (CF = 0.73) are characterized by having opposite margins roughly parallel for at least the middle one-third of the leaf (Table 1). Oblong leaves are thus a crude approximation of a rectangle (which would have a CF of 1). Oblate leaves resemble the shape of a circle. For a circle, length and width need to be multiplied by a CF of 0.79 to calculate its size, which is identical to the CF for oblate leaves.

Given various approaches have been demonstrated, guidance is required about which shape scheme should be used for leaf size estimation. As a general rule, we recommend using the finer shape schemes 2 and 3 over the coarser shape scheme 1, as the CF for finer shape schemes results in higher precision of leaf size estimation. However, the choice of leaf shape scheme depends strongly on the data source. For instance, if leaf size is estimated based on field measurements, leaf shapes should be defined a priori according to the finest shape scheme 3 as this will result in the most precise estimates. Other data sources, such as databases or species descriptions, may provide leaf shapes based on other categorizations. In such cases, we recommend carefully checking which leaf shape definitions are used in general and to which shape scheme they may fit best. In case of uncertainty, shape schemes 1 and 2 should be chosen over the finer scheme 3.

Correction factors for leaf base form, margin type, medial symmetry and size class

Adjustments for leaf base form, margin type, medial symmetry and size class had no effect or little effect on the CFs. CF for the two leaf base forms was 0.67 and 0.68, nearly identical to the CF of 2/3. A noteworthy exception was a few leaves with protruding base forms, where the leaf base extends beyond the connection point of blade and petiole. With our definition of leaf length and width, the part of the leaf extending beyond the connection point of leaf blade and petiole is excluded, resulting in higher leaf size estimates compared to leaves with similar shape but non-protruding bases (Yu et al., 2020). However, in our dataset only two species with protruding bases had a CF > 1 (i.e. Rubus parviflorus and Acer circinatum), and most such leaves had a similar CF compared to leaves with non-protruding base forms. This suggests that the bias introduced by protruding leaf bases is less important than shape for leaf size estimation. Leaf base form is difficult to define and can also exhibit high intra-specific variation (Tsukaya, 2006), leading us to recommend not taking leaf base form into account when estimation leaf size.

Leaves with entire margins had slightly higher CF than toothed leaves. This is caused by toothed leaves having small incisions (the teeth) along the margin resulting in reduced leaf size, but not length or width. However, the depth of the teeth can be difficult to quantify and is highly variable, even intra-specifically through development, between plants and between growing seasons (Baumgartner et al., 2020). Also, the differences in CF between leaves with toothed and entire margins was generally low, with a difference of the medians of Δ0.06, which suggests that differences in leaf margins do not dramatically affect leaf size estimation.

Contrary to Dolph (1977), we did not find systemic bias in CF among leaves of different sizes. Dolph (1977) hypothesized that smaller leaves had a higher CF than larger leaves because smaller leaves are nearly rectangular in shape. Dolph (1977) used leaflets of Gleditsia triacanthos that are indeed almost rectangular in shape, resulting in relatively high CF. However, such leaf shapes may be an exception also for species with very small leaves as we could not confirm this observation in our dataset.

Leaf shape-specific vs. correction factors of 2

The median CF for all leaves was nearly identical (CF = 0.68) to the CF of 2/3 proposed by Cain and De Oliveira Castro (1959; see also Dolph, 1977). However, we found large differences between leaf shapes in all three shape schemes. CF of the finest shape categorization – shape scheme 3 – showed the largest differences, ranging from 0.39 for pinnatisect leaves to 0.79 for oblate leaves. The CF of 2/3 applied to leaves with these shapes led to a 26 % overestimation and 13 % underestimation of their size, respectively. Furthermore, leaf size estimation using a CF of 2/3 resulted in overestimation of all lobed leaf shapes (shape scheme 1) and underestimation of lanceolate, oblong and oblate leaves (shape scheme 2; see also Dolph, 1977). Instead, no systemic bias occurred in leaf size estimation using the leaf shape-specific CF. Therefore, we recommend only using a CF of 0.68 when no data on leaf shape are available and to always use the leaf shape-specific CF when information on leaf shapes exist.

Family-specific correction factors

CF estimated for families provided accurate results in leaf size estimation, reflecting the assumption that leaf shape is often similar among species belonging to the same taxon (Nicotra et al., 2011; Peppe et al., 2011). In particular, species from families such as Poaceae or Lauraceae often have unlobed leaves with similar shape across species, resulting in accurate and precise leaf size estimations using the family-specific CF. Other families such as Fagaceae and Rosaceae usually include more diverse leaf shapes with both highly lobed (e.g. Rubus spp. and some species of Quercus) and unlobed leaves (e.g. Lithocarpus spp. or Prunus spp.), causing less accurate and precise leaf size estimations. This suggests that the accuracy and precision of the family-specific CF are strongly dependent on the leaf morphological variability within taxonomic groups.

Nevertheless, our results indicate that family-specific CF can provide an alternative in estimating leaf size if information about leaf shape is missing (see also Andrew et al., 2021). However, family-specific CF would require parameterization of CF for each family, and this is probably not workable for large datasets including different species identities. In principle, this approach can be applied to any taxonomic level, such as for species of the same genus or individuals belonging to the same species. With increasing taxonomic resolution, the precision and accuracy of taxonomically specific CF may also increase as leaf shapes of species within the same genus or individuals of the same species may be more similar to each other than leaf shapes across higher taxonomic levels.

Limitations

Despite the relatively high accuracy and precision of estimating leaf size using leaf shape-specific CF, some level of uncertainty remains. Leaf size estimation using CF is probably less precise compared to directly measuring leaf size, such as by image recognition software, especially for lobed leaves. This is possibly due to the incision of lobed leaves, which is difficult to quantify using only length, width and CF, but has relatively strong effect on leaf size, because for a given leaf length and width, deeply incised leaves had smaller leaf sizes than leaves with less or no lobing (see also Yu et al., 2020).

Theoretically, CF could be provided for each combination of leaf shape, level of incision and other leaf morphologies. This may enhance the precision of leaf size estimation, but would also require stricter categorization of leaf shapes and adoption of standard morphological terminology globally. Given that current categorizations offer different advantages across the breadth of leaf enthusiasts, we refrain from suggesting such an approach. An intention with our approach was to provide an easily applicable and reliable solution to estimate leaf size across different data resources. Very fine categorization of leaf morphologies would offset this, making easy and fast leaf size estimation cumbersome. For some data, such as from databases or species descriptions, very fine categorizations of leaf morphologies may not even be available.

CONCLUSION

We have presented leaf shape-specific CF values for all major leaf shapes. This will enable fast and relatively more precise and accurate estimation of leaf size than the commonly used CF of 2/3.

Our unifying framework presented here can be extended to many different data sources and advance global coverage of leaf size estimations to a large extent. For instance, leaf shape-specific CF can be used to fill gaps in global databases, such as TRY (Kattge et al., 2020) or AusTraits (Falster et al., 2021), that hold information on leaf shape, width and length for many species. Taxonomic plant species descriptions generally include information on leaf length, width and shape but rarely size (Winston, 1999). Extracting data from taxonomic descriptions could enable leaf size estimation for many described plant species worldwide, including rare or extinct species or fossils. Leaf shape-specific CF also allows for non-destructive leaf size measurements, which is important for in situ field measurements or for measuring fragile and valuable herbarium vouchers. As such, leaf shape-specific CF is a promising method to obtain reliable estimates of leaf size for many plants species worldwide.

Allometric and proportional relationships in plants offer interesting avenues to deduce complicated trait measurements from easily measurable dimensions. We hope that understanding scaling functions of plant dimensions could help to fill major gaps in knowledge, bringing us closer to a complete understanding of morphological variation in the world’s plants.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Figure S1: Correction factors for leaf base form, leaf margin, leaf medial symmetry and leaf size class. Table S1: Family and species name data. Table S2: Relative difference in leaf size and interquartile range of leaf size estimated using leaf shape-specific correction factors and a universal CF of 2/3 compared against true leaf size estimated by image recognition software. Table S3: Family-species correction factors and interquartile range for 39 families represented within our dataset with at least six taxa and ten leaves.

FUNDING

This work was supported by the Deutsche Forschungsgemeinschaft (grant number SCHR1672/1-1) to J.S. and by the Australian Research Council (grant numbers DP170103410 and DE170100208) to I.J.W. and R.V.G. respectively.