Bayesian Hypothesis Testing and Hierarchical Modeling of Ivermectin Effectiveness

To the Editor:

A recent meta-analysis of the trials evaluating ivermectin that was published in AJT¹ (referred to here as Bryant) was widely welcomed by those who argue that this antiparasitic drug is a cheap and effective treatment for COVID-19 infections. The study concluded:

“Moderate-certainty evidence finds that large reductions in COVID-19 deaths are possible using ivermectin. Using ivermectin early in the clinical course may reduce numbers progressing to severe disease. The apparent safety and low cost suggest that ivermectin is likely to have a significant impact on the severe acute respiratory syndrome coronavirus 2 pandemic globally.”

These conclusions stand in stark contrast to those of a later meta-analysis² (referred to here as Roman) that looked at a subset of the trials. Roman concluded:

“In comparison to standard of care or placebo, ivermectin (IVM) did not reduce all-cause mortality, length of stay, or viral clearance in randomized controlled trials in COVID-19 patients with mostly mild disease. IVM did not have effect on adverse events or severe adverse events. IVM is not a viable option to treat COVID-19 patients.”

Irrespective of the errors in the data and the analysis performed by Roman that were already highlighted by Crawford,³ we believe that this conclusion is not based on the results of the statistical analysis of the data, which were very similar to those of Bryant; instead, it was based on a somewhat vague and possibly biased subjective assessment of the quality of the trials themselves and erroneously concluding “no effect” from what was merely weaker evidence of a positive effect.

In a recently completed analysis⁴ we have applied a Bayesian approach, to what we believe are the relevant trials data used by Bryant and Roman (we made a number minor necessary changes to the trials, including removing the Niaee study⁵). Applying diverse alternative analysis methods, which reach the same conclusions, should increase overall confidence in the result.

The Bayesian approach brings with it several advantages over the classical statistical approaches applied to this trials' data thus far:

1. It allows the evaluation of competing causal hypotheses: we can test whether COVID-19 mortality is independent of COVID-19 severity, treatment, or both treatment and severity. The results show that the posterior probability for the hypothesis of a causal link between COVID-19 severity, ivermectin, and mortality is over 99%.

2. Given that a causal link can be established, we can explicitly evaluate the strength of impact of that causal link on mortality. These advantages can be obtained within a Bayesian meta-analysis framework using a hierarchical model that can also take account of “zero” frequency results which are not estimable in the classical statistical framework.

3. The hierarchical model produces full probability distributions for the various mortality rates. In these distributions:

   • for patients with severe COVID-19, the mean probability of death is 11.7% (confidence intervals [CI] 1.9%–27.5%) for those given ivermectin compared with 22.9% (CI 12.5%–34.9%) for those not given ivermectin.

   • for patients with mild/moderate COVID-19, the mean probability of death is 0.4% (CI 0%–3.6%) for those given ivermectin compared with 1.2% (CI 0%–6.8%) for those not given ivermectin.

In particular—as shown in Figure 1—we get full probability distributions for the risk ratio (RR) (the probability of death with ivermectin divided by the probability of death without ivermectin) and risk difference (RD) (probability of death with ivermectin minus the probability of death without ivermectin). Although we can still produce CIs for these distributions, in contrast to the classical approach, these CIs do not rely on notions of repeated trials. In addition, the classical CIs hide crucial information about where the probability mass is located. Taking this into account, there is clearly an effective RR and RD in support of ivermectin in the severe case: The probability of the RR being less than one is 90.7%. The case for ivermectin mortality improvement in mild/moderate cases is less clear: The probability of the RR being less than one is 84.1%, but it is more survivable in this case and there are fewer “events” to learn from.

FIGURE 1.

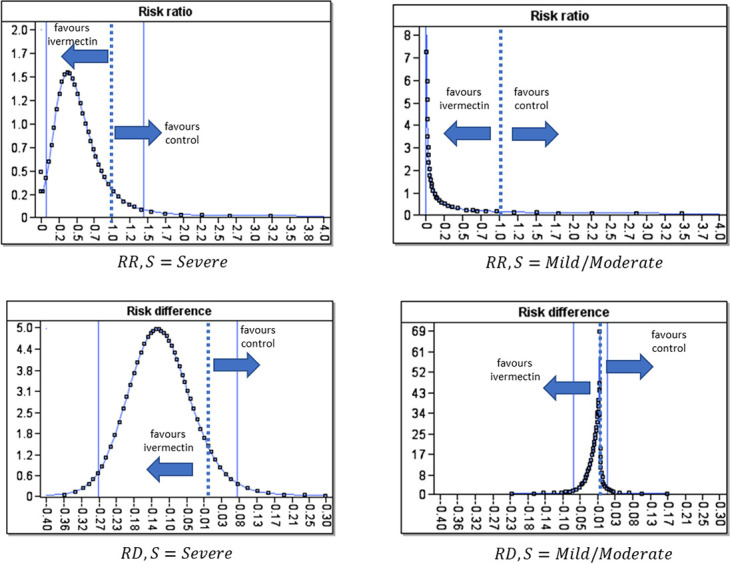
Posterior marginal probability distributions for RR and RD from the analysis. The dotted vertical line is the mean of the distribution, and the solid vertical lines are the 95% CI.

Table 1 shows the Bayesian analysis RR and RD summary statistics compared with the previous studies' results.

Table 1.

Bayesian analysis RR and RD summary statistics compared with previous studies' results.

	RR 95% CI	RD 95% CI
Roman et al, 2021 (all mild or moderate cases)	0.37 (0.12 to 1.13)
Bryant et al, 2021 (mild or moderate cases)	0.24 (0.06 to 0.94)
Bryant et al, 2021 (severe cases)	0.51 (0.22 to 1.14)
Bryant et al, 2021 (all cases)	0.38 (0.19 to 0.73)
Bayesian analysis (mild or moderate cases)	0.34 (0.00 to 26.0)	−0.013 (−0.066 to 0.020)
Bayesian analysis (severe cases)	0.48 (0.08 to 1.46)	−0.11 (−0.269 to 0.076)

To address recent widely publicized concerns about the veracity of some of the studies—notably that of Elgazzar⁶—we also evaluated the sensitivity of the conclusions to any single study by removing one study at a time (Niaee⁵ was already removed as noted above). The sensitivity analysis on the risk ratio and difference results is shown in Table 2.

Table 2.

Risk ratio and difference summary statistics for each study removed one at a time.

	Risk ratio (RR)		Risk difference (RD)		P(RD < 0)
	Median	95% CI	Mean	95% CI	P(RR < 1)
Mild to moderate
Ahmed 2020	0.03	0, 22	−0.014	−0.06, 0.02	0.84
Babalola 2020	0.03	0, 23	−0.014	−0.06, 0.02	0.84
Chaccour 2020	0.03	0, 24	−0.014	−0.07, 0.02	0.84
Elgazzar 2020	0.07	0, 156	−0.009	−0.06, 0.02	0.78
Hashim 2020	0.03	0, 17	−0.014	−0.07, 0.02	0.85
Lopez-Medina 2021	0.05	0, 36	−0.015	−0.07, 0.02	0.83
Mahmud 2020	0.06	0, 135	−0.011	−0.07, 0.02	0.79
Mohan 2021	0.04	0, 18	−0.015	−0.07, 0.02	0.85
Petkov 2021	0.03	0, 17	−0.015	−0.07, 0.02	0.85
Ravikirti 2021	0.06	0, 145	−0.005	−0.05, 0.02	0.78
Rezai 2020	2.E-04	0, 8	−0.017	−0.07, 0.01	0.91
All included	0.03	0, 26	−0.013	−0.07, 0.02	0.84
Severe
Elgazzar 2020	0.72	0.24, 1.73	−0.07	−0.23, 0.11	0.77
Fonseca 2021	0.34	0.05, 1.16	−0.15	−0.30, 0.02	0.96
Gonzalez 2021	0.41	0.04, 1.43	−0.13	−0.29, 0.07	0.92
Hashim 2020	0.63	0.09, 1.75	−0.09	−0.26, 0.12	0.86
Okumus 2021	0.43	0.04, 1.54	−0.11	−0.27, 0.08	0.90
All included	0.48	0.08, 1.46	−0.11	−0.27, 0.08	0.91

For mild-to-moderate COVID-19, the removal of any single study does not substantially affect the conclusion: The probability that the risk ratio is less than one lies in the range {78%, 91%}. For severe COVID-19, this range is {77%, 96%} suggesting that, if the Fonseca or Gonzalez studies were removed from the meta-analysis, the support for the effectiveness of the treatment would substantially improve; in the case of removing Fonseca, this would increase confidence, that the risk ratio is less than one, beyond 95%.

Removing Elgazzar, decreases confidence to 77% for severe COVID-19 and 78% for mild-to-moderate COVID-19. We also re-examined the causality hypothesis under the most unfavorable conditions to the difference hypothesis, which occurs when the Elgazzar trial is removed. The posterior probability for the hypothesis of a causal link between COVID-19 severity, ivermectin, and mortality is still strongly supported (91.2%) in the absence of Elgazzar 2020.

In our view, this Bayesian analysis, based on the statistical study data, provides sufficient confidence that ivermectin is an effective treatment for COVID-19 and this belief supports the conclusions of Bryant over those of Roman.