The mechanics of fibrillar collagen extracellular matrix

SUMMARY

As a major component of the human body, the extracellular matrix (ECM) is a complex biopolymer network. The ECM not only hosts a plethora of biochemical interactions but also defines the physical microenvironment of cells. The physical properties of the ECM, such as its geometry and mechanics, are critical to physiological processes and diseases such as morphogenesis, wound healing, and cancer. This review provides a brief introduction to the recent progress in understanding the mechanics of ECM for researchers who are interested in learning about this relatively new subject of biophysics. This review covers the mechanics of a single ECM fiber (nanometer scale), the micromechanics of ECM (micrometer scale), and bulk rheology (greater than millimeter scale). Representative experimental measurements and basic theoretical models are introduced side by side. After discussing the physics of ECM mechanics, the review concludes by commenting on the role of ECM mechanics in healthy and tumorigenic tissues and the open questions that call for future studies at the interface of fundamental physics, engineering, and medical sciences.

OVERVIEW

The extracellular matrix (ECM) is broadly defined as the non-cellular component of tissues and organs. The critical role of ECM in cell biology, and particularly in cancer physiology, has been increasingly appreciated with the realization that tumor cells and their ECM interact strongly.¹ The interaction forms a bidirectional feedback loop.² On the one hand, the ECM instructs cell morphology, migration, differentiation, and mediates cell-cell interactions. On the other hand, cells actively remodel the composition, geometry, and mechanics of the ECM.

The ECM is a hydrated polymer network with various chemical factors hosted in the liquid phase or that bind to the polymeric scaffold. Besides water and polysaccharides, the ECM is mainly composed of two categories of molecules: proteoglycans, such as perlecan and biglycan, and fibrous proteins, such as collagen and fibronectin. While the proteoglycans fill the extracellular interstitial space, fibrous proteins provide the structural support of the ECM by forming networks of interconnected fibers. This review focuses on the physical properties of the ECM, which are mainly determined by the fiber network.

There are three classes of fibrous ECM proteins: collagen, elastin, and fibronectin. Collagen is the most abundant protein in animals. Approximately 25% to 30% of human protein mass is from collagen molecules. To date, 28 subtypes of collagen have been identified. Among them, >90% of collagen molecules in the human body are type I collagen, which is the major component of organs and connective tissues such as skin, tendon, and mammary gland. Another subtype, type IV collagen, is the main component of the basement membrane, the ECM that separates the epithelium and the underlying tissue. The basement membrane usually is the first physical barrier in the route of cancer metastasis.

While collagen fibers are stiff and exhibit nonlinear responses when stretched, elastin and fibronectin fibers are much more compliant.^3,4 Elastin forms elastic fibers that are tightly bound to collagen fibrils, therefore helping tissues to resume their original shapes after compression or stretching. However, fibronectin fibers can be stretched by several times their resting length by cell traction forces.⁴ Once extended, the unfolding of fibronectin exposes integrin-binding sites to facilitate cell adhesion.⁵ This tension-activated cell-ECM adhesion is an important mechanism for the cells to probe their mechanical microenvironment using traction forces.

The structure and composition of the ECM not only vary dramatically from tissue to tissue but also evolve in time as a result of homeostasis, diseases, wounding, and aging.⁶ Many types of cells, such as fibroblasts, epithelial cells, macrophages, and cancer cells constantly rewire the ECM network.

Biochemically, molecules such as matrix metalloproteinase (MMP) secreted by cells and tissues degrade ECM fibers and crosslinks. MMPs are the critical enzymes for ECM maintenance. To date at least 23 types of MMPs have been found in human tissue with varying substrate specificity.⁷ MMP-1, for instance, is capable of cleaving gelatin, fibronectin, and collagen I, but not collagen IV. MMP-13, however, binds to collagen IV and is commonly found in cartilage and developing bones.⁸ While MMPs generally weaken ECM, cells also synthesize ECM proteins such as collagens (particularly types I and III) to create new fibers and to form crosslinks between existing fibers. These biochemical processes constantly sculpt the structure and function of ECM, keeping it at a dynamic equilibrium.

Biophysically, stroma cells apply small, fluctuating traction forces to the ECM, which deform ECM fibers, break weak bonds, and facilitate the assembly of new fibers. These biochemical and biophysical processes, often called tissue homeostasis, keep the ECM in dynamic equilibrium. One of the important consequences of tissue homeostasis is the tension homeostasis.⁹ When fibroblasts are seeded in an initially stress-free ECM, within the first few hours, cell traction forces generate an internal stress of 3–5 kPa, comparable to the stress measured at focal adhesions.^10,11 The internal stress is maintained even in the presence of environmental perturbations. For instance, if an external tensile stress is applied to the ECM, stretched fibroblasts will actively reorganize their cytoskeleton and bring back the interstitial stress to the equilibrium value.¹² Interestingly, the biophysical and biochemical remodeling of the ECM are often coupled. For example, mechanically relaxed collagen fibrils contain periodic defects in which MMPs bind as entry points of proteolysis.¹³ Once loaded with mechanical stress, collagen fibrils are strain stabilized against MMP degradation.¹⁴

The homeostasis of normal tissues is a result of highly regulated cell-cell and cell-ECM interactions, which maintain a favored environment for all physiological processes. In contrast, a hallmark of many types of tumors is the broken tissue homeostasis and aberrant tissue organization. The transformed microenvironment often promotes the growth and metastasis of tumors.

The role of ECM as a main player in the tumor microenvironment has been an active field of study. Readers may find excellent reviews covering the biochemistry of ECM,^6,15 and the molecular pathways mediating cell-ECM interactions.¹⁶ The following sections examine the mechanical properties of the ECM across different length scales and how they affect tumor progression.

This review of ECM mechanics focuses on fibrillar collagen matrices, which are mostly made of type I collagen molecules. Collagen matrices are the major mechanical component in the ECM of connective tissues. Type I collagen matrices have been used extensively as a lab model for ECM, as well as physical models of semiflexible polymer networks. It should be noted that most of the physical insights obtained from collagen matrices will apply to other types of ECM networks as well.

THE STRUCTURE OF COLLAGEN MATRICES

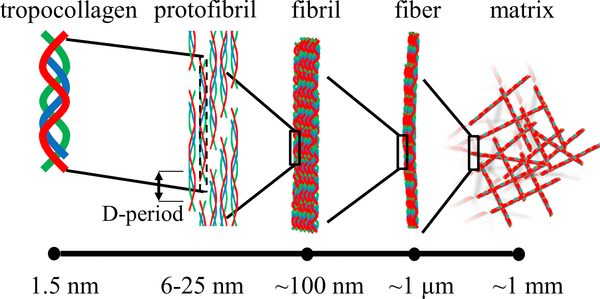
Collagen matrices feature hierarchical structures that are self-assembled through multiple steps (Figure 1). At the molecular level, fiber-forming collagens such as collagen I and IV first form polypeptides. Three polypeptide chains wrap together into a triple helix—tropocollagen—with a diameter between 1.2 and 1.5 nm, pitch ~1 nm, and typical length of 300 nm.^17,18 Multiple tropocollagens bundle together into protofibrils, including microfibrils and subfibrils, whose diameters are ~6 and 25 nm, respectively.^19,20 Within the protofibrils, the 300-nm tropocollagen segments stack laterally with alternating gap and overlapping regions. This configuration shows up in transmission electron microscopy as repeating light (gap region) and dark (overlap region) striations with a spatial period of ~67 nm, called D-periods.^21,22 The microfibrils and subfibrils further bundle into a collagen fibril, which can be as long as 1 μm, hundreds of nanometers in diameter, and denser at the rim than at the core regions.²³ Depending on the environmental condition, such as protein concentration, pH value, or temperature, collagen fibrils form collagen fibers of variable lengths and diameters. Finally, the collagen matrix is a disordered assembly of collagen fibers.²⁴ It is interesting to note that the balance between energy and entropy shifts as the spatial scale varies. At or below the nanometer scale, the binding energy of collagen molecules ensures a highly specific structure, which is crucial for the protein-protein interactions, such as between fibronectin and collagen, and ligand-receptor interactions, such as the integrin-mediated cell adhesion. At approximately the micrometer scale, the free energy of a collagen fibril has a significant entropic contribution, and the collagen fibers, like many other biopolymers, are semiflexible. Further up, entropic effects become even more evident: the microstructure of collagen matrix is spatially heterogeneous and highly sensitive to the temperature, and a collagen matrix is a porous, disordered assembly of collagen fibers.

Figure 1. The hierarchical structure of collagen matrix.

Entropic effects become increasingly important at greater spatial scales (left to right).

The self-assembly of collagen matrices is coupled with crosslinking processes, which significantly modulate the structure, stability, and mechanical properties of the ECM. As a striking contrast, skin collagen molecules have a half-life of 15 years, while cartilage has a half-life of >100 years.²⁵ Broadly speaking, there are two groups of crosslinks.²⁶ Non-enzymatic crosslinking depends on glycated lysine and hydroxylysine residues. For instance, sugar (e.g., glucose)-mediated glycation of collagen creates intermolecular connections of collagen fibrils, as well as other ECM proteins such as elastins.²⁷ These crosslinks not only impair the flexibility and permeability of the tissues but also affect cell growth, motility, and differentiation through integrin signaling.²⁸ Glycation may occur naturally with aging and pathologically in diseases such as diabetes.²⁹

Collagen matrices can also be crosslinked through enzymatic processes, which are primarily mediated by lysyl oxidase (LOX). Enzymatic crosslinks initially form difunctional covalent bonds that connect two amino acids. Over time, these crosslinks mature into trifunctional crosslinks that connect three amino acids.³⁰ Disorders associated with enzymatic collagen crosslinks can lead to fragile skin and eyes (Ehlers-Danlos syndrome type 6A), brittle bones and stiff joints (Bruck syndrome type 2), loose and inelastic skin (Cutis laxa type 4), and hardening and lesioning of skin (scleroderma).^31–34

Consistent with the scale dependence of its structure, the mechanical property of a collagen matrix also varies significantly at different spatial scales. While there is not a simple and integrated picture to understand the mechanics of collagen matrices, I focus here on three spatial scales that are most relevant to cellular dynamics.

The elasticity of single fibers

Cells probe the physical properties of the ECM by applying traction forces via cell-ECM adhesions, which are typically micron-sized protein complexes. As a result, single collagen fibers are the primary sites of cell-ECM mechanical interactions. As a defining feature, single collagen fibers are semiflexible. Unlike rigid rods and floppy strings, the bending energy of a semiflexible polymer is in tight competition with thermal fluctuation. Semiflexible polymers exhibit temperature-dependent and nonlinear elasticity, which is best understood with the help of the worm-like chain (WLC) model.

The basic assumption of the WLC model of a polymer is an elastic beam in thermal equilibrium. The WLC model has been discussed extensively. Instead of pointing readers to the vast literature, the author derives the most relevant results to make this review as self-contained as possible.

As shown in Figure 2A, the bending energy of an elastic beam can be expressed as

$$H_{bend}=\frac{\kappa }{2}\int ds{\left|\frac{\partial \mathrm{t}}{\partial s}\right|}^2$$ (Equation 1)

where s runs along the contour length, and t the tangential direction along the contour. Assume that the polymers are inextensible; therefore, their contour length l_c is fixed. A more convenient form can be obtained by substituting t = [cosθ, sinθ] into Equation 1 such that

$$H_{bend}=\frac{\kappa }{2}\int ds{\left(\frac{\partial \theta }{\partial s}\right)}^2$$ (Equation 2)

Figure 2. The worm-like chain (WLC) model of polymers explains the entropic origin of the polymer elasticity.

(A) A schematic of the WLC model of polymers. For simplicity, only planar configuration is considered, but the physics can be easily generalized into 3 dimensions, and the results differ only by numerical factors.

(B) The force-extension relation obtained by numerically inverting Equation 4. Dashed line represents the linear approximation for small strains.

Thermal fluctuations cause a WLC to wiggle so that it can no longer maintain a straight direction. This can be quantified by the two-point correlation function

$$\langle \mathbf{t}(s)\cdot \mathbf{t}(0)\rangle =e^{-\frac{s}{l_p}},l_p=\frac{\kappa }{k_{B}T}$$ (Equation 3)

Equation 3 defines an important parameter: the persistence length l_p. l_p quantifies the straightness of a polymer at thermodynamic equilibrium, as a result of competition between entropic and energetic effects. For a rigid polymer, a polymer whose contour length is much shorter compared with l_p, it can be considered as an elastic beam in which thermal fluctuation can be neglected and the mechanical property fully characterized by its Young’s modulus. For a flexible polymer, a polymer whose contour length is much longer compared with l_p, its mechanical property is characterized by an entropic spring. In between these two limits, both bending and stretching (force extension) are important for semiflexible polymers.

It is worth noting that persistence length can be defined using the correlation function as in Equation 3, and it does not restrict to the WLC model.

To straighten a WLC, we can fix one end of the chain and apply a force τ on the other end. As a result, we would expect the end-to-end distance l of the chain to increase at a larger force. Using equilibrium statistical mechanics, one can derive the force-extension relation:

$$\epsilon =\frac{\langle l_{\tau }\rangle -\langle l_{\tau =0}\rangle }{\langle l_{\tau =0}\rangle \rangle }=1-3\frac{\pi \sqrt{\varphi }\coth (\pi \sqrt{\varphi })-1}{{\pi }^2\varphi },$$ (Equation 4)

where $\varphi =\frac{\tau }{{\tau }_e}$ is dimensionless and τ_e = κπ²/l² is the Euler buckling force characterizing the pure mechanical instability of an elastic beam.

As shown in Figure 2B, Equation 4 demonstrates how nonlinear (large ϕ) and linear (small ϕ) force-extension relations can arise from a linear elastic beam. The temperature dependence has dropped out in Equation 4, and the nonlinearity is a result of mechanical instability (Euler buckling) characterized by τ_e.

In deriving this result, we have made a key assumption that the polymer is inextensible. It is useful to take a close look at this assumption. In general, an elastic beam with Young’s modulus E and radius a will have bending modulus κ ~ Ea⁴ and elongation modulus Ea². When the relative extension ε is small, we can compare the energy of entropic elongation H_ent and mechanical elongation H_mec, and find $\frac{H_{ent}}{H_{mec}}~\frac{l_P{a}^2}{l^3}$. Typically, in the ECM, lengths of collagen fibers are ~10 times greater than the radius; therefore, entropic elongation will be favored energetically. At larger ε, mechanical elongation is no longer negligible, and we expect the mechanical effect will increase the effective modulus. However, collagen fibers consist of thin fibrils. These fibrils, if not strongly crosslinked, may slide between one another and effectively elongate the contour length of the fiber. The interfibrillar sliding will decrease the effective modulus of a collagen fiber.

The micromechanics of a collagen matrix

Cells living in a three-dimensional (3D) matrix typically form tens of adhesion complexes or points of contacts with the matrix. Through mechanotransduction, cells learn the micromechanics of the ECM, which is the mechanical response of the biopolymer network measured at scales comparable to the matrix pore size.

ECM microstructure determines micromechanics

Experimental measurements of ECM micromechanics have been mostly done using optical tweezers^35–37 and atomic force microscopy (AFM).^38–40 The results show that the micromechanics of collagen and other biopolymer networks are anisotropic, heterogeneous, and stress dependent.

To better understand the experimental evidence, the author will first explain the optical tweezer measurements in detail. Assuming a micron-sized particle of radius a is embedded in a 3D matrix, a well-calibrated optical trap (modeled as a harmonic spring) is projected in the direction of angle θ in the same focal plane of the particle. We can then measure the directional compliance J_θ at the particle location:

$$J_{\theta }=6\pi a\frac{\mathbf{\Delta }\mathbf{d}\cdot \widehat{\theta }}{\mathbf{F}\cdot \widehat{\theta }}$$ (Equation 5)

Here, F is the optical force calculated by harmonic approximation, Δd is the particle displacement, and $\widehat{\theta }$ indicates the direction at which the optical tweezers are placed relative to the equilibrium positions of the probing particles.

Typical experimental measurements have a number of interesting features, as shown in Figures 3A and 3B. First, particle displacement does not follow the direction of the optical trap, in contrast to linear elastic materials such as polyacrylamide gels. This is directly related to the fact that we are probing elasticity at a scale comparable to but not much greater than the pore size. Second, the particle displacement is asymmetric. For instance, displacements with optical trap along ±x directions are not related through mirror symmetry. This is an indication of nonlinear elasticity distinct from the nonlinearity of single fibers. Finally, the directional compliance J_θ varies as the direction θ of trap position is changed. We can quantify these effects by defining the anisotropy A and compliance J:

$$A=\frac{\mathrm{Max}\left[J_{\theta }\right]-\mathrm{Min}\left[J_{\theta }\right]}{{\sum }_{\theta }{J}_{\theta }},J={\langle J_{\theta }\rangle }_{\theta }$$ (Equation 6)

Figure 3. The micromechanics of a collagen matrix is controlled by its microstructure.

(A) The confocal reflection image showing the collagen fibers and the probe particle (arrow). Inset: a holographic image showing the same field of view.

(B) The particle displacements when an optical trap is projected at θ = 0° (red), 90° (green), 180° (blue), and 270° (magenta). The optical trap is projected at the same focal plane of the particle, and 0.7 μm from the unperturbed particle center. The power of the optical trap switches on and off at a frequency of 1 Hz.

(C) Confocal reflection images showing distinct collagen fiber networks self-assembled at 2 different temperatures, 37°C and 21°C.

(D) Spatial distributions of micromechanical compliance in 2 collagen matrices formed at 37°C and 21°C, respectively.

(E) Spatial distributions of micromechanical anisotropy in 2 collagen matrices formed at 37°C and 21°C, respectively.

Scale bars in (C)–(E): 50 μm. Adapted from Jones et al.³⁶ Copyright (2016) National Academy of Sciences.

Using the two local quantities J and A, the correlation between the microstructure and micromechanics of collagen matrices is evident from Figure 3. When the chemical composition is fixed, changing the gelation temperature will direct the matrix self-assembly into distinct microstructures. As shown in Figure 3A, collagen matrices formed at a higher temperature (37°C) is spatially more uniform, with densely populated thinner fibers, while at a lower temperature (21°C), the matrices consist of thicker fibers and larger pore sizes. Correspondingly, the collagen matrix formed at a lower temperature features a broader distribution of micromechanical compliance, greater anisotropy, and more significant spatial variations.³⁶

Using structured illumination microscopy, Doyle et al.³⁹ further quantified the change of matrix microstructure. They found that while the gels formed at 37°C contained single fibrils of~310 nm in diameter, gels formed at 21°C have fibers bundled by as many as 2 to 12 fibrils. Doyle et al. also measured the temperature-dependent micromechanics of collagen ECM formed at 37°C, 21°C, 16°C, and 4°C using AFM. When averaged over the cellular size (32 × 32 μm), ECM rigidity increased by ~90% from 37°C to 4°C. However, rigidity sampled at the fibers (namely average excluding the pore area) increased by as much as 5-fold.

Theoretically, the correspondence between the microstructure and micromechanics of a fibrous network has been elegantly illustrated in a recent study.⁴¹ In this report, Beroz et al.⁴¹ used simple scaling arguments and simulations to show that micromechanics depends only on proximal network structure. In particular, by removing a single fiber in a disordered network, the local rigidity loss scales as $\frac{1}{R^6}$, where R is the distance from the removed fiber.

ECM micromechanics remodeled by cellular traction force

The micromechanics of ECM not only depend on the geometry of the network but also can be remodeled by stress, particularly by the cellular traction force. This effect has been shown by comparing the local elasticity close to and far away from cells, or before and after inhibiting cellular contractility. These measurements show that the traction force of a cell slightly increases the anisotropy, possibly due to the realignment of ECM fibers.³⁶

Traction force also stiffens the local ECM, which has been shown both in experiments and simulations. For instance, Winer et al.³⁸ measured the local stiffness of cellularized fibrin gel 10–15 μm away from the cell boundary using AFM. They found a moderate decrease (2–3 times) in stiffness after treating the cells with the myosin inhibitor blebbistatin. In another study, Kotlarchyk et al.³⁵ measured the local stiffness of fibrin gel using optical tweezers and found as much as a 10 times difference near the long axis versus short axis surrounding a smooth muscle cell.

For collagen matrices, we reported that at an ~20-μm distance from a breast cancer cell, local stiffness changed by 50% after inhibiting traction force by treating the cells with the actin polymerization inhibitor cytochalasin D.³⁶ However, a recent study by Han et al.³⁷ using optical tweezers found more than a 50 times change of stiffness 2 μm away from breast cancer cells after cytochalasin D treatment. In a different study, van Helvert et al.⁴⁰ measured the stiffening of the collagen matrix surrounding moving fibroblast and cancer cells. They observed an ~5-fold increase in the Young’s modulus at the leading edge compared to the trailing edge of cells, although this number varies significantly between different cell types.

While the ECM stiffening by cellular traction force has been observed in all of the above-mentioned studies, the magnitude of stiffening and the spatial range span several orders of magnitude in the existing literature. On the one hand, this is not surprising. The ECM micromechanics depends on local geometric and stress states, which may vary significantly from one sample to another. On the other hand, it is illuminating to note the diverse microenvironmental conditions a cell may encounter even in simple systems such as collagen or fibrin gels.

To understand the structure-mechanics relation at the microscopic scale, it is necessary to explicitly consider the geometry of the fiber network, rather than treating the matrix as a continuum. The importance of matrix geometry, such as connectivity and alignment, also propagate to much larger scales and affect the bulk property of the ECM. The next section examines the experimental and computational results related to the bulk mechanics of ECM.

The bulk mechanics

The ECM bulk mechanics, also called rheology, describes the macroscopic stress-strain relations. There are a few reasons that the bulk mechanics of tissues are under very active investigation. First, rheology can be easily measured in experiments. Most modern rheometers are capable of control or monitor strain and stress independently, and there is no need for special sample preparations. This is particularly helpful when measuring tissue samples directly from patients. Second, the bulk mechanics of tissues often changes accompanying progress in cancer, therefore providing a diagnostic signature that can be easily accessed. Finally, the physical principles that determine the bulk mechanics of a biopolymer network is still not fully understood. This fascinating problem, which involves multiscale, disordered, and many-body interactions, offers important insights to understand a wide range of systems in materials and life sciences.

Nonlinear elasticity

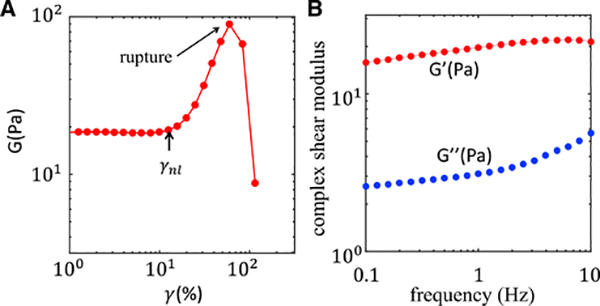
To quantify the material elasticity, a series of rheological parameters can be derived from the measured stress and strain. For instance, in a strain-sweeping experiment, in which the applied strain gradually ramps up, the ratio between stress and strain is the elastic modulus (Figure 4A). In a frequency-sweeping experiment, in which oscillatory strain with a fixed amplitude is applied, measured stress generally has a finite phase delay from the applied strain due to viscosity. The ratio between in-phase stress to strain is called storage modulus (G′), and the ratio between out-of-phase stress to strain is called loss modulus (G″). As shown in Figure 4B, the storage and loss moduli generally depend on the applied frequency.

Figure 4. The bulk rheological properties of a typical collagen matrix.

(A) The elastic modulus of a reconstituted collagen matrix. The matrix contains a collagen concentration of 1.5 mg/mL.

(B) The complex modulus-storage modulus and loss modulus of a reconstituted collagen matrix measured at various frequencies. The matrix contains a collagen concentration of 1.5 mg/mL. Adapted from Kim et al.⁴² Copyright (2017) Springer Nature Limited.

Unlike rubber and polyacrylamide gels, whose elastic moduli are nearly constant at varying strains, ECMs such as collagen and fibrin matrices exhibit nonlinear elasticity. The elastic modulus of a collagen matrix increases dramatically once the strain magnitude γ exceeds a threshold γ_nl ~ 10%–20% (Figure 4A). The nonlinear elasticity is of fundamental importance to the biomechanics of tumors because cancer cells typically induce ECM deformations that are greater than γ_nl.

To some extent, the nonlinear elasticity is not surprising. As has been demonstrated with the WLC model, semiflexible polymer fibers have nonlinear force-extension relation. When a matrix is sheared, some fibers are elongated and become stiffer as predicted by the WLC model; some fibers are compressed, and may even buckle. As a result, nonlinear stress-strain relation is expected.

To substantiate this simple picture, we can connect the WLC polymers to form a model network, the affine model. As shown in Figure 5, in the affine model, in which a fiber network is deformed by imposing a macroscopic shear strain ε, each crosslink point is assigned a displacement such that the strain field throughout the whole network is constant. The fiber between two crosslinks is stretched or compressed by εcosθ, where θ is the angle between the shear direction and the fiber orientation. Knowing the elasticity of each fiber (for instance, Equation 4), the density of fibers (proportional to the concentration), and the distribution of fiber orientation (random for an isotropic matrix), one can calculate the macroscopic stress applied on the matrix boundary. Besides the shear strain and stress, Figure 5 demonstrates another interesting observation. Under macroscopic shear, on average there are equal number of fibers being elongated and compressed. Because the collagen fibers have a higher stretching modulus than compressing modulus, there is a net pulling force on the sheared boundary. In other words, simple shear leads to negative normal stress, which is in contrast to other materials such as sand.⁴³

Figure 5. A schematic illustration of affine deformation of polymer networks.

In the affine model, every polymer in the network experiences an average strain based on its orientation. Under shear, there will be an equal number of fibers being stretched (the red fiber, for instance) and compressed (the yellow fiber, for instance).

Historically, the affine model has successfully explained the elasticity of flexible polymer networks such as rubber. For semiflexible networks, the affine model agrees well with F-actin networks and intermediate filaments, including various scaling behaviors of their nonlinear elasticity. However, there is a deep inconsistency between the assumptions of affine model and collagen matrices, which dates back to the work of James Maxwell in 1864.⁴⁴

Considering a 2D network made of springs, and the springs can freely rotate around their joints – nodes of the network. Is the network mechanically stable under infinitesimal shear? Or equivalently, does the network exhibit restoring force under shear? Clearly not every network is stable: a triangle is stable, but a rectangle is not. In fact, Maxwell⁴⁴ showed that the network is unstable if the number of nodes s is too small such that the number of springs e satisfy e> 2s — 3. For a large network, that means on average, every node must have at least four springs connected to be stable. And in d dimensions, the stability criterion generalizes to 〈z〉 > 2d, where z is the coordination number, namely the number of bonds connected to each node. The analysis of Maxwell was based on the number of degrees of freedom, and the mere effect of the springs was that they provide central forces resisting the change in their length. In other words, whether the springs are linear or nonlinear does not change the conclusion. Therefore, the criterion from Maxwell applies for collagen matrices as well. In general, when a network reaches the critical coordination number, it is called isostatic.

Collagen networks, either reconstituted in vitro or formed in vivo, has a coordination number 〈z〉 < 4.⁴⁵ As a result, collagen networks are subisostatic and should have zero shear modulus unless there are additional stabling factors.

It turns out that the small bending moduli of collagen fibers are crucial for the network to resist external stress. Bending, providing non-central force, allows an exception to the Maxwell criterion. However, bending also causes deviations from affine deformation. As a result, the mechanics of subisostatic networks goes beyond the affine model.

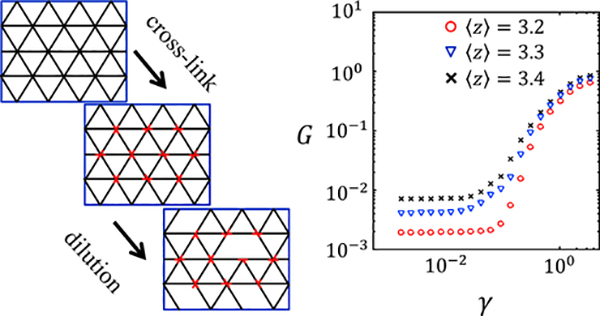
To understand the interplay of bending, stretching, compression of individual fibers, the fiber-fiber interactions governed by disordered network structure, and the constraints imposed by the macroscopic strain, multiple computational models of fiber network have been proposed.⁴⁶ These models provide many insights to understand the mechanics of biopolymer networks. As a representative example, the author recaps some basic results of the 2D phantom model.⁴⁷

In the 2D phantom model, a disordered fiber network is constructed through three steps, as shown in Figure 6: first, a fully filled network is constructed by filaments spanning the system size on a triangular lattice. Second, at each node, two out of three filaments are crosslinked with a torsion-free hinge. The third filament crossing the node is a phantom chain that does not interact with the other two filaments. Finally, the segments between any two nodes are removed with a probability p, resulting a fiber network with coordination number 〈z〉 = 4(1 – p). Notice that from the result of Maxwell, the isostatic point is 〈z〉 = 4; therefore, the network is subisostatic for any positive p.

Figure 6. An example of a lattice-based model predicts nonlinear elasticity of semiflexible polymer networks.

Left: the schematics of the model network. Right: the theoretically predicted nonlinear elasticity of the model network.

To focus on the effect of network structure, the model is athermal, meaning that the thermal effects, such as the entropic coiling discussed in the WLC model are neglected. Instead, the fibers are considered to be elastic beams of stretching modulus μ and bending modulus κ. In addition, because collagen fibers are significantly softer to bend compared with stretch, we keep $\frac{\kappa }{\mu a^2}\ll 1$. Here, a is the mesh size of the network.

The energy of the fiber network is purely mechanical and can be written as a summation of stretching and bending terms:

$$H=\frac{\mu }{2}\sum _{\langle i,j\rangle }\mathrm{\Delta }{l}_{ij}^2+\frac{K}{2}\sum _{\langle i,j,k\rangle }{\theta }_{ijk}^2$$ (Equation 7)

In this expression, Δl_ij is the change in length of any bond 〈i, j〉 and θ_ijk is the deflection angle of two connecting bonds 〈i, j〉 and 〈j,k〉.

The total energy determines the elasticity of the model network. In particular, the following protocol can be used to calculate the shear modulus. First, a fixed boundary condition is imposed on the network so that a shear strain of γ is applied to the network. Second, the network configuration is optimized to reach minimal elastic energy H_min = E(γ). Finally, the shear modulus $G=\frac{1}{\gamma }\frac{\partial E}{\partial \gamma }$ is obtained. The author has computed the shear moduli of 2D phantom networks with varying connectivity. As shown in Figure 6 and consistent with experimental results, all subisostatic networks demonstrate transitions from linear to nonlinear elasticity at increasing strains.

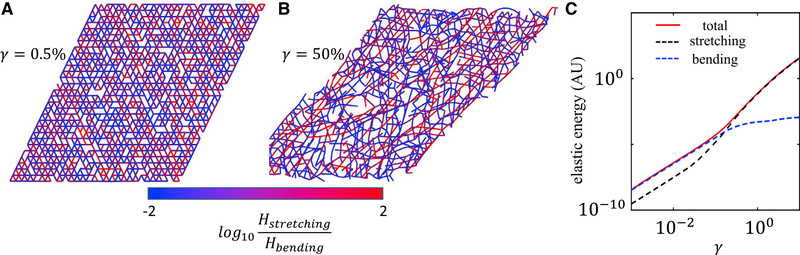
One of the most valuable insights from the simulation is the microscopic nature of nonlinear elasticity arising from perfectly linear elements—the Hamiltonian in Equation 7 has only linear elastic terms. As shown in Figure 7, the increase in elastic modulus coincides with a bending-to-stretching transition. At small strains, bending is favored to satisfy both the boundary condition and the minimizing energy. Therefore, the shear modulus is mainly controlled by the bending modulus of the fibers. At a large strain, bending modes are exhausted and most fibers must stretch to comply with the boundary condition. Therefore, the shear modulus is controlled by the stretching modulus of the fibers. It is worth noting here that the disordered nature of the network structure is necessary if the shear boundary condition is to be satisfied by mostly bending deformations.⁴⁵ Also, the physical picture revealed here is consistent with other lattice-based (e.g., kagome lattice), non-lattice-based (e.g., Mikado model), and 3D models.⁴⁶

Figure 7. Simulations of the phantom model help reveal the nature of the nonlinear elasticity of collagen matrices.

(A) The network configuration at a small shear strain of γ = 0:5%. The color represents the ratio of stretching and bending energy of each fiber.

(B) The network configuration at a large strain of γ = 50%.

(C) The contribution of bending and stretching energies to the total elastic energy at varying strains.

In (A)–(C) the network has a coordination number of 〈z〉 = 3:4.

Adapted from Kim et al.⁴² Copyright (2017) Springer Nature Limited.

The nonlinear elasticity of collagen matrices can also be understood from the point of critical phenomena.⁴⁸ As mentioned previously, collagen matrices are subisostatic networks and would be floppy without other stabling mechanisms besides central forces. Bending is one such mechanism. Interestingly, simulation of model networks shows that the network can support shear stress at zero bending modulus, when the applied strain amplitude goes beyond a critical value γc. This is analogous to the paramagnetic-to-ferromagnetic transition, where γc plays the role of the Curie temperature and the bending modulus plays the role of the external magnetic field. Both simulations and experiments show that the floppy-to-rigid transition of subisostatic networks are second-order phase transitions with non-mean-field critical exponents. The nonlinear elasticity of the collagen matrices is then naturally expected, just as the average spin in the classic Ising model is a function of temperature.

Viscoelasticity

The nonlinear elasticity of ECM characterizes its static response to a constant mechanical load. In reality, ECM is subject to forces that usually fluctuate in time. It is therefore important to characterize the frequency-dependent response of the ECM. In standard rheology, this is done by measuring the storage modulus G′ and loss modulus G″ as functions of probing frequencies.

ECMs such as collagen matrices demonstrate viscoelasticity. The origin of the viscosity lies in the microstructure. As mentioned above, ECM consists of a porous fiber network as scaffold, and the interfibrous space is filled with water and other soluble factors. When stress is applied, the frictional interaction between fibers and water will dissipate energy and generate viscous forces as the network deforms.

The viscosity of collagen matrices modulates their elasticity. When deformed with an oscillatory strain γ = γ₀sinωt, the stress generated by the matrices is typically out of phase with the strain such that τ = G′sinωt + G″cosωt. As shown in Figure 4B, the elastic (storage) modulus increases with frequency, which is qualitatively expected because the viscous interactions contribute to the total force generated. However, the frequency dependence of micromechanical compliance is not equally significant along all directions. In fact, the effect is stronger along a more compliant direction. This can be understood by the fact that viscous force is stronger when fibers move at a greater speed, and the speed is positively correlated with the displacements, or compliance, of the probe particles.

The viscoelasticity of the ECM micromechanics is important to the tumor biology because different biological processes allow the cells to probe their mechanical microenvironment at varying timescales. For instance, the integrin-ligand bond exhibits catch bond behavior, whose lifetime depends on the loading rate of mechanical force and ranges from tens of milliseconds to minutes.^11,49 However, cancer cells push their sounding matrices with membrane protrusions that only last a few minutes and apply traction forces that fluctuate on the scale of hours. These results suggest that it may be overly simplistic to consider cell mechanosensing by only referring to the bulk rigidity. Instead, much research is needed to understand how cancer cells integrate the mechanical readouts from multiple processes that probe the ECM at diverse spatiotemporal scales.

Elastoplasticity

A common assumption in cell mechanics is that the ECM is mechanically stable, at least when the applied force is comparable to the cell traction force. However, it becomes increasingly evident that the ECM demonstrates mechanical plasticity, which renders the force responses of the ECM to be history dependent.

Münster et al.⁵⁰ suggested that the ECM plasticity is due to the slippage of subfibrils that form individual fibers of the ECM. They measured the stress-strain curves of fibrin and collagen matrices under cyclic strains and found that the curves evolved in each cycle. In the meantime, the rest lengths of fibers increased over time. They proposed that the history dependence is due to the slippage of subfibrils in the ECM fibers. When the ECM is increasingly sheared, a fraction of fibers is stretched and permanently elongated. When strain returns to zero, these elongated fibers do not relax to their original lengths, but instead buckle to accommodate the increased rest lengths. In the following strain cycle, these buckled fibers do not contribute to the stress until pulled out and made taut again. As a result, the strain-stress curve shifts toward higher strains over time.

Nam et al.⁵¹ suggested a different mechanism of ECM plasticity based on the breaking and reforming of the dynamic bound between fibers. They studied the stress relaxation of fibrin and collagen networks under fixed shear strains and found that higher strains increased the stress relaxation rate. They have also observed irreversible changes of fiber orientation after removing the imposed strains. Nam et al. propose that the ECM fibers can unbind and that the rate of unbinding is exponentially accelerated by force load on the fibers. At the same time, detached fibers can freely rebind, thereby generating a different self-assembled configuration. To test the model, they have used AFM to study the interaction between a collagen-coated AFM tip and collagen matrices. They found that the lifetime of the tip-matrix attachment exponentially increases under smaller pulling forces, providing direct evidence of the force-dependent unbinding of ECM fibers.

The author has suggested that the sliding and merging of fibers contribute to the ECM plasticity and that these events can be triggered by typical cell traction forces.⁴² In these investigations, the author first held a collagen matrix at a constant shear ε₀ for a dwell time of T_d and then followed the strain relaxation kinetics ε(t). The author found that at small initial strains (ε₀ < 5%), the kinetics were single exponential characterized by a timescale, τ_v, as expected for viscoelastic solids. At larger initial strains (ε₀ > 10%), however, the author found double exponential relaxation $\epsilon (t)\approx a{e}^{-\frac{t}{{\tau }_v}}+b{e}^{-\frac{1}{{\tau }_p}}+{\epsilon }_r$. Here, τ_p is a new timescale that is >20 times longer than τ_v, and ε_r is the residual strain after prolonged relaxation (Figure 8A).

Figure 8. The strain relaxation kinetics of collagen matrices demonstrates plasticity.

(A) The shear relaxation from various initial strains.

(B) The plastic timescale increases with longer dwell time.

(C) The residual strain increases with longer dwell time.

Adapted from Kim et al.⁴² Copyright (2017) Springer Nature Limited.

The author found that by increasing the dwell time T_d, both τ_p and ε_r increased, indicating a history-dependent reconfiguration of the collagen ECM (Figures 8B and 8C). To understand these observations, the author devised a lattice-based network model and attributed the observed plasticity to the sliding and merging of fibers. The model provided good fit to the data and indicated how fiber sliding and merging allowed a matrix to search for lower energy configurations.

Qualitatively, during the dwell time, sliding and merging events accumulate to lower the energy of the strained network. As a result, the strained network becomes partially locked even after removing the external stress, leading to the residual strain ε_∞. However, sliding and merging events relax internal stresses in the network. Therefore, the fraction of highly stressed fibers, which is more likely to be reconfigured, decreases over the dwell time. Once the external stress is removed, the network strain will take longer to relax due to the reduced number of sliding or merging-ready fibers.

The history-dependent mechanics of the ECM adds a new dimension to the cancer microenvironment, and we are just beginning to uncover its biological consequences. However, there are reasons to believe that ECM plasticity is a crucial and potentially paradigm-shifting aspect of the cancer-microenvironment physical interactions.

First, the plasticity of the ECM could alter the results of previous studies that took a pure elastic approach: 3D traction force microscopy, for instance, may underestimate the cell traction force because some residual strain will persist even after releasing the traction force. Second, stress-activated “memory” of the ECM means that the cell remodeling of the ECM is a cumulative effect over time. As a result, small perturbations to the ECM structure by single cells may be integrated to produce a dramatic effect. At the same time, the notion of ECM homeostasis should be revisited to take into account the irreversible modifications of the ECM through mechanical rather than chemical processes. Finally, the plastic remodeling of the ECM provides a new channel for ECM-mediated cell-cell interaction. The ECM microstructures that are aligned and densified by traction forces may continuously guide the migration and mechanosensation of other cells for extended periods of time.

ECM MECHANICS AND TUMORIGENESIS

In a normal tissue, the structure and mechanics of the ECM are tightly regulated via homeostasis between the ECM and resident stromal cells.^6,16,52 One remarkable outcome of tissue homeostasis is the drastically divergent, yet well-maintained tissue stiffness in different parts of the human body.

There are a number of mechanisms in place to safeguard the ECM. As an example, Figure 9 shows a schematic of a wound repair process after acute injury. During wound healing, fibroblasts, which later differentiate into myofibroblasts, are recruited to synthesize and deposit ECM proteins such as collagen, fibronectin, and hyaluronic acid.⁵³ The large amount of ECM proteins often causes fibrosis, which promotes MMP synthesis, which helps restore the normal tissue structure and compositions.⁵⁴

Figure 9. The negative feedback loop mediated by the ECM synthesizes, and degradation allows the tissue to restore homeostasis after injury.

After tissue injury, the coordinated ECM synthesizes, and degradation heals the wound and restores the dynamical ECM homeostasis.

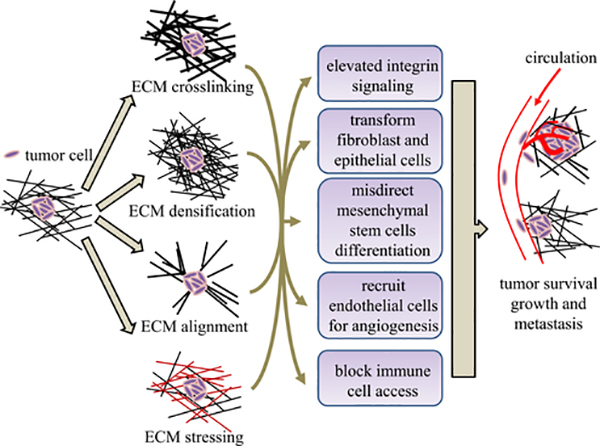
During tumorigenesis, deregulated biological processes impair the ECM homeostasis, causing aberrant ECM composition, microstructure, and, ultimately, functions. The ECM abnormality reciprocally fuels the growth and metastasis of cancers, thereby causing a fatal positive feedback cycle (Figure 10).

Figure 10. The ECM may promote tumorigenesis through a number of pathways.

Cancer cells can physically remodel the surrounding ECM, thereby creating a microenvironment promoting tumorigenesis and metastasis.

One such reciprocal interaction is mediated by ECM stiffening. Both bulk rheology and microrheology measurements have shown increased ECM stiffness concomitant with the malignant transformation of tumors.^55–57 It has been established that the observed ECM stiffening is a combined result of increased ECM crosslinking,⁵⁸ densification,⁵⁹ and mechanical stress.⁶⁰

LOX facilitates the enzymatic crosslinking of ECM fibrils. In breast, head, and neck tumors, LOX is usually excessively produced by cancer cells as well as cancer-associated fibroblasts. LOXs crosslink collagen fibers in the mammary gland and partially cause the tumor ECM to be as much as 10 times stiffer than normal breast tissue.⁵⁸ The dramatically increased ECM rigidity promotes tumorigenesis through multiple pathways. For instance, integrin signaling is upregulated, which enhances cancer cell survival and proliferation. Excessive LOX crosslinking also promotes focal adhesion-mediated ERK and phosphatidylinositol 3 (PI3) signaling, which facilitate Neu-mediated oncogenic transformation.⁵⁸

ECM stiffening also affects other types of cells and creates a favorable microenvironment for tumors.¹ For instance, endothelial cells are promoted to generate new blood vessels through sprouting angiogenesis.^61–63 The new blood vessels not only feed the growing tumor with nutrients but also provide a path for tumor metastasis. The cytotoxic CD8⁺ T cells, however, are often found to be fenced off from cancer cells by the rigid ECM surrounding solid tumors.⁶⁴ As a result, tumor cells can evade the immune defense even when these T cells have been activated. Finally, mesenchymal stem cells, whose differentiation is critically modulated by environmental rigidity, will be strongly affected by the stiffened ECM. The misdirected mesenchymal stem cells are likely to be a source of cancer stem cells and cancer-associated fibroblasts (CAFs).⁶⁵

In addition to contributing to the excessive crosslinking, tumors cause ECM densification. The ECM in the vicinity of solid tumors often consists of high levels of ECM proteins such as fibrillar collagens, fibronectin, elastin, and laminins.^66,67 In fact, for many tumors, the ECM accounts for 60% of the tumor mass.⁵⁹ These proteins are produced by tumor cells, but more prominently by CAFs.⁶⁸ Similar to the excessive ECM crosslinking, densified ECM promote cancer cell growth, transformation (e.g., epithelial-mesenchymal transition), and metastasis through integrin signaling, FAK-ERK linkages, and Rho-Rock pathways.^66,69,70

Breast tumor-associated ECM is often found to contain linearized and bundled fibers as a result of cellular traction force as well as matrix degradation via MMPs.⁷¹ It has been found that radially aligned ECM fibers projected from the original tumor site facilitate cancer invasion, leading to worse clinical outcomes.⁷² This process, called contact guidance, has been observed in vitro in both 2D and 3D migration assays.^73–75 It turns out that contact guidance is a strong signal that biases the migration of not only tumor cells but also immune cells, fibroblasts, and endothelial cells. As a result, the dynamics of many cells in the tumor microenvironment are disrupted by the remodeled ECM microstructure.¹

It is worth noting that the ECM microstructure modulates not only the mechanics but also other physical aspects of the tumor microenvironment. For instance, aligned ECM fibers lead to anisotropic diffusivity.^76,77 The transport of secreted factors and exosomes along the direction of ECM alignment is significantly enhanced, which may facilitate the tumor-stroma cell interactions.⁷⁷ As a salient example, Jung et al.⁷⁸ recently reported that traction forces of a tumor spheroid radially align the ECM fibrils in the vicinity of the spheroid. The radial alignment helps the dissemination of CAF-promoting cytokines toward normal fibroblasts, promoting the induction of cancer-associated fibroblasts.

Like the increased rigidity, the altered ECM structure has tumor-promoting effects. Using a 3D culture model, researchers found that thick collagen bundles form between Ras-transformed breast acini-rounded epithelial cell clusters. The collagen bundles accelerated the disorganization of the acini, and the epithelial cells were found to transit to an invasive mesenchymal phenotype. Removing collagen bundles by laser ablation slowed down the acini disorganization and isolated one acini completely from the others by box-cut, effectively blocking invasive phenotype transition.⁷⁹ This seminal work demonstrated the causal effect between matrix remodeling, ECM-mediated cell-cell mechanical interaction, and tumorigenesis.

CONCLUSIONS

Over the past few years, the mechanics of the ECM has emerged from a small sub-field of polymer physics to an exciting interdisciplinary subject at the forefront of physics, engineering, and medicine. While this review focuses on the multiscale mechanics of the ECM, many important topics are unfortunately being left out. For instance, readers who are interested in the poroelasticity of polymer gels will find the book by Coussy⁸⁰ and a review by Hu and Suo⁸¹ useful. Readers who are interested in computational and theoretical models can refer to an excellent review by Broedersz and MacKintosh.⁴⁶

The mechanics of the ECM is far from a mature research field. As a key element in cellular and molecular biomechanics, the author would like to point out two particular challenges that call for synergistic efforts from theoretical and experimental investigations.

One of the challenges is to develop a unifying mesoscale physics model that links the structure and mechanics of the ECM. While the bulk nonlinear elasticity of semiflexible polymers has been beautifully connected to critical behaviors of second-order phase transition,⁴⁸ such a simple picture has not been devised at the mesoscale. The micromechanics depends on many local geometrical details, such as fiber orientation and fiber density, as well as mechanical parameters, such as bending and crosslinking modulus of fibers. The complexity makes it difficult, if not impossible, to calculate the ECM micromechanics based on (often incomplete) structure data. Therefore, we do not know the exact mechanical cues presented to a cell, except when using local probes (e.g., active microrheology, AFM) in limited cases. This knowledge gap significantly restricts our understanding of the physical microenvironment of cells.

Another challenge is to experimentally produce tightly controlled ECM microstructure and micromechanics for in vitro investigations. Generally speaking, there are two classes of approaches in engineering ECM biopolymer networks. The first class seeks to harness the self-assembly of biopolymer networks by controlling the external condition. For instance, in making collagen ECM, we can modify the temperature, pH value, and protein concentration during the gelation process. However, these external conditions will simultaneously change many aspects of ECM microstructure such as the pore size, fiber thickness, and spatial heterogeneity. Independent control of these properties, while desirable for quantitative studies, has not been achieved by tuning external conditions. In this regard, recent progress suggests promising new fabrication strategies such as incorporating fluid flows^82,83 and novel crosslinkers⁸⁴ to decouple the structure, transport, and mechanical properties of collagen ECM.

Using the first class of approaches, we may determine the statistical properties of the ECM microstructure (e.g., pore size distribution) at best. In contrast, a second class of approaches aim to build the ECM from the ground up by manipulating individual construction units. For instance, in a pilot work by Kurniawan et al.,⁸⁵ fibrin fibers are carried by optical tweezers and attached to each other one by one. While such an approach offers the possibility of designing and creating ECM fiber networks on demand, it requires significant future efforts to scale up and to improve the throughput.