Predicting the trend of indicators related to Covid-19 using the combined MLP-MC model

Abstract

Although more than a year has passed since the coronavirus outbreak globally, the Covid-19 pandemic conditions still exist in many countries, including Iran. Predicting the number of future patients and deaths can help governments and policymakers make better decisions to enforce disease control restrictions. In this study, we aim to use a combined multilayer perceptron (MLP) neural network and Markov chain (MC) model to predict two indicators of the number of discharged and death cases according to their relationship with the number of hospitalized cases in Bushehr province, Iran. This hybrid model is called MLP-MC.

In this study, 136 data (days) are collected from May 13, 2020, to April 1, 2021, divided into two parts: training and test. The training data are used to train the MLP network, and the trained MLP network is used to predict the test data and the next 40 days. Then the residual errors of actual and predicted values are calculated. In the next step, the MC model is used to classify the errors and predict the values of the indicators according to the probabilities related to the error states and improve the performance of the MLP model in forecasting. Finally, the prediction accuracy of MLP and MLP-MC models are compared using three evaluation metrics: MAD, MSE and RMSE. This comparison showed that the MLP-MC model has slightly higher prediction accuracy than the MLP model.

1. Introduction

Recently, we have witnessed the rapid spread of the coronavirus pandemic, which was first reported in China and then in other countries [1]. Given the far-reaching implications of this pandemic, there is an urgent need for the scientific community to come together and present new and better methods, strategies, models and techniques, to understand and reduce the consequences of this and future pandemics [2]. Due to the unknown nature of the Covid-19 disease and its vast consequences, the continuous prediction of related indicators in different regions, time periods, and conditions are of great importance, especially for decision-makers. So far, much research has been done on using appropriate methods to predict time series associated with Covid-19. These methods have had a wide range according to factors including but not limited to purpose and subject, studied indicators, and different prevailing conditions in the region. For example, in [3], time-series modelling has been used to predict confirmed and recovered cases of Covid-19 in the world. An evolutionary data analytics method called Genetic programming (GP) has been used in [4] to mathematically model the potential effect of coronavirus in the 15 most-affected countries of the world. In [5], the Auto-Regressive Integrated Moving Average (ARIMA) model has been used to predict the irregularly patterned Covid-19 outbreaks in South Korea and Japan. In [6], a hybrid approach combining the fractal dimension and fuzzy logic has been proposed to predict the Covid-19 time series for countries in the world.

In [7], a simulation has been performed based on a trained ordinary differential equation model to describe the effect of an imported escaper and asymptomatic patients on confirmed Covid-19 infections in China's Heilongjiang Province. This study predicted the effect of strong interventions to prevent the spread of Covid-19 in this province.

In [8], an artificial neural network (ANN) curve fitting technique has been utilized to predict the Covid-19 number of rising cases and death cases in India, France, and Britain, considering the progressive trends of China and South Korea. The authors concluded that the ANN network could effectively predict the future cases of the Covid-19 outbreak in any country.

In [9], a multiple ensemble neural network model with fuzzy response aggregation has been proposed to predict the COVID-19 time series in Mexico. The results showed that the prediction errors of the proposed model are significantly lower than using traditional monolithic neural networks.

In [10], the 1st order Markov model and the Monte Carlo simulation and probability matrices have been used to predict the impact of Covid-19 in India. The approach was found useful for prediction in destiny.

In [11], the Markov Chain and the spatial Markov Chain have been used to studying the spatial distribution dynamics of Covid-19 and forecast the confirmed Covid-19 cases in 40 Asian countries. Their results showed that Covid-19 in Asia does not reach zero with current policies, and the neighbours impact the spread of Covid-19.

In [12], the hidden Markov chain modelling has been utilized to predict the evolution of Covid-19 in Morocco. Their study provided the recorded and forecasted data matrices of the cumulative number of confirmed, recovered, and active cases through the range of the studied dates.

In Iran, various studies have been conducted to predict the Covid-19 trend. For example, [13] used a mathematical model to predict the number of infected people in the second wave of the Covid-19 outbreak in Iran. In his study, several scenarios of Covid-19 progression corresponding to the second wave of the disease in Iran in the coming months have been examined. It has also been predicted that the second wave would be more severe than the first wave.

In [14], using secondary data analysis and modelling, the trend of Covid-19 in Iran until May 13, 2020, has been predicted based on severely ill patients.

In [15], various time series prediction methods have been used for modelling and forecasting the number of confirmed and death caused by Covid-19 in Iran. In their study, the performance of 9 different prediction models based on three evaluation metrics is compared. It has been concluded that based on the available data in Iran, the MLP model is the best model to predict confirmed cases, and the Holt-Winter (HW) model is the best model to predict future death cases.

In this paper, a combined MLP-MC model is used to predict the trend of Covid-19 related indicators in Bushehr province, Iran. Then, its accuracy in forecasting is compared with the MLP model using three metrics. The MLP and MC models have previously been used separately to predict various Covid-19 related indicators, e.g., in [16], [17], [18], [19], [20], [21], [22], [23], the MLP model have been used. Besides, in [10–12,24], the MC model has been used for this purpose. Combining these models simultaneously to predict Covid-19 related indicators is the main contribution of this paper. Therefore, our proposed model fills the current gap in the existing research, which is the lack of use of the combined MLP model and the Markov chain in predicting the time series associated with Covid-19. The reason for combining the Markov chain with the MLP model is to reduce prediction errors. The Markov chain is a way to reduce MLP prediction errors by addressing the errors transfer behavior using the Markov transition matrices. In summary, the main contribution of this paper is to present the hybrid model of MLP-MC to obtain an improved prediction of indicators related to Covid-19.

Moreover, most of the research conducted in Iran is mainly based on national data, and less regional and provincial data has been used in the analyses. On the other hand, if the analyses are done regionally and provincially, better and more accurate decisions can be made according to the region's conditions or province under study. A region - or province-specific model may also help discover the coronavirus pandemic's basic features [7]. Therefore, in this study, local data have been used to show the application of the proposed combined model to predict the Covid-19 related indicators.

In the present study, the only available information was the absolute number of hospitalized, discharged, and death cases per day, and other indicators are not considered due to unavailability.

The general structure of this article is as follows. Section 2 describes the research methodology and the methods used. Section 3 shows how the data are collected and used. The results and findings of the research are described in Section 4. Section 5 explains the model evaluation metrics, and Section 6 includes a discussion and conclusion.

2. Methodology

In this study, a combined MLP-MC model has been used to predict the values of Covid-19 related indicators. In general, the methodology of this study is depicted in Fig. 1 .

Fig. 1.

Research methodology.

2.1. MLP model

Artificial neural network (ANN) is one of the most efficient techniques in processing huge data sets that can be analyzed computationally to reveal patterns, trends, predictions, and more. This technique has a great perspective in engineering and medicine [8]. ANN is a computational structure that has a function similar to that of biological neurons [25]. This technique can learn from examples, and once trained, can make predictions and generalizations at high speed [26]. There are several types of artificial neural networks, including MLP as a feed-forward one [16]. The MLP has some advantages, such as ease of implementation, providing high-quality models, and keeping training time relatively low compared to more complex models [17]. The structure of the MLP network is shown in Fig. 2 . The MLP network consists of the input layer, one or more hidden layers, and the output layer. Each layer has several processing units (neurons), and each unit is fully interconnected with weighted connections to the unit in the next layer. A feed-forward network that has a hidden layer and enough neurons in the hidden layer can fit any limited input-output mapping problem [9]. The general expression of the network can be given as follows:

$$y=f_2\left(\sum _{j=1}^N(w_{\mathit{j}}{f}_1(\sum _{i=1}^n{h}_{\mathit{ij}}+b_{\mathit{j}})+b_0)\right)$$ (1)

where $h_{\mathit{ij}}$, $b_{\mathit{j}}$, and $f_1$ are respectively, the weight matrix, the bias vector, and the hidden layer activation function, and $w_{\mathit{j}}$, $b_0$, and $f_2$ are the weight vector, the bias scalar, and the output layer activation function [26].

Fig. 2.

MLP network structure.

An activation function enables the network to map an input to output, and the network also learns to displayed complex data. In other words, the MLP model performs statistically nonlinear regression [27]. A common activation function in hidden or output layer nodes is the sigmoid function. However, other functions such as the hyperbolic tangent or the quadratic can also be used. The activation function can be the same for all nodes, or a different function can be applied to each node. There are two types of activation functions commonly used in neural networks: linear and nonlinear. Selecting the activation function is important for the performance of the training algorithm [28].

The MLP network uses a back-propagation learning algorithm which consists of three steps: 1- estimating weights and biases and calculating output values, 2- calculating error on a return trip to the network acts in the negative gradient direction, and 3- updating the weights [29].

Estimating the number of neurons and hidden layers for a neural network depends on the type of database samples for which the network is designed—the more suitable the estimate, the better results in increasing accuracy and reducing complexity and training time [30]. It has been shown that few resources are needed to predict low-randomness time series, such as series related to the number of infections and deaths caused by COVID-19 [22].

2.2. MLP-MC model

The MLP-MC model is a combination of the MLP and MC models. In this hybrid model, MC is used to increase the accuracy of MLP prediction. MCs are stochastic processes whose parameters can be obtained by empirically estimating the transition probabilities between discrete states in the studied systems [31]. The MC model contains a set of states ($S_{\mathit{ij}}$) whose process starts in one of these states and moves from one state to another successively. Each move is considered a step [32]. In the first-order MC, each subsequent state depends only on the immediately previous state. While in second or higher-order MC, the next state depends on two or more preceding states [33]. In the present paper, the first-order MC is used.

In the proposed MLP-MC model, the test data is first predicted using the MLP. Then the residual errors between the predicted and actual values are calculated. The MLP-MC model considers the transition behaviour of residual errors using the Markov transition matrices and makes the necessary corrections to provide the predicted values based on the Markov matrices. The detailed procedure of this model is explained as follows.

2.2.1. Obtaining residual errors

First, the original data of time series are divided into training and test datasets, and according to the test values $X_{\left(\mathit{i}\right)}^{\mathit{0}}$, the predicted values ${\widehat{\mathit{X}}}_{\left(\mathit{i}\right)}^{\mathit{0}}$ are obtained using a trained MLP network. Then the residual errors between the actual and predicted values can be obtained using this relation [34]: $e\left(\mathit{i}\right)=X_{\left(\mathit{i}\right)}^{\mathit{0}}-{\widehat{\mathit{X}}}_{\left(\mathit{i}\right)}^{\mathit{0}}$. Here, $i(\mathit{i}=1,2,\cdots ,\mathit{n})$ is a time point.

2.2.2. Division of states

In this step, the residual errors obtained from the previous step are classified. To classify the residual errors, first, the number of classes $r$ must be determined. In this paper, the Sturges' Rule, $K=1+3.3\mathit{logN}$, is used to determination of $r$. Then, the width of classes, $I$, is calculated based on the following relation:

$$I=\frac{\text{Maximum}\text{error}-\text{Minimum}\text{error}\left(R\right)}{\text{the}\text{number}\text{of}\text{classes}\left(r\right)}$$ (2)

Each class is an interval whose width equals a fixed portion of the range between the maximum and the minimum of the total residual errors. Finally, the residual errors are classified based on the classes. Each class is a state and is denoted by $S_{\mathit{ij}}$. $S_{\mathit{ij}}$ is the $j$th state of the $i$th time step, which is defined as follows [34]:

$$S_{\mathit{ij}}\in [{\mathit{L}}_{\mathit{ij}},{\mathit{U}}_{\mathit{ij}}]$$ (3)

$L_{\mathit{ij}}$ and $U_{\mathit{ij}}$ denote the lower and upper boundaries of the $j$th state for the $i$th time step of the residual errors series, respectively [34].

2.2.3. Obtaining the transition probability matrix of states

The transition from one state to another in the next step is done with the probability of $P_{\mathit{ij}}^{\left(\mathit{m}\right)}$, which does not depend on which states the chain was in before the current state. Also, the process can stay in the state it is in with the probability of $P_{\mathit{ii}}^{\left(\mathit{m}\right)}$ [32].

The transition probability of states is calculated as follows:

$$P_{\mathit{ij}}^{\left(m\right)}=\frac{M_{\mathit{ij}}^{\left(m\right)}}{M_i},j=1,2,\cdots ,r.$$ (4)

where $P_{\mathit{ij}}^{\left(m\right)}$ is the probability of transition from state $i$ to $j$ by $m$ steps. $M_{\mathit{ij}}^{\left(m\right)}$ is the transition times from state $i$ to $j$ by $m$ steps, and $M_i$ is the number of data belonging to the $i$th state [34]. It is assumed that the transition probabilities do not change over time [35]. The probabilities of transition of any state are between zero and one. The sum of the transition probabilities in each row is equal to one, which is mathematically shown as follows [33]:

$$\sum _{j=1}{P}_{\mathit{ij}}^{\left(m\right)}=1,j=1,2,\cdots ,r.$$ (5)

Since the transition for the last $m$ entries of the series is indefinable, $M_i$ should be counted by the first as $n-m$ entries; $n$ is the value of entries of the original series. Then, the transition probability matrix of states can be obtained as follows [34]:

$$\begin{array}{c}\hfill R^{\left(m\right)}=\left[\begin{array}{cccc}{P}_{11}^{\left(m\right)}& P_{12}^{\left(m\right)}& \cdots & P_{1r}^{\left(m\right)}\\ P_{21}^{\left(m\right)}& P_{22}^{\left(m\right)}& \cdots & P_{2r}^{\left(m\right)}\\ ⋮& ⋮& \ddots & ⋮\\ P_{r1}^{\left(m\right)}& P_{r2}^{\left(m\right)}& \cdots & P_{\mathit{rr}}^{\left(m\right)}\end{array}\right],j=1,2,\cdots ,r.\end{array}$$ (6)

The transition probability matrix of states $R^{\left(m\right)}$ indicates the transition rules of the system. The transition probability of states $P_{\mathit{ij}}^{\left(m\right)}$ indicates the probability of transition from the initial state $i$ to the probable state $j$ by $m$ steps. Prediction can be made by having the Markov transition probability matrix. For example, Suppose $m=1$ and the maximum transition step is 1, then $R^{\left(1\right)}$ can be obtained. If the predicted original data is located in the $i$th state, the predicted data of the next step is obtained considering the row vector of the transition probability states, $P_{\mathit{ij}}^{\left(1\right)}$ [34].

2.2.4. Obtaining the predicted values

When the residual error series $e\left(i\right)$ is divided into $r$ states, there are $r$ transition probability vectors. The probabilities of a specified error state for the next step are obtained by the probabilities in $r$ row vectors, which are represented as $\{a_i\left(T\right),i=1,2,\cdots ,r\}$ at time step $T$. The centers of the $r$ state are defined as $\{v_i,i=1,2,\cdots ,r\}$. Then the predicted value for the next step is obtained based on the following equations [34]:

$${\tilde{X}}^{\left(0\right)}(T+1)={\widehat{X}}^{\left(0\right)}(T+1)+\sum _{i=1}^r{a}_i\left(T\right)v_i$$ (7)

where

$$a^{\left(T\right)}=[a_1\left(T\right),a_2\left(T\right),\cdots ,a_{\mathrm{r}}\left(T\right)]=a^{(T-1)}{R}^{\left(m\right)}$$ (8)

and

$$\begin{array}{c}\hfill \{\begin{array}{c}{a}^{(T+1)}=a^{\left(T\right)}{R}^{\left(m\right)}\\ a^{(T+2)}=a^{(T+1)}{R}^{\left(m\right)}\\ ⋮\\ a^{(T+k)}=a^{(T+K-1)}{R}^{\left(m\right)}\end{array}\end{array}$$ (9)

where $m=1$.

3. Data collection

In this study, to predict the future behaviour of indicators related to Covid-19, a dataset related to these indicators in the Bushehr province of Iran was used. These indicators included the number of hospitalized, discharged, and death cases caused by Covid-19. The dataset related to these indicators was available on the Bushehr University of Medical Sciences website at https://www.bpums.ac.ir/, and these data were reported daily from May 13, 2020, to April 1, 2021. It should be noted that some days were not reported on this website; therefore, there were some missing data. In total, the number of days whose statistics were available on the website at the time of the present study was 136 days, all of which were analyzed using MATLAB 15b and Excel 10.

The present study sought to predict the two indicators of the number of discharged and death cases according to their relationship with the number of hospitalized cases with the MLP-MC model. The daily trends of the number of hospitalized, discharged, and death cases caused by Covid-19 in Bushehr province from May 13, 2020, to April 1, 2021, are shown in Fig. 3 .

Fig. 3.

The daily trends of the number of hospitalized, discharged, and death cases.

4. Results

In this study, all 136 available data were initially divided into two categories of training and testing. The first 96 data (70% of the dataset) were used for training, and the second 40 data (30% of the dataset) were used for testing. After normalizing all the data, first in the training phase, the first 96 data (from May 13, 2020, to February 13, 2021) were entered into MATLAB software to train the MLP network. The best structure for the MLP network with the least MSE was determined as one input (number of hospitalized cases), sixteen neurons in the hidden layer, and two outputs (number of discharged and death cases). The number of neurons in the hidden layer was obtained by performing multiple trials and sensitivity analysis. The activation function was considered a nonlinear sigmoid function, and the model training was performed using the Bayesian Regularization (BR) algorithm in 454 iterations.

Then in the test phase, the second 40 data of the dataset were predicted using the trained network of the previous phase, and the test results were compared with the actual data. At this stage, the MSE obtained for the number of discharged and death cases were equal to 0.026 and 0.094, respectively, which showed that the MLP network has better predicted the number of discharged cases. Based on past data and the trained network, data for the next 40 days were also predicted.

In the second phase of the research, the MLP-MC model was used to improve the predictions obtained from the previous phase. For this purpose, first, the residual errors between the actual and predicted data for 40 test data per both output indicators (the number of discharged and death cases) were obtained separately. Then, these residual errors were classified. According to the Sturges' Rule, the number of classes (states) for both indicators was obtained equal to six, which were categorized in Table 1 for each indicator.

Table 1.

Classification of states per each output indicator.

The number of discharged cases	The number of death cases
$v_1$=[-15, -10]	$v_1$=[-2, -1.17]
$v_2$=[-10, -6]	$v_2$=[-1.17, -0.33]
$v_3$=[-6, -1]	$v_3$=[-0.33, 0.5]
$v_4$=[-1, 3]	$v_4$=[0.5, 1.33]
$v_5$=[3, 8]	$v_5$=[1.33, 2.17]
$v_6$=[8, 12]	$v_6$=[2.17, 3]

All residual errors were numbered based on the six classes associated with each indicator. Then, given the specified states, the transition probability matrix of states $R^{\left(m\right)}$, $m=1$, was obtained per each indicator as follows:

$$\begin{array}{c}{R}^{\left(1\right)}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0.083\\ 0\\ 0\end{array}\begin{array}{c}1\\ 0\\ 0\\ 0\\ 0.1\\ 0\end{array}\begin{array}{c}0\\ 0\\ 0\\ 0.25\\ 0.3\\ 0.333\end{array}\begin{array}{c}0\\ 0\\ 0.375\\ 0.417\\ 0.3\\ 0\end{array}\begin{array}{c}0\\ 0.5\\ 0.125\\ 0.250\\ 0.2\\ 0.5\end{array}\begin{array}{c}0\\ 0.5\\ 0.5\\ 0\\ 0.1\\ 0.167\end{array}\right]\hfill \\ \mathit{The}\mathit{tran}\mathit{siti}\mathit{on}\mathit{prob}\mathit{abil}\mathit{ity}\mathit{matr}\mathit{ix}\mathit{of}\mathit{stat}\mathit{es}\mathit{for}\mathit{the}\mathit{numb}\mathit{er}\hfill \\ \mathit{of}\mathit{disc}\mathit{harg}\mathit{ed}\mathit{cases}\hfill \\ \\ R^{\left(1\right)}=\left[\begin{array}{c}0\\ 0\\ 0.091\\ 0.077\\ 0\\ 0\end{array}\begin{array}{c}0.5\\ 0.429\\ 0\\ 0.077\\ 0.333\\ 0.333\end{array}\begin{array}{c}0\\ 0.143\\ 0.364\\ 0.385\\ 0\\ 0.333\end{array}\begin{array}{c}0\\ 0.286\\ 0.364\\ 0.308\\ 0.667\\ 0.333\end{array}\begin{array}{c}0.5\\ 0\\ 0.091\\ 0.077\\ 0\\ 0\end{array}\begin{array}{c}0\\ 0.143\\ 0.091\\ 0.077\\ 0\\ 0\end{array}\right]\hfill \\ \mathit{The}\mathit{tran}\mathit{siti}\mathit{on}\mathit{prob}\mathit{abil}\mathit{ity}\mathit{matr}\mathit{ix}\mathit{of}\mathit{stat}\mathit{es}\mathit{for}\mathit{the}\hfill \\ \mathit{numb}\mathit{er}\mathit{of}\mathit{death}\mathit{cases}\hfill \end{array}$$

According to the six states, their center values were calculated. Then $v_1=-12.5,$ $v_2=-8,$ $v_3=-3.5,$ $v_4=1,v_5=5.5,$ and $v_6=10$ were obtained corresponding to the number of discharged cases, and $v_1=-1.58,$ $v_2=-0.75,$ $v_3=0.08,$ $v_4=0.92,v_5=1.75,$ and $v_6=2.58$ were obtained corresponding to the number of death cases. Using formulas 7 to 9, the prediction values of these indicators were obtained both for the test dataset and for the next 40 days (April 2, 2021, to May 11, 2021). Figs. 4 and 5 show the predicted values of the next 40 days obtained using the MLP-MC model for both indicators. The forecast results showed that if the current trend continues and there is no nationwide vaccination in the coming months, on May 11, 2021, we will have 34 new discharged patients and 2 new death cases in Bushehr province.

Fig. 4.

Predicting the number of discharged cases by May 11, 2021, using the MLP-MC model.

Fig. 5.

Predicting the number of death cases by May 11, 2021, using the MLP-MC model.

5. Model evaluation

To evaluate the goodness of fit of MLP and MLP-MC models, the three metrics of Mean Absolute Deviation (MAD), Mean Square Error (MSE), and Root Mean Square Error (RMSE) for test data were compared. Relations 10 to 12 show how these metrics are obtained. Comparing the models for both indicators of the number of discharged and death cases are shown in Tables 2 and 3 , respectively. Also, these comparisons are demonstrated graphically in Fig. 6 . As shown in this figure and the tables, the MLP-MC model has higher accuracy in prediction than the MLP model. However, the difference between these two models is very slight, which indicates that the MLP model, which is a simpler model, can also be used alone to increase the forecast speed and reduce the calculations.

$$\text{MAD}=\frac{1}{n}\sum _{t=1}^n|X_{\mathit{t}}-{\widehat{\mathit{X}}}_{\mathit{t}}|$$ (10)

$$\text{MSE}=\frac{1}{n}\sum _{t=1}^n{(X_{\mathit{t}}-{\widehat{\mathit{X}}}_{\mathit{t}})}^2$$ (11)

$$\text{RMSE}=\sqrt{\frac{1}{n}{\sum }_{t=1}^n{(X_{\mathit{t}}-{\widehat{\mathit{X}}}_{\mathit{t}})}^2}$$ (12)

Table 2.

Comparison of accuracy of MLP and MLP-MC models in predicting the number of discharged cases.

MLP-MC	MLP	Models / Metrics
4.492	4.717	$\mathbf{MAD}$
32.820	34.723	$\mathbf{MSE}$
5.729	5.893	$\mathbf{RMSE}$

Table 3.

Comparison of accuracy of MLP and MLP-MC models in predicting the number of death cases.

MLP-MC	MLP	Models / Metrics
0.965	0.975	$\mathbf{MAD}$
1.496	1.675	$\mathbf{MSE}$
1.223	1.294	$\mathbf{RMSE}$

Fig. 6.

Comparison of models accuracy based on evaluation metrics for both indicators in the test phase.

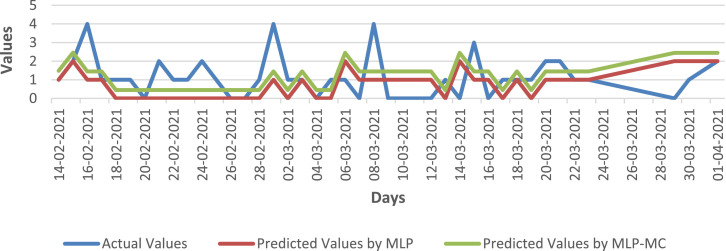
For further comparisons, the prediction results obtained by the MLP and MLP-MC models in the test phase were compared with the actual data. These comparisons for indicators of the number of discharged and death cases are shown in Fig. 7 and Fig. 8 , respectively. As can be seen in these figures, the MLP-MC model has fewer deviations from the actual data than the MLP model.

Fig. 7.

A comparison between the actual number of discharged cases and predicted values by the MLP and the MLP-MC in the test phase.

Fig. 8.

A comparison between the actual number of death cases and predicted values by the MLP and the MLP-MC in the test phase.

6. Discussion and conclusion

More than a year after the onset of the Covid-19 disease, the pandemic conditions still exist in Iran and other countries. During this period, not only has the prevalence of the disease not diminished, but in some countries, such as Iran, mutated forms of the virus have created new waves of the disease. However, Iran has not yet begun widespread vaccination. For reasons such as sanctions, specific political issues, lack of facilities, and limited domestic production capacity, widespread vaccination is improbable for at least the next few months. On the other hand, technical limitations and the high rate of coronavirus mutation have made it difficult for researchers to design an effective vaccine formula [36]. Therefore, until a widespread vaccination is carried out, government control policies and restrictions will be critical to reduce and control the disease.

The various statistical, mathematical, and artificial intelligence models used to predict future disease progression can play an essential role in government planning and policy to control the disease. Due to the high prevalence of this unknown disease and its high incidence and mortality rate, the accuracy and efficiency of the model used in forecasting are of great importance and sensitivity. The more accurately the disease prognosis is predicted, the greater the applicability, generalizability, and reliance on the model's results. Therefore, in this paper, the MLP-MC hybrid model was used to increase the accuracy of predicting the trend of Covid-19 related indicators. In other words, the main contribution of this paper was the proposed hybrid approach that combined MLP and MC models to predict the Covid-19 time series efficiently. This hybrid model simultaneously utilizes the high and fast predictive power of the MLP model and the predictive power of the MC model based on the sequence of residual errors of the MLP model.

To show the application of this model, data related to Covid-19 indicators in Bushehr province, Iran, were used. Two indicators of the number of discharged and death cases (as the model outputs) were predicted based on the number of hospitalized cases (as the model input) for test data and the next 40 days. Comparing the accuracy of the MLP-MC hybrid model showed that this model has less error than MLP alone and, therefore, higher prediction accuracy, which shows the advantage of the proposed model. However, there is a slight difference in their accuracy. This hybrid model can be seen as a general forecast model, as it can be applied to other time periods, other places, and other indicators related to Covid-19 or other areas.

It should be noted that these predictions have been made in the current situation (no widespread vaccination in the country), and the results of these predictions are valid until the mass vaccination, which is considered as a strong intervener factor. Therefore, it is suggested that if mass vaccination begins in the coming months, according to the new data collected, new predictions be made. In the case that the mass vaccination process is prolonged, it is also suggested that different scenarios be designed regarding its impact on the Covid-19 related indicators, and a re-prediction be made under these scenarios.

In future work, the proposed hybrid model can also be used for other provinces, the whole country of Iran, and other countries. This model is also applicable to simulate the effect of control schemes such as traffic restrictions on the control of indicators related to Covid-19. In addition to the Covid-19 time series, this model can also be used to predict time series in other areas such as finance, economics, and climate, especially when they have nonlinear and irregular patterns.

As another future work, the results of this model can be compared with other single or combined models, especially in the fields of artificial intelligence and machine learning. Moreover, in this study, intervention factors such as age, sex, medical history, restrictions and preventive policies, climate change, etc., have not been considered. It is suggested that these factors also be considered in future research to make more comprehensive predictions and analyses.

As mentioned earlier, no study was found that used MLP and MC models simultaneously to predict Covid-19 related indicators. However, a combination of the two models has already been used to predict indicators in other contexts. Although, the way these models are combined and used has been different. For example, [37] combined these models to predict very short-term wind speed, [38] to predict land-use change, and [39] to predict city expansion and land surface temperature. The findings of these studies showed that the MLP-MC hybrid model is suitable for predicting data with nonlinear and irregular patterns. Since the time series used in this study are also nonlinear and irregular, so it can be said that the results of this study are consistent with previous studies.

CRediT authorship contribution statement

Fatemeh Haghighat: Writing – original draft, Conceptualization, Methodology, Data curation, Investigation, Visualization, Software, Validation, Supervision, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Also, no funding was received for this work.