Abstract
Non-human primate (NHP) models are the closest approximation of human spinal cord injury (SCI) available for pre-clinical trials. The NHP models, however, include broader morphological variability that can confound experimental outcomes. We developed subject-specific finite element (FE) models to quantify the relationship between impact mechanics and SCI, including the correlations between FE outcomes and tissue damage. Subject-specific models of cervical unilateral contusion SCI were generated from pre-injury MRIs of six NHPs. Stress and strain outcomes were compared with lesion histology using logit analysis. A parallel generic model was constructed to compare the outcomes of subject-specific and generic models. The FE outcomes were correlated more strongly with gray matter damage (0.29 < R2 < 0.76) than white matter (0.18 < R2 < 0.58). Maximum/minimum principal strain, Von-Mises and Tresca stresses showed the strongest correlations (0.31 < R2 < 0.76) with tissue damage in the gray matter while minimum principal strain, Von-Mises stress, and Tresca stress best predicted white matter damage (0.23 < R2 < 0.58). Tissue damage thresholds varied for each subject. The generic FE model captured the impact biomechanics in two of the four models; however, the correlations between FE outcomes and tissue damage were weaker than the subject-specific models (gray matter [0.25 < R2 < 0.69] and white matter [R2 < 0.06] except for one subject [0.26 < R2 < 0.48]). The FE mechanical outputs correlated with tissue damage in spinal cord white and gray matters, and the subject-specific models accurately mimicked the biomechanics of NHP cervical contusion impacts.
Keywords: finite element model, non-human primate, patient-specific injury modeling, spinal cord injury, unilateral contusion injury
Introduction
Spinal cord injury (SCI) in non-human primates (NHPs) is the closest approximation to human injury available for research1,2 and provides a critical test platform for evaluating the efficacy and safety of invasive therapies such as stem cell treatments.3–5 The large scale of these animals and the inherent variability in the study population, however, make it impossible to have the same meticulous control of experimental parameters used in small animal models of SCI.6–8
Therefore, it is critical to understand and quantify potential sources of subject-specific variations in injury outcomes to minimize the variability in these experiments and provide statistical models and correlations for projecting natural recovery outcomes in each subject to maximize the sensitivity of these models to treatment outcomes and minimize the number of animals required for these experiments. Quantifying the effects of individual morphological variability on injury outcomes will also inform our understanding of human injury mechanics, the heterogeneity of human injuries,9–11 and aid in identifying individual risk factors for injury.
The significant correlation between impact biomechanics and neurological tissue damage after SCI12,13 motivates the use of computational SCI models such as finite element (FE) models to serve as a platform for understanding the SCI tissue level mechanistic behavior. This provides the foundation for defining tissue damage thresholds, directly linking FE models to injury outcomes.
Generic FE models of SCI, where the model geometry and the material specifications are generated based on a single subject14,15 or averaging several subjects,16,17 have shown tissue level stress and strain distribution,15,18 von-Mises stress,19 and maximum principal strain20 correlate with neurological/axonal damage. However, given the sensitivity of FE model outcomes to variations in model geometry,21 pre-defined constitutive material models,15,16,22,23 and injury mechanisms,20 it is unclear how the intersubject variability in spinal cord/column morphometry9–11,24,25 and material characteristics14,15,23,26–30 affects the correlations between tissue damage and injury mechanics.
To date, several studies have used generic FE models of spinal cord and SCI to extract the mechanical properties of the spinal cord and its constituent tissues,16,28 to analyze cerebral spinal fluid (CSF) interactions in SCI initiation and propagation,31–35 and to quantify tissue level deformations, stresses, or strain patterns.16,36,37 None of these studies, however, included intersubject variations in the morphometric characterizations of the spinal cord and column in their subjects, which may lessen the biofidelity of their results.
Knowing that the intersubject morphological variability is greater in large species (e.g., pigs, NHPs) and humans,9–11 and that morphological variability correlates with outcome variability in porcine SCI contusion experiments,25 motivated the need to include subject-specific morphology in this finite element study. Generating subject-specific models, however, adds cost and complexity to the modeling process. Therefore it is important to assess the differences in FE outcomes and computational costs between subject-specific and generic models.
The overall objective of the study was to assess the correlation between FE predicted mechanical outcomes and tissue damage (manifested by lesion spread) in subject-specific FE models of NHP cervical contusion SCI and compare the outcomes with a generic FE model. Our specific objectives were to: (1) generate individualized subject-specific FE models of our recent NHP unilateral cervical contusion SCI experiments using pre-injury MRIs, (2) validate the FE models' boundary conditions and material constitutive models by simulating open dura in vivo experiments, (3) calibrate the individualized FE models by comparing the FE model's overall biomechanical response with experimental outcomes and adjusting the impactor mediolateral alignment, (4) assess the correlations between FE predicted mechanical outcomes and tissue damage and investigate the effects of subject specificity on those correlations, and (5) compare the subject-specific correlations with a generic FE model of NHP by generating an average NHP FE model.
Improving the definitions of the relationships between impact biomechanics, tissue mechanics, and tissue damage is important for better understanding potential sources of variation in both large animal models and the human injury paradigm, and for defining a quantitative criteria for injury prevention technologies.
Methods
Our recent in vivo cervical spinal cord contusion experiments on NHPs1 have provided a unique opportunity to re-evaluate FE predicted tissue damage measures while exploring subject-specific variations in contusion biomechanics. Pre- and post-injury magnetic resonance imaging (MRI) scans and post-injury histology data from previous studies1,38 were used to develop FE models of each NHP test subject. These subject-specific models were then used to simulate our previous in vivo cervical unilateral contusion SCI experiments.1 The FE models were calibrated and validated against the in vivo experiments based on their biomechanical outcomes. Finally, chronic lesion histology results from the in vivo experiments were used to statistically evaluate the correlation between FE predicted tissue level mechanics and tissue damage for individual subjects.
In addition to the subject-specific models, a generic FE model was developed by averaging the cord and column morphology of four of the subjects. The generic model simulated the same impacts as the subject-specific models to assess the differences in biomechanical outcomes and injury correlations between subject-specific and generic models. Mechanical outcomes investigated in this study were: maximum/minimum principal logarithmic strain (max/min LEP), axonal logarithmic strain (LEAXON), von-Mises stress (MISES), Tresca stress (TRESCA), and strain energy density (ESEDEN).
NHP unilateral contusions
Previously, we conducted a series of in vivo unilateral cervical contusion tests on six NHPs (adult male Macaca mulatta).38,39 Briefly, experiments were performed in two groups—an open dura contusion group (n = 2) where the dura mater was perforated surgically after the laminectomy and contusion impact was applied directly to the spinal cord (open dura),38 and an intact dura group (n = 4) where the dura mater was left intact and contusion impacts were applied to the intact dura1 (Table 1).
Table 1.
Summary of Experimental Parameters and Biomechanical Outcomes for the Six Selected Non-Human Primates
 |
For all experiments, impacts were applied using a 4 mm diameter Lucite tip rod with different mediolateral impactor alignments for each test. All housing and procedures were conducted in accordance with the National Institutes of Health (NIH) Guide for the Care and Use of Laboratory Animals and were approved by The Institutional Animal Care and Use Committee at the University of California at Davis.
Open dura contusion experiments
Subjects #14 and #16 were imaged using a 3T MRI scanner approximately one week before the injury to confirm the spinal cord and CSF morphology. The surgical approach included a partial laminectomy at the fifth cervical vertebrae (C5), excising the dorsal dura mater, and visualization of the spinal cord midline. The C4 and C6 spinous processes were fixed using vertebral clamps before the impact. Before the contusion impact, the impactor tip was positioned based on a pre-set mediolateral alignment with respect to the spinal cord midline (Table 1). A pre-load of 0.3 N was used to establish a consistent starting position for impact. Blunt contusion impacts were delivered to the cord to pre-set peak displacements (Table 1). The resulting impact biomechanics (impactor displacement and force) were recorded for each subject. The contusion lesions were observed at three weeks post-injury using high-resolution 3T MRI T2-weighted isotropic scans oriented in the sagittal plane with a slice thickness of 270 μm.
Intact dura contusion experiment
Subjects #8 and 9 were scanned approximately one week before the injury with 1.5T and 3T MRI scanners, respectively (subjects #5 and 6 were not scanned pre-injury). Surgical details and biomechanical parameters were as reported previously.1 Unilateral contusion impacts were applied after a partial laminectomy at C5. The C4 and C6 spinous processes were fixed using vertebral clamps before the impact. Before the contusion impact, the impactor tip was positioned to a pre-set mediolateral alignment with respect to the spinal cord midline (Table 1). The impactor was lowered onto the dorsal dural surface to a preload of 0.5 N.
The pre-load entrapped the spinal cord against the vertebral canal, reduced the lateral motion of the spinal cord, and established a consistent starting position for impact. Peak displacements varied slightly for each test subject (-4.0 mm for subject #5 and -4.3 mm for subjects #6, #8, and #9) with pre-set impact velocities (Table 1).
Subjects were sacrificed 14–17 weeks after injury. Spinal cords were harvested, sectioned in the transverse plane at 40 μm thickness, and co-stained with eriochrome cyanine for myelin and neural red for cell bodies.1 For each subject, brightfield images were made from selected histology slices (epicenter, ±1.6 mm and ±3.2 mm rostral to the epicenter) and lesion borders were outlined.1
FE model generation
Isotropic sagittal MRI scans of each NHP subject were interpolated in Mimics (Mimics Research v19.0, Materialize N.V., Belgium) resulting in images of pixel size 0.3125 mm (intact dura subjects #5, #6, #8, and #9) and 0.2734 mm (open dura subjects #14 and #16). The three-dimensional (3D) images included the full cervical spine for all subjects (Fig. 1).
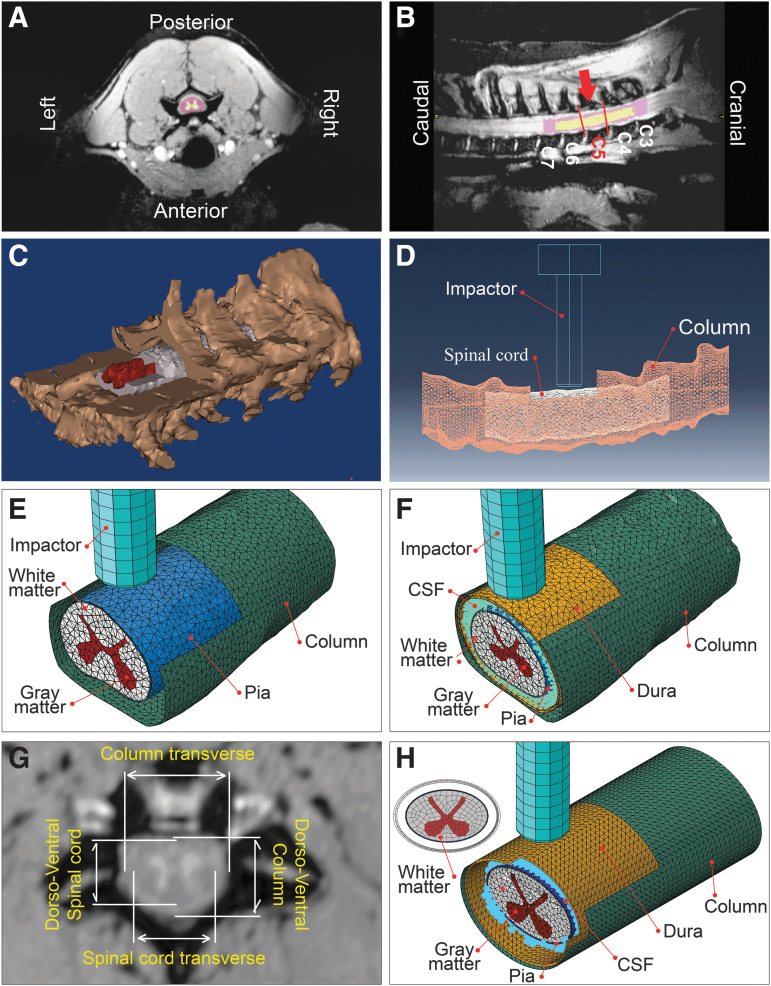
FIG. 1.
Representative magnetic resonance imaging (MRI) scan, three-dimensional (3D) segmented mask and FE models. For the subject shown here, the sagittal T2-weighted 3T MRI scans yielded 512 × 1024 pixel scans with a slice thickness of 270 μm and field of view of 140 mm. Axial view with gray and white matter masks (A), sagittal view showing target spinal cord segment (in between the red lines) and the impact position (red arrow) (B), isometric view of generated 3D mask showing C2 to C7 vertebrae, white and gray matters cut for illustration (C), a representation of FE model segment and laminectomy site (D), an isometric view of an open dura model (E), an isometric view of an intact dura FE model (F), representative of dorsoventral and transverse diameters of spinal cord and column measured for average generic model generation (G), and an isometric view of the generic model (H). CSF, cerebrospinal fluid.
Based on the post-injury MRI scans, the longitudinal location of the lesion (impact epicenter) was identified for each subject. A three-vertebrae segment was isolated using the identified epicenter as the middle vertebrae to fully include the injury site while minimizing the size of the model and the resulting computational cost.20 For open dura subjects #14 and #16, the white and gray matters and vertebral column were segmented using customized image thresholding. For intact dura subjects, the spinal cord, dura, and the vertebral column geometries were obtained via segmentation in Mimics.
Subjects #5, #6 and #8 were imaged with a 1.5T scanner; therefore, the gray matter was not clearly distinguishable and was manually added by extracting the gray matter profile from a rostral histological slide (> 4.8 mm from the epicenter). The same method was used to generate the gray matter in subject #9 for methodological consistency, even though the 3T MRI allowed for segmenting the gray matter in this subject. The spinal column, white and gray matter 3D objects were then exported to Materialise 3-Matic Research (Materialize N.V., Belgium) and meshed with tetrahedral elements (prescribed edge of 0.4 mm) after being manually partitioned. For intact dura models (#5, #6, #8, and #9), the CSF geometry was obtained by performing a Boolean operation between the spinal cord and the dural sac 3D objects in 3-Matic.
Finally, the completed orphan meshes were imported into ABAQUS (V6.14, Simulia Inc, Johnston, RI) to simulate the unilateral contusion impact. Denticulate ligaments and nerve roots were not included in the models because these components have been found to have marginal effect on the bulk cord displacement.40
For both open and intact dura experiments, the impactor was modeled as a 4 mm analytically rigid cylinder because the bulk modulus of the impactor was several orders of magnitude higher than the soft tissues of the spinal cord. Similarly, the spinal column was considered analytically rigid, because the stiffness of the vertebrae was substantially greater than spinal cord constituent materials. Three-dimensional rigid elements with quadrilateral (R3D4) and tetrahedral (R3D3) shapes were used to mesh the impactor and the spinal column, respectively. The imported orphan meshes of white and gray matters were assigned continuum C3D4 elements (continuum 3D tetrahedral) with second order accuracy. The pia mater was modeled as a skin surrounding the white matter with a thickness of 0.13 mm.41
The dura mater was modeled as a shell with a thickness of 0.35 mm.42 For open dura impacts, the dura mater was excluded from the model. For both pia and dura maters, three-node triangular shell elements (S3R elements) with second order accuracy were used. For the intact dura models, the CSF orphan mesh was imported as a solid and was converted to mass particles for further analysis using smoothed particle hydrodynamics (SPH).43,44 The posterior section of the epicenter vertebra (lamina and spinous process) was removed to mimic the in vivo surgical laminectomy.1
Finalized models comprised approximately 24,000, 98,000, 5,000, and 7,500 elements for gray matter, white matter, pia mater, and dura mater, respectively; the CSF contained ∼13,500 particles in the models (Fig. 1). To improve the computational efficiency, element distortion control, second-order accuracy, and enhanced hourglass control were applied to all the elements accordingly. The simulations were run on supercomputing clusters (Intel E5-2683 v4 CPUs, running at 2.1 GHz processors) using ABAQUS/Explicit. The open dura tests were used to validate model assumptions (contact interactions, boundary conditions, and material constitutive models), and were not further analyzed for tissue damage correlations.
Material constitutive models and properties
White matter
The rostral-caudal alignment of axonal fibers in the spinal cord white matter provides a direction-specific mechanical response.27,45 For these simulations, a conditional quasi-linear viscoelastic (QLV) transversely isotropic model16 was refined by including our recent NHP white matter compressive characterization results28 augmented with bovine tensile tests23 and derived using inverse FE optimization methods.28 The resulting conditional QLV model is a time dependent strain energy function, UWM (t), in the form of a Prony series expansion with number of terms (Equation 1):
| (1) |
where represents a conditional hyperelastic strain energy (Equation 2):
| (2) |
where represents the isotropic elastic strain energy of the glial matrix, is the contribution of the fibers in the elastic strain energy, and is the stretch in the fiber direction. Whenever the fibers are not stretched (), the matrix governs the strain energy. The matrix response is characterized by a Mooney-Rivlin model with a four-term Prony series () (Table 2)28 and combined with a quadratic reinforcing function () to capture the white matter behavior in the direction of fibers (Equation 3).16
Table 2.
Material Specifications and Properties Used in Modeling the Contusion Injury
| Tissue | Constitutive model | Hyperelastic constants | Viscoelastic constants | Density [] | Reference | |
|---|---|---|---|---|---|---|
| White matter | Mooney-Rivlin QLV with 4-term Prony series |
3.27E-3 MPa 0.91E-3 MPa 0.2393 MPa 0.4995 |
0.5256 0.3163 0.1250 0.0071 |
0.01 Sec 0.02 Sec 0.2 Sec 2.0 Sec |
1041 | This study |
| 6.172E-03 MPa | ||||||
| Gray matter | 1st order Ogden with 3-term Prony series |
4.454E-2 MPa 10.57 0.045 MPa 0.49 |
0.4793 0.2854 0.0732 |
0.64 Sec 6.40 Sec 64.0 Sec |
1045 | This study |
| Pia mater | Linear elastic |
39.3 MPa 0.3 |
- | 1075 | Kimpara41 | |
| Dura mater | 1st order Ogden with 4-term Prony series |
1.2 MPa 16.2 0.45 |
0.329 0.128 0.086 0.086 |
0.009 Sec 0.081 Sec 0.564 Sec 4.69 Sec |
1174 | Maikos30 |
| CSF | Mie-Gruneisen equation of state |
2.19 GPa 1381.7 1.979 0.11 |
- | 1007 | Kleiven56 and Panzer53 | |
QLV, quasi-linear viscoelastic.
Material density values are obtained from IT'IS website55.
| (3) |
where , and are the deviatoric invariants of the isochoric Cauchy-Green tensor, J is the determinant of the deformation gradient tensor, , , and are material parameters.
In this study, values for , and , D were assigned from the NHP white matter compressive characterization28 (Table 2). was determined through an iterative inverse FE optimization method16,28 where a series of bovine tensile tests14,23 were simulated in ABAQUS/Explicit to determine an optimized value. The conditional QLV formulation (Equation 2) was implemented as a material constitutive model using the user subroutine VUANISOHYPER_INV.16,46 The inverse FE optimization includes the off-axis loading responses and provides a more accurate FE-adoptable constitutive model for the material.
Gray matter
Unlike the white matter, axonal fibers are oriented more randomly in spinal cord gray matter; therefore, the material was considered to be isotropic. To date, only one study has managed to test isolated spinal cord gray matter, where the strips of bovine spinal cord gray matter were stretched until failure in vitro.23 The results of these bovine tests were used to determine a first order Ogden QLV model with three-term Prony series (Equation 5) for the spinal cord gray matter. The model's constitutive parameters were identified by an inverse FE optimization method,28,47–50 where the bovine gray matter tensile tests were simulated in ABAQUS and the material parameters were iteratively updated by an optimization algorithm28 to match the FE simulation results to experiments (Table 2).
| (4) |
where is the time dependent strain energy function for the gray matter and is the hyperelastic strain energy defined as (Equation 5),
| (5) |
with s defined as the deviatoric principal stretches, , and D are material properties, and J is the determinant of the deformation gradient tensor.
Pia and dura maters
Kimpara and associates41 performed a series of tensile tests on porcine cervical posterior median septum and observed a linear elastic behavior for the spinal cord pia mater at low strain rates (≤0.5 ); based on their findings, a linear elastic behavior for the pia mater was assumed (Table 2). For the dura mater, isotropic behavior was assumed and used a first order Ogden model with four-term Prony series30 (Table 2).
CSF
The mesh-free SPH method has been shown to be effective in simulating the large deformation fluid-structure interactions and complex subject-specific geometries51 for brain52 and spinal cord20 injuries. The CSF behavior was modeled as SPH particles by assuming a linear Hugoniot form of the Mie-Gruneisen equation of state46 (Equation 6).
| (6) |
where p is pressure, Em is the internal energy of the fluid per unit reference volume, c0 and s are material linear Hugoniot constants, is the nominal volumetric compressive strain with and as the reference and the current densities of the CSF, respectively, and is also a material constant.
The above equation of state, with assigned material properties of water, has been used previously to model brain CSF in FE simulations of blast brain injury.53,54 In the current study, the CSF density55 and bulk modulus (2.19 GPa)56 were used to determine c0 while the properties of water were assigned53 to s and (Table 2). Modeling CSF as SPH particles substantially decreased the stable time increments (∼1E-8 Sec) in the analysis and eliminated the possibility of parallel domain processing because of convergence difficulties. As a result, the required CPU hours for running intact dura simulations on the supercomputer cluster nodes were substantially higher than that of open dura simulations where no CSF was included in the models (about 55 CPU hours for open dura simulations versus more than 220 CPU hours for intact dura impacts).
Loading and boundary conditions
To accurately mimic the in vivo experimental conditions for both the intact and open dura impacts, the simulations were performed in two stages of pre-loading and impact. At the first stage (pre-loading), a sensor was defined on the FE impactor using the UAMP subroutine in ABAQUS to monitor the reaction force of the impactor. The impactor was lowered to touch the pia (open dura) or dura (intact dura) and then continued to trap the spinal cord against the floor of the vertebral canal. This pre-load step continued until the force readout from the sensor corresponded to the in vivo pre-load (Table 1). The CSF was not included in the models in the pre-load step because the fluid provides negligible resistance at very slow loading rates.
After the pre-load step, the impactor was held for 0.2 sec to let the viscoelastic materials relax, similar to the experimental protocol. During the pre-load step, symmetrical boundary conditions were applied to the rostral and caudal ends of the spinal cord to restrict the axial movement while allowing unrestricted dorsal/ventral and medial/lateral motion (both open and intact dura simulations). In the intact dura simulations, the rostral and caudal ends of the dura mater were fixed for the pre-loading step to prevent free rotation.
In the second stage, the actual in vivo displacement trajectory of the impactor was prescribed to the FE model impactor.1 The deformed geometries were imported from the pre-load stages. For the intact dura models, CSF particles were added to the model. The models best simulated the in vivo behavior when the symmetrical boundary conditions of the pre-load stage were substituted with fixed boundary conditions in the impact stage.
The two ends of the dura matter were prescribed axially symmetrical boundary conditions for the impact step. To confine CSF particles from escaping the dural sac during the impact, an axisymmetrical boundary condition was imposed on the first four superior/inferior rows of CSF particles at either open end of the FE model (Fig. 1). Applying this condition to less than four rows of particles did not hold the CSF particles in the dural tube during the impact. The vertebral column was secured by fixing vertebral clamps to the C4 and C6 spinous processes in the in vivo experiments1,57; therefore, fixed boundary conditions were applied to the spinal canal in the FE models. The impactor was restricted to move only in the direction of impact.
Coefficients of friction were applied at the interacting surfaces. Similar to rodent contusion SCI simulations,15,20 the coefficient of contact friction between the outer section of dura and spinal canal was assumed to be 0.15. The friction between the impactor and the dura mater (intact dura simulations) or pia mater (open dura simulations) was assumed to be slip rate dependent with the coefficient of friction equal to 0.09 and 0.18 at strain rates of 1/sec and 60/sec, respectively.58 A very low friction coefficient was assumed for the contact between the pia-dura (0.01) to simulate CSF lubrication effect. Although the CSF was removed by excising the dura in the open dura tests, there was likely some remaining fluid on the anterior side of the cord, and therefore a low contact friction coefficient (0.01) was assumed for pia-column interaction in the open dura simulations.
FE model calibration and validation
The subject-specific FE models were validated by comparing their impactor reaction force with the corresponding in vivo reaction force (force trajectory and peak value).1,39 It is known a priori that the constituent spinal cord material properties (white and gray matters and pia mater), boundary conditions, and the impactor mediolateral alignment substantially affect the impact force outcome.15,16,39 Open dura impacts were used to study and validate model assumptions without the additional complexity of the CSF. The resolved model assumptions were then applied without further alteration to the intact dura simulations.
Open dura subject #16 was used as the pilot model to systematically examine and verify modeling parameters (friction characteristics, boundary conditions, model length and mesh). A C4-C6 length model with fixed boundary conditions at the rostral and caudal free ends of spinal cord was created. Friction between the impactor and pia mater was assumed as slip rate dependent in the pilot simulation, and a constant friction coefficient of 0.01 was prescribed to pia/column contact. Model length, boundary conditions, and friction characteristics were then altered in separate models to observe their effects on the model outcome biomechanics.
Four new models were generated using the pilot model parameters: (a) a longer section of spinal cord (C3 to C7 instead of C4-C6) to examine the effects of model's length, (b) symmetrical free end boundary conditions instead of fixed, (c) frictionless contacts instead of slip rate dependent, and (d) a 25% finer mesh to evaluate mesh size effects (seed size was changed from 0.4 mm to 0.3 mm).
In these simulations, the mediolateral alignment was tuned in increments of 0.1 mm until minimum root mean square error (RMSE) between the FE predicted and experimental impactor force was obtained. Verified model parameters, boundary conditions, and friction coefficients were applied to the other open dura subject (subject #14) to validate their performance. The modeling characteristics were then used for all simulations of intact dura impacts (subjects #5, #6, #8, and #9).
Identifying the exact mediolateral positioning of the impactor during surgeries was difficult because the spinal cord was only partially visible through the laminectomy. The problem persisted for open dura experiments, with precise identification of the midline being difficult because of the limited surgical exposure. Therefore, the reported in vivo experimental alignments (Table 1) may not be accurate precisely to the submillimeter level.
Although midline contusion SCI models have reported a marginal effect of off-centered impact on their models,15,20 unilateral experiments showed that submillimeter mediolateral positioning of the impactor substantially affects in vivo impact mechanics.1,39 This is mainly due to the spinal cord's lateral shift during unilateral impacts. Therefore, preliminary studies were conducted on open dura models of this study to evaluate the reliability of mediolateral impactor positioning. These preliminary studies showed that tuning the impactor mediolateral position closely simulated the experimental impactor force output. Based on these results, because the actual reported alignments could not be confirmed, it was assumed that the tuned impactor alignment was the actual alignment.
Tissue damage correlation analysis
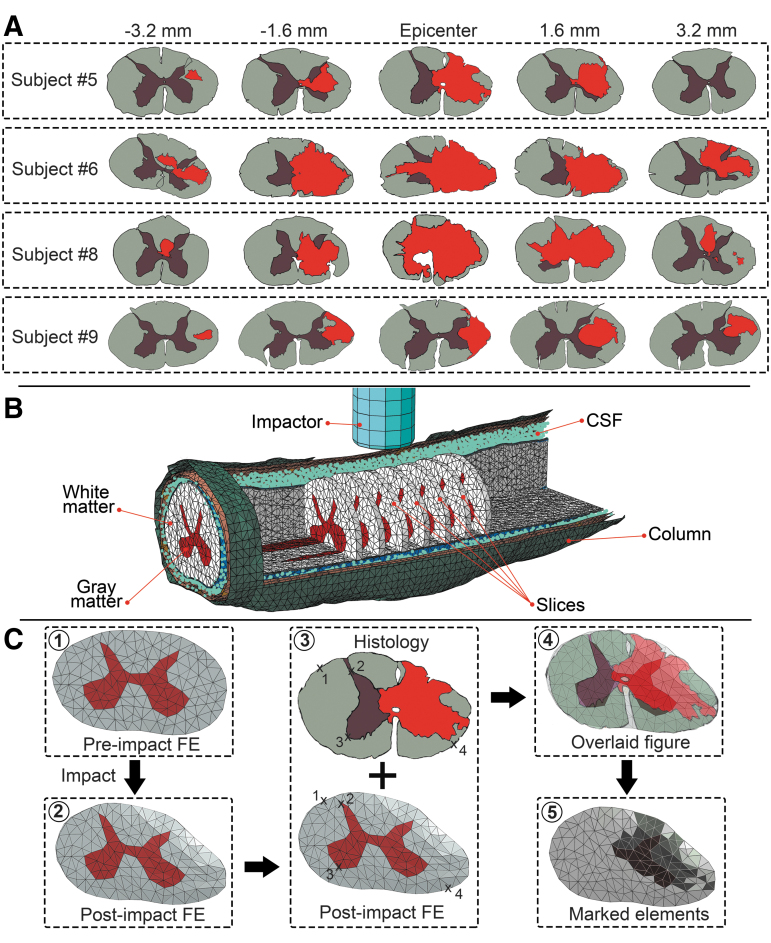
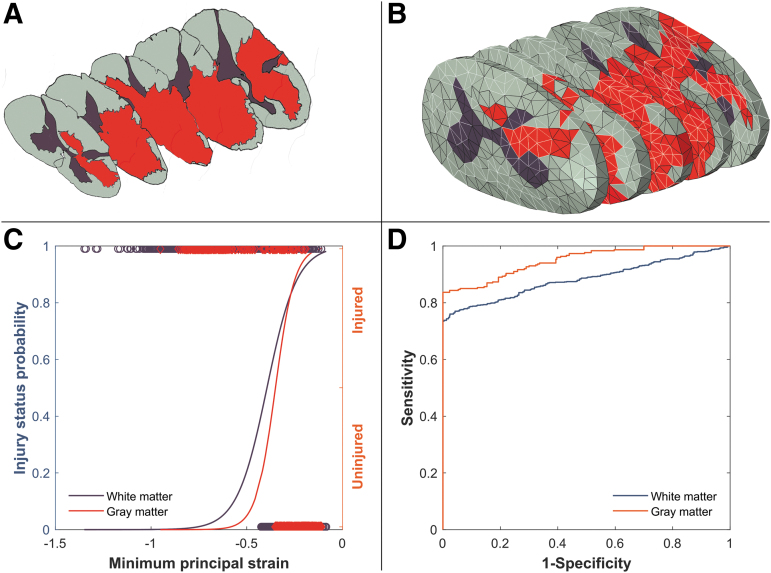
Transverse slices of one element thick (0.4 mm thick) corresponding to the histology slide positions (epicenter, 1.6 and 3.2 mm rostral and caudal) were outlined in the FE models (Fig. 2). The injury epicenter was identified as the slice centered under the impactor in the FE model and was used as a reference to locate rostral/caudal FE slices and were color-coded based on the lesion area and the spared gray and white matter regions (Fig. 2A).1
FIG. 2.
(A) Color-coded histology slides of the four intact dura subjects (gray matter, brown; white matter, gray; lesion area, red). Sections show the lesion epicenter, 3.2 mm and 1.6 mm rostral and caudal to the epicenter. (B) Isometric view of an intact dura finite element (FE) model; one element thick slices corresponding to the selected histology slides are shown. Gray and white matters, dura and pia maters, cerebrospinal fluid (CSF), and spinal column are visible in the figure. (C) Overlaying post-impact zero load FE slice onto histology slide. Arbitrary points were selected on the outline of gray and white matters in the two figures (middle) and fed to an image processing custom code to overlay the figures. Four representative points are shown in the middle figure. Injured elements are identified by dark color for both gray and white matters in the slice (right bottom).
After the impact simulation, the post-impact zero load mesh configuration of the selected slices at each level was superimposed onto the corresponding color-coded histology slide using an image processing toolbox and a custom code (MATLAB R2018a, The MathWorks Inc Natick, MA). Ventral artery and dorsal median sulcus served as the main reference landmarks. In the composite images, gray and white matter elements overlaying the injured (lesion/red) and uninjured (spared tissue colored gray for white matter and brown for gray matter) areas were identified accordingly (Fig. 2). Elements that overlaid onto both injured and uninjured tissue areas were identified as injured.59
Following previous studies of brain and spinal cord,15,18,20,23,59 several tissue level mechanical metrics were analyzed statistically to assess their correlation with tissue damage and to determine their corresponding threshold values. Because this was the first exploration of NHP contusion injury mechanics, a comprehensive assessment of several mechanical outcomes measures was performed including: min/max LEP, LEAXON, MISES, TRESCA, and ESEDEN.
For each subject, these outputs were recorded for all the elements in white and gray matters for the five selected slices during the entire impact simulation. For each element, the corresponding peak value experienced through the entire impact was listed together with the element injury status (“1” if detected as injured and “0” if uninjured). In addition to the mechanical metrics stated above, maximum/minimum principal stress and maximum/minimum pressure were investigated in our preliminary studies; however, because of their poor correlation with tissue damage, they were not included in further analysis.
Axons in the white matter were assumed to be predominantly aligned in the rostral-caudal direction before the impact. Therefore, a local coordinate system was assigned to each element of the white matter defining the axonal direction. ABAQUS traces the distortions of each element's coordinate system spatially during the impact and reports the axon direction accordingly in time intervals. Because of randomized direction distribution of axons in spinal cord gray matter, the initial alignment of the axons was not identifiable; therefore, LEAXON was not analyzed for gray matter.
Statistical analysis
For each intact dura experiment, variables were analyzed using Logit analysis in JMP (v13.2.1, SAS Institute Inc., Cary, NC) to assess their potential capability in predicting spinal cord tissue damage. In each subject, multiple random element sets (∼30) were selected from white and gray matters separately with an identical number of injured and uninjured elements. For each random set, a logistic model (Equation 7) was fit to the data of the elements' binary injury status (injured/uninjured) versus their corresponding mechanical metric peak output value experienced through the entire simulation.
| (7) |
where is the probability of the tissue being damaged, X represents a vector of the independent metrics (max/min LEP, LEAXON, MISES, TRESCA, and ESEDEN), is the model intercept and 's are the model parameters associated with and the independent metrics.
JMP uses the maximum likelihood estimation method (log-likelihood) to determine the best fit parameters for regression. A specific likelihood ratio chi-square test was performed where the observed p value of the test was judged for model goodness-of-fit assessment (significance was assumed at p < 0.05). To determine which candidate output metric provided the best correlation with the occurrence of spinal cord tissue damage, the Nagelkerke R-squared statistic60 was calculated for each fit15,61 (limits were 0 for poor and 1 for perfect correlation). Moreover, the performance of the binary classifier model at varied thresholds was evaluated by plotting receiver operating characteristic (ROC) curves for different output metrics and comparing the area under the ROC curve (AUC). The output metric with AUC closest to 1 was considered the best predictor of tissue damage.62
In addition, breakdown values (thresholds) for 50% probability of injury were determined for each output metric by inverse prediction method using confidence interval of 0.9. Mean and standard deviation of the Nagelkerke R-squares and the AUCs obtained for the random element sets were determined for the metrics in white and gray matters and was compared for each subject.
Finally, for each mechanical outcome metric, injury threshold values were compared statistically among the four subjects to determine between-subject variations. Threshold values of the element sets within a subject were grouped, and the group means were compared for individual mechanical metrics using one-way analysis of variance with significance level set at α = 0.05. Mechanical metrics with significant differences between subject thresholds should be considered as subject-specific tissue damage thresholds.
Generic NHP FE model
To evaluate the significance of generating subject-specific FE models, a generic averaged model of the four intact dura NHP subjects was generated and the model outcomes and correlations with tissue damage were compared. The generic model morphology was based on the averaged dimensions of the four subjects. The FE output and tissue damage correlations were compared with the subject-specific outcomes.
Pre-injury MRIs were used to measure the dorsoventral and transverse diameters of spinal cord and column corresponding to the injury epicenter (Fig. 1G). Resulting averages were used to generate elliptical cross-sections to represent the spinal cord. The average values for spinal cord dorsoventral and transverse diameters were 5.3 mm and 8.6 mm, respectively, and 8.2 mm and 10.9 mm for the column, respectively. The cross-sections were then extruded for 30 mm (representing the three-vertebrae cranial-caudal length of subject-specific models) with a shell cylinder for the spinal column and a solid cylinder representing the spinal cord (Fig. 1H).
A gray matter profile was created by averaging the gray matter profiles of the four intact dura subjects. Dura matter was generated by scaling down the column cylinder by 1.5% to avoid element overlap. The CSF geometry was obtained via Boolean operation using the same methods as the subject-specific methods. Impactor dimensions, CSF properties, and mesh attributes were the same as the subject-specific models.
Results
Model validation and biomechanics
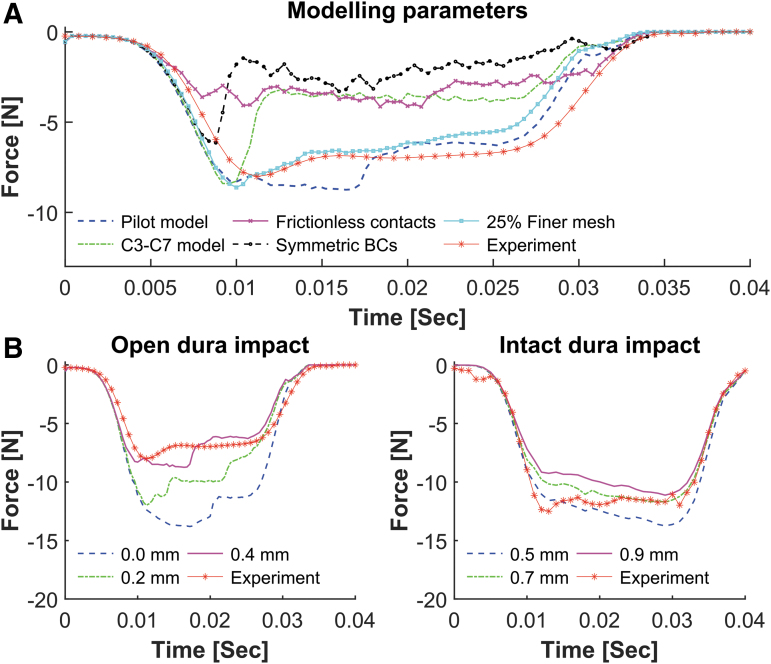
The impactor output force behavior of the pilot subject (subject #16) best matched the corresponding experimental output (RMSE = 0.93) when fixed end boundary conditions and slip rate dependent friction coefficients were applied to the model (Fig. 3A) particularly when the mediolateral alignment of the impactor was adjusted to -0.4 mm (over midline or a more centered impact) compared with the experimental alignment of -0.5 mm (Table 1).
FIG. 3.
Effects of modeling parameters on finite element (FE) predicted impactor force output. Each parameter was assessed independently. (A) Compared with the pilot model (blue dashed line), increasing the model length to C3–C7 (green dashed line) had marginal effects on the peak force; however, the force trajectory deviated from the experiment. Changing the pilot model's contacts to frictionless underestimated the reaction force of the impactor (magenta solid line). Similarly, lower reaction force was observed when using symmetrical boundary conditions (BCs) in the pilot model (black dashed line). Running the pilot model simulation with 25% finer mesh better predicted the experiment, however, was intensively costly. (B) Effects of impactor mediolateral alignment on FE model force response for subject #16 and subject #5 as representatives of open and intact dura models, respectively. Positive values show under the midline alignment of the impactor (i.e., a more lateral impact).
Using frictionless contacts did not improve the model's biomechanical outputs (RMSE >2.61) (Fig. 3A). Applying symmetrical boundary conditions to the rostral and caudal ends of the spinal cord degraded the biomechanical outcomes of the model (RMSE >3.50). Extending the pilot model length by one vertebra rostrally and caudally (i.e., extend from C4–C6 to C3–C7) did not affect the impactor's peak force; however, the force output trajectory match deteriorated (RMSE = 2.40).
Refining the model mesh by 25% (seed size = 0.3 mm) did not alter the impactor's peak force; however, the overall in vivo force trajectory was better captured when the mesh was finer (RMSE = 1.00) (Fig. 3A). Although the 25% finer mesh model better predicted the in vivo output, the simulation required nearly triple the computational time. Combined, fixed boundary conditions and slip rate dependent contact definitions with a mesh seed size of 0.4 mm best mimicked the biomechanical outcomes of the pilot model.
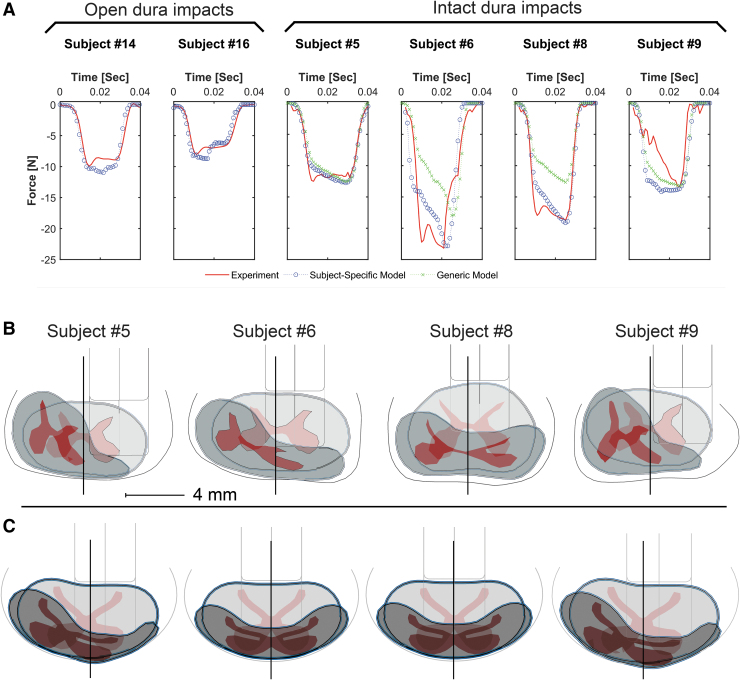
The impactor force output was affected substantially by the mediolateral alignment of the impactor in both open dura and intact dura models (Fig. 3B). In all subjects, setting the FE impactor to the reported in vivo mediolateral alignments (Table 1) overestimated the impactor output force. However, models were able to depict the in vivo force output with RMSE <0.5 and peak force difference less than 6% when the impactor mediolateral alignments were tuned (Fig. 4 and Table 1).
FIG. 4.
Impactor force outputs of subject-specific finite element (FE) models, generic FE models, and their corresponding in vivo experiments (generic models were not developed for the open dura tests) (A), superimposed deformed and undeformed configurations of intact dura subject-specific models (B), and generic models (C), showing the ultimate mediolateral positioning of the impactor in each simulation. Spinal canal, gray and white matters, pia mater, and the impactor are visible. Deformed configuration is presented at the maximum impactor stroke. Solid lines show the assumed midlines, impactor alignment over the midline (subjects #6, #8, and all generic models) is defined as negative alignment (Table 1), and the scale bar is 4 mm. Open dura subjects are not shown.
The generic models underestimated the impactor force when the experimental (actual) mediolateral alignments (Table 1) were used to simulate the impacts. In subjects #5 and #9, tuning the impactor alignment to a more centered impact (-1.2 mm and -1.4 mm over the midline, respectively) resulted in a reasonable impactor force outcome (RMSE = 1.24 and RMSE = 2.84). However, the experimental impactor force was not achieved for subjects #6 and #8, even with a centered impact (RMSE = 6.2 and RMSE = 8.42, respectively) (Fig. 4). The RMSE values for the generic models were higher compared with subject-specific models.
Subject-specific qualitative analysis of injury outcomes
The longitudinal distribution patterns showed elevated levels of the investigated metrics (min/max LEP, MISES, TRESCA, and ESEDEN) centered under the impactor. These elevated areas did not extend substantially beyond the impact zone (<2 mm) (Fig. 5). Studying the distribution patterns at the epicenter and ±1.6 mm and ±3.2 mm rostral/caudal also confirmed the rapid dissipation of stress, strain, and strain energy away from the injury epicenter. The rostral/caudal distribution of output metrics about the epicenter was not symmetrical in all the FE simulations. These observations matched the patterns of tissue damage in the corresponding experiments1 and other in vivo contusion experiments.15,63
FIG. 5.
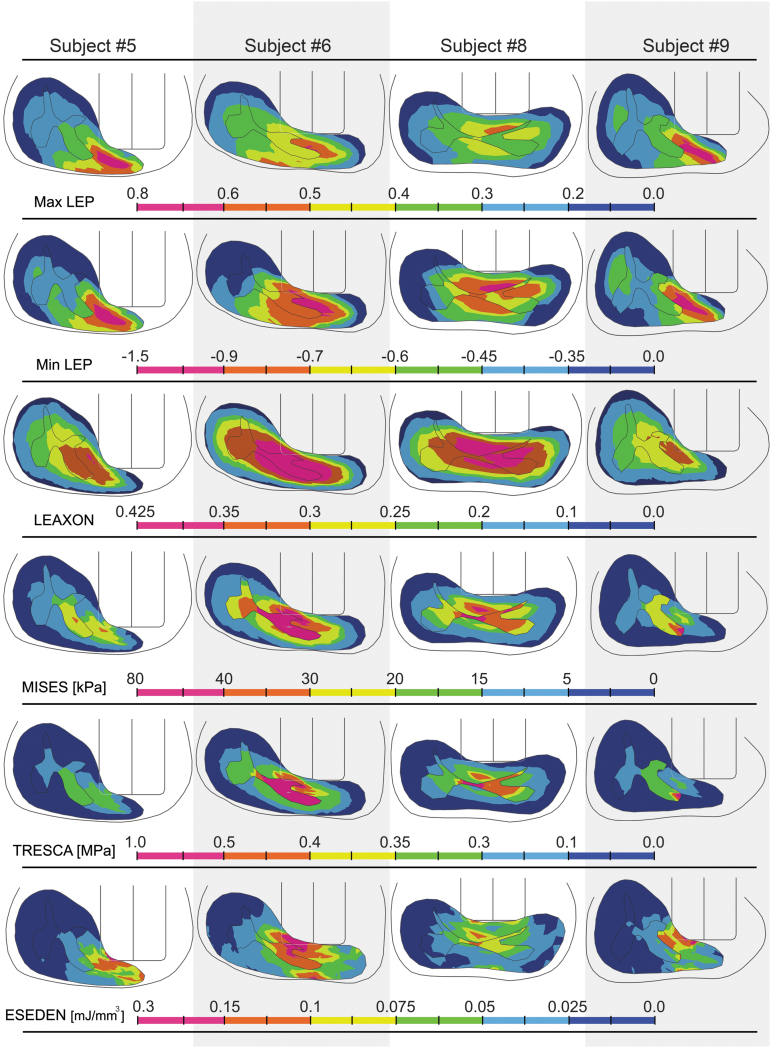
Contours representing the distribution of max/min LEP, LEAXON, MISES, TRESCA and ESEDEN at maximum impactor penetration for subject-specific models. Values of all output variables dissipate at the rostral and caudal ends of the model, demonstrating the minimum effects of end boundary conditions. max/min LEP, maximum/minimum principal logarithmic strain; LEAXON, axonal logarithmic strain; MISES, von-Mises stress; TRESCA, Tresca stress; ESEDEN, strain energy density.
Subject-specific review of the impact results showed that larger portions of the contralateral spinal cord cross-section had elevated levels of output variables in subjects #6 and #8 (Fig. 6) where the impactor position was more centered (over the midline) compared with other subjects (Fig. 4). For all of the subjects, the zone for peak strain outputs (max/min LEP and LEAXON) was localized under the tip of the impactor (Fig. 6).
FIG. 6.
Distribution of output variables at the peak displacement of the impactor in intact dura subjects. Each column is a subject and each row is an output variable for subject-specific models. The cross-sectional slice located under impactor midline is presented (injury epicenter). Deformed gray and white matters, spinal column, and the impactor are visible in the cross-section. Scale bar is 4 mm. max/min LEP, maximum/minimum principal logarithmic strain; LEAXON, axonal logarithmic strain; MISES, von-Mises stress; TRESCA, Tresca stress; ESEDEN, strain energy density.
Ipsilateral ventral gray matter horns showed the greatest stresses and strains in all subjects. In the white matter, elevated mechanical stresses and strains were located in the lateral funiculus for all subjects. Zones of high stresses (MISES, TRESCA), or strains (max/min LEP and LEAXON) were concentrated at the boundary of gray/white matters. Generally, peak output magnitudes in the white matter corresponded with the area of maximum compression. Distributions of all output metrics showed a narrow peripheral rim of ipsilateral white matter (adjacent to the pia mater) where the magnitudes were lower compared with the surrounding tissue.
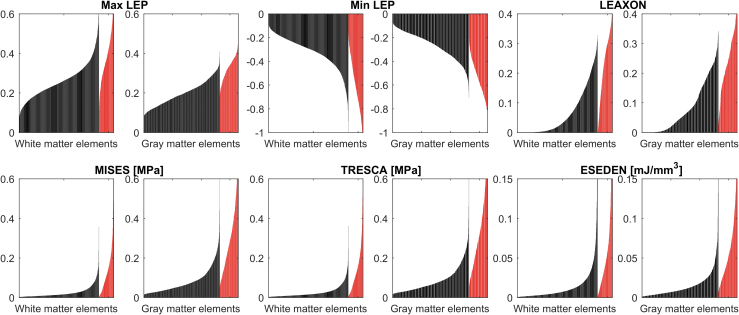
At maximum compression, min LEP, LEAXON, and MISES output patterns showed the most conformity with histology results at the epicenter. It is important to note that the spinal cord tissue may not experience the same distribution patterns of mechanical metrics during the impact. Extracting peak output values from all the elements at the selected interval for the intact dura subjects showed the general distribution of the output variables during the entire contusion simulation (Fig. 7). Rank-size distributions demonstrate the distribution of elements experiencing a given level of stress or strain. For injured/uninjured tissue to be perfectly distinguishable, there should be no overlap in the diagram. Min/max LEP in both gray and white matters showed the minimum discontinuity among the mechanical metrics, suggesting that min/max LEP may be better predictors of tissue damage than the other outcome metrics.
FIG. 7.
Rank-size distributions of peak values of each mechanical outcome experienced in the entire duration of impact for injured (red) and uninjured (black) elements (selected slices from all intact dura subjects). A smaller discontinuity between uninjured and injured section indicates the discriminative capability of the metric is stronger (less overlap in outcome values between injured and uninjured elements). The x axis shows the uninjured element rankings (black) followed by injured element rankings (red) by their magnitude. Each bar on the plot is the observation from one element. Generally, white matter elements experienced higher strain levels (max/min LEP and LEAXON) compared with gray matter elements; contrarily, higher levels of stress (MISES and TRESCA) were observed in the gray matter elements. max/min LEP, maximum/minimum principal logarithmic strain; LEAXON, axonal logarithmic strain; MISES, von-Mises stress; TRESCA, Tresca stress; ESEDEN, strain energy density.
In addition, on average, gray matter elements experienced almost double the level of stress (i.e., MISES and TRESCA) observed in white matter elements. This was opposite for strain levels (i.e., max/min LEP), where the white matter elements experienced 24.6% and 12.7% higher levels of maximum and minimum LEP, respectively, compared with gray matter (Fig. 7). Similar distributions as Figure 7 were observed in subject-specific distributions of elements' peak values in our preliminary studies.
FE outcome–tissue damage correlation analysis
Tests of goodness-of-fit resulted in statistically significant values on the chi-square term for logistic regression curves of all mechanical metrics (ρ < 0.0001) (Fig. 8). Generally, all metrics presented better potential in predicting gray matter tissue damage compared with white matter (Table 3). All AUC values were between 0.75 and 0.95, showing the discriminative capability of all selected metrics.
FIG. 8.
Example logistic analysis (minimum principal logarithmic strain [min LEP] in subject #6 in this case) on a randomly selected element set. (A) histology slides (white matter in gray, gray matter in brown, and injured tissue in red) stacked in isometric view showing epicenter, ±1.6 mm and ±3.2 rostral with corresponding (B) FE slices at approximately the same anatomical position. Random sets of elements were selected for white and gray matters from all the five slices (elements with light border) comprising approximately the same number of injured and uninjured elements for each set. (C) The peak min LEP experienced by the elements in the element set were plotted against binary status of the element, and a logit regression curve was fitted. In this case, the fit was statistically significant with p < 0.0001 for both gray and white matters, and the Nagelkerke R-square was 0.66 ± 0.04 and 0.36 ± 0.02 for gray and white matters, respectively. (D) Receiver operating characteristic (ROC) curve is higher for the gray matter (is more distanced from the diagonal line) therefore, min LEP has better predictive power for gray matter tissue damage compared with the white matter ROC curve. This is confirmed with area under the curve values equal to 0.95 and 0.88 for gray and white matters, respectively.
Table 3.
Results of Logistic Regression Analysis for Subject-Specific and Generic Models Comparing the Potential Capability of Different Mechanical Metrics for Predicting Spinal Cord Tissue Damage Computed for the Four Intact Dura Subjects
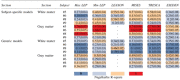 |
max/min LEP, maximum/minimum principal logarithmic strain; LEAXON, axonal logarithmic strain; MISES, von-Mises stress; TRESCA, Tresca stress; ESEDEN, strain energy density.
The heat map shows mean Nagelkerke R-square values that represent the capability of different mechanical metrics to predict tissue injury. The values in the parentheses show the standard deviation of the mean.
Subject-specific review of the results showed that in subjects #5 and #8, Min LEP, LEAXON, TRESCA and MISES were better predictors of tissue damage in white matter (higher Nagelkerke R-square) compared with max LEP or ESEDEN with some variation in the order of best fit across the subjects. Stress metrics (MISES and TRESCA) better predicted damage than strain or strain energy metrics (Min/Max LEP, LEAXON, ESEDEN) for all subjects. In subject #9, all metrics poorly depicted tissue damage except min and max LEP. For the gray matter, max LEP, min LEP, MISES, and TRESCA were the best predictors of tissue damage with Nagelkerke R-squares between 0.58 and 0.76, except for subject #9.
Using the fitted logistic curves, threshold values for each metric parameter were determined at 50% probability of tissue damage (Table 4). All the metrics had significantly different damage threshold values across subjects, indicating that tissue damage thresholds were subject-specific.
Table 4.
Threshold Values of 50% Probability of Tissue Injury (Mean±Std) for Subject-Specific and Generic Models
 |
max/min LEP, maximum/minimum principal logarithmic strain; LEAXON, axonal logarithmic strain; MISES, von-Mises stress; TRESCA, Tresca stress; ESEDEN, strain energy density; STD, standard deviation; GM, gray matter; WM, white matter.
The top and bottom rows of each cell correspond to gray and white matter results, respectively.
The AUC values for the generic models were lower than the subject-specific values for all subjects and metrics. The AUC values for subjects #5, #8, and #9 were between 0.77 and 0.89; however, the values for subject #6 were all less than 0.7. The generic models showed the same trends in the mechanical metrics in predicting tissue damage as subject-specific models, with all metrics showing better predictions in gray matter, however, with lower Nagelkerke R-squares (Table 3).
For all the subjects, the biomechanics of the impact (mediolateral impactor alignment and peak forces) better matched the corresponding histology slides and impactor outcomes in subject-specific models compared with generic models. The 50% probability tissue damage thresholds predicted by generic models were significantly different and varied from subject-specific model thresholds substantially (Table 4). No trend was observed between the threshold values obtained from the generic models and the subject-specific models.
Discussion
NHP models closely reflect human central nervous system anatomy and physiology1,2 and demonstrate a morphological heterogeneity more similar to clinical SCI. NHP contusion SCI models provide a critical test bed for invasive treatment modalities such as stem cell therapies ahead of human studies.3–5 Therefore, understanding and quantifying the link between injury mechanics and tissue damage in NHP models has important implications for developing standardized injury protocols. Establishment of a standardized SCI helps to minimize the experimental variability and provide a reliable foundation to assess clinical treatment efficacy.
This study is the first to present NHP subject-specific FE models of contusion SCI, compare these models with generic FE models of the SCI, and investigate the correlations of FE predicted outcomes with tissue damage. The primary contribution of this research was the use of NHPs as a large-scale human-like animal model in a subject-specific approach that matches the in vivo experiments. This allowed for a thorough exploration of the injury biomechanics and the potential correlations between FE mechanics and tissue damage by including intersubject anatomical and morphological variabilities in a human-like species.
Similar to previous studies, min/max LEP, MISES, and TRESCA showed stronger correlations with tissue damage than other metrics.15,18,20,64 Min/max LEP are the minimum (compressive) and maximum (tensile) strains experienced in an element in any direction. Max LEP is widely suggested as a tissue failure criteria for spinal cord injury.15,20,59 Min LEP can occur in the same element as Max LEP but in orthogonal directions (e.g., increased vertical stretch results in greater horizontal compression). MISES and TRESCA are measures of the distortional and shear stress in tissue elements, respectively, where shear is a specific form of distortion.
Mapping mechanical loading to tissue damage is a critical hurdle in making FE models capable of directly predicting damage instead of tissue mechanics. Defining this relationship has been the objective of many researchers in several animal models.15,20,21,59,61 Quantifying the relationships between mechanical loading and damage will expand the capabilities of FE models and provide the opportunity to use FE models to assess the effectiveness of injury prevention methods in reducing injury, to study the effect of impact parameters on injury, and to eventually map subject-specific impact parameters to reduce experimental variability in large animal models.
To quantify the effect of subject-specific geometry, a generic model was created by averaging the intact dura subjects similar to previous studies.15–17,20,23,59 The generic model was not able to capture the impact biomechanics of two of the four intact dura impacts despite tuning the impactor alignment. Previous studies also reported the inability of generic models to capture the experimental outcomes.15,20 In those studies, the model's constitutive material properties were adjusted to calibrate the model outcome. In the model presented here, the material properties and constitutive models were derived from experimental results. Altering the material properties moves the definitions farther from the experimentally observed characteristics.
For the two subjects where the biomechanics of the impact were captured, the mediolateral alignment of the impactor necessary to correlate with the external impact resulted in predicted patterns of tissue loading that did not align with the observed tissue damage (Fig. 2).
Besides the overall biomechanics of the impact, the FE outcome and tissue damage correlations obtained from logistic regression analysis using these generic models were generally weaker than when subject-specific models were used (Table 3). Comparing the results of the generic model with the subject-specific outcomes revealed the significance of including the natural variations in the morphometry of spinal cord and column in FE models.
The developed FE models expand the state of the art for computational models of SCI. Working with a larger scale animal model provided the opportunity to measure tissue mechanics and derive NHP-specific white matter constitutive models28 to use in the current study. The constitutive model also captured the transverse isotropy of white matter by utilizing an experimentally derived strain energy function.16 These anisotropic characteristics of the spinal cord have not been included in previous FE models of SCI.15,17,20,65 In addition, the FE models distinctly modeled the white and gray matters and the pia mater.
Discrete modeling of the pia mater has been shown to affect the SCI FE model outcome patterns.16 In contrast to previous models, which do not include the pia matter explicitly,15,20 the distributions of peak stresses and strains showed a rim of spared tissue in the white matter directly under the impactor—similar to the observed histology. This reinforces the importance of distinguishing the constituent materials to accurately capture patterns of injury. Further, treating white and gray matters as identical materials neglects the complexity of the spinal cord tissue, interactions between the two materials, and affects the intraparenchymal mechanics of the model. By integrating these material constitutive models, discrete modeling of spinal cord constituent components and tuning the impactor mediolateral alignment, the open dura simulations closely replicated their in vivo counterparts.
In a study by Maikos and colleagues,15 max LEP resulting from midline contusion FE simulations on rats was found to have significant correlation with patterns of blood–spinal cord barrier breakdown (quantified by albumin extravasation) with average Nagelkerke R-squares of 0.84 ± 0.05 for gray matter and 0.56 ± 0.12 for white matter. The R-square values determined in our study for max LEP were lower (between 0.37 ± 0.09 and 0.76 ± 0.05 for gray matter and 0.18 ± 0.03 and 0.4 ± 0.04 for white matter) (Table 3). That study did not evaluate other FE metrics.
A potential source for discrepancy may be using a chronic lesion instead of the acute injury used by Maikos and coworkers15 for correlating tissue responses to computational predictions. The primary damage to the blood–spinal cord barrier that occurs in the acute injury contributes significantly to the overall pathology, including the introduction of reactive species that induce cytotoxicity as well as secondary insults on the blood–spinal cord barrier itself. The chronic lesions that were used to establish correlations with tissue mechanics in this study were mediated by the evolution of secondary injury. These chronic lesions, however, are arguably more clinically relevant in representing the long-term implications of the mechanical impact.
Further, a stronger correlation was observed between contusion injury impact parameters (impact velocity, cord compression depth, and cord compression rate) and albumin extravasation compared with hemorrhage in rats,29 which suggests albumin extravasation should better correlate with FE predicted tissue mechanics.
The insignificant correlation between tissue damage and FE predictions in subject #9 (Table 3) may also be attributed to the milder injury generated in this subject and the limited involvement of gray matter. In subject #9, the impact was excessively lateral, resulting in a noticeably smaller lesion compared with other subjects (Fig. 2). The lateral impact was attributed experimentally to undiagnosed scoliosis,1 which may have resulted in impingement on the laminectomy opening and provided the unusual force history. Specifically, in the gray matter, the R-square values were substantially lower compared with other subjects (0.29–0.37 compared with 0.39–0.76); this is likely because of the limited involvement of the gray matter in this lesion.
The greater involvement of the gray matter in the lesion in this NHP study may account for the higher correlations between mechanical loading and damage observed in the gray matter compared with white matter (Table 3). Histological sections, processed with eriochrome cyanine and neutral red to capture the spread of damage in both the gray and white matter, showed gray matter involvement up to 100% in the lesion while white matter had a maximum of 50% involvement.1 Several studies have highlighted the particular susceptibility of the gray matter to contusion injury.15,66 This has been attributed to greater blood vessel density in spinal cord gray matter and the capillaries being finer and more susceptible to impact.67–69 Mechanical perturbation of the blood–spinal cord barrier and/or microvasculature causes hemorrhage and leads to the spread of lesion in the spinal cord.
The inclusion of a distinct pia mater membrane in our model provided a protective effect for the adjacent white matter resulting in peripheral white matter sparing in the FE model, which corresponded to histological outcomes. In addition, small adjustments to mediolateral alignment predominately affect the degree of white matter involvement in the lesion while having less effect on gray matter involvement. Consequently, the distribution patterns of all types of mechanical perturbations (stress, strain, or energy density) in the tissue more significantly matched the lesion spread for the gray matter compared with the white matter. The higher correlations observed in this study in the gray matter are in agreement with previous published evaluations in SCI studies.15,23
Strain in the axon direction (LEAXON) has been proposed by others in the fields of spinal cord18,70 and brain61,71–73 injury as a strong correlate with injury. The LEAXON was found to correlate moderately with tissue damage in two of our subjects (subjects #5 and #8 with R-square values of 0.55 ± 0.04 and 0.58 ± 0.03, respectively); however, the correlation was poor in the two other subjects (<0.37, Table 3). The LEAXON threshold values determined for white matter in our study (between 0.1 and 0.16) agreed with numerical tolerance limits reported for brain diffuse axon injury (0.1465 by Sahoo and associates61 and 0.13 by Giordano and colleagues73). These threshold results are similar to experimentally derived strain limits of isolated spinal cord and brain axons (0.18 by Bain and coworkers,71 0.2 by Morrison and associates,72 and 0.16 by Singh and colleagues74). Strains in the axon direction will be affected by the anisotropy model used to represent white matter properties in this study.
The complexity of NHP in vivo unilateral contusion injury experiments and FE modeling introduced several challenges to this study and resulted in some limitations. First, because of the limited visibility during surgery, precisely determining the mediolateral alignment of the impactor relative to the spinal cord was not possible in the experiments. Therefore, the mediolateral alignments of the impactors in the FE models were approximated and the alignment was tuned to match the experimental impactor force output. The accuracy of the tuned FE impactor positions was confirmed by comparing the FE models with their corresponding histology at the epicenter (Fig. 2A epicenter and Fig. 4B).
The ipsilateral magnitude and the contralateral extent of the tissue damage reflect the mediolateral alignment of the impactor in the corresponding simulation (except for subject #9 where scoliosis was observed). In subjects #5, #6 and #8 as the impactor alignment moved over the spinal cord midline, the mechanical tissue loading better reflected the histologically observed tissue damage, demonstrating the suitability of the calibration method.
Second, the spinal cord constituent material properties were characterized by direct in vitro mechanical tests16,23,28,30 and via FE adaptable methods. The material constitutive models were not adjusted further, and the same constitutive material models were used for all of the simulations. A considerable amount of variability has been reported in the spinal cord constituent material mechanical behavior specifically in larger animals such as porcine27 and NHPs.28 Using generic, fixed material constitutive models in the current study may limit the subject-specificity of the output results. Obtaining individualized accurate material properties for SCI simulation, however, is not trivial and requires advanced, non-invasive methods to obtain large deformation tissue characteristics. This is currently not possible.
Total Lagrangian formulation FE analysis methods (instead of the updated Lagrangian formulation used in our study) showed the ability to predict the resulting deformation field with a minimal dependency on the pre-defined constitutive material properties in studies of brain injury75–78 and the potential to circumvent the need for including material characteristic variations in subject-specific SCI models.79 However, the method is unreliable for flow-like behavior (e.g., CSF in this case) or topology changes. In addition, description of strains (and stresses) in large strain regimes (inherent to contusion impact) are complicated because of the initial displacement effects.75
The histology in this study represents the chronic phase of injury (∼20 weeks post-injury), which includes the effects of both the mechanical impact and secondary injury cascade. Although this can make the statistical analysis more variable and noisy, it is also more relevant for understanding the link between mechanical impact and long-term outcomes (which are most important to the patient). This study did not include a sham group; however, considering the localized nature of contusive SCI,15,20 preliminary analyses were performed using tissue sections remote from the injury epicenter (±4.8 mm rostral) and the significance of the study statistical results were not changed.
Finally, the small number of intact dura subjects (n = 4) in this study limited the statistical power of the presented injury thresholds. Although we tried to reduce the uncertainty of our results by choosing random sets of elements for our statistical analysis, including more subjects with consistent injuries into the analysis will reduce the risk of false-negative finding (type II error) and is beneficial. Ongoing work will expand the number of subjects to increase the fidelity of FE outcomes.
The FE modeling approach also included some limitations. Generating gray matter geometry based on histology rather than MRIs in the intact dura models was a limitation of this study because it neglects the morphometric variations of gray matter geometry along the spinal cord length. The gray matter geometry was modified along the path based on the histology slides in the corresponding cross-section. None of the models included nerve roots, denticulate ligaments, or blood vessels. Adding these exterior structures could restrict the lateral movement of the spinal cord. This is of particular importance in the simulations of this study because the impact was unilateral, and, unlike previous models of midline impact in rodents,15 the stability of the spinal cord in resistance to bulk lateral shift plays an important role. The conformity of the current FE models' biomechanical behavior with in vivo results, however, suggests that the roles of these additional structures was minimal, or adequately captured by the assigned boundary conditions.
Second, the material models used in this study have limitations because of the few available experimental results. The gray matter material model and the viscoelastic material parameters used in the FE models were based on low strain rate experiments (<0.5/sec)23 and the material behavior at higher rates is undefined. Further work is needed to characterize these properties directly, although these experiments are exceedingly complex.
The moderate to significant correlation of min LEP (compressive strain) and tissue damage observed here in white and gray matters, respectively, suggests that besides the accepted mechanisms of neurological tissue damage such as membrane permeability80,81 or axon/myelin disruption,37,70,82 that disruption to the spinal cord blood supply needs to be measured in absence not only via hemorrhage. In theory, compressive strain may contribute to blocking circulation. It has been hypothesized that disrupted circulation leads to insufficient blood supply and results in tissue damage.83,84
High accuracy computational models, such as the ones developed in the current study, could be used reliably in animal model development and testing injury prevention strategies. Translating these models to human injuries has the potential to contribute to clinical decision making and surgical planning where the effects of different surgical interventions may be assessed on the computer first. As an example, these individualized FE models may help in overcoming the challenges in the development of standardized in vivo models of traumatic SCI in large animals such as pigs and NHPs.1,25,39
Inducing a consistent injury in animal models is critically important to establish an injury baseline and to differentiate the efficacy of treatment strategies from normal recovery. Carefully controlled study populations and removing “mis-hit” animals from analysis have led to tightly correlated impact biomechanical parameters and injury in rats85–87 and mice88,89; however, these same correlations are not as clear in larger animal models such as pigs or NHPs primarily. The variation in outcomes has been attributed to more variable cord and column morphologies in large animals.1,25
Given the extensive housing and experimental costs for large animals (specifically NHPs) and the desire to minimize the use of animals, establishing methods for reducing experimental variability is critical. The sensitivity of the contusion model outcomes to different parameters observed in the current study suggests that in large animal models of SCI, getting consistent, standardized injury outcomes may require subject-specific impact parameters.
The FE predicted injury patterns may also be valuable in further refining our understanding of clinical injuries. Currently, post-injury MRI scanning provides a range of valuable data on the overall extent of the SCI and the involved tissue structures. These subject-specific images are critical in planning strategic treatments based on the individual patient and the injury severity. Currently, however, there are some important discrepancies between MRI scans and observed lesion histology—specifically, the MRI scans underestimate the extent of lesion because of the nature of MRI hyperintense signals.1 Combining MRI scans with subject-specific FE model outcomes may increase the reliability of SCI clinical evaluation because the FE models can provide high-resolution predictions of the lesion location and extent and, perhaps, its ultimate clinical consequences.
Currently, computation times are too large to be clinically feasible (∼100 CPU hours for intact dura simulations). This highlights an inherent difficulty in subject-specific modeling of neurological soft tissues (e.g., brain and spinal cord) where the low stiffness of the material substantially reduces the minimum stable time increment required for FE analysis thus extending the run times. In addition, the analysis techniques used here cannot be parallelized and therefore accessing more computing nodes (e.g., a larger super computer) would have limited effect on decreasing simulation run times. Subject-specific models aiming for neurosurgical applications (e.g., image-guided surgeries) require real-time results, therefore, long computation times are a serious obstacle.77,78,90,91
Total Lagrangian FE analysis methods75 and emerging meshless techniques92,93 have the potential to reduce the required FE analysis timing. In addition, meshless methods have the advantage of reducing the challenges associated with individualized mesh generation in subject-specific approaches. These methods, however, require further development and validation; specifically, the capability of these methods to predict parenchymal level stresses and strains has not been explored. Importantly, these techniques have been limited to simulating low to moderate strain rate phenomenon77,78,91 and the feasibility of applying them to models simulating high strain rates typical of SCI is unclear. Nevertheless, the results of our computational study highly increased the value of subject-specific SCI results and provide an important first step in justifying further exploration of these emerging methods.
Conclusion
Computational modeling of NHP contusion SCI experiments has provided important insight into the subject-specific correlations between FE predicted tissue level mechanics and spinal cord tissue damage. The results have also highlighted the effects of intersubject morphological variabilities on SCI outcomes. The findings are of particular importance to planning large animal SCI model studies where subject-specific approaches may reduce the variability of the results considerably and, consequently, minimize the costs and the use of animals. These findings also reinforce our understanding of SCI biomechanics, enhance the development of effective injury prevention and therapeutic strategies, and highlight key areas for further investigation.
Acknowledgments
The authors would like to express their appreciation to Stephanie Hawbecker and Rod Moseanko for their support in conducting in vivo experiments.
Funding Information
This work was supported by grants from the Natural Sciences and Engineering Research Council of Canada (EQPE-Q407572 and RGPIN-402007), the NIH (R-01 NS042291 and NS-105478), the Veterans Administration Gordon Mansfield Spinal Cord Research Consortium Grant, and the Craig H Neilsen Foundation. This research was enabled in part by support provided by WestGrid (www.westgrid.ca) and Compute Canada Calcul Canada (www.computecanada.ca).
Author Disclosure Statement
No competing financial interests exist.
References
- 1.Salegio, E.A., Bresnahan, J.C., Sparrey, C.J., Camisa, W., Fischer, J., Leasure, J., Buckley, J., Nout-Lomas, Y.S., Rosenzweig, E.S., Moseanko, R., Strand, S., Hawbecker, S., Lemoy, M.J., Haefeli, J., Ma, X., Nielson, J.L., Edgerton, V.R., Ferguson, A.R., Tuszynski, M.H., and Beattie, M.S. (2016). A unilateral cervical spinal cord contusion injury model in non-human primates (Macaca mulatta). J. Neurotrauma 33, 439–459 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Courtine, G., Bunge, M.B., Fawcett, J.W., Grossman, R.G., Kaas, J.H., Lemon, R., Maier, I., Martin, J., Nudo, R.J., Ramon-Cueto, A., Rouiller, E.M., Schnell, L., Wannier, T., Schwab, M.E., and Edgerton, V.R. (2007). Can experiments in nonhuman primates expedite the translation of treatments for spinal cord injury in humans? Nat. Med. 13, 561–566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kumamaru, H., Lu, P., Rosenzweig, E.S., Kadoya, K., and Tuszynski, M.H. (2019). Regenerating corticospinal axons innervate phenotypically appropriate neurons within neural stem cell grafts. Cell Rep. 26, 2329–2339.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lu, P., Gomes-Leal, W., Anil, S., Dobkins, G., Huie, J.R., Ferguson, A.R., Graham, L., and Tuszynski, M. (2019). Origins of neural progenitor cell-derived axons projecting caudally after spinal cord injury. Stem Cell Reports 13, 105–114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lien, B.V., Tuszynski, M.H., and Lu, P. (2019). Astrocytes migrate from human neural stem cell grafts and functionally integrate into the injured rat spinal cord. Exp. Neurol. 314, 46–57 [DOI] [PubMed] [Google Scholar]
- 6.Wen, J., Sun, D., Tan, J., and Young, W. (2015). A consistent, quantifiable, and graded rat lumbosacral spinal cord injury model. J. Neurotrauma 32, 875–892 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kloos, A., Fisher, L., Detloff, M., Hassenzahl, D., and Basso, D. (2005). Stepwise motor and all-or-none sensory recovery is associated with nonlinear sparing after incremental spinal cord injury in rats. Exp. Neurol. 191, 251–265 [DOI] [PubMed] [Google Scholar]
- 8.Ghasemlou, N., Kerr, B.J., and David, S. (2005). Tissue displacement and impact force are important contributors to outcome after spinal cord contusion injury. Exp. Neurol. 196 9–17 [DOI] [PubMed] [Google Scholar]
- 9.Ulbrich, E.J., Schraner, C., Boesch, C., Hodler, J., Busato, A., Anderson, S.E., Eigenheer, S., Zimmermann, H., and Sturzenegger, M. (2014). Normative MR cervical spinal canal dimensions. Radiology 271, 172–182 [DOI] [PubMed] [Google Scholar]
- 10.Kato, F., Yukawa, Y., Suda, K., Yamagata, M., and Ueta, T. (2012). Normal morphology, age-related changes and abnormal findings of the cervical spine. Part II: magnetic resonance imaging of over 1,200 asymptomatic subjects. Eur. Spine J. 21, 1499–1507 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sherman, J.L., Nassaux, P.Y., and Citrin, C.M. (1990). Measurements of the normal cervical spinal cord on MR imaging. AJNR Am. J. Neuroradiol. 11, 369–372 [PMC free article] [PubMed] [Google Scholar]
- 12.Tator, C.H. (1983). Spine-spinal cord relationships in spinal cord trauma. Clin. Neurosurg. 30, 479–494 [DOI] [PubMed] [Google Scholar]
- 13.Wagner, F.C., and Chehrazi, B. (1982). Early decompression and neurological outcome in acute cervical spinal cord injuries. J. Neurosurg. 56, 699–705 [DOI] [PubMed] [Google Scholar]
- 14.Ichihara, K., Taguchi, T., Shimada, Y., Sakuramoto, I., Kawano, S., and Kawai, S. (2001). Gray matter of the bovine cervical spinal cord is mechanically more rigid and fragile than the white matter. J. Neurotrauma 18, 361–367 [DOI] [PubMed] [Google Scholar]
- 15.Maikos, J.T., Qian, Z., Metaxas, D., and Shreiber, D.I. (2008). Finite element analysis of spinal cord injury in the rat. J. Neurotrauma 25, 795–816 [DOI] [PubMed] [Google Scholar]
- 16.Jannesar, S., Nadler, B., and Sparrey, C.J. (2016). The transverse isotropy of spinal cord white matter under dynamic load. J. Biomech. Eng. 138, 091004. [DOI] [PubMed] [Google Scholar]
- 17.Greaves, C.Y., Gadala, M.S., and Oxland, T.R. (2008). A three-dimensional finite element model of the cervical spine with spinal cord: an investigation of three injury mechanisms. Ann. Biomed. Eng. 36, 396–405 [DOI] [PubMed] [Google Scholar]
- 18.Galle, B., Ouyang, H., Shi, R., and Nauman, E. (2007). Correlations between tissue-level stresses and strains and cellular damage within the guinea pig spinal cord white matter. J. Biomech. 40, 3029–3033 [DOI] [PubMed] [Google Scholar]
- 19.Ouyang, H., Galle, B., Li, J., Nauman, E., and Shi, R. (2008). Biomechanics of spinal cord injury: a multimodal investigation using ex vivo guinea pig spinal cord white matter. J. Neurotrauma 25, 19–29 [DOI] [PubMed] [Google Scholar]
- 20.Russell, C.M., Choo, A.M., Tetzlaff, W., Chung, T., and Oxland, T.R. (2012). Maximum principal strain correlates with spinal cord tissue damage in contusion and dislocation injuries in the rat cervical spine. J. Neurotrauma 29, 1574–1585 [DOI] [PubMed] [Google Scholar]
- 21.Nishida, N., Kanchiku, T., Imajo, Y., Suzuki, H., Yoshida, Y., Kato, Y., Nakashima, D., and Taguchi, T. (2016). Stress analysis of the cervical spinal cord: impact of the morphology of spinal cord segments on stress. J. Spinal Cord Med. 39, 327–334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sparrey, C.J., Manley, G.T., and Keaveny, T.M. (2009). Effects of white, grey, and pia mater properties on tissue level stresses and strains in the compressed spinal cord. J. Neurotrauma 26, 585–595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ichihara, K., Taguchi, T., Sakuramoto, I., Kawano, S., and Kawai, S. (2003). Mechanism of the spinal cord injury and the cervical spondylotic myelopathy: new approach based on the mechanical features of the spinal cord white and gray matter. J. Neurosurg. 99, Suppl. 3, 278–285 [DOI] [PubMed] [Google Scholar]
- 24.Laing, A.C., Brenneman, E.C., Yung, A., Liu, J., Kozlowski, P., and Oxland, T. (2014). The effects of age on the morphometry of the cervical spinal cord and spinal column in adult rats: an MRI-based study. Anat. Rec. 297, 1885–1895 [DOI] [PubMed] [Google Scholar]
- 25.Kim, K.T., Streijger, F., So, K., Manouchehri, N., Shortt, K., Okon, E.B., Tigchelaar, S., Fong, A., Morrison, C., Keung, M., Sun, J., Liu, E., Cripton, P.A., and Kwon, B.K. (2019). Differences in morphometric measures of the uninjured porcine spinal cord and dural sac predict histological and behavioral outcomes after traumatic spinal cord injury. J. Neurotrauma 36, 3005–3017 [DOI] [PubMed] [Google Scholar]
- 26.Fiford, R.J., and Bilston, L.E. (2005). The mechanical properties of rat spinal cord in vitro. J. Biomech. 38, 1509–1515 [DOI] [PubMed] [Google Scholar]
- 27.Sparrey, C.J., and Keaveny, T.M. (2011). Compression behavior of porcine spinal cord white matter. J. Biomech. 44, 1078–1082 [DOI] [PubMed] [Google Scholar]
- 28.Jannesar, S., Allen, M., Mills, S., Gibbons, A., Bresnahan, J.C., Salegio, E.A., and Sparrey, C.J. (2018). Compressive mechanical characterization of non-human primate spinal cord white matter. Acta Biomater. 74, 260–269 [DOI] [PubMed] [Google Scholar]
- 29.Maikos, J.T., and Shreiber, D.I. (2007). Immediate damage to the blood-spinal cord barrier due to mechanical trauma. J. Neurotrauma 24, 492–507 [DOI] [PubMed] [Google Scholar]
- 30.Maikos, J.T., Elias, R.A.I., and Shreiber, D.I. (2008). Mechanical properties of dura mater from the rat brain and spinal cord. J. Neurotrauma 25, 38–51 [DOI] [PubMed] [Google Scholar]
- 31.Bertram, C.D., Brodbelt, A.R., and Stoodley, M.A. (2005). The origins of syringomyelia: numerical models of fluid/structure interactions in the spinal cord. J. Biomech. Eng. 127, 1099–1109 [DOI] [PubMed] [Google Scholar]
- 32.Bilston, L.E., Stoodley, M.A., and Fletcher, D.F. (2010). The influence of the relative timing of arterial and subarachnoid space pulse waves on spinal perivascular cerebrospinal fluid flow as a possible factor in syrinx development. J. Neurosurg. 112, 808–813 [DOI] [PubMed] [Google Scholar]
- 33.Loth, F., Yardimci, M.A., and Alperin, N. (2000). Hydrodynamic modeling of cerebrospinal fluid motion within the spinal cavity. J. Biomech. Eng. 123, 71–79 [DOI] [PubMed] [Google Scholar]
- 34.Persson, C., Summers, J., and Hall, R.M. (2011). The effect of cerebrospinal fluid thickness on traumatic spinal cord deformation. J. Appl. Biomech. 27, 330–335 [DOI] [PubMed] [Google Scholar]
- 35.Persson, C., Summers, J., and Hall, R.M. (2011). The importance of fluid-structure interaction in spinal trauma models. J. Neurotrauma 28, 113–125 [DOI] [PubMed] [Google Scholar]
- 36.Li, X.F., and Dai, L.Y. (2009). Three-dimensional finite element model of the cervical spinal cord: preliminary results of injury mechanism analysis. Spine (Phila. Pa. 1976). 34, 1140–1147 [DOI] [PubMed] [Google Scholar]
- 37.Li, X.F., and Dai, L.Y. (2010). Acute central cord syndrome: injury mechanisms nd stress features. Spine (Phila. Pa. 1976). 35, E955–E964 [DOI] [PubMed] [Google Scholar]
- 38.Sparrey, C.J., Salegio, E.A., Nout-Lomas, Y.S., Moseanko, R., Hawbecker, S., Pender, R., Ferguson, A.R., Rosenzweig, E.S., Tuszynski, M.H., Beattie, M.S., and Bresnahan, J.C. (2018). Open dura cervical spinal cord contusion injury in primates: effects on impact mechanics and injury patterns. J. Neurotrauma 35, A53–A54 [Google Scholar]
- 39.Sparrey, C.J., Salegio, E.A., Camisa, W., Tam, H., Beattie, M.S., and Bresnahan, J.C. (2016). Mechanical design and analysis of a unilateral cervical spinal cord contusion injury model in non-human primates. J. Neurotrauma 33, 1136–1149 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tubbs, R.S., Salter, G., Grabb, P.A., and Oakes, W.J. (2001). The denticulate ligament: anatomy and functional significance. J. Neurosurg. 94, Suppl. 2, 271–275 [DOI] [PubMed] [Google Scholar]
- 41.Kimpara, H., Nakahira, Y., Iwamoto, M., Miki, K., Ichihara, K., Kawano, S., and Taguchi, T. (2006). Investigation of anteroposterior head-neck responses during severe frontal impacts using a brain-spinal cord complex FE. Stapp Car Crash J. 50, 509–544 [DOI] [PubMed] [Google Scholar]
- 42.Shetye, S.S., Troyer, K.L., Streijger, F., Lee, J.H., Kwon, B.K., Cripton, P.A., and Puttlitz, C.M. (2014). Nonlinear viscoelastic characterization of the porcine spinal cord. Acta Biomater. 10, 792–797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lucy, L.B. (1977). A numerical approach to the testing of the fission hypothesis. Astron. J. 82, 1013–1024 [Google Scholar]
- 44.Gingold, R.A., and Monaghan, J.J. (1977). Smoothed particle hydrodynamics: theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 181, 375–389 [Google Scholar]
- 45.Meaney, D.F. (2003). Relationship between structural modeling and hyperelastic material behavior: application to CNS white matter. Biomech. Model. Mechanobiol. 1, 279–293 [DOI] [PubMed] [Google Scholar]
- 46. (2014). Abaqus documentation, 6.14. Providence, RI: Dassault Systèmes Simulia Corp
- 47.Moran, R., Smith, J.H., and García, J.J. (2014). Fitted hyperelastic parameters for Human brain tissue from reported tension, compression, and shear tests. J. Biomech. 47, 3762–3766 [DOI] [PubMed] [Google Scholar]
- 48.Chafi, M.S., Dirisala, V., Karami, G., and Ziejewski, M. (2009). A finite element method parametric study of the dynamic response of the human brain with different cerebrospinal fluid constitutive properties. Proc. Inst. Mech. Eng. H. 223, 1003–1019 [DOI] [PubMed] [Google Scholar]
- 49.Ning, X., Zhu, Q., Lanir, Y., and Margulies, S.S. (2006). A transversely isotropic viscoelastic constitutive equation for brainstem undergoing finite deformation. J. Biomech. Eng. 128, 925–933 [DOI] [PubMed] [Google Scholar]
- 50.Feng, Y., Okamoto, R.J., Namani, R., Genin, G.M., and Bayly, P. V. (2013). Measurments of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. J. Mech. Behav. Biomed. Mater. 23, 117–132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Toma, M., Bloodworth, C.H., Einstein, D.R., Pierce, E.L., Cochran, R.P., Yoganathan, A.P., and Kunzelman, K.S. (2016). High-resolution subject-specific mitral valve imaging and modeling: experimental and computational methods. Biomech. Model. Mechanobiol. 15, 1619–1630 [DOI] [PubMed] [Google Scholar]
- 52.Toma, M., and Nguyen, P. (2017). Fluid-structure interaction analysis of cerebral spinal fluid with a comprehensive head model subject to a car crash-related whiplash, in: 5th International Conference on Computational and Mathematical Biomedical Engineer CMBE2017. Pittsburgh, PA [Google Scholar]
- 53.Panzer, M.B., Myers, B.S., Capehart, B.P., and Bass, C.R. (2012). Development of a finite element model for blast brain injury and the effects of CSF cavitation. Ann. Biomed. Eng. 40, 1530–1544 [DOI] [PubMed] [Google Scholar]
- 54.Wang, C., Pahk, J.B., Balaban, C.D., Miller, M.C., Wood, A.R., and Vipperman, J.S. (2014). Computational study of human head response to primary blast waves of five levels from three directions. PLoS One 9, e113264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hasgall, P.A., Di Gennaro, F., Baumgartner, C., Neufeld, E., Gosselin, M.C., Payne, D., Klingenbock, A., and Kuster, N. (2018). IT'IS Database for thermal and electromagnetic parameters of biological tissues. Version 4.0 Available at: www.itis.ethz.ch/database. Last accessed> November 3, 2020 [Google Scholar]
- 56.Kleiven, S., and Hardy, W.N. (2002). Correlation of an FE model of the human head with local brain motion—consequences for injury prediction. Stapp Car Crash J. 46, 123–144 [DOI] [PubMed] [Google Scholar]
- 57.Choo, A.M., Liu, J., Liu, Z., Dvorak, M., Tetzlaff, W., and Oxland, T.R. (2009). Modeling spinal cord contusion, dislocation, and distraction: characterization of vertebral clamps, injury severities, and node of Ranvier deformations. J. Neurosci. Methods 181, 6–17 [DOI] [PubMed] [Google Scholar]
- 58.Rashid, B., Destrade, M., and Gilchrist, M.D. (2012). Determination of friction coefficient in unconfined compression of brain tissue. J. Mech. Behav. Biomed. Mater. 14, 163–171 [DOI] [PubMed] [Google Scholar]
- 59.Shreiber, D.I., Bain, A.C., and Meaney, D.F. (1997). In-vivo threshlolds for mechanical injury to the blood-brain barrier. SAE Tech. Pap. , No. 973335 [Google Scholar]
- 60.Nagelkerke, N.J. (1991). A note on a general definition of the coefficient of determination. Biometrika 78, 691–692 [Google Scholar]
- 61.Sahoo, D., Deck, C., and Willinger, R. (2016). Brain injury tolerance limit based on computation of axonal strain. Accid. Anal. Prev. 92, 53–70 [DOI] [PubMed] [Google Scholar]
- 62. JMP® 14 Basic Analysis. Cary, NC: SAS Institute Inc. 2018
- 63.Choo, A.M., Liu, J., Lam, C.K., Dvorak, M., Tetzlaff, W., and Oxland, T.R. (2007). Contusion, dislocation, and distraction: primary hemorrhage and membrane permeability in distinct mechanisms of spinal cord injury. J. Neurosurg. Spine 6, 255–266 [DOI] [PubMed] [Google Scholar]
- 64.Ouyang, H., Sun, W., Fu, Y., Li, J., Cheng, J.X., Nauman, E., and Shi, R. (2010). Compression induces acute demyelination and potassium channel exposure in spinal cord. J. Neurotrauma 27, 1109–1120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Imajo, Y., Hiiragi, I., Kato, Y., and Taguchi, T. (2009). Use of the finite element method to study the mechanism of spinal cord injury without radiological abnormality in the cervical spine. Spine (Phila. Pa. 1976). 34, E83–E87 [DOI] [PubMed] [Google Scholar]
- 66.Shreiber, D.I., Smith, D.H., and Meaney, D.F. (1999). Immediate in vivo response of the cortex and the blood–brain barrier following dynamic cortical deformation in the rat. Neurosci. Lett. 259, 5–8 [DOI] [PubMed] [Google Scholar]
- 67.Halder, S.K., Kant, R., and Milner, R. (2018). Chronic mild hypoxia promotes profound vascular remodeling in spinal cord blood vessels, preferentially in white matter, via an α5β1 integrin-mediated mechanism. Angiogenesis 21, 251–266 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Hassler, O. (1966). Blood supply to human spinal cord: a microangiographic study. Arch. Neurol. 15, 302–307 [DOI] [PubMed] [Google Scholar]
- 69.Turnbull, I.M., Brieg, A., and Hassler, O. (1966). Blood supply of cervical spinal cord in man. A microangiographic cadaver study. J. Neurosurg. 24, 951–965 [DOI] [PubMed] [Google Scholar]
- 70.Shi, R., and Whitebone, J. (2006). Conduction deficits and membrane disruption of spinal cord axons as a function of magnitude and rate of strain. J. Neurophysiol. 95, 3384–3390 [DOI] [PubMed] [Google Scholar]
- 71.Bain, A.C., and Meaney, D.F. (2000). Tissue-level thresholds for axonal damage in an experimental model of central nervous system white matter injury. J. Biomech. Eng. 122, 615–622 [DOI] [PubMed] [Google Scholar]
- 72.Morrison, B., Cater, H.L., Wang, C.C., Thomas, F.C., Hung, C.T., Ateshian, G.A., and Sundstrom, L.E. (2003). A tissue level tolerance criterion for living brain developed with an in-vitro model of traumatic mechanical loading. Stapp Car Crash J. 47, 93–105 [DOI] [PubMed] [Google Scholar]
- 73.Giordano, C., and Kleiven, S. (2014). Evaluation of axonal strain as a predictor for mild traumatic brain injuries using finite element modeling, in: 58th Stapp Car Crash Conference. Stapp Car Crash J. 58, 33. [DOI] [PubMed] [Google Scholar]
- 74.Singh, A., Lu, Y., Chen, C., Kallakuri, S., and Cavanaugh, J.M. (2006). A new model of traumatic axonal injury to determine the effects of strain and displacement rates, in: 50th Stapp Car Crash Conference. The Stapp Association. [DOI] [PubMed] [Google Scholar]
- 75.Miller, K., Joldes, G., Lance, D., and Wittek, A. (2006). Total Lagrangian explicit dynamics finite element algorithm for computing soft tissue deformation. Commun. Numer. Methods Eng. 23, 121–134 [Google Scholar]
- 76.Joldes, G.R., Wittek, A., and Miller, K. (2010). Real-time nonlinear finite element computations on GPU – application to neurosurgical simulation. Comput. Methods Appl. Mech. Eng. 199, 3305–3314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Miller, K., Wittek, A., and Joldes, G. (2011). Biomechanical modeling of the brain for computer-assisted neurosurgery, in: Biological and Medical Physics, Biomedical Engineering, E. Greenbaum (ed). Springer, New York, NY, pps. 111–136 [Google Scholar]
- 78.Wittek, A., Joldes, G., Couton, M., Warfield, S.K., and Miller, K. (2010). Patient-specific non-linear finite element modelling for predicting soft organ deformation in real-time; application to non-rigid neuroimage registration. Prog. Biophys. Mol. Biol. 103, 292–303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Miller, K., and Lu, J. (2013). On the prospect of patient-specific biomechanics without patient-specific properties of tissues. J. Mech. Behav. Biomed. Mater. 27, 154–166 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Pettus, E.H., Christman, C.W., Giebel, M.L., and Povlishock, J.T. (1994). Traumatically induced altered membrane permeability: its relationship to traumatically induced reactive axonal change. J. Neurotrauma 11, 507–522 [DOI] [PubMed] [Google Scholar]
- 81.Shi, R., Luo, J., and Peasley, M. (2002). Acrolein inflicts axonal membrane disruption and conduction loss in isolated guinea-pig spinal cord. Neuroscience 115, 337–340 [DOI] [PubMed] [Google Scholar]
- 82.Shi, R. (2004). The dynamics of axolemmal disruption in guinea pig spinal cord following compression. J. Neurocytol. 33, 203–211 [DOI] [PubMed] [Google Scholar]
- 83.Linssen, W.H.J.P., Praamstra, P., Gabreëls, F.J.M., and Rotteveel, J.J. (1990). Vascular insufficiency of the cervical cord due to hyperextension of the spine. Pediatr. Neurol. 6, 123–125 [DOI] [PubMed] [Google Scholar]
- 84.Schneider, R.C., and Crosby, E.C. (1959). Vascular insufficiency of brain stem and spinal cord in spinal trauma. Neurology 9, 643–656 [DOI] [PubMed] [Google Scholar]
- 85.Behrmann, D.L., Bresnahan, J.C., Beattie, M.S., and Shah, B.R. (1992). Spinal cord injury produced by consistent mechanical displacement of the cord in rats: behavioral and histologic analysis. J. Neurotrauma 9, 197–217 [DOI] [PubMed] [Google Scholar]
- 86.Dunham, K.A., Siriphorn, A., Chompoopong, S., and Floyd, C.L. (2010). Characterization of a graded cervical hemicontusion spinal cord injury model in adult male rats. J. Neurotrauma 27, 2091–2106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Gensel, J.C., Tovar, A., Hamers, F.P., Deibert, R.J., Beattie, M.S., and Bresnahan, J.C. (2006). Behavioral and histological characterization of unilateral cervical spinal cord contusion injury in rats. J. Neurotrauma 23, 36–54 [DOI] [PubMed] [Google Scholar]
- 88.Ma, M., Basso, D.M., Walters, P., Stokes, B.T., and Jakeman, L.B. (2001). Behavioral and histological outcomes following graded spinal cord contusion injury in the C57Bl/6 mouse. Exp. Neurol. 169, 239–254 [DOI] [PubMed] [Google Scholar]
- 89.Streijger, F., Beernink, T.M., Lee, J.H.., Bhatnagar, T., Park, S., Kwon, B.K., and Tetzlaff, W. (2013). Characterization of a cervical spinal cord hemicontusion injury in mice using the infinite horizon impactor. J. Neurotrauma 30, 869–883 [DOI] [PubMed] [Google Scholar]
- 90.Miller, K., Wittek, A., Joldes, G., Horton, A., Dutta-Roy, T., Berger, J., and Morriss, L. (2010). Modelling brain deformations for computer-integrated neurosurgery. Int. J. Numer. Method. Biomed. Eng. 26, 117–138 [Google Scholar]
- 91.Wittek, A., Miller, K., Kikinis, R., and Warfield, S.K. (2007). Patient-specific model of brain deformation: application to medical image registration. J. Biomech. 40, 919–929 [DOI] [PubMed] [Google Scholar]
- 92.Zhang, J.Y., Joldes, G.R., Wittek, A., and Miller, K. (2013). Patient-specific computational biomechanics of the brain without segmentation and meshing. Int. J. Numer. Method. Biomed. Eng. 29, 293–308 [DOI] [PubMed] [Google Scholar]
- 93.Chowdhury, H.A., Joldes, G.R., Wittek, A., Doyle, B., Pasternak, E., and Miller, K. (2015). Implementation of a modified moving least squares approximation for predicting soft tissue deformation using a meshless model, in: Computational Biomechanics for Medicine: New Approaches and New Applications. Doyle B., Miller K.S., Wittek A., Nielson P.M. (eds). Springer International Publishing: New York, pps. 59–71 [Google Scholar]