Segmentation of prostate and prostate zones using deep learning

Abstract

Purpose

Develop a deep-learning-based segmentation algorithm for prostate and its peripheral zone (PZ) that is reliable across multiple MRI vendors.

Methods

This is a retrospective study. The dataset consisted of 550 MRIs (Siemens-330, General Electric[GE]-220). A multistream 3D convolutional neural network is used for automatic segmentation of the prostate and its PZ using T2-weighted (T2-w) MRI. Prostate and PZ were manually contoured on axial T2-w. The network uses axial, coronal, and sagittal T2-w series as input. The preprocessing of the input data includes bias correction, resampling, and image normalization. A dataset from two MRI vendors (Siemens and GE) is used to test the proposed network. Six different models were trained, three for the prostate and three for the PZ. Of the three, two were trained on data from each vendor separately, and a third (Combined) on the aggregate of the datasets. The Dice coefficient (DSC) is used to compare the manual and predicted segmentation.

Results

For prostate segmentation, the Combined model obtained DSCs of 0.893 ± 0.036 and 0.825 ± 0.112 (mean ± standard deviation) on Siemens and GE, respectively. For PZ, the best DSCs were from the Combined model: 0.811 ± 0.079 and 0.788 ± 0.093. While the Siemens model underperformed on the GE dataset and vice versa, the Combined model achieved robust performance on both datasets.

Conclusion

The proposed network has a performance comparable to the interexpert variability for segmenting the prostate and its PZ. Combining images from different MRI vendors on the training of the network is of paramount importance for building a universal model for prostate and PZ segmentation.

Introduction

Accurate prostate segmentation on MRI datasets is required for many clinical and research applications. In addition, due to the different imaging properties of the peripheral (PZ) and transition zones (TZ) of the prostate, accurate zonal segmentation is also necessary. The prostate and zonal contours are required for computer-aided diagnosis (CAD) applications for staging, diagnosis, and treatment planning for prostate cancer. In a series of applications, prostate contours are fused with ultrasound images to guide prostate biopsies. Automatic segmentation of the prostate, PZ and TZ on MR images provides an opportunity to broaden the current scope of research by facilitating studies that include large populations of subjects or studies that incorporate serial imaging of the prostate to attain a longitudinal picture of disease progression and response. Prostate MRI image segmentation has been an area of intense research [1]. Earlier, the applied approaches varied from model-based [2, 3] to atlas-based segmentation [4–9]. Our group also evaluated the performance of an atlas-based approach for prostate and prostate zones segmentation using data from different MRI scanners and acquisition parameters [10]. The advent of deep learning techniques, such as convolutional neural networks (CNN) has led to outstanding results in image classification [11, 12]. The top ranked method of the PROMISE12 MIC-CAI Grand Challenge for the automatic segmentation of the prostate [1], used a volumetric CNN and achieved a Dice coefficient (DSC) of 89.43% [13]. Recently, the U-Net architecture has been proposed [14] for medical imaging segmentation and has been successfully applied to the prostate [15]. In this work, we implement a multistream 3D U-Net and analyze its performance for the automatic segmentation of the prostate and PZ in a multivendor MRI setting. As with our atlas-based approach [10], the goal of the described developments was to segue towards a universal approach that can segment the prostate and prostate zones, regardless of acquisition protocols, magnetic field strength or type of scanners. A core contribution is made by the preprocessing of the images in order to harmonize the data and optimize the network performance when training and testing is carried out in an image dataset from two different MRI vendors.

Methods

Datasets

An institutional review board (IRB) approved a protocol for retrospective review of MRI exams from patients with biopsy-proven prostate cancer. The IRB waived the need for informed consent. Patients with intermediate/high-risk prostate cancer, presenting for evaluation for definitive radiation treatment (RT) were considered. Patients with prior treatment for prostate cancer (RT, radical prostatectomy, focal therapies) were excluded. A total of 220 eligible patients with MRI exams carried out on Discovery MR750 3T MRI (GE, Waukesha, WI, USA) between 2012 and 2018 were identified. In addition, 330 MRI exams, publicly available from the SPIE-AAPM-NCI ProstateX Challenge, acquired on two different types of Siemens 3T MR scanners, the MAGNETOM Trio and Skyra (Siemens, Erlangen, Germany) were considered [16]. All MRI exams included acquisition of T2-weighted (T2-w) MRI in the axial, coronal and sagittal orientations using fast spin-echo (FSE) sequence with acquisition parameters (for the axial orientation) given in Table 1. T2-w sequence was acquired as a part of multiparametric (mp)MRI exam of the patients, including diffusion weighted imaging (DWI) and dynamic-contrast enhanced (DCE-) MRI and prior to contrast administration. Prostate and PZ were manually contoured on axial T2-w MRI in MIM (MIM Software Inc, Cleveland, OH, USA) by imaging experts (RS, AB, NG) with more than 25 years combined expertise in prostate imaging. The contours were cross checked by the imaging experts and reviewed by radiation oncologists (AP, MA) with extensive expertise in genitourinary malignancies.

Table 1.

MRI acquisition parameters for axial T2-weighted MRI sequence

Scanner	N	TE Min-Max	ETL	TR Min-Max	Matrix	Voxel Size (mm)
GE	112	80.88–92.73	16	3800–7078	512 × 512 × (27–30)	0.39 × 0.39 × 3
	97	81.31–105.50	16	3944–10,998	256 × 256 × (72 or 144)	1.25 × 1.25 × 2.50
	6	87.32–92.72	21	5959–6165	512 × 512 × (26–27)	0.39 × 0.39 × 3
	2	86.59, 88.79	16	3800	256 × 256 × 36	1.01 × 1.01 × 2.50
	1	117.48	30	11,226	512 × 512 × 22	0.43 × 0.43 × 3
	1	85.36	16	3800	512 × 512 × 72	0.62 × 0.62 × 2.50
	1	81.88	16	3800	256 × 256 × 27	0.78 × 0.78 × 3
Siemens	258	104	25	5360–8624	384 × 384 × (18–29)	0.5 × 0.5 × 3
	52	103	25	4480–5870	384 × 384 × (19–25)	0.56 × 0.56 × 3
	8	104	25	5660–6840	384 × 384 × (19–23)	0.5 × 0.5 × 3.50
	6	101	25	5660–7440	640 × 640 × (19–21)	0.30 × 0.30 × 3
	6	101	25	4030–6840	320 × 320 × (19–27)	0.60 × 0.60 × 3
	2	104	25	5660	384 × 384 × 19	0.5 × 0.5 × 4
	1	108	25	6250	512 × 512 × 21	0.37 × 0.37 × 3
	1	104	25	5660	384 × 384 × 19	0.5 × 0.5 × 3.30
	1	103	15	4480	320 × 320 × 19	0.56 × 0.56 × 3.50
	1	103	15	4480	320 × 320 × 19	0.56 × 0.56 × 5
	1	101	25	4000	320 × 320 × 20	0.62 × 0.62 × 3
	1	102	15	4480	256 × 256 × 19	0.70 × 0.70 × 3

TE Echo Time, ETL Echo Train Length, TR Repetition Time

Experimental design

In order to compare the robustness of the models with respect to changes in MRI vendor machines, a distinct model was trained for each dataset: GE (n = 220), Siemens (n = 330), and Combined (n = 550). Each dataset was split into 90% for training and 10% for validation. A total number of six models were built, three (GE, Siemens, Combined) for the prostate and three for the PZ. Similarly to our previous work [10], a crisscross design was used to evaluate the network performance: each of the three models for prostate and PZ segmentation was tested on GE and Siemens dataset.

Preprocessing of images and contours

The preprocessing steps for the MRIs consist of bias correction using the N4ITK algorithm [17]. N4ITK corrects for low frequency intensity nonuniformity that is present in the imaging data by least-squares B-spline data approximation. The 1 and 99% of the image intensities were normalized to an interval of [0, 1]. The image was resampled to uniform resolution, automatic selection of a region of interest (ROI), and (contour) interpolation.

The MRI series are resampled to a resolution of 0.5 × 0.5 × 0.5mm using linear interpolation [18]. The ROI, containing the prostate gland, is automatically obtained from the intersection of the rectangular prisms of the three MRI planes [15]. The resampled ROI are linearly interpolated to an isotropic volume with a resolution of 168³. Fig. 1 shows an example of an axial T2-w MRI before and after preprocessing.

Fig. 1.

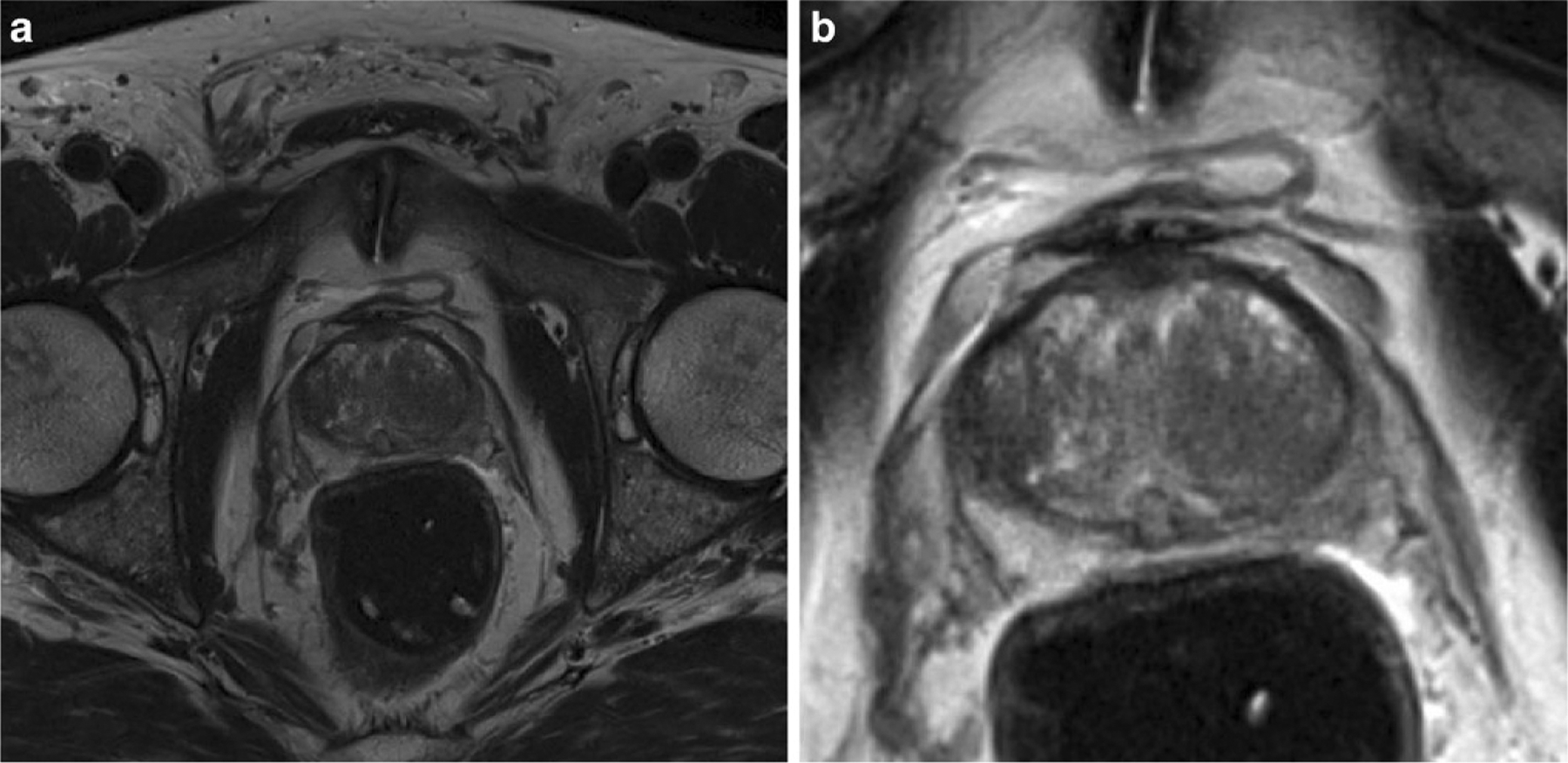
Axial T2-weighted image a before, and b after preprocessing. Preprocessing steps include bias correction, intensity normalization, resampling, and cropping

Contour preprocessing included interpolation using optical flow. The manual contours were carried out on the original T2-w MRI resolution and hence the necessity for interpolation. The proposed method estimates 2D contours in-between slices of the axial plane and computes them in dependently for every two consecutive slices. First, optical flow is obtained between the two contours of adjacent slices using the Farneback method [19]. Then, intermediate contours are generated by linearly interpolating the position of their edges following the direction of the optical flow vector field. Fig. 2 shows an example of the optical flow obtained between two horizontal slices and the resulting interpolated 3D volumes using this method.

Fig. 2.

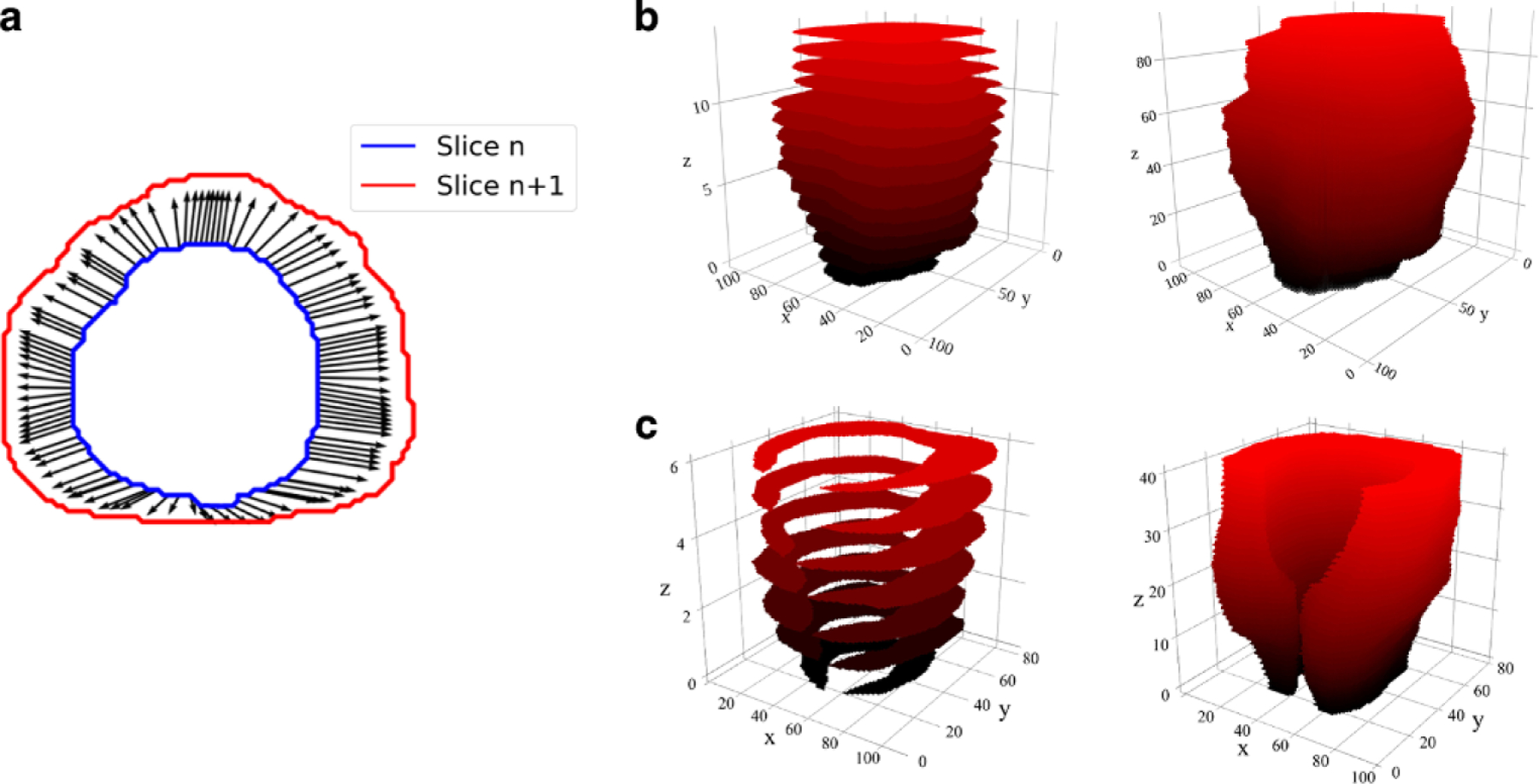
Interpolation of prostate and PZ contours. a An example of the optical flow obtained between two prostate contours from adjacent horizontal planes. Interpolation of prostate and PZ contours. In b and c original (left) and interpolated (right) prostate and PZ contours

Three-dimensional CNN architecture

The proposed CNN consist of a 3D multistream architecture that follows the encoding and decoding path of the 3D U-net [20]. Our implementation follows the one described by Meyer et al. [15]. The input of each stream is the postprocessed ROI of 168³ pixels for one of three MRI series (axial, sagittal, and coronal). During the encoding phase, a group of two convolutional layers and one max pool layer is repeated three times. The second convolutional layer in each group doubles the number of filters. In the decoding phase, a similar set of two convolutional layers and one deconvolution layer is applied three times [21]. The original network was modified by implementing batch normalization [22] and dropout of 20% [23] after each convolution in the decoding phase only (due to memory constrains in the GPU used).

The number of filters were cut from 192 to 128 in the largest convolutional layer (after the first concatenation) reducing the number of parameters from to 995k to 663k. These changes cut the training time in half. Fig. 3 shows the proposed model. All convolutional layers use a filter size of 3 × 3 × 3 and rectified linear unit (ReLU) as the activation function except the last layer which uses a filter size of 1 × 1 × 1 and Sigmoid as the activation function to match the resolution of the input MRI series. The estimated size of the complete model is 9.2 gigabytes and the accumulated memory for each layer is displayed in Fig. 3.

Fig. 3.

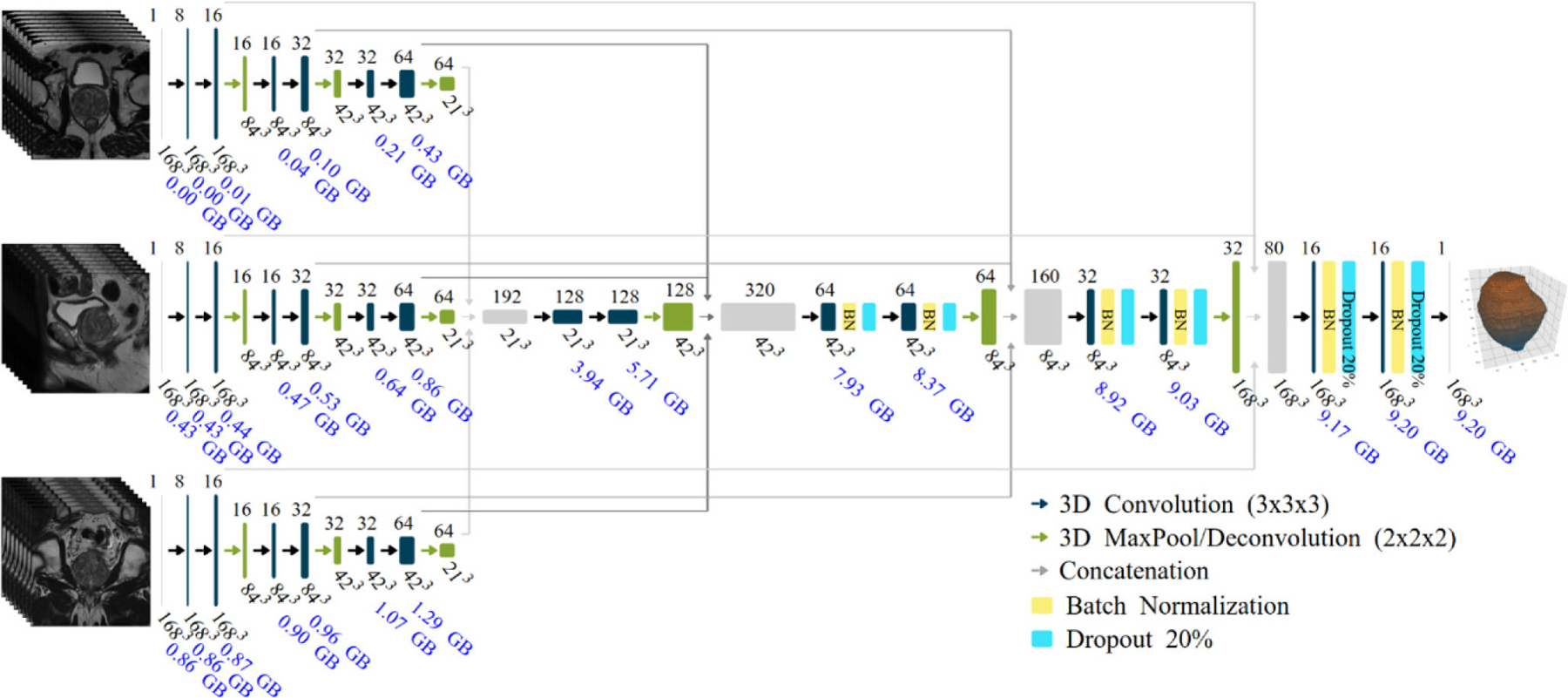
Multistream 3D convolutional networkarchitecture. The input of the network are three 168³ volumes from the MRI planes: axial, sagittal, and coronal. The estimated accumulated memory requirement is displayed in gigabytes (GB) below each layer

Data augmentation is performed on the fly by flipping the images in the x-axis and blurring them using 3D Gaussian filter randomly with 0 ≤ σ ≤ 3, the size of the filter is four times σ. Each data augmentation method is applied with a random chance of ½.

Training

The selected optimization algorithm is stochastic gradient descent (SGD) with a learning rate α = 0.001, momentum of 0.9 and decay of 10⁻⁶ after conducting a hyperparameter search (see Results section). The training is performed for 1000 epochs with a batch size of 1 and with an early stop mechanism if the loss function is not improved by at least β = 0.001 after 70 iterations. The loss function is formulated is the negative DSC [24]:

$$\text{Loss}=-\frac{2{\sum }_{j=1}^N{p}_i{t}_i}{{\sum }_{j=1}^N{p}_i^2+{\sum }_{j=1}^N{t}_i^2+\epsilon }$$ (1)

where N is the total number of voxels in the image, p_i the voxel values for the prediction of the network, t_i the true voxel values of the prostate or PZ masks, and ε = 1 for all the models. Note that the predicted probabilities, p_i, are used directly in the DSC calculation (so called “soft Dice”) instead of thresholding and converting them in a binary mask.

For each model the data was split at random 90:10 for training/validation. Training was performed on a desktop computer with an Intel Xeon(R) E5-2609 CPU and a GeForce GTX 1080 Ti NVIDIA GPU. The system is implemented using Keras [25] and Tensor Flow [26] Python libraries. The average training time for each model, independently if carried out for the prostate or the PZ, is ~7.5h, the overall training time for the six models is about two days.

Postprocessing

The CNN outputs a 3D volume of the same size of the ROI, in our case 168³ and each voxel gets the probability of belonging to the area of interest (prostate or PZ) versus the background. From this volume a binary mask is obtained with a threshold value of 0.5. After that, the largest connected volume is selected. Finally, the 3D DSC for the contour of interest in the resampled image and in the original MRI series resolution is computed. The prediction of the PZ contour is intersected with the prostate, restricting it to the prostate volume. To infer into the network layers, the activations maps of a single test input volume were visualized using Keras and Tensor Flow libraries [27].

Statistical analysis

The performance of each model (three for the prostate and three for the PZ) was assessed via DSC and 95% Hausdorff distances between manual and network contours. DSC’s distribution and 95% Hausdorff distances in the segmented GE and Siemens datasets were summarized with descriptive statistics and compared using Mann–Whitney U test. The DSCs/95% Hausdorff distances were computed from the validation set when the model is evaluated on the same MRI data, and are calculated from the whole dataset when the model is evaluated with data of a different MRI scanner. Significance was determined using probability values of p < 0.001 from two-tailed tests. The associations of the DSC and image acquisition parameters were evaluated with Spearman rank correlation coefficient (p). Significance of p was determined using probability values of p < 0.005 (to account for multiple comparisons) from two-tailed tests.

Results

In Table 1 the MRI acquisition parameters for axial T2w MRI are presented. The GE data is split almost in half between lower spatial resolution (in-plane pixel size larger than 1 × 1mm) and higher spatial resolution. This “bimodal” distribution of the voxel size contrasts the more homogeneous Siemens data. In terms of voxel size, Siemens on average is of lower resolution: (mean [mm³] ± standard deviation): 0.95 ± 0.37 (Siemens) vs 1.71 ± 1.34 (GE). The GE data is more heterogeneous also in terms of acquisition parameters.

The hyperparameter selection for stochastic gradient descent (learning rate, momentum and decay) was performed by a semi-random search on the GE training dataset. Initially, the learning rate was fixed at α = 0.001, and values in the neighborhood of 0.9 for momentum and 10⁻⁶ for decay were tested. Using 10% from the GE dataset, the performance of the hyperparameters were evaluated on two primary metrics: (i) the average DSC value of the network tested on the validation set at the specific epoch of 100; and (ii) the overall average DSC value of the network at the end of training. The values were varied semi-randomly by adding increments in the order of ±b*10^−a with the coefficient b selected randomly from 1 to 9 and the coefficient a selected randomly from 1 to 5 for momentum and from 4 to 10 for decay, ten training runs per trial. The best performing combination of momentum and decay for this set of trials would then become the start values of the next. After this search, with more than 50 different momentum and decay values, we determined that momentum and decay did not significantly impact performance across the two metrics established above. Furthermore, momentum and decay were fixed and the learning rate was varied as described above with coefficient b in the range of 1 to 5. The end result was that while network performance varied across metric (i), overall DSC scores in metric (ii) were similar, the biggest change is visible on the time that takes the network to converge. We kept the original learning rate of 0.001 because it was the fastest learning rate with similar performance than our best runs.

Table 2 shows the obtained DSCs and 95% Hausdorff distances for the segmentation of the prostate when the three trained models are used for segmenting the GE and the Siemens dataset.

Table 2.

Dice similarity coefficients (DSC) and 95% Hausdorff distances for prostate, segmented with each of the three trained models (GE, Siemens, and Combined)^a

Model	GE		Siemens
	DSC	Hausdorff distance (mm)	DSC	Hausdorff distance (mm)
	Mean (SD);	Mean (SD);	Mean (SD);	Mean (SD);
	Median (range)	Median (range)	Median (range)	Median (range)
GE	0.882 (0.058);	1.579 (1.794);	0.802 (0.106);	3.087 (2.61);
	0.897 (0.396, 0.937)	1 (0.5, 13.21)	0.833 (0.249, 0.92)	2.345 (1, 28.058)
Siemens	0.287 (0.139);	23.685 (11.607); 23.685 (8.155, 60.484)	0.905 (0.027);	1.209 (0.688);
	0.268 (0, 0.687)		0.909 (0.74, 0.955)	1 (0.5, 6.652)
Combined	0.825 (0.113);	3.226 (4.941);	0.892 (0.036);	1.285 (0.551);
	0.862 (0.285, 0.929)	1.5 (0.707, 39.617)	0.898 (0.652, 0.951)	1.118 (0.5, 5.025)

SD standard deviation

^aAll paired comparisons in the table were significantly different (p < 0.001)

When the model is trained with examples from one dataset and used to segment prostates from scans of the same MRI vendor the average DSCs are 0.882 for GE and 0.905 for Siemens. When the datasets are combined during training, the average DSCs are 0.825 for GE and 0.893 for Siemens. When the model is trained with examples from one MRI vendor and then used to process images from a different vendor, the resulting DSCs are lower (0.261 and 0.802). Fig. 4 shows the middle axial slice for the lowest, closest to mean, and highest DSC obtained for prostate segmentation on the Siemens and GE dataset. In general, the DSC increases with respect to the volume size of the prostate, and predictions for the Siemens dataset follow better the contours from the experts. It should be noted that Siemens MRIs were of higher resolution than GE and this maybe another reason why the network performs better for this MRI vendor.

Fig. 4.

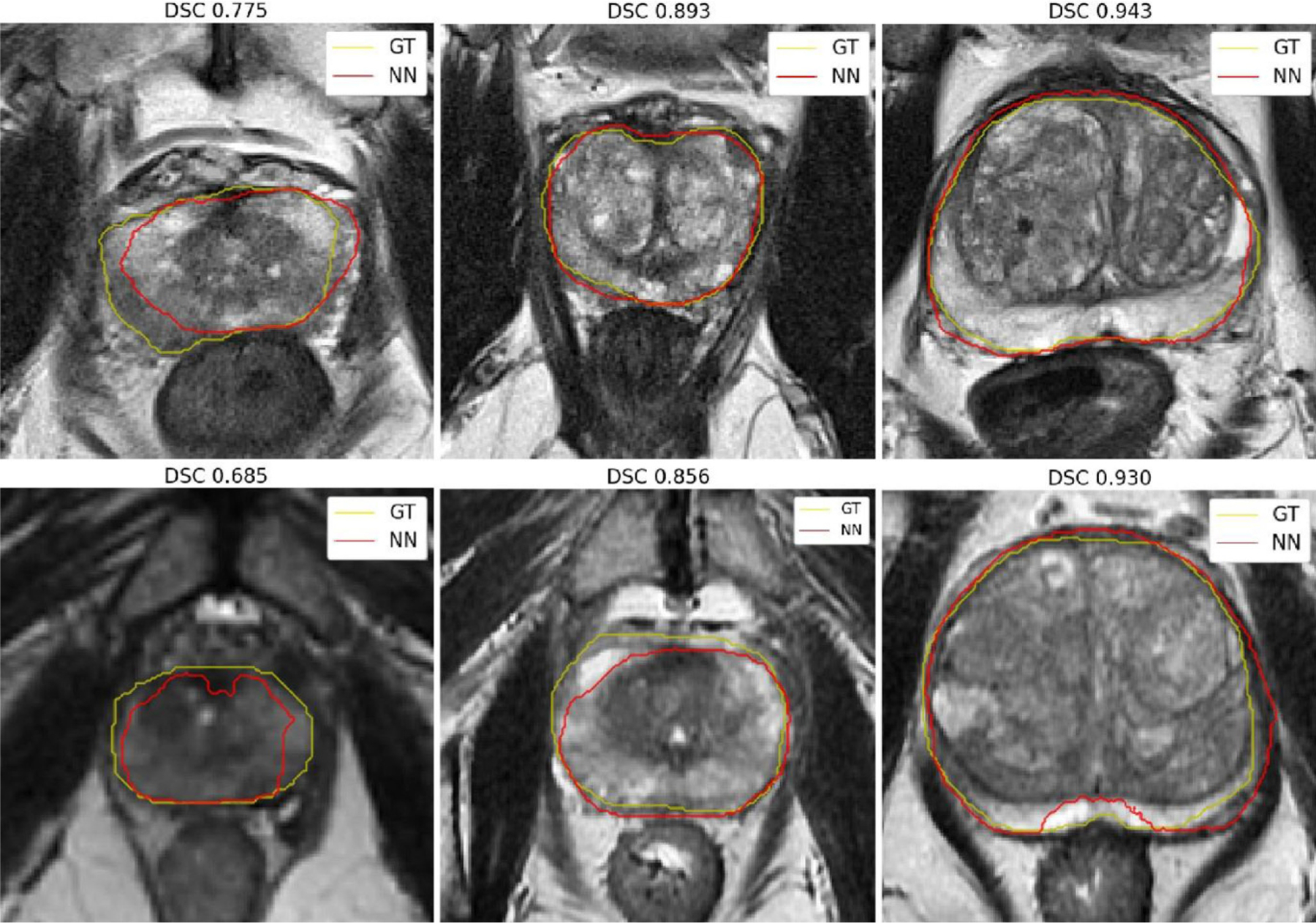
Prostate segmentation for the cases with the lowest, closest to mean, and highest 3D DSC for the Siemens (top) and GE (bottom) datasets. These segmentations are obtained with the Combined network model. Ground truth (GT) contours are in yellow and predicted contours (NN) are in red

Table 3 shows the obtained DSCs and 95% Hausdorff distances for the segmentation of the PZ for the three trained models. The best DSCs of 0.788 and 0.811 are obtained when the model is trained using the combined dataset. Fig. 5 shows the middle axial slice for the lowest, closest to mean, and highest DSC obtained for the segmentation of the PZ on the Siemens and GE dataset.

Table 3.

Dice similarity coefficients (DSC) and 95% Hausdorff distances for prostate peripheral zone, segmented with each of the three trained models (GE, Siemens, and Combined)^a

Model	GE		Siemens
	DSC	Hausdorff Distance (mm)	DSC	Hausdorff Distance (mm)
	Mean (SD);	Mean (SD);	Mean (SD);	Mean (SD);
	Median (Range)	Median (Range)	Median (Range)	Median (Range)
GE	0.765 (0.115);	2.381 (2.874);	0.539 (0.204);	7.235 (8.995);
	0.789 (0.009, 0.922)	1.5 (0.5, 22.774)	0.577 (0, 0.876)	3.536 (1, 60.815)
Siemens	0.591 (0.219);	6.161 (7.905);	0.799 (0.094);	1.868 (2.411);
	0.65 (0.015, 0.906)	3.041 (0.5, 46.005)	0.818 (0.025, 0.931)	1.118 (0.5, 27.699)
Combined	0.788 (0.093);	2.009 (2.139);	0.811 (0.079);	1.915 (2.427);
	0.811 (0.327, 0.929)	1.5 (0.5, 18.561)	0.829 (0.305, 0.933)	1.118 (0.5, 27.06)

SD standard deviation

^aAll paired comparisons in the table were significantly different (p < 0.001)

Fig. 5.

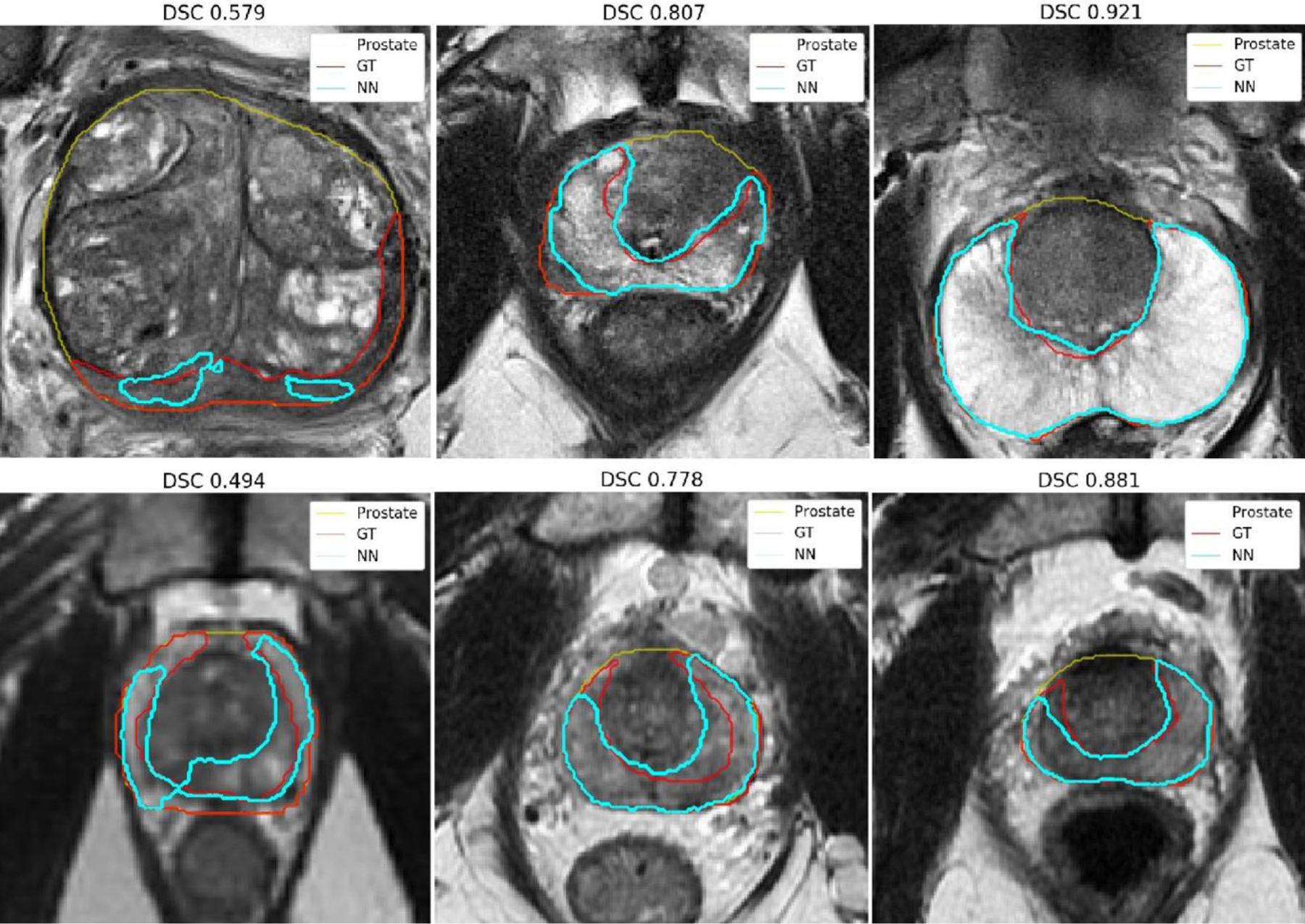
Peripheral zone segmentation for the cases with the lowest, closest to mean, and highest 3D Dice similarity coefficients (DSC) for the Siemens (top) and GE (bottom) datasets. These segmentations are obtained with the Combined network model. Ground truth (GT) PZ contours are displayed in red, predicted contours (NN) in cyan, and prostate contours in yellow

In Table 4 Spearman correlations coefficients of the DCS and four acquisition parameters: pixel size, echo time, echo train length and repetition time are displayed. The last three parameters are related in general to image contrast. Although modest, four of the Spearman coefficients reached statistical significance.

Table 4.

Spearman’s rank coefficient (ρ) between the Dice similarity coefficients (DSC) and MRI acquisition parameters. DSC is calculated between manual and automatic segmentation of the prostate and PZ with each of the three trained models (GE, Siemens, and Combined)

Test dataset	Model	Pixel size	Echo time	Echo train length	Repetition time
GE (n = 220)	GE	−0.09	0.02	0.04	−0.12
	Siemens	−0.03	0.16	0.17	−0.11
	Combined	−0.08	−0.10	0.02	−0.07
	GE_PZ	−0.034	−0.07	−0.06	0.01
	Siemens_PZ	−0.24*	0.01	0.10	−0.26*
	Combined_PZ	−0.02	−0.06	−0.07	0.00
Siemens (n = 330)	GE	0.03	−0.04	−0.05	−0.00
	Siemens	0.00	0.02	0.03	0.16*
	Combined	−0.02	0.04	0.06	0.17*
	GE_PZ	−0.06	0.04	0.03	−0.15
	Siemens_PZ	−0.09	0.09	0.09	−0.02
	Combined_PZ	−0.12	0.14	0.12	−0.03

^*p-value <0.005

Examples of activation maps for different layers are shown in Fig. 6 for the Combined model of the prostate. The activation maps of the second layer in the axial stream (Fig. 6b) show that several features are identifying the obturator muscle (areas with low intensity), and others are recognizing different types of edges. The activation maps of the fifth model layer are of low resolution (Fig. 6c) which makes it harder to identify particular structures, but some features activate a broad location of the prostate while others activate features outside the prostate. Some structures, such as the prostate, pelvic bone, obturator muscle can be identified across multiple views as the network has combined the three initial streams. And finally, the prostate and the background are clearly segmented by some of the features at the 14th layer (Fig. 6d).

Fig. 6.

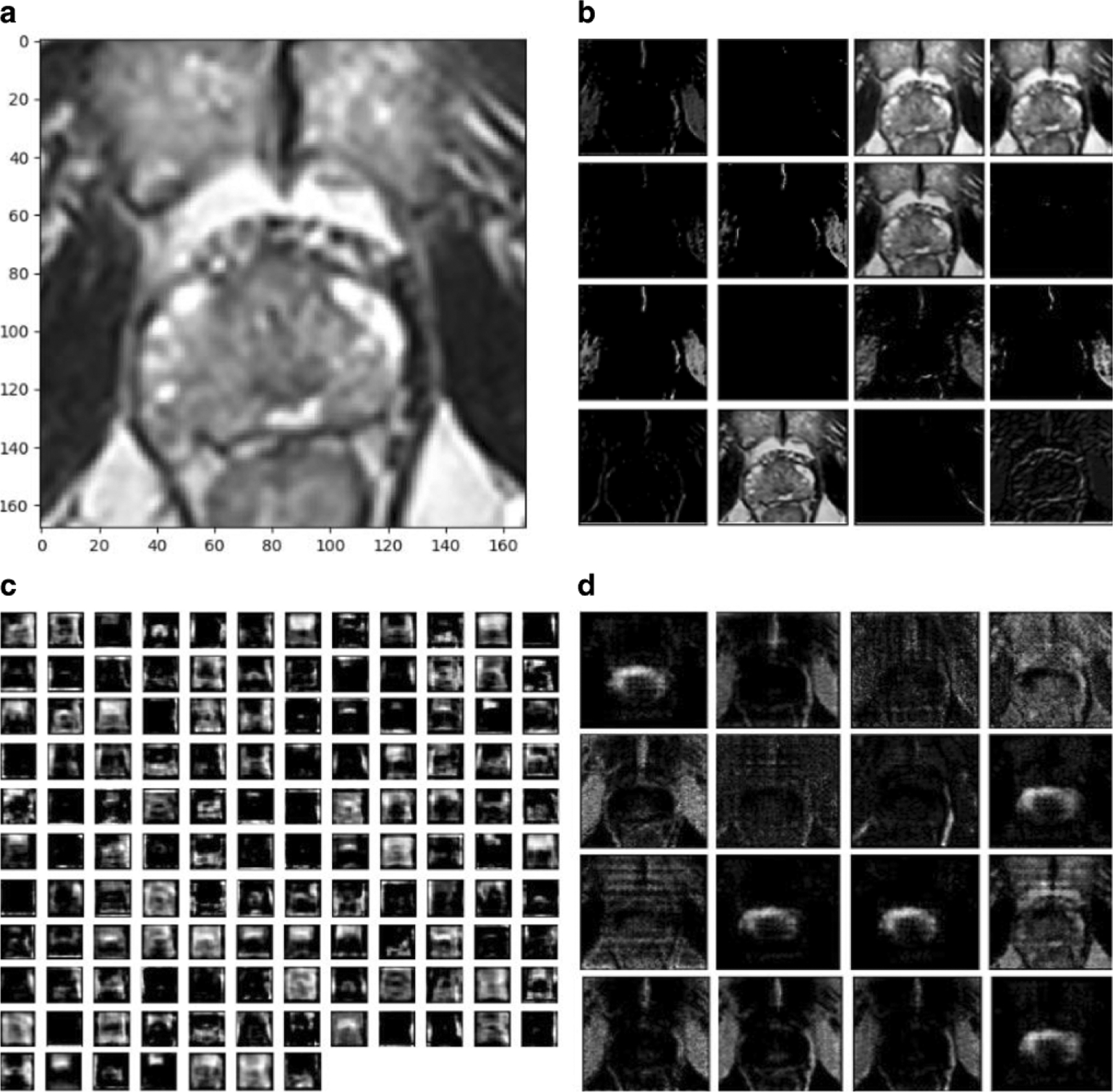
Examples of activation maps for different layers of the network. a A single axial test input; b activation maps at 2nd layer (84 × 84 × 16) from the axial input stream after convolution; c activation maps at 5th convolution layer (42, 42,128) after joining of the multistream network; and d 14th (168,168, 16) layer after convolution before fully connected output

Discussion

In this manuscript, a deep learning 3D CNN architecture for the automatic segmentation of the prostate and the zonal anatomy on T2 MRIs, collected from two MRI-vendors, is investigated. This is a continuation of our previous work [10], where a multiatlas-based segmentation method was also evaluated for different MRI vendors. In both publications, the term vendor is used with the caveat that the automatic segmentation performance is in fact related to the property of the MRI scanner. We used the same crisscross design in both projects, whereby a method trained with imaging data from one vendor was tested in segmenting images acquired on another. Recently, the inner-site variability was evaluated using similar experimental design and deep-learning-based segmentation of the prostate [28].

The objective of the paper was to build models for the segmentation of the prostate and the PZ that will perform robustly in a large variety of images and make it available to the community (the obtained models and the software for testing them are freely available at https://github.com/olmozavala/Prostate_and_PZ_DL_Segmentation_Code). Unlike Gibson et al. [28] the presented network also segments the PZ. The 3D U-Net architecture was chosen as a state of the art method for image segmentation [15]. Similarly, established methods for upsampling in the decoder phase were used [20, 29–31]. Our results on ProstateX are comparable to Meyer et al. [15], indicating that network modifications did not compromised the network. To the best of our knowledge, these developments utilized the largest collection of annotated prostate imaging datasets. The method used acquired axial, sagittal and coronal T2-weighted images for achieving high resolution segmentation of the prostate/PZ.

The combined model yielded similar DSCs for the two datasets (0.825 for GE and 0.893 for Siemens). The results obtained for the Siemens dataset are comparable with recent methods for prostate segmentation [32–34]. The average DSCs of all the PZ models are lower than the coefficients for segmenting the prostate, which is expected as segmenting the PZ is a more challenging task. The obtained DSC for segmenting the PZ with the Combined model (0.788 and 0.811) are better than what we found in the literature for similar databases (0.60, 0.68, 0.62, 0.75) [9, 35–37].

This paper brings to the forefront the need for assessment of data heterogeneity when comparing the performance of segmentation methods. While intuitively self-evident, this factor is often ignored in the quest for higher DSC scores. A robust performance of a segmentation with DCS in the 0.85 range may be more desirable than a DSC >0.9 of a model trained in a homogeneous dataset. For example, as evident from Table 1, the Siemens data are more homogeneous. The Siemens’ trained model performed with high accuracy on Siemens image data (Table 2, DCS ~0.90), but ostensibly failed on GE (DSC <0.3). It could be hypothesized that the reasons for suboptimal performance is the inability of the Siemens model on handling more heterogeneous data. Based on the results in Table 4, it also seems that the model classifies, probably erroneously, on GE image contrast properties. In the case of PZ, the Siemens model performs better on GE lower image resolution, which is expected as it is trained on images with lower resolution. Meanwhile, the GE trained model reached a more modest DSC for GE data (DSC ~0.88) but performed quite robustly on Siemens data. For these reasons, comparing the performance of our network with other CNN approaches is not straightforward. Mooij et al. [36] report DSC of 0.89 and 0.65 for TZ and PZ, respectively. The network was trained with fifty-three 3D T2-w datasets. Our results are superior; however, this most likely is a consequence of the larger training dataset. Meyer et al. [15] used a subset of forty images from ProstateX to train a network, resulting in average DCS for segmenting the prostate of 92.1%. Possible explanation for these excellent results is again the homogeneity of this data, as exemplified in Table 1. To et al. [38] tested their model with two distinct datasets and obtained DSCs of 95.11 and 89.01. The large difference of more than 6% in the performance of the network is attributable to the variation in heterogeneity of each dataset.

It should be noted that even though the CNN was trained and tested on T2-w MRIs with sizes 168³ the final model is not restricted to that input size and could be used with different resolutions as long as the field of view of the input volume is similar to the training data and the size of the image can be divided by 8 without a remainder (104³, 160³, 168³, 184³, 240³, etc.). As a test, we ran images at 200³ and the network segmented the data successfully (data not shown).

Deep learning models are sometimes considered “black box” methods because it difficult to understand how the networks work and which features of the model have some biological meaning [39]. The visualization of the activation maps for a single test input volume (Fig. 6) provide a glimpse of the image features that contribute on the network classification. Similarly, investigating the correlations of the DSC coefficients with the image acquisition parameters (Table 4) contributed to the understanding of how image contrast and resolution affect the network performance.

This study has some limitations. The Siemens and GE datasets are of different sizes and splitting the datasets in training, validation and testing of the same size would possibly provide for better comparison of the models. Even though the manual segmentation was performed by experienced operators, there is inherent error in the “ground truth” contours. The limited inter-reader study, carried out in our previously reported results [10], yielded DSC of 0.88 ± 0.04 and 0.66 ± 0.15 for the prostate and PZ, respectively. These results are similar to previously reported [4]. There is a variety of factors that affect the process of prostate segmentation. While the networks were trained on a very large dataset, there is no guarantee that this dataset encompasses all possible variations related to anatomical variability between subjects, as well as variability in imaging data.

The established network could be used as a basis and then fine tuned to a particular classifier on top of this CNN for a new dataset [40]. Future plans include incorporating other sequences of mpMRI in the model as well as investigating if segmented prostate and PZ simultaneously will improve the model. In addition, early stopping of the network will be evaluated on a separated dataset rather than on the training set.