COVID-19: Estimation of the transmission dynamics in Spain using a stochastic simulator and black-box optimization techniques

Abstract

Background and objectives: Epidemiological models of epidemic spread are an essential tool for optimizing decision-making. The current literature is very extensive and covers a wide variety of deterministic and stochastic models. However, with the increase in computing resources, new, more general, and flexible procedures based on simulation models can assess the effectiveness of measures and quantify the current state of the epidemic. This paper illustrates the potential of this approach to build a new dynamic probabilistic model to estimate the prevalence of SARS-CoV-2 infections in different compartments.

Methods: We propose a new probabilistic model in which, for the first time in the epidemic literature, parameter learning is carried out using gradient-free stochastic black-box optimization techniques simulating multiple trajectories of the infection dynamics in a general way, solving an inverse problem that is defined employing the daily information from mortality records.

Results: After the application of the new proposal in Spain in the first and successive waves, the result of the model confirms the accuracy to estimate the seroprevalence and allows us to know the real dynamics of the pandemic a posteriori to assess the impact of epidemiological measures by the Spanish government and to plan more efficiently the subsequent decisions with the prior knowledge obtained.

Conclusions:The model results allow us to estimate the daily patterns of COVID-19 infections in Spain retrospectively and examine the population’s exposure to the virus dynamically in contrast to seroprevalence surveys. Furthermore, given the flexibility of our simulation framework, we can model situations —even using non-parametric distributions between the different compartments in the model— that other models in the existing literature cannot. Our general optimization strategy remains valid in these cases, and we can easily create other non-standard simulation epidemic models that incorporate more complex and dynamic structures.

1. Introduction

The spread of SARS-CoV-2 is generating unprecedented health and socio-economical crisis worldwide, being one of the most significant challenges in Europe since World War II. In the light of this emergency, the governments ought to organize an appropriate schedule and optimize political decisions based on scientific evidence to avoid the collapse of the healthcare system, reduce virus-related mortality and minimize the potential effects of an economic recession [39], [44], [50], [51].

Given the vital capacity of the virus to spread and the lack of effectiveness of preventive measures, many countries have been systematically forced to lock down the population temporarily. Although these policies may help control the spread of the virus, they are economically unsustainable over time. In this regard, forecasting the evolution and consequences of the pandemic based on the exposure of the population becomes a critical factor in decision-making [23], [40]. However, it is first necessary to assess the current spread of the epidemic to rigorously predict these effects, which is often unknown due to the limited tracking of new infections and active cases.

At the beginning of the $20\text{th}$ century, the first mathematical models to study the dynamics of an epidemic were introduced. Probably the best-known method is the susceptible-infected-recovered model (SIR). SIR model and its variations [33], [38] divide the population into compartments, and using differential (deterministic) equations, the number of individuals in each of the compartments over time are estimated. Since then, many new variations of these models that also involved stochastic versions have been introduced in the literature (see for review [3], [5], [49], [70] or other contemporary examples [14], [59]).

Despite the enormous progress with these models in recent decades, their direct applications can be limited in several settings. First, most models explain the dynamics of the epidemic at the population level [28], [37], [41] excluding relevant individual interactions. Second, model-specific assumptions can be restrictive and abstracted from practice. For example, practitioners use Poisson’s homogeneous process to handle the mechanism of new infections or parametric distributions that determine time transitions [29], [42]. Third, introducing model reformulations in practice can be challenging and time-consuming with the current optimization strategies of the literature-based primary on designed specific procedures with likelihood equations [10]. We believe this is a critical factor limiting the performance of initial experiments and the use of novel and non-standard formulation of epidemic models in a routine and straightforward manner.

As in statistical learning theory, we can say that there is no universal model for all scenarios. Instead, we probably have to design specific models following the existing epidemiological evidence for each situation and introduce the prior knowledge obtained into models.

Simulation techniques are a prominent alternative method to build complex and more realistic epidemiological models at a high computational cost. However, their use is not new, and several agent models have appeared in the literature [75], [79], which allow modeling the possible impact of different interventions on the evolution of a pandemic. For instance, we can study the impact of vaccination, social distance, or lockdown policies in the reduction of infections or mortality [32]. More specifically, some of the specific advantages are summarized below:

• •We can introduce a wide variety of distributions in the components of the model that can be specified with intractable complex likelihood equations [17] or even non-parametric assumptions.
• •Simulation models allow the introduction of personal information of individuals, such as age and other covariates relevant to disease manifestation, without introducing challenges in the model implementation, unlike classical epidemic models.
• •Adding some constraints into the model, such as the social interactions between individuals, is not complicated from a model design perspective and only increases computation demands.

A cornerstone in expanding this area of research is the ability to obtain reliable solutions to the underlying optimization problem without resorting to problem-specific optimization strategies. Advances in computational power and the field of Black-Box optimization [66] can be an essential milestone in achieving such a goal and being able to examine different models without consuming much time using general procedures. However, sometimes, this strategy requires high-computing environments. Only by evaluating an objective function can these algorithms learn reasonable solutions performing multiple simulations.

In this paper, we explore this idea. Using a flexible yet straightforward dynamic probabilistic model that we designed based on the biological evidence of the onset of the pandemic, we estimate the seroprevalence in different regions of Spain along different waves. We also reconstruct the dynamics of infections and recoveries in different compartments to answer specific epidemiological questions, such as when the famous infection peaks happened. To do this, we solve an inverse problem with the mortality records to estimate some specific model parameters, such as the daily rate of infections. In this task, we use, for the first time in this area, the CMAES algorithm [30], one of the state-of-the-art Black-Box stochastic optimization methods that have been in our previous tests more competitive than other existing algorithms.

We must note that our primary purpose in mathematical modeling is not to make forecasts about the dynamic evolution of the pandemic. Instead, the aim of our proposal is to perform backcasting: to retrospectively reconstruct the dynamics of infections while estimating seroprevalence in the different compartments of the model. By estimating this information, we can better characterize the concrete mechanisms of virus transmission in the territories analyzed. Thus, for example, we can guide political decisions in a more refined sense by establishing more advanced and personalized epidemiological thresholds to determine lock-down policies, according to each territory’s specific socio-economic and healthcare factors and the dynamic evolution of the number of infections drawn by our model in the different compartments.

1.1. Outline

The article structure is as follows: First, we introduce our new mathematical model to estimate the spread of COVID-19 in regions and countries together with the model optimization strategy used. Then, we introduce some historical background on the evolution of the COVID-19 pandemic in Spain. Also, some demographic and economic characteristics of the Spanish population are presented. Next, we evaluate the behavior of the model and we illustrate its usefulness, performing different analyses across several Spanish regions, reporting the day-to-day evolution of susceptible, infected, and recovered patients. Finally, we discuss the results, the model limitations, and the power and value of the new methodology presented in the existing literature.

1.2. Aims of the analysis

In order to show the usefulness and broad potential of our proposal for practitioners, we perform different analyses that allow answering the following epidemiological questions:

• 1.What was the spread of the virus in the first wave in different regions of Spain like?. For example, when did the peak of infections occur?. How many infected people were there in Spain at the end of the lockdown policies?
• 2.Using a longer time frame, until March 1, 2021, how were the overall dynamics of SARS-CoV-2 in the Spanish population as a whole?. For example, the healthcare situation was critical in October of 2020, and there were discussions about applying a national lockdown; What could be the real epidemiological situation at that time?
• 3.Given that, from a theoretical point of view, we can reconstruct the dynamics of infections with our model, how was the actual day-to-day capacity to detect new cases in Spain?

2. Mathematical model and optimization strategy

2.1. Model elements

Suppose that $\mathcal{D}=\{0,1,\dots ,n\}$ is the set of days under study. Consider the following random processes whose domain is defined on $\mathcal{D}$.

• •$\mathcal{S}\left(t\right)$: Number of people susceptible to become infected on day $t$.
• •${\mathcal{I}}_1\left(t\right)$: Number of infected individuals who are incubating the virus on day $t$.
• •${\mathcal{I}}_2\left(t\right)$: Number of infected people who have passed the theoretical incubation period and who: (i) don’t show symptoms or (ii) symptoms are mild on day $t$.
• •${\mathcal{I}}_3\left(t\right)$: Number of infected people who have passed the incubation period and do show moderate or severe symptoms on the day $t$.
• •${\mathcal{R}}_1\left(t\right)$: Number of recovered cases which are still able to infect on the day $t$.
• •${\mathcal{R}}_2\left(t\right)$. Number of recovered cases that are not able to infect anymore on the day $t$.
• •$\mathcal{M}\left(t\right)$: Number of deaths on day $t$.

Henceforth, we will denote by $\mathcal{I}\left(t\right)={\mathcal{I}}_1\left(t\right)+{\mathcal{I}}_2\left(t\right)+{\mathcal{I}}_3\left(t\right)$ the number of infected people at time $t\in \mathcal{D}$ and $\mathcal{R}\left(t\right)={\mathcal{R}}_1\left(t\right)+{\mathcal{R}}_2\left(t\right)$ the number of recovered people.

The above random processes describe the dynamic of population individuals in separate compartments. We divided the infected and recovered individuals in a broader and specific taxonomy for the particular case of the COVID-19 than the classical epidemiological models [5], [38]. There are two main reasons for this. First, the patients tested by healthcare are usually those found in ${\mathcal{I}}_3$. In this case, there is an essential corpus of prior knowledge about how they evolve, and in case of death, their survival time. Second, there is evidence that there are recovered patients who can still infect others.

2.2. Basic model definition

The causal mechanism of newly infected individuals is introduced below. For each day $t\in \mathcal{D}$, we assume that the new infections ${\mathcal{I}}_1^{new}\left(t\right)$ are generated by the individual interaction of the susceptible people with infected patients and the recovered cases that they can still contaminate (patients that belong of states ${\mathcal{I}}_1$, ${\mathcal{I}}_2$, ${\mathcal{I}}_3$, ${\mathcal{R}}_1$).

Formally, we assume that if an individual can contaminate, it does so according to a random variable $X\sim Poisson\left({\mathcal{R}}_i\left(t\right)\right)$, being ${\mathcal{R}}_i\left(t\right)$ the average number of new infections that can cause each person in the day $t$. It is natural to assume that the function ${\mathcal{R}}_i\left(t\right)$ follows a decreasing trend in the first months of the epidemic, basically due to two reasons: (i) quarantine policies have been systematically introduced along with different countries and regions. (ii) the number of susceptible people decreases over time, while the number of infected people can increase. These facts indicate that in our particular setting, it is more complicated to interact with non-infected people.

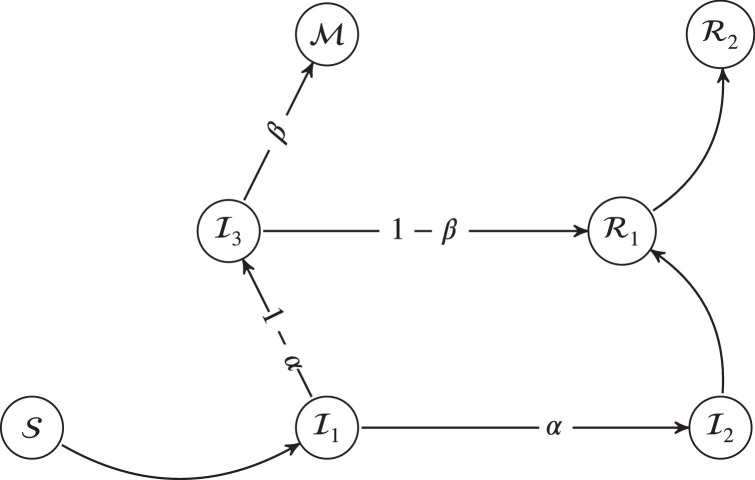
Once a new infected person arrives to the model (see Fig. 1 ), we assume that the transitions between the different graph states are modeled by a probability law that verifies the following conditions: (i) the transition probabilities are independent of the absolute instant when such transition takes place (ii) the probabilities depend only on the current state of the patient regardless of the previous path in the graph. In particular, given the $States=\{{\mathcal{I}}_1,{\mathcal{I}}_2,{\mathcal{I}}_3,{\mathcal{R}}_1,{\mathcal{R}}_2,\mathcal{M}\}$, and $\alpha ,\beta \in [0,1]$, we have: $\mathbf{P}\left({\mathcal{I}}_2\right|{\mathcal{I}}_1)=\alpha$, $\mathbf{P}\left({\mathcal{I}}_3\right|{\mathcal{I}}_1)=1-\alpha$, $\mathbf{P}\left(\mathcal{M}\right|{\mathcal{I}}_3)=\beta$, $\mathbf{P}\left({\mathcal{R}}_1\right|I_3)=1-\beta$, $\mathbf{P}\left({\mathcal{I}}_3\right|{\mathcal{I}}_2)=1$, $\mathbf{P}\left({\mathcal{R}}_2\right|{\mathcal{I}}_1)=1$; all other transitions take a value equal to zero in probability. More schematically, the $P$, probability transition matrix, between events is shown in the Eq. (1).

$$\begin{array}{c}\hfill P=\left[\begin{array}{ccccccc}& I1& I2& I3& R1& M& R2\\ I1& 0& \alpha & 1-\alpha & 0& 0& 0\\ I2& 0& 0& 0& 1& 0& 0\\ I3& 0& 0& 0& 1-\beta & \beta & 0\\ R1& 0& 0& 0& 0& 0& 1\\ M& 0& 0& 0& 0& 1& 0\\ R2& 0& 0& 0& 0& 0& 1\end{array}\right].\end{array}$$ (1)

Fig. 1.

Diagram of state changes in our model.

Additionally, Table 1 shows the random variables that model the time between transitions together with the references used in our elections for real examples of COVID-19 in Spain.

Table 1.

Random variables of the time of each transition.

Transition	Random variable	Used references
${\mathcal{I}}_1\to {\mathcal{I}}_2$	$Gamma(5.807,0.948)$	Abdel-Salam and Mollazehi [1], Lauer et al. [43]
${\mathcal{I}}_1\to {\mathcal{I}}_3$	$Gamma(5.807,0.948)$	Abdel-Salam and Mollazehi [1], Lauer et al. [43]
${\mathcal{I}}_2\to {\mathcal{R}}_1$	$Uniform(5,10)$
${\mathcal{I}}_3\to {\mathcal{R}}_1$	$Uniform(9,14)$	Abdel-Salam and Mollazehi [1]
${\mathcal{I}}_3\to \mathcal{M}$	$Gamma(6.67,2.55)$	Abdel-Salam and Mollazehi [1], Novel et al. [57], Salje et al. [68], Verity et al. [81]
${\mathcal{R}}_1\to {\mathcal{R}}_2$	$Uniform(7,14)$	Bi et al. [7], Ehmann et al. [22]

Table 2 shows the values used to model the transition probabilities. The Supplementary Material provides specific details about how the mentioned parameters and functions were selected.

Table 2.

Probability of each transition.

Coefficient	Value	Used references
$\alpha$	0.8	Day [19], Mizumoto et al. [53], Nishiura et al. [56], Tabata et al. [77]
$\beta$	0.06	Dudel et al. [20], Fauci et al. [24], Mahase [48], Rajgor et al. [65], Verity et al. [80], Wu et al. [83]

Finally, as we defined the model above, we have a continuous-time probabilistic model. However, the surrogate variables to fit and compare the model results are recorded daily in real-world situations. Consequently, in our implementation we perform the simulation between transitions and new infections on a daily basis and we truncate the corresponding continuous time in days.

2.3. Stochastic model implementation

Our model does not have a closed-form solution. Therefore, in a real-world setting, it is necessary to use statistical simulation methods to approximate specific population characteristics of the stochastic process as quantile functions. Also, we must fit some parameters of the model to characterize the behavior of the study population. For this purpose, we use a sample of the deceased patients $\{{\mathcal{M}}_1,{\mathcal{M}}_2,\dots ,{\mathcal{M}}_s\}$ along the set of days $\mathcal{O}=\{1,\dots ,s\}$.

Next, we suppose that our model ($M$) is dependent on a vector of parameters $\theta =({\theta }_1,{\theta }_2)\in {\mathbf{R}}^{p_1}\times {\mathbf{R}}^{p_2}$ (with $p_1+p_2=p$), where ${\theta }_1$ is a vector of dimension $p_1$, defined in beforehand, and ${\theta }_2$ must be estimated from the sample. Furthermore, let us assume that the initial state of the system is characterized by $\mathcal{S}=(\mathcal{S}\left(0\right),{\mathcal{I}}_1\left(0\right),{\mathcal{I}}_2\left(0\right),{\mathcal{I}}_3\left(0\right),{\mathcal{R}}_1\left(0\right),{\mathcal{R}}_2\left(0\right),\mathcal{M}\left(0\right))\in {\mathbf{N}}^7$ and $\mathcal{T}=({\mathcal{T}}_1\left(0\right),{\mathcal{T}}_2\left(0\right),{\mathcal{T}}_3\left(0\right),{\mathcal{T}}_4\left(0\right),{\mathcal{T}}_5\left(0\right),{\mathcal{T}}_6\left(0\right))\in {\mathbf{N}}^m\times \dots \times {\mathbf{N}}^m$. $\mathcal{S}$ has the number of elements for each compartment of the model on day 0. $\mathcal{T}$ also contains the amount of remaining days to complete the transition they are in for each individual in the initial state, being $m$ a natural number that represents the maximum number of registered days.

To simplify the notation, for each day $t\in \mathcal{D}$, we denote the average dead trajectory by the function $Mean({\theta }_1,{\theta }_2,\mathcal{S},\mathcal{T})\left(t\right)$.

The next step is to estimate ${\widehat{\theta }}_2$. To do this, we propose to solve the following optimization problem:

$${\widehat{\theta }}_2=\arg \underset{{\theta }_2\in S\subset {\mathbf{R}}^{p_2}}{\min }\sum _{i=1}^s{\omega }^i{({\mathcal{M}}_i-Mean({\theta }_1,{\theta }_2,\mathcal{S},\mathcal{T})\left(i\right))}^2,$$ (2)

where $\omega =({\omega }^1,\dots ,{\omega }^s)$ is a weighted vector that can help to improve model estimation. Examples of these weights may be:

${\omega }^i={\mathcal{M}}_i/{\sum }_{i=1}^s{\mathcal{M}}_i$ or ${\omega }^i=(1/{\mathcal{M}}_i)/({\sum }_{i=1}^{s}1/{\mathcal{M}}_i)$ $(i=1,\dots ,s)$.

At this point, it is relevant to note that the above optimization problem (2), as formulated, includes the possibility of introducing constraints in the parameters’ space. The previous fact is essential because we often have prior knowledge of the range of parameters, or we can even invoke the biological interpretation of parameters to answer this question. Thus, by introducing this knowledge, we can spread up the speed of optimization Black-Block techniques significantly.

In Eq. (2), we have used the real mean trajectory. However, in practice, this is unknown, and we must approximate it using simulation. Next, we run $B$ different simulations, and we denote by $\overline{M}({\theta }_1,{\theta }_2,\mathcal{S},\mathcal{T})=\frac{1}{B}{\sum }_{i=1}^B{M}^i({\theta }_1,{\theta }_2,\mathcal{S},\mathcal{T})$, the estimated mean trajectory. $M^i(\theta ,{\theta }_2,\mathcal{S},\mathcal{T})$ $(i=1,\dots ,B)$ denotes the result of simulation number $i$.

So the optimization problem to be solved is:

$${\widehat{\theta }}_2=\arg \underset{{\theta }_2\in \mathcal{S}\subset {\mathbf{R}}^{p_2}}{\min }\sum _{i=1}^s{\omega }^i{(M_i-\overline{M}({\theta }_1,{\theta }_2,\mathcal{S},\mathcal{T})\left(i\right))}^2.$$ (3)

Schematically, the overall optimization process is described below.

• 1.Define an initial ${\theta }_2^0$ and run $B$ times $M({\theta }_1,{\theta }_2,\mathcal{S},\mathcal{T})$. We denote by $M^1({\theta }_1,{\theta }_2^0,\mathcal{S},\mathcal{T}),\dots ,M^B({\theta }_1,{\theta }_2^0,\mathcal{S},\mathcal{T})$, different results are obtained.
• 2.Estimate the mean trajectory $\overline{M}({\theta }_1,{\theta }_2^0,\mathcal{S},\mathcal{T})=\frac{1}{B}{\sum }_{i=1}^B{M}^i({\theta }_1,{\theta }_2^0,\mathcal{S},\mathcal{T})$
• 3.Estimate the mean square error ${\widehat{RSS}}^0={\sum }_{i=1}^s{\omega }^i{(\overline{M}({\theta }_1,{\theta }_2^0,\mathcal{S},\mathcal{T})\left(i\right)-{\mathcal{M}}_i)}^2$.
• 4.To construct a succession of vectors ${\left\{{\theta }_2^j\right\}}_{j=1}^{R+1}$ so that ${\widehat{RSS}}^0$ $>$ ${\widehat{RSS}}^1$ $>$ ${\widehat{RSS}}^2$ $>$ $\dots$ $>$ ${\widehat{RSS}}^{R+1}$. For example with a stochastic optimization solver.
• 5.Stop after $R+1$ iterations and return ${\theta }_2^{R+1}$ as the optimal parameter of the problem.

In our particular setting, ${\theta }_2$ contains the parameter of the ${\mathcal{R}}_i\left(t\right)$ function that are defined in Section 2.2. In our preliminary experiments, we assumed that their functional form is equal to ${\mathcal{R}}_i\left(t\right)=\min \{C,a{e}^{-(bt+c{t}^2+d{t}^3+e{t}^4+f{t}^5)}\}$ where $a\in [0,3]$, $b\in [-1,1]$, $c\in [0,1]$, $d\in [0,1]$, $e\in [0,1]$, $f\in [0,1]$ with ${\theta }_2=(a,b,c,d,e,f)\in [0,3]\times [-1,1]\times [0,1]\times [0,1]\times [0,1]\times [0,1]$ and $C$ is a positive constant fixed 0.005. However, our final election after several experiments and sensitivity analysis with different family of functions that include the previously exponential or inverse sigmoid/logit functions is, ${\mathcal{R}}_i\left(t\right)=d+\frac{a}{1+b^{-(t-c)}}$, where $a\in [0,5]$, $b\in [0,1]$, $c\in [-30,30]$, $d\in [0,0.1]$.

2.4. Structural limitations of the model in COVID-19 pandemic

The behavior of our model is primarily determined by the parameters $\alpha$, $\beta$, and the function ${\mathcal{R}}_i\left(t\right)$, while small variations in the distributions function of the transitions times should not have a significant impact on the seroprevalence estimations. ${\mathcal{R}}_i\left(t\right)$ is estimated from observed mortality records. However, the parameters $\alpha ,\beta$ are fixed, with statics values over time, and perhaps, in practice, their value should vary in successive waves. In addition, $\alpha$, $\beta$, determine the infection fatality rate ($IFR$), the quotient between fatalities, and the number of infections. In particular, in our model $IFR$, is given, $IFR\%=\left(\right(1-\alpha )*\beta )*100$.

Some studies have shown that in the current pandemic, $IFR$ is the gold standard epidemiological indicator for monitoring the severity with which the virus has affected different countries [58], [60]. However, dynamic estimation of $IFR$ is challenging to perform since a precise approximation of the real number of infected people is generally only possible in a single time point, thanks to seroprevalence studies.

Several studies have investigated which factors influence the value of the $IFR$. The primary sources of variations are age and sex [76]. If the distribution of new infections is uniform along time regarding these variables, we can assume constants and statics values for $\alpha$ and $\beta$ in different time-spans.

Testing that assumption is necessary to determine if we must vary the coefficients $\alpha$, and $\beta$, over different waves. However, since we do not know about the true infections in successive waves, it is not trivial to validate this hypothesis empirically, and some statistical estimations are needed.

In Spain, heath institutions performed an ambitious and unique longitudinal epidemiological study to know the patterns of virus expansion in several time points that allow us to draw estimation about $IFR$. In particular, we have information on infections at the beginning of June and the end of November 2020. Using this information, we can estimate the differences in $IFR$ between the first and successive waves. We must note that the Spanish situation in the first wave was critical, with many problems in the elderly population, particularly in nursing homes, and and so changes in the $IFR$ along time are expected.

2.5. Model implementation to handle multi-waves

Analogous to an intervention analysis in the context of time series, we need to update the daily infection function to be able to model well the reality in at least the following two situations: at the end of each lockdown, and a new return to normal, or shortly before an explosive growth in the number of new cases or deaths occurs, and no lockdown policies are applied. In these situations, there are abrupt changes in daily infection trends, and therefore the functional form of the function ${\mathcal{R}}_i\left(t\right)$ needs to be modified.

Consider $t_0=0<t_1<t_2<\dots <t_m$, $m$ temporal points, defined with expert knowledge, and, in which, we hypothesize that the trend of the daily infection function is modifiable between different ${\left\{t_s\right\}}_{s=0}^m$, for example between two waves. Then, we propose to define the function ${\mathcal{R}}_i\left(t\right)$, as a piecewise function, dependent on the local functions ${\mathcal{R}}_i^{t_1}\left(t\right),\dots ,{\mathcal{R}}_i^{t_m}\left(t\right)$, that is,

$${\mathcal{R}}_i\left(t\right)=\{\begin{array}{cc}{\mathcal{R}}_i^{t_1}\left(t\right)\hfill & t\in [0,t_1)\hfill \\ {\mathcal{R}}_i^{t_2}\left(t\right)\hfill & t\in [t_1,t_2)\hfill \\ ⋮\hfill & \\ {\mathcal{R}}_i^{t_m}\left(t\right)\hfill & t\in [t_{m-1},t_m).\hfill \end{array}$$

In our fits in successive waves, we assume that the functional form of each ${\mathcal{R}}_i^{t_s}\left(t\right)$ $(s=1,\dots ,m)$ is identical, and equal to prior function ${\mathcal{R}}_i^{t_s}\left(t\right)=d_s+\frac{a_s}{1+b_s^{-(t-c_s)}}$ (for all $t\in [t_{s-1},t_s),\text{and}\text{any}s\in \{1,\dots ,m\}$), where, the sub-index $s$, denotes the dependence of parameters, to time-period $[t_{s-1},t_s)$. Then, the number of initial free-model parameters is multiplied by the number of periods, $m$, considered.

Regarding parameters $\alpha$ and $\beta$, our implementation allows varying these parameters between ${\left\{t_s\right\}}_{s=0}^m$. Let be ${\alpha }_s$ and ${\beta }_s$, the mentioned parameter for the interval $[t_{s-1},t_s)$. In this paper $\alpha ={\alpha }_1=\dots ={\alpha }_m$. However, in the global Spanish analysis along different waves, $\beta$ will be vary dynamically.

2.6. Conformal simulation bands to quantify model uncertainty

Quantify model uncertainty is a critical point in order to interpretate the results obtained together with their natural limits. In epidemic modeling, according to [21], we can decompose the model uncertainty in three different sources of error:

• •Data uncertainty: Uncertainty in specified model parameters, estimated externally from data, or in data to which models are fitted.
• •Stochastic uncertainty: Uncertainty derived from the method of simulation.
• •Structural uncertainty: Uncertainty in the optimal model structure, or derived from the use of more than one model structure for a given question.

In our settings, we use the dynamic evolution of mortality as a source of information. Then, directly reporting the “Stochastic Uncertainty” drawn for the stochastic simulator as a measure of uncertainty is unrealistic, since we can restrict the number of possible scenarios that happen in practice, according to mortality residuals. More formally, our source of information is a correlated time series that determines the possible reality that occurred, and for a given configuration of the vector parameter $\theta$, we should be removed a significant fraction of unrealistic simulation scenarios.

“Data uncertainty” is not trivial to incorporate in this type of model, and the non-parametric bootstrap solution proposed in D’Agostino McGowan et al. [21] have important limitations, since it does not consider the dynamic and correlation structure of daily reports. More general, bootstrap strategies that can handle the specific dependence structure of daily reports can be adapted as our setting, such as block or wild bootstrap, but it is something out of the scope of this work.

Testing “Structural uncertainty” is also challenging. There may be no universal model in an epidemic modeling context, and perhaps the best model for each situation is a combination of broad dictionary of simpler models that change dynamically as the pandemic evolves.

In this paper, we propose to use a solution similar to the one proposed in Shen et al. [73], which consists of selecting a small fraction of simulations, according to error criteria, e.g., mean squared error, that shape the possible real infection trajectories. With the remaining trajectories, we apply specific conformal inference techniques that, to the best of our knowledge, have not been applied previously to the context of stochastic simulation models. Conformal inference methods are a general methodology to quantify model uncertainty [72], with well-established theoretical foundations [45], and were used in an extensive list of machine learning and statistics problems (see for example a contemporany application [46]).

Below, we introduce the specific mathematical detail of the used conformal simulation bands that can handle heterocedastic noise. First, suppose that $\theta =({\theta }_1,{\widehat{\theta }}_2)$ is the optimal parameter configuration, where ${\widehat{\theta }}_2$ was estimated according to methodology proposed in the Section 2.3. Then,

• 1.Perform $B=10,000$ simulation of the model $M({\theta }_1,{\widehat{\theta }}_2,\mathcal{S},\mathcal{T})$ and evaluate the mean square error metric (RSS). ${\widehat{RSS}}^s$ and $M^s({\theta }_1,{\widehat{\theta }}_2,\mathcal{S},\mathcal{T})$ ($s=1,\dots ,B$), denote the results for iteration $s$ of mean square error and the estimation of mortaly records in the simulation model respectively.
• 2.Let $Sel=\{i\in \{1,\dots ,B\}:{\widehat{RSS}}^i\le {\widehat{RSS}}_{\left(1000\right)}\}$, the set of index of simulation with the lesser or equal 1000 value of $RSS$ estimations. ${\widehat{RSS}}_{\left(1000\right)}$ denote the element 1000, considering the order sample of ${\left\{{\widehat{RSS}}^s\right\}}_{s=1}^B$.
• 3.Using the subsample of death simulation trajectories ${\left\{M^i({\theta }_1,{\widehat{\theta }}_2,\mathcal{S},\mathcal{T})\right\}}_{i\in Sel}$, estimate pointwise the standart deviation $\widehat{\sigma }\left(t\right)$, $\forall t\in \mathcal{O}$.
• 4.Define the conformal score $Scor{e}_i={\max }_{t\in \mathcal{O}}\frac{|M^i({\theta }_1,{\widehat{\theta }}_2,\mathcal{S},\mathcal{T})\left(t\right)-{\mathcal{M}}_t|}{\widehat{\sigma }\left(t\right)}$ if $\widehat{\sigma }\left(t\right)>0$, $\forall i\in Sel$. Otherwise $Scor{e}_i$ is equal to 0.
• 5.Calculate the quantile $q_{\alpha }=\arg {\min }_{t\in {\mathbb{R}}^{+}}\{\frac{{\sum }_{s=1}^{1000}1\{Scor{e}_s\le t\}}{1000}\ge \alpha \}$, with $\alpha =0.95$, to guarantee distributional intervals that cover a confidence level of $90\%$.
• 6.Define for each $t\in \mathcal{O}$, the confidence interval prediction as $[\overline{M}({\theta }_1,{\widehat{\theta }}_2,\mathcal{S},\mathcal{T})\left(t\right)-\widehat{\sigma }\left(t\right)q_{\alpha },\overline{M}({\theta }_1,{\widehat{\theta }}_2,\mathcal{S},\mathcal{T})\left(t\right)+\widehat{\sigma }\left(t\right)q_{\alpha }]$, where $\overline{M}({\theta }_1,{\widehat{\theta }}_2,\mathcal{S},\mathcal{T})$ denote the simulation mean that correspond with our given mortality estimations.
• 7.Finally, to build confidence bands for the rest of the stochastic process that makes up our epidemic model, we must select simulation trajectories that lead to the mortality outcome falling within the mortality band calculated in step 6).

A key element of conformal inference is the selection of conformal scores. In this paper, the conformal score has been estimed using the geometry of the supreme norm $\left|\right|·{\left|\right|}_{\infty }$. $\left|\right|·{\left|\right|}_{\infty }$ is often used in the analysis of stochastic processes in the field of functional data analysis to estimate confidence bands (see for example [27]).

2.7. Our probabilistic model proposal in the literature

The literature on epidemic modeling is very broad and includes both mechanistic models built from causal epidemiological knowledge and more statistical approaches that exploit information from historical data with purely predictive models [9], [41]. Nowadays, it is not easy to establish a boundary between both approaches since, on many occasions, both methodologies are used from the same point of view or even jointly.

Our model definition is not very complicated from a mathematical point of view. However, it introduces new challenges from the computational and modeling point of view: the simulation of the trajectory of each individual along the population, the introduction of probability distributions that go beyond the exponential law as traditional models do [5], and the use of latent infections models through a non-homogeneous Poisson process, extending in this sense the Markovian property [5]. In [25], the authors define a model similar to ours and propose a resolution framework with Bayesian estimation methods. However, we assume that specific parameters are known from the epidemiological scientific evidence. Our approach using mortality records [61] allow us to obtain reliable seroprevalence estimates, but the difficulty of the estimation increases. We also do not introduce a Bayesian approach but a frequentist approach with its advantages and disadvantages as the need in the Bayesian paradigm of selecting prior functions. Finally, with the philosophy of our simulation model, we can consider complex extensions without making too many changes in the implementation.

2.8. Model optimization with a CMA-ES black-box solver

In our setting, we must find optimal parameters taking into account randomness in approximating the mean. To do this, we should resort to stochastic optimization algorithms.

Many stochastic algorithms are available in the literature. Still, based on the excellent preliminary results, we have decided to use a state-of-the-art evolutionary algorithm: the CMA-ES [30]. CMA-ES is an evolutionary-based derivative-free optimization technique that can optimize a wide variety of functions, including noisy functions, like the one we use in our method. One survey of Black-Box optimization strategies found that CMA-ES outranked 31 other optimization algorithms, performing exceptionally well on “difficult” functions or larger dimensional search spaces [31]. From a theoretical point of view, CMA-ES can be seen as a particular case of the Expectation-Maximization algorithm (EM) [8].

We provide specific algorithm steps in Supplementary Material.

2.9. Inverse problem behavior

The model fit with the mortality records invokes new challenges in model identification so that the inverse problem is well-defined. We fixed some model parameters according to existing scientific evidence to address this issue to make the problem more regularized. A potential alternative to fitting more parameters with the data is to transform the objective function into a multiobjective optimization problem, considering the daily cases or other ICU indicators as additional sources of information. However, in the early stages of the pandemic, and even nowadays, there were essential doubts about the real capacity of detection of new infections.

2.10. Tuning parameter

We performed multiple experiments with CMA-ES to check how the optimization solver behaves. At the same time, through statistical simulation, we estimate the variance of the empirical mean by varying fatalities in different settings. After those initial experiments, we decided to estimate the mean at 300 repetitions, that is, $B=300$. In addition, we have allowed CMA-ES to run 3000 iterations, starting the optimization algorithm from different random points. To obtain the results of this paper, CMA-ES, was able to find the optimal solution with the function ${\mathcal{R}}_i\left(t\right)$ selected in less than two hours. Finally, the loss function used is Mean Square Error (MSE) with $w^i=1$ $(i=1,\dots ,s)$ (see Section 2.3).

2.11. Software details and resources

Our proposal has been implemented in several programming languages- C++, Python and R- although the results that are shown in this article have been obtained with Python. We optimized the parameters using library pycma [2], and numpy has been used for mathematical operations.

In the different performed statistical analyses, we have used R. Plots have been made both in R with ggplot2 library and in Python with matplotlib.

Finally, the training data used to fit the models in the first wave can be downloaded at [67], and [18], that represent the daily Spanish statistics of COVID-19 fatalities. In the most extensive analysis of the overall Spanish population, we use the excess of mortality as a source of information. The raw data to estimated excess of mortality can be obtained in the public web interface related to MoMo-daily Spanish mortality surveillance system (https://momo.isciii.es/public/momo/dashboard/momo_dashboard.html), coordinated by National Institute of Health Carlos III (ISCIII).

We release the code used in this paper for the benefit of the scientific community at (https://github.com/covid19-modeling).

3. COVID-19 in Spain

Spain was one of the first countries worldwide to experience the effects of COVID-19, after China and Italy. However, the consequences were more dramatic despite the delayed outbreak start with respect to these countries. To give a better context to the evolution of Coronavirus in Spain, in the first wave, and compare it with other countries, we introduce some historical background:

• •January 31st. The first positive result was confirmed on Spanish territory in La Gomera. At that time, there were around 10,000 confirmed cases worldwide.
• •February 12th. The Mobile World Congress, one of the most remarkable technological congresses in the world, to be held in Barcelona, was cancelled.
• •March 8th. Multitudinous marches were celebrated in Spain. Also, sports competitions and other events were held as usual.
• •March 13th. Madrid reported 500 new cases of Cov-19 in one day (64 deaths total). Wuhan had gone into lockdown with 400 new cases per day (17 deaths total).
• •March 14th. With the increase in the outbreak of infections, the government declared a quarantine throughout the country.
• •March 21st. Due to an overloaded health system, the first patients started to arrive at new makeshift hospitals.
• •April 3rd. Spain accounts for a total of 117,710 confirmed cases, surpassing Italy for the first time.
• •April 6th. Spain becomes the country in the world with more deaths per million inhabitants.
• •April 9th. The FMI forecasts that 170 countries are going to fall into recession this year in the worst crisis since the Great Depression.
• •April 18th. The Spanish government changes protocols for the daily statistics of COVID-19.

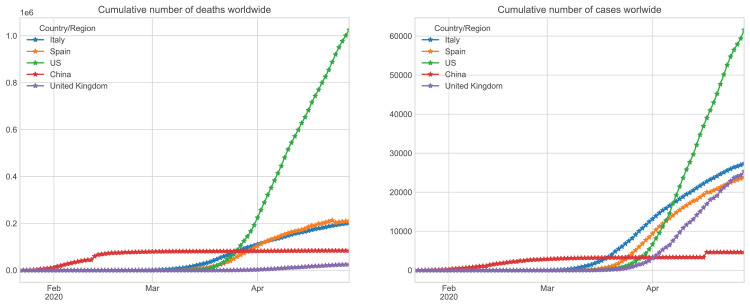
Fig. 2, shows the accumulated number of cases and deceases respectively in the previous periods in Spain, Italy, China, United Kingdom, and the United States according to the data supplied by the different governments.

Fig. 2.

Spread and number of deaths of Coronavirus in Spain, Italy, China, and the United States. Number of accumulated infected patients (left) and the number of accumulated deaths (right) [13].

Following the statistics of the Population Reference Bureau, Spain is the 20th country with the world’s oldest population [12]. The country demographic structure, poverty rates, and epidemiological profiles are essential to compare mortality between countries. In the Coronavirus disease, relative and absolute case-fatality risk (CFR) [26] increases dramatically with age and with comorbidity, as evidenced by the current literature. Relative risk can increase by more than 900% in patients over 60 [85].

Subsequently, we perform a descriptive analysis in the regions of Spain that we analyze in this paper: Galicia, País Vasco, Castilla y León, Madrid, Cataluña. Table 3 contains the essential demographic and socioeconomic characteristics of these regions. We can see that Castilla y León is the region with the highest proportion of elderly people. At the same time, Castilla y León has the most delocalized population centres, and the País Vasco is the region with the lowest poverty rate. The national poverty rate is higher than the other analyzed regions because we do not include the most poverty regions.

Table 3.

Demographic and socioeconomics characteristics of the Spanish population throughout some regions: Galicia, País Vasco, Castilla y León, Cataluńa, Madrid [34].

	Galicia	País Vasco	Castilla León	Cataluńa	Madrid	Spain
Population	2,698,763	2,181,916	2,553,301	7,609,497	6,685,470	47,100,396
At-risk-of-poverty rate	18.8	8.6	16.1	13.6	16.1	21.5
Population density	91.28	305.19	25.47	239.01	830.02	93.08
Percentage of population by age group
0–9	7.50	8.93	7.51	9.78	9.92	9.28
9–18	7.56	$8.78$	7.79	9.74	9.44	9.37
18–30	10.39	10.66	10.67	12.72	12.80	12.42
30–45	21.18	20.28	19.47	22.24	23.24	22.07
45–60	22.77	23.28	23.60	21.77	22.23	22.61
60–80	22.60	21.41	22.30	18.24	17.33	18.70
from 81 on	8.01	6.67	8.65	5.50	5.03	5.56

Spain is a multicultural country where there are significant economic, geographical, social, and demographic differences throughout the regions. All these peculiarities make Spain an interesting country to extrapolate the effects of COVID-19 spread to other regions and countries.

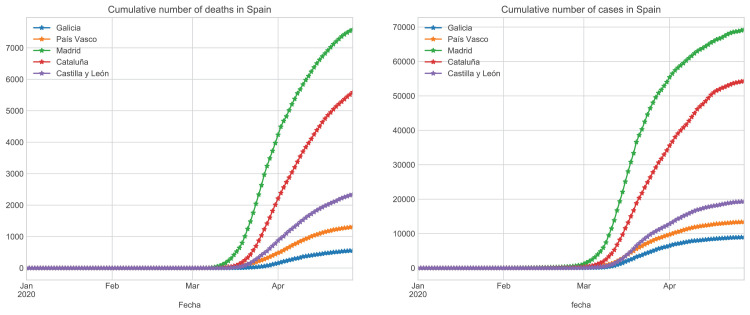
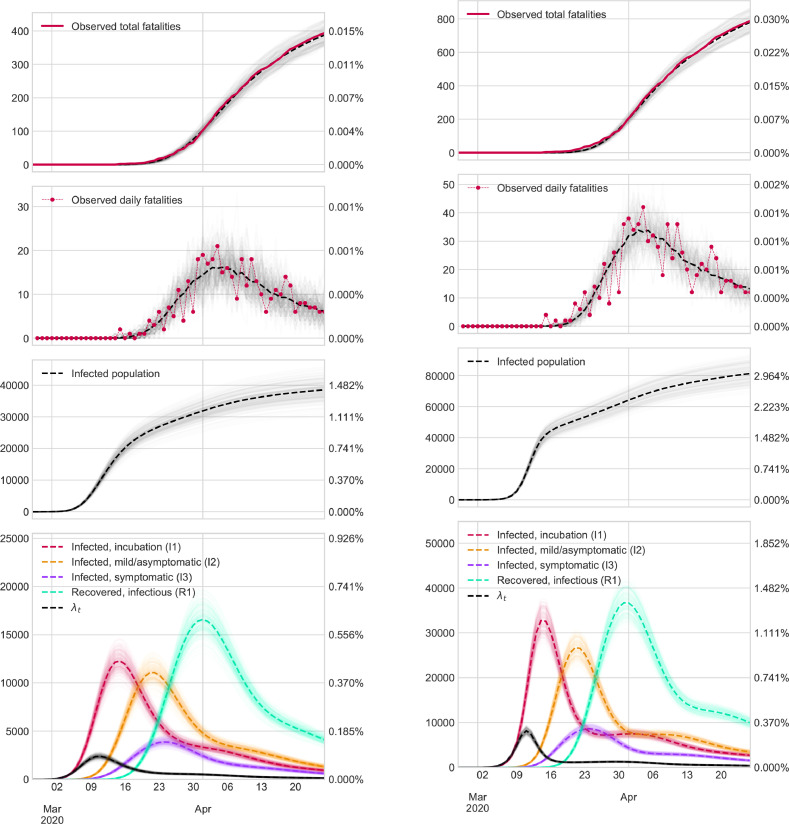
Finally, in Fig. 3 , we show the evolution of infections and fatalities among the regions under consideration in the first wave. As we can see, Madrid is the most affected region, while Galicia is the least affected, despite its older population. However, it is essential to note that the outbreak began later, and the containment was carried out earlier than in Madrid.

Fig. 3.

Evolution of accumulated infected (left) and death patients (right) in Galicia, País Vasco, Castilla y León, Madrid, Cataluña.

4. Results

4.1. First wave analysis

In order to explore the limits of the model in a more challenging scenario, we start the analysis with the first wave. In this period, most Spanish seroprevalence surveys were performed, and therefore we have a reliable estimation of the number of infections accross different Spanish regions in a single time point, allowing us to evaluate our model performance. In addition, the information is of poor quality, and epidemiological evidence is scarce; thus, making estimations in this scenario is more complicated. More specifically, we restrict the model analysis to April 26st in Galicia, País Vasco, Castilla y León, Madrid and Cataluña. As there is considerable uncertainty about mortality records, we assuming that these two scenarios hold:

• 1.We assume that the number of real deaths due to Coronavirus is reflected in official records.
• 2.We suppose a more pessimistic scenario. We assume that many people have died of Coronavirus, but they have not been included in the records because a diagnostic test was not performed. In particular, we shall suppose that the number of deaths is twice as high as those indicated in the official records each day.

To display results in an easy-to-view format, we graphically represent the evolution of some states defined at the beginning of Section 2.1 in the two cases considered. In addition, to gain further insights into the results, we show (i) the number of people who may be contaminated or have already transmitted the virus as a percentage of the population size; and (ii) the rate of new infections each day (denoted in the Figures as ${\lambda }_t$).

Finally, we introduce confidence bands of our estimations using methodology described in Section 2.6.

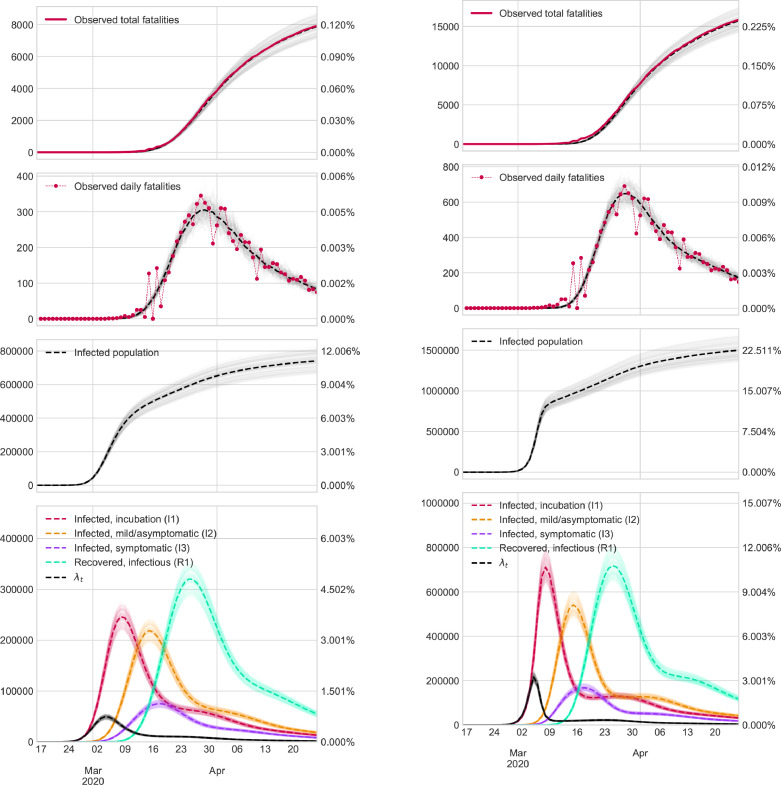
Here, we only show the Figures that contain results in Galicia and Madrid. The rest of the Figures are available in Supplementary Material.

4.2. Multi-wave analysis

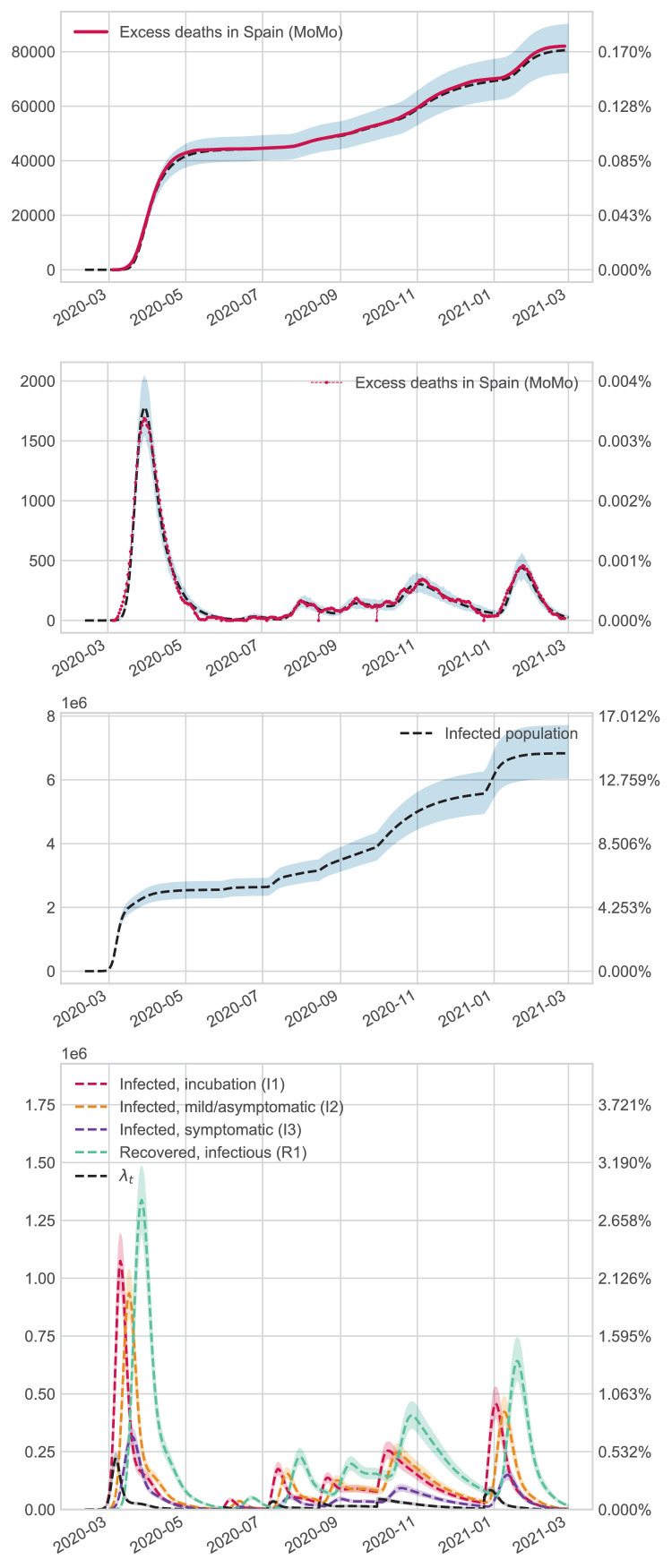
To show more recent and informative results on Coronavirus dynamics in Spain, we adjusted the model for the total Spanish population until 1 March 2021. To avoid choosing between the two scenarios above, we use excess mortality as a source of information to feed our model. $\alpha$ has been selected with the same criteria as the first wave. However, $\beta$ is fixed with a value equal to 0.085-in the first period, while the rest with 0.0425. These values were established to guarantee an $IFR$ of $1.7\%$ in the first wave and $0.85\%$ in successive periods. Specific details about $IFR$ estimations are relegated to the Supplementary Material. Daily infection function ${\mathcal{R}}_i\left(t\right)$ was fitted as a piecewise function (see Section 2.5 for details). In particular, the cut-off points selected for the jumps are as specified below ( Fig. 4, Fig. 5, Fig. 6 ).

• 1.1 March to 30 May.
• 2.1 June to 5 July.
• 3.6 July to 15 August.
• 4.16 August to 30 September.
• 5.1 October to 24 December
• 6.25 December to 1 March.

Fig. 4.

Results in Madrid.

Fig. 5.

Results in Galicia.

Fig. 6.

Results in Spain.

It is important to note that these periods correspond to critical events in pandemic evolution, such as a change in lockdown politics, holidays, or other events that led to abrupt changes in the dynamics of infections.

4.3. Analysis of results

The most relevant results in the first wave ($1\text{st}$ March 2020 to $26\text{th}$ April 2020) are outlined below:

• •Madrid was the most affected region by COVID-19. If we consider an extreme setting (e.g., the number of deaths is double that reported by the Government), 22.5% of the population could have been infected or recovered from the virus. On April 26st, there may have been almost 1,2 million of patients recovered.
• •Galicia was the region that suffered the mildest effects. The percentage of infected people was less than 2.9%.
• •Castilla y León, Pais Vasco and Cataluña could have suffered the effects of COVID-19 with a proportional magnitude. In those regions, the percentage of infections could have been between 6 and 12% of the population.
• •The peak of new infections probably occurred at the start of quarantine, while the peak of people who can contaminate took place between March 17 and 24.
• •The number of new infections have been dramatically reduced after the introduction of containment measures.
• •The most accurate scenario is the pessimistic scenario. The analysis of the excess mortality reported in the Supplementary Material justifies why this scenario is more reliable for seroprevalence estimations.

In the overall Spanish analysis, the main findings are specified below:

• •In the first wave, the number of infections reaches $5\%$, while at the end of the year, the total reaches around $10\%$. These results are in agreement with the national seroprevalence study [60].
• •After July, several lockdowns were carried out locally in different areas during specific periods. Our results show that this measure only partially controls the spread of the virus but does not sufficiently reduce the number of cases to reach a low-risk threshold of new infections. For example, active infections decreased after the global and national measures were taken from October 26th until after Christmas, but the epidemiological risk was still high during the period.
• •In the summer, the spread of the virus starts again, probably due to imported cases of tourists and high mobility patterns.
• •The peak of new infections was less severe in successive waves than at the pandemic’s beginning.
• •After Christmas, the epidemiological situation was critical. However, thanks to the new measures and the large-scale vaccination strategy, the risk of an explosion of infections was contained.

4.4. Comparison of predictions vs. seroprevalence studies during the first wave

The Spanish government launched an ambitious longitudinal epidemiological study with over 60,000 participants to assess the level of exposure of the population to the virus in at least two temporal points. The preliminary results of this study by regions can be freely downloaded at [52], and the publisher’s scientific results are available in the following article [64]. As can be seen, assuming a pessimistic scenario, our model estimates are close to the percentage of the serological survey, although there are some variations in some cases, such as in Madrid. The limitations of the epidemiological study may explain part of these discrepancies. In addition, we must consider the following factors: (i) the methodology followed in the design of the survey and in their statistical analysis; (ii) our model may need a more careful tuning of the parameters according to the study population, or should introduce more reliable sources of information. The local government of Galicia also conducted its study with more than 40,000 participants, and the results are similar [71] to those that appear in a national survey despite the different nature of the study design. Finally, the city council of Torrejón de Ardóz (Madrid), one of the most affected places in Spain, carried out its epidemiological study with more than 100,000 participants, estimating that 22 percent of the population was infected [4].

4.5. Evaluation of the testing capacity

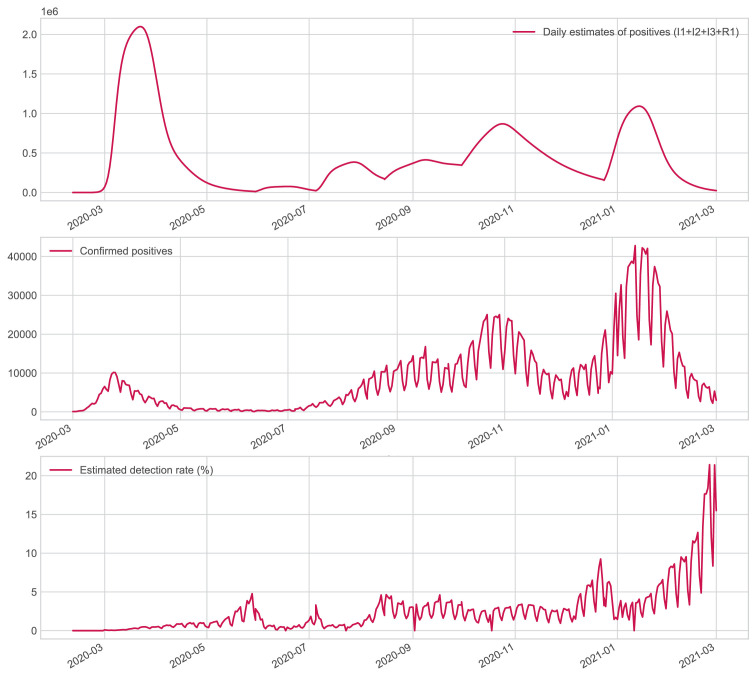
A distinctive feature of our model is that we can retrospectively reconstruct day-to-day infection dynamics with a low cost and non-invasive procedure, unlike other epidemic monitoring strategies. For example, serological surveys measure antibodies at a fixed temporal point, with the inherent limitation that we cannot answer many interesting questions about the dynamics of virus spread. Given the inherent advantage of our approach, an interesting question is to know the real number of infections detected in screening campaigns before starting large-scale vaccination. This is an essential question, as asymptomatic and pre-asymptomatic patients may be the primary transmitters of new infections. Then, this index can assess the quality and limitation of screening protocols and, more specifically, the ability of countries to manage the pandemic.

Fig. 7 shows the percentage of active cases that can be detected by public health agencies on a daily basis. At the beginning of the pandemic, we can observe that the detection capacity is minimal, and their capacity increases in May, with the end of the lockdowns and the reduction in the number of infected people. It is important to note that in the Summer, control is weak, perhaps because it coincides with the holiday period, and national mobility patterns increase, which would explain the increase of epidemiological risk in the coming months. In autumn, control is more reliable and stable. Finally, near Christmas, maximum effectiveness is obtained, partially motivated by upcoming family events, which drive a prior increase in protective measures, such as better testing capacity or stricter control of non-pharmacological measures such as social distance. In any case, in general, the Spanish government’s ability to detect daily active infections was less than $10\%$ during the period examined.

Fig. 7.

Dynamic evolution of the number of active infections in the Spanish population (top Figure). Daily cases reported by the Spanish government (middle Figure). The day-to-day percentage of active infections in the Spanish population by health agencies (bottom Figure).

5. Discussion

The Coronavirus pandemic is causing an unprecedented crisis in health, economic, and social terms. To help design better policies, estimating the number of people infected by the virus is crucial. We explore the possibility of using statistical simulation models to estimate the spread of an epidemic and Black Block Optimization techniques as a general procedure to obtain model parameters.

The estimations obtained over several regions of Spain have practical relevance. The results reveal that the number of infections was much higher than reported by the Spanish government. Two factors may explain these discrepancies: (i) The tests were carried out in a limited way among the general population, and (ii) no random sampling [84] was done among the different regions throughout the territory, shading the absolute magnitude of the pandemic. It is also worth noting that its impact was uneven across regions. Madrid was the most affected region, while Galicia was the least affected. However, according to our model, in Cataluña, Castilla y León, and the País Vasco, the effects were surprisingly similar, even though the outbreak of infections theoretically started at different time points. In addition, the geographical dispersion of Castilla y León is more significant (see Table 3). Perhaps the older population of Castilla y León (see Table 3) has a higher case fatality rate than the other communities. Therefore, our model is overestimating the number of infected people in that region. As previously mentioned, the demographic structure of the regions, together with the epidemiological profiles and other socioeconomic characteristics, is fundamental in the analysis of results.

A critical concern in epidemic modeling is feeding the models with reliable data, which is challenging due to governments’ limited tracking capacities worldwide. In this paper, the mortality records are used as a source of information to increase the reliability of estimations. However, although the information provided by this variable is more accurate than other epidemic monitoring variables as daily infections rates, our approach presents certain disadvantages. In general, fewer deaths are registered than the number of those that happened. Both Spanish and international press echoed this problem in the current Coronavirus crisis. More than twice as many deaths than those officially announced can happen in certain regions, at least at the beginning of the pandemic. A paper released in the early stages of the pandemic reported that the actual number of deaths might be even three times higher in Italy [11].

In order to alleviate this practical limitation, we consider two scenarios. An optimistic scenario in which the official number of COVID-19 caused deaths is correct, and a more extreme and pessimistic scenario, in which we assume that fatality cases are twice as much as those recorded by the government. In addition, in the overall Spanish analysis until 1 March, we use the excess of mortality as a source of information. For this purpose, to calibrate the model better, we retrospectively estimate the $IFR$ parameter and update the $\beta$ coefficients dynamically.

From a practical point of view, our approach can be essential to assess the current state of the epidemic. In particular, we can know: (i) The degree of immunity of each population; (ii) The number of people who might be infected today; (iii) The total number of recovered patients. In addition, our proposal work can be helpful in a retrospective sense to rebuild the past dynamic of infections and help plan better future decisions based on prior evaluation of the impact of epidemic policies performed in the past. As a relevant example of this modeling strategy, we estimate the capacity detection of active infections on a daily basis, which show that in the summer, the control was poor, which contributed to the substantial expansion of the virus until Christmas.

In other epidemics as influenza, data-driven approaches may be state-of-the-art because there is much evidence about the dynamic of the epidemic in many situations and the response of different agents as public health systems [9]. In this case, we point out that mechanistic models should be preferred at the beginning and in the middle of the pandemic [41]. When more information about the current epidemic and the performance of measures is gathered over time, more purely predictive models can be used. With all this information, medical institutes and governments will be able to guide the elaboration of more personalized policies for normally restoration and establish decisions thresholds to perform critical interventions as local lockdowns according to specific characteristics of each territory.

As a relevant example of our model, we can describe how the peak happened. From an epidemiological point of view, we can identify two different peaks. According to the results reported by our model in the first wave, the first one is the absolute maximum of new infections between 9 and 16 March. The second peak is related to the maximum number of potential contaminators predicted to have happened on March 17 and 24.

In general, assessing the performance of epidemic models is very hard. Practitioners do not know real epidemiological situations and monitor epidemic solutions with surrogate variables that only provide partial knowledge of epidemic dynamics. One of the most critical problems in this pandemic was that many research groups fitted their models with an official daily report of active cases, which led to inconsistent and unrealistic estimations about the number of infections and the population at epidemic risk.

In our particular case, we evaluate the performance of the model during the first wave —the most challenging scenario— against the broad number of seroprevalence studies performed in Spain. In the mentioned analysis, we restrict the expert information introduced in the models to the evidence of the first wave to evaluate model performance in an uncertain setting. In general, our results agree with different epidemiological studies in Spain and several parts of the world (https://covid19-modeling.github.io). In case of discrepancies, these can be explained as a consequence of the lack of appropriate parameter tuning. Also, there are essential discrepancies between the results of national survey studies versus more local ones such as the one carried out in Torrejón de Ardoz [4]. This might be explained by the fact that the effect of the pandemic was worse in Torrejón de Ardoz than in the majority of the population of Madrid. Another critical factor to highlight is the limitations in the statistical survey methodology employed in the national seroprevalence study. Concretely, there are more refined ways to carry on statistical inference modeling than the standard application of the Inverse Probability weight estimator. In this sense, we suggest using the recent methodology described in Ma and Wang [47] to provide more reliable results, in particular in the age groups related to the elderly population. Also, as multiple comparisons are not performed in the confidence interval estimation, coverage uncertainty is somewhat optimistic.

Despite the potential limitations, both in the parameters of our model and in the methodology of the survey, in most territories examined and assuming a pessimistic scenario, the results confirm the accuracy of our approach in the real world. In Supplementary Material, specific details are provided to explain why the pessimistic scenario was more reliable in the first wave estimates when less information on the pandemic was available.

In the more extensive analysis up to 1st March 2021, we use the excess mortality as a specific source of information. In this case, we update the daily infection function dynamically between successive waves, and $\beta$ was calibrated using our $IFR$ estimation, using the results provided by seroprevalence surveys and excess mortality records. In this sense, our results show the limited monitoring capacity of Spanish agencies and the need for more efficient large-scale testing to control the epidemic.

We hope that the recent proposals, such as the use of telecommunications information [63], or more efficient pooled testing strategies [16], [54], will allow new ways to control and monitor pandemics in a more reliable way [15], [55].

From a methodological perspective, this work aims to explore the idea that complex statistical simulation models, together with Black Box optimization techniques, are a powerful way to define new epidemic models with good empirical performance. Black-box optimization is a promising approach to optimize complex models for which it is not easy to find optimal parameters using traditional methods, such as a likelihood or gradient-based methods, due to the complex and stochastic nature of the model. The use of black-box optimization further increases the flexibility of the approach as it can be adapted to new non-standard complex epidemic formulations from a general perspective. For example, an exciting modification of our model can include non-parametric distributions to model the distribution times between model transitions. Some papers claim that this is a good general approach for estimating other parameters, for example, the virus incubation times [29].

We are unable to make a complete comparative study due to a large number of literature articles on epidemics. However, this paper aims to propose general and flexible modeling strategies to create epidemic models in a simple way, the limit of which depends on computational capabilities.

The epidemic models introduced here can improve in several directions. First, we may obtain more reliable inferences by fitting the model at simultaneous locations, for example, through multilevel simulation models. In this sense, a promising optimization strategy is to employ bayesian optimization. Second, to handle more realistic infection mechanisms, we can use other distributions such as Conway–Maxwell–Poisson [74] to handle over-under dispersion situations. Another exciting direction is introducing social interactions or genetic information about how the virus changes [78], [82]. However, nowadays, data related to this are not public in most countries or are very limited or difficult to obtain. Another significant contribution could be the use of several sources of information simultaneously to obtain more accurate estimations. In a recent paper [35], the authors used the results of seroprevalence surveys of the U.S. population to explore this idea. Finally, using machine learning approaches to accelerate parameter fitting is a promising area that may be necessary for more complex simulation models [6]. In preliminary tests with our approach, speed gains are considerable.

As for the new library for simulation that we developed, we fill some gaps in the literature. There are few computational approaches to reconstruct infection dynamics from mortality reports [36], [62], and most of the existing models are not dynamic. In this direction, we provide a well-built and reliable python library that allows estimation of seroprevalence, with interpretable and easily comparable parameters across countries. However, obtaining parameters of some prior contributions in different countries can be very challenging [62].

Traditional epidemic models are solved using well-known optimization criteria. Their properties are much better understood, but this epidemic showed the weaknesses of these classical models and the need to model and manage epidemics in an efficient way [69]. We think a general framework such as ours is an exciting and flexible direction towards adapting and designing new models that consider the particular characteristics of each territory without wasting time.

6. Conclusions

This paper has illustrated the potential of combining simulation models with a Black-Box optimization techniques to obtain new epidemic models. Despite our model’s simplicity, we have shown that the estimated results are close to those produced by different epidemiological studies. Furthermore, the proposed method can be extended in a simple way to handle more complex situations as graph structures or performing estimations in other epidemics using specific biological expert knowledge, while the same Black-Box optimization strategy remains valid.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/