Age-stratified transmission model of COVID-19 in Ontario with human mobility during pandemic's first wave

Abstract

In this work, we employ a data-fitted compartmental model to visualize the progression and behavioral response to COVID-19 that match provincial case data in Ontario, Canada from February to June of 2020. This is a “rear-view mirror” glance at how this region has responded to the 1st wave of the pandemic, when testing was sparse and NPI measures were the only remedy to stave off the pandemic. We use an SEIR-type model with age-stratified subpopulations and their corresponding contact rates and asymptomatic rates in order to incorporate heterogeneity in our population and to calibrate the time-dependent reduction of Ontario-specific contact rates to reflect intervention measures in the province throughout lockdown and various stages of social-distancing measures. Cellphone mobility data taken from Google, combining several mobility categories, allows us to investigate the effects of mobility reduction and other NPI measures on the evolution of the pandemic. Of interest here is our quantification of the effectiveness of Ontario's response to COVID-19 before and after provincial measures and our conclusion that the sharp decrease in mobility has had a pronounced effect in the first few weeks of the lockdown, while its effect is harder to infer once other NPI measures took hold.

COVID-19; Coronavirus; Infectious disease modeling; Ontario; Age stratified; Age stratification; Mobility; Google mobility; SEIR; Compartmental model

1. Introduction

Since December 2019, the novel betacoronavirus SARS-CoV-2 and its associated disease COVID-19 have spread from the point of origin in Wuhan, China [1] to virtually all corners of the globe. As of April 1, 2021 over 129 million people worldwide have been confirmed as having contracted COVID-19, resulting in over 2.82 million deaths. Despite the recent development and ongoing distribution of several vaccines, the total number of cases is increasing [2]. Predictably, the events of the last year have stimulated a robust discussion related to the nature of mathematical models in epidemiology as they inform public policy [3], [4], [5]. It seems prudent then, before describing our own model and results, to review the history of mathematical modeling in epistemology and to recall the challenges it continues to pose.

The mathematical theory required to effectively model the spread of infectious diseases throughout a homogeneous population was developed by Gottfried Leibniz in the latter half of the ${17}^{\mathrm{th}}$ century [6], [7], [8]. Leibniz's work was quickly put to use describing physical systems by early physicists, notably Jacob Bernoulli in 1695 [9]. Early contributions to the mathematical study of infectious diseases began appearing during the 18th century notably by the physicist Daniel Bernoulli in 1760 [10]. In 1866, during an epidemic of cholera in London, William Farr appears to have been the first person to (publicly) employ mathematics to predict the likely course of an epidemic [11], [12], [13]. His projection was apparently based on simple curve fitting and was seen as successful by his contemporaries, but attempts to extend his ideas to a more general context proved disappointing [13]. Further, more successful efforts to derive a mathematical model of epidemics were undergone by Brownlee [14], [15], Ross [16] and Hudson [17], [18]. The so-called ‘SIR’ model common in modern epidemiology was arrived at in 1927 by Kermack and McKendrick [19]. In the simplest case this type of model divides the population into three compartments: “susceptible”, “infected”, and “recovered”. Differential equations can then be used to describe the movement of the population between the compartments. Unfortunately, this simple model has two disadvantages which render it unsuitable for most practical purposes. Firstly, for an SIR model to produce accurate results it must use accurate values for its parameters (e.g. rate of transmission, recovery time, and mortality rate). These parameters can be difficult to measure and may not be constant across an entire population. The second disadvantage of SIR-type models is that they assume that the population in any given compartment is homogeneous, which can cause them to ignore important differences such as age, location, and travel habits. Mathematically this can always be resolved by adding more compartments, however this increases both the computational complexity of the model and the number of parameters needed to produce an output. For these reasons, contemporary models, while still recognizably related to the classic SIR model, are typically modified to accommodate the specifics of the pathogen being modeled, important variances in the population, and the intended purpose of the model [20], [21], [22], [23], [24], [25].

Some early models for the COVID-19 outbreak returned to curve-fitting as a method for projecting future outcomes [26]. Much of the epidemiological modeling is now performed with variants of the classic SIR model [27], [28], [29], [30] which fits the number of individuals in a population who are susceptible to, infected with, or have recovered from a communicable disease. The model can be extended to incorporate different phases of a disease [31], or population subtypes [32]. Studies have stratified Ontario populations by categorizing gender [33] or profession (such as healthcare workers) [34] separately. Age has also been shown to play an important factor in the transmission of COVID-19 [35] and in this paper we will further investigate that variable.

Although contact rates between individuals have previously been studied [36], [37], due to imposed social distancing and sheltering measures, absolute contact rates during the pandemic have changed drastically from baseline. Presently, governments have imposed measures in an attempt to reduce the spread of COVID-19. These include sheltering in place and isolation, travel restrictions, social distancing protocols, and the closure of public and commercial spaces. Specifically in Ontario, the government has mandated a slow relaxation of shelter-in-place measures and reopening of the economy throughout the late spring and summer of 2020 [38], and provided guidance on protective measures such as hand-washing and the use of face coverings.

Naturally, there is considerable interest in understanding the effects of the measures taken to mitigate the spread of COVID-19 [39], [40], [41], and at this stage, a year in the pandemic, looking back to what can be learned is as important as forecasting the next evolution of the pandemic. A comparative study used Google mobility data for Canada, not to model the epidemic, but to assess governmental interventions and social distancing measures, and to compare Canada's response with that of other countries [42]. A Texas study assumed two situations using arbitrary values: a 90% drop in contacts for individuals in isolation and a 40% drop in contacts for those practising social distancing [43]. More accurate estimates may be gained through anonymised location data gathered from mobile phones. Using a combination of proprietary and publicly available data, it has been shown in the United States that the adoption of shelter-in-place policies corresponds to a sharp decrease in mobility. It has also been shown that the number of infected cases is directly correlated to mobility [44], [45] in February-April 2020, which is something we see here as well. However we also show that increase in mobility in the population of Ontario stops being a good indicator of pandemic evolution past April 2020. This is likely due to the fact that while mobility has steadily risen, other NPI measures took hold, such as mask wearing, and larger testing capacity.

To estimate differences in contact during the epidemic, a team of researchers using an SEIR-type model found the overall contact-rate in British Columbia dropped by 78% due to distancing and isolation measures. The paper, however, only uses mobility data to determine the beginning and end dates of these measures, without considering that mobility will change over time due to relaxed restrictions [46]. Related studies done for France [47] and the UK [48] found similar values, in that overall contacts were reduced by 70-80%.

It is known that the contact rates between individuals of different age groups will vary significantly [49], so it is important to take this into account. An Ontario paper uses an SEIR-type model with compartments by age, but only modifies the severity of infection per age group [32]. A Brazilian study uses data from nine distinct age groups, but uses identical contact rates within and between groups [50]. [51] uses an SEIR model with age stratification to investigate the effect of various management strategies. Unfortunately, the study suffers from a lack of empirical data instead arriving at exposure rates by “making educated estimates of the effects of hygiene restrictions and specific social interactions in each place”. Research is now suggesting that children only play a minor role in transmitting COVID-19 [52]. The spread of the disease is greatest between adults in the same age group, and less frequently between parents and children. These results will have an impact on the effective contact rates between individuals.

In our work here, we use age-stratification in three broad age groups: young (less than 20 years), adults (between 20 and 60 years) and seniors (between 60 to 80 years). We use Ontario's public health onset case data, we use the Google mobility data for Canada, and we adapt the contact rates, per broad age groups from existing literature. We adapt an SEIR-type model and we successfully fit the onset case data in Ontario, per each age category, to the simulated symptomatic cases, while discounting outbreak cases in long-term care (as median age there is higher than our modeled population groups). The period of time of interest for us is February – June 2020.

What we conclude is that there is a quantification of the level of success in staving off the pandemic in Ontario via the study of a reduction of contacts coefficient q, which represents the decrease in base contacts due to lockdown and social-distancing measures. Moreover, we show that this reduction coefficient can be looked at as having two important contributors: the first is from mobility reduction in the province (at work, outdoor, retail, schools, etc. categories), while the second is due to all other NPI measures that have started to take hold or be required, such as mask wearing, restricted commerce and services, etc. We can clearly see then that mobility reduction has certainly had a pronounced impact on contact reduction in the first 4 weeks after the first lockdown was imposed, however it becomes a poor indicator (if at all) of pandemic evolution beyond that short time frame.

The structure of the paper is as follows: In Section 2 we present our methods and materials, in Section 3 we present our calibration results and reduction factor discussion, while we close with some concluding remarks and future work.

2. Methods & materials

2.1. Adapted SEIR model

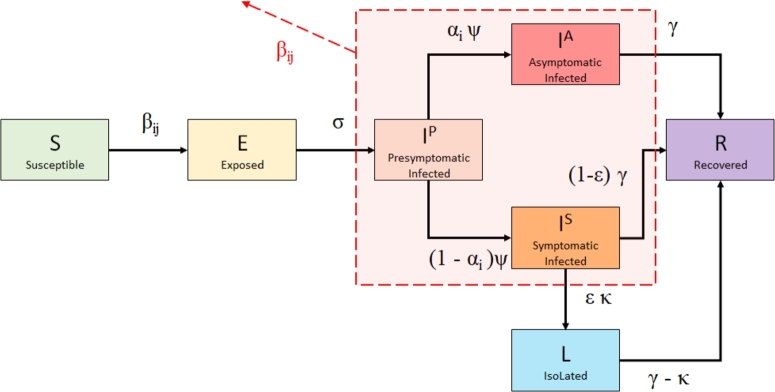
We introduce an adapted SEIR model to the question at hand by modifying and age-stratifying a variant of the SEILR model presented in [53], [54]. First, we refine the Infected compartment further into three compartments: presymptomatic ($I^P$), asymptomatic ($I^A$), and symptomatic ($I^S$). In this way, we may better examine the dynamics of the COVID-19 infection through its stages of development and consequent patient behavior due to symptom prevalence.

Second, we generalize the model to allow for age group stratification and interactions between groups. In short, we propose the extended SEILR(pas) model with the following compartments: Susceptible (S), Exposed (E) - not yet contagious, Infected (p)resymptomatic ($I^P$) - contagious, Infected (a)symptomatic ($I^A$), Infected (s)ymptomatic ($I^S$), Recovered (R), and iso(L)ated - symptomatic cases isolated to prevent spread.

In order to account for differences in disease susceptibility and infection outcomes, we divide the population of Ontario (the most populous province of Canada) in three age-stratified subgroups: Group 1, denoted by $N_1$: 0-19 years old, Group 2, denoted by $N_2$: 20-59 years old, and finally Group 3, denoted by $N_3$: (≥60) years old.

Contact rates ($c_{ij}$) within and between these age groups were inferred from Canadian contact data estimated by Prem, Cook, & Jit (2017) [37], who projected social contact patterns in 152 countries (see Collapsing age-stratified contact matrices for details). Since contact rates are a factor in determining the size of the effective contact rates, typically denoted by β, in the context of age-stratified transmission, the effective rates will be denoted by ${\beta }_{ij}$. Before we outline the equations governing our model, we include first the flow chart between the above compartments, together with classic notations of the flow rates (Fig. 1).

Figure 1.

Schematic of SEILR(pas) model for COVID-19 progression and control measures for a Group i, i ∈ {1,2,3}. The outward arrow labeled β_ij implies that the encircled compartments (Presymptomatic, Asymptomatic, and Symptomatic infected) in each age group have an impact on new transmissions to the other age groups {1,…,3}.

Considering the i-group model for $i,j\in \{1,\dots ,K\}$, the differential equations governing each of the groups are given by:

$$\{\begin{array}{cc}\hfill \frac{d{S}_i}{dt}& =-\sum _{j=1}^K{\beta }_{ij}{S}_i(t)\frac{I_j^P(t)+I_j^A(t)+I_j^S(t)}{N_j(t)},\hfill \\ \hfill \frac{d{E}_i}{dt}& =\sum _{j=1}^K{\beta }_{ij}{S}_i(t)\frac{I_j^P(t)+I_j^A(t)+I_j^S(t)}{N_j(t)}-\sigma E_i(t),\hfill \\ \hfill \frac{d{I}_i^P}{dt}& =\sigma E_i(t)-\psi I_i^P(t),\hfill \\ \hfill \frac{d{I}_i^A}{dt}& ={\alpha }_i\cdot \psi \cdot I_i^P(t)-\gamma I_i^A(t),\hfill \\ \hfill \frac{d{I}_i^S}{dt}& =(1-{\alpha }_i)\cdot \psi \cdot I_i^P(t)-(1-ϵ)\gamma I_i^S(t)-ϵ\cdot \kappa \cdot I_i^S(t),\hfill \\ \hfill \frac{d{R}_i}{dt}& =\gamma (I_i^A(t)+(1-ϵ)I_i^S(t))+(\gamma -\kappa )L_i(t).\hfill \\ \hfill \frac{d{L}_i}{dt}& =ϵ\cdot \kappa \cdot I_i^S(t)-(\gamma -\kappa )L_i(t).\hfill \end{array}$$ (1)

Individuals are all initialized in the S compartment, with the exception of a single infected individual from the largest group seeded in the $I^P$ compartment. Susceptible individuals exposed to the virus enter the E category for an average of 1/σ days before they become contagious, at which point they move into the $I^P$ category. After an average of 1/ψ days, $1-\alpha$ proportion of individuals will develop symptoms and move into the $I^S$ compartment, with the remaining α moving into the $I^A$ compartment. Individuals in $I^P$, $I^A$ and $I^S$ compartments are all contagious. ϵ proportion of individuals in $I^S$ choose to self-isolate to prevent further disease transmission, and as a result move into compartment L (isolated) and do not interact with others. They do so with a delay of 1/κ, accounting for test result waiting time and individuals who may disregard minor symptoms initially. 1/γ days after entering the $I^A$ and $I^S$ compartment, individuals all recover from (or succumb to) their infection and move into the R compartment, where they remain permanently. The model was implemented and numerically solved with R (version 4.0.2) using the packages ggplot2 and deSolve.

2.2. Ontario specific parameter values and data sources

We assume that the outbreak of COVID-19 in Ontario begins on February 14, and that the implementation of intervention and control strategies begins on March 15. Control responses in Ontario were officially enacted on Monday, March 17, [55], but commensurate with earlier institutional responses, we adjust for the fact that the public began to alter behavior before this date. For further discussion, see the Initial start date section in the Appendix. We assume individuals who recover from infection remain in the R compartment, with immunity from COVID-19 for the duration of the simulation. Given the short time frame for simulation, our model does not include births or natural deaths, and any COVID-19 deaths are captured in R. Furthermore, we assume an isolation delay of one day on average, due to individuals not always taking initial symptoms seriously enough to isolate.

Additionally, we assume an isolation compliance rate of 95%. An early study of the virus in quarantined cruise ship passengers finds that 17.9% of infected individuals were asymptomatic, and suggests the true proportion could be up to 39.9% depending on the latency period of the virus [56]. A meta-analysis of six studies estimates the asymptomatic infection rate to be anywhere in the range of 18.4% to 78.3%, and cites 46% as the most likely value [57]. We use the age stratified symptomatic rates found by Davies et al. (2020) [35] for our model, as shown in Table 1. Next, we assume that the only cases reported by Ontario's public health units (PHUs) are symptomatic cases, and that every symptomatic case will be identified and reported. In addition, we assume that asymptomatic and presymptomatic cases are not tested and therefore do not self-isolate.

Table 1.

Parameters and initial values of the SEILR system (1).

Symbol	Definition	Initial Value	Reference
K	Number of age groups	3
Ni	Subgroup population size
	$N_{total}$	14 566 547	[58]
	$N_1$: (0-19)	3 141 693	[58]
	$N_2$: (20-59)	7 977 131	[58]
	$N_3$: (60+)	3 447 723	[58]
cij	Number of daily contacts with Group j per member of Group i	Table 2
p	Transmission probability per contagious contact	Section 2.5
βij	Effective contact-rate, i,j ∈ {1,…,K}	cij⁎p
σ	Time from exposure until contagious (days)	1/2.5	[32]
ψ	Time from contagious until symptomatic (days)	1/3.5a	[32], [59]
α1	Proportion of permanently asymptomatic cases in N1	0.963	[35]
α2	Proportion of permanently asymptomatic cases in N2	0.7	[35]
α3	Proportion of permanently asymptomatic cases in N3	0.35	[35]
ϵ	Proportion of compliance with isolation	0.95	assumption
κ	Isolation delay	1	assumption
γ	Recovery/removal rate	1/7	[31]

^aThe parameter ψ is estimated from the relationship 1/σ + 1/ψ = incubation period, where 1/σ = 2.5 days and incubation period = 6 days.

The model presented above is now tailored to Ontario using the parameter values in Table 1, as well as Ontario data sources for the pandemic evolution to date.

2.3. Deriving contact rates for Ontario pre-pandemic

We first need to derive contact rates within and between the three stratified age groups introduced above. There are many examples in infectious disease modeling literature that assume uniform contact mixing for simplicity (for example, modeling Ebola dynamics in [60]), however, such an assumption neglects the significant role that age may play in relevant contact patterns [61]. The Ontario groups were partitioned as such to characterize different contact rates associated with each age group.

Group 1 represents individuals in the youngest age group (0-19). As these individuals are school-aged, they generally experience high levels of interaction with similar-aged peers, as well as some interactions with individuals in Group 2, likely including their parents and other child care providers. Group 2 represents the majority of the working population (20-59). These individuals display very high levels of interactions with other adults, likely as a combination of workplace interactions, errands such as shopping, appointments, and peer-relationships, and moderate levels of interaction with Group 1 members. The majority of these interactions are likely with their own children, but this value may be skewed up in part due to child care supervisors in Group 2 having many interactions per day. Group 3 is the oldest age group and considers seniors and retirees (60+), who make comparatively fewer overall contacts than their younger counterparts. This is to be expected as many of these individuals are retired and thus their lifestyles are more likely to be leisure-oriented ([62], [63]). Based on low transmission probability due to low contact rates, Group 3 has the lowest chance of contracting COVID-19, although they carry a much higher risk of hospitalization if they do so [64].

From [37] (a study of country-specific contact rates), a $16\times 16$ contact matrix of contact rates between Canadians aged $0-80$ was collapsed to create a condensed $3\times 3$ contact matrix stratified by our selected age groups. See Appendix for details.

From Table 2, a high degree of assortativity (intra-group contact) was found in Groups 1 and 2, shown in boldface. Group 1, comprising children and students, are most likely to interact with their peers (63% of contacts), followed by adults (parents, teachers, etc. forming 34% of contacts), with very little contact with seniors (2% of contacts). Group 2 has the highest overall number of contacts, with adults coming into contact with other adults an estimated 77% of the time. Both results may be explained by Group 2 making up the majority of the working age population, as well as holding positions requiring interaction with elderly or very young individuals (e.g. care workers, teachers). Interestingly, Group 3 individuals, while having the lowest number of overall contacts, have the most balanced spread of contact rates, and even perform contacts with Group 2 more than their own age group (53% vs. 29%, respectively). This may be due to interactions with health care workers and employees at various businesses (cashiers, wait staff, etc.), and the fact that some individuals may still be part of the workforce. We preserve our contact structure by adopting Canadian relative contact rates from [37] and assume they apply to Ontario for our time period with uniform contact scaling across all interactions. We assume our age-stratified population subgroups are homogeneously mixed, with hetereogeneous intergroup mixing.1

Table 2.

Contact rates calculated for the three Ontario population subgroups. Contact rates are taken from Canadian estimates by [37] and weighted according to census data from Statistics Canada [58].

	Group 1	Group 2	Group 3	Total Contacts
Group 1	c11=8.565645854	c12=4.661272358	c13=0.304014985	13.5309332
Group 2	c21=2.987996842	c22=11.49063721	c23=0.522285468	15.00091952
Group 3	c31=1.248771202	c32=3.686037351	c33=1.982952539	6.917761092

2.4. Case onset and mobility data

Tracked data for COVID-19 cases in Ontario were taken from Ontario's integrated Public Health Information System (iPHIS). This data set is compiled from reports from Ontario's PHUs, recording all confirmed cases of COVID-19 and qualitative factors for each case, including age group (by decade), gender, testing location, and patient outcome. In addition, iPHIS is one of the few data sources that provides both episode (case onset) date, as well as reporting date. Most other sources, including the CDC, only sort cases by reporting date. Cases organized by reporting date are highly subject to delays, including testing and submission delays, lab delays, and individual decisions regarding how soon after symptom onset one chooses to get tested. This produces noisier trend lines and both over- and under-estimates for daily counts. Since case-onset data is much more accurate, we chose it to match our simulated infection curve(s) in order to provide a more complete understanding of how transmission has changed over time since the pandemic onset.

We also incorporate some movement and behavioral activity in the population by considering Ontario mobility data compiled from Google's release COVID-19 Community Mobility Reports. Specifically, we try to capture changes in the transmission rate p, which is further explained below in Section 2.5. These reports use anonymised Google service location data to track changes in movement over time compared to baseline (pre-lockdown) activity in six broad categories: retail/recreation, groceries/pharmacies, parks, transit stations, workplaces, and domiciles. To determine the pre-lockdown average contact rate for Ontario, we used the contact rates provided by Prem et al. [37] for Canada. We weighted the average contact rates of Canada with the Ontario population to get a daily average contact rate for an individual in Ontario. We considered this value as the average baseline (pre-lockdown) contact rate, i.e.:

$$contac{t}_{av}\approx =12.5046$$

To find the mobility-influenced time-dependent contact rates post-lockdown, we considered the average contacts rate in Ontario for the home, work, and other location categories (comprising retail/recreation and groceries/pharmacies) from Prem et al., ($\approx 3.2,4.5,3.8$, respectively). Next, we used these category rates to modify the same categories of mobility data as follows:

$$contac{t}_{av}^m(t)=contac{t}_{av}^m\cdot g^m(t)\text{ where }m\in \text{{Home, Work, Other location}}$$

where the t unit is time=1 day and where $g^m(t)$ is the percentage increase or decrease in the category m of mobility as compared to Google's baseline values per category. Finally, we amalgamated the Google mobility-influenced contact rates of these categories to compute the daily mobility-influenced contact rate, by considering an average number of daily hours an average Ontarian spends in each category, i.e., 8 hours of day for work, etc.

We thus assume that changes in Google mobility data as compared to baseline activity reflect equivalent changes in contact rates as compared to average contact baseline. We also assume that the proportion of the population that has opted to provide location tracking data to Google via their personal account settings can be considered representative of the behavior of the total population of Ontario at large.

2.5. Dampening contact rates to replicate behavioral changes and preventative measures

The effective contact rate for a member of Group i with members of Group j is given by

$${\beta }_{ij}=c_{ij}\cdot p,$$ (2)

In Davies et al. (2020), authors estimated p for COVID-19 in several models under different parameters, including susceptibility/asymptomatic rates and demographic structures. They found p values of 0.046 and 0.055 in Wuhan, 0.074 in Beijing, 0.084 in Lombardy, and 0.099 in South Korea [35]. For Ontario-specific studies, Abdollahi et al. (2020) found p ranging from 0.018-0.041 [65], and Wu et al. (2020) found p of 0.145 [66]. For our model, we solve for p implicitly, fitting to the onset data recorded by iPHIS for our pre-intervention period (Feb 14 - Mar 15). We do so using a derivative-free optimization method known as the Golden Section Search algorithm to minimize the sum of squared errors (SSE) between our model output and iPHIS data (see [67]).

We find that for the pre-lockdown phase, the corresponding transmission rate in Ontario is $p=0.045$. We note that this transmission rate is much lower than the estimate of 0.145 given by [66], yet on par with the estimates given by [65]. We attribute the large difference in transmission rate compared to [66] to two main factors. Firstly, their infectious period is 5 and 7.2 days for symptomatic and asymptomatic individuals respectively. In comparison, we use an infectious period of 10.5 days in our model, allowing for many more days of contacts while infectious. Secondly, their contact rates are lower than we consider here, with a universal contact rate of <11.8, as opposed to our contact matrix which averaged ≈13 contacts per individual per day. As a result of fewer daily contacts in conjunction with fewer infectious days, one drastically reduces the total contacts each infected individual makes before recovery. To compensate for fewer contacts, a much higher transmission probability is required to produce similar case numbers.

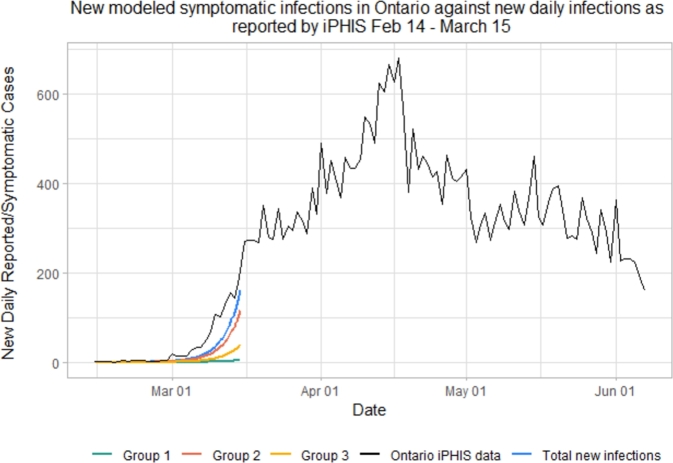
Fig. 2 depicts our simulated data from February 14 - March 15. After March 15, 2020, both the social behavior and the mobility of the population have changed, as the province adopted various preventive measures to help curb the spread of COVID-19. (For more detail on date selection, see Initial start date in the Appendix.) We therefore need our model to reflect:

• •changes in the frequency of contacts due to social distancing measures intra- and inter-groups
• •changes in the transmission probability due to mask wearing and other hygiene practices.

Figure 2.

Pre-lockdown iPHIS data (black) and simulated symptomatic infections in each of the 3 groups. The blue curve represents symptomatic infected in the overall Ontario population.

To do so, we introduce a dampening variable, denoted by $q_{\mathit{int}}\in [0,1]$ during a given time interval and generically denoted by int, such that

$${\beta }_{ij}(\mathit{int})=c_{ij}\cdot p\cdot q_{\mathit{int}},\forall \mathit{int}\in \mathit{interval}$$ (3)

where $q_{\mathit{int}}$ is constant during time interval int, interval is the number of time intervals used in the model, and int is defined as the ceiling of the number of weeks since preventive measures are introduced. Since no preventive measures were present pre-lockdown (February 14 - March 15), we will define this time period as $\mathit{int}0:=$ [Feb 14, March 15] and $q_0:=1$. We use the Golden Section Search to fit our model to iPHIS data, but this time we fix $p=0.045085$. We solve for $q_{\mathit{int}}$ and obtain the results in Fig. 3.

Figure 3.

Simulated new daily symptomatic infections in each of the 3 age groups according to the SEILR(pas) model.

Recently, Google has released data for phone mobility in various countries around the world, compared to baseline, sorted by region and mobility type. Let us now consider $M_{int}$, average mobility during interval int compared to baseline, as our relative number of total contacts as compared to baseline. Thus, q no longer needs to account for mobility changes, and we introduce a new variable $\hat{q}$ to account for changes in transmissibility. Thus, when including mobility data,

$$q_{\mathit{int}}=M_{\mathit{int}}\cdot {\hat{q}}_{\mathit{int}},$$ (4)

and thus

$${\beta }_{ij}(\mathit{int})=c_{ij}\cdot p\cdot M_{\mathit{int}}\cdot {\hat{q}}_{ij},\forall \mathit{int}\in \mathit{interval}.$$ (5)

2.5.1. The golden search method for minimizing SSE

With or without mobility, using our above model, we are left simulating a system of equations depending on a scalar unknown variable (either q or $\hat{q}$). The values of this variable change over time due to changes in mobility, mask wearing, maintaining physical distance and weather changes. However, we can compute the optimal value of q or $\hat{q}$ over given intervals such that our simulated infected symptomatic curve in Ontario (adding the 3 groups) best matches the curve of onset COVID-19 cases in Ontario:

$$I_{\mathit{new}}^S(\mathit{int})=\sum _{i=1}^3\alpha \psi I_i^P(\mathit{int}-1)$$ (6)

We solve for the optimal value of q during a preset time interval in such a way as to minimize the sum of squared errors (SSE) between $I_{new}^S(int)$ and the new daily reported cases from iPHIS. We begin this with $int0=$[Feb 14, Mar 14] as defined previously. Then due to the variable nature of new cases in Ontario after March 15, weekly time intervals are defined as before:

• •$\mathit{int}0$ := [Feb 14, Mar 14] (pre-lockdown)
• •int i := [Mar 15+7(i-1), Mar 15 + 7i] or the ceiling of the $i^{th}$ week following March 15

To minimize the SSE as described, we use the Golden Section Search algorithm, taking 2 initial approximate points for q or $\hat{q}$ and converging onto the local minimum in between the 2 points. To find the SSE, we compute

$$\begin{gathered} \text{Total New Symptomatic Infections in Ontario (TNSI)} \\ =\sum _1^{\mathit{interval}}(((\sum _{n=1}^K\alpha \cdot \psi \cdot I_i^P(\mathit{int}-1))) \end{gathered}$$

from our model on day t, and compare them to numbers reported by iPHIS.

$$\mathit{SSE}={((\sum _{n=1}^K\alpha \cdot \psi \cdot I_i^P(int-1))-\mathit{iPHIS}(\mathit{int}))}^2$$ (7)

$$\text{Standard Deviation }=\sqrt{\frac{{\mathit{TNSI}-\mathit{iPHIS}(\mathit{int}))}^2)}{\mathit{interval}}}.$$ (8)

Finally, we need to be mindful of the limitations of SEIR-type models to carefully trace delays between various stages of exposed, presymptomatic, etc. As such, a matching delay for q must be introduced before running the model. The optimal delay value was found to be 2 days, as described in Initial start date of the Appendix.

2.6. SEILR(pas) model results

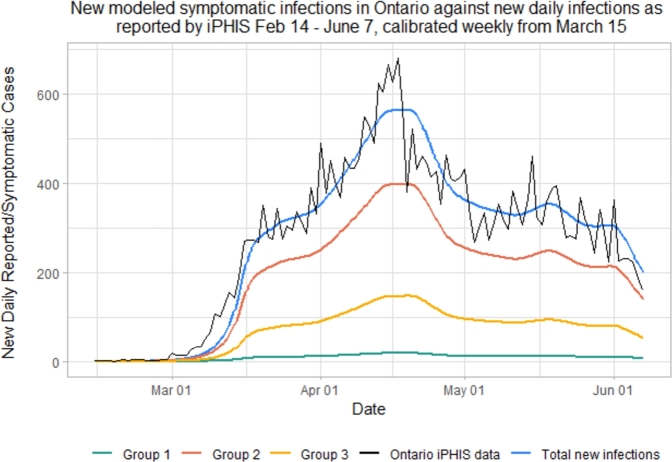
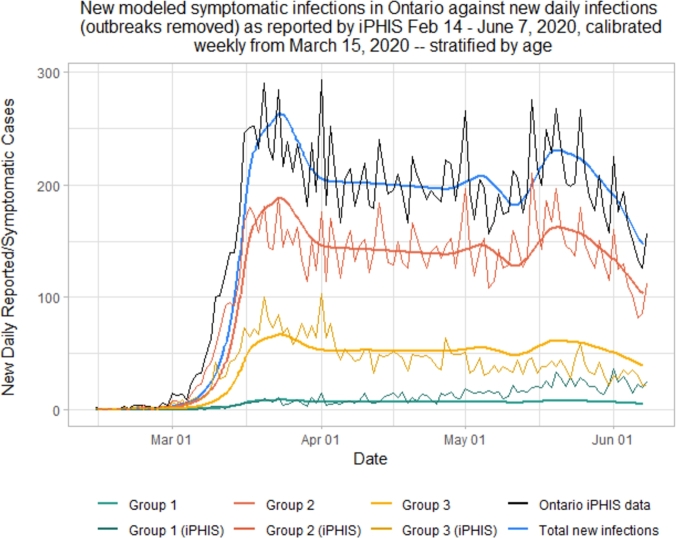
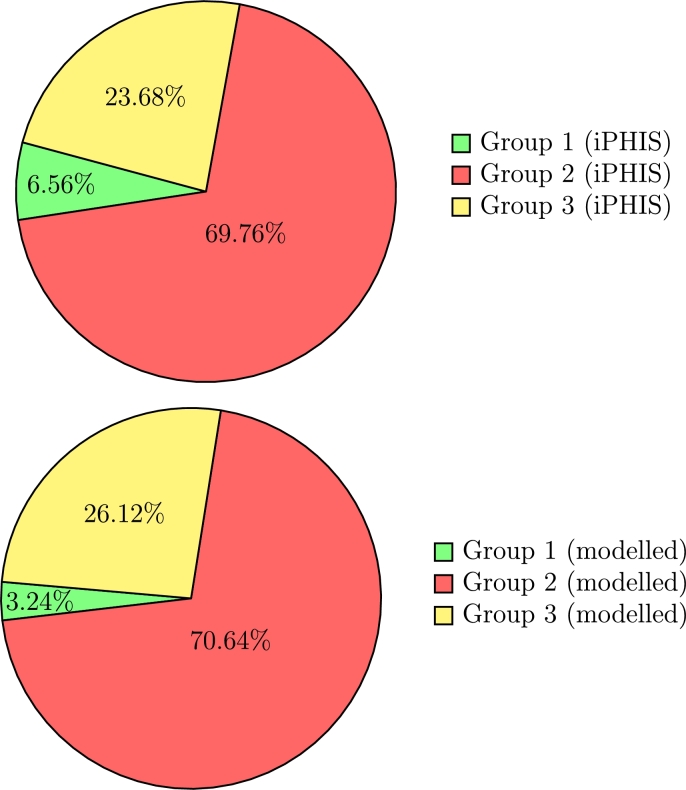
As shown in Figs. 4 and 5, while Group 1 cases are modeled quite accurately, we under-predict cases in the senior population (Group 3), and over predict cases in adults (Group 2). This is especially true during the peak of this first wave, from the third to the sixth week following the initiation of lockdown, corresponding to March 29th to April 19th. During this time period, there were many outbreaks reported in Long Term Care (LTC) facilities in Ontario, putting the senior population at a disproportionately higher risk than usual [68].

Figure 4.

Simulated new daily symptomatic infections in each of the 3 age groups compared with iPHIS reported cases, stratified by age.

Figure 5.

Proportion of COVID-19 cases in Ontario attributed to each age group for the real iPHIS reported numbers (top; total = 32,095, Group 1 = 1,336, Group 2 = 18,595, Group 3 = 12,004) vs. the SEILR(pas) model (bottom; total = 31,722, Group 1 = 1,029, Group 2 = 22,407, Group 3 = 8,286).

3. Results & discussion

3.1. Removing outbreaks to match age-specific case rates

Infection in our model is governed by our contact patterns and our contact scaling through lockdown. Our model takes a very macroscopic approach to transmission, and does not consider smaller clusters of individuals and “superspreaders”. As such, cases resulting from isolated outbreaks in long-term care homes, retirement homes, hospitals, group homes, shelters, and correctional facilities that occur as a result of close proximity are not accounted for by our model. iPHIS labels such cases “outbreak” cases, allowing us to remove them from the data and re-run the model to track only community contacts.

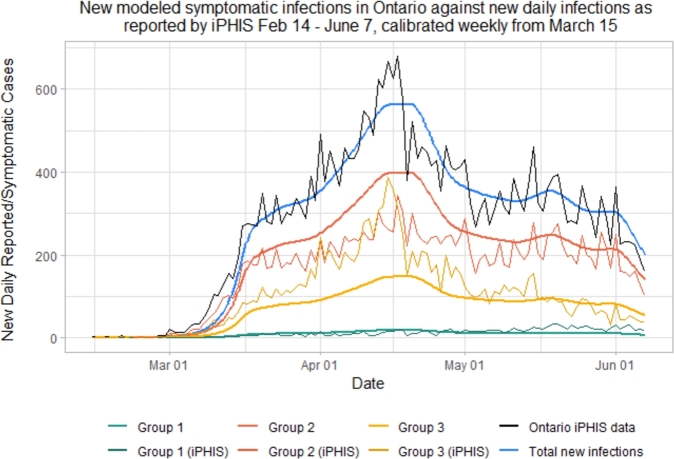
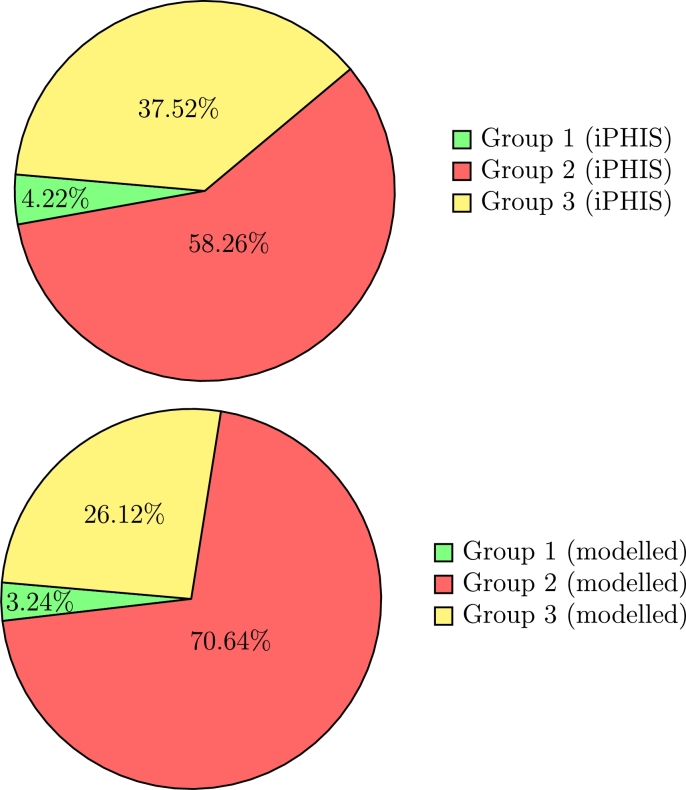
Figs. 6 and 7 show that when removing outbreak-related cases, we yield a much better match for age proportional case rates. Here, we match cases in Group 2 almost perfectly, while slightly over-predicting cases in seniors, and under-predicting cases in under-20s. This under-prediction in cases in young people can be accounted by the fact that our model does not include household transmission rates, which have been found to be much higher than external community transmission rates [69]. Since the vast majority of individuals under 20 years old live alongside adults, they inherit a higher risk than just through community transmission. The over-prediction in seniors can be attributed to the large numbers of seniors living in long-term care (LTC) facilities. Since all cases in LTC facilities are labeled ‘outbreak’, some seniors who may have gotten sick through external sources may have been labeled as ‘outbreak’ cases by iPHIS regardless. Thus, the outbreak-removed iPHIS data may be slightly under-representing non-outbreak cases in seniors.

Figure 6.

Simulated new daily symptomatic infections in each of the 3 age groups compared with iPHIS reported cases, stratified by age, with outbreaks removed.

Figure 7.

Proportion of COVID-19 cases in Ontario attributed to each age group with outbreaks removed for the real iPHIS reported numbers (top; total = 18,614, Group 1 = 1,222, Group 2 = 12,985, Group 3 = 4,407) vs. the SEILR(pas) model (bottom; total = 17,970, Group 1 = 582, Group 2 = 12,705, Group 3 = 4,683).

Note that while the total cases differ between the models with outbreaks included versus removed, the relative proportion of cases for each age group remains consistent. This is to be expected, as the model has not been altered, it simply fits q to match to a different total case number. Removing outbreaks has a significant impact on the age distribution of cases in iPHIS reported data, since outbreaks in LTC facilities disproportionately affect seniors [68].

3.2. Estimates of mobility and behavior during the pandemic's first wave

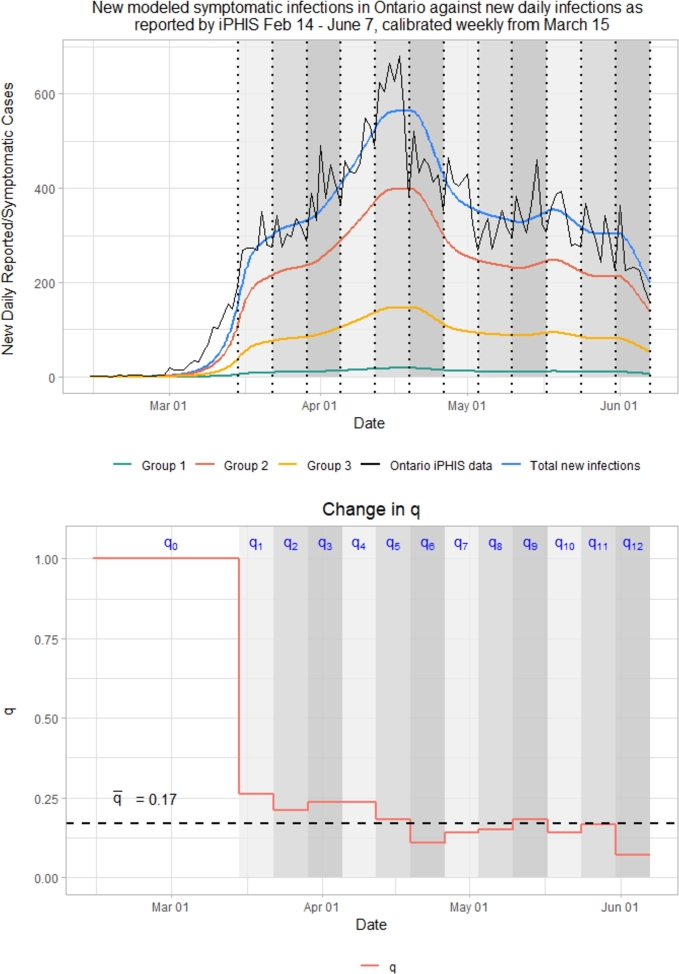
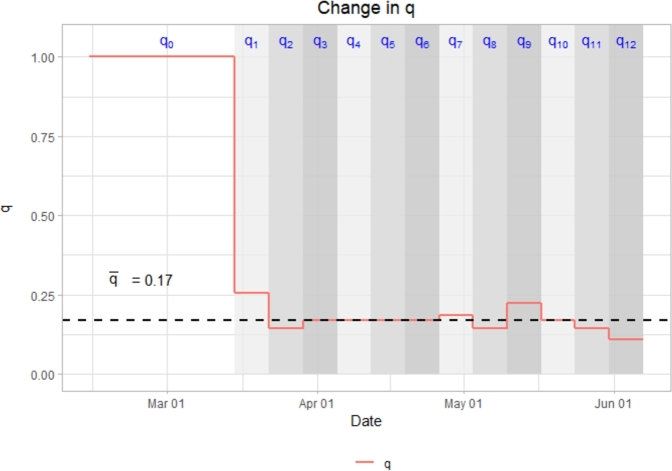
To better understand the behavior of the epidemic curve as influenced by mobility reductions, contact reductions and other NPIs, we first estimate $R_0$, the effective reproductive number of the virus near the disease-free equilibrium (pre-lockdown). We simply compute the spectral radius of the next generation matrix from the Jacobian of our model in Section 2, assuming a pre-lockdown value of $q=1$. Doing so yields an $R_0=5.88$ during this pre-lockdown phase. Consequently we find that with $p=0.045$ and q = 0.17, $R_{eff}\approx 1$.2 This implies that 0.17 is our threshold value for q, denoted $\overline{q}$, that prevents total new cases from increasing.3 At q values above this threshold we expect the disease to proliferate, and at q values below this threshold we expect case numbers to decrease over time. For this reason, it is interesting to investigate the behavior of q over time (Fig. 8).

Figure 8.

Change in q over time as compared to threshold, $\overline{q}$ = 0.17.

When comparing the placement of q relative to $\overline{q}$ to the behavior of disease spread over the same time intervals, it can be observed that when $q<\overline{q}$, case numbers decrease, when $q>\overline{q}$, case numbers rise, and when $q\approx \overline{q}$, case numbers remain relatively consistent.

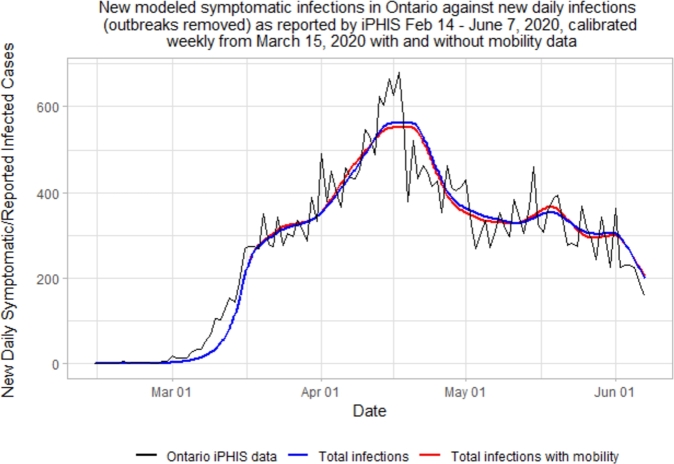
When we introduce Google mobility data to the model, the resulting epidemic curve is nearly identical to the model that did not utilize Google mobility. This is to be expected, as $q_{int}=M_{int}\cdot {\hat{q}}_{int}$, allowing ${\beta }_{ijint}$ to remain consistent between the two models. When overlaying the graphs, this is even more evident (see Fig. 9).

Figure 9.

Comparison of SEILR(pas) model epidemic curves, with and without mobility data.

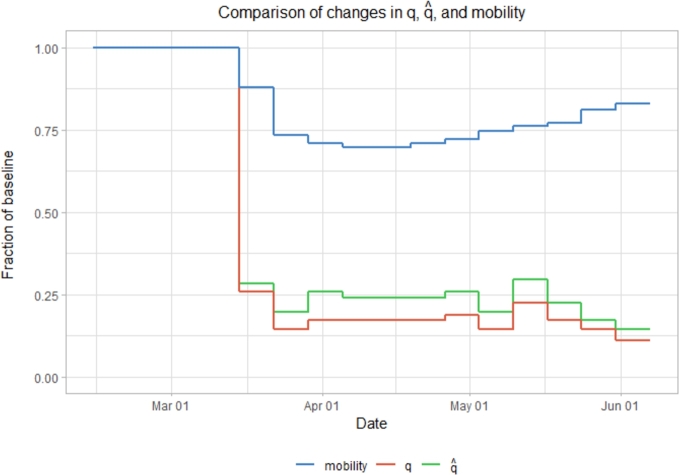
It is interesting to investigate how $\hat{q}$ and M change relative to q (Fig. 10). As expected, both M and $\hat{q}$ drop significantly as soon as lockdown measures are implemented. When comparing q to changes in Google mobility, the change vs. baseline is quite different in shape, with the exception of the initial drop in both. While mobility slowly rises over time, q slowly falls. This does not suggest that mobility is completely unassociated with q, simply that it is not necessary to keep mobility exceedingly low in order to keep q low as long as other precautionary measures are taken.

Figure 10.

Relative changes in mobility data, the transmission scaling factor (q), and the transmission scaling factor decoupled from mobility data ($\hat{q}$) from February 14 - June 7.

Conversely, when comparing q to $\hat{q}$, one notices they are actually very similar shape, just with $\hat{q}$ behaving with more drastic increases and decreases. This is because the dampening effect of $\hat{q}$ on transmission is amplified by the additional dampening effect of mobility (∼0.5), and so q must dampen ∼twice as much in order to yield a similar effect in each ${\beta }_{ij}$ (recall that $q=M\cdot \hat{q}$). It is clear from what we show here that mobility alone is not telling the whole story, on the contrary, it tends to quickly want to climb back up, however $R(t)$ does not. This is exemplified towards the end of the model as mobility begins to trend back towards baseline, causing $\hat{q}$ to trend closer to q. The closer mobility gets to 1, the less of an effect it has keeping effective contacts low, and so the more that one can attribute the decrease in disease transmission to external factors.

The values of q are quite well behaved, dropping to roughly 25% of baseline immediately following implementation of COVID-19 measures, and staying relatively stable in the time following. Mobility also drops following these implementations, though slightly more slowly, and only to about 70% of baseline, before slowly creeping above 80% by the end of the model (June 7th).

Interestingly, from $int4$ (March 30 - April 6) to $int5$ (April 6 - April 13) while Google mobility and $\hat{q}$ vary slightly, their relative changes cancel out such that $\hat{q}$ stays the same at 16.99478% of baseline, very slightly below our $\overline{q}=0.17$. During this time, case numbers remain almost completely stable, just slightly increasing over time as we are slightly below our threshold. Additionally, as more people are infected and recover from the virus, the proportion of individuals within the Susceptible compartment decreases, lowering $R_{eff}$ as well. With case numbers as low as they are for the time period modeled, this has a very small impact on the model as a whole.

The epidemic curve resulting from using outbreak-removed data (Fig. 6) is significantly flatter and more consistently behaved than the curve that included highly localized outbreaks (Fig. 4). Other than a small spike during the initial week following lockdown, and a second peak towards the end of May, new cases were consistent at approximately 200 per day. Even during the two peaks, cases never exceeded 300 new cases in a day in either the iPHIS or modeled data. This is in stark contrast to the previous iteration of the model in Section 2 that included outbreak-related cases, as case number surges and drop-offs are now comparatively stable. This suggests that community transmission in Ontario during our time period is relatively consistent and predictable over time, while the majority of surges are due to localized outbreaks. The community has been able to keep cases numbers consistent as well, suggesting a overall $R_{eff}$ value of approximately 1 given the guidelines and protocols established provincially. This is even more evident when examining the q plot (Fig. 11).

Figure 11.

Change in q over time with outbreak cases removed as compared to threshold $\overline{q}=0.17$.

From $int1$ through $int12$, $q\in [0.1101416,0.2565002]$. This yields an $R_{eff}\in [0.6487918,1.5058941]$, with an overall average of $R_{effavg}=1.007796$ during this time period. This shows that Ontario communities are living in a delicate balance, very close to an $R_{eff}=1$. This suggests that even a relatively minor shift in behavior (distancing, mask wearing, mobility, etc.) or environment (climate, virus mutations, etc.) that increases our $R_{eff}$ can easily result in further eclipsing $R_{eff}=1$, and will lead to more significant growth in case numbers over time.

4. Limitations and further work

There are some limitations to the work presented here. First, our model assumes uniform transmissibility, uniform susceptibility, and uniform contact dampening as a result of lockdown across the three age groups, which may not be true [70], [71], [72]. As well, our model only considers a period of time when non-pharmaceutical interventions (NPIs) were used to mitigate infection spread (e.g. vaccinations, and other practices which have become standard over the course of the pandemic). Now that the pandemic is much further along, different parameters may be established at new time points to reflect newly instated measures of control in our model. Additionally, when we employ the outbreaks-removed data to find a better fit for our model, we do not make adjustments to our assumed population sizes. As there are a wide range of definitions for potential outbreak locations, we cannot know from which age subgroup outbreak cases are removed.

5. Conclusion

Using our SEILR(pas) model in conjunction with Canadian contact rates and mobility data, we have successfully modeled new daily Ontario cases from February 14 to June 7, 2020 while matching age-specific case rates. We accomplish this by tracking the dampening effects of preventative measures, represented by variable q. When removing cases associated with localized outbreaks, we observe that the vast majority of variability in new cases is a result of these outbreaks. When considering community transmission only, Ontario has generally maintained an $R_{eff}\approx 1$ over the course of our modeled time period. This suggests that even a slight change that results in increasing $R_{eff}$ can result in daily case numbers growing over time, rather than remaining stable or decreasing as we observe now. When considering changes in mobility, we find that while mobility has increased towards the end of our time period, preventative measures such as hand-washing, physical distancing, and mask-wearing have been sufficient to maintain an $R_{eff}\approx 1$. It is important to note that using the mobility reduction as a signal for pandemic evolution is not easy, nor perhaps desirable, especially in a simple model such as this. We clearly see that a large suppression of mobility has helped arrest the spread, however that level is generally unsustainable beyond a few weeks and mobility will invariably be pushed back up towards baseline values over time. Disentangling mobility reduction in contacts from other NPI measures reduction teaches us that the collective impact of NPIs is perhaps a better representation for the evolution of the Ontario pandemic in the time frame considered.

We also found that the contact rates provided by Prem, Cook, & Jit (2017) [37] in combination with the age-specific symptomatic rates provided by Davies et al. (2020) [35] resulted in closely matching proportions for working-age populations and senior populations, but underestimated cases in young people. This is likely due to a combination of the effects of household transmission, differing degrees of susceptibility and transmissibility between age groups, differing responses to lockdown between age groups [70], and differing likelihoods to receive testing between age groups. This can be fixed in the future, however it would require more complete data. The lack of testing before lockdown is implemented precludes us from accurately assessing differences in susceptibility decoupled from mobility.

Declarations

Author contribution statement

R. Fields, L. Humphrey: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper. D. Flynn-Primrose, Z. Mohammadi, M. Nahirniak: Contributed reagents, materials, analysis tools or data; Wrote the paper. E. Thommes: Contributed reagents, materials, analysis tools or data. M. Cojocaru: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by the National Science and Engineering Research Council of Canada (grant no. 400684) and the Science and Engineering Research Council of Canada (grant no. 401285 and 401569).

Data availability statement

Data associated with this study is available at https://data.ontario.ca/dataset/status-of-covid-19-cases-in-ontario.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

Supplementary material related to this article can be found online at https://doi.org/10.1016/j.heliyon.2021.e07905.

No additional information is available for this paper.

Supplementary material

The following Supplementary material is associated with this article:

COVID_19_SEILR_model__Heliyon_appendix.pdf

Collapsing of age-stratified matrices and introduction of data matching delay.