Improved cortical surface reconstruction using sub-millimeter resolution MPRAGE by image denoising

Qiyuan Tian; Natalia Zaretskaya; Qiuyun Fan; Chanon Ngamsombat; Berkin Bilgic; Jonathan R Polimeni; Susie Y Huang

doi:10.1016/j.neuroimage.2021.117946

. Author manuscript; available in PMC: 2021 Sep 6.

Published in final edited form as: Neuroimage. 2021 Mar 10;233:117946. doi: 10.1016/j.neuroimage.2021.117946

Improved cortical surface reconstruction using sub-millimeter resolution MPRAGE by image denoising

Qiyuan Tian ^a,^b,^*, Natalia Zaretskaya ^a,^b,^c,^d, Qiuyun Fan ^a,^b, Chanon Ngamsombat ^a,^e, Berkin Bilgic ^a,^b,^f, Jonathan R Polimeni ^a,^b,^f, Susie Y Huang ^a,^b,^f

PMCID: PMC8421085 NIHMSID: NIHMS1716891 PMID: 33711484

Abstract

Automatic cerebral cortical surface reconstruction is a useful tool for cortical anatomy quantification, analysis and visualization. Recently, the Human Connectome Project and several studies have shown the advantages of using T₁-weighted magnetic resonance (MR) images with sub-millimeter isotropic spatial resolution instead of the standard 1-mm isotropic resolution for improved accuracy of cortical surface positioning and thickness estimation. Nonetheless, sub-millimeter resolution images are noisy by nature and require averaging multiple repetitions to increase the signal-to-noise ratio for precisely delineating the cortical boundary. The prolonged acquisition time and potential motion artifacts pose significant barriers to the wide adoption of cortical surface reconstruction at sub-millimeter resolution for a broad range of neuroscientific and clinical applications. We address this challenge by evaluating the cortical surface reconstruction resulting from denoised single-repetition sub-millimeter T₁-weighted images. We systematically characterized the effects of image denoising on empirical data acquired at 0.6 mm isotropic resolution using three classical denoising methods, including denoising convolutional neural network (DnCNN), block-matching and 4-dimensional filtering (BM4D) and adaptive optimized non-local means (AONLM). The denoised single-repetition images were found to be highly similar to 6-repetition averaged images, with a low whole-brain averaged mean absolute difference of ~0.016, high whole-brain averaged peak signal-to-noise ratio of ~33.5 dB and structural similarity index of ~0.92, and minimal gray matter–white matter contrast loss (2% to 9%). The whole-brain mean absolute discrepancies in gray matter–white matter surface placement, gray matter–cerebrospinal fluid surface placement and cortical thickness estimation were lower than 165 μm, 155 μm and 145 μm—sufficiently accurate for most applications. These discrepancies were approximately one third to half of those from 1-mm isotropic resolution data. The denoising performance was equivalent to averaging ~2.5 repetitions of the data in terms of image similarity, and 1.6–2.2 repetitions in terms of the cortical surface placement accuracy. The scan-rescan variability of the cortical surface positioning and thickness estimation was lower than 170 μm. Our unique dataset and systematic characterization support the use of denoising methods for improved cortical surface reconstruction at sub-millimeter resolution.

Keywords: High-resolution, T₁-weighted image, Convolutional neural network, Deep learning, BM4D, Non-local means, Magnetic resonance imaging

1. Introduction

Cerebral cortical surface reconstruction enables the delineation of the inner and outer boundaries of the highly folded human cerebral cortex from anatomical magnetic resonance imaging (MRI) data using geometric models of the cortex. The input for cortical surface reconstruction is typically a T₁-weighted structural MR image volume demonstrating high gray matter–white matter and gray matter–cerebrospinal fluid (CSF) contrast. The output of cortical surface reconstruction is a pair of two-dimensional surfaces represented as polyhedral (triangular) surface meshes, which represent the gray matter–white matter interface and the gray matter–CSF interface. Accurate cortical surface reconstruction can be performed automatically using several publicly available software packages (Ashburner and Friston, 2005, Bazin et al., 2014, Bazin and Pham, 2008, Dale et al., 1999, FreeSurfer, 2012, Fischl et al., 1999, Huntenburg et al., 2018, Han et al., 2004, Kim et al., 2005) and has been routinely used to quantify cortical morphology (Anderson et al., 2002, Bermudez et al., 2008, Engvig et al., 2010, Du et al., 2007, Fischl and Dale, 2000, Kuperberg et al., 2003, Lerch et al., 2004, Ly et al., 2012, Lazar et al., 2005, Schaer et al., 2008, Sailer et al., 2003, Schmaal et al., 2017, Winkler et al., 2017, Winkler et al., 2012 Wallace et al., 2010), parcellate cortical areas (Fischl et al., 2004, MF Glasser et al., 2016, Van Essen et al., 2011), and visualize and analyze anatomical (Cohen-Adad et al., 2011, Fracasso et al., 2016, Glasser and Van Essen, 2011, Marques et al., 2017, Trampel et al., 2011), microstructural (McNab et al., 2013, Kleinnijenhuis et al., 2015, Fukutomi et al., 2018, Calamante et al., 2018) and functional (Polimeni et al., 2010, Huber et al., 2015, Kok et al., 2016, Maass et al., 2014, Nasr et al., 2016, Olman et al., 2012) signals at various cortical depths and on the folded cortical manifold in a wide range of clinical and neuroscientific applications.

High-quality input T₁-weighted MR images are essential for generating accurate cortical surfaces. T₁-weighted MR images acquired with 1-mm isotropic spatial resolution have been long used for standard cortical surface reconstruction because the 1-mm voxels adequately sample the folded cortical ribbon in adult humans and because this acquisition provides an adequate trade-off between acquisition time, spatial resolution and signal-to-noise ratio (SNR). More recently, the Human Connectome Project (HCP) WU-Minn-Ox Consortium and several studies have shown the advantages of sub-millimeter isotropic spatial resolution for further improving the accuracy of the reconstructed cortical surfaces (Bazin et al., 2014, Glasser et al., 2013, Lüsebrink et al., 2013, MF Glasser et al., 2016, Q Tian et al., 2021, Zaretskaya et al., 2018). In these studies using sub-millimeter cortical surface reconstruction, the cortical surface positioning and thickness estimation in cortical regions with diminished gray–white contrast on T₁-weighted MR images exhibit improved accuracy due to reduced partial volume effects on the sub-millimeter resolution images. This effect is especially noticeable in heavily myelinated cortical areas (e.g., primary motor, somatosensory, visual and auditory cortex), where the gray matter signal appears more similar in signal intensity to the white matter, as well as in insular cortex where the superficial white matter in the extreme capsule immediately beneath the insular cortex appears darker due to partial volume effects with the claustrum (Zaretskaya et al., 2018, Q Tian et al., 2021). In general, T₁-weighted MR images with 0.8-mm isotropic resolution (half of the minimum thickness of the cortex) or higher resolution are recommended by the HCP WU-Minn-Ox Consortium (MF Glasser et al., 2016). This new standard was adopted in the healthy adult HCP (Glasser et al., 2013, MF Glasser et al., 2016) and the subsequent Lifespan HCP in Development and Aging (Bookheimer et al., 2019, Harms et al., 2018, Somerville et al., 2018). On the surface reconstruction side, several software packages, such as BrainVoyager (Goebel, 2012), CBS Tools (Bazin et al., 2014) and FreeSurfer (Zaretskaya et al., 2018) have evolved to process anatomical MRI data at native sub-millimeter resolution.

A significant barrier to the wide adoption of the cortical surface reconstruction at sub-millimeter resolution is the longer scan time. Modern accelerated MRI techniques (e.g., compressed sensing (Lustig et al., 2007) and Wave-CAIPI (Bilgic et al., 2015)) can encode a larger number of k-space data samples at the sub-millimeter acquisition with less noise enhancement and artifact penalties compared to conventional parallel imaging approaches. Nevertheless, sub-millimeter resolution MR images remain limited in image quality by the intrinsically low SNR of smaller voxels. Adequate image quality using such data for cortical surface reconstruction requires averaging data from at least two repetitions of the acquisition, resulting in scan times that last ~15 min (assuming a standard imaging acceleration factor of two) compared to ~5 min scan time for a routine 1-mm isotropic resolution acquisition. In fact, the number of the repetitions required to provide the same SNR scales with the square of the voxel size ratio (e.g., ~21.4 repetitions of 0.6-mm isotropic resolution data are needed to match the SNR of a single repetition of 1-mm isotropic resolution data, assuming all other parameters are held constant). Such long scans are uncomfortable and may result in increased vulnerability to motion artifacts and reduced scan throughput. Ultra-high field (e.g., 7-Tesla and 9.4-Tesla) MRI scanners and highly-parallelized phased-array radio frequency receive coil head arrays (i.e., 64 channels (Keil et al., 2013) and above) can significantly boost sensitivity and image SNR, but are currently still expensive and less accessible. Even at ultra-high fields, the SNR of a single repetition of sub-millimeter data may be not sufficient for accurately delineating the cortical surface in the temporal lobes because of signal dropout due to dielectric effects, and more repetitions are needed to enable high-quality whole-brain analysis.

Image denoising provides a feasible alternative strategy to obtain high-quality sub-millimeter anatomical MR images with adequate SNR from a single acquisition. Image denoising aims to recover a high-quality image from its noisy, degraded observation, which is a highly ill-posed inverse problem. Denoising algorithms often rely on prior knowledge as supplementary information to estimate high-quality images. One category of denoising methods incorporate these priors, such as sparseness (Block et al., 2007, Lustig et al., 2007, Liang et al., 2009, Murphy et al., 2012, Otazo et al., 2010) and low rank (Hu et al., 2019, Y Hu et al., 2020, Kim et al., 2019, Haldar, 2013, Shin et al., 2014, Haldar and Zhuo, 2016), during the formation of MR images. Another category of denoising methods are designed to be applied to the reconstructed images, with numerous algorithms proposed for processing 2-dimensional images (e.g., total variation denoising (Rudin et al., 1992), anisotropic diffusion filtering (Perona and Malik, 1990, Fischl and Schwartz, 1997), bilateral filtering (Tomasi and Manduchi, 1998), non-local means (NLM) filtering (Buades et al., 2005), block-matching and 3-dimentional filtering (BM3D) (Dabov et al., 2007) and K-SVD denoising (Aharon et al., 2006)) and 3-dimensional medical imaging data (Bazin et al., 2019, Coupé et al., 2008, Gerig et al., 1992, Konukoglu et al., 2013, Manjón et al., 2010, Maggioni et al., 2012). As a stand-alone processing step, these methods only take in reconstructed images from the MRI scanner as inputs, without any need to intervene in the current MRI workflow, and can be directly incorporated into the existing surface reconstruction software packages.

Convolutional neural networks (CNNs) are advantageous for learning the underlying image priors and resolving the complex high-dimensional mapping from noisy images to noise-free images. Even a simple CNN for denoising (i.e., DnCNN (Zhang et al., 2017)), comprised of stacked convolutional filters paired with rectified linear unit (ReLU) activation functions, achieves superior performance compared to the state-of-the-art BM3D denoising method. It is also relatively easy for CNNs to incorporate redundant information from other MR image contrasts (e.g., using T₁-weighted MR images to assist removal of noise in diffusion-weighted MR images (Q Tian et al., 2020)) or imaging modalities (e.g., using MR images to assist removal of noise in positron emission tomography (PET) images (Chen et al., 2018)) to boost denoising performance. Furthermore, denoising CNNs can be trained without use of noise-free target images in a self-supervised manner while still outperforming the state-of-the-art methods, which is especially useful when the noise-free target images are not available (Lehtinen et al., 2018, Krull et al., 2019). Impressively, CNN-based denoising methods can be executed extremely efficiently (in milliseconds or seconds) once trained. Thus far, CNN-based denoising has been widely applied for various biomedical imaging modalities ranging from fluorescence microscopy (Krull et al., 2019, Weigert et al., 2018), optical coherence tomography (Devalla et al., 2019) to x-ray imaging (Gondara, 2016), x-ray computed tomography (Chang et al., 2019), PET (Chen et al., 2018, Ouyang et al., 2019, Wang et al., 2018, Serrano-Sosa et al., 2020, Xu et al., 2020) and MRI (Q Tian et al., 2020, Chang et al., 2019, Gong et al., 2018, Benou et al., 2017, Jiang et al., 2018, Pierrick, 2019, Gong et al., 2020, Kidoh et al., 2019).

In the present study, we leverage multiple available denoising methods for improving cortical surface reconstruction at sub-millimeter resolution and characterize the improvement in the reconstructed surfaces offered by the different denoising approaches using empirical data. Specifically, we reconstruct cortical surfaces using single-repetition 0.6-mm isotropic resolution T₁-weighted images denoised by three classical denoising methods, including BM4D (Maggioni et al., 2012), adaptive optimized NLM (AONLM) (Manjón et al., 2010) and DnCNN (Zhang et al., 2017). These three methods have widely accepted superior denoising performance, each representing a category of denoising methods. They are often used as references for performance comparison in terms of image quality and our evaluations of them here could serve as references for performance comparison in terms of cortical surface reconstruction for different denoising methods. We systematically quantify the similarity and image contrast of denoised 0.6-mm isotropic T₁-weighted images to the corresponding high-SNR 0.6-mm isotropic images obtained by averaging 6 repetitions of the data acquired within a single scan session and compare the results to those obtained from 2- to 5-repetition averaged data. We also quantify and compare the quality and smoothness of the reconstructed surfaces as well as the similarity of cortical surface positioning and cortical thickness estimation compared to the ground truth. Finally, we characterize the scan–rescan precision of the cortical surface positioning and cortical thickness estimation derived from the sub-millimeter resolution images denoised by different methods.

2. Materials and methods

2.1. Data acquisitions

T₁-weighted images with 0.6-mm isotropic resolution of nine healthy subjects (4 for training and validation of DnCNN parameters, 5 for evaluation) were acquired on a whole-body 3-Tesla scanner (MAGNETOM Trio Tim system, Siemens Healthcare, Erlangen, Germany) using the vendor-supplied 32-channel receive coil, body transmit coil, and standard body gradients at the Athinoula A. Martinos Center for Biomedical Imaging of the Massachusetts General Hospital (MGH) with Institutional Review Board approval and written informed consent of the volunteers. The data were acquired using a 3-dimensional multi-echo magnetization-prepared rapid gradient-echo (MEMPRAGE) sequence (van der Kouwe et al., 2008). A slab-selective oblique-axial acquisition using a 13 ms FOCI adiabatic inversion pulse (Hurley et al., 2010) and acceleration factor of 2 in the partition (i.e., inner loop) direction were used to minimize the number of partition encoding steps and minimize T₁ blurring during the inversion recovery (MD Tisdall et al., 2013, Polak et al., 2018, van der Kouwe et al., 2014). Because the profile of the radiofrequency pulse for the slab excitation falls off at the slab boundaries, the signal level is lower toward the superior and inferior brain yielding lower SNR locally in the acquired images (Supplementary Fig. 1a). In order to avoid spatial blurring, partial Fourier imaging was not used in any encoding direction to help preserve the 0.6-mm isotropic resolution. The sequence parameters were: repetition time = 2510 ms, echo times = 2.88/5.6 ms, inversion time = 1200 ms, excitation flip angle = 7°, bandwidth = 420 Hz/pixel, echo spacing = 8.4 ms, 224 axial slices with 14.3% slice oversampling, matrix size = 400 × 304, slice thickness = 0.6 mm, field of view = 240 mm × 182 mm, generalized autocalibrating partial parallel acquisition (GRAPPA) factor = 2, acquisition time = 10.7 min per run × 6 separate repetitions.

2.2. Image processing

Image co-registration was performed six times for each subject. Each time, five image volumes were individually co-registered to the remaining one image volume (the reference image volume which was not resampled) using the robust registration method as implemented in the “mri_robust_template” function (Reuter et al., 2010) from the FreeSurfer software (Dale et al., 1999, FreeSurfer, 2012, Fischl et al., 1999) (version v6.0, https://surfer.nmr.mgh.harvard.edu), with “satit” and “fixtp” options and “inittp” set to the number of the reference image volume. The “fixtp” option ensures that all other image volumes are co-registered to the reference image volume specified by the “inittp” such that the reference image volume is not resampled to avoid changing its noise characteristics. The “satit” option specifies the optimal saturation value, i.e., sensitivity for outlier detection, to be automatically determined. The co-registered image volumes were gradually added to the reference image volume to create averaged image volumes with progressively increasing SNR (n = 2, 3, 4, 5, 6), which were compared to the denoised single-repetition data in order to determine the efficiency factor, i.e., the number of image volumes for averaging that would be needed to obtain equivalent image and surface metric values compared to those obtained from denoised single-repetition data. Because only results with an integer number of repetitions for averaging were available, linear interpolation between results from neighboring numbers of repetitions for averaging was performed for comparison. Consequently, 6 pairs of image volumes, each pair consisting of a noisy image volume from the single-repetition data and a high-SNR image volume from the 6-repetition averaged data, were generated for each subject. A total of 24 pairs of image volumes (6 pairs/subject × 4 training subjects) were used as the training and validation data for optimizing the CNN parameters. For evaluation, 30 pairs of image volumes, each pair consisting of a noisy image volume from the single-repetition data (or 2- to 5-repetition averaged data) and a high-SNR image volume from 6-repetition averaged data, were used.

Spatially varying intensity bias maps were estimated using the image volumes from the single-repetition data with the unified segmentation routine (Ashburner and Friston, 2005) implementation in the Statistical Parametric Mapping software (SPM, https://www.fil.ion.ucl.ac.uk/spm) with a full-width at half-maximum (FWHM) of 30 mm and a sampling distance of 2 mm (Uwano et al., 2014) (Supplementary Fig. 1b). The estimated bias maps were divided from images from the single-repetition and 2- to 6-repetition averaged data for correcting spatially varying intensity bias.

For improved DnCNN performance and evaluation of image and surface quality compared to those obtained from the 6-repetition averaged data, the images from the 6-repetition data were further non-linearly co-registered to the images from the single-repetition data, as well as from the 2- to 5-repetition averaged data, respectively. The non-linear co-registration slightly adjusted the image alignment locally, which accounted for the subtle non-linear shifts of tissue in the images due to factors such as subject bulk motion and the associated changes in distortion due to changing B0 inhomogeneity and gradient nonlinearity distortion during the acquisition of each repetition of data. The non-linear co-registration was performed using the “reg_f3d” function (default parameters, spline interpolation) from the NiftyReg software (https://cmiclab.cs.ucl.ac.uk/mmodat/niftyreg) (Modat et al., 2010, Modat et al., 2014).

The local mean values of the image intensity from the co-registered 6-repetition averaged data were also slightly scaled to match those of the corresponding single-repetition data as well as 2- to 5-repetition averaged data to remove the residual intensity bias for improved DnCNN performance and image and surface similarity evaluation. The local mean image intensity was computed using a 3-dimenstional Gaussian kernel with a standard deviation of 2 voxels (i.e., 1.2 mm).

Brain masks were created from the 6-repetition averaged image volumes by performing the FreeSurfer automatic reconstruction processing for the first five preprocessing steps (FreeSurfer’s “recon-all” function with the “-autorecon1” option). The binarized brain masks were dilated twice with holes filled using the “fslmaths” function from the FMRIB Software Library software (Smith et al., 2004, Jenkinson et al., 2012, Andersson and Sotiropoulos, 2016) (FSL, https://fsl.fmrib.ox.ac.uk).

2.3. BM4D denoising

T₁-weighted image volumes from the single-repetition data at 0.6-mm isotropic resolution were denoised using the BM4D denoising algorithm (Dabov et al., 2007, Maggioni et al., 2012). BM4D extends the widely known BM3D algorithm designed for 2-dimenstion image data to process 3-dimensional volumetric data. The BM4D method provides superior denoising performance by grouping similar 3-dimensional blocks across the entire volume (both local and non-local) into 4-dimensional data arrays to enhance the sparsity and then performing collaborative filtering. The BM4D denoising was performed assuming Rician noise with an unknown noise standard deviation and was set to estimate the noise standard deviation and perform collaborative Wiener filtering with “modified profile” option using the publicly available MATLAB-based software (https://www.cs.tut.fi/~foi/GCF-BM3D).

2.4. AONLM denoising

T₁-weighted image volumes from the single-repetition data at 0.6-mm isotropic resolution were also denoised using the AONLM algorithm (Coupé et al., 2008, Manjón et al., 2010). In AONLM, the restored intensities of a small block are the weighted average of the intensities of all similar blocks within a predefined neighborhood. The 3-dimensional AONLM extends the 2-dimensional NLM filtering by using a block-wise implementation with adaptive smoothing strength based on automatically estimated spatially varying image noise level. The AONLM was performed assuming Rician noise with 3 × 3 × 3 block and 7 × 7 × 7 search volume (Coupé et al., 2008, Manjón et al., 2010) using the publicly available MATLAB-based software (https://sites.google.com/site/pierrickcoupe/softwares/denoising-for-medical-imaging/mri-denoising/mri-denoising-software).

2.5. DnCNN denoising

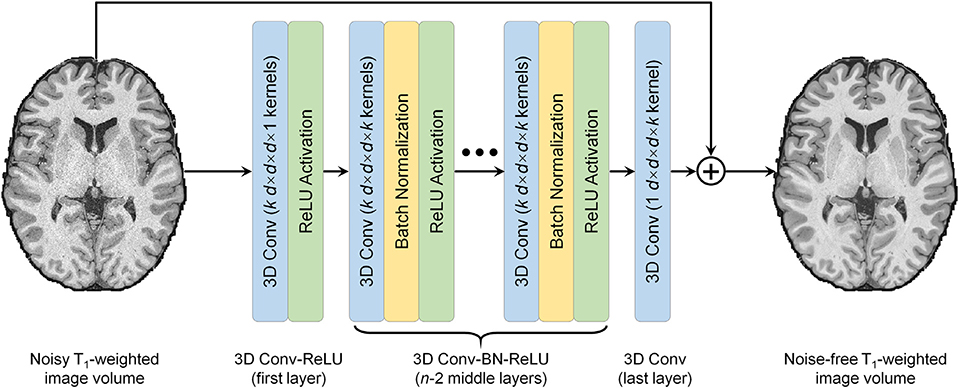
T₁-weighted image volumes from the single-repetition data at 0.6-mm isotropic resolution were also denoised using DnCNN (Zhang et al., 2017) (Fig. 1), a pioneering and classical CNN for denoising. The 2-dimensional convolution used for processing 2-dimensional images was extended to 3-dimensional for MRI to increase the data redundancy from an additional spatial dimension for improved denoising performance and smooth transition between 2-dimensional image slices. DnCNN maps the input image volume to the noise, i.e., the residual volume between the input and output image volume. Residual learning facilitates the DnCNN to only learn the high-frequency information, which boosts CNN performance, accelerates convergence and avoids the vanishing gradient problem (He et al., 2016, Kim et al., 2016, Zhang et al., 2017). DnCNN has a simple network architecture comprised of stacked convolutional filters paired with rectified linear unit (ReLU) activation functions and batch normalization functions. The n-layer DnCNN consists of a first layer of paired 3D convolution (k kernels of size d × d × d × 1 voxels, stride of 1 × 1 × 1 voxel) and ReLU activation, n − 2 middle layers of 3D convolution (k kernels of size d × d × d × k voxels, stride of 1 × 1 × 1 voxel), batch normalization and ReLU activation, and a last 3D convolutional layer (one kernel of size d × d × d × k voxels, stride of 1 × 1 × 1 voxel). The output layer excludes ReLU activation so that the output would include both positive and negative values. Parameter value settings of n = 20, k = 64, d = 3 were adopted following previous studies (Zhang et al., 2017) (~2 million trainable parameters).

Our DnCNN network was implemented using the Keras application program interface (https://keras.io) with a Tensorflow backend (Google, Mountain View, California, https://www.tensorflow.org). Training and validation were performed on image blocks of 81 × 81 × 81 voxels (12 blocks per whole-brain volume) because of the limited graphics processing unit (GPU) memory available. Sixty blocks from five random repetitions of data from each of the four training subjects (240 blocks in total) were used for training, while 12 blocks from the held-out repetition of data from each of 4 training subjects (48 blocks in total) were used for validation. The input and output image volumes were skull-stripped and image intensities were standardized by subtracting the mean intensity and then divided by the standard deviation of the image intensities of the brain voxels from the input noisy single-repetition image volumes.

All 3-dimensional convolutional kernels were randomly initialized with a “He” initialization (He et al., 2015). Network parameters were optimized by minimizing the mean squared error within the brain (excluding the cerebellum which is irrelevant for cerebral cortical surface reconstruction and has significantly different texture compared to the cerebrum) using stochastic gradient descent (LeCun et al., 1998) with an Adam optimizer (Kingma and Adam, 2014) (default parameters except for the learning rate) using a V100 GPU with 16 G memory (NVidia, Santa Clara, California) for about ~15 h. The batch size was set to 1, the largest batch the GPU memory can accommodate. The learning rate was 0.0001 for the 20 epochs, after which the network approached convergence, and 0.00005 for another 10 epochs (~0.5 hour per epoch).

The trained DnCNN was applied to the skull-stripped and standardized whole-brain image volumes from each repetition of the 5 evaluation subjects. The predicted image intensities were transformed to the original range by multiplying with the standard deviation of the image intensities and adding the mean intensity of the brain voxels from the input noisy image volumes.

2.6. Surface reconstruction

Cortical surface reconstruction at native 0.6-mm isotropic resolution was performed using the FreeSurfer sub-millimeter pipeline (Zaretskaya et al., 2018) (version v6.0) (https://surfer.nmr.mgh.harvard.edu/fswiki/SubmillimeterRecon). Specifically, the “recon-all” function was executed with the “-hires” option with an expert file that specifies 100 iterations of surface inflation in the “mris_inflate” function.

2.7. Image similarity comparison

To quantify the similarity between the image volumes from the single-repetition and 2- to 5-repetition averaged data and the denoised image volumes compared to the high-SNR image volumes from the 6-repetition averaged data at 0.6-mm isotropic resolution, the mean absolute difference (MAD), peak SNR (PSNR) and structural similarity index (SSIM) (Wang et al., 2004) were computed using custom scripts written for the MATLAB software package (MathWorks, Natick, Massachusetts). PSNR was computed using MATLAB’s “psnr” function, with larger value indicating lower mean squared error. SSIM is a perceptual metric for image similarity quantification ranging between 0 and 1 with larger value indicating higher similarity. SSIM was computed using MATLAB’s “ssim” function. For these calculations, the standardized image intensities, which virtually fell into the range [−3, 3], were normalized to the range of [0, 1] by adding 3 and dividing by 6. The group-level mean and standard deviation of the whole-brain averaged MAD, PSNR and SSIM (only within the brain mask) across 30 image volumes from the 5 evaluation subjects were computed to summarize the overall image similarity.

2.8. Gray–white boundary sharpness comparison

The sharpness of the boundary between the gray matter and white matter is essential for the accurate segmentation of the gray matter and white matter and reconstruction of the gray–white surface. Therefore, the image intensity gradient across the gray-white interface was computed from different types of images and compared. Specifically, the gray–white boundary sharpness was quantified as the percent gray–white contrast (i.e., [white − gray]/[white + gray]⋅100%) at the location of every vertex on the gray–white surface reconstructed from the 6-repetition averaged images (Supplementary Figure 2). The white matter intensity was sampled at 0.6 mm (i.e., the voxel size) below the gray–white surface. The gray matter intensity was sampled at 0.6 mm above the gray–white surface. The group-level mean and standard deviation of the whole-brain averaged vertex-wise gray–white contrast and variation of the vertex-wise gray–white contrast across 30 image volumes from the 5 evaluation subjects were computed to summarize the overall image contrast level.

2.9. Surface quality comparison

Percentage of defective vertices and surface smoothness were used for assessing the quality of surfaces reconstructed from 0.6-mm isotropic resolution data. Specifically, the percentage of defective vertices was computed as the number of vertices identified as being part of topological defects in the initial reconstructed surface prior to topology correction (Ségonne et al., 2007) (identified by FreeSurfer surface results files “lh.defect_labels” and “rh.defect_labels”) divided by the total number of vertices. Due to the reduction of noise by data averaging or denoising, the reconstructed cortical surfaces become smoother and therefore more similar to those from the 6-repetition averaged data. The cortical surfaces should not be over-smoothed, which might fail to preserve cortical folding pattens and lead to loss of anatomical details. The surface smoothness was defined as the whole-brain averaged gradient amplitude of vertex-wise mean curvature values, which were computed using FreeSurfer’s “mris_curvature” function. Specifically, for each vertex, the gradients were first computed as the differences between the mean curvature values of this vertex and all its neighboring vertices over the corresponding inter-vertex distances. The gradient amplitude was then calculated as the square root of the mean square differences. The mean curvature values of noisy surfaces are more spatially variant and therefore their gradient amplitudes are higher, and vice versa. The group-level mean and standard deviation of the percentage of defective vertices, gray–white surface smoothness, gray–CSF surface smoothness across 30 image volumes from the 5 evaluation subjects were computed to summarize the overall surface quality.

2.10. Surface accuracy comparison

The FreeSurfer longitudinal pipeline (Reuter et al., 2010, Reuter and Fischl, 2011, Reuter et al., 2012) (https://surfer.nmr.mgh.harvard.edu/fswiki/LongitudinalProcessing) was used to quantify the discrepancies of the gray–white and gray–CSF surface positioning and cortical thickness estimation from the single-repetition data, 2- to 5-repetition averaged data, and denoised single-repetition data compared to those from the 6-repetition averaged data at 0.6-mm isotropic resolution. Briefly, for any two image volumes for comparison, the longitudinal pipeline provides a vertex correspondence between the cortical surfaces reconstructed for each image volume, which enables the calculation of a vertex-wise displacement for the two bounding surfaces of the cortical gray matter as well as a per-vertex difference of the cortical thickness estimates (Fujimoto et al., 2014, Zaretskaya et al., 2018). The group-level mean and standard deviation of the mean absolute gray–white and gray–CSF surface displacement and cortical thickness difference averaged across the whole brain as well as within 34 cortical parcels (left and right hemispheres combined) from the Desikan-Killiany Atlas provided by FreeSurfer across 30 image volumes from the 5 evaluation subjects were computed to summarize the overall surface positioning accuracy.

2.11. Surface precision comparison

The FreeSurfer longitudinal pipeline was used to quantify the discrepancies of the gray–white and gray–CSF surface positioning and cortical thickness estimation from two consecutively acquired single-repetition data at 0.6-mm isotropic resolution (5 comparisons in total, i.e., repetition 1 vs. repetition 2, repetition 2 vs. repetition 3 to repetition 5 vs. repetition 6) denoised by DnCNN, BM4D and AONLM as described in the previous section to quantify the scan-rescan precision (or variability). The group-level mean and standard deviation of the mean absolute gray–white and gray–CSF surface displacement and cortical thickness difference averaged across the whole brain as well as within 34 cortical parcels (left and right hemispheres combined) from the Desikan-Killiany Atlas provided by FreeSurfer across 25 image volumes from the 5 evaluation subjects were computed to summarize the overall surface positioning precision.

2.12. Statistical comparison

Student’s t-test was performed to assess whether there were significant differences between metrics of interest (i.e., the whole-brain averaged MAD, PSNR, SSIM, vertex-wise gray–white contrast, variability of the vertex-wise gray–white contrast, gray–white surface displacement, gray–CSF surface displacement and cortical thickness difference) from different types of image volume at 0.6-mm isotropic resolution (e.g., DnCNN-denoised data vs. BM4D-denoised data, and DnCNN-denoised data vs. 6-repetition averaged data) across 5 evaluation subjects (N = 5). For the comparison, the whole-brain averaged metric values of the 6 repetitions of the data from each subject were averaged.

3. Results

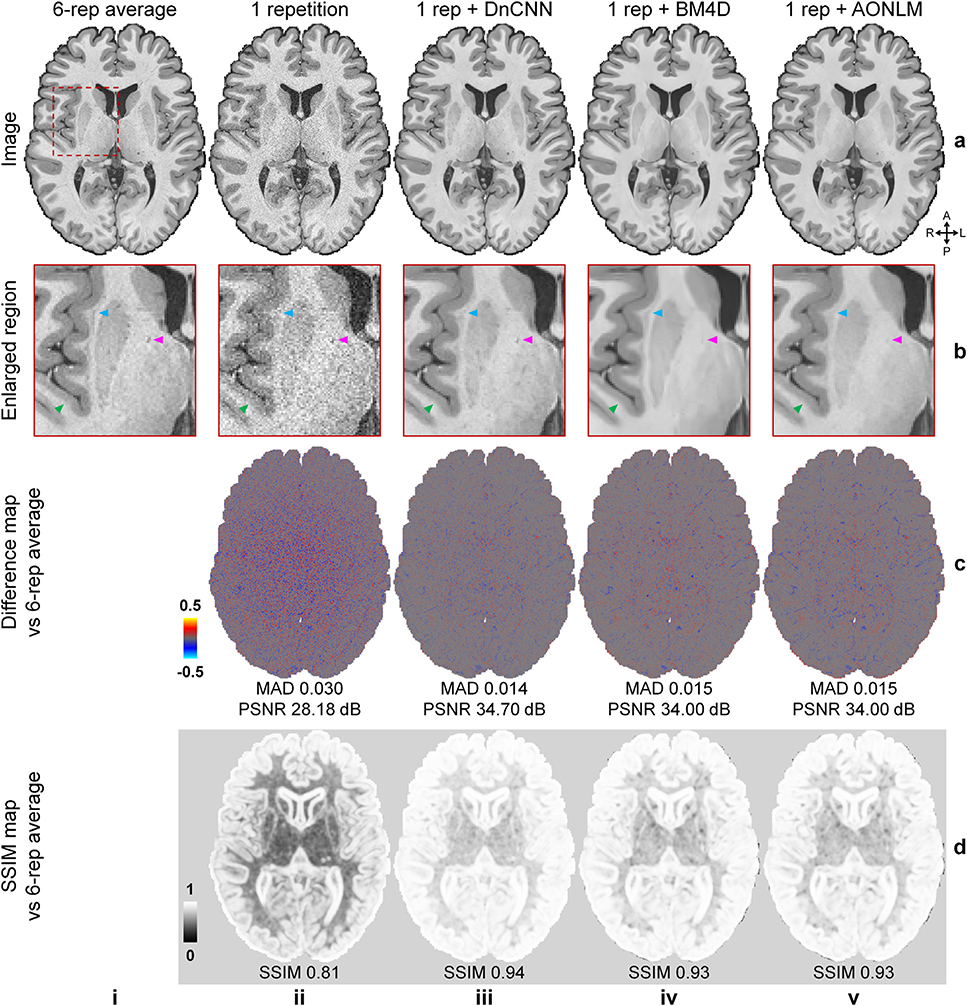
Fig. 2 shows that the T₁-weighted images (Fig. 2, rows a, b, columns iii–v) denoised using DnCNN, BM4D and AONLM were better able to delineate fine anatomical structures compared to the single-repetition data (Fig. 2, rows a, b, columns ii) and were visually more comparable to the T₁-weighted image generated from the 6-repetition averaged data (Fig. 2, rows a, b, column i). The textural details were more clearly displayed with sharper gray–white and gray–CSF boundaries in the denoised images, especially in the DnCNN-denoised images, compared to those from the single-repetition data (Fig. 2, row b, arrow heads). The image artifacts due to subject motion in the left occipital lobe were also effectively removed in the denoised images.

The differences between the denoised images and 6-repetition averaged image exhibited negligible levels of anatomical structure and were substantially lower compared to those from the single-repetition images (Fig. 2, row c), with lower whole-brain averaged MAD (0.014, 0.015, 0.015 for DnCNN, BM4D and AONLM vs. 0.03) and higher PSNR (34.7 dB, 34 dB and 34 dB for DnCNN, BM4D and AONLM vs. 28.18 dB). The SSIM maps demonstrate that the denoised images were also perceptually similar to the 6-repetition averaged image (Fig. 2, row d), with higher whole-brain averaged SSIM (0.94, 0.93, 0.93 for DnCNN, BM4D and AONLM vs. 0.81). Overall, DnCNN had slightly better denoising performance than BM4D and AONLM, which generated images of very similar quality to one another.

The noise estimated by the three methods (i.e., the residual maps between the denoised images and the acquired single-repetition image) did not contain any noticeable anatomical structure or biases reflecting the underlying anatomy (Supplementary Fig. 3, row b, columns iii-v) and were visually similar to the residual map from the 6-repetition averaged data (Supplementary Fig. 3, row b, column ii). DnCNN estimated slightly lower noise levels in the center of the brain compared to BM4D and AONLM.

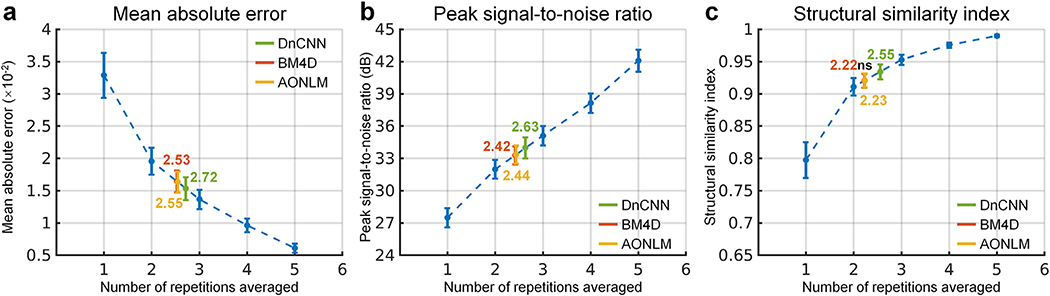
The similarity between images from the single-repetition data and the denoised single-repetition data compared to the 6-repetition averaged data was quantified at the group level and compared to those from the 2- to 5-repetition averaged data in Fig. 3. The group-level means (± the group-level standard deviation) of the whole-brain averaged MAD, PSNR and SSIM of the denoised images were approximately two times lower (0.0153 ± 0.0018, 0.0165 ± 0.0017, 0.0163 ± 0.0017 for DnCNN, BM4D and AONLM vs. 0.0329 ± 0.0035), ~6 dB higher (34.0 ± 0.98 dB, 33.3 ± 0.83 dB, 33.4 ± 0.85 dB for DnCNN, BM4D and AONLM vs. 27.5 ± 0.89 dB) and approximately 0.12 higher (0.93 ± 0.012, 0.92 ± 0.011, 0.92 ± 0.011 for DnCNN, BM4D and AONLM vs. 0.80 ± 0.028), respectively, compared to the single-repetition images. The image similarity levels of the denoised images compared to the 6-repetition averaged images were equivalent to those derived from what would be expected from averaging ~2.5 images (2.72, 2.53, 2.55 in terms of MAD, 2.63, 2.42, 2.44 in terms of PSNR, and 2.55, 2.22, 2.23 in terms of SSIM for DnCNN, BM4D and AONLM).

Fig. 3. — The blue dots and error bars represent the group mean and standard deviation of the whole-brain mean absolute difference (MAD) (a), peak signal-to-noise ratio (PSNR) (b) and structural similarity index (SSIM) (c) of the images from the single-repetition data and 2- to 5-repetition averaged data compared to the images from the 6-repetition averaged data across 30 image volumes from the 5 evaluation subjects. The green, red and yellow dots and error bars represent the group mean and standard deviation of the MAD, PSNR and SSIM of the images from the single-repetition data denoised by DnCNN (green), BM4D (red) and AONLM (yellow) compared to the images from the 6-repetition averaged data across 30 image volumes from the 5 evaluation subjects. The red dots and error bars for BM4D are virtually covered by the yellow dots and error bars for AONLM. The numbers above and below the dashed lines that link two neighboring blue dots indicate the number of image volumes for averaging that would be needed to obtain equivalent similarity metrics to those obtained from images from single-repetition data denoised by different methods. All comparisons of results from different denoising methods and numbers of repetitions for averaging are statistically significant (p<0.05), except for between the BM4D- and AONLM-denoised data for SSIM (c) (denoted with abbreviation “ns”).

The vertex-wise gray–white contrast maps depict the spatial variation of the gray–white contrast across cortical regions (Fig. 4, averaged maps across 30 image volumes from the 5 evaluation subjects available in Supplementary Fig. 4). Overall, the gray–white contrast was consistently lower in heavily myelinated regions near the central sulcus, calcarine sulcus, paracentral gyrus, Heschl’s gyrus, posterior cingulate gyrus, isthmus of the cingulate gyrus with increased gray matter image intensity on T₁-weighted images, and in the insula with decreased white matter image intensity on the T₁-weighted images arising from the partial volume effects with the claustrum (Q Tian et al., 2021). These regions are more prone to noise during the cortical surface reconstruction process.

The sharpness of the gray–white boundary is critical for the accurate segmentation of the gray matter and white matter and accurate reconstruction of gray–white surface. Therefore, gray–white contrast across the gray–white interface should be preserved as much as possible during the noise removal process, on a similar level to that from the 6-repetition averaged data. The gray–white contrast map from the single-repetition data (Fig. 4, column ii) displayed similar gray–white contrast level compared to the map from the 6-repetition averaged data (Fig. 4, column i), but was more spatially variable. The gray–white contrast maps from the denoised data (Fig. 4, columns iii–v) were smoother and less spatially variable, appearing more similar to the map from the 6-repetition averaged data (Fig. 4, column i). The gray–white contrast level in the map from DnCNN (Fig. 4, column iii) was slightly higher than those from BM4D (Fig. 4, column iv) and AONLM (Fig. 4, column v), and visibly more similar to that from the 6-repetition averaged data (Fig. 4, column i). All denoising methods unavoidably blur edges (i.e., the gray–white boundary) in input images to some extent, which leads to the loss of gray–white contrast and potentially negatively influences the accurate placement of gray–white surface.

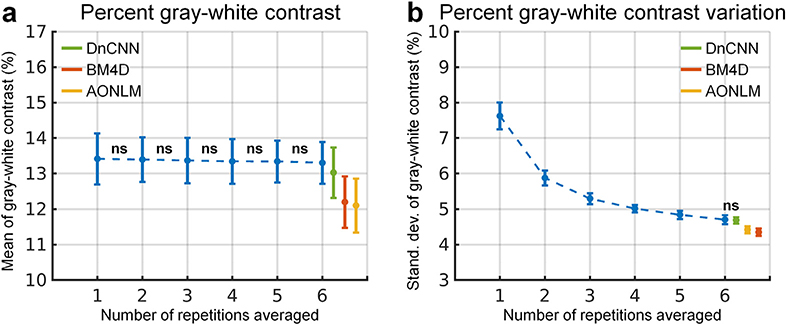
The group-level means (± the group-level standard deviation) of the spatial mean and spatial variability of the vertex-wise gray–white contrast across the whole brain were quantified to compare the capability of different denoising methods in preserving gray–white contrast (Fig. 5). The whole-brain averaged vertex-wise gray–white contrast stayed almost the same and decreased only marginally when averaging more repetitions of data (Fig. 5a, blue curve), which was consistent with visual inspection (Fig. 4, columns i, ii). The whole-brain averaged vertex-wise gray–white contrast from DnCNN was slightly higher than that from BM4D and AONLM (13.03 ± 0.71 vs. 12.20 ± 0.73 and 12.10 ± 0.76 for BM4D and AONLM) and was slightly lower than that from the 6-repetition averaged data (13.03 ± 0.71 vs. 13.30 ± 0.59).

The spatial variability of the vertex-wise gray–white contrast continued to decrease when more repetitions of the data were averaged (Fig. 5b, blue curve). This finding was also visually reflected by smoother gray–white contrast maps (Fig. 4, columns i, ii). The spatial variability of the vertex-wise gray–white contrast in the DnCNN-denoised data was nearly the same as that in the 6-repetition averaged data (4.69 ± 0.10 vs. 4.70 ± 0.13, comparison not significant). The spatial variability in the BM4D- and AONLM-denoised data (4.35 ± 0.10 vs. 4.42 ± 0.10) was further reduced than in the DnCNN-denoised data and 6-repetition averaged data, potentially due to stronger unwanted spatial smoothing effects that reduce tissue contrast.

The effects of data averaging and denoising on the reconstructed cortical surfaces are shown in Fig. 6. The cortical surfaces from the single-repetition data (Fig. 6, column ii) resembled the overall cortical geometry represented by the surfaces from the 6-repetition averaged data (Fig. 6, column i), but were noisy and unsmooth. The bumpy appearance was more obviously displayed in the superior and inferior brain (Fig. 6, column ii, arrow heads), where the SNR was further reduced because of the lower signal level resulting from the non-uniform slab excitation. The cortical surfaces from the 6-repetition averaged data and the denoised data were much smoother than those from the single-repetition data due to the reduction of noise on surfaces (Fig. 6, column i, iii–v). The surfaces from the denoised images were visually more similar to those from the 6-repetition averaged data than those from the single-repetition data. The surfaces from denoised images appeared overall slightly smoother than those from the 6-repetition averaged data, e.g., the gray–white surface near the Calcarine sulcus (Fig. 6, row d), which might be due to unwanted over-smoothing effects during the noise removal process. The over-smoothed surfaces potentially lead to loss of fine anatomical details.

The mean curvature can be used to characterize the local smoothness of cortical surfaces quantitatively (Fig. 7, averaged maps across 30 image volumes from the 5 evaluation subjects available in Supplementary Fig. 5)—the mean curvature map of a smooth surface will exhibit low levels of spatial variability. For the single-repetition data, the mean curvature map of the gray–white surface was highly spatially variable near the central sulcus, calcarine sulcus, paracentral gyrus, cingulate gyrus and insula, where the gray–white contrast was lower (Fig. 4) and the image noise had a higher impact on the reconstructed cortical surfaces. The mean curvature maps from the 6-repetition averaged data and the denoised data were much less spatially variable, but were still slightly variable near the superior portion of the central sulcus presumably because of the simultaneous reduction in gray–white contrast and lower signal levels near the edge of the excited slab.

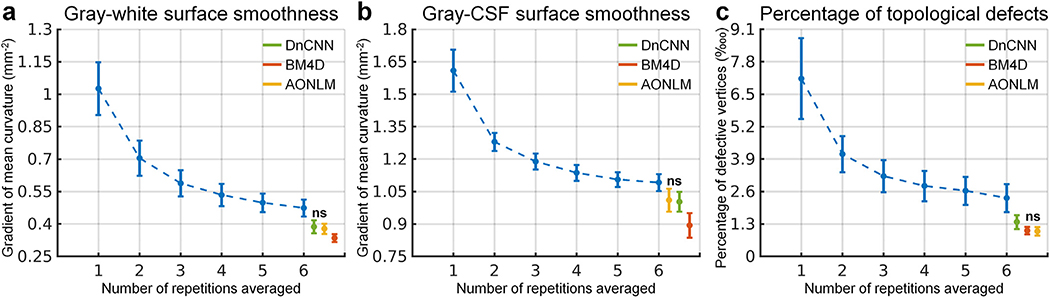
Quantitatively, the whole-brain averaged gradient amplitude of vertex-wise mean curvature values decreased as the number of the averaged repetition increased (Fig. 8a, b, blue curves), indicating increased overall surface smoothness. The cortical surfaces from the denoised data were much smoother than those from single-repetition data, indicating effective reduction of noise on surfaces. However, the cortical surfaces from the denoised data were slightly smoother than those from the 6-repetition data (0.387 ± 0.03 mm⁻², 0.335 ± 0.018 mm⁻² and 0.378 ± 0.024 mm⁻² for DnCNN, BM4D and AONLM vs. 0.474 ± 0.039 mm⁻² for 6-repetition averaged data for gray–white surface; 1.003 ± 0.046 mm⁻², 0.894 ± 0.057 mm⁻² and 1.01 ± 0.053 mm⁻² for DnCNN, BM4D and AONLM vs. 1.091 ± 0.039 mm⁻² for 6-repetition averaged data for gray–CSF surface), potentially due to unwanted spatial over-smoothing effects. The surface smoothness from DnCNN was more similar to the surface smoothness from the 6-repetition averaged data compared to those from BM4D, as well as those from AONLM for the gray–white surface.

Fig. 8. — The blue dots and error bars represent the group mean and standard deviation of the smoothness of the gray–white (a) and gray–cerebrospinal fluid (CSF) surface (b) (defined as the whole-brain averaged gradient amplitude of the vertex-wise mean curvature values), and the percentage of the vertices identified as being part of topological defects in the initial surface (c) from the single-repetition data and 2- to 6-repetition averaged data across 30 image volumes from the 5 evaluation subjects. The green, red and yellow dots and error bars represent the group mean and standard deviation of the gray–white and gray–CSF surface smoothness and percentage of the defective vertices from the single-repetition data denoised by DnCNN (green), BM4D (red) and AONLM (yellow) across 30 image volumes from the 5 evaluation subjects. All comparisons of results from different denoising methods and numbers of repetitions for averaging are statistically significant (p<0.05), except for between the AONLM- and DnCNN-denoised data for the gray–white surface smoothness (a) and for the gray–CSF surface smoothness (b), and between the BM4D- and AONLM-denoised data for the percentage of the defective vertices (c) (denoted with abbreviation “ns”).

The percentage of vertices identified as being part of topological defects in the initial surfaces reconstructed from the input data prior to automatic topological correction decreased as the number of the averaged repetitions increased (Fig. 8c, blue curve), indicating improved image quality due to data averaging. The percentage of the defective vertices (typically 0.8 to 1 million vertices in total for a subject for 0.6-mm isotropic data) was even lower in the denoised data than in the 6-repetition averaged data (0.014% ± 0.0028%, 0.01% ± 0.0015% and 0.01% ± 0.0017% for DnCNN, BM4D and AONLM vs. 0.023% ± 0.0056% for 6-repetition averaged data).

To demonstrate the effects of data averaging and denoising on the accuracy of surface positioning, cross-sections of the cortical surfaces were presented in enlarged views near the central sulcus and the calcarine sulcus (Fig. 9), chosen because they are regions with reduced gray–white contrast. The cortical surfaces reconstructed from the denoised data were similar to those reconstructed from 6-repetition averaged data and were markedly improved compared to the surface placement derived from the single-repetition data (Fig. 9, arrow heads), especially the gray–white surfaces. The discrepancy in the positioning of the gray–CSF surface across the different denoising techniques was overall smaller than that of the gray–white surface.

The cross-sections of cortical surfaces from the 1-mm isotropic resolution data were also displayed (Fig. 9, column vi) (details in the Methods for 1-mm Isotropic Resolution Data section of Supplementary Information) to demonstrate the advantages of those from the 0.6-mm isotropic resolution data. Comparing to results from the 6-repetition averaged data at 0.6-mm isotropic resolution, the gray–white surfaces from the 1-mm isotropic resolution data were placed more exterior, which is consistent with previous findings (Zaretskaya et al., 2018, Q Tian et al., 2021). The gray–CSF surfaces from the 1-mm isotropic resolution data were placed more exterior near the sulcal fundus where the space between two gyri is very tight. The displacement of the surface positioning from the 1-mm isotropic resolution data was larger than that from the 0.6-mm isotropic resolution data, especially for the gray–white surface, in the regions of interest shown in Fig. 9.

The denoised images exhibited substantially lower discrepancy in the surface positioning relative to surfaces reconstructed from the 6-repetition averaged images compared to the discrepancy seen from the single-repetition images in all cortical parcels on the single-subject level (Supplementary Fig. 6) and group level (Fig. 10). In the denoised results, the discrepancy was most prominent near the central sulcus, calcarine sulcus, Heschl’s gyrus and cingulate gyrus and insula for the gray–white surfaces (Fig. 10, rows a–d), near the Heschl’s gyrus and insula for the gray–CSF surfaces (Fig. 10, rows e–h), and near the Heschl’s gyrus and insula for the cortical thickness estimation (Fig. 10, rows i–l). Estimates from the single-repetition data and denoised data near the temporal pole and orbitofrontal cortex had larger discrepancies presumably because of the large and varying geometric distortions near air-tissue interfaces in each repetition of the data, which could not be accurately aligned for averaging the 6 repetitions of the data and therefore induced increased misalignment between each single-repetition data and the 6-repetition averaged data. The larger discrepancies near the insula might be partially due to the fact that surface reconstruction results from the 6-repetition averaged images are less robust due to insufficient spatial resolution to segment the insular cortex accurately, e.g., the boundary between the insular cortex and claustrum cannot be clearly displayed due to partial voluming effects even at a very high 0.6-mm isotropic resolution (Fig. 2, row b, column i).

Fig. 10. — The absolute average of the left-hemispheric vertex-wise displacement/difference of the gray–white surfaces (rows a–d), and gray–cerebrospinal fluid (CSF) surfaces (rows e–h) and cortical thickness estimates (rows i–l) from the single-repetition data (rows a, e, i) and the single-repetition data denoised by DnCNN (rows b, f, j), BM4D (rows c, g, k) and AONLM (rows d, h, l) compared to the surfaces estimated from the 6-repetition averaged data across 30 image volumes from the 5 evaluation subjects (rows iv–vi), displayed on inflated surface representations. Different cortical regions from the FreeSurfer cortical parcellation (i.e., *aparc.annot*) are depicted as colored outlines.

The 1-mm isotropic resolution data exhibited substantially higher discrepancy in the surface positioning and difference in cortical thickness relative to those obtained from the 6-repetition averaged data at 0.6-mm isotropic resolution compared to the discrepancy/difference seen from the denoised single-repetition data at 0.6-mm isotropic resolution in the whole brain. Consistent with previous studies (Zaretskaya et al., 2018, Q Tian et al., 2021), the gray–white surfaces from the 1-mm isotropic resolution data were placed generally more exterior, especially in heavily myelinated cortical regions such as near the central sulcus, calcarine sulcus and Heschl’s gyrus (Supplementary Fig. 6, row e, columns i–iii), which led to underestimation of the cortical thickness in these regions (Supplementary Fig. 6, row j, columns i–iii).

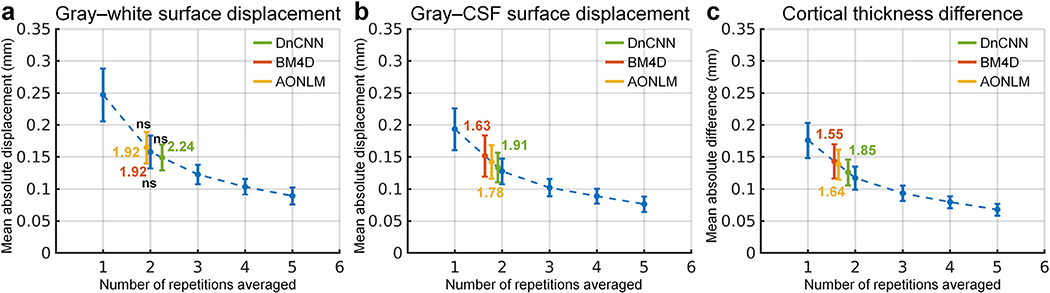
The group mean and standard deviation of the mean absolute displacement/difference of the gray–white surface, gray–CSF surface and cortical thickness was quantified for the whole brain (Fig. 11) and each cortical region (Supplementary Tables 1–3). The accuracy of surface positioning and cortical thickness estimation, especially the gray–white surface positioning was increased in the denoised data. The group-level means (± the group-level standard deviation) of the whole-brain averaged displacement of the gray–white surface in the denoised data were about two thirds of those from single-repetition images (0.15 ± 0.02 mm, 0.16 ± 0.025 mm, 0.17 ± 0.025 mm for DnCNN, BM4D and AONLM vs. 0.25 ± 0.04 mm), which were equivalent to those derived from ~2-repetition averaged images (2.24, 1.92, 1.92 for DnCNN, BM4D and AONLM, respectively). The group-level means (± the group-level standard deviation) of the whole-brain averaged displacement/difference of the gray–CSF surface and cortical thickness in the denoised data were about four fifths of those from single-repetition images (0.13 ± 0.023 mm, 0.15 ± 0.032 mm, 0.14 ± 0.026 mm for DnCNN, BM4D and AONLM vs. 0.19 ± 0.033 mm for gray–CSF surface positioning; 0.13 ± 0.02 mm, 0.14 ± 0.027 mm, 0.14 ± 0.023 mm for DnCNN, BM4D and AONLM vs. 0.18 ± 0.027 mm for cortical thickness estimation), which were equivalent to those derived from images by averaging 1.5 to 1.9 repetitions of data (1.91, 1.63, 1.78 for DnCNN, BM4D and AONLM for gray–CSF surface; 1.85, 1.55, 1.64 for DnCNN, BM4D and AONLM for cortical thickness estimation). The improvement for the gray–white surface positioning was slightly larger than for the gray–CSF surface positioning and cortical thickness estimation.

Fig. 11. — The blue dots and error bars represent the group mean and standard deviation of the whole-brain averaged absolute displacement/difference of the gray–white surface (a), gray–cerebrospinal fluid (CSF) surface (b) and cortical thickness (c) estimated from the images from the single-repetition data and 2- to 5-repetition averaged data compared to the images from the 6-repetition averaged data across 30 image volumes from the 5 evaluation subjects. The green, red and yellow dots and error bars represent the group mean and standard deviation of the whole-brain averaged absolute displacement/difference for the images from the single-repetition data denoised by DnCNN (green), BM4D (red) and AONLM (yellow) compared to the images from the 6-repetition averaged data across 30 image volumes from the 5 evaluation subjects. The red dots and error bars for BM4D are covered by the yellow dots and error bars for AONLM for the gray–white surface displacement (a). The numbers above and below the dashed lines that link two neighboring blue dots indicate the number of image volumes for averaging that would be needed to obtain equivalent similarity metrics to those obtained from images from single-repetition data denoised by different methods. All comparisons of results from different denoising methods and numbers of repetitions for averaging are statistically significant (p<0.05), except for between the BM4D- and AONLM-denoised data, between the 2-repetition averaged data and the DnCNN-denoised data, between the 2-repetition averaged data and the BM4D-denoised data and between the 2-repetition averaged data and the AONLM-denoised data for the gray–white surface displacement (a) (denoted with abbreviation “ns”).

The whole-brain averaged absolute displacement/difference of the gray–white surface, gray–CSF surface and cortical thickness of the 1-mm isotropic resolution data were around 2 to 3 times of those from the denoised single-repetition data at 0.6 mm isotropic resolution. For the two subjects with 1-mm isotropic resolution data, the whole-brain averaged absolute displacement for gray–white surfaces were 0.209 mm, 0.128 mm, 0.142 mm, 0.140 mm, 0.228 mm for subject 1, and 0.219 mm, 0.147 mm, 0.160 mm, 0.164 mm, 0.329 for subject 2 for the raw, DnCNN, BM4D and AONLM-denoised single-repetition data at 0.6-mm isotropic resolution and 1-mm isotropic resolution data. The whole-brain averaged absolute displacement for the gray–CSF surface were 0.169 mm, 0.121 mm, 0.153 mm, 0.122 mm, 0.347 mm for subject 1, and 0.166 mm, 0.107 mm, 0.113 mm, 0.115 mm, 0.381 mm for subject 2 for the raw, DnCNN, BM4D and AONLM-denoised single-repetition data at 0.6-mm isotropic resolution and 1-mm isotropic resolution data. The whole-brain averaged absolute difference for the cortical thickness estimation were 0.151 mm, 0.111 mm, 0.136 mm, 0.118 mm, 0.347 mm for subject 1, and 0.154 mm, 0.113 mm, 0.116 mm, 0.121 mm, 0.368 mm for subject 2 for the raw, DnCNN, BM4D and AONLM-denoised single-repetition data at 0.6-mm isotropic resolution and 1-mm isotropic resolution data.

The scan-rescan precision of the cortical surface position and thickness estimation using the denoised data was quantified for the whole brain and each cortical region (Fig. 12, Supplementary Figure 7, Supplementary Table 4). The reproducibility was in general lower near the temporal pole and orbitofrontal cortex presumably because of the elevated image distortions in these regions. The reproducibility was lower near the central sulcus, calcarine sulcus, Heschl’s gyrus and insula for the gray–white surfaces (Fig. 12, rows a–c), near the insula for the gray–CSF surfaces (Fig. 12, rows d–f) and cortical thickness estimation (Fig. 12, rows g–i), regions where accurate surface reconstruction is challenging.

Fig. 12. — The absolute average of the left-hemispheric vertex-wise displacement/difference of the gray–white surfaces (rows a–c), gray–cerebrospinal fluid (CSF) surfaces (rows d–f) and cortical thickness estimates (rows g–i) from two consecutively acquired single-repetition data denoised by DnCNN (rows a, d, g), BM4D (rows b, e, h) and AONLM (rows c, f, i) across 25 image volumes from the 5 evaluation subjects, displayed on inflated surface representations. Different cortical regions from the FreeSurfer cortical parcellation (i.e., *aparc.annot*) are depicted as colored outlines.

The cortical surface positioning and thickness estimation derived from DnCNN-denoised results were slightly more reproducible than those from BM4D and AONLM. The group mean and standard deviation of the whole-brain averaged absolute displacement/difference between the surface reconstruction results derived from two consecutively acquired single-repetition data denoised by DnCNN, BM4D and AONLM were 0.16 ± 0.034 mm, 0.17 ± 0.034 mm, 0.17 ± 0.035 mm for the gray–white surface, 0.16 ± 0.043 mm, 0.17 ± 0.045 mm, 0.17 ± 0.043 mm for the gray–CSF surface, and 0.15 ± 0.032 mm, 0.16 ± 0.034 mm, 0.16 ± 0.034 mm for the cortical thickness.

4. Discussion

In this study, we demonstrate improved in vivo human cerebral cortical surface reconstruction at sub-millimeter isotropic resolution using denoised T₁-weighted images. We show that three well-known classical denoising methods, including DnCNN, BM4D and AONLM, effectively remove the noise in the empirical T₁-weighted data acquired at 0.6 mm isotropic resolution (~10 min scan) and generate high-SNR T₁-weighted images with 2% to 9% loss of gray–white image intensity contrast. The superior quality of the denoised images is reflected by a low whole-brain averaged MAD of ~0.016, high whole-brain averaged PSNR of ~33.5 dB and SSIM of ~0.92, which is equivalent to those of T₁-weighted images obtained by averaging ~2.5 repetitions of the data, saving ~15 min scan time. Due to the significantly reduced noise, the reconstructed cortical surfaces are smoother than those from the single-repetition data, with similar positioning compared to those from the 6-repetition averaged data. The whole-brain mean absolute difference in the gray–white surface placement, gray–CSF surface placement and cortical thickness estimation is lower than 160 μm, which is equivalent to those of T₁-weighted images obtained by averaging ~1.55 to ~2.24 repetitions of the data, saving ~5 to ~12 min scan time, and on the same order as the test-retest precision of the FreeSurfer reconstruction (0.1 mm to 0.2 mm) (Chang et al., 2018, Fujimoto et al., 2014, Han et al., 2006).

Our study systematically characterized the effects of denoising on cortical surface reconstruction using empirical data. Three well-known classical denoising methods were evaluated in our study using this characterization framework, similar to what we have applied previously to characterize anatomical image quality in terms of cortical reconstruction precision and accuracy (Chang et al., 2018, Fujimoto et al., 2014, Q Tian et al., 2021, Zaretskaya et al., 2018), which can be applied to evaluate other image-based and k-space-based denoising methods and more sophisticated denoising CNNs. We systematically quantified and compared not only the image similarity compared to the ground truth as in most denoising studies, but also the gray–white tissue contrast across the gray–white interface that is critical for accurate gray–white surface reconstruction, surface smoothness and surface placement accuracy from the denoised data. It is noteworthy that matching the local mean image intensity of 6-repetition averaged data to the single-repetition data and the use of the FreeSurfer longitudinal pipeline in our evaluation might underestimate the positioning displacement between cortical surfaces from different data and those from the 6-repetition averaged data.

Because our ground-truth data were obtained by data averaging (6 repetitions, ~1 hour scan), we were able to evaluate the image and surface metrics from the denoised data relatively to those from 2- to 5-repetition averaged data and determine the efficiency factor, i.e., the number of image volumes for averaging that would be needed to obtain equivalent image and surface metric values compared to those obtained from denoised single-repetition images. This unique metric concisely and intuitively summarizes the denoising performance of different methods compared to data averaging, the most common practice to increase the SNR. Our results show that the denoised single-repetition data are equivalent to ~2.5-repetition averaged data in terms of image similarity quantified by MAD, PSNR and SSIM (Fig. 3), while being equivalent to 1.55 to 2.24-repetition averaged data in terms of cortical surface positioning and thickness estimation accuracy (Fig. 11). The discrepancy between the efficiency factors calculated using image and surface metrics suggests that the commonly used image similarity metrics alone cannot faithfully reflect the cortical surface reconstruction quality and the objective functions used during the denoising process, e.g., the mean squared error, can be further optimized for cortical surface reconstruction applications.

Both the spatial resolution and SNR of T₁-weighted MR images are essential for generating accurate cortical surfaces. The cortical surfaces generated from commonly used T₁-weighted images with 1-mm isotropic resolution are less noisy and smooth, but the positioning of surfaces is biased (Zaretskaya et al., 2018, Glasser et al., 2013, MF Glasser et al., 2016, Q Tian et al., 2021) (Fig. 9, e.g., gray–white surface is placed more exterior). The cortical surfaces generated from single-repetition T₁-weighted data with sub-millimeter isotropic resolution, e.g., 0.6-mm isotropic in our study, do not have biases in the positioning but are noisy and unsmooth. The choice of spatial resolution and the consequent SNR need to be determined based on available hardware systems. T₁-weighted MR images with 0.8-mm isotropic resolution, which is half of the minimum thickness of the cortex, or higher resolution are recommended by the HCP WU-Minn-Ox Consortium for generating accurate geometrical models of the human cortex (MF Glasser et al., 2016). If only a single repetition of T₁-weighted data at 0.8-mm isotropic or higher resolution is available due to limited acquisition time, denoising methods are expected to further improve the SNR of T₁-weighted images for accurately delineating the cortical surfaces, especially for low-field MR systems and phased-array radio frequency receive coil head arrays with a small number of channels. The resultant cortical surfaces from denoised images are shown to be similar to those from 2-repetition averaged data (Fig. 11), and are more similar to those from 6-repetition averaged data than those from 1-mm isotropic data with one third to half of the positioning displacement (Supplementary Fig. 6). Even for ultra-high-field MRI systems, denoising methods could be employed to improve image SNR in the temporal lobes where signals substantially drop.

In addition to improving cortical surface reconstruction at sub-millimeter resolution, denoising methods can be also useful for improving cortical surface reconstruction at standard 1-mm isotropic resolution. The ~5 min scan time of a standard 1-mm isotropic resolution acquisition (assuming a parallel imaging acceleration factor of two) is still considered long for elderly subjects, children and some patient populations prone to motion and/or discomfort. In order to save scan time, T₁-weighted images at resolutions lower than 1-mm isotropic (e.g., 3 to 5-mm thick axial slices in a 2-dimensional acquisition, ~1.5 mm resolution along the phase-encoding direction in a 3-dimensional acquisition) are also routinely acquired in clinical practice and large-scale neuroimaging studies such as the Parkinson Progression Marker Initiative (Marek et al., 2011), which preclude accurate cortical surface reconstruction and quantitative analysis of cortical morphology at 1-mm isotropic resolution. In these applications, higher parallel imaging factors (e.g., 3 or 4) can be adopted for further shortening the 1-mm isotropic acquisition duration, coupled with denoising methods for accurate cortical surface reconstruction from the noisier images. More advanced fast imaging technologies such as Wave-CAIPI (Bilgic et al., 2015) can achieve even higher acceleration factors (e.g., 9) with minimal noise and artifact penalties and have been shown to reduce the scan time of a 1-mm isotropic acquisition to 1.15 min with estimated regional brain tissue volumes comparable to those from a standard 5.2 min scan (Longo et al., 2020). Denoising methods are expected to further improve the image quality of highly accelerated 1-mm isotropic data, acquired even within a minute, for accurately delineating the cortical surface (Chang et al., 2018).

The pros and cons of different denoising methods need to be weighed for different applications. The three denoising methods evaluated here, DnCNN, BM4D and AONLM, are three well-known classical denoising methods with widely accepted superior denoising performance and are often used as references against which newly developed denoising methods are compared. Our results show that CNN-based denoising method DnCNN generates denoised images and consequently reconstructed cortical surfaces that are slightly more similar to the ground truth than BM4D and AONLM, which is achieved by effectively exploiting the data redundancy in local and non-local spatial locations as well as across numerous subjects. However, the data-driven nature of DnCNN requires additional training data (e.g., data from 4 subjects in our study) for optimizing parameters or fine-tuning the parameters of an existing DnCNN pre-trained on other datasets for improved generalization across hardware systems, pulse sequences and sequence parameters. It has been shown that results obtained by directly applying CNNs pre-trained on a different dataset are reasonably accurate but are slightly worse compared to those obtained from fine-tuned CNNs (Knoll et al., 2019, Q Tian et al., 2021, Y Hu et al., 2020). On the other hand, BM4D and AONLM only require a single input noisy image volume, which are more convenient in practice and especially useful when the training data for DnCNN are not available (e.g., denoising legacy data). In terms of computational efficiency, DnCNN, once trained, can be executed in milliseconds or seconds, much faster than BM4D and AONLM with run times that last anywhere from minutes to an hour depending on the computing platform. The extremely fast DnCNN could facilitate review of denoised images in near real-time on the host computer of the MRI console. Finally, previous research has demonstrated the advantage of incorporating information from a high-quality T₁-weighted image volume at 1 mm isotropic resolution for further boosting the denoising performance of sub-millimeter resolution T₁-weighted data (Konukoglu et al., 2013). It is also possible for DnCNN to leverage lower-resolution T₁-weighted data for improved denoising performance, simply by including the co-registered lower-resolution images interpolated to the target sub-millimeter resolution (e.g., using trilinear interpolation) as the second channel of the input. DnCNN can even incorporate high-quality lower-resolution MR images with different contrasts which are available, such as commonly acquired T₂-weighted images, T₂-weighted fluid-attenuated inversion recovery (FLAIR) images, or b = 0 images from diffusion MRI data. Multi-contrast based denoising has been proven effective for further improving the denoising performance (Chen et al., 2018, Q Tian et al., 2020).

The specific DnCNN network we chose for our study is a pioneering, classic CNN for noise removal, which is characterized by its simplest (i.e., cascaded convolutional filters and nonlinear activation functions) yet very deep (20 layers) network topology. The “plain” network architecture achieves superior performance not only in noise removal (Zhang et al., 2017), but also vision tasks such as object recognition (Simonyan and Zisserman, 2014) and super-resolution (Kim et al., 2016, Timofte et al., 2017). DnCNN has been demonstrated to outperform the state-of-the-art BM3D denoising for 2-dimension natural images, which is reproduced on empirical 3-dimenstion MRI data in our study in terms of both image quality and cortical surface positioning. The DnCNN network parameters adopted in our study (i.e., 20 layers with 64 features at each layer) were used in the original paper that proposed DnCNN and have been shown to be effective in a similar network architecture for image super-resolution (Chaudhari et al., 2018, Kim et al., 2016, Q Tian et al., 2021), and fully utilized the available memory of our GPU. More generally, network parameters of DnCNN could be adapted accordingly to GPUs with different memory sizes and further adjusted by performing a series of ablation studies on the DnCNN network following previous studies (Kim et al., 2016, Pham et al., 2019). The versatile DnCNN can be also used to perform simultaneous denoising and super-resolution (referred to as VDSR in the context of super-resolution (Kim et al., 2016)). This versatility is beneficial for obtaining high-quality images at a true, high sub-millimeter resolution using only product sequences and reconstruction provided by vendors, which can only encode a whole-brain volume at a high resolution nominally because of the use of partial Fourier imaging and the increased T₁ blurring during the inversion recovery. Simultaneous denoising and super-resolution is also helpful for obtaining images at ultra-high resolution (e.g., 0.25-mm isotropic resolution (Lüsebrink et al., 2017), which requires averaging 8 repetitions from 10 hour scan on a 7-Tesla scanner) by making a balance between extremely challenging individual denoising or super-resolution and avoiding the use of prospective motion correction to acquire input noisy images at native ultra-high resolution for denoising (Gallichan et al., 2016, Godenschweger et al., 2016, Maclaren et al., 2013, MD Tisdall et al., 2013, Watanabe et al., 2016). Image super-resolution has also been shown to be an alternative way to obtain high-quality sub-millimeter resolution images for improving cortical surface reconstruction (Q Tian et al., 2021).

It is worth noting that even though we demonstrate the advantages of denoising in improving cortical surface positioning and thickness estimation, it is still unclear whether and how surfaces from denoised images would benefit specific applications that utilize them, such as depth specific analysis of functional (Polimeni et al., 2010) and diffusion (McNab et al., 2013) MRI signals and comparison of cortical thickness between the study and control group. The effects of denoising on these scientific applications require further investigation. Further, the three classic denoising methods evaluated in our works are not necessarily the optimal denoising methods for improving cortical surface reconstruction. For example, while we only used a simple plain network DnCNN, cortical surface reconstruction might potentially benefit from denoising method based on more sophisticated CNNs, such as generative adversarial networks (Goodfellow et al., 2014). Denoising algorithms might be also optimized specifically to benefit cortical surface reconstruction in order to boost their performance.

Conclusion

Our unique dataset and systematic characterization of different denoising methods support the use of denoising methods for improving cortical surface reconstruction at sub-millimeter resolution from single-repetition anatomical MR images. The denoised images from three classical denoising methods, namely DnCNN, BM4D and AONLM, are shown to be similar to 6-repetition averaged images, with high image similarity quantified by MAD, PSNR and SSIM that are equivalent to those of T₁-weighted images obtained by averaging ~2.5 repetitions of the data. The discrepancies in the gray–white surface placement, gray–CSF surface placement and cortical thickness estimation are lower than 165 μm, equivalent to those of T₁-weighted images obtained by averaging 1.55 to 2.24 repetitions of the data and on the same order as the scan-rescan precision of FreeSurfer. The scan-rescan variability of the cortical surface positioning and thickness estimation from the denoised single-repetition data is lower than 170 μm. The proposed approach would facilitate the adoption of next-generation cortical surface reconstruction methods in a wider range of applications and neuroimaging studies that require accurate models of cortical anatomy.

Supplementary Material

NIHMS1716891-supplement-1.pdf^{(13.5MB, pdf)}

Acknowledgments

Thanks to Mr. Ned Ohringer for assistance in volunteer recruitment and data collection. We gratefully acknowledge the use of the Siemens “Works-In-Progress” package WIP900, which provided the inner-loop accelerated MPRAGE pulse sequence and image reconstruction. This work was supported by the National Institutes of Health (Grant Nos. P41-EB015896, P41-EB030006, R01-EB023281, K23-NS096056, R01-MH111419, R01-MH124004, U01-EB026996, S10-RR023401, S10-RR019307 and S10-RR023043), a Massachusetts General Hospital Claflin Distinguished Scholar Award, and the Athinoula A. Martinos Center for Biomedical Imaging. B.B. has provided consulting services to Subtle Medical.

Footnotes

Supplementary materials

Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.neuroimage.2021.117946.

Data and code availability

The source code of the DnCNN network implemented using Keras API and the pre-trained models using the MGH 0.6-mm isotropic data are available at https://github.com/qiyuantian/DnSurfer.

References

Fischl B, 2012. FreeSurfer. Neuroimage 62 (2), 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fischl B, Sereno MI, Dale AM, 1999. Cortical surface-based analysis: II: inflation, flattening, and a surface-based coordinate system. Neuroimage 9 (2), 195–207. [DOI] [PubMed] [Google Scholar]
Dale AM, Fischl B, Sereno MI, 1999. Cortical surface-based analysis: I. Segmentation and surface reconstruction. Neuroimage 9 (2), 179–194. [DOI] [PubMed] [Google Scholar]
Kim JS, Singh V, Lee JK, et al. , 2005. Automated 3-D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. Neuroimage 27 (1), 210–221. [DOI] [PubMed] [Google Scholar]
Bazin P−L, Weiss M, Dinse J, Schäfer A, Trampel R, Turner R, 2014. A computational framework for ultra-high resolution cortical segmentation at 7Tesla. Neuroimage 93, 201–209. [DOI] [PubMed] [Google Scholar]
Huntenburg JM, Steele CJ, Bazin P−L, 2018. Nighres: processing tools for high-resolution neuroimaging. Gigascience 7 (7). [DOI] [PMC free article] [PubMed] [Google Scholar]
Ashburner J, Friston KJ, 2005. Unified segmentation. Neuroimage 26 (3), 839–851. [DOI] [PubMed] [Google Scholar]
Bazin P−L, Pham DL, 2008. Homeomorphic brain image segmentation with topological and statistical atlases. Med. Image Anal. 12 (5), 616–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
Han X, Pham DL, Tosun D, Rettmann ME, Xu C, Prince JL, 2004. CRUISE: cortical reconstruction using implicit surface evolution. Neuroimage 23 (3), 997–1012. [DOI] [PubMed] [Google Scholar]
Fischl B, Dale AM, 2000. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc. Natl. Acad. Sci. 97 (20), 11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
Winkler AM, Sabuncu MR, Yeo BT, et al. , 2012. Measuring and comparing brain cortical surface area and other areal quantities. Neuroimage 61 (4), 1428–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
Winkler AM, Greve DN, Bjuland KJ, et al. , 2017. Joint analysis of cortical area and thickness as a replacement for the analysis of the volume of the cerebral cortex. Cereb. Cortex 28 (2), 738–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schaer M, Cuadra MB, Tamarit L, Lazeyras F, Eliez S, Thiran J−P, 2008. A surface-based approach to quantify local cortical gyrification. IEEE Trans. Med. Imaging 27 (2), 161–170. [DOI] [PubMed] [Google Scholar]
Du A−T, Schuff N, Kramer JH, et al. , 2007. Different regional patterns of cortical thinning in Alzheimer’s disease and frontotemporal dementia. Brain 130 (4), 1159–1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lerch JP, Pruessner JC, Zijdenbos A, Hampel H, Teipel SJ, Evans AC, 2004. Focal decline of cortical thickness in Alzheimer’s disease identified by computational neuroanatomy. Cereb. Cortex 15 (7), 995–1001. [DOI] [PubMed] [Google Scholar]
Sailer M, Fischl B, Salat D, et al. , 2003. Focal thinning of the cerebral cortex in multiple sclerosis. Brain 126 (8), 1734–1744. [DOI] [PubMed] [Google Scholar]
Kuperberg GR, Broome MR, McGuire PK, et al. , 2003. Regionally localized thinning of the cerebral cortex in schizophrenia. Arch. Gen. Psychiatry 60 (9), 878–888. [DOI] [PubMed] [Google Scholar]
Ly M, Motzkin JC, Philippi CL, et al. , 2012. Cortical thinning in psychopathy. Am. J. Psychiatry 169 (7), 743–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wallace GL, Dankner N, Kenworthy L, Giedd JN, Martin A, 2010. Age-related temporal and parietal cortical thinning in autism spectrum disorders. Brain 133 (12), 3745–3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schmaal L, Hibar D, Sämann P, et al. , 2017. Cortical abnormalities in adults and adolescents with major depression based on brain scans from 20 cohorts worldwide in the ENIGMA major depressive disorder working group. Mol. Psychiatry 22 (6), 900. [DOI] [PMC free article] [PubMed] [Google Scholar]
Anderson BJ, Eckburg PB, Relucio KI, 2002. Alterations in the thickness of motor cortical subregions after motor-skill learning and exercise. Learn. Mem. 9 (1), 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bermudez P, Lerch JP, Evans AC, Zatorre RJ, 2008. Neuroanatomical correlates of musicianship as revealed by cortical thickness and voxel-based morphometry. Cereb. Cortex 19 (7), 1583–1596. [DOI] [PubMed] [Google Scholar]
Engvig A, Fjell AM, Westlye LT, et al. , 2010. Effects of memory training on cortical thickness in the elderly. Neuroimage 52 (4), 1667–1676. [DOI] [PubMed] [Google Scholar]
Lazar SW, Kerr CE, Wasserman RH, et al. , 2005. Meditation experience is associated with increased cortical thickness. Neuroreport 16 (17), 1893. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fischl B, Van Der Kouwe A, Destrieux C, et al. , 2004. Automatically parcellating the human cerebral cortex. Cereb. Cortex 14 (1), 11–22. [DOI] [PubMed] [Google Scholar]
Glasser MF, Coalson TS, Robinson EC, et al. , 2016a. A multi-modal parcellation of human cerebral cortex. Nature 536 (7615), 171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
Van Essen DC, Glasser MF, Dierker DL, Harwell J, Coalson T, 2011. Parcellations and hemispheric asymmetries of human cerebral cortex analyzed on surface-based atlases. Cereb. Cortex 22 (10), 2241–2262. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cohen-Adad J, Benner T, Greve D, et al. , 2011. In vivo evidence of disseminated subpial T2* signal changes in multiple sclerosis at 7 T: a surface-based analysis. Neuroimage 57 (1), 55–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fracasso A, van Veluw SJ, Visser F, et al. , 2016. Lines of baillarger in vivo and ex vivo: myelin contrast across lamina at 7T MRI and histology. Neuroimage 133, 163–175. [DOI] [PubMed] [Google Scholar]
Marques JP, Khabipova D, Gruetter R, 2017. Studying cyto and myeloarchitecture of the human cortex at ultra-high field with quantitative imaging: R 1, R2* and susceptibility. Neuroimage 147, 152–163. [DOI] [PubMed] [Google Scholar]
Trampel R, Ott DV, Turner R, 2011. Do the congenitally blind have a stria of Gennari? First intracortical insights in vivo. Cereb. Cortex 21 (9), 2075–2081. [DOI] [PubMed] [Google Scholar]
Glasser MF, Van Essen DC, 2011. Mapping human cortical areas in vivo based on myelin content as revealed by T1-and T2-weighted MRI. J. Neurosci. 31 (32), 11597–11616. [DOI] [PMC free article] [PubMed] [Google Scholar]
McNab JA, Polimeni JR, Wang R, et al. , 2013. Surface based analysis of diffusion orientation for identifying architectonic domains in the in vivo human cortex. Neuroimage 69, 87–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kleinnijenhuis M, van Mourik T, Norris DG, Ruiter DJ, van Walsum A-MvC, Barth M, 2015. Diffusion tensor characteristics of gyrencephaly using high resolution diffusion MRI in vivo at 7T. Neuroimage 109, 378–387. [DOI] [PubMed] [Google Scholar]
Fukutomi H, Glasser MF, Zhang H, et al. , 2018. Neurite imaging reveals microstructural variations in human cerebral cortical gray matter. Neuroimage 182, 488–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
Calamante F, Jeurissen B, Smith RE, Tournier JD, Connelly A, 2018. The role of whole-brain diffusion MRI as a tool for studying human in vivo cortical segregation based on a measure of neurite density. Magn. Reson. Med. 79 (5), 2738–2744. [DOI] [PubMed] [Google Scholar]
Polimeni JR, Fischl B, Greve DN, Wald LL, 2010. Laminar analysis of 7T BOLD using an imposed spatial activation pattern in human V1. Neuroimage 52 (4), 1334–1346. [DOI] [PMC free article] [PubMed] [Google Scholar]
Huber L, Goense J, Kennerley AJ, et al. , 2015. Cortical lamina-dependent blood volume changes in human brain at 7 T. Neuroimage 107, 23–33. [DOI] [PubMed] [Google Scholar]
Kok P, Bains LJ, van Mourik T, Norris DG, de Lange FP, 2016. Selective activation of the deep layers of the human primary visual cortex by top-down feedback. Curr. Biol. 26 (3), 371–376. [DOI] [PubMed] [Google Scholar]
Maass A, Schütze H, Speck O, et al. , 2014. Laminar activity in the hippocampus and entorhinal cortex related to novelty and episodic encoding. Nat. Commun. 5, 5547. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nasr S, Polimeni JR, Tootell RB, 2016. Interdigitated color-and disparity-selective columns within human visual cortical areas V2 and V3. J. Neurosci. 36 (6), 1841–1857. [DOI] [PMC free article] [PubMed] [Google Scholar]
Olman CA, Harel N, Feinberg DA, et al. , 2012. Layer-specific fMRI reflects different neuronal computations at different depths in human V1. PLoS ONE 7 (3), e32536. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zaretskaya N, Fischl B, Reuter M, Renvall V, Polimeni JR, 2018. Advantages of cortical surface reconstruction using submillimeter 7 T MEMPRAGE. Neuroimage 165, 11–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
Glasser MF, Sotiropoulos SN, Wilson JA, et al. , 2013. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lüsebrink F, Wollrab A, Speck O, 2013. Cortical thickness determination of the human brain using high resolution 3 T and 7 T MRI data. Neuroimage 70, 122–131. [DOI] [PubMed] [Google Scholar]
Glasser MF, Smith SM, Marcus DS, et al. , 2016b. The human connectome project’s neuroimaging approach. Nat. Neurosci. 19 (9), 1175–1187. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tian Q, Bilgic B, Fan Q, Ngamsombat C, Zaretskaya N, Fultz NE, …, Huang SY, et al. , 2021. Improving in vivo human cerebral cortical surface reconstruction using data-driven super-resolution. Cereb. Cortex 31 (1), 463–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bookheimer SY, Salat DH, Terpstra M, et al. , 2019. The lifespan human connectome project in aging: an overview. Neuroimage 185, 335–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
Somerville LH, Bookheimer SY, Buckner RL, et al. , 2018. The lifespan human connectome project in development: a large-scale study of brain connectivity development in 5–21 year olds. Neuroimage 183, 456–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
Harms MP, Somerville LH, Ances BM, et al. , 2018. Extending the human connectome project across ages: imaging protocols for the lifespan development and aging projects. Neuroimage 183, 972–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
Goebel R, 2012. BrainVoyager—past, present, future. Neuroimage 62 (2), 748–756. [DOI] [PubMed] [Google Scholar]
Lustig M, Donoho D, Pauly JM, 2007. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58 (6), 1182–1195. [DOI] [PubMed] [Google Scholar]
Bilgic B, Gagoski BA, Cauley SF, et al. , 2015. Wave-CAIPI for highly accelerated 3D imaging. Magn. Reson. Med. 73 (6), 2152–2162. [DOI] [PMC free article] [PubMed] [Google Scholar]
Keil B, Blau JN, Biber S, et al. , 2013. A 64-channel 3T array coil for accelerated brain MRI. Magn. Reson. Med. 70 (1), 248–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
Block KT, Uecker M, Frahm J, 2007. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med. 57 (6), 1086–1098. [DOI] [PubMed] [Google Scholar]
Liang D, Liu B, Wang J, Ying L, 2009. Accelerating SENSE using compressed sensing. Magn. Reson. Med. 62 (6), 1574–1584. [DOI] [PubMed] [Google Scholar]
Murphy M, Alley M, Demmel J, Keutzer K, Vasanawala S, Lustig M, 2012. Fast ℓ₁-SPIRiT compressed sensing parallel imaging MRI: scalable parallel implementation and clinically feasible runtime. IEEE Trans. Med. Imaging 31 (6), 1250–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]
Otazo R, Kim D, Axel L, Sodickson DK, 2010. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn. Reson. Med. 64 (3), 767–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hu Y, Levine EG, Tian Q, et al. , 2019. Motion-robust reconstruction of multishot diffusion-weighted images without phase estimation through locally low-rank regularization. Magn. Reson. Med. 81 (2), 1181–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hu Y, Wang X, Tian Q, et al. , 2020a. Multi-shot diffusion-weighted MRI reconstruction with magnitude-based spatial-angular locally low-rank regularization (SPA-LLR). Magn. Reson. Med. 83 (5), 1596–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kim TH, Bilgic B, Polak D, Setsompop K, Haldar JP, 2019. Wave-LORAKS: combining wave encoding with structured low-rank matrix modeling for more highly accelerated 3D imaging. Magn. Reson. Med. 81 (3), 1620–1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
Haldar JP, 2013. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans. Med. Imaging 33 (3), 668–681. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shin PJ, Larson PE, Ohliger MA, et al. , 2014. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn. Reson. Med. 72 (4), 959–970. [DOI] [PMC free article] [PubMed] [Google Scholar]
Haldar JP, Zhuo J, 2016. P-LORAKS: low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn. Reson. Med. 75 (4), 1499–1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rudin LI, Osher S, Fatemi E, 1992. Nonlinear total variation based noise removal algorithms. Phys. D: Nonlin. Phenomena 60 (1–4), 259–268. [Google Scholar]
Perona P, Malik J, 1990. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 12 (7), 629–639. [Google Scholar]
Fischl B, Schwartz EL, 1997. Learning an integral equation approximation to nonlinear anisotropic diffusion in image processing. IEEE Trans. Pattern Anal. Mach. Intell. 19 (4), 342–352. [Google Scholar]
Tomasi C, Manduchi R, 1998. Bilateral filtering for gray and color images. In: The International Conference on Computer Vision, pp. 839–846. [Google Scholar]
Buades A, Coll B, Morel J−M, 2005. A review of image denoising algorithms, with a new one. Multisc. Model. Simul. 4 (2), 490–530. [Google Scholar]
Dabov K, Foi A, Katkovnik V, Egiazarian K, 2007. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 16 (8), 2080–2095. [DOI] [PubMed] [Google Scholar]
Aharon M, Elad M, Bruckstein AK-SVD, 2006. An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 54 (11), 4311–4322. [Google Scholar]
Gerig G, Kubler O, Kikinis R, Jolesz FA, 1992. Nonlinear anisotropic filtering of MRI data. IEEE Trans. Med. Imaging 11 (2), 221–232. [DOI] [PubMed] [Google Scholar]
Coupé P, Yger P, Prima S, Hellier P, Kervrann C, Barillot C, 2008. An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images. IEEE Trans. Med. Imaging 27 (4), 425–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
Manjón JV, Coupé P, Martí-Bonmatí L, Collins DL, Robles M, 2010. Adaptive non-local means denoising of MR images with spatially varying noise levels. J. Magn. Reson. Imaging 31 (1), 192–203. [DOI] [PubMed] [Google Scholar]
Maggioni M, Katkovnik V, Egiazarian K, Foi A, 2012. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 22 (1), 119–133. [DOI] [PubMed] [Google Scholar]
Bazin P−L, Alkemade A, Van Der Zwaag W, Caan M, Mulder M, Forstmann BU, 2019. Denoising High-field Multi-dimensional MRI with Local Complex PCA. Front Neurosci 13, 1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
Konukoglu E, van der Kouwe A, Sabuncu MR, Fischl B, 2013. Example-based restoration of high-resolution magnetic resonance image acquisitions Int. Conf. Med. Image Comput. Comput.-Assist. Intervent., 131–138. [DOI] [PubMed] [Google Scholar]
Zhang K, Zuo W, Chen Y, Meng D, Zhang L, 2017. Beyond a Gaussian denoiser: residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 26 (7), 3142–3155. [DOI] [PubMed] [Google Scholar]
Tian Q, Bilgic B, Fan Q, et al. , 2020. DeepDTI: high-fidelity six-direction diffusion tensor imaging using deep learning. Neuroimage 219, 117017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen KT, Gong E, de Carvalho Macruz FB, et al. , 2018. Ultra–low-dose 18F-Florbetaben amyloid PET imaging using deep learning with multi-contrast MRI inputs. Radiology 290 (3), 649–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lehtinen J, Munkberg J, Hasselgren J, et al. , 2018. Noise2Noise: learning image restoration without clean data. In: The International Conference on Machine Learning, pp. 2965–2974. [Google Scholar]
Krull A, Buchholz T−O, Jug F, 2019. Noise2void-learning denoising from single noisy images. In: The IEEE Conference on Computer Vision and Pattern Recognition, pp. 2129–2137. [Google Scholar]
Weigert M, Schmidt U, Boothe T, et al. , 2018. Content-aware image restoration: pushing the limits of fluorescence microscopy. Nat. Methods 15 (12), 1090–1097. [DOI] [PubMed] [Google Scholar]
Devalla SK, Subramanian G, Pham TH, et al. , 2019. A deep learning approach to denoise optical coherence tomography images of the optic nerve head. Sci. Rep. 9 (1), 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gondara L, 2016. Medical image denoising using convolutional denoising autoencoders. In: The IEEE International Conference on Data Mining Workshops (ICDMW), pp. 241–246. [Google Scholar]
Chang Y, Yan L, Chen M, Fang H, Zhong S, 2019. Two-stage convolutional neural network for medical noise removal via image decomposition. IEEE Trans. Instrum. Meas. 69 (6), 2707–2721. [Google Scholar]
Ouyang J, Chen KT, Gong E, Pauly J, Zaharchuk G, 2019. Ultra-low-dose PET reconstruction using generative adversarial network with feature matching and task-specific perceptual loss. Med. Phys. 46 (8), 3555–3564. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang Y, Yu B, Wang L, et al. , 2018. 3D conditional generative adversarial networks for high-quality PET image estimation at low dose. Neuroimage 174, 550–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
Serrano-Sosa M, Spuhler K, DeLorenzo C, Huang C, 2020. PET image denoising using structural MRI with a novel dilated convolutional neural network. J. Nucl. Med. 61, 434–434. [Google Scholar]
Xu J, Gong E, Ouyang J, Pauly J, Zaharchuk G, Han S, 2020. Ultra-low-dose 18F-FDG brain PET/MR denoising using deep learning and multi-contrast information. SPIE Med. Imaging Conf.11313, 113131P. [Google Scholar]
Gong E, Pauly JM, Wintermark M, Zaharchuk G, 2018. Deep learning enables reduced gadolinium dose for contrast-enhanced brain MRI. J. Magn. Reson. Imaging 48 (2), 330–340. [DOI] [PubMed] [Google Scholar]
Benou A, Veksler R, Friedman A, Raviv TR, 2017. Ensemble of expert deep neural networks for spatio-temporal denoising of contrast-enhanced MRI sequences. Med. Image Anal. 42, 145–159. [DOI] [PubMed] [Google Scholar]
Jiang D, Dou W, Vosters L, Xu X, Sun Y, Tan T, 2018. Denoising of 3D magnetic resonance images with multi-channel residual learning of convolutional neural network. Jpn. J. Radiol. 36 (9), 566–574. [DOI] [PubMed] [Google Scholar]
Pierrick C, 2019. MRI Denoising Using Deep Learning and Non-Local averaging arXiv preprintarXiv:1911.04798.. [Google Scholar]
Gong E, Guo J, Liu J, Fan A, Pauly J, Zaharchuk G, 2020. Deep learning and multi-contrast-based denoising for low-SNR Arterial Spin Labeling (ASL) MRI. Proc. SPIE 11313, Medical Imaging 11313 Image Processing, 113130M. [Google Scholar]
Kidoh M, Shinoda K, Kitajima M, et al. , 2019. Deep learning based noise reduction for brain MR imaging: tests on phantoms and healthy volunteers. Magn. Reson. Med. Sci. 19 (3), 195. [DOI] [PMC free article] [PubMed] [Google Scholar]
van der Kouwe AJ, Benner T, Salat DH, Fischl B, 2008. Brain morphometry with multiecho MPRAGE. Neuroimage 40 (2), 559–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hurley AC, Al-Radaideh A, Bai L, et al. , 2010. Tailored RF pulse for magnetization inversion at ultrahigh field. Magn. Reson. Med. 63 (1), 51–58. [DOI] [PubMed] [Google Scholar]
Polak D, Setsompop K, Cauley SF, et al. , 2018. Wave-CAIPI for highly accelerated MP-RAGE imaging. Magn. Reson. Med. 79 (1), 401–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
van der Kouwe AJ, Tisdall MD, Bhat H, Fischl B, Polimeni JR, 2014. Multiple echo and inversion time MPRAGE with Inner Loop GRAPPA acceleration and prospective motion correction for minimally distorted multispectral brain morphometry. Annual Meet. Int. Soc. Magn. Reson. Med. (ISMRM)22, 120. [Google Scholar]
Tisdall MD, Polimeni JR, Augustinack JC, van der Kouwe AJW, 2013a. 350 μm isotropic, high-contrast, low-blur, low-distortion MPRAGE morphometry acquisition at 3T. Annual Meet. Org. Human Brain Mapp. (OHBM) 3371. [Google Scholar]
Reuter M, Rosas HD, Fischl B, 2010. Highly accurate inverse consistent registration: a robust approach. Neuroimage 53 (4), 1181–1196. [DOI] [PMC free article] [PubMed] [Google Scholar]
Uwano I, Kudo K, Yamashita F, et al. , 2014. Intensity inhomogeneity correction for magnetic resonance imaging of human brain at 7T. Med. Phys. 41 (2). [DOI] [PubMed] [Google Scholar]
Modat M, Ridgway GR, Taylor ZA, et al. , 2010. Fast free-form deformation using graphics processing units. Comput. Methods Programs Biomed. 98 (3), 278–284. [DOI] [PubMed] [Google Scholar]
Modat M, Cash DM, Daga P, Winston GP, Duncan JS, Ourselin S, 2014. Global image registration using a symmetric block-matching approach. J. Med. Imaging 1 (2), 024003–024003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Smith SM, Jenkinson M, Woolrich MW, et al. , 2004. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 23, S208–S219. [DOI] [PubMed] [Google Scholar]
Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM., 2012. FSL. Neuroimage 62 (2), 782–790. [DOI] [PubMed] [Google Scholar]
Andersson JL, Sotiropoulos SN, 2016. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
He K, Zhang X, Ren S, Sun J, 2016. Deep residual learning for image recognition. In: The IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778. [Google Scholar]
Kim J, Kwon Lee J, Mu Lee K, 2016. Accurate image super-resolution using very deep convolutional networks. In: The IEEE Conference on Computer Vision and Pattern Recognition, pp. 1646–1654. [Google Scholar]
He K, Zhang X, Ren S, Sun J, 2015. Delving deep into rectifiers: surpassing human-level performance on imagenet classification. In: The IEEE International Conference on Computer Vision, pp. 1026–1034. [Google Scholar]
LeCun Y, Bottou L, Bengio Y, Haffner P, 1998. Gradient-based learning applied to document recognition. Proc. IEEE 86 (11), 2278–2324. [Google Scholar]
Kingma DP, Adam Ba J., 2014. A Method for Stochastic Optimization arXiv preprintarXiv:1412.6980. [Google Scholar]
Wang Z, Bovik AC, Sheikh HR, Simoncelli EP, 2004. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13 (4), 600–612. [DOI] [PubMed] [Google Scholar]
Ségonne F, Pacheco J, Fischl B, 2007. Geometrically accurate topology-correction of cortical surfaces using nonseparating loops. IEEE Trans. Med. Imaging 26 (4), 518–529. [DOI] [PubMed] [Google Scholar]
Reuter M, Schmansky NJ, Rosas HD, Fischl B, 2012. Within-subject template estimation for unbiased longitudinal image analysis. Neuroimage 61 (4), 1402–1418. [DOI] [PMC free article] [PubMed] [Google Scholar]
Reuter M, Fischl B, 2011. Avoiding asymmetry-induced bias in longitudinal image processing. Neuroimage 57 (1), 19–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fujimoto K, Polimeni JR, Van Der Kouwe AJ, et al. , 2014. Quantitative comparison of cortical surface reconstructions from MP2RAGE and multi-echo MPRAGE data at 3 and 7 T. Neuroimage 90, 60–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
Han X, Jovicich J, Salat D, et al. , 2006. Reliability of MRI-derived measurements of human cerebral cortical thickness: the effects of field strength, scanner upgrade and manufacturer. Neuroimage 32 (1), 180–194. [DOI] [PubMed] [Google Scholar]
Chang YV, Cauley SF, Liu W, et al. , 2018. Quantitative assessment of automatic cortical surface reconstructions from Wave-CAIPI MPRAGE: a validation study. In: The Annual Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM), p. 2042. [Google Scholar]
Marek K, Jennings D, Lasch S, et al. , 2011. The parkinson progression marker initiative (PPMI). Prog. Neurobiol. 95 (4), 629–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
Longo MGF, Conklin J, Cauley SF, et al. , 2020. Evaluation of ultrafast wave-CAIPI MPRAGE for visual grading and automated measurement of brain tissue volume. Am. J. Neuroradiol. 41 (8), 1388–1396. [DOI] [PMC free article] [PubMed] [Google Scholar]
Knoll F, Hammernik K, Kobler E, Pock T, Recht MP, Sodickson DK, 2019. Assessment of the generalization of learned image reconstruction and the potential for transfer learning. Magn. Reson. Med. 81 (1), 116–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hu Y, Xu Y, Tian Q, et al. , 2020b. RUN-UP: accelerated multishot diffusion-weighted MRI reconstruction using an unrolled network with U-Net as priors. Magn. Reson. Med. 85 (2), 709–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
Simonyan K, Zisserman A, 2014. Very Deep Convolutional Networks for Large-Scale Image Recognition arXiv preprint.arXiv:1409.1556. [Google Scholar]
Timofte R, Agustsson E, Van Gool L, et al. , 2017. Ntire 2017 challenge on single image super-resolution: methods and results. In: The IEEE Conference on Computer Vision and Pattern Recognition Workshops, pp. 114–125. [Google Scholar]
Chaudhari AS, Fang Z, Kogan F, et al. , 2018. Super-resolution musculoskeletal MRI using deep learning. Magn. Reson. Med. 80 (5), 2139–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pham C−H, Tor-Díez C, Meunier H, et al. , 2019. Multiscale brain MRI super-resolution using deep 3D convolutional networks. Comput. Med. Imaging Graph. 77, 101647. [DOI] [PubMed] [Google Scholar]
Lüsebrink F, Sciarra A, Mattern H, Yakupov R, Speck O, 2017. T 1-weighted in vivo human whole brain MRI dataset with an ultrahigh isotropic resolution of 250 μm. Sci. Data 4, 170032. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tisdall MD, Polimeni JR, van der Kouwe AJ, 2013b. Motion-corrected 350 μm isotropic MPRAGE at 3 T using volumetric navigators (vNavs). In: The Annual Meeting of the International Society of Magnetic Resonance in Medicine (ISMRM), p. 268. [Google Scholar]
Watanabe K, Kakeda S, Igata N, et al. , 2016. Utility of real-time prospective motion correction (PROMO) on 3D T1-weighted imaging in automated brain structure measurements. Sci. Rep. 6 (1), 38366. [DOI] [PMC free article] [PubMed] [Google Scholar]
Maclaren J, Herbst M, Speck O, Zaitsev M, 2013. Prospective motion correction in brain imaging: a review. Magn. Reson. Med. 69 (3), 621–636. [DOI] [PubMed] [Google Scholar]
Gallichan D, Marques JP, Gruetter R, 2016. Retrospective correction of involuntary microscopic head movement using highly accelerated fat image navigators (3D Fat-Navs) at 7T. Magn. Reson. Med. 75 (3), 1030–1039. [DOI] [PubMed] [Google Scholar]
Godenschweger F, Kägebein U, Stucht D, et al. , 2016. Motion correction in MRI of the brain. Phys. Med. Biol. 61 (5), R32. [DOI] [PMC free article] [PubMed] [Google Scholar]
Goodfellow I, Pouget-Abadie J, Mirza M, et al. , 2014. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 27, 2672–2680. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

NIHMS1716891-supplement-1.pdf^{(13.5MB, pdf)}

Data Availability Statement

The source code of the DnCNN network implemented using Keras API and the pre-trained models using the MGH 0.6-mm isotropic data are available at https://github.com/qiyuantian/DnSurfer.

[R1] Fischl B, 2012. FreeSurfer. Neuroimage 62 (2), 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] Fischl B, Sereno MI, Dale AM, 1999. Cortical surface-based analysis: II: inflation, flattening, and a surface-based coordinate system. Neuroimage 9 (2), 195–207. [DOI] [PubMed] [Google Scholar]

[R3] Dale AM, Fischl B, Sereno MI, 1999. Cortical surface-based analysis: I. Segmentation and surface reconstruction. Neuroimage 9 (2), 179–194. [DOI] [PubMed] [Google Scholar]

[R4] Kim JS, Singh V, Lee JK, et al. , 2005. Automated 3-D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. Neuroimage 27 (1), 210–221. [DOI] [PubMed] [Google Scholar]

[R5] Bazin P−L, Weiss M, Dinse J, Schäfer A, Trampel R, Turner R, 2014. A computational framework for ultra-high resolution cortical segmentation at 7Tesla. Neuroimage 93, 201–209. [DOI] [PubMed] [Google Scholar]

[R6] Huntenburg JM, Steele CJ, Bazin P−L, 2018. Nighres: processing tools for high-resolution neuroimaging. Gigascience 7 (7). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] Ashburner J, Friston KJ, 2005. Unified segmentation. Neuroimage 26 (3), 839–851. [DOI] [PubMed] [Google Scholar]

[R8] Bazin P−L, Pham DL, 2008. Homeomorphic brain image segmentation with topological and statistical atlases. Med. Image Anal. 12 (5), 616–625. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] Han X, Pham DL, Tosun D, Rettmann ME, Xu C, Prince JL, 2004. CRUISE: cortical reconstruction using implicit surface evolution. Neuroimage 23 (3), 997–1012. [DOI] [PubMed] [Google Scholar]

[R10] Fischl B, Dale AM, 2000. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc. Natl. Acad. Sci. 97 (20), 11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] Winkler AM, Sabuncu MR, Yeo BT, et al. , 2012. Measuring and comparing brain cortical surface area and other areal quantities. Neuroimage 61 (4), 1428–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] Winkler AM, Greve DN, Bjuland KJ, et al. , 2017. Joint analysis of cortical area and thickness as a replacement for the analysis of the volume of the cerebral cortex. Cereb. Cortex 28 (2), 738–749. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] Schaer M, Cuadra MB, Tamarit L, Lazeyras F, Eliez S, Thiran J−P, 2008. A surface-based approach to quantify local cortical gyrification. IEEE Trans. Med. Imaging 27 (2), 161–170. [DOI] [PubMed] [Google Scholar]

[R14] Du A−T, Schuff N, Kramer JH, et al. , 2007. Different regional patterns of cortical thinning in Alzheimer’s disease and frontotemporal dementia. Brain 130 (4), 1159–1166. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] Lerch JP, Pruessner JC, Zijdenbos A, Hampel H, Teipel SJ, Evans AC, 2004. Focal decline of cortical thickness in Alzheimer’s disease identified by computational neuroanatomy. Cereb. Cortex 15 (7), 995–1001. [DOI] [PubMed] [Google Scholar]

[R16] Sailer M, Fischl B, Salat D, et al. , 2003. Focal thinning of the cerebral cortex in multiple sclerosis. Brain 126 (8), 1734–1744. [DOI] [PubMed] [Google Scholar]

[R17] Kuperberg GR, Broome MR, McGuire PK, et al. , 2003. Regionally localized thinning of the cerebral cortex in schizophrenia. Arch. Gen. Psychiatry 60 (9), 878–888. [DOI] [PubMed] [Google Scholar]

[R18] Ly M, Motzkin JC, Philippi CL, et al. , 2012. Cortical thinning in psychopathy. Am. J. Psychiatry 169 (7), 743–749. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] Wallace GL, Dankner N, Kenworthy L, Giedd JN, Martin A, 2010. Age-related temporal and parietal cortical thinning in autism spectrum disorders. Brain 133 (12), 3745–3754. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Schmaal L, Hibar D, Sämann P, et al. , 2017. Cortical abnormalities in adults and adolescents with major depression based on brain scans from 20 cohorts worldwide in the ENIGMA major depressive disorder working group. Mol. Psychiatry 22 (6), 900. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] Anderson BJ, Eckburg PB, Relucio KI, 2002. Alterations in the thickness of motor cortical subregions after motor-skill learning and exercise. Learn. Mem. 9 (1), 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] Bermudez P, Lerch JP, Evans AC, Zatorre RJ, 2008. Neuroanatomical correlates of musicianship as revealed by cortical thickness and voxel-based morphometry. Cereb. Cortex 19 (7), 1583–1596. [DOI] [PubMed] [Google Scholar]

[R23] Engvig A, Fjell AM, Westlye LT, et al. , 2010. Effects of memory training on cortical thickness in the elderly. Neuroimage 52 (4), 1667–1676. [DOI] [PubMed] [Google Scholar]

[R24] Lazar SW, Kerr CE, Wasserman RH, et al. , 2005. Meditation experience is associated with increased cortical thickness. Neuroreport 16 (17), 1893. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] Fischl B, Van Der Kouwe A, Destrieux C, et al. , 2004. Automatically parcellating the human cerebral cortex. Cereb. Cortex 14 (1), 11–22. [DOI] [PubMed] [Google Scholar]

[R26] Glasser MF, Coalson TS, Robinson EC, et al. , 2016a. A multi-modal parcellation of human cerebral cortex. Nature 536 (7615), 171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] Van Essen DC, Glasser MF, Dierker DL, Harwell J, Coalson T, 2011. Parcellations and hemispheric asymmetries of human cerebral cortex analyzed on surface-based atlases. Cereb. Cortex 22 (10), 2241–2262. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] Cohen-Adad J, Benner T, Greve D, et al. , 2011. In vivo evidence of disseminated subpial T2* signal changes in multiple sclerosis at 7 T: a surface-based analysis. Neuroimage 57 (1), 55–62. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] Fracasso A, van Veluw SJ, Visser F, et al. , 2016. Lines of baillarger in vivo and ex vivo: myelin contrast across lamina at 7T MRI and histology. Neuroimage 133, 163–175. [DOI] [PubMed] [Google Scholar]

[R30] Marques JP, Khabipova D, Gruetter R, 2017. Studying cyto and myeloarchitecture of the human cortex at ultra-high field with quantitative imaging: R 1, R2* and susceptibility. Neuroimage 147, 152–163. [DOI] [PubMed] [Google Scholar]

[R31] Trampel R, Ott DV, Turner R, 2011. Do the congenitally blind have a stria of Gennari? First intracortical insights in vivo. Cereb. Cortex 21 (9), 2075–2081. [DOI] [PubMed] [Google Scholar]

[R32] Glasser MF, Van Essen DC, 2011. Mapping human cortical areas in vivo based on myelin content as revealed by T1-and T2-weighted MRI. J. Neurosci. 31 (32), 11597–11616. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] McNab JA, Polimeni JR, Wang R, et al. , 2013. Surface based analysis of diffusion orientation for identifying architectonic domains in the in vivo human cortex. Neuroimage 69, 87–100. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] Kleinnijenhuis M, van Mourik T, Norris DG, Ruiter DJ, van Walsum A-MvC, Barth M, 2015. Diffusion tensor characteristics of gyrencephaly using high resolution diffusion MRI in vivo at 7T. Neuroimage 109, 378–387. [DOI] [PubMed] [Google Scholar]

[R35] Fukutomi H, Glasser MF, Zhang H, et al. , 2018. Neurite imaging reveals microstructural variations in human cerebral cortical gray matter. Neuroimage 182, 488–499. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] Calamante F, Jeurissen B, Smith RE, Tournier JD, Connelly A, 2018. The role of whole-brain diffusion MRI as a tool for studying human in vivo cortical segregation based on a measure of neurite density. Magn. Reson. Med. 79 (5), 2738–2744. [DOI] [PubMed] [Google Scholar]

[R37] Polimeni JR, Fischl B, Greve DN, Wald LL, 2010. Laminar analysis of 7T BOLD using an imposed spatial activation pattern in human V1. Neuroimage 52 (4), 1334–1346. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Huber L, Goense J, Kennerley AJ, et al. , 2015. Cortical lamina-dependent blood volume changes in human brain at 7 T. Neuroimage 107, 23–33. [DOI] [PubMed] [Google Scholar]

[R39] Kok P, Bains LJ, van Mourik T, Norris DG, de Lange FP, 2016. Selective activation of the deep layers of the human primary visual cortex by top-down feedback. Curr. Biol. 26 (3), 371–376. [DOI] [PubMed] [Google Scholar]

[R40] Maass A, Schütze H, Speck O, et al. , 2014. Laminar activity in the hippocampus and entorhinal cortex related to novelty and episodic encoding. Nat. Commun. 5, 5547. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R41] Nasr S, Polimeni JR, Tootell RB, 2016. Interdigitated color-and disparity-selective columns within human visual cortical areas V2 and V3. J. Neurosci. 36 (6), 1841–1857. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] Olman CA, Harel N, Feinberg DA, et al. , 2012. Layer-specific fMRI reflects different neuronal computations at different depths in human V1. PLoS ONE 7 (3), e32536. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] Zaretskaya N, Fischl B, Reuter M, Renvall V, Polimeni JR, 2018. Advantages of cortical surface reconstruction using submillimeter 7 T MEMPRAGE. Neuroimage 165, 11–26. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R44] Glasser MF, Sotiropoulos SN, Wilson JA, et al. , 2013. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R45] Lüsebrink F, Wollrab A, Speck O, 2013. Cortical thickness determination of the human brain using high resolution 3 T and 7 T MRI data. Neuroimage 70, 122–131. [DOI] [PubMed] [Google Scholar]

[R46] Glasser MF, Smith SM, Marcus DS, et al. , 2016b. The human connectome project’s neuroimaging approach. Nat. Neurosci. 19 (9), 1175–1187. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] Tian Q, Bilgic B, Fan Q, Ngamsombat C, Zaretskaya N, Fultz NE, …, Huang SY, et al. , 2021. Improving in vivo human cerebral cortical surface reconstruction using data-driven super-resolution. Cereb. Cortex 31 (1), 463–482. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] Bookheimer SY, Salat DH, Terpstra M, et al. , 2019. The lifespan human connectome project in aging: an overview. Neuroimage 185, 335–348. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] Somerville LH, Bookheimer SY, Buckner RL, et al. , 2018. The lifespan human connectome project in development: a large-scale study of brain connectivity development in 5–21 year olds. Neuroimage 183, 456–468. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] Harms MP, Somerville LH, Ances BM, et al. , 2018. Extending the human connectome project across ages: imaging protocols for the lifespan development and aging projects. Neuroimage 183, 972–984. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R51] Goebel R, 2012. BrainVoyager—past, present, future. Neuroimage 62 (2), 748–756. [DOI] [PubMed] [Google Scholar]

[R52] Lustig M, Donoho D, Pauly JM, 2007. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58 (6), 1182–1195. [DOI] [PubMed] [Google Scholar]

[R53] Bilgic B, Gagoski BA, Cauley SF, et al. , 2015. Wave-CAIPI for highly accelerated 3D imaging. Magn. Reson. Med. 73 (6), 2152–2162. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R54] Keil B, Blau JN, Biber S, et al. , 2013. A 64-channel 3T array coil for accelerated brain MRI. Magn. Reson. Med. 70 (1), 248–258. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] Block KT, Uecker M, Frahm J, 2007. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med. 57 (6), 1086–1098. [DOI] [PubMed] [Google Scholar]

[R56] Liang D, Liu B, Wang J, Ying L, 2009. Accelerating SENSE using compressed sensing. Magn. Reson. Med. 62 (6), 1574–1584. [DOI] [PubMed] [Google Scholar]

[R57] Murphy M, Alley M, Demmel J, Keutzer K, Vasanawala S, Lustig M, 2012. Fast ℓ₁-SPIRiT compressed sensing parallel imaging MRI: scalable parallel implementation and clinically feasible runtime. IEEE Trans. Med. Imaging 31 (6), 1250–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R58] Otazo R, Kim D, Axel L, Sodickson DK, 2010. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn. Reson. Med. 64 (3), 767–776. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] Hu Y, Levine EG, Tian Q, et al. , 2019. Motion-robust reconstruction of multishot diffusion-weighted images without phase estimation through locally low-rank regularization. Magn. Reson. Med. 81 (2), 1181–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R60] Hu Y, Wang X, Tian Q, et al. , 2020a. Multi-shot diffusion-weighted MRI reconstruction with magnitude-based spatial-angular locally low-rank regularization (SPA-LLR). Magn. Reson. Med. 83 (5), 1596–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R61] Kim TH, Bilgic B, Polak D, Setsompop K, Haldar JP, 2019. Wave-LORAKS: combining wave encoding with structured low-rank matrix modeling for more highly accelerated 3D imaging. Magn. Reson. Med. 81 (3), 1620–1633. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R62] Haldar JP, 2013. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans. Med. Imaging 33 (3), 668–681. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R63] Shin PJ, Larson PE, Ohliger MA, et al. , 2014. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn. Reson. Med. 72 (4), 959–970. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] Haldar JP, Zhuo J, 2016. P-LORAKS: low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn. Reson. Med. 75 (4), 1499–1514. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] Rudin LI, Osher S, Fatemi E, 1992. Nonlinear total variation based noise removal algorithms. Phys. D: Nonlin. Phenomena 60 (1–4), 259–268. [Google Scholar]

[R66] Perona P, Malik J, 1990. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 12 (7), 629–639. [Google Scholar]

[R67] Fischl B, Schwartz EL, 1997. Learning an integral equation approximation to nonlinear anisotropic diffusion in image processing. IEEE Trans. Pattern Anal. Mach. Intell. 19 (4), 342–352. [Google Scholar]

[R68] Tomasi C, Manduchi R, 1998. Bilateral filtering for gray and color images. In: The International Conference on Computer Vision, pp. 839–846. [Google Scholar]

[R69] Buades A, Coll B, Morel J−M, 2005. A review of image denoising algorithms, with a new one. Multisc. Model. Simul. 4 (2), 490–530. [Google Scholar]

[R70] Dabov K, Foi A, Katkovnik V, Egiazarian K, 2007. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 16 (8), 2080–2095. [DOI] [PubMed] [Google Scholar]

[R71] Aharon M, Elad M, Bruckstein AK-SVD, 2006. An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 54 (11), 4311–4322. [Google Scholar]

[R72] Gerig G, Kubler O, Kikinis R, Jolesz FA, 1992. Nonlinear anisotropic filtering of MRI data. IEEE Trans. Med. Imaging 11 (2), 221–232. [DOI] [PubMed] [Google Scholar]

[R73] Coupé P, Yger P, Prima S, Hellier P, Kervrann C, Barillot C, 2008. An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images. IEEE Trans. Med. Imaging 27 (4), 425–441. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] Manjón JV, Coupé P, Martí-Bonmatí L, Collins DL, Robles M, 2010. Adaptive non-local means denoising of MR images with spatially varying noise levels. J. Magn. Reson. Imaging 31 (1), 192–203. [DOI] [PubMed] [Google Scholar]

[R75] Maggioni M, Katkovnik V, Egiazarian K, Foi A, 2012. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 22 (1), 119–133. [DOI] [PubMed] [Google Scholar]

[R76] Bazin P−L, Alkemade A, Van Der Zwaag W, Caan M, Mulder M, Forstmann BU, 2019. Denoising High-field Multi-dimensional MRI with Local Complex PCA. Front Neurosci 13, 1066. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R77] Konukoglu E, van der Kouwe A, Sabuncu MR, Fischl B, 2013. Example-based restoration of high-resolution magnetic resonance image acquisitions Int. Conf. Med. Image Comput. Comput.-Assist. Intervent., 131–138. [DOI] [PubMed] [Google Scholar]

[R78] Zhang K, Zuo W, Chen Y, Meng D, Zhang L, 2017. Beyond a Gaussian denoiser: residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 26 (7), 3142–3155. [DOI] [PubMed] [Google Scholar]

[R79] Tian Q, Bilgic B, Fan Q, et al. , 2020. DeepDTI: high-fidelity six-direction diffusion tensor imaging using deep learning. Neuroimage 219, 117017. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R80] Chen KT, Gong E, de Carvalho Macruz FB, et al. , 2018. Ultra–low-dose 18F-Florbetaben amyloid PET imaging using deep learning with multi-contrast MRI inputs. Radiology 290 (3), 649–656. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R81] Lehtinen J, Munkberg J, Hasselgren J, et al. , 2018. Noise2Noise: learning image restoration without clean data. In: The International Conference on Machine Learning, pp. 2965–2974. [Google Scholar]

[R82] Krull A, Buchholz T−O, Jug F, 2019. Noise2void-learning denoising from single noisy images. In: The IEEE Conference on Computer Vision and Pattern Recognition, pp. 2129–2137. [Google Scholar]

[R83] Weigert M, Schmidt U, Boothe T, et al. , 2018. Content-aware image restoration: pushing the limits of fluorescence microscopy. Nat. Methods 15 (12), 1090–1097. [DOI] [PubMed] [Google Scholar]

[R84] Devalla SK, Subramanian G, Pham TH, et al. , 2019. A deep learning approach to denoise optical coherence tomography images of the optic nerve head. Sci. Rep. 9 (1), 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R85] Gondara L, 2016. Medical image denoising using convolutional denoising autoencoders. In: The IEEE International Conference on Data Mining Workshops (ICDMW), pp. 241–246. [Google Scholar]

[R86] Chang Y, Yan L, Chen M, Fang H, Zhong S, 2019. Two-stage convolutional neural network for medical noise removal via image decomposition. IEEE Trans. Instrum. Meas. 69 (6), 2707–2721. [Google Scholar]

[R87] Ouyang J, Chen KT, Gong E, Pauly J, Zaharchuk G, 2019. Ultra-low-dose PET reconstruction using generative adversarial network with feature matching and task-specific perceptual loss. Med. Phys. 46 (8), 3555–3564. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R88] Wang Y, Yu B, Wang L, et al. , 2018. 3D conditional generative adversarial networks for high-quality PET image estimation at low dose. Neuroimage 174, 550–562. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R89] Serrano-Sosa M, Spuhler K, DeLorenzo C, Huang C, 2020. PET image denoising using structural MRI with a novel dilated convolutional neural network. J. Nucl. Med. 61, 434–434. [Google Scholar]

[R90] Xu J, Gong E, Ouyang J, Pauly J, Zaharchuk G, Han S, 2020. Ultra-low-dose 18F-FDG brain PET/MR denoising using deep learning and multi-contrast information. SPIE Med. Imaging Conf.11313, 113131P. [Google Scholar]

[R91] Gong E, Pauly JM, Wintermark M, Zaharchuk G, 2018. Deep learning enables reduced gadolinium dose for contrast-enhanced brain MRI. J. Magn. Reson. Imaging 48 (2), 330–340. [DOI] [PubMed] [Google Scholar]

[R92] Benou A, Veksler R, Friedman A, Raviv TR, 2017. Ensemble of expert deep neural networks for spatio-temporal denoising of contrast-enhanced MRI sequences. Med. Image Anal. 42, 145–159. [DOI] [PubMed] [Google Scholar]

[R93] Jiang D, Dou W, Vosters L, Xu X, Sun Y, Tan T, 2018. Denoising of 3D magnetic resonance images with multi-channel residual learning of convolutional neural network. Jpn. J. Radiol. 36 (9), 566–574. [DOI] [PubMed] [Google Scholar]

[R94] Pierrick C, 2019. MRI Denoising Using Deep Learning and Non-Local averaging arXiv preprintarXiv:1911.04798.. [Google Scholar]

[R95] Gong E, Guo J, Liu J, Fan A, Pauly J, Zaharchuk G, 2020. Deep learning and multi-contrast-based denoising for low-SNR Arterial Spin Labeling (ASL) MRI. Proc. SPIE 11313, Medical Imaging 11313 Image Processing, 113130M. [Google Scholar]

[R96] Kidoh M, Shinoda K, Kitajima M, et al. , 2019. Deep learning based noise reduction for brain MR imaging: tests on phantoms and healthy volunteers. Magn. Reson. Med. Sci. 19 (3), 195. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R97] van der Kouwe AJ, Benner T, Salat DH, Fischl B, 2008. Brain morphometry with multiecho MPRAGE. Neuroimage 40 (2), 559–569. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R98] Hurley AC, Al-Radaideh A, Bai L, et al. , 2010. Tailored RF pulse for magnetization inversion at ultrahigh field. Magn. Reson. Med. 63 (1), 51–58. [DOI] [PubMed] [Google Scholar]

[R99] Polak D, Setsompop K, Cauley SF, et al. , 2018. Wave-CAIPI for highly accelerated MP-RAGE imaging. Magn. Reson. Med. 79 (1), 401–406. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R100] van der Kouwe AJ, Tisdall MD, Bhat H, Fischl B, Polimeni JR, 2014. Multiple echo and inversion time MPRAGE with Inner Loop GRAPPA acceleration and prospective motion correction for minimally distorted multispectral brain morphometry. Annual Meet. Int. Soc. Magn. Reson. Med. (ISMRM)22, 120. [Google Scholar]

[R101] Tisdall MD, Polimeni JR, Augustinack JC, van der Kouwe AJW, 2013a. 350 μm isotropic, high-contrast, low-blur, low-distortion MPRAGE morphometry acquisition at 3T. Annual Meet. Org. Human Brain Mapp. (OHBM) 3371. [Google Scholar]

[R102] Reuter M, Rosas HD, Fischl B, 2010. Highly accurate inverse consistent registration: a robust approach. Neuroimage 53 (4), 1181–1196. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R103] Uwano I, Kudo K, Yamashita F, et al. , 2014. Intensity inhomogeneity correction for magnetic resonance imaging of human brain at 7T. Med. Phys. 41 (2). [DOI] [PubMed] [Google Scholar]

[R104] Modat M, Ridgway GR, Taylor ZA, et al. , 2010. Fast free-form deformation using graphics processing units. Comput. Methods Programs Biomed. 98 (3), 278–284. [DOI] [PubMed] [Google Scholar]

[R105] Modat M, Cash DM, Daga P, Winston GP, Duncan JS, Ourselin S, 2014. Global image registration using a symmetric block-matching approach. J. Med. Imaging 1 (2), 024003–024003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R106] Smith SM, Jenkinson M, Woolrich MW, et al. , 2004. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 23, S208–S219. [DOI] [PubMed] [Google Scholar]

[R107] Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM., 2012. FSL. Neuroimage 62 (2), 782–790. [DOI] [PubMed] [Google Scholar]

[R108] Andersson JL, Sotiropoulos SN, 2016. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R109] He K, Zhang X, Ren S, Sun J, 2016. Deep residual learning for image recognition. In: The IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778. [Google Scholar]

[R110] Kim J, Kwon Lee J, Mu Lee K, 2016. Accurate image super-resolution using very deep convolutional networks. In: The IEEE Conference on Computer Vision and Pattern Recognition, pp. 1646–1654. [Google Scholar]

[R111] He K, Zhang X, Ren S, Sun J, 2015. Delving deep into rectifiers: surpassing human-level performance on imagenet classification. In: The IEEE International Conference on Computer Vision, pp. 1026–1034. [Google Scholar]

[R112] LeCun Y, Bottou L, Bengio Y, Haffner P, 1998. Gradient-based learning applied to document recognition. Proc. IEEE 86 (11), 2278–2324. [Google Scholar]

[R113] Kingma DP, Adam Ba J., 2014. A Method for Stochastic Optimization arXiv preprintarXiv:1412.6980. [Google Scholar]

[R114] Wang Z, Bovik AC, Sheikh HR, Simoncelli EP, 2004. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13 (4), 600–612. [DOI] [PubMed] [Google Scholar]

[R115] Ségonne F, Pacheco J, Fischl B, 2007. Geometrically accurate topology-correction of cortical surfaces using nonseparating loops. IEEE Trans. Med. Imaging 26 (4), 518–529. [DOI] [PubMed] [Google Scholar]

[R116] Reuter M, Schmansky NJ, Rosas HD, Fischl B, 2012. Within-subject template estimation for unbiased longitudinal image analysis. Neuroimage 61 (4), 1402–1418. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R117] Reuter M, Fischl B, 2011. Avoiding asymmetry-induced bias in longitudinal image processing. Neuroimage 57 (1), 19–21. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R118] Fujimoto K, Polimeni JR, Van Der Kouwe AJ, et al. , 2014. Quantitative comparison of cortical surface reconstructions from MP2RAGE and multi-echo MPRAGE data at 3 and 7 T. Neuroimage 90, 60–73. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R119] Han X, Jovicich J, Salat D, et al. , 2006. Reliability of MRI-derived measurements of human cerebral cortical thickness: the effects of field strength, scanner upgrade and manufacturer. Neuroimage 32 (1), 180–194. [DOI] [PubMed] [Google Scholar]

[R120] Chang YV, Cauley SF, Liu W, et al. , 2018. Quantitative assessment of automatic cortical surface reconstructions from Wave-CAIPI MPRAGE: a validation study. In: The Annual Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM), p. 2042. [Google Scholar]

[R121] Marek K, Jennings D, Lasch S, et al. , 2011. The parkinson progression marker initiative (PPMI). Prog. Neurobiol. 95 (4), 629–635. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R122] Longo MGF, Conklin J, Cauley SF, et al. , 2020. Evaluation of ultrafast wave-CAIPI MPRAGE for visual grading and automated measurement of brain tissue volume. Am. J. Neuroradiol. 41 (8), 1388–1396. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R123] Knoll F, Hammernik K, Kobler E, Pock T, Recht MP, Sodickson DK, 2019. Assessment of the generalization of learned image reconstruction and the potential for transfer learning. Magn. Reson. Med. 81 (1), 116–128. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R124] Hu Y, Xu Y, Tian Q, et al. , 2020b. RUN-UP: accelerated multishot diffusion-weighted MRI reconstruction using an unrolled network with U-Net as priors. Magn. Reson. Med. 85 (2), 709–720. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R125] Simonyan K, Zisserman A, 2014. Very Deep Convolutional Networks for Large-Scale Image Recognition arXiv preprint.arXiv:1409.1556. [Google Scholar]

[R126] Timofte R, Agustsson E, Van Gool L, et al. , 2017. Ntire 2017 challenge on single image super-resolution: methods and results. In: The IEEE Conference on Computer Vision and Pattern Recognition Workshops, pp. 114–125. [Google Scholar]

[R127] Chaudhari AS, Fang Z, Kogan F, et al. , 2018. Super-resolution musculoskeletal MRI using deep learning. Magn. Reson. Med. 80 (5), 2139–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R128] Pham C−H, Tor-Díez C, Meunier H, et al. , 2019. Multiscale brain MRI super-resolution using deep 3D convolutional networks. Comput. Med. Imaging Graph. 77, 101647. [DOI] [PubMed] [Google Scholar]

[R129] Lüsebrink F, Sciarra A, Mattern H, Yakupov R, Speck O, 2017. T 1-weighted in vivo human whole brain MRI dataset with an ultrahigh isotropic resolution of 250 μm. Sci. Data 4, 170032. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R130] Tisdall MD, Polimeni JR, van der Kouwe AJ, 2013b. Motion-corrected 350 μm isotropic MPRAGE at 3 T using volumetric navigators (vNavs). In: The Annual Meeting of the International Society of Magnetic Resonance in Medicine (ISMRM), p. 268. [Google Scholar]

[R131] Watanabe K, Kakeda S, Igata N, et al. , 2016. Utility of real-time prospective motion correction (PROMO) on 3D T1-weighted imaging in automated brain structure measurements. Sci. Rep. 6 (1), 38366. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R132] Maclaren J, Herbst M, Speck O, Zaitsev M, 2013. Prospective motion correction in brain imaging: a review. Magn. Reson. Med. 69 (3), 621–636. [DOI] [PubMed] [Google Scholar]

[R133] Gallichan D, Marques JP, Gruetter R, 2016. Retrospective correction of involuntary microscopic head movement using highly accelerated fat image navigators (3D Fat-Navs) at 7T. Magn. Reson. Med. 75 (3), 1030–1039. [DOI] [PubMed] [Google Scholar]

[R134] Godenschweger F, Kägebein U, Stucht D, et al. , 2016. Motion correction in MRI of the brain. Phys. Med. Biol. 61 (5), R32. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R135] Goodfellow I, Pouget-Abadie J, Mirza M, et al. , 2014. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 27, 2672–2680. [Google Scholar]

PERMALINK

Improved cortical surface reconstruction using sub-millimeter resolution MPRAGE by image denoising

Qiyuan Tian

Natalia Zaretskaya

Qiuyun Fan

Chanon Ngamsombat

Berkin Bilgic

Jonathan R Polimeni

Susie Y Huang

Abstract

1. Introduction

2. Materials and methods

2.1. Data acquisitions

2.2. Image processing

2.3. BM4D denoising

2.4. AONLM denoising

2.5. DnCNN denoising

Fig. 1. Denoising convolutional neural network (DnCNN) architecture.

2.6. Surface reconstruction

2.7. Image similarity comparison

2.8. Gray–white boundary sharpness comparison

2.9. Surface quality comparison

2.10. Surface accuracy comparison

2.11. Surface precision comparison

2.12. Statistical comparison

3. Results

Fig. 2. Image quality and similarity.

Fig. 3. Image similarity quantification.

Fig. 4. Gray–white contrast.

Fig. 5. Gray–white contrast quantification.

Fig. 6. Cortical interface surface.

Fig. 7. Cortical surface smoothness.

Fig. 8. Cortical surface quality quantification.

Fig. 9. Cortical surface cross-sections.

Fig. 10. Positioning and thickness accuracy.

Fig. 11. Positioning and thickness accuracy quantification.

Fig. 12. Positioning and thickness precision.

4. Discussion

Conclusion

Supplementary Material

Acknowledgments

Footnotes

Data and code availability

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases