Current Status of Radiopharmaceutical Therapy

Abstract

In radiopharmaceutical therapy (RPT), a radionuclide is systemically or locally delivered with the goal of targeting and delivering radiation to cancer cells while minimizing radiation exposure to untargeted cells. Examples of current RPTs include thyroid ablation with the administration of ¹³¹I, treatment of liver cancer with ⁹⁰Y microspheres, the treatment of bony metastases with ²²³Ra and the treatment of neuroendocrine tumors with ¹⁷⁷Lu-DOTATATE. New RPTs are being developed where radionuclides are incorporated into systemic targeted therapies. To assure that RPT is appropriately implemented, advances in targeting need to be matched with advances in quantitative imaging and dosimetry methods. Currently, radiopharmaceutical therapy is administered by intravenous or locoregional injection and the treatment planning has typically been implemented like chemotherapy, where the activity administered is either fixed or based on a patient’s body weight or body surface area (BSA). RPT pharmacokinetics are measurable by quantitative imaging and are known to vary across patients, both in tumors and normal tissues. Therefore, fixed or weight-based activity prescriptions are not currently optimized to deliver a cytotoxic dose to targets while remaining within the tolerance dose of organs at risk. Methods that provide dose estimates to individual patients rather than to reference geometries are needed to assess and adjust the injected RPT dose. Accurate doses to targets and organs at risk will benefit the individual patients and decrease uncertainties in clinical trials. Imaging can be used to measure activity distribution in vivo and this information can be used to determine patient specific treatment plans where the dose to the targets and organs at risk can be calculated. The development and adoption of imaging-based dosimetry methods is particularly beneficial in early clinical trials. In this work we discuss dosimetric accuracy needs in modern radiation oncology, uncertainties in the dosimetry in RPT and best approaches for imaging and dosimetry of internal radionuclide therapy.

I. INTRODUCTION

The goal of each cancer therapy is to eradicate tumor cells while minimizing the potential damage to normal tissues. In radiation-based therapy, both the efficacy and morbidity depend on the radiation dose deposited in the tumor and normal tissues, respectively. External radiation therapy employs advanced imaging and sophisticated treatment planning systems to arrive at optimal dose distribution and, thereby, provide the best treatment for individual patients. Radiopharmaceutical therapy (RPT), alternatively referred to as targeted radionuclide therapy (TRT) or molecular radiotherapy (MRT), is an evolving and promising modality of cancer treatment. Through biological targeting, it provides a unique means to efficiently deliver ionizing radiation to disseminated cancer cells and small metastases while sparing healthy normal tissues. RPT sits at the junction of chemistry, radiobiology, immunology, cell biology, diagnostic imaging, physics, and multiple aspects of pharmacology [1–5].

Appropriate assessment of the radiation doses deposited in the tumor and normal tissues is crucial for the success of radiopharmaceutical therapy (RPT) but it is not typically implemented due to a general scarcity of robust dosimetry methods. Recent advances in imaging and radiation transport methods can be applied to overcome the complexities of dose-based planning and progress toward prospective RPT planning. One of the primary goals of RPT treatment planning is the implementation of personalized radiation dose calculations to meet every individual patient’s needs.

The current paradigm of prescribing dosage of radiopharmaceuticals based on a standard dose or on the patient weight or body surface is suboptimal and the full potential of RPT is not realized. Assessment of radiation doses in individual patients and their correlation with the tumor and normal tissues response to radiation is essential for analyzing the outcome of clinical trials combining RPT with new chemotherapeutic agents. In addition, the ability to assess the radiation doses delivered by RPT will enable its combination with external RT to achieve longitudinal tracking of the overall radiation dose received by a patient, subsequent treatments can be adapted accordingly.

The perceived obstacles preventing high-quality individualized therapy treatment planning include: (i) cost and effort associated with nuclear imaging exams necessary for dose calculation, image registration, and calculation of dose distribution or dose-volume histograms; (ii) lack of standard treatment planning methods; and (iii) lack of well-documented correlations between the dose assessments and outcome. It is the objective of this work to elaborate on these obstacles and discuss potential solutions.

Investigation of new cancer therapeutics typically follows an empirical paradigm; this is also true for RPT. Efficacy and tolerable toxicity observed in preclinical experiments provide a rationale for clinical evaluation of the agent. Initial clinical evaluation typically is focused on toxicity determination (phase I trial) and subsequently efficacy and comparative efficacy (phase II and III trials, respectively). Since the success of RPT depends on the differential delivery of radiation leading to significantly higher absorbed doses to targets compared to normal tissue, the treatment may be optimized by identifying a pharmaceutical dosing level most likely to show efficacy with tolerable toxicity. Properly implemented, a patient specific dosimetry-driven approach to RPT development and clinical trial design will reduce the time required to make the drug clinically available and has the potential to optimize combination treatment.

II. CHARACTERISTICS OF RADIONUCLIDES FOR THERAPY

The success of internal radionuclide therapy will depend on selecting the appropriate radionuclide for the therapeutic application at hand. Different radionuclides have inherent physical characteristics that can be beneficial or detrimental to quantitative internal radionuclide therapy. These include the half-life of the radionuclide, the emitted particle(s) and their energies.

If the half-life of RPT radionuclides is too short, administration is challenging as there is only a short period of time for the radionuclide to be distributed in the patient. Additional logistical challenges with short half-life radionuclides include distributing the radionuclide to hospitals and performing the required chemistry to create the conjugated radiopharmaceutical. Conversely, if the half-life is too long, the patient will receive a dose over a long period of time with a slow dose rate and may not receive the therapeutic benefit of radiation therapy.

Since efficacy in RPT relies on localized energy deposition, the ideal modes of decay are alpha and beta decay. Alpha particles travel 50 to 100 μm in tissue and deposit energy at a very high density over this short range (e.g. maximum range of 85 μm for ²¹³Bi) [6]. Alpha particles are helium nuclei that deposit energy along their track at a rate that is 100 to 1000 times greater than that of beta particles. The damage caused by alpha particles is predominantly double-stranded DNA breaks severe enough to make the DNA repair mechanism ineffective. Therefore, a small number of tracks through a cell nucleus can sterilize a cell and alpha-particle radiation is not susceptible to resistance as seen with external radiotherapy (e.g., in hypoxic tissue). Animal and cell culture studies have shown that the relative biological effectiveness (RBE) of alpha-particles is in the range 3 to 7, compared to RBE of beta particles at 1. This can be increased substantially by DNA DSB pathway inhibitors [7]. The short (50 – 100 micron) range of alpha-particles limits the amount of damage incurred by normal tissue. Beta particles travel 0.8 to 5 mm in tissue (mean range) and deposit energy at a lower density but over a longer range (e.g. ⁹⁰Y has a mean range of 2.5 mm and a maximum range of 11 mm with a mean energy of 0.93 MeV and a maximum energy of 2.28 MeV)[8]. For both emission types, but particularly for alpha-particles, this localized deposition of dose provides the potential to spare organs at risk.

While local energy deposition is desired, the targeting of the agent must also be a primary consideration. A radiopharmaceutical that is poorly targeted and decays via alpha or beta decay will still result in undesirably high doses to normal (untargeted) tissues. In addition, if the radionuclide readily dissociates from the targeting agent, the free radionuclide will produce increased radiation dose to untargeted tissues. Similarly, isotopes with radioactive daughters may dissociate during decay and the daughters may then re-localize to untargeted tissues.

Additional factors to consider include the production method of the radionuclides (e.g. cyclotron produced) and the ease of chemical separation and conjugation into a therapeutic agent. In the United States, the Department of Energy has active programs to increase the production levels of radionuclides of interest that are not currently produced commercially (e.g. ²¹¹At, ²¹²Pb,) or that are produced commercially in limited quantities (e.g. ⁶⁴Cu,²²³Ra).

III. QUANTITATIVE IMAGING PRINCIPLES

Image-based quantification of activity distributions can be categorized based on the decay scheme of the radionuclide. Radionuclides that decay via positron emission can be imaged using positron emission tomography (PET). Radionuclides that have a single (or multiple photons) emitted during decay can be imaged with planar methods and single photon emission tomography (SPECT).

PET/CT

In PET, the 511 keV annihilation photons are imaged to create a volumetric image. Some potential radionuclide therapeutics can be conjugated with positron-emitting analogues, allowing for a pre-treatment PET scan to be performed to determine the optimal dose of therapeutic radionuclide. This is the case for patients who may be candidates for therapy with ¹⁷⁷Lu-DOTATATE. For these patients, a pretreatment PET/CT scan may be performed with Ga-68 DOTATATE to evaluate the uptake of the agent [9].

PET relies on the coincidence detection of the annihilation photons, which travel in approximately opposing directions. This is achieved using pairs of detectors arranged in a ring geometry. Coincidence processing serves as collimation and physical collimators are not required, resulting in substantially greater sensitivity than SPECT. Clinical PET typically obtains a spatial resolution of 4–6 mm FWHM [10] [11], depending on the size of the scintillation crystals employed, the radionuclide imaged, the geometry of the PET scanner and the reconstruction methods used. For newer commercial systems, spatial resolution less than 4 mm FWHM has been reported [12]. One disadvantage of PET is that positron emitting radionuclides typically have shorter half-lives than the therapeutic radionuclides they serve as a surrogate for. This can make it difficult to obtain high quality estimates of the time-activity curve.

Planar Imaging, SPECT and SPECT/CT

In both planar imaging and SPECT, the emitted photons are detected using a gamma camera consisting of a lead collimator, scintillation crystal and electronics. The spatial resolution achieved in SPECT is 7.5 to 15 mm full-width at half maximum (FWHM) and depends on the hardware employed (crystal thickness, electronics, collimator), the radionuclide being imaged, the geometry of the patient (distance from the collimator) and reconstruction and compensation methods chosen [13, 14]. In nearly all planar and SPECT imaging studies pertaining to radionuclide therapy dosimetry, parallel-hole collimation is used. Selection of a general purpose or high resolution collimator and low-, medium-, or high- energy design is based on the desired balance of spatial resolution and sensitivity, the energies of imaged photons and the presence and abundance of higher-energy gammas [15]. In the case of planar imaging, a 2D image is created; in SPECT, a volumetric image is reconstructed from a set of 2D projections. SPECT/CT provides the potential for improved quantitation by enabling attenuation correction based on the acquired CT image. Planar imaging continues to be used in many cases because it is thought to offer the advantages of fast acquisition and ease of processing compared with SPECT and SPECT/CT. A practical compromise between fully 3-D imaging and 2D imaging is a hybrid method combining SPECT imaging at a single time point with planar imaging at multiple time points to obtain pharmacokinetics for absorbed dose estimation [16, 17], understanding that the challenge of overlapping regions exists for planar imaging.

Bremsstrahlung Imaging

A special case, bremsstrahlung imaging, is used to detect the bremsstrahlung photons generated when charged particles (electrons, positrons) slow down in tissue. Bremsstrahlung radiation is produced by decelerating electrons and positrons during beta decay, has a continuous energy spectrum, and can be imaged with a planar gamma camera or SPECT [18–20]. It is used post liver radioembolization with ⁹⁰Y to monitor extrahepatic activity of ⁹⁰Y microspheres (e.g. gastrointestinal or pulmonary), as well as deposition in the tumor and the rest of the liver. However, bremsstrahlung imaging results in images with poor contrast and limited quantitative accuracy due to low photon yield and the continuous emission spectrum, which limits its use for precise dosimetry [21]. Recently, reconstruction methods have been developed [22–24] that provide good accuracy and improved image quality[25], but these methods are not currently commercially available.

Imaging Challenges for RPT

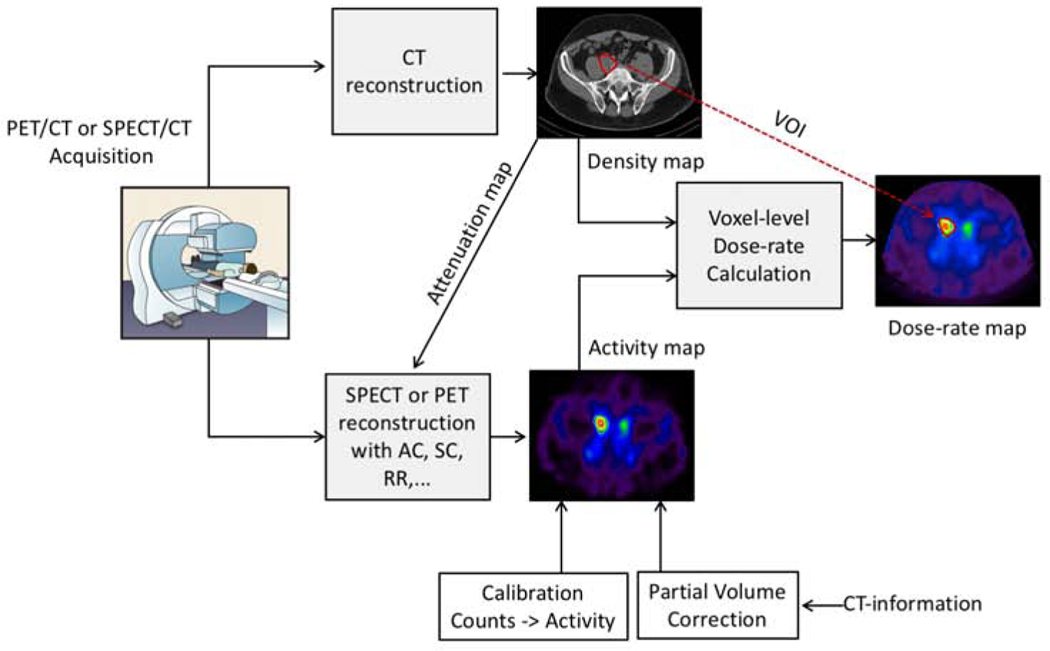
An illustration of quantitative emission tomography imaging and patient specific voxel-level dosimetry facilitated by CT information from hybrid (SPECT/CT, PET/CT) systems is shown in figure 1. Quantitative planar and SPECT imaging of therapeutic radionuclides can be more challenging than that of diagnostic radionuclides such as ^99mTc, which has a single-gamma-ray emission at 140 keV making it well suited for imaging with a standard gamma camera with a scintillator crystal and a low-energy collimator. Therapeutic radionuclides, on the other hand, are selected for their therapeutic properties, and their suitability for gamma-camera imaging is a secondary consideration. The most commonly used therapeutic radionuclides have higher energy and multiple gamma-rays both of which are not ideal for gamma-camera imaging. For example, the main gamma-ray associated with ¹³¹I is at 364 keV (82%), hence a high energy collimator with thicker septa and longer holes is used for imaging, which results in degraded spatial resolution and sensitivity compared with imaging using a low energy collimator. Moreover, the scintillator thickness of ~ 3/8” in a standard gamma-camera, though adequate to detect the 140 keV photons of ^99mTc with high efficiency is not ideal for the 364 keV gamma-rays of ¹³¹I, and hence a scanner with thicker crystals may be warranted. Furthermore, ¹³¹I has additional gamma-ray emissions at 637 keV (7.2%) and 723 keV (1.8%). Though low in intensity, these photons have a high probability of penetrating the collimator septa and ‘down scattering’ into the 364 keV photopeak acquisition window, further degrading the image quality and quantification accuracy. The multiple gamma-rays of some therapeutic radionuclides are of suitable energy and sufficient intensity for simultaneous acquisition. For example, ¹⁷⁷Lu has two relatively low intensity gamma-rays that can both be used with multi-window acquisition protocols to boost sensitivity, but accurate scatter correction becomes essential for the lower energy acquisition window because of the down scatter contribution form the higher energy emission. As with quantitative SPECT imaging, quantitative PET imaging of therapeutic radionuclides is more challenging than ¹⁸F PET. For example, ⁹⁰Y has a low-abundance positron decay mode that can be imaged with PET, but the positron branching ratio of 0.00318% introduces challenges not present in PET imaging of ¹⁸F [26, 27].

Figure 1 :

Quantitative emission tomography imaging and patient specific voxel-level dosimetry facilitated by CT information from hybrid (SPECT/CT, PET/CT) systems. This example shows imaging at a single time-point. Typically, imaging and the corresponding dose-rate maps are generated at multiple time-points to estimate absorbed dose.

In the past decade, the clinical availability of integrated functional/anatomical imaging systems (PET/CT and SPECT/CT) and iterative reconstruction that enables compensation for image degrading factors has greatly enhanced quantitative imaging of therapeutic radionuclides and facilitated patient specific dosimetry. The CT images can be used to derive patient specific non-uniform attenuation coefficient maps for attenuation correction as an alternative to maps derived from measurements with a transmission source used in the past. CT-based attenuation correction offers higher spatial resolution and contrast and rapid data acquisition compared with the long acquisitions associated with transmission measurements. The CT images can also be used in some scatter correction and partial volume correction methods as well as to define the target volumes of interest, although this is not always feasible because CT images in hybrid systems are typically acquired in low dose mode and without exogenous contrast agents. Furthermore, a CT-derived density map can be combined with the co-registered SPECT or PET based activity maps to carry-out advanced highly patient-specific voxel-level dosimetry using methods such as Monte Carlo radiation transport. The sequential acquisition of the emission and CT images on the same system reduces some of the complexity and inaccuracy associated with co-registering images acquired on separate systems, although misalignment is still present, mostly due to respiratory motion. There have been several reports on patient specific dosimetry using SPECT/CT and PET/CT systems for clinical research related to radionuclide therapy. Some examples are discussed in detail in MIRD 24 [28] and MIRD 26 [29].

PET/MR systems, in clinical use in the past few years, offer some advantages over PET/CT such as improved soft tissue contrast, simultaneous acquisition as opposed to sequential PET and CT acquisitions and potential for better motion correction. However, because MRI cannot directly assess tissue density, generation of accurate attenuation maps, a major requirement for high PET and SPECT quantitative accuracy, is a challenge[30, 31]. Use of PET/MR for clinical radionuclide therapy dosimetry studies have been reported in ⁹⁰Y radioembolization [32, 33].

Imaging System Requirements

Hardware requirements

Accurate dosimetry requires knowledge of the therapeutic radionuclide 3D distribution in the patient at one or several time points. In the past, most dosimetric calculations in internal radionuclide therapy have relied on conjugate-view planar imaging and geometric mean attenuation compensation for activity quantification. In contrast to planar imaging, SPECT and PET imaging can be used to estimate the volumes where the administered activity localizes and to estimate the 3-D activity distribution within these volumes. . This is essential in determining doses to structures and organs at risk as well as generating dose volume histograms, especially in tissues where the activity distribution is non-uniform.

System calibration

PET and SPECT imaging systems should be calibrated at regular intervals, nominally every year as currently recommended by the American College of Radiology (ACR). For centers that participate in site qualifications such as the American College of Radiology Imaging Network Centers for Quantitative Imaging Excellence (ACRIN-CQIE) for PET scanners, this involves scanning a standardized phantom and demonstrating that the imaging system achieves a Standardized Uptake Value (SUV) of 0.9 – 1.1 when imaging a uniform phantom filled with a known concentration of ¹⁸F. An additional factor is system calibration drifts, which would introduce dosimetric errors that could impact future clinical trials. As a result, use of these systems for dosimetry may require more frequent quality assurance tests performed to verify the calibration, insuring the quantitative reliability of the images.

Dose calibrators (radionuclide activity meters) are another aspect of system calibration that should be considered. These are gas-filled ionization chambers surrounding a cavity into which small volumes of radionuclides may be placed. The activity is directly reported and is routinely used to determine patient doses (how much activity is administered to the patient). Calibration of these instruments, preferably to sources with activities traceable to standards agencies, is especially important for in a therapeutic setting. Dose calibrators are also used to determine the calibration of imaging systems and an improperly calibrated dose calibrator may result in incorrect calibrations of PET and SPECT systems. The constancy of dose calibrators should be checked daily and quarterly checks of the linearity and accuracy are recommended[34].

The interplay of hardware, algorithmic, and calibration factors may limit the dosimetric accuracy and reproducibility that can be achieved with modern imaging systems. Evaluation of the effects of these factors is needed in order to make clear recommendations.

IV. DOSIMETRY

Absorbed dose calculations for RPT have traditionally followed the same schema as absorbed dose calculations for nuclear medicine imaging agents, using the absorbed fraction methodology, also known as the S value method or the medical internal radiation dosimetry (MIRD) schema. For diagnostic agents the input into this formalism is either a) planar or 3D imaging or b) by blood and urine sampling assorted with pharmacokinetic modeling. It is important to note that the absorbed fraction methodology is not in principle confined to diagnostic applications. This common miss-perception is likely rooted in the extensive use of the OLINDA/EXM software for both diagnostic and therapeutic applications, as for a long time alternative voxel-based methods were not readily available. OLINDA/EXM is indeed based on S values and was only FDA approved for use for diagnostic purposes adding to the confusion. Therapeutic dosimetry using the MIRD methodology is practicable, with a lesser degree of personalization than that of other methodologies that use patient-specific anatomical information from 3D imaging as the basis for Monte Carlo. All of the methods described below, including the absorbed fraction methodology when used for RPT, depend on personalized 3D imaging for activity or time-integrated activity (TIA) as input as well as the delineation of the tissues to be quantified and all use Monte Carlo simulations to convert the TIA values to dose rate or absorbed dose. As such, accurate imaging quantification is of paramount importance, as discussed previously, but the accuracy and precision of time point to time point image registration is equally critical to integrate the activity or the dose rate from the images, unless only one time point is required, such as for ⁹⁰Y-microspheres. The difficulty and potential inaccuracies from registration increase with smaller regions of interest. Registration accuracy can be greatly improved by positioning the patient in a reproducible and consistent position; the use of external beam-style immobilization could be a possible improvement in registration precision for RPT.

Absorbed fraction method (S value, MIRD)

In this schema, the total number of disintegrations, the TIA, in each source region is estimated and the absorbed dose to each target region is calculated by multiplying the number of disintegrations (TIA) in the source region by a dose factor specific to the source and target region pair (the S value). Classically, regions consist exclusively of organs, such that the total absorbed dose to each target organ is the sum of the absorbed dose contributions resulting from all source organs. This schema is developed in MIRD Pamphlet 21 [35] and this is the approach implemented in the commercially available OLINDA/EXM software [36]. The S values are calculated using Monte Carlo simulations with anthropomorphic phantoms and do not need to be repeated in the absorbed dose calculation by the user, who enters the TIA values (normalized to the amount of injected activity) for the relevant source regions/organs and the software provides the absorbed dose values per unit of administered activity for the desired target organs. Originally, a very schematic model of reference humans (the Christy-Eckerman phantoms [37]) were made using crude geometry for the different organs and simulations were run for a wide array of isotopes and all organs. These were the original MIRD S values. More recently, developments in technology have led a wider variety of phantoms with a greater level of realism, including voxelized, mesh, and spline phantoms and with regions that are specific to the needs of the developers, such as the use of sub-organ regions for the lungs by the ICRP Report 133. The main limitations are that i) the anatomical specificity of the patient is not taken into account. Specific patient organ masses can be input into most S value-based software which scales both the mass and the S values for greater accuracy, but the relative geometry (positions of the organs) cannot be altered. Specifically, since the phantoms represent idealized healthy humans, tumor dosimetry cannot be calculated as part of the patient dosimetry and most absorbed fraction software uses spherical models for the tumor dosimetry. ii) Uniform TIA is assumed for all regions, which for most software means uniform organ TIA However, with the development of more highly sophisticated phantoms comes an increase in the number of sub-organ regions used. Indeed, while often considered inferior to voxel-based methodologies, the absorbed fraction approach is quite versatile and is used to model and provide dosimetry for sub-organs and any regions that are below the imaging resolution of current imaging modalities.

Voxel Level Dosimetry

Voxel-level dosimetry utilizes the patient-specific three-dimensional anatomical information acquired from CT or MR scans as the basis for converting the time-integrated activity to absorbed dose and therefore has a higher level of personalization. Intrinsically, voxel-level dosimetry is more accurate than absorbed fraction dosimetry because it considers non-uniformities in the uptake and retention of the radiopharmaceutical, tissue density and tissue composition during the absorbed dose calculation, most importantly, in the lesions themselves. However, it should be noted that while information is provided at the voxel level, the quantification itself is not accurate at that level. Current imaging modalities have a resolution on the order of 4–6 mm (see previous section), such that activity can be miss-assigned to neighboring voxels, an effect known as the ‘partial volume effect’, or ‘spill-out’. Furthermore, it becomes difficult to assign voxels consistently through registration over time as they are not anatomical quantities and the TIA or absorbed dose values are further blurred across voxels. While not used in routine clinical practice, currently three main approaches exist that are capable of calculating internal dosimetry on the voxel-level: direct Monte Carlo (MC) radiation transport, dose point kernel (DPK) convolution and dose voxel kernel (DVK) convolution which uses voxel-level S-values (VSVs) based on the MIRD formalism.

Direct Monte Carlo (MC) methods

The most accurate and versatile approach for performing voxel-level dose calculations is the direct MC method. The direct MC method is a statistical approach to solving the radiation transport equation. MC simulations model each physical process that impacts transport of radiation in a medium. Individual particles are tracked from creation until the particle is absorbed, escapes the region of interest or reaches an energy that is below a user-defined threshold value. The history of the particle is determined by randomly sampling well-known probability distributions that govern the physical processes that occur during its transport. Once a desired number of particles is simulated, characteristics of the radiation field in the physical system, such as absorbed dose, can be inferred from the mean behavior of the simulated particles. In many situations, many particles (as large as hundreds of millions) may be required to accurately predict these characteristics. Therefore, direct MC simulations are more computationally demanding than other internal dosimetry approaches. Several general purpose MC codes and toolkits such as Geant4 [38], MCNP [39], or EGS [40] have been used for voxel-level internal dosimetry. Several groups have developed voxel-based MC internal dosimetry packages including DOSIMG [41], simDOSE [42], SIMDOS [43], MINERVA [44], VIDA [45], OEdipe [46], RAYDose [47], JADA [48], SCMS [49], DPM [50], and 3D-RD [51].

Dose point kernel (DPK) method

DPKs describe the dose deposition from an isotropic point source as a function of the distance from the source and are obtained from MC simulations tallying the energy deposition in concentric spherical shells around a point source in a homogeneous medium. DPK’s were first limited to monoenergetic electron sources in water [52], but eventually isotope-specific DPK’s were generated [53–55]. To account for tissue heterogeneities, the DPKs can be scaled linearly as a function of the effective density of the medium, which is proportional to the relative mass density of the medium and water [56]. The absorbed dose in a patient is determined by convolving the DPK with a patient-specific activity distribution [57]. More recently, a Collapsed cone (CC) superposition algorithm has been used to speed up the convolution of the DPK with the 3D activity distribution in heterogeneous media [58, 59].

Voxel S value (VSV) method

The VSV method was developed as an extension of the MIRD formalism from organ S values to voxel-level S values [60]. Several research and commercial software packages have been developed that utilize VSVs for internal dosimetry including: STRATOS [61], VoxelDose [62], NUKDOS [63], MrVoxel [64], VoxelMed [65], RTDS [66], and RMDP [67]. VSVs are calculated by integrating the DPK over the source and target voxels. VSVs must be tabulated for each radionuclide, voxel size, source-to-target distance, and absorbing medium. Efforts have been made to create databases of VSVs [60, 68] and different methods have been proposed for interpolating for different voxel sizes [69–71]. The voxelized dose distribution is calculated by convolving the activity distribution with the VSVs typically using a Fast Fourier Transform (FFT) or Fast Hartley Transform (FHT) [72] rather than direct convolution in order to speed up the calculation. The increase in speed comes at the cost of using a spatially invariant kernel which does not consider tissue heterogeneities. A simple density correction suggested by Dieudonné et al [73] was shown to reduce organ-level dose errors from 5.9% to 1.1% and voxel-level dose errors from 14% to 4% in the abdomen. However, the application of this technique may not be well suited for more heterogeneous regions like the thorax, head and neck, and skeletal site such as the bone marrow. For selective internal radiotherapy (SIRT) of hepatocellular carcinoma using ⁹⁰Y microspheres, VSK may be accurate in the homogeneous liver. However, in agents that may exhibit non-selective lung uptake, the differences between VSK from STRATOS [61] and MC can be up to 476% [74].

RPT dosimetry has suffered from a perceived failure to demonstrate relevance in terms of predicting biological outcome. In large part this is a result of adopting imaging and dosimetry methods that are either inaccurate (using standard planar as an imaging modality), incomplete (too few or poorly chosen time points) or devised for diagnostic imaging risk assessment rather than for therapy (using blood and urine collection). This is confounded by the fact that traditionally, no calculation of uncertainties or error bars have been associated with absorbed dose calculations in the literature, thus denying readers the ability to judge the precision and reliability of the published values. The EANM has rectified this problem by publishing a methodology and guide to calculate uncertainties for absorbed dose calculations which will benefit the field tremendously [75].

RPT dosimetry often finds itself in a vicious circle of not being used to demonstrate relevance since this relevance has not been yet demonstrated. However, a few examples that demonstrate the value of accurate dosimetry in RPT have been reported for both tumors and healthy structures[76]. These include the demonstration that progression free survival (PFS) following ¹³¹I-tositumomab radioimmunotherapy is dependent on tumor absorbed dose [77] and that red-marrow toxicity following ¹³¹I radioimmunotherapy is poorly correlated with administered activity but may be correlated to the red marrow dose or the whole body absorbed radiation dose [78]. With a critical mass of interest in the field and support by many agencies, such as the NCI, an increase in the number of dosimetric correlations with outcome can be expected soon.

There is a need for fast and accurate dosimetry for both the targets and organs at risk for patients receiving RPT. In external beam therapy, it has been demonstrated that absorbed dose differences of 7% can be clinically observed, both as additional complications to organs at risk (when the absorbed dose was later found to be higher than prescribed) and as a decrease in tumor control (when the absorbed dose was later found to be lower than prescribed) [79]. Similar observations have also been made in multi-center clinical trials[80], and this is the motivation for accurate dosimetry in external beam radiation therapy [81]. Having accurate pre-treatment estimates of absorbed dose values to targets and organs at risk may help clinicians decide between RPT and other forms of radiation therapy.

Bio-effect Modeling

Dosimetry is not limited to the calculation of absorbed dose, rather it begins with the purely physical quantity of absorbed dose and then incorporates biological input in what is known as bio-effect modeling. In external beam radiation therapy, the bio-effect quantities with the most relevance are normal tissue complication probability (NTCP), tumor control probability (TCP) and equivalent uniform dose (EUD), mostly based on the linear-quadratic model of cell survival from exposure to photon and electron radiation. This model also enables translation of absorbed dose values between different fractionation patterns using the Wither’s formula, although this model and formula is generally considered to only be valid for fractionation regimens of 5 Gy per fraction or less. This translates the biological observation that the same absorbed dose from different fractionation results in a different biological effect. The same is true in RPT, but it is the individual patient’s pharmacokinetics that regulate the dose rate, such that a same total absorbed dose for two different patients from a same radiotherapeutic will potentially have different biological effects because of the different dose rates. The dosimetric quantity used to account for these differences in traditional (beta-particle) RPT is the biological effective dose (BED); ideally, it is the BED rather than the AD which is related to effect and used for dose escalation in trials and as the basis for treatment planning. The importance of moving from AD to BED was demonstrated in the seminal study which showed a correlation between BED and kidney toxicity in peptide receptor radiation therapy [82]. Furthermore, normalization to the BED allows for translation of RPT dosimetry to external beam equivalent using the same formulas, since the BED is the equivalent of absorbed dose delivered in zero Gy fractions. This was confirmed when the MIRD Committee in Pamphlet 20 demonstrated equivalence between RPT kidney toxicity results and kidney toxicity from external beam [83].

For alpha-particle RPT (αRPT), cell-survival curves are linear rather than quadratic in the log-linear dose-survival plots, which correlates well with the observation of direct double strand break damage to the cells; furthermore the curves are generally much steeper than beta-particle curves indicating a much greater biological damage per unit of dose. The relative biological effect (RBE) relates the amount of alpha-particle absorbed dose and the amount of beta-particle absorbed dose necessary to achieve a same biological endpoint and is defined as the ratio between these two quantities, much as with particle beam therapy. Specific parameter values for the cell survival curves in response to alpha-paticle therapy are generally not well known; in practice a standard RBE value of 5 is often employed [8]; in principle, these values should be determined according to each tissue type and biological endpoint, since the RBE varies as a function of absorbed dose. Here too, an effort to standardize the RBE values by relating the alpha-particle absorbed dose either to the BED or the 2-Gy fraction equivalent dose (EQD2) has been suggested [84]. Additional dosimetric challenges for alpha αRPT include a) that localization of activity uptake often leads to localization of absorbed dose at the sub-organ level, although in principle this is not a complication that is specific to αRPT. RPT uptake of activity is driven by physiology, possibly by specific cell types or sub-structures in an organ. However, for beta-particle RPT, the range of the energy deposition often leads to a relatively uniform absorbed dose at the organ level. A notable exception is the salivary gland uptake of ¹³¹I therapy of thyroid cancer where whole organ dosimetry does not correlate well with observed toxicity [85]. This complication is more prevalent in αRPT, where the short range of emissions (50–100 μm) implies that the absorbed dose follows the localization pattern of the activity more closely. Small scale modeling has been suggested and used effectively in several instances to resolve this issue [86]. b) Many alpha-particle emitters in use have radioactive, often alpha-emitting daughters, which may re-localize after decay of the parent isotope, which can require separate activity localization measurements and dosimetric calculations. c) The high potency of alpha-emitters means that only small quantities of the radiopharmaceutical are administered therapeutically, typically on the order of several MBq (~100 μCi). This in turn makes 3D imaging difficult as the low activity results in a low count rate. These challenges will need to be addressed in order to enable a similar level of confidence and applicability in αRPT dosimetry.

IV. Pre-Clinical Testing and Clinical Trials

Pre-clinical testing for RPTs is essential to identify potential toxicities and is performed prior to clinical trials. In RPT development, dose limiting organs (DLO) and maximum tolerated absorbed dose (MTD) are identified through pre-clinical testing in relevant model systems. Compared to the administered activity (AA), the absorbed dose to DLOs or critical tissue is more closely related to potential toxicities. In preclinical studies, the administered activity is increased until toxicity is reached. Through necropsy and/or histopathology the organ responsible for dose-limiting toxicity is identified and the absorbed dose to this organ at the toxic administered activity is calculated. This is used to design Phase I trials in where the escalation variable is the absorbed dose to the dose-limiting organ. In such a trial, the activity administered is determined by a pre-treatment imaging study that is used to obtain the pharmacokinetics needed to calculate the absorbed dose to the DLO. At each dose level in the escalation scheme, the administered activity required to deliver the absorbed dose for each patient in the cohort is calculated. Patients in the same cohort may receive different administered activities as these trials are designed to maintain a maximum absorbed dose to the dose limiting organ. At this stage, if the analysis of these data suggests that there is little variation in the administered activity based on patient population, treatment based on administered activity (and not patient imaging studies) may be determined to be adequate.

In the development of a new RPT, patient-specific 3-D imaging-based dosimetry calculation methods should be implemented during Phase I trials. The clinical endpoint for Phase I trials is toxicity evaluation. Other endpoints (e.g. collection of imaging data for dosimetry, pharmacokinetic analysis) may be included to better understand the treatment. As clinical trials with internal radionuclide therapy are proposed, accurate dosimetry will serve to mitigate uncertainties in these trials and may help smaller treatment effects to be observed in a standard cohort of patients, or to observe larger effects in a smaller cohort of patients[87]. Accurate dosimetry is a prerequisite for treating patients with RPT who have the potential for a curative intent of treatment. Currently, thyroid carcinoma is treated with a curative intent with ¹³¹I, but most patients and indications treated with RPT are palliative. Outside of radiation oncology, it is not common to distinguish the intent (palliative or curative) when treating patients with RPT. Furthermore, reporting absorbed dose to tumors and normal tissues will allow for the unification and comparison of radiation absorbed dose response across the three modalities of radiation therapy: external beam radiation therapy, brachytherapy, and RPT.

V. CONCLUSIONS

We have endeavored to highlight the advantages of incorporating image-based dosimetry methodologies in the routine use of RPTs and in the design of RPT clinical trials. The tools required for calculating absorbed dose in RPT are already available. By allowing for a more efficient escalation scheme and better patient selection, use of RPT dosimetry early in the development of new RPT agents will help reduce the time required to bring these promising new agents to the clinic. Such an approach also has the advantage of unifying RPT with other forms of radiation therapy. This is achievable due to available imaging technologies where the radionuclide is imaged with either quantitative PET or SPECT, accurate volume contouring is done using anatomical images (e.g. CT, MRI) and precise dosimetric calculations based on either voxel-level Monte Carlo or absorbed fraction methods are employed. The increased availability of radionuclides with therapeutic and imaging potential will further the field of RPT. With care given to the imaging and image-based dosimetric calculations, uncertainties in the absorbed doses (or BEDs) to targets and organs at risk can be minimized, paving the way for meaningful clinical trials and routine use of RPTs that include dosimetric personalization[88, 89], combination therapy (e.g. RPT combined with chemotherapeutic agents or immunotherapies) and radiobiological treatment planning[90, 91].

The future of RPT includes a path towards targeted radiation therapy that spares healthy tissues and where user-variability is minimized. It provides the added benefit that RPT does not rely on costly infrastructure at the hospital level (e.g. linear accelerators) and can be administered at both academic and community centers, increasing patient access to cutting-edge medicine. Radiopharmaceutical therapy will be a powerful tool in the radiation therapy armament once image-based dosimetric calculations are performed for every patient.