Modeling hyperpolarized lactate signal dynamics in cells, patient-derived tissue slice cultures and murine models

Abstract

Determining the aggressiveness of renal cell carcinoma (RCC) noninvasively is a critical part of the diagnostic workup for treating this disease that kills more than 15,000 people annually in the USA. Recently, we have shown that not only the amount of lactate produced, as a consequence of the Warburg effect, but also its efflux out of the cell, is a critical marker of RCC aggressiveness and differentiating RCCs from benign renal tumors. Enzymatic conversions can now be measured in situ with hyperpolarized (HP) ¹³C magnetic resonance (MR) on a sub-minute time scale. Using RCC models, we have shown that this technology can interrogate in real time both lactate production and compartmentalization, which are associated with tumor aggressiveness. The dynamic HP MR data have enabled us to robustly characterize parameters that have been elusive to measure directly in intact living cells and murine tumors thus far. Specifically, we were able to measure the same intracellular lactate longitudinal relaxation time in three RCC cell lines of 16.42 s, and lactate efflux rate ranging from 0.14 to 0.8 s⁻¹ in the least to the most aggressive RCC cell lines and correlate it to monocarboxylate transporter isoform 4 expression. We also analyzed dynamic HP lactate and pyruvate data from orthotopic murine RCC tumors using a simplified one-compartment model, and showed comparable apparent pyruvate to lactate conversion rate (k_PL) values with those measured in vitro. This kinetic modeling was then extended to characterize the lactate dynamics in patient-derived living RCC tissue slices; and even without direct measurement of the extracellular lactate signal the efflux parameter was still assessed and was distinct between the benign renal tumors and RCCs. Across all these preclinical models, the rate parameters of k_PL and lactate efflux correlated to cancer aggressiveness, demonstrating the validity of our modeling approach for noninvasive assessment of RCC aggressiveness.

1 ∣. INTRODUCTION

Conventional cross-sectional imaging using MRI has been an important part of the diagnostic workup of renal cell carcinoma (RCC), which is responsible for more than 15,000 deaths annually in the USA. A key challenge in the management of RCCs is the inability to noninvasively assess the tumor aggressiveness for optimal treatment choice, which ranges from active surveillance to surgical resection. With the advent of metabolic imaging via hyperpolarized (HP) carbon-13 MRI, it is now feasible to assess tumor metabolism in situ. Dysregulated metabolism has been implicated as a key driver of development and progression of RCC.¹ More specifically, elevated lactate dehydrogenase A (LDHA, the enzyme isoform responsible for preferential conversion of pyruvate to lactate²) and monocarboxylate 4 (MCT4, the transporter predominantly through which the excess lactate generated via LDHA is extruded to maintain physiological pH inside the cell³), have been shown to be prognostic indicators of RCC.^4,5 HP MRI provides a means to assess these enzyme and transporter activities noninvasively.⁶ A series of work ranging from RCC cells to patient-derived RCC tissue to murine RCC models has been used to demonstrate that both lactate production and its efflux are hallmarks of aggressive cancers and can be assessed by HP ¹³C MR.⁷ This work and others^8-11 highlight the differential compartmentation of lactate that occurs during the lifetime of the HP signals, making modeling of these signals difficult. This is due in part to the challenge in measuring the membrane transport rates and intracellular relaxation rates in situ. Here, we present comprehensive modeling of the HP lactate signals arising from the intracellular and extracellular compartments following HP [1-¹³C] pyruvate administration to measure directly, in real time, the intracellular lactate longitudinal relaxation rate and the rate of transport of lactate from the intracellular compartment to outside the cell, k_LEfflux. These values are crucial in interpreting and modeling the in vivo HP data where these parameters are either assumed or fixed to values of the extracellular compartment, thereby obfuscating the subtleties in disease pathology.

2 ∣. MATERIALS AND METHODS

2.1 ∣. Cell lines

All three cell lines were grown in monolayers in Dulbeco's Modified Eagle's medium with 4.5 g/L glucose media with 10% serum. HK-2 cell line¹² and A498 cell lines were purchased from ATCC (Manassas, VA, USA). The other two cells lines, UMRC6 and UOK262, were a kind gift from Dr. Bart Grossman (MD Anderson Cancer Center, Houston, TX, USA) and Dr. W. Marston Linehan (National Cancer Institute, Bethesda, MD, USA), respectively. The UMRC6 cells were derived from a localized human clear cell RCC.¹³ The UOK262 cells were derived from a metastasis of the highly aggressive hereditary leiomyomatosis RCC.

2.2 ∣. MR experiments

2.2.1 ∣. HP ¹³C MR acquisition of cells and tissues perfused in a bioreactor

A 500 MHz Varian Inova (Agilent Technologies, Palo Alto, CA, USA) equipped with a 5-mm broadband probe was used for the bioreactor studies; 16 mol [1-¹³C] pyruvic acid was polarized in a HyperSense instrument (Oxford Instruments, Oxford, UK) and injected into a NMR-compatible cell and tissue perfusion system (bioreactor) over 90 s, as previously described.¹⁴ A 30° flip angle was used to acquire carbon data every 3 s for a total of 5 min (sweep width of 200 ppm and an acquisition time of 1 s).

2.2.2 ∣. Characterization of HP substrates’ relaxation rates and the bioreactor flow conditions

To better characterize the impact of the bioreactor flow on the metabolites’ signal dynamics and model it rigorously, the bioreactor was filled with 250 μL of cell-free alginate microspheres and perfused with the same media as if cells were present and flowing at the same rate of 0.5 ml/min with oxygen at 1 ml/min. The HP [1-¹³C] pyruvate and [1-¹³C] lactate (900 μl) were injected at 0.5 ml/min over 90 s.

2.2.3 ∣. Cells in 3D culture perfused in a MR-compatible bioreactor

As described previously,¹⁴ 200–250 μl of cells encapsulated in alginate microspheres were maintained at physiological conditions in the 5-mm MR-compatible bioreactor. The MCT4 inhibitor, 1 mM 4,4′-diisothiocyanatostilbene-2,2′-disulfonic acid, disodium salt (DiDS; Molecular Probes, Life Technologies, Foster City, CA, USA), was added to the cell perfusate medium via a filter after baseline carbon measurements were made in a subset (n = 4) of experiments with the UOK262 cells.

2.2.4 ∣. Renal tissue slice bioreactor set-up

As described in detail previously,⁷ 300-350 μm-thick tissue slices from nephrectomized samples after culturing overnight in specialized medium¹⁵ were perfused in the 5 mm MR-compatible bioreactor using a microengineered construct to hold the tissue in place to assess its metabolism in benign (n = 3) and clear RCC tissue slices (n = 6).

2.2.5 ∣. Imaging of orthotopic murine model

Mice implanted with UOK262 cells (n = 7) and A498 cells (n = 3) in the renal capsule were imaged on a 14.1-T vertical bore microimaging system (Agilent, Palo Alto, CA, USA), as detailed previously.¹⁶ Briefly, upon injection of 350 μl of 80 mM [1-¹³C] pyruvate via the tail vein, in less than 15 s, a 2D dynamic EPI sequence with spectrally and spatially selective RF pulses was used to image HP [1-¹³C] pyruvate and [1-¹³C] lactate sequentially. A constant flip angle of 90° was used for lactate, with acquisition beginning at 15 s and measured every 3 s for 17 time points; while, pyruvate was measured using a variable flip angle ranging from 2-90°, with acquisition beginning 6 s from the start of the injection and measured every 3 s thereafter for 20 time points. Additionally, T2-weighted and diffusion-weighted proton images were acquired with the following parameters: matrix size, 256 × 192; field of view, 32 × 32 mm; slice thickness, 2 mm; and b-values of 25, 180, 323 and 508 s/mm, as detailed in Sriram et al.¹⁶ Mean tumor aparent diffusion constant (ADC) was calculated from manually segmented tumor ROIs after voxel-wise monoexponential fitting of diffusion-weighted images for each slice encompassing the entire tumor.

2.3 ∣. LDH activity

Total LDH activity was measured spectrophotometrically by quantifying the linear decrease in nicotinamide adenine dinucleotide (NADH) absorbance at varying pyruvate (sodium salt) concentrations at 339 nm for 10 min.¹⁷ Semiconfluent cells were harvested and 1 million cells were lysed (in buffer with 50 mM Tris pH 8.2, 2 mM DTT, 2 mM EDTA, 1% Triton x-100). LDH assays were then carried out on the lysates added to varying concentrations of pyruvate and NADH (in excess) in a 96-well plate in triplicate using a microplate reader (Infinite, Tecan Instruments, Switzerland). LDH activity was plotted against the pyruvate concentration to arrive at the maximum velocity (Vmax) and the Michaelis–Menten constant (Km) using the Lineweaver-Burk plot.

2.4 ∣. Quantitative real-time polymerase chain reaction

Quantitative real-time polymerase chain reaction (qRT-PCR) was performed as described previously¹⁴ on the total RNA extracted from the cells with RNAeasy procedure kit (Qiagen, USA). Assays for MCT4 (Hs00358829_m1) and LDHA (Hs01378790_g1) were procured from Applied Biosystems (Foster City, CA, USA) and expressed relative to cyclophilin housekeeping gene (Amplicon: TCTCAAATCAGAATGGGACAGGTGGAGAAAGTATTTATGGTGAAAAATTTGAAGATGAAAATTTCCATTACAAGCATGATCGGGAGGGTTTACTGAGCATGGCAAATGCAGGCCGCAACACAAACGGTTCTCA. Forward: TCTCAAATCAGAATGGGACAGGT. Reverse: TGAGAACCGTTTGTGTTGCG. Probe: TTC CAT TAC AAG CAT GAT CGG GAG GGT).

2.5 ∣. Data analysis

The dynamic HP MR data were processed and analyzed using ACD/Labs software (Toronto, Ontario, Canada) with 0.5 Hz line broadening and Lorentzian peak fitting (using “peakfit” routine) after proper phasing and spline-based baseline correction for each metabolite.

2.5.1 ∣. Modeling of pyruvate and compartmentalized lactate HP signals in cells

As previously published,¹⁴ the intracellular and extracellular lactate peaks were distinguished via the 3 Hz chemical shift difference. The kinetic data were modeled using a three-compartment model (the input/supply function, the intracellular and extracellular; Figure S1) shown in the system of differential equations,

$$\frac{d}{dt}\left[\begin{array}{c}\hfill Pyr(t)\hfill \\ \hfill La{c}_{in}(t)\hfill \\ \hfill La{c}_{ex}(t)\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill -R_{1P}-k_{PL}-F_P\hfill & \hfill k_{LP}\hfill & \hfill 0\hfill \\ \hfill k_{PL}\hfill & \hfill -R_{1La{c}_{in}}-k_{LP}-k_{L_{Efflux}}\hfill & \hfill k_{L_{Influx}}\hfill \\ \hfill 0\hfill & \hfill k_{L_{Efflux}}\hfill & \hfill -R_{1La{c}_{ex}}-k_{L_{Influx}}-F_L\hfill \end{array}\right]\left[\begin{array}{c}\hfill Pyr(t)\hfill \\ \hfill La{c}_{in}(t)\hfill \\ \hfill La{c}_{ex}(t)\hfill \end{array}\right],$$

where the change in pyruvate magnetization, Pyr(t), is assumed to depend upon the longitudinal relaxation rate of HP [1-¹³C] pyruvate, R_1P, the kinetic rate constant for conversion from pyruvate to lactate by LDH, k_PL, and its backward rate constant, k_LP, as well as F_P, a rate constant that models the loss of pyruvate magnetization due to the constant flow of the bioreactor system.

Similarly, the change in intracellular lactate magnetization depends upon k_PL and k_LP, intracellular lactate relaxation rate, R_1Lacin, as well as k_LEfflux, the rate of transport of lactate out of the cell and k_LInflux, the rate of lactate uptake. Lastly, R_1Lacex is the rate of extracellular lactate relaxation and F_L is a rate constant that models the effects of loss of lactate magnetization due to the constant flow of the bioreactor system and is distinct from that of pyruvate due to transport through the alginate beads.

The kinetic data were modeled using the three-compartment model in Matlab in a stepwise manner to reliably estimate the kinetic parameters (Supplemental data S1), assuming a gamma variate input function (IF). In order to fit the data, we assumed that the IF was similar between samples. In this case, the matrix differential equation in Equation 1 can be solved as

$$Met(t)=e^{A(t-t_0)}{x}_0+I{F}^{\prime },$$

where Met = metabolite (pyruvate, lactate, etc.), A is the system matrix in Equation 1, x₀ is the metabolite's magnetization at time t₀, and IF’ is the gamma variate input function value at a given time point. This solution was implemented discretely to also include the effects of RF excitation as

$$Met[t_n]=e^{A\cdot TR}\mathsf{x}[t_{n-1}]\cos (\theta )+IF[t_{n-1}],$$

where θ is the flip angle for the discretely sampled time points at t = t_n. Fitting data to this solution was optimized using a constrained, nonlinear least squares regression solver that utilizes a trust-region-reflective algorithm in Matlab, as in Larson et al.¹⁸ The code utilized to analyze data from all experiments is located in the GitHub repository (https://github.com/FayyazA/bioreactor-kinetic-analysis).

2.5.2 ∣. Modeling of bioreactor flow parameters and solution state HP substrate relaxation rates

The pyruvate magnetization was modeled as an IF based on the gamma-variate distribution, Γ(k), as

$$IF(t)=\frac{t^{k-1}{e}^{-t∕\theta }}{{\theta }^k\Gamma (k)},\text{where}\Gamma (k)={\int }_0^{\infty }{t}^{k-1}{e}^{-t}dt.$$

The shape parameters k and θ were characterized by repeated injections (n = 2) of HP [1-¹³C] pyruvate, [1-¹³C] lactate and ¹³C urea into bioreactors loaded with cell-free alginate microspheres, as described in Sriram et al.¹⁴ Furthermore, the HP [1-¹³C] pyruvate, ¹³C urea and [1-¹³C] lactate magnetization relaxation rates were modeled using a simplified equation for each metabolite, Met(t), magnetization as a function of its relaxation rate, R₁, and flow due to the bioreactor alone, with the IF modeled as described above with tight constraints based on the a priori knowledge of the solution state relaxation rates of the HP ¹³C substrates at this field (11.7 T):

$$\frac{dMet(t)}{dt}=-(R_1-F)\mathsf{x}Met(t).$$

2.5.3 ∣. Synthetic data analyses to assess parameter interdependencies and model robustness

Synthetic data were generated by using the objective function, which calculates the input function and matrix exponential to generate Pyr(t), Lac_in(t) and Lac_ex(t), then combining them to provide an estimate of the fit. Two sets of analyses were performed using synthetic data.

1). Influence of initial value in modeling:

In the first experiment, the 12 kinetic parameters were each set to their average value across all cell lines and synthetic data were generated using these average values. This was then refit over 120 trials, where each parameter had its initial value varied (within the boundary conditions) in linear increments of 1/10th of that range. The normalized error as a percentage of the expected parameter estimate was then calculated by:

$$\text{Normalized error}=\frac{\text{Estimated value}-\text{Known value}}{\text{Known value}}\times 100\%.$$

The Pearson correlation coefficient between the initial conditions and normalized errors, as well as the range of each parameter's normalized errors, are then calculated to demonstrate how much of an effect the initial condition has on the final estimate of the parameter.

2). Interdependence of parameter estimates:

The second experiment used largely the same set of 12 average values for each parameter but kept all the initial conditions the same throughout all 60 trials. Instead, 11 parameters were held fixed at the previous average values, while one was varied over the numerical range (set as the boundary condition for modeling) in linear increments of 1/5th of that range. The normalized error was calculated using the same formula as above. The Pearson correlation coefficient between the parameter that was modulated to generate new synthetic data and every parameter's normalized error at these parameter values was calculated; each parameter's maximum normalized error was also denoted to determine what the worst case error was in a given parameter when another parameter used to generate synthetic data was modulated. With a perfect model, changing any parameter used to generate synthetic data should still result in a normalized error of 0, thus revealing which parameters are correlated. Due to computational issues with certain parameters like k_LP and k_LInflux having infinitesimally small values, normalized errors at minimum boundary conditions reached extremely large values, and thus, the first out of five trials were discarded for each parameter so that only 48 trials were counted in the results.

2.5.4 ∣. Modeling of HP [1-¹³C] pyruvate and [1-¹³C] lactate HP signals in patient-derived tissue slices

Tissue slice modeling was carried out similar to the cell culture bioreactor model, with a few notable exceptions. Due to insufficient homogeneity in the tissue slices, the intracellular and extracellular lactate peaks could not be distinguished, and the system of differential equations was simplified to

$$\frac{d}{dt}\left[\begin{array}{c}\hfill Pyr(t)\hfill \\ \hfill Lac(t)\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill -R_{1P}-k_{PL}-F_P\hfill & \hfill k_{LP}\hfill \\ \hfill k_{PL}\hfill & \hfill -R_{1L}-k_{LP}-F_L\hfill \end{array}\right]\left[\begin{array}{c}\hfill Pyr(t)\hfill \\ \hfill Lac(t)\hfill \end{array}\right],$$

where R_1L describes the apparent relaxation rate of lactate due to the impact of different microenvironments. The IF was kept the same, as detailed in Equation 4.

2.5.5 ∣. Modeling of murine HP [1-¹³C] lactate

The most simplified, unidirectional, single-compartment, inputless model¹⁹ was used to fit the dynamic HP [1-¹³C] lactate signal from mice bearing UOK262 and A498 orthotopic tumors. The system of differential equations used to analyze the signals was

$$\frac{d}{dt}\left[\begin{array}{c}\hfill Pyr(t)\hfill \\ \hfill Lac(t)\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill -R_{1P}-k_{PL}\hfill & \hfill 0\hfill \\ \hfill k_{PL}\hfill & \hfill -R_{1L}\hfill \end{array}\right]\left[\begin{array}{c}\hfill Pyr(t)\hfill \\ \hfill Lac(t)\hfill \end{array}\right].$$

Because the model is unidirectional, it assumes only a conversion from the pyruvate pool to the lactate pool. The model also allows for variable flip angles by utilizing a hybrid discrete-continuous model that converts the measured signal to the magnetization after RF excitation. The model only fits the output lactate signal and does not compute a pyruvate signal fit.

3 ∣. RESULTS AND DISCUSSION

3.1 ∣. Characterization of bioreactor flow parameters as well as relaxation rates of HP signals

Because the flow conditions and infusion were maintained between experiments in the bioreactor set-up, we sought to characterize the flow parameters and relaxation rates in a cell-free setting. For this purpose, simultaneous infusions of copolarized pyruvate, lactate and urea into cell-free alginate microspheres were performed to assess the parameters of k and θ of the gamma variate input function. Furthermore, urea was used as a control substrate that should yield similar results for flow and input function characteristics as the metabolites of interest, namely, pyruvate and lactate. The cell-free alginate microspheres provided a similar filling factor of the bioreactor in terms of flow features while excluding metabolism of the substrates. Upon modeling of the parameters, as shown in Equation 5, the bounds for the relaxation rates of the three substrates were restricted to ± 3 s of the measured solution state relaxation of the three substrates at the 11.7 T field strength of 48, 38 and 44 s for pyruvate lactate and urea, respectively.^20,21 We quantified the following values: F = 0.169 ± 0.029, k = 2.96 ± 0.03, and θ = 16.05 ± 1.31. Additionally, the R₁ of each substrate was estimated as follows: pyruvate = 0.0206 ± 0.0001, lactate = 0.0272 ± 0.0000, and urea = 0.0221 ± 0.0001. These values were then used for subsequent modeling of biological data for all bioreactor experiments, while using the lower and upper bounds for each parameter, based on the maximum and minimum from these results (Table S1). Because flow is a significant parameter, which is an order of magnitude higher than the relaxation rate (or more), estimating this value carefully is of paramount importance. We were able to achieve this by modeling the data from the cell-free bioreactor set-up.

3.2 ∣. Estimation of intracellular relaxation and efflux rate of lactate in cells encapsulated in alginate microspheres and perfused in the microengineered bioreactor

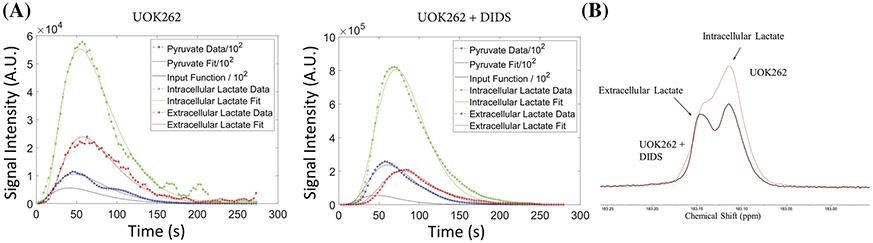
The excellent magnetic field homogeneity obtainable in the cell culture bioreactor allowed for distinction of intracellular and extracellular lactate peaks (0.02 ppm apart), as detailed and validated in Sriram et al.¹⁴ Figure 1 shows representative data and resultant modeled curves for pyruvate, intracellular lactate, and extracellular lactate signal curves versus time for the UOK262 cells and the UOK262 cells treated with DIDS inhibitor. The constraints used for the various parameters are detailed in Table S2. The black line shows the modeled input function that accounts for a sub-stantial percentage of the pyruvate signal as expected, because the lactate signal (arising from the pyruvate signal) is two orders of magnitude lower than that of pyruvate. This is also in line with our prior observation²² in a similar bioreactor set-up with a comparable filling factor using the same UOK262 cells, that the intracellular pyruvate signal constituted ~1% of the injected dose. Representative fits for the other cell lines are shown in the supporting information (Figure S2), and a mean R-squared value ranging from 0.968 to 0.997 (Table S3) demonstrates robust fitting. The average normalized root mean square error (NRMSE) ranges from 8% to 25%. The pyruvate signal yielded the best fits of all modeled HP signals, averaging 8% ± 0.6% NRMSE, largely attributable to the iterative stepwise fitting approach, while the lactate signals (intracellular and extracellular) had a slightly lower NRMSE (15% ± 1.2%). The R₁ parameter for pyruvate was tightly constrained between 0.0196 and 0.0213 s⁻¹ and, as can be seen from Table 1, there is no significant difference between R₁ values across the cells (including the ones treated with small molecule inhibitor). The mean R₁ of pyruvate across the cells is 0.0200 ± 8.65 x 10⁻⁵ s⁻¹. Similarly, the R₁ of extracellular lactate constrained between 0.0265 and 0.028 s⁻¹ resulted in a mean value of 0.0273 ± 0.0013 s⁻¹ across the cells (Table 1). The ability to measure the compartmentalization of the lactate HP signal enables the modeling and thereby measurement of the intracellular lactate relaxation rate. Similar to pyruvate and extracellular lactate values, the intracellular lactate relaxation rate also converged to a mean intracellular lactate relaxation rate of 0.0609 ± 0.0057 s⁻¹ (Table 1). This is the first measure of intracellular lactate relaxation rate in situ, which was made feasible by the excellent homogeneity afforded by the bioreactor set-up. Prior measures of intracellular relaxation rates were indirect and involved the use of paramagnetic species (in the form of gadolinium-based contrast agents)^9,10 to quench the extracellular signal and determine the intracellular lactate signal alone; or it required the use of artificial systems^10,23 (mimicking the viscosity of the intracellular component), or modeling the single lactate signal using multiple relaxation rates (and other variables).²⁴ Such measurements of lactate relaxation times were in the range of 15 to 25 s. Our measure of 16.42 s suggests that the lower end of the range is a more realistic estimate of the intracellular longitudinal relaxation time.

FIGURE 1.

Representative plots of HP pyruvate, intracellular lactate and extracellular lactate signal over time (individual points) and the resultant fits (smooth lines) for each metabolite for (A) UOK262 control, (B) UOK262 with DiDS treatment and (C) shows the region of intracellular and extracellular HP lactate region of UOK262 cells with and without DiDS treatment

TABLE 1.

Average ± standard error of pyruvate, intracellular lactate, and extracellular lactate R₁s in cell culture bioreactor model calculated by kinetic model

Relaxation rate (s−1)	HK-2	UMRC6	UOK262	UOK + DIDS
Pyruvate	0.0203 ± 3.05E-04	0.0201 ± 7.96E-06	0.02 ± 1.45E-04	0.0199 ± 1.38E-04
Lactate intracellular	0.06 ± 0.0208	0.0584 ± 0.0171	0.0586 ± 0.0054	0.0677 ± 0.0156
Lactate extracellular	0.0266 ± 4.51E-05	0.0274 ± 3.73E-04	0.0275 ± 1.79E-04	0.0273 ± 2.97E-04

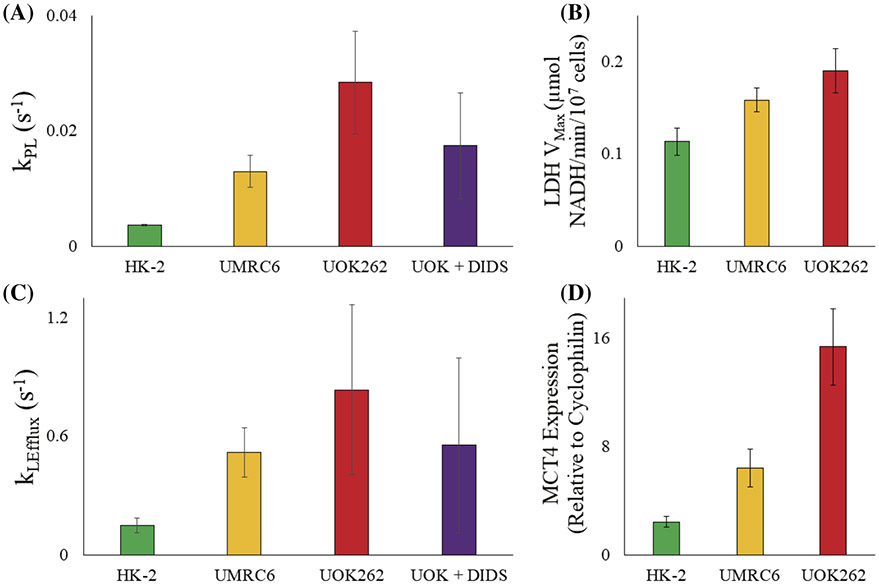
Figure 2 depicts the trends in the apparent kinetic rate constant and the corresponding protein activity or expression in the different cell lines. The apparent rate of conversion of pyruvate to lactate (k_PL) increases from HK-2 (0.0037 ± 0.0001 s⁻¹) to UMRC6 (0.013 ± 0.003 s⁻¹) to UOK262 (0.028 ± 0.009 s⁻¹). This is corroborated with the LDH activity of the three cell lines, which also increased from HK2 to UMRC6 to UOK262, with a highest mean V_Max of 0.113 ± 0.015, 0.158 ± 0.013 and 0.190 ± 0.024 μmoles NADH/min/10⁷ cells, respectively, congruent with our prior observations.¹⁴ Similar trends between the modeling parameter k_LEfflux, the rate of lactate transport from inside to out of the cell, and MCT4 expression, the transporter predominantly responsible for efflux of lactate out of the cell,^25,26 were found. The HK-2 cell line had the lowest average k_LEfflux value at 0.147 ± 0.038 s⁻¹ and the lowest MCT4 expression relative to cyclophilin of 2.43-fold, followed by UMRC6 of 0.519 ± 0.126 s⁻¹ and 6.41-fold, respectively, with the highest in UOK262 of 0.835 ± 0.430 s⁻¹ and 15.39-fold. Furthermore, upon inhibition of the MCT4 transporter using a small molecule (DiDS), which is nonspecific for MCT4, a reduction in both k_PL and k_LEfflux of 39% (0.028 to 0.017 s⁻¹) and 34% (0.834 to 0.553 s⁻¹) was observed, respectively, compared with the untreated UOK262 cells. These results showcase the range of transport and enzymatic conversion rates and highlight their dependence on the underlying biological system. For the renal cell lines studied here, the rate of MCT-facilitated transport of lactate is consistently much higher (greater than 2-fold) than the LDH-mediated conversion from pyruvate. It is important to note that while we expect LDH to be operating at near equilibrium, MCT will be functioning well below its Km, which ranges from 3.5 (for MCT1) to 30-40 mM (for MCT4).^3,27 Because only 750 μL of 12 mM pyruvate was injected into the bioreactor over a 90-s period, and was further diluted by a flowing bioreactor (0.5 ml/min) with a media volume of 2.5 ml before it reached the cell-laden alginate microspheres, we expected that during the course of the HP experiments that MCT4 was not saturated, even if 100% of the injected pyruvate was taken up by the cells and converted to lactate. Other measures of lactate efflux rate using the HP lactate signal ranged from 0.038²⁴ to 0.3²⁸ s⁻¹ in PC3 cells and from 0.009²⁴ to 0.25⁹ s⁻¹ in MCF-7 cells. These ranges of values highlight the nuances in assessment of the lactate transport rate using HP signals, which is characteristic of the cell line under study and is heavily influenced by the modeling parameters as well as the experimental set-up. For instance, the study by Breukels et al.²⁸ was performed in a highly homogenous modified Shigemi NMR tube that allowed the intracellular and extracellular HP lactate signals to be resolved. However, the modeling used to extract the lactate transport value assumed that intracellular and extracellular lactate magnetization had the same longitudinal relaxation, as it best fitted their data. This would have a direct impact on the transport rate as both the movement of lactate out of the cell, as well as that of the longitudinal relaxation rate, would be additive in their contribution to the decrease in the intracellular lactate signal. Furthermore, the experimental set up of 2.5–5 mM pyruvate concentration injected into the NMR tube (and retained in the same space for the entirety of the measurement) combined with the efflux of lactate in the same extracellular space could alter the MCT rate kinetics. This work strives to circumvent some of these hurdles by minimal assumptions and a well-characterized continuous perfusion system that allows the cell metabolism to be studied in situ with little alteration to the physiological parameters in the extracellular space.

FIGURE 2.

Average ± standard error for apparent rate constants, associated LDH activity and MCT4 expression from cell culture bioreactor model. (A) Model-calculated mean kPL for the three cell lines and UOK262 cells treated with DiDS inhibitor; (B) lactate dehydrogenase activity (n = 3) for the three cell lines, as determined by calorimetric assay; (C) model-calculated mean kLefflux for the three cell lines and UOK262 cells treated with DiDS inhibitor; and (D) MCT4 tRNA expression (n = 3) for each cell line relative to its cyclophilin expression, as determined by qRT-PCR

The average value ± standard error for the remaining parameters fit by the model are provided in the supporting information (Table S4). Notably, the average values for k_LP and k_Linflux were found to be effectively 0 s⁻¹. The F_P parameter was largely constant across cell lines, in the 0.1–0.2 s⁻¹ range, which indicates that the flow was affecting the pyruvate magnetization roughly equally across cell lines. However, F_L, the loss of lactate magnetization attributed to flow, increased from HK-2 to UOK262 by 0.08 to 1.82 s⁻¹. This suggests that the flow parameter for lactate is convolved with the efflux rate due to cellular processes and merits further investigation. In fact, k_Lefflux and F_L are strongly correlated (R-squared of 0.8259 and p < 0.0001 using Pearson two-tailed correlation; Figure S2). While most parameters fit well within the bounds used for each variable, Table S5 shows the details for each replicate of the cell lines.

One of the shortcomings of the experimental set-up is the use of a large RF flip angle (30°), which could have an impact on the modeling parameters. Our fitting approach used a hybrid discrete-continuous model that specifically includes RF flip angle compensation and can ideally account for these large flip angles. Although the calibration of the RF coil was performed regularly, the flip angle compensation becomes challenging in the presence of flow and RF coil edge or slice profile effects.²⁹

3.3 ∣. Assessing model stability and parameter interdependence using synthetic data

The synthetic data experiments largely show that the model is effective at finding minima (local or global) regardless of a parameter's initial value and confounding effects from other kinetic rate parameters.

1. Influence of the initial value in modeling: Ideally, if our model was perfect, the normalized errors would be equal to 0; however, because there is variation in errors, the impact of the initial value used for modeling is expressed as the range of normalized error for each parameter in Table 2. Overall, most of the parameters (R_1P, k_PL, F_P, K_Lefflux, R_1Lex, and F_L) had ranges of normalized errors within fractions of a percent to 15%, so the magnitude of the effect of the initial condition is negligible. However, the parameter R_1Lin had a strong correlation between the initial value and the normalized error (p = 0.99) with a maximal error of 102%. The parameters K_LP and K_Linflux were not considered, as they were found to be negligible in the modeling results from the cell data. This validates the model as 10 out of 12 parameters successfully converge to their correct local minima in such a way that the errors in their estimates are negligible.

2. Interdependence of parameter estimates: The Pearson correlation matrix is computed for non-negligible parameters (Table S6). As can be noted, every parameter is incidentally correlated with the error in the other parameter estimates; this is because, as the synthetic data changes slightly, different parameters in the main diagonal of the matrix (Equation 1) can shift relative to one another slightly to improve the fit during optimization. These adjustments likely result in these correlations with the other parameters, but the magnitude of the association between parameters also plays a major role in the final parameter estimates. To parse out the importance of this interdependence we then looked at the maximal normalized error in the other parameter's estimate by varying the first parameter's true value, as shown in Table S7. As can be seen, the maximal error for other estimates are no more than 30%. Using a threshold of 0.7 for Pearson correlation and more than 30% maximal error as the cutoff between negligible and non-negligible changes in estimates, the only significant interactions were between k_LP and k_LInflux with the other parameters. These interactions are inconsequential because both parameters are negligible compared with the kinetic parameters describing the reverse reaction, k_PL and k_LEfflux. Because both parameters have known values that are infinitesimally small, this again causes extremely large errors when other parameters are adjusted slightly in the matrix, making it appear as though there are large changes in the estimates of these parameters when in reality they are negligible.

TABLE 2.

Impact of the initial parameter estimate on the resulting model fit, as characterized by the range of the normalized error of each parameter. The initial values were varied between its minimum and maximum value from cell modeling, n = 5

	Range of % error (max.-min.)
R 1P	6.5125
k PL	10.0147
FP	0.2925
R 1Lin	103.6789
k LEfflux	0.1282
R 1Lex	5.4421
FL	15.8624

3.4 ∣. Modeling of kinetic rate parameters of patient-derived renal tissue slices perfused in the microengineered bioreactor

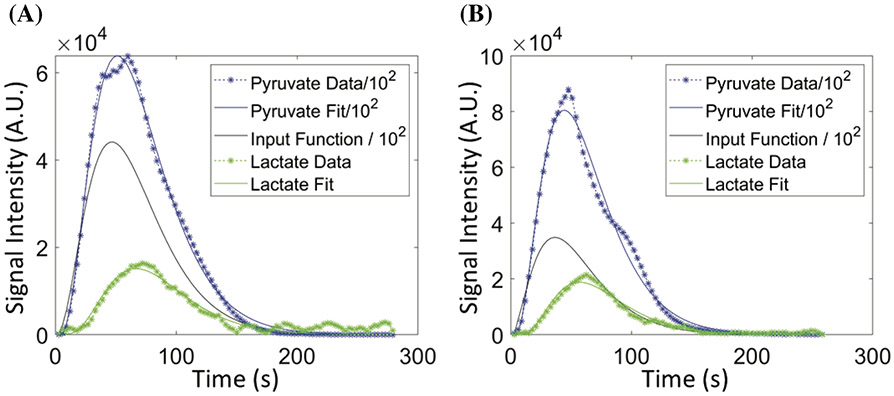
Due to larger inhomogeneity in the tissue slices compared with cells in the bioreactor, intracellular lactate and extracellular lactate peaks could not be distinguished in the majority of the data sets, and only a larger combined lactate peak could be observed. Figure 3A,B depict representative plots of HP [1-¹³C] pyruvate and [1-¹³C] lactate signal over time and model-produced fits. Because of the negligible k_Linflux (based on the modeling results from the cell data) and simplification of the differential equations (Equation 6), the parameter F_L is representative of the lactate magnetization loss not only attributable to the flow of the perfusate media, but also to that of the physical transport across cell membrane. The boundary conditions of all the kinetic rates and input function were set to be similar to those of the cells, and the fit within these constraints for each data set are given in Tables S8 and S9. Similar to the fits of the HP signals from the cells in the bioreactor, the fits were robust, resulting in mean R-squared values ranging from 0.956 to 0.997 across both tissue slice categories (Table S10). Similarly, the mean NRMSE across the tissue slice categories ranged from ~ 8% to 29% of the measured signal, similar to the cell modeling data. These measures of fit demonstrate that the simplified two-compartment model used in these experiments model the data well. As expected, the input function descriptors are identical between the tissue slices (Table 2) as well as to the cell bioreactor modeling (Table S4), reinforcing the consistency of the infusion of the HP [1-¹³C] pyruvate (over both time and amount) between experiments and model systems.

FIGURE 3.

Representative plots of pyruvate (blue) and lactate (green) signal versus time depicting both data (points) and the resultant fit (line) for (A) benign and (B) RCC renal tissue slice. The solid black line represents the fitted input function

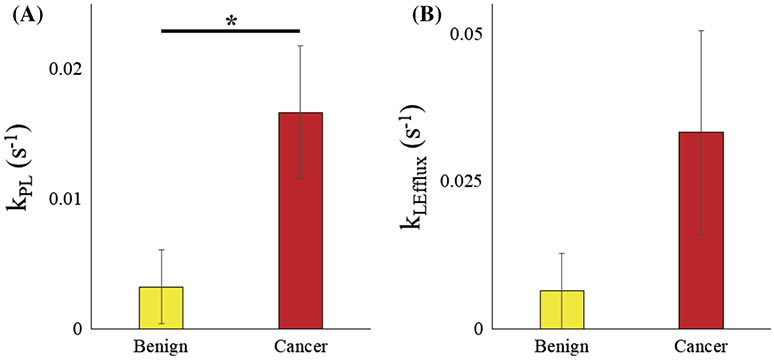
The apparent enzymatic conversion rate of pyruvate to lactate, k_PL, in the patient-derived renal tissue slice bioreactor largely followed trends similar to those of the cell culture model (Figure 4), in that the malignant tissues had higher values than those of the benign tissues. The average k_PL of benign tissue slices was 0.003 s⁻¹, and significantly lower (p = 0.0275, one tail assuming unequal variances) than that of malignant tissue slices (0.017 s⁻¹). These values are similar to the HK-2 cells and in between UMRC6 and UOK262 cells, respectively, thereby validating the range of k_PL values for RCC across models that stratifies aggressiveness.

FIGURE 4.

Kinetic rate parameters from modeling dynamic HP signal changes in tissue slice cultures. Average ± standard error of (A) kPL and (B) FL (lactate signal loss due to flow) in benign and RCC tissue slices

The rest of the kinetic rate parameters are given in Table 3. The average R₁ of pyruvate for benign as well as malignant tissue slices was 0.02 ± 1.7 x 10⁻⁴ s⁻¹, and matches that measured from the cell-laden bioreactors. The mean R₁ of lactate for both benign and malignant tissue slices was 0.03 s⁻¹, even when the bounds of the R_1L ranged from 0.02 to 0.1 s⁻¹. The flow parameter F_L in this model reflects a combined effect of lactate magnetization loss as a function of both the efflux rate out of the cells as well as the decrease in lactate magnetization as a function of the flow of the perfusate in the bioreactor. Similar to cell-laden bioreactor modeling (see the prior section), the flow parameter is correlated to the efflux rate, and hence in this setting it can be used as a surrogate for efflux rate because the physical flow rate setting, as well as the loading of the amount of tissue in the RF-sensitive region of the coil, were identical for all tissue slice samples. As described previously, the efflux rate is a reflection of the amount of the transporter MCT4, the monocarboxylate transporter isoform that is predominantly responsible for the export of lactate out of the cell. The mean F_L was 0.006 s⁻¹ for benign and 0.033 s⁻¹ for malignant tissue slices. This 5.5-fold increase in F_L in malignant tissues matches the trend of increased expression of the MCT4 protein between benign tissue slices and clear cell RCC, as observed in previous work,⁷ and also mimics the 5-fold difference between HK-2 and UOK262 cells (see the prior section) representing benign and aggressive tumor cells. Although we did not see the expected difference in the estimated lactate relaxation rates between the benign and malignant tissues, as would be an effectiveT₁ of intracellular and extracellular compartments weighted by the amount of lactate that are present in the respective compartments, we believe it is recapitulated in the F_L parameter. The F_P was 1.52 ± 1.31 s⁻¹ on average for the benign and 14.06 ± 3.13 s⁻¹ for the malignant tissues. This huge increase in the loss of pyruvate signal in malignant tissue, attributed to the flow of the perfusate in the bioreactor, could be a consequence of the cancerous tissue morphology, all else being considered equal. The average for benign samples is influenced by an outlier of 4.13 s⁻¹, while all the other samples are in the 0.1–0.5 s⁻¹ range, similar to that of the cell-modeling data. The k_LP of both benign and malignant samples were predominantly zero (with the exception of one data set, Figure S3).

TABLE 3.

Average ± standard error for all kinetic rate parameters for benign and RCC tissue slices

	Benign	Cancer
R1P (s−1)	0.02 ± 3.19E-04	0.02 ± 1.18E-04
R1L (s−1)	0.03 ± 4.22E-04	0.03 ± 7.25E-04
FP (s−1)	1.52 ± 1.31	14.06 ± 3.13
FL (s−1)	0.006 ± 0.006	0.033 ± 0.017
kLP (s−1)	0.01 ± 0.01	3.39E-03 ± 3.39E-03
k	3.79 ± 0.67	3.33 ± 0.21
θ	18.46 ± 1.82	19.66 ± 0.61
γ	3.71E+08 ± 1.91E+08	6.18E+08 ± 1.30E+08

3.5 ∣. Modeling HP signal kinetics of orthotopic murine RCC models

The inputless model¹⁹ was used to fit a simplified one-compartment model (Equation 7) without modeling the pyruvate signal or determining the input function. To compute the k_PL, the model was fit by holding the R₁s of pyruvate and lactate fixed at 0.04 and 0.05 s⁻¹, respectively. The values of the R₁ parameter were chosen based on the intracellular lactate relaxation rates quantified from the cell bioreactor and empirically adjusted for compartmentalization (25% for lactate) and the field effect (11.7 vs. 14.1 T). The initial value and boundary conditions are shown in Tables S11 and 12.

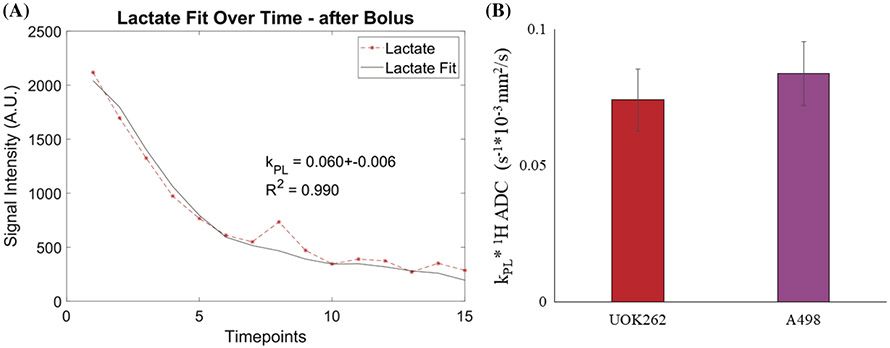
Dynamic HP signals from mice bearing orthotopic renal tumors inducted using either A498 (n = 3) or UOK262 cells (n = 7) were used for this analysis. Figure 5A depicts a representative fit of the lactate signal kinetics from a mouse bearing an orthotopic renal tumor of UOK2 62 cells. The k_PL values thus obtained were 0.044 ± 0.010 for UOK262 and 0.047 ± 0.005 for A498 tumors. These values are similar to the upper range of k_PL values observed for UOK262 cells when perfused in the bioreactor. The apparently higher k_PL value could arise from the contribution of the extracellular lactate signal in the in vivo tumors that are not effectively washed away, unlike in the bioreactor set-up. Prior work¹⁶ on these two tumor xenografts showed that while the LDH activity of A498 tumors was significantly higher, the apparent glycolytic rate (presented as the ratio of HP [1-¹³C] lactate to [1-¹³C] pyruvate signal, equivalent to k_PL) was lower in comparison with UOK262 tumors. This was attributed to the lower cell density of the A498 tumors contributing to the lactate signal (for the same voxel volume). Prior work in Sriram et al.¹⁶ has demonstrated that cellular density and proton ADC are inversely correlated (cellular density ~ 1/ADC) for these RCC tumors. Thus, using the same rationale and data, cell density-normalized k_PL values can be calculated by using the k_PL x ADC product. Consequently, we can retrieve the expected biological trend reflected in the apparent glycolytic rate, the density-normalized k_PL, as shown in Figure 5B. Pursuant to prior work,^19,30,31 we only considered unidirectional conversion of pyruvate to lactate as it would make it an underdetermined problem. However, this could be explored in future work with the modeling of diffusion-encoded HP signals. Overall, this seems to indicate that (1) the apparent rate of pyruvate to lactate conversion k_PL is similar between the in vitro study as well as in the in vivo tumor model for the aggressive cells, giving us an estimate of the range of k_PL values for aggressive RCC tumors; and (2) the simplified model is a good approximation (not requiring the two-compartment model) as the high lactate efflux effect is blunted in the in vivo model because of the crowded interstitial space.

FIGURE 5.

Modeling in vivo HP signals from tumor-bearing mice. (A) Representative plot of pyruvate and lactate HP signal versus time (each timepoint = 3 s), including computed kPL values and fits of the lactate data acquired from orthotopically implanted UOK262 cells. (B) Average ± standard error for kPL * 1H ADC product for mice injected with UOK262 cells (left) and A498 cells (right)

4 ∣. CONCLUSIONS

Having already demonstrated the importance of lactate efflux as a biomarker of cancer presence and metastatic potential using novel bioengineering tools and model systems in conjunction with metabolic imaging, we have demonstrated here that rigorous analysis of HP ¹³C data can yield greater insights into cellular biophysical processes. The results of these studies demonstrate that robust modeling of this data can reliably and noninvasively measure previously inaccessible biological parameters such as intracellular relaxation rates and molecular transport rates in situ using HP metabolic imaging.

Abbreviations used:

ADC

apparent diffusion constant

DiDS

4,4′-diisothiocyanatostilbene-2,2′-disulfonic acid, disodium salt

HP

hyperpolarized

IF

input function

Km

Michaelis–Menten constant

LDH

lactate dehydrogenase

MCT

monocarboxylate

NADH

nicotinamide adenine dinucleotide

NRMSE

normalized root mean square error

RCC

renal cell carcinoma

Vmax

maximum velocity

DATA AVAILABILITY STATEMENT

The software scripts that were used for the modeling are freely available at https://github.com/FayyazA/bioreactor-kinetic-analysis and Larson P, eugene17uf, Gordon J, et al. LarsonLab/hyperpolarized-mri-toolbox: Demo notebooks, new datasets. March 2020. doi:10.5281/zenodo.3711662.