Abstract
The coronavirus disease 2019 (COVID-19) pandemic has fatalized 216 countries across the world and has claimed the lives of millions of people globally. Researches are being carried out worldwide by scientists to understand the nature of this catastrophic virus and find a potential vaccine for it. The most possible efforts have been taken to present this paper as a form of contribution to the understanding of this lethal virus in the first and second wave. This paper presents a unique technique for the methodical comparison of disastrous virus dissemination in two waves amid five most infested countries and the death rate of the virus in order to attain a clear view on the behaviour of the spread of the disease. For this study, the data set of the number of deaths per day and the number of infected cases per day of the most affected countries, the USA, Brazil, Russia, India, and the UK, have been considered in the first and second waves. The correlation fractal dimension has been estimated for the prescribed data sets of COVID-19, and the rate of death has been compared based on the correlation fractal dimension estimate curve. The statistical tool, analysis of variance, has also been used to support the performance of the proposed method. Further, the prediction of the daily death rate has been demonstrated through the autoregressive moving average model. In addition, this study also emphasis a feasible reconstruction of the death rate based on the fractal interpolation function. Subsequently, the normal probability plot is portrayed for the original data and the predicted data, derived through the fractal interpolation function to estimate the accuracy of the prediction. Finally, this paper neatly summarized with the comparison and prediction of epidemic curve of the first and second waves of COVID-19 pandemic to visualize the transmission rate in the both times.
Keywords: Coronavirus disease, Fractal time series, Correlation dimension, Fractal interpolation function, Autoregressive model, Prediction analysis
Introduction
The world is in a state of havoc and turmoil due to the increasing fatality of the epidemic virus, called the Severe Acute Respiratory Syndrome Corona Virus 2 (SARS-CoV-2) which is the most prevalent coronavirus. The Coronavirus Disease 2019 (COVID-19) has put the world in a mode of panic, which has led to a state of emergency that has profoundly affected the manner in which we see our reality and our day-by-day lives. This COVID-19 pandemic has presented both health and financial crises across the world. Fortunately, there are medications available to avert or to treat the infection such as amantadine hydrochloride, dexamethasone, hydroxychloroquine, and remdesivir and also used in the representative countries. With reference to the report of WHO, the first mass vaccination programme started in the early of December 2020, and as of 15 February 2021, 175.3 million of at least 7 different vaccine doses have been administered. The World Health Organization (WHO) advises not to treat the infection with any self-medication. Also, WHO recommends prevention, controlling infections and adopting health policies as key health priorities in dealing with the disease. However, there are many clinical trials involving western and traditional medicines. According to a report given by WHO and other world eminent organizations in the arena of public health, as on 07 August 2020, the total number of confirmed cases and deaths of coronavirus disease is 19,172,505 and 716,327, respectively. Exclusively in USA, Brazil, Russia, India and UK, the total number of COVID-19 confirmed cases is significantly increasing and unfortunately reports indicate that the total number of death cases is also gradually increasing. The increasing number of infected cases and deaths of the pandemic demands a continuous data analysis, so that the dynamical behaviour of the virus can be understandable, and it leads us towards the growth control of the epidemic.
Controlling the outbreak of COVID-19 infections requires systematic planning and strategies, so the researchers can utilize the mathematical modelling for COVID-19 data analysis. In mathematical perspective, one can recognize the patterns and general mechanisms in the process of disease, which can assist to identify some of the basic structures that govern eruptions and epidemics. Recently, several researchers have focused on predictions based on some mathematical analysis of the exact number of COVID-19 cases. In particular, ARIMA model is applied on COVID-19 data set to predict the spread and occurrence of the virus [1]. Mishra et al. [2] described three quarantine models to handle the pandemic disease by considering several compartments called susceptible population, immigrant population, home isolation population, infectious population, hospital quarantine population, and recovered population in 2020. Kassa et al. [3] developed a mathematical model for analysing the disease COVID-19. Bouchnita and Jebrane [4] designed a multiscale model, which simulates the transmission dynamics of COVID-19. Also, the authors demonstrated that the stability of SARS-CoV-2 on hard surfaces determines the number of events reached during the peak of the infection. Djilali and Ghanbari [5] estimated a predictive mathematical analysis for the epidemiological outbreak of coronavirus infection in South Africa, Turkey and Brazil in 2020. Furthermore, the authors investigated the impact of isolation of affected individuals on the spread of COVID-19 disease. Fanelli and Piazza used the susceptible-infected-recovered-deaths (SIRD) model for forecasting COVID-19 spreads to Italy, China and France in 2020 [6]. Sun and Wang [7] developed a mathematical model to classify imported escapes and asymptomatic patients. Using the described model, the authors accomplished some stochastic simulations for the pandemic. Ayinde et al. [8] proposed some curve estimation models with an autoregressive model of order 1 to contemplate the pattern of the COVID-19 cases from Nigeria. Ghosal et al. [9] predicted a linear regression analysis for the number of deaths due to SARS-CoV-2. The qualitative evaluation has been made based on the implemented prevention and control interventions to control the epidemic of COVID-19 [10]. Creating models that can interpret the infection and the general trend parameters are useful for prediction purposes; it may be useful for future planning for viral respiratory illnesses by other countries that are at an early stage of the epidemic. Two models are developed by the authors one model for analysing the spread during the fast phase and the other for interpreting the entire data set and those models reasonably agree with the data [11]. In order to analyse this harmful COVID-19 outbreak, a modified SEIRS model has been constructed to extend prediction on the current projections of the pandemic into three possible outcomes: death, recovery, and recovery with a possibility of re-susceptibility [12]. A power law with Pareto exponent has also been modelled nearly equal to the exponent estimated directly from the distribution of confirmed cases across counties [13].
As the fractal and multifractal analyses have been applied to time series and experimental signals, the dimensional measures have mainly been used to analyse the change in the chaotic nature in different physiopathological conditions and to estimate the complexity in forecasting process [14–18]. Among all the nonlinear schemes, the correlation fractal dimension measurement is more accessible in dealing with diffusion data with more complexity in nature for prediction [19–28]. Due to an uncertainty in the spread of coronavirus, the empirical data of the number of infected cases and death cases are being analysed based on the power law kinetics with fractal exponent, which gives a best fit to the contemporary data than the traditional epidemiology method. Hence, the fractal-based comparative study of COVID-19 has been provoked at different situations [29–33]. This study proposes the correlation fractal dimension and the autoregressive moving average model-based comparative prediction analysis of COVID-19 death rate in the first and second waves.
The main goal of this study is to provide a technique for a systematic comparison of COVID-19 spread among five most infected countries and the death rate to understand the chaotic behaviour of the disease transmission. We have considered the data sets of the number of deaths per day and the number of infections per day in the five most affected nations, namely the United States of America (USA), Brazil, Russia, India and the United Kingdom (UK). The correlation dimension is estimated for the representative data sets of daily infections, daily deaths and daily death rate of COVID-19. Further, the mean differences of the actual data sets and its computed correlation dimension estimates are compared by the analysis of variance. At last, the comparative analysis is performed to depict the structure of the transmission and death rate of the corona virus in both phases.
The present work is organized as follows: Sect. 2 succinctly portrays the mathematical techniques of the correlation dimension, fractal interpolation and the necessary statistical methods. The data set information is described in Sect. 3. In Sect. 4, the estimation of the correlation dimension and the fractal interpolation representation for COVID-19 data set are explored. The ARMA processes and the parametric statistical technique one-way analysis of variance are also performed on the actual data sets and the calculated correlation dimension estimates in the same section. Additionally, the second wave analysis is done by comparative study and also discussed elaborately in Sect. 4. The concluding remarks of the research work are presented in Sect. 5.
Mathematical methods
Mainly the noisy data sets can be modelled and analysed by the basic probability distributions. Based on that impression, the Renyi entropy and the correlation fractal dimension are generally defined in terms of discrete probability measures. As per the definition, the probability distributions are mainly involved in the Renyi entropy and the fractal dimensions. Hence, the Renyi entropy is very appropriate and widely used for describing the generalized fractal dimension method in order to analyse the noisy data for getting more information about the uncertainty and complexity. So the Renyi entropy and the correlation fractal dimension are used as generalized techniques in our proposed methods to analyse/predict the complex time series. The preliminaries of the Renyi entropy, the correlation fractal dimension and the fractal interpolation function are depicted mathematically in this section.
Renyi Entropy
One of the most important concepts in modern science is entropy, and it is a measure to estimate the multiformity, unsureness or randomness of a system in the theory of information. If the value of the random variable is unsure, one can use Shannon entropy, which is a measure of the average information. Renyi entropy is Shannon’s generalization entropy, which is also used to define the correlation fractal dimension. The Renyi entropy of order is denoted as , and it is defined by
| 1 |
where is a non-negative and non-increasing function on q, and q is a positive real number. Further, are the probabilities of the discrete random variable X which takes N possible values , that is for [34] .
Correlation fractal dimension
Correlation fractal dimension is one of the nonlinear measures, which imparts the data about the kind of dynamics available and also describes the presence of chaotic dynamics in the time series. The correlation dimension is a measure of the dimensionality of the space occupied by a number of random points in complex systems. The correlation dimension is an example of a fractal dimension measurement because it permits non-integer dimensional values. A mathematical model of a system that evolves over time is known as a dynamical system. Even though the time series appears irregular in the time domain, the linearity is manifested in the frequency domain as sharp peaks. If the time series comes from a nonlinear dynamical system, with or without small added noise, or a random process (large noise), the time series will be irregular in both the time and frequency domains [35–37].
The various methods for calculating the dimension are the Hausdorff dimension, the box-counting dimension and the information dimension are available to analyse the signals or time series, but the correlation dimension has a predominant scope of being computed immediately, performed on the reconstructed path, and generated the different values reflecting the different types of correlations in the reconstruction. The correlation dimension is the easiest dimension measurement to perform and is the most commonly used dimension in random time-series analysis. The correlation dimension is also associated with the smallest number of variables required to model the behaviour of the system in phase space [38–40].
This section concisely presents the necessary materials of the correlation dimension. Based on the Renyi entropy, the correlation dimension (correlation fractal dimension) of a fractal time series is defined by constructing the probability distribution as follows [19–28].
Let be the points of a fractal time series and the total range of the time series is divided into N intervals (bins) such that
| 2 |
where and are the maximum and the minimum values of the time series for the corresponding experiment, respectively, and r is the uncertainty factor.
Define where is the number of points of the time series lies in the ith bin of length r.
Then, the correlation fractal dimension () for the known probability is defined by:
| 3 |
Fractal interpolation function
Fractal interpolation functions are generated by a special type of iterated function system (IFS) of affine transformations. This section concisely presents the necessary materials to construct the fractal interpolation functions; more rigorous treatment of the fractal interpolation is given in [41–46].
Let the sample data with be given and ’s are not necessary at equal distances. Let , for and , be contractive homeomorphisms satisfying the endpoint conditions
| 4 |
Let and Let continuous functions obeys
| 5 |
Moreover, is a contraction with respect to the second variable. Define the functions , by The iterated function system corresponds to the self-mapping F on defined by for any . Then, the space is complete with respect to the Hausdorff metric, since X is complete metric space. Further, F is contraction on ; hence, by the IFS theory, F has a unique fixed point G whose graph is a continuous function , which satisfies for The function g generated by the IFS is termed as fractal interpolation function corresponding to the data points .
As the paper deals with the prediction of the infected and death rates from COVID-19 information, the data set , where represents the ith day and denotes the death rate on ith day due to COVID-19 infections, is considered along with the following IFS to generate the fractal interpolation function: where
| 6 |
and for all . Here, the free parameter is called the vertical scaling factor, which decides the pattern and fractal dimension of the fractal interpolation function. By Eq. (5), maps the terminals of given data to the terminal of each sub-interval. That is, maps first day and its death rate to th day and its death rate . Similarly, image of nth day and its death rate under the mapping is kth day and its death rate for each k. Hence, the mapping has the following constructions.
| 7 |
for all . If is a predefined variable in system (6) with constraints (7), then it provides a unique solution for (6). Therefore, the constants can be obtained uniquely as follows:
| 8 |
The coefficients are required parameters to define the contractive homeomorphisms between days in the IFS given in Eq. (6). Further, the constants are required to obtain the death rate on kth day under the mapping in Eq. (6). If for all , then it gives the classical piecewise linear interpolation function. The scaling factor determines the fractal dimension of fractal interpolation function, since the image of lines parallel to the y-axis under the mapping is the line parallel to y-axis. Further, if the length of the line L is l, then the length of its image is times of l, for all . That is, the ratio between the length of the lines L and is .
ARMA processes
The time-series analysis has an extensive range of applications in forecasting, spectral estimation and modelling of time-domain system. The time series can be analysed by means of time domain and frequency domain. Frequency-domain approach is the study of nonparametric decay using a spectral function in which the time series is used in its different frequency components. Albeit, the time-domain approach focuses on parametric models to investigate the future values of the time series as a parameter function of the present and past values. One of the foremost methods to investigate the time series is autoregressive moving average (ARMA), which provides an intimate description of a standard random process based on two polynomials such as autoregression (AR) and moving average (MA). Besides, the complex time series can be analysed, modelled and forecasted in both the time and the frequency domains in detail by this superlative method. ARMA(p, q) notion indicates the model with p autoregressive terms AR(p) and q moving-average terms MA(q).
The random process is an ARMA(p, q) process, if is stationary and for every t,
| 9 |
where c is a constant, is a random variable representing the number of infected or death cases in the tth day, is a random variable denotes the noise term at the tth day, and & are model parameters of AR(p) and MA(q), respectively.
Statistical methods
One-way analysis of variance (ANOVA) is a parametric statistical technique used to compare data sets based on the mean and the variance of the given data sets. In ANOVA, the inferences about means are made by analysing the variance. If the observed differences are high, then it is considered to be statistically significant. The p-value can be determined by F-test statistic in the analysis of variance between groups, which is the probability of getting a result. In ANOVA test, if the p-value is near zero, the null hypothesis is rejected and recommends the conclusion that at least one sample mean is significantly different from the other sample means. We can establish the fact that the significant differences between the data set increases when the p-value approaches to zero.
The F-test statistic associated with ANOVA test is defined as the ratio of the between-group variance to the within-group variance.
| 10 |
A box plot is a graphical tool used to analyse the prescribed data if there are any variations between the levels of a one-way model. A graphical alternative to the one-way ANOVA test is the box plot. It is also a good way to summarize and compare the data from two or more samples. A box plot is a consistent method of viewing a data set based on a five-number summary such as minimum, maximum, sample median, first and third quartiles. In addition, the whiskers are also occurred in the box plot like outliers, if the numerical values are deviated from the prescribed range of the data.
The power spectrum of a time series in statistical analysis describes the distribution of power into frequency components that make up the signal. The spectrum is the statistical average of a particular time signal or sort of signal (including noise) as evaluated in terms of frequency content. Since the cumulative energy of such a signal over all time will be infinite, the power spectral density (PSD) refers to the spectral energy distribution that would be found per unit time. The spectral density, in simple terms, describes the signal’s frequency content. One aim of the spectral density estimation is to detect any periodicities in the data by looking for peaks at the frequencies that correspond to these periodicities. As COVID-19 infected and death cases are complex data sets, the logarithmic power spectral density can be estimated for all representative time series to analyse the complexity, to predict the values smoothly in terms of frequencies and also to estimate the periodicities and peak values.
Data description
The empirical data have been accessed in the data repository of COVID-19 provided by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University [47] and Statistics & Research Coronavirus Pandemic (COVID-19) available in the database “Our World in Data” [48]. The daily infection count and the daily death count data sets of the five most affected countries have been selected and utilized in this research work as on 18 January 2021, and the same information of the representative data sets is meticulously presented in Table 1 [49]. The initial date of the experimental data considered in this research study is 23 June 2020 for the first wave and 01 October 2020 for the second wave of COVID-19.
Table 1.
Countries with the most number of COVID-19 cases as on 18 January 2021
| Country | Total infected cases | Total deaths |
|---|---|---|
| USA | 24,438,935 | 406,162 |
| Brazil | 8,638,249 | 212,831 |
| Russia | 3,616,680 | 66,810 |
| India | 10,610,883 | 152,869 |
| UK | 3,515,796 | 93,469 |
Results and discussion
In this study, the five most disease-ridden countries have been considered and the data set of each country comprises a total of around 100 observations, which is end on the date 30 September 2020 for exploring the first phase.
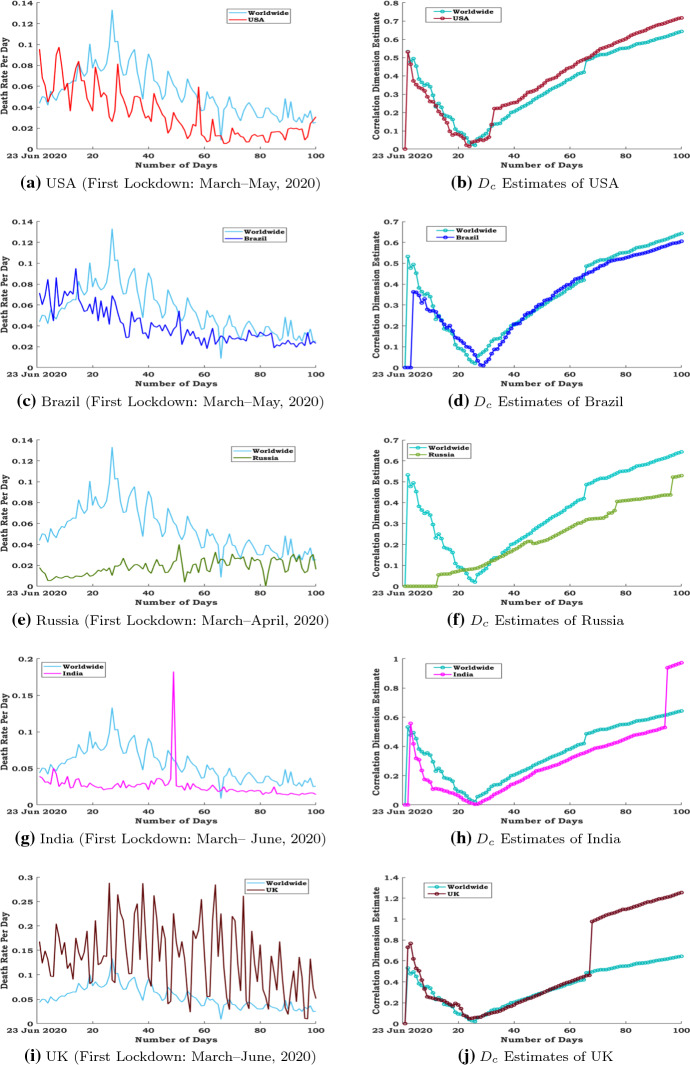
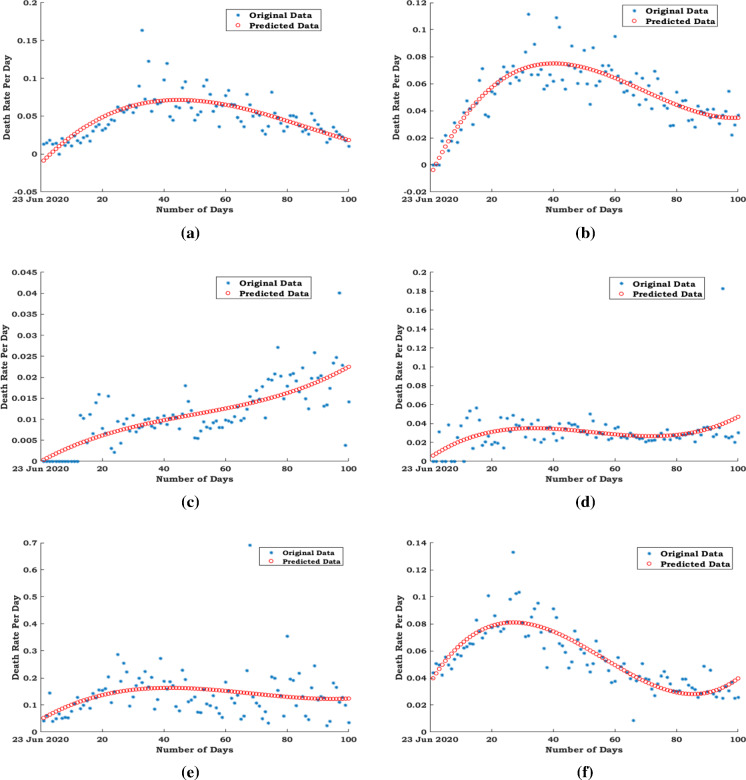
The day-wise total number of reported cases is subject to change with the amount of testing that has been completed in a particular day; henceforth, we have decided to intensely examine the total number of death cases and the ratio of death cases with the total number of infected cases per day. The death rate or case fatality rate, also known as case fatality risk, is described in epidemiology as the proportion of people who die from a predetermined infection among all people diagnosed with the disease over a given time period. The case fatality rate is commonly used as an indicator of disease severity and is often used for prognosis (predicting disease outcome), with higher rates indicating worse outcomes. It may also be used to assess the effectiveness of new therapies, with tests declining as treatments become more effective. The case fatality rate (death rate) is calculated in this paper by dividing the number of confirmed deaths per day by the number of confirmed cases per day. The mortality rate or case fatality rate would be estimated with respect to one day as a fixed time frame since the COVID-19 is a short-term infectious disease (not a chronic disease) [50]. In case of case fatality rate or the death rate, the number of identified deaths out of the total number of confirmed cases is classified in terms of its correlation dimension estimate curve. The daily death rate of COVID-19 as a function of the number of days is elucidated in Fig. 1a, c, e, g, i, respectively, for USA, Brazil, Russia, India, UK. Also, the correlation dimension estimates as a function of the number of days for the death rate are plotted in Fig. 1b, d, g, h, j, respectively, for USA, Brazil, Russia, India and UK. Figure 1 narrates that the peak of death rate of USA and Brazil occurred in the initial timeline and conspicuously reduced at the end, though the fatality rate of Russia and India is significantly less in the onset period, getting contrary progress in the end phase.
Fig. 1.
First wave: comparison between the worldwide daily death rate and the representative countries’ daily death rate: a USA, c Brazil, e Russia, g India, i UK and analogies of the correlation dimension estimates between daily death rate of the country and worldwide daily death rate: b USA, d Brazil, f Russia, h India, j UK
Further, the actual data set of the death rate of each country is compared with the death rate of the world which is exhibited in Fig. 1a USA, (c) Brazil, (e) Russia, (g) India, (i) UK. Similarly, analogies of the correlation dimension estimate between the total death rate of each country and the total death rate of the world per day are displayed in Fig. 1b USA, (d) Brazil, (f) Russia, (h) India, (i) UK. Figure 1a shows that the death rate is approximately periodic curve in USA as well as in worldwide. It was a consequence of delay in reporting the cases and also not conducting the regular tests during the weekend. Similarly in Fig. 1i, it is observed that the death rate per day fluctuates periodically with time period of one week. It is implied that the mortality rate of UK is not much stable comparatively with other countries during the prescribed time frame. Comparison in Fig. 1 demonstrates that the daily death rate of UK is in an increased amount than the daily death rate of the world from the beginning to end. It can be noted that the daily death rate of USA and Brazil is fluctuating over the death rate of the world, whereas the death rate of Russia and India is lower than the death rate of the world except one point at the end. Moreover, Fig. 1g depicts that there is a certain noise occurred at 49th day due to the sudden peak in the death rate of India. It has to be denoised for further analysis as the preprocessing step to perform the prediction process in the accurate manner.
The minimum of correlation fractal dimension estimates of death rates per day for all representative countries is graphically illustrated to examine the effect of execution of the actions on decreasing the spread of this fatal virus. Figure 1b, d, f, h and j manifestly uncovers that the correlation dimension estimates for death rates of representative countries except Russia are nearly zero (minimum) during the period from 20th day to 30th day, and it indicates the less intricacy in death rates, due to the effectiveness of continuous lockdowns and other preventative activities taken severely during the first wave by the administration of all countries represented in this research work, whereas in Russia the intervention strategies including the progressive lockdown implemented on 28 March 2020 eventually reduced the positive cases of COVID-19 initially, and hence, the lockdown was ended on 30 April 2020. This results the correlation dimension estimates for death rates of Russia are nearly zero during the initial period from 23rd June 2020 and then gradually increased without attaining the minimum (zero) again.
It is noted that the country India was positioned under the first phase of the full lockdown from the Middle of March to April. Also, the phases 2, 3 and 4 of the lockdown were prolonged till the end of May, with the incremental relaxations. Beginning of the June month, India has started a lifting of restrictions in a phased manner, which was continued and extended by a series of unlocks till the month of November 2020. The jump of the correlation fractal dimension estimates of the daily death rates for India in Fig. 1h displays the gradual increase in death rates per day, which was happened due to certain exemptions from the lockdown. Consequently in UK, the first wave of the pandemic occurred from March to April 2020. By the middle of April, it was reported that the severe lockdowns are flattened the epidemic curves. Hence, the daily new cases and deaths were cut down between the months of May and June, and it was also continued at low levels over the summer of 2020. The lockdowns in the UK were gradually reduced by the authorities between the months of June and July. It causes that the number of daily new infections was continuously declined until the beginning of August 2020. In Fig. 1j, the jump of the correlation fractal dimension values of the daily death rates in UK indicates the sign of the second wave in UK from August 2020 to September 2020. The mentioned jumps are occurred in the correlation fractal dimension measures of the daily death rates, and those changes cannot be treated as noise for the death rate time series, as it was caused by the series of lockdowns.
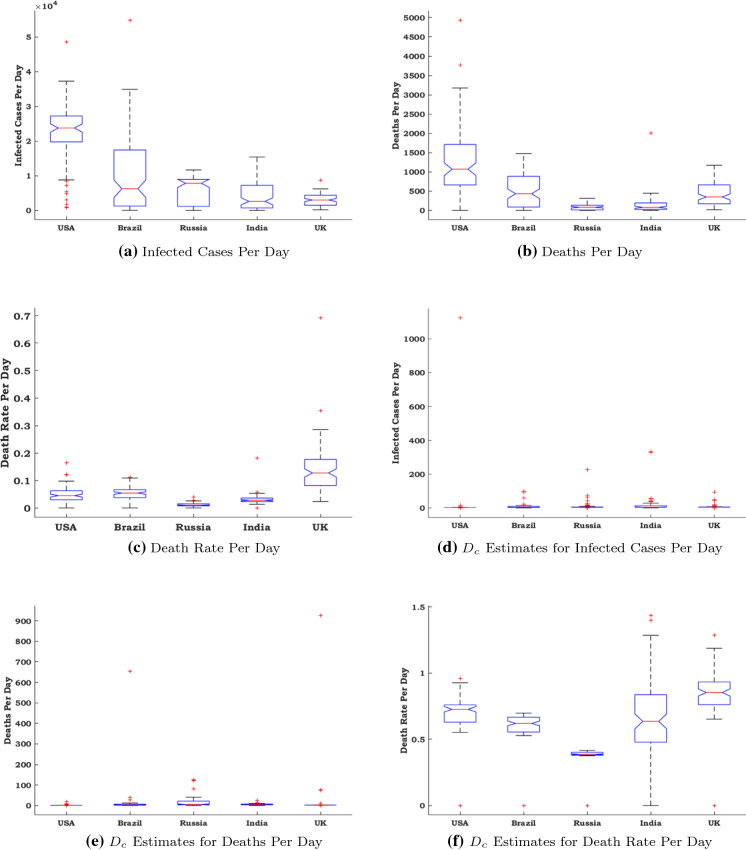
The correlation dimension estimates for the number of infected cases per day, the number of deaths per day and the daily death rate are estimated using Eq. 3 and are plotted in Fig. 2. The minimum of correlation fractal dimension estimates of the infected, deaths and death rates per day for all representative countries is visually observed in Fig. 2 as minimum (nearly zero) around the 25th bin of the experiment. It would validate the competence of enactment of many safety procedures and progressive lockdowns, and it marks the reduction in the diffusion process of the corona virus due to the precautionary steps. Comparison in Fig. 2 narrates that though the total number of infections of UK is less than the other four countries, the correlation dimension estimates of the daily infected cases and the daily death rate of UK are notably higher. The correlation dimension estimate curve of the daily death rate of USA is of concern, it stands behind UK, but the total deaths of USA are at peak. In the onset phase, the correlation dimension estimate curve of the daily death rate of India is very low, later crossing Russia’s curve around 100 bins, which gradually increases to overtake the Brazil death rate curve. Computational results reveal that the death rate of UK significantly increases, so this study recommends that the necessary control measures are to be taken by the public health authorities to stabilize the death rate of UK. The correlation fractal dimension for COVID-19 data sets of the five most diseased countries are computed, and the gained results are tabulated in Table 2.
Fig. 2.
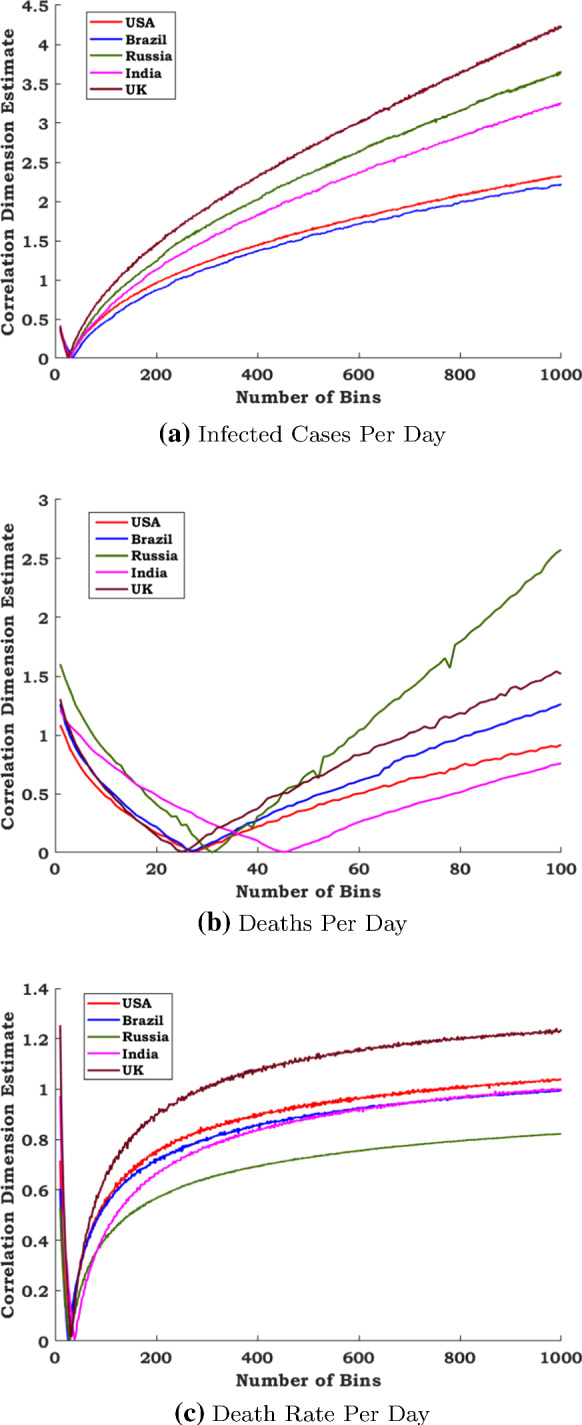
First wave (initial date of experimental data is 23rd June 2020): correlation fractal dimension estimates of COVID-19. The initial lockdown was introduced in all representative countries as follows: i USA—first lockdown: March–May, 2020; ii Brazil—first lockdown: March–May, 2020; iii Russia—first lockdown: March–April, 2020; iv India—first lockdown: March–June, 2020; v UK—first lockdown: March–June, 2020
Table 2.
Correlation fractal dimension for the first phase of COVID-19 data sets
| Country | Infected cases per day | Deaths per day | Death rate per day |
|---|---|---|---|
| USA | 2.3163 | 1.0171 | 1.3026 |
| Brazil | 2.4918 | 4.7337 | 0.9665 |
| Russia | 3.5853 | 0.9429 | 0.7580 |
| India | 3.4152 | 1.4693 | 1.0801 |
| UK | 4.0864 | 1.7201 | 1.3026 |
The F-test statistic is associated with the ANOVA test as a statistical measure to test the significance differences, and the statistical test is performed with 95% level of confidence. The mean differences of the data sets, the number of infections per day, the number of deaths per day and the daily death rate of the five countries USA, Brazil, Russia, India and UK are statistically tested by one-way analysis of variance associated. The statistical measures of one-way ANOVA are shown in Table 3. The one-way ANOVA test statistically substantiates the proposed procedure in this study, since the p-value in Table 3 for infected cases, death cases and death rates is almost near to zero. Hence, one-way ANOVA suggests the conclusion that at least one sample mean is significantly differed from the other sample means in actual data sets of infections, deaths and death rates. It is statistically implied that the representative countries are varied sufficiently in the level of infections, deaths and death rates with respect to collected data sets and its correlation dimension estimates except the correlation dimension estimates for infected cases. Thus, the infected cases for all the representative countries are not much fluctuated during the period of research with respect to the correlation dimension estimates. The same status on infected cases may be changed in near future due to the various regional settings of infectious diseases.
Table 3.
One-way ANOVA table—original COVID-19 data sets: a infected cases per day, b deaths per day, c death rate per day. Correlation fractal dimension () estimates: d infected cases per day, e deaths per day, f death rate per day
| ANOVA table | |||||
|---|---|---|---|---|---|
| Source | SS | df | MS | F | Prob > F |
| (a) Infected cases per day | |||||
| Columns | 2.35743e10 | 4 | 5.89358e09 | 128.89 | 2.4571e−75 |
| Error | 2.26342e10 | 495 | 4.57257e07 | ||
| Total | 4.62086e10 | 499 | |||
| (b) Deaths per day | |||||
| Columns | 7.77547e07 | 4 | 19438678.7 | 89.14 | 5.07082e−57 |
| Error | 1.07942e08 | 495 | 218063.7 | ||
| Total | 1.85696e08 | 499 | |||
| (c) Death rate per day | |||||
| Columns | 0.65621 | 4 | 0.16405 | 53.87 | 1.08402e−37 |
| Error | 1.50735 | 495 | 0.00305 | ||
| Total | 2.16356 | 499 | |||
| (d) Estimates of infected cases per day | |||||
| Columns | 9527.47 | 4 | 2381.87 | 0.7 | 0.593 |
| Error | 1,687,131.86 | 495 | 3408.35 | ||
| Total | 1,696,659.33 | 499 | |||
| (e) Estimates of death rate per day | |||||
| Columns | 33,493.6 | 4 | 8373.39 | 2.43 | 0.0471 |
| Error | 1,429,702.7 | 415 | 3445.07 | ||
| Total | 1,463,196.3 | 419 | |||
| (f) Estimates of death rate per day | |||||
| Columns | 14.7229 | 4 | 3.68073 | 122.68 | 1.13754e−72 |
| Error | 14.8516 | 495 | 0.03 | ||
| Total | 29.5745 | 499 | |||
The box plots with red lines and whiskers for data sets of daily infections, daily deaths and daily death rates, and the corresponding correlation fractal dimension estimates among all five mostly affected countries are elucidated in Fig. 3. In box plot, the median values of daily infections, daily deaths and daily death rates, and the median values of its correlation fractal dimension estimates of USA, India, Brazil, Russia, UK are marked in red lines as in Fig. 3. The whiskers in box plots are representing the outliers of the data sets. It is perceived that the statistical differences among the countries are occurred significantly in the infections, deaths and death rates. In Fig. 3a, the median of the infected cases for USA is very high in the prescribed time span, when compared to the other countries, and also the standard deviation of infected cases of Brazil is comparatively high, as the corresponding box plot has greater variances. In addition, more number of outliers is occurred with minimum values in USA. Likewise, Fig. 3b demonstrates that the median and the standard deviation of death cases for USA is large, when compared with the other countries and also infers that there was huge variances in the number of deaths during the mentioned period in that country. Figure 3c reveals that the median and the standard deviation of the daily death rates of UK take the upper hand and also indicate that the daily death rates varied notably in UK during the prescribed period, when compared to the other countries. Besides that, the box plots in Fig. 3d–f sketched on correlation fractal dimension values for infected cases, death cases and death rates would be differed notably among the countries. In Fig. 3d, the standard deviation of correlation dimension estimates of the infected cases in India is varied higher than other countries with more variations, whereas the correlation dimensions estimate of the infected cases for USA is conspicuously less as the box plot is constructed with less variance. In Fig. 3e, the standard deviation of correlation dimension estimates of the death cases in Russia is reasonably high, since there is a significant variation in the box plot. But the standard deviation of correlation estimates of the death cases for USA and UK is evidently less with fewer variations. In Fig. 3f, the standard deviation of correlation dimension estimates of the death rate of India is remarkably high, as the corresponding box plot has significant variations. However, the standard deviation of the correlation fractal dimension estimates of the death rate for Russia is comparatively less than other countries as shown in the respective box plot with the small amount of variance. As far as the median is concerned in the box plot, the value is higher in UK and lesser in Russia.
Fig. 3.
First wave (initial date of experimental data is 23 June 2020): box plots for original COVID-19 data sets: a infected cases per day, b deaths per day, c death rate per day. Box plots for correlation fractal dimension () estimates: d infected cases per day, e deaths per day, f death rate per day
It is curiously observed in Fig. 3d, e that the variations in the vertical scale are too large due to the occurrence of the unexpected extremal values in the database and its correlation fractal dimension estimates as well. In Fig. 3d, f, there are certain outliers occurred in India with respect to maximum values, which are comparatively higher than other countries. There are some extremal points occurred in the maximum values of the correlation dimension values for the countries UK and Brazil, as it is clearly revealed in Fig. 3e. In Fig. 3f, there is a significant difference in the box plot of correlation estimate of death rates among the countries than the box plots for the original death rate data sets. Especially, the box plot for the correlation dimension for death rates in India is varied significantly with the wider range consisting of more whiskers plots. This will indicate the sign of the second wave to India that there will be increasing in the infected cases, death cases and death rates gradually.
As the data sets are realistic in nature, there are certain noises occurred in the time series considered for this study. For instance, there is a sudden peak observed in Fig. 1g. It may affect the accuracy of the prediction and comparison analysis in the proposed method. In order to overcome this issue, the denoising process has been done strongly for all data sets as the preprocessing step by using the Gaussian process before applying the ARMA process to predict the required information.
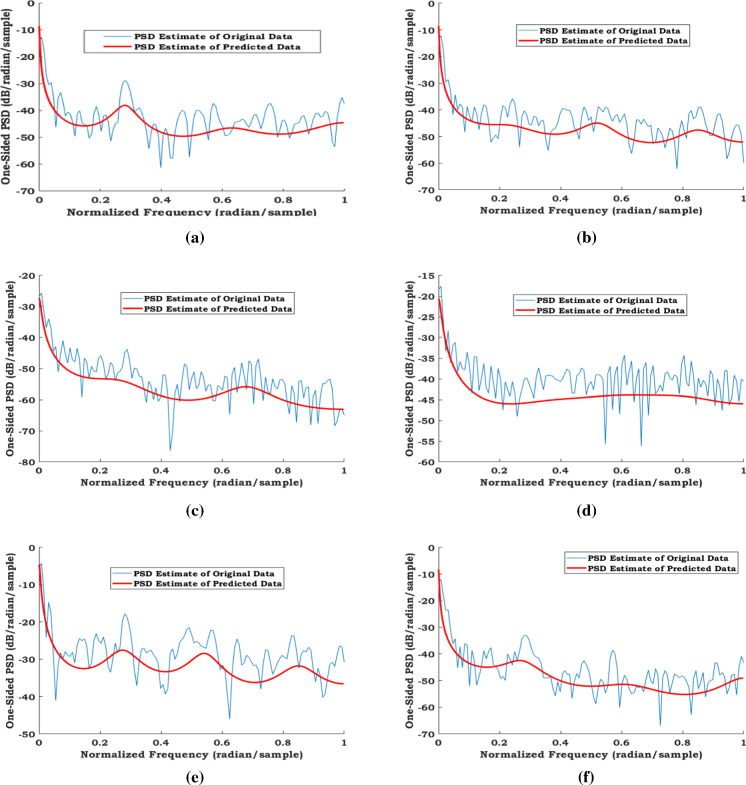
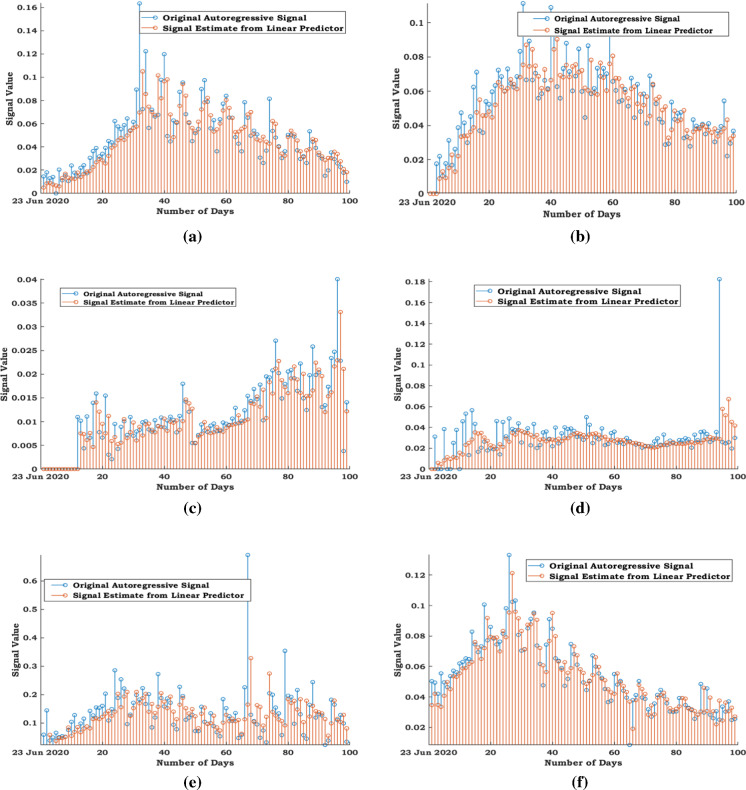
The periodograms in Fig. 4 sequentially demonstrate the logarithmic power spectral density estimate for the original and the predicted data representing the daily death rate in USA, Brazil, Russia, India and UK. The time span of this research study is around 100 observations (days). The maximum frequency of the logarithmic power spectral density periodogram is 0.5 (1/day), and the minimum frequency of the same spectrum is 1/(100 days). The basic frequency is considered as 1/week, as this study observes the week-based periodical death rates. In Fig. 5, the autoregressive signal transformed from the original death rate data and the predicted signal from the corresponding linear predictor coefficient for the death rate are sketched against the number of days to compare the day-wise information in the form of stem plots. Figure 6 portrays the predicted data of the death rate along with the corresponding original death rate of COVID-19 of the represented countries. In order to predict the day-wise death rate data, the autoregressive moving-average polynomial coefficients and are optimally determined by using the ARMA process and depicted in Table 4 to construct the following polynomial.
| 11 |
where t represents the number of days and D(t) is the death rate in the tth day of COVID-19 infection. The polynomial in Eq. (11) predicts the death rate for near future by using the ARMA polynomial coefficients. The representations of the predicted data from the original data by using the ARMA process are depicted with different geometrical settings in Figs. 4, 5 and 6.
Fig. 4.
First wave (initial date of experimental data is 23 June 2020): periodogram of logarithmic power spectral density estimate for original data and predicted data with the frequency, f = 1/(7 days): a USA, b Brazil, c Russia, d India, e UK, f World
Fig. 5.
First wave: stem plots of original autoregressive signal and the predicted signal by linear predictor against the number of days: a USA, b Brazil, c Russia, d India, e UK, f World. (Color figure online)
Fig. 6.
First wave: representation of death rate in time domain for original COVID-19 data and predicted data by ARMA process versus number of days: a USA, b Brazil, c Russia, d India, e UK, f World
Table 4.
Autoregressive moving-average polynomial coefficients for prediction
| Country | Autoregressive moving-average polynomial coefficients | ||||
|---|---|---|---|---|---|
| Error | |||||
| USA | 1 | e−04 | |||
| Brazil | 1 | e−04 | |||
| Russia | 1 | e−05 | |||
| India | 1 | e−04 | |||
| UK | 1 | ||||
| World | 1 | e−04 | |||
A phenomenal time, the rapid rise of the death cases in several countries of the world, is representing a major lacuna on what the future will carry for us. The top five countries together significantly account in the total infected cases and death cases. In Fig. 4, the periodogram of the logarithmic power spectral density estimate is exposed graphically for the original and the predicted data indicating the daily death rate in the representative countries USA, Brazil, Russia, India, UK, and World Wide. The logarithmic power spectral density is projected against the normalized frequency values after normalizing the usual frequencies in Fig. 4 with respect to the preferred basic frequency 1/week, so that the predicted data curve is obtained smoothly by the investigational system. It is evident that the logarithmic power spectral estimate is too irregular for original data of daily death rate with noises, whereas the power spectral estimate is so smooth for predicted data of daily death rate in the frequency domain. Thus, the logarithmic power spectral density estimates the predicted data as a smooth curve to represent the original data appropriately in frequency phase. It is an advantage for the governing authorities, and it will help them to predict the data for future span approximately with the less amount of error for taking the precautionary measures vigorously. Figure 5 demonstrates a stem plot representation of the autoregressive signal (blue stems) transformed from the original death rate data and the predicted signal (red stems) from the corresponding linear predictor coefficient for the death rate in terms of days. It is observed from Fig. 5 that the actual data extracted from the autoregressive technique may be constructed with the certain noises or outliers, and the same deviations are controlled or reduced by the suitable estimator of the linear predictor coefficient. In addition, the peak values of original data (blue stems) observed for all countries in Fig. 5 are denoised and the same those peak values corresponding to the predicted data (red stems) have been normalized and represented by using the ARMA process. Hence, Fig. 5 evidently reveals that the daily death rate data are predicted in the accepted level with less deviation and considered for the further study of comparison. Figure 6 illustrates a comparative analysis of death rate prediction. Countries around the world are working to flatten the death rate curve of this pandemic. As a comparison in Fig. 6 elucidates that predicted death rate curves of USA and Brazil are set to peak in early time and gradually reducing the peak at the end. Though the death rate curve of Russia and India is flatten throughout the prediction timeline, it is not seen a declining trend at the terminal. Hence, the public health authorities of Russia and India should cautiously maintain the stabilized action to uphold the current status of the death rate.
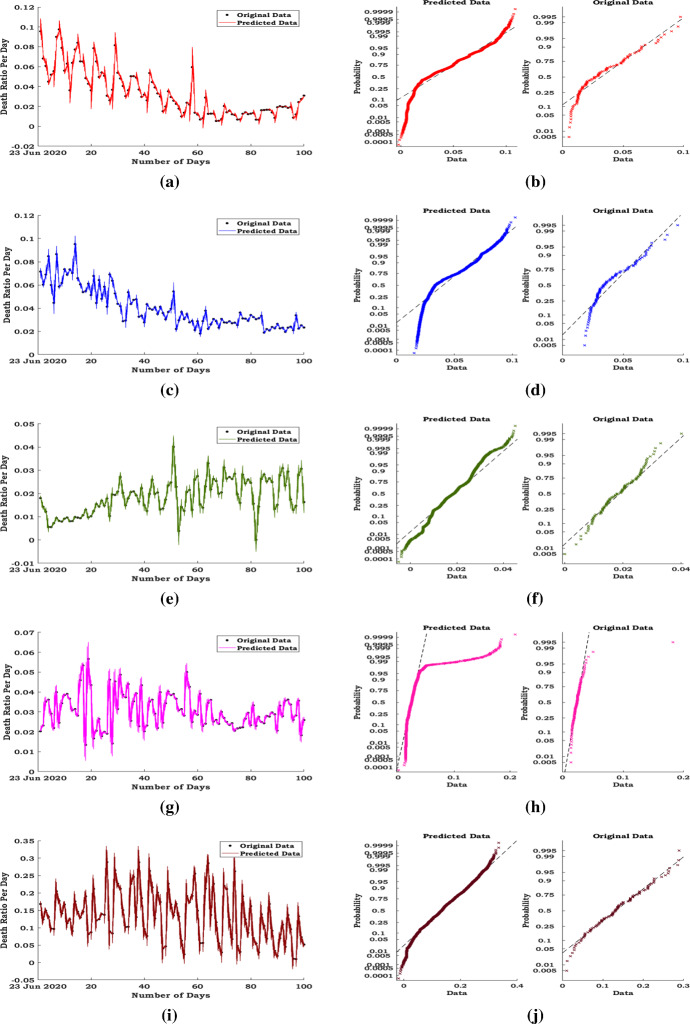
The predicted death ratio of USA, Brazil, India, Russia and UK using the model framed by the fractal interpolation function of the iterated function system given in Eq. (6) is exhibited in Fig. 7. Besides, the five most disease-ridden countries have been considered and the death ratio is predicted for the data set of each country, which comprises of nearly 100 observations (days) that ends on the date 30 September 2020 for exploring the first phase. Comparing the results of the fractal interpolation forecasting method, the predicted death rate curve of India follows a uniform pattern, but not has more fluctuation, whereas other countries have more oscillation in death rate. The probability plots for normal distribution of the original death rate and the predicted death rate of USA, Brazil, Russia, India and UK are depicted in Fig. 7. The normal probability plot generates each sample data point in death rate represented by markers and also compared with the reference line theoretically given by the normal probability distribution. Basically, the reference line is obtained by connecting the first and third quartiles of the sample data and extending to the extremum of the data. The sample data points appear along with the reference line provided the information that the sample data follow the normal distribution. Perhaps, the sample data does not possess the normal distribution, if those points are significantly deviated from the reference line. Comparisons illustrated in Fig. 7 elucidate that the predicted death rate by the fractal interpolation method obeys normal distribution, if the actual death rate follows normal distribution.
Fig. 7.
First wave: comparison between the original and predicted daily death rate of the representative countries by fractal interpolation function: a USA, c Brazil, e Russia, g India, i UK and analogies of the probability plot for normal distributions between predicted and original daily death rate: b USA, d Brazil, f Russia, h India, j UK
Second wave analysis of COVID-19
In the first phase of COVID-19 pandemic, the massive public health interventions have been encountered across the world. Additionally, the most affected countries have executed stringent social measures based on local risk assessments, such as lockdown, mobility restrictions, compulsory face mask-wearing, telecommuting for non-essential community services, and virtual meeting in educational institutes as well as business sectors. However, the reduced COVID-19 positive count could undoubtedly resurge when the social measures are relaxed for economic and educational factors. As on 30 September 2020, there were 7,228,526 (USA), 4,810,935 (Brazil), 1,170,799 (Russia), 6,312,584 (India), 455,846 (UK), confirmed cases of COVID-19 infections reported in the database. It was collated publicly available officially confirmed cases of each country to construct the epidemic curve on January 18, 2021 in which 24,078,772 (USA), 8,511,770 (Brazil), 3,552,888 (Russia), 10,581,823 (India), 3,443,350 (UK), total number of confirmed cases of COVID-19 were reported. Moreover, the countries like Russia, UK and USA are recording with the infected rate at the beginning of January 2021 comparatively higher than the infected rate of those detected from March to September, 2020. On the contrary, India’s infected cases are lower than the other countries from the second week of January, 2021. The attributes of the high severity of the first wave of pandemic in these countries seem to be unpredictable.
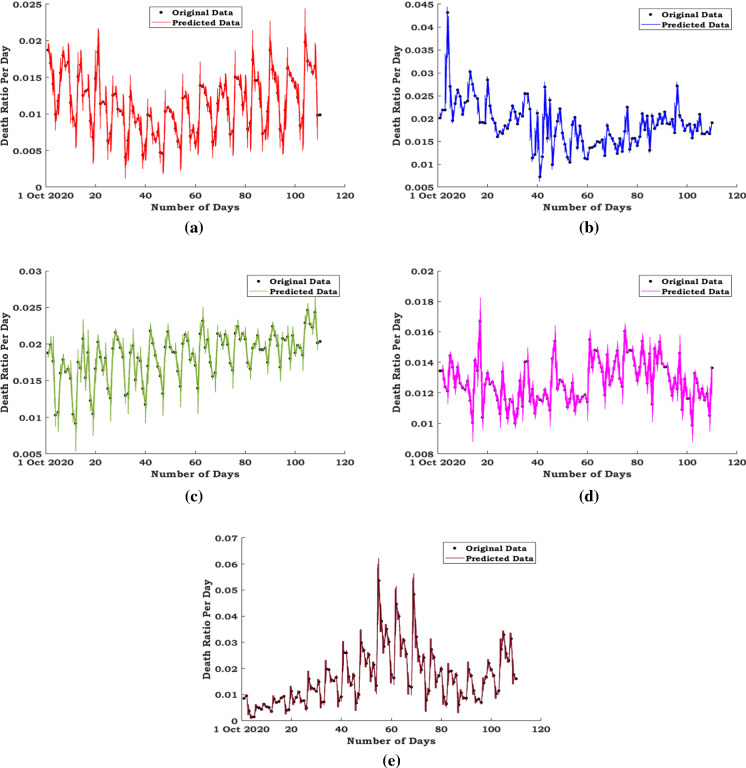
In the view of second wave, the death ratio of USA, Brazil, India, Russia and UK is analysed and predicted by using the fractal interpolation function of the given iterated function system mentioned in Eq. (6) and demonstrated in Fig. 8, based on the data recorded from 01 October 2020 to 18 January 2021. In [14], the authors have proposed a reconstruction method of the epidemic curves from the fractal interpolation function with constant vertical scaling factor. In particular, the vertical scaling factor is fixed as 0.1 for all the data constantly. The proposed technique highlights the feasible reconstruction of the death rate based on the fractal interpolation function with the constant scaling factor. In addition, the vertical scaling factor is optimized in the proposed model, and hence, the scaling factor will be automatically selected based on the nature of COVID-19 data set, whereas the vertical scaling factor was a fixed value and not optimized in [14]. Hence, the proposed method is performed superior to the existing reconstruction method as in [14] with respect to the vertical scaling factor. Moreover, the predicted data can be noisy, as it is an extrapolation of the proposed method. The vertical scaling factor is selected based on the data in the proposed technique to reduce or to avoid the occurrence of noises significantly in the predicted data. Further, the correlation fractal dimension is estimated for the prescribed data sets of COVID-19 for the second phase as reported in Table 5. Also, the correlation dimension estimates for the number of infected cases per day, the number of deaths per day and the daily death rate are plotted in Fig. 9. Table 5 narrates the comparison that the correlation fractal dimension of infected cases per day, number of deaths per day and daily death rates of for all representative countries. It will marks the significant jump in the number of infected cases and the number of deaths in second wave of coronavirus in the mentioned countries.
Fig. 8.
Second wave: comparison between the original and predicted daily death rates of the representative countries by fractal interpolation function: a USA, b Brazil, c Russia, d India, e UK
Table 5.
Correlation fractal dimension for second wave of COVID-19 data sets
| Country | Infected cases per day | Deaths per day | Death rate per day |
|---|---|---|---|
| USA | 0.4646 | 0.9574 | 0.4311 |
| Brazil | 0.5312 | 1.3153 | 0.4163 |
| Russia | 0.6942 | 2.2627 | 0.4834 |
| India | 0.5277 | 1.4541 | 0.3743 |
| UK | 0.5193 | 1.2297 | 0.4613 |
Fig. 9.
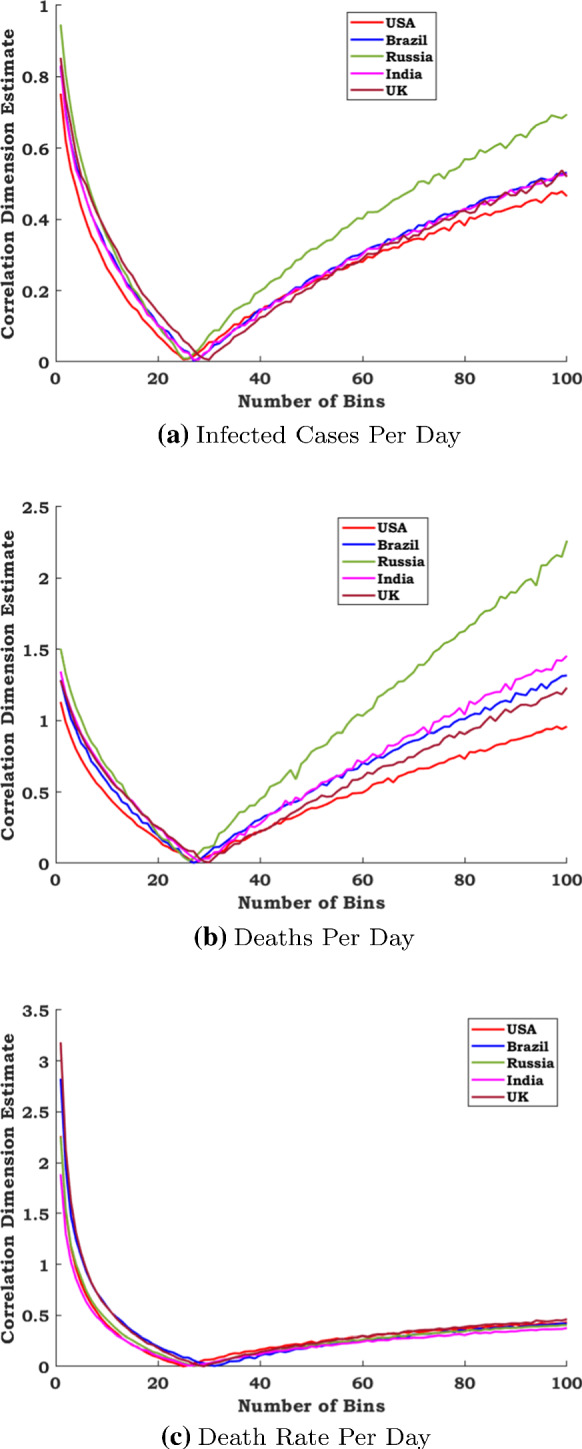
Second wave (initial date of experimental data is 1 October 2020): correlation fractal dimension estimates of COVID-19 second wave database
Influence of lockdown
The nonlinear measures and statistical tools have been calculated and applied to COVID-19 data sets (infected cases, death cases and death rates) to understand the dynamics of the disease transmission. Especially, the correlation fractal dimension, the fractal interpolation function and the autoregressive moving average model have been applied to analyse the chaotic behaviour and also to perform the comparison-based prediction analysis for COVID-19 death rates of the five most disease-ridden countries. The local minima of correlation fractal dimension estimates of death rates for all representative countries are graphically explored to investigate the impact of implementation of the action on reducing the spread of SARS-CoV-2 viruses. Figure 2 evidently shows that there is a period in which the correlation dimension estimates for death rates are nearly zero (minimum), and refers the less complexity, due to the efficacy of precautionary measures taken strictly during the first wave by the government of all countries reflected in this study. It infers that the intervention strategies including the progressive lockdown implemented since March 2020 have influenced the spread of the outbreak. The effectiveness of COVID-19 has been reduced dramatically during the first wave as a result of the respective governing authorities’ incessant lockdown, social distancing, medical precautions and early safety steps. As a result, the mortality rate has been noticeably reduced. Another important point can be identified that the infected cases and the death rate have been increased slowly during the first wave after restrictions relaxed by the governing bodies. It will advise world nations to strictly adhere to the preventive measures so that the respective countries can suppress the death rate as outlined in Sect. 4.1 and save the lives of many people.
Conclusion
The alarming and rapid rise of the COVID-19 positive cases and the rate of mortality due to the second wave of the COVID-19 in several countries of the world are becoming a major threat for the world economy and the livelihood. During this period of pandemic, a detailed study on the virus growth, death rates, recovering rate and on many more parameters has become inevitable to pursue future research on this dreadful virus. In this context, this study has provided a systematic exploration on the comparative analysis and prediction of the spread of the contagion in the first and second waves. The data sets of the number of deaths and the number of infected cases per day of the five most affected countries have been considered for a comparative and prediction analysis. The correlation fractal dimension is estimated for the prescribed data sets of COVID-19 in the first and second waves. Moreover, the comparative analysis of the death rates has been performed based on the correlation fractal dimension estimate curve. The performance of the proposed method has been supported by ANOVA statistical tool. Moreover, the prediction of the daily death rate has been demonstrated through the fractal interpolation function and autoregressive moving average model for both first and second waves. This proposed method has successfully predicted the progress of this dreadful contagion and expressively implemented with the second wave analysis of COVID-19 by comparison based on the reported data provided by WHO and other prestigious organizations. It is observed generically from this study that the prediction of the death rate is liable to change depending on the increase in size of the data set available, and in such a scenario, the rudiments of epidemic prevention, testing, tracking and treating must be concentrated severely.
Availability of data and materials
The experimental data sets analysed in this research study are publicly available [47–49].
Declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
D. Easwaramoorthy, Email: easandk@gmail.com
A. Gowrisankar, Email: gowrisankargri@gmail.com
A. Manimaran, Email: marans2011@gmail.com
S. Nandhini, Email: nandhini.s@vit.ac.in
Lamberto Rondoni, Email: lamberto.rondoni@polito.it.
Santo Banerjee, Email: santoban@gmail.com.
References
- 1.Benvenuto D, Giovanetti M, Vassallo L, Angeletti S, Ciccozzi M. Application of the ARIMA model on the COVID-2019 epidemic data set. Data Br. 2020;29:105340. doi: 10.1016/j.dib.2020.105340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mishra BK, Keshri AK, Rao YS, Mishra BK, Mahato B, Ayesha S, Rukhaiyyar BP, Saini DK, Singh AK. COVID-19 created chaos across the globe: three novel quarantine epidemic models. Chaos, Solitons Fractals. 2020;138:109928. doi: 10.1016/j.chaos.2020.109928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kassa SM, Njagarah JB, Terefe YA. Analysis of the mitigation strategies for COVID-19: from mathematical modelling perspective. Chaos, Solitons Fractals. 2020;138:109968. doi: 10.1016/j.chaos.2020.109968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bouchnita A, Jebrane A. A hybrid multi-scale model of COVID-19 transmission dynamics to assess the potential of non-pharmaceutical interventions. Chaos, Solitons Fractals. 2020;138:109941. doi: 10.1016/j.chaos.2020.109941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Djilali S, Ghanbari B. Coronavirus pandemic: a predictive analysis of the peak outbreak epidemic in South Africa, Turkey, and Brazil. Chaos, Solitons Fractals. 2020;138:109971. doi: 10.1016/j.chaos.2020.109971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fanelli D, Piazza F. Analysis and forecast of COVID-19 spreading in China. Italy and France. Chaos Solitons Fractals. 2020;134:109761. doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sun T, Wang Y. Modeling COVID-19 epidemic in Heilongjiang Province, China. Chaos, Solitons Fractals. 2020;138:109949. doi: 10.1016/j.chaos.2020.109949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ayinde K, Lukman AF, Rauf RI, Alabi OO, Okon CE, Ayinde OE. Modeling Nigerian Covid-19 cases: a comparative analysis of models and estimators. Chaos, Solitons Fractals. 2020;138:109911. doi: 10.1016/j.chaos.2020.109911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ghosal S, Sengupta S, Majumder M, Sinha B. Linear regression analysis to predict the number of deaths in India due to SARS-CoV-2 at 6 weeks from day 0 (100 cases–March 14th 2020) Diabetes Metab. Syndr. 2020;14(4):311–315. doi: 10.1016/j.dsx.2020.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dai C, Yang J, Wang K. Evaluation of prevention and control interventions and its impact on the epidemic of coronavirus disease 2019 in Chongqing and Guizhou Provinces. Math. Biosci. Eng. 2020;17(4):2781–2791. doi: 10.3934/mbe.2020152. [DOI] [PubMed] [Google Scholar]
- 11.Radiom M, Berret JF. Common trends in the epidemic of Covid-19 disease. Eur. J. Phys. Plus. 2020;135:517. doi: 10.1140/epjp/s13360-020-00526-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ng KY, Gui MM. COVID-19: development of a robust mathematical model and simulation package with consideration for ageing population and time delay for control action and resusceptibility. Phys. D. 2020;411:132599. doi: 10.1016/j.physd.2020.132599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Beare BK, Toda AA. On the emergence of a power law in the distribution of COVID-19 cases. Phys. D. 2020;412:132649. doi: 10.1016/j.physd.2020.132649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cristina-Maria P, Bogdan-Radu N. An analysis of COVID-19 spread based on fractal interpolation and fractal dimension. Chaos, Solitons Fractals. 2020;139:110073. doi: 10.1016/j.chaos.2020.110073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sharma M, Pachori RB, Rajendra Acharya U. A new approach to characterize epileptic seizures using analytic time-frequency flexible wavelet transform and fractal dimension. Pattern Recogn. Lett. 2017;94:172–179. doi: 10.1016/j.patrec.2017.03.023. [DOI] [Google Scholar]
- 16.Sharma M, Pachori RB. A novel approach to detect epileptic seizures using a combination of tunable-Q wavelet transform and fractal dimension. J. Mech. Med. Biol. 2017;17(7):1740003. doi: 10.1142/S0219519417400036. [DOI] [Google Scholar]
- 17.Uthayakumar R, Gowrisankar A. Mid-sagittal plane detection in magnetic resonance image based on multifractal techniques. IET Image Process. 2016;10(10):751–762. doi: 10.1049/iet-ipr.2016.0003. [DOI] [Google Scholar]
- 18.Banerjee, S., Hassan, M.K., Mukherjee, S., Gowrisankar, A.: Fractal Patterns in Nonlinear Dynamics and Applications. CRC Press (2019)
- 19.Easwaramoorthy, D., Uthayakumar, R.: Estimating the complexity of biomedical signals by multifractal analysis. In: Proceedings of the IEEE Students’ Technology Symposium. IEEE Xplore Digital Library, IEEE, USA, pp. 6–11 (2010)
- 20.Easwaramoorthy, D., Uthayakumar, R.: Using advanced generalized fractal dimensions. In: Proceedings of the 2nd International Conference on Computing, Communication and Networking Technologies, IEEE Xplore Digital Library, IEEE, USA, pp. 1–6 (2010)
- 21.Easwaramoorthy, D., Uthayakumar, R.: Analysis of biomedical EEG signals using wavelet transforms and multifractal analysis. In: Proceedings of the IEEE International Conference on Communication Control and Computing Technologies, IEEE Xplore Digital Library, IEEE, USA, pp. 544–549 (2010)
- 22.Easwaramoorthy D, Uthayakumar R. Improved generalized fractal dimensions in the discrimination between healthy and epileptic EEG signals. J. Comput. Sci. 2011;2(1):31–38. doi: 10.1016/j.jocs.2011.01.001. [DOI] [Google Scholar]
- 23.Uthayakumar R, Easwaramoorthy D. Multifractal-wavelet based denoising in the classification of healthy and epileptic EEG signals. Fluct. Noise Lett. 2012;11(4):1250034. doi: 10.1142/S0219477512500344. [DOI] [Google Scholar]
- 24.Uthayakumar, R., Easwaramoorthy, D.: Generalized fractal dimensions in the recognition of noise free images. In: Proceedings of the International Conference on Computing, Communication and Networking Technologies, IEEE Xplore Digital Library, IEEE, USA, pp. 1–5 (2012)
- 25.Uthayakumar, R., Easwaramoorthy, D.: Multifractal analysis in denoising of color images. In: Proceedings of the International Conference on Emerging Trends in Science, Engineering and Technology, IEEE Xplore Digital Library, IEEE, USA (2012)
- 26.Uthayakumar R, Easwaramoorthy D. Epileptic seizure detection in EEG signals using multifractal analysis and wavelet transform. Fractals. 2013;21(2):1350011. doi: 10.1142/S0218348X13500114. [DOI] [Google Scholar]
- 27.Uthayakumar, R., Easwaramoorthy, D.: Fuzzy generalized fractal dimensions for chaotic waveforms. In: Chaos, Complexity and Leadership 2012, Springer Proceedings in Complexity, pp. 411—422 (2014)
- 28.Easwaramoorthy D, Eliahim Jeevaraj PS, Gowrisankar A, Manimaran A, Nandhini S. Fuzzy generalized fractal dimensions using inter-heartbeat interval dynamics in ECG signals for age related discrimination. Int. J. Eng. Technol. (UAE) 2018;7(4.10):900–903. doi: 10.14419/ijet.v7i4.10.26784. [DOI] [Google Scholar]
- 29.Ziff, A.L., Ziff, R.M.: Fractal kinetics of COVID-19 pandemic. Int. J. Educat Excell. 6(1), 43–69 (2020)
- 30.Yolanda GS, Sabir Z, Guirao JG. Design of a nonlinear SITR fractal model based on the dynamics of a novel coronavirus (covid-19) Fractals. 2020;28(8):2040026. doi: 10.1142/S0218348X20400265. [DOI] [Google Scholar]
- 31.Namazi H, Kulish VV. Complexity-based classification of the coronavirus disease (COVID-19) Fractals. 2020;28(5):2050114. doi: 10.1142/S0218348X20501145. [DOI] [Google Scholar]
- 32.Ganan-Calvo, A.M., Hernandez Ramos, J.A.: The fractal time growth of COVID-19 pandemic: an accurate self-similar model and urgent conclusions (2020). arXiv:2003.14284
- 33.Gowrisankar A, Lamberto R, Banerjee S. Can India develop herd immunity against COVID-19? Eur. Phys. J. Plus. 2020;135:526. doi: 10.1140/epjp/s13360-020-00531-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Renyi A. On a new axiomatic theory of probability. Acta Math. Hungar. 1955;6:285–335. doi: 10.1007/BF02024393. [DOI] [Google Scholar]
- 35.Grassberger P, Procaccia I. Measuring the strangeness of strange attractors. Phys. D: Nonlinear Phenom. 1983;9(1):189–208. doi: 10.1016/0167-2789(83)90298-1. [DOI] [Google Scholar]
- 36.Grassberger P. Generalized dimensions of strange attractors. Phys. Lett. A. 1983;97:227–320. doi: 10.1016/0375-9601(83)90753-3. [DOI] [Google Scholar]
- 37.Hentschel HGE, Procaccia I. The infinite number of generalized dimensions of fractals and strange attractors. Phys. 8D. 1983;8(3):435–444. [Google Scholar]
- 38.Theiler J. Statistical precision of dimension estimators. Phys. Rev. A. 1990;41(6):3038–3051. doi: 10.1103/PhysRevA.41.3038. [DOI] [PubMed] [Google Scholar]
- 39.Nerenberg MAH, Essex C. Correlation dimension and systematic geometric effects. Phys. Rev. A. 1990;42(12):7065–7074. doi: 10.1103/PhysRevA.42.7065. [DOI] [PubMed] [Google Scholar]
- 40.Jaquette J, Schweinhart B. Fractal dimension estimation with persistent homology: a comparative study. Commun. Nonlinear Sci. Numer. Simul. 2020;84:105163. doi: 10.1016/j.cnsns.2019.105163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Barnsley MF. Fractal functions and interpolation. Constr. Approx. 1989;2(1):303–329. doi: 10.1007/BF01893434. [DOI] [Google Scholar]
- 42.Banerjee, S., Easwaramoorthy, D., Gowrisankar, A.: Fractal functions, dimensions and signal analysis. 1st ed. Springer, Cham (2021)
- 43.Mazel DS, Hayes MH. Using iterated function systems to model discrete sequences. IEEE Trans. Signal Process. 1992;40(7):1724–1734. doi: 10.1109/78.143444. [DOI] [Google Scholar]
- 44.Zhai MY, Juan Luis FM, Rector JW. A new fractal interpolation algorithm and its applications to self-affine signal reconstruction. Fractals. 2011;19(3):355–365. doi: 10.1142/S0218348X11005427. [DOI] [Google Scholar]
- 45.Prasad PK, Gowrisankar A, Saha A, Santo B. Dynamical properties and fractal patterns of nonlinear waves in solar wind plasma. Phys. Scr. 2020;95(6):065603. doi: 10.1088/1402-4896/ab833c. [DOI] [Google Scholar]
- 46.Fataf NAA, Gowrisankar A, Santo B. In search of self-similar chaotic attractors based on fractal function with variable scaling approximately. Phys. Scr. 2020;95(7):075206. doi: 10.1088/1402-4896/ab8f45. [DOI] [Google Scholar]
- 47.Dong, E., Du, H., Gardner, L.: An interactive web-based dashboard to track COVID-19 in real time. Lancet Inf Dis. 20(5), 533–534 (2020) [DOI] [PMC free article] [PubMed]
- 48.Roser, M., Ritchie, H., Ortiz-Ospina, E., Hasell, J.: Coronavirus pandemic (COVID-19). OurWorldInData.org (2020). https://ourworldindata.org/coronavirus
- 49.WHO, Coronavirus Disease (COVID-2019) Situation Reports. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/
- 50.Rebecca, A.: Harrington. Case fatality rate, Encyclopedia Britannica (2020)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The experimental data sets analysed in this research study are publicly available [47–49].