Abstract
Assessing the impact of environmental fluctuations on species coexistence is critical for understanding biodiversity loss and the ecological impacts of climate change. Yet determining how properties like the intensity, frequency or duration of environmental fluctuations influence species coexistence remains challenging, presumably because previous studies have focused on indefinite coexistence. Here, we model the impact of environmental fluctuations at different temporal scales on species coexistence over a finite time period by employing the concepts of time-windowed averaging and performance curves to incorporate temporal niche differences within a stochastic Lotka–Volterra model. We discover that short- and long-term environmental variability has contrasting effects on transient species coexistence, such that short-term variation favours species coexistence, whereas long-term variation promotes competitive exclusion. This dichotomy occurs because small samples (e.g. environmental changes over long time periods) are more likely to show large deviations from the expected mean and are more difficult to predict than large samples (e.g. environmental changes over short time periods), as described in the central limit theorem. Consequently, we show that the complex set of relationships among environmental fluctuations and species coexistence found in previous studies can all be synthesized within a general framework by explicitly considering both long- and short-term environmental variation.
Keywords: fluctuating environment, temporal scale of variation, disturbance, thermal niche
1. Introduction
Environmental fluctuations not only influence an organism's physiology and reproduction directly, but they can also impact an organism's fitness indirectly by driving species interactions [1–3]. Hutchinson [4] suggested that fluctuations in environmental conditions may allow for the coexistence of species competing for limiting resources. For example, one of the key arguments behind the intermediate disturbance hypothesis is that species can reach an equilibrium state and exclude other competing species under reduced environmental fluctuations, whereas increased fluctuations prevent species from reaching equilibrium and therefore prevent competing species from excluding others [4–8] (but see [9]). By contrast, May [10–12] argued that for competing species to coexist in a fluctuating environment, niche differences need to be greater because random environmental fluctuations may favour one species while occasionally excluding another. In a series of influential articles, Chesson et al. [13–16] developed the ‘modern coexistence theory’ of when and how environmental fluctuations mediate species coexistence through nonlinear averaging and storage effects. They found that species can coexist only when the fitness differences [17,18] between species are smaller than their niche differences in a shared environment (i.e. differences in resource utilization in space and time) [17]. Accordingly, environmental fluctuations potentially promote species coexistence by minimizing average fitness differences (equalizing mechanism) [17] or by creating different temporal niches (stabilizing mechanism) [13,16].
The theory of species coexistence was mainly aimed at discussing indefinite coexistence [19–21] (i.e. species persist through infinite time), so fluctuating environments can be represented by the stationary distribution of environmental conditions because the environmental state at any given time recurs with a predictable long-run frequency [22]. Although the analysis of indefinite coexistence has helped us to better understand the mathematical nature of species coexistence, there are significant limitations in its practical application, including how species extinction can be affected by the time scale of environmental variation. For example, a species that specializes in arid environments could survive a certain period of dormancy in a wet year and reproduce again in the next dry year. However, if the wet conditions continue for a thousand years (as opposed to alternating dry and wet years over a short period of time), the probability of extinction of an arid specialist would be much higher [20,23]. Therefore, although the average distribution of the environment (the mean and variance of the environmental conditions) on a long time scale is the same for both the annual alternation of wet and dry years and the alternation of wet and dry years once every thousand years, the effects on the coexistence of species are obviously different. This situation is similar to the process behind the central limit theorem, which was proposed by de Moivre in 1733 and proved by Lyapunov in 1901 [24]. According to the central limit theorem, small samples (e.g. environmental variation over long time periods) are more likely to show large deviations from the expected mean than large samples (e.g. environmental variation over short time periods) and are less predictable. As many practical experiments have confirmed, species rarely (if ever) coexistent indefinitely in the real world [25–27]. Therefore, considering the transient coexistence of species at ecologically meaningful time scales will be crucial for understanding real-world scenarios that might influence species coexistence, particularly in a period of increased global climate change where environmental fluctuations are increasing across much of the world.
Past research on the effects of temporal scales of environmental fluctuations on species coexistence has been based largely on the temporal autocorrelation of the environment. For example, red noise represents low-frequency environmental fluctuations, and thus the time scale of environmental fluctuations is longer. Schreiber [28] investigated the effect of temporal autocorrelation of the environment on species coexistence in relation to the link between environmental conditions and interspecific competition. He found that species can coexist in negatively autocorrelated environments through a different form of storage effect [28], a mechanism that emphasizes that populations are less sensitive to interspecific competition in unfavourable years and can therefore ‘store’ their population increments in favourable years [14,17]. On the other hand, Caswell & Cohen [29] found that the greater the temporal autocorrelation of environmental fluctuations, the more likely that species exclusion is promoted. However, these studies did not consider that the environment may have different magnitudes of variation at different time scales. Moreover, it is difficult to directly compare the distribution of the environmental states at different time scales by using temporal autocorrelation to investigate environmental variation (e.g. the effect of the time scale of environmental variation on species coexistence under different mean environmental conditions). This limits our understanding of the effects of environmental variation on species coexistence at different time scales.
Here, we explore the patterns of species coexistence in fluctuating environments using a stochastic Lotka–Volterra competition model framework. We use windowed averaging to discuss the effects of temporal scales of environmental variation on the mean state of the transient environment. We also employ the newly developed standardized approach for characterizing temperature variation across temporal scales [30], adjusting the magnitude of environmental variation at different time scales to simulate environmental fluctuations in close proximity to real-world situations. We use thermal performance curves to explicitly describe temperature-dependent fitness [31,32]. Although we focus on temperature, our approach can be applied to other climatic measures like precipitation (though a different performance curve would be needed to represent it). In addition, we limit our study to transient coexistence [4,17,33] in order to explore environmental fluctuations at different time scales in nonequilibrium systems. Ultimately, our model provides a basic framework for understanding patterns of species coexistence in fluctuating and unpredictable environments, a topic that will have critical implications for studying and conserving biodiversity in an era of anthropogenic climate change.
2. Methods
(a) . Population dynamics
We investigate the conditions promoting coexistence using a stochastic Lotka–Volterra competition model with two competing species regulated by the population density of its own and the opposing species. Although this design is similar to the classic form of this model [10,12], instead of integrating all fitness responses of environmental conditions, we leave them as continuous responses to the environment (i.e. temperature) and explicitly model environmental conditions through time. That is, the population dynamics follow
| 2.1 |
where i, j identifies the species, T is temperature and N stands for population density. Similarly, K, r, α and d denote carrying capacities, intrinsic growth rates, levels of interspecific interaction and temperature-dependent mortality, respectively. We also assume that the populations will go extinct if the density is too low (i.e. Ni = 0 if Ni < Next = 0.5) in order to prevent the dynamics staying at extremely small positive values.
Although most parameters remain constant, the population growth rate changes with temperature and depends on the thermal performance function (wi(T)), which is adapted from previously published estimates of thermal performance curves [34,35],
| 2.2 |
This function has a maximum value of 1 at Topt. When T is below Topt, thermal performance decreases exponentially with decreasing temperature, whereas when T is above Topt, thermal performance decreases quadratically and eventually reaches the minimum value, wbase, at Tmax (wbase > 0). We assume that there is a high temperature-adapted species (orange; species 1) and a low temperature-adapted species (blue; species 2) (figure 1a). Species 1 is a relative specialist at warm temperatures and species 2 is a relative specialist at cool temperatures (Topt,1 > Topt,2). Although broadly similar in the shapes of their performance curves, we assume that species 1 performs well in a wider range of environments that species 2 (σ1 > σ2). From a biological perspective, our model can be applied to a variety of species for which thermal performance can be quantified; the performance component can be the survival of the species, its reproduction or other fitness components. Although in the literature the thermal performance curve is most often applied to the performance of ectotherms at different body temperatures [36,37], the concept of the thermal performance curve has been extended to the performance of different fitness components of organisms at different environmental or body temperatures [34,38,39]. As a result, our model can be applied to both endotherms and ectotherms. For simplicity, we do not consider the possibility that the thermal performance curve may change over a relatively short time frame [30]. Instead, we assume that the thermal performance curve of a species is fixed.
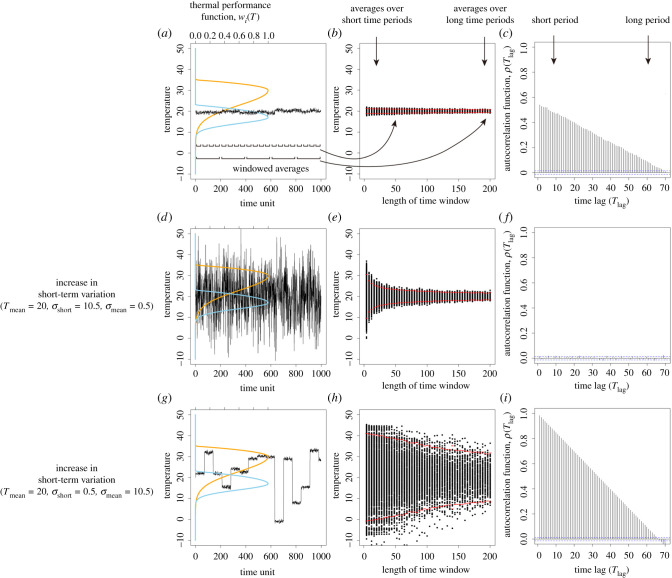
Figure 1.
A demonstration of the species and environmental variation properties in our model. (a) Following the concept of biological performance curves, the difference between the two species can be depicted by the per capita growth rates across all environments (i.e. temperatures). We assume that there is a high temperature-adapted species (orange curve; species 1) and a low temperature-adapted species (blue curve; species 2) competing against one another (see also Methods). The solid black line describes the time series of temperature variation. (b) To better visualize the fluctuations at different temporal scales, we divide the time series into many fractions with equal durations (i.e. window lengths) and calculate the windowed averages of each fraction. This visualization allows us to visualize the rate of convergence of the windowed average, where the red dots are the average plus or minus two standard deviations of the windowed averages for different time windows. (c) Alternatively, the temperature time series can be analysed using the autocorrelation function, where autocorrelation coefficients are plotted along with each time lag. The blue dashed lines indicate the confidence interval of the autocorrelation function; autocorrelation coefficients larger than the interval are statistically significant. (d–f) The time series, windowed averages and autocorrelation function of another temperature time series with an increased short-term variation. (g–i) The same analyses for the other temperature time series where long-term variation is increased. (Online version in colour.)
(b) . Temporal scales of environmental variation
We introduce stochasticity into the model by allowing environmental conditions (i.e. temperature) to change over time. We design two types of environmental variation with different temporal scales that differ in resampling frequency to capture this idea. Specifically, temperatures are determined by the mean and variation of the short-term distribution,
| 2.3a |
where the mean of the short-term distribution and Tsmean, is sampled from a long-term distribution,
| 2.3b |
Note that T is resampled in every time unit, Tsmean is resampled in every δ = 70 time units and population size is updated 200 times in each time unit. We ensure that changes in population size respond to changes in the environment in real time by updating the population size frequently. Although we did not directly consider the effect of species' generation length, we can account for this by adjusting the timing of environmental effects on population renewal to be less frequent, or by allowing the intrinsic growth rate to be smaller (meaning that populations grow or shrink more slowly). The result of doing this demonstrates that species with long generation times are relatively less sensitive to environmental changes in population size (electronic supplementary material, figure S5).
Under our settings, environmental fluctuations are controlled by three factors: (i) the mean temperature of the long-term distribution (Tmean), (ii) long-term variation (); and (iii) short-term variation (). Thus, we model a nonequilibrium system in the sense that environmental conditions vary stochastically and, therefore, the carrying capacities and growth rates of competing species can change dynamically, which prevents populations from reaching the equilibrium points of the Lotka–Volterra equations. Note that equilibrium can be defined more broadly; for example, an equilibrium state describes having some system converge and return to those points upon perturbation, not just the equilibrium points that we define here [25].
The characteristics of short- and long-term environmental variation can be visualized by using an autocorrelation function, a windowed average approach and a fast Fourier transformation. Temporal autocorrelation, used frequently in the literature, describes the probability that the same environmental conditions will remain constant over time [28,29,40]. In essence, when the autocorrelation is large, the chance that the environment remains constant over time is high, and vice versa (figure 1c,f,i). Further, we show that when the time scale of species coexistence is not indefinite and the environmental variation is stochastic, we can also use windowed averaging to resolve the difference between the long- and short-term environmental mean conditions due to the sampling bias as indicated by the central limit theorem (figure 1b,e and h, see also Introduction). Windowed averaging with temporal autocorrelation makes it easier to understand the transient coexistence of species over a finite period of time (e.g. hundreds, thousands or tens of thousands of years). Lastly, the time scale of environmental fluctuations can also be visualized through fast Fourier transformation (FFT) to decompose the time series of temperature into frequency and amplitude domains (electronic supplementary material, figure S1b,c) [30]. Since frequencies with the greatest amplitudes contribute more to the pattern of variation, if we change one type of variation at a time, we can see that larger long-term variation increases the amplitude of low frequencies more than that of higher frequencies (electronic supplementary material, figure S1i). Conversely, larger short-term variation increases the amplitudes of all frequencies uniformly (electronic supplementary material, figure S1f). Thus, increasing long-term variation makes the temperature time series more similar to red noise, while increasing short-term variation makes the time series closer to white noise.
Our temperature fluctuation settings capture the characteristics of stochastic fluctuations at different temporal scales. For instance, body temperature may vary over the course of a few minutes due to a difference in wind speed, whereas variation in weather (e.g. a tropical storm or heat wave) may last for weeks. Further, global events like El Niño may occur at considerably irregular intervals at the temporal scale of years. These examples illustrate how stochastic events can occur at both short- and long-term temporal scales. Importantly, long- and short-term variation should be viewed as two points along with a continuum of temporal environmental variation. Although we do not directly focus on the number of variation types or the relative temporal scale of updating the environmental conditions (i.e. δ), it is possible to extend our model to incorporate more complex and realistic patterns of environmental variation (see table 1 for a summary of all parameters).
Table 1.
List of model parameters.
| name | values | description |
|---|---|---|
| r1, r2 | 0.5 | scaling factor of intrinsic growth rate |
| K1, K2 | 10 000 | scaling factor of carrying capacity |
| d1, d2 | 0.01 | scaling factor of environmental-dependent mortality |
| α | 0.4 | level of interspecific competition |
| δ | 70 | relative duration of long-term variation to short-term variation |
| Topt,1, Topt,2 | 30, 17 | optimum temperature of the two species |
| Tmax,1, Tmax,2 | 35, 23 | upper boundary of fitness function of the two species |
| σ1, σ2 | 5, 2 | width parameter of the fitness function for temperature below optimum |
| wbase | 0.001 | minimum value of fitness function, designed to avoid population deadlock at extreme temperatures |
| Next | 0.5 | the threshold at which a population goes extinct |
3. Results
(a) . Short- versus long-term environmental variation
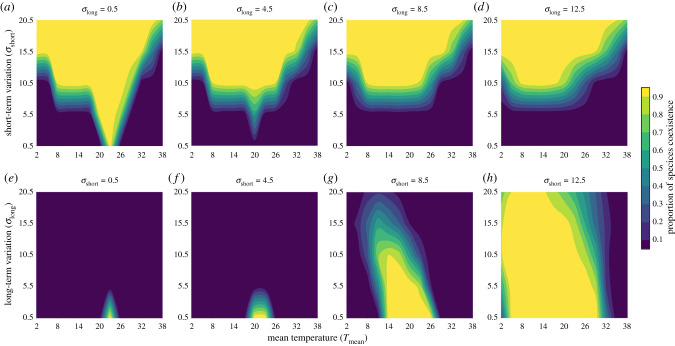
We first explore how combinations of temperature variation at different time scales and different mean temperatures affect species coexistence under (i) continuous short-term variations with different long-term variation (figure 2a–d) and (ii) continuous long-term variations with different short-term variations (figure 2e–h). We found a uniform trend such that the proportion of replicate experiments with species coexistence increases with an increase in short-term variation, regardless of the magnitude of the long-term variation, when short-term variation is continuous along the x-axis and long-term variation is discrete across panels (figure 2a–d). Similarly, when that the range of continuous long-term variation is constant, the area of high coexistence also increases with increasing short-term variation (figure 2e–h). By contrast, we observe the opposite effect of long-term variation, which mainly promotes exclusion (figure 2a–d and e–h). To confirm the generality of this result, we also control for the sum of variances and only change the distribution of variances in the ratio of long- to short-term variation, finding qualitatively similar results (electronic supplementary material, figure S2). In addition, we also confirm that the environmental conditions examined here are such that both species can survive individually in the absence of competition. Therefore, our coexistence and exclusion results are largely driven by species competition (electronic supplementary material, figure S3). Together, these results suggest that greater short-term environmental variation promotes coexistence, whereas greater long-term environmental variation leads to a reduction in species coexistence.
Figure 2.
Short- and long-term temperature variations have contrasting impacts on species coexistence. (a–d) Proportion of simulations producing species coexistence dynamics, where brighter colours indicate greater proportions of coexisting species. Each panel has constant long-term variation (σlong, labelled above each panel) but variable mean temperature (Tmean, x-axis) and short-term variation (σshort, y-axis). Species coexistence occurs if both species sustain through 20 000 short-term variations and 286 long-term variations (4-million calculations of population change). A species becomes extinct if its density is too low (Ni < Next); each combination of mean and variability is repeated for 100 times. (e–h) The proportion of coexistence with the same definition, but each panel has a constant short-term variation (σshort, labelled above each panel) and variable long-term variation (σlong, y-axis). (Online version in colour.)
(b) . Mechanisms of long- and short-term environmental variation on species coexistence
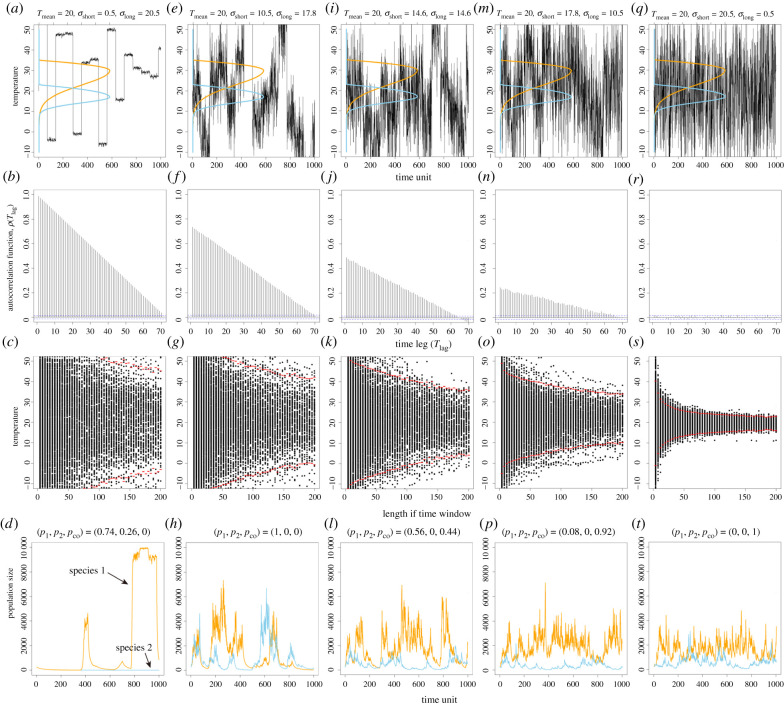
Our results demonstrate that long-term environmental variation promotes competitive exclusion, while short-term environmental changes promote species coexistence (figures 2 and 3; electronic supplementary material, figure S3). Here, we show that when the environmental variation is large at long time scales and small at short time scales (figure 3a), the temporal autocorrelation of the temperature is larger at short time scales and decreases with longer time scales (figure 3b). Interestingly, the mean temperature varies considerably in this case across time periods, showing the windowed average property (figure 3c). Combining the short time period mean temperature with the above results of temporal autocorrelation, we find that the temperature is more likely to remain in a state for a long period of time while the variation is small at short time scales, thus promoting competitive exclusion (figure 3d). Conversely, when the environmental variation is large at short time scales and small at long time scales (figure 3q), the temperature has little temporal autocorrelation at either time scale (figure 3r). The mean temperature is more variable in the short term because it changes many times in a short period of time, but it tends to converge as the time period becomes longer (figure 3s). Therefore, temperature changes a lot at short time scales but very little at long time scales, thus promoting species coexistence (figure 3t).
Figure 3.
Under the same degree of environmental variability, time series with more short-term variation favour species coexistence. Here, we fix the sum of long- and short-term variation (σlong − 0.5)2 + (σshort − 0.5)2 = 400 and examine the fluctuations with different combinations of the two time scales of environmental variation. Specifically, we analyse the temperature time series and the probability of three population-dynamic outcomes: species 1 dominates (p1), species 2 dominates (p2) and species coexistence, (pco). (a) The temperature time series when most of the variation occurs as long-term variation (σlong = 20.5, σshort = 0.5) and thermal performance curves of the two species. (b,c) Autocorrelation function and windowed averages of the temperature time series. (d) The population dynamics corresponding to (a) and the probabilities of coexistence or when a single species dominates. (e–t) The same analyses for another four variation settings where short-term variation increases, but long-term variation decreases. Note that we can only keep the total variance approximately constant. In other words, the difference in variances in the parameter space is marginal, but the variance is not actually constant. (Online version in colour.)
(c) . Effects of environmental averaging on species coexistence
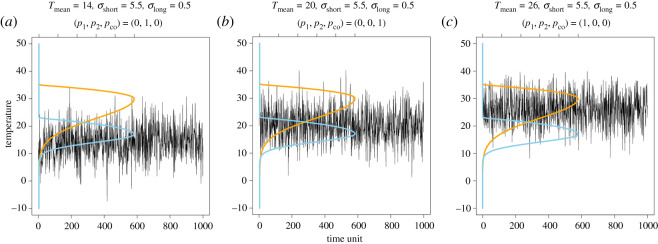
In the case of fixed environmental variation, the effects of the environmental mean on species coexistence are relatively easy to understand. If the mean temperature of the environment is close to the optimal performance temperature of species 1, then species 1 can easily outcompete species 2, resulting in the extinction of species 2 (figure 4a). If the average temperature is intermediate between the optimal temperatures of the two competing species, then the two competing species are likely to coexist (figure 4b). Finally, if the mean temperature is close to the optimal temperature of species 2, then species 1 is easily excluded by species 2 (figure 4c).
Figure 4.
Mean temperature (Tmean) affects species coexistence even when long- and short-term variations remain unchanged. (a) When the mean is lower than the optimal temperature of species 2 (blue curve), species 2 excludes species 1. (b) However, when the mean is between the optima of the two species, species coexistence can occur. (c) Finally, when the mean is above the optimum of species 1, it excludes species 2. Temperature variability is the same in all three cases, where σlong = 0.5, σshort = 5.5. Additionally, p1, p2 and pco represent the probability of species 1 dominating, species 2 dominating and species coexistence, respectively. Note that the mean temperature is different from windowed averages (e.g. figure 3s), as the mean is the actual average of the temperature distribution used for generating time series. (Online version in colour.)
(d) . Environmental variation can both promote and inhibit species coexistence
We have shown that while long-term environmental variation tends to hinder species coexistence and short-term variation tends to promote coexistence, the mean state of the environment also has a critical influence on the pattern of species coexistence. Therefore, by combining these three environmental characteristics, a wide variety of relationships between environmental variation and species coexistence can be generated. Here, we use the above framework to explain the relationship between species coexistence and environmental variation for four seemingly contradictory scenarios. We found that the previous coexistence–exclusion–coexistence result occurs at a mean temperature (17 degrees) that lies in between the optimal temperatures of the two competing species and allows for coexistence in a stable environment (figures 3a and 4g). However, if the mean temperature increases (and becomes closer to the optimum of species 1), species coexistence only occurs when variation is large (figure 4f). Moreover, if the mean temperature increases further, even greater environmental variation will not generate species coexistence. In other words, when mean temperature deviates from the intermediate temperature that is non-optimal for both competing species and approaches the optimum of either species, the relationship between environmental variation and species coexistence may shift from coexistence–exclusion–coexistence (figure 4g–i) to one that promotes coexistence (figure 4d–f) to one that favours coexistence but has relatively weaker influence (figure 4a–c).
4. Discussion
We have shown that the mean and variability of environmental fluctuations can have complex yet predictable effects on patterns of species coexistence. Notably, environmental variation can either promote or hinder species coexistence depending on the temporal scale of variation. This is because short-term environmental variation, at least with our model settings, generally favours species coexistence, whereas long-term environmental variation promotes exclusion of competing species. Our model settings include competitive effects that are linear, competitive effects that are not directly affected by the environment and a range of temperature variation averages over a largely concave fitness surface. In addition, the mean environmental condition also plays a critical role in shaping the effects of environmental variation on species coexistence, depending on whether the mean condition approaches the optimal condition of one of the species or whether it occurs between the optimal conditions of the competing species. In general, large short-term environmental variation promotes species coexistence. However, if the mean environmental conditions are intermediate between the optimal conditions for the two species, large long-term environmental variation will promote competitive exclusion in most of the parameter space. Moreover, when the mean environmental conditions are closer to the optimal conditions for one of the species, there is a small parameter space for large long-term environmental variation to promote species coexistence as a result of environmental variation that suits different species at different times. Thus, if environments fluctuate simultaneously on different temporal scales (e.g. daily, seasonal or annual patterns of temperature fluctuation), which commonly occurs in nature, diverse relationships between environmental variability and species coexistence are expected.
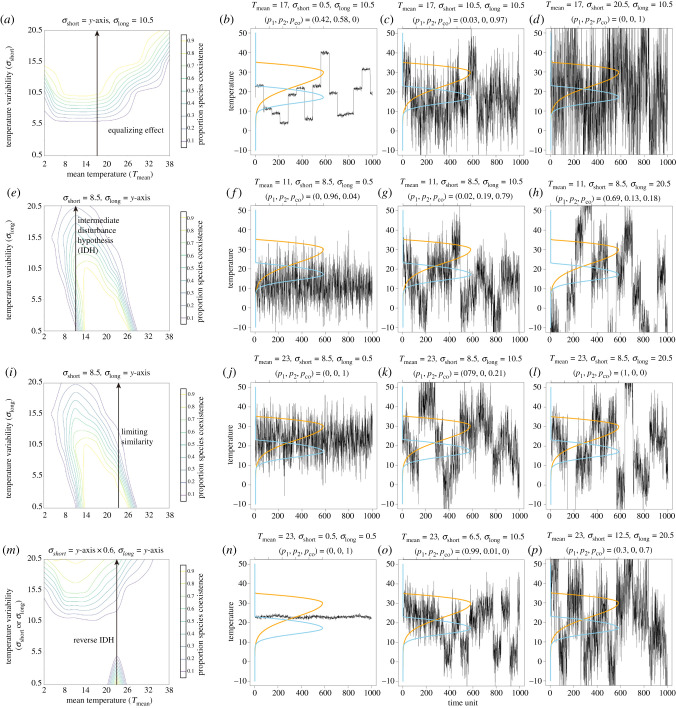
Many seemingly contradictory results of species coexistence and environmental fluctuations from previous studies can be viewed as special cases of a more general result described here (figure 5). For example, Hutchinson [4,5] discussed the impact of temporal scales of environmental variation on species coexistence in a nonequilibrium setting (i.e. species could go extinct by chance due to environmental fluctuations). He argued that both overly fast and overly slow fluctuations promote competitive exclusion between competing species because whichever species competes best on average will exclude the other. Thus, only environmental fluctuations occurring at an intermediate temporal scale will favour species coexistence. Interestingly, analyses of Hutchinson's theory, based on modern coexistence theory, generally conclude that Hutchinson's predictions about the time scales of environmental change and species coexistence are misleading [41]. This is because in the discussion of indefinite coexistence, the mean environmental condition rather than the time scale of environmental fluctuations affects the pattern of species coexistence. By contrast, our model partially agrees with Hutchinson's hypothesis such that intermediate- and long-term environmental fluctuations favour species coexistence and exclusion, respectively. Nevertheless, our model demonstrates that short-term fluctuations are also predicted to facilitate species coexistence rather than exclusion. The key difference between long- and short-term environmental fluctuations is that fast-changing environments allow each competing species to experience their optimal and adverse environmental conditions prior to extinction, which prevents competitive exclusion, whereas slow-changing environments last longer and, thus, can favour one of the competing species in excluding the other. However, May et al. [10–12] proposed that niche differences need to be larger in fluctuating environments than in stable environments for species to coexist. Consequently, competitive exclusion is predicted to occur more easily in fluctuating environments than in stable environments. Yet our model shows that May and colleagues' prediction is a special case such that it is only valid for long-term environmental variation in a nonequilibrium, stochastic model setting.
Figure 5.
Different combinations of short-term temperature variation, long-term temperature variation and mean temperature can generate diverse patterns of species coexistence. (a–d) Coexistence can be promoted by greater temperature variability when the increase is in short-term variation (σshort). (e–h) Coexistence may also occur when variability is intermediate when the increase is in long-term variation (σlong) [4,6]. (i–l) Alternatively, coexistence can be hindered by temperature variability [10] when the increased variability is of long-term variation (σlong) at a different mean temperature (Tmean). (m–p) Finally, it is also possible that coexistence is promoted when variability is very high or very low, when the increased variability contains both short- and long-term variation (both σshort and σlong). We provide examples of temperature time series for each pattern with the probability of species coexistence and single-species dominance above each panel. (Online version in colour.)
Our model may also help resolve the long-standing debate over the intermediate disturbance hypothesis [6,7,42,43], which states that species richness of competing species will be ‘maximized at intermediate frequencies and/or intensities of disturbance or environmental change’ [42]. We show that there can be diverse patterns of species coexistence in relation to environmental variability. Therefore, with the right combination of long- and short-term environmental variation, intermediate disturbance can generate higher species richness relative to higher or lower disturbance scenarios (e.g. figure 5b, left arrow). However, it is also true that intermediate disturbance does not always lead to the highest species richness because species coexistence depends at least partially on the temporal scale of environmental variation. The main differences between our model and previous models are that (i) environments in our model fluctuate stochastically, and therefore species can go extinct by chance if they happen to experience unfavourable environments for an extended period of time [44–46], and (ii) we explicitly consider the temporal scale of environmental variation, while simultaneously considering the effect of the mean environmental condition (i.e. environmental mean, variance and their interaction are included in our model). Accordingly, we urge future studies testing the intermediate disturbance hypothesis to carefully distinguish between different properties of environmental disturbance (e.g. intensity and frequency) on the richness of competing species [30,47].
Since previous research on species coexistence has focused on indefinite coexistence, environmental fluctuations at different time scales have little effect on the relationship between the average environment and species coexistence. To achieve indefinite coexistence, species must be able to invade competing species with low population densities (termed mutual invisibility) [48,49]. Consequently, to achieve indefinite coexistence, there are usually two non-mutually exclusive mechanisms. The first is that species are less sensitive to the interspecific competition when population density is low or the environment is of poor quality [14,17,28]. The second is that the population growth rate increases when population density is low or the environment is of poor quality [16,17]. However, in our model, we deliberately do not assume that the coefficient of interspecific competition (α) is directly influenced by the environment. Yet the intensity of interspecific competition is still influenced by population size (αN), and therefore by environmental conditions. Thus, we do not assume that the population has a buffering effect in poor quality environments or at low population densities, so that we can explore more directly the effect of the environment on competitive exclusion and species coexistence (i.e. assuming that the interspecific competition coefficient becomes smaller when the population density is small or the environment is of poor quality, the coexistence probability is bound to increase). In the terminology of modern coexistence theory, we do not assume a stabilizing effect; our transient coexistence is due to environmental changes that equalize the average performance of the two species (i.e. equalizing effect).
Previous discussions of indefinite coexistence have provided great insights into the mathematical investigation of species coexistence. Here, we echo past calls for discussion of non-equilibrium or transient coexistence [20,23], and the importance of understanding the spatial and temporal scales at which patterns occur, something that has long been emphasized in ecology [50]. We believe that exploring the temporal scales of species coexistence has critical implications for understanding real-world biodiversity loss. Because of the stochastic nature of the environment, the average state of the environment will be different for different time scales (e.g. decades, centuries and millennia) and thus will probably result in different patterns of species coexistence, as described in the central limit theorem [24].
In conclusion, we show that contrasting results from previously published studies linking environmental variation to species interactions [4,10,17] can be viewed as special cases of a more general framework that we develop here (figure 5). By explicitly taking different temporal scales of environmental variation into account [51,52], simultaneously considering the mean environmental condition and modelling different types of stochastic environments, we develop a framework that can be used to explore rich patterns of species coexistence. This framework will be useful for developing testable predictions at a time when environmental fluctuations are increasing globally.
Supplementary Material
Acknowledgements
We thank Po-Ju Ke, Hong-Yan Shih and two anonymous referees for their helpful comments.
Data accessibility
All simulated data were generated using C. The codes and generated data used for this study are available at: https://github.com/mingpapilio/Codes_Coexistence_and_Variation.
Authors' contributions
M.L.: formal analysis, investigation, methodology, visualization, writing-original draft, writing-review and editing; D.R.R.: conceptualization, investigation, visualization, writing-review and editing; S.A.C.: formal analysis, investigation, methodology, validation, writing-review and editing; S.-F.S.: conceptualization, formal analysis, funding acquisition, investigation, supervision, visualization, writing-original draft, writing-review and editing.
All authors gave final approval for publication and agreed to be held accountable for the work performed therein.
Competing interests
We declare we have no competing interests.
Funding
S.-F.S. was supported by Academia Sinica (Career Development Award and Investigator Award, grant no. AS-IA-106-L01) and Minister of Science and Technology of Taiwan (S.-F.S., grant nos. 100-2621-B-001-004-MY3 and 104-2311-B-001-028-MY3). D.R.R. was supported by the US National Science Foundation (grant nos. IOS-1439985 and IOS-1656098).
References
- 1.Tylianakis JM, Didham RK, Bascompte J, Wardle DA. 2008Global change and species interactions in terrestrial ecosystems. Ecol. Lett. 11, 1351-1363. ( 10.1111/j.1461-0248.2008.01250.x) [DOI] [PubMed] [Google Scholar]
- 2.Gilman SE, Urban MC, Tewksbury J, Gilchrist GW, Holt RD. 2010A framework for community interactions under climate change. Trends Ecol. Evol. 25, 325-331. ( 10.1016/j.tree.2010.03.002) [DOI] [PubMed] [Google Scholar]
- 3.Davis AJ, Jenkinson LS, Lawton JH, Shorrocks B, Wood S. 1998Making mistakes when predicting shifts in species range in response to global warming. Nature 391, 783-786. ( 10.1038/35842) [DOI] [PubMed] [Google Scholar]
- 4.Hutchinson GE. 1961The paradox of the plankton. Am. Nat. 95, 137-145. ( 10.1086/282171) [DOI] [Google Scholar]
- 5.Hutchinson GE. 1953The concept of pattern in ecology. Proc. Acad. Natl Sci. Philadelphia 105, 1-12. [Google Scholar]
- 6.Connell JH. 1978Diversity in tropical rain forests and coral reefs. Science 199, 1302-1310. ( 10.1126/science.199.4335.1302) [DOI] [PubMed] [Google Scholar]
- 7.Grime JP. 1973Competitive exclusion in herbaceous vegetation. Nature 242, 344-347. ( 10.1038/242344a0) [DOI] [Google Scholar]
- 8.Roxburgh SH, Shea K, Wilson JB. 2004The intermediate disturbance hypothesis: patch dynamics and mechanisms of species coexistence. Ecology 85, 359-371. ( 10.1890/03-0266) [DOI] [Google Scholar]
- 9.Chesson P, Huntly N. 1997The roles of harsh and fluctuating conditions in the dynamics of ecological communities. Am. Nat. 150, 519-553. ( 10.1086/286080) [DOI] [PubMed] [Google Scholar]
- 10.May RM, MacArthur RH. 1972Niche overlap as a function of environmental variability. Proc. Natl Acad. Sci. USA 69, 1109-1113. ( 10.1073/pnas.69.5.1109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.May RM. 1973Stability in randomly fluctuating versus deterministic environments. Am. Nat. 107, 621-650. [Google Scholar]
- 12.May RM. 1974On the theory of niche overlap. Theor. Popul. Biol. 5, 297-332. ( 10.1016/0040-5809(74)90055-0) [DOI] [PubMed] [Google Scholar]
- 13.Chesson PL, Warner RR. 1981Environmental variability promotes coexistence in lottery competitive systems. Am. Nat. 117, 923-943. ( 10.1086/283778) [DOI] [Google Scholar]
- 14.Chesson PL. 1983Coexistence of competitors in a stochastic environment: the storage effect, pp. 188-198. Berlin, Germany: Springer. [Google Scholar]
- 15.Chesson PL. 1988Interactions between environment and competition: how fluctuations mediate coexistence and competitive exclusion, pp. 51-71. Berlin, Germany: Springer. [Google Scholar]
- 16.Chesson P. 1994Multispecies competition in variable environments. Theor. Popul. Biol. 45, 227-276. ( 10.1006/tpbi.1994.1013) [DOI] [Google Scholar]
- 17.Chesson P. 2000Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 31, 343-366. ( 10.1146/annurev.ecolsys.31.1.343) [DOI] [Google Scholar]
- 18.Chesson P. 2018Updates on mechanisms of maintenance of species diversity. J. Ecol. 106, 1773-1794. ( 10.1111/1365-2745.13035) [DOI] [Google Scholar]
- 19.Armstrong RA, McGehee R. 1976Coexistence of species competing for shared resources. Theor. Popul. Biol. 9, 317-328. ( 10.1016/0040-5809(76)90051-4) [DOI] [PubMed] [Google Scholar]
- 20.Hubbell SP. 2001The unified neutral theory of biodiversity and biogeography. Princeton, NJ: Princeton University Press. [Google Scholar]
- 21.Ellner SP, Snyder RE, Adler PB, Hooker G. 2019An expanded modern coexistence theory for empirical applications. Ecol. Lett. 22, 3-18. ( 10.1111/ele.13159) [DOI] [PubMed] [Google Scholar]
- 22.Chesson P. 2017AEDT: a new concept for ecological dynamics in the ever-changing world. PLoS Biol. 15, e2002634. ( 10.1371/journal.pbio.2002634) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cooper G. 2001Must there be a balance of nature? Biol. Phil. 16, 481-506. ( 10.1023/A:1011935220219) [DOI] [Google Scholar]
- 24.Tijms H. 2007Understanding probability: chance rules in everyday life, 2nd edn. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 25.Rohde K. 2005Nonequilibrium ecology. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 26.Donohue I, et al. 2016Navigating the complexity of ecological stability. Ecol. Lett. 19, 1172-1185. ( 10.1111/ele.12648) [DOI] [PubMed] [Google Scholar]
- 27.Shimadzu H, Dornelas M, Henderson PA, Magurran AE. 2013Diversity is maintained by seasonal variation in species abundance. BMC Biol. 11, 98. ( 10.1186/1741-7007-11-98) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schreiber SJ. 2021Positively and negatively autocorrelated environmental fluctuations have opposing effects on species coexistence. Am. Nat. 197, 405-414. ( 10.1086/713066) [DOI] [PubMed] [Google Scholar]
- 29.Caswell H, Cohen JE. 1995Red, white and blue: environmental variance spectra and coexistence in metapopulations. J. Theor. Biol. 176, 301-316. ( 10.1006/jtbi.1995.0200) [DOI] [Google Scholar]
- 30.Dillon ME, Woods HA, Wang G, Fey SB, Vasseur DA, Telemeco RS, Marshall K, Pincebourde S. 2016Life in the frequency domain: the biological impacts of changes in climate variability at multiple time scales. Integr. Comp. Biol. 56, 14-30. ( 10.1093/icb/icw024) [DOI] [PubMed] [Google Scholar]
- 31.Huey RB, Kingsolver JG. 1989Evolution of thermal sensitivity of ectotherm performance. Trends Ecol. Evol. 4, 131-135. ( 10.1016/0169-5347(89)90211-5) [DOI] [PubMed] [Google Scholar]
- 32.Angilletta MJ Jr, Angilletta MJ. 2009Thermal adaptation: a theoretical and empirical synthesis. Oxford, UK: Oxford University Press. [Google Scholar]
- 33.Loreau M. 2010The maintenance and functional consequences of species diversity. In From populations to ecosystems, pp. 19-55, Princeton, NJ: Princeton University Press. [Google Scholar]
- 34.Deutsch CA, Tewksbury JJ, Huey RB, Sheldon KS, Ghalambor CK, Haak DC, Martin PR. 2008Impacts of climate warming on terrestrial ectotherms across latitude. Proc. Natl Acad. Sci. USA 105, 6668-6672. ( 10.1073/pnas.0709472105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vasseur DA, DeLong JP, Gilbert B, Greig HS, Harley CD, McCann KS, Savage V, Tunney TD, O'Connor MI. 2014Increased temperature variation poses a greater risk to species than climate warming. Proc. R. Soc. B 281, 20132612. ( 10.1098/rspb.2013.2612) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Huey RB, Stevenson RD. 2015Integrating thermal physiology and ecology of ectotherms: a discussion of approaches. Am. Zool. 19, 357-366. ( 10.1093/icb/19.1.357) [DOI] [Google Scholar]
- 37.Sinclair BJ, et al. 2016Can we predict ectotherm responses to climate change using thermal performance curves and body temperatures? Ecol. Lett. 19, 1372-1385. ( 10.1111/ele.12686) [DOI] [PubMed] [Google Scholar]
- 38.Tsai HY, Rubenstein DR, Chen BF, Liu M, Chan SF, Chen DP, Sun SJ, Yuan TN, Shen SF. 2020Antagonistic effects of intraspecific cooperation and interspecific competition on thermal performance. eLife 9, e57022. ( 10.7554/eLife.57022) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Levesque DL, Marshall KE. 2021Do endotherms have thermal performance curves? J. Exp. Biol. 224, jeb141309. ( 10.1242/jeb.141309) [DOI] [PubMed] [Google Scholar]
- 40.Schreiber SJ, Benaïm M, Atchadé KAS. 2011Persistence in fluctuating environments. J. Math. Biol. 62, 655-683. ( 10.1007/s00285-010-0349-5) [DOI] [PubMed] [Google Scholar]
- 41.Li L, Chesson P. 2016The effects of dynamical rates on species coexistence in a variable environment: the paradox of the plankton revisited. Am. Nat. 188, E46-E58. ( 10.1086/687111) [DOI] [PubMed] [Google Scholar]
- 42.Fox JW. 2013The intermediate disturbance hypothesis should be abandoned. Trends Ecol. Evol. 28, 86-92. ( 10.1016/j.tree.2012.08.014) [DOI] [PubMed] [Google Scholar]
- 43.Huston MA. 2014Disturbance, productivity, and species diversity: empiricism vs. logic in ecological theory. Ecology 95, 2382-2396. ( 10.1890/13-1397.1) [DOI] [Google Scholar]
- 44.Adler PB, Ellner SP, Levine JM. 2010Coexistence of perennial plants: an embarrassment of niches. Ecol. Lett. 13, 1019-1029. ( 10.1111/j.1461-0248.2010.01496.x) [DOI] [PubMed] [Google Scholar]
- 45.Gravel D, Guichard F, Hochberg ME. 2011Species coexistence in a variable world. Ecol. Lett. 14, 828-839. ( 10.1111/j.1461-0248.2011.01643.x) [DOI] [PubMed] [Google Scholar]
- 46.Adler PB, Drake JM. 2008Environmental variation, stochastic extinction, and competitive coexistence. Am. Nat. 172, E186-E195. ( 10.1086/591678) [DOI] [PubMed] [Google Scholar]
- 47.Vázquez DP, Gianoli E, Morris WF, Bozinovic F. 2017Ecological and evolutionary impacts of changing climatic variability. Biol. Rev. (Cambridge) 92, 22-42. ( 10.1111/brv.12216) [DOI] [PubMed] [Google Scholar]
- 48.Grainger TN, Levine JM, Gilbert B. 2019The invasion criterion: a common currency for ecological research. Trends Ecol. Evol. 34, 925-935. ( 10.1016/j.tree.2019.05.007) [DOI] [PubMed] [Google Scholar]
- 49.Siepielski AM, McPeek MA. 2010On the evidence for species coexistence: a critique of the coexistence program. Ecology 91, 3153-3164. ( 10.1890/10-0154.1) [DOI] [PubMed] [Google Scholar]
- 50.Levin SA. 1992The problem of pattern and scale in ecology: the Robert H. Macarthur award lecture. Ecology 73, 1943-1967. ( 10.2307/1941447) [DOI] [Google Scholar]
- 51.Shibasaki S, Mobilia M, Mitri S. 2021Exclusion of the fittest predicts microbial community diversity in fluctuating environments. bioRxiv. ( 10.1101/2020.07.22.216010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Liu M, Rubenstein DR, Liu W-C, Shen S-F. 2019A continuum of biological adaptations to environmental fluctuation. Proc. R. Soc. B 286, 20191623. ( 10.1098/rspb.2019.1623) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All simulated data were generated using C. The codes and generated data used for this study are available at: https://github.com/mingpapilio/Codes_Coexistence_and_Variation.