Morphological determinants of bite force capacity in insects: a biomechanical analysis of polymorphic leaf-cutter ants

Abstract

The extraordinary success of social insects is partially based on division of labour, i.e. individuals exclusively or preferentially perform specific tasks. Task preference may correlate with morphological adaptations so implying task specialization, but the extent of such specialization can be difficult to determine. Here, we demonstrate how the physical foundation of some tasks can be leveraged to quantitatively link morphology and performance. We study the allometry of bite force capacity in Atta vollenweideri leaf-cutter ants, polymorphic insects in which the mechanical processing of plant material is a key aspect of the behavioural portfolio. Through a morphometric analysis of tomographic scans, we show that the bite force capacity of the heaviest colony workers is twice as large as predicted by isometry. This disproportionate ‘boost’ is predominantly achieved through increased investment in muscle volume; geometrical parameters such as mechanical advantage, fibre length or pennation angle are likely constrained by the need to maintain a constant mandibular opening range. We analyse this preference for an increase in size-specific muscle volume and the adaptations in internal and external head anatomy required to accommodate it with simple geometric and physical models, so providing a quantitative understanding of the functional anatomy of the musculoskeletal bite apparatus in insects.

1. Introduction

Colonies of social insects are stereotypically characterized by a division of labour, i.e. individuals favour some tasks over others [1,2]. Such task preferences may be the ‘plastic’ result of complex interactions between genetic predisposition, neural and hormonal factors, and varying levels of experience [2,3], but they may also correlate with more ‘rigid’ morphological differences in the colony workforce [4,5]. A natural aim, then, is to connect morphological variation with the task specialization it enables.

A textbook example of polymorphic social insects are leaf-cutter ants, in which workers fall on a more or less continuous size spectrum covering more than two orders of magnitude in body mass (figure 1). Workers may not only differ in size, but also in shape, i.e. specific body parts may not scale according to geometric similarity hypotheses [6–10]. Both size and shape variation may indicate task specialization and so help to increase colony fitness through ergonomic task allocation [8,11–16], but this link is speculative where it is not rationalized through a quantitative functional analysis. For some tasks, e.g. brood care or gardening, such an analysis may be difficult to conduct, but there exists a subset of tasks where it can be made both explicit and quantitative: where tasks have a physical foundation, it is possible to derive exact relationships between morphology and performance from first principles.

Figure 1.

(a) Atta vollenweideri leaf-cutter ants cut and carry fresh plant fragments using their mandibular bite apparatus to supply a fungus used as crop (photo: Samuel T. Fabian). (b) This task is performed by workers which may vary by approximately two orders of magnitude in body mass, as illustrated here with photographs of head capsules representing this size spectrum (dorsal view).

A key mechanical task arising in leaf-cutter ants is to cut leaf or fruit fragments to supply and maintain a fungus used as crop (figure 1; [16,17]). Leaf cutting occurs on an almost industrial scale, and at significant metabolic cost: leaf-cutter ants are responsible for up to 15% of the defoliation in the Neotropics [15,18], and the aerobic scope of leaf cutting is comparable to that of insect flight [19]. It thus appears both plausible and necessary that leaf-cutter ants show morphological adaptations which render them particularly apt at cutting plants.

In all insects with chewing mouthparts, bite forces are generated by large muscles located in the head capsule, and transmitted to the cutting edge of the mandible via an apodeme and a mandibular joint [20,21]. Because this musculoskeletal bite system is of behavioural, ecological and evolutionary relevance and can be analysed with first principles, it has received increasing attention from biomechanists [22–25], evolutionary biologists [26–30], functional morphologists [24,31–38] and (behavioural) ecologists alike [21,39–44]. Concretely, for an isometric contraction at zero fibre stretch, the force exerted at any point of the mandible, F_b, may be written as the product between the ratio of muscle volume V_m and the average fibre length L_f (the physiological cross-sectional area of the muscle, A_phys = V_m/L_f), the muscle stress σ_m, the cosine of the average pennation angle φ, and the mechanical advantage MA [21,31,39,41]:

$$F_b=\underset{\mathrm{Physiology}}{\underbrace{{\sigma }_m}}\cdot \stackrel{A_{\mathrm{eff}}}{\overbrace{\underset{\mathrm{Investment}}{\underbrace{V_m}}\cdot \underset{\mathrm{Geometry}}{\underbrace{L_f^{-1}\cdot \cos \phi \cdot \mathrm{M}\mathrm{A}}}}}.$$ 1.1

Parametrizing the bite force in this way has two distinct advantages. First, it illustrates that F_b may be modulated by changing one of three distinct determinants: muscle physiology (represented by muscle stress), total muscle investment (represented by muscle volume) and the geometry of the musculoskeletal apparatus, defined by the arrangement of muscle fibres and the lever system. The product between the latter two terms may be interpreted as the effective cross-sectional area A_eff of a muscle which acts directly at the point of force application; A_eff is thus a suitable proxy for bite force capacity.

Second, because A_eff is defined entirely by morphological quantities, it is possible to quantitatively link both size and shape variation across workers to a specialization in terms of bite force capacity. Concretely, the parsimonious assumption of geometric similarity implies V_m ∝ m, L_f  ∝ m^1/3 and cosφ ∝ MA ∝ m⁰, so that A_eff  ∝ m^2/3 (where m is body mass). Any deviation from this prediction indicates shape variation that correlates with a modulation of bite force capacity. Here, we use this predictive model as a quantitative guideline for a morphometric analysis of the bite force apparatus of Atta vollenweideri leaf-cutter ants across the entire size range. We (i) investigate if bite force capacity is modulated solely by size or also by shape differences; (ii) analyse if and why such specialization may occur predominantly via changes in muscle investment versus geometry; and (iii) discuss how any specialization requires a variation of the external and internal head morphology, due to geometric and mechanical constraints.

2. Material and methods

2.1. Study animals

Individual ants were sampled from a colony of A. vollenweideri, founded and collected in Uruguay in 2014. The colony was kept in a climate chamber at 25°C, 60% relative humidity, in a 12/12 h light and dark cycle (FitoClima 12.000 PH, Aralab, Rio de Mouro, Portugal), and was fed with bramble and honey water ad libitum. About 30 ants, across the size spectrum, were collected from the foraging area and weighed (Explorer Analytical EX124, max. 120 g × 0.1 mg, OHAUS Corp., Parsippany, NJ, USA). From these 30 ants, we then selected 16 individuals including the heaviest (43.3 mg) and lightest (0.3 mg) specimen to achieve an approximately even spacing between log-transformed masses. The sample size was limited by the time-intense segmentation process. However, the consistently high R² values of our scaling regressions, and the narrow confidence intervals of the associated slopes suggest that our conclusions are robust (see Results).

Ants were sacrificed by freezing and decapitated using a razor blade. In order to facilitate fixative penetration, the antennae and labrum were removed with fine forceps (Dumont #5, Montignez, Switzerland), and about five holes were pierced into the head capsule using ‘00’ insect pins for specimens heavier than 1 mg. All heads were fixed in a paraformaldehyde solution (4% in PBS, Thermo Fisher Scientific, Waltham, MA, USA) for 18 h and subsequently stored in 100% ethanol.

2.2. Micro computed tomography and tissue segmentation

Computed tomography (CT) scans were performed at the Imaging Cluster at the KIT light source (see electronic supplementary material for details). Prior to segmentation, the tomographic image stacks were preprocessed using ‘Fiji’ [45]. Each stack was aligned such that the lateral, dorso-ventral and antero-posterior axes coincided with the principal axes of Fiji’s coordinate system (figure 2). The lateral and dorso-ventral axes were defined based on the bilateral symmetry of the heads. The antero-posterior axis was defined as the line connecting the distal end of the dorsal mandible with the centre of the posterior head opening in lateral view. The oriented image stacks were imported in ‘ITK-SNAP’ (v. 3.6, [46]) for threshold-based segmentation (see electronic supplementary material).

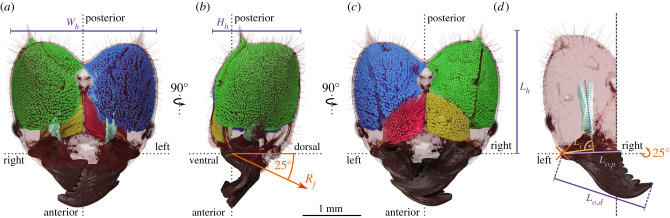
Figure 2.

(a) Dorsal, (b) lateral and (c) ventral view of the internal head anatomy of a medium-sized Atta vollenweideri worker (10.9 mg). Tissues as segmented from micro-computed tomography scans are shown in green (closer muscle), yellow (opener muscle), turquoise (closer apodeme) and light brown (opener apodeme). Muscle fibres as reconstructed with a custom fibre-tracking algorithm are coloured in blue (closer muscle) and red (opener muscle); dashed lines indicate the lateral (left–right), antero-posterior and dorso-ventral axes. We also indicate head width W_h, height, H_h and length L_h. (d) The effective inlever L_i, proximal and distal outlevers, L_o,p and L_o,d, respectively, are defined as the perpendicular distances to the rotational axis of the mandible joint R_j.

2.3. Morphometric analysis

We extracted a series of parameters from the CT scans in order to quantify the key morphological determinants of bite force. These parameters include head dimensions (width, height and length), volume occupancy, apodeme dimensions and orientation, the mechanical advantage of the mandibular lever system, and the volume, physiological cross-sectional area, fibre lengths and orientation of the mandibular closer muscle. The definition of these parameters and their extraction from the segmented data are described in detail in the electronic supplementary material. Most crucially, we extracted the length and pennation angle of 62 380 closer muscle fibres with a custom tracking algorithm written in Python 3.7.6 ([47]. The pennation angle was defined with respect to the main axis of the apodeme. For details, see electronic supplementary material). In brief, the origins of individual muscle fibres were identified by dilating the head capsule, and extracting the intersections with the muscle tissue. These intersections were used as ‘seed points’ to grow fibres in an iterative process, designed to maximize fibre length and homogeneity. A detailed error analysis—explicitly evaluating (i) identification error; (ii) intrinsic error; (iii) segmentation error; and (iv) tracking error—suggests that our methods compare favourably to the performance of commercial alternatives ([48], for details, see electronic supplementary material).

2.4. Data analysis

All data analysis was performed in jupyter lab v. 2.1.2 [49], using R v. 3.6.1 [50] and Python v. 3.7.6 [47]. Unless stated otherwise, all values are given as mean ± s.d. There was no significant difference between tissues in the left and right head hemispheres (ANCOVA: p > 0.05), so we used the average. Analyses involving morphological traits, their derived quantities and body mass were performed on log₁₀-transformed data. We used ordinary least squares (OLS) and standardized major axis (SMA) regressions models implemented in the R package ‘SMATR’ to describe scaling relationships [51]. The suitability of these models is subject to debate, as they involve assumptions on ‘observational’ and ‘biological’ errors [52]. Fortunately, the main conclusions of this paper are supported by either model. The text reports the results for OLS regressions for simplicity; SMA regression results are provided in the electronic supplementary material, table S2.

Allometric scaling in polymorphic ants has sometimes been described with bi- or curvilinear models, i. e. a single log-log slope may not allow an adequate description of the observed allometry [6,7,53–56]. Visual inspection of key morphological traits in our data suggested an approximately linear relationship on a log-log-scale, i.e. a constant differential growth factor. However, the smallest workers (head width <1 mm), appeared to depart from this linear relationship: ‘Minims’ systematically ‘underperformed’, i.e. they had significant negative residuals (e.g. figure 3d). Indeed, the assumptions of a linear model were only met when minims were excluded (assessed via a global procedure following [57]), which also increased the coefficient of determination R² considerably for all regressions on opener and closer muscle volumes, inlever and outlevers. On the basis of this statistical observation, as well as the biological argument that minims preferentially engage in brood care and gardening and only rarely partake in foraging activities which involve cutting [12], we excluded them from all subsequent analyses.

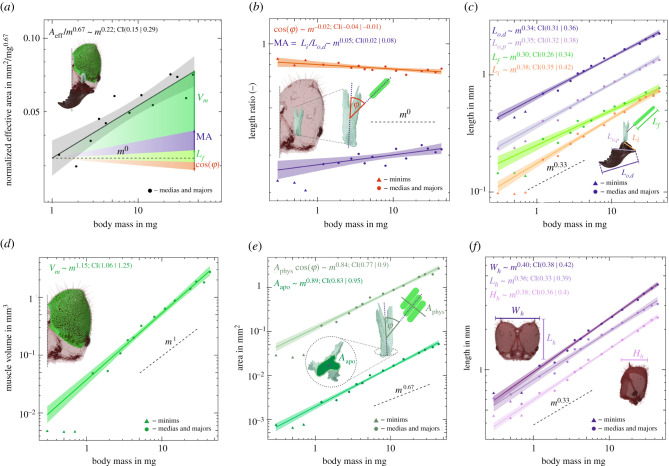
Figure 3.

Scaling of bite force capacity, its morphological determinants and associated allometric changes in internal and external head anatomy in A. vollenweideri leaf-cutter ants. Solid lines show the results of ordinary least-squares regressions on log-log-transformed data excluding the minims (triangles, see Methods), shadings show the 95% confidence intervals, and dashed lines show predictions from isometry. (a) Bite force capacity is determined by investment in muscle volume V_m and the geometry of the musculoskeletal apparatus, and shows strong positive allometry. The shaded areas indicate the extent to which the size-specific increase in bite force capacity is determined by the different morphological determinants. (b) The mechanical advantage, MA and cosine of the average pennation angle, cosϕ, both change systematically but moderately with size. (c) The change in mechanical advantage is solely achieved by a positive allometry of the inlever L_i; both the distal and proximal effective outlevers, L_o,p and L_o,d, respectively, are isometric. Fibre length, L_f, shows a weak but non-significant trend to negative allometry. (d) Muscle volume grows with strong positive allometry, and because fibre length is isometric, this increase largely reflects an increase in the physiological cross-sectional area of the muscle. (e) The apodeme cross-sectional area A_apo also scales with positive allometry. As a result, apodeme stress remains approximately constant despite the increase in bite force capacity. (f) The increase in size-specific muscle volume is accommodated mainly by a positive allometry of head width W_h and height H_h; head length L_h is isometric.

3. Results and discussion

Cutting plant fragments is a central part of the behavioural repertoire of leaf-cutter ants. Bite force capacity is thus a biologically relevant performance metric for the suitability of an individual worker to partake in foraging. All morphological determinants of bite force capacity apart from fibre length differ significantly from isometry (see electronic supplementary material, tables S1 and S2 for detailed statistics). As a cumulative result of these changes, the effective cross-sectional area, A_eff scales as A_eff ∝ m^0.88 [95% CI: (0.81| 0.95)], in significant excess of the isometric prediction, A_eff ∝ m^0.67. This difference in scaling coefficients may appear small, but it results in a substantial enhancement of the absolute bite force capacity: the largest workers have an effective cross-sectional area twice as large as predicted from changes in size alone, (45/1)^0.88−0.67 ≈ 2; achieving this increase in bite force capacity through mere size variation would require workers approximately 2^3/2 ≈ 3 times larger than the largest workers in the colony. Two key questions emerge from this result. First, which of the ‘morphological dials’ are turned to achieve the departure from isometry? Second, what additional adaptations of internal and external head anatomy are required to implement those changes?

3.1. Functional constraints on mechanical advantage and pennation angle favour positive allometry of A_phys

The maximum bite force capacity is determined by the investment in muscle volume V_m, the average fibre length L_f, the average pennation angle φ, and the mechanical advantage MA of the force transmission system (see equation (1.1)). About 70% of the observed disproportionate increase in A_eff is achieved by a disproportionate increase in muscle volume V_m. MA and L_f, in turn, make a contribution of about 40%; the systematic decrease of φ seemingly reduces size-specific bite force capacity by about 10% (figure 3a). Thus, bite force capacity is substantially enhanced through an increased investment in muscle volume as opposed to adjustments in the geometry of the musculoskeletal apparatus. What are the advantages and disadvantages of altering the relative force capacity through a systematic increase in volume investment over changes in geometry, and what constraints may limit one strategy or favour another?

3.1.1. Mechanical advantage

Across worker sizes, MA shows limited but significant positive allometry; MA increases by about 20%, irrespective of whether it is defined with respect to the distal or proximal sections of the gnathal edge (figure 3b). A systematic change in MA may be achieved by an increase of the effective inlever (L_i), a decrease in the effective outlever (L_o), or a combination of both. In A. vollenweideri, the positive allometry in MA is solely driven by the first option (figure 3c). Although halving L_o would result in the same numerical change of MA as doubling L_i, these two changes are not functionally equivalent: an increase in L_i increases the force available at any point along the mandibular cutting edge. By contrast, a shortening of L_o merely reduces the functional length of the mandible without providing a clear functional advantage—smaller outlevers can also be achieved by simply biting with a more proximal part of the mandible. Because this behavioural flexibility is not afforded to L_i—which is anatomically fixed—it is functionally sensible to drive systematic changes in MA through changes in inlever length.

Notably, both the absolute value of the MA and its variation, 0.27 < MA < 0.32 for the distal outlever, are at the lower end of values reported across numerous insect taxa (typically 0.3 < MA < 0.8, see [58]). Thus, the ants appear to use only a small fraction of the theoretically available scaling capacity—a change from 0.3 to 0.8 across worker sizes would result in MA ∝ m^0.26, a factor of five in excess of the observed scaling. We argue that the scaling capacity of MA is constrained for at least two reasons. First, systematic increases in L_i are difficult to implement, because inlevers are internal to the head capsule. Second, the magnitude of the bite force is not the sole functional determinant of bite performance. Instead, ant workers may have to maintain an approximately similar opening range across sizes, which results in a functional coupling of in- and outlever. To retain an equivalent mandibular opening range, a strong positive allometry of MA would require relatively longer muscle fibres, or an increase in characteristic muscle strain. Implementing either option likely requires substantial changes to head anatomy or muscle physiology, and may therefore only be possible across more distantly related species, where developmental and phylogenetic constraints are relaxed. Indeed, the MA of the mandibular system contains significant phylogenetic signal [58], and extreme variations in outlever such as between male and female stag beetles are matched by corresponding changes in inlever [22], both consistent with this interpretation.

3.1.2. Pennation angle

Across worker sizes, the cosine of the average pennation angle φ decreases significantly by about 8%, i.e. φ increases from about 37° to 43° (figure 3b). Thus, the systematic change in φ seemingly decreases the bite force capacity of larger workers. However, this conclusion is premature. Pennate muscle fibres require an attachment area which exceeds their cross-sectional area by a factor csc(φ) [39,41,42,59]. This dependency of the physiological cross-sectional area on φ introduces a sin term into equation (1.1), so that the maximum bite force capacity occurs not for $\phi =0^{\circ }$, as may be concluded from equation (1.1). Instead, the maximum occurs for d/dφ [sinφcosφ] = 0, i.e. for $\phi ={45}^{\circ }$, remarkably close to the values measured for the largest workers (also see [41]). Concretely, although the fraction of the force acting along the apodeme decreases as m^−0.02, the potential for an increase in physiological cross-sectional area A_phys scales as m^0.03 so that the net result of the increase in φ may well be an increase in bite force capacity; we discuss how the disproportionate increase in A_phys is implemented below. Because small workers already have average pennation angles close to the theoretical optimum for force capacity, the net change in bite force capacity arising from changes in φ is negligible. Indeed, the similarity of φ across sizes likely reflects a functional limitation in analogy to the constraint imposed on L_i: changes in φ at constant size-specific muscle length would either alter the functional opening range of the mandible, or require a systematic variation in characteristic muscle strain.

3.1.3. Muscle length and volume

The segmented volume of the closer muscles fibres scales with positive allometry, V_m ∝ m^1.15. By contrast, the length of the muscle fibres scales close to isometry, L_f ∝ m^0.30. Thus, the positive allometry of V_m exclusively reflects a strong positive allometry of A_phys ∝ m^0.86, and hence bite force capacity. Leaf-cutter ants thus deploy a ‘hybrid strategy’ of combining positive allometry of muscle volume with isometry of fibre length, simultaneously satisfying two biological demands: the differential growth of L_f and $\sqrt{A_{\mathrm{phys}}}$ systematically increases bite force capacity, and the isometric growth of L_f ensures that mandibular opening range remains approximately size invariant.

3.2. Positive allometry of bite force capacity requires substantial changes to external and internal head anatomy

We have demonstrated that larger A. vollenweideri leaf-cutter ants boost their bite force capacity via an increased investment in muscle volume, while the geometric arrangement defined by muscle length, pennation angle and the mechanical advantage only shows minor size-specific changes. This positive allometric growth results in a substantial increase of bite force capacity (figure 3a), but poses a significant challenge for external and internal head anatomy: internal adaptations are required to provide the attachment area for a relatively larger A_phys; external adaptations are necessary to combine the positive allometry of A_phys with isometry of L_f, and to provide sufficient space for other functional tissues.

3.2.1. Internal anatomy

The disproportionate increase in A_phys needs to be matched by an equivalent increase of the internal attachment area. In order to model this increase, we approximate the shape of each half of the head capsule as a cylinder with radius R and height h = f_h R (with f_h ≥ 0). This cylinder is terminated with a spherical cap, also with radius R, at its posterior end. The internal attachment area, in turn, is defined by a cylindrical part with equal height h, but radius r = f_r R for the cylindrical section and the spherical cap (with 0 ≤ f_r ≤ 1. The internal area is not equal to the apodeme surface area, because most muscle fibres attach via filaments, see figure 4a). We estimate h as the apodeme length, R as a quarter of the head width, and r = R − L_fsinφ. This simple model predicts the functional volume occupied by muscle to 3% accuracy (V_func ≈ V_ext), and A_phys to 19% accuracy (A_phys ≈ sinφA_int). Having demonstrated that our geometric approximation captures the salient features of the internal and external head geometry pertaining to the arrangement of the closer muscle, we turn our attention to two functional predictions it enables.

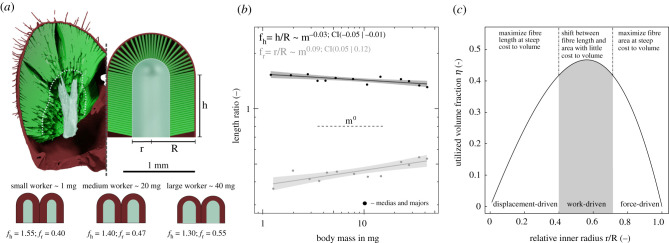
Figure 4.

(a) The volume of half a head capsule may be modelled as a cylinder of length h and radius R, terminated by a spherical cap. The internal fibre attachment area surrounds and internal volume of identical geometry, but with radius r ≤ R; this volume contains both the apodeme, and muscle filaments (see main text). (b) The ratio h/R is negatively allometric so that heads of larger ants appear more ‘heart-shaped’. The ratio r/R, in turn, is positively allometric, indicating a change in the surface to volume ratio of the attaching muscle (see main text). (c) The internal head morphology of A. vollenweideri leaf-cutter ants achieves approximately optimal volume utilization (here shown for a mean value of h/R = 1.4), and lies in a morphological region where fibre length and area can be ‘exchanged’ without a significant variation in used volume.

First, we note that, although A_phys can be increased by increasing either h or r, deviating from the isometric prediction of $A_{\mathrm{phys}}\propto V_m^{0.67}$ requires a systematic variation in r/R = f_r, which controls the surface to volume ratio of the muscle (see electronic supplementary material):

$$\frac{A_{\mathrm{phys}}}{V_m}=\frac{\sin \phi }{R(1-f_r)}.$$ 3.1

Indeed, in A. vollenweideri, r grows more quickly than R, so that f_r increases systematically with size [r ∝ m^0.49. 95% CI: (0.45|0.52); f_r ∝ m^0.09× 95% CI: (0.05|0.12), see figure 4b]. As a consequence of this shift in internal anatomy, the positive allometry of muscle volume is disproportionally invested into A_phys instead of L_f. Additional support for the hypothesis that a disproportionate increase in A_phys is the dominant objective is provided by the observation that h grows more slowly with mass than r, [h ∝ m^0.37× 95% CI: (0.34|0.39)].

Second, we seek to demonstrate that heads of A. vollenweideri workers occupy a morphological space where a shift of volume from fibre length to area can be achieved without a significant variation of the total muscle volume. The origin of the complex relationship between length, area and volume is rooted in the space constraint imposed by an exoskeleton: the area occupied by a cross-section through a muscle fibre is independent of its length, but the internal area available to attach it decreases as the fibre gets longer [41,42]. For a given head volume, there thus exist a trade-off between maximizing fibre length or fibre cross-sectional area: at one extreme are fibres of maximum length which have no internal area to attach to; at the other extreme are fibres with a maximum A_phys equal to the internal surface area of the head capsule, but of miniscule length. The volume of the muscle, then, is maximized at some compromise between investment in fibre length versus area. In order to calculate the geometric arrangement which optimizes muscle volume, we consider the fraction of the available head volume occupied by the closer muscle, η, which is a function of f_r and f_h (see electronic supplementary material):

$$\frac{V_m}{V_{\mathrm{ext}}}=\eta =\frac{\hspace{0.17em}{f}_r^2(1-f_r)+f_h{f}_r(1-f_r)}{1/3+f_h/2}.$$ 3.2

The maximum for η falls between two extremes set by a high-aspect ratio cylinder (f_h ≫ f_r, η_max = 0.5, f_r(η_max) = 0.5) and a hemisphere (f_h = 0, η_max = 0.44, f_r(η_max) = 0.67; see electronic supplementary material). Thus, the maximum volume that can be used is roughly half of the head capsule, which requires f_r ≈ 0.5. For Atta workers, our data suggest 0.36 < f_r < 0.55 and 1.30 < f_h < 1.53, covering a functionally meaningful range (figure 4b): For f_r ≪ 0.5, muscle length is favoured over area at the steep expense of muscle volume. For f_r ≫ 0.5, in turn, volume is sacrificed to maximize area. For f_r ≈ 0.5 as observed in A. vollenweideri, the partitioning of volume into fibre length and cross-sectional area can be altered without a large variation in total muscle volume (figure 4c): The geometric changes in internal head morphology increase the size-specific A_phys by more than 50%, but only alter η by about 12%.

The internal attachment area surrounds an internal volume. In principle, this internal volume could be filled entirely with apodeme, but in insects, individual muscle fibres may alternatively attach via a single, thin, filament-like process of the apodeme [40]. The fraction of filament- versus directly attached muscle fibres differs across species, and likely reflects functional specialization [40–42]. In A. vollenweideri, $98\pm 2\text{\%}$ of muscle fibres are filament attached, independent of worker size [ANOVA: F_1,11 = 1.98, p = 0.18]. What is the advantage of such a strong bias towards filament-attached fibres?

Hypotheses on the functional significance of filament-attached muscle fibres are scarce, but previous work has suggested that using filaments optimizes area utilization [41,42]. Although filaments indeed result in an increase in the available attachment area, this is only a sufficient condition, but not a necessary condition: the same increase could be achieved by increasing the volume occupied by the apodeme instead. Indeed, filament-attached fibres appear to be an alternative to secondary and tertiary branching of the apodeme [41,42], suggesting that optimizing volume utilization may not be the dominant driving factor for filament attachment. We demonstrate in the electronic supplementary material that the use of filaments in A. vollenweideri substantially reduces the required cuticle volume by an amount approximately equal to the cuticle volume of the entire head capsule. Thus, filament attachment has the advantage of significantly reducing material investment; such ‘light-weight’ construction may be particularly important in insects which operate close to maximum volume occupancy.

Filament attachment of muscle fibres constitutes a powerful strategy to reduce material investment, but the apodeme itself cannot be arbitrarily small. Instead, apodeme size is bound by two constraints. First, the apodeme needs to have a surface area large enough to attach all muscle fibres. Only about 6±4% of the apodeme surface area is covered with either filaments or directly attached muscle fibres (see electronic supplementary material). Consequently, the surface area is unlikely to be a limiting constraint for apodeme size. Second, the apodeme needs to have a cross-sectional area sufficiently large to withstand the muscle force without risking failure. This demand may be formally described as the condition that the ratio between two characteristic forces is to remain constant:

$$\mathrm{apodeme}\hspace{0.17em}\mathrm{safety}\hspace{0.17em}\mathrm{factor}=\frac{{\sigma }_{\mathrm{apo}}{A}_{\mathrm{apo}}}{{\sigma }_m{A}_{\mathrm{phys}}\cos \phi }\propto m^0.$$ 3.3

Here, A_apo is the cross-sectional area of the apodeme at the location of maximum stress, and σ_apo is the yield strength of the apodeme. If both characteristic stresses are size invariant, the above condition is satisfied if the scaling of A_apo is close to the scaling of A_physcosφ ∝ m^0.84. Consistent with this condition, we find that A_apo ∝ m^0.89 [95% CI: (0.83| 0.95), figure 3e; see electronic supplementary material for how we determined A_apo]. Hence, ants possess apodemes with cross-sectional areas just large enough to keep the stress approximately constant, σ_apo ∝ m^−0.06 [95% CI: (−0.10| −0.02)]. The simple expression for the safety factor highlights a second important functional demand: the extent to which volume can be saved through the use of filament-attached fibres is modulated by the ratio σ_apo/σ_m. For an approximate value of σ_m ≈ 0.30 MPa [60], and σ_apo ≈ 100 − 600 MPa (see electronic supplementary material), this ratio is typically σ_apo/σ_m ≈ 300 − 1800. The implemented area ratio, in turn, is cosφA_phys/A_apo = 55 ± 5, suggesting that the apodeme operates at a safety factor of ≈ 5 − 30.

3.2.2. External anatomy

The positive allometry of muscle volume poses a challenge, as larger ants need to accommodate disproportionally larger closer muscles. This challenge can be addressed by (i) increasing volume occupancy, and/or (ii), increasing the relative head volume. Volume occupancy χ indeed increases from 70 to over 80% (in accordance with previous studies on ant mandible muscles, e.g. [40,42]), χ ∝ m^0.05 [95% CI: (0.03| 0.06)]. This increase accounts for about 20% of the increase in the functional volume in excess of isometry V_func ∝ m^1.19, as (45/1)^1.19−1.00 ≈ 2. The remaining 80% are enabled by disproportionally larger head capsules, V_h ∝ m^1.15 [95% CI: (1.08|1.21)]. Larger ants tend to have proportionally smaller brains [10,36,55,61], which may provide some flexibility for muscle occupancy. However, smaller ants already have the majority of their heads filled by muscle, and larger ants likely need to provide space for other tissues inside the head capsule, so that the strong allometry of V_func must be predominantly achieved by a positive allometry of overall head volume.

The positive allometry of head volume can be modulated by scaling head length, width and height. We find that head width displays the strongest positive allometry W_h ∝ m^0.40 (as previously reported for Atta, see [8,9,12]), followed by head height, H_h ∝ m^0.38. Head length, in turn, only shows a weak tendency for positive allometry L_h ∝ m^0.36 [95% CI: (0.33| 0.39)] (figure 3f). What explains this seeming preference for increasing some head dimensions more strongly than others?

One possible explanation might lie in the expansion of the internal attachment area: changing the surface-to-volume ratio requires a strong positive allometry of the internal radius r ∝ m^0.49 (see above). Coupled with the isometric growth of fibre length, this allometric expansion affects the relative spatial demand in width and height more strongly than it does in length, as a larger fraction of head width and height is occupied by r. In other words, the effect of the strong positive allometry of r on head length is likely attenuated by the apodeme length, and the space occupied by the opener muscle (figure 2). Head width allometry, in comparison to head height, might be further driven by the need to accommodate longer mandible inlevers, which are approximately aligned with the lateral axis.

3.3. Why vary shape to boost bite performance?

The bite force capacity in A. vollenweideri leaf-cutter ants shows strong positive allometry, mainly achieved by a disproportionate increase in muscle investment. Bite force capacity is of particular relevance for leaf-cutter ants, as it influences the diversity of plant material that can be processed by colony workers [12,13,62,63]. Hence, our results add further support to the hypothesis that size-polymorphism in leaf-cutter ants, and the associated adaptations in shape, may enable them to forage on a broader spectrum of food sources [8,12,16,64,65]. Why alter force capacity not only via size but also via shape differences?

We propose three potential reasons. First, achieving the same bite force with isometry would require a worker three times heavier than the largest worker in an allometric colony workforce. The positive allometry thus increases the effective size range of the colony workforce by a factor of three, but at reduced ‘production cost’ (which is proportional to mass). It is well established that larger workers cut tougher leaves [12,13,62,63,66,67], and our results suggest that they may even cut relatively tougher leaves. Second, a disproportionate increase in bite force may be required to compensate for an increase in mandibular cutting force—the force required to cut a material with mandibles—which may scale in proportion to a characteristic mandible length [68]. Third, disproportionally large heads may enable an increase in size-specific bite force capacity, but they may limit or reduce the ability of workers to perform other tasks, i.e. they render them less generalist. For example, the increased head size may reduce mobility at the nest entrance and within the nest where small heads may be beneficial to successfully manoeuvre through the close-knit structure of the fungal garden (figure 3f; [69]). Indeed, significant numbers of larger workers typically only exist in colonies which exceed a minimum size [14], consistent with the hypothesis of specialized large workers but generalist small workers.

Leaf-cutter ant workers show substantial, size-specific modifications to internal and external anatomy which increase their bite force capacity. The extent to which this specialization improves colony performance requires to integrate the morphological findings of this study with quantitative measurements of cutting performance to assess ‘efficiency’, and with behavioural assays to assess how differences in efficiency are reflected in task allocation. We hope that such work will provide a comprehensive and integrative picture of the interaction between worker polymorphism, task specialization and foraging efficiency.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

This research has received funding (i) from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 851705, to David Labonte), and (ii) from the German Research Foundation (DFG) through grant nos. INST 35/1314-1 FUGG and INST 35/1503-1 FUGG.