A competing risks model with binary time varying covariates for estimation of breast cancer risks in BRCA1 families

Abstract

Mammographic screening and prophylactic surgery such as risk-reducing salpingo oophorectomy can potentially reduce breast cancer risks among mutation carriers of BRCA families. The evaluation of these interventions is usually complicated by the fact that their effects on breast cancer may change over time and by the presence of competing risks. We introduce a correlated competing risks model to model breast and ovarian cancer risks within BRCA1 families that accounts for time-varying covariates. Different parametric forms for the effects of time-varying covariates are proposed for more flexibility and a correlated gamma frailty model is specified to account for the correlated competing events.We also introduce a new ascertainment correction approach that accounts for the selection of families through probands affected with either breast or ovarian cancer, or unaffected. Our simulation studies demonstrate the good performances of our proposed approach in terms of bias and precision of the estimators of model parameters and cause-specific penetrances over different levels of familial correlations. We applied our new approach to 498 BRCA1 mutation carrier families recruited through the Breast Cancer Family Registry. Our results demonstrate the importance of the functional form of the time-varying covariate effect when assessing the role of risk-reducing salpingo oophorectomy on breast cancer. In particular, under the best fitting time-varying covariate model, the overall effect of risk-reducing salpingo oophorectomy on breast cancer risk was statistically significant in women with BRCA1 mutation.

1 Introduction

Between 10% and 15% of all breast cancers (BCs) are caused by a hereditary predisposition.¹ Hereditary breast and ovarian cancer syndrome (HBOC) is an autosomal dominant disease characterized by germline pathogenic mutations in the BRCA1 and BRCA2 genes for the majority of cases. It is the most common cause of hereditary forms of both breast and ovarian cancer (OC).² The overall prevalence of BRCA1/2 mutations is estimated to be from 1 in 400 to 1 in 800 with a higher prevalence in the Ashkenazi Jewish population (1 in 40). Estimates of penetrance (cancer risk) for BRCA1/2 mutations vary considerably.² Previous large meta-analyses reported mean cumulative BC risks at age 70 of 57% for BRCA1 and 49% for BRCA2 mutation carriers.^3,4 The OC risks were 40% for BRCA1 and 18% for BRCA2 mutation carriers. Mutation carriers are also at an elevated risk of developing contralateral breast cancer (CBC) after a previous unilateral BC.⁴ A recent meta-analysis estimated the five-year CBC risk at 15% for BRCA1 mutation carriers and 9% for BRCA2 mutation carriers after a first BC.⁵ Risk prediction models can be used to assess these risks in BRCA1/2 mutation positive families. These statistical models can help health practitioners to guide women who could benefit from genetic counseling and also in their clinical management, which currently comprise intensified surveillance for early BC detection using multimodal imaging techniques or prophylactic surgery such as bilateral mastectomy for the risk of BC and risk-reducing salpingo oophorectomy (RRSO) for the risk of OC.⁶

Competing risks’ models for clustered failure times data have already been proposed by Gorfine and Hsu,⁷ which extended the competing risks model of Prentice et al.⁸ to incorporate the frailty variables to cause-specific hazards models for all the causes. In a subsequent article, Gorfine et al.⁹ showed through a simulation study that naively treating competing risks as independent right censoring events resulted in non-calibrated predictions of cancer risks, with the expected number of events overestimated. Recently, we have also proposed a competing risks approach for clustered family data applicable to successive time-to-event outcomes (i.e. the first and second cancer event could each have a competing risk event).¹⁰ However, to our knowledge, none of these approaches was developed to include time-varying covariates (TVCs).

In a clinical setting, assessing the effect of TVCs is important especially when the follow-up duration is long. For example, we can consider a binary variable, x, for an intervention occurring at a certain time t_x during the follow-up period, which takes the value 0 before t_x and 1 afterwards. Such a variable that changes its value over the follow-up time is referred to as a TVC. If we treat this variable as time-invariant (i.e., coded as 1 for the entire follow-up period), this could result in a biased estimate of its effect since the duration of exposure to the intervention would be overestimated. In addition, this could lead to an immortal time bias when evaluating an intervention in a clinical trial as those individuals who were assigned to an intervention arm cannot have an event of interest until they received the intervention, i.e., they are “immortal” up to time t_x. This is also referred to as survivor selection bias because individuals who have survived (or are event free) are more likely to have received the intervention.

To avoid immortal time bias, the TVC and its effect over time should be appropriately specified. In this context, either a variable, or its effect or both can be assumed to vary with time. In our setting, we have a binary TVC whose value is 0 before intervention at time t_x and 1 thereafter. When the value is one, the effect of the TVC can either be constant or vary with time. It can be formulated as permanent exposure (PE) if the effect of TVC is constant after the time of intervention because the effect stays constant “permanently,” or as exponential decay (ED)¹¹ if the effect of TVC decays over time exponentially and converges to zero. Moreover, if the effect of TVC decays exponentially but converges to a certain fixed value, other than zero, it is referred to as Cox and Oakes (CO)¹² formulation, which allows the decaying effect to remain positive or negative as time goes.

In this article, our goal is to extend previous competing risks approach^7,10 to the situations where the cause-specific hazard function for the event of interest (BC in our application) can depend on TVCs such as mammography screening (MS) or RRSO and where the competing events are correlated within families. The second main extension is to propose an ascertainment correction that specifically accounts for the fact that the BRCA1 families have been recruited through a proband affected by either BC or OC before her study entry, or through an unaffected proband. That is, the ascertainment correction accounts for both the biased sampling and competing events issues. With our proposed approach, we have BC, OC and death from other causes as competing events in BRCA1 mutation families. We also demonstrated a very relevant application of our model to a large series of BRCA1 families, in particular, with an assessment of RRSO. For a woman who has not experienced menopause, removing her ovaries greatly reduces the amount of the hormones, estrogen and progesterone, circulating in her body. This surgery can halt or slow BCs that need these hormones to grow. The possibility that RRSO prevents future BC has however been the subject of some debate. Terry et al.¹³ did not find an association after accounting for the time-varying nature of the covariate. There may be some benefits in RRSO; however, women may elect for RRSO close to menopause limiting the impact. Here we consider the impact of the timing of RRSO in addition to MS through both simulations and applied analyses.

2 Methods

2.1 Correlated gamma frailty model for competing events with time-varying covariates

Consider data arising from n independent families, with family f, $f=1,\dots ,n$, each family consisting of n_f members, $i=1,\dots ,n_f$. For family member i in family f, we denote by $T_{f_i}^{\ast }$ and $C_{f_i}$ the time to the first event and the right censoring time, respectively, and by ${\delta }_{f_i}\in \{1,\dots ,J\}$ the type of the first observed event among J competing events and ${\delta }_{f_i}=0$ if right censored. The observed time is then defined as $T_{f_i}=\text{min}(T_{f_i}^{\ast },C_{f_i})$. We denote by $Z_{f_j}$ the unobserved frailty shared within family f for event $j(j=1,\cdots ,J)$. To allow covariates to vary over time, let ${\mathit{x}}_{f_i}(t)$ be the vector of TVCs at time t for individual i in family f and ${\mathit{X}}_{f_i}(t)=\{{\mathit{x}}_{f_i}(u);0\le u<t\}$ represent the covariate history up to time t.

Consider a binary TVC $x_{f_i}(t)$ = 0 at $t<t_x$ and 1 at $t\ge t_x$, where t_x is the time that changes in value of covariate occurred. We can describe the effect of the TVC that changes over time, denoted by $\mu (·)$, in three different structures: PE, ED, and CO as follows

$$\mu (t,x_{f_i}(t))=\{\begin{array}{l}0\text{ if }t<t_x(\text{PE},\text{ED},\text{CO})\hfill \\ \beta \text{ if }t\ge t_x\text{ (PE) }\hfill \\ \beta \text{exp}\{-\eta (t-t_x)\}\text{ if }t\ge t_x\text{ (ED) }\hfill \\ \beta \text{exp}\{-\eta (t-t_x)\}+{\eta }_0\text{ if }t\ge t_x\text{ (CO) }\hfill \end{array}$$

where for time $t\ge t_x$, the effect of TVC stays at β for PE, whereas it starts to decrease exponentially with a rate of $e^{-\eta }$ to 0 for ED or to η₀ for CO. This time-dependent effect is not limited to TVCs but can be applied to time-invariant covariates. Then the cause-specific hazard for event j for individual i from family f conditional on the covariate history ${\mathit{X}}_{f_i}(t)$ and cause-specific familial frailty $Z_{f_j}$ can be written as

$$\begin{array}{l}{h}_{f_{ij}}(t|{\mathit{X}}_{f_i}(t),Z_{f_j})=\underset{dt\to 0}{\lim }\frac{1}{dt}P(t\le T_{f_i}^{\ast }<t+dt,{\delta }_{f_i}=j|T_{f_i}^{\ast }\ge t,{\mathit{X}}_{f_i}(t),Z_{f_j})\\ =h_{0j}(t)Z_{f_j}\text{exp}\{\mu (t,{\mathit{x}}_{f_i}(t))\}\end{array}$$ (1)

where $h_{0j}(t)$ is the baseline hazard function. We assume the TVCs are exogenous—the future values of covariates up to any time t > u are not affected by the occurrence of any event at time u.

The corresponding cause-specific cumulative hazard function can be expressed as

$$H_{f_{ij}}(t|{\mathit{X}}_{f_i}(t),Z_{f_j})={\displaystyle {\int }_0^t{h}_{0j}}(u)Z_{f_j}\text{exp}\{\mu (u,{\mathit{x}}_{f_i}(u))\}du$$

where calculation details for cause-specific cumulative hazard for PE, ED, and CO models are presented in supplementary Web Appendix A.

The family-specific frailties $Z_{f_j}$ for event j are random effects shared within families. We assume that the frailties are independent across families given event j, but the event-specific frailties could be correlated with each other within families. The correlated frailties can be constructed by defining each event-specific frailty $Z_{f_j}$ within families using two independent random variables $Y_{f_0}$ and $Y_{f_j}$^14,15 so that any pair of family members with different events shares the common frailty $Y_{f_0}$ to induce possible dependence across competing events within families. Gamma frailties are commonly used in the literature because of their mathematical convenience for constructing likelihoods with closed form expressions.

Other distributions such as log-normal or compound Poisson distributions can be used as well for frailties. For correlated log-normal frailties, a multivariate log-normal distribution can be directly used to construct the dependence via the covariance matrix. However, there is no closed form expression for such distribution when integrating out the frailties to construct marginal likelihood and numerical integration is needed. In our article, we present correlated gamma frailties to provide closed form expressions of marginal likelihood and cause-specific penetrance functions, i.e., absolute risk of event given the mutation status for each individual.

We construct the correlated gamma frailties by defining

$$Z_{f_j}=\frac{{\omega }_0}{{\omega }_j}{Y}_{f_0}+Y_{f_j}$$

where $Y_{f_0},Y_{f_j},j=1,\dots ,J$ are independent gamma distributed frailties following $Y_{f_0}\sim \text{Gamma}(k_0,1/k_0)$ and $Y_{f_j}\sim \text{Gamma}(k_j,1/(k_0+k_j))$ and ${\omega }_0=k_0,{\omega }_j=k_0+k_j.$ Then, $Z_{f_j}$ follows $\text{Gamma}({\omega }_j,1/{\omega }_j)$ with mean 1 and variance $=1/{\omega }_j$ and the covariance of the frailties of two events j and $j\prime ,j\ne j\prime$ can be expressed as $\text{cov}(Z_{f_j},Z_{f_{j\prime }})=\frac{{\omega }_0}{{\omega }_j{\omega }_{j\prime }}$, and the correlation as $\rho =\frac{{\omega }_0}{\sqrt{{\omega }_j{\omega }_{j\prime }}}$. As a special case, ${\omega }_0=0$ corresponds to the independent frailties.

The overall survival function is defined as the probability of surviving from all competing events conditional on the covariate history and frailties

$$S_{f_i}(t|{\mathit{X}}_{f_i}(t),{\mathit{Z}}_f)=\text{exp}\{-{\displaystyle \sum _{j=1}^J{H}_{f_{ij}}}(t|{\mathit{X}}_{f_i}(t),Z_{f_j})\}$$ (2)

where ${\mathit{Z}}_f=(Z_{f_1},\dots ,Z_{f_J})$ and $H_{f_{ij}}(t|{\mathit{X}}_{f_i}(t),Z_{f_j})$ is the cause-specific cumulative hazard function at time t.

2.2 Likelihood construction

Let $\mathit{\theta }$ be the vector of parameters involved in the model, which consists of baseline parameters for specifying baseline hazard functions, regression coefficients, parameters related to specifying TVC effects and frailty parameters. Then, the likelihood of the data from n families can be constructed simply by the product of the likelihoods of all families

$$L(\mathit{\theta })={\displaystyle \prod _{f=1}^n{L}_f}(\mathit{\theta })$$

Under the shared frailty competing risk model framework, the likelihood for family f is obtained by integrating over the frailty distribution

$$\begin{array}{l}{L}_f(\mathit{\theta })={\displaystyle \prod _{i=1}^{n_f}{\displaystyle {\int }_0^{\infty }\cdots }}{\displaystyle {\int }_0^{\infty }\left\{{\displaystyle \prod _{j=1}^J{h}_{f_{ij}}}{(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}),Z_{f_j})}^{\text{I}({\delta }_{f_i}=j)}\right\}}\\ \times S_{f_i}(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}),{\mathit{Z}}_f)g_Z(Z_{f_1},\dots ,Z_{f_J})d{Z}_{f_1}\dots d{Z}_{f_J}\end{array}$$

To compute the integrals, we replace $Z_{f_j}$ by $Y_{f_0}+Y_{f_j},j=1,\dots ,J$ and integrate out the independent random variables $Y_{f_j},j=0,\dots ,J$, utilizing their Laplace transform ${\varphi }_j(·)$ and their dth derivative, ${\varphi }_j{(·)}^{(d)}$, which have the following expressions

$$\begin{array}{l}{\varphi }_j(s)={\displaystyle {\int }_0^{\infty }{e}^{-sz}}{g}_j(z)dz\\ {\varphi }_j(s{)}^{(d)}={(-1)}^d{\displaystyle {\int }_0^{\infty }{z}^d}{e}^{-sz}{g}_j(z)dz\end{array}$$

where $g_j(·)$ represents the density function of the random variable $Y_{f_j}$.

With $Y_{f_j}\sim \text{Gamma}(k_j,\frac{1}{{\omega }_j}),{\omega }_0=k_0,{\omega }_j=k_0+k_j,j=1,\dots ,J,$ they have closed form expressions

$$\begin{array}{l}{\varphi }_j(s)={\left(1+\frac{s}{{\omega }_j}\right)}^{-k_j}\\ {\varphi }_j(s{)}^{(d)}=(-1{)}^d\frac{\Gamma (k_j+d)}{\Gamma (k_j){\omega }_j^d}{\left(1+\frac{s}{{\omega }_j}\right)}^{-k_j-d}\end{array}$$

Thus, the likelihood for family f can be obtained as

$$\begin{array}{l}{L}_f(\mathit{\theta })={\displaystyle \prod _{i=1}^{n_f}{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{\infty }\cdots }}}{\displaystyle {\int }_0^{\infty }{\displaystyle \prod _{j=1}^J{h}_{f_{ij}}}}(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}),Y_{f_0},Y_{f_j}{)}^{\text{I}({\delta }_{f_i}=j)}\\ \times S_{f_i}(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}),{\mathit{Y}}_f)g_0(Y_{f_0})g_1(Y_{f_1})\cdots g_J(Y_{f_J})d{Y}_{f_0}d{Y}_{f_1}\dots d{Y}_{f_J}\\ ={\displaystyle \prod _{i=1}^{n_f}{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{\infty }\cdots }}}{\displaystyle {\int }_0^{\infty }{\displaystyle \prod _{j=1}^J{\left\{\left(\frac{{\omega }_0}{{\omega }_j}{Y}_{f_0}+Y_{f_j}\right)h_{ij}(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}))\right\}}^{\text{I}({\delta }_{f_i}=j)}}}\\ \times \exp \left\{-{\displaystyle \sum _{j=1}^J\left(\frac{{\omega }_0}{{\omega }_j}{Y}_{f_0}+Y_{f_j}\right)}{\dot{H}}_j\right\}{g}_0(Y_{f_0})g_1(Y_{f_1})\cdots g_J(Y_{f_J})d{Y}_{f_0}d{Y}_{f_1}\dots d{Y}_{f_J}\\ =\left\{{\displaystyle \prod _{i=1}^{n_f}{\displaystyle \prod _{j=1}^J{h}_{ij}}}{(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}))}^{\text{I}({\delta }_{f_i}=j)}\right\}{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{\infty }\cdots }}{\displaystyle {\int }_0^{\infty }{\displaystyle \prod _{j=1}^J{\left(\frac{{\omega }_0}{{\omega }_j}{Y}_{f_0}+Y_{f_j}\right)}^{d_{f_j}}}}\\ \times \exp \left\{-Y_{f_0}\left({\displaystyle \sum _{j=1}^J\frac{{\omega }_0}{{\omega }_j}}{\dot{H}}_j\right)-{\displaystyle \sum _{j=1}^J{Y}_{f_j}}{\dot{H}}_j\right\}\\ \times g_0(Y_{f_0})g_1(Y_{f_1})\cdots g_J(Y_{f_J})d{Y}_{f_0}d{Y}_{f_1}\dots d{Y}_{f_J}\\ =\left\{{\displaystyle \prod _{i=1}^{n_f}{\displaystyle \prod _{j=1}^J{h}_{ij}}}{(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}))}^{\text{I}({\delta }_{f_i}=j)}\right\}{\displaystyle \sum _{b_1=0}^{d_{f_1}}\cdots }{\displaystyle \sum _{b_J=0}^{d_{f_J}}{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{\infty }\cdots }}}{{\displaystyle \int }}_0^{\infty }\\ Y_{f_0}^B\exp \left\{-Y_{f_0}\left({\displaystyle \sum _{j=1}^J\frac{{\omega }_0}{{\omega }_j}}{\dot{H}}_j\right)\right\}\left\{{\displaystyle \prod _{j=1}^J\left(\begin{array}{c}{d}_{f_j}\\ b_j\end{array}\right)}{\left(\frac{{\omega }_0}{{\omega }_j}\right)}^{b_j}{Y}_{f_j}^{d_{f_j}-b_j}\right\}\exp \left\{-{\displaystyle \sum _{j=1}^J{Y}_{f_j}}{\dot{H}}_j\right\}\\ \times g_0(Y_{f_0})g_1(Y_{f_1})\cdots g_J(Y_{f_J})d{Y}_{f_0}d{Y}_{f_1}\dots d{Y}_{f_J}\\ =\left\{{\displaystyle \prod _{i=1}^{n_f}{\displaystyle \prod _{j=1}^J{h}_{ij}}}{(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}))}^{\text{I}({\delta }_{f_i}=j)}\right\}{\displaystyle \sum _{b_1=0}^{d_{f_1}}\cdots }{\displaystyle \sum _{b_J=0}^{d_{f_J}}{(-1)}^B}{\varphi }_0^{(B)}\left({\displaystyle \sum _{j=1}^J\frac{{\omega }_0}{{\omega }_j}}{\dot{H}}_j\right)\\ \times \left\{{\displaystyle \prod _{j=1}^J\left(\begin{array}{c}{d}_{f_j}\\ b_j\end{array}\right)}{\left(\frac{{\omega }_0}{{\omega }_j}\right)}^{b_j}{(-1)}^{d_{f_j}-b_j}{\varphi }_j^{(d_{f_j}-b_j)}\left({\dot{H}}_j\right)\right\}\end{array}$$ (3)

where $d_{f_j}={\displaystyle {\sum }_{i=1}^{n_f}\text{I}}({\delta }_{f_i}=j)$ is the number of family members affected by event j, ${\dot{H}}_j={\displaystyle {\sum }_{i=1}^{n_f}{H}_{ij}}(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}))$ and $B={\displaystyle {\sum }_{j=1}^J{b}_j}$ are used for notational simplicity, and the products of binomials are written using summations based on the binomial theorem

$$\begin{array}{l}{\displaystyle \prod _{j=1}^J{\left(\frac{{\omega }_0}{{\omega }_j}{Y}_{f_0}+Y_{f_j}\right)}^{d_{f_j}}}={\displaystyle \sum _{b_1=0}^{d_{f_1}}\cdots }{\displaystyle \sum _{b_J=0}^{d_{f_J}}\left(\begin{array}{c}{d}_{f_1}\\ b_1\end{array}\right)}{\left(\frac{{\omega }_0}{{\omega }_1}{Y}_{f_0}\right)}^{b_1}{Y}_{f_1}^{d_{f_1}-b_1}\cdots \left(\begin{array}{c}{d}_{f_J}\\ b_J\end{array}\right){\left(\frac{{\omega }_0}{{\omega }_J}{Y}_{f_0}\right)}^{b_J}{Y}_{f_J}^{d_{f_J}-b_J}\\ ={\displaystyle \sum _{b_1=0}^{d_{f_1}}\cdots }{\displaystyle \sum _{b_J=0}^{d_{f_J}}\left(\begin{array}{c}{d}_{f_1}\\ b_1\end{array}\right)}{\left(\frac{{\omega }_0}{{\omega }_1}\right)}^{b_1}\cdots \left(\begin{array}{c}{d}_{f_J}\\ b_J\end{array}\right){\left(\frac{{\omega }_0}{{\omega }_1}\right)}^{b_J}{Y}_{f_0}^B{Y}_{f_1}^{d_{f_1}-b_1}\cdots Y_{f_J}^{d_{f_J}-b_J}\\ ={\displaystyle \sum _{b_1=0}^{d_{f_1}}\cdots }{\displaystyle \sum _{b_J=0}^{d_{f_J}}{Y}_{f_0}^B}\left\{{\displaystyle \prod _{j=1}^J\left(\begin{array}{c}{d}_{f_j}\\ b_j\end{array}\right)}{\left(\frac{{\omega }_0}{{\omega }_j}\right)}^{b_j}{Y}_{f_j}^{d_{f_j}-b_j}\right\}\end{array}$$

With the Laplace transform of the gamma frailties, the likelihood can be further simplified as

$$\begin{array}{l}{L}_f(\mathit{\theta })=\left\{{\displaystyle \prod _{i=1}^{n_f}{\displaystyle \prod _{j=1}^J{h}_{ij}}}{(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}))}^{\text{I}({\delta }_{f_i}=j)}\right\}{\displaystyle \sum _{b_1=0}^{d_{f_1}}\cdots }{\displaystyle \sum _{b_J=0}^{d_{f_J}}\frac{\Gamma (k_0+B)}{\Gamma (k_0)k_0^B}}{\left(1+{\displaystyle \sum _{j=1}^J\frac{{\dot{H}}_j}{k_0+k_j}}\right)}^{-k_0-B}\\ \times \left\{{\displaystyle \prod _{j=1}^J\left(\begin{array}{c}{d}_{f_j}\\ b_j\end{array}\right)}{\left(\frac{{\omega }_0}{{\omega }_j}\right)}^{b_j}\frac{\Gamma (k_j+d_{f_j}-b_j)}{\Gamma (k_j){(k_0+k_j)}^{d_{f_j}-b_j}}{\left(1+\frac{{\dot{H}}_j}{k_0+k_j}\right)}^{-k_j-d_{f_j}+b_j}\right\}\\ =\left\{{\displaystyle \prod _{i=1}^{n_f}{\displaystyle \prod _{j=1}^J{h}_{ij}}}{(t_{f_i}|{\mathit{X}}_{f_i}(t_{f_i}))}^{\text{I}({\delta }_{f_i}=j)}\right\}{\displaystyle \prod _{j=1}^J{(k_0+k_j)}^{-d_{f_j}}}\\ \times {\displaystyle \sum _{b_1=0}^{d_{f_1}}\cdots }{\displaystyle \sum _{b_J=0}^{d_{f_J}}\frac{\Gamma (k_0+B)}{\Gamma (k_0)}}{\left(1+{\displaystyle \sum _{j=1}^J\frac{{\dot{H}}_j}{k_0+k_j}}\right)}^{-k_0-B}\\ \times \left\{{\displaystyle \prod _{j=1}^J\left(\begin{array}{c}{d}_{f_j}\\ b_j\end{array}\right)}\frac{\Gamma (k_j+d_{f_j}-b_j)}{\Gamma (k_j)}{\left(1+\frac{{\dot{H}}_j}{k_0+k_j}\right)}^{-k_j-d_{f_j}+b_j}\right\}\end{array}$$ (4)

2.3 Ascertainment correction

It is common in familial cancer studies that families are ascertained via a proband (indexed as p) who is affected with cancer. A correction for ascertainment needs to be applied to get valid inference about the penetrance function and genetic relative risk and we have previously proposed and evaluated several approaches for this problem in the context of a single time to event outcome.¹⁶ We generalize here the prospective likelihood approach of ascertainment correction that we introduced before, to the situation where the proband has at least one of the three competing events (BC, OC or death from other causes) before her age at examination ($a_{f_p}$). We also consider death as an ascertainment event because our real application includes a small number of probands who were unaffected at study entry but died during the follow-up period.

The rationale of the prospective likelihood method of ascertainment correction is to weight the likelihood of each family f, $L_f(\mathit{\theta })$, by the inverse probability of a proband being affected before her age at examination, assuming that the proband could have been ascertained anytime within this interval. If a proband has high probability of being selected before her age at ascertainment, then the risk of events for the selected family will be overestimated in the model, and they are therefore down-weighted. We denote by $A_f(\mathit{\theta })=P(T_{f_p}\le a_{f_p}|{\mathit{X}}_{f_p}(a_{f_p}))$ the probability for a proband to experience at least one event by her age of ascertainment, which can be derived as

$$\begin{array}{l}{A}_f(\mathit{\theta })=1-{\displaystyle \int \cdots }\int \text{exp}\{-{\displaystyle \sum _{j=1}^J{Z}_{f_j}}{H}_{f_{pj}}(a_{f_p}|{\mathit{X}}_{f_p}(a_{f_p}))\}{g}_Z(Z_{f_1},\dots ,Z_{f_J})d{Z}_{f_1}\dots d{Z}_{f_J}\\ \hspace{1em}\hspace{1em} =1-{\{1+{\displaystyle \sum _{j=1}^J\frac{H_{f_{pj}}(a_{f_p}|{\mathit{X}}_{f_p}(a_{f_p}))}{{\omega }_j}}\}}^{-k_0}{\displaystyle \prod _{j=1}^J\{}1+\frac{H_{f_{pj}}(a_{f_p}|{\mathit{X}}_{f_p}(a_{f_p}))}{{\omega }_j}{\}}^{-k_j}\end{array}$$ (5)

In our real data application, we also consider unaffected probands. The ascertainment correction for them is given by the probability of surviving all events

$$A_f(\mathit{\theta })={\{1+{\displaystyle \sum _{j=1}^J\frac{H_{f_{pj}}(a_{f_p}|{\mathit{X}}_{f_p}(a_{f_p}))}{{\omega }_j}}\}}^{-k_0}{\displaystyle \prod _{j=1}^J\{}1+\frac{H_{f_{pj}}(a_{f_p}|{\mathit{X}}_{f_p}(a_{f_p}))}{{\omega }_j}{\}}^{-k_j}$$

Therefore, the ascertainment corrected likelihood for all the families is expressed as

$$L_C(\mathit{\theta })={\displaystyle \prod _{f=1}^n\frac{L_f(\mathit{\theta })}{A_f(\mathit{\theta })}}$$

and maximum likelihood estimates of the parameters are obtained by maximizing the corresponding log-likelihood.

2.4 Cause-specific penetrance function with time-varying covariates

Our main interest is to estimate the jth cause-specific cumulative incidence function $F_j(·)$, also called cause-specific penetrance. We first express the conditional cause-specific penetrance given the random frailty variables $\mathit{Z}=(Z_1,\dots ,Z_J)$ as

$$\begin{array}{l}{F}_j(t|{\mathit{X}}_{f_i}(t),\mathit{Z})=P(T_{f_i}\le t,{\delta }_{f_i}=j|{\mathit{X}}_{f_i}(t),\mathit{Z})\\ ={\displaystyle {\int }_0^t{h}_{f_{ij}}}(u|{\mathit{X}}_{f_i}(u),Z_j)\text{exp}\{-{\displaystyle \sum _{j=1}^J{H}_{f_{ij}}}(u|{\mathit{X}}_{f_i}(u),Z_j)\}du.\end{array}$$

We derived the marginal cause-specific penetrance function for event j by integrating over the frailties $\mathit{Z}=(Z_1,\dots ,Z_J)$ as follows

$$\begin{array}{l}{F}_j(t|{\mathit{X}}_{f_i}(t))={\displaystyle {\int }_0^{\infty }\cdots }{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^t{h}_{f_{ij}}}}(u|{\mathit{X}}_{f_i}(u),Z_j)S_{f_i}(u|{\mathit{X}}_{f_i}(u),\mathit{Z})g_Z(\mathit{Z})dud\mathit{Z}\\ ={\displaystyle {\int }_0^t{\displaystyle {\int }_0^{\infty }\cdots }}{\displaystyle {\int }_0^{\infty }{h}_{f_{ij}}}(u)\left(\frac{{\omega }_0}{{\omega }_j}{Y}_0+Y_j\right)e^{-{\displaystyle \sum _{l=1}^J\left(\frac{{\omega }_0}{{\omega }_l}{Y}_0+Y_l\right)H_{f_{il}}(u)}}\\ \times g_0(Y_0)g_1(Y_1)\cdots g_J(Y_J)d{Y}_{0}d{Y}_1\cdots d{Y}_{J}du\\ ={\displaystyle {\int }_0^t{h}_{f_{ij}}}(u){\displaystyle \prod _{l\ne j}{\displaystyle {\int }_0^{\infty }{e}^{-H_{f_{il}}(u)Y_l}}}{g}_l(Y_l)d{Y}_l\\ \times [\frac{{\omega }_0}{{\omega }_j}{\displaystyle {\int }_0^{\infty }{Y}_0}{e}^{-{\displaystyle \sum _{l=1}^J\left\{\frac{{\omega }_0}{{\omega }_l}{H}_{f_{il}}(u)\right\}{Y}_0}}{g}_0(Y_0)d{Y}_0{\displaystyle {\int }_0^{\infty }{e}^{-H_{f_{ij}}(u)Y_j}}{g}_j(Y_j)d{Y}_j\\ +{\displaystyle {\int }_0^{\infty }{e}^{-{\displaystyle \sum _{l=1}^J\left\{\frac{{\omega }_0}{{\omega }_l}{H}_{f_{il}}(u)\right\}{Y}_0}}}{g}_0(Y_0)d{Y}_0{\displaystyle {\int }_0^{\infty }{Y}_j}{e}^{-H_{f_{ij}}(u)Y_j}{g}_j(Y_j)d{Y}_j]du\\ ={\displaystyle {\int }_0^t{h}_{f_{ij}}}(u){\displaystyle \prod _{l\ne j}{\varphi }_l}\left\{H_{f_{il}}(u)\right\}[\frac{{\omega }_0}{{\omega }_j}(-1){\varphi }_0^{(1)}\left\{{\displaystyle \sum _{l=1}^J\frac{{\omega }_0}{{\omega }_l}}{H}_{f_{il}}(u)\right\}{\varphi }_j\{H_{f_{ij}}(u)\}\\ +{\varphi }_0\left\{{\displaystyle \sum _{l=1}^J\frac{{\omega }_0}{{\omega }_l}}{H}_{f_{il}}(u)\right\}(-1){\varphi }_j^{(1)}\{H_{f_{ij}}(u)\}]du\\ ={\displaystyle {\int }_0^t{h}_{f_{ij}}}(u){\displaystyle \prod _{l\ne j}}(1+\frac{H_{f_{il}}(u)}{{\omega }_l}{)}^{-k_l}[\frac{{\omega }_0}{{\omega }_j}{\left\{1+{\displaystyle \sum _{l=1}^J\frac{H_{f_{il}}(u)}{{\omega }_l}}\right\}}^{-k_0-1}{\left\{1+\frac{H_{f_{ij}}(u)}{{\omega }_j}\right\}}^{-k_j}\\ +{\left\{1+{\displaystyle \sum _{l=1}^J\frac{H_{f_{il}}(u)}{{\omega }_l}}\right\}}^{-k_0}\frac{k_j}{{\omega }_j}{\left\{1+\frac{H_{f_{ij}}(u)}{{\omega }_j}\right\}}^{-k_j-1}]du\\ ={\displaystyle {\int }_0^t{h}_{f_{i1}}}(u){\displaystyle \prod _{l\ne j}{\left\{1+\frac{H_{f_{il}}(u)}{{\omega }_l}\right\}}^{-k_l}}{\left\{1+\frac{H_{f_{ij}}(u)}{{\omega }_j}\right\}}^{-k_j}{\left\{1+{\displaystyle \sum _{l=1}^J\frac{H_{f_{il}}(u)}{{\omega }_l}}\right\}}^{-k_0}\times \\ [\frac{k_0}{{\omega }_j}{\left\{1+{\displaystyle \sum _{l=1}^J\frac{H_{f_{il}}(u)}{{\omega }_l}}\right\}}^{-1}+\frac{k_j}{{\omega }_j}{\left\{1+\frac{H_{f_{ij}}(u)}{{\omega }_j}\right\}}^{-1}]du\end{array}$$ (6)

where the covariate history ${\mathit{X}}_{f_i}(u)$ is removed from the hazard and cumulative hazard functions for notational simplicity and calculation details for PE, ED, and CO models are specified in supplementary Web Appendix B.

2.5 Variance estimation

The variance–covariance matrix of $\widehat{\mathit{\theta }}$ is estimated using a robust sandwich variance estimator

$$V(\widehat{\mathit{\theta }})=I_o{(\mathit{\theta })}^{-1}J(\mathit{\theta })I_o{(\mathit{\theta })}^{-1}$$

where $I_o(\mathit{\theta })$ is the observed information matrix and $J(\mathit{\theta })$ is the expected information matrix. They can be obtained by

$$\begin{array}{l}{I}_o(\mathit{\theta })=-\frac{{\partial }^2{\ell }_C(\mathit{\theta })}{\partial {\mathit{\theta }}^T\partial \mathit{\theta }}\\ J(\mathit{\theta })={\displaystyle \sum _f{U}_f}(\mathit{\theta })U_f^{\mathrm{\top }}(\mathit{\theta })\\ U_f(\mathit{\theta })=\frac{\partial \text{log}{L}_f(\mathit{\theta })}{\partial \mathit{\theta }}-\frac{\partial \text{log}{A}_f(\mathit{\theta })}{\partial \mathit{\theta }}\end{array}$$

The variance estimates $\widehat{V}(\widehat{\mathit{\theta }})$ are obtained by evaluating $I_o(\mathit{\theta })$ and $J(\mathit{\theta })$ at the maximum-likelihood estimate $\widehat{\mathit{\theta }}$.

The robust variance estimator for the cause-specific penetrance estimate, $F_j(t|\widehat{\mathit{\theta }})$, is obtained using Delta method

$$V(F_j(t|\widehat{\mathit{\theta }}))=D_{\mathit{\theta }}^{\mathrm{\top }}(t)V(\widehat{\mathit{\theta }})D_{\mathit{\theta }}(t)$$

where $D_{\mathit{\theta }}(t)$ is the vector of partial derivatives of $F_j(t|\mathit{\theta })$ with respect to $\mathit{\theta }$. The variance estimates $\widehat{V}(F_j(t|\widehat{\mathit{\theta }}))$ are obtained by plugging in $\widehat{\mathit{\theta }}$.

2.6 Confidence interval estimations

The confidence interval (CI) for each (transformed) parameter was obtained by Wald method based on the variance estimates. The parameters whose space is restricted to be positive including baseline parameters (Weibull or piecewise constant), exponential rate parameters ($\eta \prime$s) frailty parameters ($k\prime$s) were log transformed.

The CI for cause-specific penetrance is obtained based on Monte Carlo stimulations of the parameter estimates following a multivariate normal distribution with the mean equal to the estimated parameters from the model and variance equal to the estimated robust variance–covariance matrix. Each simulated set of parameters was plugged in the penetrance function for given time t and covariate values. The 95% CI of the penetrance is obtained from the 2.5th and 97.5th percentiles of the penetrance estimates from 1000 Monte Carlo simulations.

Similarly, the CI for the time-dependent hazard ratio (HR) of a TVC is obtained by exponentiating the CI for $\mu (t,x(t))$ obtained using TVC effect estimates at given time t from 1000 Monte Carlo simulations of related parameters.

2.7 Implementation

Our proposed model was implemented in R (version 3.6.1) and optimization of the likelihood to estimate parameters was based on optim function in R using Nelder and Mead method.¹⁷ Calculation of the cumulative hazards and cause-specific penetrances was done by numerical integration based on adaptive quadrature method using integrate function in R. We also provide R codes in supplementary to simulate family data with time-dependent covariates and also to obtain the parameter estimates based on our proposed model.

3 Simulation study

3.1 Simulation study design

We conducted simulation studies to assess the finite-sample properties of our proposed approach. We considered J = 2 competing events with a TVC affecting a single event. Our simulated datasets mimic BRCA1 mutation positive families from the Breast Cancer Family Registry (BCFR) used in our application with respect to family structure and inclusion criteria. True parameter values were obtained after fitting our model to the real data. For each dataset, 500 families were generated under PE, ED, and CO TVC models, each with low, medium, and high familial dependence, which corresponds to $k_1=7$ ($\tau =0.07$), 3.5 ($\tau =0.13$), and 1 ($\tau =0.33$), respectively, where τ represents a Kendall’s tau. A value close to 1 indicates higher dependence among the family relatives’ failure times. The parameter k₂ was fixed at the estimated value obtained from the real data analysis. We consider the situation where k₀ goes to zero, i.e., independent frailties, as in our real data analysis, the parameters associated with the TVCs and penetrance functions (which are our main interests in these simulations) were not very sensitive to the presence of correlation between the frailties. All combinations of parameters can be found in Table 1. The model included a mutation status as a time-invariant covariate affecting both events and a TVC, which can be either MS or RRSO, for event 1. Detailed steps of data generation are presented in supplementary Web Appendix C. For each scenario, the model parameters and penetrance estimators are evaluated based on 500 simulations by comparing bias, empirical standard error (ESE), average standard error (ASE), and empirical coverage probability (ECP). Bias is defined as the difference between mean estimate, $\overline{\widehat{\beta }}$ and the true value of the parameter, β; ESE is obtained by the standard deviation of the estimates over all simulations, $\sqrt{{\displaystyle {\sum }_{i=1}^M{(\widehat{{\beta }_i}-\overline{\widehat{\beta }})}^2}/(M-1)},$ where M = 500 is the number of simulations and ${\widehat{\beta }}_i$ is the parameter estimate from simulation i, $i=1,\dots ,M$ and $\overline{\widehat{\beta }}$ is the average of the estimates from M simulations; ASE is obtained by ${\displaystyle {\sum }_{i=1}^{M}S}E(\widehat{{\beta }_i})/M$, the average of robust standard errors (SEs) from each simulation. Finally, ECP is the proportion of times 95% CI defined as $\widehat{{\beta }_i}\pm Z_{0.975}$SE($\widehat{{\beta }_i}$) include true value β for $i=1,\dots ,N$.

Table 1.

Empirical parameter estimates from the competing risks model with a time-varying covariate (TVC) under low ($k_1=7$), medium ($k_1=3.5$), and high ($k_1=1$) familial dependence; permanent exposure (PE), exponential decay (ED) or Cox and Oakes (CO) models are considered for TVC.

TVC		True	$k_1=7,\tau =0.07$				True	$k_1=3.5,\tau =0.13$				True	$k_1=1,\tau =0.33$
model		value	Bias	ESE	ASE	ECP	value	Bias	ESE	ASE	ECP	value	Bias	ESE	ASE	ECP
PE	$\text{log}({\lambda }_1)$	−4.83	−0.01	0.06	0.06	0.95	−4.83	0.00	0.06	0.06	0.95	−4.83	0.00	0.06	0.06	0.94
	$\text{log}({\rho }_1)$	0.88	0.00	0.03	0.03	0.94	0.88	0.00	0.03	0.03	0.93	0.88	0.00	0.03	0.03	0.96
	$\text{log}({\lambda }_2)$	−4.96	−0.01	0.09	0.10	0.95	−4.96	−0.02	0.10	0.10	0.94	−4.96	−0.01	0.09	0.10	0.96
	$\text{log}({\rho }_2)$	1.12	0.00	0.07	0.07	0.95	1.12	0.00	0.07	0.07	0.95	1.12	0.00	0.06	0.07	0.96
	${\beta }_{1g\mathit{ene}}$	1.95	0.01	0.12	0.12	0.95	1.95	0.01	0.12	0.12	0.96	1.95	0.00	0.12	0.11	0.94
	${\beta }_{2g\mathit{ene}}$	1.19	0.03	0.23	0.23	0.96	1.19	0.03	0.24	0.23	0.95	1.19	0.02	0.22	0.24	0.96
	${\beta }_{1tvc}$	0.67	0.01	0.11	0.11	0.95	0.67	0.00	0.10	0.11	0.96	0.67	0.00	0.11	0.11	0.96
	$\text{log}(k_1)$	1.95	0.24	1.08	0.85	0.92	1.25	0.13	0.69	0.48	0.95	0.00	0.02	0.25	0.25	0.95
	$\text{log}(k_2)$	1.06	0.62	2.17	1.38	0.80	1.06	0.72	2.20	1.41	0.84	1.06	0.61	2.05	1.46	0.86
ED	$\text{log}({\lambda }_1)$	−4.83	−0.01	0.05	0.06	0.96	−4.83	0.00	0.06	0.06	0.95	−4.83	0.00	0.06	0.06	0.96
	$\text{log}({\rho }_1)$	0.83	0.00	0.03	0.03	0.96	0.83	0.00	0.03	0.03	0.95	0.83	0.00	0.03	0.03	0.96
	$\text{log}({\lambda }_2)$	−4.96	0.00	0.09	0.09	0.95	−4.96	−0.01	0.09	0.09	0.96	−4.96	−0.01	0.09	0.09	0.95
	$\text{log}({\rho }_2)$	1.08	0.00	0.06	0.06	0.95	1.08	0.00	0.06	0.06	0.95	1.08	0.00	0.06	0.06	0.95
	${\beta }_{1g\mathit{ene}}$	1.86	0.00	0.12	0.12	0.96	1.86	0.01	0.11	0.12	0.95	1.86	0.01	0.11	0.11	0.94
	${\beta }_{2g\mathit{ene}}$	1.22	0.01	0.20	0.21	0.95	1.22	0.03	0.22	0.21	0.96	1.22	0.02	0.21	0.22	0.96
	${\beta }_{1tvc}$	1.87	0.03	0.25	0.25	0.94	1.87	−0.01	0.25	0.25	0.95	1.87	0.03	0.24	0.24	0.94
	$\text{log}(\eta )$	−1.28	0.02	0.32	0.31	0.94	−1.28	0.00	0.32	0.31	0.94	−1.28	0.03	0.30	0.30	0.94
	$\text{log}(k_1)$	1.95	0.23	0.99	0.88	0.93	1.25	0.08	0.49	0.48	0.97	0.00	0.02	0.23	0.24	0.96
	$\text{log}(k_2)$	1.18	0.51	2.04	1.18	0.85	1.18	0.53	1.70	1.26	0.84	1.18	0.48	1.47	1.28	0.84
CO	$\text{log}({\lambda }_1)$	−4.83	0.00	0.05	0.06	0.95	−4.83	0.00	0.05	0.06	0.94	−4.83	0.00	0.05	0.06	0.96
	$\text{log}({\rho }_1)$	0.83	0.00	0.03	0.03	0.94	0.83	0.00	0.03	0.03	0.96	0.83	0.00	0.03	0.03	0.97
	$\text{log}({\lambda }_2)$	−4.96	0.00	0.07	0.09	0.95	−4.96	0.00	0.07	0.09	0.97	−4.96	0.00	0.08	0.09	0.95
	$\text{log}({\rho }_2)$	1.07	0.00	0.05	0.06	0.96	1.07	0.00	0.05	0.06	0.97	1.07	0.00	0.05	0.06	0.96
	${\beta }_{1g\mathit{ene}}$	2.08	0.01	0.10	0.12	0.94	2.08	0.01	0.10	0.12	0.95	2.08	0.01	0.09	0.11	0.96
	${\beta }_{2g\mathit{ene}}$	1.57	0.00	0.17	0.21	0.98	1.57	0.00	0.17	0.21	0.94	1.57	0.01	0.16	0.21	0.97
	${\beta }_{1tvc}$	1.52	0.04	0.32	0.42	0.96	1.52	0.04	0.33	0.42	0.94	1.52	0.02	0.32	0.42	0.96
	$\text{log}(\eta )$	−0.18	−0.02	0.50	0.58	0.90	−0.18	0.01	0.50	0.60	0.91	−0.18	−0.03	0.48	0.62	0.91
	η 0	0.21	−0.02	0.12	0.14	0.95	0.21	−0.01	0.12	0.14	0.96	0.21	−0.02	0.12	0.14	0.95
	$\text{log}(k_1)$	1.95	0.20	0.74	0.86	0.91	1.25	0.10	0.39	0.46	0.96	0.00	0.02	0.18	0.22	0.97
	$\text{log}(k_2)$	1.26	0.38	1.15	1.39	0.86	1.26	0.35	0.98	1.40	0.90	1.26	0.36	1.10	1.32	0.87

For each scenario, the mean bias, empirical standard error (ESE), average standard error (ASE), and estimated 95% coverage probability (ECP) are obtained from 500 replicates each with n = 500 families. λ_j and ρ_j are baseline hazard parameters for event $j,j=1,2$; β_jgene is the regression coefficient of a time-invariant covariate for event j; ${\beta }_{1tvc}$, η, and η₀ are parameters to describe TVC effects; k_j is the frailty parameter for event j.

In addition, we also investigated the robustness of the proposed model to the misspecification of TVC function in our simulations. Bias and efficiency of the mis-specified TVC function are evaluated in comparison to the true TVC model. Simulations results based on n = 500 families are presented below while Tables S1 and S2 include simulation results for n = 1000 families.

3.2 Simulation results

The simulation results for the model parameter estimates are summarized in Table 1. Biases of the parameter estimates related to the baseline hazard function (${\rho }_1,{\lambda }_1,{\rho }_2,{\lambda }_2$) and regression coefficients (${\beta }_{1tvc},{\beta }_{1g\mathit{ene}},{\beta }_{2g\mathit{ene}}$) are negligible across all the TVC models and the levels of familial dependences. ASEs and ESEs are very close to each other and ECPs are within acceptable range, i.e., between 0.93 and 0.97. The frailty parameter estimates are more biased especially for event 2 and their ECP is lower than the nominal level, 0.95 (ranged between 0.80 and 0.90). We also observed that ASEs tend to be larger than ESEs in the CO model. Coverage probability for k₁ was better than for k₂ and the bias decreases with the level of familial dependence.

Table 2 summarizes the simulation results related to the penetrance estimators. While frailty parameter estimators suffer from bias, penetrance estimators by age 70 for both event 1, $F_1(70;\mathit{X})$, and event 2, $F_2(70;\mathit{X})$, performed well. The bias was negligible (<1%) and the ECPs were close to the 0.95 nominal level and within acceptable range (between 0.93 and 0.97) regardless of the level of familial dependence. ASEs and ESEs agree with each other in PE model but ASEs tend to be slightly higher than ESEs in the ED and CO models.

Table 2.

Empirical penetrance estimates by age 70 for the competing risks model with a time varying covariate (TVC) under low ($k_1=7$), medium ($k_1=3.5$), and high ($k_1=1$) familial dependence; permanent exposure (PE), exponential decay (ED) or Cox and Oakes (CO) models are considered for TVC; $F_1(70;\text{ TVC, G})$ and $F_2(70;\text{ TVC, G})$ are cause-specific penetrance estimators (%) by age 70 for event 1 and event 2, respectively, given TVC and mutation status (G), and TVC occurred at age 35 if $\text{TVC}=1$.

TVC		True	$k_1=7,\tau =0.07$				True	$k_1=3.5,\tau =0.13$				True	$k_1=1,\tau =0.33$
model		value	Bias	ESE	ASE	ECP	value	Bias	ESE	ASE	ECP	value	Bias	ESE	ASE	ECP
PE	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	12.56	−0.10	1.38	1.36	0.95	12.45	0.01	1.33	1.40	0.94	11.93	0.07	1.48	1.45	0.94
	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	21.92	−0.01	2.45	2.45	0.94	21.58	0.02	2.37	2.48	0.95	20.09	0.13	2.49	2.50	0.96
	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	56.52	−0.33	3.20	3.18	0.94	54.51	0.12	3.39	3.42	0.94	46.80	−0.02	3.84	3.92	0.95
	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	75.63	−0.23	3.75	3.74	0.94	72.59	0.03	4.08	4.06	0.94	61.08	−0.04	4.61	4.79	0.94
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	4.73	−0.08	0.82	0.85	0.94	4.73	−0.08	0.87	0.85	0.93	4.74	−0.05	0.79	0.88	0.95
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	4.45	−0.08	0.77	0.80	0.94	4.45	−0.08	0.82	0.80	0.93	4.49	−0.05	0.75	0.83	0.95
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	9.68	0.04	1.16	1.15	0.94	9.85	−0.04	1.16	1.18	0.95	10.52	0.02	1.29	1.28	0.95
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	7.12	0.01	0.91	0.89	0.94	7.42	−0.04	0.91	0.92	0.95	8.56	0.00	1.04	1.04	0.95
ED	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	13.55	−0.05	1.39	1.42	0.94	13.42	−0.02	1.41	1.44	0.94	12.82	−0.04	1.47	1.47	0.94
	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	15.49	0.03	1.64	1.64	0.94	15.32	0.05	1.62	1.66	0.94	14.54	0.00	1.61	1.68	0.97
	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	55.65	−0.28	2.70	3.07	0.97	53.68	−0.05	3.03	3.27	0.96	46.14	0.12	3.56	3.68	0.96
	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	60.49	−0.10	2.99	3.33	0.97	58.24	0.10	3.26	3.54	0.97	49.69	0.21	3.67	3.94	0.96
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	5.39	0.01	0.90	0.91	0.95	5.39	−0.07	0.86	0.92	0.95	5.41	−0.05	0.85	0.93	0.96
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	5.26	0.01	0.87	0.89	0.95	5.26	−0.07	0.83	0.89	0.95	5.28	−0.06	0.83	0.91	0.95
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	11.38	0.05	1.18	1.22	0.96	11.57	0.04	1.29	1.24	0.95	12.34	−0.05	1.34	1.35	0.95
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	9.97	0.01	1.05	1.09	0.96	10.22	0.01	1.12	1.12	0.95	11.20	−0.07	1.20	1.22	0.95
CO	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	13.54	0.02	1.36	1.42	0.95	13.41	0.02	1.44	1.43	0.95	12.81	0.08	1.34	1.43	0.96
	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	16.60	−0.04	2.00	2.03	0.95	16.41	−0.04	2.02	2.03	0.94	15.52	−0.02	1.89	1.99	0.95
	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	61.12	0.07	2.90	2.93	0.96	58.82	0.25	3.15	3.10	0.94	50.11	0.32	3.32	3.49	0.97
	$F_1(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	67.55	−0.15	3.94	3.73	0.93	64.90	0.06	3.80	3.86	0.95	54.88	0.09	3.94	4.09	0.95
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	5.53	0.04	0.87	0.93	0.95	5.53	0.05	0.88	0.93	0.95	5.55	−0.02	0.89	0.95	0.95
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}0})$	5.39	0.03	0.85	0.90	0.95	5.39	0.04	0.85	0.91	0.95	5.42	−0.02	0.87	0.93	0.95
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	14.27	−0.06	1.24	1.37	0.98	14.61	−0.02	1.38	1.41	0.94	15.91	−0.08	1.51	1.55	0.95
	$F_2(70;\text{\hspace{0.17em}TVC\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}G\hspace{0.17em}=\hspace{0.17em}1})$	12.35	−0.06	1.22	1.28	0.96	12.77	−0.02	1.31	1.32	0.95	14.36	−0.07	1.41	1.45	0.95

For each scenario, the mean bias, empirical standard error (ESE), average standard error (ASE), and estimated 95% coverage probability (ECP) are obtained from 500 replicates each with n = 500 families.

Additional simulations were conducted to evaluate the robustness of the proposed model to misspecification of the TVC function. We generated datasets under each TVC model assumption considering a medium familial dependence level ($k_1=3.5$) and then fitting the wrong TVC models to them. Tables S3 and S4 summarize the simulation results for penetrance estimates under TVC misspecification. As expected, fitting ED and CO models on the dataset generated under a PE TVC leads to minimal biases. However, we note that the coefficient ${\beta }_{1tvc}$ of a TVC is largely biased under the CO model. Table S3 shows the TVC effect ${\beta }_{1tvc}$ is underestimated while η₀ is overestimated. The overall effect on penetrance is however unbiased since the bias on these two parameters is in opposite direction. Fitting a CO model on ED-generated data does not result in any bias. In other situations where a simpler TVC model is fitted to more complex true TVC models, substantial biases are observed for the individuals with TVC = 1. Therefore, in practice, it is necessary to fit all three models and select the best model according to the lowest Akaike information criterion (AIC) values. In our simulations, we note that the correct model is selected about 88% of the time with this selection criterion. In Tables S1 and S2, we present additional simulation results for parameter and penetrance estimators for a larger number of families n = 1000. In brief, when n = 1000 the bias is substantially lower for all parameters, especially the frailty parameters, and their ECPs greatly improve (0.88–0.93 for k₂). Similarly, penetrance estimators are less biased, i.e. less than 0.1%.

4 Application to BRCA1 families from BCFR

4.1 Data

Our analyses focus on BRCA1 carrier families recruited through the BCFR.¹⁸ The BCFR was established in 1995 with six participating sites from the USA, Australia and Canada including Ontario Cancer Care. It enrolled most of the families from 1996 to 2000 while continuing to recruit additional families satisfying its criteria, i.e., families were included whenever they segregate BRCA1 or BRCA2 mutations, exhibit multiple cases of breast or OC, are Ashkenazi Jewish ancestry or from specific racial and ethnic groups. For the population-based families, each family includes the proband, i.e. the initial member of the family to be identified, as well as the first and the second degree relatives. The BCFR is not a traditional cohort but a family-based cohort over-sampled for increased BC familial risks. It is not a cohort of mutation carriers. We assumed all the family members entered the study at 16 years of age, which is the start of the time scale and were followed up to age at the occurrence of the first event (either BC, OC or death), or to age at last follow-up. The follow-up ages range from 18.1 to 102.5 years (median = 55.8, interquartile range (IQR) = 40.5, 70.5). Women did not have a mammography screen at study entry; RRSO and mammography screens could occur anytime during follow-up. When the age at RRSO was less than one year from the age at BC onset, we considered that both events occurred at the same time and thus RRSO did not affect BC (n = 12). Our data include 586 censored individuals and their last follow-up ages range from 18.1 to 95.0 years (median = 50.5, IQR = 38.3, 61.5). Vital and cancer statuses have been updated through phone interviews, mailed questionnaires, clinic visits, and linkages to cancer registries. In addition, there have been systematic updates of risk factors and clinical outcomes data. Families with no BRCA mutation carriers were not included in our analysis and we only used BRCA1 carrier families identified from 498 probands including a total of 2650 relatives. A complete description of the families is given in Table 3.

Table 3.

Characteristics of 498 BRCA1 positive families from the BCFR.

	Breast cancer	Ovarian cancer	Death	Unaffected	Total
N (%)	924 (34.9%)	182 (6.9%)	958 (36.2%)	586 (22.1%)	2650
N (%) of probands	391 (78.5%)	43 (8.6%)	5 (1.0%)	59 (11.9%)	498
N (%) of probands at study entry
	386 (77.5%)	31 (6.2%)	0 (0%)	81 (16.3%)	498
Event age
Mean (SD)	44.2 (12.0)	53.0 (11.5)	70.5 (17.9)	50.9 (16.2)	55.8 (19.1)
Min, max	21.0, 86.0	28.0, 89.0	18.5, 102.5	18.1, 95.0	18.1, 102.5
BRCA1 mutation status
Non-carrier	29 (3.1%)	4 (2.2%)	14 (1.5%)	229 (39.1%)	276 (10.4%)
Carrier	483 (52.3%)	55 (30.2%)	16 (1.7%)	192 (32.8%)	746 (28.2%)
Untested	412 (44.6%)	123 (67.6%)	928 (96.9%)	165 (28.2%)	1628 (61.4%)
# of mammographic screening
0	722 (78.1%)	158 (86.8%)	944 (98.5%)	257 (43.9%)	2081 (78.5%)
1	160 (17.3%)	19 (10.4%)	7 (0.7%)	174 (29.7%)	360 (13.6%)
2	31 (3.4%)	4 (2.2%)	3 (0.3%)	63 (10.8%)	101 (3.8%)
3+	11 (1.2%)	1 (0.5%)	4 (0.4%)	92 (15.7%)	108 (4.1%)
RRSO	28 (3.0%)	0 (0%)	9 (0.9%)	129 (22.0%)	166 (6.3%)

RRSO: risk-reducing bilateral salpingo oophorectomy; SD: standard deviation.

The statistics given are computed over the whole follow-up period, i.e., from study entry to time of first event (BC, OC, or death) or the last observation.

4.2 Analyses

Our main event of interest is the time to a first primary BC while a first primary OC and death (from other causes than BC or OC) are considered as competing events in our analyses. We used a Weibull distribution for the baseline hazard in our application as it is a common choice and it provides a flexible functional form to describe the baseline hazard with a small number of parameters (two parameters). Age is considered as the time scale, i.e. age at diagnosis for women with either BC or OC, and age at last follow-up or death for women free of BC and OC. RRSO status is our main TVC of interest while the successive MS events are assumed to be confounding TVCs. We considered up to three possible MS events and each MS as a binary TVC (see supplementary Web Appendix E). Prophylactic bilateral mastectomy was considered as a censoring variable for BC and RRSO as a censoring variable for OC. We only accounted for screening and surgery histories before any events of interest (BC, OC, death or censored). The proportion of individuals with OC as first cancer is much lower than that of BC (6.9% vs. 34.9%). The proportion of women who underwent RRSO among the BC cohort is 3%.

4.3 Selection of the best TVC model

For both RRSO and MS variables, we used the AIC to select the best TVC model and evaluated the three models, i.e. PE, ED, and CO, for each of them. The best model corresponds to the CO model for both RRSO and the three MS-related variables with an AIC of 19,077.43 (Table S6). The form of the hazard function corresponding to the best model and that of other TVC models are displayed in Figure S2. The choice of the CO model means that for women with BRCA1 mutations, the effect of RRSO on BC reduces over time until reaching a threshold.

4.4 Correlation between the competing events

We found a significant correlation between the two competing events BC and OC conditional on the mutation status, estimated at 0.52 (95% CI = 0.17, 0.79; see Methods section). The variance of each frailty is 0.29 (SE = 0.04) for BC and 0.40 (SE = 0.13) for OC, corresponding to a Kendall’s tau of 0.13 (95% CI = 0.09, 0.20) and 0.17 (95% CI = 0.11, 0.37), respectively, representing within familial correlation for each event. The correlation between BC and death and between OC and death was close to 0 and the frailty parameter corresponding time to death was not significant at the 5% level. Therefore, we only considered the correlation between BC and OC in our final model, which involves the frailty parameters k₀, k₁, and k₂ in Table 4.

Table 4.

Parameter estimates based on the correlated competing risks (BC, OC, and death) models with frailties and without frailties, assuming Cox–Oakes models for mammography screening (MS) and risk-reducing salpingo oophorectomy (RRSO) effects on BC in the BRCA1 families from the Breast Cancer Family Registry.

		Shared frailty			No frailty
		Competing risks model			Competing risks model
	Parameter	Estimate	SE	p value	Estimate	SE	p value
BRCA1 on BC	${\beta }_{1g\mathit{ene}}$	2.25	0.13	<0.01	2.18	0.11	<0.01
First MS on BC	${\beta }_{MS1}$	3.44	0.26	<0.01	3.43	0.26	<0.01
	$\log ({\eta }_{MS1})$	1.54	0.24	<0.01	1.49	0.25	<0.01
	${\eta }_{0_{MS1}}$	0.36	0.14	0.01	0.31	0.14	0.03
Second MS on BC	${\beta }_{MS2}$	3.97	0.46	<0.01	3.43	0.26	<0.01
	$\log ({\eta }_{MS2})$	0.87	0.37	0.02	0.66	0.36	0.07
	${\eta }_{0_{MS2}}$	−0.43	0.41	0.29	−0.47	0.43	0.27
Third MS on BC	${\beta }_{MS3}$	3.95	0.97	<0.01	3.72	0.52	<0.01
	$\log ({\eta }_{MS3})$	1.55	1.24	0.21	−0.80	1.11	0.47
	${\eta }_{0_{MS3}}$	−0.38	0.60	0.53	−1.92	1.51	0.21
RRSO on BC	βRRSO	−1.79	0.71	0.01	−1.65	0.78	0.03
	$\log ({\eta }_{\mathit{RRSO}})$	−0.19	0.45	0.68	−0.30	0.27	0.27
	${\eta }_{0_{\mathit{RRSO}}}$	−0.41	0.24	0.08	−0.56	0.24	0.02
BRCA1 on OC	${\beta }_{2g\mathit{ene}}$	1.48	0.23	<0.01	1.51	0.19	<0.01
BRCA1 on death	${\beta }_{3g\mathit{ene}}$	−0.36	0.14	0.01	−0.15	0.11	0.17
Frailties	$\log (k_1)$	0.63	0.41	0.12	–	–	–
	$\log (k_2)$	−0.04	0.79	0.96	–	–	–
	$\log (k_0)$	0.43	0.40	0.29	–	–	–
−loglik		9515			9532
−loglik0		9523			9539
p value*		<0.001			0.003

−loglik is the negative log-likelihood value for the fitted model.

−loglik0 is the negative log-likelihood value based on the model without RRSO.

β_MSj, η_MSj, ${\eta }_{0_{\mathit{MSj}}}$ represents baseline, exponential decay rate, threshold values for the jth MS.

β_RRSO, η_RRSO, ${\eta }_{0_{\mathit{RRSO}}}$ are baseline, exponential decay rate, and threshold values for RRSO.

k₁ is the frailty parameter only for BC, k₂ only for OC, k₀ for shared between the two frailties.

*For testing RRSO effect compared to the null model using the likelihood ratio test with df = 3.

4.5 Effects of mutation status on the competing events, RRSO and MS on breast cancer

The parameter estimates for the correlated competing risk models are given in Table 4. The parameters ${\beta }_{1g\mathit{ene}},{\beta }_{2g\mathit{ene}}$, and ${\beta }_{3g\mathit{ene}}$ correspond to the BRCA1 mutation effect on the time to BC, OC, and death, respectively. The three parameters are all significant at the 5% level and yield HRs of 9.53 (95% CI = 7.44, 12.19), 4.41 (95% CI = 2.81, 6.92), and 0.70 (95% CI = 0.47, 0.81), respectively. This last HR for death is smaller than 1 as 8% and 57% of women died from other causes (other than BC or OC) among carriers and non-carriers, respectively, after imputing the mutation carrier status for untested women. The parameters β_MSj, η_MSj, and ${\eta }_{0_{\mathit{MSj}}}$ for the jth MS, j = 1, 2, 3, and β_RRSO, η_RRSO, and ${\eta }_{0_{\mathit{RRSO}}}$ for RRSO, respectively, correspond to baseline, ED rate, and threshold value (see Methods section and supplementary Web Appendix E). The RRSO and the three MSs were highly significant (p < 0.001) based on the likelihood ratio test when comparing a model with RRSO versus no RRSO (the 3 MSs included) and a model with the three MSs versus no MS (RRSO included), respectively. The forms of the hazard functions and penetrance functions for women with one MS or three MSs under the different TVC models are given in Figures S2 and S3, respectively.

4.6 Time-dependent effect of RRSO on relative risk of BC in women with BRCA1 mutations

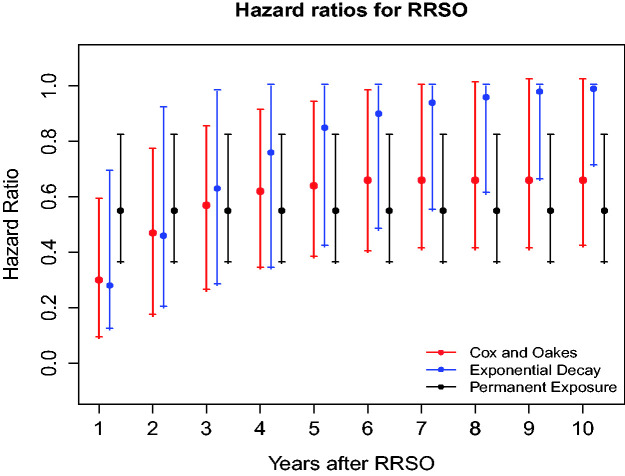
The time-dependent association of the RRSO on BC can be assessed by its effect on the hazard function assessed by the HR given by $\exp \{\mu (t,x_{fi}(t))\}$ or on BC cumulative incidence (i.e., penetrance function), which are both defined as cause-specific functions. The time-dependent effect of RRSO was estimated on a continuous scale from 1 to 10 years after surgery (Figure 1, Table S6). Under the best fitting TVC model (i.e., the CO model) and assuming competing risks and MS adjustment, the overall effect of RRSO on BC risk is statistically significant in women with BRCA1 (p < 0.001). Under this TVC model, the effect of RRSO reduces over time, i.e., HR = 0.30 (95% CI = 0.09, 0.59) to HR = 0.66 (95% CI = 0.42, 1.02) from 1 to 10 years post surgery in BRCA1 mutation carriers. The very low HR estimated shortly after surgery could be imposed by the functional form chosen for RRSO. As sensitivity analysis, we also found that the CO model (AIC = 19077) fits the data better in comparison to a piece-wise constant functional form (AIC = 19086) for RRSO (that we used for sensitivity analyses), even for the short-term effect of RRSO (see Tables S7 and S8).

Figure 1.

Hazard ratios (and their 95% confidence intervals) measuring the time-dependent effect of risk-reducing salpingo oophorectomy (RRSO) on BC risks based on different TVC models (Cox and Oakes (red), exponential decay (blue), and permanent exposure (black)) in BRCA1 families from the BCFR; best TVC model for BRCA1 families is Cox and Oakes model (red).

4.7 Time-dependent effect of RRSO on cumulative risk of BC among women with BRCA1 mutations

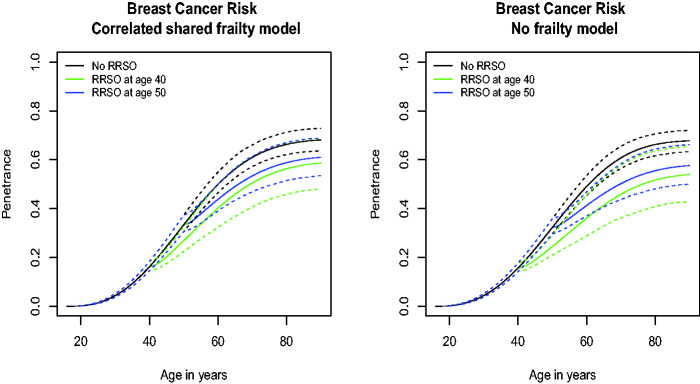
The cause-specific penetrance for BC for women without a RRSO is 61.0% (95% CI = 57.2, 66.0) by age 70 for women with a BRCA1 mutation and 12.0% (95% CI = 9.9, 14.2) for women within BRCA1 families but who do not carry a mutation (Figure 2 and Table 5). The cause-specific penetrance of BC for women with RRSO at 40 years with no MS is 50.5% (95% CI = 40.6, 61.4) by age 70 for women with BCRA1 mutations (Figure 2 and Table 5). For women with RRSO at 50 years with MS, this penetrance is 53.4% (95% CI = 46.9, 61.3) while for women with RRSO at 30 years it is 49.0% (95% CI = 36.7, 62.3). For women with RRSO at age 40 and screened once at age 35, their penetrance by age 70 is 61.2% (95% CI = 49.9, 73.4; Figure S4 and Table 5). This penetrance decreases as the number of MSs increase: i.e., 52.6% (95% CI = 38.9, 71.6) for women with two MSs at age 35 and 40, 47.9% (95% CI = 33.2, 73.1) for women with three MSs at age 35, 40 and 45. The corresponding penetrances for women with RRSO at 50 years and from 1 to 3 MSs are 64.1% (95% CI = 55.8, 74.2), 57.9% (95% CI = 44.8, 75.7), and 54.4% (95% CI = 40.2, 74.8), respectively.

Figure 2.

Breast cancer-specific penetrance estimates for mutation carriers with respect to risk-reducing salpingo oophorectomy (RRSO) from the correlated competing-risks model (left) and the competing risks model without frailties (right). The black line represents a woman who did not have RRSO, the green line a woman who had RRSO at age 40 years, and the blue line a woman who had RRSO at age 50 years. The dashed lines represent the 95% confidence intervals.

Table 5.

Penetrance estimates and their 95% confidence intervals based on the best TVC model for the BRCA1 families from the BCFR.

	Age 50	Age 70
Breast cancera
Carriersb	33.4% (30.6, 37.3)	61.0% (57.2, 66.0)
Non-carriersb	4.5% (3.6, 5.5)	12.0% (9.9, 14.2)
RRSOc at 30 years	24.4% (17.5, 33.5)	49.0% (36.7, 62.3)
RRSOc at 35 years	25.3% (19.6, 32.5)	49.6% (38.3, 61.6)
RRSOc at 40 years	26.8% (22.4, 32.5)	50.5% (40.6, 61.4)
+MS at 35 years	35.6% (29.6, 43.9)	61.2% (49.9, 73.4)
+MS at 35 and 40 years	32.3% (26.1, 43.5)	52.6% (38.9, 71.6)
+MS at 35, 40, and 45 years	32.9% (26.1, 43.5)	47.9% (33.2, 73.1)
RRSOc at 50 years	33.4% (30.6, 37.3)	53.4% (46.9, 61.3)
+MS at 35 years	43.2% (38.0, 51.2)	64.1% (55.8, 74.2)
+MS at 35 and 40 years	42.5% (34.5, 57.8)	57.9% (44.8, 75.7)
+MS at 35, 40, and 45 years	43.2% (34.5, 57.8)	54.4% (40.2, 74.8)
Ovarian cancerd
Carriers	4.7% (3.9, 6.0)	11.2% (9.1, 14.2)
Non-carriers	1.4% (1.0, 1.9)	5.0% (3.9, 6.6)

+MS: mammography screening(s) in addition to RRSO.

^aCorresponds to a first breast cancer.

^bCorresponds to women without RRSO or MS.

^cCorresponds to women without MS.

^dCorresponds to a first ovarian cancer.

4.8 Sensitivity to RRSO modeling assumptions

Our best TVC models assume a parametric form (ED) for the variation of RRSO effect over time. To assess this assumption, we fitted a more general piece-wise TVC for RRSO, where the HR was constant within intervals but did not follow any particular functional form. We considered three time intervals: $\le$2, 2–5, and > 5 years. The HR estimates from this model are close to the best TVC model and confirm that the ED for RRSO effect over time is a reasonable assumption (data not shown).

4.9 Goodness-of-fit of the TVC model

We evaluated the goodness-of-fit of our best TVC model using martingale residuals for each competing event, which are defined as the difference between the number of events of subject i in family f at time $T_{f_i}$ and the expected number of events computed by the cumulative hazard by the last observed time $T_{f_i}$. The martingale residuals are derived at both the individual level and the family level (supplementary Web Appendix D) and their martingale residuals plots are given in Figures S7 and S8. At both levels, their means are close to zero, indicating the good fit of the TVC model to the data.

5 Discussion

Members of BRCA1 mutation positive families are exposed to a very high risk of developing BC or OC as first cancer and the risk of BC is likely to depend on TVCs such as MS and RRSO in a complex manner. Most risk prediction models developed for these families do not account for competing risks nor for time-varying effects on BC. In this article, we developed a flexible approach based on competing risks model, where the risk of the first competing event (BC) could depend on TVCs. Our model provides cause-specific hazard functions and cumulative incidence functions that estimate age-specific risks of BC and OC, accounting for death and the other event as competing events and residual familial correlation not due to the BRCA1 mutation segregating within the family. We also proposed an ascertainment correction that specifically accounts for the fact that the BRCA1 families have been recruited through a proband affected by either BC or OC before her study entry, or through an unaffected proband (i.e., the ascertainment correction was extended specifically to the competing events framework).

In our framework, death prevents the occurrence of BC or OC, so it was more natural to treat it as competing event as it precludes the occurrence of BC and OC. Regarding BC and OC, we were interested in the time to the first event, which also justified why they were treated as competing events. In future developments, we will consider modeling successive events such as OC after BC, BC after OC or cause-specific death after BC or OC. It would be, however, more challenging computationally and would require a more complex multi-state type of model but designed for family data. Our model framework does not consider death as a non-informative censoring for BC and OC, but instead as a competing event correlated with the two other events within families. As sensitivity analysis, we treated death as non-informative censoring for BC in a model with just BC and then in another model where BC and OC are two competing events. Our results show that the parameter estimates related to MS and RRSO tended to be negatively biased and penetrance estimates after RRSO appeared to be slightly underestimated while the penetrance for a woman with no RRSO was slightly overestimated (see supplementary Table S10, Figure S6). Therefore, treating death as non-informative censoring could lead to potential biases of the parameters of interest in our model.

We assumed a gamma distribution for the frailties to account for correlated competing events within families and derived closed form expressions for the marginal likelihood and cause-specific penetrance functions. The choice of frailty distributions is not limited to the gamma distribution and other distributions such as multivariate log-normal distribution can be used alternatively. However, except for the gamma distribution, other distributions do not have a closed form for the likelihood and require numerical approximations of the integrals over frailties, such as Gaussian quadrature, to obtain the marginal likelihood. They are therefore more computationally challenging. Related works also reported that the model parameter estimates are not sensitive to the choice of the frailty distribution in both competing risks⁷ and non-competing risks models.^19,20 However, further studies are needed to evaluate in more details the sensitivity of parameter estimates to the choice of the frailty distribution under the competing risks models with TVCs. As pointed out by several authors,^21,22 we would expect biased parameter estimates when the frailties from the model are omitted. We added a comparison in our application by fitting a model without frailties (see Table 4 and Figure 2). The model with frailties was significantly better than the model ignoring frailties (p value <0.001, based on the likelihood ratio test). In addition, the HRs for RRSO estimated with and without frailties under the CO model are given in Figure S1 and Table S6. We found that the parameter estimates and penetrance estimates as well as HR estimates for RRSO are slightly underestimated when ignoring the frailties from the competing risk model.

Our simulation studies demonstrate the good performances of our approach in terms of bias and precision of the estimators of model parameters and cause-specific penetrances over different levels of familial correlations. The frailty-related parameter estimators had larger biases and lower coverage probability than other parameter estimators but these biases did not result in any biases of the cause-specific hazard functions and penetrances. A possible explanation for the difficulties in estimating the frailty parameters would be that in our simulations and application, the family sizes were relatively small: 3–8 in our simulations, 1–8 for most of families (88%) in our application. Within families, the observed number of OC (ranged 0 to 3, median = 0) was also relatively small compared to the number of BC (ranged 0 to 7, median = 2). These limitations might have impacted the estimation of the frailty parameters. The robustness of other parameters and the penetrance estimates to the frailty misspecification is a very important result since the cause-specific penetrance is used by genetic counselors to guide clinical decisions such as prophylactic surgery or intensive screening for known mutation carriers or the decision to have genetic testing for unknown mutation carriers in BRCA families. Another important result is that, applying models with the wrong TVC function could also result in substantial biases of the parameter estimators when fitting a simpler model to a more complex time-varying function. It is therefore critical to select the correct TVC function to obtain accurate HR and cause-specific penetrance estimates.

A more flexible choice for the baseline hazard could have been to use a piecewise-constant function but to the price of a larger number of parameters to estimate (i.e., depending on the number of cut points considered). The piecewise-constant hazard function can also be used for diagnostic purposes. We graphically display penetrance estimates and their 95% CIs in Figure S5, using a piecewise constant baseline (right panel) compared to a Weibull hazard (left panel) and present the parameter estimates in the correlated competing risks model with piecewise constant baselines in Table S5 and selected penetrance estimates in Table S9. We found that the parameter and penetrance estimates from the model with Weibull baseline are very similar to those with piecewise baseline. In addition, models with Weibull baselines are easier to fit and provide smooth curve estimation of the penetrance function whereas models with piecewise-constant baselines could take longer time to fit and the numerical integration to estimate penetrance accounting for multiple TVCs could be challenging. For these reasons, we opted for the Weibull baseline hazard.

Our application to 498 BRCA1 mutation positive families from the BCFR illustrates the importance of accounting for both competing risks and TVCs when estimating cause-specific penetrance of BC among mutation carriers. In addition, our results demonstrate the importance of the functional form of the TVC when assessing the role of RRSO on BC, in line with our simulation results. In particular, under the best fitting TVC model (i.e., the CO model) with competing risks and MS adjustment, the overall effect of RRSO on BC risk was statistically significant in women with BRCA1 mutations. Under this TVC model, the effect of RRSO reduces over time, i.e., HR = 0.30 (95% CI = 0.12, 0.69) to HR = 0.66 (95% CI = 0.42, 1.02) from 1 to 10 years post surgery in BRCA1 mutation carriers. In terms of cumulative risks, our penetrance estimate for BC at age 70 is 61.0% (95% CI = 57.2, 66.0) for women without RRSO and no MS. It is close to previous publications who reported a mean cumulative BC risks of 57% for BRCA1 mutation carriers⁴ but this latter estimate is likely an average over women with different histories of MSs and surgical interventions. For a woman with RRSO at age 40 years and no MS, the cause-specific cumulative risk of BC is 50.5% (95% CI = 40.6, 61.4) by age 70. It is 47.9% (95% CI = 33.2, 73.1) for women with three MSs at age 35, 40, and 45 and RRSO at age 40 (see Table 5, Figure S4). This result could have some implications for the clinical management of women carrying BRCA1 mutations but warrants further confirmation.

Our model assumes the TVCs as exogenous variables, i.e., the future path of the covariate is independent of the occurrence of BC,²³ so that the hazard function at a specific time t is influenced by the observed covariate history up to time t in the regression model. This assumption is realistic for prophylactic RRSO and scheduled MS in our application since the observation of RRSO and MS does not carry information about the status of BC; however, if the MSs were performed in symptomatic women, the MS would not be exogenous since it could carry information about the status of BC. We did not have evidence that MS frequency could be associated with other BC-related diagnosis such as ductal carcinoma in situ, as this information was not well recorded in our data. Even in that latter situation, our inference is based on the likelihood conditional on the covariate process up to the time t, so does not involve the future path of the covariate after BC.

We should also mention that in our application, we considered MSs as confounding variables for the association between RRSO and BC risk as our primary interest is to evaluate RRSO effect on BC risk. The history of MSs was rather incomplete in our data and denser information would be needed to improve its modeling and effect on BC in this family. A joint modeling framework, as we developed recently,²⁴ could be applied for this purpose, although it would need to be extended to the competing risks framework.

Our model could also help evaluating more intervention options on BC risk, such as combinations of RRSO and MSs as well as the ages they could be introduced. It could be further extended to account for additional competing risks events, e.g. prophylactic mastectomy, and also to estimate the risks of successive cancer events after a first BC or OC, for example following our previous work.¹⁰ Finally, we are planning to incorporate information on polygenic risk score from known genetic variants,²⁵ that could modify BC and OC risks by incorporating a kinship matrix into the cause-specific model for BC and/or OC.²⁶ These future developments should lead to a more comprehensive risk prediction model applicable to BRCA families as well as other families with increased genetic risks.