Visual Abstract
Keywords: cardiovascular disease, chronic kidney disease, clinical epidemiology, atrial fibrillation
Abstract
Background and objectives
Atrial fibrillation (AF) is common in CKD and associated with poor kidney and cardiovascular outcomes. Prediction models developed using novel methods may be useful to identify patients with CKD at highest risk of incident AF. We compared a previously published prediction model with models developed using machine learning methods in a CKD population.
Design, setting, participants, & measurements
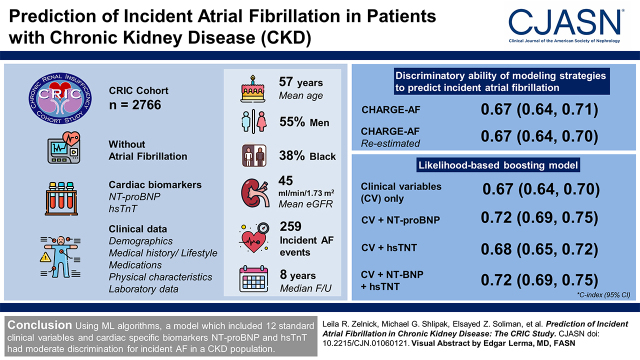
We studied 2766 participants in the Chronic Renal Insufficiency Cohort study without prior AF with complete cardiac biomarker (N-terminal pro–B-type natriuretic peptide and high-sensitivity troponin T) and clinical data. We evaluated the utility of machine learning methods as well as a previously validated clinical prediction model (Cohorts for Heart and Aging Research in Genomic Epidemiology [CHARGE]-AF, which included 11 predictors, using original and re-estimated coefficients) to predict incident AF. Discriminatory ability of each model was assessed using the ten-fold cross-validated C-index; calibration was evaluated graphically and with the Grønnesby and Borgan test.
Results
Mean (SD) age of participants was 57 (11) years, 55% were men, 38% were Black, and mean (SD) eGFR was 45 (15) ml/min per 1.73 m2; 259 incident AF events occurred during a median of 8 years of follow-up. The CHARGE-AF prediction equation using original and re-estimated coefficients had C-indices of 0.67 (95% confidence interval, 0.64 to 0.71) and 0.67 (95% confidence interval, 0.64 to 0.70), respectively. A likelihood-based boosting model using clinical variables only had a C-index of 0.67 (95% confidence interval, 0.64 to 0.70); adding N-terminal pro–B-type natriuretic peptide, high-sensitivity troponin T, or both biomarkers improved the C-index by 0.04, 0.01, and 0.04, respectively. In addition to N-terminal pro–B-type natriuretic peptide and high-sensitivity troponin T, the final model included age, non-Hispanic Black race/ethnicity, Hispanic race/ethnicity, cardiovascular disease, chronic obstructive pulmonary disease, myocardial infarction, peripheral vascular disease, use of angiotensin-converting enzyme inhibitor/angiotensin receptor blockers, calcium channel blockers, diuretics, height, and weight.
Conclusions
Using machine learning algorithms, a model that included 12 standard clinical variables and cardiac-specific biomarkers N-terminal pro–B-type natriuretic peptide and high-sensitivity troponin T had moderate discrimination for incident AF in a CKD population.
Introduction
Atrial fibrillation is common in patients with CKD and associated with greater risk of poor clinical outcomes, including other types of cardiovascular disease, death, and progression to kidney failure (1–8). Development of prediction models for atrial fibrillation in patients with CKD may help identify those who may benefit from enhanced cardiovascular care to prevent atrial fibrillation and related complications.
Atrial fibrillation prediction models have been developed and validated in non-CKD community–based populations. For example, the Cohorts for Heart and Aging Research in Genomic Epidemiology-Atrial Fibrillation (CHARGE-AF) consortium developed a 5-year predictive model including the variables age, race, height, weight, systolic and diastolic BP, current smoking, use of antihypertensive medication, diabetes, and history of myocardial infarction and heart failure, which demonstrated moderate discrimination (C statistic, 0.765) (9). However, the CHARGE-AF model and others were not developed specifically in patients with CKD and did not include kidney-specific risk factors for atrial fibrillation, such as alterations in mineral metabolism. Further, our prior work has demonstrated that clinically available biomarkers of myocardial injury (high-sensitivity troponin T [hsTnT]) and hemodynamic stress (N-terminal pro–B-type natriuretic peptide [NT-proBNP]) are strongly associated with atrial fibrillation in patients with CKD (10), and we hypothesized that they may also improve discrimination of incident atrial fibrillation in this population.
Therefore, we evaluated the performance of the CHARGE-AF risk equation and also derived new models using a variety of machine learning approaches to predict incident atrial fibrillation in persons with CKD. In all algorithms, we investigated the incremental prognostic value of NT-proBNP and hsTnT for atrial fibrillation prediction compared with standard clinical variables. We hypothesized that (1) the CHARGE-AF model would have poor discrimination for incident atrial fibrillation in a CKD population and (2) a machine learning model that utilized a combination of clinical variables plus NT-proBNP and hsTnT would predict incident atrial fibrillation better, with improved discrimination in a cohort of patients with CKD.
Materials and Methods
Study Design and Population
The Chronic Renal Insufficiency Cohort (CRIC) study is an ongoing, prospective, multicenter cohort study of 3939 adult participants with mild to moderate CKD (eGFR of 20–70 ml/min per 1.73 m2) at study entry. Participants were enrolled at seven clinical centers across the United States; details on study design and baseline characteristics of participants have been previously published (11,12). All study participants provided written informed consent, and the study protocol was approved by institutional review boards at each site.
For this analysis, we excluded participants with prevalent atrial fibrillation at study entry (n=666), those with missing NT-proBNP or hsTnT (n=105) or other covariates (n=380), and those who were lost to follow-up after baseline (n=22), leaving a final analytic population of 2766 participants (Supplemental Figure 1).
Atrial Fibrillation
Incident atrial fibrillation was defined as a hospitalization for atrial fibrillation and confirmed by physician adjudication (13). At each study visit, participants were asked if they had visited an emergency department or had been hospitalized. Medical records from corresponding hospitals or health care systems were queried for qualifying encounters. Diagnostic codes for atrial fibrillation (International Classification of Diseases, Ninth Revision, Clinical Modification 427.31 or 427.32) prompted retrieval of medical records and centralized review for the ascertainment of incident atrial fibrillation. Final adjudication of events was done after at least two study physicians reviewed all possible events by manual review of relevant medical records. Discordances were resolved by discussion between adjudicators. Hospitalized electrocardiograms (when available) were reviewed and were part of the adjudication process.
Candidate Predictor Variables
At each visit, participants provided information on sociodemographic characteristics, medical history, medication usage, and lifestyle behaviors. Race/ethnicity was categorized as non-Hispanic White, non-Hispanic Black, Hispanic, and other by self-report. Tobacco use was categorized as current, former, or never. Diabetes mellitus was defined as a fasting glucose >126 mg/dl, a nonfasting glucose >200 mg/dl, or use of insulin/other antidiabetic medication. Comorbid conditions, including cardiovascular disease, myocardial infarction, congestive heart failure, stroke, peripheral vascular disease, and chronic obstructive pulmonary disease, were determined by self-report. BP was obtained in a standardized setting by trained coordinators using the mean of three seated resting BP readings. Body mass index was derived as weight in kilograms divided by height in meters squared. Hemoglobin, 24-hour urine albumin, LDL cholesterol, HDL cholesterol, fibroblast growth factor-23, and total parathyroid hormone were measured from fasting blood samples at baseline. eGFR was calculated from serum creatinine using the Chronic Kidney Disease Epidemiology Collaboration equation (14), where serum creatinine was measured using an enzymatic method on an Ortho Vitros 950 at the CRIC Central Laboratory and standardized to isotope dilution mass spectrometry–traceable values (15,16). Medication use (e.g., diuretics, angiotensin-converting enzyme inhibitors, angiotensin receptor blockers, and other antihypertensive medications) was determined by self-report. Heart rate was derived from digitally recorded 12-lead electrocardiograms using standardized procedures (17) and identical electrocardiographic equipment (MAC 1200; GE Medical Systems Information Technologies, Milwaukee, WI).
NT-proBNP and hsTnT were measured at baseline after cohort entry from frozen serum or plasma samples. Both cardiac biomarkers were measured at baseline in 2008 from EDTA plasma stored at −70°C using a chemiluminescent microparticle immunoassay (www.roche-diagnostics.us) on the ElecSys 2010 at the University of Maryland. The range of values for NT-proBNP was from 5 to 35,000 pg/ml, and the coefficient of variation was 9% at a level of 126 pg/ml and 6% at 5319 pg/ml. hsTnT was measured using the highly sensitive assay with a range of values from 3 to 10,000 pg/ml. The coefficient of variation was 6% at a level of 26 pg/ml and 5% at 2140 pg/ml. The value at the 99th-percentile cutoff from a healthy reference population was 13 pg/ml for hsTnT with a 10% coefficient of variation.
Statistical Analyses
We summarized participant demographic and clinical characteristics using descriptive statistics, such as mean and SD for continuous variables and frequency and percentage for categorical variables. We investigated the ability of a series of models that incorporated clinical variables and cardiac biomarkers to predict incident atrial fibrillation. For all models, the outcome was the time to incident atrial fibrillation measured from study enrollment and censored for death, loss to follow-up, or end of study.
We first evaluated the performance of a previously published risk equation from the CHARGE-AF consortium (9), which used Cox regression together with a backward stepwise elimination procedure to predict the 5-year risk of developing atrial fibrillation. In this study, we examined using both published coefficients and re-estimated coefficients using data from the CRIC cohort, because the CHARGE-AF model was developed and validated in a general population.
In addition to these models, we evaluated the performance of a variety of machine learning approaches. We considered a Cox backward stepwise regression procedure with the stopping rule determined by the Akaike information criterion (18). The least absolute shrinkage and selection operator (LASSO) is a penalized regression approach (using the L1-norm penalty) that shrinks regression coefficients toward zero, leading to parsimonious models (19,20). Ridge regression is also a penalized regression approach, but it uses the L2-norm penalty; estimates are shrunk toward zero compared with usual Cox regression estimation, but resulting models contain all eligible covariates (21). We explored two boosting algorithms (likelihood-based boosting and gradient-boosting machines), an iterative technique originally developed for binary outcomes that has been extended to survival analysis (22,23). Likelihood-based boosting estimates a single parameter at each iteration, incorporating the previous boosting step as an offset in penalized partial likelihood estimation, which tends to result in LASSO-like sparse solutions. The gradient-boosting machine approach is based on the correlation between the negative gradient of the negative log partial likelihood and the observations (24).
For each of these machine learning methodologies, we evaluated the performance of models that could select from (1) clinical variables, which included demographics, lifestyle factors, medical history, and laboratory values (Supplemental Table 1); (2) clinical variables and NT-proBNP; (3) clinical variables and hsTnT; and (4) clinical variables, NT-proBNP, and hsTnT.
For each algorithm, we assessed the overall discriminatory performance via Harrell’s C-index (25), a measure of goodness of fit for models producing risk scores that is often used with survival outcomes when data may be censored. For each estimate, we obtained associated 95% confidence intervals (95% CIs) using nonparametric bootstrap methods with 2000 replicates (26). For models that required estimation (e.g., all models except the previously published CHARGE-AF model), we chose to estimate performance using ten-fold cross-validation. In this approach, data are split into ten folds, nine of which are used to fit the model, which is then used to create predictions about the remaining fold. The process is repeated ten times, holding out a different fold each time. Predictions in each fold are derived from models that did not use that fold’s data, avoiding an overoptimistic assessment of the model’s discriminatory ability; estimating performance via ten-fold cross-validation has also been shown to make more efficient use of data compared with splitting data into training/validation sets (27). Calibration of top models was assessed graphically by plotting the predicted versus observed 5-year probability of incident atrial fibrillation by decile of the predicted probabilities, and formally through the Grønnesby and Borgan goodness of fit test (28,29).
Prediction derived from standard Cox regression models has been shown to substantially overestimate predicted probabilities in the face of strong competing risks (30,31). Death was common among CRIC participants; therefore, to account for the competing risk of death, we utilized a Fine and Gray approach in all models to estimate the actual risk of atrial fibrillation as accurately as possible (32). A sensitivity analysis examined the performance of top models compared with CHARGE-AF by category of baseline eGFR (<30, 30–44, 45–59, or ≥60 ml/min per 1.73 m2).
Finally, we considered the ability of both clinical and cardiac biomarkers data to predict incident atrial fibrillation using a super learning approach (33–35). In this machine learning framework, the super learning algorithm estimates the optimal weighted combination of a given set of potential algorithms under a specified loss function, which in this case, was the cross-validated negative log partial likelihood. In particular, this approach leverages observed data to inform which candidate algorithms will provide the most accurate predictions for future observations. The “best” algorithm for prediction of each outcome is a weighted combination of the candidate algorithms described above. Weights are chosen to optimize predictive performance and identified by the super learner via ten-fold cross-validation; better-performing algorithms tend to receive higher weight from the super learner.
In a secondary analysis, we calculated the net reclassification improvement (NRI), with accompanying 95% bootstrap CIs (36). Because there are not established categories of risk for atrial fibrillation in CKD, we calculated the continuous NRI, which quantifies model improvement by comparing risk prediction between models but within event groups and can be seen as another measure of improvement in discrimination.
The use of race in medicine and clinical research is a controversial issue and has been repeatedly challenged in recent publications (37,38), and guidance for researchers continues to evolve (39). Race is a complex social construct that reflects social determinants of health and systemic racism, among others, yet self-described race may contain information that helps to predict an individual’s risk of cardiovascular outcomes. Much previously published work in this field (including the CHARGE-AF equation that forms the basis of comparison in this manuscript) includes race as a potential predictor, so we felt it was important to also include race for face validity as well as comparability with previously published research. However, given the ongoing conversation within the scientific community, we considered models that did not include race/ethnicity as a potential clinical predictor in a sensitivity analysis.
All analyses were conducted using the R 3.6.2 software environment (R Foundation for Statistical Computing, Vienna, Austria).
Results
Participant Characteristics
The mean (SD) age of the 2766 participants included in this study was 57 (11) years, and the mean (SD) eGFR at baseline was 45 (15) ml/min per 1.73 m2; 55% of participants were men, and 38% self-identified as non-Hispanic Black (Table 1). There were 259 incident atrial fibrillation events that occurred during a median of 8.0 (interquartile range, 5.6–9.4) years of follow-up, and 514 participants died without having developed atrial fibrillation. The incidence of atrial fibrillation among the study population was 12.9 per 1000 person-years overall, with 6.7, 11.0, 16.4, and 15.7 per 1000 person-years among those with eGFR≥60, 45–59, 30–45, and <30 ml/min per 1.73 m2, respectively.
Table 1.
Baseline characteristics of the Chronic Renal Insufficiency Cohort analytic population (n=2766)
| Variables | Overall, n=2766 | Participants Not Experiencing Incident Atrial Fibrillation during Follow-Up, n=2507 | Participants Experiencing Incident Atrial Fibrillation during Follow-Up, n=259 |
|---|---|---|---|
| Age, yr | 57 (11) | 57 (11) | 62 (8) |
| Men | 1521 (55) | 1358 (54) | 163 (63) |
| Race/ethnicity | |||
| Non-Hispanic White | 1203 (43) | 1061 (42) | 142 (55) |
| Non-Hispanic Black | 1064 (38) | 985 (39) | 79 (31) |
| Hispanic | 380 (14) | 351 (14) | 29 (11) |
| Other | 119 (4) | 110 (4) | 9 (3) |
| Diabetes at baseline | 1327 (48) | 1181 (47) | 146 (56) |
| History of myocardial infarction | 506 (18) | 426 (17) | 80 (31) |
| History of congestive heart failure | 165 (6) | 137 (5) | 28 (11) |
| History of stroke | 245 (9) | 219 (9) | 26 (10) |
| History of peripheral vascular disease | 169 (6) | 149 (6) | 20 (8) |
| History of chronic obstructive pulmonary disease | 73 (3) | 60 (2) | 13 (5) |
| Antihypertensive medications | 2530 (91) | 2279 (91) | 251 (97) |
| ACEi/ARB | 1888 (68) | 1694 (68) | 194 (75) |
| β-blockers | 1272 (46) | 1127 (45) | 145 (56) |
| Calcium channel blockers | 1110 (40) | 988 (39) | 122 (47) |
| Diuretics | 1569 (57) | 1388 (55) | 181 (70) |
| Height, cm | 168.6 (9.7) | 168.5 (9.7) | 169.9 (9.3) |
| Weight, kg | 90.8 (23.2) | 90.2 (23.1) | 96.4 (23.4) |
| BMI, kg/m2 | 31.9 (7.8) | 31.7 (7.7) | 33.4 (7.6) |
| Systolic BP, mmHg | 128 (22) | 128 (22) | 131 (21) |
| Diastolic BP, mmHg | 72 (13) | 72 (13) | 69 (13) |
| Heart rate, bpm | 65 (12) | 65 (12) | 65 (11) |
| eGFR by CKD-EPI, ml/min per 1.73 m2 | 45 (15) | 45 (15) | 41 (13) |
| 24-h urine albumin, g, median (IQR) | 0.1 (0.0–0.6) | 0.1 (0.0–0.6) | 0.1 (0.0–0.6) |
| Total PTH, pg/ml, median (IQR) | 52 (34–87) | 52 (33–85) | 60 (39–105) |
| FGF-23, RU/ml, median (IQR) | 139 (94–224) | 136 (93–220) | 164 (106–255) |
| Hemoglobin, g/dl | 12.6 (1.8) | 12.6 (1.7) | 12.4 (1.9) |
| LDL, mg/dl | 103 (35) | 103 (35) | 98 (31) |
| HDL, mg/dl | 48 (16) | 48 (16) | 46 (16) |
Entries are mean (SD) for continuous variables and N (percentage) for categorical variables, except as noted. ACEi, angiotensin-converting enzyme inhibitor; ARB, angiotensin receptor blocker; BMI, body mass index; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; IQR, interquartile range; PTH, parathyroid hormone; FGF-23, fibroblast growth factor-23.
Performance of CHARGE-AF Models for Prediction of Incident Atrial Fibrillation
CHARGE-AF prediction equations that used the original and re-estimated coefficients had ten-fold cross-validated C-indices of 0.674 (95% CI, 0.64 to 0.71) and 0.667 (95% CI, 0.64 to 0.70), respectively; these were not significantly different from one another (Table 2). The original CHARGE-AF prediction equation performed best among participants with eGFR≥60 ml/min per 1.73 m2, with a C-index of 0.750 (95% CI, 0.64 to 0.86); discriminatory ability was substantially poorer among participants with eGFR<60 ml/min per 1.73 m2 (Table 3). Calibration was adequate for the CHARGE-AF original equation (Supplemental Figure 2) (Grønnesby and Brogan P=0.39).
Table 2.
Discriminatory ability of several modeling strategies to predict incident atrial fibrillation compared with the published Cohorts for Heart and Aging Research in Genomic Epidemiology-Atrial Fibrillation (CHARGE-AF) model
| Predictive Modeling Strategy | C-Index (95% Confidence Interval) | Difference from CHARGE-AF C Index (95% Confidence Interval) | Net Reclassification Index (95% Confidence Interval)a |
|---|---|---|---|
| CHARGE-AF | 0.674 (0.64 to 0.71) | NA | NA |
| CHARGE-AF (re-estimated) | 0.667 (0.64 to 0.70) | −0.007 (–0.02 to 0.01) | NA |
| Stepwise regression | |||
| Clinical variables only | 0.649 (0.62 to 0.68) | −0.025 (–0.04 to −0.01) | −23 (−35 to −11) |
| Clinical variables + NT-proBNP | 0.704 (0.67 to 0.73) | 0.030 (0.00 to 0.06)b | 15 (2 to 28)b |
| Clinical variables + hsTnT | 0.668 (0.64 to 0.70) | −0.006 (–0.03 to 0.02) | −9 (−21 to 4) |
| Clinical variables + NT-proBNP + hsTnT | 0.707 (0.68 to 0.74) | 0.033 (0.01 to 0.06)b | 13 (1 to 26)b |
| LASSO | |||
| Clinical variables only | 0.665 (0.63 to 0.70) | −0.009 (–0.03 to 0.01) | −22 (−34 to −10) |
| Clinical variables + NT-proBNP | 0.714 (0.68 to 0.75) | 0.040 (0.02 to 0.06)b | 9 (−4 to 22) |
| Clinical variables + hsTnT | 0.681 (0.65 to 0.71) | 0.007 (–0.01 to 0.03) | −1 (−13 to 12) |
| Clinical variables + NT-proBNP + hsTnT | 0.716 (0.69 to 0.75) | 0.041 (0.02 to 0.07)b | 16 (3 to 29)b |
| Ridge regression | |||
| Clinical variables only | 0.669 (0.64 to 0.70) | −0.005 (–0.03 to 0.02) | −24 (−36 to −12) |
| Clinical variables + NT-proBNP | 0.701 (0.67 to 0.73) | 0.027 (0.00 to 0.05)b | 11 (−2 to 24) |
| Clinical variables + hsTnT | 0.679 (0.65 to 0.71) | 0.005 (–0.02 to 0.03) | −14 (−26 to −2) |
| Clinical variables + NT-proBNP + hsTnT | 0.706 (0.66 to 0.74) | 0.032 (0.01 to 0.06)b | 15 (2 to 28)b |
| Likelihood-based boosting model | |||
| Clinical variables only | 0.668 (0.64 to 0.70) | −0.006 (–0.03 to 0.01) | −11 (−24 to 1) |
| Clinical variables + NT-proBNP | 0.717 (0.69 to 0.75) | 0.042 (0.02 to 0.07)b | 18 (5 to 31)b |
| Clinical variables + hsTnT | 0.683 (0.65 to 0.72) | 0.009 (–0.01 to 0.03) | 2 (−10 to 14) |
| Clinical variables + NT-proBNP + hsTnT | 0.718 (0.69 to 0.75) | 0.044 (0.02 to 0.07)b | 21 (8 to 34)b |
| Generalized boosting regression model | |||
| Clinical variables only | 0.663 (0.63 to 0.70) | −0.011 (–0.04 to 0.01) | −28 (−41 to −16) |
| Clinical variables + NT-proBNP | 0.701 (0.67 to 0.74) | 0.027 (–0.00 to 0.06)b | 4 (−9 to 17) |
| Clinical variables + hsTnT | 0.676 (0.64 to 0.71) | 0.002 (–0.03 to 0.03) | −17 (−30 to −5) |
| Clinical variables + NT-proBNP + hsTnT | 0.711 (0.68 to 0.74) | 0.037 (0.01 to 0.07)b | 10 (−3 to 24) |
| Super learner algorithm | 0.720 (0.69 to 0.75) | 0.046 (0.02 to 0.07)b | 15 (2 to 28)b |
The entry for CHARGE-AF is C index and the associated 95% bootstrap confidence interval; all other entries are ten-fold cross-validated C indices or difference in C indices and associated 95% bootstrap confidence intervals compared with the CHARGE-AF model with the original coefficients. CHARGE-AF models predict atrial fibrillation from age, White race/ethnicity, height, weight, systolic BP, diastolic BP, smoking, use of antihypertensives, diabetes, congestive heart failure, and myocardial infarction. Predictions from the super learner algorithm are derived from individual algorithm predictions; weights are shown in Supplemental Table 2. CHARGE-AF, Cohorts for Heart and Aging Research in Genomic Epidemiology-Atrial Fibrillation; NA, not applicable; NT-proBNP, N-terminal pro–B-type natriuretic peptide; hsTnT, high-sensitivity troponin T; LASSO, least absolute shrinkage and selection operator.
Net reclassification index is compared with the CHARGE-AF model with re-estimated coefficients.
Indicates statistical significance at the α=0.05 level.
Table 3.
Discriminatory ability of likelihood-based boosting models to predict incident atrial fibrillation compared with the published Cohorts for Heart and Aging Research in Genomic Epidemiology-Atrial Fibrillation (CHARGE-AF) model by category of eGFR
| Predictive Modeling Strategy | N at Risk (N Events) | C-Index (95% Confidence Interval) | Difference from CHARGE-AF C Index (95% Confidence Interval) |
|---|---|---|---|
| eGFR<30 ml/min per 1.73 m2 | 505 (53) | ||
| CHARGE-AF | 0.640 (0.56 to 0.72) | NA | |
| Likelihood-based boosting | |||
| Clinical variables only | 0.641 (0.57 to 0.71) | 0.001 (–0.04 to 0.04) | |
| Clinical variables + NT-proBNP | 0.682 (0.61 to 0.76) | 0.043 (–0.01 to 0.09) | |
| Clinical variables + hsTnT | 0.667 (0.60 to 0.74) | 0.027 (–0.02 to 0.07) | |
| Clinical variables + NT-proBNP + hsTnT | 0.682 (0.61 to 0.76) | 0.043 (–0.01 to 0.09) | |
| eGFR 30 to <45 ml/min per 1.73 m2 | 977 (112) | ||
| CHARGE-AF | 0.649 (0.60 to 0.70) | NA | |
| Likelihood-based boosting | |||
| Clinical variables only | 0.649 (0.60 to 0.70) | 0.000 (–0.03 to 0.03) | |
| Clinical variables + NT-proBNP | 0.686 (0.64 to 0.73) | 0.037 (0.00 to 0.07)a | |
| Clinical variables + hsTnT | 0.652 (0.60 to 0.70) | 0.003 (–0.03 to 0.04) | |
| Clinical variables + NT-proBNP + hsTnT | 0.686 (0.64 to 0.73) | 0.037 (0.00 to 0.07)a | |
| eGFR 45 to <60 ml/min per 1.73 m2 | 861 (72) | ||
| CHARGE-AF | 0.673 (0.61 to 0.73) | NA | |
| Likelihood-based boosting | |||
| Clinical variables only | 0.654 (0.59 to 0.72) | −0.019 (–0.06 to 0.02) | |
| Clinical variables + NT-proBNP | 0.729 (0.67 to 0.79) | 0.056 (0.01 to 0.10)a | |
| Clinical variables + hsTnT | 0.671 (0.61 to 0.73) | −0.002 (–0.04 to 0.04) | |
| Clinical variables + NT-proBNP + hsTnT | 0.733 (0.67 to 0.79) | 0.060 (0.01 to 0.11)a | |
| eGFR≥60 ml/min per 1.73 m2 | 423 (22) | ||
| CHARGE-AF | 0.750 (0.64 to 0.86) | NA | |
| Likelihood-based boosting | |||
| Clinical variables only | 0.693 (0.56 to 0.82) | −0.057 (–0.12 to 0.01) | |
| Clinical variables + NT-proBNP | 0.761 (0.65 to 0.88) | 0.011 (–0.08 to 0.10) | |
| Clinical variables + hsTnT | 0.728 (0.61 to 0.85) | −0.022 (–0.09 to 0.05) | |
| Clinical variables + NT-proBNP + hsTnT | 0.761 (0.64 to 0.88) | 0.011 (–0.08 to 0.10) |
The entry for CHARGE-AF is C index and the associated 95% bootstrap confidence interval; all other entries are ten-fold cross-validated C indices or difference in C indices and associated 95% bootstrap confidence intervals. CHARGE-AF models predict atrial fibrillation from age, White race/ethnicity, height, weight, systolic BP, diastolic BP, smoking, use of antihypertensives, diabetes, congestive heart failure, and myocardial infarction. CHARGE-AF, Cohorts for Heart and Aging Research in Genomic Epidemiology-Atrial Fibrillation; NA, not applicable; NT-proBNP, N-terminal pro–B-type natriuretic peptide; hsTnT, high-sensitivity troponin T.
Indicates statistical significance at the α=0.05 level.
Performance of Machine Learning Models for Prediction of Incident Atrial Fibrillation
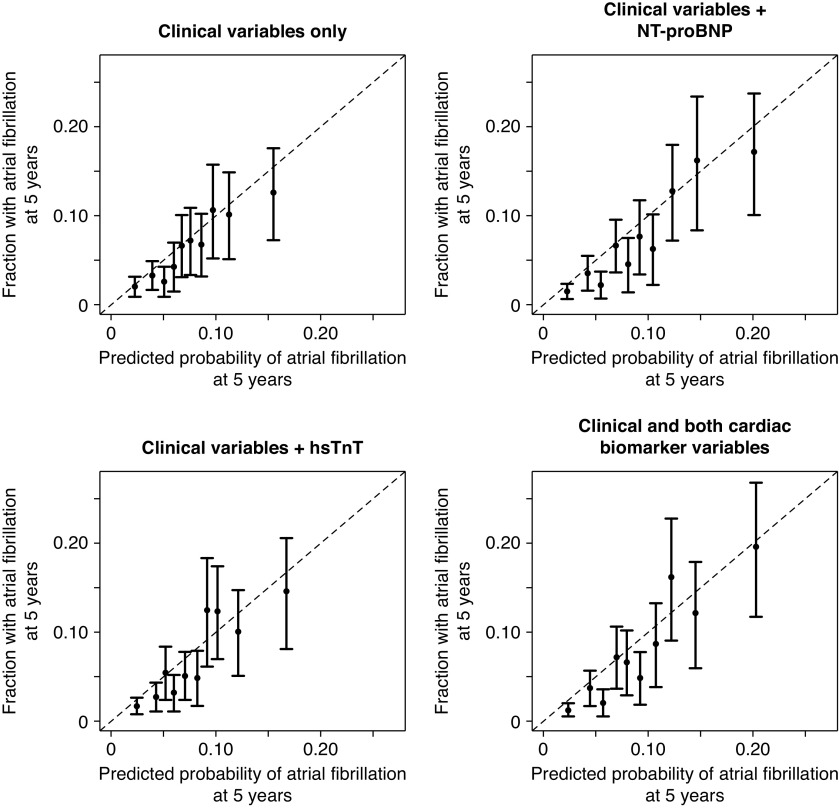
All machine learning methodologies had similar discriminatory ability to predict incident atrial fibrillation (Table 2). Clinical data alone paired with machine learning techniques showed no improvement over the CHARGE-AF model; however, the addition of NT-proBNP to clinical data improved the discriminatory ability of the model in all cases. For example, a likelihood-based boosting model using clinical data had a ten-fold cross-validated C-index of 0.668 (95% CI, 0.64 to 0.70). Adding NT-proBNP, hsTnT, or both biomarkers improved the C-indices to 0.717 (95% CI, 0.69 to 0.75), 0.683 (95% CI, 0.65 to 0.72), and 0.718 (0.69 to 0.75), respectively (variable estimates of the full model are shown in Table 4), with associated NRIs of 18% (5%, 31%), 2% (−10%, 14%), and 21% (8%, 34%), respectively. This model included 12 clinical variables, NT-proBNP, and hsTnT. Calibration of all likelihood-based boosting models was adequate (Figure 1) (all Grønnesby and Brogan P>0.10).
Table 4.
Final coefficient estimates of the likelihood-based boosting model using all clinical and cardiac biomarker data
| Variable | Estimated Coefficient |
|---|---|
| Age, yr | 0.391 |
| Non-Hispanic Black race/ethnicity | −0.206 |
| Hispanic race/ethnicity | −0.0492 |
| History of cardiovascular disease | 0.0306 |
| History of chronic obstructive pulmonary disease | 0.0411 |
| History of myocardial infarction | 0.0135 |
| History of peripheral vascular disease | −0.0589 |
| Use of ACEi/ARBs | 0.0509 |
| Use of calcium channel blockers | 0.00599 |
| Use of diuretics | 0.062 |
| Height, cm | 0.0686 |
| Weight, kg | 0.217 |
| log(NT-proBNP), pg/ml | 0.456 |
| log(hsTnT), pg/ml | 0.0864 |
Predicted 5-year risk of atrial fibrillation is 1–, where β is the regression coefficient and X is the level for each risk factor listed above. ACEi, angiotensin-converting enzyme inhibitor; ARB, angiotensin receptor blocker; NT-proBNP, N-terminal pro–B-type natriuretic peptide; hsTnT, high-sensitivity troponin T.
Figure 1.
Calibration plots of likelihood-based boosting models show predicted and observed probabilities of atrial fibrillation at 5 years by decile of predicted probability. All associated Grønnesby and Borgan P values are greater than 0.10. hsTnT, high-sensitivity troponin T; NT-proBNP, N-terminal pro–B-type natriuretic peptide.
Performance of Machine Learning Models for Prediction of Incident Atrial Fibrillation across eGFR Categories
Participants with lower eGFR tended to have greater predicted 5-year risk of atrial fibrillation (Supplemental Figure 3). Similar to the CHARGE-AF model, all likelihood-based boosting models had better absolute predictive performance among participants with higher eGFR (Table 3). However, improvement over the CHARGE-AF model was only seen among participants with eGFR of 30 to <45 ml/min per 1.73 m2 (difference in C index for full model, 0.037; 95% CI, 0.00 to 0.07) and 45 to <60 ml/min per 1.73 m2 (difference in C index for full model, 0.060; 95% CI, 0.01 to 0.11). Likelihood-based boosting models showed no statistically significant improvement from the CHARGE-AF model among participants with eGFR<30 ml/min per 1.73 m2.
Super Learner Performance
The super learner algorithm had discriminatory ability to predict incident atrial fibrillation that numerically had the greatest improvement over the CHARGE-AF model (Table 2) (C index of 0.720; 95% CI, 0.69 to 0.75); the difference in the C index from the CHARGE-AF model was 0.046 (95% CI, 0.02 to 0.07), and the associated NRI was 15% (2%, 28%). Estimated super learner weights are shown in Supplemental Table 2. Greatest weight (65%), indicating better-performing algorithms, was placed on likelihood-based boosting algorithms that incorporated NT-proBNP, with smaller weights placed on generalized boosting regression (10%), ridge regression (10%), and stepwise regression (9%) models that incorporated the biomarker. No weight was placed on LASSO models. Notably, only 3% of weight was placed on CHARGE-AF predictions. Calibration of the super learner algorithm was adequate (Supplemental Figure 4) (Grønnesby and Borgan P=0.47).
Performance of Machine Learning Models for Prediction of Incident Atrial Fibrillation Excluding Race/Ethnicity
Machine learning models that used clinical data and cardiac biomarkers but excluded information on self-described race/ethnicity had performances that were comparable with models that included this information (Supplemental Table 3). Although the machine learning method used made little difference with respect to the discriminatory ability, addition of NT-proBNP significantly improved the ten-fold cross-validated C-index compared with that from the previously published CHARGE-AF equation for most machine learning methods. A top-performing likelihood-based boosting model included 11 clinical variables, NT-proBNP, and hsTnT (Supplemental Table 4) and had adequate calibration (P=0.14).
Discussion
In this analysis, we found that machine learning prediction models for incident atrial fibrillation that incorporated the cardiac biomarker NT-proBNP had the best discrimination in a CKD population compared with models that involved only clinical data or the previously published CHARGE-AF model. A parsimonious likelihood-based boosting model including cardiac biomarkers and 12 additional readily available clinical variables was the top-performing individual model. Developing tools to predict atrial fibrillation in patients with CKD may provide opportunities for enhanced cardiovascular primary prevention.
We found that addition of NT-proBNP improved discrimination for atrial fibrillation in addition to standard clinical variables; the improvement in prediction with NT-proBNP was seen across all machine learning approaches. Our findings related to NT-proBNP are similar to findings in the community-based cohort study, Atherosclerosis Risk in Communities, in which inclusion of cardiac biomarkers modestly improved discrimination of incident atrial fibrillation (40). In the CHARGE-AF consortium of multiple community-based studies, B-type natriuretic peptide substantially improved prediction beyond the clinical CHARGE-AF risk score (41). Our findings extend the use of NT-proBNP to possibly help identify patients with CKD at the greatest risk for developing atrial fibrillation. NT-proBNP is widely available, and thus, it is plausible to incorporate the use of this biomarker into clinical care after appropriate risk thresholds for models including NT-proBNP are identified.
We did not find meaningful differences across various machine learning approaches when similar clinical variables were used. We hypothesized a priori that ensemble methods, such as boosting, could leverage higher-order interactions between predictor variables, resulting in better predictive performance. Contrary to this hypothesis, we found no advantage of any particular machine learning model. The best-performing models were the likelihood-based boosting and LASSO methods that incorporated NT-proBNP. Both methods produce parsimonious models that are appropriate for clinical use, and predictions from corresponding likelihood-based boosting and LASSO models were highly correlated (r>0.99 for models with the same predictors).
We also explored the performance of a super learning approach to prediction, which incorporates predictions from a number of candidate algorithms. The super learner has been shown to have asymptotic optimal properties provided the number of algorithms is large (42); excellent performance has been observed in practice as well (43,44). Despite this, super learning has been used less often with survival outcomes and is novel to nephrology (45,46). In our analysis, the super learner had the highest numeric discrimination and placed a majority of weight on predictions from the top-performing individual likelihood-based boosting models. Because it requires predicted probabilities from a large number of individual predictive models, the super learner is unlikely to enter routine clinical practice as a predictive tool. However, it can provide insight by suggesting the algorithm or algorithms likely to provide the best predictions in future datasets.
The predicted probability of incident atrial fibrillation was higher with lower eGFR in this CKD population. We found that the previously published CHARGE-AF equation performed best at higher eGFR (eGFR>60 ml/min per 1.73 m2), with only modest discrimination among those with lower eGFR. It is likely that those with higher eGFR aligned more closely with the study population in which the CHARGE-AF equation was developed. Our likelihood-based boosting model, which included clinical variables and cardiac biomarkers, performed significantly better in participants with eGFR 30–44 and 45–60 ml/min per 1.73 m2 compared with the CHARGE-AF model. These results reaffirm that prediction models for cardiovascular disease derived in general populations often cannot be applied to the CKD population, in which the influence of risk factors and trajectory of disease differ.
There are numerous potential applications of prediction models for atrial fibrillation in patients with CKD. These models could potentially be used in the design of clinical trials to identify participants who are most likely to derive benefit from cardiovascular therapies for primary prevention of atrial fibrillation. Further, prediction scores (e.g., the Framingham risk score) have been used successfully in clinical medicine to risk-stratify patients, make decisions, and advise patients on use of primary prevention pharmacotherapies, BP targets, and lifestyle modifications. This may be particularly useful in patients with CKD, a population that often has unrecognized cardiovascular disease from either differing pathology or symptomology compared with the general population, which ultimately may affect how many patients with CKD receive primary cardiovascular treatment. Clinical models to identify patients with CKD who are highest risk of atrial fibrillation may guide decisions around primary treatment strategies for cardiovascular disease in general (because there are currently no specific evidence-based primary prevention therapies for atrial fibrillation in patients with CKD).
Our study had several strengths. We studied a well-characterized, multicenter CKD cohort. All atrial fibrillation events were adjudicated by two physicians. We included a broad range of candidate predictors for our models, and unlike previous research, we accounted analytically for the competing risk of death. We recognize a few limitations as well. Our outcome only captured hospitalized atrial fibrillation; thus, it is unknown whether our prediction model performs well for ambulatory-detected atrial fibrillation not requiring hospitalization. However, a similar approach could be applied and tested. Our models were developed in a cohort of research volunteers, so the performance of the models may differ in other patient populations.
In conclusion, a prediction model developed using machine learning, which included clinical variables and cardiac biomarkers, demonstrated moderate discrimination and calibration for incident atrial fibrillation in a cohort of CKD participants, and it performed better compared with a published prediction model used in the general population. Use of prediction models in patients with CKD may offer opportunities to identify high-risk individuals who may benefit for enhanced cardiovascular care.
Disclosures
N. Bansal reports serving as an associate editor of Kidney360. R. Christenson reports consultancy agreements with Babson Diagnostics, Beckman Coulter, Becton Dickenson, PixCell, Quidel, Roche Diagnostics, Siemens Healthineers, and Sphingotec; ownership interest in Babson Diagnostics; receiving research funding from Abbott Diagnostics, Astute, Beckman Coulter, Becton Dickinson, Critical Care Diagnostics, DiadexUS, Ortho Clinical Diagnostics, Procise, Quidel, Roche Diagnostics, and Siemens Healthcare Diagnostics; receiving honoraria from Babson, Beckman Coulter, Becton Dickinson, PixCell, Roche Diagnostics, and Siemens Healthcare Diagnostics; and serving as a scientific advisor or member of Babson, Becton Dickinson, Roche Diagnostics, Siemens Healthcare Diagnostics, and Sphingoec. D.L. Cohen reports consultancy agreements with Medtronic; receiving research funding from the CRIC study and Medtronic; receiving honoraria from Medtronic; and serving as section editor of Currents in Clinical Cardiology and on the editorial board of Journal of Clinical Hypertension. R. Deo reports consultancy agreements with Boehringer Ingelheim, Janssen Pharmaceuticals, and Pfizer; receiving research funding from iRhythm Technologies; serving on the editorial board of Circulation and on the editorial board of Heart Rhythm O2; and serving on the steering committee for Kidney Disease Improving Global Outcomes. A. Go reports employment with Kaiser Permanente Northern California and receiving research funding from Amarin, Bristol Meyers-Squibb, CSL Behring, and Novartis. J. Lash reports serving as a scientific advisor or member of Kidney360. P. Rao reports receiving honoraria from AstraZeneca and serving as a scientific advisor or member of the AstraZeneca Nephrology Fellowship Advisory Board, the GSK scientific advisory board, and the Renal Research Institute. S. Seliger reports consultancy agreements with Tricida, Inc. (Endpoint Adjudication Committee); receiving research funding from Critical Diagnostics, Kadmon Pharmaceuticals, Palladio Biosciences, Reata Pharmaceuticals, Roche Diagnostics, Inc., and Sanofi US; patents and inventions with the University of Maryland, Baltimore and the University of Texas Southwestern: Methods for Assessing Differential Risk for Developing Heart Failure; and serving as a member of the editorial board of Circulation, an Associate Editor of CJASN, Chair of the Board of Directors of ESRD Network 5, a member of Medical Review Board ESRD Network 5, and a member of the Endpoint Adjudication Committee of the Evaluation of Effect of TRC101 on Progression of Chronic Kidney Disease in Subjects with Metabolic Acidosis (VALOR-CKD) trial (Tricida, Inc.). M.G. Shlipak reports employment with the San Francisco Veterans Affairs Medical Center; consultancy agreements with Cricket Health, Intercept Pharmaceuticals, the University of North Carolina at Chapel Hill, the University of Washington Cardiovascular Health Study, and the Veterans Medical Research Foundation; ownership interest in Tai Diagnostics; receiving research funding from Bayer Pharmaceuticals; receiving honoraria from the University of California, Irvine; serving as a scientific advisor or member of American Journal of Kidney Disease, Circulation, JASN, and TAI Diagnostics; and serving as a board member of the Northern California Institute for Research and Education. R. Townsend reports consultancy agreements with Axio, IONIS, Medtronic, and Regeneron; receiving research funding from the National Institutes of Health; serving on the editorial boards of Journal of Clinical Hypertension and Pulse; and receiving royalties as an UpToDate contributor. L.R. Zelnick reports consultancy agreements with the Veterans Medical Research Foundation and serving as a statistical editor for CJASN. All remaining authors have nothing to disclose.
Funding
This study was supported by National Institute of Diabetes and Digestive and Kidney Diseases grant R01 DK103612 (to N. Bansal). This research was supported in part by an unrestricted gift from the Northwest Kidney Centers to the Kidney Research Institute. Roche Diagnostics provided partial funding for the NT-proBNP and hsTnT assays. Funding for the CRIC study was obtained under a cooperative agreement from National Institute of Diabetes and Digestive and Kidney Diseases grants U01DK060990, U01DK060984, U01DK061022, U01DK061021, U01DK061028, U01DK060980, U01DK060963, and U01DK060902. In addition, this work was supported in part by the Perelman School of Medicine at the University of Pennsylvania Clinical and Translational Science Award National Institutes of Health (NIH), National Center for Advancing Translational Sciences grant UL1TR000003; Johns Hopkins University grant UL1 TR-000424; University of Maryland General Clinical Research Center grant M01 RR-16500; the Clinical and Translational Science Collaborative of Cleveland; NIH and NIH Roadmap for Medical Research, National Center for Advancing Translational Sciences grant UL1TR000439; Michigan Institute for Clinical and Health Research grant UL1TR000433; University of Illinois at Chicago Clinical and Translational Science Award grant UL1RR029879; Tulane COBRE for Clinical and Translational Research in Cardiometabolic Diseases grant P20 GM109036; and Kaiser Permanente NIH/National Center for Research Resources University of California, San Francisco-Clinical and Translational Science Institute grant UL1 RR-024131.
Supplementary Material
Acknowledgments
Parts of this study were presented at the American Society of Nephrology Kidney Week, October 20–25, 2020.
Because Dr. Stephen Seliger is an Associate Editor of CJASN, he was not involved in the peer review process for this manuscript. Another editor oversaw the peer review and decision-making process for this manuscript.
Data Sharing Statement
Deidentified participant data, protocol, and data dictionary from the CRIC study are available upon request through the National Institute of Diabetes and Digestive and Kidney Diseases repository website. New data from the CRIC study are periodically added to the repository per National Institutes of Health guidelines.
Footnotes
Published online ahead of print. Publication date available at www.cjasn.org.
Supplemental Material
This article contains the following supplemental material online at http://cjasn.asnjournals.org/lookup/suppl/doi:10.2215/CJN.01060121/-/DCSupplemental.
Supplemental Figure 1. CONSORT diagram of the analytic population.
Supplemental Figure 2. Calibration plot for the CHARGE-AF equation with original coefficients.
Supplemental Figure 3. Distribution of predicted probabilities of atrial fibrillation at 5 years from the likelihood-based boosting model (all clinical and cardiac biomarker data), by category of eGFR.
Supplemental Figure 4. Calibration plot for super learner-predicted probabilities.
Supplemental Table 1. List of clinical and cardiac biomarker variables available for use in predictive models.
Supplemental Table 2. Percentage weighting used for super learner predictions.
Supplemental Table 3. Discriminatory ability of several modeling strategies not including race/ethnicity to predict incident atrial fibrillation, compared with the published CHARGE-AF model.
Supplemental Table 4. Final coefficient estimates of the likelihood-based boosting model using clinical and cardiac biomarker data, excluding race/ethnicity.
References
- 1.Piccini JP, Stevens SR, Chang Y, Singer DE, Lokhnygina Y, Go AS, Patel MR, Mahaffey KW, Halperin JL, Breithardt G, Hankey GJ, Hacke W, Becker RC, Nessel CC, Fox KA, Califf RM; ROCKET AF Steering Committee and Investigators: Renal dysfunction as a predictor of stroke and systemic embolism in patients with nonvalvular atrial fibrillation: Validation of the R(2)CHADS(2) index in the ROCKET AF (Rivaroxaban Once-daily, oral, direct factor Xa inhibition Compared with vitamin K antagonism for prevention of stroke and Embolism Trial in Atrial Fibrillation) and ATRIA (AnTicoagulation and Risk factors In Atrial fibrillation) study cohorts. Circulation 127: 224–232, 2013 [DOI] [PubMed] [Google Scholar]
- 2.Nakagawa K, Hirai T, Takashima S, Fukuda N, Ohara K, Sasahara E, Taguchi Y, Dougu N, Nozawa T, Tanaka K, Inoue H: Chronic kidney disease and CHADS(2) score independently predict cardiovascular events and mortality in patients with nonvalvular atrial fibrillation. Am J Cardiol 107: 912–916, 2011 [DOI] [PubMed] [Google Scholar]
- 3.Go AS, Fang MC, Udaltsova N, Chang Y, Pomernacki NK, Borowsky L, Singer DE; ATRIA Study Investigators: Impact of proteinuria and glomerular filtration rate on risk of thromboembolism in atrial fibrillation: The anticoagulation and risk factors in atrial fibrillation (ATRIA) study. Circulation 119: 1363–1369, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nelson SE, Shroff GR, Li S, Herzog CA: Impact of chronic kidney disease on risk of incident atrial fibrillation and subsequent survival in Medicare patients. J Am Heart Assoc 1: e002097, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bansal N, Fan D, Hsu CY, Ordonez JD, Go AS: Incident atrial fibrillation and risk of death in adults with chronic kidney disease. J Am Heart Assoc 3: e001303, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Olesen JB, Lip GY, Kamper AL, Hommel K, Køber L, Lane DA, Lindhardsen J, Gislason GH, Torp-Pedersen C: Stroke and bleeding in atrial fibrillation with chronic kidney disease. N Engl J Med 367: 625–635, 2012 [DOI] [PubMed] [Google Scholar]
- 7.Bansal N, Fan D, Hsu CY, Ordonez JD, Marcus GM, Go AS: Incident atrial fibrillation and risk of end-stage renal disease in adults with chronic kidney disease. Circulation 127: 569–574, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bansal N, Xie D, Sha D, Appel LJ, Deo R, Feldman HI, He J, Jamerson K, Kusek JW, Messe S, Navaneethan SD, Rahman M, Ricardo AC, Soliman EZ, Townsend R, Go AS: Cardiovascular events after new-onset atrial fibrillation in adults with CKD: Results from the Chronic Renal Insufficiency Cohort (CRIC) study. J Am Soc Nephrol 29: 2859–2869, 2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Alonso A, Krijthe BP, Aspelund T, Stepas KA, Pencina MJ, Moser CB, Sinner MF, Sotoodehnia N, Fontes JD, Janssens AC, Kronmal RA, Magnani JW, Witteman JC, Chamberlain AM, Lubitz SA, Schnabel RB, Agarwal SK, McManus DD, Ellinor PT, Larson MG, Burke GL, Launer LJ, Hofman A, Levy D, Gottdiener JS, Kääb S, Couper D, Harris TB, Soliman EZ, Stricker BH, Gudnason V, Heckbert SR, Benjamin EJ: Simple risk model predicts incidence of atrial fibrillation in a racially and geographically diverse population: The CHARGE-AF consortium. J Am Heart Assoc 2: e000102, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lamprea-Montealegre JA, Zelnick LR, Shlipak MG, Floyd JS, Anderson AH, He J, Christenson R, Seliger SL, Soliman EZ, Deo R, Ky B, Feldman HI, Kusek JW, deFilippi CR, Wolf MS, Shafi T, Go AS, Bansal N; CRIC Study Investigators: Cardiac biomarkers and risk of atrial fibrillation in chronic kidney disease: The CRIC study. J Am Heart Assoc 8: e012200, 2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Feldman HI, Appel LJ, Chertow GM, Cifelli D, Cizman B, Daugirdas J, Fink JC, Franklin-Becker ED, Go AS, Hamm LL, He J, Hostetter T, Hsu CY, Jamerson K, Joffe M, Kusek JW, Landis JR, Lash JP, Miller ER, Mohler ER 3rd, Muntner P, Ojo AO, Rahman M, Townsend RR, Wright JT; Chronic Renal Insufficiency Cohort (CRIC) Study Investigators: The Chronic Renal Insufficiency Cohort (CRIC) study: Design and methods. J Am Soc Nephrol 14[Suppl 2]: S148–S153, 2003 [DOI] [PubMed] [Google Scholar]
- 12.Lash JP, Go AS, Appel LJ, He J, Ojo A, Rahman M, Townsend RR, Xie D, Cifelli D, Cohan J, Fink JC, Fischer MJ, Gadegbeku C, Hamm LL, Kusek JW, Landis JR, Narva A, Robinson N, Teal V, Feldman HI; Chronic Renal Insufficiency Cohort (CRIC) Study Group: Chronic Renal Insufficiency Cohort (CRIC) Study: Baseline characteristics and associations with kidney function. Clin J Am Soc Nephrol 4: 1302–1311, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mehta R, Cai X, Lee J, Scialla JJ, Bansal N, Sondheimer JH, Chen J, Hamm LL, Ricardo AC, Navaneethan SD, Deo R, Rahman M, Feldman HI, Go AS, Isakova T, Wolf M; Chronic Renal Insufficiency Cohort (CRIC) Study Investigators: Association of fibroblast growth factor 23 with atrial fibrillation in chronic kidney disease, from the Chronic Renal Insufficiency Cohort study. JAMA Cardiol 1: 548–556, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Inker LA, Schmid CH, Tighiouart H, Eckfeldt JH, Feldman HI, Greene T, Kusek JW, Manzi J, Van Lente F, Zhang YL, Coresh J, Levey AS; CKD-EPI Investigators: Estimating glomerular filtration rate from serum creatinine and cystatin C. N Engl J Med 367: 20–29, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Joffe M, Hsu CY, Feldman HI, Weir M, Landis JR, Hamm LL; Chronic Renal Insufficiency Cohort (CRIC) Study Group: Variability of creatinine measurements in clinical laboratories: Results from the CRIC study. Am J Nephrol 31: 426–434, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Levey AS, Coresh J, Greene T, Marsh J, Stevens LA, Kusek JW, Van Lente F; Chronic Kidney Disease Epidemiology Collaboration: Expressing the Modification of Diet in Renal Disease Study equation for estimating glomerular filtration rate with standardized serum creatinine values. Clin Chem 53: 766–772, 2007 [DOI] [PubMed] [Google Scholar]
- 17.Kligfield P, Gettes LS, Bailey JJ, Childers R, Deal BJ, Hancock EW, van Herpen G, Kors JA, Macfarlane P, Mirvis DM, Pahlm O, Rautaharju P, Wagner GS; American Heart Association Electrocardiography and Arrhythmias Committee, Council on Clinical Cardiology; American College of Cardiology Foundation; Heart Rhythm Society: Recommendations for the standardization and interpretation of the electrocardiogram. Part I. The electrocardiogram and its technology. A scientific statement from the American Heart Association Electrocardiography and Arrhythmias Committee, Council on Clinical Cardiology; the American College of Cardiology Foundation; and the Heart Rhythm Society. Heart Rhythm 4: 394–412, 2007 [DOI] [PubMed] [Google Scholar]
- 18.Lawless JF, Singhal K: Efficient screening of nonnormal regression-models. Biometrics 34: 318–327, 1978 [Google Scholar]
- 19.Tibshirani R: The lasso method for variable selection in the Cox model. Stat Med 16: 385–395, 1997 [DOI] [PubMed] [Google Scholar]
- 20.Tibshirani R: Regression shrinkage and selection via the Lasso. J R Stat Soc Series B Methodol 58: 267–288, 1996 [Google Scholar]
- 21.Simon N, Friedman J, Hastie T, Tibshirani R: Regularization paths for Cox’s proportional hazards model via coordinate descent. J Stat Softw 39: 1–13, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Binder H, Allignol A, Schumacher M, Beyersmann J: Boosting for high-dimensional time-to-event data with competing risks. Bioinformatics 25: 890–896, 2009 [DOI] [PubMed] [Google Scholar]
- 23.Friedman JH: Greedy function approximation: A gradient boosting machine. Ann Stat 29: 1189–1232, 2001 [Google Scholar]
- 24.Golmakani MK, Polley EC: Super learner for survival data prediction [published online ahead of print February 22, 2020]. Int J Biostat 10.1515/ijb-2019-0065 [DOI] [PubMed] [Google Scholar]
- 25.Harrell FE Jr., Lee KL, Mark DB: Multivariable prognostic models: Issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med 15: 361–387, 1996 [DOI] [PubMed] [Google Scholar]
- 26.Efron B, Tibshirani R: Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat Sci 1: 54–75, 1986 [Google Scholar]
- 27.James G, Witten D, Hastie T, Tibshirani R: An Introduction to Statistical Learning: With Applications in R, New York, Springer, 2013 [Google Scholar]
- 28.May S, Hosmer DW: A cautionary note on the use of the Grønnesby and Borgan goodness-of-fit test for the Cox proportional hazards model. Lifetime Data Anal 10: 283–291, 2004 [DOI] [PubMed] [Google Scholar]
- 29.Grønnesby JK, Borgan O: A method for checking regression models in survival analysis based on the risk score. Lifetime Data Anal 2: 315–328, 1996 [DOI] [PubMed] [Google Scholar]
- 30.Wolbers M, Koller MT, Witteman JC, Steyerberg EW: Prognostic models with competing risks: Methods and application to coronary risk prediction. Epidemiology 20: 555–561, 2009 [DOI] [PubMed] [Google Scholar]
- 31.Austin PC, Lee DS, Fine JP: Introduction to the analysis of survival data in the presence of competing risks. Circulation 133: 601–609, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fine J, Gray R: A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc 94: 496–509, 1999 [Google Scholar]
- 33.Cooper JN, Minneci PC, Deans KJ: Postoperative neonatal mortality prediction using superlearning. J Surg Res 221: 311–319, 2018 [DOI] [PubMed] [Google Scholar]
- 34.van der Laan MJ, Polley EC, Hubbard AE: Super learner. Stat Appl Genet Mol Biol 6: Article25, 2007 [DOI] [PubMed] [Google Scholar]
- 35.Polley EC, van der Laan MJ: Super Learning for Right-Censored Data, New York, Springer, 2011 [Google Scholar]
- 36.Pencina MJ, D’Agostino RB Sr., Steyerberg EW: Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Stat Med 30: 11–21, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Neal RE, Morse M: Racial health inequities and clinical algorithms [published online ahead of print March 5, 2021]. Clin J Am Soc Nephrol 10.2215/CJN.01780221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Boulware LE, Mohottige D: The seen and the unseen: Race and social inequities affecting kidney care. Clin J Am Soc Nephrol 16: 815–817, 2021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Flanagin A, Frey T, Christiansen SL, Bauchner H: The reporting of race and ethnicity in medical and science journals: Comments invited. JAMA 325: 1049–1052, 2021 [DOI] [PubMed] [Google Scholar]
- 40.Li L, Selvin E, Lutsey PL, Hoogeveen RC, O’Neal WT, Soliman EZ, Chen LY, Alonso A: Association of N-terminal pro B-type natriuretic peptide (NT-proBNP) change with the risk of atrial fibrillation in the ARIC cohort. Am Heart J 204: 119–127, 2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sinner MF, Stepas KA, Moser CB, Krijthe BP, Aspelund T, Sotoodehnia N, Fontes JD, Janssens AC, Kronmal RA, Magnani JW, Witteman JC, Chamberlain AM, Lubitz SA, Schnabel RB, Vasan RS, Wang TJ, Agarwal SK, McManus DD, Franco OH, Yin X, Larson MG, Burke GL, Launer LJ, Hofman A, Levy D, Gottdiener JS, Kääb S, Couper D, Harris TB, Astor BC, Ballantyne CM, Hoogeveen RC, Arai AE, Soliman EZ, Ellinor PT, Stricker BH, Gudnason V, Heckbert SR, Pencina MJ, Benjamin EJ, Alonso A: B-type natriuretic peptide and C-reactive protein in the prediction of atrial fibrillation risk: The CHARGE-AF Consortium of community-based cohort studies. Europace 16: 1426–1433, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.van der Vaart A, Dudoit S, van der Laan MJ: Oracle inequalities for multi-fold cross-validation. Stat Decis 24: 351–371, 2006 [Google Scholar]
- 43.Rose S: Mortality risk score prediction in an elderly population using machine learning. Am J Epidemiol 177: 443–452, 2013 [DOI] [PubMed] [Google Scholar]
- 44.Pirracchio R, Petersen ML, Carone M, Rigon MR, Chevret S, van der Laan MJ: Mortality prediction in intensive care units with the Super ICU Learner Algorithm (SICULA): A population-based study. Lancet Respir Med 3: 42–52, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sachs MC, Discacciati A, Everhov AH, Olen O, Gabriel EE: Ensemble prediction of time-to-event outcomes with competing risks: A case-study of surgical complications in Crohn’s disease. J R Stat Soc Ser C Appl Stat 68: 1431–1446, 2019 [Google Scholar]
- 46.Biccler JL, Eloranta S, de Nully Brown P, Frederiksen H, Jerkeman M, Jørgensen J, Jakobsen LH, Smedby KE, Bøgsted M, El-Galaly TC: Optimizing outcome prediction in diffuse large B-cell lymphoma by use of machine learning and nationwide lymphoma registries: A Nordic Lymphoma Group Study. JCO Clin Cancer Inform 2: 1–13, 2018 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.