Learning and Representation of Hierarchical Concepts in Hippocampus and Prefrontal Cortex

Abstract

A key aspect of conceptual knowledge is that it can be flexibly applied at different levels of abstraction, implying a hierarchical organization. It is yet unclear how this hierarchical structure is acquired and represented in the brain. Here we investigate the computations underlying the acquisition and representation of the hierarchical structure of conceptual knowledge in the hippocampal-prefrontal system of 32 human participants (22 females). We assessed the hierarchical nature of learning during a novel tree-like categorization task via computational model comparisons. The winning model allowed to extract and quantify estimates for accumulation and updating of hierarchical compared with single-feature-based concepts from behavior. We find that mPFC tracks accumulation of hierarchical conceptual knowledge over time, and mPFC and hippocampus both support trial-to-trial updating. As a function of those learning parameters, mPFC and hippocampus further show connectivity changes to rostro-lateral PFC, which ultimately represented the hierarchical structure of the concept in the final stages of learning. Our results suggest that mPFC and hippocampus support the integration of accumulated evidence and instantaneous updates into hierarchical concept representations in rostro-lateral PFC.

SIGNIFICANCE STATEMENT A hallmark of human cognition is the flexible use of conceptual knowledge at different levels of abstraction, ranging from a coarse category level to a fine-grained subcategory level. While previous work probed the representational geometry of long-term category knowledge, it is unclear how this hierarchical structure inherent to conceptual knowledge is acquired and represented. By combining a novel hierarchical concept learning task with computational modeling of categorization behavior and concurrent fMRI, we differentiate the roles of key concept learning regions in hippocampus and PFC in learning computations and the representation of a hierarchical category structure.

Introduction

Concepts are organizing structures that help to assign meaning to novel information (Kemp, 2012). Depending on the situation, we flexibly use conceptual knowledge at different levels of abstraction (e.g., identify a Ferrari as a vehicle, or specifically as a racing car). Such superordinate and subordinate category levels are connected via relational rules (Skorstad et al., 1988) that define subcategorization-relevant features in dependence of the superordinate level (e.g., speed distinguishes subcategories within the category 'cars', but not within the category 'animals'). It is largely unclear how this hierarchical structure inherent to conceptual knowledge is acquired and represented by the brain. Many brain regions contribute to concept learning in different functions (Seger and Miller, 2010). The key aspect of generalization over experiences to abstract commonalities and build organized knowledge is supported by hippocampus and (ventro-)medial PFC (mPFC), given their roles in relational processing and memory integration (Kumaran et al., 2009; Zeithamova et al., 2012; Schlichting et al., 2015; Mack et al., 2018; Spalding et al., 2018). Recent work specifically suggests that the hippocampus and mPFC encode information in cognitive maps that represent multiple relationships in a common representational space defined along behaviorally relevant dimensions (hippocampus: Tavares et al., 2015; Theves et al., 2019, 2020; vmPFC: Constantinescu et al., 2016; Bao et al., 2019). For instance, the hippocampus maps distances between stimuli in a space spanned by feature dimensions that were relevant to categorization during prior concept learning (Theves et al., 2020). Such cognitive maps might provide a flexible representation enabling inference and transfer of meaning to novel encounters, critical to the use of concepts. Previous neuroimaging studies mostly defined categories either by discrete features shared by their exemplars (Davis et al., 2012, 2017; Mack et al., 2016, 2020; Bowman and Zeithamova, 2018) or by the ratio of continuous features (Seger et al., 2015; Theves et al., 2020). Conceptual similarity between stimuli as defined by their distance in a continuous feature space was reflected in scaled similarity between their hippocampal representations (Theves et al., 2020). It has not been investigated whether conceptual similarity between exemplars as defined by the number of shared nodes in a hierarchical category structure is likewise captured by graded neural similarity in these regions. Nested hippocampal representations have so far been observed in rodents performing a spatial context-dependent object discrimination task, with population activity in dorsal hippocampus representing both superordinate and subordinate distinctions (McKenzie et al., 2014). Further insight in multiscale representations is provided by Bernadi et al. (2020). By comparing the generalization performance of a neural decoder to new task conditions with the number of decodable variables, they show that the representational geometry of hippocampal and prefrontal ensembles can simultaneously be abstract and high-dimensional. Another strand of research points toward a key role of the rostro-lateral PFC (rlPFC) in acquiring hierarchical concepts. Most prior fMRI studies used simpler feature-based categorization rules and focused on memory processes and similarity-based mechanism, where concept representations ground on common features and new exemplars are judged based on representational overlap (Zeithamova et al., 2019). However, memory processes are thought to be complemented by more abstract reasoning strategies (Smith and Sloman, 1994; Ashby et al., 1998) specifically during early concept learning (Erickson and Kruschke, 1998). As a hierarchical concept is defined by dependent rules, its acquisition might specifically engage relational reasoning. Abstract reasoning (Christoff et al., 2001; Kroger et al., 2002; Watson and Chatterjee, 2012) and relational category learning in specific (Davis et al., 2017) have been linked to rlPFC. Here, rlPFC was shown to track the representational distance between test and training examples during acquisition of relational versus feature-based concepts, whereas mPFC supported general decision-making functions (Davis et al., 2017). It has been debated (Badre, 2010; Speed, 2010) whether rlPFC processes information stored elsewhere with respect to task-relevant relations, or whether it reflects the storage site of relational concepts.

In sum, it has not been explicitly investigated how hierarchical levels of concepts are acquired and represented. Here we evaluate the roles of hippocampus, mPFC, and rlPFC in (1) learning operations and (2) representations of a hierarchical category structure, respectively. We compare behavior during a novel hierarchical categorization task to different learning models and use the winning model's parameters to identify learning-related brain activity. Further, we probe the site of representation of the hierarchical category structure at the end of learning and evaluate its connectivity to regions involved in learning computations.

Materials and Methods

Experimental design and subject details

Thirty-seven participants, recruited from Radboud University, Nijmegen, gave written informed consent and were paid as agreed by the local Research Ethics Committee (CMO region Arnhem-Nijmegen, the Netherlands). Five participants were excluded from the analyses because of excessive motion (n = 2; cutoff criteria: mean absolute displacement >2 mm or peak in absolute displacement >3.9 mm; mean and SD of absolute displacement of analyzed sample: 0.64 ± 0.39 mm), corrupted MRI data files (n = 1), and lacking engagement in the task (n = 2). Inside the scanner, participants were trained on a hierarchical categorization task with the intention to capture computations during concept learning as well as the emergence of neural concept representations in the final stages of learning. The categorization task was followed and preceded by stimulus viewing blocks which are not subject of the present report. Thirty-two participants (age: 23 ± 3 years; 22 females) were included in the analysis of learning-related activity. In the representational similarity analysis (RSA), we intended to measure the representation of the entire hierarchical concept structure. Therefore, we excluded 3 participants whose postexperimental debriefing (no explicit knowledge of Level 2 rule) as well as Level 2 categorization accuracy (Level 2 accuracy rates stayed <50%) indicated that they did not acquire both levels of the concept. One participant did not perform the multidimensional sorting task following scanning.

Method details

Behavioral procedures

In the learning phase, participants were trained to categorize 32 different stimuli, creatures generated with the video game Spore (http://www.spore.com/), into two superordinate and four subordinate categories according to a hierarchical rule. Creatures had five body features which could take two values each (i.e., wings: present-absent, ears: big-small, eyes: big-small, leaf on belly: big-small, knee-pads: big-small). Diagnostic for the subcategory was the specific combination of a subset of critical features. The value of a first feature (wings) defined a creature's superordinate category and which second feature is relevant for further subcategorization within the superordinate category. That is, depending on whether the creature has wings or not, either the size of the eyes or the size of the ears was relevant for further subcategorization. Importantly, both ear and eye size varied for all creatures, yet their relevance for subcategorization depended on the superordinate category. Thus, the subcategory was determined by a dependent relational rule and was not predicted by the secondary feature alone. The mapping of features to categories was constant across participants. Participants were instructed to categorize the creatures into four families, that evolved from two different species. In each trial, participants selected the subcategory (family) by pressing one of four buttons and received feedback that indicated up to which level in the hierarchy their categorization was correct: “100%” was displayed when the correct subcategory was selected, “50%” when only the category but not the subcategory was correct, and “0%” when the category (and consequently the subcategory) was incorrect. The learning phase comprised 8 blocks of 32 stimuli, each of which were followed by feedback. The 8 blocks were preceded by a practice block in which the superordinate category had to be selected from two response options (Fig. 2B, shaded area). Stimuli were presented for 2 s, followed by 0.5 s feedback and intertrial intervals of 2, 3.5, or 5 s (33.3% each). In a final debriefing questionnaire, participants' explicit knowledge of the categorization rules was assessed. Each of the eight learning blocks was followed by six probe trials (three congruent, three incongruent) during which no feedback was displayed. Probe stimuli were creatures with features missing. For incongruent probes, missing features included the categorization-relevant features (i.e., the eyes for “wing creatures”), implying that the categorization rule was nonapplicable. Congruent probes had all features relevant for categorization. Given the equal amount of congruent and incongruent probes, the absence of feedback, and the fact that other features in addition to the relevant ones were missing, probe trials were noninformative for learning. As participants reported difficulties with intermittingly adapting to the probe-block task structure within only six trials and further found the presentation of noncategorizable stimuli (which was not announced in the instruction) confusing, we refrained from interpreting this measurement. The presence of probe trials was included as a regressor in all GLMs of the learning data. Performance accuracy (mean ± SD) across these 24 trials was 75.26 ± 15.26% for Level 1 and 63.54 ± 20.49% for Level 2. In a multidimensional sorting task subsequent to the scanning session, 20 stimuli (three exemplars of each category and eight probe stimuli) had to be arranged according to their relatedness within a circular arena displayed on a computer screen (Kriegeskorte and Mur, 2012) to probe perceived similarity across stimuli as function of their category membership. All tasks were conducted using Presentation 16.4 (NBS), except the multidimensional sorting task, which was conducted using MATLAB.

Figure 2.

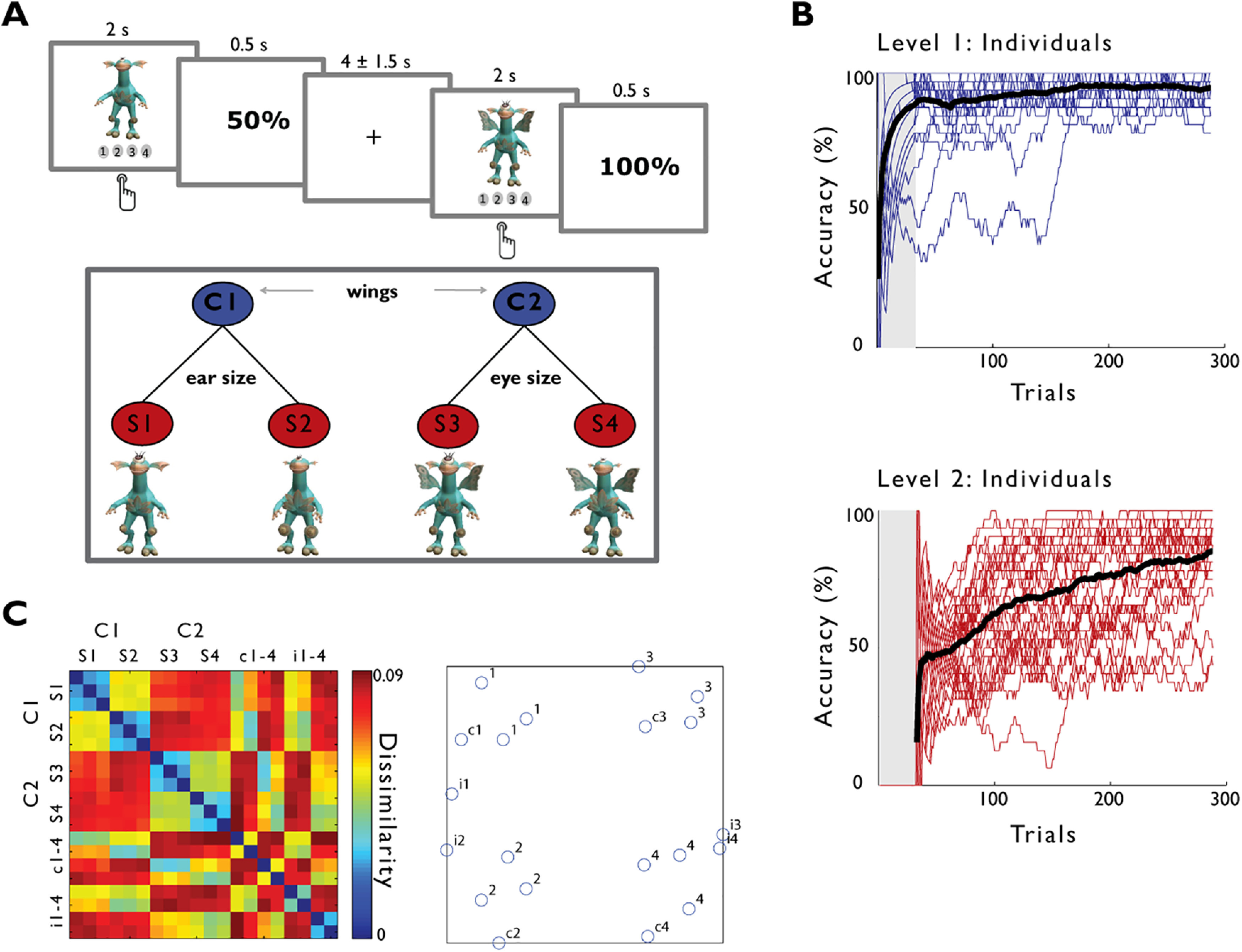
Hierarchical concept learning task and behavior. A, Stimuli (artificial creatures) were presented with a jittered intertrial interval of 3.5 ± 1.5 s for 2 s during which participants had to select the correct subcategory out of four options. Subcategories were defined by a hierarchical rule: The value of a first feature (wings) determined which second feature (ears or eyes) became relevant to further subcategorization. Responses were followed by 0.5 s of feedback indicating up to which level in the conceptual hierarchy the stimulus was correctly categorized (100% = subordinate category, 50% = superordinate category, 0% = none). The task comprised 8 blocks of 32 different stimuli each. In an additional preceding practice block (B, shaded gray), stimuli had to be sorted into the two superordinate categories. B, Categorization performance on the superordinate (blue) and subordinate category level (red) of the hierarchy showing the percentage of correct trials for a moving average over 32 trials for individual participants (colored) and averaged across participants (black). C, Pairwise similarity judgments derived from a subsequent multidimensional sorting task in which the 20 stimuli (3 per subcategory + 8 probe stimuli) had to be arranged according to their relatedness in a circular arena. Stimuli from the same (sub) category were judged as more similar than stimuli from different (sub) categories (left). Multidimensional scaling of single subject data visualizes how congruent (c1–c4), but not incongruent probe stimuli (i1-i4) cluster with their respective category members (right).

MRI methods

All images were acquired using a 3T PrismaFit MR scanner equipped with a 32-channel head coil (Siemens). A 4D multiband sequence (84 slices, multislice mode, interleaved, voxel size 2 mm isotropic, TR = 1500 ms, TE = 28 ms, flip angle = 65 degrees, acceleration factor PE = 2, FOV = 210 mm) was used for functional image acquisition. In addition, a structural T1 sequence (MPRAGE, 1 mm isotropic, TE = 3.03 ms, TR = 2300 ms, flip angle = 8 degrees, FOV = 256 × 256 × 192 mm) was acquired. Separate magnitude and phase images were used to create a gradient field map to correct for distortions (multiband sequence with voxel size of 3.5 × 3.5 × 2.0 mm, TR = 1020 ms, TE = 10 ms, flip angle = 45 degrees). Preprocessing of functional images was performed with FSL 5.0.9 (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/). Motion correction, high pass filtering at 100 s, and distortion correction were applied to the functional datasets. Spatial smoothing was only performed before the univariate analysis, but not before being subjected to RSA. The FSL brain extraction toolbox was used to create a skull-stripped structural image. The structural scans were downsampled to 2 mm (matching the functional image resolution) and segmented into gray matter, white matter, and CSF. Mean intensity values at each time point were extracted for white matter and used as nuisance regressors in the GLM analyses. Structural images were registered to the MNI template. For the functional data, the preprocessed mean image was registered to the individual structural scan and the MNI template. The coregistration parameters of the mean functional image were applied to all functional volumes.

Quantification and statistical analysis

Model specification

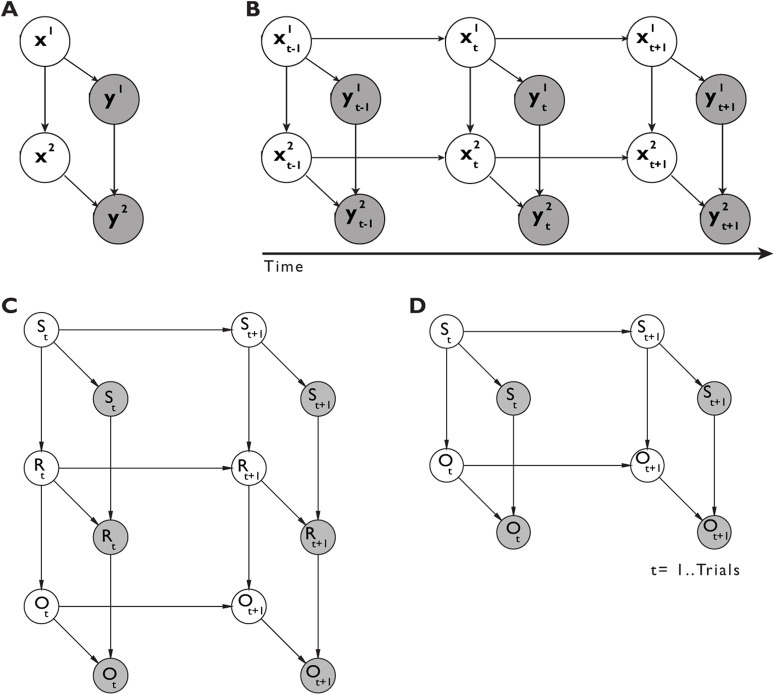
In order to estimate the relative contribution of the knowledge accumulated for each level of the hierarchical concept to categorization performance, we modeled the sequence of behavioral responses for each subject with a Dynamic Bayesian Network (DBN) model. DBNs are a class of probabilistic graphical models (Murphy, 2002; Bishop, 2006; Koller and Friedman, 2009) where complex causal dependencies between variables of interest, either latent or observed, can be expressed in the formalism of directed acyclic graphs. A DBN model is defined by a set of variables or nodes, a set of links or edges reflecting the causal dependencies among the variables, and the parameters describing the probability distributions governing each node given its parents. In the present study, we first defined a static Bayesian Network (BN) model that is a model for a single experimental trial with no dependencies across time. The BN is defined by the set of random variables Z = (X, Y), with X and Y representing latent and observed variables, respectively. The probability of being correct at any level of the hierarchy on a given trial was assumed to be dependent on two latent variables, x₁ and x₂, representing the contribution of either Level 1 or Level 2 knowledge, respectively. Each latent variable was also endowed with its own private observation node (y₁ and y₂), representing the correctness of subjects' responses at any level of the hierarchy. The coding of the behavioral responses (0%/50%/100%) over observation nodes (y₁ and y₂) followed the coding of the feedback provided during the task with 0% being incorrect on both levels (y₁, y₂ = [0, 0]), 50% being correct on only Level 1 (y₁, y₂ = [1, 0]) and 100% being correct on Levels 1 and 2 (y₁, y₂ = [1, 1]). Furthermore, to reflect the structure of the concept used in the task, we also assumed that the amount of information accumulated at Level 2, x₂, was causally dependent on the contribution of Level 1 knowledge, x₁ (Fig. 1A). All of the nodes were assumed to be discrete variables with two possible states [0, 1] and the conditional probability distributions (CPDs) over the nodes were defined by multinomial distributions expressed as tabular CPDs. Tabular CPDs, also called conditional probability tables, are multidimensional arrays particularly efficient for describing CPDs in networks with only discrete valued nodes. The CPD for any node Z_i of the graph given its parents, Pa(Z_i), is expressed by the following function:

$$P(Z_i|Pa(Z_i))$$

with the full joint distribution over all the nodes of the directed acyclic graph given by the following:

$$P\left(Z_1...Z_N\right)={\displaystyle \prod }_{i=1}^{N}P(Z_i|Pa(Z_i))$$

Figure 1.

DBN model. A, Bayesian network for one single trial with hierarchical rule representation. B, DBN extension of the single-trial model (A) unrolled for three time slices. C, Graph structure of control models DBN_ERO and DBN_FRO. D, Graph structure of control models DBN_FO and DBN_CO. Empty nodes represent latent variables and shaded nodes observed variables. Links indicate statistical causal dependencies between variables, either across layers of the network or across time slices. The superscript index indicates the level of the hierarchical rule (e.g., x¹ = level 1).

Next, we extended the BN to a DBN to capture the evolution of causal dependencies among variables across time. This was done by “copying” the BN for each time step (or time slice) and then connecting the BN of different time slices. The term “dynamic” refers to the fact that we are modeling a dynamical system and not that the network structure changes over time. To fully specify a DBN, we only need to specify two temporal slices since the structure of the graph is assumed to stay constant over time slices; therefore, it is common practice to refer to a DBN as a two-slice Temporal Bayes Network. The two-slice Temporal Bayes Network is defined over the set of variables, Z_t = (X_t, Y_t) by means of a directed acyclic graph as follows:

$$P(Z_t|Z_{t-1})={\displaystyle \prod }_{i=1}^{N}P(Z_t^i|Pa(Z_t^i))$$

where $Z_t^i$ is the i'th node at time t, which could be an element of $X_t$, or $Y_t$ and $Pa(Z_t^i)$ are the parents of $Z_t^i$given the graph structure. The nodes in the first slice of a two-slice Temporal Bayes Network do not have any probability distribution associated with them, whereas for the following temporal slices each node has an associated CPD, which defines $P(Z_t^i|Pa(Z_t^i))$ for all t > 1. The parents of a node, $Pa(Z_t^i)$, can be part of either the same time slice or any of the previous time slices. Here we assumed a first-order Markov process over the latent nodes, meaning that $X_i$ was dependent only on the latent nodes of the immediately previous temporal slice (Fig. 1). The semantics of the DBN can be defined by “unrolling” the two-slice Temporal Bayes Network until we have as many time slices as the number of experimental trials with the resulting joint distribution being given by the following:

$$P\left(Z_{1:T}\right)={\displaystyle \prod }_{t=1}^T{\displaystyle \prod }_{i=1}^{N}P(Z_t^i|Pa(Z_t^i))$$

Model selection

In order to test the adequacy of the hierarchical DBN model (DBN_H) as the most parsimonious description of the behavioral data, we fitted four additional competing DBN models with different levels of complexity and assumptions regarding the learning mechanism to the same data. In addition to the hierarchical DBN_H model, we tested the following competing models with increasing degree of generalization: A DBN with mappings between single stimuli (32 exemplars), response (buttons 1-4), and outcome (feedback 0%, 50%, 100%) variables (DBN_ERO), a DBN with mappings between all combinations of the critical features (8 combinations), response, and outcome variables (DBN_FRO), a DBN with mappings between all combinations of the critical features (8 combinations) and outcome variables (DBN_FO), and a DBN with mappings between subcategory (four categories) and outcome variables (DBN_CO). DBN_ERO assumes that participants do not generalize over experiences and simply learn the correct response to each of the 32 unique stimuli. The DBN_FRO and DBN_FO assume that participants do generalize over experiences that features of the stimuli are critical to categorization, but do not make use of the dependent rule which makes the concept hierarchical. This 'flat' learning strategy would entail representing all eight possible combinations of the relevant features. The inclusion relative to the exclusion of a response node in DBN_FRO versus DBN_FO does not reflect a different learning mechanism per se, but resulted from stepwise reduction of model complexity. The DBN_CO instead assumes that participants do use the hierarchical rule and thus need to represent only the four relevant combinations of features. DBN_H additionally collapses over the specific categories and incorporates only two nodes, one per level of the hierarchy, representing generalization of the rule over categories. For each model and for each subject, the relative Bayesian information criterion (BIC) was calculated to provide a quantitative measure of how well the model accounts for the data while penalizing for the number of free parameters to be estimated. For each participant, we first rank-ordered the BIC score of each model from the best (lowest BIC) to the worst (highest BIC). Next, we averaged the ranks for each model across participants. Model comparison was conducted by selecting the model with the lowest rank as the most parsimonious account of the data. BIC scores, ranks, likelihoods, and number of free parameters for all five DBN models are reported in Table 1. In a Bayesian statistical framework, overly complex models are already penalized at the level of marginal log-likelihood estimation when the a priori component decreases the posterior predictive power (Wagenmakers et al., 2008).

Table 1.

Model statistics for the five DBN models^a

Model	LL	d′	BIC	Rank	Z
DBNERO	−1599	1535	3690	5	Stimulus exemplar (32) – Response (4) – Outcome (3)
DBNFRO	−1146	215	512	4	Stimulus feature combinations (8) – Response (4) - Outcome (3)
DBNFO	−905	127	295	3	Stimulus feature combinations (8) – Outcome (3)
DBNCO	−975	47	107	2	Stimulus categories (4) – Outcome (3)
DBNH	−272	15	31	1	Knowledge leve1 (2) – Knowledge level2 (2)

^aLL, Maximum log-likelihood; d′, number of free parameters; BIC: average score; Rank: average rank of BIC score; Z, random variables of interest with number of states (in parentheses).

Model inference

Exact inference at the single-subject level on the model parameters was conducted in two steps by first updating the model with available evidence and then calculating the posterior model parameters (after having seen the data). In the first step, the probability distributions of the DBN models for each participant were updated with evidence (time-series of the behavioral responses for one subject) yielding subject-level posterior probability distributions. This step was accomplished using a two-pass message-passing scheme implemented in the junction tree algorithm (Murphy, 2002). Next, we extracted parameters reflecting accumulation and updating of hierarchical knowledge for the subsequent fMRI analyses. To this end, we extracted the unique contribution of Level 2 knowledge (Level 2, node x2) on behavior, by summing out the contribution of Level 1 knowledge (Level 1, node x1) from the joint probability distribution of Levels 1 and 2 as follows:

$$P\left(X_2\right)={\displaystyle \sum }_{i}P(X_2,Pa{(X_2)}_i)$$

and by calculating the posterior estimates for the Level 2 node (accumulation). From the posterior estimates, we further computed the first derivative in time, $\frac{d{x}_i}{dt}$, which can be interpreted as a measure of the instantaneous change of accumulated evidence, that is, how much updating is needed for the variable after having seen the evidence (updating). The model-based analysis was conducted in MATLAB using customized scripts for the Bayes Net Toolbox (Murphy, 2001).

fMRI statistical analysis

All first-level and whole-brain group-level analyses (Table 2) were performed using FSL 5.0.9 (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/).

Table 2.

Whole-brain results of accumulation and updating analyses (cluster-based threshold z = 2.3, p = 0.5)^a

Cluster index	Voxels	p	Z-max	Z-max x (mm)	Z-max y (mm)	Z-max z (mm)	Region
Univariate: Accumulation > baseline
12	6797	0	5.47	−24	−94	−10	Occipital pole
11	1440	4.93E-24	4.3	48	−10	58	Precentral gyrus
10	697	4.95E-14	4.41	−54	−6	42	Precentral gyrus
9	472	2.36E-10	4.03	−48	−44	10	Supramarginal gyrus
8	209	3.70E-05	3.51	−16	−32	78	Postcentral gyrus
7	200	5.98E-05	3.85	−62	−8	−8	Middle temporal gyrus
6	188	0.000115	3.81	22	10	−10	Frontal orbital cortex
5	159	0.000587	3.84	−2	−2	64	Supplementary motor cortex
4	152	0.000883	4.04	62	−4	−10	Superior temporal gyrus
3	119	0.00663	3.73	−18	8	−10	Putamen
2	112	0.0104	3.43	−2	42	−16	Frontal medial cortex
1	110	0.0118	3.44	52	−28	22	Parietal operculum
Univariate: Accumulation < baseline
12	3501	4.20E-45	4.51	32	60	20	Frontal pole
11	2160	3.97E-32	4.39	−50	−68	−26	Cerebellum
10	2123	9.78E-32	5.47	2	28	42	Paracingulate, superior frontal gyrus
9	1625	3.20E-26	4.24	−44	36	24	Middle frontal gyrus
8	1415	9.90E-24	4.26	38	−54	44	Angular gyrus
7	809	1.04E-15	4.49	48	20	6	Inferior frontal gyrus
6	794	1.72E-15	4.47	−6	−68	50	Precuneus
5	606	1.34E-12	3.81	−28	−56	40	Superior parietal lobule
4	544	1.39E-11	4.56	−42	16	0	Frontal operculum
3	441	8.36E-10	4.05	8	−14	10	Thalamus right
2	327	1.19E-07	3.81	62	−38	−16	Inferior temporal gyrus
1	198	6.66E-05	3.81	38	−64	−50	Lateral occipital cortex
Univariate: Updating > baseline
5	230	2.56E-06	3.4	−46	−60	52	Lateral occipital cortex
4	201	1.36E-05	3.42	56	−48	46	Angular gyrus
3	88	0.0245	3.61	0	16	52	Superior frontal gyrus
2	86	0.0285	3.27	38	40	30	Frontal pole
1	80	0.0454	3.32	−32	−54	50	Superior parietal lobule
Univariate: Updating < baseline
1	605	6.15E-14	4.25	0	56	−6	Frontal medial cortex, paracingulate
2	115	0.00336	3.93	−10	−56	14	Precuneus
PPI, Accumulation (seed: mPFC)
4	180	9.70E-05	3.37	−16	−52	10	Precuneus
3	130	0.00207	3.55	18	−68	12	Intracalcarine/precuneus
2	124	0.00305	3.66	−22	26	44	Middle frontal gyrus/superior frontal gyrus
1	108	0.00894	4.07	−14	56	26	Frontal pole
PPI, Updating (seed: mPFC)
2	166	6.32E-05	3.55	−30	52	22	Frontal pole
1	100	0.00665	3.35	2	40	26	Paracingulate gyrus
PPI, Updating (seed: HPC)
1	126	0.000852	3.54	−44	34	20	Middle frontal gyrus, extending to frontal pole

^aClusters activated, their voxels, p values, and peaks. Local maxima labels are based on the Harvard-Oxford Atlas. The coordinates are in standard MNI space.

Model-informed univariate analysis: accumulation and updating

To examine the roles of hippocampus, mPFC, and rlPFC in computations underlying hierarchical concept learning, we estimated knowledge accumulation and updating from behavior using the DBN_H model and regressed each subject's individual parameters against brain activity in these regions. For this purpose, we set up a GLM with one regressor modeling the feedback period and a second regressor of interest weighted parametrically by the respective model parameters. Additionally, stimulus presentation, trial type, and button presses were added as regressors of no interest together with six motion parameters and the time course in white matter as covariates. In the GLM with the updating values as regressor of interest, accumulation was additionally included as a regressor of no interest to identify updating-specific activity beyond accumulation. Resulting β maps were transformed to MNI space to extract the average β value of each ROI (hippocampus, frontal medial cortex, and frontal pole masks from Harvard-Oxford Atlas) for subsequent analysis. First-level β estimates of the parametric regressor were averaged across all voxels within an ROI for each participant, and the distribution of these values was tested for significance (at α = 5%) using two-sided permutation t tests (n permutations = 1000) (Groppe, 2010; corrected for multiple comparisons: tmax method, Blair and Karniski, 1993).

Control analysis: model contrast

In a post hoc analysis, we further probe whether activity in the regions, revealed by the analysis above, is also significantly better tracked by estimates derived from DBN_H compared with estimates derived from a stimulus-response-outcome model (DBN_ERO, Table 1) that assumes a mapping between each stimulus exemplar and respective response without making use of generalization over exemplars of which features (combinations) are relevant. The DBN_ERO incorporates a stimulus node, which can take 32 values (for 32 exemplars); a response node, which can take 4 values (four buttons); and an outcome node with three values of feedback (0%, 50%, and 100%). Accumulation of subcategory knowledge would in this model be reflected in the parameter estimates for the outcome node (state 100% correct). To this end, we included accumulation and updating of subcategory knowledge as estimated by the DBN_ERO model as regressors in addition to accumulation and updating as estimated by the DBN_H model in otherwise identical GLMs and took the respective contrasts (accumulation_H vs accumulation_ERO; updating_H vs upadting_ERO) to significance testing (one-sided, mc-corrected).

RSA

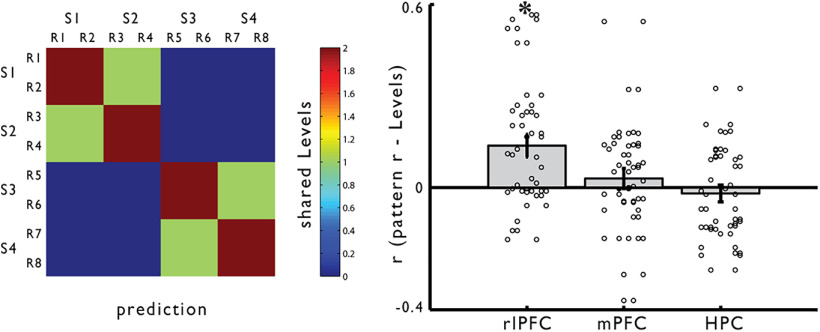
We quantified the emergence of hierarchical concept representations in the final stages of the learning phase (i.e., when both levels of the concept had been learned) in hippocampus, mPFC, and lateral PFC via RSA (Kriegeskorte and Kievit, 2013). The late learning stage was defined as blocks 7-9 (counting the practice block as block 1) to achieve a compromise between distance to the average Level 2 learning trial (within block 4) and sufficient stimulus repetitions. We did not set up stimulus-specific regressors because of the small number of repetitions per stimulus (n = 3) in the late learning stage. Instead, to achieve a sufficient number of trials per regressor as well as the minimal number of regressors necessary to probe a hierarchical representation, we set up a GLM with two stimulus presentation regressors per subcategory (R1-R8; see Fig. 4). Stimuli of each subcategory were alternatingly assigned to one of the two respective regressors (i.e., every other subcategory 1 stimulus presentation contributed to R1, the rest to R2; every other subcategory 2 stimulus presentation contributed to R3, the rest to R4, etc.). As this assignment was based on participant-specific presentation sequences, different stimuli contributed to these eight regressors across participants, diminishing effects of visual similarity. The GLM included eight stimulus regressors for the late learning stage and eight stimulus regressors for the remaining phase, regressors for the different feedback scores, trial type, and button press, as well as six motion parameters and signal change in white matter as covariates. For every ROI, the multivoxel activation pattern of first-level β estimates of each late learning stimulus regressor was correlated with the multivoxel activation patterns of all other late learning stimulus regressors, yielding an 8 × 8 neural pattern similarity matrix per ROI. Pattern similarity matrices were correlated (Spearman) with a prediction matrix that indicated the number of shared levels between stimulus pairs in the category tree (0, 1, or 2; see Fig. 4). That is, pattern similarity was expected to be lowest for stimuli in different categories, higher for stimuli in the same superordinate category, and highest for stimuli in the same subordinate category. The distribution of correlation coefficients was tested for significance (α = 5%) across participants for each ROI using two-sided one-sample permutation t test (Groppe, 2010; MC correction: tmax method, Blair and Karniski, 1993).

Figure 4.

Hierarchical concept representations in lateral PFC after learning. Right, Correlations between hierarchical prediction matrix (left), indicating the number of shared levels (0 = blue, 1 = green, 2 = red) between stimuli modeled via eight “late-learning” regressors (R1-R8: two regressors per subcategory S1-S4) and neural pattern similarity in rlPFC, mPFC, and hippocampus. Bars represent the mean across participants. Error bars indicate SEM. Circles represent individual participants. *p < 0.05 (mc-corrected).

RSA: perceptual similarity control analysis

To ensure that the hierarchical representation reflects conceptual similarity beyond perceptual similarity, we correlated neural similarity matrices with a hierarchical prediction matrix that was baseline-corrected by pixel similarity across stimuli. Therefore, we created an 8 × 8 matrix reflecting pixel similarity across stimuli for every participant (as the assignment of stimuli to the 8 regressors was based on the individual presentation sequence). First, we vectorized the R, G, and B values of all pixels per image. Next, we averaged the pixel-intensity vectors of each image across all images that were included in the same regressor. Finally, we correlated each of the eight pixel-intensity vectors with all other pixel-intensity vectors, resulting in subject-specific 8 × 8 pixel similarity prediction matrices. We subtracted each subject's pixel similarity prediction matrix from the hierarchical prediction matrix to obtain baseline-corrected hierarchical prediction matrices, which we correlated with the neural pattern similarity matrices. Resulting correlation values were tested for significance via one-sample permutation t tests (Groppe, 2010; MC correction: tmax method, Blair and Karniski, 1993). A sanity check of the pixel similarity matrix as a measure of perceptual similarity was given by its significant correlation with neural pattern similarity in visual cortex (occipital pole: t₍₂₈₎ = 6.142, p < 0.0001). (An additional control for visual similarity at the group level could have been achieved by counterbalancing the relevant features across participants.)

RSA: time of learning control analysis

To further ensure that the hierarchical representation reflects acquired knowledge and is hence specifically present at the end of learning, we applied the same analysis we ran for the late phase of learning to the early phase of learning. The early learning phase was modeled as the first three blocks of subcategorization to be of equal length as the late learning phase regressors (blocks 7-9). Corresponding to the analysis of late learning phase representations, we set up a GLM with 8 stimulus regressors for the early phase of interest and 8 stimulus regressors for the remaining phase. All further analyses steps were identical to the late-learning RSA.

Model-informed psychophysiological interaction (PPI) analysis: accumulation and updating

In a final step, we evaluated learning-dependent connectivity of hippocampal and prefrontal regions in separate PPI analyses using the model estimates for accumulation (for mPFC) and updating (for mPFC and hippocampus) as the respective psychological variable. GLMs included the time course of the seed region, model estimates of the learning parameter (accumulation or updating), and the interaction term between the two (PPI regressor), along with the remaining regressors used in the respective GLMs of the univariate analyses described above. Finally, the PPI regressor was contrasted against baseline to reveal the regions that show learning-dependent connectivity with the seed. Resulting β estimates for the PPI regressor were subjected to group-level analysis, where we used cluster-based thresholding (z threshold = 2.3, p = 0.05) to control for multiple comparisons.

Results

Performance in a hierarchical concept learning task

Participants were trained on a hierarchical categorization task with the intention to capture computations during concept learning as well as the emergence of concept representations in the final stages of learning. Participants learned to categorize 32 different creatures into four subordinate categories emerging from two superordinate categories according to a hierarchical rule: The value of a first binary feature (wings) defined a creature's superordinate category and which second binary feature (ear size or eye size) is relevant for further subcategorization within the superordinate category. Thus, the subordinate category was not determined by the secondary feature alone, that is, superordinate and subordinate category level followed a hierarchical organization (Fig. 2). In each trial, participants selected the subordinate category by pressing one of four buttons and received feedback that indicated up to which level in the hierarchy their categorization was correct. The time of learning Level 1 (superordinate category) and Level 2 (subordinate category) of the hierarchical categorization rule was each defined as the trial in which a participant's performance exceeded the respective chance level for all remaining trials at a confidence level of 95%. The Level 1 of the categorization rule was acquired early by all participants (Trial 8.53 ± 26.37), while there was high intersubject variability in the subsequent acquisition of the hierarchical Level 2 rule (Trial 140.63 ± 95.99) (Fig. 2B). A final debriefing questionnaire confirmed explicit knowledge of the Level 1 rule in all participants, and of the Level 2 rule in all but 3 participants. In a multidimensional sorting task subsequent to the scanning session, 20 stimuli had to be arranged according to their relatedness (three exemplars of each category and 8 novel incomplete probe stimuli, of which four were categorizable, while four could not be categorized because of critical features missing). Stimuli from the same category were judged as more similar than stimuli from different categories (category: t₍₃₀₎ = −17.87, p = 0.001; subcategory: t₍₃₀₎ = −22.16, p < 0.001). Multidimensional scaling (example participant, Fig. 2C, right) visualizes how categorization-rule congruent probe stimuli clustered with their respective category members, confirming the ability to transfer the concept to novel information. This transfer effect was significant on the group level when comparing the dissimilarity of novel probe items to their respective category members against their dissimilarity to noncategory members (t₍₃₀₎ = −15.45, p < 0.001).

Computations underlying hierarchical concept learning

In order to estimate the relative contribution of specific knowledge accumulated for each level of the hierarchical concept to categorization performance, we modeled the sequence of behavioral responses for each subject with a DBN model (Bishop, 2006; Koller and Friedman, 2009). To first test whether the present concept was indeed learned in a hierarchical fashion, we compared the ability of five different DBNs, differing in their assumption on the underlying learning mechanisms (i.e., the degree of generalization), to account for the data at the single-subject level using the BIC (Table 1; for model description, see Materials and Methods). In brief, a first model (DBN_ERO) assumes simple stimulus-response mapping (associations between each of the 32 exemplars to their respective subcategory) without any generalization. The second and third model (DBN_FRO and DBN_FO) assume that participants do generalize over experiences which features are relevant to categorization but do not make use of the dependent rule connecting both levels (e.g., only if a creature has wings, the size of the eye is relevant), which makes the concept hierarchical. The fourth model (DBN_CO) instead assumes that participants use the hierarchical rule and thus need to represent only the four relevant combinations of features, one per subcategory. A final hierarchical model DBN_H further collapses over the specific categories and incorporates only the two levels of the hierarchy, representing generalization of the rule over categories. We find that both hierarchical models (DBN_CO, DBN_H) outperform the other models as assessed by the BIC score, while DBN_H provided the most parsimonious description of behavior (Table 1) in all participants (i.e., DBN_H was on rank 1 for all 32 participants).

Accumulation and updating of hierarchical concepts in hippocampus and PFC

We set out to test whether hippocampal and prefrontal activity during learning reflects hierarchical concept learning as estimated by the winning model DBN_H. For each trial, the model computes the probabilities of using Level 1 (superordinate category) and Level 2 (subordinate category) knowledge to produce a response. We extracted the impact of Level 2 knowledge on behavior by summing out the contribution of the Level 1 node from the joint probability distribution. The resulting posterior estimates for the Level 2 node thus reflect the unique accumulation of hierarchical knowledge over the course of learning. In addition, the first derivative of the accumulation parameter reveals the instantaneous rate of change in Level 2 knowledge from trial to trial, which can be interpreted as updating current knowledge of the hierarchy. We regressed the accumulation and the updating parameters against brain activity in hippocampus, mPFC, and rlPFC. We find that mPFC activity increased as a function of accumulation of hierarchical knowledge (t₍₃₁₎ = 3.137, p = 0.005), while rlPFC activity decreased with accumulation (t₍₃₁₎ = −3.825, p = 0.001); the hippocampus did not track accumulation (t₍₃₁₎ = 0.703, p = 0.822). Both mPFC (t₍₃₁₎ = −4.271, p = 0.0001) and hippocampus (t₍₃₁₎ = −2.756, p = 0.015) tracked updating from trial to trial by responding stronger to negative updating values (i.e., an error follows a correct response), while rlPFC did not track updating (t₍₃₁₎ = 0.237; p = 0.993) (Fig. 3B; for whole-brain results, see Table 2). We further show that mPFC, hippocampus, and rlPFC signals are also significantly better explained by learning parameters derived from the hierarchical model compared with learning parameters from a nonhierarchical control model DBN_ERO (accumulation_H vs accumulation_ERO: mPFC: t₍₃₁₎ = 2.707, p = 0.0045; rlPFC: t₍₃₁₎ = −3.478, p = 0.001; updating_H vs upadting_ERO: mPFC: t₍₃₁₎ = −2.397, p = 0.0150; HPC: t₍₃₁₎ = −2.099, p = 0.033).

Figure 3.

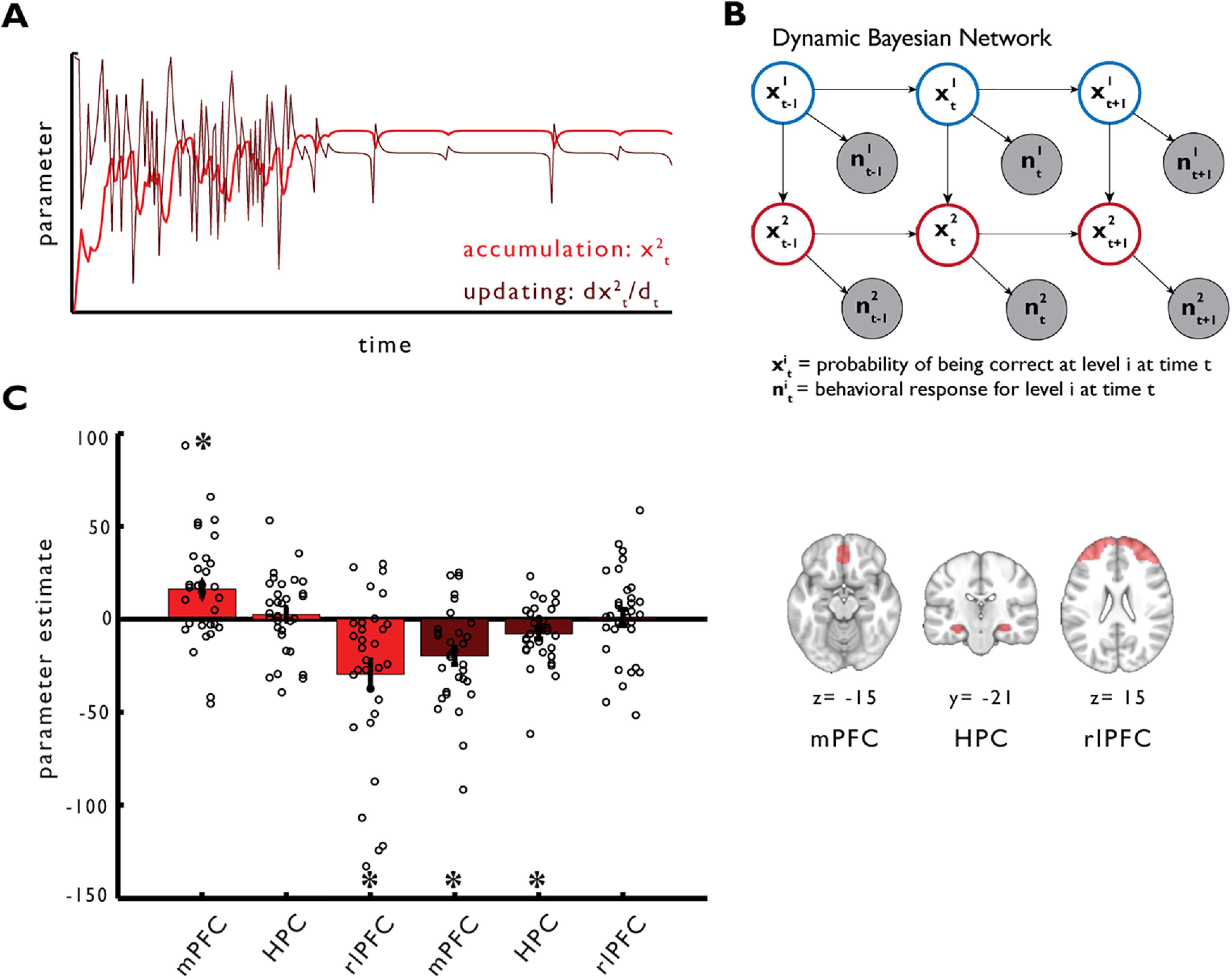
Computations underlying hierarchy formation. A, Level-specific accumulation of knowledge over trials and updating was estimated from behavior using a Bayesian Network with a hierarchical rule representation (DBN_H). Parameter estimates for accumulation (light red) and updating (first derivative of accumulation parameter, dark red) of an example subject. Negative updating values reflect that an error follows correct responses; positive updating values reflect the reverse. B, The DBN_H model unrolled for three time slices. Empty nodes represent latent variables. Shaded nodes represent observed variables. Links indicate statistical causal dependencies between variables, either across layers (incorporating the constraint that correct categorization at the subordinate level depends on correct categorization at the superordinate level) or across time slices. The superscript index indicates the level of the hierarchical rule (e.g., x¹ = Level 1). C, Regression of individual knowledge accumulation and updating parameters against brain activity in mPFC, hippocampus, and rlPFC (see ROI masks on the right). Bars represent mean of β estimates across participants. Error bars indicate SEM. Circles represent individual participants. *p < 0.05 (mc-corrected).

Hierarchical concept representations emerge in rlPFC

So far, we investigated how the brain acquires new conceptual knowledge at a hierarchical level. But where is the acquired concept represented? Does the neural representation of the concept follow a hierarchical tree-like structure that comprises, but distinguishes between, both levels of abstraction to eventually enable the flexible use of knowledge? We probed the emergence of concept representations in hippocampus and PFC in the final stages of the learning phase when both levels of the concept had been learned by participants, using RSA (Kriegeskorte and Kievit, 2013). We set up a GLM, including two stimulus regressors per subordinate category for the final learning stage. For each ROI, we correlated the multivoxel activation pattern of each stimulus regressor with the multivoxel activation patterns of all other stimulus regressors. To probe whether neural pattern similarity between stimuli scaled with their distance in the category tree, neural similarity matrices were correlated with a hierarchical prediction matrix that indicated the number of shared levels (0 = different category, 1 = same category, or 2 = same subcategory) (Fig. 4). We find that this hierarchical prediction significantly correlates with neural pattern similarity in rlPFC (t₍₂₈₎ = 3.666, p = 0.001), but not in medial PFC (t₍₂₈₎ = 0.889, p = 0.722) nor in the hippocampus (t₍₂₈₎ = −0.676, p = 0.873). To confirm that this representation reflects learned conceptual information beyond perceptual similarity of the stimuli, we further show that the representation persists when baseline-correcting for pixel similarity across stimuli (rlPFC: t₍₂₈₎ = 4.357, p = 0.0001; mPFC: t₍₂₈₎ = 1.326; p = 0.410; HPC: t₍₂₈₎ = −0.571; p = 0.891). In addition, we show that the representation was not present in the early stage of learning in any region (rlPFC: t₍₂₈₎ = 2.288, p = 0.081; mPFC: t₍₂₈₎ = 0.558, p = 0.917; HPC: t₍₂₈₎ = −1.217, p = 0.518).

Learning-dependent connectivity of mPFC and hippocampus to rlPFC

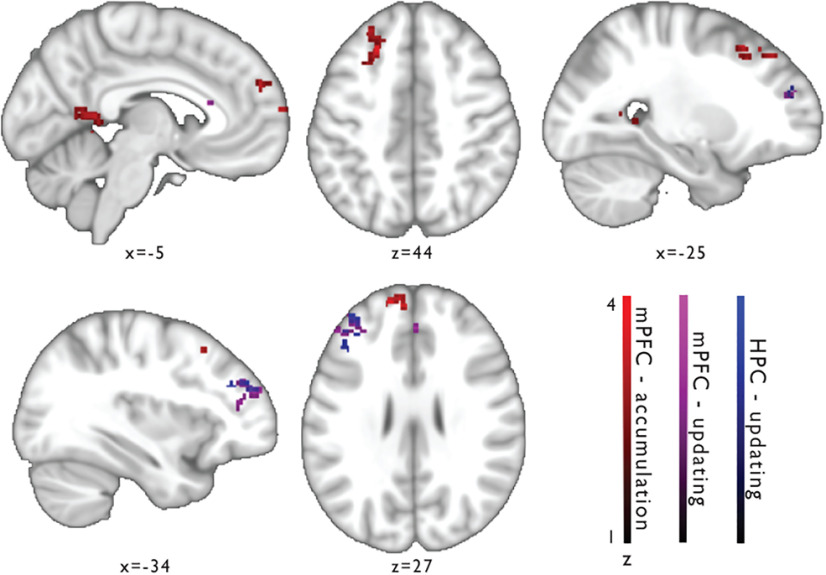
We observed that the hippocampus and mPFC support learning computations, while the acquired hierarchical concept structure was finally represented in rlPFC. Also rlPFC responses scaled with accumulation of hierarchical knowledge, yet this relation was reverse in sign compared with the mPFC accumulation signal. While mPFC activation increased with accumulation of hierarchical knowledge, rlPFC activation decreased. This negative relation with accumulation is congruent with finding the concept representation being formed in rlPFC, given that the demand to incorporate information in the concept representation decreases with increasing knowledge. One might ask whether accumulation and updating related activity in mPFC and hippocampus are associated with the emergence of concept representations in rlPFC. To probe whether the mPFC and hippocampus interact with rlPFC as a function of hierarchical learning, we examined their learning-dependent connectivity patterns in separate PPI analyses using the model estimates for accumulation (seed: mPFC) and updating (seeds: mPFC; hippocampus) as respective psychological variables. We find that mPFC shows foremost accumulation-dependent correlation of time-courses with clusters in lateral PFC, including the rlPFC (z = 4.07, MNI = −14/56/26) and middle frontal gyrus (peak z = 3.66, MNI=−22/26/44), as well as the precuneus (z = 3.37, MNI = −16/−52/10) (Fig. 5, red; Table 2). Updating of hierarchical conceptual knowledge also modulated mPFC's connectivity to a cluster in rlPFC (z = 3.55, MNI = −30/52/22), and furthermore to paracingulate gyrus (spreading to anterior cingulate gyrus; z = 3.35, MNI: 2/40/26) (Fig. 5, violet; Table 2). Moreover, the PPI analysis with the hippocampal seed revealed updating-dependent connectivity to a cluster of rlPFC (z = 3.18, MNI = −34/47/24) and middle frontal gyrus voxels (z = 3.54, MNI: −44/34/20) (Fig. 5, blue; Table 2), partly overlapping with the rlPFC cluster that showed updating-modulated connectivity to the mPFC seed (Fig. 5, violet).

Figure 5.

Connectivity changes in mPFC and hippocampus as a function of hierarchical concept learning. Significant clusters of whole-brain PPI analyses showing regions with accumulation-dependent connectivity to mPFC (red), updating-dependent connectivity to mPFC (violet), and updating-dependent connectivity to the hippocampus (blue). Plotted are the thresholded z maps (cluster threshold z = 2.3; p threshold: 0.05) of each PPI regressor.

Discussion

The present study elucidates the roles of hippocampus and PFC in both learning and representation of the hierarchical structure inherent to conceptual knowledge. Participants learned to categorize unfamiliar cartoon stimuli according to a tree-like category structure entailing a superordinate and a subordinate category level. Comparing fits of different computational models on the learning mechanism to categorization performance revealed that a hierarchical rule representation explained learning behavior best. The winning model allowed to extract each choice's probability of being correct based on knowledge at the hierarchical level beyond the superordinate level, resulting in measures of two learning computations, accumulation of hierarchical knowledge over time and trial-to-trial updating, to be regressed against brain activity. We found that mPFC activation scaled with the accumulation of hierarchical knowledge over time, whereas both mPFC and hippocampus signaled updating. Further, as a function of these learning computations, both regions changed their connectivity to lateral frontal regions, including the rlPFC, which in contrast to mPFC and hippocampus, represented the hierarchically nested category structure at the end of learning. In sum, our findings suggest that mPFC and hippocampus support the integration of accumulated evidence and instantaneous updates into hierarchical concept representations in rlPFC.

The present work significantly extends previous studies on the involvement of hippocampus, mPFC, and rlPFC in category learning (HPC and (v)mPFC: Mack et al., 2016, 2020; Bowman and Zeithamova, 2018; Bowman et al., 2020; HPC: Davis et al., 2012; Theves et al., 2019, 2020; rlPFC: Davis et al., 2017) by explicitly investigating their functions in the acquisition and the representation of the hierarchical structure inherent to conceptual knowledge. Specifically, the combination of a novel hierarchical categorization task and modeling approach first allowed to evaluate the learning mechanism of hierarchal concept acquisition, and to extract and quantify its hierarchical aspect for a targeted evaluation of related brain effects. Comparing models with different assumptions on the degree of generalization involved (from direct stimulus response mapping, to the abstraction of relevant features, up to the abstraction of features and relational rules) revealed that a high degree of generalization over experiences to abstract a hierarchical representation explains categorization performance best. This provides the first relevant insights on the learning mechanisms underlying such a task. Future accounts might further elaborate on this by modeling variations in aspects other than degree of generalization.

Importantly, the best fitting model allowed to extract and quantify the accumulation and updating of hierarchical category knowledge to inform our main research question regarding the roles of hippocampus and prefrontal regions in learning and representation of hierarchical levels within a concept. Indeed, previous reports in the literature led to diverse predictions on their respective contributions: In previous, non-hierarchical, categorization studies, hippocampus and vmPFC were shown sensitive to conceptual similarity as defined by feature overlap (Bowman and Zeithamova, 2018) or by distances in continuous feature space (Theves et al., 2019, 2020), leaving open the question whether this would transfer to the representation of conceptual similarity defined along dependent rules of a hierarchical structure. Hippocampus and PFC could have been considered suitable to represent different levels of abstraction within a concept given their specific coding properties (McKenzie et al., 2014; Bernadi et al., 2020). rlPFC might be specifically relevant, given that a hierarchical concept is defined by relational rules and its acquisition might thus engage more abstract reasoning processes associated with rlPFC (Christoff et al., 2001; Kroger et al., 2002; Watson and Chatterjee, 2012; Davis et al., 2017). In sum, our results suggest a division of labor between hippocampus and mPFC as opposed to rlPFC in operational aspects of learning versus representation of a hierarchical category structure, respectively.

Our paradigm first allowed to probe how actual hierarchical levels of a newly acquired concept are represented in key regions involved in concept learning. Specifically, 'hierarchical' refers to the property that superordinate and subordinate levels are connected via relational rules, such that subcategory-relevant features alone are not informative (while 'speed' distinguishes subcategories within the category 'cars' [racing car vs family van], speed is not relevant to subcategorization of 'animals' [mammals vs birds], although also animals vary in speed). We find that conceptual similarity between exemplars increasing from superordinate to subordinate categories is captured by graded neural similarity in the rlPFC. This fits well with the notion that rlPFC is critical to abstract relational processing (Christoff et al., 2001), that rlPFC was shown to track the representational distance between novel test and old training examples during relational compared with feature-based categorization (Davis et al., 2017), and has also been discussed as a potential storage site of relational concepts (Speed, 2010). As the present study focused on the acquisition phase, the endurance of the rlPFC representation over time remains to be investigated. Contrary to considerations in theoretical accounts on cognitive maps (Bellmund et al., 2018; Morton and Preston, 2021), we did not observe the respective representation in the hippocampus and mPFC.

The model-based analyses of learning-related activity revealed that mPFC and rlPFC track accumulation of hierarchical knowledge, while mPFC and hippocampus track updating. Interestingly, mPFC and rlPFC effects were reversed in sign. While mPFC activity increased as a function of hierarchical knowledge accumulation, rlPFC activity decreased. This pattern is in line with our finding of rlPFC forming the representation of the concept, given that the demand to incorporate information in the representation decreases with increasing knowledge. The positive relation between mPFC activity and accumulation might be interpreted in light of previous theories on context-dependent memory retrieval in mPFC (Preston and Eichenbaum, 2013): With increasing hierarchical knowledge, the Level 1 feature might increasingly set the context for retrieving the appropriate Level 2 rule. Alternatively, one might consider context (Level 1 feature)-dependent sampling of respectively relevant information in a given trial (Level 2 feature) (Braunlich and Love, 2021) to underlie the accumulation effect in mPFC. Contemporary cognitive models of concept learning (e.g., SUSTAIN, Love et al., 2004; ALCOVE, Kruschke, 1992) mostly operated by accentuating behaviorally relevant stimulus dimensions the same way for every stimulus and would as such have been unable to account for learning problems, such as the present. Indeed, the assumption of dimension-wide attention is challenged by a new model (SEA; Braunlich and Love, 2021), showing that dynamic and sequential allocation of attention within a trial for active sampling of context-relevant information can likewise account for a range of classical category learning phenomena. Future work might explore the explanatory power of this active sampling model for PFC activation in hierarchical learning problems. Further, negative updating parameters in mPFC and hippocampus reflect their increased activity when an error follows a correct response (i.e., mismatch signal) and might serve to correct the current representation. Updating-related rapid signal changes in mPFC can be expected during a rule-based category learning task. Indeed, changing the used rule has been shown to be reflected in abrupt and sometimes transient activity changes of mPFC neurons in rats (Rich and Shapiro, 2009; Durstewitz et al., 2010) and in a predictive representation of decision-relevant stimulus features in human mPFC before the strategy shift (Schuck et al., 2015). More specifically, it has further been suggested that mPFC disadvantages processing of task-irrelevant information to focus on goal-relevant features (Mante et al., 2013; Mack et al., 2020). The hippocampal role in updating fits well with the notion that hippocampal codes are highly dynamic (Horner and Doeller, 2017) and involved in novelty detection (Knight, 1996; Kumaran and Maguire, 2007; Fenker et al., 2008). A study on memory-based prediction errors in the hippocampus during concept learning found model-based (Love et al., 2004) estimates of decisional uncertainty during categorization to correlate with anterior hippocampus engagement throughout learning (Davis et al., 2012), suggesting that the hippocampus does not merely signal novelty but rather indicates the deviation of the current experience from existing conceptual knowledge. Recent work further indicates that prediction errors bias the hippocampus toward encoding versus retrieval, as reflected in increased connectivity of CA1 to entorhinal cortex and decreased connectivity to CA3 (Bein et al., 2020).

While our PPI analysis was not sensitive to intrahippocampal connectivity changes, we were primarily interested in a potential communication between the regions involved in learning operations (mPFC, hippocampus) and regions representing the final hierarchical category structure (rlPFC). Here we observed both accumulation- and updating-dependent connectivity changes between mPFC and hippocampus to rlPFC. This might indicate that, during hierarchical concept learning, mPFC and hippocampus serve to incorporate accumulated evidence and trial-to-trial updates into lateral prefrontal representations of the hierarchical concept structure.

In conclusion, our study provides a first targeted fMRI investigation to study category learning with respect to the hierarchical nature of concepts (i.e., different abstract levels connected via dependent rules). Our modeling approach revealed insight in the learning mechanism by which humans acquire hierarchical concepts and informed fMRI analyses to evaluate the respective roles of candidate regions in learning computations versus representation of hierarchical concepts. As such, the study lays important ground for future investigations of this relevant aspect of human higher-level cognition.