Abstract
Vaccination remains a critical element in the eventual solution to the COVID-19 public health crisis. Many vaccines are already being mass produced and supplied in many countries. However, the COVID-19 vaccination programme will be the biggest in history. Reaching herd immunity will require an unprecedented mass immunisation campaign that will take several months and millions of dollars.
Using different network models, COVID-19 pandemic dynamics of different countries can be recapitulated such as in Italy. Stochastic computational simulations highlight that peak epidemic sizes in a population strongly depend on the network structure. Assuming a vaccine efficacy of at least in a mass vaccination program, at least of a given population should be vaccinated to obtain herd immunity, independently of the network structure. If the vaccine efficacy reports lower levels of efficacy in practice, then the coverage of vaccination would be needed to be even higher. Simulations suggest that the “Ring of Vaccination” strategy, vaccinating susceptible contact and contact of contacts, would prevent new waves of COVID −19 meanwhile a high percent of the population is vaccinated.
Keywords: SARS-CoV-2, Networks, Vaccination, Epidemics, COVID-19, Mass vaccination, Ring of Vaccination
1. Introduction
The novel Coronavirus SARS-CoV-2 epidemic which first emerged from Wuhan, China in December 2019 has spread globally, causing high levels of mortality and morbidity worldwide. To curb the spread, governments across the world have implemented measures ranging from quarantining, social distancing, wearing of face masks among others. Amidst this crisis, national health care systems such as in Italy and the United States of America have been overwhelmed by the ever-increasing number of infection cases (Miller et al., 2020).
In studying infectious diseases, mathematical models play a significant role in estimating disease transmission parameters as well as the severity and intensity of an outbreak (Brauer et al., 2012). The development of these models is crucial in providing insights and making predictions about the disease so as to effectively plan mitigation strategies and policies (Scarpino and Petri, 2019, Colizza et al., 2007). For instance, during the Severe Acute Respiratory Syndrome (SARS) outbreak, mathematical models were used to forecast transmission risks of the disease as well as to develop relevant vaccination strategies (Chretien et al., 2015, Meyers et al., 2005, Colizza et al., 2007).
COVID-19 epidemiological models have been formulated to understand and curb the spread of the disease. Many of these models follow an SIR framework (Bailey et al., 1975, Kermack and McKendrick, 1927) either in the deterministic or stochastic form or both (Anderson et al., 2020a, Weitz et al., 2020, Sameni, 2020, Simha et al., 2020, Calafiore et al., 2020, Chatterjee et al., 2020). Other variations and modifications to this general model have been considered including SEIR (Kucharski et al., 2020, Peng et al., 2020, Ricardo-Azanza and Hernandez-Vargas, 2020) and SIRD (Fanelli and Piazza, 2020) compartmental models. Some models also include parameters such as age-heterogeneity (Singh and Adhikari, 2020), guiding the flow of users in supermarkets (Hernandez-Mejia and Hernandez-Vargas, 2020), and governmental policies (Lin et al., 2020, Arenas et al., 2020, Ricardo-Azanza and Hernandez-Vargas, 2020). In addition, a few studies incorporate the dynamics of the disease within an individual host (Hernandez-Vargas and Velasco-Hernandez, 2020, Almocera et al., 2020). However, only a few of these models, currently predicting the SARS-CoV-2 pandemic, consider the structure of the population and the underlying interactions between individuals (Firth et al., 2020, Zaplotnik et al., 2020, Herrmann and Schwartz, 2020).
The assumption of random homogeneous mixing in epidemiological models has been documented to be unrealistic as populations have underlying structural properties and individuals tend to interact with each other (Ferretti et al., 2012). Increasingly, network theory is being used in epidemiology (Meyers et al., 2005, Keeling and Eames, 2005, Rizzo et al., 2016, Getz et al., 2019). In particular, social networks have gained popularity in conceptualising the effects of social interaction during epidemics in a given population (Moinet et al., 2018, Kabir et al., 2019, Sharma et al., 2017). Contacts between individuals in a given population can be captured in a network where nodes represent individuals and the edges represent the connections between them (Hernandez-Vargas et al., 2019). Social networks are thus important determinants of infectious disease transmission, for example, infections transmitted by close contact can easily spread along the paths of a network.
Many studies in network theory have found that networks may display varying connectivity properties such as randomness and regularity. Some well-known network models include random networks, scale-free networks, and small-world networks. Random networks such as the Erdos–Renyi network, are characterised by a Poisson distribution of nodes whereby there is equal distribution of nodes. Such models do not have hubs and clustering effect is absent. However, scale-free networks such as the Barabási and Albert model, follow a power-law distribution and have an inhomogeneous degree distribution of nodes (Barabási, 2003) (that is, the number of connections a node has to other nodes). In small-world networks such as the Watts and Strogatz model, the pattern of connectivity between nodes is more localized (Watts and Strogatz, 1998) and the average path length is comparable with a homogeneous random network, without any regard to clustering.
During a disease outbreak, it is less likely for the disease to reach epidemic proportions in the power-law network than it is in random networks (Dezső and Barabási, 2002, Volz, 2008). This is because power-law networks are made up of vertices with few contacts and a very small proportion of hubs (or superspreaders) whereas vertices in random networks are fairly homogeneous. Thus, while it is possible to reach an epidemic in power law networks with a high enough transmissibility, a random network reaches an epidemic threshold only when the outbreak leads to an epidemic (Eguiluz and Klemm, 2002, Meyers et al., 2005).
Since the declaration of SARS-CoV-2 as a pandemic, initial control efforts have relied heavily on the use of non-pharmaceutical interventions (NPIs), including physical distancing, wearing of masks, and hand hygiene. In many countries across the globe, school closures and national lockdowns have been implemented as part of NPIs to mitigate infection (Flaxman et al., 2020, Viner et al., 2020, Lavezzo et al., 2020). However, with the continuation of SARS-CoV-2 in many parts of the world, the push for a vaccine has become highly necessary. Pharmaceutical companies are in a race to develop suitable vaccines as there is a lack of other alternatives. As of October 2020, there were 17 candidate vaccines undergoing trial at various stages. Because it is a novel viral disease, it is still unclear what levels of vaccine efficacies will be sufficient to curb the spread of the virus. Identifying such efficacies earlier can direct vaccine development and administration in the population (Hodgson et al., 2020). Previous studies suggest that vaccination would be effective for protecting the host against SARS-CoV-2 (Krammer, 2020), however, there have not been many studies to evaluate the potential effects of different vaccination programs over a network model.
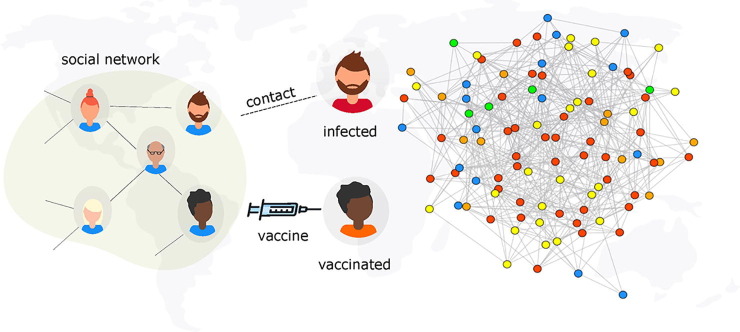
A key question to be answered is, how many vaccines are required to create herd immunity to dismantle SARS-CoV-2 transmission? (Anderson et al., 2020c). In other words, how many people need to be vaccinated to reach herd immunity? Here, we employ a network-based approach to explore the potentials of two vaccination schemes, classical mass vaccination and ring vaccination, in minimizing the spread of SARS-CoV-2, see Fig. 1 . Ring vaccination is a vaccination strategy in which infected cases and contacts of cases are identified and vaccinated (Greenhalgh, 1986, Müller et al., 2000). This strategy is especially efficient in controlling rare pathogens and has been successful in the eradication of Smallpox and the Ebola virus disease (Geddes, 2006, Foege et al., 1971, Wells et al., 2015).
Fig. 1.
Model scheme. An illustration of infection spread with vaccination on a social network. Individuals in the social network are considered as nodes and contact between nodes exposed to the virus and those who do not have the virus can potentially lead to a transmission. Persons who are vaccinated are considered to be immune to infection. The epidemic state of each node is represented by a colour: Susceptible, , ( ), Exposed, , (
), Exposed, , ( ), infectious, , (
), infectious, , ( ), Vaccinated, , (
), Vaccinated, , ( ) and Recovered, , (
) and Recovered, , ( ).
).
Our analysis uses different stochastic network simulation models of SARS-CoV-2 transmission to examine its control by mass and ring vaccination strategies with varying vaccine efficacies in the presence of non-pharmaceutical disease control interventions. Given that vaccinating millions of people will require a lot of time, this study implements a lockdown period as a further control measure during vaccination strategies in our simulations. It is important to note that the roll out of vaccines can play an increasing role in reducing the number of infections – thereby causing governments to ease lockdown measures. However, in order to keep our model mathematically tractable, we assume that social contacts follow lockdown-period patterns throughout the vaccination campaign. The main objective here is to identify the necessary vaccine efficacy thresholds capable of preventing an epidemic under such conditions.
2. Modelling epidemic spread on networks
2.1. Model setup
Network Generation. To study the impact of vaccination on the epidemic dynamics of SARS-CoV-2, the underlying structure of human interactions is represented by a complex network. As heterogeneous networks are often used to explore epidemic spread, we consider the infection dynamics on a random Erdos-Renyi (ER) network and a scale-free Barabási-Albert (BA) network due to their tractability and practicability (Kepes, 2007, Barabási, 2003). The ER network is based on the random graph model characterized by two parameters; the network size n and the number of edges M which assigns exactly M edges to each graph. In the ER networks used for this study, , that is , which yields an average degree distribution . On the other hand, the BA network is created using consisting of N vertices and m outgoing edges for each vertex with a power constant p of the nonlinear model equal to one. For the simulations using the BA network, and which ensures a degree distribution of as in the ER network.
Epidemic Spread. SARS-CoV-2 is a disease which spreads primarily through close contact with an infected person. Following the exposure to the SARS-CoV-2 virus and before symptom onset, individuals go through an incubation period of about days with the average being about days (Liu et al., 2020a, Russell et al., 2020, Burke, 2020). After this incubation period, infectious individuals become symptomatic and can transmit to others through respiratory droplets or by direct contact (Liu et al., 2020a).
Epidemic States. We simulated a Susceptible – Asymptomatic – Infectious – Recovered – Vaccinated (SAIRV) process on an Erdos–Renyi and a Barabási-Albert network with nodes and in both networks. At any instant during the infection process, the status of a node can be in any one of five possible states: Susceptible (S, not infected but can be infected), Asymptomatic (A, infectious, may not show symptoms and can transmit to others), Infectious (I, infectious and symptomatic, capable of transmission to others), Recovered (R, recovered and immune to the disease) and Vaccinated (V, vaccinated). Therefore, at any time, t, in the infection process, .
Epidemic Process. The model (depicted in Algorithm 1) proceeds in discrete one-day time steps for a period of 360 days to determine the dynamics of the disease. Simulation codes can be found in https://github.com/systemsmedicine/COVID-19-Network-Model. At the initial state of the epidemic process, all individuals in the network are susceptible except one (patient zero) which is in the exposed state. On each day during the epidemic process, there is an interaction between individuals and infected persons can potentially transmit to their susceptible contacts. If a susceptible individual comes into contact with someone who has the virus (that is, a person in the A or I state), a Binomial trial is used to determine if the contact results in an infection. If yes, the newly infected susceptible individual moves from the S state to the A state. Any individual exposed to the disease remains in the A state for the duration of the incubation period. After the incubation period, infected nodes either move to the I state with a probability or to the R state with a probability . Infectious individuals can transmit to their neighbours, when they come into contact, in a Binomial trial with a given probability, and then move into the R state after the infectious period.
| Algorithm 1. Epidemic process on social network |
 |
In the course of an epidemic, the effective rate of infection is never constant. As interventions are being executed, the per-capita transmission rate of infection decreases, and when these interventions cease, this rate will increase towards its pre-intervention level. To model this response, we consider a double logistic function to model the various phases of the infection dynamics leading to a decline in cases when interventions are initiated and a resurgence in cases when interventions cease. The double logistic function used to define a time-dependent probability of infection, is as follows:
| (1) |
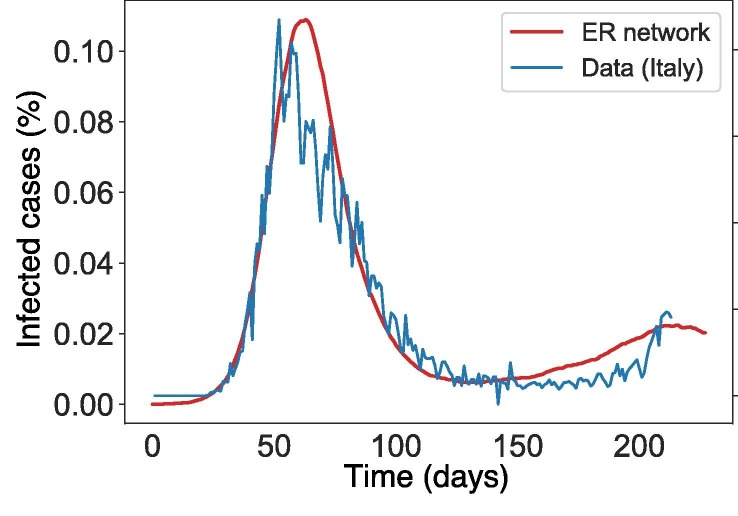
where is the first boundary (i.e. function value at time zero), is the second boundary, is the rate of change of first period, is rate of change of second period, is the midpoint of the first period (start of interventions), is the midpoint of the second period (end of interventions) and t is time. Note that if the function increases first and then decreases, and vice versa. To get a good set of parameters for , we applied Eq. (1) to emulate infection data (from February 22 to September 1 2020) from Italy, one of the worst hit countries during the first wave of SARS-CoV-2 pandemic (see Fig. 2 ).
Fig. 2.
Infection cases between the network model simulation using and Italian SARS-CoV-2 data from February 22 2020 to September 1 2020. The y-axis shows the infection cases. Parameter values used are .
The main goal of vaccination in this model is to prevent transmission. At the beginning of each epidemic simulation, a fraction of the population () is given a vaccine. Due to delayed immunity of the vaccine, these vaccinated individuals remain in the S state for a period of 14 days. Within this 14 day window, these individuals, which we denote as , are still prone to interaction with asymptomatic and infectious individuals which can lead to more infections with a probability . After 14 days, individuals in who do not have the virus, move to V state. Individuals in V that become exposed to the virus due to contact with an exposed individual move into the A state with probability , where is the efficacy of the vaccine. Individuals for whom the vaccine is effective remain in the V state whilst those for whom the vaccine is not effective move into the A state. Furthermore, depending on the vaccination strategy being modelled, the time of vaccination as well as population coverage varies.
For the first strategy which we refer to as the classical mass vaccination strategy, a fraction of individuals start in the V state (denoted ) with one index case (patient zero) and the rest in the S state. The population coverage in this case ranges from . The modelling process follows as in Algorithm 1.
For the second strategy which we refer to as ring vaccination, vaccination occurs after a percentage ( or ) of the population has been exposed to the virus during the epidemic. In this case, we simulate the epidemics as described above (in Algorithm 1) with no vaccination and only begin vaccine administration after a proportion of the population () has been exposed (see Algorithm 2 for more details). We assume that once a case is diagnosed, all the contacts or neighbours are traceable and vaccinated. To initiate the ring vaccination, susceptible contacts of exposed individuals can be vaccinated in a binomial trial with probability . This vaccination is further extended to susceptible contacts of these first contacts with the assumption that contacts are identified through contact tracing. Contacts of contacts are also vaccinated with the same probability. In our model, we also assume that traced and identified susceptible contacts and contacts of contacts are vaccinated. This process is described in Algorithm 2 and detailed implementation can be found at https://github.com/systemsmedicine/COVID-19-Network-Model.
In both strategies, we assume that the vaccine does not have an effect on infectious or asymptomatic individuals. Table 1 summarizes all parameters and key terms used in this study.
| Algorithm 2. Ring vaccination model on social network |
 |
Table 1.
Definition of key terms and parameters.
| Key term | Definition | Value |
|---|---|---|
| N | number of nodes in the network | |
| average degree distribution of nodes in the network | ||
| transmission probability | the probability that infection is spread due to contact between an infectious node and a susceptible node | Eq. (1) |
| incubation period | the interval between exposure to virus and initial occurrence of symptoms | days (Burke, 2020) |
| infection period | interval between symptom onset to recovery | days (Liu et al., 2020a) |
| vaccine efficacy | efficacy of vaccine | varies (Callaway and Mallapaty, 2021) |
| percentage of population vaccinated prior to infection (before case zero) | varies | |
| epidemic duration | 360 days | |
| percentage of population exposed to virus before onset of vaccination | varies | |
| symptomatic probability, | the probability that a person in the class moves to the class | 0.2 (Anderson et al., 2020b) |
Epidemic Process in Mathematical Form
The model depicted in Algorithm 1 proceeds in discrete one-day time steps for a period of 360 days to determine disease dynamics.
Each node has an individual state at time t. We initialize the model simulation by randomly assigning nodes to the infectious state (I), that is setting and the rest of the nodes to the susceptible state, for . We denote by the set of nodes with state at time t. Conditional on current state , the next state for node i is determined as follows.
-
•Susceptible nodes
(2) -
•Asymptomatic nodes
(3) -
•Infectious nodes
(4) -
•Recovered nodes
(5) -
•Vaccinated nodes
(6) (7)
2.2. Simulation scenarios
Several scenarios are explored here. First, we consider an epidemic implemented with no vaccination. This scenario is evident of the epidemic outcome without the discovery of a vaccine. Subsequent scenarios consist of the overall performance of the vaccine by considering its efficacy in preventing transmission and symptomatic infection using either the classical mass vaccination or the ring vaccination strategy. In our simulations, vaccine efficacy varied between whereas population coverage for classical vaccination varied between . For ring vaccination, the proportion of exposed individuals () varied as and (see Table 2 ). For ER simulations: = day 50, = day 126 and days. For BA simulations: = day 50, = day 126 and days. Each scenario is repeated 100 times and the mean of infection cases taken for analysis.
Table 2.
Vaccination scenarios with corresponding population coverages and vaccine efficacies considered in this study.
| Scenario | Coverage | Time of vaccination | Effect of vaccine () |
|---|---|---|---|
| No vaccination | – | – | |
| Mass vaccination | Before case zero | ||
| Ring vaccination | 1st order and identified contacts AND contacts of contacts | After percentage of population infectious (varies between ) |
2.3. High-performance computing
Implementations of this network model were computationally demanding and challenging using conventional resources. For instance, one simulation can take up to several hours or days to complete on a modern desktop computer. Thus, due to these limitations, we employed a High-Performance Computing (HPC) cluster for our simulations. The cluster used is FUCHS-CSC from the Center for Scientific Computing (CSC, Frankfurt, Germany). It is based on 72 dual-socket AMD Magny-Cours CPU compute nodes with 64 GB of RAM, 250 dual-socket AMD Istanbul compute nodes with 32 GB of RAM and 36 quad-socket AMD Magny-Cours compute nodes with 128 GB of RAM each. A simulation in the HPC takes about 5 h to complete for the classical vaccination scenarios and about days for the ring vaccination scenarios. This project is coded in Python and the codes can be found in this https://github.com/systemsmedicine/COVID-19-Network-Model.
3. Results
The parameter value of shows infection peaks at comparable time points with varying population percentages but essentially a qualitative fit of the data (see Fig. 2). The parameter values used to fit are: .
3.1. COVID-19 dynamics – control scenario
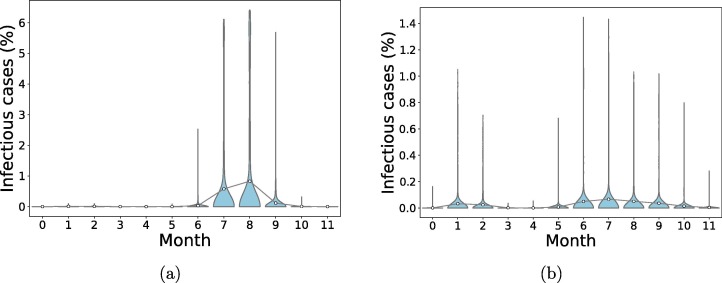
In a completely susceptible population, the introduction of one exposed individual leads to the spread of the infection with more than one peak of cases of infection after some months. In Fig. 3 , the mean number of infectious cases peaks at for ER network and for BA network.
Fig. 3.
Distribution of the final infectious cases in different timing for scenarios without vaccination in both networks. A population of N = 106 individuals was generated and 100 simulations were run to simulate the epidemic in the course of one year. An individual was chosen randomly as patient zero for each run. Circles represent mean infection cases for each month connected by lines. (a): Erdos–Renyi network, (b): Barabasi-Albert network.
3.2. Mass vaccination scenarios
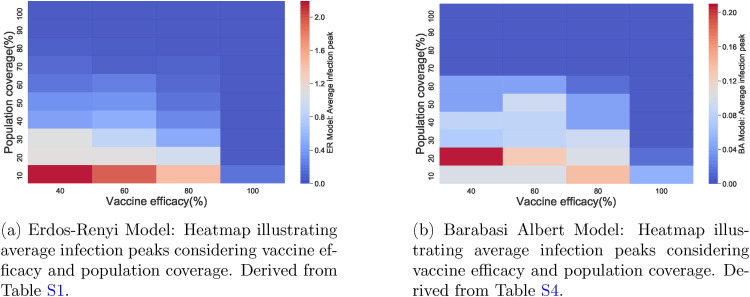
These scenarios determine the outcome of vaccination in both networks when Algorithm 1 is used. From Fig. 4 and Tables S1 and S4, we observe that generally, infection peaks are much lower in Barabasi-Albert network than in the Erdos–Renyi network.
Fig. 4.
Comparing infection peaks in both networks.
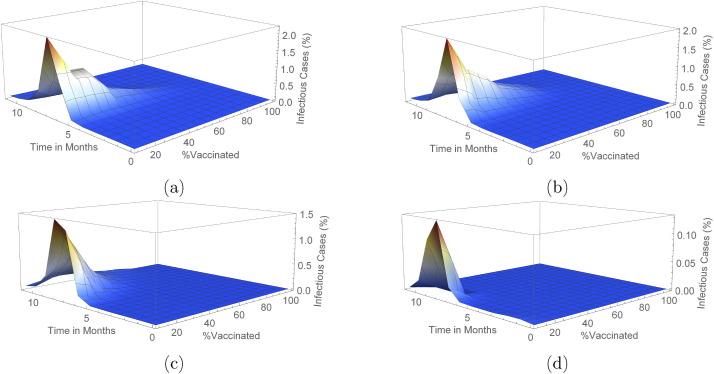
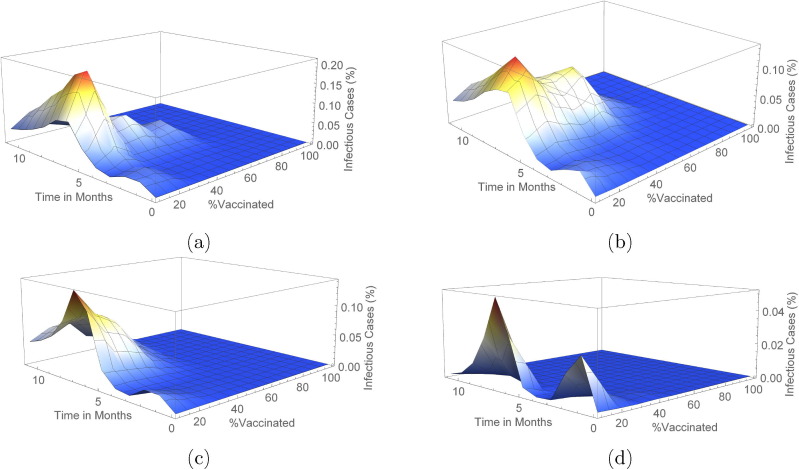
In the Erdos–Renyi network, when vaccine efficacy is , a population coverage of or more is needed to achieve infection peak with less than infection cases in the population. Table S1 (and also Fig. 4) reveals that with vaccine efficacy of , a coverage more than keeps mean infection cases on the low with elimination of the peak occurring when coverage is more than . Furthermore, low cases of infection are observed when or more of the population is vaccinated and vaccine efficacy is . On the other hand, a vaccine which is efficacious requires just or more of the population to be vaccinated to ensure there is no peak of infections.
In the Barabasi-Albert network, with a vaccine efficacy of , a population coverage of more than ensures elimination of infection peaks whereas when vaccine efficacy is , a coverage more than achieves elimination. In addition, when or more of the population is vaccinated with an efficacious vaccine, infection cases are almost negligible. In the case when a efficacious vaccine is administered, a population coverage more than keeps infection peaks at bay.
As seen in Fig. 5, Fig. 6 (see also Figs. S1–S4 and S7–S10 in Supplementary Material), peak(s) of infection cases are observed when a small percentage of the population is vaccinated in both networks with double infection peaks more frequent in the Barabasi-Albert network. For instance, in both networks, there is at least one peak of infection for vaccine coverage between and even when varies. Therefore, vaccinating a small proportion of the population is not useful in these instances as cases can still peak even with a vaccine with efficacy. Thus, the key to eliminating infection peaks is to administer very efficacious vaccines to many individuals.
Fig. 5.
Outcome for mass vaccination scenarios for each vaccine efficacy percentage on an Erdos–Renyi network. This shows the changes in mean infected cases over time under the different vaccine efficacies. In (a), (b), (c) and (d) vaccine efficacies are and respectively.
Fig. 6.
Outcome for mass vaccination scenarios for each vaccine efficacy percentage on a Barabasi Albert network. This shows the changes in mean infected cases over time under the different vaccine efficacies. In (a), (b), (c) and (d) vaccine efficacies are and respectively.
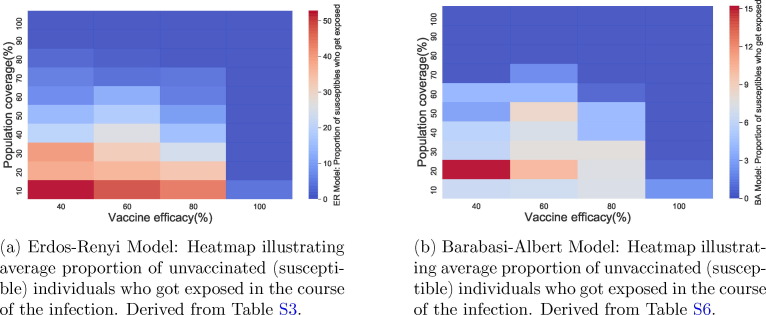
Furthermore, infection cases in vaccinated and unvaccinated individuals is much higher in the ER model than in the BA model (see Fig. 7, Fig. 8, Fig. 7, Fig. 8 b and Tables S6, S5, S3, S2). In both networks, a efficacious vaccine ensures that no susceptible (unvaccinated) individual gets exposed to the disease (Fig. 7). Similar results are observed in the proportion of vaccinated individuals who later become exposed (Fig. 8). For the ER network, the highest infection cases occur when vaccine efficacy is and only of the population is vaccinated. In the BA network however, this is seen at a vaccine efficacy of and population coverage.
Fig. 7.
Comparing average proportion of unvaccinated individuals who got exposed in the course of the infection in both networks.
Fig. 8.
Comparing average proportion of vaccinated individuals who got exposed in the course of the infection in both networks.
In the population of unvaccinated individuals for the ER network, higher cases of infection are observed with a vaccine efficacy of or less and population coverage less than (Fig. 7a). However, for the BA network, observed cases of infection are usually low in comparison with the ER network (Fig. 7b). In the population of vaccinated individuals for the ER network, higher cases of infection are observed with a vaccine efficacy of or less and population coverage less than (Fig. 8a). Again, for the BA network, observed cases of infection are usually low in comparison with the ER network (Fig. 8b).
3.3. Ring vaccination scenarios
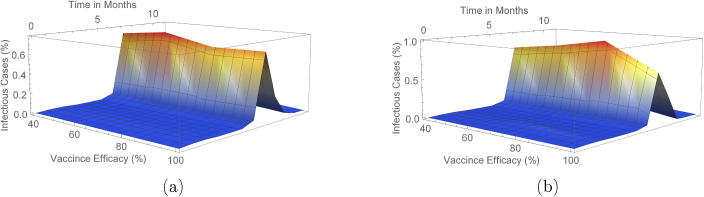
We carried out simulations using Algorithm 2 to determine the infection outcome when ring vaccination is used in both networks. In Fig. 9, Fig. 10 (see also Figs. S5, S6, S11, S12 and Table 3 ), we show these outcomes with varying scenarios of vaccine efficacy and when or of the population is already exposed to the disease before the onset of vaccination.
Fig. 9.
Outcome for ring vaccination scenarios for each vaccine efficacy percentage on a Erdos-Renyi network. This shows the changes in mean infected cases over time when there is and prior exposed population in (a) and (b) respectively.
Fig. 10.
Outcome for ring vaccination scenarios for each vaccine efficacy percentage on a Barabasi Albert network. This shows the changes in mean infected cases over time when there is and prior exposed population in (a) and (b) respectively.
Table 3.
Average population coverage (in ) for ring vaccination scenarios in both ER and BA networks considering vaccine efficacy.
| Vaccine Efficacy |
||||
|---|---|---|---|---|
| (ER Network) | ||||
| ( of population exposed before vaccination) | ||||
| ( of population exposed before vaccination) | ||||
| (BA Network) | ||||
| ( of population exposed before vaccination) | ||||
| ( of population exposed before vaccination) | ||||
We see that in both networks, there are less cases realised with a exposed population before the start of vaccination as compared to a exposed population. In addition, the number of infected cases in these scenarios are considerably lower than that of the classical vaccination method. Also, even with a efficacious vaccine, total eradication of the peak is not achieved irrespective of the exposed population prior to vaccination and regardless of the network. This can be seen in Figs. S5, S6, S11 and S12.
In comparison to mass vaccination, a lower percentage of the population has to be vaccinated when using a ring vaccination protocol in order to attain low infection cases (see Table 3). This is especially so as with effective contract tracing, more individuals can be vaccinated and thus decreasing the number of infections. It is worth noting also that even with the above results, the percentage of vaccinated individuals is lesser when only of the population is exposed prior to vaccination than when the prior exposed population is . Also, from Table 3 we see that for each network, the vaccinated populations are very similar in both scenarios (that is when or of the population is exposed) irrespective of the efficacy of the vaccine.
Table 4 shows the average proportion of unvaccinated (susceptible) individuals who got exposed in the course of the infection in both ER and BA networks under ring vaccination. Similar to the average infection peaks, there are fewer cases in unvaccinated individuals in the BA network than in the ER network. In addition, more cases are seen when of the population is exposed than when is exposed. From our simulations for ring vaccination in both networks, vaccinated individuals remain vaccinated and do not get exposed during the course of the infection.
Table 4.
Average proportion (in ) of unvaccinated (susceptible) individuals who got exposed in the course of the infection in both ER and BA networks under ring vaccination.
| Vaccine Efficacy |
||||
|---|---|---|---|---|
| (ER Network) | ||||
| ( of population exposed before vaccination) | ||||
| ( of population exposed before vaccination) | ||||
| (BA Network) | ||||
| ( of population exposed before vaccination) | ||||
| ( of population exposed before vaccination) | ||||
4. Discussion
With the ongoing spread of SARS-CoV-2 worldwide, pharmaceutical companies have also been in a race to produce safe and highly effective vaccines to counter the transmission of the disease. As of December 2020, there were 52 vaccine candidates in clinical trials in humans, 13 of which were in Phase 3 trials (World Health Organisation, 2020). In November 2020, some pharmaceutical companies and institutes, including Pfizer Inc and BioNTech, Moderna, the University of Oxford (in collaboration with AstraZeneca), announced positive results from the first interim analyses of their Phase 3 vaccine trials (Moderna, 2020, Oxford University, 2020, Pfizer Inc, 2020). Initial data released from these trials report that the vaccines manufactured by Pfizer Inc/BioNTech and Moderna both yielded efficacy whereas that by University of Oxford (in collaboration with AstraZeneca) yielded efficacy. On 2 December 2020, the UK medicines regulator MHRA granted temporary regulatory approval for the Pfizer-BioNTech vaccine (Mullard, 2020) which was under evaluation for emergency use authorization (EUA) status by the United States Food and Drug Administration (United States Food and Drug Authority, 2020) and approved for use on 11 December 2020 (Mullard, 2020) in the United States.
Although the Pfizer, Moderna and University of Oxford/AstraZeneca vaccines are being used worldwide, in other countries such as China and Russia, other vaccines (from Sinovac in China and Gameleya Research Institute in Russia) have been developed and are currently in limited use. Table 5 summarizes candidate vaccines currently in use as well as their manufacturers and vaccine platform (that is, a system that uses certain basic components as the backbone but is relatively flexible and can be adapted quickly to be used against different pathogens Hume and Lua, 2017).
Table 5.
List of candidate vaccines currently in use. Adapted from World Health Organisation, 2020, BioSpace, 2021.
| SARS-CoV-2 Vaccine Manufacturer/ Developer | Vaccine platform | Timing of doses | Overall Efficacy (from BioSpace, 2021) |
|---|---|---|---|
| University of Oxford/AstraZeneca | Non-replicating viral vector | 0, 28 days | |
| Sinovac | Inactivated | 0, 14 days | |
| Janssen Pharmaceutical Companies | Non-replicating viral vector | 0 or 0, 56 days | |
| Moderna/NIAID | RNA | 0, 28 days | |
| CanSino Biological Inc./Beijing Institute of Biotechnology | Non-replicating viral vector | ||
| BioNTech/Fosun Pharma/Pfizer | RNA | 0, 21 days | |
| Beijing Institute of Biological Products/Sinopharm | Inactivated | 0, 21 days | |
| Novavax | Protein subunit | 0, 21 days | |
| Gameleya Research Institute/ Sputnik | Non-replicating viral vector | 0, 21 days | |
| Medicago Inc. | Virus-like particle (VLP) | 0, 21 days | – |
In this study, we modelled the spread of SARS-CoV-2 infection using an SAIRV model structure on social networks. We run stochastic simulations to determine vaccine efficacy and population coverage limits capable of extinguishing the disease. We considered two vaccination strategies, each with varying scenarios regarding vaccine efficacy and population coverage. We found that the introduction of a single infectious person into a completely susceptible population leads to the spread of infection giving rise to more infectious cases and subsequently more than one infection peak. This is an indication that in the absence of a good enough vaccine, there is a much higher chance of more than one infection peak which is already being observed in some countries (Cacciapaglia et al., 2020, Bontempi, 2020).
In addition, the introduction of vaccination lowered the number of infectious cases irrespective of the type of vaccination and contact network. Our simulations and analysis show that when using a mass vaccination strategy, the lower the efficacy of the vaccine, the more people needed to be vaccinated against the disease in order to eliminate infection peak(s). This is true for both ER and BA networks. For instance, in an ER network, a vaccine with an efficacy of will require more than of the entire population to be vaccinated in order to reach low infection peak values less than whereas in a BA network, a population coverage more than with a vaccine efficacy of achieves negligible infection cases. In both networks, a effective vaccine will require just about of the population to be vaccinated.
Even though there are some vaccines which require a single dose regimen to achieve acclaimed efficacy levels, from Table 5, it can be seen easily that the majority of vaccines require more than one dose to achieve the levels of efficacy claimed by manufacturers. Given that this is a simplified model to explore the effects of vaccination strategies in general, it is worth pointing out that our model is limited when considering a two-dose vaccine regimen and hence results from our model can likely be influenced under such circumstances.
Given the experimental nature and limited initial supply of vaccines, a classical mass vaccination campaign might not be feasible in many countries. However, ring vaccination of likely case contacts and contacts of cases could provide an effective alternative in distributing the vaccine to ensure low levels of infection and subsequently preventing infection peaks. This is with the assumption of effective contract tracing of infectious people.
Researchers, policy makers and the general public are of the opinion that the discovery of a vaccine will allow the return to normality of life before the SARS-CoV-2 pandemic. It is worth noting that, the discovery of a proven-to-be effective vaccine however, might not reduce transmission completely. This is because a vaccine that effectively reduces the severity of transmission does not necessarily reduce virus transmission to a comparable degree (Kissler et al., 2020).
It is also important to consider the potential impact of voluntary mass vaccination in the efforts of clearing the epidemic (Omer et al., 2009, Phadke et al., 2016, Larson et al., 2014, Cooper et al., 2008). In years past, the roll-out of vaccination has been faced with declining vaccine confidence in the general public which could lead to hesitancy in getting vaccinated (de Figueiredo et al., 2020). Such instances could easily lead to a disruption of people receiving a vaccine voluntarily thus, having a detrimental effect on efforts to eradicate the disease, and hence such situations should not be underestimated.
4.1. Limitations and future work
Though exploring the effects of SARS-CoV-2 transmission on social networks, in this study we have limited our analysis to two types of social network which are the Erdos–Renyi network and the Barabasi-Albert network models. To proceed towards increasing practicality, the analysis performed in this study can be extended to consider disease spread and vaccination on other social networks and small-world network (Watts and Strogatz, 1998) models, using similar scenarios and protocols. Such network models can be compared with each other and the outcomes analysed. Data on known social networks such as contact matrices and age mixing patterns can also be used for further analysis and evaluation. Some of these social contact networks include existing survey data social networks such as from the POLYMOD study in Mossong et al. (2008), age-related social networks in Kenya (Kiti et al., 2014) and social contact networks in Great Britain (Danon et al., 2013).
Simulations in this study were performed with the assumption of an optimistic condition in which all infectious individuals are identified. In reality, contact tracing is especially difficult in the course of an ongoing epidemic. In the particular case of SARS-CoV-2, traditional interview based approaches as well as recent digital contact-tracing apps have proven to be less effective (Li and Guo, 2020, Bashir et al., 2020). Thus identifying all infectious contacts and their secondary contacts (especially for the ring vaccination strategy) becomes difficult and comes at a higher cost (McClain and Rainie, 2020, Kretzschmar et al., 2020). In effect, these challenges can potentially reduce the impact of vaccination efforts, as presented in this study.
Also, the model used here assumes there is equal mixing of individuals and their neighbours in the network whereas in reality, this is not the case (Herrmann and Schwartz, 2020, Newman, 2002, Prem et al., 2020). Consequently, infection cases could be lower and population coverage may be reduced.
The model also assumes that all infectious people recover from the disease and are immune. The effect of mortality on the dynamics of the disease is not considered as this model aims to study the general transmission dynamics and the effects of varying vaccination strategies. Within-host dynamics such as the viral dynamics and immune responses would be important to be included in a framework with higher resolution (Nguyen et al., 2018).
Epidemiological models of disease spread and transmission generally take into account the reproduction number () of the disease to gain knowledge on the transmission process (You et al., 2020, Alimohamadi et al., 2020). Estimates of vary widely as data continue to emerge in an ongoing epidemic (Pan et al., 2020, Liu et al., 2020b). This study however, does not examine this parameter since it does not directly impact the transmission dynamics.
In summary, this study describes the transmission dynamics of SARS-CoV-2 on a social contact network and the vaccine efficacy thresholds needed to prevent new waves of the disease. For future work, we will focus on other social network models and their analysis with respect to SARS-CoV-2. We will also consider the transmission potential based on and the dynamics in this regard.
CRediT authorship contribution statement
Josephine N.A.Tetteh: Simulations and draft preparations. Van Kinh Nguyen: Writing - review & editing. Esteban A. Hernandez-Vargas: Conceptualization, Resources, Supervision, Writing - review & editing.
Declaration of Competing Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgements
This work was supported by the Universidad Nacional Autonoma de Mexico (UNAM) – PAPIIT with the number IA102521. This work was also supported by the Alfons und Gertrud Kassel-Stiftung and the Deutsche Forschungsgemeinschaft through the project HE7707/5-1.
Footnotes
Supplementary data associated with this article can be found, in the online version, athttps://doi.org/10.1016/j.jtbi.2021.110894.
Supplementary data
The following are the Supplementary data to this article:
References
- Alimohamadi Y., Taghdir M., Sepandi M. Estimate of the basic reproduction number for COVID-19: a systematic review and meta-analysis. Journal of Preventive Medicine and Public Health. 2020;53(3):151. doi: 10.3961/jpmph.20.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almocera, A.E.S., Quiroz, G., Hernandez-Vargas, E.A., 2020. Stability analysis in COVID-19 within-host model with immune response. Communications in Nonlinear Science and Numerical Simulation, p. 105584. ISSN 1007-5704. URL: http://www.sciencedirect.com/science/article/pii/S1007570420304147. [DOI] [PMC free article] [PubMed]
- Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? The Lancet. 2020 doi: 10.1016/S0140-6736(20)30567-5. ISSN 0140-6736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the covid-19 epidemic? The Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M., Vegvari C., Truscott J., Collyer B.S. Challenges in creating herd immunity to SARS-CoV-2 infection by mass vaccination. The Lancet. 2020;396(10263):1614–1616. doi: 10.1016/S0140-6736(20)32318-7. ISSN 1474547X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas, A., Cota, W., Gómez-Gardenes, J., Gómez, S., Granell, C., Matamalas, J.T., Soriano-Panos, D., Steinegger, B. 2020. A mathematical model for the spatiotemporal epidemic spreading of COVID-19. medRxiv.
- Bailey, N.T., et al., 1975. The Mathematical Theory of Infectious Diseases and Its Applications. Charles Griffin & Company Ltd, 5a Crendon Street, High Wycombe, Bucks HP13 6LE.
- Barabási A.-L. 2003. Linked: The new science of networks. [Google Scholar]
- Bashir, A., Lone, A., Zahoor, S., Khan, A.. Naaz, R., 2020. Applicability of mobile contact tracing in fighting pandemic (COVID-19): Issues, challenges and solutions. [DOI] [PMC free article] [PubMed]
- BioSpace (2021). Updated comparing COVID-19 vaccines: Timelines, types and prices. URL: https://www.biospace.com/article/comparing-covid-19-vaccines-pfizer-biontech-moderna-astrazeneca-oxford-j-and-j-russia-s-sputnik-v/. Accessed: 2021-22-06.
- Bontempi E. The europe second wave of COVID-19 infection and the italy “strange” situation. Environmental Research. 2020:110476. doi: 10.1016/j.envres.2020.110476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brauer F., Castillo-Chavez C., Castillo-Chavez C. vol. 2. Springer; 2012. (Mathematical Models in Population Biology and Epidemiology). [Google Scholar]
- Burke, R.M., 2020. Active monitoring of persons exposed to patients with confirmed COVID-19–united states, january–february 2020. MMWR. Morbidity and mortality weekly report, 69. [DOI] [PMC free article] [PubMed]
- Cacciapaglia G., Cot C., Sannino F. Second wave COVID-19 pandemics in europe: a temporal playbook. Scientific Reports. 2020;10(1):1–8. doi: 10.1038/s41598-020-72611-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calafiore, G.C., Novara, C., Possieri, C., 2020. A modified SIR model for the COVID-19 contagion in italy. arXiv preprint arXiv:2003.14391. [DOI] [PMC free article] [PubMed]
- Callaway E., Mallapaty S. Novavax covid vaccine protects people against variants. Nature. 2021;590:17. doi: 10.1038/d41586-021-00268-9. [DOI] [PubMed] [Google Scholar]
- Chatterjee K., Chatterjee K., Kumar A., Shankar S. Healthcare impact of COVID-19 epidemic in india: A stochastic mathematical model. Medical Journal Armed Forces India. 2020 doi: 10.1016/j.mjafi.2020.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chretien J.-P., Swedlow D., Eckstrand I., George D., Johansson M., Huffman R., Hebbeler A. Advancing epidemic prediction and forecasting: a new us government initiative. Online Journal of Public Health Informatics. 2015;7(1) [Google Scholar]
- Colizza V., Barrat A., Barthélemy M., Vespignani A. Predictability and epidemic pathways in global outbreaks of infectious diseases: the sars case study. BMC Medicine. 2007;5(1):1–13. doi: 10.1186/1741-7015-5-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper L.Z., Larson H.J., Katz S.L. Protecting public trust in immunization. Pediatrics. 2008;122(1):149–153. doi: 10.1542/peds.2008-0987. [DOI] [PubMed] [Google Scholar]
- Danon L., Read J.M., House T.A., Vernon M.C., Keeling M.J. Social encounter networks: characterizing great britain. Proceedings of the Royal Society B: Biological Sciences. 2013;280(1765):20131037. doi: 10.1098/rspb.2013.1037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Figueiredo A., Simas C., Karafillakis E., Paterson P., Larson H.J. Mapping global trends in vaccine confidence and investigating barriers to vaccine uptake: a large-scale retrospective temporal modelling study. The Lancet. 2020;396(10255):898–908. doi: 10.1016/S0140-6736(20)31558-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dezső Z., Barabási A.-L. Halting viruses in scale-free networks. Physical Review E. 2002;65(5) doi: 10.1103/PhysRevE.65.055103. [DOI] [PubMed] [Google Scholar]
- Eguiluz V.M., Klemm K. Epidemic threshold in structured scale-free networks. Physical Review Letters. 2002;89(10) doi: 10.1103/PhysRevLett.89.108701. [DOI] [PubMed] [Google Scholar]
- Fanelli D., Piazza F. Analysis and forecast of COVID-19 spreading in china, italy and france. Chaos, Solitons & Fractals. 2020;134 doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferretti L., Cortelezzi M., Yang B., Marmorini G., Bianconi G. Features and heterogeneities in growing network models. Physical Review E. 2012;85(6) doi: 10.1103/PhysRevE.85.066110. [DOI] [PubMed] [Google Scholar]
- Firth J.A., Hellewell J., Klepac P., Kissler S., Kucharski A.J., Spurgin L.G. Using a real-world network to model localized COVID-19 control strategies. Nature Medicine. 2020;26(10):1616–1622. doi: 10.1038/s41591-020-1036-8. [DOI] [PubMed] [Google Scholar]
- Flaxman S., Mishra S., Gandy A., Unwin H.J.T., Mellan T.A., Coupland H., Whittaker C., Zhu H., Berah T., Eaton J.W., et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in europe. Nature. 2020;584(7820):257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- Foege W.H., Millar J.D., Lane J.M. Selective epidemiologic control in smallpox eradication. American Journal of Epidemiology. 1971;94(4):311–315. doi: 10.1093/oxfordjournals.aje.a121325. [DOI] [PubMed] [Google Scholar]
- Geddes A.M. The history of smallpox. Clinics in Dermatology. 2006;24(3):152–157. doi: 10.1016/j.clindermatol.2005.11.009. [DOI] [PubMed] [Google Scholar]
- Getz W.M., Salter R., Mgbara W. Adequacy of seir models when epidemics have spatial structure: Ebola in sierra leone. Philosophical Transactions of the Royal Society B. 2019;374(1775):20180282. doi: 10.1098/rstb.2018.0282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenhalgh D. Optimal Control of An Epidemic By Ring Vaccination. Communications in Statistics. Stochastic Models. 1986;2(3):339–363. ISSN 08820287. [Google Scholar]
- Hernandez-Mejia, G., Hernandez-Vargas, E.A., 2020. When is SARS-CoV-2 in your shopping list? Mathematical Biosciences 328, 108434. ISSN 0025-5564. URL: http://www.sciencedirect.com/science/article/pii/S0025556420301036. [DOI] [PMC free article] [PubMed]
- Hernandez-Vargas E.A., Alanis A.Y., Tetteh J. A new view of multiscale stochastic impulsive systems for modeling and control of epidemics. Annual Reviews in Control. 2019;48:242–249. doi: 10.1016/j.arcontrol.2019.06.002. [DOI] [Google Scholar]
- Hernandez-Vargas, E.A., Velasco-Hernandez, J.X., 2020. In-host modelling of COVID-19 kinetics in humans. Annual Reviews in Control. (50), 448-456. URL: https://www.sciencedirect.com/science/article/abs/pii/S1367578820300638 [DOI] [PMC free article] [PubMed]
- Herrmann H.A., Schwartz J.-M. Why COVID-19 models should incorporate the network of social interactions. Physical Biology. 2020;17(6) doi: 10.1088/1478-3975/aba8ec. [DOI] [PubMed] [Google Scholar]
- Hodgson S.H., Mansatta K., Mallett G., Harris V., Emary K.R., Pollard A.J. What defines an efficacious COVID-19 vaccine? a review of the challenges assessing the clinical efficacy of vaccines against SARS-CoV-2. The Lancet Infectious Diseases. 2020 doi: 10.1016/S1473-3099(20)30773-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hume H.K.C., Lua L.H. Platform technologies for modern vaccine manufacturing. Vaccine. 2017;35(35):4480–4485. doi: 10.1016/j.vaccine.2017.02.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabir K.A., Kuga K., Tanimoto J. Effect of information spreading to suppress the disease contagion on the epidemic vaccination game. Chaos, Solitons & Fractals. 2019;119:180–187. [Google Scholar]
- Keeling M.J., Eames K.T. Networks and epidemic models. Journal of the Royal Society Interface. 2005;2(4):295–307. doi: 10.1098/rsif.2005.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepes F. vol. 3. World Scientific; 2007. (Biological Networks). [Google Scholar]
- Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. 1927;115(772):700–721. [Google Scholar]
- Kissler S.M., Tedijanto C., Goldstein E., Grad Y.H., Lipsitch M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science. 2020;368(6493):860–868. doi: 10.1126/science.abb5793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiti M.C., Kinyanjui T.M., Koech D.C., Munywoki P.K., Medley G.F., Nokes D.J. Quantifying age-related rates of social contact using diaries in a rural coastal population of kenya. PloS One. 2014;9(8) doi: 10.1371/journal.pone.0104786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krammer F. SARS-CoV-2 vaccines in development. Nature. 2020;586(7830):516–527. doi: 10.1038/s41586-020-2798-3. ISSN 14764687. [DOI] [PubMed] [Google Scholar]
- Kretzschmar M.E., Rozhnova G., Bootsma M.C., van Boven M., van de Wijgert J.H., Bonten M.J. Impact of delays on effectiveness of contact tracing strategies for COVID-19: a modelling study. The Lancet Public Health. 2020;5(8):e452–e459. doi: 10.1016/S2468-2667(20)30157-2. ISSN 24682667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R.M., Sun F., Jit M., Munday J.D., et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. The Lancet Infectious Diseases. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson H.J., Jarrett C., Eckersberger E., Smith D.M., Paterson P. Understanding vaccine hesitancy around vaccines and vaccination from a global perspective: a systematic review of published literature, 2007–2012. Vaccine. 2014;32(19):2150–2159. doi: 10.1016/j.vaccine.2014.01.081. [DOI] [PubMed] [Google Scholar]
- Lavezzo E., Franchin E., Ciavarella C., Cuomo-Dannenburg G., Barzon L., Del Vecchio C., Rossi L., Manganelli R., Loregian A., Navarin N., et al. Suppression of a SARS-CoV-2 outbreak in the italian municipality of vo’. Nature. 2020;584(7821):425–429. doi: 10.1038/s41586-020-2488-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, J., Guo, X., 2020. COVID-19 contact-tracing apps: A survey on the global deployment and challenges. arXiv preprint arXiv:2005.03599.
- Lin Q., Zhao S., Gao D., Lou Y., Yang S., Musa S.S., Wang M.H., Cai Y., Wang W., Yang L., et al. A conceptual model for the outbreak of coronavirus disease 2019 (COVID-19) in wuhan, china with individual reaction and governmental action. International Journal of Infectious Diseases. 2020 doi: 10.1016/j.ijid.2020.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J., Liao X., Qian S., Yuan J., Wang F., Liu Y., Wang Z., Wang F.-S., Liu L., Zhang Z. Community transmission of severe acute respiratory syndrome coronavirus 2, shenzhen, china, 2020. Emerging Infectious Diseases. 2020;26(6) doi: 10.3201/eid2606.200239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Gayle A.A., Wilder-Smith A., Rocklöv J. The reproductive number of covid-19 is higher compared to sars coronavirus. Journal of Travel Medicine. 2020 doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClain, C., Rainie, V., 2020. The Challenges of Contact Tracing as U.S. Battles COVID-19 — Pew Research Center. Technical Report October. https://www.pewresearch.org/internet/2020/10/30/the-challenges-of-contact-tracing-as-u-s-battles-covid-19/.
- Meyers L.A., Pourbohloul B., Newman M.E., Skowronski D.M., Brunham R.C. Network theory and sars: predicting outbreak diversity. Journal of Theoretical Biology. 2005;232(1):71–81. doi: 10.1016/j.jtbi.2004.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller I.F., Becker A.D., Grenfell B.T., Metcalf C.J.E. Disease and healthcare burden of COVID-19 in the united states. Nature Medicine. 2020:1–6. doi: 10.1038/s41591-020-0952-y. [DOI] [PubMed] [Google Scholar]
- Moderna, 2020. Moderna’s COVID-19 vaccine candidate meets its primary efficacy endpoint in the first interim analysis of the phase 3 cove study. URL: https://investors.modernatx.com/node/10316/pdf. Accessed: 2020-12-10.
- Moinet A., Pastor-Satorras R., Barrat A. Effect of risk perception on epidemic spreading in temporal networks. Physical Review E. 2018;97(1) doi: 10.1103/PhysRevE.97.012313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mossong J., Hens N., Jit M., Beutels P., Auranen K., Mikolajczyk R., Massari M., Salmaso S., Tomba G.S., Wallinga J., et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Medicine. 2008;5(3) doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller J., Schönfisch B., Kirkilionis M. Ring vaccination. Journal of Mathematical Biology. 2000;41(2):143–171. doi: 10.1007/s002850070003. ISSN 03036812. [DOI] [PubMed] [Google Scholar]
- Newman M.E. Assortative mixing in networks. Physical Review Letters. 2002;89(20) doi: 10.1103/PhysRevLett.89.208701. [DOI] [PubMed] [Google Scholar]
- Nguyen V.K., Mikolajczyk R., Hernandez-Vargas E.A. High-resolution epidemic simulation using within-host infection and contact data. BMC Public Health. 2018;18(1) doi: 10.1186/s12889-018-5709-x. ISSN 14712458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omer S.B., Salmon D.A., Orenstein W.A., Dehart M.P., Halsey N. Vaccine refusal, mandatory immunization, and the risks of vaccine-preventable diseases. New England Journal of Medicine. 2009;360(19):1981–1988. doi: 10.1056/NEJMsa0806477. [DOI] [PubMed] [Google Scholar]
- Mullard A., 2020. COVID-19 vaccines buoy hope. Nature Reviews Drug Discovery 20(1), 8. URL: https://www.nature.com/articles/d41573-020-00215-9. Accessed: 2020-12-12. [DOI] [PubMed]
- Oxford University, 2020. Oxford university breakthrough on global COVID-19 vaccine. URL: https://www.research.ox.ac.uk/Article/2020-11-23-oxford-university-breakthrough-on-global-covid-19-vaccine. Accessed: 2020-12-10.
- Pan A., Liu L., Wang C., Guo H., Hao X., Wang Q., Huang J., He N., Yu H., Lin X., et al. Association of public health interventions with the epidemiology of the COVID-19 outbreak in wuhan, china. Jama. 2020;323(19):1915–1923. doi: 10.1001/jama.2020.6130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng, L., Yang, W., Zhang, D., Zhuge, C., Hong, L., 2020. Epidemic analysis of COVID-19 in China by dynamical modeling. arXiv. http://arxiv.org/abs/2002.06563.
- Phadke V.K., Bednarczyk R.A., Salmon D.A., Omer S.B. Association between vaccine refusal and vaccine-preventable diseases in the united states: a review of measles and pertussis. Jama. 2016;315(11):1149–1158. doi: 10.1001/jama.2016.1353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prem K., Liu Y., Russell T.W., Kucharski A.J., Eggo R.M., Davies N., Flasche S., Clifford S., Pearson C.A., Munday J.D., et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in wuhan, china: a modelling study. The Lancet Public Health. 2020;5(5):e261–e270. doi: 10.1016/S2468-2667(20)30073-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzo A., Pedalino B., Porfiri M. A network model for ebola spreading. Journal of Theoretical Biology. 2016;394:212–222. doi: 10.1016/j.jtbi.2016.01.015. [DOI] [PubMed] [Google Scholar]
- Russell C.D., Millar J.E., Baillie J.K. Clinical evidence does not support corticosteroid treatment for 2019-nCoV lung injury. The Lancet. 2020;395(10223):473–475. doi: 10.1016/S0140-6736(20)30317-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricardo-Azanza, C.L., Hernandez-Vargas, E.A., 2020. Epidemiological Characteristics of COVID-19 in Mexico and the Potential Impact of Lifting Confinement Across Regions. Frontiers in Physics 21:1-9. URL: https://https://www.frontiersin.org/articles/10.3389/fphy.2020.573322/full.
- Pfizer Inc., 2020. Pfizer and biontech announce vaccine candidate against COVID-19 achieved success in first interim analysis from phase 3 study. URL: https://www.pfizer.com/news/press-release/press-release-detail/pfizer-and-biontech-announce-vaccine-candidate-against. Accessed: 2020-12-10.
- Sameni, R., 2020. Mathematical modeling of epidemic diseases; a case study of the COVID-19 coronavirus. arXiv preprint arXiv:2003.11371.
- Scarpino S.V., Petri G. On the predictability of infectious disease outbreaks. Nature Communications. 2019;10(1):1–8. doi: 10.1038/s41467-019-08616-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma, A., Menon, S.N., Sasidevan, V., Sinha, S., 2017. Epidemic prevalence information on social networks mediates emergent collective outcomes in voluntary vaccine schemes. arXiv preprint arXiv:1709.07674. [DOI] [PMC free article] [PubMed]
- Simha, A., Prasad, R.V., Narayana, S., 2020. A simple stochastic sir model for COVID-19 infection dynamics for karnataka: Learning from europe. arXiv preprint arXiv:2003.11920.
- Singh, R., Adhikari, R., 2020. Age-structured impact of social distancing on the COVID-19 epidemic in india. arXiv preprint arXiv:2003.12055, 2020.
- United States Food and Drug Authority (2020). Emergency use authorization. URL: https://www.fda.gov/emergency-preparedness-and-response/mcm-legal-regulatory-and-policy-framework/emergency-use-authorization. Accessed: 2020-12-10.
- Viner R.M., Russell S.J., Croker H., Packer J., Ward J., Stansfield C., Mytton O., Bonell C., Booy R. School closure and management practices during coronavirus outbreaks including COVID-19: a rapid systematic review. The Lancet Child & Adolescent Health. 2020;4(5):397–404. doi: 10.1016/S2352-4642(20)30095-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz E. Sir dynamics in random networks with heterogeneous connectivity. Journal of Mathematical Biology. 2008;56(3):293–310. doi: 10.1007/s00285-007-0116-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts D.J., Strogatz S.H. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Weitz J.S., Beckett S.J., Coenen A.R., Demory D., Dominguez-mirazo M., Dushoff J., Leung C.-Y., Li G., Magalie A., Park S.W., Rodriguez-gonzalez R., Shivam S., Zhao C.Y. Modeling shield immunity to reduce COVID-19 epidemic spread. Nature Medicine. 2020 doi: 10.1038/s41591-020-0895-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells C., Yamin D., Ndeffo-Mbah M.L., Wenzel N., Gaffney S.G., Townsend J.P., Meyers L.A., Fallah M., Nyenswah T.G., Altice F.L., et al. Harnessing case isolation and ring vaccination to control ebola. PLoS Negl Trop Dis. 2015;9(5) doi: 10.1371/journal.pntd.0003794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organisation, 2020. Draft landscape of COVID-19 candidate vaccines. URL: https://www.who.int/publications/m/item/draft-landscape-of-covid-19-candidate-vaccines. Accessed: 2020-12-10.
- You C., Deng Y., Hu W., Sun J., Lin Q., Zhou F., Pang C.H., Zhang Y., Chen Z., Zhou X.-H. Estimation of the time-varying reproduction number of COVID-19 outbreak in china. International Journal of Hygiene and Environmental Health. 2020;228 doi: 10.1016/j.ijheh.2020.113555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaplotnik, Z., Gavric, A., Medic, L., 2020. Simulation of the COVID-19 pandemic on the social network of slovenia: estimating the intrinsic forecast uncertainty. arXiv preprint arXiv:2005.13282. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.