Forecasting of Oxidant/Antioxidant levels of COVID-19 patients by using Expert models with biomarkers used in the Diagnosis/Prognosis of COVID-19

Graphical abstract

Abstract

Background

Early detection of oxidant-antioxidant levels and special care in severe patients are important in combating the COVID-19 epidemic. However, this process is costly and time consuming. Therefore, there is a need for faster, reliable and economical methods.

Methods

In this study, antioxidant/oxidant levels of patients were estimated by Expert-models using biomarkers, which are effective in the diagnosis/prognosis of COVID-19 disease. For this purpose, Expert-models were trained and created between the white-blood-cell-count (WBC), lymphocyte-count (LYM), C-reactive-protein (CRP), D-dimer, ferritin values of 35 patients with COVID-19 and antioxidant/oxidant parameter values of the same patients. Error criteria and R² ratio were taken into account for the performance of the models. The validity of the all models was checked by the Box-Jenkis-method.

Results

Antioxidant/Oxidant levels were estimated with 95% confidence-coefficient using the values of WBC, LYM, CRP, D-dimer, ferritin of different 500 patients diagnosed with COVID-19 with the trained models. The error rate of all models was low and the coefficients of determination were sufficient. In the first data set, there was no significant difference between measured antioxidant/oxidant levels and predicted antioxidant/oxidant levels. This result showed that the models are accurate and reliable. In determining antioxidant/oxidant levels, LYM and ferritin biomarkers had the most effect on models, while WBC and CRP biomarkers had the least effect. The antioxidant/oxidant parameter estimated with the highest accuracy was Native-Thiol divided by Total-Thiol.

Conclusions

The results showed that the antioxidant/oxidant levels of infected patients can be estimated accurately and reliably with LYM, ferritin, D-dimer, WBC, CRP biomarkers in the COVID-19 outbreak.

1. Introductıon

Coronavirus disease 2019 (COVID-19) is an infectious disease caused by coronavirus 2 (SARS-CoV-2), which causes severe acute respiratory syndrome. This disease spreads far beyond the China in a few weeks and reached every part of the world. Real-time reverse transcription polymerase chain reaction (rRT-PCR), which is used in the diagnosis of COVID-19, can give negative results in 30–50% of cases, even if they are infected with the virus [1], [2]. As with immunodiagnostic testing, RT-PCR testing may have difficulties distinguishing between true positive and true negative individuals infected with COVID-19 [3], [4]. Since the test may fail in a significant proportion of suspected and confirmed patients with clinical results, it is prudent not to rely solely on PCR test results and to consider other clinical and molecular evidence [3], [5]. In addition, considering the difficulties in the RT-PCR test results, it was stated that the test should be repeated on more than one sample and the application methodology should be improved in order to increase the overall sensitivity of the test [3]. However, this is a difficult process for the staff and the patient. These difficulties in diagnosing COVID-19 have further increased the importance of routine laboratory results [1], [2].

Also, while the number of COVID-19 cases is increasing day by day, there is limited information about the effects of hematological and laboratory findings associated with this disease on other parameters such as antioxidant-oxidant balance [1]. In addition, although the emergence of new technologies has accelerated the development of vaccines, there is limited information on the pathophysiology of the COVID-19 virus [6]. Therefore, many studies are still being conducted to determine the place and importance of routine laboratory parameters in COVID-19 [7], [8], [9], [10].

Covid 19 disease is a multifactorial disease that can affect many parameters in the living body [1]. The studies showed that there was significant increases in proinflammatory cytokine levels in patients infected with covid 19 and a decrease in antioxidant capacity with an increase in oxidative stress [11], [12].

When a new pathogen such as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), emerges, all new information can assist in the monitoring and diagnosis of coronavirus disease (COVID-19) [13]. In many previous studies, it has been reported that oxidative stress is associated with the occurrence or prognosis of many diseases such as diabetes, alzheimer, obesity, immune deficiency, cardiovascular diseases and prognosis of viral diseases [14], [15], [16]. In order to reduce the effect of oxidative stress, there are antioxidant enzymes or systems such as superoxide dismutase, catalase and glutathione peroxidase, which provide the main antioxidant defense in the cell [17], [18]. However, in the disease state, oxidative stress increases with mutated antioxidant enzymes, toxins, or decreased consumption of natural antioxidants [19]. Since natural phenolic compounds show antioxidant activity, they play a vital role in suppressing oxidative stress both in the food industry and in the human body [20], [21]. For this reason, it was reported that supplements such as antioxidant vitamin E and C, and also vitamin D were important in patients infected with covid 19 [22], [23]. CRP, ferritin and D-dimer parameters among routine biochemistry parameters are especially used as determinants in the prognosis of in Covid 19 [1]. In many studies, it was stated that patients infected with COVID-19 started to increase in proinflammatory cytokines such as TNF-α and IL-1β and oxidants such as lipid peroxidation, disulfide level and oxidative DNA damage [24], [25], [26]. In these studies, it was also stated that patients infected with COVID-19 started to decrease in antioxidants such as superoxide dismutase (SOD), glutathione (GSH), glutathione peroxidase (GPx), total thiol, and native thiol [24], [25], [26].

However, CRP, ferritin and D-dimer, which are among the routine parameters, can be measured easily and cheaply, while proinflammatory cytokine levels, antioxidant and oxidative stress markers can be measured manually by spectrophotometric methods (such as ELISA) by spending more money, effort and time.

Mathematical Models, which provide great advantages in terms of prevention of the time, economy and labor losses, continue to be one of the useful and popular methods in estimating the parameters that may affect the prognosis of many diseases. In this respect, Expert Models and tools (AR-ARMA-ARIMA) are thought to be useful in overcoming difficulties in obtaining values of the antioxidant and oxidant parameters.

Indeed, one study used expert methods to predict key epidemiological parameters and the evolution of COVID-19 [27]. Another study used a generalized logistic growth model, Richards growth model, and a wave growth model to estimate cases reported in Guangdong and Zhejiang, China [28]. Additionally, this study obtained real-time predictions for COVID-19 in China using three phenomenological models [28]. One study used ARIMA expert models to predict confirmed cases of COVID-19 [29]. In addition, different expert models were used in one study for the prediction of avian influenza H5N1 and another study for the prediction of COVID-19 cases [30], [31].

In terms of predictive ability, ARIMA models are known to perform better than complex structural models [32], [33]. With expert models, one of the population estimation methods, the risk of choosing an individual wrong model is reduced and the hypothesis is generalize [33], [34], [35]. Depending on the accuracy and diversity of individual models, ARIMA models have excellent generalization performance in predicting the population trend. ARIMA methods, also known as expert models, can make strong predictions using only the historical data of the cases. When the method is created with the right models, it can also be used to estimate the antioxidant-oxidant parameter values of the patients and help the treatment system to serve new patients more quickly and safely.

As far as we know, this manuscript is the first study to estimate antioxidant-oxidant values using routine blood values. In this study, antioxidant-oxidant levels of patients were estimated accurately and reliably with Expert-models using routine biochemistry and hematological laboratory parameters that are effective in the diagnosis-prognosis of COVID-19 disease.

2. Material and method

This retrospective single-center study was conducted in accordance with the 1989 Helsinki Declaration. This study was approved by the Ministry of Health and the Ethics Committee. Data matching our criteria were collected from Erzincan Binali Yıldırım University Mengücek Gazi Training and Research Hospital information system between March 2020 and December 2020 and were included in the study. The research only covered people over 18 years old. Laboratory data of the patients were the first blood values measured at the time of first admission to the hospital.

2.1. Participants criteria, study design and workflow

Demographic data and blood values of 535 patients diagnosed with COVID-19 on the specified dates were obtained. The diagnosis of COVID-19 was defined only in cases detected as SARS-CoV-2 by rRT-PCR in nasopharyngeal or oropharyngeal swabs at the dates covered by this study in our hospital. Routine laboratory parameters used in the diagnosis-prognosis of COVID-19 were determined by scanning the literature. Determined biochemical and hematological values were obtained from all patients. The all data sets were obtained digitally from the hospital registry system.

The study consists of two data sets. In the first data set, there were routine blood values (white blood cell count “WBC”, lymphocyte count “LYM”, C-reactive protein “CRP”, D-dimer, ferritin) and antioxidant-oxidant values (SOD, GPx, GSH, Native thiol, Total thiol, Native thiol/Total thiol, Malondialdehyde “MDA”, 8-OHdG “8-hydroxy-2-deoxy guanosine”, Disulfide, Disulfide/Native thiol and Disulfide/Total thiol) of COVID-19 patients consisting of 35 individuals (Table 1 ).

Table 1.

Descriptive statistical results of antioxidant-oxidant levels and routine laboratory parameter values of the patient group in the first data set.

n = 35	Median	Mean	St. d	Min	Max
SOD (ng/mL)	29.03	28.77	2.43	22.08	33.11
GPx (ng/mL)	14.86	14.95	2.52	11.23	18.83
GSH (uM)	8.48	9.22	2.51	4.43	15.36
MDA (uM)	9.89	9.97	5.09	1.10	22.37
8-OHdG/106 dG	3.87	3.75	1.24	1.68	6.86
Total Thiol (µmol/L)	389.39	387.44	63.79	272.43	516.38
Native Thiol (µmol/L)	345,31	333.77	65.43	220.39	474.13
Disulfide (µmol/L)	25.86	24.89	5.77	11.17	36.89
Disulfide / Native Thiol (%)	7.72	7.77	2.45	2.75	13.07
Disulfide / Total Thiol (%)	6.56	6.69	1.79	2.65	10.55
Native Thiol/Total Thiol (%)	86.69	86.45	3.65	78.73	93.87
LYM x103/μL	1.30	1.44	0.73	0.30	3.9
CRP (mg/L)	5.0	24.27	43.87	0.2	187.0
D-dimer (μg/L)	136.0	446.25	1285.9	27.0	7700.00
Ferritin (mL/ng)	154.0	218.6	252.6	1.0	1419.00
WBC x103/μL	4.4	5.11	2.5	1.4	13.00

CRP: C-reactive protein; LYM: lymphocyte count; WBC: white blood cell count; NEU: neutrophil count; SOD: Superoxide dismutase; GPx: Glutathione peroxidase; GSH: Reduced glutathione; MDA: Malondialdehyde; 8-OHdG: 8-hydroxy-2-deoxy guanosine; St. d: Standard deviation; Min: Minimum; Max: Maximum.

The second data set consists of WBC, LYM, CRP, D-dimer, ferritin values of 500 different patients diagnosed with COVID-19 in the same time period as the first data set (Table 2 ).

Table 2.

Descriptive statistical results of routine laboratory parameters of the patient group in the second data set.

	Parameters	Mean	Median	St. d	Min	Max
Second Patient Group (n = 500)	LYM x103/μL	1.95	1.92	0.86	0.43	14.74
	CRP (mg/L)	30.76	19.1	45.58	3.02	356.0
	D-Dimer (μg/L)	2065.1	2154.3	1586.6	101.0	2230.0
	Ferritin (ml/ng)	166.8	166.4	184.7	3.7	1650.0
	WBC x103/μL	7.93	7.8	3.31	2.8	35.8

CRP: C-reactive protein; LYM: lymphocyte count; WBC: white blood cell count; NEU: neutrophil count; St. d: Standard deviation; Min: Minimum; Max: Maximum.

In this study, routine laboratory variables were included in the Autoregressive Integrated Moving Average (ARIMA) model as independent variables and antioxidant-oxidant variables as dependent variables. The ARIMA Model was run for each dependent variable. The antioxidant-oxidant values of these patients were estimated by the ARIMA model using the independent variables of 35 patients in our first data set. In order to test the accuracy and reliability of the models obtained, the actual measured antioxidant-oxidant values of the first data set were compared with the estimated antioxidant-oxidant values. After ensuring the accuracy and reliability, the upper and lower limits of the 95% confidence coefficient of the models were determined. Accordingly, antioxidant-oxidant parameter values of 500 patients in our second data set, which had the same independent variables as the models obtained, were estimated and confidence limits were determined.

2.2. Outcome measures

Our primary aim in this study is to estimate the antioxidant-oxidant parameter values of the patients in the second data set with ARIMA models trained with the first data set. Our secondary aim is to determine which routine biochemistry or hematological blood values are more effective in predicting antioxidant-oxidant parameters of COVID-19 patients.

2.3. Statistical analysis

IBM SPSS Statistics 25 (Chicago, IL) software was used for statistical analysis. In this study, patients' routine blood values and antioxidant-oxidant values were estimated by the ARIMA model. The ARIMA model, also known as the Box-Jenkins methodology, uses the most recent observations as default values and describes past forecast errors to accurately set the next period [36]. The Box-Jenkins method is a prognostic tool with advanced mathematical and statistical procedures for dealing with complex situations. The method can be easily applied in risk analysis and uncertainty analysis [37], [38].

Analysis of variance and classical regression will likely be misleading when autocorrelation exists between prediction errors. These data can be analyzed with the ARIMA model [38]. The ARIMA methodology analyzes the stochastic properties of various data series according to a particular philosophy, not the construction of a single or multiple equation model, as, for example, in regression analysis [36], [39], [40], [41], [42].

Problems such as autocorrelation of lags, linearity problem and residual independence in our data series are solved with ARIMA model and predictions are made with low error rate. Equations from the ARIMA models were run to estimate the antioxidant-oxidant levels of each patient in the study.

2.3.1. Basic Autoregressive integrated moving average (ARIMA Model)

The ARIMA model is defined by parameters p, d or q. Here, p: lagged values of autoregressives; q: parts of the moving average, and d; indicates the number of differences in the data series. ARIMA assumes that the volatility (delays) of stationary data series can be expressed as a linear combination of observed values and errors of current values [35], [43]. If the data series is stationary, the process turns into ARMA (p,q) model and is defined by the following equation.

$${\widehat{Y}}_t=\stackrel{\mathit{constant}}{\overbrace{C}}+\stackrel{\mathit{AR}\mathit{terms}\left(laggedvaluesofy\right)}{\overbrace{{\alpha }_1{Y}_{t-1}+\cdots +{\alpha }_p{Y}_{t-p}}}+{\epsilon }_t+\underset{\mathit{MA}\mathit{terms}\left(laggederrors\right)}{\underbrace{{\beta }_1{\epsilon }_{t-1}+\cdots {\beta }_q{\epsilon }_{t-q}}}$$

More details about the mathematical model can be found in [44]. The time series based model was modified for this study as follows. Here${\widehat{y}}_t$, t. the patient's predicted antioxidant-oxidant level; Y, t. the patient's actual antioxidant-oxidant level; c, initial ground level (intercept); α₁,…,α_p autoregressive (coefficient of each p parameter);β₁,…,β_q the moving average (coefficient of each q parameter) and ε_t, is the amount of residual error in the t-th patient's predicted parameter.ε_t, determines the white noise criterion whose mean is 0 variance ${\sigma }^2$.

Since the data used in the study were stationary, the minimum difference order and moving average (d, q parameter) was chosen as zero (0) and the AR model (p) was used. White noise (ındependence of autocorrelations of errors in the prediction model) is an indicator of how well the data fit the model in ARIMA models [44], [45], [46]. Auto Correlations Figures (ACF) and Partial Auto Correlation Figures (PACF) were obtained for the independence of errors in the estimation and for white noise control. While creating the best estimation models, mean absolute percent error (MAPE), mean absolute error (MAE), maximum absolute percent error (Max APE), root mean square error (RMSE), bayesian information criterion (BIC) and explained variance ratio (R²), which are commonly used error criteria in the literature, were taken into account [46], [47].

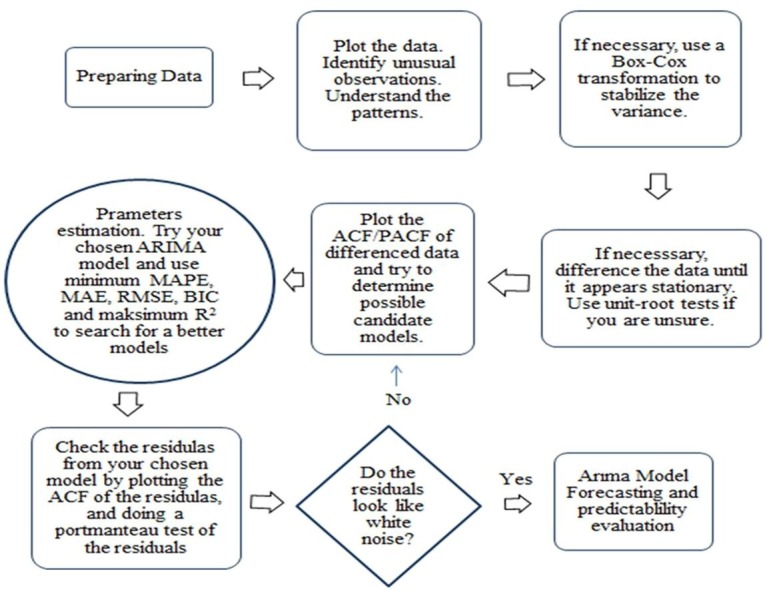
Accordingly, the p parameter were determined by considering the lowest value of the error criteria and the highest value of the R² (determination) coefficient. The work flow of the study is summarized in the diagram below (Fig. 1 ).

Fig. 1.

Work flow diagram of the study; ACF: Auto Correlation Figure; PACF: Partial Auto Correlation Figure; ARIMA: Autoregressive Integrated Moving Average; MAPE: Mean Absolute Percent Error, MAE: Mean Absolute Error; RMSE: Root Mean Square Error; BIC: Bayesian Information Criterion; R²: Determınatıon coeffıcıent.

3. Results

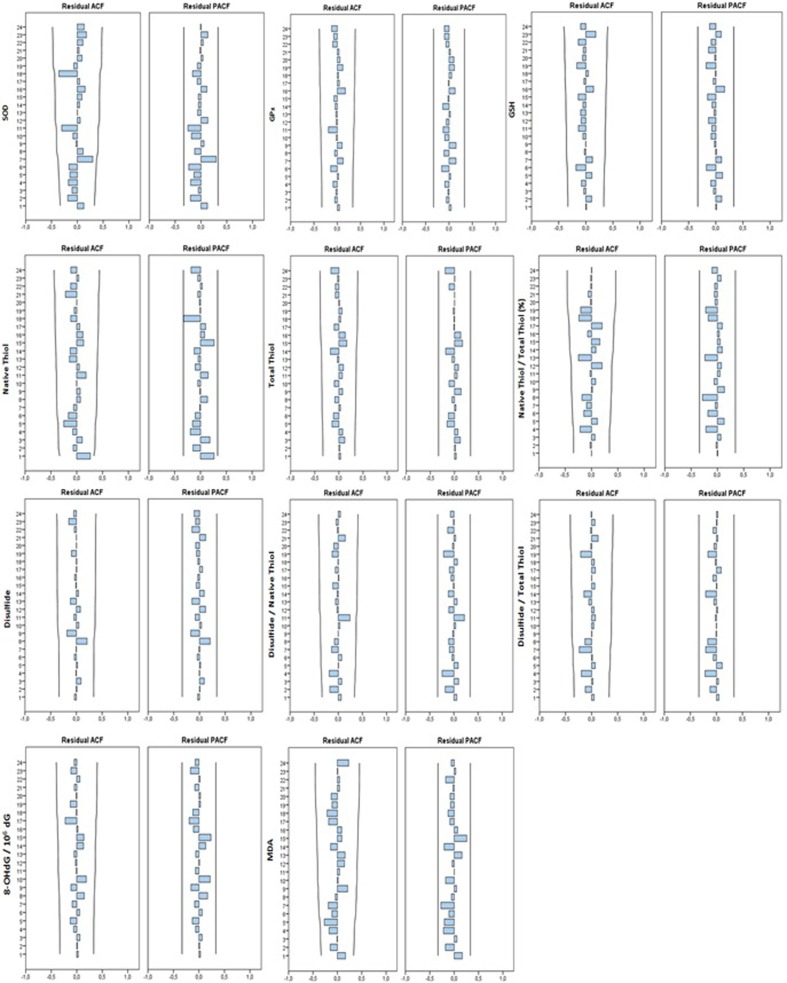
The best ARIMA models were obtained for estimating the antioxidant-oxidant levels of COVID-19 patients with the CRP, D-Dimer and Ferritin parameters, which are frequently used in the prognosis of COVID-19 disease (Table 3 ). After ensuring the stability of the obtained models, Ljung-Box test was used for autocorrelation control. The validity of all the models appears to be satisfactory according to the Ljung-Box test (p > 0.05) (Table 3). In addition, when ACF and PACF graphs were examined, it was seen that autocorrelation or partial autocorrelation coefficients were not significant (p > 0.05). In addition, the randomness and independence of the residuals in the prediction were checked by ACF/PACF plots (Fig. 2 ). Accordingly, none of the residul was significantly different from zero. According to this result, the data series was evaluated as stationary.

Table 3.

Performance results of AR models obtained to estimate antioxidant-oxidant parameters.

Model Statistics
Model	Number of Predictors	R2 (%)	RMSE	MAPE	MAE	Max APE	Normalized BIC	Ljung-Box Q (sig.)	Number of Outliers
Dissulfide/Native Thiol	5	64.4	1.84	7.56	1.16	13.86	2.57	0.14	1
Dissulfide	5	41.8	5.4	6.45	3.65	18.08	4.5	0.95	0
Dissulfide /Total Thiol	5	52.3	1.50	7.8	0.98	14.20	1.85	0.91	0
GPx	5	61.9	3.6	8.6	7.06	17.9	3.5	0.38	0
GSH	5	57.1	2.16	13.5	6.8	16.2	2.7	0.74	0
MDA	5	62.1	3.65	12.02	5.68	19.68	3.5	0.35	1
Native Thiol	5	59.7	9.02	9.8	12.9	18.6	6.71	0.65	1
Native Thiol/Total Thiol	5	78.4	2.3	1.4	1.2	4.35	3.4	0.84	0
8-OHdG/106 dG	5	58.8	1.2	11.8	0.81	16.14	1.5	0.08	0
SOD	5	64.3	1.8	4.3	1.1	14.7	2.15	0.61	1
Total Thiol	5	63.8	8.9	7.3	5.6	9.84	3.11	0.96	1

SOD: Superoxide dismutase; GPx: Glutathione peroxidase; GSH: Reduced glutathione; MDA: Malondialdehyde; 8-OHdG: 8-hydroxy-2-deoxy guanosine; MAPE: Mean absolute percent error; MAE: Mean absolute error; Max APE: Maximum absolute percent error; RMSE: Root mean square error; BIC: Bayesian information criterion; R²: Coefficient of determination.

Fig. 2.

The graphs of ACF and PACF of residuals. ACF: Auto Correlation Figure; PACF: Partial Auto Correlation Figure.

When (Table 3) is examined, the most successful prediction was seen in Native Thiol/Total Thiol model according to all criteria, while the most unsuccessful prediction was seen in Native Thiol model. The algorithm left out of analysis the extreme values that do not fit the model. Errors were seen at acceptable levels in the all models. However, R² (amount of variance explained in the estimation of antioxidant-oxidant levels of the patient group in the first data set) was found to be normal on average. Exponential smoothing was found to be significant in the models obtained to stabilize the lags in the estimation of SOD and GSH levels (p < 0.05).

The statistical results of the parameters of the models obtained by ARIMA technique for estimating antioxidant-oxidant levels are given in detail in the (Table 4 ). However, only the parameters that significantly affected the models were reported in the (Table 4) (p < 0.05). Considering all prediction models, it was seen that LYM and ferritin were the most effective parameters. This result was followed by D-dimer, CRP and WBC parameters, respectively (Table 4). It was observed that only D-dimer was effective in estimating GSH, MDA and GPx levels, and only ferritin parameter was effective in estimating SOD levels. The LYM parameter was the most effective promoting variable in predicting the disulfide level. In the estimation of the total thiol level, it was observed the WBC parameter had a significant decreasing effect.

Table 4.

Statistical results of the AR models obtained.

ARIMA Model Parameters
Model				Estimate	St EM	t	p
Disulfide	AR (2,0,0)	Constant		22.980	3.069	7.487	0.000
		AR	Lag 1	1.887	0.325	5.808	0.000
			Lag 2	−1.533	0.397	−3.867	0.001
		LYM	Lag 0	3.022	1.357	2.227	0.036
		CRP	Lag 0	0.079	0.033	2.362	0.027
GPx	AR (2,0,0)	Constant		14.954	1.470	10.170	0.000
		AR	Lag 1	0.129	0.043	2.965	0.007
			Lag 2	−0.987	0.036	−27.438	0.000
		D-Dimer	Lag 0	0.001	0.000	2.306	0.031
GSH	AR (3,0,0)	Constant		10.404	1.725	6.031	0.000
		AR	Lag 1	0.926	0.287	3.225	0.004
			Lag 2	−0.902	0.317	−2.849	0.009
			Lag 3	0.686	0.247	2.780	0.011
		D-Dimer	Lag 0	0.029	0.012	2.385	0.026
MDA	AR (2,0,0)	Constant		8.923	1.616	5.522	0.000
		AR	Lag 1	0.527	0.182	2.890	0.008
			Lag 2	−0.484	0.190	−2.548	0.017
		D-Dimer	Lag 0	0.001	0.001	2.316	0.029
Native Thiol	AR (0,0,0)
		Constant		298.148	21.610	13.797	0.000
		LYM	Lag 0	32.139	7.552	4.255	0.000
		CRP	Lag 0	−0.565	0.265	−2.137	0.043
		Ferritin	Lag 0	0.084	0.034	2.449	0.022
Total Thiol	AR (4,0,0)	Constant		427.233	22.964	18.605	0.000
		AR	Lag 1	1.294	0.186	6.946	0.000
			Lag 2	−1.311	0.238	−5.514	0.000
			Lag 3	1.008	0.233	4.334	0.000
			Lag 4	−0.629	0.176	−3.584	0.002
		CRP	Lag 0	−0.517	0.232	−2.225	0.037
		WBC	Lag 0	−7.673	2.952	−2.600	0.016
Disulfide / Native Thiol	AR (2,0,0)	Constant		5.487	0.986	5.565	0.000
		AR	Lag 1	1.434	0.415	3.452	0.002
			Lag 2	−1.031	0.493	−2.092	0.049
		LYM	Lag 0	1.156	0.403	2.865	0.009
		Ferritin	Lag 0	−0.006	0.002	−3.208	0.004
		WBC	Lag 0	0.290	0.136	2.126	0.046
Disulfide / Total Thiol	AR (2,0,0)	Constant		6.285	0.835	7.527	0.000
		AR	Lag 1	1.163	0.180	6.462	0.000
			Lag 2	−0.657	0.172	−3.809	0.001
		LYM	Lag 0	1.209	0.360	3.358	0.003
		Ferritin		−0.003	0.002	−2.128	0.044
Native Thiol /Total Thiol	AR (0,0,0)	Constant		90.575	2.663	34.018	0.000
		LYM	Lag 0	−1.588	0.433	−3.669	0.002
		D-Dimer	Lag 0	−0.001	0.000	−2.456	0.025
Native Thiol /Total Thiol	AR (0,0,0)	Constant		90.575	2.663	34.018	0.000
		LYM	Lag 0	−1.588	0.433	−3.669	0.002
		D-Dimer	Lag 0	−0.001	0.000	−2.456	0.025
8-OHdG / 106 dG	AR (2,0,0)	AR	Lag 2	−0.714	0.270	−2.647	0.014
		Ferritin	Lag 0	0.004	0.001	3.338	0.003
		WBC	Lag 0	0.220	0.091	2.421	0.023

CRP: C-reactive protein; LYM: Lymphocyte count; WBC: White blood cell count; NEU: Neutrophil count; SOD: Superoxide dismutase; GPx: Glutathione peroxidase; GSH: Reduced glutathione; MDA: Malondialdehyde; 8-OHdG: 8-hydroxy-2-deoxy guanosine; St EM: Standart error of mean; p < 0.05 was considered significant.

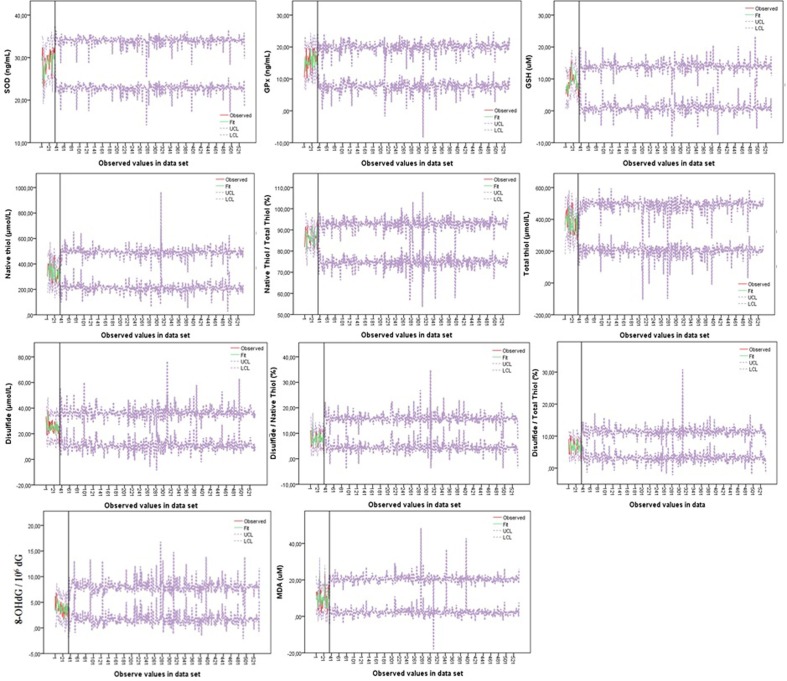
It was clearly seen how compatible the models obtained for the prediction with the antioxidant-oxidant levels of the patients in the first data set in Fig. 3 . This figure showed that all models provide the fit between the predicted values and the measured values in the first data set. The predicted values showed that the model has a satisfactory level of predictability. The data set of antioxidant-oxidant levels in the first data set did not show a clear upward or downward trend, and these data set showed multiple peaks, most of which were not equally spaced. This result indicates that the data set is stationary for the general trend (Fig. 2, Fig. 3). Confidence limits of the predicted antioxidant-oxidant levels of the second data set were visualized, according to the agreement obtained from the first data set (Fig. 3).

Fig. 3.

Graphs showing the agreement between antioxidant-oxidant levels measured in the first data set and the confidence limits of the estimation models obtained accordingly. SOD: Superoxide dismutase; GPx: Glutathione peroxidase; GSH: Reduced glutathione; MDA: Malondialdehyde; 8-OHdG: 8-hydroxy-2-deoxy guanosine.

The descriptive statistics and confidence limits of the antioxidant-oxidant parameters of the patients included in the second data set with the models obtained from the study are shown in detail in (Table 5 ). Descriptive statistics were obtained with a 95% confidence coefficient.

Table 5.

Descriptive statistical results of antioxidant-oxidant levels estimated in the patient group in the second data set.

Predicted Value	Median	Mean	St. d	Min	Max	Predicted Value	Median	Mean	St. d	Min	Max
SOD Model	28.41	28.32	1.19	19.94	32.42	Native Thiol Model	354.16	351.19	42.88	167.71	823.85
LCL – SOD Model	22.73	22.71	1.29			LCL - Native / Thiol Model	213.32	212.46	42.95
UCL - SOD Model	34.04	33.92	1.18			UCL - Native / Thiol Model	493.40	489.93	45.22
GPx Model	14.37	14.40	1.52	2.49	20.36	Disulfide Model	23.43	23.90	4.98	4.27	63.73
LCL - Gpx Model	7.66	7.78	1.64			LCL – Dissulfide Model	10.63	11.13	5.04
UCL – Gpx Model	21.05	21.03	1.48			UCL - Dissulfide Model	36.16	36.68	4.97
GSH Model	7.40	7.52	1.77	3.63	16.77	Disulfide / Native Thiol Model	9.98	10.09	2.26	1.76	29.03
LCL – GSH Model	0.86	1.12	1.98			LCL–Dissulfide/Native Thiol Model	4.25	4.47	2.21
UCL - GSH Model	13.88	13.92	1.72			UCL - Dissulfide / Native Thiol Model	15.72	15.70	2.44
MDA Model	11.20	11.24	2.51	5.84	35.95	Disulfide / Total Thiol Model	7.24	7.28	1.64	1.95	26.70
LCL - MDA-Model	1.77	1.87	2.49			LCL - Dissulfide / Total Thiol Model	3.17	3.23	1.65
UCL - MDA Model	20.67	20.61	2.61			UCL – Dissulfide / Total Thiol Model	11.33	11.34	1.68
8-OHdG /106 Model	3.55	3.57	0.70	1.24	8.35	Native Thiol / Total Thiol Model	83.97	83.83	3.21	62.77	98.82
LCL – 8-OHdG / 106 dG Model	0.89	0.91	0.70			LCL– NativeThiol / TotalThiol Model	74.85	74.95	3.59
UCL – 8-OHdG / 106 dG Model	6.20	6.23	0.70			UCL – NativeThiol / Total Thiol Model	92.98	92.71	3.16
Total Thiol Model	353.77	348.12	43.22	40,95	484.93
LCL – Total Thiol Model	209.35	206.30	46.56
UCL - Total Thiol Model	497.96	489.94	43.11

SOD: Superoxide dismutase; GPx: Glutathione peroxidase; GSH: Reduced glutathione; MDA: Malondialdehyde; 8-OHdG: 8-hydroxy-2-deoxy guanosine; LCL: Lower confidence level; UCL: Upper confidence levels; St. d: Standard deviation; Min: Minimum; Max: Maximum.

In addition, antioxidant-oxidant levels of the patients in the first data set with the models obtained from the study were estimated as SOD: 28.96 ± 0.30, GPx: 15.53 ± 0.29, GSH: 8.94 ± 0.38, MDA: 10.15 ± 0.67, 8-OHdG: 3.83 ± 0.11, Total Thiol: 384.60 ± 9.02, Native Thiol: 336.60 ± 9.02, Disulfide: 6.67 ± 0.23, Disulfide/Native Thiol: 7.74 ± 0.37, Disulfide/Total Thiol: 6.67 ± 0.23, Native/Total Thiol: 86.59 ± 0.54. These findings were compared with the actual (measured) antioxidant-oxidant results of the patients in the first data set. Accordingly, all antioxidant-oxidant prediction results were similar to the measured results and there was no significant difference between them (p > 0.05) (Fig. 4 ). This showed that the models produced accurate and reliable results.

Fig. 4.

Comparison of the predicted antioxidant-oxidant values and actual values for the first data set. SOD: Superoxide dismutase; GPx: Glutathione peroxidase; GSH: Reduced glutathione; MDA: Malondialdehyde; 8-OHdG: 8-hydroxy-2-deoxy guanosine, Native Thiol, Total Thiol, Native Thiol/Total Thiol levels were divided into 10 in order to obtain a harmonious view among all parameters in the graph.

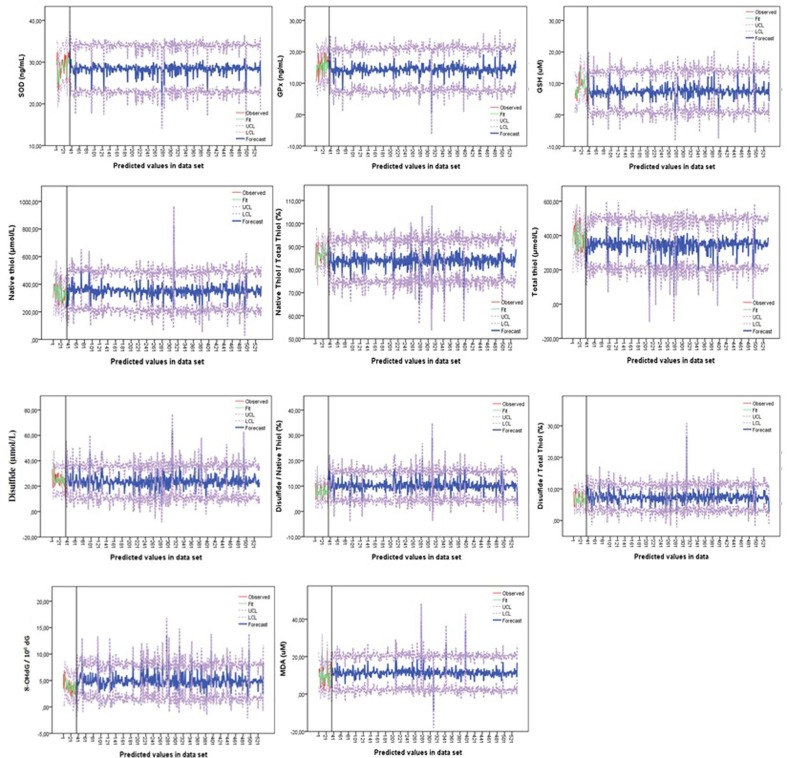
The estimated antioxidant-oxidant levels and confidence limits of the patient group in the second data set were visualized (Fig. 5 ). The visuals in Fig. 5 consist of two stages. The first step (up to the black line in the images) shows the agreement of the models between the antioxidant-oxidant levels and the predicted levels of the patients in the first data set. The second stage (the part after the black line in the images) shows the estimated antioxidant-oxidant levels of the patient group in the second data set according to the confidence limits obtained.

Fig. 5.

The consistency of the prediction models in the first data set and the predicted antioxidant-oxidant levels of the second data set. SOD: Superoxide dismutase; GPx: Glutathione peroxidase; GSH: Reduced glutathione; MDA: Malondialdehyde; 8-OHdG: 8-hydroxy-2-deoxy guanosine.

While the predicted antioxidant-oxidant levels for SOD and MDA in men were higher than in the women, GPx and GSH values in woman were higher than in the men. Other antioxidant-oxidant levels were not different according to gender (Table 6 ).

Table 6.

Comparison of estimated antioxidant-oxidant levels according to the gender.

	Female (n = 306)					Male (n = 229)
	Mean	Median	Min	Max	St EM	Mean	Median	Min	Max	St EM	p
Age	49.07	46.50	19.00	93.00	1.09	47.90	46.00	19.00	100.00	1.30	0.394
Antioxidan-OxidanParameters
SOD	27.79	27.99	19.94	31.37	0.06	29.02	29.15	22.72	32.42	0.06	0.000
GPx	14.53	14.46	0.49	20.19	0.09	14.23	14.21	7.68	20.36	0.09	0.004
GSH	7.65	7.55	−1.63	14.46	0.10	7.34	7.24	−0.96	16.77	0.11	0.004
MDA	11.07	10.99	−5.84	35.95	0.15	11.46	11.41	4.63	31.03	0.16	0.009
OHdG	3.57	3.56	1.44	8.11	0.04	3.57	3.53	1.24	8.35	0.04	0.833
Total Tiyol	346.80	352.50	40.95	484.93	2.63	349.89	354.19	136.32	469.85	2.59	0.601
Native Tiyol	350.17	352.70	193.69	823.85	2.80	352.56	355.03	167.71	499.40	2.18	0.397
Dissulfide	24.15	23.68	4.27	63.73	0.32	23.57	23.28	7.24	50.07	0.28	0.211
Dissulfide/NativeTiyol	10.10	9.96	2.07	29.03	0.14	10.06	9.99	1.76	16.98	0.13	0.887
Dissulfide/Total Tiyol	7.38	7.32	1.95	26.70	0.11	7.15	7.14	2.44	12.94	0.08	0.136
Native Tiyol/TotalTiyol	83.91	84.11	62.77	98.82	0.20	83.71	83.87	66.86	91.97	0.18	0.126

SOD: Superoxide dismutase; GPx: Glutathione peroxidase; GSH: Reduced glutathione; MDA: Malondialdehyde; 8-OHdG: 8-hydroxy-2-deoxy guanosine; Min: Minimum; Max: Maximum; St EM: Standart error of mean; p < 0.05 was considered significant.

4. Discussion

It has been reported that oxidative stress plays an important role in the pathogenesis of various diseases [11], [12], [14], [19]. Many studıes showed that the levels of parameters such as MDA, IL-1B and TNF-alpha associated with oxidative stress in various viral diseases were high compared to the control group while the levels of antioxidan parameters such as GSH, SOD, CAT and GSH-Px were low [24], [25]. Because the measurement of antioxidant-oxidant parameters is a manual process, it is a costly and time consuming endeavor. As in other viral diseases, it is inevitable that antioxidant-oxidant levels in patients with COVID-19 will vary according to healthy people [26]. For this reason, the fact that the data set on antioxidant-oxidant parameters consists of patients diagnosed with COVID-19 has further increased the importance of the study.

In this study, antioxidant-oxidant values of patients in the second data set were estimated at 95% confidence level with ARIMA models trained with the first data set. Next, it was determined which routine biochemistry or hematological blood values were more effective in predicting the antioxidant-oxidant parameters of COVID-19 patients. The best parameters of the prediction model were determined by evaluating the error criteria and the level of determination (R²) [46], [47]. According to our literature review, this study is the first study about the estimation of some antioxidant-oxidant levels with routine blood laboratory findings.

It is known that Expert-ARIMA models perform better than structural models in terms of prediction performance [32], [33]. Expert models based on certain statistical calculations can be used for forward estimation using only the historical data of the cases [33]. For this reason, many studies have been conducted in the future predictions of COVID-19 cases with Expert models and are still being to carried out [48], [49], [50].

The fact that ARIMA models provide various evaluation possibilities for the predicted dependent variable (for antioxidant-oxidant levels in this study) also reduces the need for a control group in studies [45], [46]. As a matter of fact, the scarcity of the control group in this study did not affect the success in the prediction negatively.

However, most prediction models only take into account the minimization of errors and constitute a single target for the estimation of data series. This may result with overfitting of the population estimation model in data series [35]. However, it is known that ARIMA models have successful generalization performance in estimating the dependent variable [33]. When the ARIMA method was created with the right models, it was emphasized that the method can also be used estimation of different parameters of the patients and it will help the treatment system to provide faster service to new patients [33].

In this study, the lack of significant difference between the predictive antioxidant-oxidative results obtained for the first patient group and the measured antioxidant-oxidant levels of these patients (Fig. 4, p > 0.05) showed that the models produced reliable results. Similarly, in two different studies using Expert models, a linear combination of past and present values and errors in the data set was created and reliable predictive values were obtained [45], [46].

Considering all prediction models in this study, it was found that LYM and ferritin were the most effective parameters in predicting antioxidant-oxidant levels. It has been reported that the decrease in the LYM level and the increase in the ferritin level indicate an increase in the COVID-19 prognosis [1], [48], [51], [52]. Accordingly, considering the ferritin and lymphocyte values in the epidemic of COVID-19, the antioxidant-oxidant values of severe patients can be learned and special effective treatment can be assisted for these patients.

Also, D-dimer, CRP and WBC parameters were less effective in predicting antioxidant-oxidant levels than LYM and ferritin. It was observed that only the D-dimer parameter was effective to the model in the prediction of GSH, MDA and GPx levels, and only the Ferritin parameter in the prediction of the SOD level. While LYM parameter was the most effective variable in estimating disulfide level (increasing effect), it was observed that WBC parameter had a significant decreasing effect in estimation of Total Thiol level. In the study, the antioxidant-oxidant levels that varied most among individuals were SOD and GSH (see Table 4). These results showed that it can be possible to predict oxidant/antioxidant status through parameters such as LYM, ferritin, D-dimer and CRP, which are the most effective routine laboratory parameters in the prognosis of COVID-19 disease. While the predicted antioxidant-oxidant levels for SOD and MDA were higher in men than in women, GPx and GSH values were higher in women than in men.

In the first patient group, antioxidant-oxidant values of a limited number of COVID-19 patients could be obtained. The reason for this is that a limited number of studies have been conducted to measure antioxidant-oxidant levels in COVID-19 patients. However, this did not increase the margin of error in the prediction due to the strong performance of ARIMA models. Also, the low number of patients in the first data set prevented the amount of variance explained (R²) in the estimate from being high. However, the variance amounts explained by the models in the estimation of antioxidant-oxidant levels in the first data set were found to be about 60%, and the amount of error was found to be <10%. With these results, when the data set of the dependent variable (measured antioxidant-oxidant levels) is augmented, it is expected that the amount of R² predicted by the prediction models will definitely increase.

5. Conclusion

In this study, some antioxidant-oxidant levels were estimated in COVID-19 patients. The results showed that especially LYM and ferritin may be important in predicting antioxidant-oxidant levels in patients with COVID-19. Thus, it was evaluated that by predicting antioxidant-oxidant levels with Expert Models without loss of money, time and effort, faster and more effective health service could be provided. However, while the results are encouraging, it is necessary to study a larger COVID-19 population that antioxidant-oxidant levels were measured, to have a more reliable estimate of accuracy rates. In addition, factors such as age and gender that affect antioxidant-oxidant levels in COVID-19 patients can be included, as well as different laboratory parameters not included in the study. Studies to be conducted in multicenter and larger patient groups will further clarify the importance of routine laboratory parameters used in the prognosis of COVID-19 in predicting antioxidant-oxidant status. In this context, it is thought that this study can pioneer many new studies.

6. Limitations of the study

The first data set was conducted on a relatively small population, because limited number of studies have been conducted to measure antioxidant-oxidant levels in COVID-19 patients. For this reason, in order for the amount of variance to be high, it is necessary to make estimation studies in larger data sets. Our data is derived from an electronic recording system that places restrictions on the provision of old information. Retrospective studies naturally lack control of variables. Therefore, prospective cohorts are also needed to validate our study data. In addition, other differential data such as comorbidity of the patients could not be achieved.

Author Contributions

¹HUYUT MT; He designed the study; scanned the literature; planned and implemented methodology and analyzed; organized figures and tables, evaluated the data; commented, wrote and revised the work.

²HUYUT Z; scanned the literature, collected material, evaluated and interpreted the results.

Ethical approval

This retrospective observational study was conducted in accordance with the 1989 Helsinki Declaration and was approved by the Ministry of Health and Erzincan University Faculty of Medicine Clinical Research Ethics Committee.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.