Precision vibratome for high-speed ultrathin biotissue cutting and organ-wide imaging

Summary

Cutting tissues into ultrathin slices is highly desired in sectioning-based organ-wide imaging. However, it is difficult to perform tissue cutting at a high speed with excellent quality. Here, we design a precision vibratome based on a paired double parallelogram flexure, which enables a vibrating blade to move strictly along a straight line. Meanwhile, we develop a high-speed cutting method that does not compromise cutting quality, which the vibratome operated at a high frequency mode. The characterized parasitic motion errors of a 180-Hz vibratome were less than 300 nm. It achieved a cutting speed six times that of an 85-Hz vibratome with acceptable quality. The capacity of the vibratome was investigated by organ-wide imaging, and the results revealed that it can be adapted in different tissues, such as the mouse brain and liver. This new vibratome shows great potential in speeding up organ-wide imaging applications especially for large volume biotissues.

Graphical abstract

Highlights

• •Flexure-based vibratome was designed to cut soft tissue into thin slice
• •High vibration frequency strategy was proposed for high-speed cutting
• •New vibratome was used to speed up sectioning-based organ-wide imaging technologies
• •3D microstructure was acquired from different tissues of mouse brain and liver

Biological sciences; Biological sciences research methodologies; Biology experimental methods; Biotechnology

Introduction

Obtaining organ-wide 3D continues anatomy information at submicron resolution is highly desired in biomedical research, such as connectome science and brainsmatics study (Oh et al., 2014; Luo, 2017; Shi et al., 2019). Traditional medical imaging technologies such as magnetic resonance imaging (MRI) and micro-computed tomography (μCT) can perform organ-wide imaging, but insufficient imaging resolution makes them difficult to identify fine structures such as capillaries (Hegab et al., 2016; Chung et al., 2020). While the electron microscope owns ultra-high resolution, it is hard to cover large-volume biotissues due to the time-consuming imaging mode (Kislinger et al., 2020). In between, light microscopy is a suitable tool for whole-organ precision imaging because it owns diffraction-limited resolution as well as centimeter-level imaging range. However, the occurrence of light absorption and scattering in thick tissues constrain its imaging depth. Recently, tissue clearing techniques that aim to reduce the scattering effect within the tissues are developed rapidly. In combination with light sheet microscopy, it can perform high-throughput imaging over an entire organ (Ueda et al., 2020). However, chemical clearing reagents cannot penetrate the tissue indefinitely, leading to a significant decrease in imaging resolution as the imaging depth increases (Xu et al., 2020). To obtain organ-wide 3D information at a consistently high resolution, sectioning-based optical imaging is a feasible solution; it includes micro-optical sectioning tomography (MOST) series technologies (Li et al., 2010; Gong et al., 2013, 2016; Zhong et al., 2021), serial two-photon tomography (Ragan et al., 2012; Amato et al., 2016), and block-face serial microscopy tomography (Seiriki et al., 2017, 2019). In these technologies, optical imaging and tissue cutting are performed alternately. To be more specific, a microtome is used to remove the imaged tissues layer by layer after each layer imaging is completed, which can help to break the imaging depth limitation and capture whole-organ 3D information. In these technologies, both optical imaging and tissue cutting are key techniques, but in the reported work, most were focused on the innovation of optical imaging but little on tissue cutting. Here, we aim to develop a novel vibratome that can be applied in sectioning-based optical imaging with superior cutting quality and speed, which can help to improve the efficiency and applicability in organ-wide imaging.

Cutting fresh/non-embedded tissue into thin slices with a thickness at micron level is difficult because fresh tissue is a kind of high elasticity material like jelly, which will deform randomly when interacting with a blade. Hence, resin or paraffin is used as embedding mediums that can provide stiff physical support for the soft tissue (Luo et al., 2020; Yang et al., 2013). In combination with a rotary or sliding microtome, it can generate thin slices even up to submicron thickness. However, the dehydration treatment in the sample preparation process will cause nonlinear shrinkage of the tissue, leading to undesired distortions to original anatomical structures. Recently, elastic materials such as agarose and hydrogel are developed rapidly, which have advantages of shorter sample preparation cycle and less tissue distortion (Seiriki et al., 2019). However, these materials own relative low Young's modulus in comparison with resin and paraffin (1–10³ vs. 10⁴–10⁷ kPa) (Benetti et al., 2014; DeSain et al., 2009; Normand et al., 2000); therefore, they deform to a great extent if suffer a large cutting force. Typically, a vibration cutting manner is used to reduce the cutting force (Atkins et al., 2004; Cheng and Huo, 2013; Huo and Cheng, 2019). In the implementation, a vibrating microtome (vibratome) is used to cut these elastic embedded tissues. But limited by the imperfect mechanical mechanism as well as the vibration cutting mode, the existing vibratomes fail to cut tissues into ultrathin slices (<10 μm) and in high speed (>50 mm/min) at the same time, which becomes a bottleneck for their usage in sectioning-based organ-wide imaging.

To date, two types of vibratomes have been reported, which are the vibratome with crank-slider mechanism and the vibratome with flexure mechanism (Hroncová et al., 2012; Jiang et al., 2017; Wang et al., 2019). The crank-slider design is simple but prone to the wearing problem and the unwanted parasitic motion errors (Hroncová et al., 2012). In the flexure-based vibratome, two different flexures have been studied, which are parallelogram and paired parallelogram (P–P) flexures, which can avoid the wearing problem because no rigid joints are used. However, the parallelogram flexure still suffers considerable swing/Z-rotation errors, especially when operated at large amplitudes (Jiang et al., 2017; Zhao et al., 2017), while the P–P flexure is restricted by the limited stroke, which compromises cutting quality (Wang et al., 2019). To address these problems, we proposed a novel double paired parallelogram (DP–DP) flexure that can operate in a large stroke with minimized motion errors.

Another problem that constrains existing vibratome usage is the slow cutting process. The reported vibratomes were operated in a low vibration frequency mode, e.g., 85 Hz, which the cutting quality degrades with an increase in the sample feed rate, limiting the feed rate to be less than 30 mm/min (Jiang et al., 2017). Here, based on the tissue destruction mechanics, we propose a conjecture that a vibratome working at a high-frequency mode can help to increase the sample feed rate without compromising the cutting quality. To demonstrate this theory, we aim to develop a high-speed cutting strategy by constructing a high-frequency vibratome.

In this work, we developed a high-precision and high-speed vibratome integrating with an optical imaging technique for organ-wide imaging. A novel DP–DP flexure, as the key transmission mechanism in the vibratome, was designed and performed a theoretical analysis. A set of mechanical testing and cutting experiments were designed to characterize the performance of the proposed vibratome. To demonstrate the unique capability and advantages of the vibratome, structured illumination microscopy (SIM) was performed to acquire the 3D anatomy information of different organs.

Results

High-precision and high-frequency vibratome design

The design goal of the vibratome is to obtain a high cutting speed as well as quality, which generates design requirements as summarized in Table 1. Overall, the frequency of the vibratome was set to 180 Hz, which is about twice that of state-of-the-art commercial vibratomes, such as VT 1000S from Leica (Rivera et al., 2013). The maximum vibration amplitude was designed to be 1 mm that is the same as VT 1000S. To ensure high cutting quality, the parasitic z-motions that affect the fluctuation of cutting cross section were constrained within 1 μm. The novel vibratome was designed to cut tissues with a thickness ranging from 4 to 1000 μm.

Table 1.

Design requirements for the high frequency vibratome

Specification	Vibration frequency	180 Hz
	Vibration amplitude	0–1 mm
Capacity	Feed rate	0–120 mm/min
	Section thickness	4–1000 μm
Performance	Parasitic z-motion	<1 μm

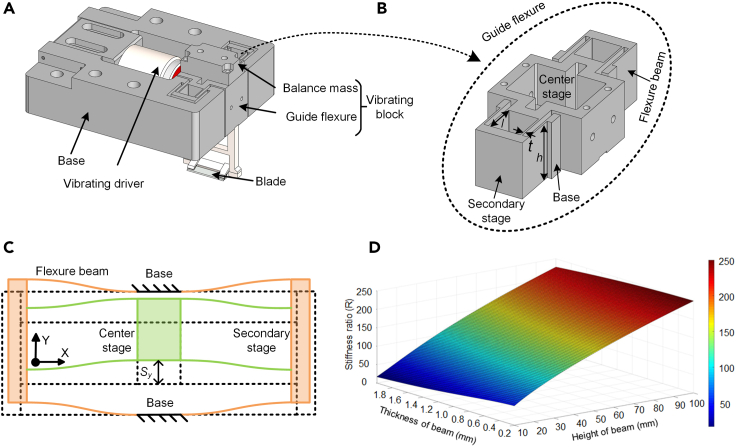
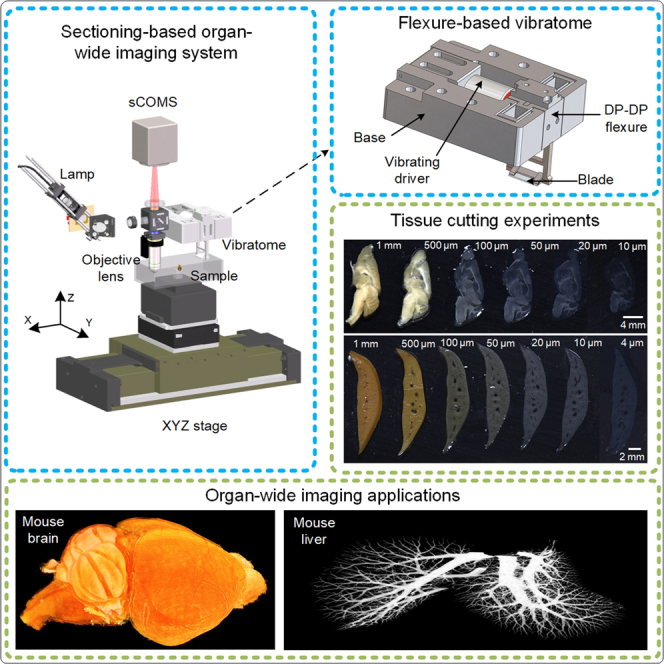
The proposed vibratome consists of four main components, namely the base, vibrating driver, vibrating block, and blade, which was modeled by SOLIDWORKS software (Figure 1A). The base functions as the ground, with both the vibrating driver and vibrating block mounted on it. When the cutting process starts, the vibrating block is actuated by a vibrating driver, such as a voice coil motor (VCM) and operated at the resonance mode. The blade is fixed on the vibrating block, moving along with it. Among these four parts, the vibrating block is the key module because it acts as a motion transmission between the vibrating driver and the blade.

Figure 1.

Design of a DP–DP flexure-based vibratome

(A) 3D model of the novel vibratome comprising the base, the vibrating driver, the vibrating block, and the blade.

(B) 3D model of the guide flexure shown in (A), it is a DP–DP flexure that consists of a center stage, two secondary stages, and eight flexure beams; the key structural parameters of the flexure beam include thickness, length, and height (t, l, h).

(C) Schematic diagram of the DP–DP flexure shown in (B); the center stage, two secondary stages, and four flexure beams have formed two inner parallelograms (green); two secondary stages, the base, and the other four flexure beams have formed two outer parallelograms (orange).

(D) Stiffness ratio R as a function of beam thickness t and height h.

In this design, the vibrating block consists of two components, namely the balance mass and guide flexure. The balance mass is used to adjust the center of the mass of the vibrating block to ensure it is coincident with the center of stiffness and the vibration driving force. If these three are not coincident, the vibrating block moves in a motion that is a combination of the translation and rotation motions, which cannot be a straight line. The guide flexure acted as a motion guide as well as a mechanical filter at the same time. The motion guide ensures a linear motion of the vibrating blade, and the mechanical filter suppresses parasitic motion errors caused by the harmonic motion. Besides, the guide flexure should achieve a large vibration amplitude because according to soft tissue cutting theory, the larger vibration amplitude can lead to better cutting quality (Wang et al., 2019).

To satisfy the motion guide and mechanical filter requirements, a novel DP–DP flexure was designed and used in our vibratome (Figure 1B). Essentially, it is a symmetric cantilever beam mass system that can therefore generate linear harmonic motion while suppressing Z-rotation errors to a greater extent compared with the parallelogram flexure (Zhao et al., 2017). The video of the linear harmonic motion of the DP–DP flexure is also given (see Video S1, an animation of the DP-DP flexure motion diagram, related to Figure 1B). Besides, the compensation of the outer parallelograms results in the center stage undergoing a larger stroke S_y than with the P–P flexure (Figure 1C). Note that although the DP–DP flexure is much complex than the parallelogram and P–P flexures, it still can be fabricated as a whole through wire electrical discharge machining (wire-EDM) to ensure no assembly errors are introduced.

Video S1. Animation to reveal the linear harmonic motion of the DP-DP flexure, related to

Figure 1B

Now the flexure mechanism has been determined; next, we need to design the structural parameters of the flexure, including the beam thickness, length, and height (t, l, h) (Figure 1B). Because the flexure is operated at the resonate mode, the natural frequency should be matched with the designed vibration frequency, i.e., 180 Hz. The natural frequency f₀ can be calculated using the following equation:

$$f_0=\frac{1}{2\mathrm{\pi }}\sqrt{\frac{2Eh{t}^3}{m{l}^3}}$$ (Equation 1)

Based on this design condition, we still have countless combinations of the structural parameters. So, next, we use the stiffness design approach to select an optimized solution. Note that the DP–DP flexure is also a stiffness anisotropic structure, that is, the stiffness is different in three directions. With proper design, we can further reduce the unwanted out-of-plane motion errors. The stiffness in the y and z direction, K_Y, and K_Z of the DP–DP flexure can be calculated as follows:

$$K_Y=\frac{2Eh{t}^3}{l^3}$$ (Equation 2)

$$K_Z=\frac{10Et{h}^3}{5l^3+12l{h}^2\left(1+\mathrm{\mu }\right)}$$ (Equation 3)

where E is the elastic modulus of the material (For Al, 7075, E = 72 GPa). To minimize the parasitic motion error in the z axis, the stiffness ratio K_Z/K_Y should be as large as possible. From Equations 1, 2, and 3, the stiffness ratio R can be expressed as follows:

$$R=\frac{K_Z}{K_Y}=\frac{5t^2{h}^2\left(\frac{2Eh}{4{\mathrm{\pi }}^{\mathrm{2}}{f}_0^{2}m}\right)2/3}{5t^4\left(\frac{2Eh}{4{\mathrm{\pi }}^{\mathrm{2}}{f}_0^{2}m}\right)2/3+12t^2{h}^2\left(1+\mathrm{\mu }\right)}$$ (Equation 4)

Based on Equation 4, the relationship between R and t and h can be obtained using MATLAB software, as depicted in Figure 1D. Here, R increased with a smaller t and larger h. According to the workspace permit, h was set to 50 mm. Because the flexure was fabricated through EDM, to maintain fabrication precision, t was set as 1 mm. Here, l calculated using (Equation 3) was 22.4 mm.

Characterization of the mechanical performance of the high-frequency vibratome

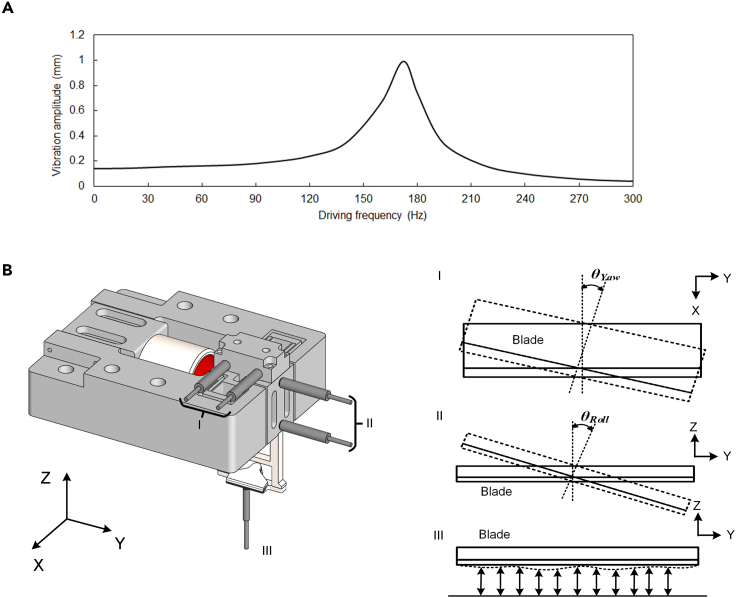
To prove the validity of the designed vibratome, we have performed a set of mechanical tests to characterize its performance. In these experiments, a 180-Hz DP–DP flexure-based vibratome was actuated by a VCM (NCC05-18-060-2PBS, H2W, USA). A capacitive sensor (Lion Precision C9.5/CPL290, resolution: 3 nm) was used to record the vibration amplitude of the system driven under different frequencies. The measurement results presented in Figure 2A revealed that the amplitude reached the maximum (1 mm) when the vibration frequency was set to 172 Hz, which indicated that the natural frequency of the DP–DP flexure was 172 Hz. The frequency of the actual instrument was slightly different from that of the theatrical design because of the inevitable manufacturing errors. Because the difference is small, in the following sections, this vibratome was assumed as 180 Hz.

Figure 2.

Schematic diagram of mechanical test and actual test result of resonance frequency

(A) Measured vibration amplitude under different driving frequency with a harmonic driving force.

(B) Three sets of sensors I, II, and III are used to measure the yaw, roll, and beating errors of the vibrating blade, respectively.

Theoretically, the DP–DP flexure guides the blade to move only on a horizontal axis. However, because of unavoidable manufacturing errors of the flexure and the assembly error of VCM, most of the time the vibration driving force cannot be exactly horizontal and penetrates the center of mass. Therefore, even with the proper stiffness design, the blade still undergoes slight parasitic motions in other axes. To characterize these errors, three sets of sensors were used (Figure 2B). Sensor I is a couple of capacitive sensors (Lion Precision C5/CPL290, resolution: 1 nm) used to measure the yaw error, sensor II is a couple of capacitive sensors (Lion Precision C9.5/CPL290, resolution: 3 nm) used to measure the roll error, and sensor III is a capacitive sensor (Lion Precision C5/CPL290, resolution: 1 nm) used to record the longitudinal beating. The measured θ_yaw and θ_roll errors were 20.8 and 4.1 μrad, respectively, and the root-mean-square longitudinal beating was 212 nm, which satisfies the proposed design requirement listed in Table 1.

Characterization of the tissue cutting capacity of the high-frequency vibratome

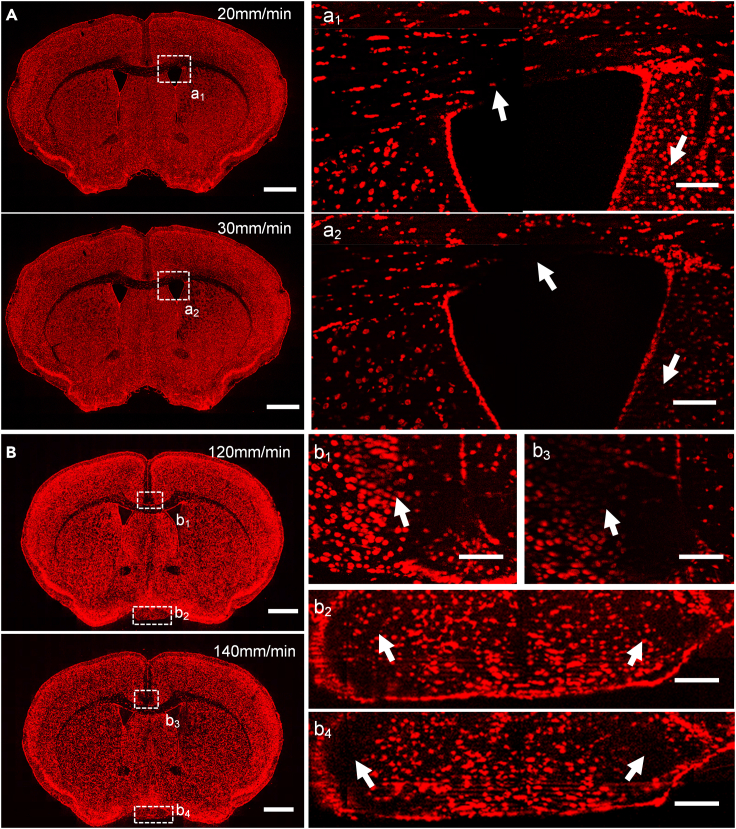
To prove that a high-frequency vibratome can increase the sample feed rate without comprising cutting quality, two DP–DP flexure-based vibratomes with different frequencies, namely 90 and 180 Hz, were used to cut the agarose-embedded brain tissue at different feed rates. The superficial layer of the newly exposed block surface was then counterstained using propidium iodide (PI) solution and imaged using the SIM system. In the following experiments, vibratomes were equipped with ceramic blades (38 × 7 × 0.5 mm, model 7550-1-C, Campden Instruments, UK). Figure 3 presents the imaging results of an agarose-embedded C57BL/6J mouse brain. Figure 3A depicts the block cut using a 90-Hz vibratome. The cutting quality decreased when the feed rate was larger than 20 mm/min, that is, a₁ and a₂ were the same region close to the ventricle, and the structures indicated by arrowheads in a₁ were lost in a₂. Figure 3B presents the block cut using the 180-Hz vibratome; the optimized sample feed rate was 120 mm/min. Some structural information was lost when the sample feed rate was increased to 140 mm/min, as indicated in b₁–b₄. These results confirmed that high frequency can speed up the whole sample cutting process with high quality.

Figure 3.

Cutting the agarose-embedded mouse brain tissue via DP–DP-based vibratomes with a thickness of 10 μm under different vibration frequencies and feed rates

(A) Slices were cut in the frequency of 90 Hz and the feed rate of 20 and 30 mm/min, respectively. Scale bars, (A) 1 mm; (a₁, a₂) 100 μm.

(B) Slices were cut in the frequency of 180 Hz and the feed rate of 120 and 140 mm/min, respectively. Scale bars, (B) 1 mm; (b₁, b₂, b₃, b₄) 100 μm.

Another key evaluation indicator of a vibratome is the thickness range of the cut slices that it can achieve. Here, the success of cutting is defined as the cut slice without any defects. Under this definition, the 180-Hz vibratome was used to cut an agarose-embedded C57BL/6J mouse brain and liver, respectively. Figure 4A depicts the cut brain slices of thickness ranging from 10 to 1000 μm (also see Video S2, an demonstrative video to show the successed in cutting the brain slice with a thickness of 20 μm, related to Figure 4A). The micro-optical imaging of the 10-μm brain slice was performed through light microscopy (Olympus IX73, Japan) that no visible defects were observed. Figure 4B depicts the liver slices of thickness ranging from 4 to 1000 μm and the micro-optical imaging of the 4-μm liver slice. It can be observed that all vascular cavities well persevered. These results indicated that the new vibratome could cut the brain tissue into slices at least as thin as 10 μm and the liver tissue as thin as 4 μm.

Figure 4.

The mouse brain and liver tissue cutting thickness test of 180-Hz vibratome

(A) Agarose-embedded brain tissue sections of different cut thickness ranging from 10 μm to 1 mm (left), and the microscopic imaging of the PI-stained 10 μm slice (right). Scale bars, 4 mm and 1 mm, respectively.

(B) Agarose-embedded liver tissue section of different cut thickness ranging from 4 μm to 1 mm (left), and the microscopic imaging of the PI-stained 4 μm slice (right). Scale bars, 4 mm and 1 mm, respectively.

Video S2. Demostrative video of cutting agarose-embedded brain sample with a thickness of 20 μm, related to

Figure 4A

Perform the mouse brain and liver organ-wide imaging via the vibratome-based fluorescent MOST system

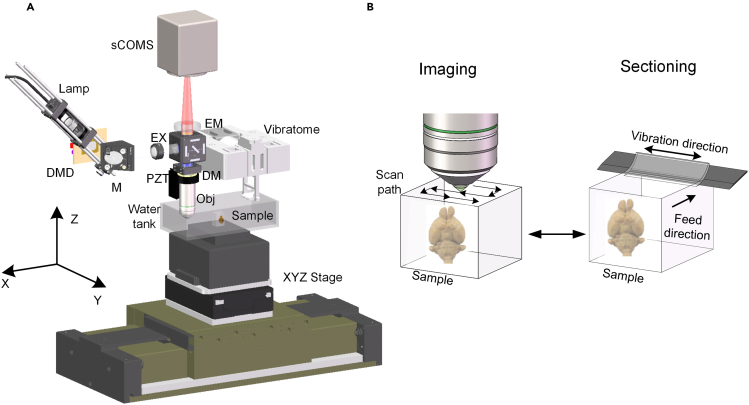
To further demonstrate the superior capacity and potential application of the new vibratome, it was integrated with an SIM system to form a fluorescent MOST system, as depicted in Figure 5A. The SIM system was reported in our previous paper (Gong et al., 2016; Jiang et al., 2017), in which a DMD (XD-ED01N, X-digit, China) was used to add period patterns in the incident beam. To perform optical sectioning illumination, an objective (XLUMPLFLN 20X/1.0NA, Olympus, Japan) was mounted on a piezo stage to perform stack scanning, and a 3-axis linear stage (X: ABL20030, Y: ALS130-050, Z: AVL125, Aerotech, USA) was used to move the sample for mosaic scanning and tissue sectioning. A sCMOS camera (ORCA-Flash 4.0, Hamamatsu, Japan) was used to capture images. This optical imaging system can perform the data acquisition at a voxel resolution of 0.32 × 0.32 × 2 μm³. Figure 5B presents the organ-wide imaging process; we first used the SIM to perform in situ imaging combined with a mosaic scanning strategy to acquire the superficial layer information of the sample. We then used the vibratome to remove the imaged layer and repeat this process until the whole organ was imaged.

Figure 5.

Integration of the new vibratome with SIM for whole-organ imaging

(A) Schematic diagram of the SIM system. It comprises a wide-field fast structured illumination microscope to obtain images and a high-frequency vibratome to remove the imaged layer. (DMD, digital micromirror device; M, mirror; EX, excite filter; DM, dichroic mirror; PZT, piezo stage; Obj, objective lens; and EM, emission filter).

(B) Schematic representation of the whole-organ imaging process. The agarose-embedded sample moves between the SIM and the vibratome alternately. The SIM acquires the entire cross-sectional data in a mosaic scanning imaging manner. After the imaging process is completed, the imaged tissue is removed via the vibratome.

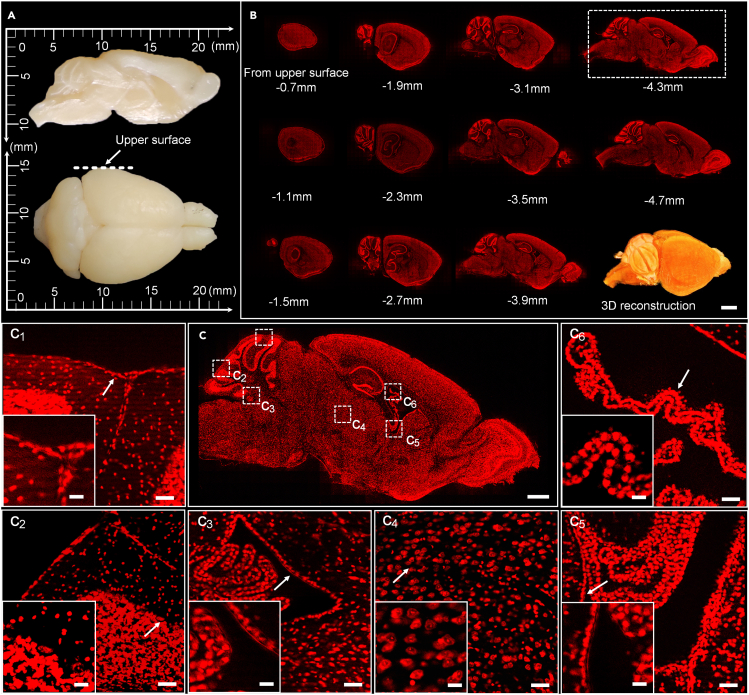
In the first experiments, an agarose-embedded brain sample (C57BL/6J mouse) was immersed in a PI solution, in which the cytoarchitecture was counterstained automatically. Figure 6A displays an actual mouse brain of size approximately 18 × 10 × 6 mm³. Figure 6B presents the imaging results of the brain in the sagittal planes. Because of the symmetrical form of the brain, only images of one-half of the brain are displayed in Figure 6B. The PI-stained results indicated that the cutting quality of the cross section was excellent for submicron resolution precision imaging. The data integrity demonstrated the high repeatability of the vibratome and the stability of the cutting process. Figure 6C depicts the enlarged view of the dashed rectangle in Figure 6B, which was in the middle of the brain (4.7 mm from the upper surface). Here, c₁–c₆ regions in Figure 6C represent different characteristic parts. To be more specific, c₁ depicts the boundary between tissues and the embedding medium; c₂ depicts the junction of cerebellar gray and white matter with a difference in cell density; c₃ depicts the junction of the cerebellum and medulla oblongata that contains cavity and membrane structures; c₄ depicts the part with uniformly distributed cell body; c₅ and c₆ depict the edge and the meninges of the ventricle. Conventionally, the parts such as c₁ and c₂ that with microstructures of a great difference in mechanical properties are difficult to obtain consistently high quality, while the parts such as c₃, c₅, and c₆ are located at the edge of cavities or containing membrane structures can be easily damaged during the cutting process because of lacking support/stiffness. But the results in Figure 6 proved that the new vibratome can avoid these problems.

Figure 6.

Imaging of a mouse brain

(A) Main view (top) and top view (bottom) of the PFA-fixed mouse brain.

(B) Sagittal images of PI-stained cytoarchitecture which are spaced 400 μm apart. Scale bar, 2 mm.

(C) Enlarged view from the dashed box in (B), while c₁–c₆ are enlarged views of the dashed in (C). Scale bars, (C) 1 mm; (C₁, C₂, C₃, C₄, C₅, C₆), 50 μm; inset graphs, 20 μm.

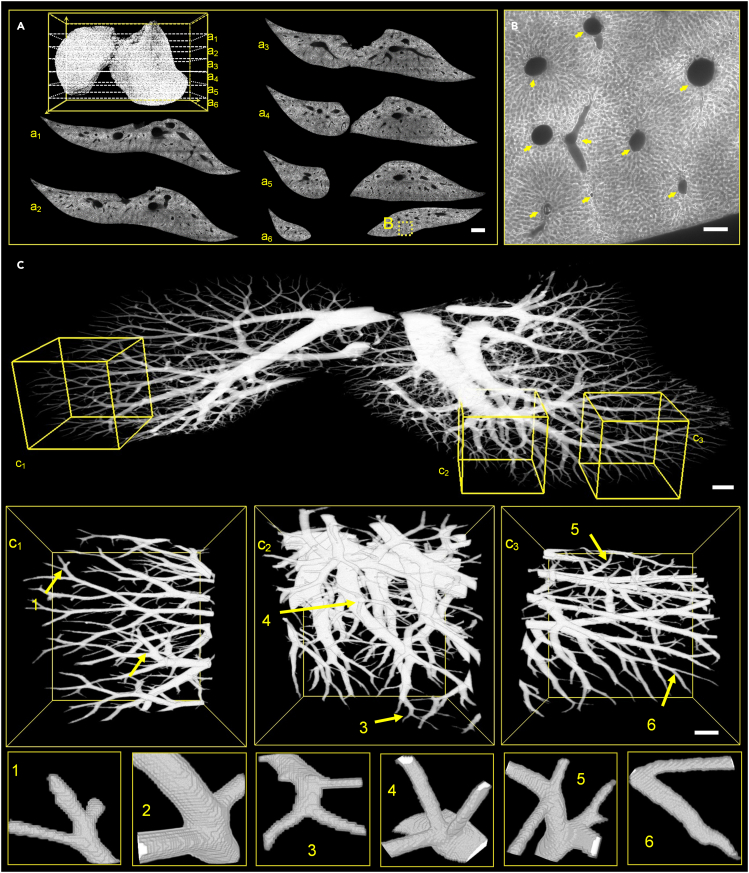
In the second experiment, an agarose-embedded liver sample (mT/mG mouse) was used, where the cell membrane was labeled with tdTomato fluorescence. Figure 7A presents the 3D reconstruction of the median lobe of mouse liver from 5,600 acquired images, which was approximately 18 × 7 × 6 mm³ in size. Here, a₁–a₆ were six selected cross sections, showing that the shape of the liver lobe was gradually changed from a connected whole to two separated halves. Figure 7B depicts the enlarged view of the dashed rectangle in a₆, where the pointed black holes were vascular structures. These features can be extracted and used to reconstruct the vascular network via Amira software (6.1.1) as displayed in Figure 7C. The entire network is 3D continuous without breakage, which proved that the new vibratome can provide excellent cutting quality for organs containing dense cavity structures. To show finer details, c₁, c₂, and c₃ depict the enlarged view of the dashed cube in Figure 7C, where c₁ and c₃ were parts located at the entry side and exit side of the vibration cutting process, indicating that the whole cutting process is stable; and c₂ was the part of dense vascular structures with sharp changes in size, which still can be well cut. Subgraphs 1–6 denote vessel branches in c₁, c₂, and c₃, showing that the vibratome can cut vascular structures at arbitrary angles. These results again confirmed that the new vibratome can be used for cutting tissues containing cavities.

Figure 7.

Imaging of a mouse liver

(A) 3D reconstruction of a liver lobe, where a₁–a₆ are selected cross sections in (A). Scale bar, 1 mm.

(B) Enlarged view from the dashed box in a₆. Scale bar, 100 μm.

(C) 3D reconstruction of the vessel network from the dataset, while c₁, c₂ and c₃ are enlarged views of the dashed in (C), subgraphs 1–6 are vessel branches pointed in c₁, c₂ and c₃. Scale bars, (C) 500 μm; (C₁, C₂, C₃), 200 μm.

Discussion

Advantages of high-frequency vibration cutting mode

A vibratome operated at a high frequency exhibits two benefits when used for cutting soft tissues. From the cutting results presented in Figure 4, first, the sample feed rate increased at a high-frequency cutting mode. To the best of our knowledge, this phenomenon has not been explained previously, and the mechanism of the vibrating blade cutting on the soft tissue has not been fully deciphered. According to our understanding, a high-frequency vibrating blade, coupled with an advancing tissue, can increase the number of destructions per unit time at the contact edge, resulting in an easier cut, which increases the sample feed rate without compromising the cutting quality. This advantage is particularly important in whole-organ imaging, especially for large volume biological samples (Herculano-Houzel, 2009). As depicted in Table 2, for a mouse brain with an average size of 20 × 11 × 8 mm³, if cutting with a thickness of 20 μm and a feed rate of 20 mm/min via the traditional 85-Hz vibratome, the overall acquisition time for organ-wide imaging is about 77 hr, where the cutting time accounts for about a quarter, i.e., 20 hr (Gong et al., 2016). Using the novel 180-Hz vibratome with a feed rate of 120 mm/min, the cutting time can be reduced to 3.3 hr. In the near future, for a macaque brain of size 75 × 55 × 45 mm³, the cutting time can be reduced from 625 hr (26 days) to 104 hr (4.3 days), and for a human brain of size 167 × 149 × 93 mm³, the cutting time can be shortened from 2615 hr (109 days) to 436 hr (18.2 days), which can greatly improve the mesoscopic brain science study efficiency.

Table 2.

Estimation of various brain tissues cut by 85-Hz and 180-Hz vibratomes

		Mouse	Macaque	Human
Size (mm3)		20 × 11×8	75 × 55×45	167 × 149×93
Estimate of whole-brain cutting time	85 Hz (Jiang et al., 2017)	20 hr	625 hr	2615 hr
	180 Hz	3.3 hr	104 hr	436 hr

Second, a high-frequency vibrating blade can cut tissues with cavities. The anatomical structures of most organs contain cavities, such as ventricles in the brain and central veins in the liver. Conventionally, such structures are destroyed when cut by commercial vibratomes because they lack sufficient physical support, that is, agarose molecules cannot penetrate the interior of these tissues. However, the cutting results depicted in Figures 6 and 7 indicate that the local hardening effect is enhanced at a higher frequency, to more specific, Young's modulus/shear modulus of the soft tissue increases as the vibration frequency increases, which improves the cutting quality (Arbogastal and Marguliesal, 1998).

Comparison with state-of-the-art vibratomes

Table 3 presents a comparison of performance between our DP–DP flexure-based vibratome with the P–P flexure-based system (Wang et al., 2019). It shows that our vibratome has a larger amplitude (1.0 vs. 0.3 mm). Because based on theory calculations, for the beam of the same size, the stiffness K_{Y_DP–DP} was two times smaller than K_{Y_P–P}. That means the DP–DP flexure has two times larger stroke/amplitude than the P–P flexure when driven by the same force, which can help to improve the cutting quality as mentioned before. Besides, for the same frequency, the P–P flexure either uses larger l or smaller b, both with a lower stiffness ratio R, which reduces the effect of suppressing motion errors. Therefore, as depicted in Table 3, our DP–DP flexure achieved a thinner cutting thickness and a higher cutting precision (4 μm and 212 nm, respectively) than did the P–P flexure. The commercial system using the parallelogram flexure, such as the Leica VT 1000S, can only obtain complete slices with a thickness larger than 30 μm (Rivera et al., 2013).

Table 3.

Comparison with state-of-the-art vibratome

Flexure	DP-DP flexure-based vibratome	P-P flexure-based vibratome
Frequency (Hz)	180	0–250
Amplitude (mm)	0–1.0	0–0.3
Feed rate (mm/min)	0–120	0–12
Cutting thickness (μm)	4–1000	10–500
Longitudinal beating (nm, RMS)	212	500

Except whole-organ imaging, other fields such as histology or pathological examination also need to cut various organs into thin slices, i.e., researchers or doctors obtain well-cut thin slices from the target tissue and then examine their microanatomy under a light microscope (Annese et al., 2014; Chen et al., 2020). To observe precision structures at cellular resolution, cut slices of thickness less than 10 μm and flatness better than 1 μm are ideal (Schmitt et al., 2019). As illustrated in Table 3, our new vibratome can fully meet these needs.

Limitations of the study

In the present study, we developed a high-precision vibratome for agarose-embedded tissue cutting. Recently, another high elastic material, i.e., the hydrogel, has also been widely used in the tissue imaging field, such as expansion microscopy (Gotz et al., 2020) and optical clearing (Chung and Deisseroth, 2013; Yang et al., 2014). The superior biocompatibility and permeability make it ideal for large-volume tissue embedding (Zhou et al., 2020). Through online optical clearing methods that combine hydrogel embedding with high-frequency vibration cutting, potentially it can be used to obtain complete 3D data of a marmoset or even human brain at a consistent submicron resolution (Wu et al., 2019). But compared with agarose, the hydrogel has a much lower Young's modulus (1–10² vs 1–10³ kPa) (Czerner et al., 2015), meaning it is a kind of extremely soft material. Hence, to make this broad application prospect material practical, it needs to introduce a material modification to reinforce Young’s modulus as well as develop a higher frequency vibratome to match with mechanical properties of the material. It still has a great effort to make.

In general, we modeled and designed a precision vibratome based on the DP–DP flexure and achieved a longitudinal motion error better than 250 nm. Based on this model, a high-frequency vibratome can be developed. Here, we built a 180-Hz vibratome and integrated it with an SIM system to perform whole-organ imaging, such as imaging of the brains and livers of mice. The results confirmed the high-speed and high-quality cutting capacity of the novel vibratome.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
PBS	Sigma-Aldrich	P3563
Paraformaldehyde	Sigma-Aldrich	158127
NaIO4	Sigma-Aldrich	311448
Agarose	Sigma-Aldrich	A6013
PI	Sigma-Aldrich	P4170
Experimental models: Organisms/strains
C57BL/6J	Jackson Laboratory	000664
mT/mG	Jackson Laboratory	007676
Software and algorithms
Amira software (6.1.1)	FEI, Mérignac Cedex, France	http://www.fei.com/software/amira-avizo
MATLAB 2017a	Mathworks, Inc.	https://www.mathworks.com
SOLIDWORKS 2017	Dassault Systemes	https://www.solidworks.com

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Jianwei Chen (jchen1@ hust.edu.cn).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Animals

Three eight-week-old C57BL/6J male mice (Jackson Laboratory, Bar Harbor, ME, USA) and a twelve-week-old mT/mG male mouse (Jackson Laboratory, Bar Harbor, ME, USA) were used in this study. The mice were kept in a 12-h light/dark cycle with food and water provided ad libitum. All the experiments on animals were performed according to procedures approved by the Institutional Animal Ethics Committee of Huazhong University of Science and Technology.

Method details

Tissue preparation

The mice were anesthetized with a 1% sodium pentobarbital solution and subsequently intracardially perfused with 0.01 M PBS (Sigma-Aldrich, USA), followed by 4% PFA (Sigma-Aldrich, USA) in 0.01 M PBS. Then, the organs, such as the brains or livers, were excised and post-fixed in 4% PFA at 4°C for 24 h. Next, each intact organ was rinsed overnight at 4°C in 0.01 M PBS and prepared for embedding.

Embedding method

To prepare the embedding medium, oxidized agarose was prepared by adding agarose Type I-B (Sigma-Aldrich, USA) to a 10 mM NaIO₄ (Sigma-Aldrich, USA) solution and stirred for 2–3 h at room temperature without exposure to sunlight. Then, the solution was repeatedly washed and resuspended in PBS to increase the final concentration to 2%–6%. To form the final sample, the organs were pat-dried and placed in a cubic silicone mold filled with melted oxidized agarose. The mold was then placed in a 55–65°C water bath for 0.5 h until the surfaces of the organs were fully crosslinked with agarose. Then, the mold and organs were left at room temperature for 0.5 h to allow the agarose to solidify. Finally, the agarose-embedded organs were separated from the mold and stored in PBS at 4°C before imaging.

The mouse brain and liver imaging

To demonstrate the wide applicability of the vibratome, the mouse brain and liver were imaged via the vibratome-integrated fMOST (Gong et al., 2016). The brian sample was immersed in a water bath that containing PI solution for real-time staining of cytoarchitecture, while liver sample was immersed in a water bath that containing PBS solution. Shallow tissue of a thickness of 8 μm was imaged with a voxel resolution of 0.32 × 0.32 × 2 μm and four consecutive images were obtained. Then the imaged tissue was cut via the vibratome to expose a smooth new block surface for next round imaging. The full-volumetric imaging was performed with repeated cycle of tissue imaging and cutting until the whole sample data was acquired. For experiments of cutting thickness test, the collected slices was imaged with a light microscopy (Olympus IX73,10X/0.4NA).

The reconstruction of partial vascular network of mouse liver

We labeled the contours of the blood vessels of the mouse liver using threshold segmentation in Amira software, and reconstructed the vascular network based on their connectivity.

Published: September 24, 2021

Data and code availability

Any additional information required to reanalyze the data reported in this paper is available from the Lead Contact upon request.