Abstract
Various studies have been conducted to examine the effect of COVID-19 on stock prices. However, these studies failed to examine the effect across quantile distributions of both dependent and independent variables. This study pays particular attention to the emerging 7 countries and examines the effect of the novel coronavirus 2019 (COVID-19) pandemic on stock prices. We use quantile unit root and quantile cointegration tests to examine the integrating properties of COVID-19 cases and deaths with stock prices and use quantile-on-quantile regression (QQR) to examine the relationship across quantile distributions of both dependent and independent variables. Quantile cointegration estimates indicate that stock prices are integrated with COVID-19 cases whereas QQR estimates indicate a weak positive relationship at the upper quantiles of stock prices, and a strong negative effect is found at the lower quantiles of stock prices. Policy implications are recommended based on the findings of this study.
Keywords: Quantile-on-quantile regression, COVID-19, Quantile cointegration, E7 stock markets
1. Introduction
A new type of coronavirus disease, discovered in Wuhan city of China, was officially named COVID-19 on December 31, 2019. Within three months, this disease spread to many parts of the world through international travel. Since then, it has affected various social, political, medical, and economic activities at the global level. Goodell (2020), also highlighted that COVID-19 will likely affect financial markets, institutions, and financial systems. Therefore, different governments have reacted in different ways by announcing various economic relief packages to mitigate the adverse effects of the COVID-19 pandemic.1
It is expected that the financial impact of COVID-19 in financial markets would be more severe than other global pandemic viruses such as Severe Acute Respiratory Syndrome (SARS) and Middle Eastern Respiratory Syndrome (MERS). Within 4 months, it has imposed a more significant negative impact on the global economy than MERS and SARS. A recent report by the Organization of Economic Cooperation and Development (OECD) (2020) also demonstrated that COVID-19 has had a more severe effect on the agricultural, manufacturing, and service sectors, which ultimately caused a decline in gross domestic product around the world.
The rapid spread of the COVID-19 virus affected every economic sector, including stock markets. There have been large fluctuations in the stock markets of both developed and emerging countries. However, due to the strong foundations of the stock markets in developed countries, COVID-19’s effect on stock market performance may be temporary and those markets may pick up during the economic recovery. However, emerging countries may be affected for a longer period by the pandemic. The United Nations supported this view that the negative effect of the COVID-19 pandemic may be more severe in less developed countries than in more developed countries (Bruckner and Mollerus, 2020). Prior research supports the view that, as compared to those in developed countries, return and risk profiles are higher in developing countries (Harvey, 1995). This study, therefore, analyzes the asymmetric impact of the COVID-19 pandemic on stock prices of emerging 7 (E7) countries, namely, China, Mexico, Turkey, Indonesia, India, Russia, and Brazil. We select the E7 countries since they represent a major part of the emerging economies. These countries stock markets are more vulnerable to unfavorable consequences (Hashmi and Chang, 2021; Hashmi et al., 2021; Chang et al., 2019a, b).
Few studies have examined the effect of COVID-19 on financial stock markets. Ramelli and Wagner (2020) indicated that as the spread of the pandemic increases, it negatively affects the stock markets, whereas Gormsen and Koijen (2020) concluded that this pandemic did not affect the stock markets of Iran, South Korea, and Italy until February 20, 2020. However, these stock markets started declining after February 20, 2020. Likewise, the United States (US) stock market started declining after March 18, 2020. Liu et al. (2020) also supported the negative influence of this pandemic on stock markets. He, Sun et al. (2020) found that COVID-19’s effect on stock prices depends upon the severity of the crisis. Alfaro et al. (2020) concluded an adverse effect of COVID-19 on stock market prices. Heyden and Heyden (2020) determined that the information about the first death and first pandemic case affected stock markets differently wherein the stock market is negatively affected by the announcement of the first death. However, the limitation of these studies is that they did not consider emerging markets. As discussed above, the emerging markets are more likely to be affected than developed markets since there are higher returns and risks in developing countries.
Keeping with the above limitations, this study contributes to the existing literature in two ways. First, this is the first study that pays special attention to the E7 countries. Second, this study uses advanced techniques, such as quantile cointegration, quantile unit root testing, and quantile-on-quantile regression (QQR) approaches. These advanced techniques enable an examination of the relationship across the distribution of the series as well as on conditional means and thus exhibit a comprehensive relationship between the COVID-19 pandemic and E7 stock prices Bhutto and Chang (2019); Chang and Rajput (2018); Chang et al. (2018) and Anjum et al. (2017).
The remainder of this paper is organized as follows. Section 2 discusses the empirical literature; Section 3 mentions the data sources and measurement and discusses the quantile cointegration test, quantile unit test, and QQR approach. Section 4 discusses the findings, and Section 5 provides the conclusion of the study as well as policy implications.
2. Literature review
This section is discusses the empirical literature that exists examining the relationship between the COVID-19 pandemic and stock market performance. He et al. (2020) examined the spillover and direct impact of COVID-19 on the stock markets of the US, Japan, Germany, Spain, France, South Korea, Italy, and the People’s Republic of China using t-tests as well as non-parametric Mann–Whitney tests. Their estimates indicate that stock markets negatively respond to the COVID-19 pandemic in the short run. They also established a feedback spillover effect between American and European, and Asian countries. Liu et al. (2020) analyzed the short-run effect of COVID-19 on the stock markets of the 21 countries. Using an event study method, their findings concluded that stock markets adversely responded to the COVID-19 pandemic. Yan et al. (2020) analyzed the impact of COVID-19 on the stock market and suggested how an individual investor can profit from the market during the pandemic. They examined the effect of past outbreaks and pandemics and concluded that those events negatively affected the stock markets in the short run, but in the long run, the markets adjusted and, as a result, stock prices increased in the long run. Therefore, they recommended that to profit from such events, investors should initially sell the shares of those industries that are quickly affected by the virus, whereas those shares may be bought back when prices in those industries have significantly decreased. Baker et al. (2020) examined the effect of COVID-19 on US stock markets using text-based methods and concluded that although previous pandemics like the Spanish flu had a moderate effect on the US market, COVID-19 adversely affected the US stock market. Adenomon et al. (2020) analyzed the effect of COVID-19 on the stock market performance of Nigeria. Using the GARCH model, their study concluded that the Nigerian stock market negatively responded to the COVID-19 pandemic.
Yilmazkuday (2020) also analyzed the effect of COVID-19 on the S&P 500 index. For this purpose, he used a structural VAR (SVAR) model and found that a daily 1 % cumulative rise in COVID-19 cases caused a 0.01 % cumulative decrease in the S&P 500 index stock market prices after one day, whereas it caused a 0.03 % a cumulative decrease after one month. Ahundjanov et al. (2020) also examined the impact of Google search queries related to COVID-19 on the stock market performance of developing and developed countries. Their findings, using a structural VAR (SVAR) model based on Bayesian inference, concluded that concluded Google search queries negatively affected the financial indices. More specifically, their estimates indicate that a 1 unit increase in Google search queries related to COVID-19 caused a cumulative decrease in global financial indices from around 0.38 % to 0.069 % after one day, whereas it caused a cumulative decrease in global financial indices from around 0.054 % to 0.150 % in one week. Papadamou et al. (2020) analyzed the relationship between the COVID-19 pandemic and stock market volatility in various countries in Asia, Europe, Australia, and the US. Their findings, based on a panel VAR model, concluded a positive relationship between Google trend metrics for stock market volatility and the COVID-19 pandemic.
Goodell and Goutte (2021a, 2021b) examined whether assets become more correlated during crisis periods. Using advanced econometric techniques like wavelet coherence and neural network analyses, they examined the role of COVID-19 on the comovements of four cryptocurrencies with seven equity indices. Their findings indicated that, as the COVID-19 progressed, the comovement between cryptocurrencies and equity indices increased, however, this correlation was moderate positive or negligible for most of the cases, which suggests that cryptocurrencies can not be used as diversification during economic downturns. An exception was found in the movement of tether. It negatively moves with equity indices which therefore suggests that tether can be used as a safe haven during economic downturns. Using wavelet methods, Goodell and Goutte (2021a, 2021b) examined the relationship between COVID-19 world deaths and Bitcoin prices and found that in post-April 5, 2020 period, COVID-19 caused an increase in Bitcoin prices.
Although there is a growing amount of literature that focuses on the effect of COVID-19 on stock market prices, the empirical literature related to E7 countries is limited. This study contributes to the existing literature by focusing on the effects of COVID-19 on the stock market performance of the E7 countries, namely, Indonesia, Mexico, India, China, Brazil, Russia, and Turkey. We employ novel techniques, namely, quantile cointegration test, quantile unit root test, and QQR approach. As per the authors’ knowledge, these techniques have not been used in the extant literature to examine the effect across various quantiles of the distribution as well as on the conditional mean. Specifically, the quantile-on-quantile approach helps analyze the effect on various quantiles of the total number of COVID-19 cases on stock market prices. For robustness purposes, we also examine the effect of the total number of deaths on stock market prices at various quantiles of both independent and dependent variables.
3. Data and methodology
3.1. Data analysis
To examine the relationship between COVID-19 cases and E7 stock prices, we use daily data from January 20, 2020, to June 19, 2020. Starting and end periods were selected based on the availability of data at the time of this study. The adjusted closing prices for each country were obtained from Bloomberg, whereas COVID-19 confirmed cases and death data for each country was obtained from the World Health Organization website. COVID-19 case data were deleted for the days with missing stock price data. We use the log of both COVID-19 and stock price data, except the data used in descriptive statistics (Table 1 ).
Table 1.
Descriptive statistics of stock prices and COVID-19 cases.
| Country | Mean | Maximum | Minimum | Standard dev. | Jarque–Bera | p-value |
|---|---|---|---|---|---|---|
| Panel A: Stock prices | ||||||
| Brazil | −0.123 | 13.908 | −14.779 | 4.137 | 6.432 | 0.048 |
| Russia | −0.136 | 7.71 | −8.282 | 2.275 | 9.211 | 0.010 |
| India | −0.150 | 8.975 | −13.525 | 2.945 | 8.679 | 0.013 |
| China | −0.0420 | 3.14 | −7.725 | 1.668 | 7.562 | 0.021 |
| Turkey | −0.200 | 6.938 | −10.568 | 2.679 | 7.619 | 0.021 |
| Mexico | −0.172 | 4.269 | −6.423 | 2.054 | 3.492 | 0.172 |
| Indonesia | −0.212 | 10.191 | −6.579 | 2.278 | 8.652 | 0.013 |
| Panel B: COVID-19 cases | ||||||
| Brazil | 25189016 | 69074 | 34.00 | 16900.06 | 11.671 | 0.003 |
| Russia | 9685.653 | 29039 | 4.000 | 7341.759 | 60.282 | 0.000 |
| India | 36073.03 | 97894 | 3.000 | 29715.32 | 19.849 | 0.000 |
| China | 40.24088 | 352.00 | 0.000 | 47.771 | 1417.175 | 0.000 |
| Turkey | 3633.099 | 33198 | 0.000 | 7162.06 | 1839.062 | 0.000 |
| Mexico | 4561.442 | 22089 | 0.000 | 3174.108 | 399.934 | 0.000 |
| Indonesia | 2254.467 | 8369.0 | 0.000 | 1792.099 | 19.677 | 0.000 |
Note: This table presents descriptive statistics for stock returns and COVID-19 cases data. Panel A presents the descriptive statistics for stock returns of emerging 7 countries whereas Panel B presents the descriptive statistics related to COVID-19 cases. Jarque–Bera test is used to test the null hypothesis that the data is normally distributed. P-values below 0.05 indicate the rejection of the null hypothesis.
The mean returns, presented in Table 1 (Panel A), are negative for stock prices of all E7 countries, which indicates that these stock markets have, on average, performed below average during the COVID-19 period. The mean returns are highest for China, whereas its standard deviation is lowest, indicating that the Chinese stock market was the least affected compared to other emerging countries. Indonesian stock prices have the lowest means of returns (–0.212), followed by Turkish stock prices (–0.200). The Jarque–Bera values are statistically significant for all countries, except Mexico, which indicates that the returns of these countries are not normally distributed. The mean number of cases (Table 1, Panel B) is the lowest for China, indicating that China successfully dealt with the COVID-19 pandemic, whereas other countries were highly affected by this crisis (Chang et al., 2020a).
3.2. Quantile unit root test
Galvao (2009) extended the quantile unit root test initially proposed by Koenker and Xiao (2004). This test statistic checks the data stationarity across different quantiles as well as the conditional mean of the variable. However, the test statistics proposed by Koenker and Xiao (2004) do not incorporate covariate and time trends in the quantile autoregressive (QAR) model (Chang et al., 2020b; 2020c; 2020d; Chang, 2020). Galvao (2009) extended Koenker and Xiao (2004) by considering these issues. To check the stationarity of the variables across various quantiles and the conditional mean of the series, we use the quantile autoregressive (QAR) unit root test proposed by Galvao (2009). The following quantile regression model is used to check the unit root properties of the variables.2
| (1) |
where represents the quantile of ), represents the drift term, indicates persistent parameter, shows linear trend, shows the error for different quantiles of the conditional distribution.
3.3. Quantile cointegration approach
Recent studies related to finance and economics indicate that cointegration among the variables varies across different quantiles (Syed et al., 2019). Therefore, this study focuses on the novel quantile cointegration test proposed by Xiao (2009). This test analyzes the effect on the shape, scale, and location of the conditional distribution of the feedback variable. Xiao (2009) further extended the cointegration model used by previous studies (Saikkonen, 1991) by dividing the cointegrating equation errors into lead-lag terms. This extended model is an innovation of previous traditional models since it accounts for the endogeneity issues characteristic of previous cointegration techniques. Xiao (2009) defined quantile cointegration in such a way that the coefficients of quantile cointegration vary across different quantile levels.
In this model, indicates the vector of constants. The model is represented as follows:
| (2) |
| (3) |
is defined as in Eq. (1), and is the drift term, indicates persistent parameters, and shows the errors for different quantiles of the conditional distribution.
Next, the model based on the quadratic term is shown as follows:
| (4) |
The terms in Eq. (4) are defined as above. To measure the stability of cointegrating coefficients, Xiao (2009) proposed a test as given in Eq. (4). The null hypothesis in this test is that , where represents all quantiles. Further, the supremum norm function is derived as test statistics by Xiao for the change of absolute values . Therefore, this study uses test statistic for all quantities, as well as 1,000 Monte Carlo simulations to obtain the critical values of test statistics.
3.4. Quantile-on-quantile regression
Next, to examine the comprehensive relationship between COVID-19 cases and E7 stock indices, we use the QQR approach proposed by Sim and Zhou (2015). This model is an extended version of standard quantile regression, which is established by combining the non-parametric estimation and the standard quantile regression technique. The standard quantile regression examines the impact of the independent variables across various quantiles as well as the conditional mean of the explained variable. Therefore, the quantile regression technique gives better results than the ordinary least squares method. Stone (1977) and Cleveland (1979) proposed traditional linear regression, which examines the effect of specific quantiles of the independent variable on the conditional mean of the dependent variable. Therefore, combining traditional linear regression and standard quantile regression enable us to analyze the effect on various quantiles of both the independent and dependent variables. Therefore, it provides deeper insight into the relationship between the independent and dependent variables.
In this study, we use the extended version called the QQR technique proposed by Sim and Zhou (2015) to analyze the effect of various quantiles of COVID-19 cases on different quantiles of E7 stock indices. For this purpose, we use the following non-parametric quantile regression model.
| (5) |
where indicates the stock prices for each of the E7 stock markets in time represents the number of COVID-19 cases in time and denotes quantile distribution of the number of COVID-19 cases. Next, the quantile error term is represented by where becomes zero. is not known because the information is not available on the relationship between COVID-19 cases and E7 stock indices. The choice of bandwidth is very important to identify when the non-parametric technique is applied. When the bandwidth is large, it may increase the deviation of estimation but would decrease the variance and vice versa. In this study, the bandwidth parameter h = 0.05 is selected following the previous research such as Sim and Zhou (2015).
4. Results discussion and analysis
This section discusses the results related to the impact of COVID-19 cases on the stock indices of the E7 countries. We use the quantile cointegration test and quantile unit root test to analyze the integrating properties across the quantile distribution of the dependent variable. In addition, this study uses quantile regression to analyze the effect on quantiles of stock prices as well as COVID-19 cases. The following subsections provide the findings related to these test statistics.
4.1. Quantile unit root and quantile cointegration test
First, we check the stationarity of the variables using the quantile autoregressive (QAR) unit root test proposed by Xia (2009). Table 2 presents the results of the quantile unit root test in which persistent values are represented by , t statistics are represented by t-stats, and the critical values are represented by the critical values (CV) against each quantile. The null hypothesis against each quantile is that where the null hypothesis indicates the non-stationary behavior of the variables. The bold values in Table 2 indicate the rejection of null hypothesis at a 5% significance level. In this study, the null hypothesis for stock prices in Turkey is rejected at lower quantiles, which suggests that Turkish stock prices are stationary at lower quantiles, whereas Turkish stock prices are non-stationary at the upper and median quantiles. The rest of the variables for stock prices as well as COVID-19 cases are non-stationary for all quantiles.
Table 2.
Results of the quantile unit root test.
| Quantile | Brazil |
Russia |
India |
China |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α(τ) | t-stats | CV | α(τ) | t-stats | CV | α(τ) | t-stats | CV | α(τ) | t-stats | CV | |
| Panel A: Unit root test for stock prices | ||||||||||||
| 0.05 | 1.121 | 0.546 | −1.321 | 0.995 | −1.54 | −2.231 | 0.875 | −1.325 | −1.987 | 0.897 | −1.642 | −1.814 |
| 0.25 | 0.897 | −1.542 | −1.895 | 0.958 | −1.512 | −2.231 | 0.897 | −0.725 | −1.654 | 0.985 | −1.214 | −1.895 |
| 0.50 | 0.895 | −2.542 | −2.897 | 0.895 | −1.941 | −2.785 | 1.110 | 0.325 | −2.391 | 0.985 | −1.578 | −2.452 |
| − | 0.954 | −1.231 | −3.214 | 0.854 | −1.321 | −3.124 | 1.121 | 0.421 | −2.514 | 0.875 | −0.912 | −2.895 |
| 0.95 | 0.998 | −2.124 | −3.124 | 1.124 | −1.389 | −3.231 | 0.987 | −0.523 | −2.452 | 0.897 | −0.692 | −3.325 |
| Quantile | Turkey |
Mexico |
Indonesia |
||||||
|---|---|---|---|---|---|---|---|---|---|
| α(τ) | t-stats | CV | α(τ) | t-stats | CV | α(τ) | t-stats | CV | |
| Panel A: Unit root test for stock prices | |||||||||
| 0.05 | 0.875 | −2.425 | −1.312 | 0.895 | −0.810 | −1.695 | 0.524 | −1.754 | −1.422 |
| 0.25 | 0.985 | −2.598 | −2.412 | 0.895 | −1.312 | −1.951 | 0.952 | −2.231 | −2.515 |
| 0.50 | 0.895 | −0.791 | −2.321 | 1.121 | 0.299 | −2.125 | 0.895 | −0.852 | −2.527 |
| 0.75 | 0.985 | −1.810 | −2.543 | 1.124 | 1.211 | −2.652 | 1.121 | −0.124 | −2.844 |
| 0.95 | 0.897 | −0.521 | −2.845 | 1.124 | 1.823 | −2.921 | 1.125 | 1.124 | −2.989 |
| Quantile | Brazil |
Russia |
India |
China |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α(τ) | t-stats | CV | α(τ) | t-stats | CV | α(τ) | t-stats | CV | α(τ) | t-stats | CV | |
| Panel B: Unit root test for COVID-19 cases | ||||||||||||
| 0.05 | 1.111 | 0.556 | −1.521 | 0.965 | −1.64 | −2.531 | 0.955 | −1.465 | −1.977 | −1.95 | 0.544 | −1.774 |
| 0.25 | 0.877 | −1.572 | −1.695 | 0.978 | −1.712 | −2.631 | 0.697 | −0.765 | −1.684 | −1.97 | 0.972 | −2.531 |
| 0.50 | 0.855 | −2.342 | −2.697 | 0.795 | −1.841 | −2.685 | 1.410 | 0.425 | −2.491 | −2.25 | 0.865 | −0.872 |
| 0.75 | 0.954 | −1.431 | −3.514 | 0.554 | −1.521 | −3.224 | 1.321 | 0.451 | −2.554 | −2.56 | 1.126 | −0.126 |
| 0.95 | 0.968 | −2.324 | −3.324 | 1.324 | −1.489 | −3.431 | 0.977 | −0.623 | −2.652 | −2.95 | 1.425 | 1.324 |
| Quantile | Turkey |
Mexico |
Indonesia |
||||||
|---|---|---|---|---|---|---|---|---|---|
| α(τ) | t-stats | CV | α(τ) | t-stats | CV | α(τ) | t-stats | CV | |
| Panel B: Unit root test for COVID-19 cases | |||||||||
| 0.05 | 0.857 | −1.662 | −1.714 | 0.795 | −0.820 | −1.795 | 0.624 | −1.764 | −1.622 |
| 0.25 | 0.975 | −1.314 | −1.795 | 0.695 | −1.512 | −1.751 | 0.852 | −2.531 | −2.715 |
| 0.50 | 0.875 | −0.491 | −2.421 | 1.321 | 0.399 | −2.155 | 0.795 | −0.862 | −2.557 |
| 0.75 | 0.985 | −1.810 | −2.543 | 1.124 | 1.211 | −2.652 | 1.121 | −0.124 | −2.844 |
| 0.95 | 0.897 | −0.521 | −2.845 | 1.124 | 1.823 | −2.921 | 1.125 | 1.124 | −2.989 |
Note: This table indicates critical values (CV), t statistics, (t-stats), and the persistence estimates α(τ), of the quantile unit root test by Galvao (2009) and Koenker and Xiao (2004). Bold values indicate that the null hypothesis is rejected at the 5 % significance level.
Next, this study uses the quantile cointegration test (Xiao, 2009) to examine the cointegration between COVID-19 cases and stock prices in the E7 countries. Table 3 presents these quantile cointegration test results in which β and γ coefficients are the supremum norm values. Moreover, this table presents critical values at the 1 % (CV1), 5 % (CV5), and 10 % (CV10) significance levels. The results indicate that the coefficient values for γ and β are greater than the CV at the 1% significance level. These results, therefore, indicate that cointegration exists between COVID-19 cases and stock prices for all E7 countries.
Table 3.
Results of quantile cointegration test.
| Model | Coeff. | Supτ | Vn(τ) | | CV10 | CV5 | CV1 |
|---|---|---|---|---|---|
| Brazil | |||||
| COVIDt vs. SPt | γ | 290.544 | 121.848 | 274.548 | 360.212 |
| β | 2361.980 | 1258.329 | 2038.357 | 3415.317 | |
| Russia | |||||
| COVIDt vs. SPt | γ | 3471.425 | 1946.786 | 2257.118 | 2842.457 |
| β | 8482.446 | 3931.471 | 4832.778 | 5834.221 | |
| India | |||||
| COVIDt vs. SPt | γ | 289.325 | 98.329 | 124.553 | 193.332 |
| β | 537.436 | 233.466 | 293.567 | 321.392 | |
| China | |||||
| COVIDt vs. SPt | γ | 673.428 | 289.653 | 302.474 | 453.548 |
| β | 938.239 | 402.227 | 542.553 | 748.432 | |
| Mexico | |||||
| COVIDt vs. SPt | γ | 948.557 | 348.971 | 493.672 | 684.369 |
| β | 1835.632 | 993.580 | 1039.654 | 1546.328 | |
| Indonesia | |||||
| COVIDt vs. SPt | γ | 783.557 | 375.448 | 499.256 | 589.578 |
| β | 1246.449 | 204.345 | 548.539 | 934.410 | |
| Turkey | |||||
| COVIDt vs. SPt | γ | 202.898 | 89.547 | 100.006 | 142.475 |
| β | 1598.332 | 861.157 | 1066.499 | 1372.322 | |
Note: In this table, we mention the estimates of the quantile cointegration test for COVID-19 cases and E7 stock prices. We use the quantile cointegration model in Eq. (3) to check the stability of the coefficients γ and β. CV10, CV5, and CV1 denote critical values at the 10 %, 5 %, and 1 % significance levels where these critical values are generated using 1,000 Monte Carlo simulations. This study uses 19 quantiles [0.05–0.95] of the equally spaced grid for generating the test statistics of the quantile cointegration model between COVID-19 cases and E7 stock prices.
4.2. Results based on quantile-on-quantile regression approach
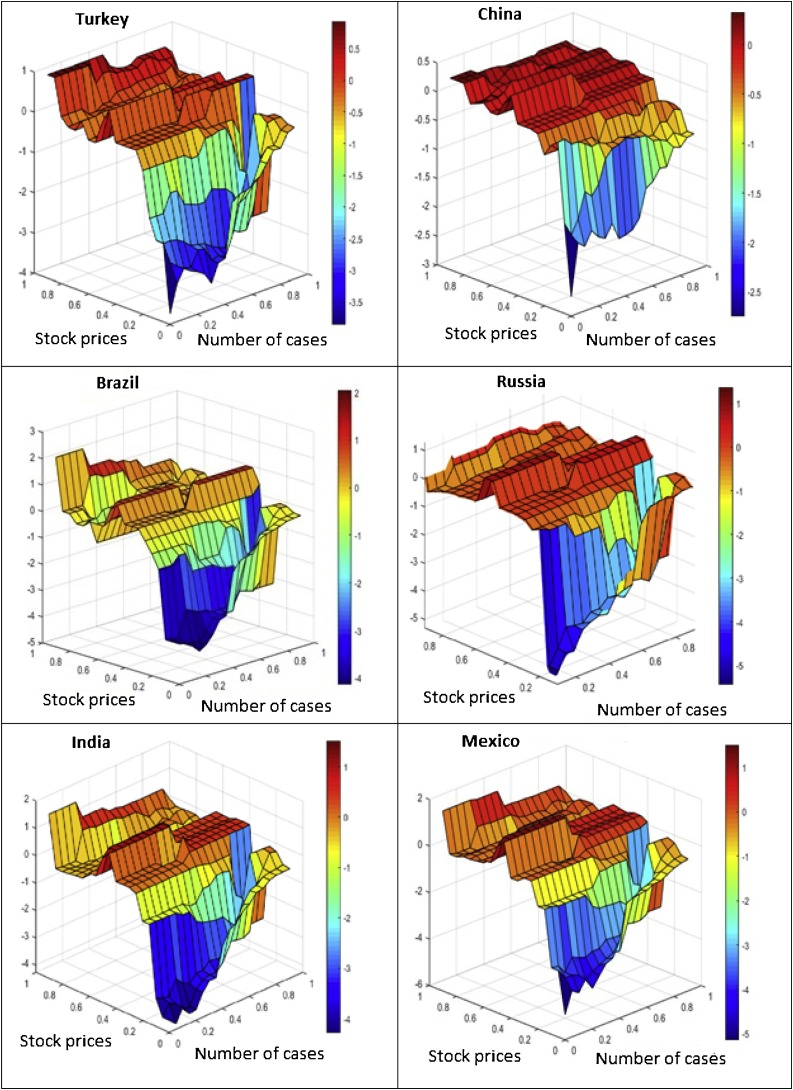
This section provides the results based on the QQR approach. We use this approach to examine the relationship between COVID-19 cases and E7 stock indices. Fig. 1 presents the slope coefficients which indicate the effect of the quantile of the number of COVID-19 cases on the quantile of E7 stock indices. The results indicate that the effect of each quantile of COVID-19 cases on stock indices varies across various quintiles of stock prices.
Fig. 1.
This figure presents the results of quantile-on-quantile regression for COVID-19 cases and stock price data for the emerging 7 countries.
Fig. 1 indicates that Turkey’s COVID-19 cases positively affect stock prices at upper quantiles of stock prices (0.65–0.95). This positive effect continues across all quantiles of COVID-19 cases. This effect becomes negligible during average quantiles of stock prices (0.4–0.65) and becomes negative at lower quantiles (0.05–0.4) of stock prices. It can further be observed that the positive effect observed at the upper quantiles of stock prices is weak since the maximum positive coefficient is one, whereas the negative coefficient observed at lower quantiles of stock prices reaches around four. These results indicate that COVID-19 cases have a weak positive correlation with Turkish stock prices at upper quantiles of stock prices; however, this effect becomes strongly negative at lower quantiles of the stock prices.
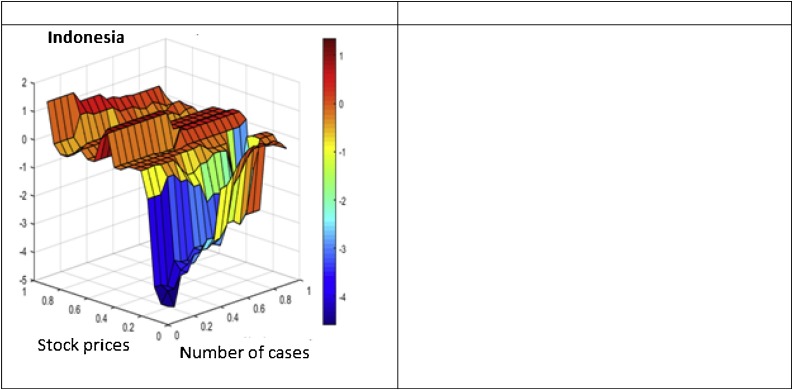
For China, we also find a weak positive relationship between COVID-19 cases and stock prices at upper quantiles (0.65–0.95) of stock prices. This weak positive relationship is consistent across all quantiles of COVID-19 cases. However, this effect becomes negative when we move to the lower quantiles (0.05–0.4) of the stock prices. This negative effect during lower quantiles of stock prices is much stronger during lower and middle quantiles (0.05–0.75) of COVID-19 cases. Conversely, this negative effect becomes weaker when we move to the upper quantiles (0.75–0.95) of the number of cases. The findings for Russia, Mexico, and Indonesia are consistent with the findings for Turkey and China. These results suggest that the number of COVID-19 cases has a strong negative effect on the stock prices of emerging markets like Turkey, China, Russia, Mexico, and Indonesia, especially when these stock markets are in a bearish state.
In Brazil, a positive relationship is found between the upper quantiles of stock prices (0.9–0.95) and lower quantiles (0.05–0.2) of the number of cases where this positive coefficient is around two. The positive effect of the number of cases is weak across all quantiles of COVID-19 cases when stock prices are in the average (0.35–0.65) quantiles. This indicates that an increase in COVID-19 cases increases stock prices during bullish states of the stock market, whereas these cases do not affect stock prices when the Brazilian stock market is in a normal state. Finally, a strong negative effect is observed during lower quantiles of both stock prices and the number of cases. This suggests that the number of cases reduces stock prices when the stock market is in a bearish state. The findings for India are consistent with the findings for Brazil. Like other stock markets, the Brazilian and Indian stock markets are negatively affected by COVID-19 cases when these markets are in a bearish state.
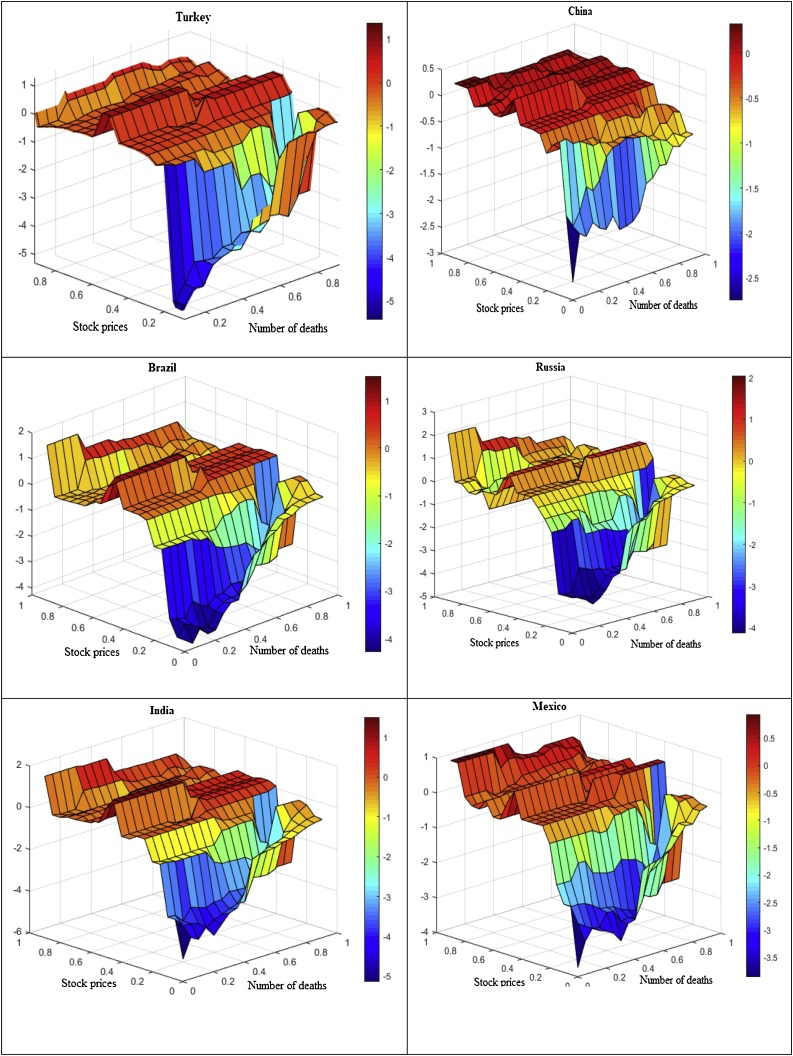
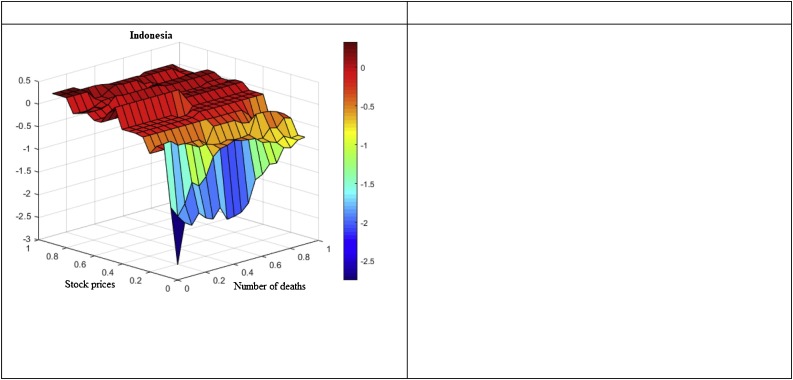
Fig. 2 presents the results using the number of deaths instead of the total number of cases. We present these results to check whether our findings for the total number of deaths are consistent with the findings for the total number of cases. Our estimates (see Fig. 2) conclude that the findings obtained using the total number of deaths are consistent with the findings for the total number of cases.
Fig. 2.
This figure presents the results of quantile-on-quantile regression on number of COVID-19 deaths and stock price data for the emerging 7 countries.
The overall results conclude that total number of cases and deaths positively affect stock prices during upper quantiles of the stock markets; however, this positive effect is weak. Moreover, an almost negligible effect is found during the middle quantiles of stock prices. Finally, a strong negative effect is found during lower quantiles of the stock markets. These results, therefore, suggest that E7 stock markets are more susceptible to COVID-19 cases, especially when these markets are in a bearish state. This may be because the bearish state of the stock market creates more panic for investors and other stakeholders. During this panic state, investors may withdraw their investments fearing that their investment will suffer further losses if they hold it for a longer period. However, when the stock market is in a normal or bullish state, the increase or decrease in COVID-19 cases does not significantly affect stock market returns since investors do not bother much during normal and booming states of stock markets.
5. Conclusion and policy implications
In Wuhan City in China, a new type of virus was discovered and given the official name COVID-19 on December 31, 2019. It rapidly spread to many other parts of the world through international travel and affected various activities such as medical, political, social, and economic indicators including stock markets. It is, therefore, important to gain a deeper understanding of the relationship between COVID-19 cases and emerging stock markets.
This study examined the effect of COVID-19 cases on the stock prices of E7 (i.e., Brazil, Russia, India, China, Mexico, Indonesia, and Turkey) stock indices across various quantiles of both stock prices and the number of COVID-19 cases. For this purpose, we used a quantile unit root test and quantile cointegration test to examine the integrating properties of COVID-19 cases and E7 stock prices. Further, we used the QQR approach proposed by Sim and Zhou (2015), as this technique helps to determine the effect of COVID-19 cases on E7 stock indices across various quantiles of both the independent and dependent variables.
Quantile unit root test estimates indicate that stock prices for Turkey are stationary at lower quantiles but are not stationary at middle and upper quantiles. On the contrary, the stock prices for the rest of the countries as well as the number of COVID-19 cases are not stationary for all emerging countries. The quantile cointegration technique indicates that COVID-19 cases are integrated with stock prices for all E7 stock prices. Finally, the estimates from QQR indicate that the findings varied across different quantiles of COVID-19 cases and stock prices. For example, the number of COVID-19 cases positively affects stock prices for upper quantiles of stock prices. However, this positive effect is weak for upper quantiles of stock prices. Conversely, a strong negative effect is found during lower quantiles of stock markets. These findings are consistent across all E7 countries.
The negative findings for lower quantiles indicate that investors and other stakeholders lose their confidence during bearish states of the stock market. Therefore, the effect is stronger during these states. These findings suggest that government should announce economic relief packages and devise policies to minimize sharp declines in prices. Central banks may also adjust their monetary policies by decreasing interest rates so that investors’ and other stakeholders’ confidence may be developed to minimize losses during stock market declines. Finally, other policies should be devised for companies such as a reduction in taxes, providing social security, and providing loans with low-interest rates so that losses due to COVID-19 cases may be minimized.
Author statement
Shabir Mohsin Hashmi: Software, Visualization, Investigation, Supervision, Validation. Bisharat Hussain Chang: Data curation, Writing- Original draft preparation, Conceptualization, Software, Methodology. Li Rong: Writing- Reviewing and Editing.
Footnotes
See this link for further details about economic relief packages https://www.imf.org/en/Topics/imf-and-covid19/Policy-Responses-to-COVID-19.
For further details about quantile unit root test please refer Chang et al. (2020).
References
- Adenomon M.O., Maijamaa B., John D.O. 2020. On the Effects of COVID-19 Outbreak on the Nigerian Stock Exchange Performance: Evidence From GARCH Models. Preprints. [DOI] [Google Scholar]
- Ahundjanov B.B., Akhundjanov S.B., Okhunjanov B.B. Information search and financial markets under COVID-19. Entropy. 2020;22(7):791. doi: 10.3390/e22070791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alfaro L., Chari A., Greenland A.N., Schott P.K. National Bureau of Economic Research; 2020. Aggregate and Firm-Level Stock Returns During Pandemics, in Real Time (No. w26950) [Google Scholar]
- Anjum N., Ghumro N.H., Husain B. Asymmetric impact of exchange rate changes on stock prices: empirical evidence from Germany. Int. J. Econ. Financ. Res. 2017;3(11):240–245. [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Kost K.J., Sammon M.C., Viratyosin T. National Bureau of Economic Research; 2020. The Unprecedented Stock Market Impact of COVID-19. Working Paper No. 26945. [Google Scholar]
- Bhutto N.A., Chang B.H. The effect of the global financial crisis on the asymmetric relationship between exchange rate and stock prices. High Freq. 2019:1–9. doi: 10.1002/hf2.10033. [DOI] [Google Scholar]
- Bruckner M., Mollerus R. 2020. UN/DESA Policy Brief #66: COVID-19 and the Least Developed Countries.https://www.un.org/development/desa/dpad/publication/un-desa-policy-brief-66-covid-1-and-the-least-developed-countries/ Retrieved from: [Google Scholar]
- Chang B.H. Oil prices and E7 stock prices: an asymmetric evidence using multiple threshold nonlinear ARDL model. Environ. Sci. Pollut. Res. 2020:1–12. doi: 10.1007/s11356-020-10277-2. [DOI] [PubMed] [Google Scholar]
- Chang B.H., Rajput S.K.O. Do the changes in macroeconomic variables have a symmetric or asymmetric effect on stock prices? Evidence from Pakistan. South Asian J. Bus. Stud. 2018;7(3):312–331. [Google Scholar]
- Chang B.H., Rajput S.K.O., Ghumro N.H. Asymmetric impact of exchange rate changes on the trade balance: does global financial crisis matter? Ann. Financ. Econ. 2018;13(4) [Google Scholar]
- Chang B.H., Meo M.S., Syed Q.R., Abro Z. Dynamic analysis of the relationship between stock prices and macroeconomic variables. South Asian J. Bus. Stud. 2019;8(3):229–245. [Google Scholar]
- Chang B.H., Rajput S.K.O., Bhutto N.A. The asymmetric effect of extreme changes in the exchange rate volatility on the US imports: evidence from multiple threshold nonlinear ARDL model. Stud. Econ. Finance. 2020;37(2):293–309. [Google Scholar]
- Chang B.H., Rajput S.K.O., Bhutto N.A. Impact of exchange rate volatility on the US exports: a new evidence from multiple threshold nonlinear ARDL model. J. Int. Commer. Econ. Policy. 2019;10(02) [Google Scholar]
- Chang B.H., Sharif A., Aman A., Suki N.M., Salman A., Khan S.A.R. The asymmetric effects of oil price on sectoral Islamic stocks: new evidence from quantile-on-quantile regression approach. Resour. Policy. 2020;65 [Google Scholar]
- Chang B.H., Rajput S.K.O., Ahmed P., Hayat Z. Does gold act as a hedge or a safe haven? Evidence from Pakistan. Pak. Dev. Rev. 2020;59(1):69–80. [Google Scholar]
- Chang B.H., Sharif A., Aman A., Suki N.M., Salman A., Khan S.A.R. The asymmetric effects of oil price on sectoral Islamic stocks: new evidence from quantile-on-quantile regression approach. Resour. Policy. 2020;65 [Google Scholar]
- Cleveland W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979;74(368):829–836. [Google Scholar]
- Galvao A.F., Jr. Unit root quantile autoregression testing using covariates. J. Econom. 2009;152(2):165–178. [Google Scholar]
- Goodell John W. COVID-19 and finance: agendas for future research. Finance Res. Lett. 2020:35. doi: 10.1016/j.frl.2020.101512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodell J.W., Goutte S. Diversifying equity with cryptocurrencies during COVID-19. Int. Rev. Financ. Anal. 2021;76 [Google Scholar]
- Goodell John W., Goutte Stéphane. Co-movement of COVID-19 and Bitcoin: evidence from wavelet coherence analysis. Finance Res. Lett. 2021;38 doi: 10.1016/j.frl.2020.101625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gormsen N.J., Koijen R.S. University of Chicago, Becker Friedman Institute for Economics Working Paper; 2020. Coronavirus: Impact on Stock Prices and Growth Expectations. 2020-22. [Google Scholar]
- Harvey C.R. Predictable risk and returns in emerging markets. Rev. Financ. Stud. 1995;8(3):773–816. [Google Scholar]
- Hashmi S.M., Chang B.H. Asymmetric effect of macroeconomic variables on the emerging stock indices: a quantile ARDL approach. Int. J. Finance Econ. 2021 doi: 10.1002/ijfe.2461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashmi S.M., Chang B.H., Shahbaz M. Asymmetric effect of exchange rate volatility on India’s cross‐border trade: evidence from global financial crisis and multiple threshold nonlinear autoregressive distributed lag model. Aust. Econ. Pap. 2021;60(1):64–97. [Google Scholar]
- He Q., Liu J., Wang S., Yu J. The impact of COVID-19 on stock markets. Econ. Polit. Stud. 2020:1–14. [Google Scholar]
- He P., Sun Y., Zhang Y., Li T. COVID?19’s impact on stock prices across different sectors—An event study based on the Chinese stock market. Emerging Markets Finance Trade. 2020;56(10):2198–2212. [Google Scholar]
- Heyden K.J., Heyden T. 2020. Market Reactions to the Arrival and Containment of COVID-19: an Event Study. Available at SSRN 3587497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenker R., Xiao Z. Unit root quantile autoregression inference. J. Am. Stat. Assoc. 2004;99(467):775–787. [Google Scholar]
- Liu H., Manzoor A., Wang C., Zhang L., Manzoor Z. The COVID-19 outbreak and affected countries stock markets response. Int. J. Environ. Res. Public Health. 2020;17(8):1–19. doi: 10.3390/ijerph17082800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- OECD . 2020. COVID-19 and the Food and Agriculture Sector: Issues and Policy Responses 29 April 2020.https://www.oecd.org/coronavirus/policy-responses/covid-19-and-the-food-and-agriculture-sector-issues-and-policy-responses-a23f764b/ Retrieved from. [Google Scholar]
- Papadamou S., Fassas A., Kenourgios D., Dimitriou D. 2020. Direct and Indirect Effects of COVID-19 Pandemic on Implied Stock Market Volatility: Evidence From Panel Data Analysis. MPRA Working Paper No. 100020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramelli S., Wagner A.F. University of Zurich; 2020. Feverish Stock Price Reactions to covid-19. Working paper. [Google Scholar]
- Saikkonen P. Asymptotically efficient estimation of cointegration regressions. Econom. Theory. 1991;7(1):1–21. [Google Scholar]
- Sim N., Zhou H. Oil prices, US stock return, and the dependence between their quantiles. J. Bank. Finance. 2015;55:1–8. [Google Scholar]
- Stone C.J. Consistent nonparametric regression. Ann. Stat. 1977:595–620. [Google Scholar]
- Syed Q.R., Malik W.S., Chang B.H. Volatility spillover effect of federal reserve’s balance sheet on the financial and goods markets of Indo-Pak Region. Ann. Financ. Econ. 2019;14(03) [Google Scholar]
- Xiao Z. Quantile cointegrating regression. J. Econom. 2009;150(2):248–260. [Google Scholar]
- Yan H., Tu A., Stuart L., Zhang Q. 2020. Analysis of the Effect of COVID-19 on the Stock Market and Potential Investing Strategies. Working Article. SSRN. https://ssrn.com/abstract, 3563380. [Google Scholar]
- Yilmazkuday H. 2020. COVID-19 Effects on the S&P 500 Index.https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3555433 Retrieved from. [Google Scholar]