Protein interaction interface region prediction by geometric deep learning

Abstract

Motivation

Protein–protein interactions drive wide-ranging molecular processes, and characterizing at the atomic level how proteins interact (beyond just the fact that they interact) can provide key insights into understanding and controlling this machinery. Unfortunately, experimental determination of three-dimensional protein complex structures remains difficult and does not scale to the increasingly large sets of proteins whose interactions are of interest. Computational methods are thus required to meet the demands of large-scale, high-throughput prediction of how proteins interact, but unfortunately, both physical modeling and machine learning methods suffer from poor precision and/or recall.

Results

In order to improve performance in predicting protein interaction interfaces, we leverage the best properties of both data- and physics-driven methods to develop a unified Geometric Deep Neural Network, ‘PInet’ (Protein Interface Network). PInet consumes pairs of point clouds encoding the structures of two partner proteins, in order to predict their structural regions mediating interaction. To make such predictions, PInet learns and utilizes models capturing both geometrical and physicochemical molecular surface complementarity. In application to a set of benchmarks, PInet simultaneously predicts the interface regions on both interacting proteins, achieving performance equivalent to or even much better than the state-of-the-art predictor for each dataset. Furthermore, since PInet is based on joint segmentation of a representation of a protein surfaces, its predictions are meaningful in terms of the underlying physical complementarity driving molecular recognition.

Availability and implementation

PInet scripts and models are available at https://github.com/FTD007/PInet.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Due to the importance of protein–protein interactions in driving cellular machinery, numerous experimental and computational techniques have been developed to identify putative partners (Shoemaker and Panchenko, 2007). While these methods yield information about which pairs of proteins might interact, they don’t characterize how they interact (Fig. 1). Further experimental investigations or computational analyses are then necessary to determine or predict binding modes, provide mechanistic insights and guide subsequent efforts to, e.g. design mutations to change binding affinity or specificity or identify small molecule inhibitors of an interaction. Likewise, recent advances in repertoire sequencing have enabled the collection of millions or billions of antibody sequences from different individuals and conditions (Briney et al., 2019), and promise to provide valuable insights into vaccination and natural infection, especially if how the sequenced antibodies recognize their antigen targets could also be characterized. The same holds for display-based development of antibody therapeutics (Feldhaus et al., 2003), where different antibodies may have different modes of interacting with an antigen that may manifest different trade offs, and thus early characterization could drive better selection of leads. Unfortunately, while experimental structure determination provides ‘gold standard’ insights into recognition, these and even alternative less precise/confident methods (e.g. alanine scanning) cannot keep up with the scale of experimental discovery of interacting partners.

Fig. 1.

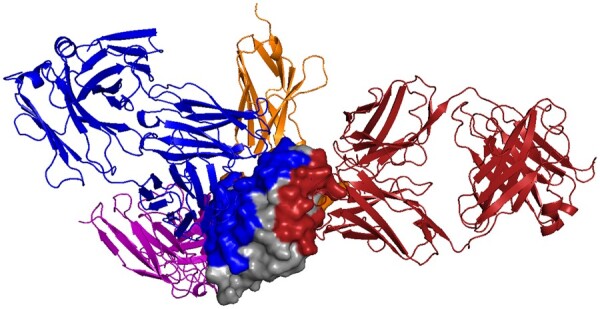
Different proteins can recognize the same protein partner in very different ways, as shown here for hen egg lysozyme (HEL; gray surface, 3LZT) and different antibodies (colored cartoon; purple: 1BVK, blue: 1DQJ, red: 1MLC and orange: 2I25). Partner-independent predictions seek to label, in general, what parts of one protein might be recognized by unknown other proteins. In this example, even with just these few example antibodies, much of the HEL surface is recognized by one antibody or another, so partner-independent prediction of binding region would largely cover the surface. Thus when information about particular partners is available, partner-specific predictions can be beneficial, providing a more specific characterization of recognition by separately localizing each partner. (Color version of this figure is available at Bioinformatics online.)

Computational methods to predict how two given proteins interact can be roughly split into those methods based on physical models and those leveraging data-driven models. Physically based approaches include protein–protein docking, e.g. (Comeau et al., 2004; Pierce et al., 2014; Schneidman-Duhovny et al., 2005; Weitzner et al., 2017; Yan et al., 2020), wherein structures or models of the individual partners are computationally rotated and translated (and in some cases, modified) to generate possible ‘poses’ in which they interact. Beyond the computational cost of sampling or computing a sufficient set of poses, a key difficulty is scoring them. Scoring functions are often carefully crafted to integrate multiple factors, with shape complementarity as the foundation (Lawrence and Colman, 1993). Typically, as has been studied with a state-of-the art physically based docking program, ClusPro, near-native structures are generally included among the top poses, but it remains difficult to identify which one(s) (Vajda et al., 2017).

In contrast to physically based approaches, data-driven/machine learning approaches seek to leverage existing databases of characterized interactions to learn properties underlying recognition. While some methods are based on sequence alone (Murakami and Mizuguchi, 2010; Porollo and Meller, 2007), structural information can be extremely important and has been shown to yield more accurate predictions (Zhang et al., 2012), since recognition is largely based on surface regions that may not be contiguous in primary sequence, and as discussed above overall surface complementarity is critical. Fortunately, in many important cases, structures of the individual proteins are already available, or high-quality homology models can be readily obtained, so a number of structure-based data-driven predictors have emerged. The impact of using structural information instead of sequence is demonstrated, for example, by BIPSPI (Sanchez-Garcia et al., 2019) and PAIRPred (Afsar Minhas et al., 2014), which gain on average a 10% improvement in precision and recall using structure versus sequence alone.

Machine learning approaches can further be classified into those that seek to predict which residues are in the interface regions, which we call here ‘interface region prediction’, and those that seek to predict which pairs of residues (one from each partner) are interacting, which we call here ‘contact prediction’. For example, MASIF (Gainza et al., 2020) and PECAN (Pittala and Bailey-Kellogg, 2020) predict interface regions, ComplexContact (Zeng et al., 2018) and SASNet (Townshend et al., 2019) predict contacts, and the BIPSPI and PAIRPred methods mentioned above predict contacts and post-process the results to predict interface regions. As discussed above, antibody recognition of cognate antigens is one particularly important special case of interface region prediction (the ‘epitope’ on the antigen and the ‘paratope’ on the antibody are the interaction regions). Epitope prediction has been the subject of much study, with DiscoTope (Kringelum et al., 2012) focusing on learning general surface properties, EpiPred (Krawczyk et al., 2014) combining conformational matching and a machine learning boosted scoring function, and PECAN (Pittala and Bailey-Kellogg, 2020) employing graph convolution networks. Paratope prediction is also well studied, though it is somewhat easier, due to the regularity of immunoglobulin sequence and structure (Pittala and Bailey-Kellogg, 2020).

Different interface region prediction tasks leverage different available information to achieve different goals. Partner-independent prediction seeks to predict, in general, what portions of the surface of a protein may serve as interface regions for other proteins (known or unknown). In contrast, partner-specific prediction accounts for a particular partner in identifying the binding regions most suitable for that partner. As illustrated in Figure 1, deconvolving the surface into partner-specific predictions for different partners provides a better characterization of the recognition; this can be important for subsequent engineering, for understanding underlying immune responses, and so forth. In the specific case of antibodies, while many classic epitope predictors are partner-independent, Sela-Culang et al. (2015) motivated the paradigm of antibody-specific approach, since antibodies may be developed by the immune system against a variety of different epitopes on an antigen (Fig. 1). Further studies (Hua et al., 2017; Sela-Culang et al., 2014) have demonstrated the utility of this framework when information about the partner antibody is available.

To bring deep learning to bear in developing new structure-based interface region prediction methods, a central question is how to represent the protein structures and thus develop a suitable neural network. Since geometry is one of the key principles underlying interface complementarity (as exploited by physical modeling methods), but protein structures are not regularly sampled grids like the images studied by traditional deep learning, this task belongs to the general area of geometric deep learning. Graph Convolutional Networks (GCNs) (Kipf and Welling, 2017) are one geometric deep learning method that has been leveraged for protein interface region prediction. GCNs generalize Convolutional Neural Networks (CNNs) from 2D grids to graphs by employing spectral convolution, enabling them to avoid the unnecessary and potentially costly direct Euclidean domain representations of structured data (e.g. 3D voxelization might waste a great deal of memory at high resolution, or might lose important features at low resolution). A recent study (Fout et al., 2017) employed a GCN to learn a representation for each residue in a protein and used that representation to classify whether or not two residues interact. This study showed that convolution is able to capture interaction information from basic physicochemical properties of residues. Recently, PECAN (Pittala and Bailey-Kellogg, 2020) combined the advantages of GCNs and attention mechanisms (Bahdanau et al., 2014) in an integrated model for predicting both epitopes and paratopes, learning better representations of residues and their interaction preferences in order to focus predictions on complementary regions.

Another recent protein interface region prediction method, MaSIF (Gainza et al., 2020), used a different form of geometric deep learning to learn and utilize geometric features, mapping 3D surface patches of an input protein to 2D using a soft polar coordinate system, and then using CNNs to predict the likelihood of a surface vertex being involved in an interaction region. MaSIF was also trained on a substantially larger dataset than previous studies, using thousands rather than hundreds of complex structures. We note that in contrast to the methods above, as well as ours, MaSIF is partner-independent, predicting likely binding sites in general for a protein, rather than making predictions that are specific to given partner proteins.

In order to directly encode and exploit surface geometry and interface complementarity in a deep learning framework, we pursue here a point cloud based representation. Traditional ways of dealing with point clouds, e.g. aggregating points into discrete voxels for a 3D voxel CNN (Maturana and Scherer, 2015), or sorting them into a linear sequence for an RNN (Vinyals et al., 2015), can ruin the detailed geometry of the data or result in an unstable ordering of the inherently non-linear set of points into a sequence. PointNet (Qi et al., 2017) was developed to directly learn geometrical information from point clouds, overcoming these problems by learning functions to make points order invariant, as well as aggregating local and global features over the cloud. More specifically, PointNet utilizes a Spatial Transformer Network (Jaderberg et al., 2015) to render the input point cloud invariant to geometric transformations, employs a multi-layer perceptron to learn high-dimensional local feature vectors for the points, and subsequently applies a max pooling layer over each channel to produce global feature vectors describing overall shape features. This global feature vector can be concatenated with local feature vectors to enable semantic segmentation by learning which subset of global features should be assigned to a point. When different points share similar global signatures, their neighborhood information is also extracted, thereby helping group points for segmentation. PointNet was shown to achieve state of the art performance on problems including 3D object classification, part segmentation and scene semantic segmentation.

Our contribution. In order to leverage the advantages of both physically based modeling and data-driven modeling, we develop a partner-specific geometric deep learning approach to interface region prediction that is based on an explicit representation of a pair of molecular surfaces. Our approach thereby enables characterization of shape and physicochemical complementarity driving molecular recognition, using existing data to learn how best to score this complementarity and thereby identify interface regions of a given pair of structures. In addition to predicting interface regions in general protein–protein pairs, we also address the specific case of epitope-paratope prediction in antibody-antigen (Ab-Ag) recognition. Our approach, PInet, achieves state of the art performance on each of the different interface region prediction tasks on which we evaluate it. Strikingly, even when trained on a dataset largely comprised of other types of protein–protein interactions rather than one focused specifically on antibody-antigen interactions, PInet performs better than state-of-the-art epitope predictors, demonstrating that it has learned generalized representations of protein interface complementarity.

2 Methods

2.1 Problem setup

Given individual structures or high-quality homology models of two proteins, traditionally termed the ‘ligand’ and ‘receptor’ (the distinction is not important in our approach), our goal is to predict their interface regions, i.e. the portions that are contacting each other. While ultimately the predicted interface regions will be characterized in terms of the involved residues, in order to directly represent recognition in terms of two complementary molecular surfaces, we encode both proteins as surface point clouds $P^l=\left\{P_i^l\right|i=1\dots n_l\}$ and $P^r=\left\{P_i^r\right|i=1\dots n_r\}$, where each point cloud includes both (x, y, z) coordinates (G_i) along with physicochemical properties (H_i, E_i) described below. We then seek to label each point as being in the interface or not, yielding an $n_l+n_r$ by 1 output probability score. The point cloud representation enables simultaneously capturing both geometric and physicochemical properties mediating recognition, and yields meaningful predictions in terms of segmented surface regions potentially mediating interactions.

2.2 Data preparation

Geometry. We first preprocess input PDB (Berman et al., 2002) files using PDB2PQR (Dolinsky et al., 2007) to remove solvent molecules and fill in missing atoms. We then generate surface meshes for each protein separately and use the mesh vertices as the input point clouds; results presented here are based on PyMOL-generated meshes (DeLano, 2002) with a water probe radius of 1.4 Å. Point coordinates in G_i are translated so that the point cloud’s centroid is at the origin.

Physicochemical features. PInet allows physicochemical properties to be associated with each point. For the results shown here, we employed representative encodings of the two most important classes of properties: electrostatics (E_i) and hydrophobicity (H_i). Combined with the 3D geometry G_i, these features make P^l and P^r 5 dimensional point sets.

• Electrostatics Poisson–Boltzmann electrostatics are computed by APBS (Baker et al., 2001) for both proteins separately, and the continuum electrostatics value for each point (E_i) is taken as the value of the voxel containing that point normalized by the maximum value over the whole grid.

• Hydrophobicity. The hydrophobicity value for each point (H_i) is computed as a distance-normalized weighted sum of the Kyte-Doolittle scale (Kyte and Doolittle, 1982) values for the amino acid types of the three closest residues (R_k):

  $$H_i=\sum _{k=1}^3\text{KD}(R_k)\times \frac{1}{D(P_i,R_k)}$$

where $\text{KD}(R_k)$ is the Kyte-Doolittle value for residue type R_k and $D(P_i,R_k)$ is distance between the surface point and the centroid of the residue.

Interface labels. The label sets L^l and L^r assign each point a value of 1 if it is in the interface region and 0 if it isn’t. Here, we define interface points as those within 2 Å of a point on the partner protein (known in training from the complex structure). The 2 Å threshold was selected based on an analysis of the distribution of the shortest pairwise distances across interacting proteins (Supplementary Fig. S1).

2.3 Architecture

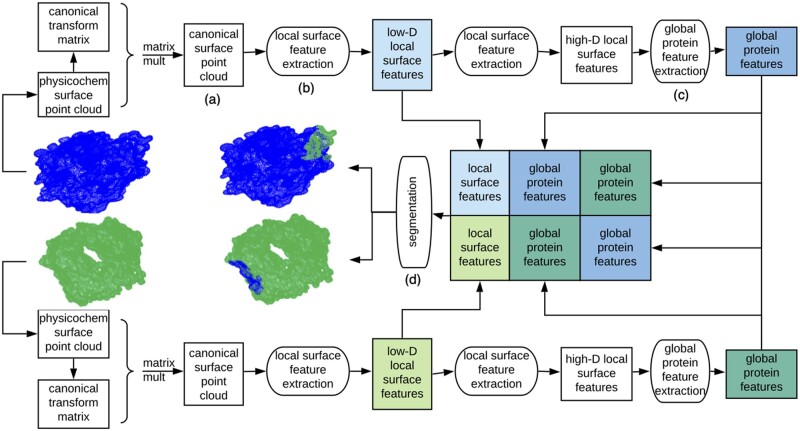
We use this representation as the basis for a geometric deep learning framework (Fig. 2) that seeks to segment points in the interface region from the rest for both input point clouds simultaneously. The architecture is rooted in that pioneered by PointNet (Qi et al., 2017). While PointNet was developed for semantic segmentation of a single point cloud in an image according to its own features, our goal here is to learn to simultaneously segment two point clouds into interacting and non-interacting regions. Whether or not regions interact is revealed by shape and physicochemical complementarity of their sub-regions, i.e. segmentation of a set of points also depends on features of potential partner points. We thus adapt the architecture to take two point clouds as input and learn to extract feature signatures that capture complementarity between sub-regions of the clouds and enable simultaneous segmentation of both clouds into interface versus non-interface.

Fig. 2.

Overview of our Protein Interface Network (PInet) approach for predicting interaction regions on pairs of proteins. PInet consumes two 5 dimensional point clouds representing geometry and physicochemical properties of each protein surface, and performs a semantic segmentation on all points from both point clouds simultaneously. It first processes each point cloud separately. For each protein, a Spatial Transformation Network renders the surface point clouds invariant to rigid-body transformations. Then a multi-layer perceptron (MLP) extracts local surface features. These local surface features are then aggregated into a global protein feature vector. With each protein thus processed, the protein local surface features and global protein features from both proteins are concatenated in order to be segmented by another MLP. The trainable weights for canonical transformation, local and global feature extraction are shared for the two proteins

Point cloud canonical transformation ( Fig. 2a). The first step transforms the points in a cloud into a canonical space in a way that is invariant to linear transformations. The underlying problem is that there is no standard coordinate system for protein structures, and indeed the key problem in physically based methods is to find the right transformation (rotation and translation) to bring the two separate proteins together. Rather than sampling different poses, we use a canonical representation approach, and in fact, learn the transformation into the canonical space rather than hand-crafting a canonical representation. In particular, we use a simplified Spatial Transformation network (Jaderberg et al., 2015) to learn a k × k transformation matrix (where k is the dimension of the point cloud, 5 in our case) that maps each point into the new space.

Local surface feature extraction ( Fig. 2b). The next step moves beyond individual points in a cloud to a richer representation of properties of the protein surface. This local surface feature extraction block is implemented by a sequence of fully connected layers on points, forming a Multilayer perceptron (MLP). Here the MLP is learning a set of functions that map input surface point features (3D geometry and 2D physicochemical) to a higher-dimensional vector of protein surface features. Inspection of the first fully connected layer of a trained model from the results reveals that some weights focus on the coordinates, aggregating geometry-related features, while other weights focus more on electrostatics and hydrophobicity channels, capturing physicochemical properties.

Global protein feature extraction ( Fig. 2c). After re-representing each point in terms of local surface features, the next step summarizes the entire protein surface in order to later support segmentation via comparison of local features to this global feature. The global feature is obtained by max pooling over all points’ local features. This max pooling layer reveals points with dominant impact on each feature, and uses the associated features of these points to summarize the whole protein surface.

Segmentation ( Fig. 2d). Finally, the binding interfaces for both proteins are simultaneously segmented. Our segmentation block is also implemented by an MLP, taking as input a combination, over both proteins, of all the local surface features and the two global feature vectors. The MLP learns complementarity from the two global feature vectors, and uses the relationship between the complementarity signature and the local feature vectors in order to predict for each point its probability of being in the binding interface.

2.4 Loss function

We train the model with Binary Cross Entropy loss $L_{\text{BCE}}$ balanced by the weight of the positive labels. In addition, we designed a regularization term, $L_{\text{Hist}}$, based on the intuition that the binding regions on both input point clouds should have complementary shapes (Osada et al., 2002). To describe the shapes of the binding regions, we use D₂ shape distributions, which are the distance distributions (represented by histograms) of subsets of random points in the positive labeled point clouds. We then use the difference of distributions as a regularization loss. In particular, given the normalized distances D between all pairs of point from a random subset, we implemented a backpropagatable 10 bin histogram defined in terms of the bins‘centers c_i and radii r_i:

$$\begin{array}{c}\text{bin}(d)=\sum _{i=0}^9\left(\text{sigmoid}\left(\frac{d-c_i+r_i}{\sigma }\right)-\text{sigmoid}\left(\frac{d-c_i-r_i}{\sigma }\right)\right)b_i\\ \text{Hist}(D)=\sum _{d\in D}\text{bin}(d)\end{array}$$

where σ is a coefficient (set by grid search in the training data) controlling the steepness of the sigmoid function and b_i is a 10-dimensional vector with the ith dimension set to 1 and rest to 0. Consequently, $L_{\text{Hist}}$ is then defined as the L2 norm of the difference between $D_{\text{ligand}}$ and $D_{\text{receptor}}$:

$$L_{\text{Hist}}=\left|\right|\text{Hist}(D_{\text{ligand}})-\text{Hist}(D_{\text{receptor}})\left|\right|$$

The loss function with regularization $L_{\text{Hist}}$ is then defined by:

$$L=L_{\text{BCE}}+\alpha L_{\text{Hist}}$$

where the hyperparameter α setting the relative weight between the losses is found by grid search in the training data.

2.5 Training

Since the input point cloud sizes can vary significantly and the memory size of the GPU used in implementation is limited, we do not pad all input point clouds; but for particularly large protein pairs, we uniformly subsample them, without replacement, so as to reduce the cardinality of each to at most 20000. We feed one protein pair at a time into the network, performing backpropagation on the average loss of every set of complexes (16 for smaller datasets and 32 for larger ones). Thus the model is still essentially trained using mini-batch gradient descent. We use the Adam optimizer and train each model for 160 epochs with initial learning rate 0.001 decreasing by half every 20 epochs. The keep rate for the dropout layer in the segmentation block is set to be 0.7. All these parameters were determined by grid search within the training set.

2.6 Data augmentation

Since there is relatively little training data available (tens to hundreds of protein complex structures in curated datasets), we sought to augment it artificially. In particular, since the spatial transformation network needs sufficient data to learn the mapping from point clouds to a canonical space, and the reference coordinate system in each structure is essentially arbitrary, a natural augmentation is to add randomly rotated instances of the training data. For each input pair of point clouds in the training set, we generated a fixed number of additional input point clouds, each randomly rotated from the original, i.e. by a random angle around a random axis. For smaller datasets, we compared the performance using 10 or 50 additional training instances for each original; for a large dataset, we were only able to augment with 5 additional instances each due to memory limitations.

2.7 Residue-level Prediction

While PInet’s predictions are in terms of surface point clouds, most methods (and indeed, subsequent experiments, e.g. site-directed mutagenesis) focus on which amino acids are in the interfaces. Thus for interpretation and direct comparison with other methods, we compute predictions for residues based on predictions for nearby surface points. In order to ensure potential representation of all atoms in a residue, we identify the closest surface points for each of its atoms and then the closest of those points over all atoms in the residue. We then average the probabilities for those nearby surface points to give the residue’s probability. More precisely, for atom A_j let C_j be the corresponding k₁ closest points in the point cloud (we used $k_1=3$), and for residue R_k, let D_k be the k₂ closest points (we used $k_2=10$) from the set of points $\underset{A_j\in R_k}{\cup }{C}_j$ of atoms comprising the residue and their closest points. Then we compute the probability $P(R_k)$ that R_k is in the binding site by summing the evidence provided by the points associated with its constituent atoms.

$$P(R_k)=\frac{1}{k_2}\sum _{P_i\in D_k}P(P_i)$$

3 Results

3.1 Benchmarks

We evaluated PInet on three previously collected and evaluated benchmarks, summarized in Supplementary Table S1 and Supplementary Figure S2, and associated state-of-the-art predictors. Different steps were taken by each in order to clean and reduce redundancy, as briefly summarized here.

• DBD5. The Protein–Protein Docking Benchmark 5.0 (DBD5) (Vreven et al., 2015) is a non-redundant set of high-resolution structures of 225 general protein–protein complexes. The redundancy is handled at the structural family level according to the Structural Classification of Proteins (SCOP) (Murzin et al., 1995). We also considered the DBD3 dataset (Hwang et al., 2008), a previous version that is a subset of DBD5 of size 73. We compare our model with representative state-of-the-art methods BIPSPI (Sanchez-Garcia et al., 2019) and PAIRpred (Afsar Minhas et al., 2014), which are partner-specific predictors (i.e. for a given pair of proteins) using both sequence- and structure-based features. All models followed the same protocol of leave-one-out cross-validation. We tested on both bound conformations (i.e. the structures of the individual proteins are extracted from the complex structure), as well as on unbound conformations (i.e. the structures of the individual proteins were solved separately).

• MaSIF The authors of MaSIF compiled a massive dataset by combining the PRISM (Murakami and Mizuguchi, 2010) dataset (Ogmen et al., 2005), the ZDock benchmark (Pierce et al., 2014), PDBBind (Wang et al., 2005) and the SAbDab antibody database (Dunbar et al., 2014) filtered for a maximum of 30% sequence identity using psi-cd-hit (Huang et al., 2010). In all, the original dataset used 3003 proteins for training and 359 for testing. The overall dataset was not curated for redundancy and overlap between training and testing, so for comparison we use the same test-train split, except for one small bit of curation: we discarded complexes whose binding site was smaller than 1% of the size of ligand, since from inspection these complexes have little interaction. Thus our training and testing set sizes are 2689 and 345. We compared our model with MaSIF and SPPIDER (Porollo and Meller, 2007), another partner-independent predictor based on relative solvent accessibility, whose performance is included in the MaSIF publication (Gainza et al., 2020). The provided benchmark uses bound conformations.

• EpiPred EpiPred (Krawczyk et al., 2014) is one of the state-of-the art antibody epitope predictors, though recently PECAN (Pittala and Bailey-Kellogg, 2020) outperformed it on the same dataset. The EpiPred dataset comprises a non-redundant set of high-resolution antibody-antigen complex crystal structures, filtered from SAbDab (Dunbar et al., 2014) according to structural quality and dissimilarity. It includes 148 Ab-Ag complexes with Ab sequence identity less than 99% and corresponding Ag sequence identity less than 90%, and all Ags at least 50 residues. Of these complexes, 118 are used for training and 30 for testing. Here we compare our model with EpiPred along with the partner-independent epitope predictor DiscoTope (Kringelum et al., 2012) and the recent partner-dependent epitope predictor PECAN, which holds the current state-of-the-art performance for the EpiPred dataset, achieving 15.7% precision with 73.0% recall and AUC-PR of 65.5%. Here too, the provided benchmark uses bound conformations.

We first evaluated PInet on DBD5 in order to establish a comparison with the general state of the art in predicting how pairs of proteins interact. We also used DBD5 to show the importance of partner-specific methods, accounting for the other protein when predicting on the one protein, rather than just generally predicting what part of a protein might be recognized by any partner (see again Fig. S1). DBD5 also provided the opportunity to assess the utility of data augmentation for our method. We then used the MaSIF dataset to evaluate our approach on this much larger and richer (though uncurated) dataset. As we can see in Supplementary Figure S2, in MaSIF, the sizes of ligands and receptors tend to be more similar compared to DBD5 and EpiPred, but the proportions of residues in interface regions (i.e. percentages of positive labels) varies substantially. We further leveraged the MaSIF dataset to explore different variations of the the PInet model, including architecture and feature choices. Finally we turned to the special case of antibody-antigen prediction and used the EpiPred benchmark to evaluate PInet’s performance on this important task.

In general, due to the imbalance between positive labels (about 8%) and negative labels (Supplementary Table S1), we advocate the use of precision and recall as performance metrics, both as single values at the 0.5 probability cut-off, as well as in a precision-recall curve. To allow comparison with some other approaches, we also compute AUC-ROC even though the classes are very imbalanced. For consistency of comparison, PInet’s point-based predictions are converted to residue-level predictions as described in the methods. In order to illustrate the power of PInet in enabling further computational modeling or experimental evaluation, we provide illustrative examples of resulting segmentations.

3.2 DBD5

We trained and tested PInet on the DBD5 and older DBD3 benchmarks using leave-one-out cross-validation and found that, compared to representative predictors trained and tested the same way, it attains significantly better average precision, recall and AUC-PR (Table 1 and Supplementary Table S2). For example, for the DBD5 benchmark, using a probability cutoff of 0.5, the average precision of the model trained without data augmentation is over 51% and average recall nearly 75%, both more than 10% higher than previous methods, while the average AUC-PR is almost 0.67, more than 0.20 higher. Clearly the model does a good job of identifying the binding regions, but also expands them to include some false positives. For the model trained with 10× augmentation, the performance improves slightly, while for model trained with 50× augmentation, the performance further improves substantially, attaining average precision of 54%, average recall of 82% and average AUC-PR of 0.73. To evaluate the impact of conformational change on the predictions, we further tested PInet on the unbound structures using the 50× augmentation model. We note that BIPSI’s performance was more or less the same in application to bound or unbound structures, presumably because its features are less sensitive to the conformational changes induced by binding in these test cases. As might be expected for PInet, which uses features based on higher-resolution point clouds, performance did drop, but it still outperformed these other predictors in terms of both precision and recall.

Table 1.

Performance evaluation for DBD3 and DBD5 datasets, with published values for PAIRPred and BIPSI, compared to PInet with no augmentation or augmented with 10 or 50 random rotations per training complex

Struct	Method	precision	recall	AUC-ROC	AUC-PR
DBD3
B	PInet	0.494	0.723	0.812	0.639
B	PInet (Aug 10)	0.480	0.732	0.846	0.669
B	PInet (Aug 50)	0.491	0.845	0.867	0.710
U	PAIRpred	0.371	0.419	0.774	0.341
U	BIPSPI	0.383	0.545	0.816	0.405
U	PInet (Aug 50)	0.518	0.745	0.775	0.626
DBD5
B	BIPSPI	0.394	0.599	0.827	0.429
B	PInet	0.511	0.749	0.837	0.667
B	PInet (Aug 10)	0.523	0.755	0.851	0.685
B	PInet (Aug 50)	0.538	0.824	0.877	0.734
U	BIPSPI	0.391	0.558	0.822	0.410
U	PInet (Aug 50)	0.492	0.723	0.753	0.596

Note: Bolded entries are the best in that column for that dataset. Testing is performed on either bound (B) or unbound (U) structures, as indicated in the first column.

Figure 3 illustrates epitope predictions (Supplementary Fig. S3 gives paratopes) for hen egg lysozyme and antibodies illustrated in Figure 1. The PInet predictions clearly demonstrate a very important point: it is not just memorizing binding sites during training—while it sees the antigen and one specific antibody during training, it is still able to predict the very different interface of that antigen for different partner antibodies during testing. The result also demonstrates the importance of partner-specific prediction, as for example DiscoTope covers much of the surface as possible binding interface without distinguishing for which antibody. In contrast, the PInet predictions leverage antibody specific models to distinguish different binding regions and support prioritization and follow-up studies for the different antibodies.

Fig. 3.

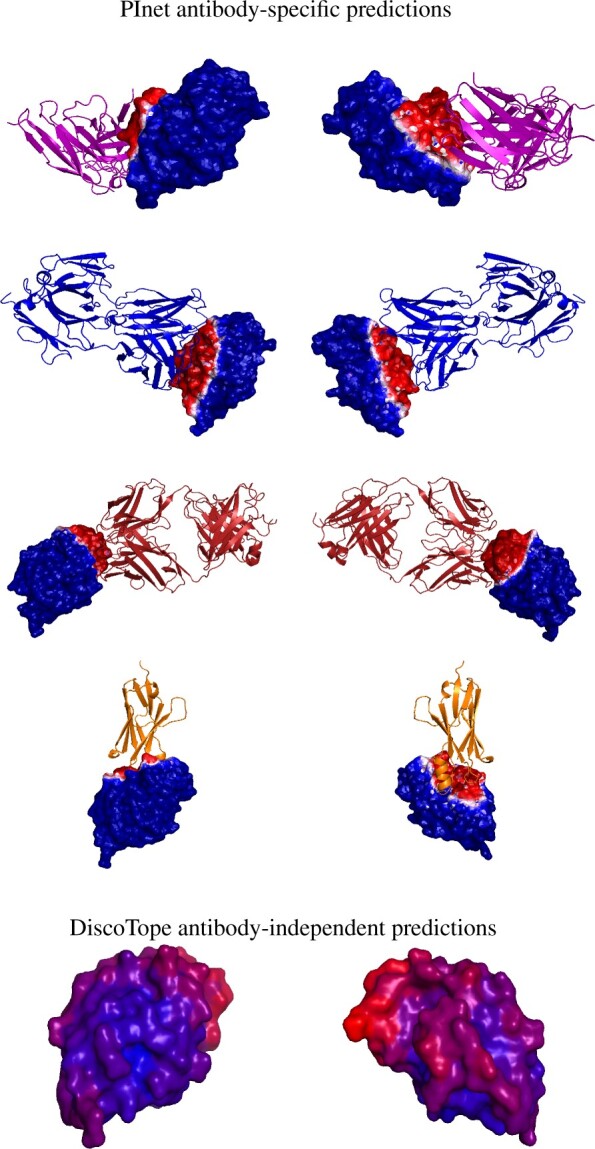
Binding interface prediction for one protein (hen egg lysozyme) with four different antibodies. (Top four rows) PInet predictions, from two different viewpoints. The heatmap shows predicted probability of being in the interface, with darker red for higher probability and darker blue for lower. (Bottom row) Discotope prediction for 3LZT, again with a heatmap showing predicted probability (darker red higher, darker blue lower). (Color version of this figure is available at Bioinformatics online.)

Figure 4 visualizes the PInet interface region predictions for the median performance complexes from the DBD5 Enzyme-Partner category test cases. Here too—even at the median level of performance—PInet is able to provide high-quality interface region segmentations. Overall (Supplementary Fig. S4), the prediction performance is consistent across different types of protein interactions, suggesting that PInet is learning robust, general models of interaction specificity.

Fig. 4.

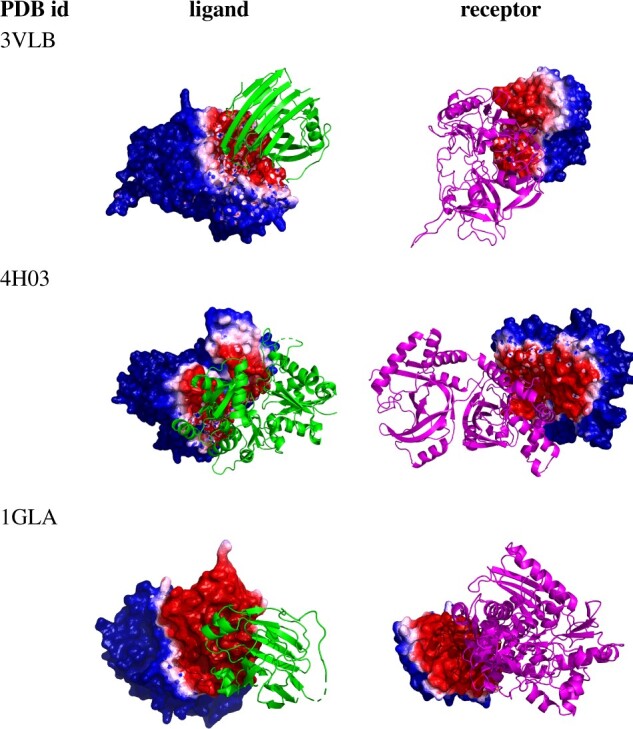
Segmentation visualization for three example (median PInet prediction performance) Enzyme-Partner pairs from DBD5: Enzyme-Inhibitor 3VLB (top), Enzyme-Substrate 4H03 (middle) and Enzyme complex with a regulatory or accessory chain 1GLA (bottom). Heatmaps for the partner indicate the predicted probability of being in the interface, with darker red for higher probability and darker blue for lower. (Color version of this figure is available at Bioinformatics online.)

3.3 MaSIF

The MaSIF benchmark is substantially larger, and provides more diverse but uncurated training and testing data. The MaSIF paper also presents results for a model using geometric features only, as compared to the one using both geometry and physicochemical features. We trained PInet following the same protocol and, as the top rows in Table 2 indicate, PInet outperforms MaSIF when using just geometric features, and attains the same performance when using both geometric and physicochemical properties. The relatively better performance of PInet on geometry alone leads us to conjecture that PInet could benefit from a different encoding of physicochemical features or a more direct aggregation of the features (e.g. as convolution would do), In addition to the full dataset, the MaSIF paper also includes a comparison to SPPIDER (Porollo and Meller, 2007) on predicting for the subset of single-chain transient interactions. We also tested on the transient interactions subset; the bottom section of Table 2 shows that we again match MaSIF’s performance in terms of AUC-ROC. For completeness, since the dataset is quite imbalanced, we also provide AUC-PR for PInet; though a comparison can’t be made to the other methods, we do see that it is substantially lower than we obtained for the DBD5 dataset, suggesting that a carefully curated training and testing regime can yield better performance.

Table 2.

Performance (area under the PR and ROC curves) on the Masif benchmark

Test case	Method	AUC-PR	AUC-ROC
Full	MaSIF	n/a	0.87
Full	PInet	0.45	0.88
Full	MaSIF (geom only)	n/a	0.68
Full	PInet (geom only)	0.30	0.75
Transient	SPPIDER	n/a	0.65
Transient	MaSIF	n/a	0.81
Transient	PInet	0.30	0.82

Note: (top) full test set, with each model using geometric features and physicochemical features. (middle) full test set, with each model using geometric features only. (bottom) transient interaction subset. Bolded values indicate the best performance within each category: full, full (geom only), and transient.

Finally, we used the MaSIF dataset to compare different versions of the PInet modeling approach; performance is summarized in Supplementary Table S3. The top two rows shows the full model and the geometry-only model, as already presented in Table 2. The next two rows summarize the impact of adding each of our two physicochemical features separately; each helps, though hydrophobocity helps more on this dataset. To evaluate the effects of point cloud resolution, we also evaluated a model using at most 2000 points, instead of the default 2 00 000 points. As shown in Supplementary Figure S2, most point clouds are in the 10 000 to 20 000 range, so this subsampling reduces the grid resolution and consequently hurts performance all around. Finally, we compared the difference between models with or without the data augmentation. The extent of augmentation we could perform was limited due to memory constraints, and the dataset was already quite large, so augmentation had little effect on the performance here.

3.4 EpiPred

The final dataset covers the important special case of antibody-antigen interactions. While our model simultaneously predicts both interfaces, the epitope (the part of the antigen recognized by the antibody) is usually most important, so we focus on comparison with the state-of-the-art antibody-specific epitope predictors PECAN (Pittala and Bailey-Kellogg, 2020) and EpiPred (Krawczyk et al., 2014), along with the state-of-the-art antibody-independent DiscoTope (Kringelum et al., 2012), using Epipred’s training and testing sets.

Table 3 summarizes the performance of the various approaches. The basic PInet approach, training and testing on the EpiPred dataset alone, is directly comparable to the state-of-the-art PECAN, and we see that it substantially outperforms it (as well as the other methods) in terms of recall while also doing better on precision. Data augmentation further improves precision and also achieves the best AUC-PR and AUC-ROC. Strikingly, the PInet models trained above on augmented DBD5 data (performance numbers averaged over all models trained during the leave-one-out cross-validation) achieve performance comparable to that of the other state of the art methods, though suffer a loss in recall compared to the model trained directly on EpiPred data. This result implies that our model robustly learns generalizable determinants of protein–protein binding interfaces.

Table 3.

Epitope prediction performance on the EpiPred test set. Bolded values indicate the best performance for each metric.

Method	Precision	Recall	AUC-ROC	AUC-PR
EpiPred	0.136	0.436	NA	NA
DiscoTope	0.214	0.110	NA	NA
Sppider	0.153	0.363	NA	NA
PECAN	0.157	0.730	0.655	0.226
PInet [EpiPred]	0.181	0.931	0.654	0.291
PInet [EpiPred & Aug]	0.216	0.774	0.687	0.368
PInet [DBD5 Aug] ave	0.206	0.752	0.651	0.321

Figure 5 visualizes the PInet epitope predictions for representative good and not-so-good test cases. Corresponding paratope predictions are included in Supplementary Figure S5. Consistent with the performance metrics, PInet identifies most or all of the epitope regions, but extends the segmentation out a bit further beyond them. By the median performance example, we see that PInet also produces a secondary binding site; these false positives would need to be ruled out by subsequent computational or experimental analysis. Finally, we evaluated the overall performance for simultaneous paratope and epitope prediction (Supplementary Table S4). We see that indeed the precision and recall for combined epitope+paratope prediction tends to be higher than that for epitope prediction since, as discussed, paratope prediction is generally easier than epitope prediction, due to the structural and functional similarity of the complementarity determining regions of antibodies.

Fig. 5.

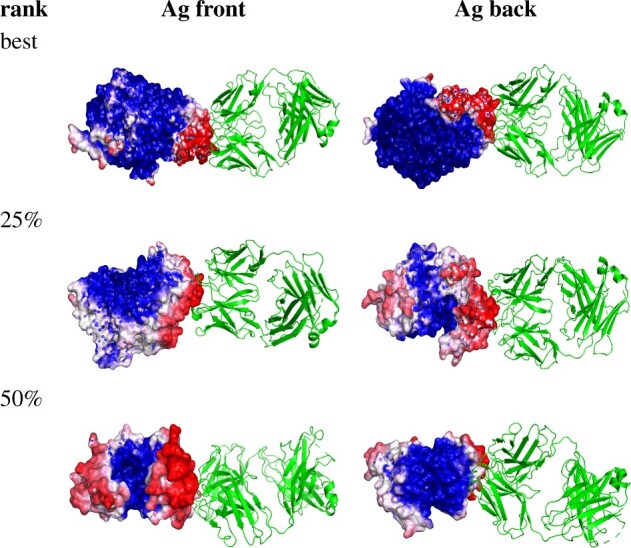
Segmentation visualization for 3 example Ab-Ag pairs: best 4JR9, top 25% 3LIZ and 50% 3RAJ (according to AUC-PR). For these three pairs, precision ranges from 13% to 23% and recall ranges from 65% to 93%. Green structures are antibodies and gray structures are antigens, while heatmaps for the partner indicate the predicted probability of being in the interface, with darker red for higher probability and darker blue for lower. (Color version of this figure is available at Bioinformatics online.)

4 Discussion

In order to improve the state of the art in predicting how proteins interact, aiming to scale up to support large-scale analyses, we bridge physical modeling approaches and data-driven approaches training a data-driven model using the same types of features leveraged by physically based modeling methods. Our unified geometric deep neural network encodes geometry and physicochemical properties by way of point clouds and leverages this encoding to learn how to recognize the complementarity underlying molecular recognition. This leads to interface region prediction that outperforms state of the art methods in precision, recall and AUC-PR. Moreover, our model could be directly used as a protein surface fingerprint for more applications such as pose recovery.

The model trained on the general DBD5 dataset performed quite well on the specific EpiPred dataset, but could potentially benefit from additional training with antibody-antigen data. Thus we evaluated the utility of transfer learning, pre-training a model with DBD5 and then fine tuning it with EpiPred training data. The transfer learning process did boost the performance on the EpiPred test set relative to a model trained on EpiPred alone with no augmentation, but the benefit was not significant compared to that of a model trained on EpiPred with augmentation (Supplementary Table S4). This suggests that, at least as far as this dataset goes, the model learned from general protein complexes already represents antibody-antigen recognition as well as it can.

While it can be very challenging to discern what a neural network has learned and how exactly it is representing information, we sought to explore some of the key properties of PInet. Since the global vector is summarized by a pooling layer, we plotted those points that most strongly activates channels in the global vector for a couple of example proteins, and found that PInet’s global feature extraction layer is essentially sampling landmarks on the protein surface and using them to summarize the protein (Supplementary Fig. S6a). The following MLP layer then segments the surface based on predictions from these points as to where interactions are most likely. We also noticed that the global vectors of different classes of interaction in DBD5, Ab-Ag versus Enzyme-Partner, are distinguishable when projected into 2D via t-SNE embedding (Supplementary Fig. S6b). Even though the model was not trained for this type of classification, it appears to be representing differently these different types of interfaces. These preliminary investigations point to the potential value of unsupervised pre-training on single proteins (for which there is much more data) and using a better encoding as the basis for learning models of interaction specificity.

The strength of PInet lies in its point cloud representation of protein surfaces and its ability to learn representations of complementarity in interacting surfaces. Table 2 and Supplementary Table S3 show that PInet receives much less benefit from augmenting its geometric representation with biophysical properties, compared to MASIF. This could be due to the discrete encoding of electrostatic features employed by PInet, which lacks a convolutional kernel that would more naturally capture electrostatic locality. Future work may seek to incorporate a CNN like approach into the point cloud architecture, or use a different encoding of electrostatics to better leverage this important information as MASIF does.

The point cloud representation makes PInet more sensitive to conformational change upon binding (B versus U in Table 1). In general, physically based methods such as docking depend on such details, while the features used by and representations learned by data-driven methods may not (e.g. solvent accessibility features may be generally unaffected by modest conformational change). As a hybrid physics/data-driven approach, PInet falls somewhere in the middle. Thus an interesting angle for future work is to train models that learn the features of complementary surfaces while robustly accounting for deformations to those surfaces induced during binding.

PInet pursues a partner-specific prediction approach, reasoning that in theory, one partner’s sequence ‘encodes’ information regarding what it will recognize on the other, and nature is able to ‘decode’ this information reliably. Thus it is worthwhile to attempt to learn such a representation, which could be useful, e.g. to identify which of a set of isolated antibodies target which sites on the antigen, which representative subset is thus worth functionally characterizing, which antibodies are more likely to be neutralizing, and so forth. The partner-specific approach clearly pays off in the hen egg lysozyme example, where PInet deconvolves the different antibody specificities and gives much better localizations of their putative epitopes compared to the partner-independent method. However, the overall precision across the benchmarks still remains low, and there is clearly still much work to be done to achieve sufficiently accurate predictions. While partner-specific methods have more information than partner-independent ones, simply knowing the partner doesn’t necessarily help all by itself, since it isn’t known a priori which part of the partner’s surface is the interface. In fact, simultaneous prediction of both interfaces goes a long way toward solving the docking problem. Indeed, we hope that further development of data-driven methods explicitly encoding geometric and biophysical complementarity may indeed enable direct prediction of binding modes with high precision and recall over large diverse sets of protein partners.