Abstract
Motivation
Integrative multi-feature fusion analysis on biomedical data has gained much attention recently. In breast cancer, existing studies have demonstrated that combining genomic mRNA data and DNA methylation data can better stratify cancer patients with distinct prognosis than using single signature. However, those existing methods are simply combining these gene features in series and have ignored the correlations between separate omics dimensions over time.
Results
In the present study, we propose an adaptive multi-task learning method, which combines the Cox loss task with the ordinal loss task, for survival prediction of breast cancer patients using multi-modal learning instead of performing survival analysis on each feature dataset. First, we use local maximum quasi-clique merging (lmQCM) algorithm to reduce the mRNA and methylation feature dimensions and extract cluster eigengenes respectively. Then, we add an auxiliary ordinal loss to the original Cox model to improve the ability to optimize the learning process in training and regularization. The auxiliary loss helps to reduce the vanishing gradient problem for earlier layers and helps to decrease the loss of the primary task. Meanwhile, we use an adaptive weights approach to multi-task learning which weighs multiple loss functions by considering the homoscedastic uncertainty of each task. Finally, we build an ordinal cox hazards model for survival analysis and use long short-term memory (LSTM) method to predict patients’ survival risk. We use the cross-validation method and the concordance index (C-index) for assessing the prediction effect. Stringent cross-verification testing processes for the benchmark dataset and two additional datasets demonstrate that the developed approach is effective, achieving very competitive performance with existing approaches.
Availability and implementation
1 Introduction
Breast cancer has been one of the most common form of diseases worldwide. Reported data emphasize the importance of a more profound understanding of the factors that trigger breast cancer and contribute to its development. Genetic alterations driven by multiple factors motivate frequent applications to identify biomarkers of breast carcinoma progression. Two ‘omics dimensions easy to measure refer to DNA methylation and mRNA expression processes. DNA methylating process and mRNA levels exhibit differential expressions in a variety of tissues (Suzuki et al., 2012). To elucidate the interacting mechanisms of various genomics-related characteristics, more sophisticated modeling and analysis processes are required. It is noteworthy that the causal associations between DNA methylation information and gene expression data receive wide interest and analysis (Anjum et al., 2014; Jiao et al., 2014; Yang et al., 2014). Methylation’s and mRNA’s influence in cancer have been introduced with great success. mRNA epigenetic regulating processes via DNA methylation at CpG sites can be maintained, with methylating patterns termed as epigenetic markers (Lobo, 2008).
In early studies on cancer prognosis, the use of single-feature biomarkers was often performed. Yet in the mentioned researches, some useful Supplementary Information between different data modalities was ignored. With the advances of modern genomic technologies, integrative analysis on heterogeneous data to find important information for diagnosis, staging and prognosis of cancers has received considerable attention (Jeong et al., 2015; Kim et al., 2017, 2018). Multi-feature fusion analysis is receiving widespread attention from pathologists in practical clinics-related affairs. Some studies have explored a combination of different genomic biomarkers for survival analysis. Kim et al. (2018) proposed an integrative robust pathway-based directed random walk (DRW) method on survival prediction processes of breast carcinoma utilizing the interaction between gene expressing state and DNA methylating process. Yuan et al. (2012) integrated image and genomic records for improving the survival prediction of breast cancer cases. Cheng et al. (2017) constructed an emerging framework capable of predicting the survival outcome of renal cell carcinoma cases by combining image features and gene expression features. As indicated by the aforementioned existing researches, different forms of data complement each other and present more effective case stratification if employed jointly. Though the combination of genomic features is capable of more effectively predicting the clinical evolution of carcinoma cases, simple combinations of the mentioned characteristics are likely to present redundant characteristics, thus reducing the prediction effect, so that some feature selection process is critical to multimodal feature fusion. In previous research, the multimodal data were commonly linked, and subsequently conventional feature selection approaches were adopted for selecting the parts associated with carcinoma prediction.
In clinical practice, pathologists make a diagnosis and predict evolution by clinical examination. The clinics-related behaviors of breast carcinoma are significantly diverse, covering aggressive metastatic disease and slowly developing localized tumors (Gulati et al., 2014). Thus, prediction-related biomarkers are critical to split cases for personalized carcinoma management, which could avoid over treatment or under treatment (Chen et al., 2015). For example, those patients classified in high-risk groups may benefit from more aggressive therapies, closer follow-up and more advanced care plans (Kim et al., 2004; Yu et al., 2016). Cox proportional hazard model (Lin et al., 1993) is one of the most popular survival prediction model. Recently, based on the Cox model, several regularization approaches have been proposed in the literature. The Least Absolute Shrinkage and Selection Operator COX model (LASSO-COX) (Ryall et al., 2017; Shao et al., 2018; Tibshirani, 1997) applies the lasso feature selection method for selecting parts associated with carcinoma prediction. Random survival forests (RSF) (Ishwaran et al., 2008) calculates a random forest with the log-rank test as the splitting standard. It determines the cumulative hazards of the leaf nodes while averaging them over the totality of elements. Cox regression with neural networks by a one hidden layer multilayer perceptron (MLP) (Xiang et al., 2000) was proposed to replace the linear predictor of the Cox model. Some novel networks were suggested to be capable of outperforming typical Cox models (Amiri et al., 2008). DeepSurv (Katzman et al., 2016; Katzman et al., 2018) refers to a deep Cox proportional hazards neural network as well as a survival approach to model interacting processes of a case’s covariates and treatment modalities for providing individual treatment suggestions. DeepSurv is developed upon Cox proportional assumption with a cutting-edge deep neural network. MTLSA (Li et al., 2016) is a recently proposed model which regards survivL study to be a multi-task learning issue. It transforms the problem into several binary classifying processes, and employs a multi-task learning approach to model the event probability at different times. Though much progress has been made using above approaches, Yet the prediction performance of the previously proposed approaches remains far from satisfying, and many areas remain for subsequent advancement. In addition, the afore mentioned approaches assume that the survival data of one patient is not determined by others, thereby losing the robust ordinal association of the survival times of a range of cases.
Motivated by all the previously mentioned considerations, we present a novel method for survival prediction of breast cancer using bidirectional Long Short-Term Memory (biLSTM) (Hochreiter and Schmidhuber, 1997) ordinal Cox model network from gene mRNA expression and DNA methylation multi-modal data. In this model, the original Cox losses are combined with the auxiliary ordinal losses as a multi-task loss. The losses of auxiliary tasks added to the original objective help to improve the ability to optimize the learning process in biLSTM training and regularization. Because the performance of multi-task systems strongly depends on the relative weight between the losses of each task, adjusting these weights manually is a difficult and expensive process, which makes multi-task learning difficult in practice. So, we use an adaptive approach to multi-task learning which weighs multiple loss functions by considering the homoscedastic uncertainty of each task. This allows us to learn all kinds of quantities in the regression settings of different units at the same time. This study demonstrates the effective properties of the developed approach through cross validation tests on the benchmark dataset.
2 Materials and methods
2.1 Benchmark datasets
In this study, the used survival analysis benchmark datasets including gene expression data, DNA methylation data and clinical data. The clinical data are included in the main clinical file downloaded from The Cancer Genome Atlas (TCGA) (Tomczak et al., 2015), which provides an extensive collection of genomics and clinical outcome data for large cohorts of patients of more than 30 types of cancers. The main files contain 1097 breast cancer patients’ clinical annotations and information. In our case, two clinical variables are used: Overall Survival Status (1 if the patient deceased, 0 if he/she is living at the time of the last follow-up) and Overall Survival (Months), which represent the number of months between diagnosis and date of death or last follow-up. In clinical data, patients with missing follow-up were excluded.
The gene expression data and DNA methylation data of breast cancer cases pertain to the TCGA dataset of the Broad Institute GDAC Firehose (Deng et al., 2017). Gene expression information from mRNA sequence consisted of 20 533 genes. mRNA expression profiles received the transformation from Illumina HiSeq 2000 RNA-seq readcounts to normalized reads per kilobase per million (RPKM). This study acquires DNA methylation data as a gene-related characteristic of 20 106 genes through the selection of the probe exhibiting a minimal relation to expressing information for the respective gene. This study removes genes achieving genes expressing values of 0. Gene expression data, DNA methylation data and clinical data were merged and filtered to keep only matching samples. This study removes cases with survival months not recorded or not correctly recorded having negative data. For the latter reason, among 1097 cases, this study extracts 485 instances that comprised both mRNA sequencing and DNA methylation information. The benchmark dataset including gene data and survival data was obtained. Table 1 lists the gene- and clinic-related features for the selected cases.
Table 1.
Gene and clinical characteristics of breast cancer
| Characteristics | Summary |
|---|---|
| Instance no. | 485 |
| Gene no. | |
| Methylation | 20 106 |
| mRNA | 20 533 |
| Survival status | |
| Living | 413 |
| Deceased | 63 |
| Follow-up (months) | 0.03–282.69 |
| Age (years) | |
| Range | 26–90 |
| Median | 57.23 |
A challenging point facing the present research is that other significant cohorts of breast cancer cases with matched DNA methylation and gene expression information are lacking. Thus, this study firstly applies the cross-validation process in the respective steps of downstream machine learning research, then adopts a second dataset to validate the efficacy of the proposed method.
2.2 Gene feature extraction
The large number of genes in mRNA and methylation data posed a challenge to obtaining sufficient statistical power. Recently, a weighted network mining algorithm termed as local maximum quasi-clique merging (lmQCM) (Cheng et al., 2017) has been developed and received favorable results when applied in gene co-expression research. lmQCM could detect weak quasi-clique modules in weighted graphs with applications in functional gene cluster discovery. This algorithm features a greedy approach that uses hierarchical clustering and does not allow overlap between modules, Meanwhile, it allows genes to be shared among multiple modules. This is consistent with the fact that genes often participate in multiple biological processes. In addition, lmQCM can find smaller coexpressed gene modules that are often associated with structural mutations such as copy number variation in cancers. Another well-known gene clustering algorithm is weighted gene co-expression network analysis (WGCNA) (Langfelder and Horvath, 2008). WGCNA is a powerful technique used to extract co-expressed gene networks from gene expressions, and is widely used in genomic data analysis.
In our study, we tested the effectiveness of the methods of lmQCM and WGCNA respectively. By comparing the effects, we chose lmQCM as gene feature extraction method. Instead of focusing on individual genes, we firstly use the lmQCM algorithm to cluster genes into coexpressed modules, then summarized each module as an eigengene. The lmQCM algorithm has four parameters γ, t, α, β. Among these parameters, γ is the most influential, as it determines if a new module can be initiated by setting the weight threshold for the first edge of the module representing a subnetwork. In the lmQCM algorithm, the absolute values of the spearman correlation coefficients between expression profiles of genes are transformed into weights using a normalization procedure adopted from spectral clustering. Thus, lmQCM algorithm yields 17 coexpressed gene modules (features) for methylation data and 116 coexpressed gene modules for mRNA data. It is worth noting that to avoid overfitting, we applied gene feature selection methods to the training set and test set in cross-validation respectively.
2.3 Ordinal Cox model
In survival analysis, prediction of the time duration until a certain event occurs is the goal of the task being modeled and the death of a cancer patient is the event of interest in our study (Kourou et al., 2015). Cancer patients in our study can be divided into two categories, i.e. censored patients and non-censored patients. For censored patients, the death events were not observed for them during the follow-up period, and thus their genuine survival times are longer than the recorded data; while for non-censored patients, their recorded survival times are the exact time from initial diagnosis to death. We use a triplet to represent each observation in survival analysis, where is the feature vector, is the observed time and is the censoring indicator. Here, or indicates a non-censored or censored instance, respectively.
The primary goals in survival analysis are estimating the survival function and hazard function (Wang et al., 2019), both of which can be used to model the distribution of the event time over the timeline. Survival function represents the probability that the event has not happened earlier than a specified time t (Lee and Wang, 2003). We define O as the variable of the true occurrence time for the event of interest and is the probabilistic density function (P.D.F.) of the true event time. So we have,
| (1) |
By defining the survival function as the probability that a patient will survive after time t, the hazard function that can assess the instantaneous rate of death is defined as following:
| (2) |
where corresponds to the covariate variable of dimensionality n. Among the hazards modeling methods, cox proportional hazard model (Lin et al., 1993), which is built based on the hypothesis that the hazard ratio between two instances is time-independent, is defined as:
| (3) |
Here, is the baseline hazard, and is called survival function, in which can be estimated by minimizing its corresponding partial likelihood function. The partial likelihood is defined as follows:
| (4) |
where ti denotes the event time, is a binary value indicating whether the event happened or not, and denotes the set of all individuals at risk at time, which represents the set of patients that are still at risk before time. Therefore, the coefficient vector can be learned via minimizing the negative partial log-likelihood function () of the Cox model, which is defined as following (Sy and Taylor, 2000):
| (5) |
Although we could use the above Cox model to directly make survival prediction, it does not take the ordinal survival information between different cases (e.g. the survival time for case A is longer than that for case B) into consideration. In the hazard ratio-based model, the ordinal relationship of the hazard risk between patient and patient can be easily derived by calculating the ratio (i.e. recij):
| (6) |
In practice, if, the survival time for patientshould be shorter than that for patient, and vice versa. By utilizing the above ordinal relationship indicated by Cox model, we design a ranking loss function (to capture the ordinal survival information among different patients as follows:
| (7) |
where I = 1 if the survival time for patientis shorter than that for patient. Otherwise, I = 0.
By combining the Cox negative partial log-likelihood function with the above ordinal loss , the weighted sum of the losses can be formulated as a multi-task model. Numerous existing approaches learning multiple tasks at the same time employ a naive weighted sum of losses, in which the loss weights are uniform, or altered in a crude and manual manner. However, the model effect exhibits extreme sensitivity to weight selecting process. The afore mentioned weight hyper-parameters can be tuned at high costs. Thus, a more convenient approach capable of learning the optimal weights is required. We developed a method to integrate several loss functions for learning objectives in an adaptive manner.
2.4 Adaptive weighting losses
In this study, we use gene expression and methylation features to make survival predictions for breast cancer patients. Our main task is obtaining the training model. The main task has a corresponding loss Lmain, which can be the expected return loss used for calculating the policy gradient. The present study employs the Cox negative partial log-likelihood function as the main loss Lmian, i.e. Lmain=LCox. To improve data efficiency, besides the main task, one has access to one or more auxiliary tasks that share some unknown structure with the main task (Papoudakis et al., 2018). In this study, the ordinal survival deep network model is employed as an auxiliary task, and the ordinal loss can be used as auxiliary loss of this auxiliary task, i.e. Laux=Lord. Our goal is to optimize the main loss Lmian. However, auxiliary tasks are commonly used to help to learn a good feature representation. We can combine the main loss with the loss from the auxiliary tasks as:
| (8) |
where is the set of all training model parameters, and are the weights for the main task and the auxiliary task respectively. Let , in which ,are the weight variables with an initial value of 0. Under the intuition that modifying , and to minimizewill improve and if the two tasks are sufficiently related. We propose to modulate the weight variable at each learning iteration (epoch) by adding a custom-multi-loss layer in the deep network. Given that is the set of all model parameters at training step , and,are the weight variables at step , we assume that we update the parameters, and using gradient descent on this combined objective:
| (9) |
whereis the gradient step size, and denotes the gradient of the loss function L. At each optimization iteration, we can efficiently approximate the solution to . The weights are discouraged from decreasing too much by the negative exponential functions. The modeling task-dependent weighting can improve the model’s representation and the performance of each task when compared to separate model trained on each task individually.
2.5 Flowchart of system algorithm
Figure 1 shows the algorithm process of our proposed method. There are several stages including the gene co-expression cluster stage, main/auxiliary biLSTM network stage and the COX model stage etc. In the gene co-expression cluster stage, the feature dimensions of the mRNA and methylation data can be reduced. lmQCM algorithm is used to cluster genes, and so mRNA and methylation eigengenes are obtained respectively. The directly concatenated eigengenes of mRNA and methylation will be main task input features for the machine learning network to train the model. Meanwhile, we also use the concatenated eigengenes as auxiliary task input. In the main task, multiple biLSTM layers, timeDistributed layers, dropout layers and full connected layers are used to predict patient survival risk with the negative partial log-likelihood function, and then the main loss (i.e. Lmain) is obtained. In the auxiliary task, we use one auxiliary biLSTM layer and one fully connected layer to obtain the ordinal loss (i.e. auxiliary loss Laux). We designed a custom multi-loss layer which can combine the main loss with the auxiliary loss: at each learning iteration t. We use a proposed adaptive optimization iteration method to tune the weight variables (λ1t, λ2t) of the main and auxiliary loss. Finally, through iterative training, the deep cox hazard model is built for survival analysis to ensure that the ordinal relationship among the survival time of different patients can be preserved. We termed this multi-task loss ordinary COX model procedure as ML_ordCOX.
Fig. 1.
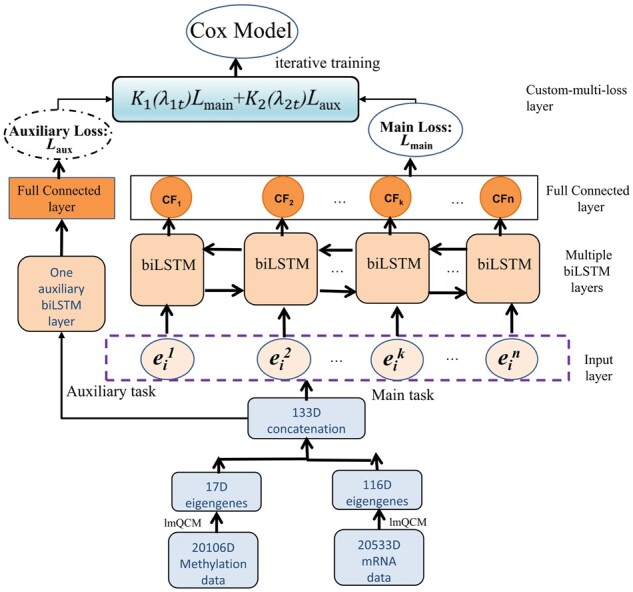
Illustration of the proposed model and framework
2.6 Evaluation indexes
This study assesses the performance of the developed approach and other comparing method using Concordance index (C-index). C-index quantifies the fraction of all pairs of cases with predicted survival times ordered in a correct manner as:
| (10) |
where k denotes the set of validly orderable pairs when ; represents the number of comparable pairs among them; is the prediction of survival time; I is the indicator function of whether the condition in parentheses is satisfied or not. C-index gives probability. In terms of a random individual pair, the predicted survival time of the two individuals is in the same order as their actual survival time. Since the C-index is determined only by variations in the predicted results, it is very useful for evaluating proportional hazard models. Because the order of proportional-risk models doesn't change over time. Therefore, we were able to use relative risk functions rather than measures used to predict survival time.
3 Results and discussions
3.1 Coexpressed gene modules clustering help to improve prediction accuracy
In this section, we test three gene feature selection methods: Denoising Autoencoder (DA) (Liu et al., 2020), lmQCM and WGCNA. DA has proven to be effective in selecting robust features against input noise and extracting more specific cancer-related pathways or genes. In the experiments, we choose the optimal parameter settings for these three methods. We set the number of DA encoder layer nodes as 100, and activation function as ‘sigmoid’. In lmQCM, we set parameters with For WGCNA, we set minModuleSize = 30. Through these three different methods, methylation and mRNA features after dimensionality reduction can be obtained. We use DA algorithm to obtain 100 methylation features and 100 mRNA features respectively. We use lmQCM algorithm to obtain 17 methylation features and 116 mRNA features respectively. Similarly, by WGCNA, we obtain 12 methylation features and 26 mRNA features respectively. We combine methylation and mRNA features in series and obtain 200, 133 and 38-dimensional features in three different methods. It should be noted that the number of features is automatically selected by these algorithms. We test each integrated feature and compare performance between different methods with C-index value. Table 2 lists the performance comparison of three methods. For the sake of fairness and convenience, we only carry out the same single task loss function, i.e. main loss (Lmain), and the same biLSTM structure.
Table 2.
Comparison of performance of three gene feature selection methods with C-index
| Gene Selection Methods | C-index |
|---|---|
| DA | 0.5507 |
| WGCNA | 0.6423 |
| lmQCM | 0.6894 |
As shown in Table 2, it can be found that lmQCM and WGCNA methods have better performance than DA. In the cross validation on the standard dataset, lmQCM is superior to WGCNA. Compared with the DA and WGCNA methods, the C-index of lmQCM is improved by 13.87% and 4.71%. Considering the similar computational complexity of lmQCM and WGCNA, we decided to adopt lmQCM method to extract gene features.
3.2 Multi-feature fusion is superior to single feature
In this part, this study assesses the performance concerning the integrated feature set with different single feature set. After obtaining 116 mRNA eigengenes and 17 methylation eigengenes from lmQCM algorithm respectively, we take the two eigengenes as two different single gene feature (named GmRNA and Gmeth) inputs. We combine mRNA and methylation features in sequence and obtain a 133-dimensional feature vector which will be viewed as integrated gene feature (Named GmRNA+meth) input. Moreover, for the sake of fairness, this study carries out the same multiple losses ordinary COX model procedure (i.e. ML_ordCOX). The experiments compare the performance of three feature sets over ten-fold cross validation and run 1000 epochs (iterations). It should be noted that the learning rate will be set with an initial value of 0.001 and will be reduced gradually by half every 100 epochs during training phase in order to improve model performance. Table 3 summarizes the performance comparison of the three feature sets with the values of the C-index.
Table 3.
Performance comparison among integrated feature set and single feature sets with C-index
| Feature Sets | C-index |
|---|---|
| GmRNA+meth | 0.7222 |
| GmRNA | 0.6707 |
| Gmeth | 0.5573 |
As demonstrated in Table 3, in the 10-fold cross validation on standard datasets, the GmRNA+meth outperforms the two single feature sets. Compared with them, Gmeth and GmRNA, the C-index of the GmRNA+meth is improved by 5.15% and 16.49% respectively. The integrated feature set, by leveraging the combination of the single feature sets, can effectively improve the performance.
Figure 2 reflects the loss decrease during training phase by applying different feature sets. From Figure 2, we find that as the number of iterations increases, the training loss of the multi-feature fusion methods (GmRNA+meth) decreases obviously faster than that of the other two single feature set methods (i.e. Gmeth and GmRNA). The faster gradient descent helps the training loss converge to the optimal solution. It demonstrates the advantage of the integrated patterns of sequential mRNA data and methylation data. It is worth noting that the continuous decay of the learning rate makes the training loss curve finally converge.
Fig. 2.
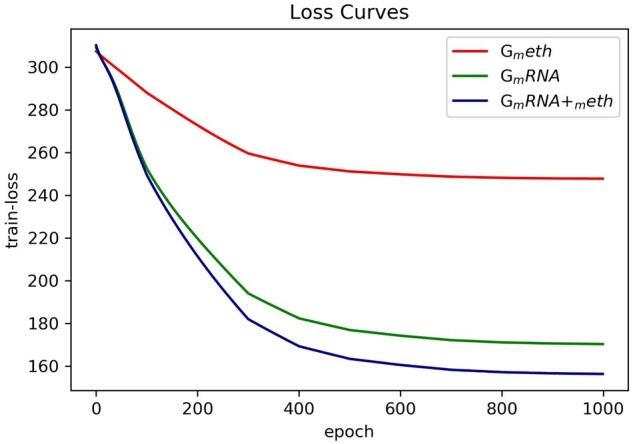
The training loss curves by applying different feature sets
3.3 Multi-task losses method performs better than single task loss alone
We compare the proposed multi-task losses method (i.e. ML_ordCOX), which combines the main loss (Lmain) with the auxiliary loss (Laux) from the auxiliary task, with two single task alone loss methods (i.e. only main task loss and only auxiliary task loss). In 3.2 section experiments, GmRNA+meth is the best feature set. So, we use GmRNA+meth as input feature set to assess the performance concerning the proposed approach. Table 4 presents the performance comparison of the ML_ordCOX and the two single task loss methods with the values of the C-index.
Table 4.
Performance comparison between three different loss methods with C-index
| Methods | C-index |
|---|---|
| Multi-task losses (ML_ordCOX) | 0.7222 |
| Only main task loss | 0.6894 |
| Only auxiliary task loss | 0.5056 |
From Table 4, we can find that the multi-task ML_ordCOX method has the best performance when compared with the other two single task methods. Compared with only the main task loss and only the auxiliary task loss, the C-index of the ML_ordCOX is improved by 3.28 percent and 21.66 percent respectively. It means that the proposed multi-task method can dynamically adapt the weights for the multiple tasks to perform better than or as well as the best single task.
Figure 3 shows the training loss curves of three different loss methods. As can be seen from this Figure 3, the curve of the only auxiliary task loss method converges fastest, and the curve of the multi-task method ML_ordCOX, which combines the two single tasks, decreases faster than that of the only main task. It indicates that the auxiliary task will help multi-task to converge to the optimal solution if we add an auxiliary loss term to the total loss function.
Fig. 3.
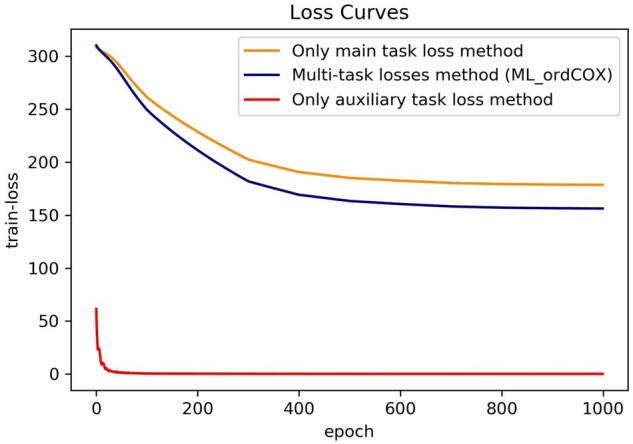
The training loss curves of three different task loss methods
We develop an adaptive optimization iteration method to tune the weight variables (λ1, λ2) of the main and auxiliary loss. In the experiments, we also tracked the weight variables and represented the weight change curve. Figure 4 shows the curves of weight variables ,, (i.e. lambda1, lambda2), and weights for the main task loss and the auxiliary task loss. Here, . In Figure 4(a), weight variables ,are set with initial value of (0,0), and the values are changed to (0.1488, 0.01303) when the model converges. As also can be seen from Figure 4(b), weights are set with initial value of (1,1) and converge to (0.8617, 0.9871) when 1000 epochs are completed. As demonstrated in Figure 4, firstly, we could use the negative exponential functions of weight variables to effectively discourage the weights from decreasing too much. Secondly, compared with the auxiliary task, the main task weight plays a major tuning role in training the multi-task model.
Fig. 4.
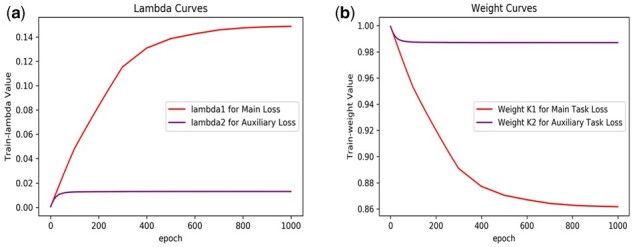
The weight variable and weight curves of the main task loss and the auxiliary task loss. (a) the curves of weight variables , for the main task loss; (b) the curve of weights for the auxiliary task loss
3.4 Comparison with existing survival prediction methods over cross-validation test
We compare the prediction effects of the developed ML_ordCOX method with five machine learning approaches: RSF (Ishwaran et al., 2008), LASSO (Tibshirani, 1997), MLP (Amiri et al., 2008), DeepSurv (Katzman et al., 2016) and MTLSA (Li et al., 2016). The C-index is used to evaluate the prediction performance. To ensure fairness, this study runs the identical feature set in all cross-validation tests.
Table 5 lists the performance comparisons between the proposed method, MTLSA, DeepSurv, MLP, Lasso and RSF by the measurements of C-index. From Table 5, we find that the cross validation of the developed method on the standard training set is better than the other five methods. Compared with the methods: RSF, LASSO, MLP, DeepSurv and MTLSA, the C-index of the developed method is improved by 14.93%, 11.78%, 7.33%, 6.99% and 7.74% respectively. As can be seen from Table 5, firstly, the prognosis power of the regularized Cox models (i.e. RSF and LASSO) is inferior to the other deep model-based methods (i.e. MLP and DeepSurv). This is because the deep model can better represent gene features than the hand-crafted low-level features. Secondly, the proposed biLSTM method can achieve higher C-index values than the comparing methods, which demonstrates the advantage of LSTM that can represent the integrated patterns of sequential mRNA data and methylation data. The experiment also demonstrates the efficacy of the proposed method.
Table 5.
Performance comparison among different survival prediction methods by the measurements of C-index (along with their standard deviations)
| Methods | C-index |
|---|---|
| The proposed method (ML_ordCOX) | 0.7222 (0.0145) |
| MTLSA | 0.6448 (0.0232) |
| DeepSurv | 0.6523 (0.0271) |
| MLP | 0.6489 (0.0663) |
| LASSO | 0.6044 (0.0097) |
| RSF | 0.5729 (0.0178) |
3.5 Survival stratification prediction
Another important task in survival analysis is to stratify cancer patients into subgroups with different predicted outcomes, by which we can develop personalized treatment plans during cancer disease progression. The median risk score method is used in the training set as a threshold to stratify patients in the test set into low-risk and high-risk groups, and then test if these two groups have significantly different survival time using the log-rank test. Better prognosis prediction performance comes with smaller P-value from the log-rank test. We show the stratification performance of different prediction methods in Figure 5.
Fig. 5.
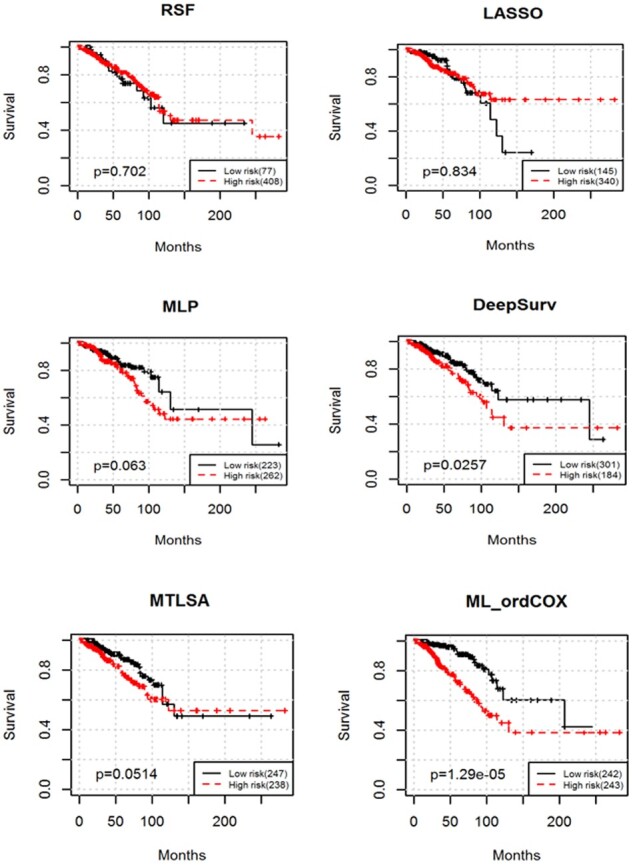
The survival curves by applying different methods
As shown in Figure 5, the proposed prediction method (ML_ordCOX) achieves significantly superior stratification performance (log-rank test P = 1.29e-05) when compared with the other methods (log-rank test P = 0.702, 0.834, 0.063, 0.0257 and 0.0514 for RSF, LASSO, MLP, DeepSurv and MTLSA, respectively) on mRNA and methylation datasets, which shows the advantage of using auxiliary loss. In addition, it is worth noting that the proposed method could provide better prognostic prediction than the comparing methods, this is because our proposed model considers both the ordinal characteristics and the integrative patterns in survival analysis. Thus, its prognostic power is effectively improved.
3.6 Performance generalization and comparison over independent validation sets
To further explore the effectiveness of the proposed method, we carry out experiments on two additional cancer type datasets, i.e. Glioma cohort (GBMLGG) and Pan-kidney cohort (KIPAN). The two datasets were also obtained from Firehose (Deng et al., 2017). We selected these two cohorts because they have a high number of cases, which allows us to draw more valid inferences, and construct stronger comparisons for our breast cancer results. The GBMLGG datasets include 1129 samples for clinical data, 17 184 gene expression features for mRNA sequencing data, and 20 116 gene-level features for DNA methylation data. We obtained 563 instances that had both mRNA sequencing and DNA methylation data after merging and filtering. For GBMLGG datasets, by using lmQCM algorithm, we extracted 17 coexpressed features for methylation data and 36 coexpressed features for mRNA data. The KIPAN datasets contain 973 samples, 25 055 gene expression features, and 20 533 DNA methylation features. Similarly, we also extracted 656 instances that had both mRNA sequencing and DNA methylation data. For KIPAN, lmQCM algorithm yields 25 coexpressed features for methylation data and 28 coexpressed features for mRNA data.
Firstly, we compare the performance concerning the integrated feature set with two different single feature sets. In order to be consistent with breast cancer, for GBMLGG and KIPAN, we still take the obtained mRNA eigengenes and methylation eigengenes from lmQCM algorithm as GmRNA and Gmeth respectively. The integrated feature set is still referred to as GmRNA+meth. Table 6 summarizes the performance comparison of the three feature sets on GBMLGG and KIPAN datasets. Secondly, we use the two additional datasets to further validate the effectiveness of our proposed multi-task losses method (i.e. ML_ordCOX). We compare ML_ordCOX with two single task loss methods (i.e. only main task loss Lmain and only auxiliary task loss Laux). Table 7 presents the performance comparison between these three different loss methods.
Table 6.
Performance comparison among integrated feature set and single feature sets by C-index on GBMLGG and KIPAN datasets
| Feature Sets | GBMLGG | KIPAN |
|---|---|---|
| GmRNA+meth | 0.8236 | 0.7748 |
| GmRNA | 0.8011 | 0.7624 |
| Gmeth | 0.8102 | 0.4785 |
Table 7.
Performance comparison between three different loss methods by C-index on GBMLGG and KIPAN datasets
| Methods | GBMLGG | KIPAN |
|---|---|---|
| ML_ordCOX | 0.8236 | 0.7748 |
| Only main task loss | 0.8117 | 0.7613 |
| Only auxiliary task loss | 0.5272 | 0.7528 |
From Table 6, we can find that the GmRNA+meth still outperforms the two single feature sets. For GBMLGG, compared with GmRNA and Gmeth, the C-index of the GmRNA+meth is improved by 2.25% and 1.34%; and for KIPAN, the performance of integrated feature has an increase of 1.24% and 29.63%. It once again shows the superiority of integrated features. As shown in Table 7, compared with only main task loss and only auxiliary task loss, the C-index of the ML_ordCOX is improved by 1.19 percent and 29.64 percent on GBMLGG, and is improved by 1.35% and 2.20% on KIPAN. From Table 7, we can also find that the proposed multi-task method still has the best performance than the other two single task methods on the additional datasets.
Figures 6 and 7 show the performance curves concerning the GBMLGG and KIPAN respectively. The plotted curves include the training loss curves by three different feature sets, the training loss curves of three different loss methods, the curves of weight variables (λ1, λ2), and weights curves. Compared with Breast Cancer, Figures 6 and 7 show the similar performance curves on GBMLGG and KIPAN. It further demonstrates the advantage of the integrated feature and the proposed multi-task losses method.
Fig. 6.
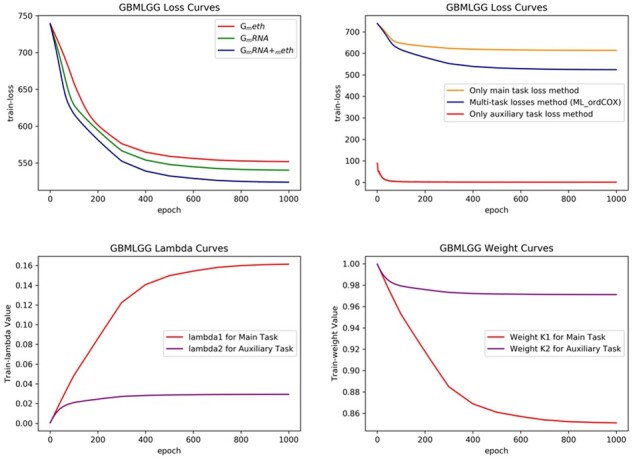
The performance comparison curves on GBMLGG dataset
Fig. 7.
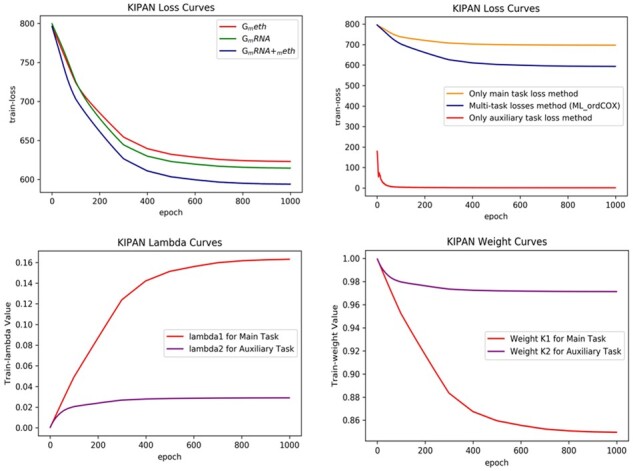
The performance comparison curves on KIPAN dataset
Finally, we compare the proposed method ML_ordCOX with the aforementioned five survival prediction methods on GBMLGG and KIPAN datasets. Table 8 lists the performance comparisons between the proposed method ML_ordCOX, MTLSA, DeepSurv, MLP, Lasso and RSF by the measurements of the C-index on GBMLGG and KIPAN datasets. To ensure fairness, we still use the same feature set in all cross-validation tests.
Table 8.
Performance comparisons among different survival prediction methods by C-index on GBMLGG and KIPAN datasets over ten-fold cross-validation (with standard deviations)
| Methods | GBMLGG | KIPAN |
|---|---|---|
| ML_ordCOX | 0.8236 (0.0201) | 0.7748 (0.0142) |
| MTLSA | 0.7103 (0.0193) | 0.6984 (0.0264) |
| DeepSurv | 0.7647 (0.0216) | 0.7347 (0.0173) |
| MLP | 0.7494 (0.0227) | 0.7253 (0.0363) |
| LASSO | 0.6235 (0.0147) | 0.6346 (0.0286) |
| RSF | 0.5932 (0.0278) | 0.6233 (0.0233) |
From Table 8, we can find that our method ML_ordCOX achieved the best performance on GBMLGG and KIPAN data. For GBMLGG, compared with RSF, LASSO, MLP, DeepSurv and MTLSA, the C-index of the developed approach ML_ordCOX is improved by 23.04%, 20.01%, 7.42%, 5.89% and 11.33% respectively; and for KIPAN, the performance of ML_ordCOX has an increase of 15.15%, 14.02%, 4.95%, 4.01% and 7.64% in C-index respectively.
Hence, the test results demonstrate that the generalization capabilities of the developed approach are superior to those of the other five reported approaches. The good performance of these independent tests further demonstrates the effectiveness of the developed method for survival analysis of other cancer types.
4 Conclusions
This study develops a survival analysis framework for breast cancer cases, considering cases’ ordinal survival information. Cross-validation experiments on the mRNA gene expression data and DNA methylation data were carried out. Experimental results demonstrate the superiority of the proposed method over the existing RSF, Lasso, MLP, DeepSurv and MTLSA methods. The good performances of the proposed method come from the use of the combined bidirectional LSTM predictor and ordinal information. Experimental results also show the importance of DNA methylation and gene expression signatures for breast cancer survival analysis. In this work, we have shown that dynamically combining an auxiliary task and adaptively adjusting the weights for the multiple tasks in an online manner can give a significant performance improvement for biLSTM Cox model network. The proposed method uses the idea that auxiliary tasks should provide a gradient update direction that helps to decrease the loss of the main task. In addition, we carried out experiments on Glioma cohort and Pan-kidney cohort. The good performance on the two additional cancers also demonstrates that our method is not limited to breast cancer and can be applied to other carcinoma types with many samples in TCGA.
Financial Support: none declared.
Conflict of Interest: none declared.
Contributor Information
Isabelle Bichindaritz, Intelligent Bio Systems Laboratory, Biomedical and Health Informatics, Department of Computer Science, State University of New York at Oswego, Syracuse, NY 13202, USA.
Guanghui Liu, Intelligent Bio Systems Laboratory, Biomedical and Health Informatics, Department of Computer Science, State University of New York at Oswego, Syracuse, NY 13202, USA.
Christopher Bartlett, Intelligent Bio Systems Laboratory, Biomedical and Health Informatics, Department of Computer Science, State University of New York at Oswego, Syracuse, NY 13202, USA.
References
- Amiri Z. et al. (2008) Assessment of gastric cancer survival: using an artificial hierarchical neural network. Pak. J. Biol. Sci., 11, 1076–1084. [DOI] [PubMed] [Google Scholar]
- Anjum S. et al. (2014) A BRCA1-mutation associated DNA methylation signature in blood cells predicts sporadic breast cancer incidence and survival. Genome Med., 6, 47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.-M. et al. (2015) New breast cancer prognostic factors identified by computer-aided image analysis of HE stained histopathology images. Sci. Rep., 5, 10690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng J. et al. (2017) Integrative analysis of histopathological images and genomic data predicts clear cell renal cell carcinoma prognosis. Cancer Res., 77, e91–e100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng M. et al. (2017) FirebrowseR: an R client to the Broad Institute’s Firehose Pipeline. Database, 2017, baw160. () [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulati S. et al. (2014) Systematic evaluation of the prognostic impact and intratumour heterogeneity of clear cell renal cell carcinoma biomarkers. Eur. Urol., 66, 936–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochreiter S., Schmidhuber J. (1997) Long short-term memory. Neural Comput., 9, 1735–1780. [DOI] [PubMed] [Google Scholar]
- Ishwaran H. et al. (2008) Random survival forests. Ann. Appl. Stat., 2, 841–860. [Google Scholar]
- Jeong H-h. et al. (2015) Integrative network analysis for survival-associated gene-gene interactions across multiple genomic profiles in ovarian cancer. J. Ovarian Res., 8, 42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiao Y. et al. (2014) A systems-level integrative framework for genome-wide DNA methylation and gene expression data identifies differential gene expression modules under epigenetic control. Bioinformatics, 30, 2360–2366. [DOI] [PubMed] [Google Scholar]
- Katzman J.L. et al. (2016) Deep survival: a deep cox proportional hazards network. Stat, 1050, 2. [Google Scholar]
- Katzman J.L. et al. (2018) DeepSurv: personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol., 18, 24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim D. et al. (2017) Using knowledge-driven genomic interactions for multi-omics data analysis: metadimensional models for predicting clinical outcomes in ovarian carcinoma. J. Am. Med. Inf. Assoc., 24, 577–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H.L. et al. (2004) Using protein expressions to predict survival in clear cell renal carcinoma. Clin. Cancer Res., 10, 5464–5471. [DOI] [PubMed] [Google Scholar]
- Kim S.Y. et al. (2018) Integrative pathway-based survival prediction utilizing the interaction between gene expression and DNA methylation in breast cancer. BMC Med. Genomics, 11, 68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kourou K. et al. (2015) Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J., 13, 8–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langfelder P., Horvath S. (2008) WGCNA: an R package for weighted correlation network analysis. BMC Bioinformatics, 9, 559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee E.T., Wang J. (2003) Statistical Methods for Survival Data Analysis. John Wiley & Sons, Hoboken, NJ. [Google Scholar]
- Li Y. et al. (2016) A multi-task learning formulation for survival analysis. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. pp. 1715–1724. 10.1145/2939672.2939857 [DOI]
- Lin D.Y. et al. (1993) Checking the Cox model with cumulative sums of martingale-based residuals. Biometrika, 80, 557–572. [Google Scholar]
- Liu G. et al. (2020) Bioimage-based Prediction of Protein Subcellular Location in Human Tissue with Ensemble Features and Deep Networks. IEEE/ACM Trans. Comput. Biol. Bioinf., 17, 1966–1980. [DOI] [PubMed] [Google Scholar]
- Lobo I. (2008) Genomic imprinting and patterns of disease inheritance. Nat. Educ., 1, 5. [Google Scholar]
- Papoudakis G. et al. (2018) Deep reinforcement learning for Doom using unsupervised auxiliary tasks, arXiv preprint arXiv:1807.01960. 2018 Jul 5.
- Ryall S. et al. (2017) A comprehensive review of paediatric low-grade diffuse glioma: pathology, molecular genetics and treatment. Brain Tumor Pathol., 34, 51–61. [DOI] [PubMed] [Google Scholar]
- Shao W. et al. (2018) Ordinal multi-modal feature selection for survival analysis of early-stage renal cancer. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 648–656.
- Suzuki H. et al. (2012) DNA methylation and microRNA dysregulation in cancer. Mol. Oncol., 6, 567–578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sy J.P., Taylor J.M. (2000) Estimation in a Cox proportional hazards cure model. Biometrics, 56, 227–236. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. (1997) The lasso method for variable selection in the Cox model. Stat. Med., 16, 385–395. [DOI] [PubMed] [Google Scholar]
- Tomczak K. et al. (2015) The Cancer Genome Atlas (TCGA): an immeasurable source of knowledge. Contemporary Oncol., 19, A68–A77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang P. et al. (2019) Machine learning for survival analysis: a survey. ACM Comput. Surv. (CSUR), 51, 1–36. [Google Scholar]
- Xiang A. et al. (2000) Comparison of the performance of neural network methods and Cox regression for censored survival data. Comput. Stat. Data Anal., 34, 243–257. [Google Scholar]
- Yang X. et al. (2014) Gene body methylation can alter gene expression and is a therapeutic target in cancer. Cancer Cell, 26, 577–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu K.-H. et al. (2016) Predicting non-small cell lung cancer prognosis by fully automated microscopic pathology image features. Nat. Commun., 7, 12474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan Y. et al. (2012) Quantitative image analysis of cellular heterogeneity in breast tumors complements genomic profiling. Sci. Transl. Med., 4, 157ra143. [DOI] [PubMed] [Google Scholar]


