Abstract
Summary
Cox-nnet is a neural-network-based prognosis prediction method, originally applied to genomics data. Here, we propose the version 2 of Cox-nnet, with significant improvement on efficiency and interpretability, making it suitable to predict prognosis based on large-scale population data, including those electronic medical records (EMR) datasets. We also add permutation-based feature importance scores and the direction of feature coefficients. When applied on a kidney transplantation dataset, Cox-nnet v2.0 reduces the training time of Cox-nnet up to 32-folds (n =10 000) and achieves better prediction accuracy than Cox-PH (P<0.05). It also achieves similarly superior performance on a publicly available SUPPORT data (n=8000). The high efficiency and accuracy make Cox-nnet v2.0 a desirable method for survival prediction in large-scale EMR data.
Availability and implementation
Cox-nnet v2.0 is freely available to the public at https://github.com/lanagarmire/Cox-nnet-v2.0.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Large-scale population data, including electronic medical records (EMR) data are sources of informative data that can be used for patient’s survival prediction. It is also found that machine-learning-based models outperformed conventional models, such as Cox-Proportional Hazard (Cox-PH) model (Cox, 1972), Random Survival Forests model (Ishwaran et al., 2008) and elastic net regression (Fan et al., 2010) on the prediction of coronary artery disease mortality using EMR data (Steele et al., 2018). Although it is challenging to develop prediction models driven by EMR data, the large sample size and clinical features in these data provide valuable information in survival prediction (Goldstein et al., 2017).
We previously proposed Cox-nnet (Ching et al., 2018), a deep-learning-based neural-network prognosis prediction model, which achieved comparable or better performance than Cox-PH on high-throughput omics data. We recently applied Cox-nnet to histopathology imaging data with pre-extracted features and demonstrated its advantage in combining gene-expression data and image data for survival prediction (Zhan et al., 2020). However, it remains to be tested if Cox-nnet is suitable to predict survival in large-scale population data, where the sample size is usually magnitudes larger than genomics data. Toward this, we propose Cox-nnet v2.0, which significantly improves computational speed, with enhanced interpretability. Additionally, Cox-nnet v2.0 also achieves better prediction accuracy than Cox-PH.
2 Materials and methods
2.1 Cox-nnet method improvement
The original Cox-nnet is a neural-network-based extension to Cox-PH method, using the log partial likelihood as its loss function. In Cox-nnet v2.0, we have made the following improvements:
(i) speed-up in calculating log partial likelihood loss function. The log partial likelihood is calculated by:
| (1) |
where is the linear predictor of patient and is defined by patient is not censored. To avoid nested summation in Theano, the previous version of Cox-nnet calculates the log partial likelihood by matrix multiplication:
| (2) |
where and are vectors of and respectively. is a by at risk set indicator matrix, and each entry is defined by:
| (3) |
where is the sample size of the input data, and and are the event time of patient and , respectively. This implementation is memory intensive and time consuming when dealing with large sample sizes.
In the new version, instead of pairwise comparison, we sorted the observations by event time. Then by definition of the at-risk set, is converted to an upper triangular matrix filled with 1. Intuitively, can be calculated using cumulative summation that no longer requires storing matrix and nested summation (double loops).
(ii) Adding permutation-based feature importance scores. Previously the variable importance score of Cox-nnet is calculated by pseudo drop-out, which replaced the variable with its mean. The drawback is that it is hard to interpret categorical variables. Here, we introduce a more general feature evaluation method using permutation importance score (Breiman, 2001). The main idea is to measure the model error increase after shuffling the feature’s values, since the permutation breaks the relationship between the feature and the outcome. We implement the algorithm proposed in (Fisher et al., 2019).
(iii) Adding the directionality of the feature coefficient. Similar to estimating the sign of for Cox-PH, we develop a framework, which approximates the direction of feature coefficients in Cox-nnet. The linear predictor in Cox-nnet is:
| (4) |
where is the activation function, is the coefficient weight matrix between input and hidden layer and is the bias term. Suppose each column in is defined by:
| (5) |
Similar to the interpretation of in Cox-PH, the direction of each feature coefficient in Cox-nnet is approximated by the sign of
| (6) |
where is defined by . Intuitively, the risk increases if the sign of is positive.
(iv) Adding additional optimization algorithms and activation functions for parameter tuning. We add Adam (Kingma and Ba, 2015) optimizer as an alternative optimization strategy, which further accelerates the training process. We also use the Scaled Exponential Linear Unit activation function (Klambauer et al., 2017) in the Cox-nnet v2.0.
2.2 Evaluation metrics
As in Cox-nnet v1.0, we evaluate the prediction accuracy by C-IPCW (Uno et al., 2011), which is the C-index weighted by inverse censoring probability.
2.3 Dataset
The first large-scale population data used for the study is the national kidney transplant registry data obtained from the US Organ Procurement and Transplantation Network (OPTN) (https://optn.transplant.hrsa.gov/data/). A total of 80 019 patients, which includes all patients with ages >18, who received transplant between January 2005 and January 2013 with deceased donor type were used in the analysis. A total of 117 clinical variables describing up-to transplant characteristics are used in the analysis.
The second large-scale population data used for the study is Study to Understand Prognoses Preferences Outcomes and Risks of Treatment (SUPPORT), which has the survival time of seriously ill hospitalized adults. We obtained the preprocessed SUPPORT data from URL: https://github.com/jaredleekatzman/DeepSurv/tree/master/experiments/data/support. The dataset contains 9105 patients and 14 features including age, sex, race, number of comorbidities, presence of diabetes, presence of dementia, presence of cancer, mean arterial blood pressure, heart rate, respiration rate, temperature, white blood cell count, serums’ sodium and serums’ creatinine. The patients with any missing features are dropped from the dataset.
To test the effect of feature size on the model, a pan-cancer dataset from 10 TCGA cancers types is used, as done before (Ching et al., 2018). It includes the following cancer types: Bladder Urothelial Carcinoma, Breast invasive carcinoma, Head and Neck squamous cell carcinoma, Kidney renal clear cell carcinoma, Brain Lower Grade Glioma, Liver hepatocellular carcinoma, Lung adenocarcinoma, Lung squamous cell carcinoma, Ovarian serous cystadenocarcinoma and Stomach adenocarcinoma. The RNA-Seq expression and clinical data are downloaded from the Broad Institute GDAC (Broad Institute TCGA Genome Data Analysis Center, 2014). This pan-cancer dataset contains 5031 patients and 20 315 gene features in total. Raw count data are normalized using the DESeq2 R package (Srivastava et al., 2014) and then log-transformed.
3 Results
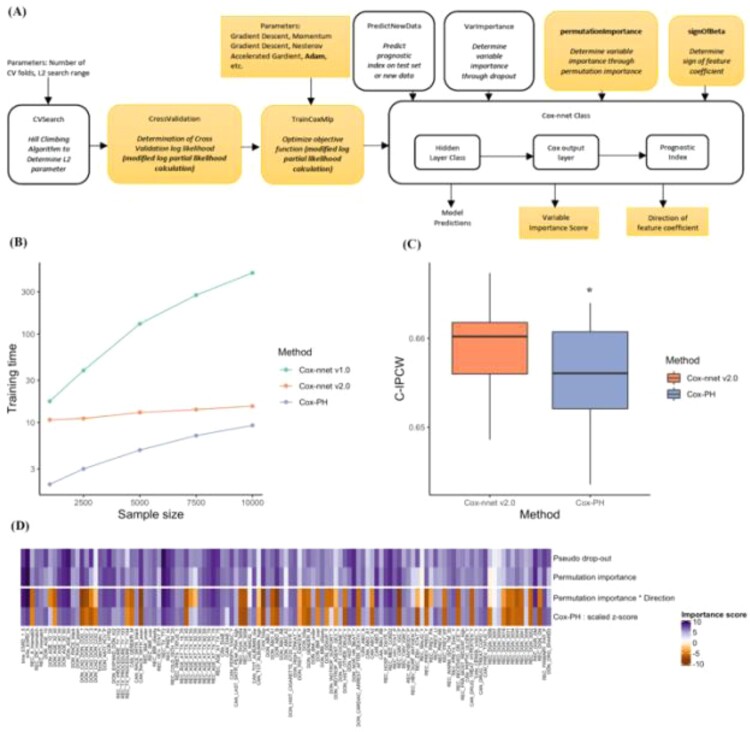
The structure of Cox-nnet v2.0 is shown in Figure 1A. The newly updated functionalities are highlighted.
Fig. 1.
Overview of Cox-nnet v2.0 and its performance improvement. (A) The modules in Cox-nnet. The names of new modules and functions are in bold with highlight background. The other modules are inherited from Cox-nnet v1.0. (B) Training time comparison among Cox-nnet v2.0 (red), Cox-nnet v1.0 (green) and Cox-PH (purple), varying from sample size of 1000 to 10 000 in OPTN kidney transplant registry data. (C) Prediction accuracy measured by C-IPCW on the EMR dataset (n=80 019), over 10 repetitions. *: P<0.05 (1-tail t-test) (D). Heatmap to compare feature importance scores in different methods. From top to bottom row: pseudo drop-out (Cox-nnet v1.0), permutation importance score (Cox-nnet v2.0), permutation importance score times direction of feature coefficient (Cox-nnet v2.0) and scaled z-score (Cox-PH)
We randomly split the OPTN kidney transplant registry data into training (80%) and testing (20%) sets, and used C-IPCW to evaluate on the hold-out testing set. We repeated this process 10 times to access the overall prediction performance. Cox-nnet v2.0 is not sensitive to the sample size and dramatically reduces the training time, compared to Cox-nnet v1.0, where the computing time increases polynomially with the sample size (Fig. 1B). Cox-nnet v2.0 also achieves significantly better C-IPCW than Cox-PH (Fig. 1C), without any drop of C-IPCW compared to Cox-nnet v1.0. We performed feature evaluation by calculating the feature importance scores using the new permutation method, where the values are close to those by the previous pseudo drop-out method. With the directionality (+/− signs) of the feature coefficients, our feature evaluation results are more interpretable: a positive (+) sign indicates increased risk of graft failure, whereas a negative (−) sign means decreased risk of graft failure. As additional confirmation, the pattern of important scores matches well with that of coefficients obtained from Cox-PH (Fig. 1D).
In summary, Cox-nnet v2.0 significantly accelerates the training process of Cox-nnet without loss in the prediction accuracy. In addition, it also enables better interpretation for all features in the model. Cox-nnet v2.0 is the new version suitable for prognosis prediction in large-scale EMR dataset.
To confirm the gain of efficiency without loss of accuracy, we tested Cox-nnet v2.0 on an additional SUPPORT data, similar to the previous kidney transplant data. Cox-nnet v2.0 is not sensitive to the sample size and dramatically reduces the training time, compared to Cox-nnet v1.0 where the computing time increases polynomially with the sample size (Supplementary Fig. S1A). It also achieves significantly better C-IPCW than Cox-PH on the whole dataset (Supplementary Fig. S1B). We also tested the effect of feature size on the three models. Since the two datasets above have very modest feature sizes, we used the third TCGA pan-cancer dataset (a combination of 10 cancer types), whose total feature size is large (over 20 000). As shown in Supplementary Figure S2A, when the feature size varies from 4000 to 20 000, Cox-nnet v2.0 is still more efficient than Cox-nnet v1.0 in all feature sizes. Cox-nnet v2.0 is both significantly faster at training the model (Supplementary Fig. S2A) and more accurate in prediction (Supplementary Fig. S2B), compared to Cox-PH.
In summary, Cox-nnet v2.0 is a much more efficient neural-network model from Cox-nnet v1.0 without loss of the predictive performance. Such characteristics make Cox-nnet v2.0 a desirable method for survival prediction in large-scale population (e.g. EMR) data.
Author’s contribution
L.X.G. conceived the project, D.W. conducted model improvement and major data analysis, Z.J. conducted additional data analysis. K.H. provided the dataset and helped with the analysis. D.W., Z.J. and L.X.G. wrote the manuscript with the help of K.H. All authors read, revised and approved the manuscript.
Funding
L.X.G. is supported by grants K01ES025434 awarded by NIEHS through funds provided by the trans-NIH Big Data to Knowledge (BD2K) initiative (www.bd2k.nih.gov), R01 LM012373 and R01 LM012907 awarded by NLM and R01 HD084633 awarded by NICHD. K.H. is supported by funds through The University of Michigan Office of Research (UMOR).
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Di Wang, Department of Biostatistics, University of Michigan, Ann Arbor, MI 48109, USA.
Zheng Jing, Department of Statistics, University of Michigan, Ann Arbor, MI 48109, USA.
Kevin He, Department of Biostatistics, University of Michigan, Ann Arbor, MI 48109, USA.
Lana X. Garmire, Department of Computational Medicine and Bioinformatics, University of Michigan, Ann Arbor, MI 48109, USA.
References
- Breiman L. (2001) Random forests. Mach. Learn., 45, 5–32. [Google Scholar]
- Broad Institute TCGA Genome Data Analysis Center. (2014) Analysis overview for 15 July 2014 Broad Institute of MIT and Harvard.
- Ching T. et al. (2018) Cox-nnet: an artificial neural network method for prognosis prediction of high-throughput omics data. PLoS Comput. Biol., 14, e1006076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox D.R. (1972) Regression models and life‐tables. J. R. Stat. Soc. Series B Stat. Methodol., 34, 187–220. [Google Scholar]
- Fan J. et al. (2010) High-dimensional variable selection for Cox’s proportional hazards model. In: Borrowing Strength: Theory Powering Applications–a Festschrift for Lawrence D. Brown. Institute of Mathematical Statistics, Beachwood, OH, pp. 70–86. [Google Scholar]
- Fisher A. et al. (2019) All models are wrong, but many are useful: learning a variable’s importance by studying an entire class of prediction models Simultaneously. J. Mach. Learn. Res., 20, 1–81. [PMC free article] [PubMed] [Google Scholar]
- Goldstein B.A. et al. (2017) Opportunities and challenges in developing risk prediction models with electronic health records data: a systematic review. J. Am. Med. Inform. Assoc., 24, 198–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishwaran H. et al. (2008) Random survival forests. Ann. Appl. Stat., 2, 841–860. [Google Scholar]
- Kingma D.P., Ba J. (2015) Adam: a method for stochastic optimization. In: Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015). [Google Scholar]
- Klambauer G. et al. (2017) Self-normalizing neural networks. In: Guyon I. et al. (eds) Advances in Neural Information Processing Systems 30. Curran Associates, Inc., Red Hook, NY, pp. 971–980. [Google Scholar]
- Srivastava N. et al. (2014) Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res., 15, 1929–1958. [Google Scholar]
- Steele A.J. et al. (2018) Machine learning models in electronic health records can outperform conventional survival models for predicting patient mortality in coronary artery disease. PLoS One, 13, e0202344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uno H. et al. (2011) On the C-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Stat. Med., 30, 1105–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan Z. et al. (2020) Two-stage biologically interpretable neural-network models for liver cancer prognosis prediction using histopathology and transcriptomic data. medRxiv, doi:10.1101/2020.01.25.20016832. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.