Learning number patterns through computational thinking activities: A Rasch model analysis

Abstract

Despite the increasing presence of computational thinking (CT) in the mathematics context, the connection between CT and mathematics in a practical classroom context is an important area for further research. This study intends to investigate the impact of CT activities in the topic of number patterns on the learning performance of secondary students in Singapore. The Rasch model analysis was employed to assess differences of ability between students from the experimental group and control group. 106 Secondary One students (age 13 years old) from a secondary school in Singapore took part in this study. A quasi-experimental non-equivalent groups design was utilized where 70 students were assigned into the experimental group, and 36 students were assigned into the control group. The experimental group was given intervention with CT-infused activities both on- and off-computer, while the control group received no such intervention. Both groups were administered the pretest before the intervention and the posttest after the intervention. The data gathered were analyzed using the partial credit version of the Rasch model. Analysis of pretest and posttest results revealed that the performance of the experimental group was similar to the control group. The findings did not support the hypothesis that integrating CT in lessons can result in improved mathematics learning. However, the drastic improvement was observed in individual students from the experimental group, while there is no obvious or extreme improvement for the students from the control group. This study provides some new empirical evidence and practical contributions to the infusion of CT practices in the mathematics classroom.

Number patterns; Computational thinking; Rasch model; Quasi-experiment; Mathematics education.

1. Introduction

In recent years, computational thinking (CT) has become a topic of high interest in mathematics education (Broley et al., 2017) because some, such as English (2018), have considered CT and mathematics to be natural companions. In a similar vein, Gadanidis et al. (2017) argued that a natural connection existed between CT and mathematics in terms of logical structure and in the capability to explore and model mathematical relationships. Kallia et al. (2021) claimed that both CT and mathematical thinking approach thinking by adopting concepts of cognition, metacognition, and dispositions central to problem-solving. In addition, they also recognize and foster socio-cultural learning opportunities that shape ways of thinking and practicing that reflect the real world.

The key motivation for introducing CT practice into mathematics classrooms is the fast-changing nature of mathematics in professional field practice (Bailey and Borwein, 2011). The infusion of CT into mathematics lessons can deepen and enrich the learning of mathematics, and vice versa (Weintrop et al., 2016; Ho et al., 2017). It can also acquaint learners with the practice of mathematics in the real world (Weintrop et al., 2016) and cultivate students' ability to acquire knowledge and apply it to new situations (Kallia et al., 2021). Taking into account these advantages, many researchers and educators began to integrate CT in the mathematics classroom. Thus, there is a growing body of literature on CT and mathematics education, and this includes review studies conducted by Barcelos et al. (2018), Hickmott et al. (2018), and Kallia et al. (2021).

While acknowledging that coding or digital making activities are the most prevalent means of learning CT, the authors of this paper have joined a growing set of researchers and educators who are stretching the boundaries of how CT can be learned or used to enrich existing school subjects. In this project, CT is defined as the thought process involved in formulating problems and developing approaches to solving them in a manner that can be implemented with a computer (human or machine) (Wing, 2011). This process involves several problem-solving skills, including abstraction, decomposition, pattern recognition, and algorithmic thinking. The term Math + C refers to the integration of CT and mathematics in the design and enactment of lessons (Ho et al., 2021).

Some of the Singapore secondary schools have started to teach CT in the mathematics curriculum. For instance, a recent study was conducted by Lee et al. (2021) with secondary students in the School of Science and Technology, Singapore (SST). Descriptive qualitative research was performed with 51 Secondary 2 students of mixed to high ability in the study. Students were asked to solve a mathematical problem about quadratic functions by writing a program using Python programming language. The students also had to complete the individual student's reflections and worksheets that had a series of questions involving the four components of CT, i.e., decomposition, pattern recognition, abstraction, and algorithm design. The results showed that CT can assist students to strengthen the learning of mathematics process and synthesize their mathematical concepts. In addition, student responses to CT questions and survey questions also appear to strongly indicate that math questions support students to apply CT skills.

Nevertheless, there are some challenges when infusing CT into the mathematics classroom. One of the challenges is the insufficiency of CT expertise. Most of the teachers do not have computing or computer science backgrounds as they do not take computer science courses during their studies. They even do not receive any training or are exposed to the pedagogies on how to teach CT effectively, so they lack confidence in teaching CT in math class. Besides, students from backgrounds with little experience in computers and students with learning difficulties found it difficult to keep up with the course (Choon and Sim, 2021).

This study provides an initial exploration of the link between CT and mathematics at the secondary level. It aims to determine the effect of Math + C lessons on students’ performance on typical test problems in the lower secondary mathematics topic of number patterns. Based on the findings from the previous studies, it is hypothesized that the CT research done in this study would have a positive impact on the math learning performance of secondary students in Singapore. This can be examined from the comparison of the ability between the experimental students and the control students. By using the Rasch model analysis, we can analyze the results as a pattern among the scores of individual students, not only aggregated data. Specifically, this study was guided by one overarching research question: What are the differences of ability between the students from the experimental group and the control group?

2. Literature review

2.1. Computational thinking and mathematics

The earliest mention of the phrase ‘CT’ appeared in Mindstorm: Children, computers, and powerful ideas, in which Papert (1980) briefly used the term to describe a kind of thinking that might be integrated into everyday life. The term CT was recently refreshed by Wing (2006), in which she argued that everyone should learn CT, that CT involves “thinking like a computer scientist”, and that computer science should not be reduced to programming. CT was further defined by Wing (2011) as “the thought processes involved in formulating problems and their solutions so that the solutions are represented in a form that can be effectively carried out by an information-processing agent” (p. 1).

A popular breakdown of CT into identifiable practices is Hoyles and Noss (2015)'s and Tabesh (2017)'s description of CT as including pattern recognition (seeing a new problem as related to previous problems), abstraction (seeing a problem at diverse detail levels), decomposition (solving a problem comprises solving a set of smaller problems), and algorithm design (seeing tasks as to smaller associated discrete steps). To operationalize the definition of CT in this project, Ho et al. (2021) adapted these four processes in the mathematics context. Decomposition referred to the procedure by which the mathematical problem was broken down into smaller sub-problems. Through decomposition, the complicated or complex problem became more manageable as smaller sub-problems can be solved easily. Meanwhile, pattern recognition was the action of finding common patterns, features, trends, or regularities in data. It was common in mathematical practice to find out the patterns from the disordered data. Besides, abstraction was the procedure of formulating the general principles that create these identified patterns. It happened when a problem in the real-world setting was expressed in mathematical terms. Algorithm design was the development of accurate step-by-step instructions or recipes to solve the problem at hand or similar problems. The solution to the problem can be computed by using a computer program.

Many efforts and initiatives have been conducted to bring CT into the mathematics curriculum and cover various mathematical topics, such as geometry and measurement (Sinclair and Patterson, 2018; Pei et al., 2018), algebra (Sanford, 2018), number and operations (Sung et al., 2017), calculus (Benakli et al., 2017), and statistics and probability (Fidelis Costa et al., 2017). Weintrop et al.’s (2016) taxonomy of CT practices for science and mathematics, which included data practices, modeling & simulation practices, computational problem-solving practices, and systems thinking practices, has provided comprehensive descriptions of how CT was applied across science, technology, engineering, and math (STEM) subjects. Engineers and scientists use CT and mathematics to construct accurate and predictive models, to analyze data, as well as to execute investigations in new ways (Wilkerson and Fenwick, 2016).

2.2. Earlier studies of the impact of CT on mathematics performance

A recent quasi-experiment was performed by Rodriguez-Martínez et al. (2020) to investigate the impact of Scratch on the development of CT and the acquisition of mathematical concepts of sixth-grade students. 47 students from a primary school in Spain were divided into an experimental group (24 students) and a control group (23 students). There were two phases in this experiment, namely the programming phase and the mathematics phase. The programming phase was associated with the instructions in Scratch and emphasized acquiring the basic concepts of CT such as conditionals, iterations, events-handling, and sequences. Meanwhile, the mathematics phase stressed instruction on calculating the least common multiple (LCM) and the greatest common divisor (GCD) and solving problems involving these concepts. The experimental group employed Scratch as a pedagogical tool, while the control group worked in a traditional paper-and-pencil environment. The pretest and posttest were administered before and after the instruction. The findings seem to demonstrate that Scratch can be employed to augment both students’ CT and mathematical concepts.

Fidelis Costa et al. (2017) implemented a quasi-experiment to explore the influence of CT on the math problem-solving ability of 8th-grade students. The students were selected randomly into the experimental group with CT and the control group without CT. The experimental group was trained using the mathematics questions that were prepared to be more aligned with CT, while the control group was given traditional questions prepared by mathematics teachers. The findings were statistically significant, indicating that the integration of CT and mathematics through appropriate adjustments of classroom practice can have a positive impact on students' problem-solving abilities.

Another quasi-experiment was conducted by Calao et al. (2015) to test whether the usage of coding in mathematics classes could have a positive effect on 42 sixth-graders’ mathematical skills. The sample included 24 students from the experimental group and 18 students from the control group. The experimental group students received the intervention which comprised three months of Scratch programming training, while the control group received no such intervention. Both the experimental group and the control group performed pre-intervention and post-intervention tests. A rubric had been developed to assess students’ skills and performance in the mathematical processes including reasoning, modeling, exercising, and formulation, and problem-solving. The findings demonstrated that the experimental group trained in Scratch has a statistically significant improvement in the understanding of mathematical knowledge.

3. Materials and methods

3.1. Instructional design of CT activities

Singapore students learn to find patterns in number sequences since primary year one. In the secondary year one topic of Numbers and Algebra, students are expected to learn how to recognize and represent patterns or relationships by finding an algebraic expression for the nth term.

3.1.1. Instructional design of plugged Math + C activities using a spreadsheet

The instructional design of plugged Math + C activities using a spreadsheet was demonstrated in Table 1. There were four-lesson design principles for integrating CT into number patterns lessons anchored on the CT practices, i.e., complexity principle, data principle, mathematics principle, and computability principle (Ho et al., 2021). The first principle was the complexity principle. The task related to the learning of the Number Patterns topic was sufficiently complex to be decomposed into sub-tasks. If the task was routine and can be solved easily using a well-known and simple approach, then the decomposition cannot be applied well. The second principle was the data principle. The task ought to include the quantifiable and observable data which could be utilized, transformed, treated, and stored. Besides, the mathematics principle was regarded as the third principle. We needed to identify whether the task gave rise to a problem or situation that could be mathematized. Mathematization was the construction of the problem using mathematical terms. It involved changing a real-world problem setting accurately and abstractly to a mathematical problem. The task should be formulated abstractly so that it could be reasoned, described, and represented meticulously. The last principle was the computability principle where we were required to ensure that the solution to the task could be executed on a computer via a finite process (Ho et al., 2021).

Table 1.

Instructional design for plugged Math + C activities using a spreadsheet.

Teaching Move	CT Practices	Description of Instructional Design
Induction	Pattern recognition	The students worked in pairs and set up driver-navigator roles. The navigator was the one who handles the computer part, and the driver was the one who gave instructions. The students were given hands-on worksheets to complete the tasks. The students were shown a video about patterns. Then, the students recalled prior knowledge about number patterns.
Development I	Algorithm Design	The students were taught the concepts of CT, a way of thinking about and solving problems so that we can make use of the computers to help us. The students were informed about the lesson objectives, i.e., (a) learn how to generate number patterns using computers, and (b) construct the general term of a given number pattern.
	Pattern Recognition	The teacher demonstrated how to use the spreadsheet software. The teacher introduced the spreadsheet as a large array of boxes that we called ‘cells’ and each cell was a place to store a piece of datum. Each cell was named by its coordinates, which we learned in mathematics. For example, the default position of the cursor rested in the cell named A1. After that, the teacher provided guidance to the students to enter the word ‘Figure Number (n)’ in cell A1. A cell can be populated with English words which were data called ‘Strings’. The teacher showed how to enter the number ‘1’ in A2 and a cell can be populated with numerical data called ‘Numbers’. Then, the teacher demonstrated how to enter the formula = A2 + 1.
	Algorithm Design	The teacher hovered the cursor near the corner of cell A3, and the Fill Handle appeared with a small cross. The students dragged the Fill Handle downwards till it reached cell A11, i.e., cell range A2:A11 as displayed in the figure below. The students were taught about the recursion method for number patterns.
Development II	Algorithm Design	The students created the algorithm that calculates the nth term of the number pattern based on the questions in the hands-on worksheet as exhibited in the figure below. Then, the students produced the final product in the spreadsheet as shown in the figure below.
	Decomposition	The students broke down the problem into two smaller problems: Problem 1: What is the starting number? Where to key in?; Problem 2: How do I use the recursive method to generate the number pattern? The students used the spreadsheet to find T10 and T100.
Development III	Pattern Recognition	When the number n gets larger, the recursive method is troublesome to use, even though we have a computer. If we have a formula in terms of n, such a direct method will be faster. To find the direct relationship between n and Tn, the students drew a scatter plot as a graphical representation to show the patterns as exhibited in the figure below.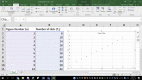
	Pattern Recognition	The students were shown a ‘staircase’ structure in the scatter plot as illustrated in the figure below.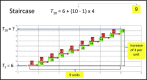 After that, the students filled in the blanks based on the ‘staircase’ scatter plot as displayed in the figure below.
	Abstraction	The students generated the general formula using abstraction skills as shown in the figure below. The nth term of the arithmetic sequence was given by $T_n=T_1+\left(n-1\right)d,$ where $T_1$is the first term of the sequence and d is the common difference. Finally, the student constructed the general formula of 4n + 2.
	Algorithm Design	The students checked the abstracted formula using the spreadsheet as revealed in the figure below. It was found that the answer to the direct method was the same as the recursive method.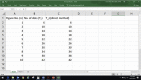
Consolidation	Algorithm Design	The students did the hands-on exercise in the worksheets. Lastly, the teacher recapped the lesson.

In this lesson, we believe that CT can help students deepen their understanding of number patterns in two ways. First, recursive relationships can be easily coded in any programming language. This algorithm method always provides an accurate (numerical) solution to the problem, even if there is no closed formula—the power of the numerical method. Secondly, the graphical features in the spreadsheet are employed to analyze the relationship between n and T_n (Ho et al., 2021).

The computational tool used in the plugged Math + C activities was a spreadsheet. A spreadsheet was chosen as it was readily accessible and available in most of the schools. It has been widely applied in education as a computational tool to promote CT skills (Sanford, 2018). In this study, it was utilized to teach number sequences which enabled the learners to make sense of recursive and explicit formulas. The spreadsheet served as the valuable element to visualize the Left-Hand-Side (LHS) and Right-Hand-Side (RHS) of “sum = product” characteristics in a synchronized way, to comprehend and differentiate between the explicit forms and recursion forms of LHS = RHS characteristics, as well as to link the visualizations which lead to the understanding of formal proof and mathematical induction (Caglayan, 2017).

3.1.2. Instructional design of unplugged Math + C activities

Unplugged Math + C activities played a transitional role in that teachers and students who have never used computers in learning mathematics can still acquire or use some aspects of CT without the use of the computer. Math + C worksheets were created to be used in the unplugged Math + C activities. The CT practices were utilized in the Math + C worksheets, namely pattern recognition, decomposition, algorithm design, and abstraction. The sample items of Math + C worksheets were demonstrated in Table 2. Through guided questions, the students were required to use pattern recognition to recognize the common difference of the number sequence. For the decomposition, the students had to analyze the parts of a number sequence. Regarding algorithm design, the students were led to understand the steps or processes to obtain a solution for number sequence. The students ought to generate the general formula of the number sequence for the abstraction.

Table 2.

Sample items of Math + C worksheets.

CT Practices	Sample Items
Pattern recognition	13, 17, 21, 25, …
	What is the difference between each term in the sequence?
Decomposition
Algorithm design	Let's further investigate.
	1.What do you notice about the highlighted numbers in the last column?
	2.What is the relationship between the position number and the highlighted number?
Abstraction	What is the general formula that we can use to find any number in the sequence that you see in the previous page?

The lesson objectives for the unplugged Math + C activities were: (a) recognizing simple patterns from various number sequences, and (b) determining the next few terms and find the general formula of a number sequence. During the unplugged Math + C lesson, the students were asked to guess the next two terms for the sequence “2, 5, 8,11, 14, …, …”. The term “number sequence” and “terms” were introduced. These numbers followed specific rules or patterns, e.g., start with 2 and add 3 to each term to get the next term. Next, the students did the exercises in the textbook. The teacher highlighted the rules governing number sequences need not an addition but can be subtraction, multiplication, and division and can involve negative numbers. The students completed the ‘Practice Now 1’ in the textbook to write down the next two terms. Upon completion, the students were called one by one to answer the questions.

Then, the students were given the Math + C worksheets and had to complete pages 1 and 2 to find the general formula for number patterns. The teacher stressed the patterns in the last column titled “further breakdown the numbers”, namely, what does the n^th term mean with regards to the position of the number and the relationship between the position and the numbers that changed in the last column. The students had to find the general formula based on the worksheet and simplify the expression. Next, the students completed the questions on pages 3 and 4 in the Math + C worksheets. The teacher discussed the solutions with the students. Lastly, the teacher recapped the lesson and assigned homework to the students.

3.2. Lesson in the control group

In the lessons for the control group, the students were not given Math + C intervention. They were taught the topic of number patterns using the two worksheets as demonstrated in Table 3. In the worksheet, the students were required to find the next two terms for the number sequences. The teacher asked the students to come to the front to show their answers on the whiteboard. Next, the students were given the general term of a number sequence and they had to find the terms of the sequence. The students were guided on how to obtain the 1001^st term for the sequence of 2, 4, 6, 8, … For this question, the general term is T_n = 2n, T₁₀₀₁ = 2 (1001) = 2002. Then, the students were taught how to generate the general term from the number sequences in the worksheet. The students had to complete the questions in the worksheets. After that, the teacher discussed the solutions with the students and gave them homework. Further, the teacher also gave worksheet 2 to the students and discussed it with them.

Table 3.

Sample items of two worksheets.

Worksheet	Sample Items
1	Write down the next two terms in the following number sequence. (a) 1, 3, 5, 7, ___, ___ (b) 6, 10, 14, 18, ___, ___ (c) 8, -3, -2, ___, ___
	(a) If the nth term of a sequence is Tn = 5n + 4, find the first 5 terms of the sequence. (b) If the nth term of a sequence is Tn = nˆ2–3, find the first 4 terms of the sequence. (c) If the nth term of a sequence is Tn = - 4n+9, find the 35th and 50th of the sequence.
	Find the general term, Tn. 1, 3, 5, 7, … Tn = ?
	Write down the nth term in the following number sequence. (a) 5, 9, 13, 17, 21, … (b) 7, 12, 17, 22, 27, … (c) 2, 4, 14, 20, 26
2	The diagram shows the first three patterns of dots in a sequence. (a) Draw the 4th pattern of dots. (b) How many dots are there in the 5th pattern?

3.3. Participants

In this study, a quasi-experimental non-equivalent groups design was employed where the students were non-randomly chosen to be in the experimental group or the control group (Lochmiller, 2018). There were 106 Secondary One students (who have the age of 13 years old) from a Singapore secondary school who participated in this study. These students were chosen as this was the first year they entered secondary school which would have provided us with the longest track for students' CT skills development. Three intact classes were involved: two classes were assigned to the experimental group and one class was assigned to the control group. These three classes were taught by three different teachers as the teachers who taught mathematics subjects were different. There were 70 students in the experimental group and 36 students in the control group. In the experimental group, there were 37 males and 33 females. Meanwhile, there were 20 males and 16 females in the control group. The sample size of both groups was large enough to ascertain that the results of the results were well established and justified as Gall et al. (1996) claimed that there should be at least 15 participants in experimental and control groups for comparison. Following Institutional Review Board (IRB) regulations, students’ consent to participate in this study was requested. Their data were kept confidential and anonymous, for instance, A in A15 referred to the experimental group, 15 represented the student ID, B in B23 referred to the control group, 23 represented the student ID.

3.4. Instrumentation

The pretest and posttest were designed and constructed based on the topic of Number Patterns in the Singapore Secondary Mathematics syllabus. They were validated by the experts who were two authors of this paper to make sure that the items were appropriate to the targeted construct and assessment objectives. The scope covered in the pretest and posttest included recognizing simple patterns from various number sequences, determining the next few terms and finding a formula for the general term of a number sequence, and solving problems involving number sequences and number patterns. The pretest and posttest comprised short answer items including fill-in-the-blank questions. Both tests had eight items respectively and were labeled as Q1, Q2, Q3, Q4A, Q4B, Q4C, Q5A, and Q5B. The majority of the question types for both tests was an arithmetic sequence, and there was only one question of quadratic sequence and geometric sequence. In this study, all the items were under the numeral category, except for Q4A (figural). The skills tested and the sample items in the number patterns were demonstrated in Table 4. There was only one item (Q4A) with a dichotomous response which had two values of 0 and 1. The other items were the polytomous responses which had more than two values such as 0, 1, 2; 0, 1, 2, 3, and so on (Bond and Fox, 2015).

Table 4.

Test items.

Type	Skill Tested	Sample Items
Arithmetic sequence (Numeral)	Identify terms of simple number sequences when given the initial terms	Q1. Fill in the missing terms in the following sequence: 41, ___, 29, 23, ___, 11
Quadratic sequence (Numeral)	Identify terms of quadratic sequences when given the rule	Q2. Find the 8th term of the sequence: 1, 4, 9, 16, …
Geometric sequence (Numeral)	Identify terms of geometric sequences when given the rule	Q3. Write down the next two terms of the number sequence: 4, 16, 64, 256, ____,____
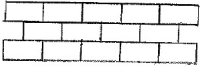
Arithmetic sequence (Figural task with successive configurations)	(a) Use visual cues established directly from the structure of configurations to illustrate the pattern. (b) Identify terms of arithmetic sequences when given the rule (c) Generate the rule of a pattern (d) Obtain an unknown input value when given the formula and an output value	Q4. The diagram indicates a sequence of identical square cards. (a) Draw Figure 4. (b) Complete the following table. (c) Calculate the number of squares in the 130thfigure. Explain or show how you figured out.
Arithmetic sequence (Numeral)	(a) Use only cues established from any pattern when listed as a sequence of numbers or tabulated in a table. (b) Generate the rule of a pattern	Q5. Consider the following number pattern: 4 = 2 $\times$ 3 - 2 10 = 3 $\times$4 - 2 18 = 4 $\times$ 5 - 2 28 = 5 $\times$ 6 - 2 $⋮$ 208 = $n\times \left(n+1\right)-2$ (a) Write down the equation in the 6th line of the pattern. (b) Deduce the value of n. Explain or show how you figured out.

The construct validity of the pretest and posttest were identified through assessing unidimensionality. The unidimensionality assumption was investigated using the Principal Components Analysis of Rasch measures and residuals. It can be asserted that the data is fundamentally one-dimensional if the Rasch measurement indicates a relatively elevated percentage of explained variance (at least 40 percent) and the first residual components of the unexplained variances are less than 2 eigenvalues (Linacre, 2012). All the unexplained values are less than 15%, showing supporting unidimensionality (Bond and Fox, 2015). The values of raw variance explained by measures were 55.6% and 59.9% for pretest and posttest respectively. They were viewed as strongly measured variances as they were greater than 40%. It means that the construct validity was good for both tests.

The reliability of the pretest and posttest were determined using item reliability and separation indices. The item reliability showed the replicability of item placements along the trait continuum (Bond and Fox, 2015). It was noticed that the item reliability for pretest and posttest were 0.94 and 0.95, which were regarded as high (>0.90) (Qiao et al., 2013). Item separation was an estimate of the separation or spread of items along with the measured variable (Bond and Fox, 2015). The item separation of 4.06 for the pretest and 4.20 for the posttest indicated the items were well separated by the students who took the test (Chow, 2013) as it was greater than 2 as suggested by Bond and Fox (2015). The Outfit mean-square (MNSQ) of pretest and posttest item mean was 1.29 and 1.01 were within the acceptance ranges of 0.5–1.5 (Boone et al., 2014). This implied that the items were productive and acceptable for a good measurement.

3.5. Procedure

This study utilized five days to complete the data collection as revealed in Table 5. The first day and last day were used for testing, while another three days were used for instruction. The data collection was implemented during the mathematics period in the school. At the beginning of this study, the researcher administered the 15-minutes pretest to the students of the experimental group and control group. Then, the experiment group was given the intervention by involving the unplugged Math + C activities and plugged Math + C activities using a spreadsheet. For the unplugged activities, the students were required to solve the problems in the Math + C worksheets. During the computer lesson, the students worked in pairs using laptops. The control group received no intervention and was given mathematics instruction the usual way by the teacher. After the instruction, both groups were administered the 15-minute posttest.

Table 5.

The procedure of data collection.

Day	Time	Activities	Remark
1	10:40am–12:00pm	-Administer pretest -Conduct unplugged Math + C lesson	30 students from experimental group involved
	1:30pm–1:45pm	Administer pretest	40 students from experimental group involved
2	10:40am–12:00pm	-Administer pretest -Conduct traditional lesson	36 students from control group involved
3	12:00pm–12:50pm	Conduct unplugged Math + C lesson	30 students from experimental group involved
	12:00pm–12:50pm	Conduct traditional lesson	36 students from control group involved
	12:50pm–2:15pm	Conduct plugged Math + C computer lesson using spreadsheet	40 students from experimental group involved and they work in pairs using laptops
4	8:40am–10:00am	Conduct unplugged Math + C lesson	40 students from experimental group involved
	9:20am–10:40am	Conduct plugged Math + C computer lesson using spreadsheet	30 students from experimental group involved and they work in pairs using laptops
	9:20am–10:40am	Conduct traditional lesson	36 students from control group involved
5	9:20am–9:35am	Administer posttest	36 students from control group involved
	11:20am–11:35am	Administer posttest	40 students from experimental group involved
	12:00pm–12:15pm	Administer posttest	30 students from experimental group involved

The difference between the experimental group and the control group can be examined from two aspects. The first aspect was that the teachers in the experimental group taught the students by using Math + C worksheets in the unplugged Math + C activities where the mathematical problems were specially designed to align with CT practices, i.e., pattern recognition, abstraction, algorithm design, and decomposition. But for the control group, the teacher utilized the routine mathematical problems to teach the students without the use of CT practices. The second aspect was that the students from the experimental group were instructed using a computational tool which was a spreadsheet, but the students from the control group were taught without any computational tool.

3.6. Rasch model analysis

In this study, the pretest and posttest results were analyzed using the partial credit version of the Rasch model. The partial credit model (PCM) was used as it enables the likelihood of having different numbers of response levels for different items on the same test (Bond and Fox, 2015). It was a “unidimensional model for ratings in two or more ordered categories” (Engelhard, 2013, p. 50). The software used for PCM was Winsteps version 3.73. To conduct the PCM analysis, a scoring rubric for pretest and posttest was created as shown in Table 6. There were four categories of code for PCM, i.e., code A for a maximum score of 2, code B for a maximum score of 1, code C for a maximum score of 3, and code D for a maximum score of 4.

Table 6.

Scoring rubric for pretest and posttest.

Question	Code	Score	Description	Examples of Answers in Pretest	Examples of Answers in Posttest
Q1	A	2	Complete or correct response	35, 17	1, -17
		1	Only correctly answer one of the solutions	35, 16	1, 17
		0	Incorrect response	30, 16	3, 6
Q2	A	2	Complete or correct response	64	45
		1	Provide evidence of correct way to find the number sequences, but obtain incorrect solution	+3, +5, +7, +9…	26 (+2, +3, +4…)
		0	Incorrect response	40	T0 = -1 Tn = -1+2n T9 = -1 + 2 (9) = 17
Q3	A	2	Complete or correct response	1024, 4096	729, 2187
		1	Only correctly answer one of the solutions	1024, 6020	-
		0	Incorrect response	556, 664	17496, 3779136
Q4(a)	B	1	Complete or correct drawing	3	4
		0	Incorrect drawing	5	6
Q4(b)	C	3	Complete or correct response	14, 17, 20	14, 17, 20
		2	Only correctly answer two of the solutions	14, 17, 21	14, 17, 21
		1	Only correctly answer one of the solutions	14, 18, 22	14, 18, 21
		0	Incorrect response	15, 18, 21	16, 22, 29
Q4(c)	D	4	Complete or correct response and justification	124 × 3 = 372, 372 + 20 = 392, The pattern was plus three all the way so I subtract the figure number that had been shown on the table with figure number 130 and I get 124 then I multiply it by the pattern, 3	No. The general equation is 2+3n. So, 136-2 = 134. 134÷3 = 44 $\frac{2}{3}$. The result to that equation is a decimal hence there is no figure number in the sequence that contains 136 bricks.
		3	Obtain correct response, but partially correct justification	-	No. 131 divided by 3 is a decimal.
		2	Obtain correct response, but incorrect justification	392. 130 × 2 = 260, 260 + 132 = 392	No. 5 + 3 (95-1) = 137 5 + 3 (44-1) = 134
		1	Provide evidence of correct way to find the solution, but obtain incorrect solution	130 × 3 = 390, 390 + 5 = 395	-
		0	Incorrect response and justification	394. I calculated with my calculator and I got this	Yes. Seeing that the number of bricks increases by 3, 136-3 = 133. So, 136 bricks can be possible.
Q5(a)	A	2	Complete or correct response	54 = 7 × 8 - 2	96 = 3 × 62–2 × 6
		1	Partially correct response	7 × 8–2 or 54	96
		0	Incorrect response	6 x (6 + 1) – 2 = 40	3 × 62–2 × 5
Q5(b)	D	4	Complete or correct response and justification	n = 14. Guess and check method 14 x (14 + 1) -2 = 208	n = 11. I used guess and check on my calculator. I started with 3 × 8 × 8–2 × 8 until I got 3 × 11 × 11–2 × 11 = 341
		3	Obtain correct response, but partially correct justification	14. I guessed the answer	11. I used guess and check to figure it out
		2	Obtain correct response or justification, but incorrect response or justification	208 = 14 × 15-2	11. I used algebra.
		1	Provide evidence of correct way to find the solution, but obtain incorrect solution	-	-
		0	Incorrect response and justification	208–4 = 204, 204 × 2 = 408	3 x n2 – 2 x n = 341 3n2 – 2n = 341 n2 = 341 n = 18.466

There were some missing data in the pretest and posttest as some of the students skipped one or more items without giving any answer. Such a situation may due to the item was difficult to understand or may not be printed on the test paper. However, the Rasch model was rarely influenced by any missing data and did not require to have all the items to be answered as it involved a single trait where the response measures can be calculated based on the items completed (Boone et al., 2014).

To determine the differences of abilities between the students from the experimental group and the control group, the average person measure for all the students was computed. As Winsteps was employed to run a Rasch analysis of data, all persons were represented on the same linear scale. The logit units of Rasch measurement express where each person was positioned on that same variable. Therefore, the person can be compared to other persons, for example, Mary has a higher ability than Julia (Boone et al., 2014). The logit value person (LVP) was conducted to compare the level of students' abilities from the experimental group and control group in the pretest and posttest. In other words, students' mathematical knowledge in number patterns from both groups was measured and compared. The Wright map was also utilized to present the students’ abilities and item difficulties comprehensively. Three criteria, i.e., Outfit mean-square (MNSQ), Outfit z-standardized (ZSTD), and Point-measure correlation (Pt-Measure Corr) were used for person-fit analysis (Bond and Fox, 2015).

4. Findings and discussion

The Rasch analysis demonstrated that the average mean of pretest for the experimental group and the control group was 1.22. In the posttest, the average mean of the posttest for the experimental group was 1.49, and the control group is 1.48. The experimental group had only 0.01 logit higher than the control group. This means that the abilities between the experimental group and control were similar and not much different. The results of this study were not consistent with the results of previous studies with a positive impact of CT on students’ understanding of mathematical knowledge such as Calao et al. (2015), Fidelis Costa et al. (2017).

The possible reason for this occurrence may be due to the students in the experimental group being involved in CT activities for a short intervention time. The plugged Math + C activities using a spreadsheet had only one session and the duration was less than one and a half hours, while the unplugged Math + C activities were less than two hours in duration. Experimental students might have only participated in certain features of the problem-solving process in CT activities, but these features are not enough to reveal significant differences with control students. This was supported by the statement from Wright and Sabin (2007) who said that learning may not happen if sessions were too short. The warrant to suggest that CT elements of the Math + C treatment influenced students’ learning needs to be further investigated through interviews.

Another possible reason was that the students might not so familiar with the operations in the spreadsheet required for the plugged Math + C activities. Such a situation might hinder the effects of the intervention in the experimental group. According to cognitive load theory, the design of teaching materials needs to follow some principles in order to effectively utilize spreadsheet to learn mathematics. If you need to learn specific spreadsheet skills first to be useful in learning mathematics, then the sequencing order is critical. The interactivity and intrinsic cognitive load of the elements of spreadsheets and math tasks are high. If two learning tasks are performed at the same time, the cognitive load is likely to increase. Therefore, the learning of these two tasks may be constrained; hence, in order to maximize the learning of mathematics, you should first master and consolidate spreadsheet skills (Clarke et al., 2005). When the students were not competent enough in the use of the spreadsheet, the students had to learn some about the spreadsheet in addition to number sequences. This would cause them not to assign all their cognitive load to the learning contents and consequently inhibit the intervention.

The logit value person (LVP) analysis for the experimental group can be seen in Table 7. The students were classified into four levels of abilities, namely very high level, high level, moderate level, and low level. The grouping of students’ abilities was based on the mean (1.17) and standard deviation (0.54) of all LVPs. For instance, the LVP value for a very high-level group was gained from the sum of the mean and standard deviation, i.e. 1.71. It was noticed that there were 13 out of 70 students (19%) from the experimental group had a very high of CT in the pretest. Meanwhile, 22 of them (31%) possessed a high ability of CT. 26 of them (37%) had a moderate ability and 9 of them (13%) had a low ability. For the posttest, the high ability was achieved by the 31 students from the experimental group, i.e. 44%. This followed by 17 of them (24%) had a very high ability, 15 of them (21%) had a moderate ability and 7 of them (10%) had a low ability.

Table 7.

Logit value person (LVP) analysis for experimental group.

Group	Very High LVP > +1.71	High $+1.71\ge LVP\ge +1.17$	Moderate $+1.17\ge LVP\ge +0.63$	Low $LVP\le +0.63$
Pretest	13	22	26	9
Posttest	17	31	15	7

Table 8 demonstrates the logit value person (LVP) analysis for the control group. Each group's level of abilities was computed based on the mean value of 1.13 and standard deviation value of 0.49. For example, the value of LVP for the low-level group was obtained from the difference between the mean and standard deviation, which was 0.64. 6 out of 36 students (17%) from the control group had a very high ability of CT in the pretest, while 14 out of 36 students (39%) had a high ability of CT. 8 of them (11%) had a moderate ability and 8 of them (11%) had a low ability. There were 10 students from the control group who had very high ability in the posttest, which was 28%. Students with high ability were 14 (39%), students with moderate ability were 8 (22%) and students with low ability were 4 (11%). From Tables 7 and 8, it can be said that some students from both groups have improved their abilities from low and moderate ability to high and very high ability. The percentage for experimental group students with high and very high ability increased by 13% and 5% respectively. Meanwhile, the percentage for control group students with very high ability enhanced by 11%, but the percentage for high ability remained the same.

Table 8.

Logit value person (LVP) analysis for control group.

Group	Very High LVP > +1.62	High $+1.62\ge LVP\ge +1.13$	Moderate $+1.13\ge LVP\ge +0.64$	Low $LVP\le +0.64$
Pretest	6	14	8	8
Posttest	10	14	8	4

Figure 1 and Figure 2 display the Wright map which visually presenting the distribution of items and person-measures in an equal logit scale (Bond and Fox, 2015). The left side of the Wright map showed the difficulty of items, while the right side showed the ability of the students. Logit 0 was the average of the test items. The items with higher difficulty levels were at the top left of the logit scale, while the items with lower difficulty levels were at the bottom left of the logit scale. By comparing Figure 1 and Figure 2, it can be seen that the logit scale increase from +2.0 to +3.0. Meanwhile, the person average for the pretest was +1.22 logits and the person average for the posttest was +1.49 logits. The increment was +0.27 logits. This indicated that the performance of the students from both groups became greater and a number of them were able to solve the difficult items. In Figure 2, we can see that all the students from both groups also were found to be above the item logit average (0.00), except for one student (A30) from the experimental group. It can be said that the overall performance of the students from both groups was over the expected performance.

Figure 1.

The Wright map for pretest.

Figure 2.

The Wright map for posttest.

In Figure 1 and Figure 2, item Q5B was the most difficult item to be solved by the students from the experimental group and control group as the item difficulty was above the person measure average. This means that the probability for the students to solve this item accurately was less than 50%. Item Q5B asked the students to explain how to deduce the value of n. Hence, it can be asserted that the students always faced difficulties in generating algebraic rules from patterns as argued by Stacey and MacGregor (2001). The easiest item in both tests was item Q4A as it was positioned below the item logit average and at the lowest part of the logit scale. It was categorized as an arithmetic sequence (Figural task with successive configurations). Students were required to draw the fourth identical square card in item Q4A. All the students from both groups were able to solve this type of item easily. This finding was contrasted with the study of Becker and Rivera (2006) that claimed that students fail to recognize the figural patterns.

From Figure 1, item Q1 and item Q4B in the pretest were located below the item logit average. This implied that these two items were easy for the students to solve. Item Q1 asked the students to fill in the missing terms in the arithmetic sequence. This item involves operations on a single specific number in order to find the next term in the sequence. 69 out of 70 experimental group students (99%) were able to solve item Q1, while all the control group students were able to solve this item correctly. Meanwhile, item Q4B required the students to identify terms of arithmetic sequences when given a rule. Item Q4B was solved correctly by 68 experimental group students (97%) and all the control group students.

Item Q2 asked the students to recognize the eighth term of quadratic sequences, while item Q3 required the students to find the next two terms of geometric sequences. These two items were positioned at the logit 0.00 which indicated that half of the students obtained correct answers and another half of the students obtained an incorrect answer. Furthermore, the students were requested to write down the equation in the sixth line of the pattern based on the number pattern shown for item Q5A. Seven of the experimental group students (10%) answered this item wrongly, while one of the control group students (3%) answered it wrongly. For item Q4C, 30 out of 70 students from the experimental group (43%) solved it incorrectly and 11 out of 36 students from the control group (31%) solved it incorrectly. Such a situation was probably due to the students might not know how to generate the rule of a pattern and obtain an unknown input value.

Regarding the posttest, three items (Q3, Q1, Q4B) were also situated below the item logit average as shown in Figure 2. All the students from the experimental group solved these three items correctly, except for item Q4B. 69 of them (99%) were able to solve item Q4B. Meanwhile, all these items were solved successfully by all the students from the control group. Item Q5A was answered by two students from the experimental group (3%) and all the students from the control group unsuccessfully. For item Q2, 5 students from the experimental group and one student from the control group solved it wrongly. Meanwhile, 18 experimental group students (26%) and 10 control group students (28%) were unable to answer item Q4C.

Several students in the experimental group had poor performance in the pretest as their logits were below the mean item logit 0.00 including A19 (-0.90 logits), A66 (-0.39 logits), A05 (-0.09 logits), and A49 (-0.08 logits). After they were exposed to the intervention, their performance was improved significantly and their logits were located above the mean item logit 0.00 in the posttest, i.e., A19 (+0.40 logits), A66 (+0.27 logits), A05 (+1.92 logits), and A49 (+0.88 logits). There were also students in the experimental group whose performance augmented drastically, for instance, students A53 and A59. Their performance in the pretest was located at +0.10 and +0.84 logits respectively. But after they participated in the CT activities, their performance in the posttest increased almost three times until maximum logits, i.e., +3.24. On the other hand, for the students from the control group, there was only one student B15 who improved by +2.12 logits. It can be said that there was no obvious or extreme improvement for the students from the control group compared to the experimental group.

As seen in Figure 1 and Figure 2, there were some big gaps between the items of the pretest and posttest, indicating the need for additional items to fill the gaps. The Wright map also demonstrated the redundancy of the item or item with the same difficulty level such as items Q2 and Q3 in the pretest. Q4A was the item-free person in the pretest and too easy for the students to solve it correctly. In the posttest, there was three items free person which means all the students were able to answer correctly, i.e. Q1, Q3, and Q4A. Besides, there were no items that cover the top of the scale where the best-performing students were located. This suggested that the more difficult items are required to assess the full range of person abilities.

To detect the “misfitting” students, person-fit statistics were employed including Outfit MNSQ, Outfit ZSTD, and Pt-Measure Corr. The person-fit indicated how well the responses given by the students matched with the model used to produce the level of attainment (Walker and Engelhard, 2016). In the pretest, there were two most “misfitting” students in the control group, i.e., B18, and B28. There were no “misfitting” students from the experimental group. These two students (B18 and B28) had Outfit MNSQ, Outfit ZSTD, and Pt-Measure Corr that did not in the range. It means that they had an unusual response pattern in the pretest. These unusual response patterns can be further scrutinized by looking at the Guttman Scalogram as exhibited in Figure 3. In other words, we can examine the causes of these unusual response patterns that did not fit the model through the Guttman Scalogram.

Figure 3.

Guttman Scalogram of responses for pretest.

A Guttman Scalogram comprises a unidimensional set of items that were ranked in order of difficulty (Bond and Fox, 2015), where item 4 (Q4A) was the easiest item and item 8 (Q5B) was the most difficult item. It can be observed that student B18 obtained correct for the difficult items, but did wrongly for the easier item. For student B28, he or she also managed to solve the difficult items but obtained the wrong answer for the easiest item in the pretest. It was most probably the student who made the careless mistake when solving the item.

Regarding the posttest, three students were considered as misfit persons, i.e., A22, A33, and B09. This was because of their Outfit MNSQ, Outfit ZSTD, and Pt-Measure Corr that did not fulfill the range. In the Guttman Scalogram in Figure 4, these three students tended to answer the difficult items correctly but solved the easy items wrongly. Most probably they knew how to solve the item, but made a careless mistake during the test. All these misfit students were considered as the person under-fits the model (Aghekyan, 2020).

Figure 4.

Guttman Scalogram of responses for posttest.

5. Conclusion, implications and recommendations

This study focused on examining the differences in performances between the students from the experimental group and the control group in learning the mathematics topic of number sequences. It was found that the academic performances of the students in the experiment group were similar to that of the control group. This indicated that the intervention of plugged Math + C activities using a spreadsheet and unplugged Math + C activities did not have much impact on the learning performance of the students in number patterns. Thus, the CT activities did not influence the learning of the students in mathematics. The results did not support the hypothesis that the quasi-experimental done in this study would have a positive impact on the learning performance of secondary students in Singapore. This situation might be due to the short intervention time for the experimental group students who are not so familiar with spreadsheet operations required in the learning of number sequences. Nevertheless, it can be observed that the performance of several students from the experimental group improved from pretest to posttest drastically, while the students in the control group experienced no obvious or extreme improvement.

Although the results did not meet the expectations, this study still provides some new empirical evidence and practical contributions to the integration of CT practices in the mathematics classroom. It also adds to the literature review on the effectiveness of didactic activities that involves CT in mathematics instruction, especially at the secondary level. Despite several challenges such as teacher education and institutional willingness are not fully invested in integration (Pollak and Ebner, 2019), this research shows the possibilities to bring CT into existing school subjects. The development of the CT instructions and assessments serve as resources for the school teachers, curriculum developers, researchers, administrators, and policymakers. These resources give them a clearer and concrete set of practices to guide curriculum development and classroom implementation of CT concepts.

The Rasch analysis performed in this study allows the researchers and instructors to identify whether the tests work for this pool of participants and able to differentiate participants according to their ability level, as well as uncover outlier responses for person-fit analysis. The use of the Wright map also provides direction for the researchers to perform refinement and resolve some negative issues in further studies such as gaps between the items, and item redundancy. For further investigation, it is recommended to add more items to reduce the existing gaps between the items and revise the items that had the same level of difficulty, as well as create items that can fully assess the abilities of the students.

This study has developed valid and reliable pretest and posttest for measuring mathematical knowledge of number patterns, which can be used for any kind of pedagogical intervention on this topic, including ones involving CT. This work proposes a path to address the blank spot of a lack of validated tools in mathematics education, specifically at the lower secondary level. The report of acceptable validity and reliability evidence ensure the quality of the research findings. This allows the instructors and researchers to utilize these assessments in the classroom confidently and strengthens the wide distribution of instruments as they tend to employ valid and reliable tools (Tang et al., 2020).

There were several limitations found in this study. One limitation was that it was hard to get more time for the intervention due to the tight timetables in the school. Therefore, a longer duration is needed in future studies to promote the students’ learning in mathematics, as well as to obtain additional evidence. Furthermore, there was only a small number of students involved in this study which could not be representative of the whole population. Therefore, it is suggested that the number of participants in future studies can be increased. Further studies need to be executed in terms of different mathematics topics, grade level, age, school, computational tools, and so forth.

Another limitation was that this study only involved only a single data source for the assessment, which was the pretest and posttest. Such a situation might limit the final verification result (Barcelos et al., 2018). It is suggested to conduct the triangulation of the method by complementing the quantitative method with the qualitative method such as interviews and observation to obtain more comprehensive and richer data in the research (Neuman, 2014).

Additionally, we only developed the instrument to measure students' mathematical knowledge in number patterns, but there was no specific instrument to measure CT. Hence, in future studies, it is recommended that we develop assessments to measure both CT and mathematics as the identification of domains assessed by specific assessment tasks may instrumental for the interplay of integrated domains in an assessment context, thereby gaining a more comprehensive understanding of students ’strengths and weaknesses in various domains (Bortz et al., 2020).

Declarations

Author contribution statement

Weng Kin Ho: Conceived and designed the experiments; Performed the experiments.

Wendy Huang: Performed the experiments; Wrote the paper.

Shiau-Wei Chan: Analyzed and interpreted the data; Wrote the paper.

Peter Seow, Longkai Wu: Contributed reagents, materials, analysis tools or data.

Chee-Kit Looi: Performed the experiments; Wrote the paper.

Funding statement

This work was supported by the Singapore Ministry of Education’s project grant (OER 10/18 LCK) and by Universiti Tun Hussein Onn Malaysia and the UTHM Publisher’s Office via Publication Fund E15216.

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.