Characterizing change in vagal tone during the first three years of life: A systematic review and empirical examination across two longitudinal samples

Abstract

Functioning of the parasympathetic nervous system (PNS), most often indexed by respiratory sinus arrhythmia (RSA), influences the volitional, cognitively-mediated forms of self-regulation across development. However, despite its clear relevance to children’s self-regulation, and its utility as a transdiagnostic biomarker of emotion dysregulation and psychopathology, the ontogeny of vagal tone under conditions of homeostasis across infancy and early childhood is not well understood. The current research is comprised of two complementary studies. The first aims to address this gap by conducting a systematic review of the literature which has assessed resting RSA in the first three years of life. The second study uses data from two diverse, longitudinal datasets (n = 203 and n = 370) to model change in RSA from infancy to toddlerhood. Results from a systematic review of 62 studies meeting inclusion criteria suggest that measures of resting RSA increase over time and demonstrate moderate stability across infancy, toddlerhood, and preschool ages. Results from a series of models fit to longitudinal data in study two suggest that baseline RSA is characterized by stable increases across infancy and early childhood. Moreover, although there was equivocal evidence for individual variability in trajectories of RSA, the findings suggest that the individual differences in resting RSA may become entrenched in early life based on observed significant variance in growth model intercepts. In all, the current study contributes to our understanding of the developmental trajectories of baseline RSA across infancy and early childhood and should support future research examining links between children’s parasympathetic regulation and their adjustment in early life.

The capacity to self-regulate is a key milestone of early childhood development (Nigg, 2016). Self-regulation is often defined in terms of volitional, cognitively-mediated processes such as inhibitory control, or aggregates of these processes, such as executive functions. However, a more complete definition of self-regulation includes not only these volitional processes but also the largely involuntary activity of neurophysiological systems that have evolved to modulate metabolic output under conditions of both homeostasis and challenge (Blair & Raver, 2012). Indeed, the consolidation and emergent coordination of these systems in the first years of life establishes the foundation on which the development of volitional, cognitively-mediated forms of self-regulation are built (Calkins & Keane, 2004; Porges, 1992). As such, gaining a clear descriptive understanding of how these neurophysiological systems develop across infancy and early childhood has the potential to contribute a meaningful foundation on which future research investigating self-regulation can rest.

Research examining the neurophysiological underpinnings of self-regulation typically focuses on the activity of the two systems that are most closely associated with stress response: the hypothalamic-pituitary-adrenal (HPA) axis and the sympathetic branch of the autonomic nervous system (ANS). The other branch of the ANS, the parasympathetic nervous system (PNS), has received less attention. This omission understates the role of the PNS in modulating metabolic output under conditions of homeostasis, the breadth of environmental conditions encompassed by that term, and the insights into cortical and, specifically, prefrontal cortical function that examining PNS activity may allow. Through efferent fibers originating with the cranial and spinal nerves, the PNS innervates tissues and organs throughout the body, collectively known as visceral effectors. Via these projections the PNS makes moment-to-moment adjustments in metabolic output in response to the shifting environmental demands presented under conditions of homeostasis, conditions that encompass all situations that do not constitute an aversive challenge or threat (Porges, 1992). As we have noted elsewhere, “for most children threats are a rare occurrence…and therefore the phasic or moment-to-moment activity of the PNS may be particularly relevant” to a child’s day-to-day experience, including the many contexts that demand self-regulation (Holochwost et al., 2019, p. 732).

Although PNS activity is not generally subject to direct, volitional control, its activity is modulated by input from sub-cortical and cortical structures that mediate self-regulation and are under volitional control. Chief among these are the same prefrontal cortical areas that are active during the exercise of volitional self-regulatory processes (Buhle et al., 2014). Moreover, there is a large body of research establishing PNS functioning as a valid measure of those volitional self-regulatory processes and as a transdiagnostic biomarker of emotion dysregulation and psychopathology (Beauchaine, 2015; Wagner & Waller, 2020). In sum, measures of PNS activity in infancy and early childhood have the potential to inform our understanding of fundamental processes of self-regulation, as well as pathways of adaptation and maladaptation. Therefore, developing a clear and comprehensive understanding of the development of the PNS in the first three years of life is important insofar as it contributes to a foundational understanding of these processes from which applied research can be conducted. The current research is comprised of two complementary studies designed to advance this understanding. The first study aims to address this need by conducting a systematic review of literature which has assessed children’s PNS functioning in the first three years of life; the second uses data from two diverse, longitudinal datasets to model change in PNS functioning from infancy to toddlerhood.

PNS Functioning Under Conditions of Homeostasis

A single efferent pathway – the X^th cranial, or vagus nerve – accounts for nearly 80% of efferent cranial parasympathetic activity (Fox & Fitzgerald, 1990). One visceral effector innervated by the vagus is the heart. Each beat of the heart can be represented as a QRS waveform on an electrocardiogram, with the distance between any two consecutive R-peaks referred to as the interbeat interval (IBI). The variability of the IBI is referred to as heart-rate variability (HRV), and HRV can be decoupled into high frequency HRV (or HF-HRV) and low frequency components (LF-HRV). HF-HRV is one way to measure PNS activity. Another is to isolate the input from the nucleus ambiguus (NA) of the vagus to the sino-atrial (SA) node of the heart, which is possible because this input is subject to modulation by respiration (Hirsch & Bishop, 1981). The variability associated with respiration is referred to as respiratory sinus arrhythmia (RSA; Bornstein & Suess, 2000) or vagal tone. Although HF-HRV and RSA are closely related and both reflect PNS function (Lewis et al., 2012; Thayer et al., 2012), measures of RSA may offer the purest measure of parasympathetic activity (Saul et al., 1991) because it conforms to the assumptions of parametric analysis, is not moderated by respiration, is robust to non-stationarity, and is the most sensitive to vagal blockade (Lewis et al., 2012).

To paraphrase Thayer and Lane (2000, 2009), the reason we are interested in HF-HRV and RSA is not because of what these measures can tell us about the function of the heart, but rather because of what they can tell us about the PNS, the brain, and their interface during processes of self-regulation. The PNS and brain are part of a super-system of cortical and sub-cortical structures that function in a coordinated manner to regulate cognitive, behavioral, and metabolic activity under conditions of homeostasis and stress (Lewis & Todd, 2007). This coordination is permitted by the continuous and reciprocal flow of information among these structures, which are arranged in a vertical fashion, with the phylogenetically-oldest structures (including the spinal nerves) at the bottom or rostral end, and the most phylogenetically-recent structures such as the brain at the top or caudal end.

The oldest structures, including the sympathetic nervous system and those of the diencephalon (e.g., the hypothalamus) and limbic system (e.g., the amygdala) mediate the default response to stress, novelty, and uncertainty observed in lizards, lower mammals, and humans: fight or flight (Herry, 2007; Thayer & Lane, 2009). The more recent structures – including the NA, which is unique to mammals (Porges, 2009), and the prefrontal cortex (PFC), which is unique to humans – permit a more varied and, in most modern contexts that humans inhabit, appropriate range of cognitive and behavioral responses (LeDoux, 1996; Mesculam, 2002). At the sub-cortical level, this is accomplished, in part, by the inhibitory influence of the PNS on the SNS; at the cortical level, it is facilitated by the inhibitory projections from the PFC to limbic and sub-cortical structures (Amat et al., 2006; Lewis & Todd, 2007; Thayer, 2006), including projections to the SA node of the heart via the vagus nerve (Porges, 2007; Saul et al., 1991).

When we measure HRV, we are indexing the regulatory activity of the PFC (see Thayer et al., 2012, for a meta-analysis) and the PNS. Under conditions of homeostasis, it is adaptive for the PFC and PNS to regulate neurophysiological function in a way that promotes metabolic conservation, which would be reflected in higher levels of HRV. It is therefore not surprising that higher levels of HRV are associated with better emotion regulation (Appelhaus & Luecken, 2006; Melzig et al., 2009; Ruiz-Padial et al., 2009), while lower levels are associated with mental (Shook et al., 2007; Smets et al., 2011) and physical illness (Thayer & Lane, 2007; Thayer et al., 2010). When we measure HF-HRV, and RSA, we are focusing more narrowly on PNS activity, though the indirect influence of the PFC is present in the signal (Porges, 2007, 2009). Again, under homeostatic conditions, the PNS should promote states of calm engagement, which would be reflected in higher levels of RSA. Indeed, the extant literature does reveal a link between higher RSA and better outcomes.

For example, increased RSA (i.e., higher vagal tone) has been linked to enhanced attentional capacity (Linnemeyer & Porges, 1986) and task engagement (Doussard-Roosevelt et al., 1994), whereas lower vagal tone (i.e., lower RSA) has been linked to poorer sustained attention, more impulsiveness, and greater disinhibition (Rash & Aguirre-Camacho, 2012). Intriguingly, higher levels of vagal tone have not only been associated with variability in emotional reactivity and expression, but with enhanced emotional regulation as well (Gentzler et al., 2009; Stifter & Jain, 1996). A similar relationship has been found with respect to behavioral and attentional regulation: at 9 months, infants with higher levels of vagal tone were rated as having a more difficult temperament (i.e., increased behavioral reactivity), while at 3 years, children with higher levels of vagal tone were rated as having less difficult temperament (i.e., increased behavioral self-regulation). Infants with higher levels of vagal tone spend less time fixating on a novel stimulus (Bornstein & Suess, 2000a; Richards, 1985) and are more able to attend to a relevant stimulus despite distractors (Richards, 1987, Stifter et al., 1989). In addition, a large body of research has established RSA to be a valid transdiagnostic biomarker of psychopathology (Beauchaine 2015; Wagner & Waller, 2020). Whereas higher levels of vagal tone are associated with positive psychosocial outcomes (Calkins et al., 2013), lower resting vagal tone and either hyper- or hypo-reactivity when confronted by threat or challenge are characteristic of both internalizing and externalizing psychopathology (Beauchaine & Cicchetti, 2019; Wagner & Waller, 2020).

Despite its clear relevance to volitional processes of self-regulation, the ontogeny of vagal tone under conditions of homeostasis in early childhood is not well understood. This is due, in part, to the fact that a relatively small number of longitudinal studies have examined vagal tone at multiple ages, while fewer still have modeled longitudinal data to examine what functional forms may best capture patterns of change in vagal tone over time. One recent paper reported stability in resting RSA from age 2 years to age 15 years, showing that the rate of change in resting RSA slowed across these ages and plateaued around age 10 years (Dollar et al., 2020). Although this study makes important contributions to our understanding of the developmental characteristics of RSA, it did not investigate changes across infancy and toddlerhood.

This is a particularly important gap in our understanding of children’s development. In an example of ontogeny recapitulating phylogeny, the development of the prefrontal cortex in humans is protracted, with neurogenesis, synaptogenesis, and pruning continuing well into the preschool and early elementary school years (Dumontheil et al., 2008). Given this, in the first three years of life the modulation of cognitive and behavioral responses away from the sympathetically-mediated, fight-or-flight default may rest much more heavily on the function of the PNS. As such, insight into the ontogeny of RSA in early childhood has the potential to provide insight into the development of the young child’s primary means of self-regulation in contexts that do not demand fight or flight behaviors.

The current paper presents the results of two studies designed to address this gap in our knowledge. The first is a systematic review of all published studies that examined vagal tone under homeostatic conditions across infancy and early childhood. The second study presents a series of models that were fit to longitudinal data drawn from two demographically-diverse samples encompassing the same developmental period. In both studies, we focus on RSA due to its relative purity as a measure of PNS activity, and because the similarities in study design and measurement between the two samples used in the second study allow for meaningful comparison of RSA trajectories across infancy and toddlerhood. Therefore, unless otherwise noted we will use the term ‘vagal tone’ to refer to RSA as defined by Porges (1985). We conclude with a general discussion that interprets the models considering our systematic review and outlines directions for future research.

Study 1: The Development of Vagal Tone in Early Childhood – A Systematic Review

Method

A protocol for reviewing the literature was developed according to the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines (Shamseer et al., 2015). Three databases (PsycInfo, PubMed, and Web of Science) were searched using the keywords “vagal tone*” OR “respiratory sinus arrhythmia” OR “RSA.”); a priori search criteria at this stage of the literature search were: 1) that papers were published in English in a peer-reviewed journal, 2) that they reported the results of an empirical study, and 3) that those studies were conducted with human children who were neonates, infants, or preschoolers. The resulting list of titles and abstracts was screened, and studies were retained only if they met the following inclusion criteria: 1) participants were young children (birth to age 8 years) who were healthy and developing normally; 2) vagal tone was indexed by RSA (rather than HF-HRV); and 3) RSA (thus defined) was measured under homeostatic conditions (i.e., not during a stress or challenge paradigm) at least once when children were between 0 and 36 months of age. No date limitations were placed on the search results, and the final search was conducted in August 2020. The full texts of papers that passed these criteria were reviewed and the inclusion criteria were applied again to determine whether the paper should be included or excluded. These inclusion criteria were also applied to additional studies taken from the reference lists of papers included in the review. All studies were screened by the first and third authors. Disagreements about whether inclusion criteria were met were resolved by the first and second authors.

The following information was extracted from the studies included in the review: 1) sample size; 2) sample composition (mean age and standard deviation, gender, and race/ethnicity); 3) mean RSA value and its standard deviation for each age at which RSA was measured. The authors of studies that did not report mean RSA value at each age were contacted and this information was incorporated if available. Those studies without mean RSA values were excluded from the review. For studies that modeled repeated-measures data the intercorrelation of RSA values across ages was noted, as was the approach and results for the subset of studies that modeled change in vagal tone over time.

Results

The literature search using the specified keywords yielded 3,119 records, 317 of which were duplicates. Titles and abstracts were screened for the remaining 2,802 records, and based on this screening, 212 articles were selected for eligibility assessment. Of the 132 studies deemed eligible for inclusion in the review, 70 were excluded due to insufficient data being reported, leaving 62 studies in the present review. This process is summarized in Figure 1.

Figure 1.

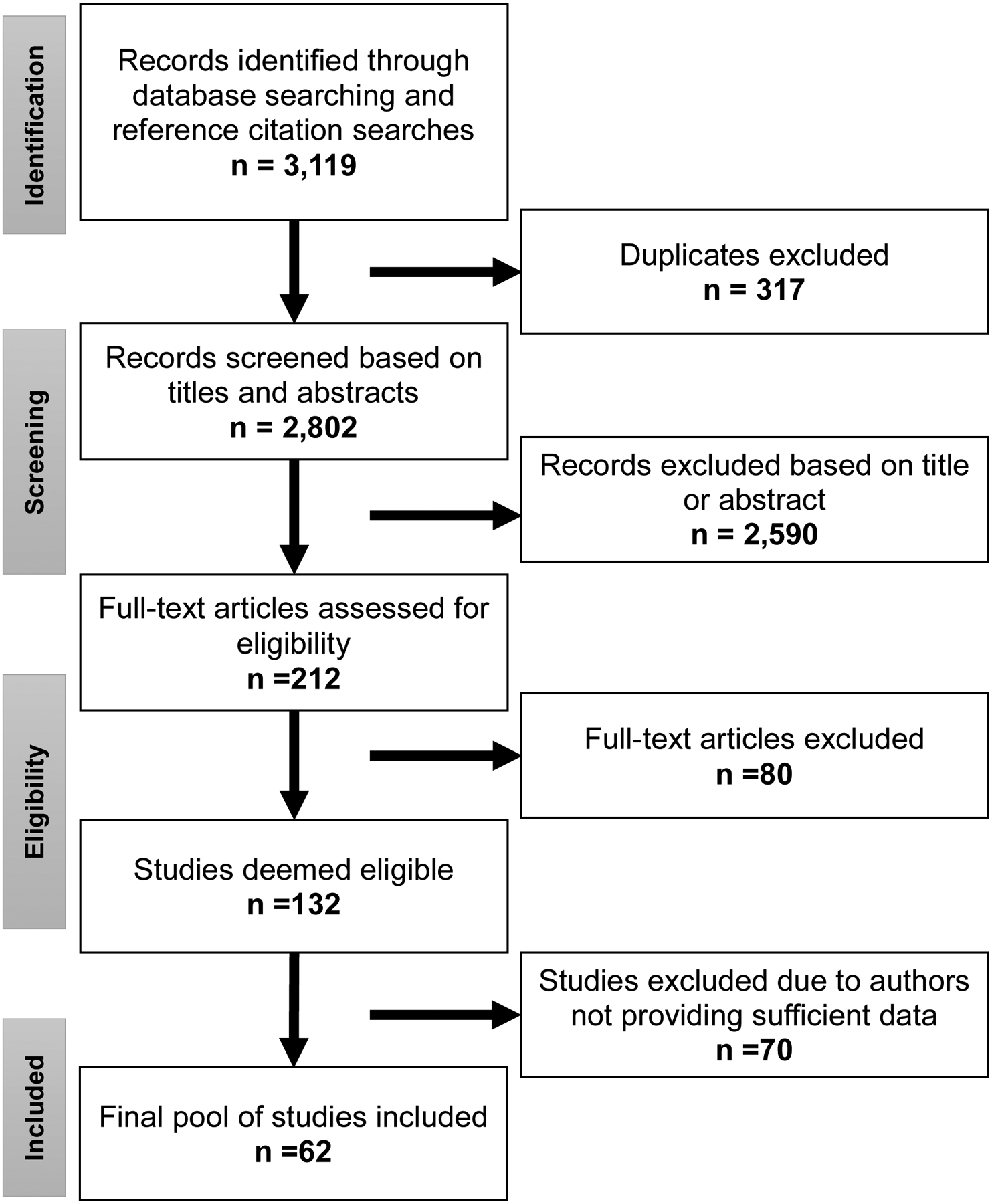
Summary of the results of the literature search.

Table 1 reports the sample composition for each study included in the review, as well as the mean and standard deviation for RSA at every age for which it was measured in each study. Values of RSA assessed at multiple ages within the same study were modestly to moderately intercorrelated not only within infancy (Fracasso et al., 1994: r = [.50, .60]; Izard et al., 1991: r = [.36, .49]; Porter et al., 1995: r = .39; Stifter & Jain, 1996: r = .30), but also between infancy and toddlerhood (Porges et al., 1994: r = .55), and between infancy and preschool (Bornstein & Suess, 2000a, b: r = [.30, .55]). Studies with measures spanning early childhood reported consistent results: Bar-Haim et al. (2000) reported that among 10 correlations among measures of basal vagal tone taken at 4, 9, 14, 24, and 48 months, all but two were significant (r = [.36, .55]); Patriquin et al. (2013) reported the same proportion of significant correlations among measures at 5, 10, 24, 36, 48 months (r = [.27, .67]). Additional details regarding the intercorrelations for measures of RSA for studies included in the review can be found in supplemental Table S1.

Table 1.

Summary of studies employing repeated measures of RSA during early childhood

		Age By Month		Demographics		RSA
Brief Citation	n	Timepoint (month)	M(SD)	% Male	Race/Ethnicity	M	SD
Alkon et al., 20061	150	6	6.66(0.97)	54%	89% Mexican	3.30	0.90
	142	12	12.44(0.8)	47%	11% Mixed	3.80	0.90
					1% Other
Alkon et al., 20111	159	6	6.66(0.97)	50.2%	97% Latino	3.32	0.82
	152	12	12.44(0.8)	50.2%	3% Multiracial	3.74	0.93
	136	42	NR	50.2%		6.44	1.13
	297	60	NR	50.2%		6.8	1.19
Arditi et al., 20062	62	newborn	51.9hr(7.31)	46.78%	100% Israeli	3.99	1.10
Bar-Haim et al., 2000	24	4	NR	37.5%	100% White	3.22	0.86
	24	9	NR	37.5%		3.60	0.87
	24	14	NR	NR		3.91	1.11
	24	24	NR	NR		4.74	1.08
	24	48	NR	NR		6.01	1.27
Berry et al., 20183	748	7	NR	NR	Ethnicity NR	3.82	0.76
	748	15	NR	NR		4.29	0.92
	748	24	NR	NR		4.89	1.12
	748	35	NR	NR		5.52	1.09
Bockneck et al., 2018	130	24 to 31	27.02(2.6)	59.2%	90% Black 3.8% White 3.8% Multiracial 2.3% Other	2.95	0.86
Bornstein & Suess, 2000	77	2	1.98(0.32)	50.65%	Ethnicity NR	2.60	0.76
	66	5	5.39(0.37)	45.45%		3.24	0.79
Brooker et al., 2013	124	6	NR	NR	95% White 1.7% Black 0.9% Asian	3.55	0.77
Buss et al., 2005	68	24	24.5(0.4)	64.7%	94.1% White 1.5% each Black/ Asian/ Hispanic/ Indigenous	5.06	0.95
Busuito et al., 2019	158	6	6.31(0.3)	57%	75% White 8% Black 17% Other	3.18	0.85
Calkins & Keane, 2004	140	24	NR	50.6%	65% White 30% Black 5% Other	5.76	1.40
Cho & Buss, 2017	124	24	24.43(0.47)	50%	90.4% White 6.4% Asian 1.6% Indigenous 1.6% Other	4.46	1.07
Cruz et al., 2018	28	1	1.12(0.24)	57.1%	100% White	3.10	1.30
DiPietro et al., 2006	137	24	24.8(0.9)	49%	85.1% White 11.7% Black 3.2% Asian	4.27	1.02
Esposito et al., 2016	156	28	28.5(5.91)	52%	90% White 8% Multiracial 2% Asian	5.22	1.31
	156	36	35.34(6.18)	52%		5.79	1.32
	156	42	43.42(6.09)	52%		6.21	1.22
Feldman & Eidelman, 20072	52	newborn	NR	55.8%	100% Israeli	2.28	1.46
Fox, 19894	63	5	4.65(0.29)	47.6%	Ethnicity NR	2.99	0.88
	52	14	14.1(4.2)	45.5%		3.45	0.79
Fracasso et al., 1994	58	5	NR	44.8%	100% White	3.02	0.71
	53	7	NR	45.3%		3.25	0.72
	44	10	NR	43.2%		3.27	0.72
	49	13	NR	51%		3.20	0.71
Gormally et al., 2001	21	newborn	53hr(12)	42%	Ethnicity NR	3.80	1.50
Grady & Callan, 2019	37	24	23.28(0.65)	35.1%	56% Hispanic/Latino 26.5% White 6% Asian 5.9% Black	5.58	1.04
Gueron-Sela et al., 20175	137	3	NR	52%	58% Black 46.1% White	3.41	0.96
	137	6	NR	52%		3.65	0.88
	137	12	NR	52%		3.67	0.93
	137	18	NR	52%		4.50	1.57
	137	24	NR	52%		4.92	1.49
	137	30	NR	52%		4.86	1.40
	137	36	NR	52%		5.34	1.25
Gunnar et al., 1995	50	newborn	46.4hr(19.7)	50%	84% White 8% Black 4% Asian 4% Other	3.90	1.20
Haley et al., 20086	104	3	3.04(0.20)	52.9%	80% White Other NR	3.46	1.12
Haley et al., 20106	151	6	NR	50.3%	80% White Other NR	3.44	0.87
Holochwost et al., 20145	95	6	NR	47.4%	53.7% Black 46.3% White	3.72	0.91
Holochwost et al., 20185	112	24 to 36	NR	51.5%	58.7% Black 41.3% White	5.16	1.26
Hsu & Porter, 2004	53	1	NR	43.18%	92% White	3.35	1.20
	53	3	NR	38.46%	Other NR	3.35	0.89
Huffman et al., 1998	65	3	2.69(0.12)	51.7%	“Predominantly White”	2.6	0.82
Izard et al., 1991	86	3	NR	NR	100% White	2.56	0.80
	83	4.5	NR	NR		2.76	0.81
	58	6	NR	NR		2.96	0.93
	54	9	NR	NR		3.49	0.81
	47	13	NR	NR		3.61	0.76
Jewell et al., 2018	312	1.4	NR	46%	87% Mexican	2.50	0.97
	205	2.8	NR	46%	13% White	2.81	1.00
	210	4.1	NR	46%		2.86	0.94
	210	5.5	NR	46%		3.10	0.85
	206	12	NR	46%		3.66	0.95
	237	18	NR	46%		4.25	0.98
	244	24	NR	46%		6.23	1.12
Johnson et al., 2014	329	6	6(0.53)	55%	91% White Other NR	3.58	1.76
Kennedy et al., 2004	104	24	NR	48.1%	97% White	4.86	0.98
	104	27	3m follow up	51%	Other NR	4.86	0.98
Lewis et al., 2004	56	4	3.93(0.28)	48.2%	91.1% White 7.14% Asian 1.78% Hispanic	2.76	0.13
Maikranz et al., 2000	68	4	NR	48.5%	Ethnicity NR	5.76	0.83
Mammen et al., 2017	46	8	7.6(0.95)	56%	89% White Other NR	3.37	0.80
Mateus et al., 2018	23	1	1.15(0.23)	65.2%	100% White	3.11	1.24
Mills-Koonce et al., 20153	150	6	NR	NR	Ethnicity NR	3.95	0.90
	161	15	NR	NR		4.37	1.07
Montirosso et al., 2014	83	4	4.08(0.06)	46.3%	Ethnicity NR	3.14	0.92
	83	4.5	4.56(0.2)	44.4%		3.24	1.02
Moore, 20095	89	6	6.81(0.68)	51%	52.1% White 47.9% Black	3.68	0.85
Moore et al., 2004	73	3	2.87(0.29)	58.9%	81% White 14% Black 4% Mixed	2.82	0.75
Morales et al., 2015	125	24	NR	NR	90% White 5% Asian 2% Indigenous 1% each Black/ Hispanic/ Mixed/ Other	4.46	0.87
	124	42	NR	NR		5.38	0.79
Patriquin et al., 2014 7	91	5	NR	47.2%	87.7% White 8.5% Multiracial	3.77	0.89
	94	10	NR	47.2%		4.44	1.02
	69	24	NR	47.2%		5.52	1.52
	56	36	NR	47.2%		6.14	1.11
	56	48	NR	47.2%		6.58	1.07
Patriquin et al., 20157	287	5	NR	49.7%	77% White 16% Black 7% Multiracial	4.02	1.27
	261	10	NR	49.7%		4.74	1.16
	228	24	NR	49.7%		5.44	1.23
	207	36	NR	49.7%		6.49	1.53
	190	48	NR	49.7%		6.80	1.38
Perry et al., 20188	388	5	5.4(0.26)	49%	78% White 13% Black	3.97	1.21
	352	10	10.4(0.37)	49%		4.64	1.13
	320	24	25.2(0.95)	49%		5.43	1.3
Poehlmann et al., 2011	120	newborn	NR	52%	70% White 11% Black 16% Multiracial	3.43	0.87
Porges et al., 1994	25	9	NR	45.7%	Ethnicity NR	4.03	1.00
	20	36	NR	45.7%		5.73	1.4
Porter et al., 2003	56	6	6.2(NR)	44.6%	95% White	3.32	0.96
					5% Hispanic
Porter et al., 1995	26	1	1.12(NR)	26.9%	“Predominantly White”	3.20	1.10
	26	3	3.2(NR)	26.9%		3.13	0.80
	26	6	6.25(NR)	26.9%		3.73	0.90
Quigley et al., 20175	151	6	NR	51%	52.1% White 47.9% Black	3.68	0.87
Riniolo et al., 19979	36	5	NR	NR	EthnicityNR	3.82	0.80
	36	5	NR	NR		4.12	0.86
Somers et al., 2019	322	1.4	1.38(0.32)	46.3%	86.3% Mexican 13.7% Mexican-American	2.52	0.96
Stifter & Jain, 1996	90	5	NR	51.1%	96% White 2% Black	2.98	0.70
	84	10	NR	48.8%		3.64	0.80
	74	18	NR	50%	1% each Asian/Hispanic	4.3	1.00
Stifter & Fox, 19904	88	newborn	48hr(24)	45.5%		3.94	0.97
	63	5	4.65(0.29)	47.6%	Ethnicity NR	2.99	0.88
Stifter & Corey, 2001	136	12	12.21(0.28)	48.5%	91.8% White 3.4% Black 3.4% Asian	3.81	0.92
	127	13	13.28(0.31)	47.2%		3.84	0.94
Sturge-Apple et al., 2016	201	24	25.14(1.68)	56%	56% Black 23% White 11% Latino 7% Multiracial 3% Other	6.62	1.36
Sullivan et al., 201610	160	5	4.83(0.46)	50%	65% White 17% Multiracial/Other 9% Black/Hispanic 8% East Asian/Indian	3.54	1.45
	160	5	4.83(0.46)	50%		3.72	1.31
Thompson et al., 1993	20	newborn	47.37hr(NR)	NR	Ethnicity NR	1.48	0.22
Wagner et al., 20165	186	6	NR	48%	56% Black 44% White	3.4	0.85
Wagner et al., 20175	169	3	NR	49%	57% Black	3.41	0.98
	96	6	NR	49%	43% White	3.66	0.88
	102	12	NR	49%		3.7	0.99
	122	18	NR	49%		4.56	1.61
	79	24	NR	49%		4.82	1.58
Wagner et al., 2018	84	24	24.99(1.08)	50%	97% White Other NR	4.86	0.98
Waters et al., 2016	64	6 to 36	13.12(1.21)	51.5%	58% White 19% Asian 9% Multiracial 7% Latina 7% Black/ Biracial	3.96	0.98
Whedon et al., 20188	357	5	NR	NR	76% White	3.97	1.21
	336	10	10.27(0.32)	51%	Other NR	4.64	1.13
	273	24	24.85(0.87)	51%		5.43	1.30

Note: n = number; m = mean; SD = standard deviation; NR = not reported.

Across studies with multiple measures of vagal tone, comparing mean values of RSA typically revealed higher levels of vagal tone as a function of age. Thus vagal tone has been found to be higher at earlier months as compared to later months across infancy (Jewell et al., 2018; Bornstein & Suess, 2000a; Gueron-Sela et al., 2017; Porter et al., 1995; Fracasso et al., 1994; Bar-Haim et al., 2000; Perry et al., 2018; Stifter, Fox, & Porges, 1996; Whedon et al., 2018; Alkon et al., 2006, 2011; Jewell et al., 2018, toddlerhood (Izard et al., 1991; Fox, 1989; Berry et al., 2018; Gueron-Sela et al., 2017; Jewell et al., 2018; Stifter & Jain, 1996; Gueron-Sela et al., 2017; Jewell et al., 2018; Berry et al., 2018; Perry et al., 2018; Whedon et al., 2018), and early childhood (Gueron-Sela et al., 2017; Esposito et al., 2016; Berry et al., 2018; Porges et al., 1994; Esposito et al., 2016; Bar-Haim et al., 2000; Calkins & Keane, 2004; Kennedy et al., 2004; Bornstein & Suess, 2000b). A parallel trend towards increasing values of RSA with age was revealed by plotting the weighted means of RSA across studies (see Figure 2).

Figure 2.

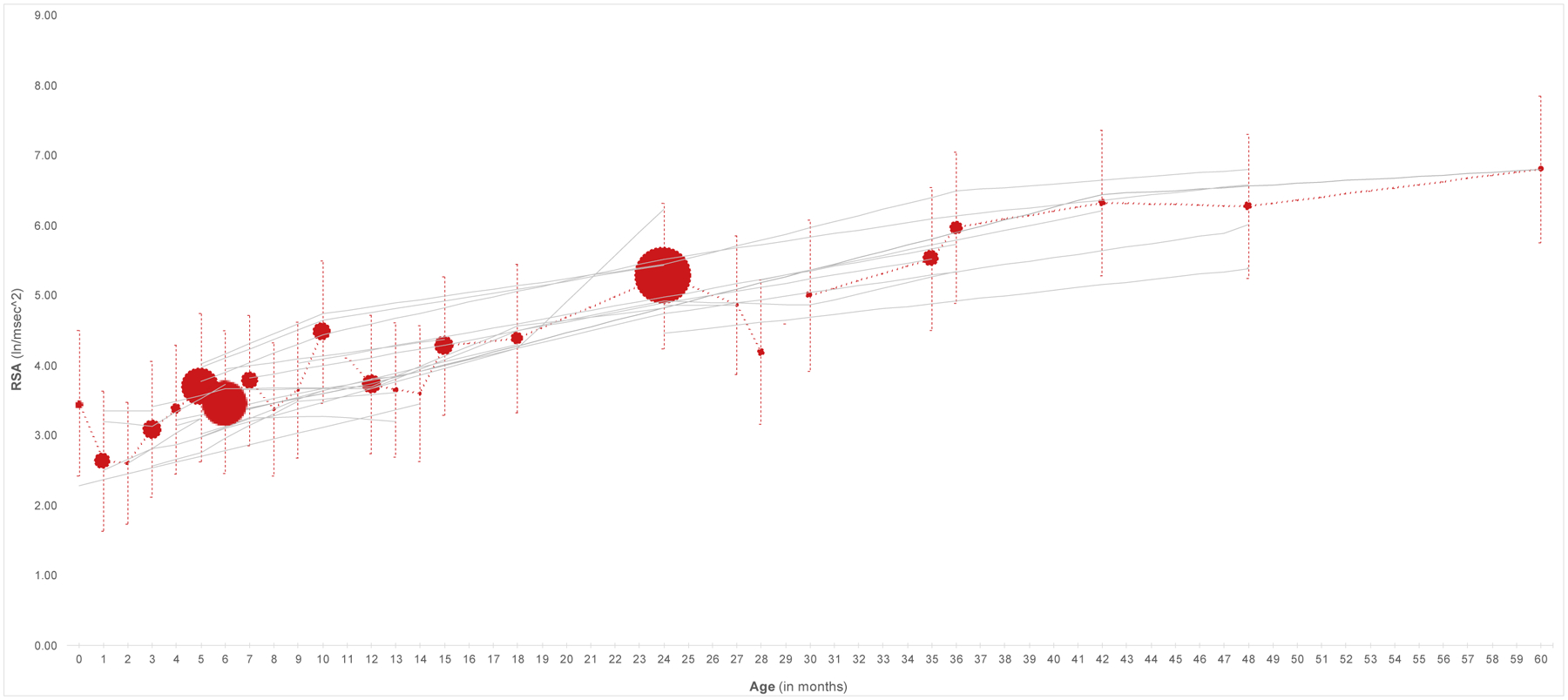
Graphical summary of studies included in the systematic review. The red line represents the weighted means and pooled standard deviations across studies at each age. The sizes of the red markers are proportionate to the number of studies on which each weighted mean is based. Timepoints reported in Table 1 were used to locate each study on the x-axis. When a range of timepoints were provided, the mid-point of that range was used (except for Waters et al. (2016), which was omitted from the figure due to the width of the range). For Riniolo et al. (1997), the sub-sample with higher temperatures is depicted; for Sullivan et al. (2016) the children who participated in the study on day 1 are included.

Study 2: Modeling the Development of Vagal Tone in Early Childhood

Method

Participants

Durham Child Health and Development Study.

The Durham Child Health and Development Study (DCHDS) is a prospective longitudinal study consisting of 206, full-term infants who were recruited at 3 months of age. Approximately equal numbers of African and European American families from lower- and higher-income groups were targeted for recruitment. Families from a largely urban community who were expecting a new child were contacted by telephone using birth record information as well as through fliers and postings at birthing classes. The study included only infants who were healthy, full-term, and born without significant complications. Family’s race and income status were determined from mother self-report.

The current study uses baseline cardiac data collected at 3 (n = 171), 6 (n = 96), 12 (n = 102), 18 (n = 122), 24 (n = 79), 30 (n = 100), and 36 (n = 74) month laboratory visits. Of the 206 children who were recruited into the DCHDS, 203 (98.5%) had cardiac data at one or more of the time points. Participants that were missing cardiac data at every time point were excluded from the analyses. No significant differences on demographic variables exist between those missing data and those who were included in these analyses. The final sample consisted of 103 (50.7%) males, 100 (49.3%) females and was 56.7% African American. The average income-to-needs ratio over the seven time points was 3.4 (SD = 2.5). Families were compensated monetarily for their participation in the study.

Family Life Project.

The Family Life Project (FLP) is a large longitudinal study with the overarching goal of understanding the multiple interacting processes in early childhood that act to alter developmental outcomes. Sampling procedures were designed to study families that lived in two of the four major geographical areas of high child rural poverty (Appalachia and the Black South). As such, six counties were selected, three in North Carolina (NC) and three in Pennsylvania (PA), and a stratified random sampling procedure was used to recruit a representative sample of 1,292 families at the time mothers gave birth to a child. For more information on the recruitment of the FLP sample, see Willoughby et al., (Willoughby et al., 2013). The participants’ homes were visited at 6 (n = 196), 15 (n = 208), 24 (n = 237), and 36 (n = 136) months. Of the 1,292 families in the study, 370 (28.6%) had cardiac data at one or more of the time points and were included in the analyses. Fewer African American participants had missing data than European Americans (475 vs. 394; x2 = 7.8, p = 0.003). Participants missing cardiac data at every time point did not significantly differ from those included on any other demographic variable. The sample used in the current study is comprised of 190 (51.4%) females, 136 (36.8%) African American, and 209 (56.5%) from North Carolina. The average income-to-needs ratio over the four time points was 1.8 (SD = 1.3). Families who participate in FLP receive a $50-dollar gift card to Wal-Mart. Children are given age-appropriate gifts for participation such as balls, stickers, and books.

Measures

DCHD RSA.

The Mini Logger 2000 was used to collect IBIs (Mini Logger 2000; Mini-Mitter Corp., Bend, OR). Researchers placed two electrodes cross-diagonally (i.e., from upper right to lower left) on the child’s chest at the beginning of the 3, 6, 12, 18, and 24-month visits for a 2–4-minute measure of baseline cardiac function while at rest. Electrodes were connected to a preamplifier, which transmitted IBIs to a monitor. Porges’ (U.S. Patent No. 4,510,944; Porges, 1985) method of calculating RSA and HP, in which a moving polynomial filter is used to remove frequencies lying outside a normal physiological range (0.24 + 1.04 Hz), was used, and the estimate of RSA is reported in units of ln(ms)2. The data files were transferred to a computer, and were edited by two reliable researchers using MXEdit software. The two researchers were trained to reliability in MXEdit software (Delta Biometrics, Bethesda, MD) with Porges’s Lab at the University of Maryland, and edited the files by visually scanning the data for outlier points relative to adjacent data and replacing those points by dividing them or summing them so that they would be consistent with surrounding data. Consistent with previous work (Moore et al., 2009), only participants who had full and sufficient data with less than 10% editing were included in the final dataset. RSA and HP were calculated every 15 seconds for the baseline period using Porges’s (1985) method.

FLP RSA.

The experimenter placed three disposable pediatric electrodes in a triangular pattern on the child’s chest while seated in caregiver’s lap. The electrodes were connected to a preamplifier, the output of which was transmitted to a laptop computer which was equipped with data collection hardware and software (Mindware Technologies, Westerville, OH). Cardiac IBI data were continuously collected for a 4-min period during which the child was stimulated as little as possible to assess baseline RSA and HP. Data files were edited for bodily movements, tugging on electrodes, and physical force. Data files that required editing of more than 10% of the data were not included in the analyses and were considered missing data. The integral of the power in the RSA band (0.24–1.04) was extracted and the natural log of this measure as calculated as an average across 30 s epochs and reported in units of ln(ms)².

Additional Covariates.

The sex and race of the child were reported by primary caregivers at entry into the study for both the DCHDS and the FLP. These covariates were included in all analyses.

Statistical Analyses

The main goal of the statistical analyses was to gain insight into the functional form of the development of RSA across infancy and early childhood in two separate longitudinal studies while controlling for relevant covariates. To ascertain the shape of change in baseline RSA between 3 and 36 months, two analytic frameworks were used. The modeling approach adopted in the current study allowed for both the examination of inter- and intra-individual change using latent curve modeling (LCM) as well as an investigation of potential patterns of homogeneity in the form of latent classes using latent class growth analysis (LGCA). First, an LCM was used to model both within-person change and between-person differences in RSA change over time. In these models, individual change is modeled according to a set of growth parameters which specify a mean and a variance across individuals. Likelihood ratio tests of nested models were conducted to test increasingly complex models, proceeding from an intercept only model, to a linear slope, to a quadratic term.

Second, a series of LGCAs (Muthen and Muthen, 2000; Nagin, 1999) were conducted. First, unconditional LGCAs were performed to determine the number of classes which best fit the data. Covariates were included after this step because class enumeration may be sensitive to the addition of covariates (Enders and Tofighi, 2007). In each of these models, growth in RSA over time within class was characterized by intercept, linear slope, and quadratic components. This mixture modeling framework determines whether and how significant heterogeneity in the growth of RSA over time can be captured in the form of discrete groupings based on these trajectories. All statistical analyses were conducted separately for each sample using Mplus version 7.2 (Muthen and Muthen, 2014). In the LCGA, race and sex were added as predictors of class membership; class structure was examined for differences between the unconditional and conditional models.

Model fit indices.

For both the LCM and LCGA, the Akaike Information Criterion (AIC; Akaike, 1973) and Bayesian Information Criterion (BIC; Schwarz, 1987) were consulted in choosing the optimal model. Both the AIC and the BIC decrease in value when the likelihood of the data is greater, but increase in value when the number of parameters is larger; thus, smaller values indicate a better balance of fit and parsimony. For the LCM, several absolute fit indices were consulted to consider the overall goodness of model fit. The root mean squared error of approximation (RMSEA; Browne and Cudeck, 1993) measures the closeness of the model-implied covariance matrix to the observed covariance matrix; models producing values below .05 are considered to fit the data well. The comparative fit index (CFI; Bentler, 1992) and Tucker-Lewis Index (TLI; Tucker and Lewis, 1973) both compare the fit of the model to the fit of a null model; values range from 0 to 1, with values above .95 indicating good fit.

For the LCGA, several tests were consulted in addition to the BIC and AIC in choosing the optimal solution. The Lo-Mendell-Rubin likelihood ratio test (LMR; Lo, Mendell, and Rubin, 2001) and parametric bootstrap likelihood ratio test (BLRT; McLachlan and Peel, 2001; Nylund et al., 2007) are tests of the null hypothesis that a model with K-1 classes fits the data as well as a model with K classes. As such, a significant result indicates that a model with K classes fits better than a model with one fewer class, and therefore the model favored by these tests is the last one for which a significant result is obtained. Finally, entropy (Celeux and Soromenho, 1996) is a value ranging from zero to one which represents the separation between the classes; though it is not a measure of fit per se, values close to one suggest that individuals in the sample are classified very well by the solution.

Results

Descriptive Statistics

In DCHD, means of baseline RSA increased steadily across the 3 (mean = 3.41, SD = .98), 6 (mean = 3.67, SD = .88), 12 (mean = 3.70, SD = .99), 18 (mean = 4.56, SD = 1.6), 24 (mean = 4.82, SD = 1.58), 30 (mean = 4.90, SD = 1.3), and 36 (mean = 5.82, SD = 1.7) month visits. Bivariate correlations between baseline RSA at each time point were positive and significant, ranging from r = .23 to r = .64. In FLP, means of baseline RSA also increased steadily across the 6 (mean = 3.92, SD = .86), 15 (mean = 4.36, SD = 1.1), 24 (mean = 4.99, SD = 1.3), and 36 (mean = 5.51, SD = 1.1) month time points. Bivariate correlations between baseline RSA at each time point were positive and significant, ranging from r = .16 to r = .44.

Latent Curve Model

In both datasets, all LCMs include sex and race as covariates. In the DCHD analysis, an intercept-only model, in which the mean and variance of the intercept were freely estimated, was first fit to the data; this model did not show adequate fit as measured by the test of model fit, χ²(38) = 296.04, p < .001, as well as absolute fit indices, with RMSEA = .183 and a CFI and TLI indices below zero. Adding a linear slope component improved fit but still did not yield good fit to the data, as indicated by the test of model fit, χ²(33) = 62.16, p = .0016, as well as absolute fit indices, with RMSEA = .066, CFI = .800, and TLI = .788. Though fit was still poor, it was significantly better than in the intercept-only model, χ²(5) = 233.86, p < .001. To further improve fit, a quadratic term was added to the model; this model still did not fit the data well, χ²(30) = 55.267, p = .0033, as well as absolute fit indices, with RMSEA = .064, CFI = .827, and TLI = .798. Though this model still fit poorly, the fit was marginally better than that of a model with a linear slope, χ²(3) = 6.89, p = .075; thus, a quadratic term was retained. Relative fit indices (AIC = 2317.453; BIC = 2380.404) were recorded to allow comparison to LCGA results. The mean intercept and slope parameters (point estimates = 3.403 and 0.818, respectively) were significantly different from zero, z = 30.457, p < .001 and z = 4.189, p < .001 respectively; the quadratic parameter’s mean was not significant. The variances of the intercept and slope parameters (point estimate = .364 and 0.067, respectively) were significantly different from zero, z = 4.584, p < .001 and z = 2.111, p = .035 respectively. There was no effect of sex on any of the model parameters, but race did have an effect such that African American participants had a higher predicted linear slope (β = .783, z = 3.246, p < .001), but a lower predicted quadratic term (β = −0.188, z = −2.303, p = .021).

As in the DCHD dataset, an intercept-only model did not show acceptable fit to the FLP data, χ²(14) = 218.321, p < .001, as well as absolute fit indices, with RMSEA = .212, CFI and TLI both below zero. However, unlike in the DCHD analysis, adding a linear slope yielded very good fit, χ²(9) = 6.813, p = .657, RMSEA = .000, CFI = 1.000, and TLI = 1.044; as predicted, adding this linear slope produced a significant difference in fit, χ²(5) = 211.51, p < .001. A model including a quadratic term also fit the data well, χ²(6) = 3.726, p = 0.7136, RMSEA = .000, CFI = 1.000, and TLI = 1.068, but did not produce a significant improvement in fit, χ²(3) = 3.086, p = .379. Relative fit indices (AIC = 2054.278; BIC =2114.770) were recorded to allow comparison to LCGA results. The mean intercept and slope parameters (point estimates = 3.839 and 0.409, respectively) were significantly different from zero, z = 39.390, p < .001 and z = 3.801, p = .002 respectively; the quadratic parameter’s mean was not significant. The variance of the intercept (point estimate = 0.383) was significantly different from zero, z = 2.891, p = .004; however, the variance of the linear slope was not significantly different from zero. As in the DCHD dataset, there was no effect of sex on any model parameters; however, unlike in the DCHD dataset, race did not influence the slope and quadratic components but did influence the intercept, such that African American participants showed higher initial levels of RSA (β = .431, z = 3.365, p < .001).

Latent Class Growth Analysis

Unconditional models.

Fit statistics for the unconditional model are shown in the top panel of Table 2. As is typical of mixture models, fit indices did not unequivocally converge on one solution, but a three-class solution was chosen for both the DCHD and FLP datasets. In both FLP and DCHD, the AIC favored an increasingly large number of classes, whereas the BIC favored a three-class solution. In the FLP dataset, the LMR favored a four-class solution, whereas in the DCHD dataset the LMR favored a two-class solution. The BLRT favored an increasing number of classes in the DCHD data, but in the FLP dataset it favored a three-class solution. Entropy was relatively low in all solutions, but was highest in the four-class solution in FLP and in the three-class solution in DCHD. Importantly, the four-class solution might appear to be the best-fitting solution in the FLP dataset, but it included classes with extremely small proportions of the sample (i.e., one class with <1% of the sample), and thus a three-class solution was chosen. Importantly, the BIC and AIC do not strongly favor the three-class model over the latent curve models fit in the previous analyses; indeed, in the FLP dataset the BIC is lower in the LCM than the three-class model.

Table 2.

Fit statistics for LCGA models

Unconditional models
	Number of classes	AIC	BIC	Entropy	LMR		BLRT
					Value	p. value	Value	p. value
FLP	1	2125.456	2151.921	--	--	--	--	--
FLP	2	2082.808	2124.396	0.513	48.549	0.4747	50.648	<.001
FLP	3	2062.225	2118.936	0.593	27.398	0.115	28.583	<.001
FLP	4	2060.148	2131.982	0.685	9.659	0.0413	10.077	0.0984
DCHD	1	2438.852	2471.246	--	--	--	--	--
DCHD	2	2354.852	2401.237	0.535	87.16	0.0022	91.262	<.001
DCHD	3	2324.121	2383.759	0.661	36.99	0.3526	38.731	<.001
DCHD	4	2313.218	2386.109	0.598	18.054	0.1515	18.903	<.001
Conditional models
	Number of classes	AIC	BIC	Entropy	LMR		BLRT
					Value	p. value	Value	p. value
FLP	2	2073.162	2122.312	0.437	62.493	0.0818	64.294	<.001
FLP	3	2053.306	2125.140	.614	30.963	0.3349	31.856	<.001
FLP	4*	2049.907	2144.425	.664	14.968	0.1495	15.399	0.3636
DCHD	2	2349.042	2402.053	0.558	97.995	0.0099	101.069	<.001
DCHD	3	2317.012	2389.902	0.668	42.691	0.2548	44.03	<.001
DCHD	4*	2308.839	2401.607	0.612	19.56	0.3345	--	--

Note.

^*indicates that model parameters needed to be fixed in order to ensure convergence

Conditional models.

Fit statistics for the conditional model are shown in the bottom panel of Table 2. As in the unconditional model, fit indices did not unequivocally favor one model in either dataset. In the DCHD, conditional models performed almost identically to the unconditional models: a three-class solution was arguably best-fitting, as suggested by the BIC and entropy values, though the LMR did favor the two-class solution. In the FLP dataset, a two-class solution was very narrowly favored by the BIC over the three-class solution, although all other fit indices suggested increasing the number of classes past four. Importantly, in both datasets a four-class solution encountered estimation difficulties such that parameter values needed to be fixed; results from these solutions should be interpreted with caution. In both datasets we proceeded with the three-class model, given the fact that the growth patterns in RSA defined by the conditional models were essentially identical to the unconditional model, indicating that this is a relatively stable solution. As in the unconditional model, the BIC and AIC do not strongly favor the three-class model over the conditional latent curve models; here the AIC and BIC are lower in the LCMs than in the three-class models in both datasets.

The three-class solution.

In addition to being equivocally favored by fit indices, the three-class solution was of particular interest because it was confirmed across both the FLP and DCHD datasets, in both conditional and unconditional models. This suggests that the results are relatively stable: while there are not three discrete classes that exist in the development of RSA over time which have been definitively uncovered by these data, our findings do suggest that a three-class solution is a valid way to summarize the patterns of change over time.

Growth parameters for the conditional and unconditional three-class solutions are shown in Table 3 and trajectories for each class are shown in Figure 3. All solutions were characterized by a class with intermediate levels of RSA that increased linearly over time (class 1). This was the largest class, containing 60.7% and 58.8% respectively in the DCHD and FLP datasets under the unconditional model, and 59.8% and 59.6% respectively in the DCHD and FLP datasets under the conditional model. In all solutions, the second-largest class (class 2) was characterized by lower initial levels of baseline RSA that also increased linearly over time; this pattern contained 29.0% and 36.5% respectively in the DCHD and FLP datasets under the unconditional model, and 29.8% and 34.2% respectively in the DCHD and FLP datasets under the conditional model. Finally, in all analyses there was a small class with high levels of baseline RSA that increased slightly and then decreased (class 3), and were thus best described using a quadratic pattern; this pattern contained 10.3% and 4.7% respectively in the DCHD and FLP datasets under the unconditional model, and 10.4% and 6.0% respectively in the DCHD and FLP datasets under the conditional model.

Table 3.

Growth parameters for LCGA models

DCHD
	Class 1 (59.8%)				Class 2 (29.8%)				Class 3 (10.4%)
Parameter	Est.	S.E.	Est/S.E.	p. val	Est.	S.E.	Est/S.E.	p. val	Est.	S.E.	Est./S.E.	p. val
Intercept	3.682	0.151	24.411	<0.001	2.742	0.384	7.14	<0.001	4.086	0.18	22.748	<0.001
Slope	0.181	0.157	1.158	0.247	0.392	0.265	1.482	0.138	2.768	0.547	5.056	<0.001
Quadratic	0.173	0.076	2.275	0.023	0.022	0.08	0.278	0.781	−0.628	0.182	−3.453	0.001
FLP
	Class 1 (59.8%)				Class 2 (34.2%)				Class 3 (6.0%)
Parameter	Est.	S.E.	Est./S.E.	p. val	Est.	S.E.	Est./S.E.	p. val	Est.	S.E.	Est./S.E.	p. val
Intercept	4.091	0.158	25.858	<0.001	3.425	0.2	17.147	<0.001	5.062	0.341	14.828	<0.001
Slope	0.663	0.168	3.959	<0.001	0.141	0.271	0.522	0.602	2.266	0.432	5.245	<0.001
Quadratic	−0.011	0.074	−0.15	0.881	0.102	0.079	1.282	0.2	−0.632	0.159	−3.976	<0.001

Figure 3.

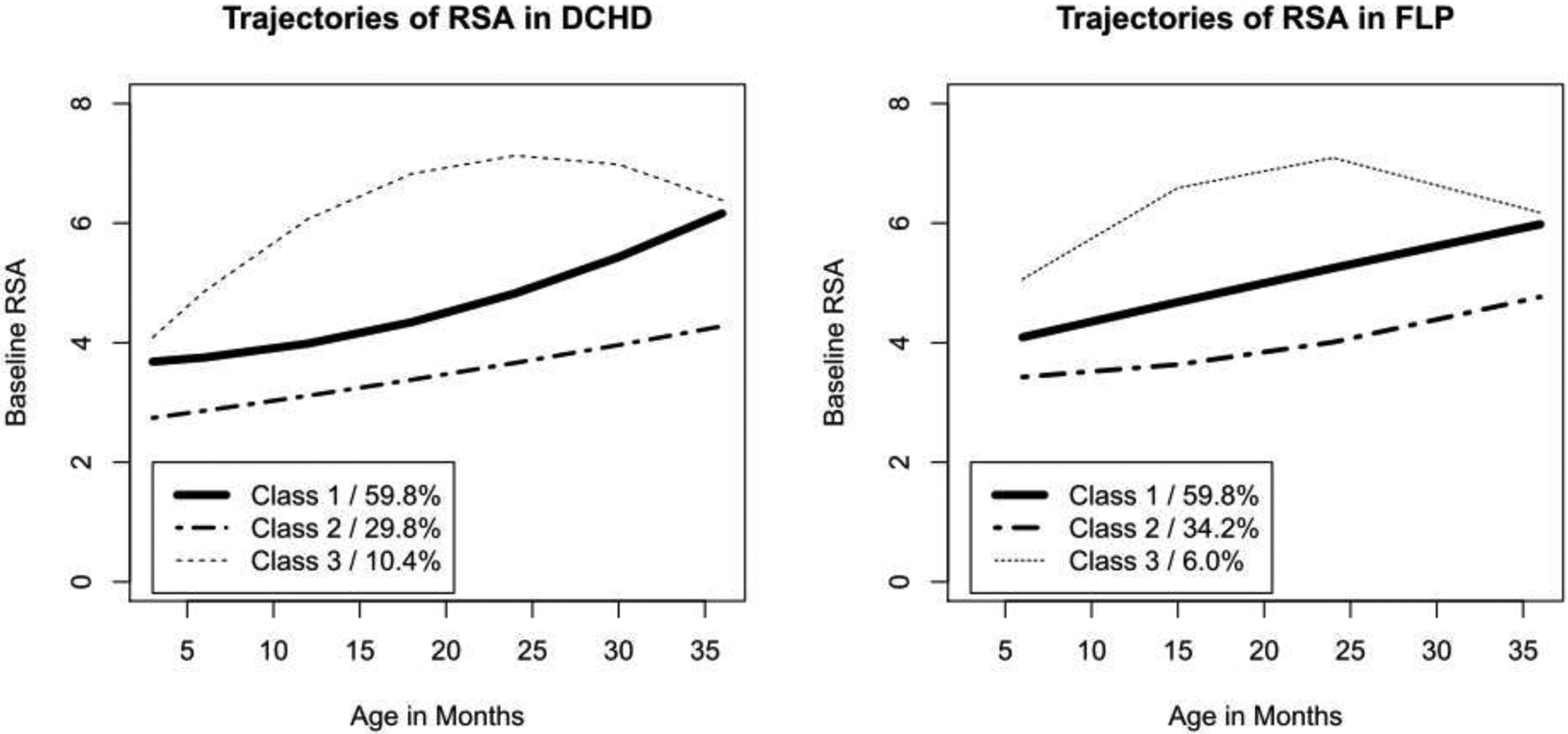
Model-implied trajectories under conditional LCGA models in both datasets.

In the conditional model, there were no sex differences across classes. In both the DCHD and FLP datasets, there was a race effect such that African American subjects were more likely to be in class 3 than class 1 (DCHD: β = 3.147, p = .013 / FLP: β = 2.306, p = . 011); in DCHD, African American subjects were more likely to be members of class 1 than class 2, but in the FLP dataset this effect did not reach significance (DCHD: β = 2.589, p = .040 / FLP: β = 1.299 , p = .072).

Summary and General Discussion

The functioning of the PNS supports key emotional, behavioral, and social regulatory processes across the lifespan (Dollar et al., 2020) and is linked with many adjustment outcomes in childhood and adolescence, including emotional (Abaied et al., 2018) and social competence (Eisenberg & Fabes, 1992), educational attainment (Holochwost et al., 2019), executive functioning (Nigg, 2016), and psychopathology (Beauchaine, 2015; Wagner et al., 2015; Wagner et al., 2018; Wagner & Waller, 2020). Although there has been considerable research elucidating the correlates of resting RSA across infancy and early childhood (Calkins & Dedmon, 2000), less work has been done to characterize its development across infancy and early childhood. We report findings from two complementary studies to address this gap. The first presents the results of a systematic review of the literature examining longitudinal measures of resting RSA starting in infancy or early childhood. The second study tests a series of models that were fit to longitudinal data drawn from two demographically-diverse samples. Consistent with previous studies (Dollar et al., 2020; Hinnant et al., 2011; Patriquin et al., 2014), findings from both studies suggest that baseline RSA is characterized by stable increases across infancy and early childhood. Although study 2 provides equivocal evidence for individual variability in trajectories of RSA, the findings suggest that the individual differences in resting RSA may become entrenched in early life, thus supporting the view of resting RSA as a biomarker of children’s arousal and regulation.

Stability and Discontinuity of Vagal Tone in Infancy and Early Childhood

Bar-Haim et al. (Bar-Haim et al., 2000) and Calkins and Keane (Calkins & Keane, 2004) have noted that, if homeostatic vagal tone is a stable physiological substrate or endophenotype of temperament (Derryberry & Rothbart, 1997; Posner & Rothbart, 2000), it should be stable over time. That is, the relative positions of any group of individuals on measures of vagal tone under homeostatic conditions at one age should resemble the relative positions of individuals at other ages (Bornstein & Suess, 2000). The results of the studies included in the systematic review generally support this view, with modest-to-moderate stability in measures of vagal tone taken under homeostatic conditions across age-spans of varying lengths during early childhood. Moreover, the observed patterns of modest-to-moderate stability in measures of baseline vagal tone from the DCHD and FLP samples used in study 2 align with the pattern of results obtained in study 1.

However, this stability in vagal tone appears to be accompanied by discontinuity, or change in the absolute levels of vagal tone over time (Bornstein & Suess, 2000b). Both within studies that measured vagal tone at multiple ages and across all studies included in the systematic review, increasing age was generally associated with higher levels of vagal tone. The results of the models featured in study 2 were consistent with this association, indicating a linear increase in vagal tone across early development, as evidenced by the significant, linear slope across models. However, there were substantial individual differences within this overall trend. First, in one of three classes revealed by our analyses (class 3), levels of RSA decreased following a period of initial increase. Second, there was considerable variation between subjects is in the intercept parameter, indicating large differences in subjects’ initial vagal tone at 3 months of age.

These results are broadly consistent with prior work by Patriquin and colleagues (2014). Although Patriquin found that a quadratic function best fit repeated measures of vagal tone collected between 5 and 48 months, most participants in her study (93.3%) were assigned to a group for which the trend in basal vagal tone was positive and generally linear. And, as was also the case in Patriquin’s study, the majority of participants in both samples included in study 2 were assigned to one of two of patterns characterized by low levels of vagal tone that increased gradually over time, whereas a small number of participants (10.4% in DCHD and 6.0% in FLP) were assigned to an ‘atypical’ class characterized by higher initial levels of vagal tones that increased slightly before plateauing and then decreasing after the second year of life. This pattern of change over time supports the assertion made by Patriquin and colleagues that levels of vagal tone for most children may surpass those of children in the ‘atypical’ group due to the combined influence of the plateau and subsequent decline in vagal tone after the first year.

Taken together, these results suggest that: 1) vagal tone is somewhat stable under homeostatic conditions across early childhood, but that 2) it is also discontinuous, in that for most children it increases linearly over this period, and 3) there are considerable individual differences in both the trajectory and, in particular, the initial values of vagal tone. The first of these findings reinforces the fact that while homeostatic vagal tone may indeed be a substrate or endophenotype of temperament (Calkins & Keane, 2004; Posner & Rothbart, 2000), like the regulatory dimensions of temperament (e.g., effortful control; Nigg 2016) and other aspects of neurophysiological function (Fox & Porges, 1985), vagal tone is open to environmental influence in early childhood (Propper & Holochwost, 2013). Were this not the case, we would expect to observe a much higher level of stability in vagal tone over time.

The specific nature of the discontinuity in vagal tone reported here, wherein vagal tone increased over time both across studies (as reported in study 1) and for the overwhelming majority of children (in study 2), may reflect deeply-ingrained developmental phenomena at the multiple levels of organization. At the sub-cortical level, increasing vagal tone reflects the emergent capacity of the PNS to inhibit sympathetic and limbic mechanisms of neurophysiological response. At the cortical level, these same increases reflect the nascent, higher-level regulation of parasympathetic function, cognitive, and behavior by a rapidly-developing PFC. Finally, at the behavioral level these increases are reflected in and indeed support young children’s emergent capacity to volitionally regulate emotions, behavior, and cognitive processes (Bar-Haim et al., 2000; Izard et al., 1991).

As noted above, in study 2 there were individual differences in the specific nature of the discontinuity in vagal tone over time. First, a small number of children do not display a pattern of linearly increasing vagal tone. In one sense, the antecedents for this finding are clear: a reduced rate of development in parasympathetic and/or prefrontal regulatory mechanisms. The explanation for such a deviation from typical developmental trend is necessarily speculative, and could include injury, illness, or extremely harsh conditions in the developmental environment. The consequences of decreasing vagal tone over development are, however, not speculative: progressively lower levels of vagal tone would be associated with poorer emotional and behavioral regulation as well as a reliance on sympathetic and limbic mechanisms of neurophysiological self-regulation that would impose a heavy allostatic load.

Second, there were significant individual differences in initial levels of vagal tone among children who did exhibit linear increases over time. This may be traced to both genetic and environmental influences; the latter may include experiences in very early infancy (i.e., prior to three months of age) as well as the conditions of the neonatal and prenatal environments (Propper et al., 2008). Given similar, linear trajectories in vagal tone, a child with initially-lower level of vagal tone will exhibit lower levels of vagal tone at all subsequent points in development. Whether these particular individual differences are of a sufficient magnitude to result in meaningful differences in children’s ability to regulate their emotions, behavior and cognitive processes is, as of yet, unclear, but the results reported here certainly suggest that individual variability in the rate of intra-individual change in vagal tone may serve as a biomarker for meaningful differences in children’s capacity to exercise volitional processes of self-regulation.

Limitations and Future Directions

The current research underscores the importance of understanding the nature and, ultimately, the etiology of individual differences in the degree and rate of change in vagal tone over time. However, the current review should be considered in the context of the following limitations. Although stringent exclusionary and inclusionary criteria were imposed during the selection and review of articles, there are other confounding influences that should be kept in mind when considering the associations between RSA and developmental age. For example, individual studies vary in their procedures for the collection “resting state” data or their analytic strategies for adjusting for potential confounds such as body weight or time of day of assessment. The current review is descriptive in nature and is meant to provide a foundation on which future empirical work can build.

With regard to study 2, one limitation of the LCM framework applied in study 2 is its assumption that the same general model applies to all individuals in the sample. This limitation motivated the application of a LCGA to the data, which when applied to both the FLP and DCHD datasets revealed three classes or patterns of change in vagal tone over time. Although the LCGA solution was not a conclusively-superior fit to the data than the latent curve models it did provide somewhat more generalizable patterns of vagal tone that were consistent with previous studies, including the study conducted by Patriquin and colleagues (2014). One clear direction for future research is to understand the socioemotional and social-cognitive coincident and sequalae of exhibiting this pattern of vagal tone in early childhood, which may indicate less neurophysiological flexibility in the face of changing environmental and social stimuli.

One strength of study 2 was that it examined change in vagal tone within two racially-diverse samples. Of the 51 studies included in the systematic review that reported the racial/ethnic composition of their samples, the majority (27) were conducted with samples that were at least 80% European American (including two that reported their samples as “predominantly white”). However, the small number of studies that have explicitly examined the associations between race and change in vagal tone under homeostatic conditions suggested that while African-American children demonstrate higher levels of vagal tone under these conditions than white children (Dollar et al., 2020), they may also show less increase in vagal tone over time (Hinnant et al., 2011). Our findings partially align with these results, in that African American participants in the DCHD study had higher predicted linear slope and African American participants in the FLP study demonstrated higher initial levels of vagal tone. Consistent with these findings, LCGA models also suggested that African American participants were also more likely to be in the groups classifying higher initial levels of vagal tone. While intriguing, the dearth of studies that have explicitly tested racial differences in the development of vagal tone precluded us from interpreting this finding. A clear direction for future research is to investigate the biological, environmental, and societal factors that have the potential influence the consolidation of neurophysiological systems, including pervasive experiences of systematic racism.

Conclusion

The current study contributes to our understanding of how vagal tone under homeostatic conditions changes across infancy and early childhood by presenting results from a systematic review of studies reporting these data across these ages, and by demonstrating two complementary approaches to modeling trajectories of baseline RSA across infancy and toddlerhood in two, diverse, longitudinal studies. Although the findings from the LCM and LCGA modeling approaches converged to tell a similar story, there may be situations in which mixture modeling, group-based analytic approaches provide insight into patterns of homogeneity which otherwise may go unobserved. Researchers should consider a full complement of analytic techniques to determine which approach best aligns with extant literature and study hypotheses. Baseline RSA is often presented as modifying or linking early experience with child adaptation and both the LCM and LCGA modeling approaches can be expanded to incorporate exogenous outcomes. In all, the current study contributes to our understanding of the developmental trajectories of baseline RSA across infancy and early childhood, and should support future research examining links between children’s parasympathetic regulation and their adjustment in early life.

Highlights.

• Despite its clear relevance to children’s self-regulation, and its utility as a transdiagnostic biomarker of emotion dysregulation and psychopathology, the ontogeny of vagal tone under conditions of homeostasis across infancy and early childhood is not well understood.

• A systematic review of 62 articles suggest that measures of respiratory sinus arrhythmia (RSA) increase over time and demonstrate moderate stability across infancy, toddlerhood, and preschool ages.

• A series of models fit to two diverse, longitudinal datasets suggest that baseline RSA is characterized by stable increases across infancy and early childhood and that individual differences in resting RSA may become entrenched in early life.

• This study contributes to our understanding of the developmental trajectories of baseline RSA across infancy and early childhood and should support future research examining links between children’s parasympathetic regulation and their adjustment in early life.