Applying a Computational Model Credibility Framework to Physiological Closed-loop Controlled Medical Device Testing

Abstract

Physiological closed-loop controlled medical devices are safety-critical systems that combine patient monitors with therapy delivery devices to automatically titrate therapy to meet a patient’s current need. Computational models of physiological systems can be used to test these devices and generate pre-clinical evidence of safety and performance before using the devices on patients. The credibility, utility, and acceptability of such model-based test results will depend on, among other factors, the computational model used. We examine how a recently developed risk-informed framework for establishing the credibility of computational models in medical device applications can be applied in the evaluation of physiological closed-loop controlled devices.

I. Introduction

Physiological closed-loop controlled (PCLC) medical devices combine monitoring and therapeutic devices to maintain or adjust a physiological variable by automatically adjusting therapy. This technology can assist in providing supportive therapy in critical care scenarios by, for example, automating fluid delivery (1, 2) or mechanical ventilation (3). The condition of patients in these scenarios and potential consequences related to the therapy being controlled engenders these to be safety-critical systems.

An international standard describes requirements for demonstrating safety and performance of physiological closed-loop controllers (IEC 60601–1-10) such as controller response and controller disturbance properties during normal and worst-case conditions (4). One possibility for testing related specifications of a PCLC medical device is to use computational simulations by incorporating a mathematical model of the patient physiology either with models of the device components or as part of a loop with the actual medical devices (i.e., hardware-in-the-loop testing). These computational and bench test methods can enable relevant and realistic testing of system performance prior to use on patients and with reduced costs compared to animal testing. The utility and acceptability of test results using computational patient models to demonstrate device safety and effectiveness will depend on the computational model used and the evidence available to support simulation results from that model (5).

Demonstrating that a computational physiological model is appropriate to use for a specific task can be open-ended and subjective. The need to validate computational physiological models has been suggested previously along with various approaches (6). This can be established through model assessment activities including verification, validation and uncertainty quantification. Recent community-wide efforts to improve the use of computational models in medical device applications have led to the development of a framework for establishing the credibility of computational models and has been proposed as a standard for this purpose (7, 8). This framework defines credibility as ‘the trust, through the collection of evidence, in the predictive capability of a computational model for a context of use’ (7). By applying the framework, which includes defining the specific role and scope of the computational model, risk of the decision consequence that the model is to be used for, and then goals and verification and validation plans that are commensurate with those aspects, one can collect evidence to support the model in the testing it is being applied to.

In this article, we examine how the proposed credibility framework could support testing of physiological closed-loop controllers with computational physiological models. We consider two questions of interest related to the safety and performance of an example closed-loop fluid resuscitation system that may be addressed with computational testing. In Section II we describe an example PCLC system and highlight two properties that may be evaluated with computational testing. In Section III we provide an overview of the proposed model credibility framework. In Section IV we consider how this framework could be applied to models used in testing for the two properties outlined in Section II including defining the questions of interest, role of the model, and risks associated with the decision consequence. Establishing specific credibility goals for the model and developing and performing verification and validation activities are beyond the current scope.

II. Example Physiological Closed-loop Controlled Fluid Delivery System

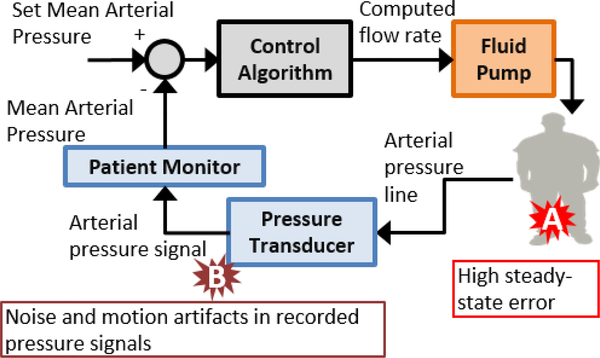
The following provides a simplified description of an example closed-loop fluid resuscitation device for maintaining a patient’s mean arterial pressure (MAP) at a prescribed set-point, Fig. 1. A pressure transducer measures the continuous arterial pressure from a radial artery fluid-filled catheter, and a patient monitor measures MAP from this signal. A desired MAP value is established as a set-point set by the caregiver. The controller compares the MAP to the set-point and sends a signal to an infusion pump to automatically adjust the fluid infusion rate per its control algorithm. The patient’s physiology then serves as a transfer element that converts the infused fluid into the pressure signal to be recorded.

Fig. 1.

Example block diagram of fluid resuscitation system and example hazardous situations.

Risks to the patient may include over resuscitation leading to edema or under resuscitation leading to hypovolemia. Controller performance aspects that may exacerbate these risks could be related to, for example, controller response that results in high steady-state error between MAP and the set-point or disturbances to the arterial pressure signal resulting in inaccurate MAP values being sent to the controller. The controller should be designed to minimize these risks, and computational testing could be applied to verify the performance of the controller response during normal and worst-case conditions and in the presence of such disturbances. A computational patient model may be used as the patient transfer element when verifying the controller response during normal and worst-case conditions. For disturbances related to the arterial pressure signal, the PCLC system requirements may include mechanisms to detect the presence of noise and artifacts in the recorded arterial waveform and provide an alarm or otherwise modify the controller response. A computational patient model that includes the generation of realistic noise and arterial pressure artifacts may be used to verify the controller response during such disturbances. The computational test configuration and the evidence necessary to demonstrate that the computational patient model is credible for these two types of tests may not be the same for these two types of tests.

III. Overview of Model Credibility Framework

A risk-informed computational modeling credibility assessment framework has been developed by The American Society of Mechanical Engineers (see V&V 40 Subcommittee on Verification and Validation (V&V) in Computational Modeling of Medical Devices) that focuses on establishing the credibility of computational models applied to medical devices (7, 8). The framework begins with defining the question(s) of interest, which includes identifying a decision to be made, and the specific role, scope, i.e., context of use of the computational model as well as the simulation results. These enable an assessment of the model risk, which is a combination of both the influence of the model on the question of interest as compared to the other available evidence (such as animal or clinical test results), and the decision consequence, which is the potential outcome of an incorrect decision. Model risk directly drives the selection of goals for the V&V activities to be performed to establish credibility. This approach acknowledges that the computational model will be used in a specific context and that the evidence provided from computational testing, or other sources, will likely not be used in isolation. By considering these points, model performance goals necessary to support the current context of use, can be defined. After establishing credibility goals, the next step in the framework is to plan the V&V activities (e.g., verification, validation, uncertainty quantification, applicability analysis (9)) to achieve the credibility goals, and then perform those V&V activities. Then the V&V evidence along with any other pertinent information (such as historical evidence of model performance) is gathered to assess whether the computational model meets the established goals. If the model does not meet the goals after the V&V assessment, then the context of use or aspects of the model can be changed, or additional V&V activities can be performed. The final stage is to document and report the findings. Documentation should include the rationale to support the assumptions and credibility goals for using the model in the proposed context of use.

IV. Applying the Model Credibility Framework

In Section II, two safety and performance aspects that could be tested with computational modeling and simulation prior to using the example closed-loop fluid resuscitation system on patients were highlighted: steady-state error (hazard A) and analysis of the response to arterial pressure signal disturbances (hazard B). Here, we consider how the credibility assessment framework summarized in Section III could be applied to support the computational testing. We begin by defining the two questions of interest that computational testing may be used to answer (Table I). We then provide an example summary of a simulation that might be performed to answer these questions and more broadly the context of use that explains how the computational testing results using the model will be applied in the decision making related to the question of interest.

TABLE 1.

Example Questions of Interest, Contexts of Use of Computational Modeling, and Potential Decision Consequences Associated with Potential Hazardous Situations Identified in Fig. 1

	Question of Interest	Proposed Simulation Setup	Context of Use	Consequence of Incorrect Decision
A	Is the average root-mean squared error of the controller during normal and worst-case steady-state conditions within the specifications?	A computational model of the patient transfer element that includes fluid as the input and mean arterial pressure as the output will be used to evaluate the steady-state response of the system at various MAP set-points. Parameters in the patient transfer element will be varied to represent normal and worst-case conditions.	Computational simulations will be performed to estimate the controller steady-state response at a range of set-points and patient transfer element conditions. The results will be used to verify that the steady-state error is within performance specifications during normal and worst-case conditions.	The device may be used on patients and in scenarios where the system does not perform within pre-specified criteria possibly leading to the development of edema or hypovolemia in some patients. Alternatively, patient populations that may benefit from the device may be excluded from use.
B	What is the controller’s response to transient disturbances in the arterial pressure signal?	Hardware-in-the-loop testing that incorporates a computational patient model with the physical patient monitor and infusion pump will evaluate the controller response during disturbances to the arterial pressure signal (e.g., noise in the recorded signal).	Results from the computational simulations will verify the performance of arterial pressure signal artifact detection mechanism and that the controller responds safely responds when these artifacts are detected.	Signal noise and artifacts in the arterial pressure waveform may not be detected during device use resulting in inaccurate arterial pressure measurement and potentially inappropriate therapy being delivered to the patient for short time periods.

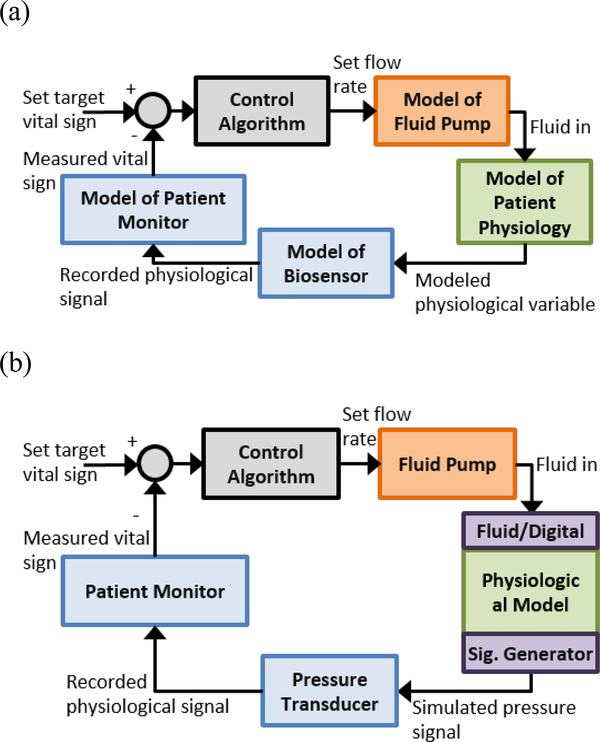
For Hazard A, our question of interest is whether the root-mean squared error of MAP during steady-state is within specifications during normal and worst-case conditions. To address this question, a simulation is proposed that will use the computational patient model alongside computational models of the device components (including a patient monitor, fluid infusion pump, and controller, Fig. 2a). The computational patient model will be used as the patient transfer element during representative normal and worst-case conditions. We assume that only evidence from the computational testing will be used to address this question. The context of use (COU-A) of the computational simulations is to verify that the steady-state error is within performance specifications during normal and worst-case conditions. The consequence of an incorrect decision related to this question is that inappropriate fluid may be delivered to the patient potentially resulting in patient injury. Combined with the high influence of the computational model on the decision making and risk to the patient if the decision is incorrect, this leads to a high model risk, and thus translates to higher credibility goals. If the simulation results were to be used alongside evidence from pre-clinical animal studies or other software/bench testing, or if an incorrect decision would not lead to patient injury, the model risk could be reduced.

Fig. 2.

Block diagram of system test setups for (a) computational testing used in COU-A where all components are modeled and (b) bench (hardware-in-the-loop) setup where physical device components are used in combination with a computational model of the patient for COU-B.

For Hazard B, our question of interest is whether the controller responds safely when transient disturbances (noise) in the arterial pressure signal are present. The response may include not adjusting the infusion rate while the disturbance is present or initiating an alarm. To address this question, a bench simulation is proposed that will use the computational patient model in a loop with the physical devices that are part of the system (Fig. 2b). The computational patient model will be used as the patient transfer element, but there is an additional element that includes adding noise and artifacts to the arterial pressure signals. Additional evidence may be available including design documentation, software, and bench testing to verify the functionality of the fallback mechanisms. The context of use (COU-B) is to support that the system responds as intended in the presence of arterial pressure disturbances. The consequence of incorrect information from this testing may include short periods of inappropriate therapy delivered to the patient, since we are only concerned with transient disturbances for this scenario. We may conclude there is a moderate level of risk of injury to the patient compared to the steady-state error example, and since additional information from other testing will be available to support the decision, overall risk of using this computational patient model may be low, translating to lower credibility goals.

The two questions we identified that may be addressed with computational modeling result in two different contexts of use and model use. For both scenarios, there are many aspects related to the simulation setup that may influence the results. We are focusing only on the computational patient model here that is serving as the patient transfer element in our simulation. In COU-A, we described a simulation that uses computational models of the device components, and for COU-B we require simulation techniques to produce the arterial pressure artifacts. The proposed framework could be applied to these components of the testing, as well as the overall testing.

Shortcomings in the performance of the computational patient model in each context of use may lead to incorrect or misleading test results. Performing relevant V&V activities reduce the chance of misuse and provide confidence in the results obtained from the model. The ASME V&V40 framework presents credibility criteria related to model verification (including characterizing software and numerical code errors), model validation (related to the model form and assessment), and applicability analysis. Model characteristics that may impact the results can be related to model form (equations representing the physiological mechanisms and known phenomena), model implementation (code used to implement and run the mathematical model), model parameters (selection of values used to define the properties of the model including initial and boundary conditions), and model validation domain (assessment of the model performance throughout the parameter space). For each characteristic, there may be several V&V activities with associated low to high credibility goals. For example, the model form may vary between the two scenarios presented. For COU-A, the steady-state error that is being evaluated that may be affected by physiologic variability as well as external disturbances. The model form will therefore need to account for sources of physiological variability such as interactions between different physiological systems and be influenced by disturbances such as other delivered therapies. For COU-B, since only the response to transient arterial pressure disturbances is being evaluated, the physiological sources of variability might not be as important to consider, but the model form should provide realistic response times to enable an assessment of short-term disturbances. COU-A and COU-B will likely have different credibility goals for model form given the uses and risks of each testing.

V. Conclusion

Evaluation of PCLC medical devices with computational patient models can be used to generate substantial amounts of information related to device safety and performance. Methods to establish the credibility of computational patient models for specific contexts of use can advance the utility of the simulation results such that they can serve as pre-clinical evidence of device performance. Here, we introduced a framework to establish the credibility of the computational models to testing PCLC medical devices. This could aid in demonstrating the utility and acceptability of computational testing in relation to PCLC medical device standards (e.g., IEC 60601–1-10) which may provide a range of contexts of use for the computational model. The next steps in applying the framework are to define the relevant V&V activities for the model to generate the evidence necessary to establish the appropriate model credibility for each context of use, perform those V&V activities, and consider if the results demonstrate that the model meets the credibility goals. Following such a process can provide assurance that the computational model provides credible simulation results to support the decision being made (i.e., verifying design requirements related to safety and performance) and further the use of computational modeling and simulations in medical device testing.