Temperature-Corrected Proton Density Fat Fraction Estimation using Chemical Shift-Encoded MRI in Phantoms

Abstract

Purpose:

Chemical shift-encoded MRI (CSE-MRI) is well-established to quantify proton density fat fraction (PDFF) as a quantitative biomarker of hepatic steatosis. However, temperature is known to bias PDFF estimation in phantom studies. In this study, strategies were developed and evaluated to correct for the effects of temperature on PDFF estimation through simulations, temperature-controlled experiments, and a multi-center, multi-vendor phantom study.

Methods:

A technical solution that assumes and automatically estimates a uniform, global temperature throughout the phantom is proposed. Computer simulations modeled the effect of temperature on PDFF estimation using magnitude-, complex-, and hybrid-based CSE-MRI methods. Phantom experiments were performed to assess the temperature correction on PDFF estimation at controlled phantom temperatures. To assess the temperature correction method on a larger scale, the proposed method was applied to data acquired as part of a nine-site multi-vendor phantom study and compared to temperature-corrected PDFF estimation using an a priori guess for ambient room temperature.

Results:

Simulations and temperature-controlled experiments show that as temperature deviates further from the assumed temperature, PDFF bias increases. Using the proposed correction method and a reasonable a priori guess for ambient temperature, PDFF bias and variability were reduced using magnitude-based CSE-MRI, across MRI systems, field strengths, protocols, and varying phantom temperature. Complex and hybrid methods showed little PDFF bias and variability both before and after correction.

Conclusion:

Correction for temperature reduces temperature-related PDFF bias and variability in phantoms across MRI vendors, sites, field strengths, and protocols for magnitude-based CSE-MRI, even without a priori information about the temperature.

INTRODUCTION:

Non-alcoholic fatty liver disease (NAFLD) is the most common form of chronic liver disease in the Western world, prevalent in up to 30–40% of adults¹. The hallmark feature of NAFLD is hepatic steatosis, the excess accumulation of triglycerides in hepatocytes. For many patients, the presence of fat is associated with hepatocyte injury, inflammation, fibrosis, and even cirrhosis and its complications². Biopsy is the current reference standard for detection and quantitative grading of NAFLD, but is limited by its invasive nature, cost, and high sampling variability³. Thus, there is a need for non-invasive methods with high accuracy and precision for early detection and treatment monitoring of NAFLD.

Over the past decade, confounder-corrected chemical shift-encoded magnetic resonance imaging (CSE-MRI) has become the leading MR method to quantify proton density fat fraction (PDFF), an accurate noninvasive biomarker of tissue fat content⁴. PDFF maps can be reconstructed using either magnitude-based CSE-MRI methods⁵, which use only the magnitude of the acquired signal, or complex-based CSE-MRI methods⁶, which use both the magnitude and the phase of the acquired signal. While complex-based methods can robustly estimate PDFF from 0–100%, they are susceptible to phase errors. Magnitude-based methods are insensitive to phase errors but have lower SNR performance in general and are unstable at PDFF values near 50%. Hybrid methods combine the higher noise performance and stability of complex methods with the insensitivity to phase errors of magnitude methods⁷. Now commercially available on most vendor platforms, PDFF is increasingly used for detection^8,9, quantitative staging^8,10, treatment monitoring of liver fat content^11,12, and as an endpoint for drug trials^11,12.

Multiple confounders can impact the accuracy of PDFF estimation. These include T₁-related bias¹³, R₂* signal decay^5,14, noise-related bias¹³, and inaccuracies in the spectral modeling of fat^5,6. In response, CSE-MRI methods have evolved to incorporate strategies that minimize the deleterious impact of these confounders on PDFF estimation. However, it is well-known that the proton resonance frequency (PRF) of water relative to fat varies with temperature^15–18. Previous studies have investigated the use of chemical shift to measure the effects of temperature in similar contexts^5,17–20. If uncorrected, temperature-dependent PRF shifts lead to inaccuracies in the spectral model of fat relative to water that can introduce bias into PDFF estimates²¹.

Commercially available CSE-MRI methods for quantifying PDFF assume a multi-peak spectral model of fat relative to water with a chemical shift at body temperature (37°C). This is a reasonable assumption for typical in vivo human studies. However, quantitative fat-fraction phantoms are playing an increasingly important role in the development and validation of new methods to quantify PDFF, system validation and acceptance testing, and periodic system quality assurance. These phantoms, as well as ex vivo tissue specimens with variable fat content^22,23, are usually imaged at lower temperatures, often unknown to the user since temperature measurement is often impractical. In this context, the use of CSE-MRI to quantify fat content is impacted by temperature.

Previous work has shown that both magnitude-^21,24 and complex-based²¹ CSE-MRI methods are susceptible to temperature-related PDFF bias if correction for the temperature is not included in the spectral model of fat. Further, Hernando et al²¹ has successfully demonstrated temperature correction when the PRF of water relative to fat, or fat-water frequency shift, is known. However, the true temperature of the phantom, and therefore fat-water frequency shift, is often unknown. Consequently, there is an unmet need to understand and mitigate PDFF estimation bias related to unknown temperature deviations from 37°C. Therefore, the purpose of this work is to develop and evaluate temperature correction strategies to mitigate temperature-related bias in PDFF estimation in phantoms without a priori information about the phantom’s true temperature.

THEORY:

PDFF is typically quantified on a voxel-by-voxel basis using a multi-echo spoiled gradient echo (SGRE) CSE-MRI method that uses the signal from a voxel containing both fat and water, sampled at multiple echo times (TE). The signal is typically modeled assuming a known multi-peak spectral model of fat relative to water, as well as R₂* signal decay^5,6, i.e.:

$$S\left(T{E}_n\right)=\left[W+F{c}_N\right]e^{i2\pi f_{B}T{E}_n}{e}^{-R_2^{*}T{E}_n}$$ [1]

where W and F are the complex signal amplitudes of water and fat, respectively. The sum of weighted exponentials $c_N={\sum }_{p=1}^P{\alpha }_p{e}^{i2\pi f_{F,p}T{E}_n}$ serves as the multi-peak spectral model of fat with P peaks of amplitude α_p (with ${\sum }_{p=1}^P{\alpha }_p=1$) and frequencies f_F,p (Hz) relative to the water resonance as described in previous works^6,25, changed slightly to match the fat-water frequency shift in phantoms as described in Hernando et al²¹. In addition, f_B (Hz) is the local magnetic field inhomogeneity, and TE_n (s) is the nth echo time (n = 1, …, N). The effects of T₁-related bias are typically avoided by using a small flip angle¹³.

The parameters W, F, f_B, and/or $R_2^{*}$ can be estimated using a non-linear least squares fitting algorithm²⁶, from either magnitude or complex signals. Magnitude fitting is represented as:

$$\left\{{\widehat{W}}_m,{\widehat{F}}_m,{\widehat{R}}_{2,m}^{*}\right\}= \underset{W,F,R_2^{*}}{\text{argmin}} \sum _{TE}{\left(\left|S_{est, TE}\left(W, F, R_2^{*}\right)\right|-\left|S_{\mathit{\text{meas}}, TE}\right|\right)}^2$$ [2]

where the subscript, m, denotes magnitude fitting; whereas complex fitting, denoted by the subscript, c, is represented as:

$$\left\{{\widehat{W}}_c,{\widehat{F}}_c,{\widehat{f}}_{B,c}, {\widehat{R}}_{2,c}^{*}\right\}= \underset{W,F, f_B,R_2^{*}}{\text{argmin}} \sum _{TE}{\left|S_{est, TE}\left(W, F, f_B, R_2^{*}\right)-S_{\mathit{\text{meas}}, TE}\right|}^2$$ [3]

Water and fat signals can be combined and PDFF calculated using a magnitude discrimination method to avoid noise related bias¹³.

Hybrid methods, which are weighted combinations of magnitude- and complex-based PDFF estimation, have also been proposed as a means to minimize unanticipated phase shifts caused by eddy currents⁷. The hybrid estimates of water and fat are given as:

$${\widehat{W}}_h=\lambda \cdot {\widehat{W}}_c+\left(1- \lambda \right)\cdot {\widehat{W}}_m$$ [4]

$${\widehat{F}}_h=\lambda \cdot {\widehat{F}}_c+\left(1- \lambda \right)\cdot {\widehat{F}}_m$$ [5]

where the subscript, h, denotes hybrid fitting and where λ is a weighting based on a Fermi function⁷ to maintain the stability of complex fitting near a PDFF of 50%, where λ approaches 1, and the low bias of magnitude fitting near a PDFF of 0 or 100%, where λ approaches 0.

The proton resonance frequency (PRF) of water in part depends on temperature^15–18. Current CSE-MRI methods model the spectrum of fat relative to the water resonance frequency at body temperature (37°C). The temperature dependence of the PRF of water is due in part to temperature-dependent changes in the electron shielding of protons in the water molecule. By comparison, the PRF of triglycerides, is negligibly affected by temperature. As a result, the fat-water frequency shift will change with variations in temperature, as depicted in Figure 1.

Figure 1.

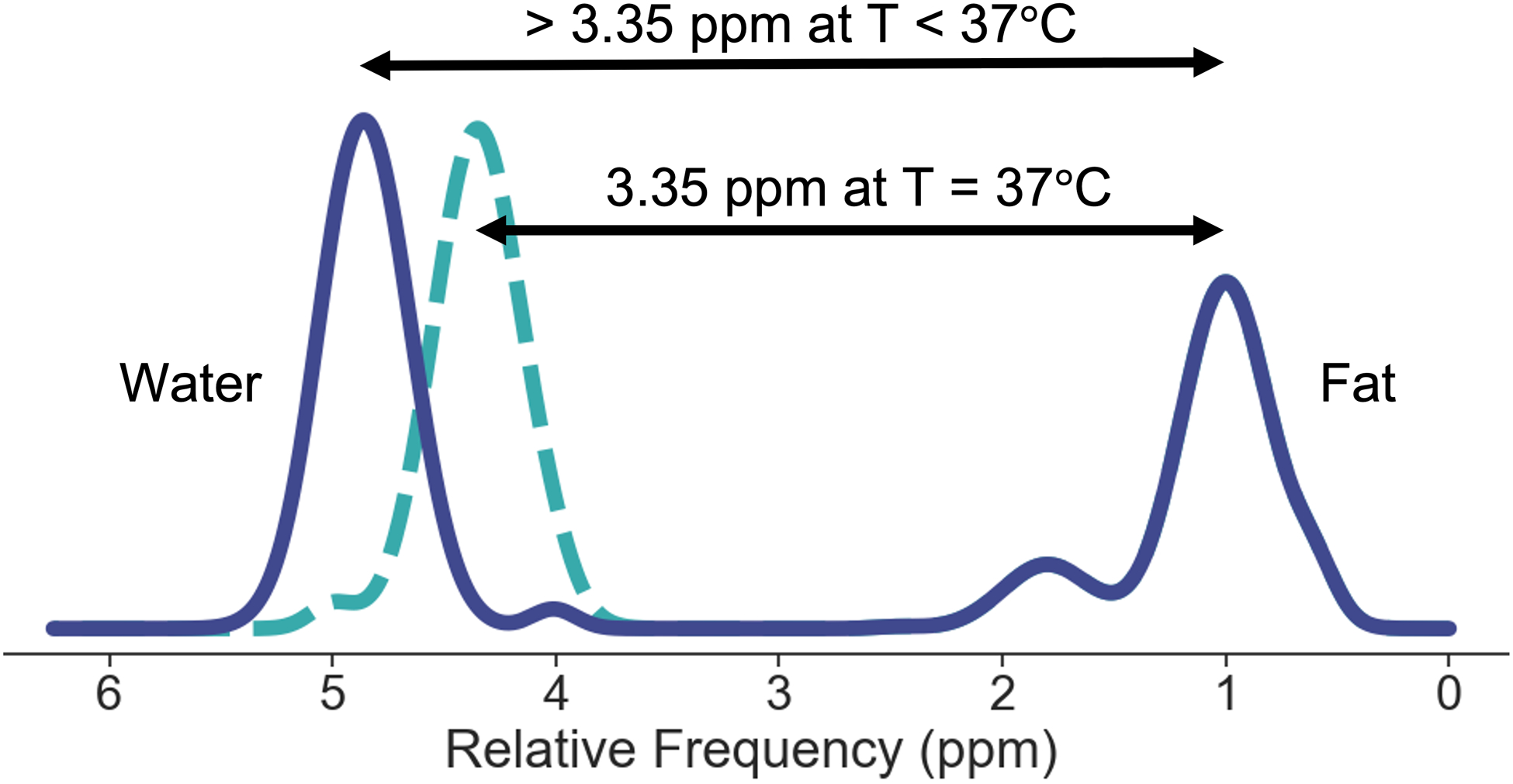
Diagram of the effect of temperature (T) on the fat-water frequency shift. At body temperature, 37°C, the fat-water frequency shift in phantoms is approximately 3.35 ppm²¹. As the temperature lowers, due to the temperature dependence of the water resonance peak and the temperature independence of the fat resonance peaks, the fat-water frequency shift increases at a rate of approximately 0.01 ppm/°C^15,17. Note that the relative amplitudes and frequencies of the fat peaks are assumed to be constant with changes in temperature.

Incorporating the effects of temperature into Eq. 1, the temperature-corrected signal²¹ can be modeled as:

$$S\left(T{E}_n\right)=\left[W{e}^{i2\pi f_{T}T{E}_n}+F{c}_N\right]e^{i2\pi f_{B}T{E}_n}{e}^{-R_2^{*}T{E}_n}$$ [6]

where f_T (Hz) is the frequency offset of water from its value at 37°C. In units of ppm, its dependence on temperature is defined as:

$$f_T=-0.01 \text{ppm/}°\text{C} \times \left(T- 37°\text{C}\right)$$ [7]

where T is the temperature (°C), and the coefficient −0.01 ppm/°C corresponds to the rate of change of the water PRF as a function of temperature^15,17. Notice that the model assumes that the spectral model of fat, including relative amplitudes and frequencies of the various fat peaks is unaffected by changes in temperature; the only change is the shift between water and fat.

If unaccounted for (Eq. 1), deviations in temperature from 37°C result in incorrect modeling of water-fat chemical shift, which can lead to bias in PDFF estimates²¹. To mitigate temperature-related PDFF bias, several approaches can be taken.

First, if the temperature of the phantom is known, the spectral model of fat relative to water can be adjusted accordingly with Eq. 6. However, measuring the temperature during an acquisition is often impractical, requires human intervention, and assumes that the measured temperature represents the actual temperature throughout the phantom and throughout the imaging experiment. Temperature can be measured using an MR-visible thermometer such as that developed by Keenan et al²⁷ instead, but only if this thermometer is available at the time of imaging.

A second approach is to estimate voxel-wise temperature, T(r), as an independent parameter when fitting the spectral model to the data:

$$\left\{\widehat{T}\left(\mathbf{r}\right),\widehat{W}\left(\mathbf{r}\right),\widehat{F}\left(\mathbf{r}\right),{\widehat{f}}_B\left(\mathbf{r}\right),{\widehat{R}}_2^{*}\left(\mathbf{r}\right)\right\}=\underset{T,W,F, f_B,R_2^{*}}{\text{argmin}} \left[\sum _{\mathbf{r}}\sum _{TE}{\left|S_{est, TE}\left(T\left(\mathbf{r}\right),W\left(\mathbf{r}\right), F\left(\mathbf{r}\right), f_B\left(\mathbf{r}\right), R_2^{*}\left(\mathbf{r}\right)\right)-S_{\mathit{\text{meas}}, TE}\right|}^2\right]$$ [8]

where r is the vector representation of the voxel location. Note that Eq. 8 makes use of complex fitting as in Eq. 3. A similar adjustment can be made for magnitude fitting as in Eq. 2. Please note that for voxels containing only water or only fat, T cannot be estimated, and the solution to this estimation problem is unstable. Even in voxels containing both fat and water, the additional degree of freedom will degrade the noise performance of the fit and introduce random error into the PDFF estimation²⁸.

Here, we propose a fully automated solution which relies on the assumption that the temperature is uniform throughout the phantom. A global temperature value, T_G, is estimated for the phantom:

$$\left\{{\widehat{T}}_G\right\}=\underset{T_G}{\text{argmin}} \left[\sum _{\mathbf{r}}\underset{W,F, f_B,R_2^{*}}{\text{argmin}} \left[\sum _{TE}{\left|S_{est, TE}\left(T_G, W\left(\mathbf{r}\right), F\left(\mathbf{r}\right), f_B\left(\mathbf{r}\right), R_2^{*}\left(\mathbf{r}\right)\right)-S_{\mathit{\text{meas}}, TE}\right|}^2\right]\right]$$ [9]

Note again that Eq. 9 makes use of complex fitting as in Eq. 3. Since the temperature of the phantom and the true PDFF is unknown, we make use of a fit error metric for determining the true phantom temperature. For various temperatures, the voxel-wise fit error, or sum of squared residuals, ${\sum }_{TE}{\left|S_{est}\left(T_G, TE\right)-S_{\mathit{\text{meas}}}\left(TE\right)\right|}^2$, can be calculated and averaged over all voxels. In the case of hybrid fitting, the voxel-wise fit error is a weighted combination of the complex voxel-wise fit error and the magnitude voxel-wise fit error using the same weights described in Eqs. 4–5. The global fit error is minimized at an input temperature equal to the global temperature of the phantom. The temperature at which fit error is minimized is subsequently used in the temperature-corrected signal model for all voxels (Eq. 6) to minimize PDFF bias.

Note that if the global temperature of the phantom is already known, then it can be directly used in the temperature-corrected signal model for temperature correction. However, using the automatically estimated temperature facilitates temperature correction regardless of whether the temperature is known or not. In this study, we evaluate temperature-related PDFF bias with simulations, temperature-controlled experiments, and a multi-center, multi-vendor phantom study. As part of the multi-center study, we compared the performance of the proposed temperature correction algorithm with a reasonable guess for room temperature, for magnitude-, complex-, and hybrid-based estimation algorithms.

METHODS:

Simulations:

The effect of using an uncorrected spectral model (Eq. 1) on PDFF bias while the true temperature deviates from the modeled temperature is studied using simulations. Noiseless multi-echo SGRE signals were simulated in digital voxels containing mixtures of water and fat, at both 1.5T and 3T assuming $R_2^{*}=40{ s}^{-1}$ and f_B = 50 Hz, with PDFF values of 0, 10, 20, 50 (%). Simulated signals were generated at temperatures over a range of 0–40°C in increments of 0.1°C. Six echoes with echo times typical for CSE-MRI PDFF estimation were used. For magnitude-based CSE-MRI simulations, an initial TE of 2.3 ms (1.15 ms) and ΔTE of 2.3 ms (1.15 ms) at 1.5T (3T) were used. For complex- and hybrid-based simulations, an initial TE of 1.0 ms (0.5 ms) and ΔTE of 1.6 ms (0.8 ms) at 1.5T (3T) were used. PDFF was quantified using magnitude (Eq. 2), complex (Eq. 3), and hybrid (Eqs. 4–5) fitting from the temperature uncorrected spectral model (Eq. 1).

Temperature-Controlled Phantom Data Acquisition:

A fat-fraction phantom was constructed according to the method of Hines et al²⁹ including 12 vials with PDFF values of 0, 4.1, 4.2, 7.6, 10.1, 14.3, 19.2, 23.3, 26.7, 35.6, 44.2, 100 (%). These values were obtained from a PDFF map generated from a high SNR, complex-based CSE-MRI image of the phantom with automated temperature-correction applied. The vials were placed in a water fill solution in a spherical housing unit (Calimetrix, Madison, WI). The phantom was imaged at 1.5T (Optima 450w, GE Healthcare, Waukesha, WI) using an 8-channel phased-array head coil, and at 3T (Signa Premier, GE Healthcare, Waukesha, WI) using a 48-channel phased-array head coil. Complex data were acquired using a 3D multi-echo SGRE acquisition (which makes use of echo times optimized for complex fitting) and magnitude data were acquired using a 2D multi-echo SGRE acquisition (which makes use of echo times optimized for magnitude fitting) similar to the protocols used in the multi-center study as described below.

All acquisitions had an echo train length of 6, 1 (2) echo train(s) at 1.5T (3T), field of view of 26×26 cm², and a matrix size of 256×256. Magnitude acquisitions had an initial TE of 1.55 ms (1.30 ms) and ΔTE of 2.61 ms (1.16 ms) at 1.5T (3T), bipolar readout, flip angle of 10°, TR of 120 ms, and a slice thickness of 6 mm. Complex acquisitions had an initial TE of 1.12 ms (1.09 ms) and ΔTE of 1.94 ms (0.88 ms) at 1.5T (3T), a monopolar readout, flip angle of 10° (3°) at 1.5T (3T), TR of 25.6 ms (7.4 ms) at 1.5T (3T), and a slice thickness of 3 mm.

At both 1.5T and 3T, 2D and 3D CSE-MRI data were acquired at three nominal temperatures: 10°C, 20°C, and 40°C. The low temperature (10°C), room temperature (20°C), and high temperature (40°C) were achieved by placing the phantom in a refrigerator, room temperature environment, and contrast agent warmer, respectively. To achieve a steady-state temperature, the phantom was kept in these environments for at least six hours prior to image acquisition. The temperature of the phantom was measured using a standard glass thermometer (Serial No. 308756, Thermco, Lafayette, NJ) inserted in the fill solution next to the vials. Temperature was measured before and after each acquisition, and then averaged to estimate the thermometer-measured temperature, T_t, during acquisition.

Multi-Center Phantom Data Acquisition:

Data acquired from a separate commercial fat-fraction phantom (Model 300, Calimetrix, Madison, WI) as part of a multi-center Quantitative Imaging Biomarkers Alliance (QIBA) study³⁰ were used for this study. The commercial fat-fraction phantom contained twelve vials with fat-water emulsions with PDFF values ranging from 0 to 100%, fixed in a spherical acrylic phantom. The vials were then immersed in a contrast-doped water fill solution to create a homogeneous magnetic field. The fill solution was additionally doped with CuSO₄ to minimize T₁ bias. A CSE-MRI-generated PDFF map showing true PDFF values labeled for the commercial phantom vials are shown in Figure 2.

Figure 2.

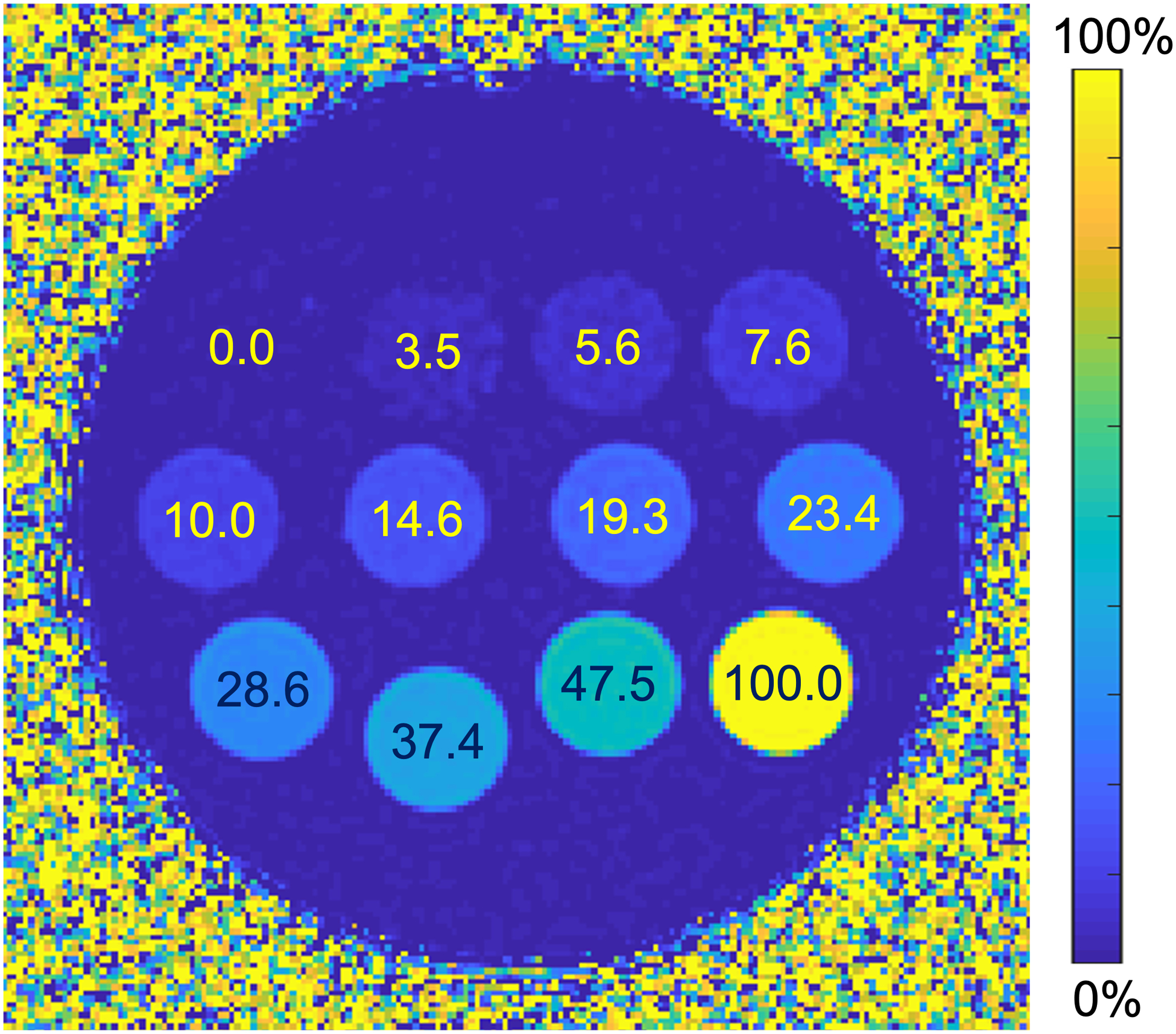
Example CSE-MRI generated PDFF map with true PDFF values labeled for each vial in the multi-center QIBA study commercial fat-fraction phantom.

The QIBA PDFF validation study³⁰ collected a total of 128 datasets (68 magnitude, 60 complex), from 26 unique MR systems (12 GE, 7 Siemens, 7 Philips), at both 1.5T (10 MR systems) and 3T (16 MR systems) at 9 sites across the United States. While there were only 26 unique MR systems, multiple CSE-MRI data sets had been collected using different protocols and during different sessions to produce the total 128 acquisitions in the multi-center study. MR systems and acquisition parameters are listed in Tables S1–S3 in Supporting Information S2. All acquisitions had been performed at the ambient room temperature after allowing at least 1 hour for the phantom to equilibrate at room temperature. No explicit temperature recording was performed as part of the multi-center study.

The CSE-MRI image data were submitted to a central data processing center not affiliated with Calimetrix, LLC or any MRI vendor. A single image analyst at the data processing center reviewed the images from each imaging center to confirm absence of gross artifacts. For both the temperature-controlled experiments and the multi-center datasets, a phase correction for multi-echo complex acquisitions was performed as described in Supporting Information S1.

Reconstruction:

For automated temperature correction in both temperature-controlled experiments and the multi-center phantom data, magnitude (Eq. 2), complex (Eq. 3), and hybrid (Eqs. 4–5) fitting was performed over a wide range of modeled temperatures (0–40°C) at increments of 1°C. PDFF maps were generated at each modeled temperature, adjusting the spectral model of fat relative to water as appropriate (Eq. 6). For each reconstructed PDFF map, voxel-wise fit error, or the sum of squared residuals, ${\sum }_{TE}{\left|S_{est}\left(T_G, TE\right)-S_{\mathit{\text{meas}}}\left(TE\right)\right|}^2$, was also measured and the average fit error over all voxels in the PDFF maps was calculated. Please note that some sites in the multi-center study placed an oil-filled bag adjacent to the phantom. As the precise type of oil, and therefore the fat spectrum, were unknown, this region of the image was cropped in these cases prior to global temperature fitting. The modeled temperature at which fit error was minimized (Eq. 9) was assumed to represent the actual global temperature and was used for subsequent temperature correction in Eq. 6, even if the actual temperature of the phantom was unknown.

Further, CSE-MRI-measured PDFF before and after correction were estimated as a means of validating the performance of the temperature correction method. Circular regions of interest (ROIs) (having approximately half the radius of a vial, corresponding to an area of 143 mm²) were centered within each of the 12 vials. The PDFF was averaged across all voxels in the vial’s ROI to quantify the average MRI PDFF in each vial. This was done on two sets of PDFF maps: (1) before temperature correction and (2) after the automated temperature correction. In the case of the multi-center study, this was also performed on PDFF maps corrected using a temperature of 20°C since all acquisitions were performed in room temperature environments.

Statistical Analysis:

To simplify the validation metric of PDFF bias for our phantoms containing multiple PDFF vials, a slope difference metric was used to compare the PDFF estimation before and after correction. In a plot of MRI PDFF vs. true PDFF, the slope is estimated using linear regression. The slope difference, defined as the difference between the slope of the identity line and the regression slope (i.e.: 1.0 – regression slope), was calculated for the uncorrected and for the corrected PDFF values. The slope difference metric was chosen since a change in temperature is assumed to maintain a similar r² in a plot of MRI PDFF vs. true PDFF but change slope.

Because of its lack of fat content, the 100% PDFF vial is expected to have no temperature-related PDFF bias, thus distorting the slope calculation. Furthermore, the 100% vial has an oversized effect on the linear regression because of its statistical leverage with respect to the other vials. Therefore, the 100% vial was excluded from the slope difference analysis.

The mean of the slope differences for all datasets in the multi-center study before and after correction were compared. Further, the standard deviation of the slope differences before and after temperature correction was calculated as a measure of reproducibility of the temperature correction method on PDFF estimation made across MRI systems. A single team member performed statistical analyses on the results. Statistical analyses were performed using Matlab (Mathworks, Natick, MA) and Python (Python Software Foundation, Beaverton, OR).

RESULTS:

Simulations:

Simulations demonstrate increasing absolute bias in PDFF with increasing temperature deviations from that presumed in the uncorrected spectral model, for magnitude-, complex-, and hybrid-based methods as shown in Figure 3. In addition, increasing absolute bias is seen as PDFF values approach 50% for magnitude and complex methods. Note that when using hybrid methods, however, the PDFF bias behavior is similar to that of complex methods at PDFFs near 50% and similar to that of magnitude methods otherwise due to how hybrid methods are defined (Eqs. 4–5). Also, especially at PDFF values approaching 50%, magnitude-based CSE-MRI has significantly greater bias than both complex and hybrid methods, with large PDFF biases approaching 5% absolute PDFF at room temperature. Since the simulations assumed noiseless signal, there is no bias at 37°C for any method.

Figure 3.

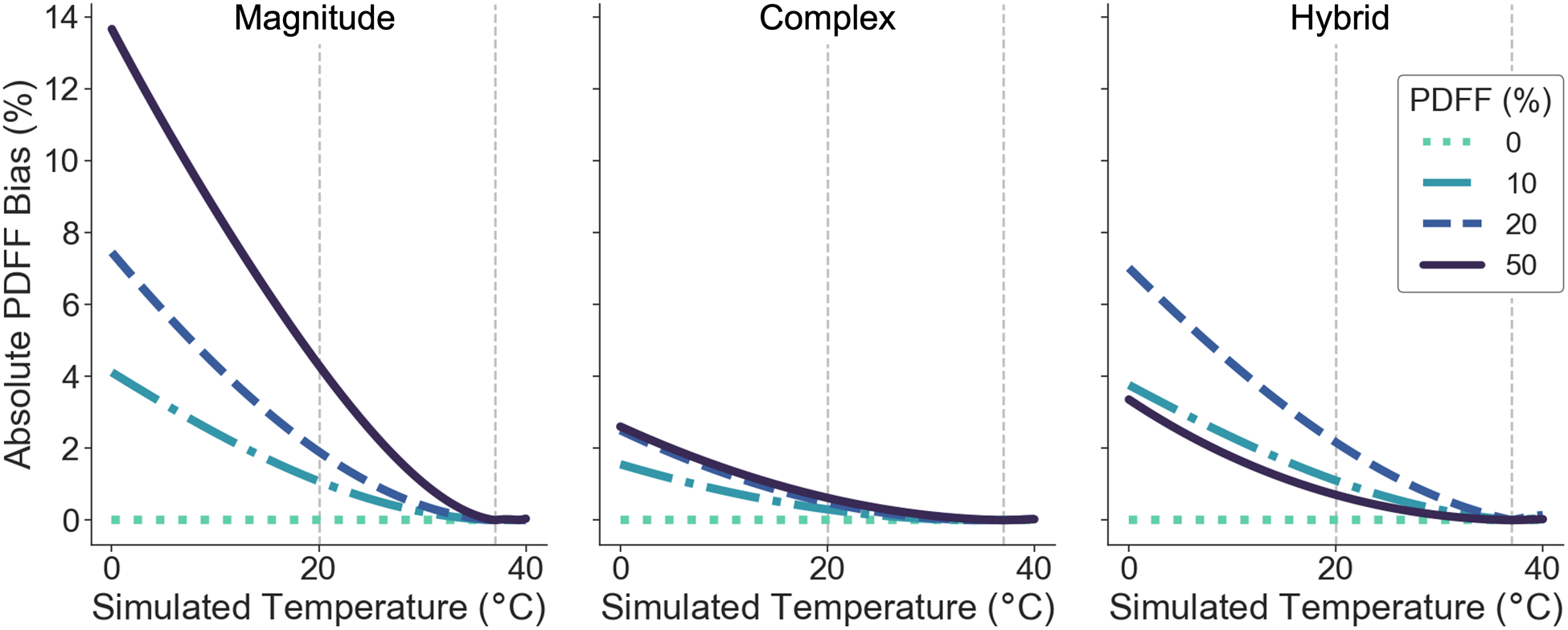
Absolute PDFF bias increases as temperature deviates further from the assumed 37°C. Simulations show absolute PDFF bias as a function of simulated temperature for four different true PDFF values with no temperature correction to the signal model (Eq. 1) at 1.5T using a) magnitude-based b) complex-based c) hybrid-based methods. Note that when using hybrid methods, the PDFF bias behavior is similar to that of complex methods at PDFFs near 50% and similar to that of magnitude methods otherwise due to how hybrid methods are defined (Eqs. 4–5).

Temperature-Controlled Phantom Experiments:

Experiments demonstrate that fit error minimizes at approximately the true temperature of the phantom as shown in Figure 4. The fit error as a function of modeled temperature of the phantom for each temperature-controlled, magnitude-based acquisition is shown. Similar results for complex and hybrid methods are shown in Figure S1 in Supporting Information S3. We note that the measured temperature, recorded before and after image acquisition, changed at most by 1°C after acquisition. The temperature averaged between these two measurements, or T_t, is shown in the figure.

Figure 4.

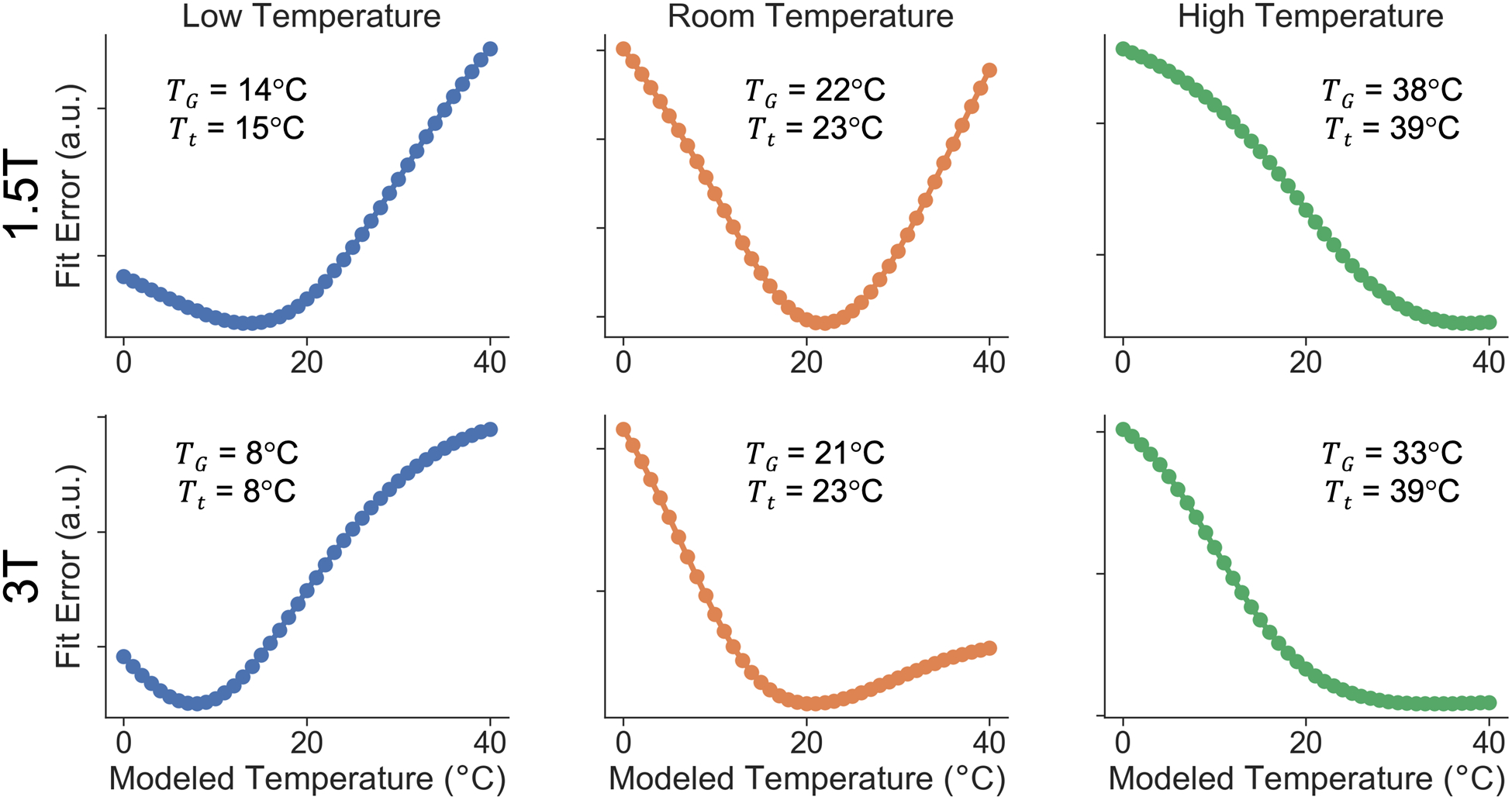
Global fit error can be used to estimate the true temperature of the phantom in order to correct for temperature-dependent errors in PDFF quantification. Fit error as a function of modeled temperature is shown in temperature-controlled experiments using two different field strengths (1.5T and 3T) at three different phantom temperatures (approximately 10°C, 20°C, 40°C) using magnitude-based methods. Global temperature at minimum fit error, T_G, and thermometer-measured phantom temperature, T_t are shown.

PDFF bias in magnitude-based CSE-MRI, as demonstrated through plots of MRI PDFF vs. true PDFF, are shown in Figure 5 for different phantom temperatures, T_t, before and after temperature correction using the automatically estimated temperature, T_G, shown in Figure 4. Similar plots for complex and hybrid methods are shown in Figure S2 in Supporting Information S3. Bias in PDFF is reduced after temperature correction, especially when the true temperature of the vials deviates further from body temperature and when using magnitude-based methods. For example, using magnitude-based methods, for the vial with a true PDFF of 44% at 3T at room temperature, before correction the PDFF bias is 11% and after correction the PDFF bias is 0.45%.

Figure 5.

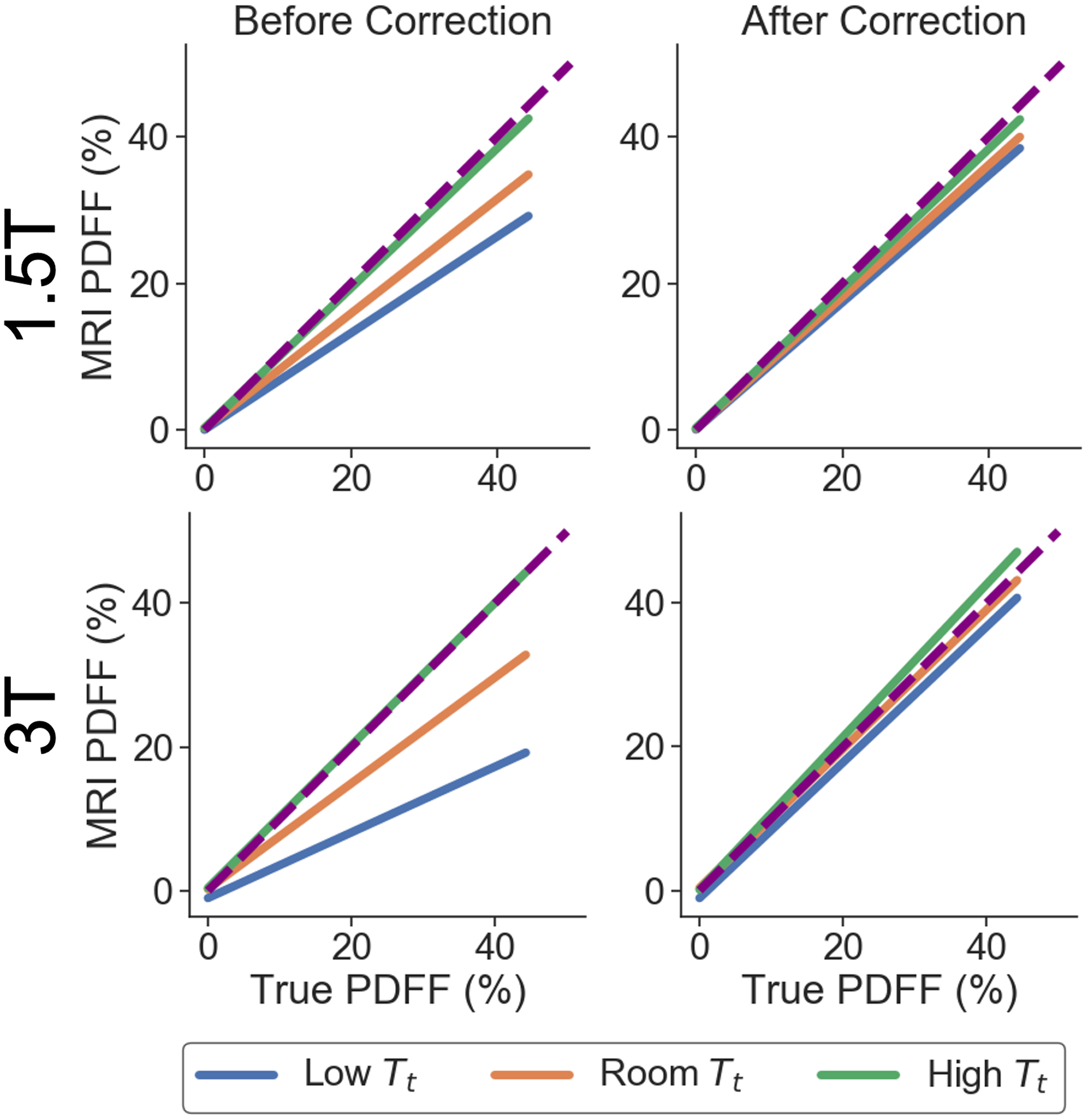
PDFF bias is reduced for all given true phantom temperatures (T_t) using the proposed temperature-correction method with T_G found in Figure 4. Linear regression plots of MRI PDFF as a function of the true PDFF are shown for the temperature-controlled experiments at 1.5T and 3T, before and after temperature correction, using magnitude-based methods. The identity line is also plotted as a dashed line.

Multi-Center Phantom Experiments:

An example of MRI PDFF vs. true PDFF is shown in Figure 6a before and after the proposed automated temperature-correction. Figure 6a demonstrates the concept of using regression slope difference before and after correction as a validation metric of the temperature-correction method. Figure 6b displays the corresponding fit error plot as a function of modeled temperature for the data set shown in Figure 6a.

Figure 6.

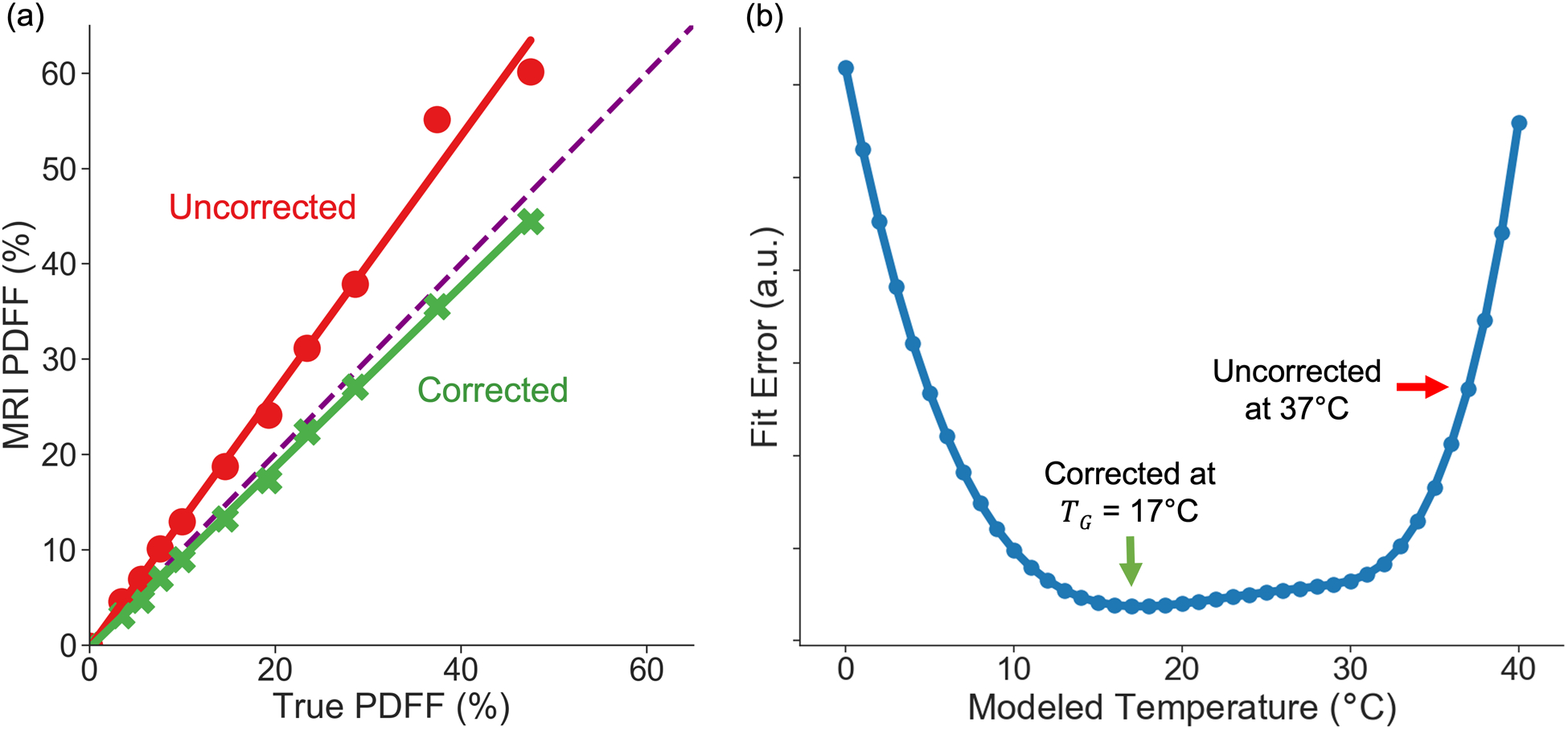
The proposed automated temperature correction method reduces slope difference. a) MRI PDFF vs. True PDFF in one example multi-center phantom acquisition. Linear regression is used to estimate the slope. The identity line is also shown as a dashed line. The corrected signal model reduces the difference in slope: identity slope (1.0) – regression slope. b) The corresponding fit error plot for the example shown in (a).

For the multi-center phantom data, temperature correction reduced overall PDFF estimation bias and variability across acquisitions, as assessed by the slope difference (Figure 7). Although the mean of the slope difference distributions did not change greatly after temperature correction, variability in slope difference did. For magnitude-based CSE-MRI, temperature correction reduced the slope difference variability from σ = 0.128 to σ = 0.027 using the assumed multi-center acquisition temperature of 20°C and σ = 0.042 using T_G. In terms of PDFF bias, in magnitude-based acquisitions, in the vial with a true PDFF of 47.5%, the temperature correction reduced absolute PDFF bias from 5.3 ± 3.6% to 1.0 ± 0.9% using the assumed multi-center acquisition temperature of 20°C and 2.4 ± 2.2% using T_G. The corrections also eliminated three outlier PDFF values (Figure 6). These outliers had suboptimal echo times (TE_init = 1.66 ms, ΔTE = 2.3 ms) for magnitude fitting, known to affect PDFF bias²¹. Similar results were observed at a trend level for complex and hybrid fitting, though these differences in mean and standard deviation were generally less.

Figure 7.

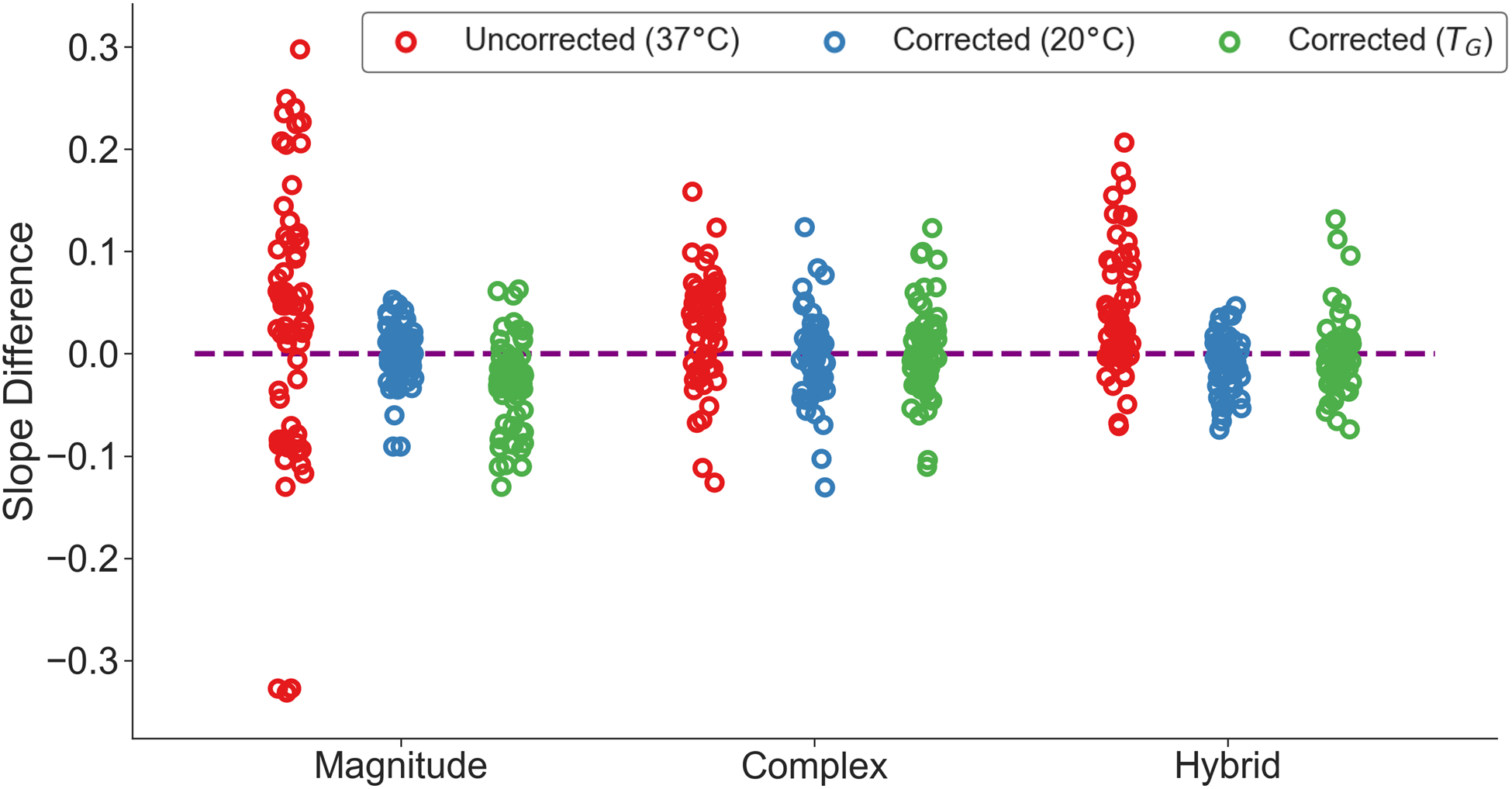
Slope differences for all scans from the QIBA study (acquired at room temperature) are reduced using a temperature-corrected (using 20°C or the automatically estimated temperature, T_G) signal model compared to the uncorrected model. The identity line is also plotted as a dashed line. The mean (μ) and standard deviation (σ) of the uncorrected and corrected slope differences are also shown. The three outliers (bottom left) in the uncorrected model in magnitude-based CSE-MRI had sub-optimal echo times (TE_init = 1.66 ms, ΔTE = 2.3 ms), where differences in echo times are known to affect PDFF bias²¹. An example of one such outlier is shown in Figure 6.

DISCUSSION:

In this work, we developed and evaluated strategies to correct for the effects of temperature through simulations, temperature-controlled experiments, and a multi-center, multi-vendor phantom study when the temperature of the phantom is unknown. Furthering the work of Hernando et al²¹, we demonstrated that significant bias in PDFF estimation can occur among multiple sites, vendors, etc., particularly using magnitude-based CSE-MRI methods. These effects increased with increasing divergence from the modeled temperature. Based on the assumption that the phantom temperature is uniform, we proposed and implemented a correction method that estimates the global temperature and subsequently corrects the multi-peak spectral model of fat relative to water. We validated the proposed method with simulations, temperature-controlled phantom experiments, and a large multi-center phantom study, using multiple vendors at 1.5T and 3T. Our results demonstrated that the proposed temperature-correction method not only reduced bias in phantom PDFF estimation, but also reduced the variability in PDFF estimates across different acquisition protocols. Similar results were observed when a reasonable guess for the ambient temperature, 20°C, was used to correct for the spectral model of fat relative to water. Our results demonstrate the importance of temperature correction in phantom imaging, particularly when using magnitude-based CSE-MRI. Similar benefits are expected for measuring PDFF in ex vivo tissue specimens, typically acquired near 0°C²², although this was not explicitly tested in this work.

Importantly, it is known that the choice of echo time has a significant impact on fat quantification errors. Some echo time combinations can result in the signal being more sensitive to temperature inaccuracies²¹. However, we note that the proposed temperature-correction method minimizes temperature-related bias, regardless of echo time combination. This feature is potentially important for improving the reproducibility of CSE-MRI in phantom/ex vivo imaging across sites that use different acquisition protocols.

The proposed method has important implications in the use of phantoms and ex vivo tissue studies with CSE-MRI, particularly for those studies using magnitude-based CSE-MRI methods. Because many currently available CSE-MRI techniques do not provide a means to correct for temperature, this could produce significant PDFF bias in phantom studies, especially in magnitude-based CSE-MRI³¹. The proposed temperature-correction method can reduce this bias in ex vivo tissue studies and in phantom studies, which are often used for clinical quality assurance, qualification for trial participation, and for drug development clinical trials that use liver PDFF as endpoints in efficacy and safety studies.

Hernando et al²¹ characterized the effect of temperature in CSE-MRI and demonstrated temperature correction via correction of the multi-peak spectral model given the actual fat-water frequency shift. While it is possible to measure the temperature of the object with a standard thermometer or heat/cool the phantom to the modeled temperature in order to correct the spectral model, this approach may be impractical in many circumstances, and requires operator input, potentially leading to further errors. Other techniques to measure the temperature of the object such as using MR-visible liquid crystal thermometers²⁷ or MR thermometry³² are possible if the operator has access to this thermometer/protocol. It is also possible to create a temperature map of the phantom by including a free parameter temperature term in the spectral model. However, this degrades SNR performance due to instability of the estimation process²⁸. Here, we have extended the work in Hernando et al by performing a multi-center, multi-vendor validation of temperature-correction of PDFF estimation and developing a global temperature-correction strategy without the need to measure temperature or the use of additional imaging protocols. Importantly, the proposed temperature-correction method is fully automated and requires no segmentation or operator input. The only assumptions are that the phantom has a uniform temperature, which can be easily achieved by allowing a phantom to equilibrate with its environment prior to imaging, and that temperature only affects the fat-water frequency shift.

If a reasonable guess of the global temperature of the phantom can be made, such as in the QIBA multi-center study shown, this provides a valid solution for temperature correction. However, using the automatically estimated temperature allows for temperature correction regardless of whether the temperature can be reasonably assumed or not. This is evidenced by the multi-center study, where both types of correction reduced PDFF bias, regardless of site, vendor, or protocol. The automated correction could especially be useful when the true temperature of the phantom or ex vivo sample cannot be reasonably guessed (e.g. using a phantom brought in from another environment or trying to perform retrospective temperature correction when the sample temperature is unknown/forgotten).

It is important to note that this method likely has negligible effects in in vivo imaging. The assumption already made in CSE-MRI PDFF estimation is the use of a multi-peak spectral model with a fat-water frequency shift at body temperature. Since the fit error plots are flat near 37°C, the proposed temperature-correction method is not likely to be accurate for in vivo temperature mapping.

Limitations of this study include the lack of phantom temperature measurements in the QIBA multi-center acquisitions. Such measurements were not feasible, however, as this would have required access of a thermometer into the interior of the commercial phantom. Measuring the room temperature at the time may have been insufficient, as the phantom is expected to heat up due to RF deposition, although this effect is likely to be small. However, the automated temperature correction inherently accounts for any changes in temperature due to RF deposition in the phantom. Also, we have shown that a reasonable global temperature guess reduces PDFF bias, suggesting that a precise measurement of temperature is not needed for correction.

After temperature correction, little PDFF bias remained for some protocols and some systems. However, we note that the degree of bias is markedly reduced. With any measurement, there is always some degree of bias, and there are other sources of bias other than temperature-related errors in the signal model. For example, complex-based CSE-MRI acquisitions using bipolar readout acquisitions require the use of phase correction methods that may not have entirely eliminated phase-related PDFF errors as described in Supporting Information S1. These remaining phase errors, which can vary significantly in multi-center studies, could result in the remaining PDFF bias. We note that other CSE-MRI reconstruction methods used to correct for the effects of eddy currents, such as mixed fitting methods³³, should also be evaluated using the proposed strategy. In addition, some T1-related PDFF bias may exist, but this bias is likely small due to the use of small flip angles in all acquisitions.

In summary, we have developed and evaluated strategies to correct for the effects of temperature on PDFF estimation through simulations, temperature-controlled experiments, and a multi-center, multi-vendor phantom study. This work demonstrates the importance of temperature-correction in phantoms via correction of the multi-peak spectral model. To correct for temperature without any a priori temperature information, we developed and validated a fully automated method using a global temperature assumption in phantoms using CSE-MRI. This strategy was very similar in performance to an approach where a reasonable guess for the a priori ambient temperature could be assumed (e.g. 20°C). However, the proposed method allows for retrospective temperature correction, even if the phantom temperature is unknown, and reduces both temperature-related PDFF bias and variability, especially in magnitude-based CSE-MRI. This work may have important implications for phantom and ex vivo studies, including quality assurance for multi-center clinical drug development studies that rely on phantoms for assuring data integrity.

Supplementary Material

Figure S1a

Figure S1. Global fit error can be used to estimate the true temperature of the phantom in order to correct for temperature-dependent errors in PDFF quantification. Fit error as a function of modeled temperature is shown in temperature-controlled experiments using two different field strengths (1.5T and 3T) at three different phantom temperatures (approximately 10°C, 20°C, 40°C) using a) magnitude-based b) complex-based c) hybrid-based methods. Global temperature at minimum fit error, T_G, and thermometer-measured phantom temperature, T_t are shown.

Figure S2

Figure S2. PDFF bias is reduced for all given true phantom temperatures (T_t) using the proposed temperature-correction method with T_G found in Figure S1. Linear regression plots of MRI PDFF as a function of the true PDFF are shown for the temperature-controlled experiments at 1.5T and 3T, before and after temperature correction, using magnitude-based, complex-based, and hybrid-based methods. The identity line is also plotted as a dashed line.

Supporting Information

Table S1: List of unique MR systems used in the multi-center study.

Table S2: All unique magnitude-based CSE-MRI protocols used in the multi-center study. Some protocols were performed multiple times to produce the total 68 magnitude-based CSE-MRI acquisitions. For all acquisitions, vials were oriented along B₀ and a multi-echo spoiled gradient echo was used. Details of the MR systems are listed in Table S1. Abbreviations: ETL = echo train length, TE = echo time, TR = repetition time, FOV = field of view.

Table S3: All complex-based CSE-MRI protocols used in the multi-center study. Some protocols were performed multiple times to produce the total 60 complex-based CSE-MRI acquisitions. For all acquisitions, vials were oriented along B₀ and a multi-echo spoiled gradient echo was used. Details of the MR systems are listed in Table S1. Abbreviations: ETL = echo train length, TE = echo time, TR = repetition time, FOV = field of view.