A fairer way to compare researchers at any career stage and in any discipline using open-access citation data

Corey J A Bradshaw; Justin M Chalker; Stefani A Crabtree; Bart A Eijkelkamp; John A Long; Justine R Smith; Kate Trinajstic; Vera Weisbecker

doi:10.1371/journal.pone.0257141

. 2021 Sep 10;16(9):e0257141. doi: 10.1371/journal.pone.0257141

A fairer way to compare researchers at any career stage and in any discipline using open-access citation data

Corey J A Bradshaw ^1,^2,^*, Justin M Chalker ³, Stefani A Crabtree ^4,^5,⁶, Bart A Eijkelkamp ⁷, John A Long ⁷, Justine R Smith ⁸, Kate Trinajstic ⁹, Vera Weisbecker ^2,⁷

Editor: Sergi Lozano¹⁰

PMCID: PMC8432834 PMID: 34506560

Abstract

The pursuit of simple, yet fair, unbiased, and objective measures of researcher performance has occupied bibliometricians and the research community as a whole for decades. However, despite the diversity of available metrics, most are either complex to calculate or not readily applied in the most common assessment exercises (e.g., grant assessment, job applications). The ubiquity of metrics like the h-index (h papers with at least h citations) and its time-corrected variant, the m-quotient (h-index ÷ number of years publishing) therefore reflect the ease of use rather than their capacity to differentiate researchers fairly among disciplines, career stage, or gender. We address this problem here by defining an easily calculated index based on publicly available citation data (Google Scholar) that corrects for most biases and allows assessors to compare researchers at any stage of their career and from any discipline on the same scale. Our ε′-index violates fewer statistical assumptions relative to other metrics when comparing groups of researchers, and can be easily modified to remove inherent gender biases in citation data. We demonstrate the utility of the ε′-index using a sample of 480 researchers with Google Scholar profiles, stratified evenly into eight disciplines (archaeology, chemistry, ecology, evolution and development, geology, microbiology, ophthalmology, palaeontology), three career stages (early, mid-, late-career), and two genders. We advocate the use of the ε′-index whenever assessors must compare research performance among researchers of different backgrounds, but emphasize that no single index should be used exclusively to rank researcher capability.

Introduction

Deriving a fair, unbiased, and easily generated quantitative index serving as a reasonable first-pass metric for comparing the relative performance of academic researchers is—by the very complexity, diversity, and intangibility of research output across academic disciplines—impossible [1]. However, that unachievable aim has not discouraged bibliometricians and non-bibliometricians alike from developing scores of citation-based variants [2–4] in an attempt to do exactly that, from the better-known h-index [5, 6] (h papers with at least h citations), m-quotient [5, 6] (h-index ÷ number of years publishing), and g-index [7] (unique largest number such that the top g papers decreasingly ordered by citations have least g² citations), to the scores of variants of these and other indices—e.g., h²-index, e-index [8], χ-index [9], h_m-index [10], g_m-index [11], etc. [3]. Each metric has its own biases and strengths [12–14], suggesting that several should be used simultaneously to assess citation performance. For example, the arguably most-popular h-index down-weights quality relative to quantity [15], ignores the majority of accumulated citations in the most highly cited papers [16], has markedly different distributions among disciplines [17], and tends to increase with experience [18]. As such, It has been argued that the h-index should not be considered for ranking a scientist’s overall impact [19]. The h-index can even rise following the death of the researcher, because the h-index can never decline [2] and citations can continue to accumulate posthumously.

Despite their broad use for inter alia assessing candidates applying for academic positions, comparing the track records of researchers applying for grants, to applications for promotion [3, 20], single-value citation metrics are rarely meant to (nor should they) be definitive assessment tools [3]. Instead, their most valuable (and fairest) application is to provide a quick ‘first pass’ to rank a sample of researchers, followed by more detailed assessment of publication quality, experience, grant successes, mentorship, collegiality and all the other characteristics that make a researcher more or less competitive for rare positions and grant monies. But despite the many different metrics available and arguable improvements that have been proposed since 2005 when the h-index was first developed [5, 6], few are used regularly in these regards. This is because they are difficult to calculate without detailed data of a candidate’s publication history, they are not readily available on open-access websites, and/or they tend to be highly correlated with the h-index anyway [21]. It is for these reasons that the admittedly flawed [19, 22, 23] h-index and its experienced-corrected variant, the m-quotient, are still the dominant (h-index much more so than the m-quotient) [2] metrics employed given that they are easily calculated [2, 24] and found for most researchers on open-access websites such as Google Scholar [25] (scholar.google.com). The lack of access and detailed understanding of the many other citation-based metrics mean that most of them go unused [3], and are essentially valueless for every-day applications of researcher assessment.

The specific weaknesses of the h-index or m-quotient make the comparison of researchers in different career stages, genders, and disciplines unfair because they are not normalized in any way. Furthermore, there is no quantitatively supported threshold above or below which assessors can easily ascertain minimum citation performance for particular applications—while assessors certainly use subjective ‘rules of thumb’, a more objective approach is preferable. For this reason, an ideal citation-based metric should only be considered as a relative index of performance, but relative to what, and to whom?

To address these issues and to provide assessors with an easy, rapid, yet objective relative index of citation performance for any group of researchers, we designed a new index we call the ‘ε-index’ (the ‘ε’ signifies the use of residuals, or deviance from a trend) that is simple to construct, can be standardized across disciplines, is meaningful only as a relative index for a particular sample of researchers, can be corrected for career breaks (see Methods), and provides a sample-specific threshold above and below which assessors can determine whether individual performance is greater or less than that expected relative to the other researchers in the specific sample.

With the R code and online app we provide, an assessor need only acquire four separate items of information from Google Scholar (or if they have access, from other databases such as Scopus—scopus.com) to calculate a researcher’s ε-index: (i) the number of citations acquired for the researcher’s top-cited paper (i.e., the first entry in the Google Scholar profile), (ii) the i10-index (number of articles with at least 10 citations), (iii) the h-index, and (iv) the year in which the researcher’s first peer-reviewed paper was published. While the last item requires sorting a researcher’s outputs by year and scrolling to the earliest paper, this is not a time-consuming process. We demonstrate the performance of the ε-index using Google Scholar citation data we collected for 480 researchers in eight separate disciplines spread equally across genders and career stages to show how the ε-index performs relative to the m-quotient (the only other readily available, opportunity-corrected citation index available on Google Scholar) across disciplines, career stages, and genders. We also provide a simple method to scale the index across disciplines (ε′-index) to make researchers in different areas comparable despite variable citation trends within their respective areas.

Materials and methods

Researcher samples

Each co-author assembled an example set of researchers from within her/his field, which we broadly defined as archaeology (S.A.C.), chemistry (J.M.C.), ecology (C.J.A.B.), evolution/development (V.W.), geology (K.T.), microbiology (B.A.E.), ophthalmology (J.R.S.), and palaeontology (J.A.L.). Our basic assembly rules for each of these discipline samples were: (i) 20 researchers from each stage of career, defined here arbitrarily as early career (0–10 years since first peer-reviewed article published in a recognized scientific journal), mid-career (11–20 years since first publication), and late career (> 20 years since first publication); each discipline therefore had a total of 60 researchers, for a total sample of 8 × 60 = 480 researchers across all sampled disciplines. (ii) Each sample had to include an equal number of women and men from each career stage. (iii) Each researcher had to have a unique, publicly accessible Google Scholar profile with no obvious errors, inappropriate additions, obvious omissions, or duplications. The entire approach we present here assumes that each researcher’s Google Scholar profile is accurate, up-to-date, and complete.

We did not impose any other rules for sample assembly, but encouraged each compiler to include only a few previous co-authors. Our goal was to have as much ‘inside knowledge’ as possible with respect to each discipline, but also to include a wide array of researchers who were predominantly independent of each of us. The composition of each sample is somewhat irrelevant for the purposes of our example dataset; we merely attempted gender and career-level balance to show the properties of the ranking system (i.e., we did not intend for sampling to be a definitive comment about the performance of particular researchers, nor did we mean for each sample to represent an entire discipline). Finally, we completely anonymized the sample data for publication.

Citation data

Our overall aim was to provide a meaningful and objective method for ranking researchers by citation history without requiring extensive online researching or information that was not easily obtainable from a publicly available, online profile. We also wanted to avoid an index that was overly influenced by outlier citations, while still keeping valuable performance information regarding high-citation outputs and total productivity (number of outputs).

For each researcher, the algorithm requires the following information collected from Google Scholar: (i) i10-index (the number of publications in the researcher’s profile with at least 10 citations, which we denoted i₁₀); one condition is that a researcher must have i₁₀ ≥ 1 for the algorithm to function correctly; (ii) h-index—the researcher’s Hirsch number [5]: the number of publications with at least as many citations, which we denoted h; (iii) the number of citations for the researcher’s most highly cited paper (denoted c_m); and (iv) the year the researcher published her/his first peer-reviewed article in a recognized scientific journal (denoted Y₁). For the designation of Y₁, we excluded any reports, chapters, books, theses or other forms of publication that preceded the year of the first peer-reviewed article; however, we included citations from the former sources in the researcher’s i₁₀, h, and c_m.

Ranking algorithm

The algorithm first computes a power-law-like relationship between the vector of frequencies (as measured from Google Scholar): i₁₀, h, and 1, and the vector of their corresponding values: 10, h, and c_m, respectively. Thus, h is, by definition, both a frequency (y-axis) and value (x-axis). We then calculated a simple linear model of the form y ~ α + βx, where

y = \log_{e} [\begin{matrix} i_{10} \\ h \\ 1 \end{matrix}] and x = \log_{e} [\begin{matrix} 10 \\ h \\ c_{m} \end{matrix}]

(y is the citation frequency, and x is the citation value) for each researcher (S1 Fig). The corresponding $\hat{α}$ and $\hat{β}$ for each relationship allowed us to calculate a standardized integral (area under the power-law relationship, A_rel) relative to the researcher in the sample with the highest c_m. Here, the sum of the predicted y derived from incrementing values of x (here in units of 0.05) using $\hat{α}$ and $\hat{β}$ is divided by the product of c_m and the number of incremental x values. This implies all areas were scaled to the maximum in the sample, but avoids the problem of truncating variances near a maximum of 1 had we used the maximum area among all researchers in the sample as the denominator in the standardization procedure.

A researcher’s A_rel therefore represents her/his citation mass, but this value still requires correction for individual opportunity (time since first publication, t = current year–Y₁) to compare researchers at different stages of their career. This is where career gaps can be taken into account explicitly for any researcher in the sample by subtracting a_i = the total cumulative time absent from research (e.g., maternity or paternity leave, sick leave, secondment, etc.) for individual i from t, such that an individual’s career gap-corrected $t_{i}^{'} = t_{i} - a_{i}$ . We therefore constructed another linear model of the form A_rel ~ γ + θlog_et across all researchers in the sample, and took the residual (ε) of an individual researcher’s A_rel from the predicted relationship as a metric of citation performance relative to the rest of the researchers in that sample (S2 Fig). This residual ε allows us to rank all individuals in the sample from highest (highest citation performance relative to opportunity and the entire sample) to lowest (lowest citation performance relative to opportunity and the entire sample). Any researcher in the sample with a positive ε is considered to be performing above expectation (relative to the group and the time since first publication), and those with a negative ε fall below expectation. This approach also has the advantage of fitting different linear models to subcategories within a sample to rank researchers within their respective groupings (e.g., such as by gender; S3 Fig). An R code function to produce the index and its variants using a sample dataset is available from github.com/cjabradshaw/EpsilonIndex.

Discipline standardization

Each sampled discipline has its own citation characteristics and trends [17], so we expect that the distribution of residuals (ε) within each discipline to be meaningful only for that discipline’s sample. We therefore endeavoured to scale (‘normalize’) the results such that researchers in different disciplines could be compared objectively and more fairly.

We first scaled the A_rel within each discipline by dividing each i researcher’s A_rel by the sample’s root mean square:

A_{{rel}_{i}}^{'} = \frac{A_{{rel}_{i}}}{\sqrt{\frac{\sum_{i = 1}^{n} A_{{rel}_{i}}}{n - 1}}}

where n = the total number of researchers in the sample (n = 60). We then regressed these discipline-scaled $A_{rel}^{'}$ against the log_e number of years since first publication pooling all sampled disciplines together, and then ranked these scaled residuals (ε′) as described above. Comparison between disciplines is only meaningful when a sufficient sample of researchers from within specific disciplines first have their ε calculated (i.e., discipline-specific ε), and then each discipline sample undergoes the standardization to create ε′. Then, any sample of researchers from any discipline can be compared directly.

Results

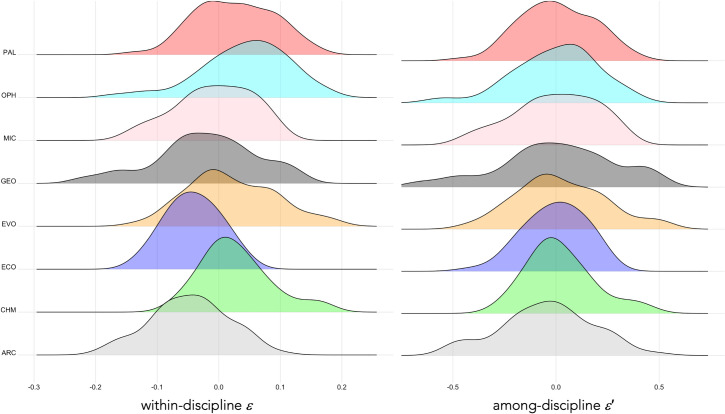
Despite the considerable variation in citation metrics among researchers and disciplines, there was broad consistency in the strength of the relationships between citation mass (A_rel) and log_e years publishing (t) across disciplines (Fig 1), although the geology (GEO) sample had the poorest fit (^ALLR² = 0.43; Fig 1). The distribution of residuals ε for each discipline revealed substantial difference in general form and central tendency (Fig 2), but after scaling, the distributions of ε′ became aligned among disciplines and were approximately Gaussian (Shapiro-Wilk normality tests; see Fig 2 for test values).

Fig 1 — Relationship between a researcher’s citation mass (A_rel; area under the citation frequency–value curve—see S2 Fig) and log_e years (t) since first peer-reviewed publication (Y₁) for eight disciplines (ARC = archaeology, CHM = chemistry, ECO = ecology, EVO = evolution and development, GEO = geology, MIC = microbiology, OPH = ophthalmology, PAL = palaeontology) comprising 60 researchers each (30 ♀, 30 ♂) in three different career stages: Early career researcher (ECR), mid-career researcher (MCR), and late career researcher (LCR). The fitted lines correspond to the entire sample (solid black), women only (dashed black), and men only (dashed red). Information-theoretic evidence ratios for all relationships > 180; adjusted R² for each relationship shown in each panel.

Fig 2 — Left panel: Distribution of within-discipline residuals (ε) of the relationship between A_rel and log_e years publishing (t) by discipline (ARC = archaeology, CHM = chemistry, ECO = ecology, EVO = evolution and development, GEO = geology, MIC = microbiology, OPH = ophthalmology, PAL = palaeontology), each comprising 60 researchers (30 ♀, 30 ♂). Right panel: Distribution of among-discipline residuals (ε′) of the relationship between $A_{rel}^{'}$ (scaled) and t by discipline. All $A_{rel}^{'}$ distributions are approximately Gaussian according to Shapiro-Wilk normality tests (ARC: W = 0.985, p = 0.684; CHM: W = 0.961, p = 0.051; ECO: W = 0.980, p = 0.409; EVO: W = 0.984, p = 0.630; GEO: W = 0.929, p = 0.398; MIC: W = 0.971, p = 0.170; OPH: W = 0.980, p = 0.416; PAL: W = 0.986, p = 0.720).

After scaling (Fig 3A), the relationship between ε′ and the m-quotient is non-linear and highly variable (Fig 3B), meaning that m-quotients often poorly reflect actual relative performance (and despite the m-quotient already being ‘corrected’ for t, it still increases with t; S4 Fig). For example, there are many researchers whose m-quotient < 1, but who perform above expectation (ε′ > 0). Alternatively, there are many researchers with an m-quotient of up to 2 or even 3 who perform below expectation (ε′ < 0). Once the m-quotient > 3, ε′ reflects above-expectation performance for all researchers in the example sample (Fig 3B). The corresponding ε′ indicate a more uniform spread by gender and career stage (Fig 3C) than do m-quotients (Fig 3D). Further, the relationship between h-index and t (from which the m-quotient is derived is neither homoscedastic nor Normal (S5–S12 Figs). Another advantage of ε′ versus the m-quotient is that the former has a threshold (ε′ = 0) above which researchers perform above expectation and below which they perform below expectation, whereas the m-quotient has no equivalent threshold. Further, the m-quotient tends to increase through one’s career, whereas ε′ is more stable. There is still an increase in ε′ during late career relative to mid-career, but this is less pronounced that that observed for the m-quotient (Fig 4).

Fig 4 — Violin plots of scaled residuals (ε′) and m-quotient across all eight disciplines relative to career stage (ECR = early career; MCR = mid-career; LCR = late career). Treating career stage as an integer in a linear model shows no difference among stages for ε′ (p = 0.205), but there is evidence for a career stage effect for the m-quotient (p = 0.000073). Likewise, treating career stage as an ordinal factor (ECR < MCR < LCR) in a linear model shows no difference among stages for ε′ (MCR: p = 0.975; LCR: p = 0.205), but there is evidence for a divergence of LCR for the m-quotient (MCR: p = 0.388; LCR: p = 0.000072).

Examining the ranks derived from ε′ across disciplines, genders and career stage (Fig 5), bootstrapped median ranks overlap for all sampled disciplines (Fig 5A), but there are some notable divergences between the genders across career stage (Fig 5B). In general, women ranked slightly below men in all career stages, although the bootstrapped median ranks overlap among early and mid-career researchers. However, the median ranks for late-career women and men do not overlap (Fig 5B), which possibly reflects the observation that senior academic positions in many disciplines are dominated by men [26–28], and that women tend to receive fewer citations than men at least in some disciplines, which often tends to compound over time [29–32]. The ranking based on the m-quotient demonstrates the disparity among disciplines (Fig 5C), but it is perhaps somewhat more equal between the genders (Fig 5D) compared to the ε′ rank (Fig 5B), despite the higher variability of the m-quotient bootstrapped median rank.

However, calculating the scaled residuals across all sampled disciplines for each gender separately, and then combining the two datasets and recalculating the rank (producing a gender-‘debiased’ rank) effectively removed the gender differences (Fig 6).

Fig 6 — (a) Bootstrapped (10,000 iterations) ε′ ranks by gender and career stage (ECR = early career researcher, MCR = mid-career researcher, LCR = late-career researcher); (b) bootstrapped debiased (i.e., calculating the scaled residuals for each gender separately, and then ranking the combined dataset) ε′ ranks by gender and career stage.

Discussion

Todeschini and Baccini [33] recommended that the ideal author-level indicator of citation performance should (i) have an unequivocal mathematical definition, (ii) be easily computed from available data (for a detailed breakdown of implementation steps and the R code function, see github.com/cjabradshaw/EpsilonIndex; we have also provided a user-friendly app available at cjabradshaw.shinyapps.io/epsilonIndex that implements the code and calculates the index with user-provided citation data), (iii) balance rankings between more experienced and novice researchers (iv) while preserving sensitivity to the performance of top researchers, and (iv) be sensitive to the number and distribution of citations and articles. Our new ε-index not only meets these criteria, it also adds the ability to compare across disciplines by using a simple scaling approach, and can easily be adjusted for career gaps by subtracting research-inactive periods from the total number of years publishing (t). In this way, the ε-index could prove invaluable as we move toward greater interdisciplinarity, where tenure committees have had difficulty assessing the performance of candidates straddling disciplines [34, 35]. The ε-index does not ignore high-citation papers, but neither does it overemphasize them, and it includes an element of publication frequency (i₁₀) while simultaneously incorporating an element of ‘quality’ by including the h-index.

Like all other existing metrics, the ε-index does have some disadvantages in terms of not correcting for author contribution—such as the h_m-index [10] or g_m-index [11]—even though these types of metrics can be cumbersome to calculate. Early career researchers who have published but have yet to be cited will not yet be able to calculate their ε-index, as they will not have an h-index score, so would require different types of assessment. Another potential limitation is that the ε-index alone does not correct for any systemic gender biases associated with the many reasons why women tend to be cited less than men [26–32, 36], but it does easily allow an assessor to benchmark any subset of researchers (e.g., women-only or men-only) to adjust the threshold accordingly. Thus, women can be compared to other women and ranked accordingly such that the ranks are more comparable between these two genders. Alternatively, dividing the genders and benchmarking them separately followed by a combined re-ranking (Fig 6) effectively removes the gender bias in the ε-index, which is difficult or impossible to do with other ranking metrics. We certainly advocate this approach when assessing mixed-gender samples (the same approach could be applied to other subsets of researchers deemed a priori to be at a disadvantage).

The ε-index also potentially suffers from the requirement of the constituent citation data upon which it is based being accurate and up-to-date [37, 38]. It is therefore important that users correct for obvious errors when compiling the four required data to calculate the ε-index (i₁₀, h-index, c_m, t). This could include corrections for misattributed articles, start year, or even i₁₀. In some cases, poorly maintained Google Scholar profiles might exclude certain researchers from comparative samples. Regardless, should an assessor have access to potentially more rigorous citation databases (e.g., Scopus), the ε-index can still be readily calculated, although within-sample consistency must be maintained for the ranks to be meaningful. Nonetheless, because the index is relative and scaled, the relative rankings of researchers should be maintained irrespective of the underlying database consulted to derive the input data. We also show that the distribution of the ε-index is relatively more Gaussian and homoscedastic than the time-corrected m-quotient, with the added advantage of identifying a threshold above and below which individuals are deemed to be performing better or worse than expected relative to their sample peers. While there are potentially subjective rules of thumb for thresholds to be applied to the m-quotient, the residual nature of the ε-index makes it a more objective metric for assessing relative rank, and the ε-index is less-sensitive than the m-quotient regarding the innate rise of ranking as a researcher progresses through her/his career (Fig 4).

We reiterate that while the ε-index is an advance on existing approaches to rank researchers according to their citation history, a single metric should never be the sole measure of a researcher’s productivity or potential [39]. Nonetheless, the objectivity, ease of calculation, and flexibility of its application argue that the ε-index is a needed tool in the quest to provide fairer and more responsible [39, 40] initial appraisals of a researcher’s publication performance.

Supporting information

S1 Fig. Citation frequency versus citation value.

Relationship between log_e citation frequency (y) and log_e citation value (x) for 60 researchers within the discipline of ophthalmology. Each light grey, dashed line is the linear (on the log_e-log_e scale) fit for each individual researcher. The area under the fitted line (A_rel) is shown for individual 32 (ID32; red horizontal hatch) and individual 27 (orange vertical hatch).

(TIF)

Click here for additional data file.^{(3.4MB, tif)}

S2 Fig. Example citation mass relative to years since first publication.

Relationship between a researcher’s citation mass (A_rel; area under the citation frequency–value curve—see S1 Fig) and log_e years since first peer-reviewed publication (Y₁) for an example sample of 60 microbiology researchers in three different career stages: early career researcher (ECR), mid-career researcher (MCR), and late-career researcher (LCR). The residuals (ε) for each researcher relative to the line of best fit (solid black line) indicate relative citation rank—researchers below this line perform below expectation (relative to the sample), those above, above expectation. Also shown are the lines of best fit for women (black dashed line) and men (red dashed line—see also S3 Fig). Here we have also selected two researchers at random (1 female, 1 male) from each career stage and shown their results in the inset table. The residuals (ε) provide a relative rank from most positive to most negative. Also shown is each of these six researchers’ m-quotient (h-index ÷ number of years publishing).

(TIF)

Click here for additional data file.^{(1.1MB, tif)}

S3 Fig. Gender-specific rankings.

Gender-specific researcher ranks versus ranks derived from the entire sample (in this case, the microbiology sample shown in S2 Fig). For women who increased ranks when only compared to other women (negative residuals; top panel), the average increase was 1.50 places higher. For women with reduced ranks (positive residuals; top panel), the average was 1.88 places lower. For men who increased ranks when only compared to other men (negative residuals; bottom panel), or who declined in rank (positive residuals; bottom panel), the average number of places moved were both 1.75 for both.

(TIF)

Click here for additional data file.^{(4.2MB, tif)}

S4 Fig. m-quotient relative to years since first publication.

Relationship between the m-quotient and log_e years publishing (t) for 480 researchers in eight different disciplines. There is a weak, but statistically supported positive relationship (information-theoretic evidence ratio = 68.7).

(TIF)

Click here for additional data file.^{(631.9KB, tif)}

S5 Fig. Normality and homoscedasticity diagnostics for the archaeology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of archaeology (ARC). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.1MB, tif)}

S6 Fig. Normality and homoscedasticity diagnostics for the chemistry sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of chemistry (CHM). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.8MB, tif)}

S7 Fig. Normality and homoscedasticity diagnostics for the ecology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of ecology (ECO). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.6MB, tif)}

S8 Fig. Normality and homoscedasticity diagnostics for the evolution/development sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of evolution and development (EVO). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.7MB, tif)}

S9 Fig. Normality and homoscedasticity diagnostics for the geology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of geology (GEO). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.7MB, tif)}

S10 Fig. Normality and homoscedasticity diagnostics for the microbiology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of microbiology (MIC). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.4MB, tif)}

S11 Fig. Normality and homoscedasticity diagnostics for the ophthalmology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of ophthalmology (OPH). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.7MB, tif)}

S12 Fig. Normality and homoscedasticity diagnostics for the palaeontology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of palaeontology (PAL). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.6MB, tif)}

Acknowledgments

We acknowledge our many peers for their stewardship of their online citation records. We acknowledge the Indigenous Traditional Owners of the land on which Flinders University is built—the Kaurna people of the Adelaide Plains.

Data Availability

Example code and data to calculate the index are available at: github.com/cjabradshaw/EpsilonIndex. A R Shiny application is also available at: cjabradshaw.shinyapps.io/epsilonIndex, with its relevant code and example dataset available at: github.com/cjabradshaw/EpsilonIndexShiny.

Funding Statement

The authors received no specific funding for this work.

References

1.Phelan TJ. A compendium of issues for citation analysis. Scientometrics. 1999;45(1):117–36. doi: 10.1007/BF02458472 [DOI] [Google Scholar]
2.Barnes C. The h-index debate: an introduction for librarians. J Acad Libr. 2017;43(6):487–94. doi: 10.1016/j.acalib.2017.08.013 [DOI] [Google Scholar]
3.Wildgaard L. An overview of author-level indicators of research performance. In: Glänzel W, Moed HF, Schmoch U, Thelwall M, editors. Springer Handbook of Science and Technology Indicators. Cham: Springer International Publishing; 2019. p. 361–96. [Google Scholar]
4.Egghe L. The Hirsch index and related impact measures. Ann Rev Inf Sci Tech. 2010;44(1):65–114. doi: 10.1002/aris.2010.1440440109 [DOI] [Google Scholar]
5.Hirsch JE. An index to quantify an individual’s scientific research output. Proc Natl Acad Sci USA. 2005;102(46):16569–72. doi: 10.1073/pnas.0507655102 [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Schubert A, Schubert G. All along the h-index-related literature: a guided tour. In: Glänzel W, Moed HF, Schmoch U, Thelwall M, editors. Springer Handbook of Science and Technology Indicators. Cham: Springer International Publishing; 2019. p. 301–34. [Google Scholar]
7.Egghe L. How to improve the h-index. The Scientist. 2006;20(3):15. [Google Scholar]
8.Zhang C-T. The e-Index, complementing the h-Index for excess citations. PLoS One. 2009;4(5):e5429. doi: 10.1371/journal.pone.0005429 [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Fenner T, Harris M, Levene M, Bar-Ilan J. A novel bibliometric index with a simple geometric interpretation. PLoS One. 2018;13(7):e0200098. doi: 10.1371/journal.pone.0200098 [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Schreiber M. A modification of the h-index: The h_m-index accounts for multi-authored manuscripts. J Informetr. 2008;2(3):211–6. doi: 10.1016/j.joi.2008.05.001 [DOI] [Google Scholar]
11.Schreiber M. How to modify the g-index for multi-authored manuscripts. J Informetr. 2010;4(1):42–54. doi: 10.1016/j.joi.2009.06.003 [DOI] [Google Scholar]
12.Thompson DF, Callen EC, Nahata MC. New indices in scholarship assessment. Am J Pharm Educ. 2009;73(6):111. doi: 10.5688/aj7306111 [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Bornmann L, Mutz R, Daniel H-D. Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. J Am Soc Inf Sci Tech. 2008;59(5):830–7. doi: 10.1002/asi.20806 [DOI] [Google Scholar]
14.Bornmann L, Mutz R, Hug SE, Daniel H-D. A multilevel meta-analysis of studies reporting correlations between the h index and 37 different h index variants. J Informetr. 2011;5(3):346–59. doi: 10.1016/j.joi.2011.01.006 [DOI] [Google Scholar]
15.Costas R, Bordons M. The h-index: advantages, limitations and its relation with other bibliometric indicators at the micro level. J Informetr. 2007;1(3):193–203. doi: 10.1016/j.joi.2007.02.001 [DOI] [Google Scholar]
16.Anderson TR, Hankin RKS, Killworth PD. Beyond the Durfee square: enhancing the h-index to score total publication output. Scientometrics. 2008;76(3):577–88. doi: 10.1007/s11192-007-2071-2 [DOI] [Google Scholar]
17.Batista PD, Campiteli MG, Kinouchi O. Is it possible to compare researchers with different scientific interests? Scientometrics. 2006;68(1):179–89. doi: 10.1007/s11192-006-0090-4 [DOI] [Google Scholar]
18.Kelly CD, Jennions MD. The h index and career assessment by numbers. Trends Ecol Evol. 2006;21(4):167–70. doi: 10.1016/j.tree.2006.01.005 [DOI] [PubMed] [Google Scholar]
19.Waltman L, van Eck NJ. The inconsistency of the h-index. J Am Soc Inf Sci Tech. 2012;63(2):406–15. doi: 10.1002/asi.21678 [DOI] [Google Scholar]
20.Hirsch JE. Does the h index have predictive power? Proc Natl Acad Sci USA. 2007;104(49):19193. doi: 10.1073/pnas.0707962104 [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Bornmann L. Redundancies in h index variants and the proposal of the number of top-cited papers as an attractive indicator. Measurement. 2012;10(3):149–53. doi: 10.1080/15366367.2012.716255 [DOI] [Google Scholar]
22.Costas R, Franssen T. Reflections around ‘the cautionary use’ of the h-index: response to Teixeira da Silva and Dobránszki. Scientometrics. 2018;115(2):1125–30. doi: 10.1007/s11192-018-2683-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Abramo G, D’Angelo CA, Viel F. The suitability of h and g indexes for measuring the research performance of institutions. Scientometrics. 2013;97(3):555–70. doi: 10.1007/s11192-013-1026-4 [DOI] [Google Scholar]
24.Bhattacharjee Y. Impact factor. Science. 2005;309(5738):1181. [DOI] [PubMed] [Google Scholar]
25.Delgado López-Cózar E, Orduña-Malea E, Martín-Martín A. Google Scholar as a data source for research assessment. In: Glänzel W, Moed HF, Schmoch U, Thelwall M, editors. Springer Handbook of Science and Technology Indicators. Cham: Springer International Publishing; 2019. p. 95–127. [Google Scholar]
26.Tregenza T. Gender bias in the refereeing process? Trends Ecol Evol. 2002;17(8):349–50. doi: 10.1016/S0169-5347(02)02545-4 [DOI] [Google Scholar]
27.Larivière V, Ni C, Gingras Y, Cronin B, Sugimoto CR. Global gender disparities in science. Nature. 2013;504(7479):211–3. doi: 10.1038/504211a [DOI] [PubMed] [Google Scholar]
28.Howe-Walsh L, Turnbull S. Barriers to women leaders in academia: tales from science and technology. Stud High Educ. 2016;41(3):415–28. doi: 10.1080/03075079.2014.929102 [DOI] [Google Scholar]
29.Aksnes DW. Characteristics of highly cited papers. Res Eval. 2003;12(3):159–70. doi: 10.3152/147154403781776645 [DOI] [Google Scholar]
30.Maliniak D, Powers R, Walter BF. The gender citation gap in international relations. Intl Organ. 2013;67(4):889–922. doi: 10.1017/S0020818313000209 [DOI] [Google Scholar]
31.Beaudry C, Larivière V. Which gender gap? Factors affecting researchers’ scientific impact in science and medicine. Res Policy. 2016;45(9):1790–817. doi: 10.1016/j.respol.2016.05.009 [DOI] [Google Scholar]
32.Atchison AL. Negating the gender citation advantage in political science. PS-Polit Sci Polit. 2017;50(2):448–55. doi: 10.1017/S1049096517000014 [DOI] [Google Scholar]
33.Todeschini R, Baccini A. Handbook of Bibliometric Indicators: Quantitative Tools for Studying and Evaluating Research. Weinheim: Wiley-VCH; 2016. [Google Scholar]
34.Austin J. Interdisciplinarity and tenure. Science. 2003;10 January. [Google Scholar]
35.Evans E. Paradigms, Interdisciplinarity, and Tenure [PhD]. Palo Alto, California, USA: Stanford University; 2016. [Google Scholar]
36.Carter TE, Smith TE, Osteen PJ. Gender comparisons of social work faculty using H-Index scores. Scientometrics. 2017;111(3):1547–57. doi: 10.1007/s11192-017-2287-0 [DOI] [Google Scholar]
37.Teixeira da Silva JA, Dobránszki J. Multiple versions of the h-index: cautionary use for formal academic purposes. Scientometrics. 2018;115(2):1107–13. doi: 10.1007/s11192-018-2680-3 29628536 [DOI] [Google Scholar]
38.Teixeira da Silva JA, Dobránszki J. Rejoinder to “Multiple versions of the h-index: cautionary use for formal academic purposes”. Scientometrics. 2018;115(2):1131–7. doi: 10.1007/s11192-018-2684-z [DOI] [Google Scholar]
39.Schmoch U, Schubert T, Jansen D, Heidler R, von Görtz R. How to use indicators to measure scientific performance: a balanced approach. Res Eval. 2010;19(1):2–18. doi: 10.3152/095820210X492477 [DOI] [Google Scholar]
40.Ràfols I. S&T indicators in the wild: contextualization and participation for responsible metrics. Res Eval. 2019;28(1):7–22. doi: 10.1093/reseval/rvy030 [DOI] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0257141.r001

Decision Letter 0

Sergi Lozano

10 May 2021

PONE-D-21-03358

A fairer way to compare researchers at any career stage and in any discipline using open-access citation data

PLOS ONE

Dear Dr. Bradshaw,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

Despite considering the paper interesting, both reviewers have raised a number of methodological concerns (please, note PLOS ONE's publication criterion #3, https://journals.plos.org/plosone/s/criteria-for-publication#loc-3). Some of such concerns might have a deep impact in the presented results (i.e. data source or discipline selection) and, therefore, should be paid special attention in your revision of the manuscript. In addition, Reviewer 2 initial comments might help you to better embed your work in the already huge literature of scientific performance indicators.

Please submit your revised manuscript by Jun 24 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols.

We look forward to receiving your revised manuscript.

Kind regards,

Sergi Lozano

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. Please note that PLOS ONE has specific guidelines on software sharing (http://journals.plos.org/plosone/s/materials-and-software-sharing#loc-sharing-software) for manuscripts whose main purpose is the description of a new software or software package. In this case, new software must conform to the Open Source Definition (https://opensource.org/docs/osd) and be deposited in an open software archive. Please see http://journals.plos.org/plosone/s/materials-and-software-sharing#loc-depositing-software for more information on depositing your software.

3. Please include captions for your Supporting Information files at the end of your manuscript, and update any in-text citations to match accordingly. Please see our Supporting Information guidelines for more information: http://journals.plos.org/plosone/s/supporting-information.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Partly

Reviewer #2: Yes

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: This is an interesting paper that develops a measure to evaluate scholars' performance across career stages and disciplines. The algorithms and results are easy to understand with cool visualizations. However, I have several concerns about the experiments and evaluations of the proposed measure.

First, the authors focused on eight disciplines when selecting researchers. But the selected disciplines do not seem to cover major disciplines in science. Most of them are subfields in biomedical research. Some important disciplines such as engineering, math and physics, social science, and computer science are missing in the list. Thus the experimental result does not necessarily support the claim that this measure works across all academic disciplines. I would recommend consulting a standard discipline catalog to reduce selection bias, such as the UCSD map of science (defines 13 disciplines): https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0039464. This catalog is also used in a recent paper: https://advances.sciencemag.org/content/7/17/eabb9004.

Second, the algorithm fits a linear line to each researcher based on three data points. This gives the area under the line A_{rel} for each researcher, which is then scaled to the maximum value in the sample (the one with the highest c_m). But why does the researcher with the highest c_m has the highest A_{rel}? Also, with this framework, if I understand the ranking algorithm correctly, there should exist a data point whose A_{rel} equals 1.0 in Fig. S3, but it's missing.

Third, there is no external validation of the measure. The authors did compare the ranking obtained with the proposed measure to that based on the m-quotient (Fig. 3b), but this is not a proper validation. The paper assumes that this measure just works as expected and then is used as a ground truth to evaluate the m-quotients (by stating that "the relationship between ε′ and the m-quotient is non-linear and highly variable, meaning that m-quotients often poorly reflect actual relative performance"). What if it is the other way around --- the m-quotients ranks researchers in a meaningful way, which would then indicate that the proposed measure fits poorly. The paper does show that there is a level of relationships between A_{rel} and log_e(t) across disciplines with reported R^2 at the beginning. But how much R^2 is needed to support a strong correlation and the fitness of the model? I would recommend the authors validate the ranking against external ground truth data, such as the evaluation of researchers from experts via survey.

Fourth, another limitation of this relative measure is that it's sensitive to the samples used in the ranking, especially when comparing researchers across disciplines. Let's imagine a scenario where one needs to compare two scholars (A and B) in two different disciplines. In one case, the peers we choose for A's discipline all perform worse than A; in another case, the peers selected all outperform A. Both conditions have the same samples for B's discipline. However, the ranking between A and B could be very different in the two conditions. Indeed, it is not meaningful and of little practical value to even considering comparing a computer scientist with a biologist in the first place.

I think the paper could be improved based on these suggestions.

Minor issue: Fig. 4 does not prove that "the m-quotient tends to increase through one's career, whereas sigma' is more stable" because the errorbars all seem to overlap with each other.

Reviewer #2: Overall I find very interesting and well-written this article. It is well structured, conceived, and executed.

I must confess that yet another article about h-index variants is not the road that the Bibliometrics community is looking for. A lot of (unused) variants have been published and, at the end of the day, only few of them add something to the discussion. In practical terms (availability of the indicator), only h-index is really used (g-index is rarely used in research evaluation in most countries).

We need to separate the advancements of Bibliometrics, on the one hand, and the use of indicators for research evaluation, on the other. Despite the clear intersections among these fields, we find significant differences in their approaches and interests.

Therefore, I would recommend authors to emphasize the limitations of previous indicators (and such uncovered things that research evaluation tasks still need) in greater detail, in order to justify properly the new proposal. Without a clear description of literature (and professional use of these indicators) gaps, new proposals feel incomplete.

I find excessive the use of the term “fair”, not only in the title but also throughout the text. It is somewhat subjective, and no fair indicator exists. Moreover, I recommend linking strongly the proposal of new indicator with responsible indicators and responsible research movements.

Please find below some minor comments, suggestions and recommendations oriented to make stronger the proposal.

Among the many disadvantages of the h-index (I fully agree with most of them), I do not find its accumulative nature as a limitation, as long as evaluators use it as wisely as possible. The problem lies with the poor use of the indicator. Obviously a person with 50 years may have more experience and years worked than a 25 years old person. That not makes 'number of years working' a bad indicator itself, it is just incomplete if we want to measure applicant skills.

Despite Google Scholar is free to access, data cannot be massively exported. No API exists, and this database shows some limitations (information noise, duplicates, errors, etc.). Google Scholar Profiles is a filter of Google Scholar, which depends on the author to create the profile accurately. These points should be discussed as it is the database used as a test-bed. Authors include some comments about it, but I believe they need to make stronger the reason to use this database and, later, how we can move to other databases in order to extrapolate the indicator to other controlled environments. If the indicator can only be operated with Google Scholar, it is a limitation.

“The entire approach we present here assumes that each researcher’s Google Scholar profile is accurate, up-to-date, and complete.”

� This is a dangerous approach. Real life shows us that profiles are noisy, with errors (some of them on purpose). It is clear that here the important thing is to test the statistical nature of the indicator. However, the sensitive of the indicator to the nature of the database in real conditions can add robustness to this proposal.

Why authors selected these specific disciplines? Why the number of researchers is equal? The demography of these disciplines is not equal.

� I understand the research design and the underlying reasons. However, again, the real conditions of the database should be acknowledged, and decisions should be strongly justified. With the results obtained I cannot be sure if the indicator would be useful for other disciplines and, then, generalizing the strengths of the indicator.

“we did not intend for sampling to be a definitive comment about the performance of particular researchers, nor did we mean for each sample to represent an entire discipline”

� While I understand this point, this is important, as authors are trying to operate an indicator with a particular dataset. Biases of this dataset can be inherited in the conclusions achieved. If the sample does not represent the entire discipline, then how I can infer its usefulness to this discipline?

“peer-reviewed article published in a recognized scientific journal”

� What a recognized scientific journal is for authors in the context of google scholar profiles?

“For the designation of Y1, we excluded any reports, chapters, books, theses or other forms of publication that preceded the year of the first peer-reviewed article; however, we included citations from the former sources in the researcher’s i10, h, and cm.”

� I disagree with this procedure. I do not see justifiable to exclude book chapters as document, and later include their citations, it can introduce citation biases. Please justify this decision.

All figures performed are of excellent quality and are very informative. The data segregation according to gender is so interesting and adds new debates and discussions. I congratulate authors for this effort in data visualization.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2021 Sep 10;16(9):e0257141. doi: 10.1371/journal.pone.0257141.r002

Author response to Decision Letter 0

18 Jul 2021

Reviewer #1

This is an interesting paper that develops a measure to evaluate scholars' performance across career stages and disciplines. The algorithms and results are easy to understand with cool visualizations. However, I have several concerns about the experiments and evaluations of the proposed measure.

https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0039464. This catalog is also used in a recent paper: https://advances.sciencemag.org/content/7/17/eabb9004.

RESPONSE #1: Had our goal been to test the universality of our proposed metric across all disciplines, we would have followed a procedure similar to the one the reviewer proposes. But this was not our goal. Rather, we aimed to choose a sample of widely divergent disciplines in terms of citation trends, that had an equal number of men and women in each sample, as well as an equal number of researchers in each of the three career stages we identified.

To achieve such a gender- and career-stage-balanced sample required knowledge about the discipline and a good deal of experience in ranking researchers therein. That was why each co-author was chosen from a different discipline, and not across the entire array of disciplines. We also aimed to have as much gender and career-level diversity in our authorship team.

We disagree that the sample disciplines were primarily “biomedical”; in fact, only one was strictly in the biomedical and clinical sciences (ophthalmology), three were in biological sciences (ecology, evolution/development, microbiology), two were in earth sciences (geology, palaeontology), one was in chemical sciences (chemistry), and one in history, heritage and archaeology (archaeology). The discipline categories we provide here are the official Field of Research major categories from the Australian Bureau of Statistics (www.abs.gov.au/statistics/classifications/australian-and-new-zealand-standard-research-classification-anzsrc/2020).

Did we cover a sufficient spread of disciplines according to citation trends? Yes. According to InCites Essential Science Indicators™, highly cited papers range from 24.56 to 4.85 cites/paper across 22 disciplines — our sample covered 83.4% of that range: molecular biology/genetics 24.56; chemistry 16.30; environment/ecology 14.64, geosciences 14.04, clinical medicine 13.72, social sciences 8.12.

More importantly, we never claimed that our metric applies universally across “all disciplines”. Throughout the text where we stated “all disciplines”, this was explicitly with references to “all [sampled] disciplines”. To clarify, we have now added the word ‘sampled’ where appropriate.

Second, the algorithm fits a linear line to each researcher based on three data points. This gives the area under the line A_(rel) for each researcher, which is then scaled to the maximum value in the sample (the one with the highest c_m). But why does the researcher with the highest c_m has the highest A_(rel)?

RESPONSE #2: We concede that we had not adequately explained the standardisation procedure. The algorithm predicts a series of slices across the triangle made by the slope and intercept estimated from the fit between the 3 points in the citation frequency by citation value graph (e.g., previously Fig. S2; now Fig. S1). The citation mass — the sum of these slices (i.e., predicted loge citation frequency for incrementing values of loge citation value) — is then standardised by taking the sum and dividing it by the number of slices multiplied by the maximum of loge cm across all researchers. The main reason we did this is explained more in the following response (Response #4), but we have now added some clarifying text in the Methods:

“Here, the sum of the predicted y derived from incrementing values of x (here in units of 0.05) using α ^ and β ^ is divided by the product of cm and the number of incremental x values. This implies all areas were scaled to the maximum in the sample, but avoids the problem of truncating variances near a maximum of 1 had we used the maximum area among all researchers in the sample as the denominator in the standardization procedure.”

Also, with this framework, if I understand the ranking algorithm correctly, there should exist a data point whose A_(rel) equals 1.0 in Fig. S3, but it's missing.

RESPONSE #3: Because we do not standardise each researcher’s triangle area via division by the largest triangle area in the sample, the citation masses do not have a maximum of 1. The principal reason for avoiding this is to prevent truncation of variances closer to the ‘extreme’ values near 1. This could violate the homoscedasticity property of the ε index, which is a problem with the m-quotient (see Response #4)

Third, there is no external validation of the measure. The authors did compare the ranking obtained with the proposed measure to that based on the m-quotient (Fig. 3b), but this is not a proper validation. The paper assumes that this measure just works as expected and then is used as a ground truth to evaluate the m-quotients (by stating that "the relationship between ε′ and the m-quotient is non-linear and highly variable, meaning that m-quotients often poorly reflect actual relative performance"). What if it is the other way around --- the m-quotients ranks researchers in a meaningful way, which would then indicate that the proposed measure fits poorly. The paper does show that there is a level of relationships between A_(rel) and log_e(t) across disciplines with reported R^2 at the beginning. But how much R^2 is needed to support a strong correlation and the fitness of the model? I would recommend the authors validate the ranking against external ground truth data, such as the evaluation of researchers from experts via survey.

RESPONSE #4: We had originally designed an internal ‘evaluation’ of the researcher lists we compiled for each discipline, where each co-author would subjectively rank the researchers in their respective discipline according to their own qualitative and quantitative criteria. This is yet another reason we kept the sample of disciplines to those in which our eight co-authors were most experienced.

However, we ultimately abandoned this line of inquiry because there was really no way to guarantee any standardisation or ‘truth’ in the subjective rankings. Whether these subjective rankings were well-correlated or not with ε does not insinuate that ε is any worse or better than existing metrics per se. This is, after all, the entire aim of our study — to provide a better metric than what is currently available. We never insinuated that it reflects absolute reality (whatever that might mean, in the nebulous world of researcher-ranking algorithms). Because everyone uses a different set of criteria to rank researchers, such a “ground truth” ends up being none at all.

From a statistical perspective, there is no threshold beyond which the R2 between citation mass (Arel) and loge years publishing (t) becomes ‘acceptable’ — it is a range (i.e., higher is better, lower is worse). However, we can show that the relationship between the h-index and years publishing (the quotient of which is the m-index) violates several statistical assumptions, whereas ε does not. We did not include these statistical assumption checks in the first submission, but realise now that they are useful for justifying our approach.

The following plots, which we have now added to the Supplementary Material (Fig. S5–S12), show the residual vs. fitted, scale-location, and normal quantile-quantile plots for the relationship between Arel and loge(t) (top rows) and between h-index and t (bottom rows) for all eight disciplines — the latter relationship represents the m-quotient (h-index ÷ t):

In all disciplines, the Arel ~ loge(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line).

In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

In other words, our ε index does not violate base statistical assumptions in its derivation like the m-quotient does. This demonstration is, however, intuitive given that one can clearly see how the m-quotient is truncated at lower values and its variance inflates at larger values relative to the non-bounded ε index (Fig. 3b).

Importantly — and this is really an essential characteristic of the ε index relative to the m-quotient — the latter has no intrinsic threshold to which one can compare relative performance. On the contrary, the ε index explicitly defines a mid-point (value = 0) above which researchers are relatively higher performers, and below which they are relatively poorer performers. The m-index does not have this highly useful characteristic.

RESPONSE #5: We disagree that this is a weakness and strongly argue the opposite — this is a particular strength of the ε index.

First, we disagree that comparing researchers in different disciplines is not meaningful, because people do it all the time. Whether it is for ranking job applicants, or members of a multidisciplinary centre, the utility is without question.

The lead author (CJAB) has done exactly this sort of comparison on many occasions, having interviewed ecologists, mathematicians, physicists, economists, and engineers for the same position (all requiring mathematical skills for an ecological application). He has also been requested to rank the Chief Investigators in Centres of Excellence spanning the sciences and humanities, as well as rank applicants for nationally competitive grants (e.g., the Australian Research Council and the New Zealand Marsden Fund). Indeed — this necessity was one of the underlying rationales for developing the ε index in the first place.

This justification aside, the reviewer’s example is not how we proposed that the interdisciplinary comparisons should be done, and how the discipline-standardised ε′ index is calculated.

Consider the example provided above. If one wishes to compare researcher A to researcher B, the first step is to accumulate the data for a sample of A’s colleagues in A’s same discipline, and then do the same for a sample of B’s colleagues in B’s discipline. Once the ε index is calculated for discipline A and B separately, the standardisation is applied to each discipline in turn. Then, and only then, can one use A’s ε′ and compare it to B’s ε′. In other words, the within-discipline standardisation of ε to ε′ ensures that A’s and B’s indices are on the same scale.

Given this confusion, we have added the following text in the ‘Discipline standardization’ section of the Methods to clarify:

“Comparison between disciplines is only meaningful when a sufficient sample of researchers from within specific disciplines first have their ε calculated (i.e., discipline-specific ε), and then each discipline sample undergoes the standardization to create ε′. Then, any sample of researchers from any discipline can be compared directly.”

Minor issue: Fig. 4 does not prove that "the m-quotient tends to increase through one's career, whereas sigma' is more stable" because the errorbars all seem to overlap with each other.

RESPONSE #6: Generally speaking, quantile derivation of confidence bounds cannot be substituted for actual statistical tests. It was our fault not to have included such tests, which we now supply in the caption of Fig. 4.

Treating career stage either as an integer (early = 1, mid = 2, late = 3), or as an ordinal factor, in a linear model clearly shows that ε′ does not differ among career stages, but that the late-career m-quotient in particular diverges statistically from the earlier stages:

career stage as an integer

ε′ index:

Estimate SE t value Pr(>|t|)

(Intercept) -0.02891 0.02461 -1.175 0.241

stage 0.01446 0.01139 1.269 0.205

m-quotient:

Estimate SE t value Pr(>|t|)

(Intercept) 1.14857 0.09261 12.403 < 2e-16 ***

stage 0.17152 0.04287 4.001 7.3e-05 ***

career stage as an ordinal factor

ε′ index:

Estimate SE t value Pr(>|t|)

(Intercept) -0.00987 0.01612 -0.612 0.541

stage2 0.00070 0.02280 0.031 0.975

stage3 0.02891 0.02280 1.268 0.205

m-quotient:

Estimate SE t value Pr(>|t|)

(Intercept) 1.35259 0.06058 22.328 < 2e-16 ***

stage2 0.07402 0.08567 0.864 0.388

stage3 0.34304 0.08567 4.004 7.22e-05 ***

We have elected not to include all this detail in the caption, but have provided the Type I error estimates Pr(>|t|) for both the integer- and ordinal factor-based linear models. The new text in the caption of Fig. 4 is now:

“Treating career stage as an integer in a linear model shows no difference among stages for ε′ (p = 0.205), but there is evidence for a career stage effect for the m-quotient (p = 0.000073). Likewise, treating career stage as an ordinal factor (ECR < MCR < LCR) in a linear model shows no difference among stages for ε′ (MCR: p = 0.975; LCR: p = 0.205), but there is evidence for a divergence of LCR for the m-quotient (MCR: p = 0.388; LCR: p = 0.000072).”

Finally, we have replaced Fig. 4 with a violin plot as a better reflection of the distribution and trends in the underlying data.

Reviewer #2

RESPONSE #7: We could not agree more, and is exactly why we derived this new, easily calculated, relative, and less-biased metric. Here, it was a delicate balance between ease of calculation and improvement over existing metrics in terms of career stage and gender biases (prevalent in both the h-index and m-quotient as we show). We contend that the main reason most people default to the h-index is because it is provided by most citation-accumulation engines. With a little additional effort, a few more readily available data points can make a world of difference.

Is our ε-index all-encompassing and free of all biases? Does it account for variable contribution in co-authorship? Does it consider non-citation-based metrics of performance? Of course not, and we did not claim that it does. But it is easy to derive, and vastly improves rankings compared to those based on the h-index/m-quotient.

RESPONSE #8: We disagree. This is not a review of the pros and cons of different metrics. That has been done in gory detail many times before [1-7] (note that we have cited all but two of these reviews in the original submission, and have now added them to the Introduction). Our aim was instead to point the reader to these extensive reviews, highlight the remaining problems, and propose one way to account for issues without having to spend too much effort to derive this new index.

In fact, one bibliometric paper recently published in PLoS One [8] (which we also cited) followed a similar approach to us in these terms.

RESPONSE #9: We have now modified most occasions of ‘fair’ to ‘fairer’, and ‘fairly’ to ‘more fairly’.

While our index does not really fall under the FAIR principles (Findable, Accessible, Interoperable, Reusable) per se (but the article in PLoS One will), we have added a few new citations along the lines of responsible indicators, and adjusted the final paragraph to:

“We reiterate that while the ε-index is an advance on existing approaches to rank researchers according to their citation history, a single metric should never be the sole measure of a researcher’s productivity or potential [9]. Nonetheless, the objectivity, ease of calculation, and flexibility of its application argue that the ε-index is a needed tool in the quest to provide fairer and more responsible [9, 10] initial appraisals of a researcher’s publication performance.”

RESPONSE #10: Agreed. The problem unfortunately is that many people do not use the h-index wisely. A correction for experience is therefore essential.

RESPONSE #11: The lack of an API provided for Google Scholar is a problem, and one of which the lead author has been acutely aware since he developed the ε-index app (https://cjabradshaw.shinyapps.io/epsilonIndex). It would have been ideal to develop a scraper using an API to make the acquisition of the necessary data (i10, h-index, cm, t) automatic. He has even developed the code to do this should Google Scholar ever supply a public API.

But as we stated in the submitted manuscript: “Regardless, should an assessor have access to potentially more rigorous citation databases (e.g., Scopus), the ε-index can still be readily calculated, although within-sample consistency must be maintained for the ranks to be meaningful.”, other databases can be readily used to provide the necessary data. The only limitation, as we stated, is that the same database must be used for all researchers in the sample.

Databases like Scopus are subscription-only, but most universities appear to have subscriptions. Thus, as long as people desiring to construct the ε-index follow this simple rule of consistency, any database can be potentially used.

We have updated the relevant section along these lines:

“The ε-index also potentially suffers from the requirement of the constituent citation data upon which it is based being accurate and up-to-date [11, 12]. It is therefore important that users correct for obvious errors when compiling the four required data to calculate the ε-index (i10, h-index, cm, t). This could include corrections for misattributed articles, start year, or even i10. In some cases, poorly maintained Google Scholar profiles might exclude certain researchers from comparative samples. Regardless, should an assessor have access to potentially more rigorous citation databases (e.g., Scopus), the ε-index can still be readily calculated, although within-sample consistency must be maintained for the ranks to be meaningful. Nonetheless, because the index is relative and scaled, the relative rankings of researchers should be maintained irrespective of the underlying database consulted to derive the input data.”

“The entire approach we present here assumes that each researcher’s Google Scholar profile is accurate, up-to-date, and complete.”

This is a dangerous approach. Real life shows us that profiles are noisy, with errors (some of them on purpose). It is clear that here the important thing is to test the statistical nature of the indicator. However, the sensitive of the indicator to the nature of the database in real conditions can add robustness to this proposal.

RESPONSE #12: Please see the previous response (Response #11) and the new text clarifying this point.

Why authors selected these specific disciplines? Why the number of researchers is equal? The demography of these disciplines is not equal.

RESPONSE #13: Please see Response #1 to Reviewer #1.

I understand the research design and the underlying reasons. However, again, the real conditions of the database should be acknowledged, and decisions should be strongly justified. With the results obtained I cannot be sure if the indicator would be useful for other disciplines and, then, generalizing the strengths of the indicator.

RESPONSE #14: Please see Responses #11 and #15.

“we did not intend for sampling to be a definitive comment about the performance of particular researchers, nor did we mean for each sample to represent an entire discipline”

While I understand this point, this is important, as authors are trying to operate an indicator with a particular dataset. Biases of this dataset can be inherited in the conclusions achieved. If the sample does not represent the entire discipline, then how I can infer its usefulness to this discipline?

RESPONSE #15: We reiterate that the ε-index is not designed to encompass a discipline; rather, it is designed to compare a sample of individual researchers and compare their relative performance to each other. That someone not included in the sample has a higher h-index or m-quotient (or some other metric) is irrelevant. Because they are not included in the sample, they are not being compared. This is a severe limitation of other metrics because no one can objectively judge what a ‘good’ or ‘bad’ h-index is in any discipline.

“peer-reviewed article published in a recognized scientific journal”

What a recognized scientific journal is for authors in the context of google scholar profiles?

RESPONSE #16: The eight co-authors from eight separate disciplines had no issues in distinguishing peer-reviewed journals from other types of output. We suspect that in extremely rare occasions when a compiler is unfamiliar with the journals in a particular discipline that questions might arise; however, there are several publicly (e.g., Journals Directory; Wikipedia) and subscription-based (e.g., Web of Knowledge; Scopus) databases where one can verify if an article is published in a peer-reviewed journal.

I disagree with this procedure. I do not see justifiable to exclude book chapters as document, and later include their citations, it can introduce citation biases. Please justify this decision.

RESPONSE #17: In nearly all cases, reports, chapters, books, theses, etc. listed prior to the first peer-reviewed did not contribute to any of the metrics required for the calculation of ε. None of the researchers’ most highly cited item (cm), h-index, or even i10 were influenced by anything appearing before the first peer-reviewed paper. Even in cases where this might occur (e.g., most likely with the i10), it makes little difference to the relative position of the researcher.

Given that earlier entries are often missing details or have incorrect attribution to the researcher in question (e.g., in Google Scholar), the only way to standardize career length was to establish a rule such as this to identify the start of one’s career. We concede that in disciplines where peer-reviewed articles are the minority of a researcher’s output (e.g., many of the humanities), this type of threshold might be a disadvantage. However, in such cases it is simple to shift the beginning of a researcher’s publication career to a different rule (e.g., first book chapter). Because the number of publication years can be easily manipulated to account for career gaps, it can also easily be manipulated to take into account any aspects of debatable start year discussed above.

RESPONSE #18: Thank you. No response required.

References cited in this response

1. Phelan TJ. A compendium of issues for citation analysis. Scientometrics. 1999;45(1):117-36. doi: 10.1007/BF02458472.

2. Wildgaard L. An overview of author-level indicators of research performance. In: Glänzel W, Moed HF, Schmoch U, Thelwall M, editors. Springer Handbook of Science and Technology Indicators. Cham: Springer International Publishing; 2019. p. 361-96.

3. Schubert A, Schubert G. All along the h-index-related literature: a guided tour. In: Glänzel W, Moed HF, Schmoch U, Thelwall M, editors. Springer Handbook of Science and Technology Indicators. Cham: Springer International Publishing; 2019. p. 301-34.

4. Bornmann L, Mutz R, Daniel H-D. Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. J Am Soc Inf Sci Tec. 2008;59(5):830-7. doi: 10.1002/asi.20806.

5. Bornmann L, Mutz R, Hug SE, Daniel H-D. A multilevel meta-analysis of studies reporting correlations between the h index and 37 different h index variants. J Informetr. 2011;5(3):346-59. doi: 10.1016/j.joi.2011.01.006.

6. Egghe L. The Hirsch index and related impact measures. Annual Review of Information Science and Technology. 2010;44(1):65-114. doi: 10.1002/aris.2010.1440440109.

7. Waltman L, van Eck NJ. The inconsistency of the h-index. J Am Soc Inf Sci Tec. 2012;63(2):406-15. doi: 10.1002/asi.21678.

8. Fenner T, Harris M, Levene M, Bar-Ilan J. A novel bibliometric index with a simple geometric interpretation. PLoS One. 2018;13(7):e0200098. doi: 10.1371/journal.pone.0200098.

9. Schmoch U, Schubert T, Jansen D, Heidler R, von Görtz R. How to use indicators to measure scientific performance: a balanced approach. Res Eval. 2010;19(1):2-18. doi: 10.3152/095820210X492477.

10. Ràfols I. S&T indicators in the wild: contextualization and participation for responsible metrics. Res Eval. 2019;28(1):7-22. doi: 10.1093/reseval/rvy030.

11. Teixeira da Silva JA, Dobránszki J. Multiple versions of the h-index: cautionary use for formal academic purposes. Scientometrics. 2018;115(2):1107-13. doi: 10.1007/s11192-018-2680-3.

12. Teixeira da Silva JA, Dobránszki J. Rejoinder to “Multiple versions of the h-index: cautionary use for formal academic purposes”. Scientometrics. 2018;115(2):1131-7. doi: 10.1007/s11192-018-2684-z.

Attachment

Submitted filename: PONE-D-21-03358.R1 response.docx

Click here for additional data file.^{(8.8MB, docx)}

PLoS One. doi: 10.1371/journal.pone.0257141.r003

Decision Letter 1

Sergi Lozano

25 Aug 2021

A fairer way to compare researchers at any career stage and in any discipline using open-access citation data

PONE-D-21-03358R1

Dear Dr. Bradshaw,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Sergi Lozano

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #2: All comments have been addressed

Reviewer #3: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #2: Yes

Reviewer #3: Partly

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #2: Yes

Reviewer #3: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #2: Yes

Reviewer #3: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #2: Yes

Reviewer #3: Yes

**********

6. Review Comments to the Author

Reviewer #2: Authors have addressed correctly all my previous doubts and concerns. The revised manuscript has also fixed some minor errors. I believe the manuscript offers new interesting findings to the discipline.

Reviewer #3: I think the authors did a good job addressing most of the comments in the previous round of reviews. Optionally, I suggest them to reconsider their response #4 to Reviewer #1, as I think that evaluating the correlation between their subjective opinions (or those of other experts) of the researchers in their pool and the ranking they obtain from their index would add substantial value to the paper. They clearly went through a lot of effort to assemble a large multidisciplinary team, so in my opinion this is very much low hanging fruit.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #2: No

Reviewer #3: No

PLoS One. doi: 10.1371/journal.pone.0257141.r004

Acceptance letter

Sergi Lozano

31 Aug 2021

PONE-D-21-03358R1

A fairer way to compare researchers at any career stage and in any discipline using open-access citation data

Dear Dr. Bradshaw:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Sergi Lozano

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Fig. Citation frequency versus citation value.

(TIF)

Click here for additional data file.^{(3.4MB, tif)}

S2 Fig. Example citation mass relative to years since first publication.

(TIF)

Click here for additional data file.^{(1.1MB, tif)}

S3 Fig. Gender-specific rankings.

(TIF)

Click here for additional data file.^{(4.2MB, tif)}

S4 Fig. m-quotient relative to years since first publication.

(TIF)

Click here for additional data file.^{(631.9KB, tif)}

S5 Fig. Normality and homoscedasticity diagnostics for the archaeology sample.

(TIF)

Click here for additional data file.^{(3.1MB, tif)}

S6 Fig. Normality and homoscedasticity diagnostics for the chemistry sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of chemistry (CHM). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.8MB, tif)}

S7 Fig. Normality and homoscedasticity diagnostics for the ecology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of ecology (ECO). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.6MB, tif)}

S8 Fig. Normality and homoscedasticity diagnostics for the evolution/development sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of evolution and development (EVO). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.7MB, tif)}

S9 Fig. Normality and homoscedasticity diagnostics for the geology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of geology (GEO). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.7MB, tif)}

S10 Fig. Normality and homoscedasticity diagnostics for the microbiology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of microbiology (MIC). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.4MB, tif)}

S11 Fig. Normality and homoscedasticity diagnostics for the ophthalmology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of ophthalmology (OPH). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.7MB, tif)}

S12 Fig. Normality and homoscedasticity diagnostics for the palaeontology sample.

Residual vs. fitted (a & b), scale-location (c & d), and normal quantile-quantile (e & f) plots for the relationship between log_e A_rel (area under the power-law relationship) and log_e t (years publishing) used to derive the ε-index (top row), and for the relationship between the h-index and t used to derive the m-quotient (bottom row) for 60 researchers in the discipline of palaeontology (PAL). The A_rel ~ log_e(t) relationships show homoscedasticity (i.e., a random pattern in the residual vs. fitted plots, and no trend in the scale-location plots) and a near-Normal distribution (points fall on the expected quantile-quantile line). In contrast, the h-index ~ t relationships all show heteroscedasticity (i.e., a ‘fan’ pattern in the residual vs. fitted plots, and a positive trend in the scale-location plots) and a non-Normal distribution (points diverge considerably more from the expected quantile-quantile line).

(TIF)

Click here for additional data file.^{(3.6MB, tif)}

Attachment

Submitted filename: PONE-D-21-03358.R1 response.docx

Click here for additional data file.^{(8.8MB, docx)}

Data Availability Statement

[pone.0257141.ref001] 1.Phelan TJ. A compendium of issues for citation analysis. Scientometrics. 1999;45(1):117–36. doi: 10.1007/BF02458472 [DOI] [Google Scholar]

[pone.0257141.ref002] 2.Barnes C. The h-index debate: an introduction for librarians. J Acad Libr. 2017;43(6):487–94. doi: 10.1016/j.acalib.2017.08.013 [DOI] [Google Scholar]

[pone.0257141.ref003] 3.Wildgaard L. An overview of author-level indicators of research performance. In: Glänzel W, Moed HF, Schmoch U, Thelwall M, editors. Springer Handbook of Science and Technology Indicators. Cham: Springer International Publishing; 2019. p. 361–96. [Google Scholar]

[pone.0257141.ref004] 4.Egghe L. The Hirsch index and related impact measures. Ann Rev Inf Sci Tech. 2010;44(1):65–114. doi: 10.1002/aris.2010.1440440109 [DOI] [Google Scholar]

[pone.0257141.ref005] 5.Hirsch JE. An index to quantify an individual’s scientific research output. Proc Natl Acad Sci USA. 2005;102(46):16569–72. doi: 10.1073/pnas.0507655102 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0257141.ref006] 6.Schubert A, Schubert G. All along the h-index-related literature: a guided tour. In: Glänzel W, Moed HF, Schmoch U, Thelwall M, editors. Springer Handbook of Science and Technology Indicators. Cham: Springer International Publishing; 2019. p. 301–34. [Google Scholar]

[pone.0257141.ref007] 7.Egghe L. How to improve the h-index. The Scientist. 2006;20(3):15. [Google Scholar]

[pone.0257141.ref008] 8.Zhang C-T. The e-Index, complementing the h-Index for excess citations. PLoS One. 2009;4(5):e5429. doi: 10.1371/journal.pone.0005429 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0257141.ref009] 9.Fenner T, Harris M, Levene M, Bar-Ilan J. A novel bibliometric index with a simple geometric interpretation. PLoS One. 2018;13(7):e0200098. doi: 10.1371/journal.pone.0200098 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0257141.ref010] 10.Schreiber M. A modification of the h-index: The h_m-index accounts for multi-authored manuscripts. J Informetr. 2008;2(3):211–6. doi: 10.1016/j.joi.2008.05.001 [DOI] [Google Scholar]

[pone.0257141.ref011] 11.Schreiber M. How to modify the g-index for multi-authored manuscripts. J Informetr. 2010;4(1):42–54. doi: 10.1016/j.joi.2009.06.003 [DOI] [Google Scholar]

[pone.0257141.ref012] 12.Thompson DF, Callen EC, Nahata MC. New indices in scholarship assessment. Am J Pharm Educ. 2009;73(6):111. doi: 10.5688/aj7306111 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0257141.ref013] 13.Bornmann L, Mutz R, Daniel H-D. Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. J Am Soc Inf Sci Tech. 2008;59(5):830–7. doi: 10.1002/asi.20806 [DOI] [Google Scholar]

[pone.0257141.ref014] 14.Bornmann L, Mutz R, Hug SE, Daniel H-D. A multilevel meta-analysis of studies reporting correlations between the h index and 37 different h index variants. J Informetr. 2011;5(3):346–59. doi: 10.1016/j.joi.2011.01.006 [DOI] [Google Scholar]

[pone.0257141.ref015] 15.Costas R, Bordons M. The h-index: advantages, limitations and its relation with other bibliometric indicators at the micro level. J Informetr. 2007;1(3):193–203. doi: 10.1016/j.joi.2007.02.001 [DOI] [Google Scholar]

[pone.0257141.ref016] 16.Anderson TR, Hankin RKS, Killworth PD. Beyond the Durfee square: enhancing the h-index to score total publication output. Scientometrics. 2008;76(3):577–88. doi: 10.1007/s11192-007-2071-2 [DOI] [Google Scholar]

[pone.0257141.ref017] 17.Batista PD, Campiteli MG, Kinouchi O. Is it possible to compare researchers with different scientific interests? Scientometrics. 2006;68(1):179–89. doi: 10.1007/s11192-006-0090-4 [DOI] [Google Scholar]

[pone.0257141.ref018] 18.Kelly CD, Jennions MD. The h index and career assessment by numbers. Trends Ecol Evol. 2006;21(4):167–70. doi: 10.1016/j.tree.2006.01.005 [DOI] [PubMed] [Google Scholar]

[pone.0257141.ref019] 19.Waltman L, van Eck NJ. The inconsistency of the h-index. J Am Soc Inf Sci Tech. 2012;63(2):406–15. doi: 10.1002/asi.21678 [DOI] [Google Scholar]

[pone.0257141.ref020] 20.Hirsch JE. Does the h index have predictive power? Proc Natl Acad Sci USA. 2007;104(49):19193. doi: 10.1073/pnas.0707962104 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0257141.ref021] 21.Bornmann L. Redundancies in h index variants and the proposal of the number of top-cited papers as an attractive indicator. Measurement. 2012;10(3):149–53. doi: 10.1080/15366367.2012.716255 [DOI] [Google Scholar]

[pone.0257141.ref022] 22.Costas R, Franssen T. Reflections around ‘the cautionary use’ of the h-index: response to Teixeira da Silva and Dobránszki. Scientometrics. 2018;115(2):1125–30. doi: 10.1007/s11192-018-2683-0 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0257141.ref023] 23.Abramo G, D’Angelo CA, Viel F. The suitability of h and g indexes for measuring the research performance of institutions. Scientometrics. 2013;97(3):555–70. doi: 10.1007/s11192-013-1026-4 [DOI] [Google Scholar]

[pone.0257141.ref024] 24.Bhattacharjee Y. Impact factor. Science. 2005;309(5738):1181. [DOI] [PubMed] [Google Scholar]

[pone.0257141.ref025] 25.Delgado López-Cózar E, Orduña-Malea E, Martín-Martín A. Google Scholar as a data source for research assessment. In: Glänzel W, Moed HF, Schmoch U, Thelwall M, editors. Springer Handbook of Science and Technology Indicators. Cham: Springer International Publishing; 2019. p. 95–127. [Google Scholar]

[pone.0257141.ref026] 26.Tregenza T. Gender bias in the refereeing process? Trends Ecol Evol. 2002;17(8):349–50. doi: 10.1016/S0169-5347(02)02545-4 [DOI] [Google Scholar]

[pone.0257141.ref027] 27.Larivière V, Ni C, Gingras Y, Cronin B, Sugimoto CR. Global gender disparities in science. Nature. 2013;504(7479):211–3. doi: 10.1038/504211a [DOI] [PubMed] [Google Scholar]

[pone.0257141.ref028] 28.Howe-Walsh L, Turnbull S. Barriers to women leaders in academia: tales from science and technology. Stud High Educ. 2016;41(3):415–28. doi: 10.1080/03075079.2014.929102 [DOI] [Google Scholar]

[pone.0257141.ref029] 29.Aksnes DW. Characteristics of highly cited papers. Res Eval. 2003;12(3):159–70. doi: 10.3152/147154403781776645 [DOI] [Google Scholar]

[pone.0257141.ref030] 30.Maliniak D, Powers R, Walter BF. The gender citation gap in international relations. Intl Organ. 2013;67(4):889–922. doi: 10.1017/S0020818313000209 [DOI] [Google Scholar]

[pone.0257141.ref031] 31.Beaudry C, Larivière V. Which gender gap? Factors affecting researchers’ scientific impact in science and medicine. Res Policy. 2016;45(9):1790–817. doi: 10.1016/j.respol.2016.05.009 [DOI] [Google Scholar]

[pone.0257141.ref032] 32.Atchison AL. Negating the gender citation advantage in political science. PS-Polit Sci Polit. 2017;50(2):448–55. doi: 10.1017/S1049096517000014 [DOI] [Google Scholar]

[pone.0257141.ref033] 33.Todeschini R, Baccini A. Handbook of Bibliometric Indicators: Quantitative Tools for Studying and Evaluating Research. Weinheim: Wiley-VCH; 2016. [Google Scholar]

[pone.0257141.ref034] 34.Austin J. Interdisciplinarity and tenure. Science. 2003;10 January. [Google Scholar]

[pone.0257141.ref035] 35.Evans E. Paradigms, Interdisciplinarity, and Tenure [PhD]. Palo Alto, California, USA: Stanford University; 2016. [Google Scholar]

[pone.0257141.ref036] 36.Carter TE, Smith TE, Osteen PJ. Gender comparisons of social work faculty using H-Index scores. Scientometrics. 2017;111(3):1547–57. doi: 10.1007/s11192-017-2287-0 [DOI] [Google Scholar]

[pone.0257141.ref037] 37.Teixeira da Silva JA, Dobránszki J. Multiple versions of the h-index: cautionary use for formal academic purposes. Scientometrics. 2018;115(2):1107–13. doi: 10.1007/s11192-018-2680-3 29628536 [DOI] [Google Scholar]

[pone.0257141.ref038] 38.Teixeira da Silva JA, Dobránszki J. Rejoinder to “Multiple versions of the h-index: cautionary use for formal academic purposes”. Scientometrics. 2018;115(2):1131–7. doi: 10.1007/s11192-018-2684-z [DOI] [Google Scholar]

[pone.0257141.ref039] 39.Schmoch U, Schubert T, Jansen D, Heidler R, von Görtz R. How to use indicators to measure scientific performance: a balanced approach. Res Eval. 2010;19(1):2–18. doi: 10.3152/095820210X492477 [DOI] [Google Scholar]

[pone.0257141.ref040] 40.Ràfols I. S&T indicators in the wild: contextualization and participation for responsible metrics. Res Eval. 2019;28(1):7–22. doi: 10.1093/reseval/rvy030 [DOI] [Google Scholar]

PERMALINK

A fairer way to compare researchers at any career stage and in any discipline using open-access citation data

Corey J A Bradshaw

Justin M Chalker

Stefani A Crabtree

Bart A Eijkelkamp

John A Long

Justine R Smith

Kate Trinajstic

Vera Weisbecker

Roles

Abstract

Introduction

Materials and methods

Researcher samples

Citation data

Ranking algorithm

Discipline standardization

Results

Fig 1. Citation mass relative to years since first publication.

Fig 2. Within-discipline residuals from the relationship between citation mass and years since first publication.

Fig 3. ε-index versus m-quotient.

Fig 4. Career-stage differences in the ε′-index and m-quotient.

Fig 5. Gender differences in the ε′-index and m-quotient.

Fig 6. Gender differences in the ε′-index and gender-debiased ε′-index.

Discussion

Supporting information

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Sergi Lozano

Roles

Author response to Decision Letter 0

Decision Letter 1

Sergi Lozano

Roles

Acceptance letter

Sergi Lozano

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases