Conceptual-based design of an ultrabroadband microwave metamaterial absorber

Significance

While microwave absorption is a widely pursued topic, a conceptual-based design can offer a theoretical basis for generalization and improvements. We offer a design recipe for ultrabroadband absorption based on the use of electrical dipole resonance in a metallic ring to generate, via interaction with its image resonance, two high-impedance resonances. Impedance matching over the frequency range in between the two resonances is obtained by adding resistance to the metallic ring. To extend the absorption to an ultrabroadband spectrum, we employ a double-layer self-similar structure in conjunction with absorption of the diffracted waves at the higher frequency end. The resulting absorber pushes the overall performance close to the causality limit over a large absorption bandwidth.

Abstract

By introducing metallic ring structural dipole resonances in the microwave regime, we have designed and realized a metamaterial absorber with hierarchical structures that can display an averaged −19.4 dB reflection loss (∼99% absorption) from 3 to 40 GHz. The measured performance is independent of the polarizations of the incident wave at normal incidence, while absorption at oblique incidence remains considerably effective up to 45°. We provide a conceptual basis for our absorber design based on the capacitive-coupled electrical dipole resonances in the lateral plane, coupled to the standing wave along the incident wave direction. To realize broadband impedance matching, resistive dissipation of the metallic ring is optimally tuned by using the approach of dispersion engineering. To further extend the absorption spectrum to an ultrabroadband range, we employ a double-layer self-similar structure in conjunction with the absorption of the diffracted waves at the higher end of the frequency spectrum. The overall thickness of the final sample is 14.2 mm, only 5% over the theoretical minimum thickness dictated by the causality limit.

The advent of fifth generation (5G) technology implies an order of magnitude, or more, microwave power permeating the 5G-active space, owing to the usage of multiple high-frequency microwave bands (1), a significant increase in transmission stations, and the fact that the microwave power varies quadratically as a function of frequency. Associated with this microwave power increase, there is a need for balancing the necessary monitoring activities and privacy as well as for remediating health concerns (2–4) arising from the long-term exposure to a much higher microwave power environment. A suitable microwave absorption structure can play an important role in resolving such issues. Meanwhile, there also exists extensive demands for electromagnetic absorption, with applications in electromagnetic compatibility (5), radar cross-section reduction (6), energy harvesting (7), etc. The recent development of metamaterial absorbers, based on designed structures with subwavelength thickness, has injected new momentum to this subject, with potential applications (8) to broad frequency bands ranging from microwave to terahertz (9–11), infrared (12–14), and visible light (15, 16). Due to microwave’s long wavelength and high penetrability through solids, its absorption has always been the most challenging.

An ideal microwave absorber should absorb over a wide frequency bandwidth, with simple geometry for both experimental implementation and mass production. However, recent metamaterial-based absorbers can only display near-perfect absorption at either one frequency (13, 17–19) or several discretized frequencies (9, 20) due to the inherent resonance-based mechanism of metamaterials and their attendant dispersive characteristics (21). In order to extend the absorption frequency spectrum, many efforts have been devoted to either increasing the dissipation (22–26), for example, by using resistive sheets or loading with lumped elements, or superposing resonant units (27–31), for example, by exploiting multilayer patch absorbers. Yet, the broadband performance has still been limited, and the geometry of such structures has evolved toward ever-more complexity and sophistication. In this work, the basic building block in our design is just a metallic ring that is fabricated by the printed circuit board (PCB) technology. The final integrated sample can exhibit near-perfect absorption from 3 to 40 GHz, covering the whole high-frequency 5G bands (32). Another crucial measure of an absorber is its thickness. While a thick enough absorber can absorb everything over all frequency regimes, it is nevertheless impractical in terms of applications. For a passive absorber, there is a common standard set by the causality-dictated minimum sample thickness that is associated with any given reflection spectrum (33). In our case, the overall thickness of the absorber is 14.2 mm, only 5% over the minimum thickness dictated by the causality limit. This theoretical limit also plays a crucial role in the impedance design of the acoustic (34–38) and microwave transmission line network systems (6, 39, 40). The causal optimality of broadband metamaterial absorber has been reported in acoustic systems (35, 36). However, to the best of our knowledge, the electromagnetic counterpart has not yet been experimentally realized, which therefore serves as one of our motivating targets. Although metallic ring structures have been extensively studied in the literature (8, 21, 41, 42), it has not been found that they can serve as the basis for broadband microwave absorption. We show that the crucial underlying physics lies in the generation of two high-impedance resonances from the interaction of the electric dipole resonance of the metallic ring with its image resonance, and the resulting impedance matching attained by adding resistive loss to the metallic ring. The latter is usually denoted dispersion engineering (21).

Here, we iterate the following four conceptual-based elements that underpin our absorber design and its excellent performance. First is the use of electrical dipole resonance and the interaction with its image that insures an appreciable magnetic permeability with the generation of two high-impedance resonances in the microwave regime. Second is the use of dispersion engineering via the tuning of the dissipative resistance to achieve broadband impedance matching. Third is the use of self-similar hierarchical structure to extend the absorption spectrum to the ultrabroadband regime. Fourth is the absorption of the diffraction orders in the higher frequency regime by using foam patches. Below, we detail each of the conceptual elements together with their structural realizations.

Results

Metallic Ring.

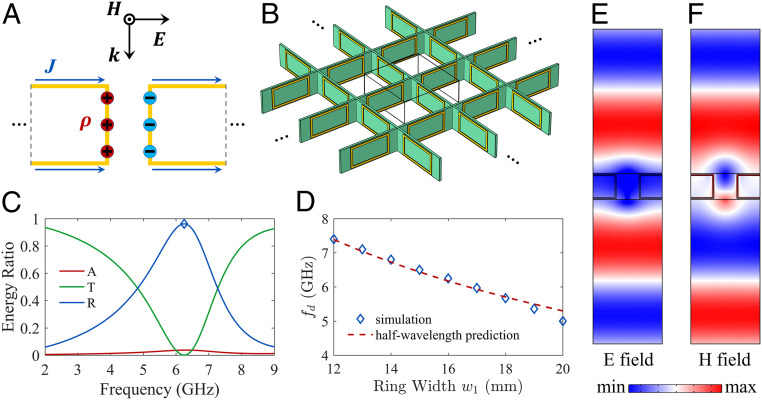
The basic element of our absorber is a rectangular metallic ring, each separated from its neighbor by a capacitive gap (Fig. 1A, two of the half rings are plotted to show the periodic configuration). The rings are embedded on PCB stipes [FR4 with relative permittivity ${\mathit{ϵ}}_1=4.3(1+0.025i)$], which are structured to form a two-dimensional checkerboard array (Fig. 1B) to attain polarization-independent properties. The lattice constant (i.e., lateral spatial periodicity) is a₁ = 24 mm. Detailed geometry information is available in SI Appendix, Sample geometry.

Fig. 1.

(A) The geometry of the metallic ring structure (yellow) and its capacitive gap, serving as the basis for a resonant electrical dipole. Here, only half of the ring is drawn, and the dashed lines imply the periodic conditions. The arrows and circles illustrate the current density and charge density, respectively. (B) The periodic two-dimensional array constructed by the ring structures embedded in the PCB substrates (green plates). The black box denotes one unit cell. (C) Energy ratios of the absorption A, transmission T, and reflection R. (D) A comparison between the simulation results and the half wavelength prediction. The resonant frequencies are plotted as a function of varying the lateral width of the ring. (E and F) The scattered radiating electric field and magnetic field at the 6.25 GHz resonance.

Capacitively-Coupled Electrical Dipole Resonance.

A metallic ring can be regarded as two metallic segments fused together on their two ends. If the length of each metallic segment corresponds to half wavelength of the incident wave, an electrical dipole resonance can be excited. The occurrence of this resonance may be further enhanced through capacitive coupling between the neighboring rings (Fig. 1A). To investigate this dipole resonance through simulations, we apply the periodic boundary condition around the unit cell (indicated by the black frame in Fig. 1B), with an incident plane wave from the top side. The excited dipole mode would radiate upward and downward, and the resulting fields in steady state can be divided into the incident field plus the scattered radiating field. In particular, the energy ratios can be extracted from the S parameters, that is, reflection $R={\left|S_{11}\right|}^2$, transmission $T={\left|S_{21}\right|}^2$, and the absorption A = 1 – R − T. It is shown in Fig. 1C that a resonance is located at 6.25 GHz for our rectangular metallic ring (with width w₁ = 16 mm and height h₁ = 8.3 mm), characterized by the minimal transmission and a maximum in reflection. To verify our understanding that this is indeed a half wavelength electrical dipole resonance, we deviate the width of the ring from its original value w₁ = 16 mm and compare the predicted frequency f_d = c/λ = c/[2(w₁+h₁)] with the resonance peaks given by the simulations. Good agreements are obtained as seen in Fig. 1D. We note that the resonance also occurs with enhanced electric field in the gap between two nearby rings, which means that the resonance is of a collective response. The fact that it is an electric dipole resonance can be further confirmed by the symmetrical radiating electric field pattern and the anti-symmetrical magnetic field pattern (Fig. 1 E and F). Owing to the scattered radiation, the width of the resonance peak is noted to be fairly broad.

Interaction with the Image Mode and the High-Impedance Resonances.

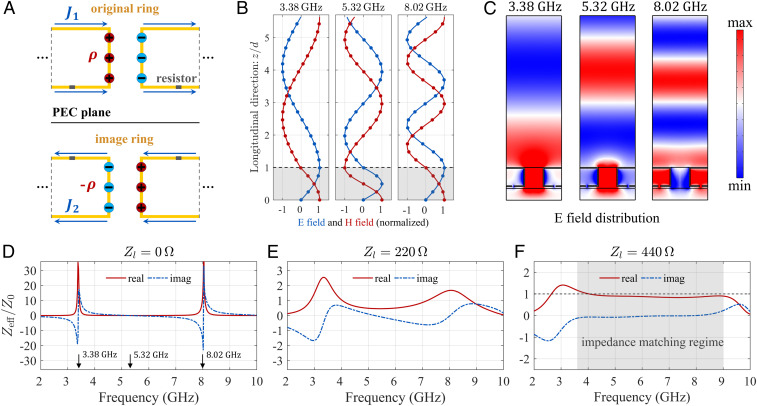
In Fig. 2A, we show the effect of introducing a metallic boundary at the bottom side of the sample. By approximating the metallic boundary as a perfect electric conductor (PEC) plane, its effect can be determined through the interaction of the current loop with its image. At specified frequencies, the retardation effect can lead to high-impedance resonances as detailed below. Consider the current densities J₁ and J₂ in Fig. 2A, equally distant from the PEC plane with a separation d = 14.2 mm. Under the Lorentz gauge (43), the current density is the source term of the wave equation for the vector potential A. In Fig. 2A, J₁ is positive (to the right); it emits a signal that travels with the speed of light toward J₂. Provided the distance between J₁ and J₂—2d in the present case—corresponds to a phase difference of π, then when the signal reaches J₂, it would have acquired an opposite sign. However, since J₂ is along the negative direction, the arrival signal is exactly in phase with the signal emitted by J₂, leading to an enhancement. The enhanced signal would travel back to J₁ with a phase change of π again and encounters an in phase–emitted signal from J₁, and in this manner, the wave amplitude is reinforced back and forth, leading to a longitudinal resonant behavior. Since the electric field corresponds with the time derivative of A, one can expect a maximum of the electric field to occur at the J₁ plane, implying a perfect magnetic conductor (PMC) condition, that is, a high-impedance resonance. Indeed, through simulations, it was found that at 3.38 and 8.02 GHz, the upper surface of the ring structure, that is, the J₁ plane, is indeed an antinode of the electric field, which can be recognized as the artificial PMC effect induced by a magnetic resonance (44–46). Between the two high-impedance magnetic resonances, there exists a magnetic antiresonance with zero impedance at 5.32 GHz, at which the retardation effect leads to a phase change of 2π between J₁ and J₂. It should be noted that the magnetic antiresonance is the electric resonance, and vice versa (13, 28), due to the distinct symmetries of the resonant modes. Similar correspondences were also reported in acoustic systems (47–49).

Fig. 2.

(A) Schematics of the original ring and its mirror image with the presence of the PEC plane. The rings are loaded with two tunable resistors (gray patches). (B) The simulated standing wave patterns for effective medium with n_eff, indicated by gray regions. The blue and red curves denote the E field and H field respectively, with its amplitude normalized to be unity. (C) The simulated standing electric fields for the real ring structure excited by an incident plane wave from the top side. At 3.38 and 8.02 GHz, the upper surface of the ring exhibits antinodes of the E field (PMC effect), while at 5.32 GHz, it is a node for the E field (PEC effect). (D–F) The comparison of the effective normalized impedance with the loaded resistance of 0, 220, and 440 Ω, respectively. The shadowed gray region in F highlights the impedance matching regime from 3.6 to 9 GHz.

We can replace the metallic ring structure by an effective medium with an effective refraction index n_eff (see gray regions in Fig. 2B). It turns out that by setting n_eff = 1.6, 2.0, and 0.66 for 3.38, 5.32, and 8.02 GHz, respectively, the resulting far fields (Fig. 2B) can be fitted to be identical with those shown in Fig. 2C. The same PMC effects are also seen at the upper plane of effective medium, characterized by the electric field antinode and magnetic field node (Fig. 2B). Inside the effective medium, the fields undergo a phase shift of π/2, π, and π/2 for 3.38, 5.32, and 8.02 GHz, respectively. The only “surprise” here is that the phase shift at 8.02 GHz is only π/2 instead of the intuitively expected 3π/2. This is because the metallic ring structure prevents the electric field from having a node inside the ring as one can see in the 8.02 GHz subplots of Fig. 2C. It should be noted that similar considerations leading to a resonance behavior can be applied to the current component in Fig. 2A close to the PEC plane in conjunction with the interaction with its image. That turns out to be unnecessary because the small distance of separation between the current (close to the PEC plane) and its image implies a much higher resonance frequency in which the diffraction effect appears and therefore the underlying physical picture of our description above is no longer valid.

Dispersion Engineering for Broadband Impedance Matching.

The resonant behaviors can be quantitatively reflected in the effective impedance Z_eff(ω). Details of the extraction method (28, 50) for the effective parameters are available in SI Appendix, Extraction method for the effective parameters. For a small loaded resistance ($Z_l\to 0\hspace{0.17em}\text{Ω}$), the effective impedance can be written in Lorentz forms (28, 47):

$$Z_{\text{eff}}\left(\omega \right)={\displaystyle \sum _i\frac{-i\omega {\alpha }_i}{{\omega }_i^2-{\omega }^2-i{\beta }_i\omega }},$$ [1]

where ω_i is the ith resonant frequency, α_i is its oscillation strength, and β_i denotes its dissipation coefficient. In Fig. 2D, we show that at 3.38 and 8.02 GHz, the real part of Z_eff exhibits high peaks, while at 5.32 GHz, the impedance is the zero (magnetic antiresonance). Since the impedance matching condition requires $Z_{\text{eff}}\cong Z_0$ (see more details on theoretical requirements for near-perfect absorption in SI Appendix, Theoretical requirements for near-perfect absorption), we would like to spread the high impedance of the two magnetic resonances evenly over the frequency range in between the two resonances. This can be achieved by fixing two chip resistors symmetrically at the bottom of the ring (see gray patches in Fig. 2A). By adjusting the load resistance Z_l, it can be seen from Fig. 2 D–F that at an optimal value of Z_l = 440 Ω, the real part of Z_eff is almost matched to Z₀, while the imaginary part is close to zero (see the gray highlighted regime from 3.6 to 9.0 GHz in Fig. 2F). In this manner, we have shown that the metallic ring structure, together with the PEC backing, can exhibit excellent absorption from 3.6 to 9 GHz with more than −20 dB reflection loss (Fig. 3A). It should be noted that the dispersion engineering for impedance matching can only be effective over a limited frequency range. This is due to the fact that over all frequencies, the causality-governed Kramer–Kronig relations (43) must hold.

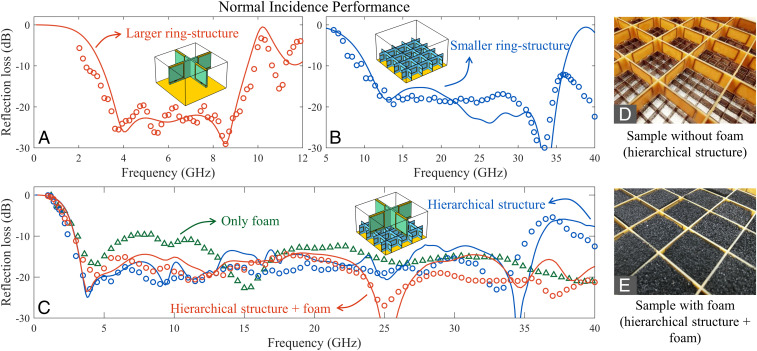
Fig. 3.

Normal incidence performance. (A and B) The reflection loss spectra (in dB scale) of the individual larger-ring structure and the smaller ring structure, respectively. (C) The spliced reflection loss spectra (in dB scale) of the hierarchical structures with and without the foam patches together with the same results for the foam with identical thickness as the sample. The solid lines denote the simulation results with the unit cells shown in Insets in each figure, and the circles/triangles are the measured results. (D) A photo of the fabricated sample assembled into two-dimensional arrays with hierarchical structures. (E) The same for the structure with foam patches filled in the interstitial space.

Self-Similar Hierarchical Structures.

The physical phenomena of waves are closely linked to the ratio between the wavelength and the size of the structure, usually denoted the scaling factor (34). For instance, if the dimensions of the ring structure are uniformly scaled by α (<1), while the material properties (e.g., the resistance, dielectric constant of the substrate) are kept unchanged, the operating band can be extended to a higher frequency range, that is, from 3.6/α-9/α GHz. In our case, the optimal value of α is chosen to be 1/4 simply because the other values cannot cover either the high-frequency or the low-frequency end of the absorption spectrum as well as 1/4. Details on the scaling factor determination is given in SI Appendix, Scaling factor determination. In actual implementation of the scaled structures, not every material property can be kept the same under realistic considerations [e.g., the dielectric constant of the high-frequency PCB substrate is usually smaller in the industrial production, which is Rogers 5880 with relative permittivity ${\mathit{ϵ}}_2=2.2\left(1+0.0009i\right)$ in our case]. Therefore, the geometric parameters for the smaller ring structure have to be slightly adjusted to retain the scaling property of the operating frequency band by a repeat application of dispersion engineering. However, the loaded resistance (Z_l = 440 Ω) remains unchanged, and the lattice constant is strictly scaled by the 1/4 factor (i.e., a₂ = a₁/4). Geometry information for optimized smaller ring structures is also available in SI Appendix, Sample geometry. In this way, it turns out that the reflection loss of smaller ring structures is close to −20 dB from 10 to 36 GHz (Fig. 3B).

Splicing the Reflection Loss Spectra.

The ultimate purpose of designing two similarly structured arrays with scaled spatial dimensions is to splice the absorption spectra to attain the ultrabroadband regime. Remarkably, the integrated hierarchical structure (see Fig. 3 C, Inset for the schematic of the unit cell and Fig. 3D for a photo of fabricated sample) exhibits spliced ultrabroadband reflection loss spectrum from 3 to 35 GHz (see the blue circles in Fig. 3C). Good agreements are witnessed between the simulation and experimental results. Note that the overall thickness is the summation of the height of the first layer l₁ and second layer l₂ (i.e., d = l₁ + l₂ = 14.2 mm). However, diffraction invariably arises in the higher frequency range over such an ultrabroadband coverage. A generalized definition of “absorption” is needed by including diffraction into consideration (25) because our absorber works beyond the subwavelength regime, that is, f > c/a₁ = 12.5 GHz. In the absence of transmission, reflection loss in the linear scale is defined by 1 – R, which is actually the summation of diffraction and absorption (i.e., 1 – R = D + A). Here, the energy ratios can be expressed by the S parameters: $R={\left|S_{11}\right|}^2$, $D={\displaystyle \sum }_{i>1}{\left|S_{i1}\right|}^2$. In logarithmic dB scale, reflection loss is defined by the value of 10 log₁₀(R) in accordance with the textbook definition in microwave engineering (6).

Ultrabroadband Reflection Loss.

We interpret the reflection loss mechanisms of the integrated hierarchical structure as follows. Absorption in the lower frequency range (by the upper layer) is minimally affected by the lower layer, owing to the smaller dimensions of the rings as compared to the relevant wavelength. The individual layer’s absorption mechanism has been guaranteed by impedance matching as described in Fig. 2 D–F. In the higher frequency regime, however, the upper layer would diffract a part of the incident wave, while the lower layer would absorb the remaining part. In order to dissipate the diffracted components, we use the microwave-absorbing foam patches (Dalian Dongxin FCT40) to fill the upper layer interstitial spaces of the checkerboard array without increasing the overall thickness (Fig. 3E). The foam patches (with a thickness of 9 mm) are chosen to be porous and dissipative with low mass density and small loss angle (see details on the simulation modeling of the foam in SI Appendix, Modeling the foam by using the Debye model). In this way, the reflection loss spectrum is extended to 40 GHz (see the orange circles in Fig. 3C) with a large fraction of the diffraction effectively absorbed inside the sample, which can be verified through simulations (see the calculation of diffraction orders in SI Appendix, Diffraction orders and their absorption). In fact, we believe that with the foam patches, the sample can exhibit excellent absorption at frequencies much higher than 40 GHz, which is the limit of our measurement system.

Performance Evaluation and Comparison.

We introduce two quantitative indicators to evaluate the measured performance as well as to facilitate the comparison with published prior results. The first indicator is the causality ratio defined by R_c = d/d_min in which the actual thickness of our absorber d = 14.2 mm, and the causality-dictated minimum thickness (33, 36) is given by

$$d_{\text{min}}=\frac{1}{4{\pi }^2}\frac{{\mu }_0}{{\mu }_{\text{eff}}}\left|\underset{0}{\overset{\infty }{{\displaystyle \int }}}\text{ln}\left(R\left(\lambda \right)\right)\right|d\lambda ,$$ [2]

where R(λ) is the reflected energy as a function of the wavelength λ, and ${\mu }_0/{\mu }_{\text{eff}}\cong 1$ for nonmagnetic absorbers, which is the case considered in this work. By inserting the measured reflection spectrum (orange circles in Fig. 3C) of the hierarchical structures with foam patches into Eq. 2, we obtain d_min = 13.5 mm and R_c = 1.05, which means that our absorber closely approaches the causality limit. The causality ratio R_c for the hierarchical structure without the foam patches (Fig. 3D) does not deviate from 1.05 too much since the higher frequency part has negligible contribution to the integral of Eq. 2. The second indicator is the relative bandwidth, defined by

$$B_w=2(f_2-f_1)/(f_2+f_1),$$ [3]

where f₁ and f₂ denote the minimum and maximum frequencies corresponding to the operating band for at least −10 dB reflection loss (25). In our case, f₁ = 3 GHz and f₂ = 40 GHz, so B_w = 1.72. It should be noted that if $f_2/f_1\to \infty$, B_w approaches the limiting value of 2. While the second indicator B_w attaches the importance to the effective frequency bandwidth, the causality ratio R_c emphasizes the optimal trade-off between the low-frequency performance and the actual sample thickness. Based on these two indicators (R_c and B_w), we are able to comprehensively evaluate the overall performance of an absorber.

We summarize in Table 1 the performance of the present absorber and a number of competitive metamaterial absorbers (22, 23, 25, 28) as well as the conventional foam absorber with the same thickness (14.2 mm). The latter comparison is obligated by our use of the foam patches in our sample, with the purpose of showing the foam to be only partially responsible for the success of our absorber. It can be seen that our absorber has a larger B_w and a smaller R_c than all the competitors. For example, while the absorber of ref. 28 has a better absorption performance, its thickness is relatively large, and the operating bandwidth is limited. Also, despite a thin thickness of 3.53 mm for the absorber in ref. 25, the reflection loss is not as competitive as others. It is worth mentioning that the conventional foam is already an effective absorber, especially for higher frequencies (see green triangles in Fig. 3C). In fact, other carbon-based materials (51–54) also exhibit similar excellent absorption capabilities at higher frequencies.

Table 1.

The performances of our absorber compared with the microwave-absorbing foam and other selected competitive metamaterial absorbers

Reference	Thickness	Operating band	B w	Averaged reflection loss (dB)	R c
Our work	14.2 mm	3 to 40 GHz	1.72	−19.4 dB	1.05
Foam	14.2 mm	3 to 40 GHz	1.72	−15.4 dB	1.40
Ref. 22	10.0 mm	5.2 to 18.0 GHz	1.10	−14.3 dB	N.A.
Ref. 23	13.3 mm	2.1 to 9.1 GHz	1.25	−17.7 dB	1.23
Ref. 25	3.5 mm	6.8 to 19.4 GHz	0.96	−14.0 dB	N.A.
Ref. 28	40.0 mm	1.1 to 2.0 GHz	0.58	−20.9 dB	1.43

The operating bands and the related averaged reflection loss are evaluated from the published experimental results. The displayed values of R_c are from the relevant references. Here, N.A. means not available in cited works.

Polarization Independence and Oblique Incidence Performance.

In a complex electromagnetic environment, the performance of a microwave absorber must be averaged over various oblique incident angles under random polarizations. Hence, it is of great importance to check the absorption performance with different polarizations as well as with oblique incident angles. Because of the symmetry of the designed structure, at normal incidence, the transverse electric field (TE) excitation and transverse magnetic field (TM) excitation are identical and therefore lead to the same reflection loss. Hence, it can be concluded that the absorber is polarization independent at normal incidence (SI Appendix, Polarization independence and oblique incidence performance).

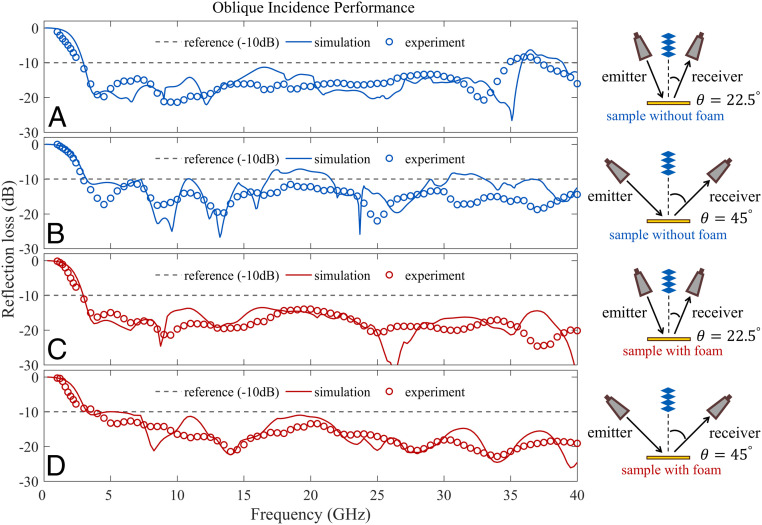
At oblique incidence, the reflection coefficients are different for the TE and TM polarizations (12). The reflection loss spectra of the two cases are separately displayed in SI Appendix, Polarization independence and oblique incidence performance. Here, for simplicity, we average the reflection loss with TE and TM polarizations and plot the results in Fig. 4. Both the simulation and experimental results show that under 22.5° oblique incidence (Fig. 4 A and C), the reflection loss averaged over 3 to 40 GHz is −17.6 dB, comparable with that under normal incidence in Fig. 3C, indicating the sample’s insensitivity to the incidence angle. For a larger oblique incident angle of 45°, even without the foam, the hierarchical structure can already display efficient performance with over −10 dB reflection loss (Fig. 4B). With the assistance of the dissipative foam patches, the reflection loss spectrum is smoothed (Fig. 4D) and displays an average reflection loss of −16.3 dB. The dissipation of the foam patches converts the majority of diffraction components into absorption inside the sample. This is evidenced through simulations by a direct calculation of the diffracted energy, presented in SI Appendix, Diffraction orders and their absorption.

Fig. 4.

Oblique incidence performance. (A and B) The reflection loss of the sample without the foam patches. (C and D) The reflection loss of the sample with the foam patches. The reflection loss spectra (in dB scale) under oblique incidence are averaged using the data of TE and TM polarizations. The solid lines are the simulation results of the reflection loss, while the open circles denote the measured results. For comparison, A and C show the results under an oblique incidence angle of 22.5°, while B and D are corresponding to 45°. The gray dashed lines denote the reference for −10 dB reflection loss.

Conclusion and Outlook

We report a microwave absorber design based on the collective (electrical) dipole resonance that, upon interaction with its image through a PEC plane, leads to two high-impedance resonances. With deliberately controlled loss in conjunction with a staggered hierarchical structure, near-perfect absorption is achieved from 3 GHz onward, covering the whole 5G high-frequency bands. The thickness of the hierarchically structured absorber very closely approaches the causality limit as dictated by the reflection spectrum. Despite the excellent performance, the basic building element is a simple metallic ring printed on PCB substrate, which is foreseen to facilitate the future applications with low-cost mass production. In past works, the metamaterial absorbers often work in the subwavelength regime, below a cutoff frequency determined by the lattice constant. Our absorber breaks this limit by introducing self-similar structures attendant with the absorption of the diffracted beams by dissipative foam, thereby extending the absorption capability to a much higher frequency regime. The basic conceptual elements adopted in this work may have potential in designing versatile devices with broadband performance, such as tunable waveguides (55–57), electromagnetic cloak (58, 59), metamaterial-based antenna (60), achromatic metalens (61), etc.

Materials and Methods

Sample Fabrication.

The PCB technology was adopted to fabricate the sample. All the metallic rings were printed with electro-deposited copper, which is available for high etching accuracy and large circuit density. With the surface-mounted technology, the lumped chip resistors (R0201 or R01005) were soldered on either the larger or the smaller rings. The resistor dimensions were chosen to be small enough to minimize the parasitic effects (6) at higher frequencies. The circuit board was subsequently cut into long strips with equally spaced rectangular slots. The stripes were then assembled into a square checkerboard array for both the larger and smaller metallic rings. Finally, the microwave-absorbing foam (Dalian Dongxin FCT40) was cut into square patches to fill the interstitial spaces of the square larger-ring array. The lateral dimension of the measured sample is 22 × 22 cm.

Far-Field Measurements.

The sample performance was measured inside a microwave dark room with the dimensions of 1.5 × 1.5 × 2.5 m. The six inner walls of the dark room were covered by pyramidal-shaped, thick microwave-absorbing foam to create a reflection-free space. We adopted three pairs of double-ridge antennas, which were responsible for the frequency bands 1 to 20 GHz (HZ-10200-DRHA-10), 6 to 18 GHz (MX-0618-DRHA-16), and 18 to 40 GHz (MX-1840-DRHA-16). For a targeted frequency band, one antenna served as an emitter and the other as the receiver. If the characteristic diameter of the antenna is D_h, the distance between the antenna and the sample should satisfy the relation $L_{hs}>2D_h^2/\lambda$ so as to reach the far-field plane wave radiation condition. The antennas were connected to the vector network analyzer (Keysight N5320B) via the coaxial cables (Lair UF40) whose cutoff frequency is higher than 40 GHz. A flat, 3.2-mm-thick aluminum plate with the same lateral dimensions as the sample was used to calibrate each measurement. We varied the polarizations of the incident microwave by rotating the azimuth of the antenna horn.

Simulation Methods.

In numerical simulations, the CST Studio Suite was adopted for fast and efficient computation of the individual layer of the absorber, thanks to the finite-difference time-domain method. The optimization toolbox and parametric-scanning function of CST Studio Suite can be used to find the best parameters. Another commercial software we used is COMSOL Multiphysics (Radio Frequency Module) based on the finite element method. The COMSOL Multiphysics was responsible for the calculation of reflection and diffraction for the hierarchical structure. Both software support the lumped elements used to model the loaded resistors. For the absorption frequency band without diffraction (in the subwavelength region $a_1<\lambda$), there was no difference whether we used PEC and PMC side boundaries or the Floquet periodic boundary conditions to guide the plane wave with normal incident angle. However, for the case involving diffraction orders and oblique incidence, only the Floquet periodic boundary condition was appropriate, and the diffraction was calculated by using only COMSOL Multiphysics. The mesh size was set to be smaller than 1/6 wavelength in order to ensure accurate outcomes.

Data Availability

All study data are included in the article and/or SI Appendix.