H₂ in Antarctic firn air: Atmospheric reconstructions and implications for anthropogenic emissions

Significance

Atmospheric molecular hydrogen (H₂) levels influence the lifetime of greenhouse gases and the levels of tropospheric ozone. The extent to which human activities have influenced the global H₂ budget is not well established due to our limited knowledge of past variations in atmospheric H₂ levels. Here, we reconstruct atmospheric H₂ over the last 150 y using Antarctic firn air. We find a roughly 70% rise in atmospheric H₂ over the twentieth century that can be attributed to human activities. Surprisingly, there is no evidence that anthropogenic emissions of H₂ decreased during the late twentieth century due to reduced automotive emissions associated with air pollution controls. It is likely that nonautomotive anthropogenic H₂ emissions have been underestimated.

Abstract

The atmospheric history of molecular hydrogen (H₂) from 1852 to 2003 was reconstructed from measurements of firn air collected at Megadunes, Antarctica. The reconstruction shows that H₂ levels in the southern hemisphere were roughly constant near 330 parts per billion (ppb; nmol H₂ mol⁻¹ air) during the mid to late 1800s. Over the twentieth century, H₂ levels rose by about 70% to 550 ppb. The reconstruction shows good agreement with the H₂ atmospheric history based on firn air measurements from the South Pole. The broad trends in atmospheric H₂ over the twentieth century can be explained by increased methane oxidation and anthropogenic emissions. The H₂ rise shows no evidence of deceleration during the last quarter of the twentieth century despite an expected reduction in automotive emissions following more stringent regulations. During the late twentieth century, atmospheric CO levels decreased due to a reduction in automotive emissions. It is surprising that atmospheric H₂ did not respond similarly as automotive exhaust is thought to be the dominant source of anthropogenic H_2. The monotonic late twentieth century rise in H₂ levels is consistent with late twentieth-century flask air measurements from high southern latitudes. An additional unknown source of H₂ is needed to explain twentieth-century trends in atmospheric H₂ and to resolve the discrepancy between bottom-up and top-down estimates of the anthropogenic source term. The firn air–based atmospheric history of H₂ provides a baseline from which to assess human impact on the H₂ cycle over the last 150 y and validate models that will be used to project future trends in atmospheric composition as H₂ becomes a more common energy source.

Molecular hydrogen (H₂) is an abundant and reactive constituent of Earth’s atmosphere. The utilization of H₂ as an energy source emits no carbon to the atmosphere if produced from water using renewables, and increasing adoption of H₂ as a substitute for fossil fuels is likely (1). As the H₂ energy sector expands, anthropogenic emissions are expected to increase due to leakage. Projecting the effects of increasing anthropogenic emissions requires a comprehensive understanding of the biogeochemical cycle of H₂. Reconstructing the paleoatmospheric levels of H₂ contributes to that understanding by establishing the baseline for quantifying anthropogenic emissions since the industrial revolution.

Presently, the average atmospheric abundance of H₂ is 530 parts per billion (ppb; nmol H₂ mol⁻¹ air), and the atmospheric lifetime is about 2 y (2). The budget of H₂ is complex, including both natural and anthropogenic terms. Globally, the largest source of H₂ is the photolysis of formaldehyde, formed by the atmospheric oxidation of methane and nonmethane hydrocarbons (NMHCs). Other major sources include direct emissions from fossil fuel combustion and biomass burning. N₂ fixation both on land and in the ocean is a small additional source. The major sink for atmospheric H₂ is uptake by soil microbes, with oxidation by OH accounting for the remaining losses. H₂ levels are higher by about 3% in the southern hemisphere than in the northern hemisphere due to the hemispheric asymmetry of the soil sink (2–5).

Atmospheric H₂ levels impact Earth’s radiative budget and air quality. H₂ serves as a sink for the OH radical, increasing the atmospheric lifetime of radiatively important trace gases like methane. Additionally, the reaction of H₂ with OH results in the catalytic production of O₃ in the troposphere (2, 6–8). Oxidation of H₂ by OH in the stratosphere leads to increased concentrations of HO₂ and water vapor. The increase in these species will have indirect radiative effects due to losses of ozone and alterations to the distribution of polar stratospheric clouds. Increased stratospheric concentrations of water vapor will also have direct radiative effects via increased infrared absorption (7, 9–12).

The modern instrumental record of tropospheric H₂ abundance began in the late 1980s (2, 13). Mid-twentieth century studies reported a wide range (400 to 2,000 ppb), which likely reflects analytical issues and/or influence from urban pollutants (14–16). The surface flask air measurements of Khalil and Rasmussen (13), the National Oceanic and Atmospheric Administration Global Monitoring Laboratory (NOAA/GML; refs. 2, 17), and the Commonwealth Scientific and Industrial Research Organisation (CSIRO; ref. 18) show atmospheric levels of H₂ of 510 to 550 ppb during the late 20th and early 21st centuries at background sites around the world. In situ measurements from Cape Grim, Tasmania, and Mace Head, Ireland, made by the Advanced Global Atmospheric Gases Experiment (AGAGE) show similar levels of atmospheric H₂ during the same time period (19). To date, there have been two published firn air studies of the historical trends of atmospheric H₂. Petrenko et al. (20) reconstructed northern hemisphere H₂ from Greenland firn air measurements. Their results show an increase in atmospheric H₂ levels from 450 to 520 ppb during the 1960s to a peak near 550 ppb during the late 1980s or early 1990s, then a recent decline to about 515 ppb in 2010. The peak and recent decline are inconsistent with modern flask measurements that show roughly constant H₂ levels during the 1990s (2, 17, 19). The authors note that the firn air model used for the reconstruction does not include pore close-off fractionation of H₂, and it is possible that the inferred peak is a modeling artifact (20, 21). Firn air measurements of H₂ from the South Pole showed that atmospheric H₂ increased from 350 ppb to 550 ppb over the twentieth century in the high southern latitudes (22). This reconstruction does not include a late twentieth century peak or decline, and the reconstructed levels of H₂ are consistent with available modern flask measurements beginning in the late 1980s. The increase in atmospheric H₂ is primarily attributed to increasing anthropogenic emissions and increasing atmospheric concentrations of methane over the twentieth century.

Here we report H₂ measurements in firn air samples collected from the Megadunes site (80.78 °S, 124.49 °E, Alt: 2,283 m) in central Antarctica during January of 2004 and analyzed at NOAA/GML in April 2004 (23, 24). Megadunes is a complex site, with very low annual accumulation rates and an unusually large amplitude of surface topography. The oldest firn air ever recovered, with a mean CO₂ age of 140 y, was sampled during this campaign (23). A firn air model is used to reconstruct southern-hemisphere atmospheric H₂ levels since the 1850s. The reconstruction is compared to the existing South Pole firn air reconstruction (22), and implications of the reconstructed atmospheric history for the global budget of H₂ are discussed.

Firn Air Model Inversion and Recovering the Atmospheric History

The Megadunes firn air H₂ data were corrected for detector nonlinearity and calibration drift and adjusted from the NOAA96 to the MPI09 calibration scale (SI Appendix; ref. 25). Then the firn air data were corrected for gravitational fractionation and depth-averaged (SI Appendix). To recover an atmospheric history of H₂, the measurements are inverted using depth-dependent age distributions or Green’s functions (G(z,t); ref. 26). The Megadunes firn air model is initialized with no H₂ in the firn air column, then forced with a 1-y pulse of H₂ at the surface, after which the surface concentration is set to 0. The model is integrated for 300 y, and the evolution of the pulse is tracked as a function of depth and time to produce the Green’s functions, which allow us to determine the modeled levels of H₂ in the firn (H₂(z)_model) from a given atmospheric history (H_2(atm)(t)) according to Eq. 1:

$$H_2{\left(z\right)}_{model}=\sum _{t=0}^{300}{H}_{2\left(\text{atm}\right)}\left(t\right)\ast G\left(z,t\right),$$ [1]

This technique is computationally efficient and allows for rapid iteration over many possible atmospheric histories in order to optimize the fit between the modeled and measured depth profiles. This inversion problem is under-constrained, and there are an infinite number of atmospheric histories that give good fits to the measured depth profile. To prevent unrealistic extreme fluctuations in the reconstructions, we employ a cost function which includes a smoothing term (26):

$$f={\chi }_{\text{red}}^2+S=\sum _{i=1}^n\frac{\left(\frac{{\left(H_2{\left(z\right)}_{\text{model}}-H_2{\left(z\right)}_{\text{obs}}\right)}^2}{{\sigma }^2}\right)}{n-1}+\alpha \sum _{t=0}^{300}{\left(\frac{{\partial }^2{H}_{2\left(\text{atm}\right)}\left(t\right)}{\partial t^2}\right)}^2,$$ [2]

where f is the cost, χ²_red is the reduced χ² statistic, S is the smoothing term, σ is the analytical uncertainty (Fig. 1B), n is the number of unique depths, and α is a prescribed, dimensionless weighting parameter for the smoothing term. The MATLAB solver “fmincon” is used to minimize f.

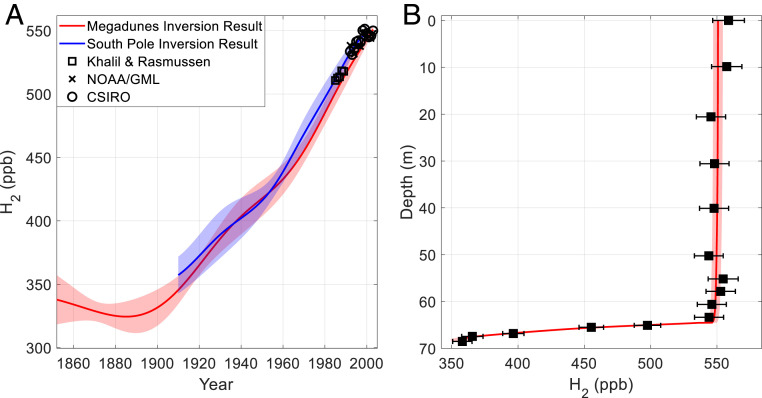
Fig. 1.

Reconstructions of atmospheric H₂ and associated Megadunes firn air depth profiles. (A) Red line and shading—mean inferred atmospheric history and ±1σ uncertainty from 4,000 Monte Carlo inversions on the Megadunes firn air measurements (see Firn Air Model Inversion and Recovering the Atmospheric History) using α = 8*10⁻²; blue line and shading- inferred atmospheric history and ±1σ uncertainty from a South Pole firn air reconstruction (22); and black squares, black x’s, and black circles—observed atmospheric H₂ annual means from high southern latitude sites from 1985 to 1989 and 1992 to 2003 (2, 13, 17, 18); (B) Black squares and error bars—depth-averaged Megadunes firn air H₂ measurements corrected for detector nonlinearity, calibration drift, and gravitational fractionation as described in SI Appendix. Error bars are the propagated ±2% measurement uncertainty; red line and shading show the mean modeled H₂ depth profile and ±1σ uncertainty resulting from the inferred atmospheric history plotted in red in A.

The initial guess for the atmospheric H₂ history is a linear ramp from some “preindustrial” level of H₂ in 1704 to 540 ppb in 2003. The 1704 level is fixed at its initial value, and the H₂ levels for 1705 to 2003 are allowed to vary to minimize f. In order to assess the sensitivity of the inversion to the initial guess, the H₂ level in 1704 is initialized at four different values: 270 ppb, 310 ppb, 350 ppb, and 390 ppb based on the early twentieth century levels from Patterson et al. (22). The inversion is run for each initial guess and the results are compared. To assess sensitivity to smoothing, we vary α across an order of magnitude (8*10⁻³ and 8*10⁻²). To determine the impact of analytical uncertainty, we use a Monte Carlo method in which we repeatedly sample the normal distributions defined by the depth-averaged measurements and the analytical uncertainty at each depth (Fig. 1B). We then invert the synthetic depth profiles that are generated by the repeated sampling. We performed 1,000 Monte Carlo samplings at each combination of initial condition and α for a total of 8,000 inversion runs, accounting for uncertainties due to initial conditions, smoothing, and analytical uncertainties. The Monte Carlo runs do not assess bias in the modeling parameterizations or Green’s functions. Model uncertainties and bias are addressed in a later section.

Inversion Results and the Atmospheric History

The Monte Carlo inversion results show that the reconstruction after 1852 is insensitive to the assumed “preindustrial” level of H₂ (SI Appendix, Fig. S4). Here, only results after 1852 for α = 8*10⁻² are discussed. The choice of α does not affect the main conclusions of this work. Results using α = 8*10⁻³ are given in SI Appendix (SI Appendix, Fig. S5). The inversion result is the average of the 4,000 Monte Carlo runs (Fig. 1A). H₂ levels were 330 ± 15 ppb from 1852 to 1890. In 1890, atmospheric H₂ begins to increase at a rate of 1.5 ppb y⁻¹ until 1960. After 1960, the rate of atmospheric increase rises to 2.5 ppb y⁻¹. Atmospheric H₂ levels reach 550 ppb in 2002. The inversion result is broadly consistent with the previous South Pole firn air reconstruction of H₂ (Fig. 1A; ref. 22). Notably, the firn air history includes a late twentieth century rise in southern-hemisphere H₂ levels.

Modern flask air measurements are in good agreement with the inversion result and support the late twentieth century rise in H₂ (Fig. 1A). These include flask air measurements from 1985 to 1989 at Palmer Station, Antarctica, and Cape Grim Observatory, Tasmania, made by Khalil and Rasmussen (13), from 1992 to 2003 at Palmer, Syowa, South Pole, and Halley Stations, Antarctica, and Cape Grim Observatory, Tasmania, made by NOAA/GML (2, 17), and from Casey, South Pole, and Mawson Stations, Antarctica, and Cape Grim and Macquarie Island, Tasmania, made by CSIRO (18). The NOAA/GML flask measurements were adjusted from the NOAA96 to the MPI09 calibration scale (SI Appendix). One feature in the flask air measurements that is not evident in the firn air history is the abrupt increase in atmospheric H₂ from 1997 to 1998 likely due to El Niño–Southern Oscillation-related biomass burning. This H₂ pulse is not evident in the firn air history because of diffusive smoothing in the firn air column (see Fig. 3, Insets; refs. 18, 19, 27). The surface flask air measurements were not used to constrain the inversion.

Bias and Uncertainty in the Inversion Technique

The Monte Carlo method described above assesses uncertainty in the inversion resulting from measurement uncertainty, but it does not assess bias or uncertainty in the model parameterizations (e.g., molecular diffusion) or the Green’s functions used in the inversion. To assess bias or uncertainty in the inversion technique, we use the same methods to invert the measured depth profiles of CH₄ and CO₂ at Megadunes. The inversion results are then compared to the established atmospheric histories of CH₄ and CO₂. Atmospheric CH₄ and CO₂ levels over the last several centuries are well constrained by high-resolution ice core measurements from Law Dome and modern flask measurements from NOAA/GML (28–31). When the firn air model is forced with these atmospheric histories, modeled depth profiles show a small bias in the lock-in zone relative to measured depth profiles (SI Appendix, Fig. S3).

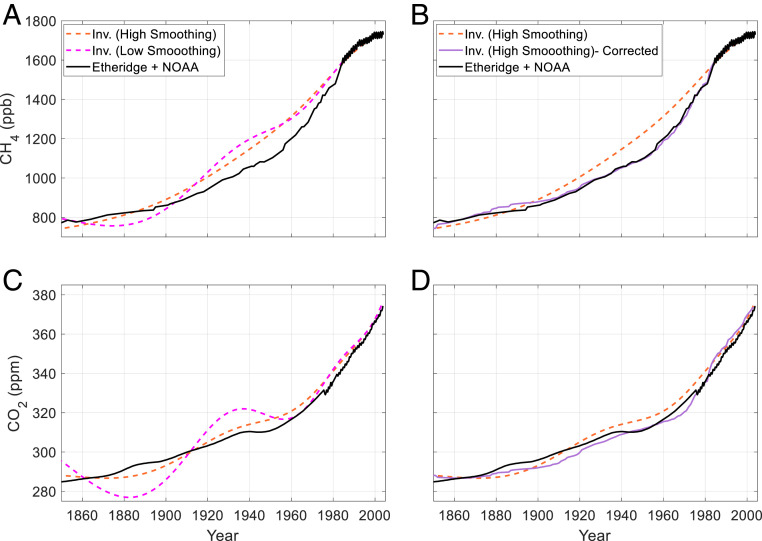
For CH₄, the bias between the inversion result and the Law Dome/modern flask record increases from near 0 early in the record to about 15 y in the mid-twentieth century, then decreases to 0 around 1980 (Fig. 2A). The R² between the firn air history and the established history is 0.954 with an average error of 4.8% (52 ppb). The CO₂ firn air history shows less bias than the CH₄ history with an R² of 0.978 and average error of 1.0% (2.9 ppm; Fig. 2C). The smaller bias for CO₂ is expected because the model diffusivities were tuned using CO₂ (Methods).

Fig. 2.

Inversion results and empirically corrected inversion results for CO₂ and CH₄ compared to the Law Dome/modern flask atmospheric histories. (A) Dashed orange line: inversion result for CH₄ using high smoothing; dashed magenta line: inversion result for CH₄ using 10% of the smoothing used for the “high smoothing” inversion, included for comparison; and solid black line: well-established atmospheric history of CH₄ from Etheridge et al. (29) and Dlugokencky (30). (B) Dashed orange line and solid black line: as in A; solid purple line: inversion result with high smoothing with the empirical correction applied (see Bias and Uncertainty in the Inversion Technique). (C and D) As in A and B, respectively, for CO₂; the established atmospheric history is from Etheridge et al. (28) and Dlugokencky (31).

We assume that the differences between the reconstructions and the Law Dome/modern flask atmospheric histories reflects uncertainty in the physical parameterizations or tuning of the diffusivities in the firn air model. We can use the results from the CH₄ and CO₂ reconstructions to further refine the inversion. This was done by calculating the age correction required to optimize the fit between the firn air CH₄ and CO₂ reconstructions to the Law Dome/modern flask atmospheric histories. The correction is formulated as a time-dependent age offset (B(t)) for the CH₄ and CO₂ mixing ratios at each year of the reconstruction. We use the MATLAB solver “fmincon” to minimize a new cost function (j) and optimize B(t):

$$j=R^2+S$$

$$=\sum _{t=0}^{300}{\left[X_{\left(CH4\_inv\right)}\left(t+B\left(t\right)\right)-X_{\left(CH4\_hist\right)}\left(t\right)\right]}^2+\sum _{t=0}^{300}{\left[X_{\left(CO2\_inv\right)}\left(t+B\left(t\right)\right)-X_{\left(CO2\_hist\right)}\left(t\right)\right]}^2+\beta \sum _{t=0}^{300}{\left(\frac{{\partial }^{2}B\left(t\right)}{\partial t^2}\right)}^2,$$ [3]

where R² is the sum of the squared residuals for both CO₂ and CH₄, S is a smoothing term, X_{(CH4_inv)}(t) and X_{(CO2_inv)}(t) are the reconstructed firn air history of CH₄ and CO₂ respectively, X_{(CH4_hist)}(t) and X_{(CO2_hist)}(t) are the well-constrained atmospheric histories of CH₄ and CO₂, respectively, and β is an arbitrary weighing parameter for the smoothing term. As expected, applying this correction to the CH₄ and CO₂ reconstructions yields better agreement with the established atmospheric histories. For CH₄, R² increases from 0.954 to 0.998, and the average error decreases from 4.8 to 1.2% (52 to 11 ppb). For CO₂, R² increases from 0.977 to 0.982 and the average error decreases from 1.0 to 0.8% (2.9 to 2.6 ppm).

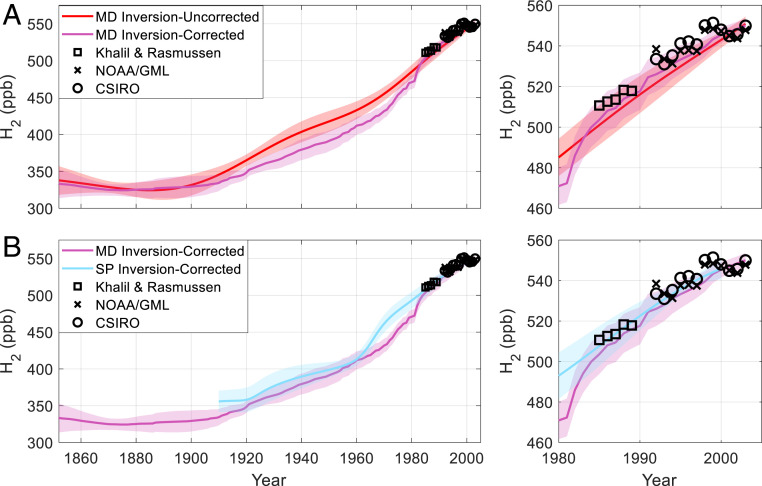
This correction has little effect on the Megadunes H₂ reconstruction before 1900 and after 1980 (Fig. 3). Between 1900 and 1980, the corrected result is on average 4.6% (18.9 ppb) lower than the uncorrected inversion result. We conducted a similar exercise for the South Pole firn air H₂ reconstruction from Patterson et al. (22). CH₄ and CO₂ depth profiles from that firn air campaign were inverted, and Eq. 3 was used to calculate an empirical correction. As with Megadunes, this correction has a relatively minor effect on the H₂ reconstruction, and there is good agreement between the corrected reconstructions from the two sites (Fig. 3B).

Fig. 3.

Atmospheric reconstructions of H₂ with empirical corrections applied. (A) Red line and shading: Megadunes inversion result and ±1σ uncertainty as in Fig. 1A; purple line and shading: Megadunes Inversion result and ±1σ uncertainty using the empirical correction; black squares, black x’s, and black circles: atmospheric H₂ annual means from high southern latitude sites from 1985 to 1989 and 1992 to 2003 as in Fig. 1A. (B) Purple line and shading, black squares, black x’s, and black circles: as in A; blue line and shading: corrected South Pole inversion and ±1σ uncertainty; and right panels: expanded view of the late twentieth century.

Modeling the H₂ Budget

A steady-state box model of the troposphere was used to develop a simulation of atmospheric H₂ based on estimated changes in various H₂ emissions over the past century. The model is comprised of six 30°-wide zonal boxes. Transport between boxes is parameterized from the modern atmospheric distribution of SF₆ (32). First-order losses of H₂ to soils, OH radicals, oceans, and the stratosphere are included. H₂ sources consist of the following: anthropogenic H₂ emissions (including direct emissions from fossil fuel burning and oxidation of anthropogenic NMHCs), biomass-burning emissions, oxidation of CH₄, oxidation of biogenic NMHCs, and terrestrial and marine N₂ fixation. Annual H₂ emissions are prescribed for 1852 through 2003, and the steady-state H₂ abundance is calculated for each year. The geographic distribution of sources and sinks is assumed to be constant in time, and first-order loss rates for all sinks are fixed.

H₂ emissions change over time due to changes in atmospheric CH₄ levels, biomass burning, and anthropogenic H₂ (Fig. 4 A and B). CH₄ oxidation was scaled with the atmospheric history of CH₄ based on the ice core and instrumental records (29, 30). Biomass burning and anthropogenic emissions were scaled to estimates of historical CO emissions. Sources of atmospheric H₂ and CO are thought to be tightly coupled because incomplete combustion and photochemical oxidation of formaldehyde are the most important sources of both gases (SI Appendix, Table S2; refs. 2–4, 20). We followed the approach of Verhulst (33), who used the biomass-burning CO emissions inventory of Lamarque et al. (34) and an anthropogenic CO inventory based on a top-down analysis of firn air–derived CO atmospheric histories. This approach yields substantially larger anthropogenic CO emissions than bottom-up inventories with an earlier peak (∼1970) and a larger late twentieth century decline (33–35). Bottom-up inventories of anthropogenic CO have previously been shown to underestimate atmospheric CO levels (34–39). The CO inventories used here agree well with the instrumental record and firn reconstructions from Greenland and Antarctica (SI Appendix; refs. 20, 33, 40, 41) and are also consistent with firn air reconstructions of other NMHCs (e.g., refs. 42, 43). We assumed constant H₂/CO molar emissions ratios of 0.46 for biomass burning and 0.23 for anthropogenic emissions. These ratios were chosen to achieve agreement between the box model and the 2003 atmosphere. A small time-dependent change in H₂ emissions from terrestrial N₂ fixation was also assumed based on Fowler et al. (44). A full description of the treatment of each source and sink is given in SI Appendix.

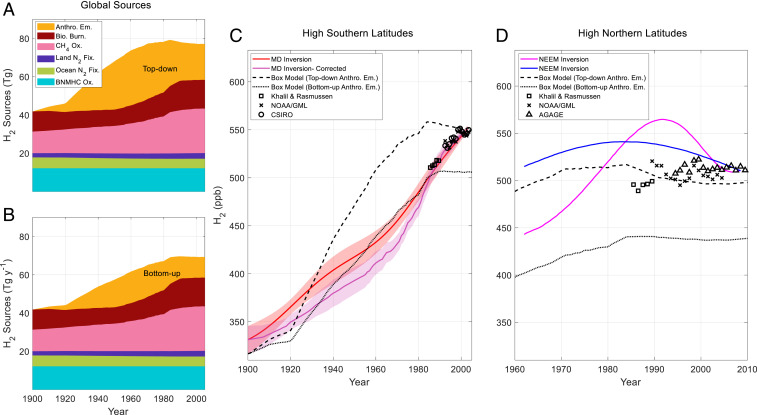
Fig. 4.

H₂ global sources and atmospheric history for the twentieth century from firn air and the box model. (A and B) Global sources estimated from Pieterse et al. and Verhulst (SI Appendix; refs. 5, 33). In A, anthropogenic emissions are estimated using the top-down inventory of Pieterse et al. (5). In B, anthropogenic emissions are estimated from the bottom-up inventory of Vollmer et al. (50). (C) High southern latitude atmospheric H₂ reconstructed from Antarctic firn air (red, purple lines, and shading: as in Fig. 3A) and 60 to 90° S box model simulations using top-down (dashed black line) and bottom-up (dotted black line) anthropogenic emissions. Observed atmospheric H₂ annual means from high southern latitude sites from 1985 to 1989 and 1992 to 2003 are shown (2, 13, 17, 18). (D) High northern latitude northern hemisphere atmospheric histories of H₂ from Petrenko et al. based on firn air measurements at the Northeast Greenland Eemian drill site (NEEM) using the Institute of Arctic and Alpine Research firn air model (blue line) and using the firn air model of Witrant et al. (magenta line: ref. 62) adjusted from the NOAA96 to the MPI09 calibration scale (20). Observed atmospheric H₂ annual means for high northern latitude sites from 1985 to 2008 are shown (2, 13, 17, 19). Box model simulations are shown for 60 to 90° N using top-down (dashed black line) and bottom-up (dotted black line) anthropogenic emissions.

Modeled high southern latitude H₂ levels rise slowly from 306 to 341 ppb from 1852 to 1920, then more rapidly to 558 ppb in 1985. From 1985 to 2000, H₂ levels decrease slowly to 550 ppb (Fig. 4C). The general increasing trend in the box model simulation is consistent with the firn air–derived history. The increase is attributable to growing anthropogenic emissions and rising production from CH₄ oxidation. However, the pace of the rise and rollover in modeled H₂ levels after 1980 does not agree with the steady, gradual increase in the firn air history. Forcing the firn air model with the modeled atmospheric history gives a modeled depth profile that is inconsistent with the measured depth profile (SI Appendix, Fig. S6). This demonstrates that the slower, steady rise in H₂ levels from the firn air history is not the result of over-smoothing in the firn air reconstruction but rather reflects a real inconsistency between the CO-based inventory and the firn air data. A historical H₂ budget with anthropogenic emissions that rise monotonically produces a much better fit to the firn air–derived atmospheric history (SI Appendix, Fig. S7). Such a history is generated by scaling anthropogenic H₂ emissions to CO₂ emissions rather than CO emissions.

The mismatch between the firn air history and the box model simulation calls into question the assumed relationship between H₂ and CO emissions. The plateau and decrease in anthropogenic CO emissions during the late twentieth and early twenty-first centuries was due to stricter air pollution controls, increased use of automotive catalytic converters, and improvements in the efficiency of catalytic converters (35, 45–47). Automobile exhaust has been estimated to make up >80% of total anthropogenic H₂ emissions (4), and pollution controls are believed to have dramatically reduced H₂ emissions along with CO. Assuming that there were no unexplained compensating changes to the natural budget terms, a plateau or decline in anthropogenic H₂ should be evident in atmospheric levels. By contrast, both the firn air history and flask air measurements show increasing trends in H₂ in the southern hemisphere during the late twentieth century. Furthermore, atmospheric measurements by CSIRO (18) and AGAGE (19) show that H₂ was largely constant from 2000 to 2015 when automotive exhaust emissions of H₂ were decreasing (48–50). This implies that there must be other important sources of anthropogenic H₂ which are increasing rapidly enough to offset the decreasing emissions from automotive exhaust.

The need for additional anthropogenic H₂ emissions that do not scale directly with CO is also evident in the difference between bottom-up and top-down estimates of anthropogenic H₂ emissions for the modern atmosphere. Top-down estimates require 17 to 18 Tg y⁻¹ of total anthropogenic emissions in 2008 (5, 51) as prescribed in the box model. By contrast, bottom-up estimates are 11 Tg y⁻¹ or less (4, 48–50). In their top-down estimate, Pieterse et al. (51) bridged this gap with 9.0 Tg y⁻¹ of emissions from residential combustion, much larger than the bottom-up estimate of 2.8 Tg y⁻¹ from Vollmer et al. (50).

This is further illustrated by forcing the box model with an H₂/CO anthropogenic emissions ratio calculated from the bottom-up estimate of anthropogenic H₂ from Vollmer et al. (Fig. 4B; ref. 50). With this historical inventory, the model yields good agreement with the firn air–derived history prior to 1985 but significantly underestimates the firn air history thereafter (Fig. 4C). Closing the gap between the box model result and the firn history would require an additional source that rose from 0 Tg y⁻¹ in 1985 to ∼8 Tg y⁻¹ in 2003.

Bottom-up estimates of anthropogenic H₂ emissions do not consider leakage from industrial processes. H₂ production for industrial use rose from roughly 40 Tg y⁻¹ to 80 Tg y⁻¹ between 1985 and 2005 (52). Estimated leakage rates are substantial, ranging from 0.5 to 12% with most estimates falling in the 1 to 4% range (7–9, 12). To our knowledge, direct measurements of H₂ leakage rates have not been published, and the uncertainties associated with these estimates are large. A 10% leakage rate would result in H₂ leakage increasing from 4 to 8 Tg y⁻¹ between 1985 and 2005 or roughly half of the late twentieth century disagreement between the box model and the firn air–derived history.

Northern Hemisphere Trends

Anthropogenic H₂ emissions are concentrated in the northern hemisphere, so it is informative to compare northern hemisphere atmospheric and Greenland firn air observations with the box model (Fig. 4D). Petrenko et al. (20) produced two reconstructions of atmospheric H₂ based on NEEM firn air measurements using two different firn air models. The reconstructions show a peak in atmospheric H₂ of 520 to 560 ppb during the 1980s and/or 1990s followed by a decrease to modern levels of about 515 ppb. The H₂/CO emissions ratios that produce agreement with the 2003 atmosphere yield modeled Greenland H₂ levels that increase during the mid-twentieth century and then plateau near 515 ppb from 1975 to 1985. Between 1985 and 2000, the box model shows H₂ levels decreasing to about 500 ppb (Fig. 4D).

Both the firn air–derived atmospheric histories and the box model show a distinct maximum in northern hemisphere H₂ during the late twentieth century. However, there is little evidence of such a maximum in the atmospheric measurements that remain roughly constant near modern levels throughout the late twentieth century (2, 13, 17, 19, 20). In addition, the timing of the maxima in the box model and firn air histories do not agree. The anthropogenic H₂/CO emissions ratio calculated from Vollmer et al. (50) yields modeled Greenland H₂ levels that rise from 400 to 440 ppb between 1960 and 1985. After 1985, H₂ levels remain approximately constant into the modern (Fig. 4D). Modeled H₂ levels using this emissions history are substantially lower than the firn air–derived histories and the flask measurements. It is clear that further work is needed to develop a clear understanding of northern hemispheric atmospheric H₂ trends and the factors determining those trends.

Sources versus Sinks

In this analysis, we attribute the model/data mismatch in the southern hemisphere to uncertainty in sources rather than sinks. It is difficult to construct a scenario whereby the observed trends in H₂ are dominated by changes in the losses. For example, if the late twentieth century rise in southern hemispheric H₂ was due to a reduction in the soil microbial sink, one would expect an even larger rise in the northern hemisphere where the soil sink is primarily located. Large changes in atmospheric OH would be required to drive the observed trends, whereas photochemical models suggest that global atmospheric OH concentrations were relatively stable over the past century (53, 54). In addition, the reduction in OH required to cause the observed late twentieth century increase would cause an even larger relative increase in CO at a time when CO levels were stabilizing or declining (SI Appendix; refs. 33, 40, 54).

Conclusions

Measurements and modeling of firn air at Megadunes, Antarctica, were used to reconstruct the atmospheric history of southern-hemisphere atmospheric levels of H₂ from 1852 to 2003. This reconstruction shows that the atmosphere was relatively constant during the mid-late 1800s around 330 ppb, followed by a steady rise to the modern level of 550 ppb. The magnitude of the rise in atmospheric H₂ is consistent with increasing anthropogenic emissions and production from CH₄ oxidation. The Megadunes reconstruction validates the South Pole firn air record, providing confidence in the atmospheric history of H₂ and modeling of the transport of a highly permeable gas in firn (22). Developing such records for atmospheric H₂ is particularly important because the instrumental record over the twentieth century is limited in duration and subject to challenging calibration issues.

The firn air reconstruction shows a late twentieth century increase in atmospheric H₂ that has not previously been discussed in the literature (Figs. 1 and 3). Rising H₂ levels at this time are also evident in atmospheric measurements from Khalil and Rasmussen (13), CSIRO (18), and AGAGE (19). The same trend is evident in NOAA/GML data after empirical correction to the MPI09 calibration scale (SI Appendix). This trend raises questions about the assumption of tight coupling between anthropogenic H₂ and CO emissions during the entire twentieth century. Firn air–derived histories of atmospheric CO clearly show the expected decline due to reduced automotive emissions after 1970s (20, 33, 40). However, a similar trend is not evident in the Antarctic firn air–based H₂ atmospheric histories. Instead, H₂ continues to rise through the end of the twentieth century. This rise cannot be attributed to increasing CH₄ oxidation alone and requires increasing emissions from another anthropogenic source barring unexplained changes in natural sources or sinks. An additional nonautomotive anthropogenic source of H₂ would also help reconcile the significant (7 to 8 Tg) gap between bottom-up and top-down estimates of anthropogenic H₂ emissions.

It is notable that flask measurements in the southern hemisphere display a monotonic rise in atmospheric H₂ throughout the late twentieth century, while they show a plateau in H₂ levels in the northern hemisphere. For a gas with an atmospheric lifetime of ∼2 y, it is difficult to construct a realistic emissions scenario whereby a strong trend exists in one hemisphere and not the other. Firn air records from Antarctica and Greenland at sites with a wide range of accumulation rates are needed to validate late twentieth century H₂ flask measurements and improve understanding of the global budget and emissions history.

Methods

Firn Air Sampling and Measurements.

During January of 2004, firn air was sampled at the Megadunes site in central Antarctica (23). A 3” diameter hole was bored to a depth of 70 m using an ice core drill. Drilling was paused at 15 unique depths so that firn air could be sampled. The sampling method was similar to techniques from previous published firn air studies (21, 55, 56). The hole was sealed above each sampling depth with an inflatable rubber packer to prevent contamination from the modern atmosphere. A waste air intake was positioned directly below the rubber packer. The waste air intake was separated from the sample air intake by a 2 3/4” diameter baffle. Air was pumped from the waste air intake 3 times faster than from the sample air intake to ensure that no air that had been in contact with the rubber packer was sampled. In total, 34 2-L glass flasks with Teflon seals were filled for analysis by the NOAA/GML Carbon Cycle group.

The firn air samples were analyzed for H₂ at NOAA/GML using gas chromatography with a mercuric oxide reduction gas analyzer. Relative measurement uncertainty is estimated at ±2%. The H₂ measurements are reported as dry air mole fraction. The data were corrected for calibration drift, detector nonlinearity, and gravitational fractionation as described in SI Appendix. The raw and corrected H₂ measurements are shown in SI Appendix, Fig. S2 and Fig. 1B.

Firn Air Model.

A one-dimensional, finite-difference, advective-diffusive model was used to simulate the evolution of H₂ levels in firn air. The model is largely derived from the work of Severinghaus et al. (23), and a complete model description is given in that work. The model also includes the pore close-off fractionation module from Patterson et al. (22) The model is broadly divided into an upper “diffusive zone” and lower “lock-in zone.” In the diffusive zone, vertical gas transport occurs via wind-driven convective mixing and molecular diffusion. Diffusive mixing decreases with depth due to the increasing tortuosity of the firn. In the lock-in zone, vertical molecular diffusion ceases due to the presence of impermeable winter layers. Gas transport in the lock-in zone occurs primarily due to advection with a small nonfractionating mixing term. The model uses a forward Euler integration scheme and a time step of 324 s. The primary differences between our model and that of Severinghaus et al. (23) are the omission of thermal diffusion which is unimportant for H₂ and the inclusion of the pore close-off fractionation module. The model tracks the air content and composition in both open pores and closed bubbles as a function of time and depth. The model code is written and executed in MATLAB R2020a (Mathworks Inc.).

Firn physical properties are taken from Severinghaus et al. (23). The annual average temperature is 224 K. The bulk density profile (ρ_firn) is calculated from an empirical fit to density measurements of the firn core. Total porosity (s_total) is estimated from the density profile:

$$s_{total}=1-\frac{{\rho }_{firn}}{{\rho }_{ice}},$$ [4]

where ρ_ice is the temperature dependent density of ice from Bader (kg m⁻³; ref. 57). Porosity is partitioned between open pores and closed bubbles using an empirical fit to measurements of density and closed porosity from Summit, Greenland (58). The accumulation rate at Megadunes has not been empirically constrained. The model accumulation rate is 2.8 cm y⁻¹ ice equivalent after Severinghaus et al. (23). The onset of the lock-in zone is at 64.5 m, as determined by the sharp gradient in the CO₂ and CH₄ depth profiles (SI Appendix, Fig. S3).

In the diffusive zone, model grid spacing is 0.5 m. Gas transport is dominated by convective mixing in the upper part of the diffusive zone and by molecular diffusion in the lower part of the diffusive zone. To simulate nonfractionating convective mixing, an eddy diffusivity term is added to the classical one-dimensional firn air transport equation (23, 58, 59). Additionally, we neglect the typical gravitational term and instead empirically correct the firn air measurements using the δ¹⁵N depth profile as described in SI Appendix. Eq. 5 governs the evolution of the concentration of the gas of interest in the open pores (23):

$$s_o\frac{\partial C}{\partial t}=\frac{\partial }{\partial z}\left(\frac{\partial C}{\partial z}\ast \left[s_o{D}_{mol}\left(z,T,P\right)+s_o{D}_{eddy}\left(z\right)\right]\right)-s_{o}w\left(z\right)\frac{\partial C}{\partial z},$$ [5]

where s_o is the open porosity, C is concentration of the gas of interest (mol m⁻³), D_mol is the depth, temperature, and pressure-dependent molecular diffusivity constant (m²s⁻¹), D_eddy is the depth-dependent eddy diffusivity (m²s⁻¹), and w is the downward velocity of the firn column (ms⁻¹). D_mol and D_eddy are tuned using the measured CO₂ and δ¹⁵N depth profiles. D_mol is then scaled using the ratio of the gas phase diffusivity of CO₂ to the gas phase diffusivity of H₂ (or other gas of interest). Temperature- and pressure-dependent gas phase diffusivities are calculated from Reid et al. (60). A detailed description of the tuning of the diffusivity profile is given in Severinghaus et al. (23).

Model grid spacing in the lock-in zone is one annual layer (∼3 cm). There is no molecular diffusivity in the lock-in zone, and gas transport occurs via downward advection of annual layers once per year. Small values of eddy diffusivity are prescribed in the upper part of lock-in. This nonfractionating mixing term is included to account for vertical airflow caused by barometric pressure fluctuations. The model parameterizations were validated by forcing the model with the atmospheric history of CH₄ from Law Dome and the NOAA flask air network and comparing the resulting modeled and measured depth profiles (SI Appendix, Fig. S3; refs. 28–31).

In addition to diffusion and advection, pore close-off fractionation is parameterized in the firn air model. As closed pores (bubbles) are advected downward in the firn, internal pressure increases, creating a partial pressure gradient which drives a net diffusive flux of highly mobile trace gases out of the bubbles, through the ice lattice, and into the open pores. The open pores are therefore enriched in these gases. This phenomenon affects gases with kinetic diameters (KD) <3.6 Å such as Ne and He due to their large diffusivity in ice (21, 22). As a result of pore close-off fractionation, enrichments of nearly 10% in ²²Ne (KD = 2.75 Å) content were observed in the base of lock-in at Megadunes.

Pore close-off fractionation must also affect H₂ (20, 22). Patterson et al. (22) examined both “kinetic” and “equilibrium” parameterizations for pore close-off fractionation of H₂ (21, 22). In the kinetic parameterization, the time scale for diffusion between closed and open pores is assumed to be slow relative to the advective time scale. A small constant flux out of a given bubble is maintained until the bubble has compressed by 5% after which the flux out of the bubble decreases to 0. In the equilibrium parameterization, permeation through the ice lattice is assumed to be fast enough to achieve equilibrium between open pores and closed bubbles throughout the model domain. Reconstructions of atmospheric H₂ from South Pole firn air measurements were relatively insensitive to the choice of parameterization (22). Recent laboratory measurements indicate that the permeability of H₂ in ice is sufficiently fast to equalize the partial pressure of H₂ in the open porosity and closed bubbles under the conditions at Megadunes (61). The equilibrium parameterization was used in this study as described by Eqs. 6–8:

$$P_n=(P_{bubble}{x}_{n\left(bubble\right)}{s}_c+P{x}_{n\left(firn\right)}{s}_o)/s_{total}$$ [6]

$$x_{n\left(bubble\right)}=P_n/P_{bubble}$$ [7]

$$x_{n\left(firn\right)}=P_n/P_{ambient},$$ [8]

where P is pressure, x is mole fraction, and s_c is closed porosity. The subscripts bubble and firn distinguish between the closed and open porosity. Eqs. 6–8 are executed at every timestep in each grid cell in the model. Patterson et al. (22) demonstrated that dissolution and vertical diffusion through the ice lattice may have effects on the order of 2 to 3% in the lock-in zone if a permeation constant of 5.0*10⁻¹⁵ mol m⁻¹s⁻¹Pa⁻¹ is assumed. Recent measurements of the permeation of H₂ in ice yield an estimate more than 100 times lower (61). The lower permeation constant greatly reduces the magnitude of these effects. For the purposes of this work, dissolution and vertical diffusion through the ice lattice are neglected.

Data Availability

Firn air and atmospheric measurements of H₂ data have been deposited in the DRYAD Data Repository (https://doi.org/10.7280/D18698; ref. 24).