Spin-textured Chern bands in AB-stacked transition metal dichalcogenide bilayers

Significance

The long-wavelength moiré superlattices in twisted two-dimensional (2D) structures have emerged as a highly tunable platform for strongly correlated electron physics. In this work, we reveal the displacement field–induced topological moiré bands in AB-stacked transition-metal dichalcogenide (TMD) heterobilayer ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$. Valley-contrasting Chern bands with nontrivial spin texture are formed from interlayer hybridization between ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ bands of nominally opposite spins. The general mechanism for band inversion we uncovered in AB-stacked TMD bilayers is quite robust and can be applied to other material combinations as well. Our study establishes a recipe for creating topological bands in AB-stacked TMD bilayers in general, which provides a highly tunable platform for realizing quantum-spin Hall and interaction-induced quantum anomalous Hall effects.

Abstract

While transition-metal dichalcogenide (TMD)–based moiré materials have been shown to host various correlated electronic phenomena, topological states have not been experimentally observed until now [T. Li et al., Quantum anomalous Hall effect from intertwined moiré bands. arXiv [Preprint] (2021). https://arxiv.org/abs/2107.01796 (Accessed 5 July 2021)]. In this work, using first-principle calculations and continuum modeling, we reveal the displacement field–induced topological moiré bands in AB-stacked TMD heterobilayer ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$. Valley-contrasting Chern bands with nontrivial spin texture are formed from interlayer hybridization between ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ bands of nominally opposite spins. Our study establishes a recipe for creating topological bands in AB-stacked TMD bilayers in general, which provides a highly tunable platform for realizing quantum-spin Hall and interaction-induced quantum anomalous Hall effects.

Two-dimensional (2D) transition-metal dichalcogenides (TMDs) ${\mathrm{M}\mathrm{X}}_2$ exhibit a host of interesting electronic phases, such as charge-density wave and Ising superconductivity (1, 2) and magnetism (3), ferroelectricity (4, 5), and quantum-spin Hall insulator (6–10). More recently, semiconductor TMD moiré superlattices (11–32) have emerged as a highly tunable quantum simulator of correlated electron physics (33). Unlike graphene with highly mobile Dirac electrons, semiconductor TMDs have an intrinsic large effective mass that strongly enhances interaction effects at low density.

In TMD heterobilayer ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}}_2$ (11–13, 15–17), the moiré pattern due to lattice mismatch introduces a periodic effective potential for low-energy electrons or holes. At long moiré wavelength, interaction and potential energies dominate over the kinetic energy, leading to a plethora of strong-coupling phases, including Mott insulators, generalized Wigner crystals, and stripe charge order. In twisted homobilayer ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$, the bandwidth is continuously tunable by the twist angle $\theta$. At $\theta \sim 4°$ to $5°$, where the bandwidth is comparable to interaction energy, metal–insulator transitions and quantum critical phenomena tuned by the displacement field have been observed at half-band filling (14). A candidate state for the correlated insulator is an intervalley spin-density wave (28) that is smoothly connected to an $xy$-ordered antiferromagnet (29, 30). Signs of superconductivity have also been observed below half-filling (14). The remarkably rich physics of TMD moiré systems is being uncovered at a rapid pace.

Due to strong spin-orbit coupling and broken inversion symmetry, monolayer TMDs in the 2H phase, such as ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ and ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$, feature large spin-orbit splitting in the valence band (34). The topmost valence bands at $\pm K$ are spin-polarized with $s_z=\uparrow ,\downarrow$, respectively. The spin-valley locking opens the possibility of topological bands and quantum-spin Hall effect in TMD moiré systems (32). Using a continuum model approach, Wu et al. (22) predicted topologically nontrivial $\pm K$-valley moiré bands with spin/valley Chern number in twisted homobilayer TMD. Based on first-principles calculations, we recently identified flat topological bands in twisted bilayer ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ and further predicted interaction-induced spin/valley polarization at half-band filling, which leads to a quantum anomalous Hall (QAH) insulator (25).

The above theoretical works are concerned with TMD homobilayers with a small twist angle starting from the AA stacking, where every metal (M) or chalcogen (X) atom on the top layer is aligned with the same type of atom on the bottom layer. The formation of topological bands relies on spin- and valley-conserving tunneling between the two layers. In contrast, in AB-stacked TMD bilayers, where the top layer is rotated by $180°$ relative to the bottom layer, the valence bands of two layers in the same valley carry different spins. It is commonly believed that the spin mismatch blocks interlayer tunneling, and, therefore, the two layers are electronically decoupled.

Unexpectedly, a recent experiment discovered a QAH state in the AB-stacked ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ heterobilayer in a range of displacement fields (35). Magnetic hysteresis behavior is observed in both Hall resistance and Kerr rotation below 5K. At zero field, the Hall resistance reaches the quantized value $h/e^2$ below 2.5K. The origin of this QAH state calls for theoretical understanding.

In this work, by performing large-scale, first-principles calculations, we find that the displacement field induces band inversion in AB-stacked ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ and leads to valley Chern bands with nontrivial spin and layer characters. In contrast to twisted homobilayers, interlayer coupling between ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ bands of different spins is essential for gap opening after band inversion. We introduce a continuum model to describe the low-energy moiré bands of TMD heterobilayers and the displacement field–induced topological transition. Our findings suggest spontaneous valley polarization in topological bands as the mechanism for the observed QAH state in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$.

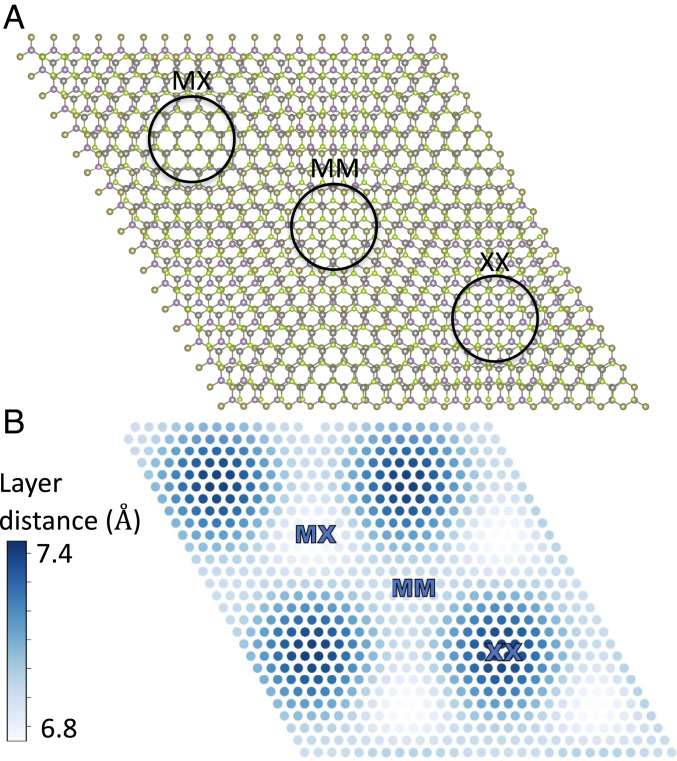
We consider a heterobilayer TMD ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$, with $a_b\left(a_t\right)$ as the lattice constant of the bottom (top) layer and $\theta$ as the twist angle. The lattice mismatch leads to a moiré superlattice in Fig. 1, with superlattice constant $a_M=a_b/\sqrt{{\delta }^2+{\theta }^2}$, where $\delta =\left(a_b-a_t\right)/a_t$. In AB-stacked TMD bilayers, the orientation of the top layer is antiparallel to that of the bottom layer. Here, we study the moiré superlattice at $\theta =0$, where the moiré wavelength $a_M\sim 5$ nm is maximum. In this superlattice, there are three high-symmetry regions, denoted as MM, XX, and MX. In the MX region, the M atom on the bottom layer is locally aligned with the X atom on the top layer, and likewise for MM and XX (Fig. 1A). The bilayer structure in these stacking configurations is invariant under threefold rotation about the $z$ axis, $C_{3z}$, centered at the high-symmetry regions.

Fig. 1.

Lattice structure for AB-stacked ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ heterobilayer. (A) MM, XX, and MX stacking regions. (B) spatial dependent layer distance in $2\times 2$ moiré superlattice with strong out-of-plane corrugation.

A unit cell of the ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ superlattice at $\theta =0$ contains $13\times 13\hspace{0.17em}{\mathrm{MoTe}}_2$ unit cells and $14\times 14\hspace{0.17em}{\mathrm{W}\mathrm{S}\mathrm{e}}_2$ unit cells. As well studied in previous works on various homobilayers and AA-stacked heterobilayers (15), lattice relaxation significantly modifies the low-energy electronic states, especially the real space features of the moiré bands and the relative energy level of the $\mathrm{\Gamma }$- and $K$-valley moiré bands (23, 36). In order to obtain accurate moiré lattice structures, we perform large-scale density functional theory (DFT) calculations with the SCAN+rVV10 van der Waals density functional (37), which captures the intermediate-range van der Waals interaction through its semilocal exchange term, resulting in a better estimation of layer spacing. Owing to the different local atomic alignments in MM, XX, and MX regions, the layer distances have a strong spatial variation as shown in Fig. 1B, which are 6.8, 7.0, and 7.4 Å for MX, MM, and XX regions, respectively.

At zero displacement field, there is a large valence band offset $\mathrm{\Delta }{E}_g\sim 110$ meV (consistent with ref. 38) between ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ (Fig. 2B), and the holes are first filled to the ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ layer. The primary effect of the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ layer on ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$, and vice versa, is through the lattice corrugation effect. Therefore, we first study the moiré band structures for the separated ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ layer and the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ layer with corrugation extracted from relaxed aligned heterobilayers. The $z$ corrugation in the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ layer is around 0.7 Å, while the height variation in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ is at the order of 0.2 Å. Due to the relatively smaller moiré wavelength, here, the built-in strain is 0.5%, smaller than the 1% in the case of 8.2-nm AA-stacked ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}}_2$ (15).

Fig. 2.

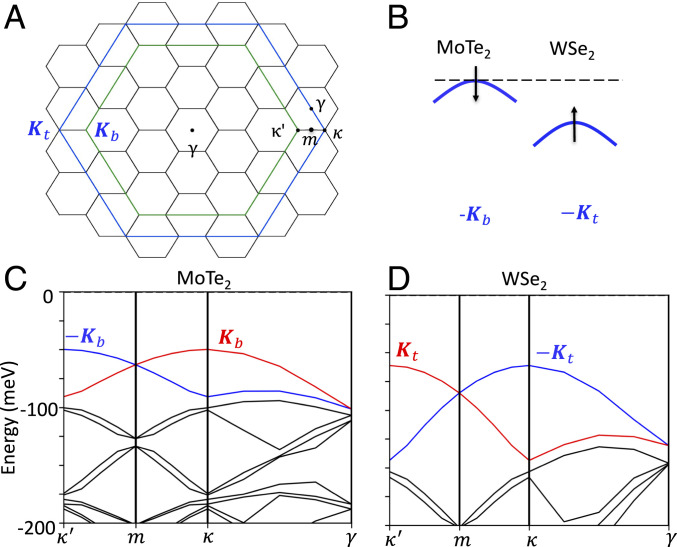
(A) Schematic figure for BZ folding. Black lines are mBZ of the moiré supercell, and $\gamma$, $\mathrm{m}$, $\kappa$, and ${\kappa }^{\prime }$ are labels in the mBZ. Green and blue lines are the full BZ for the primitive cell in the $3N+1$ and $3N+2$ supercell, which apply to 13$\times$13 ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and $14\times 14\hspace{0.17em}{\mathrm{W}\mathrm{S}\mathrm{e}}_2$. (B) Band offset between the ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2\hspace{0.17em}-K$ valley. (C and D) DFT Band structures of $13\times 13\hspace{0.17em}{\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ (C) and $14\times 14\hspace{0.17em}{\mathrm{W}\mathrm{S}\mathrm{e}}_2$ (D) with lattice corrugation extracted from relaxed untwisted heterobilayers. Note that we move the moiré bands in C and D to the same energy level, and band offset is therefore not presented.

Owing to strong Ising spin-orbit coupling in the valence-band side, valley and spin are locked (34) in monolayer TMD, resulting in the top valence bands being mostly spin-$\uparrow$ at $+K$ valley and spin-$\downarrow$ at $-K$. The moiré Brillouin zone (mBZ) is constructed by folding the full Brillouin zone (BZ), as illustrated in Fig. 2A. The $K$ and $-K$ valley fold to $\kappa$ and ${\kappa }^{\prime }$, respectively, in the $13\times 13\hspace{0.17em}{\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ supercell, while in ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ with $14\times 14$ supercell, the $K$ and $-K$ valley instead fold to ${\kappa }^{\prime }$ and $\kappa$. Since the moiré wavelength is relatively small ($a_M\sim 5$ nm), the kinetic energy scale $\sim -\frac{|\mathit{\kappa }{|}^2}{2_{m_b}}\sim 40$ meV ($m_b=0.65m_0$ is the effective mass of bottom layer ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$, $m_t=0.35m_0$ for the top layer ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ and therefore even larger kinetic energy) is much larger than the potential energy scale, giving rise to a nearly-free electron dispersion with small band gaps at the mini BZ boundaries in Fig. 2 C and D.

Due to the large valence-band offset $\mathrm{\Delta }{E}_g$ between ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$, we expect the top moiré valence bands in the heterobilayer to be quite similar to the ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ layer with corrugation. When the band offset is reduced by displacement field, the top moiré bands of the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ layer is lifted and intersects with the band bottom of the first set of moiré bands in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$, causing a band inversion at $\kappa$ between the $-K$ valleys of ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and $180°$ rotated ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$, of mostly spin-$\downarrow$ and -$\uparrow$, respectively.

To substantiate this picture, we calculate the band structure of the AB-stacked ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ heterobilayer from DFT. With zero out-of-plane displacement field, the top two valence moiré bands are well separated from the other moiré bands with a band gap around 10 meV at $\kappa$ in the mBZ. Compared to the band structure of monolayer ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ with corrugation, it is clear that the majority of the dispersive bands in heterobilayer ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ are developed from ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ layer, and in the energy range of interest, there is only one additional moiré band coming from the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ band maximum, as shown in Fig. 3A.

Fig. 3.

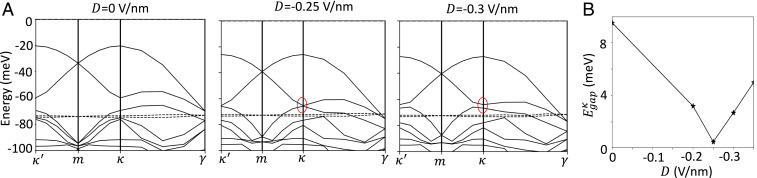
(A) DFT band structure of AB-stacked ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ heterobilayer with displacement field D = 0, −0.25 (critical field), and −0.3 V/nm, showing gap reopening and band inversion. (B) Displacement field–dependent band gap at $\kappa$: The band gap reduces from 9 to 0 meV and then increases to 4 meV.

When the displacement field strength is increased, the single-particle band gap at $\kappa$ between the two $-K$-valley dispersive moiré bands gradually reduces from 9 meV and closes at a critical field of around $-0.25$ V/nm, as shown in Fig. 3B. At a displacement field $-0.3$ V/nm, we observe a band inversion near $\kappa$ with a direct gap of $\sim 1.5$ meV.

Besides the dispersive moiré bands, we find two flat bands (dashed lines). In order to determine the origin of various moiré bands, we plot the Kohn–Sham wavefunctions in real space. The wavefunction of the flat band at $\kappa$ (dashed lines in Fig. 3A) is formed of the bonding and antibonding orbitals between ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ and is therefore spread out in two layers, indicating that it arises from the $\mathrm{\Gamma }$ valley of the monolayer TMDs. The dispersive moiré valence bands at $\kappa$ are instead strongly localized at one layer with around 80% weight from $d$ orbitals of metallic atoms, forming a triangular network, and we conclude that they arise from the $\pm K$ valley of ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$. In real space, the first two $-K$-valley moiré bands are peaked at the MM region in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and the XX region in ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$, respectively, forming an effective honeycomb lattice with band gap tunable by displacement field.

While the $\mathrm{\Gamma }$-valley bands of monolayer ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ and ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ are significantly lower in energy than their $\pm K$-valley counterparts, interlayer tunneling in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ substantially pushes up the energy of $\mathrm{\Gamma }$-valley moiré bands, which overlaps with the $\pm K$-valley moiré bands. Nonetheless, due to large separation between $\mathrm{\Gamma }$ and $\pm K$ in momentum space, these two sets of moiré bands are decoupled at the single-particle level. The $\mathrm{\Gamma }$-valley flat bands are not relevant to our discussion concerning the band gap and topological properties between two $\pm K$-valley moiré bands.

To reveal the origin of topological gap closing, we further analyze the wavefunction around the band-inversion point $\kappa$. Inspecting the band structure of separated monolayers, we find that the pair of topological moiré bands are developed from the $-K$ valley of ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and the $-K$ valley of ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$, which should have nominally opposite spins due to AB stacking. Tunneling between these bands is only possible if spin $s_z$ is not fully conserved, as is generally true in systems with strong spin-orbit coupling.

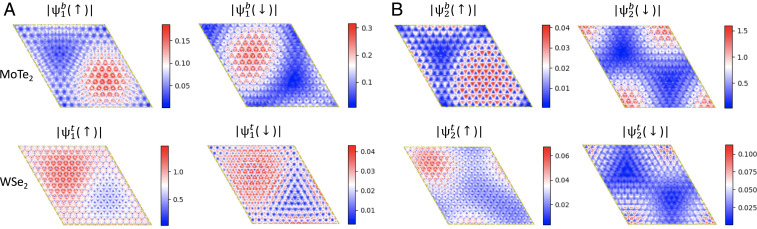
The validity of this scenario can be further tested by layer- and spin-resolved (projected in the $s_z$ direction) wavefunction of the two $-K$-valley bands at $\kappa$. At the displacement field $D=-0.3$ V/nm in the inverted regime, the wavefunction of the first band is dominantly located at the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ layer, with 6% charge density at the ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ layer shown in Fig. 4A. In the spin channel, the amplitude of spin-up and spin-down resolved wavefunctions in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$, $\sqrt{\int d\mathit{r}|{\psi }_1^b\left(\uparrow \right){|}^2/\int d\mathit{r}|{\psi }_1^b\left(\downarrow \right){|}^2}\sim 0.6$ is of comparable magnitude, a direct proof of $s_z$ nonconservation and spin mixing in the AB-stacked heterobilayer. Even in corrugated monolayers, we find that $s_z$ is not conserved, due to the breaking of mirror symmetry $m_z$.

Fig. 4.

At $D=-0.3$ V/nm after topological transition, spin- and layer-resolved $\kappa$ wavefunction for the first topological band (A) and second topological band (B). Both the spin and layer are mixed in these two bands. And the first topological band is dominantly localized at the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ layer spin-up channel, with sizeable component localized at the ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ layer spin-up channel.

In Fig. 5, we plot the layer-resolved real space spin texture, $\mathit{s}\left(\mathit{r}\right)$, for the two topological bands at $\kappa$. For the top topological band, the majority layer ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ is almost fully spin up. The spin moment in the minority layer ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$, on the other hand, very clearly forms a real-space Skyrmion lattice, with spins at the MX regions pointing down and spins at the XX regions pointing up, and a vortex structure in the in-plane spin around these regions. In the second topological band, the minority layer ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ similarly exhibits a Skyrmion texture.

Fig. 5.

At $D=-0.3$ V/nm after topological transition, spin texture at $\kappa$ for the first topological band projected at the ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ layer (A) and the second topological band projected at the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ layer (B). We plot the $\left(s_x,s_y\right)$ as in plane vector and $s_z$ as a colormap for both bands. The spin component in the majority layer is almost fully up or down at the $s_z$ direction, while the spin texture in the minority layer forms a real space Skyrmion lattice.

The absence of spin $s_z$ conservation allows interlayer tunneling between same-valley bands in the AB-stacked heterobilayer. We expect the tunneling amplitude to be much weaker in this case, compared to the AA-stacked case, which involves tunneling between matching spin bands [which for ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ homobilayer is around 18 meV (25)]. From the amplitude ratio between same-spin wavefunctions in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$, we estimate that the tunneling magnitude in our case should be of order $\sim 1$ meV. The relatively weak tunneling amplitude is fully consistent with the small topological gap in the inverted regime, which is $\sim$1.5 meV from DFT calculation. This value is close to the $\sim$2 meV inferred from capacitance measurement. Thus, our DFT calculation and wavefunction analysis clearly show that there is a nonzero, albeit small, interlayer tunneling, despite the two bands being of primarily opposite spin.

We now develop a continuum model for AB-stacked heterobilayers, which well captures the physics of the band inversion. As a first step, the moiré band structures of single-layer ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ or ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ can be modeled by a continuum model with kinetic and potential term, one for each valley $\pm K$. We focus on only the $-K$ valley,

$$H_{-K}^{b,t}=-\frac{{\left(\mathit{k}-{\mathit{\kappa }}^{\left(\prime \right)}\right)}^2}{2m_{b,t}}+V_{b,t}\left(\mathit{r}\right),$$ [1]

$$V_{b,t}\left(\mathit{r}\right)=2V_{b,t}\sum _{i=\mathrm{1,3,5}}\cos \left({\mathit{g}}_{\mathit{i}}\cdot \mathit{r}+{\varphi }_{b,t}\right),$$ [2]

where $\mathit{k}=-i\nabla$, and $m_{b,t}>0$ is the effective mass in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ (bottom layer) and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ (top layer). The potential term is expressed as the first-order harmonics with moiré wave vectors ${\mathit{g}}_{\mathit{j}}=\frac{4\pi }{\sqrt{3}{a}_M}\left(-\sin \frac{\pi \left(j-1\right)}{3},\cos \frac{\pi \left(j-1\right)}{3}\right)$ (16). Due to the BZ folding, take the minimum of the dispersion, ${\mathit{\kappa }}^{\left(\prime \right)}$, to be $\mathit{\kappa }=\frac{4\pi }{3a_M}\left(-\frac{1}{2},\frac{\sqrt{3}}{2}\right)$ for the bottom layer and ${\mathit{\kappa }}^{\prime }=\frac{4\pi }{3a_M}\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)$ for the top layer.

The continuum Hamiltonian involving both layers is given by

$$H_{-K}=\left(\begin{array}{cc}{H}_{-K}^b\hfill & W\left(\mathit{r}\right)\hfill \\ W^{†}\left(\mathit{r}\right)\hfill & H_{-K}^t-\mathrm{\Delta }{E}_g\hfill \end{array}\right),$$ [3]

where $m_{t,b}$ are effective masses, $V_{b,t}\left(\mathit{r}\right)$ is an effective potential arising due to corrugation effects, $W\left(\mathit{r}\right)$ is an interlayer tunneling term, and $\mathrm{\Delta }{E}_g$ is the energy between the two layers, which can be tuned experimentally by the displacement field. The continuum model has threefold counterclockwise rotation symmetry $C_{3z}$ about the origin, chosen to be between the metal atoms of the two layers at an MM-stacking region.

The interlayer tunneling term is

$$W^{†}\left(\mathit{r}\right)=W\left(1+{\omega }^{\nu }{e}^{i{\mathit{g}}_2\cdot \mathit{r}}+{\omega }^{2\nu }{e}^{i{\mathit{g}}_3\cdot \mathit{r}}\right),$$ [4]

where $\omega =e^{2\pi i/3}$, and $C_{3z}$ symmetry fixes $\nu$, depending on the difference in $C_{3z}$ eigenvalue of the $-K_{b,t}$ states in the two layers. Specifically, if the state at $-K_{b\left(t\right)}$ on the bottom (top) layer, $|-K_{b\left(t\right)}\rangle$, has $C_{3z}$ eigenvalue ${\omega }^{n_{b\left(t\right)}}$, then $\nu =n_b-n_t$ mod 3. The eigenvalues ${\omega }^{n_{b,t}}$ can be determined from monolayer DFT calculations by computing the $C_{3z}$ eigenvalues of the valence band top at $-K$. We find $n_b=-\frac{1}{2}$ and $n_t=\frac{1}{2}$. Since the $-K$ valley ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ band is mostly spin-$\downarrow$ and the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ band mostly spin-$\uparrow$, these $C_{3z}$ eigenvalues can be decomposed as $n_b=-1+\frac{1}{2}$ and $n_t=1-\frac{1}{2}$, where the integer part is due to the orbital wavefunction and the half-integer part is due to spin.

Again, we note that if the spin-$U\left(1\right)$ symmetry was exact and $s_z$ a good quantum number, interlayer tunneling would be forbidden. However, as observed in the DFT band structure, there is indeed interlayer hybridization between bands of different spin. Thus, the interlayer tunneling is nonzero, albeit weak, and arises due to the fact that the bands are not fully spin-polarized. The continuum model is agnostic of the microscopic origin of the interlayer tunneling, and $W\left(\mathit{r}\right)$ is simply the first harmonic approximation of a generic complex-valued tunneling term that is allowed by $C_{3z}$ symmetry.

This continuum model differs from the previously studied continuum model for TMD heterobilayers (16), as it takes into account both layers that are coupled through interlayer tunneling, rather than just keeping a single layer, which is only valid in the limit of large $\mathrm{\Delta }{E}_g$. At the displacement fields at which the band inversion takes place, both layers are important. The continuum model also differs from that of AA-stacked TMD homobilayers (22) with a displacement field, for which the interlayer tunneling term always has $\nu =0$ due to the alignment of spins on the two layers. Depending on $\nu$, the tunneling $\left|W\left(\mathit{r}\right)\right|$ will be peaked at one of either MM, MX, or XX regions and zero at the other two, due to the difference in the $C_{3z}$ eigenvalue.

The BZ folding (Fig. 2) is such that the $-K_b\hspace{0.17em}{\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ band maximum is at ${\kappa }^{\prime }$ in the mBZ, with narrow gaps opened at $\gamma$ and $\kappa$ at energy $E\approx -\frac{|\mathit{\kappa }{|}^2}{2_{m_b}}$. Meanwhile, the $-K_t\hspace{0.17em}{\mathrm{W}\mathrm{S}\mathrm{e}}_2$ band maximum is located at $\kappa$ at energy $E\approx -\mathrm{\Delta }{E}_g$. By tuning displacement field to $\mathrm{\Delta }{E}_g\sim \frac{|\mathit{\kappa }{|}^2}{2m_b}$, the ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ valence-band top can cause a band inversion with the ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ bands at $\kappa$.

Let us focus on the bands at $\kappa$ relevant to the band inversion. When $V_b=W=0$, there are three exactly degenerate ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ bands at $\kappa$, given in the continuum model by plane waves ${\left\{|-{\mathit{k}}_b+{\mathit{\delta }}_j\rangle \right\}}_{j\in \left\{\mathrm{1,2,3}\right\}}$, where ${\mathit{\delta }}_j$ are counterclockwise $2\pi \left(j-1\right)$ rotations of ${\mathit{\delta }}_1=\frac{4\pi }{3a_M}\left(\mathrm{1,0}\right)$. The $C_{3z}$ symmetry acts as $|-{\mathit{k}}_b+{\mathit{\delta }}_j\rangle \to {\omega }^{n_b}|-{\mathit{k}}_b+{\mathit{\delta }}_{j+1}\rangle$. For nonzero $V_b$, the degeneracy is split, and the resulting eigenstates (restricted to this three-state subspace) are $C_{3z}$ eigenstates

$$|n\rangle =\frac{1}{\sqrt{3}}\sum _{j=\mathrm{1,2,3}}{\omega }^{jn}|-{\mathit{k}}_b+{\mathit{\delta }}_j\rangle ,$$ [5]

with energy

$$E_n=-\frac{|\mathit{\kappa }{|}^2}{2m_b}+2V_b\cos \left(2\pi n/3+{\varphi }_b\right),$$ [6]

and $C_{3z}$ eigenvalue ${\omega }^{n_b-n}$. These eigenstates also have characteristic spatial dependence. Let ${\mathit{R}}_m=\frac{m{a}_M}{\sqrt{3}}\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)$, for $m\in \left\{\mathrm{0,1,2}\right\}$, be the high-symmetry positions MM (${\mathit{R}}_0$), MX (${\mathit{R}}_1$), and XX (${\mathit{R}}_2$). Then, $\left|⟨{\mathit{R}}_m|n⟩\right|\propto |1+{\omega }^{m-n}+{\omega }^{n-m}|$ is maximized at ${\mathit{R}}_{m=n}$ and zero at ${\mathit{R}}_{m\ne n}$. Thus, the state $\left\{|n\rangle \right\}$ is peaked at the high-symmetry position ${\mathit{R}}_n$, and their energy splitting is also proportional to the potential $V_b\left({\mathit{R}}_n\right)$.

We can obtain the relevant continuum model parameters by fitting to the band structure at displacement field $-0.3$ V/nm. Since the essential physics involves only the band maximum of ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$, the potential $V_t\left(\mathit{r}\right)$ is unimportant, and we simply set $V_t=0$. From fitting to the energies, and using the long-wavelength features of the DFT majority-spin wavefunctions at $\kappa$, we find the following parameters: ($V_b,{\varphi }_b,W$) = (4.1 meV, $14°,1.3$ meV), ($m_b,m_t$) = $\left(0.65m_0,0.35m_0\right)$, where $m_0$ is the electron mass (using lattice constants $a_b=3.575$ Å and $a_t=3.32$ Å), and $\mathrm{\Delta }{E}_g=36.8$ meV. The fitted effective mass is very close to the monolayer value reported in previous experimental and theoretical study (39, 40).

The resulting continuum model bands are shown in Fig. 6A, in comparison with DFT bands. The continuum model agrees very well with DFT along the $\mathrm{m}$–$\kappa$ path, but differs slightly near $\gamma$, as a result of neglected time-reversal symmetry-breaking terms within one valley, which makes $\gamma$ and $\kappa$ nonequivalent. This effect, present even in the corrugated monolayer, arises from spatially varying strain that produces a valley-contrasting pseudomagnetic field (41, 42), but does not play an important role in the band inversion in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$. In Fig. 6B, we show the direct gap between the first two bands at $\kappa$, as well as the minimum over all $\mathit{k}$, as a function of $\mathrm{\Delta }{E}_g$. The gap closes at $\kappa$ at $\mathrm{\Delta }{E}_g\approx 40$ meV, and the first band remains topological below it. We compute the Chern number from the continuum model after inversion to be ${\mathcal{C}}_{-K}=1$. The $+K$-valley band will have the opposite Chern number due to time-reversal symmetry.

Fig. 6.

(A) Band structure of the continuum model with parameters mentioned in the main text. Blue lines indicate $-K$-valley bands, and red lines indicate $+K$-valley bands. The black dots represent the DFT bands computed for the heterobilayer at displacement field $-0.3$ V/nm (dashed lines are states originating from the Gamma pocket). A, Inset shows the avoided crossing due to interlayer hybridization near $\kappa$. (B) The direct gap between the first two $-K$-valley bands at $\mathit{k}=\mathit{\kappa }$ and minimized over $\mathit{k}$, as a function of $\mathrm{\Delta }{E}_g$. The first band has a nontrivial Chern number for $\mathrm{\Delta }{E}_g<40$ meV.

Importantly, the physics of topological band inversion in TMD bilayers is essentially dictated by the $C_{3z}$ symmetry eigenvalues of the top ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ and ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ bands at $\kappa$. Provided that $C_{3z}$ eigenvalues of the two are different, decreasing the layer bias potential beyond $\mathrm{\Delta }{E}_g\lesssim \frac{|\mathit{\kappa }{|}^2}{2m_b}$ will close the gap and drive a band inversion. Prior to band inversion, the first $-K$-valley band at $\kappa$ has $C_{3z}$ eigenvalue ${\omega }^{n_b-n_0}$ at $\kappa$, where $n_0=\lfloor \frac{{\varphi }_b+\pi /3}{2\pi /3}\rfloor$ mod 3 is determined by the location of the maximum of $V_b\left(\mathit{r}\right)$ ($n_0=0$ for ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$). After the band inversion, the state at $\kappa$ of the first band will instead have $C_{3z}$ eigenvalue ${\omega }^{n_t}$ and consist mainly of the state $|-K_t\rangle$ of the top layer. The resulting band after inversion has $C_{3z}$ eigenvalues ${\omega }^{n_b}$ at ${\kappa }^{\prime }$, ${\omega }^{n_b+n_0}$ at $\gamma$, and ${\omega }^{n_t}$ at $\kappa$. The interlayer tunneling $W\ne 0$ is crucial in opening a direct gap in the inverted regime. As long as $n_t\ne n_b-n_0\mathrm{mod}3$, this eigenvalue structure cannot be captured by a single-band tight-binding model with any choice of Wannier centers and will have a nontrivial Chern number. Note that, here, $n_t\ne n_b$ due to the different spin of $-K$-valley monolayer bands in the AB-stacked case. In the AA-stacked case, we would have had $n_t=n_b$, and the resulting bands would not be topological for $n_0=0$.

We note that the relative $C_{3z}$ eigenvalues at $\kappa$, ${\kappa }^{\prime }$, and $\gamma$ dictate the position of the Wannier centers for the first moiré bands from each layer that participate in band inversion. For the first $-K$-valley ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$ moiré band, all $C_{3z}$ eigenvalues are identical, ${\omega }^{-\frac{1}{2}}$, indicating that the Wannier centers should be at the MM regions. For ${\mathrm{W}\mathrm{S}\mathrm{e}}_2$, we calculate the $C_{3z}$ eigenvalues directly from DFT to be ${\omega }^{\frac{1}{2}},{\omega }^{-\frac{1}{2}}$, and ${\omega }^{\frac{3}{2}}$, at $\kappa ,{\kappa }^{\prime }$, and $\gamma$. This eigenvalue structure corresponds to Wannier functions centered at the XX region, consistent with the peak of the DFT wavefunctions at the XX region. A tight binding description of the first bands from each layer is therefore a honeycomb lattice with sites centered at the MM and XX regions of the moiré superlattice.

Discussion

The low-energy theory near topological band inversion in AB-stacked TMD bilayers is described by a massive Dirac Hamiltonian

$$H_D=v\left(q_x{\sigma }_x+q_y{\tau }_z{\sigma }_y\right)+m{\sigma }_z,$$ [7]

where ${\sigma }_{\alpha }$ and ${\tau }_{\alpha }$ are layer and valley Pauli matrices, respectively, and $\mathit{q}\equiv \mathit{k}-{\tau }_z\mathit{\kappa }$. The Dirac mass determines the band gap between the first and second moiré bands at $\kappa ,{\kappa }^{\prime }$ and is controlled by the displacement field. The sign reversal of Dirac mass $\mathrm{m}$ leads to a change of valley Chern number from $C=0$ to $C=1$. The displacement field–induced band inversion in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ is reminiscent of the case of InAs/GaSb quantum wells (43, 44). Due to spin-valley locking, the complete filling of Chern bands in both valleys, corresponding to two holes per moiré unit cell, gives rise to a quantum-spin Hall insulator.

While our calculation focused on ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$, the general mechanism for band inversion we uncovered in AB-stacked TMD bilayers is quite robust and can be applied to other material combinations as well. In such bilayer systems with a tunable band offset, the formation of valley-contrasting Chern bands depends only on the difference of $C_{3z}$ eigenvalues between the bands at the band-inversion point.

Including the effect of Coulomb interaction in these valley-contrasting Chern bands may lead to a number of interesting electronic phases, such as the recently observed QAH insulator at half-band filling in AB-stacked ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ (35). This phase may occur as a result of interaction-induced valley polarization. In this scenario, holes would fully fill a Chern band from one of the two valleys $K$ or $-K$, realizing a QAH state at the filling of one hole per moiré unit cell. Our comprehensive DFT calculation and theoretical analysis show that the envelope wavefunctions of the two dispersive bands form a honeycomb lattice structure. Therefore a theoretical framework for studying interaction effects in ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ is the Kane–Mele–Hubbard model. As shown in our recent work (25), this model exhibits a variety of insulating phases at half-band filling, including the QAH and Mott insulating phases. A detailed phase diagram for ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ will be presented in our follow-up work. Finally, we remark that specific details, such as the negative overlap, $\mathrm{\Gamma }$ pocket bands, and interaction-induced band renormalization, will depend on the specific materials, moiré wavelength, and the choice of van der Waals density functionals; however, the displacement field–induced band inversion and band topology is generic and depends only on the $C_{3z}$ eigenvalues and nonzero interlayer tunneling.

Method

We perform the density functional calculations using generalized gradient approximation (45) with SCAN+rVV10 van der Waals density functional (37), as implemented in the Vienna Ab Initio Simulation Package (46). Pseudopotentials are used to describe the electron–ion interactions. We first construct AB-stacked ${\mathrm{M}\mathrm{o}\mathrm{T}\mathrm{e}}_2$/${\mathrm{W}\mathrm{S}\mathrm{e}}_2$ heterobilayer with vacuum spacing larger than 20 Å to avoid artificial interaction between the periodic images along the $z$ direction. Dipole correction is added to the local potential in order to correct the errors introduced by the periodic boundary conditions in out-of-plane direction. The structure relaxation is performed with force on each atom less than 0.01 eV/A. We use Gamma-point sampling for structure relaxation and self-consistent calculation, due to the large moiré unit cell.

Data Availability

All study data are included in the article and/or supporting information.