Semiempirical method for examining asynchronicity in metal–oxido-mediated C–H bond activation

Significance

There is considerable interest in understanding the role that asynchronicity plays in metal–oxido-mediated C–H bond activation. A semiempirical method is presented for gauging the relative importance of the free energies for proton transfer (PT) and electron transfer (ET) in determining the rate constants for C–H bond cleavage. The method deviates from traditional Bell–Evans–Polanyi analyses by examining the behavior of log (k) vs. a linear combination of PT and ET terms, rather than bond strengths. The appropriate combination of free energy terms is determined by the linearity of plots vs. log (k). We developed the approach by examining substrate oxidations by a Mn^IV–oxido complex and applied it to data for other M–O(H) systems, indicating it has general applicability to other proton-coupled electron transfer (PCET) processes.

Abstract

The oxidation of substrates via the cleavage of thermodynamically strong C–H bonds is an essential part of mammalian metabolism. These reactions are predominantly carried out by enzymes that produce high-valent metal–oxido species, which are directly responsible for cleaving the C–H bonds. While much is known about the identity of these transient intermediates, the mechanistic factors that enable metal–oxido species to accomplish such difficult reactions are still incomplete. For synthetic metal–oxido species, C–H bond cleavage is often mechanistically described as synchronous, proton-coupled electron transfer (PCET). However, data have emerged that suggest that the basicity of the M–oxido unit is the key determinant in achieving enzymatic function, thus requiring alternative mechanisms whereby proton transfer (PT) has a more dominant role than electron transfer (ET). To bridge this knowledge gap, the reactivity of a monomeric Mn^IV–oxido complex with a series of external substrates was studied, resulting in a spread of over 10⁴ in their second-order rate constants that tracked with the acidity of the C–H bonds. Mechanisms that included either synchronous PCET or rate-limiting PT, followed by ET, did not explain our results, which led to a proposed PCET mechanism with asynchronous transition states that are dominated by PT. To support this premise, we report a semiempirical free energy analysis that can predict the relative contributions of PT and ET for a given set of substrates. These findings underscore why the basicity of M–oxido units needs to be considered in C–H functionalization.

The functionalization of C–H bonds is one of the most challenging synthetic transformations in chemistry, in part because of the inherent large bond dissociation-free energies (BDFEs) associated with C–H bonds (BDFE_C–H) (1, 2). Monomeric metal–oxido species can overcome these barriers and cleave C–H bonds in a diverse set of substrates. The utility of metal–oxido species is exemplified within the active sites of metalloenzymes, such as heme and nonheme Fe monooxygenases (3–6) and in related, synthetic Mn– (7–15), Co– (16), and Fe–oxido complexes (17–25). Even with the advances made with these natural and synthetic metal–oxido species, key mechanistic questions about which properties of the metal complexes contribute to productive C–H cleavage persist (26–30). Much of our current understanding of metal–oxido-mediated C–H bond activation is predicated on a relationship between ground-state thermodynamics and the height of the activation barrier. Reactions of metal–oxido species with organic substrates often show a correlation between variations in substrate C–H bond strength, (BDFE_C–H, Eq. 1, where C_G is a constant that is dependent on the reference electrode and solvent) and the log of the rate constant for C–H bond cleavage. Systems for which these correlations are highly linear are said to follow a linear free energy relationship or display Bell–Evans–Polanyi (BEP)-like correlations (31, 32).

$$BDF{E}_{C–H}=\hspace{0.17em}23.06\left(E˚\right)\hspace{0.17em}+\hspace{0.17em}1.37\left(p{K}_a\right)\hspace{0.17em}+\hspace{0.17em}{C}_G.$$ [1]

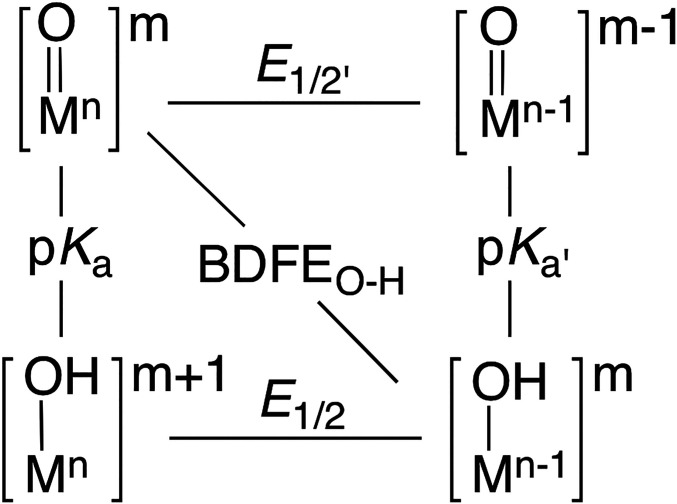
The ground-state thermodynamics for C–H bond cleavage are determined by comparing the BDFE_C–H of the C–H bond to be cleaved to that of the O–H bond formed in the resulting M^n-1–OH species; this BDFE_O–H value is obtained from the reduction potential of the M = O species and its basicity, in a manner analogous to Eq. 1 (1, 33). The relationship between BDFE_O–H, reduction potential and basicity can be conveniently represented using a thermodynamic square scheme that contains three limiting, mechanistic paths (Fig. 1) (26): 1) proton transfer/electron transfer (PT-ET); 2) electron transfer/proton transfer (ET-PT); and 3) synchronous, proton-coupled electron transfer (PCET). An important outcome of the approach of comparing BDFE values is the recognition that the basicity of the M–oxido unit can be a key contributor to C–H bond cleavage. This concept is exemplified by the high-valent Fe–oxido intermediate in cytochrome P450s (compound I). The reduced intermediate is highly basic, promoting the abstraction of H atoms from strong C–H bonds at relatively low, one-electron reduction potentials (34, 35).

Fig. 1.

Thermodynamic square scheme for M–oxido complexes involved in C–H bond cleavage. For 1, E_1/2' = −1.0 V; E_1/2 = −0.18 V; pK_a = 15; pK_a' = 28.1(2); and BDFE_O–H = 87(2) kcal/mol (SI Appendix, Eq. S1). Values measured in DMSO at room temperature. Potentials are referenced to [Fe^III/IICp₂]^+/0.

We have also shown that the basicity of the oxido ligand drives the reactivity of a low-valent Mn^III–oxido complex that is competent at cleaving C–H bonds, even though its reduction potential is less than −2.0 V versus [Fe^III/IICp₂]^+/0 (7). Our initial mechanistic suggestion for this Mn^III–oxido complex was a stepwise PT-ET pathway with proton transfer (PT) being rate limiting. However, subsequent kinetic studies on a related series of Mn^III–oxido complexes showed that electron transfer (ET) must also be involved in the rate-determining step (8). To reconcile these results, we proposed a mechanism with an imbalanced transition state, in which PT precedes ET (8). This type of asynchronous PCET mechanism (36) was examined computationally (37) and experimentally to explain the cleavage of C–H bonds with Co^III–oxido (16), Ru^IV–oxido (38), and Cu^III−O₂CAr complexes (39). The involvement of asynchronous PCET processes in the cleavage of C–H bonds by high-valent M–oxido complexes, such as Fe^IV/Mn^IV–oxido species, is still uncertain. In fact, most reactions have synchronous PCET mechanisms that follow the BEP principle (31, 32) and exhibit the correlations between the BDFE_C–H values of the substrates and the log of the second-order rate constants [log (k)]. However, C–H bond cleavage via an asynchronous PCET mechanism that is driven by the basicity of the M–oxido unit would be beneficial because reactivity could occur at lower redox potentials, while still achieving the efficiency that is often associated with PCET processes. We reasoned that this type of mechanism could occur if the high-valent M–oxido complex was relatively basic and could therefore favor mechanisms that involve PT-driven, asynchronous transition states. The high-valent Mn^IV–oxido complex [Mn^IVH₃buea(O)]⁻ (1) is a suitable candidate for testing this premise because it has a relatively high basicity, as gauged by its conjugate acid, [Mn^IVH₃buea(OH)], which has an estimated pK_a of ∼15 in DMSO (7).

We report here the kinetic studies of 1 with a variety of substrates, and the results of these studies support the involvement of PT-dominated, asynchronous transition states and show the applicability of this type of mechanism in the cleavage of C–H bonds by high-valent M–oxido complexes. To further evaluate our findings, we developed a semiempirical free energy analysis to estimate the relative contributions from the free energies of PT and ET within an asymmetric transition state. This analysis supports the assertion that the observed reactivity of 1 is driven by the pK_a, leading to PT-controlled, asynchronous transition states for the substrates examined. Moreover, we demonstrate that this analysis is useful in predicting whether a PCET reaction will be synchronous or asynchronous based on reactivity and thermodynamic parameters. Our method deviates from traditional, BEP-like analyses, in that it examines the behavior of log (k) versus a linear combination of PT and ET terms, rather than bond strengths. The appropriate combination of these free energy terms is determined by the linearity of plots versus log (k).

Results and Discussion

Reactivity Studies.

Prior reactivity studies of 1 with 9,10-dihydroanthracene (DHA) (7) were expanded in this study to include a variety of substrates with differing BDFE_C–H and pK_a values (Scheme 1 and Table 1). Kinetic results were acquired by monitoring the change in the absorption feature at λ_max = 640 nm for 1 during its reaction with excess substrate in DMSO at 20 °C (SI Appendix, Fig. S1). Under these conditions, all reactions showed pseudo–first-order kinetic data with observed rate constants (k_obs) that varied linearly with the concentration of substrate (SI Appendix, Fig. S2), consistent with the second-order rate law of rate = k[1][substrate]. The slopes of the k_obs versus [substrate] plots (Table 1 and SI Appendix, Fig. S2) provided k₂ values, which were then adjusted for the number of activable C–H bonds to give corrected, second-order rate constants, k (Table 1) (7).

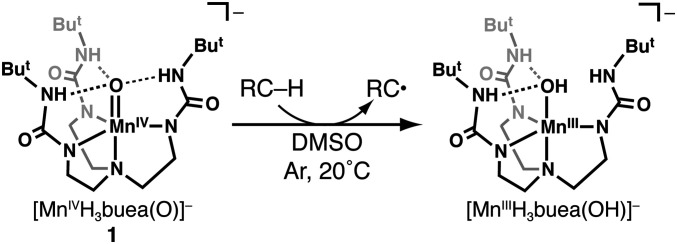
Scheme 1.

Generalized reaction for the homolytic C–H bond cleavage by [Mn^IVH₃buea(O)]⁻(1).

Table 1.

Thermodynamic parameters for the substrates and kinetic data for their reactivity with 1^*

Substrate	pKa†	BDFE†,‡	k § , ¶
Diphenylmethane	32.2	79.7	0.0006(2)
9-methylanthracene	31.1	79.4	0.0012(4)
1,4-cyclohexadiene	—	—	0.013(2)
DHA	30.1	76	0.026(2)
Xanthene	30.0	73.3	0.089(5)
4-benzylpyridine	26.7	80.9	0.008(4)
Fluorene	22.6	77.4	0.91(8)
Indene	20.1	76.7	1.07(6)
9-tolyl-fluorene	18.3	71.5	3.94(5)
9-phenyl-fluorene	17.9	71.9	11.04(6)

^*In DMSO.

^† Refs. 26, 40, 52.

^‡Kilocalories per mole.

^§Molarity⁻¹ second⁻¹.

^¶ 20 °C.

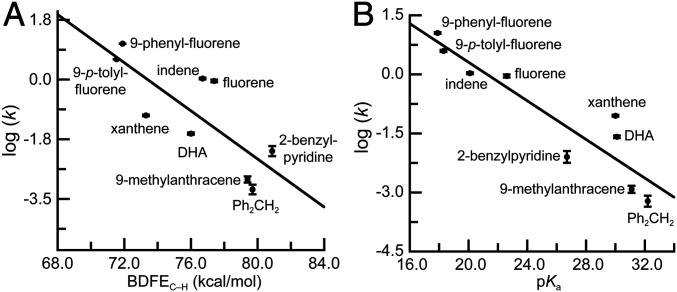
The second-order rate constants for the substrates span four orders of magnitude, while the BDFE_C–H values of the substrates differ by less than 10 kcal/mol. As discussed in the Introduction, high-valent M–oxido complexes normally follow the BEP principle and exhibit a strong correlation between log (k) and BDFE_C–H of the substrates; this type of correlation was not found for 1 (Fig. 2A). For example, the BDFE_C–H value for fluorene is 4.1 kcal/mol larger than that for xanthene, and yet fluorene reacted significantly faster than xanthene with a k value that is 10-fold larger. A better correlation was found between log (k) and the pK_a(C–H) values of the substrates (Fig. 2B), which again shows the importance of PT in C–H bond cleavage. For instance, the k value for 9-phenyl-fluorene with a more acidic C–H bond [pK_a(C–H) = 17.9] is 124 times larger than that for xanthene [pK_a(C–H) = 30.0] (40).

Fig. 2.

Plot of log (k) versus BDFE with R² = 0.62 (A) and plot of log (k) versus pK_a with R² = 0.85 (B).

While the plot of log (k) versus pK_a(C–H) gave insight into the mechanism of C–H bond cleavage by 1, some of the data did not agree with this process being dependent on only PT. We point to the data for DHA and xanthene, which have identical pK_a(C–H) values (Fig. 2B), but whose k values differ by a factor of 3. To gain a further understanding of these reactions, we compared the kinetic isotope effects (KIEs) for DHA, xanthene, and fluorene; of these three substrates, fluorene has a more acidic C–H bond (Table 2). We have previously reported a KIE value of 6.8 for DHA and determined values of 22 and 82 for xanthene and fluorene, respectively (SI Appendix, Figs. S3 and S4). These values are consistent with a primary KIE and support the hypothesis that C–H bond breakage is rate limiting. However, the KIE values for xanthene and fluorene are significantly higher than those found within the semiclassical limit, which suggests that tunneling effects may be applicable (SI Appendix). The possibility of tunneling was examined by measuring the temperature-dependent reactivity of fluorene and d₂-fluorene. The criteria for H atom tunneling include a KIE value greater than 6.4 at 20^οC; a difference in activation energies, ΔE_a = [E_a(D) − E_a(H)], of greater than 1.2 kcal/mol; and a ratio of preexponential factors, A(H)/A(D), of less than 0.7 (41, 42). An Arrhenius analysis of the data for fluorene and d₂-fluorene (SI Appendix, Fig. S5) gave a ΔE = 3 kcal/mol and A(H)/A(D) = 0.6, which provides further experimental support that appreciable H atom tunneling is involved in the C–H bond cleavage of fluorene. We also examined the temperature dependence of the rate constant for fluorene and xanthene (SI Appendix, Fig. S6) (the values for DHA have been reported previously) and found that the E_a values for xanthene and DHA are similar, but they differ significantly from that of fluorene. In addition, there is a large difference between the A values of these substrates with the value for fluorene being exceptionally large (Table 2)—we do not yet understand the cause(s) of these differences. Eyring analyses (SI Appendix, Fig. S6) found that xanthene and DHA have similar activation parameters, which again differ substantially from those found for fluorene (Table 2). Notice that for fluorene, ΔH^‡ > −TΔS^‡, which implies that C–H bond cleavage occurs under enthalpic control, whereas for xanthene and DHA, −TΔS^‡ > ΔH^‡, showing that reactivity is entropically controlled.

Table 2.

Activation parameters and KIE values for the reactivity of 1^*

Substrate	ΔH†,‡	ΔS‡	ΔG†,‡, §	E a †	A (105)¶	k H /k D
DHA	5(1)	−49(4)	19(2)	5.6(3)	0.004	6.8
Xanthene	5.9(6)	−43(3)	18(1)	6.5(6)	0.0672	22.3
Fluorene	11.5(2.0)	−19(7)	17(4)	12.0(2)	12,860	82.6

^*In DMSO.

^†Kilocalories per mole.

^‡ Entropy unit.

^§ 20 ^οC.

^¶ Second⁻¹.

Mechanistic Considerations.

Several mechanisms were considered to explain the kinetic and thermodynamic data obtained from the reaction of 1 with C–H bonds. As discussed in the Introduction, ET-PT, PT-ET, and synchronous PCET mechanisms are often discussed as possibilities for the cleavage of C–H bonds by metal–oxido complexes (Fig. 1). We have ruled out rate-limiting ET because the observed correlation between log (k) and the pK_a(C–H) clearly indicate that PT is involved in the rate-determining step. Fast ET, followed by rate-limiting PT, was also rejected because the low redox potential of 1 (−1.0 V versus [Fe^III/IICp₂]^+/0) would not facilitate the fast oxidation of these substrates. Moreover, a plot of log (k) versus the gas phase ionization energies of the substrates does not show any correlation (SI Appendix, Fig. S7). The moderate correlation between log (k) and pK_a (Fig. 2B) could suggest a stepwise process with rate-limiting PT, followed by ET. However, the discrepancies in the k values between DHA and xanthene, that we discussed in Reactivity Studies, discount rate-limiting PT. Comparison of the data between fluorene and indene is also inconsistent with PT being the sole determinant of the rates—these substrates have nearly the same second-order rate constants, but their pK_a values differ by 2.5. One would expect a larger difference in the k values if only PT was involved in the transition state. Finally, the lack of a linear correlation between log (k) and BDFE_C–H of the substrates ruled out synchronous PCET as a viable mechanistic pathway.

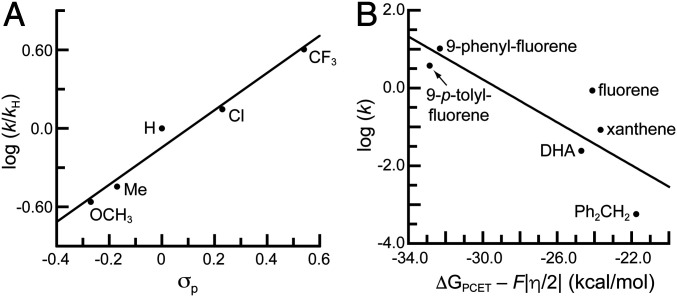
A basic, asynchronous PCET pathway, in which PT is dominant within the transition state, was then considered as a possible mechanism. For this type of mechanism, appreciable negative charge should accumulate on the substate within the transition state. To examine this possibility, the reactivity of 1 with 9-(p-X-phenyl)-fluorenes (X = OCH₃, Me, H, Cl, and CF₃) was investigated (SI Appendix, Fig. S2). We found larger second-order rate constants for substrates having stronger electron-withdrawing groups, and a Hammett analysis showed a strong correlation between log (k/k_H) and the σ_p values of the para substituents of the substrates (Fig. 3A). The data gave a positive slope of 1.42, which is consistent with a build-up of negative charge on the reactive carbon center within the transition state and further supports an asynchronous PCET mechanism.

Fig. 3.

Hammett plot for 1 with substituted 9-(p-X-Ph)-fluorenes (X = OCH₃, Me, H, Cl, and CF₃) (A) and plot of log (k) versus ΔG_PCET – F|η|/2, where η is the asynchronicity parameter, with R² = 0.70 (B).

We also used the data from 1 to experimentally determine the asynchronicity parameter (37) η for the reactions with DHA, xanthene, diphenylmethane, fluorene, 9-phenyl-fluorene, and 9-p-tolyl-fluorene (the only substrates with reported thermodynamic data to complete this analysis) and assess the usefulness of this parameter in probing the mechanism. Srnec introduced this parameter to predict whether PT or ET makes the dominant contribution to the thermodynamic driving force for a PCET process (37). The theory states that a negative η value indicates a PT-dominated asynchronous processes, while a positive value signifies an ET-dominated asynchronous process—a synchronous transition state is operative when an η = 0. The value of η is dependent on the pK_a value and redox potential of both the substrate and metal–oxido complex (SI Appendix, Eq. S2); however, experimental verification of this parameter has been difficult because, except for 1 and its Fe^IV=O analog (43), these values have not been measured for high-valent M–oxido complexes. For the substrates examined, negative η values were obtained, which agrees with the premise that a PT-driven asynchronous process occurs during C–H bond cleavage by 1. In addition, a plot of log (k) versus the η values shows a general trend of larger rate constants with more asynchronicity (SI Appendix, Fig. S8 and Table S1); however, the correlation is weak (R² = 0.26). Srnec has argued that asynchronous processes have smaller activation barriers and that the changes in the barriers are a function of $\mathrm{\Delta }{G}_{PCET}^o$ – F|η|/2, where F is the Faraday constant (37). This premise suggests that log (k) will be better correlated with $\mathrm{\Delta }{G}_{PCET}^o$ – F|η|/2 than differences in BDFEs. Our findings lend some support to this premise: Although the data are scattered, an improved correlation was observed for the plot of log (k) versus $\mathrm{\Delta }{G}_{PCET}^o$– F|η|/2 (R² = 0.70; Fig. 3B and SI Appendix, Table S1).

Linear Free Energy Analysis.

To examine asynchronicity within the transition states of the reactions of 1 with C–H bonds, we explored if a semiempirical free energy analysis, with weighted contributions from ET and PT, could more accurately describe the PT-dominated trends observed in our data. Using the Brønsted catalysis law and the Eyring equation, we obtained Eq. 2 that relates the free energy of activation ($\mathrm{\Delta }{G}^{o‡}$) to the thermodynamic driving force for a reaction (SI Appendix),

$$\mathrm{\Delta }{G}^{o‡}=\alpha \mathrm{\Delta }{G}^o\hspace{0.17em}+\hspace{0.17em}\beta .$$ [2]

For a PCET process, the overall thermodynamic driving force ($\mathrm{\Delta }{G}_{PCET}^o$) is a combination of the free energies of PT ($\mathrm{\Delta }{G}_{PT}^o$) and ET ($\mathrm{\Delta }{G}_{ET}^o$) (44, 45),

$$\mathrm{\Delta }{G}_{PCET}^o=\hspace{0.17em}\mathrm{\Delta }{G}_{PT}^o+\hspace{0.17em}\mathrm{\Delta }{G}_{ET}^o,$$ [3]

where for our system

$$\mathrm{\Delta }{G}_{PT}^o=\hspace{0.17em}-2.303RT(p{K}_a^{Mn\left(IV\right)OH}\hspace{0.17em}-\hspace{0.17em}p{K}_a^{substrate}),$$ [4A]

$$\mathrm{\Delta }{G}_{ET}^o=\hspace{0.17em}-F\left(E_{1/2}^{Mn\left(IV/III\right)OH}\hspace{0.17em}-\hspace{0.17em}{E}_{1/2}^{\left(substrate\right)\bullet /-}\right)\hspace{0.17em}.$$ [4B]

For BEP-like systems, changes in the free energy of activation for C–H bond cleavage correlate with the thermodynamic driving force for PCET ($\mathrm{\Delta }{G}_{PCET}^o$; Eq. 3), which can be obtained from the sum of the individual free energies associated with ET and PT, Eqs. 4A and 4B (via the thermodynamic scheme shown in Fig. 1),

$$\mathrm{\Delta }{G}^{o‡}=\alpha \left(\mathrm{\Delta }{G}_{PT}^o+\mathrm{\Delta }{G}_{ET}^o\right)\hspace{0.17em}+\hspace{0.17em}\beta .$$ [5]

Eq. 5 describes a synchronous PCET process, in which the electron and proton move concomitantly through the transition state, with $\mathrm{\Delta }{G}_{PT}^o$ and $\mathrm{\Delta }{G}_{ET}^o$ playing equal roles (i.e., receiving equal weighting) in determining changes in the activation barrier.

In an asynchronous process, the electron and proton proceed along the reaction coordinates at different rates, and their motions can be thought to contribute to the activation barrier in different degrees. In an effort to model this behavior, we have explored the possibility that a specific semiempirically determined, weighted combination of $\mathrm{\Delta }{G}_{PT}^o$ and $\mathrm{\Delta }{G}_{ET}^o$ would better correlate with observed changes in activation barrier for a PT-controlled asynchronous processes. For this type of mechanism, Eq. 5 was modified to

$$\mathrm{\Delta }{G}_{asyn}^{o‡}=\alpha (\mathrm{\Delta }{G}_{PT}^o+x\mathrm{\Delta }{G}_{ET}^o)\hspace{0.17em}+\hspace{0.17em}\beta ,$$ [6]

with 0 < x < 1, and $\mathrm{\Delta }{G}_{asyn}^{o‡}$ is the free energy of activation for a PT-controlled asynchronous process. Moreover, combining Eq. 6 with the Eyring equation gives

$$log\hspace{0.17em}\left(k\right)=\hspace{0.17em}–\left(\frac{\alpha }{2.303RT}\right)(\mathrm{\Delta }{G}_{PT}^o+x\mathrm{\Delta }{G}_{ET}^o)+\beta \text{'},$$ [7]

where ${\beta }^{\prime }=\log \left(\frac{\kappa k_{B}T}{h}\right)-\raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$2.303RT$}\right.$.

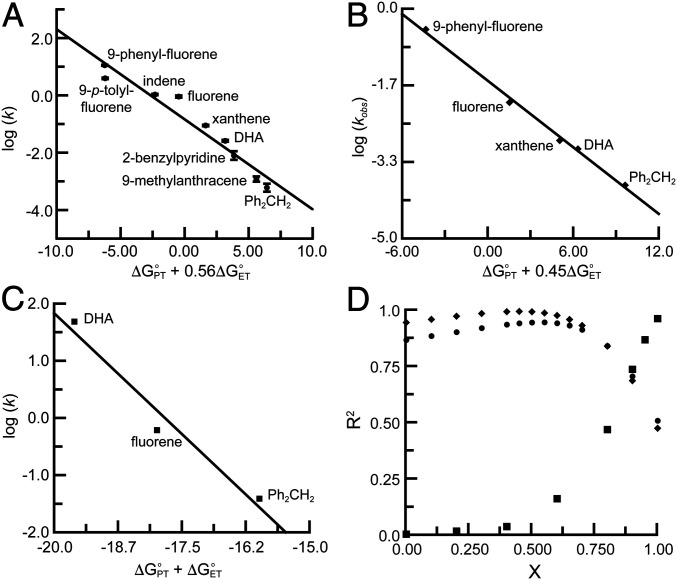
Based on Eq. 7, a PT-dominated asynchronous process will show a linear dependency between log (k) and $\mathrm{\Delta }{G}_{PT}^o+x\mathrm{\Delta }{G}_{ET}^o$ for a specific x value that gives the best fit to the data (Fig. 4A and SI Appendix, Fig. S9). A graphical representation of how the linearity varied with the x value was obtained from a plot of R² versus x, which indicated that the best correlation occurred for x = 0.56 with R² = 0.94 (Fig. 4D and SI Appendix, Fig. S10). Notice that this correlation is a statistically significant improvement on those shown in the plots for either log (k) versus BDFE_C–H (R² = 0.62 and P value = 0.0082; Fig. 2A) or log (k) versus pK_a(C–H) of the substrate (R² = 0.85 and P value = 0.10; Fig. 2B), which suggests that although PT is the major contributor to the transition state, the ET component also plays a role in the observed reactivity.

Fig. 4.

Plots of log (k) versus $\mathrm{\Delta }{G}_{PT}^o+x\mathrm{\Delta }{G}_{ET}^o$for 1, where x = 0.56 with R² = 0.94 (A); for a Co^III–oxido complex, where x = 0.45 with R² = 0.996 (B); and for a Cu^III–OH complex, where x = 1.0 with R² = 0.96 (C); plot of R² versus x for 1 (circles), Co^III–oxido complex (diamonds), and Cu^III–OH complex (squares) (D).

We also examined how our approach can provide insight into other systems that cleave C–H bonds. For instance, Anderson has shown that the reactivity of his Co^III–oxido complex does not correlate with the substrate BDFE_C–H but instead trends with the acidity of the substrate C–H bonds, with a relatively modest correlation: A plot of log (k_obs) versus pK_a(C–H_subsrate) gave an R² value of 0.65 (16). To examine the utility our approach, we reanalyzed these data for all substrates used and found a more linear relationship for a plot of log (k_obs) versus $\mathrm{\Delta }{G}_{PT}^o+x\mathrm{\Delta }{G}_{ET}^o$ with x = 0.55 (R² = 0.85; SI Appendix, Fig. S11). We also examined just the five substrates that are common to both our studies (Fig. 4B). This gave a significantly better R² value of 0.94 for the plot of log (k_obs) versus pK_a(C–H_subsrate). The correlation was further improved using our approach to give a nearly linear fit R² = 0.996 if log (k_obs) was plotted versus $\mathrm{\Delta }{G}_{PT}^o+x\mathrm{\Delta }{G}_{ET}^o$ with x = 0.45 (Fig. 4 B and D). The observation of similar outcomes for the Co^III–oxido and Mn^IV–oxido complexes is consistent with the M–oxido units having similar basicities (Co^III–OH/Mn^IV–OH: pK_a = ∼15/15) and redox potentials (Co^III/II–hydroxido/Mn^IV/III–hydroxido: E° = −0.23/−0.18 V versus [Fe^III/IICp2]^+/0) (7, 16, 46). We also examined C–H cleavage by the Cu^III–OH complex of Tolman [pK_a(Cu^III–OH₂) = 11.7, E°(Cu^III/II–OH₂) = 0.345 V versus [Fe^III/IICp₂]^+/0] (47), which had previously been proposed to follow a synchronous PCET process based on a strong correlation between log (k) and BDFE_C–H. Our analyses using common substrates agreed with this premise: We found that the best linear correlation for log (k) and $\mathrm{\Delta }{G}_{PT}^o+x\mathrm{\Delta }{G}_{ET}^o$ was obtained with x = 1 (R² = 0.96), which is characteristic of a synchronous PCET mechanism (Fig. 4 C and D and SI Appendix, Fig. S12). It appears that the significant increase in Cu^III/II redox potential (∼0.55 V) and decrease in pK_a of the Cu^III–OH, relative to those of the Co^III–oxido/Mn^IV–oxido species, results in more synchronous reactions with C–H bonds.

Conclusions

Studies using ground-state thermodynamics to probe the reactivity of high-valent M–oxido complexes with C–H bonds generally describe the reactions as PCET processes with synchronous transition states; this description indicates that the energetics of PT and ET contribute equally to the overall reactivity. However, within a broader context, the energetics of PCET are often viewed as a continuum, in which the contributions of the ground-state free energies for PT and ET are not necessarily equivalent (28, 48, 49). Our results for the reactivity of 1 illustrate this broader concept and show how asynchronous PCET serves as a relevant mechanistic explanation for the reactivity of high valent M–oxido complexes with C–H bonds. The semiempirical free energy analysis, introduced here to explain the reactivity of 1, relates log (k) to the fractional component of the free energy of ET (that is $\mathrm{\Delta }{G}_{PT}^o+x\mathrm{\Delta }{G}_{ET}^o$). This approach is useful in identifying synchronous and asynchronous processes for PCET reactions involving metal–oxido/hydroxido complexes and, more generally, should be applicable in probing other types of PCET processes. These findings highlight the need to consider PT in the cleavage of C–H bonds by metal–oxido complexes and the important functional role of the basicity of metal–oxido groups (50). In proteins, a more basic M–oxido unit would allow the metallocofactor to react at a lower redox potential (1), thereby explaining how highly reactive species like compound I can be generated without oxidizing the surrounding amino acid residues. Including basic metal–oxido units in the design of synthetic complexes could lead to more selective reagents whose targets are determined by the acidity of the C–H bonds, which would be advantageous in chemical syntheses.

Materials and Methods

The [Mn^IVH₃buea(O)]⁻ complex was prepared, as previously described (7, 51). Kinetic experiments were done in triplicate under pseudo–first-order conditions by following the disappearance of the absorption band at λ_max = 640 nm. Product analyses were done using gas chromatography–mass spectrometry methods. Regression analyses to determine the P values were done with “F-Test Two-Sample for Variances” routines in Microsoft Excel (version 16.23) data analysis tools. For full descriptions and details of experimental methods, derivations of equations used to generate the semiempirical linear free energy approach, regression analysis, and all spectral and statistical data, reference SI Appendix.

Data Availability

All study data are included in the article and/or SI Appendix.