Energy penalties enhance flexible receptor docking in a model cavity

Significance

The dynamic nature of biomolecules is typically neglected in docking screens for ligand discovery. The key to benefitting from various receptor conformations is not only structural but also thermodynamic information. Here, we test a general approach that uses conformational preferences from enhanced and conventional molecular dynamics simulations to account for the cost of transitions to high-energy states. Including this information as a conformational penalty term in a docking, scoring function, we perform retrospective and prospective screens and experimentally confirm predicted ligands with T_m upshift and X-ray crystallography. This not only allows us to test the predicted ligands for binding, it also tests whether they bind to the conformation of the binding site for which they were predicted.

Abstract

Protein flexibility remains a major challenge in library docking because of difficulties in sampling conformational ensembles with accurate probabilities. Here, we use the model cavity site of T4 lysozyme L99A to test flexible receptor docking with energy penalties from molecular dynamics (MD) simulations. Crystallography with larger and smaller ligands indicates that this cavity can adopt three major conformations: open, intermediate, and closed. Since smaller ligands typically bind better to the cavity site, we anticipate an energy penalty for the cavity opening. To estimate its magnitude, we calculate conformational preferences from MD simulations. We find that including a penalty term is essential for retrospective ligand enrichment; otherwise, high-energy states dominate the docking. We then prospectively docked a library of over 900,000 compounds for new molecules binding to each conformational state. Absent a penalty term, the open conformation dominated the docking results; inclusion of this term led to a balanced sampling of ligands against each state. High ranked molecules were experimentally tested by T_m upshift and X-ray crystallography. From 33 selected molecules, we identified 18 ligands and determined 13 crystal structures. Most interesting were those bound to the open cavity, where the buried site opens to bulk solvent. Here, highly unusual ligands for this cavity had been predicted, including large ligands with polar tails; these were confirmed both by binding and by crystallography. In docking, incorporating protein flexibility with thermodynamic weightings may thus access new ligand chemotypes. The MD approach to accessing and, crucially, weighting such alternative states may find general applicability.

Proteins interchange between conformational states of varying probabilities (1). These rearrangements, naturally, also alter its physicochemical properties (2, 3). Exploiting these varying features can benefit ligand discovery (4–7) but also presents several challenges. Key among them is weighting the different states by their energies, which has been shown to be crucial for docking success (4, 8); without such weights, high-energy protein conformations, often better suited to ligand complementarity but harder to access, can dominate docking results, acting effectively as decoy conformations.

Structural models of proteins in distinct conformational states can be obtained from experiments like X-ray crystallography, NMR, or cryoelectron microscopy. The choice of the single structure used for a docking campaign contributes to its likelihood of success and choosing any single conformation inevitably leads to false negatives, even in successful campaigns. A solution to this problem is to consider multiple protein conformations, often referred to as ensemble docking or flexible receptor docking (4, 9–15). Yet incorporating multiple protein conformations only increases accuracy in ligand discovery when they are weighted according to their ensemble probabilities (10, 16, 17). When such energies have been incorporated in docking campaigns, they have enabled the discovery of ligands that are inaccessible to single-state docking, often with high fidelity to the subsequent structure determination of ligand–protein complexes. However, incorporating these weights has relied on experimental observables, such as occupancies from high-resolution structures. This has both limited the range of states that may be used—since states higher in energy than a few kilocalories per mole above the ground state will not be observed experimentally—and cannot be generalized to the vast number of targets for which such information is unavailable. Even when alternative conformational states can be observed in complex with different ligands (4, 11, 18, 19), their thermodynamic weights in the apo ensemble are typically unknown. It would be useful to have a general method of sampling and energy-weighting conformational states that would enable their exploitation in ligand discovery, in general, and for molecular docking in particular.

In principle, computationally modeled conformations, such as those derived from molecular dynamics (MD) simulations, can sample such states (9, 20, 21) and can estimate their thermodynamic weighting (22–24). Encouraging studies on how MD simulation can be leveraged to explore the flexibility of ligand binding sites include work from the Bowman group, in which exhaustive MD simulations aided the discovery of allosteric binders (6, 10). More recently, exascale simulations of proteins central to SARS-CoV-2 immune evasion were able to explain and predict cryptic binding sites (25, 26). In practice, however, challenges with many MD simulations include insufficient sampling and the difficulty in weighting states by relative energies. The free energy minima, representing conformational states of a protein, are often separated by high-energy barriers, which are rarely overcome on time scales covered by conventional MD (cMD) simulations (1). Enhanced sampling algorithms, such as accelerated MD (aMD) (27), introduce a bias potential to lower the barriers between individual conformational states. This makes the sampling of a diverse, conformational ensemble, including higher-energy conformational states, more efficient by increasing the sampling by up to three orders of magnitude (28–30). A core question is whether the assumptions and approximations made in aMD affect its ability to usefully weight the conformations sampled.

Here, we test energetic weights from MD simulation for ligand discovery in the engineered cavity site of T4 lysozyme L99A (L99A). This hydrophobic cavity was first introduced by Eriksson, Morton, Baase, and Matthews (31–34), as a model system to explore ligand binding and thermodynamics. While binding to this site is not thought to affect the enzymes function (it is over 20 Å from the catalytic aspartate and does not overlap with the muramyl peptide binding site; SI Appendix, Fig. S7), it has important advantages for exploring terms in ligand binding and docking (here, protein flexibility). The cavity site is relatively small, only 150 ų in its apo state, and is completely enclosed from solvent in that conformation (Fig. 1A). Combined with its dominance by apolar interactions, this simplifies the determinants of ligand binding. Despite its small size, there are still many hundreds of likely ligands that are readily available and testable from within docking libraries, enabling prospective predictions to test new docking terms and methods (11, 32, 33, 35–37). Previous studies have revealed at least 68 ligands for this cavity, many of which have protein-bound crystal structures determined (31, 38), enabling detailed retrospective studies. Despite its simplicity, L99A has complexities that make it interesting and relevant as a model site, and its thermodynamics (34, 39–41), dynamics (28, 42–50), and ligand (un)binding (33, 36, 51–59) have been intensely studied.

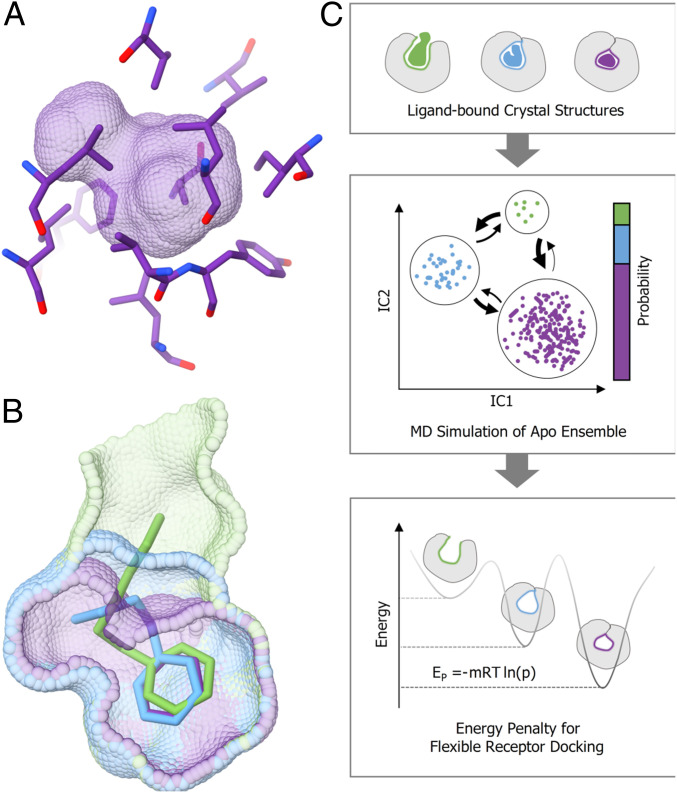
Fig. 1.

Three conformations of the L99A cavity binding site. (A) Crystal structures of T4 lysozyme L99A in its apo state show a small, buried, and entirely apolar cavity. (B) Structures of the protein in complex with ligands of increasing size show three major conformational states of the binding site: closed (purple), intermediate (blue), and open (green). (C) Workflow.

Particularly germane to this study, the cavity undergoes a conformational change as larger and larger ligands bind to it, adopting three principal conformations termed closed (150 ų), intermediate (∼200 ų), and open (<300 ų) (35) (Fig. 1B). As larger ligands bind, the cavity opens owing to the unwinding of helix F from an α- to a 3 to 10-helix. In the most voluminous state of the cavity (twice that of the closed state), it opens to form a channel between bulk solvent and the hydrophobic cavity. Thus, despite being a simplified model system, L99A exhibits substantial structural rearrangements, making it a useful site to test flexible receptor docking (11, 60).

For this study, we derive conformational state definitions from apo and holo crystal structures of L99A in its closed, intermediate, and open state (Fig. 1C). Removing the ligands, we perform aMD and cMD simulations for exhaustive and efficient sampling. We then construct a Markov state model (MSM) (61–64) to estimate the relative probability of each crystallographic conformational state in the apo ensemble. Converted into a conformational energy penalty $E_p$ (Eq. 1), we incorporate the state probabilities into our flexible receptor docking scoring function (4).

$$E_p=-m\cdot k_B\cdot T\cdot \text{ln}\left(p\right),$$ [1]

where k_B is the Boltzmann constant, T is the temperature in K, P is the population, and m is the weighting multiplier.

The multiplier m weights the conformational penalty energy to bring it into balance with the other terms in the DOCK3.7 scoring function, which are typically higher in magnitude than true ligand-binding energies. As in earlier studies that used crystallographic occupancies to measure populations, this m value may need to be optimized for each system studied, at least for DOCK3.7 (4); for scoring functions whose energies are already aligned with experimental binding energies, this may not be necessary. While this is admittedly a weakness, we test the reliability of the applied penalties in retrospective screens based on the known ligands and their property-matched decoys, as we do with the normal scoring function (see Results). Thus, while this weighting may change from system to system, doing so fits with the retrospective control calculations that are already typical in docking.

Crucially, we evaluate the ability of the approach to predict ligands with new chemotypes selective for each of the three relevant conformations of the cavity in a prospective docking screen. We consider the usefulness of this approach to the general problem of predicting weighted, conformational ensembles of proteins for docking and ligand discovery.

Results

Thermodynamic Weighting from Apo MD Simulations.

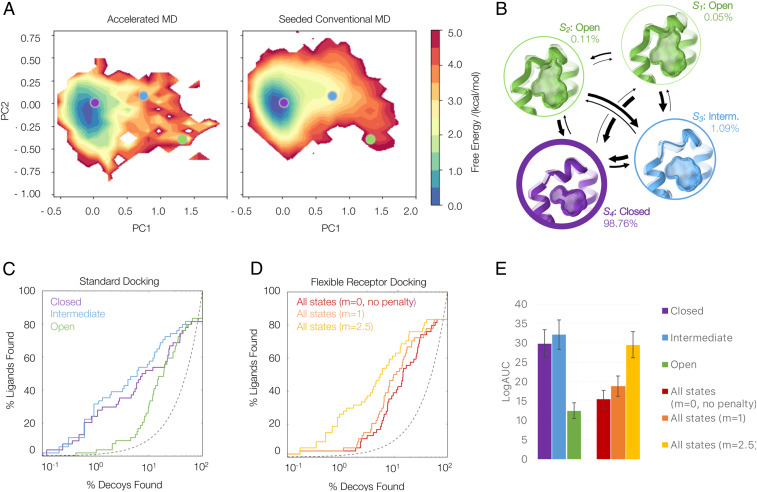
We perform both enhanced (i.e., aMD) (SI Appendix, Fig. S1) and conventional (cMD) simulations to estimate the population of the three crystallographic states in the apo ensemble (Fig. 2). On the one hand, we directly derive reweighted populations from clustering 500 ns aMD. This analysis suggests a probability of 0.5% for the open, 1.4% for the intermediate, and 98% for the closed state (SI Appendix, Table S2). On the other hand, we assess the stability of these populations from unbiased cMD simulations. From extensive structural sampling (7.75 µs), we construct an MSM to estimate the thermodynamic weight of each crystallographic state in solution with no ligand present. In addition to providing populations of and by extension weights for the states, this analysis also allows an assessment of the involved kinetics. The MSM analysis finds four distinct states (S₁ to S₄), which closely resemble the three distinct conformations observed in ligand-bound structures (Fig. 2 and SI Appendix, Figs. S2–S4). States S₁ (0.05% of the population) and S₂ (0.11% of the population) both resemble the open state, which, for example, occurs in complex with n-hexyl-benzene (Protein Data Bank [PDB]: 4W59). State S₃ (1.09% of the population) resembles the intermediate conformational state, as found in the complex with n-butyl-benzene (PDB: 4W56). The closed conformation, which is found for most apo structures or in the complex with benzene (PDB: 4W52), is modeled by state S₄ (98.76% of the population). Encouragingly, we thus obtain state populations within the same order of magnitude from the reweighted aMD ensemble and the unbiased simulations.

Fig. 2.

Retrospective docking with MD-based weightings. (A) Conformational space covered with aMD and the seeded cMD simulations as a projection onto the combined principal component analysis space; representative crystal structures of the closed (4W52, purple), intermediate (4W55, blue), and open (4W59, green) state are depicted as circles. (B) The MSM built from the unbiased cMD trajectories identifies four states (S₁ to S₄); S₁ and S₂ both represent the open state, S₃ the intermediate, and S₄ the closed state of L99A. Adjusted log receiver operating characteristic (ROC) curves from standard docking (C) to individual conformational states (purple: closed, blue: intermediate, and green: open) and flexible receptor docking (D) with varying weighting multipliers m. (E) Adjusted areas under the log ROC curves quantifying the enrichment of known ligands against decoys for classic and flexible docking screens with and without penalties.

The kinetic information provided by the MSM is not required to perform flexible receptor-docking calculations. Nevertheless, this analysis highlights that the structurally highly similar closed and intermediate state have fast transition time scales, consistent with experimental spectroscopy (57, 65) and the ability to soak ligands into apparently closed cavities in crystals. Expanding the closed conformation toward the intermediate state is observed with a mean first passage time (mfpt) of 106 ns. Observing a full opening of the cavity, however, takes an order of magnitude longer in simulation time, with mfpts of 1,555 to 8,474 ns.

Retrospective Testing of MD-Based Penalties.

We converted these populations into an energy penalty term using Eq. 1 (4). To test the benefits and shortcoming of flexible receptor docking and MD-based penalties, we docked 68 known ligands into the three conformational states of the binding site. We then calculated the log-adjusted enrichment of the known ligand over property-matched decoys (66), docking to each receptor state individually (standard dock—Fig. 2 C and E) and using all three states combined with and without the energy penalty (flexible receptor docking—Fig. 2 D and E). Previously (4, 10), we find that the enrichment of known ligands over decoys depends on the receptor conformational state. Docking to the higher-energy open state without a conformational penalty enables many decoy molecules to be accommodated and, moreover, to score better than known ligands that bind to the smaller closed and intermediate states. Accordingly, docking against all three states without an energy penalty (Fig. 2D, red curve) led to poor overall enrichment of known ligands over property-matched decoys and domination by the higher-energy open state (Fig. 2E and SI Appendix, Fig. S5). Including a penalty term calculated directly from the MD slightly improves enrichment in the retrospective docking. When we weigh this MD penalty term to bring it into line with the magnitude of the other energy terms in the DOCK3.7 scoring function, as similarly done in previous studies (4), ligand enrichment improves substantially, and the distribution of molecules docked to each conformational state becomes more balanced (less dominated by the open conformation). We note that even weighted, the enrichment from docking against the multiple receptor conformation (Fig. 2D, gold curve) does not exceed that from docking against the single closed conformation (Fig. 2C, blue curve). This reflects the bias of the past, however, as most ligands known for the L99A cavity bind to the closed conformation of the receptor. Including the alternate higher-energy conformations of the receptor, without having them dominate, enables the discovery of newer molecules that bind to these more open states.

In addition to its accuracy in identifying known ligands, we test whether the approach can reproduce the crystallographic state occupancies. We calculate the conformational preferences from the docking score of seven ligands, as described previously (4). Applying a weighting multiplier of m = 2.5 to the energy penalty term, we find a Pearson correlation coefficient of 0.93 between experimental and predicted conformational preferences (SI Appendix, Fig. S6). Based on ligand enrichment and the correlation between crystallographic occupancies and predicted conformational preferences, we proceeded with prospective prediction using the optimized value of m = 2.5.

Prospective Screening to Identify Binders for Each Conformational State.

Encouraged by the retrospective performance, we applied the energy penalties in a prospective screen of a library of over 900,000 purchasable molecules from the ZINC database. From among the top ranking 0.25% of these docked molecules, we selected 33 molecules for experimental testing, choosing the same number of compounds for each conformational state of the cavity (closed, intermediate, and open). In addition to being high ranking—which concentrated the molecules under consideration among the top 99.75%—we applied a typical “hit-picking” criteria (67), insisting that they not be conformationally strained nor bear high-energy tautomers, features that the method can miss. We also biased toward molecules that were topologically at once diverse and unrelated to previously known ligands (Table 1, Tanimoto column).

Table 1.

Summary of newly identified L99A binders based on T_m upshift and X-ray crystallography

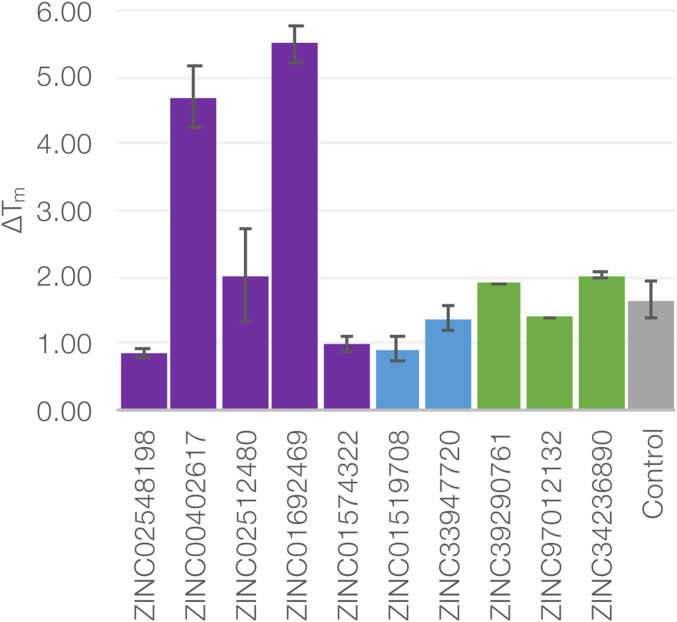
Each of the prioritized molecules was measured for binding by temperature of melting upshift using a SYPRO orange binding assay (Materials and Methods). Of these 33, 10 increased the T_m of melting of L99A by between 0.9 and 5.5 °C when tested at 100 μM (P values ranging from <0.01 to 0.0001 versus DMSO control; without a crystal structure, a molecule had to have a T_m upshift >0.9 to be considered a ligand) (Fig. 3). In addition to the change in melting temperatures, we also determined crystal structures of 13 compounds bound to L99A; any molecule for which a cocomplexed crystal structure could be determined was considered a ligand. Taking together that both change in melting temperature and crystal structures, we consider 18 molecules to be L99A ligands, a docking hit rate of 55%, with seven confirmed by both X-ray structure determination and T_m upshift assay, five confirmed by T_m upshift assay alone, and six confirmed by X-ray structure alone (in total 18 confirmed of 33 predicted, Table 1). We note that as ligands for a designed cavity in lysozyme, one distant from the active site, none are expected to substantially modulate enzyme activity, c.f. SI Appendix, Fig. S7. If one were to only consider the 13 crystallographically confirmed molecules as ligands, the hit rate would be 39% (Fig. 4). On a state-by-state basis, 8 of 11 molecules predicted for the closed conformation were confirmed experimentally and 7 of 11 molecules predicted for the intermediate conformation were confirmed experimentally, while for molecules predicted for the open state, which is more challenging because so many more ligands can fit it, 3 of 11 were confirmed to bind (Figs. 3 and 4).

Fig. 3.

T_m upshift experiments with DSF. In a thermal shift assay (DSF), 10 ligands were identified as binders. Five of these were predicted to bind to the closed state (purple), two to the intermediate state (blue), and three to the open state (green). The previously known binder ethylbenzene is shown as positive control in gray.

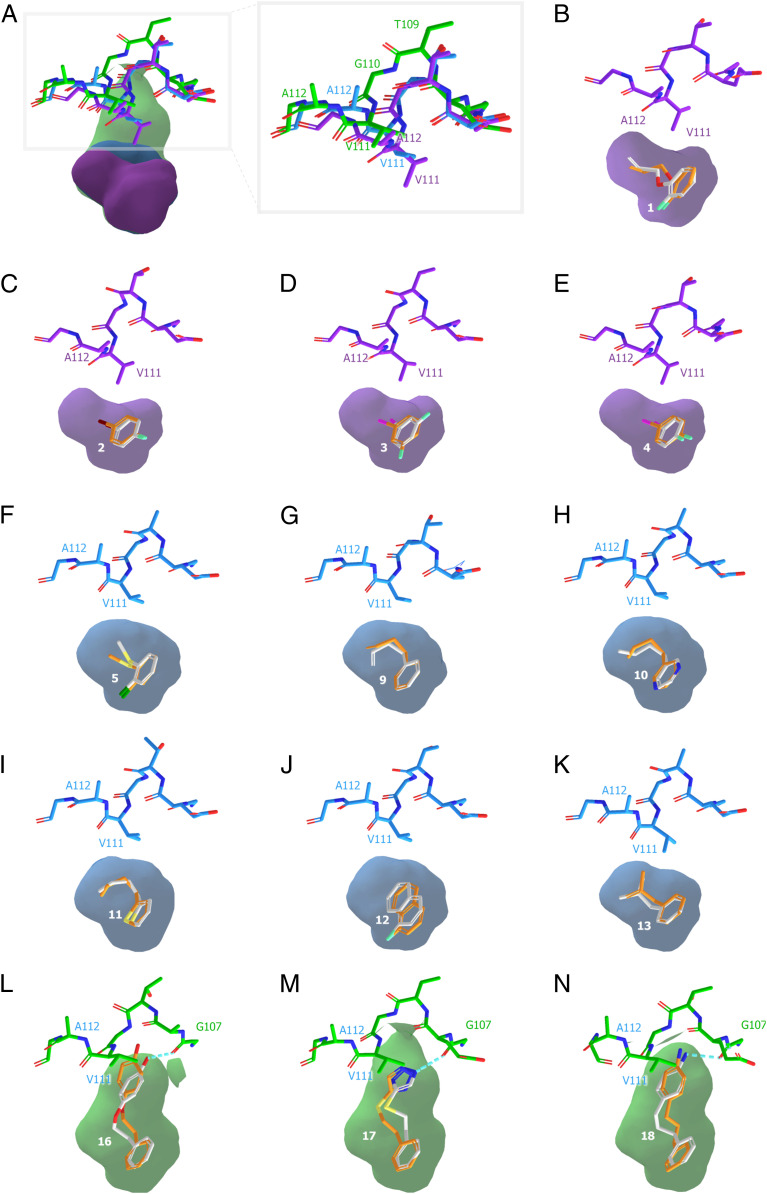
Fig. 4.

Predicted and experimental ligand poses and site conformations. (A) Closed (violet), intermediate (blue), and open (green) conformation of the L99A cavity site—characterized by a shift of the F-helix residues T109 to A112. (B–N) Superposition of predicted (orange) and crystallographic (white) ligand poses for crystals structures 7LOB, 7LOC, 7LOA, 7LOD, 7LX8, 7LX9, 7LOG, 7LOF, 7LOE, 7LXA, 7LX7, 7LX6, and 7LOJ, respectively.

For 13 of these ligands, we determined that X-ray crystal structures bound to L99A (Table 1 and SI Appendix, Fig. S8 and Table S3). Crystals diffracted from 0.99- to 1.5-Å resolution. In all 13 of the crystal structures, we can see the unrefined difference electron density maps (F_o-F_c) clearly defining both ligand positions and that of the F-helix, whose opening defines the three conformational states of the cavity. Crystals diffracted from 0.99- to 1.5-Å resolution. In all 13 of the crystal structures, we can see the unrefined difference electron density maps (F_o-F_c) clearly defining both ligand positions and that of the F-helix, whose opening defines the three conformational states of the cavity (SI Appendix, Fig. S8). The quality of these observations made us confident on our ability to predict these structures. Of the five closed state structures, four (PDB: 7LOB, 7LOC, 7LOA, and 7LOD) also had the alternate electron density for the intermediate state in the F-helix, thus both intermediate and closed conformation existed in the same structures with the dominant conformation being closed. For PDB 7LOB, the closed cavity conformation occupied 77% of the observed electron density, while the rest was modeled as intermediate. The percentage of closed cavity conformation for the other three closed state structures with PDB ID’s 7LOC, 7LOA, and 7LOD were 56, 71, and 63%, respectively. The only intermediate structure that also had an alternate conformation for closed state included PDB ID 7LOG, with 92% of the conformation being intermediate and the rest modeled as closed state. Alternate conformational states with less than 8% occupancy were not modeled in the crystal structures. Encouragingly, the docked poses of the predicted ligands closely resembled the crystallographic geometries, with rmsds ranging from 0.42 to 2.3 Å and a mean rmsd of 0.90 Å (Fig. 4). Crucially, all ligands but one (compound 5) bound to the conformational state for which it had been predicted in the weighted-ensemble docking (Table 1). Thus, ligands predicted to bind to the closed state, compounds 1 through 4, were observed to bind to that state; the seven ligands predicted to bind to the intermediate state, compounds 9 through 13, bound to it; and the three ligands predicted to bind to the open state, compounds 16, 17, and 19, bound to it. Only compound 5, which was predicted to bind to the closed state, was found to bind to the intermediate state. For all of these complexes, there was little ambiguity in making these state assignments—in the four closed state structures, the F-helix adopted a classic α-helical geometry, with residues V111 and A112 adopting a “down” conformation into the site, and no pathway between the cavity and bulk solvent—the ligands were completely enclosed by the residues defining the cavity. For the six intermediate state structures, residues T109 to G113 shift “upwards,” with Val111 rotating about its $\chi$₁ angle, enlarging the cavity. Finally, in all three open state structures, the F-helix adopts a 3 to 10 helix, and a clear channel opens up to solvent, which the docked ligands exploit. Whereas the docking hit rate for this state was relatively low, all three ligands bound in geometries that corresponded to the docking predictions (Fig. 4 L–N). Clearly, the driving force for binding in the closed, intermediate, and open states was sterics, but in the open state, there is also a role for the orientation of polar groups, which typically interacted with the backbone of residue G107 in the unwound F-helix and also with bulk solvent. Encouragingly, these interactions were captured in the docking (Fig. 4).

Discussion

Three key results emerge from this study. First, MD simulations, including aMD, can access and energy weight alternative conformational states of binding sites; second, these weighted conformations substantially improve docking hit rates versus unweighted states; and third, the docking hits predicted for each state actually bind to those states. Using MD—and, indeed, other methods, such as simply relying on experimental observables—to access and weight protein conformations for docking has confronted two problems: accessing the correct states and weighting them by energy. In previous work, even when states are sampled correctly, docking can be biased by those states that best fit ligands, which are often those that are higher in energy. These high-energy states, thus, act as decoys, crowding out more favorable solutions. Drawing on experimental observables, several studies have shown that when states are properly weighted by conformational energies, docking results improve (4, 11). However, depending only on experimental observables, such as multiple state occupancies, restricts this approach to the relatively few targets that afford such high-quality observables. Thus, a crucial result of this study is that both cMD and, encouragingly, also aMD can both sample experimentally accessible states and usefully weigh them (Fig. 2A). Tested retrospectively in the model cavity site L99A, docking hits are dominated by the highest-energy open conformation of the site, which is the one that can accommodate the largest ligands. With the aMD-derived population weights applied, retrospective hit rates improve substantially (Fig. 2 C–E). More compellingly, in prospective screens, a high 55% hit rate is found for new ligands, topologically different from those previously known (Table 1). The ability to readily determine structures with L99A allowed us to interrogate these new ligands at atomic resolution. For 12 out of 13 structures determined, each new ligand was predicted to be bound to the conformational state in which it was observed (Fig. 4).

Besides its high sampling efficiency compared to cMD, an advantage of the aMD approach is its pathway independence (68). In aMD, no prior knowledge of a system’s free energy landscape needs to be incorporated, for instance, in the form of a reaction coordinate or a collective variable. Instead, the required parameters can be derived from energetic averages of short cMD simulations. The workflow we present can thus be applied to any system of interest. Here, we focus on benchmarking the reliability of aMD-derived energy weights, which we then apply on experimental holo structures. However, especially when exhaustive sampling can be achieved, it has been shown that MD simulations can also suggest and refine protein binding site conformations for ligand discovery, even those that have not been observed before or were not well defined (10, 26). Selecting single structures from thousands of snapshots visited within MD trajectories is a tedious and typically ambiguous challenge. The kinetic clustering and coarse graining embedded in a typical MSM workflow represents a most robust and straight-forward approach to this problem. In summary, aMD can provide a sampling speedup of three orders of magnitude versus cMD simulations (29, 69), but the cMD-based MSM workflow provides more accurate estimations of state probabilities. The combination of enhanced and cMD simulations (Fig. 1 A and B) may be an efficient method for extensive phase space exploration, with ultimately unbiased transition rates, and thus may offer reliable energetic weightings for the sampled states. Similar simulation strategies, differing in the initial step of assuring exhaustive sampling, have been applied to a broad range of biomolecular systems, such as the miniproteins WW domain and NTL9 (70), beta-lactamase (10), allergen proteins (71, 72), serine proteases (24, 73), antibodies (74), and proteins central to SARS-CoV-2 evasion (25, 26). This workflow should thus be transferrable to most biomolecular system.

The energy weights, which we derived from the aMD simulations, substantially improved our docking hit rates, both for retrospective and prospective screens. We find that the energetic penalty term is crucial, in particular, for the high-energy open state. Without accounting for the energetic cost of the cavity opening, large decoy molecules dominate the top ranks of the retrospective docking (Fig. 2D). Larger ligands are inherently favored by the docking scoring function, for this and for other sites, simply because they can make more interactions. Incorporating energy weights helps balance the ligands and states among the top-ranked molecules. While similar observations have been made based on high-quality experimental weighting, an advantage of the MD approaches investigated here is that they should be applicable to the majority of targets for which such weighted states are not available directly from experimental observables.

Encouragingly, predicted and experimental binding site conformations corresponded well. For 12 of 13 ligand-bound structures, the flexible receptor docking predicted the correct dominant receptor conformation. This is most compelling for the open state, in which the site doubles in volume and opens it to the bulk solvent, making it substantially more complicated in terms of its potential interactions and biophysics. The three molecules that bind to this conformation, compounds 16 through 18, include polar groups, such as a phenolic hydroxyl, a triazole, and an amine (Fig. 4 L–N), which hydrogen bond with the backbone of G107 in the F-helix, a group previously unavailable to them in the closed and intermediate conformations. In the open state, these groups are also open to bulk solvent, which likely has a role in reducing the desolvation penalty they would otherwise pay. Balanced against the ability to predict this state for these ligands, and to predict the ligand-bound geometries with high fidelity, was the relatively low hit rate for molecules predicted to bind to the open state. This at least partly reflects the loss of the steric constraint that effectively separates ligands from many larger nonbinders in the much smaller closed and intermediate cavity conformations—in the open state, the L99A “cavity” begins to reflect the more open sites typical of drug targets, as do its docking hit rates (3 of the 11). Likely also contributing was the relatively low solubility of the larger molecules versus smaller ligands for a site whose maximal affinity is close to 10⁻⁴ M.

Certain limitations of this study merit airing. While we believe that aMD can be used to not only weigh but to sample relevant conformations, we relied on crystallographically defined conformational states, for which we calculated MD-based probabilities. Until this is demonstrated prospectively, a substantial undertaking, the generalizability of this approach will remain tentative. Correspondingly, while we achieved relatively exhaustive sampling for L99A, for larger and more complex drug targets, this will be more challenging. And just when sufficient sampling is achieved, remains one of the general challenges with MD simulations. It may be that, for the foreseeable future, reaching full convergence for a large biomolecular system may be unfeasible; still, local convergence, for instance for motions within a specific binding site, may be reachable. We do note that MSM-based workflows have shown promise in ligand discovery by estimating the uncertainty of such local equilibria (10). Naturally, our study was conducted in a model system that intentionally simplifies the problem, eliminating many challenges typically faced in docking (e.g., a usually heterogenous recognition surface, partly exposed to solvent, is radically simplified). The hit rates experienced here, and the sampling challenges, will be increased in more complicated, drug-relevant binding sites. By the same standard, the simplifications afforded by L99A, like all model systems, allowed us to focus on the challenge at hand, sampling and including multiple protein conformations. Finally, we note that though the overall hit rate for the docking was high, at 55%, the hit rate for the more challenging open cavity, though not disreputable at 27%, was substantially lower, reflecting the challenges emerging as one moves from an enclosed cavity to the more typical binding sites. The lower hit rate reflects well-known problems with docking, we believe, not really challenges attending the weighted ensemble approach; all but one of the ligands predicted, after all, bound in the states to which they were docked.

These caveats should not distract from the central observations of this study—MD simulations, including the resource-efficient aMD, can sample relevant states and usefully energy-weight them. The resulting energy penalties, incorporated into multiconformer receptor docking, allow one to access a much broader range of chemotypes without being dominated by high-energy structures. The approach has the promise of generality and potentially may be applied to the vast number of systems in which such states are unavailable from experimental data but are likely to play a key role in the success of large library-docking screens.

Materials and Methods

MD Simulation Setup and Analysis.

Structures, coordinates, and topologies for the MD simulations were prepared using modules implemented in AMBER14 (75). The analysis was performed using in-house python scripts, cpptraj (76), and PyEMMA 2.5.7 (77). Further details are available in SI Appendix.

Flexible Receptor Docking.

All library screens were performed using the flexible, receptor-docking protocol, scripts, and programs implemented in DOCK3.7 (78). A detailed description is included in SI Appendix.

Protein Purification.

L99A was cloned, as previously described (35). Briefly, pET-29 plasmid (EMD Biosciences) containing the gene L99A T4 lysozyme gene was transformed into Escherichia coli BL21(DE3) cells. The C-terminally hexa-histidine–tagged L99A T4 lysozyme was expressed in BL21 cells for 4 h, following induction with 0.5 mM IPTG overnight at 18 °C in presence of kanamycin. Cells were harvested by centrifugation at 4,000 rpm for 20 min followed by resuspension of cells in lysis buffer containing 20 mM Hepes pH 6.8, 10 mM imidazole, and 5 mM β-mercaptoethanol and lysed using a sonicator. Following lysis, the His-tagged protein was bound to Ni-NTA agarose and subjected to wash with buffer containing 20 mM Hepes pH 6.8, 20 mM imidazole, and 5 mM β-mercaptoethanol. Finally, the protein was eluted using elute buffer containing 20 mM Hepes pH 6.8, 250 mM imidazole, and 5 mM β-mercaptoethanol. The eluted protein was dialyzed in 200 mM KCl, 5 mM β-mercaptoethanol, and 50 mM phosphate buffer pH 6.6 and concentrated to 20 mg/mL before flash freezing in liquid nitrogen to store the protein at −80 °C.

Differential Scanning Fluorimetry.

L99A was incubated with SYPRO orange dye (Thermo Fisher Scientific, S6650) in a 384-well PCR microplate (VWR, 10011–194), with a final volume of 15 μL per well, including 2.5 μM T4 Lys and 2.5× SYPRO dye in 50 mM KPi, pH 6.5. The temperature was ramped from 30 to 95 °C at a rate of 1 °C/min and fluorescence of the dye monitored by qPCR machine. Melting temperatures were determined by the Life Cycler Thermal Shift Analysis software. L99A was mixed with a final 100-μM concentration of small molecules prior to differential scanning fluorimetry (DSF). The difference in the melting temperature was calculated for each small molecule–L99A mixture.

Protein Crystallization.

Crystals for L99A were set at a protein concentration of 10 mg/mL using vapor diffusion hanging drop method. Crystals grew overnight at 20 °C in buffer containing 0.1 M Tris pH 8.0, 22% PEG, 4% isopropanol, 50 mM BME, and 50 mM 2-hydroxyethyl disulfide. Ligands were soaked in the crystals, and crystals were left overnight at 20 °C before cryocooling them in 25% ethylene glycol for data collection.

Structure Determination and Refinement.

L99A–ligand datasets were collected at beamline 8.3.1 of the Advanced Light Source (Lawrence Berkeley Laboratory) with wavelength of 0.95386 and a temperature of 100 K. All datasets belonged to P3₂2₂1, with one molecule in the asymmetric unit. The datasets were processed, scaled, and merged using XDS and AIMLESS. MOLREP was used for molecular replacement using the protein model from PDB ID 4W57. The F-helix residues 107 to 115 and ligand were removed from PDB ID 4W57 during molecular replacement, giving unbiased electron density for the ligands and F-helix in the initial electron density maps. Geometry restraints of ligands were created in eLBOW-PHENIX. Initial model fitting and addition of waters was done in COOT (79) followed by refinement in REFMAC (80). Following modeling of the ligand in COOT, several rounds of refinement were carried out using PHENIX. For each structure, geometry was assessed using Molprobity and PHENIX polygon. Structures were not compared until the completion of the refinement for each ligand to prevent the biasing of refinement of different states of lysozyme. Datasets have been deposited to the PDB as 7LOA, 7LOB, 7LOC, 7LOD, 7LOE, 7LOF, 7LOG, 7LOJ, 7LXA, 7LX6. 7LX7, 7LX8, and 7LX9.

Data Availability

All crystallographic structures have been deposited to the PDB as 7LOA, 7LOB, 7LOC, 7LOD, 7LOE, 7LOF, 7LOG, 7LOJ, 7LXA, 7LX6, 7LX7, 7LX8, and 7LX9. All other study data are included in the article and/or SI Appendix.