Abstract
Polymers are often used in medical applications, therefore, some novel polymers and their interactions with photons have been studied. The gamma-ray shielding parameters for Polymethylpentene (PMP), Polybutylene terephthalate (PBT), Polyoxymethylene (POM), Polyvinylidenefluoride (PVDF), and Polychlorotrifluoroethylene (PCTFE) polymers were determined using the Geant4 simulation and discussed in the current work. The mass attenuation coefficients (μ/ρ) were simulated at low and high energies between 0.059 and 1.408 MeV using different radionuclides. The accuracy of the Geant4 simulated results were checked with the XCOM software. The two different methods had good agreement with each other. Exposure buildup factor (EBF) was calculated and discussed in terms of polymers under study and photon energy. Effective atomic number (Zeff) and electron density (Neff) were calculated and analyzed at different energies. Additionally, the half-value layer (HVL) of the polymers was evaluated, and the results of this parameter showed that PCTFE had the highest probability of interaction with gamma photons compared to those of the other tested polymers.
Keywords: Geant4 simulation, radiation shielding, polymers, attenuation coefficients, XCOM software, exposure buildup factor and effective atomic number
1. Introduction
Nuclear technology is widely used in fields such as agriculture, medical applications, nuclear power plants, material identification, science, and space exploration. Researchers have developed and studied several new shielding materials [1,2,3,4] to safe humans from the hazards of ionizing radiation that originates from radioactive sources. Generally, the attenuation coefficients of gamma-rays characterize the interaction of radiation with the materials. It was observed that the absorption materials containing elements with high Z, or atomic numbers (such as Pb, Bi, and Ba) are utilized to attenuate the photons. However, medical applications often use materials containing low Z (such as H, C, N, and O).
Substances containing low Z (such as plastics and polymers) are commonly used as phantom materials and tissue equivalents in medical applications. In this case, linear attenuation coefficient, mass attenuation coefficient, effective atomic number, exposure buildup factor, and half- and tenth-value layers must be studied because they serve as indicators of the interactions of polymers with photons. The literature reports on the interaction between polymers with neutrons and/or gamma rays [5,6,7,8,9].
Polymehtylpentene (PMP) has useful properties, including excellent electrical insulator, extremely low water absorption, and good chemical resistance. In addition, it has high transparency, with a light transmittance of over 90%, which is equivalent to that of acrylic and glass. PMP also has a relatively high melting point of about 230 °C [10]. The second most important commercial polyester is Polybutylene terephthalate (PBT). PBT can easily be thermoformed and molded. Depending on the molding process and the cooling rate, it can be amorphous or semi-crystalline. PBT has some attractive properties, such as high durability and strength, heat resistance, good abrasion, excellent dimensional stability, and good chemical resistance, especially when reinforced with glass fiber [11].
Polyoxymethylene (POM), also called Acetal, is the most important Polyacetal. The crystalline thermoplastic is known for its high tensile and flexural strength, hardness, low creep under stress, and stiffness. It also has a low friction coefficient, excellent fatigue properties, and excellent chemical resistance, but has moderate thermal stability. Polyvinylidene fluoride (PVDF) is a highly inert specialty thermoplastic with a melting point of about 175 °C. It is produced by the radical polymerization of 1,1-difluoroethylene (CH2 = CF2) [10,11]. Polychlorotrifluoroethylene (PCTFE) is a transparent, non-flammable, semi-crystalline high-performance thermoplastic with excellent moisture resistance and high thermal resistance and chemical stability. It provides a balance of chemical, mechanical, and electrical properties, which is not available in any other engineered thermoplastics [10,11].
These characteristics of polymers make them important in the radiation industry. Understanding the interaction of these polymers with radiation will help applications that utilize radiation. The purpose of the current work is to evaluate the gamma-ray attenuation properties of the present polymers. Using a Geant4 simulation and the XCOM program [12,13], the shielding parameters of the polymers were determined to evaluate their attenuation characteristics against gamma-rays.
2. Materials and Methods
2.1. Shielding Parameters
The linear attenuation coefficient (μ) is a key factor for evaluating the effect of gamma radiation of appropriate energy with the studied material and can be deduced from Beer-Lambert Law [14] as follows in Equation (1):
| (1) |
The initial and transmitted intensities are I0 and I respectively, across a target material of thickness x. I0 and I were determined by evaluating the area under the photopeak in without the polymer absorber Areawithout and with the polymer sample Areawith respectively.
The ability of the considered polymers to be checked as radiation protecting materials by calculating the mass attenuation coefficient (μ/ρ) by dividing the calculated linear attenuation coefficient (μ) of a particular polymer by its density (ρ). Theoretically, (μ/ρ) can be evaluated using Equation (2) [15]:
| (2) |
where wi and (μ/ρ)i was the weight fraction and the mass attenuation coefficient of the ith constituent element in the polymer material, respectively.
The half, tenth value layers or HVL and TVL are two important parameters in designing a suitable radiation shielding material. These parameters are defined as the attenuator thicknesses needed to decrease the γ-ray intensity to 50% and 10% of its initial value and estimated using Equations (3) and (4), respectively [16]:
| (3) |
| (4) |
Due to the interaction of gamma rays with the polymer sample, the mean-free path (MFP) is known as the medium distance traveled by a photon between two successive reactions is defined as and described in Equation (5) [17,18]:
| (5) |
The MFP is also, practically, the attenuator distance which decreases the initial photon intensity of 36.8% when passing across the polymer absorber. The (Zeff) is another useful radiation interaction factor used to discuss the attenuating properties of the mixtures or compounds in terms of pure elements and depends on the incoming photon energy. Zeff values for the studied polymers can be obtained using Equation (6) [18]:
| (6) |
where fi, Zi and Ai, refer to the molar fraction, atomic number and atomic weight of the ith constituent element in the selected polymer, respectively.
The effective electron density (Neff), measured in electrons/g, defined as the number of electrons per unit mass of the polymer material and is derived using the calculated Zeff according to Equation (7) [19]:
| (7) |
where represents the mean atomic mass of the polymer, and NA is Avogadro’s number.
When choosing a shielding material, the exposure buildup factor (EBF) must be considered to edit the absorption calculations resulting from buildup of secondary photons resulting from Compton scattering [20]. To determine the EBF for the selected polymers, the Geometric-Progression fitting method (GP) was employed, and the computations were determined according to the three following steps [7]:
The (Zeq), which is an energy-dependent parameter describing the properties of the investigated polymers in terms of their equivalent elements, was first calculated using the next formula [21,22]:
| (8) |
where R1 and R2 are the (μComp/μtotal) ratios corresponding to the elements with atomic numbers Z1 and Z2, respectively, and R is the (μComp/μtotal) ratio for the selected polymer at a specific energy, which lies between the ratios R1 and R2.
The computed Zeq values of the investigated polymers were then used to interpolate the GP fitting EBFs (b, c, a, XK, d) in the range of energy 0.015–15 MeV using the interpolation formula [22] (9):
| (9) |
where C1 and C2 are GP fitting parameters, taken from the ANSI/ANS-6.4.3 standard database [23], corresponding to Z1 and Z2 between which Zeq of the selected polymer lies. As an example, the GP fitting parameters and the Zeq for PMP (C6H12) in the energy range 0.015–15 MeV are listed in Table 1.
Table 1.
The (Zeq) and GP fitting parameters for PMP (C6H12) in the range 0.015–15 MeV.
| Energy (MeV) | Zeq | b | c | a | XK | d |
|---|---|---|---|---|---|---|
| 0.015 | 5.488 | 1.553 | 0.610 | 0.121 | 14.66 | −0.059 |
| 0.02 | 5.494 | 2.240 | 0.842 | 0.051 | 15.20 | −0.029 |
| 0.03 | 5.494 | 4.085 | 1.400 | −0.070 | 13.62 | 0.029 |
| 0.04 | 5.495 | 6.053 | 1.985 | −0.156 | 14.25 | 0.068 |
| 0.05 | 5.499 | 7.443 | 2.371 | −0.195 | 14.40 | 0.085 |
| 0.06 | 5.501 | 7.862 | 2.652 | −0.221 | 14.45 | 0.097 |
| 0.08 | 5.505 | 7.391 | 2.917 | −0.244 | 14.54 | 0.106 |
| 0.1 | 5.506 | 7.007 | 2.884 | −0.239 | 15.18 | 0.100 |
| 0.15 | 5.510 | 5.111 | 2.966 | −0.251 | 14.72 | 0.106 |
| 0.2 | 5.512 | 3.832 | 2.942 | −0.254 | 14.64 | 0.114 |
| 0.3 | 5.514 | 3.151 | 2.652 | −0.236 | 14.21 | 0.110 |
| 0.4 | 5.516 | 2.852 | 2.397 | −0.216 | 13.06 | 0.095 |
| 0.5 | 5.516 | 2.667 | 2.179 | −0.195 | 13.49 | 0.091 |
| 0.6 | 5.516 | 2.545 | 1.994 | −0.173 | 13.64 | 0.080 |
| 0.8 | 5.517 | 2.334 | 1.784 | −0.149 | 13.61 | 0.075 |
| 1 | 5.517 | 2.222 | 1.604 | −0.122 | 13.66 | 0.062 |
| 1.5 | 4.779 | 2.090 | 1.408 | −0.091 | 13.62 | 0.053 |
| 2 | 4.762 | 1.978 | 1.229 | −0.054 | 14.18 | 0.031 |
| 3 | 4.754 | 1.803 | 1.073 | −0.019 | 12.81 | 0.012 |
| 4 | 4.749 | 1.697 | 0.980 | 0.005 | 15.34 | −0.003 |
| 5 | 4.747 | 1.609 | 0.933 | 0.018 | 15.48 | −0.010 |
| 6 | 4.745 | 1.551 | 0.900 | 0.027 | 14.82 | −0.015 |
| 8 | 4.744 | 1.455 | 0.868 | 0.036 | 14.27 | −0.020 |
| 10 | 4.742 | 1.396 | 0.834 | 0.048 | 13.62 | −0.025 |
| 15 | 4.726 | 1.291 | 0.823 | 0.050 | 13.58 | −0.024 |
Finally, the EBF for the selected polymers were then estimated with the help of the obtained GP fitting parameters, using the following relations [24,25]:
| (10) |
and
| (11) |
where
| (12) |
where E is incident γ-ray energy and x is the penetration depth in terms of mfp.
2.2. Geant4 Simulation
Geant4 toolkit is a universal Monte Carlo code that can be used to study the history of the electron, neutron and photon or their coupling within a medium. With its huge cross-section database, Geant4 can simulate the interaction between these particles and energies from 1 keV to 100 MeV [26]. The input of the detector form will be explained as a Monte Carlo symbol and the calculated physical quantity. Geant4 was divided into different sizes, and the largest was called the "universal size". The simulation is set up inside this folder.
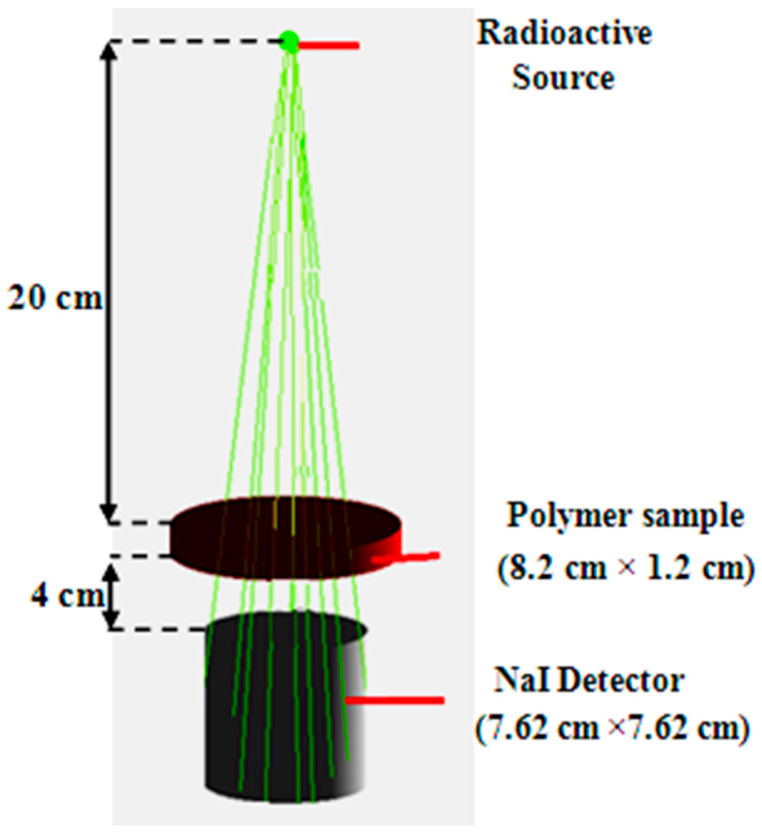
Within the large volume “world”, the design and construction of the detector, attenuating material, and radioactive source are shown in Figure 1. The detector was modeled with a NaI crystal, which was cylindrical and surrounded by aluminum housing (0.5 mm), and the reflective material was modeled with magnesium oxide. For the attenuation material, it was modeled by using different attenuation materials in the simulation process, and different polymer materials with a constant thickness were placed between the source and the detector. There are two methods for modeling radioactive sources: the first method is to use radionuclides, which is necessary to understanding the decay scheme of each radioactive source, and the second method is the method used in a recent article, [27], using monoenergetic gamma-ray photons in each simulation.
Figure 1.
Sketch of the used Geant4 simulation geometry set-up.
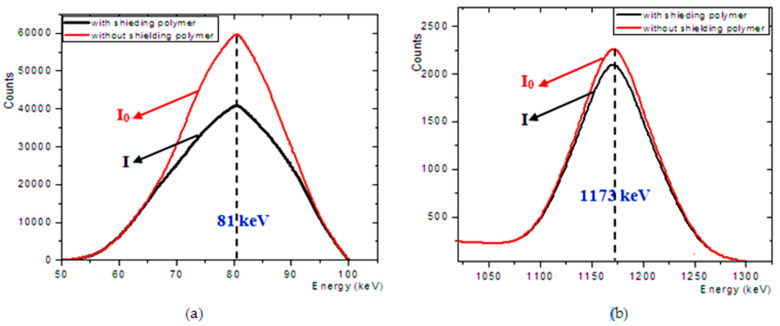
For this purpose, the Gaussian distribution of the parameters (standard deviation σ and mean x) obtained from the analytical data was utilized to the deposition energy E0 [27,28,29]. First, the full width at half maximum (FWHM) on the energy deposited (E0) was evaluated. The second step was to create random energy or (Er) by using a Gaussian distribution with mean <x> = E0 and σ = 2.356 * FWHM (E0)). If it was a random in the interval (E0 ± 2.96 σ), then the peak value was energy E0. In the ROOT analysis framework, an algorithm written in C++ was used to process the Gaussian distribution spectrum [30]. The algorithm performed a peak search process and calculated the area under the peak using the same mathematical algorithm as in Genie2000 [31] (see Figure 2). The weighted peak area with and without attenuating material at different energies was obtained (see Table 2) and used in Equation (1) to calculate the attenuation coefficient of present polymer materials. To reduce the error within 1%, no less than 2 × 107 events were used in each simulation, otherwise, the error would increase as the number decreased.
Figure 2.
The energy spectra from shielded and unshielded simulations at different two energies (a) at 81 and (b) 1173 keV.
Table 2.
Comparison between mass attenuation coefficients for the polymer materials using XCOM software online [32] and Geant4 code at various photon energies.
| Sample | Energy (keV) | Area without | Uncert. | Area with | Uncert. | Linear Attenuation Coefficient Geant4 (cm−1) |
Mass Attenuation Coefficient (cm2 g−1) |
||
|---|---|---|---|---|---|---|---|---|---|
| Geant4 | XCOM | Δ% | |||||||
| PMP | 59.53 | 1.50 × 105 | 6.71 × 102 | 1.09 × 105 | 5.72 × 102 | 0.15866 | 0.19047 | 0.18880 | 0.88% |
| 80.99 | 1.67 × 105 | 7.07 × 102 | 1.24 × 105 | 6.10 × 102 | 0.14755 | 0.17713 | 0.17690 | 0.13% | |
| 121.78 | 1.71 × 105 | 7.17 × 102 | 1.31 × 105 | 6.26 × 102 | 0.13428 | 0.16120 | 0.16070 | 0.31% | |
| 244.69 | 1.52 × 105 | 6.76 × 102 | 1.22 × 105 | 6.05 × 102 | 0.10924 | 0.13114 | 0.13040 | 0.56% | |
| 344.30 | 1.19 × 105 | 5.98 × 102 | 9.80 × 104 | 5.46 × 102 | 0.09583 | 0.11504 | 0.11520 | −0.14% | |
| 661.66 | 5.98 × 104 | 4.24 × 102 | 5.17 × 104 | 4.20 × 102 | 0.07317 | 0.08784 | 0.08802 | −0.21% | |
| 778.90 | 5.08 × 104 | 3.91 × 102 | 4.44 × 104 | 3.65 × 102 | 0.06759 | 0.08114 | 0.08174 | −0.74% | |
| 964.13 | 4.09 × 104 | 3.51 × 102 | 3.62 × 104 | 3.30 × 102 | 0.06185 | 0.07425 | 0.07387 | 0.51% | |
| 1173.23 | 3.33 × 104 | 3.17 × 102 | 2.98 × 104 | 3.23 × 102 | 0.05577 | 0.06695 | 0.06708 | −0.19% | |
| 1332.50 | 3.02 × 104 | 3.01 × 102 | 2.72 × 104 | 2.86 × 102 | 0.05273 | 0.06330 | 0.06283 | 0.75% | |
| 1408.01 | 2.78 × 104 | 2.89 × 102 | 2.51 × 104 | 2.75 × 102 | 0.05101 | 0.06123 | 0.06107 | 0.27% | |
| PBT | 59.53 | 1.50 × 105 | 6.71 × 102 | 9.42 × 104 | 8.20 × 102 | 0.23234 | 0.17873 | 0.17750 | 0.69% |
| 80.99 | 1.67 × 105 | 7.07 × 102 | 1.08 × 105 | 5.77 × 102 | 0.21465 | 0.16512 | 0.16420 | 0.56% | |
| 121.78 | 1.71 × 105 | 7.17 × 102 | 1.16 × 105 | 5.91 × 102 | 0.19281 | 0.14831 | 0.14860 | −0.19% | |
| 244.69 | 1.52 × 105 | 6.76 × 102 | 1.11 × 105 | 6.19 × 102 | 0.15771 | 0.12132 | 0.12040 | 0.75% | |
| 344.30 | 1.19 × 105 | 5.98 × 102 | 9.01 × 104 | 5.67 × 102 | 0.13814 | 0.10626 | 0.10640 | −0.13% | |
| 661.66 | 5.98 × 104 | 4.24 × 102 | 4.83 × 104 | 4.31 × 102 | 0.10656 | 0.08197 | 0.08128 | 0.84% | |
| 778.90 | 5.08 × 104 | 3.91 × 102 | 4.17 × 104 | 3.54 × 102 | 0.09886 | 0.07604 | 0.07548 | 0.74% | |
| 964.13 | 4.09 × 104 | 3.51 × 102 | 3.42 × 104 | 3.21 × 102 | 0.08948 | 0.06883 | 0.06823 | 0.88% | |
| 1173.23 | 3.33 × 104 | 3.17 × 102 | 2.83 × 104 | 3.38 × 102 | 0.08114 | 0.06242 | 0.06195 | 0.75% | |
| 1332.50 | 3.02 × 104 | 3.01 × 102 | 2.60 × 104 | 3.29 × 102 | 0.07504 | 0.05772 | 0.05803 | −0.54% | |
| 1408.01 | 2.78 × 104 | 2.89 × 102 | 2.40 × 104 | 2.86 × 102 | 0.07338 | 0.05644 | 0.05641 | 0.06% | |
| POM | 59.53 | 1.50 × 105 | 6.71 × 102 | 8.95 × 104 | 5.42 × 102 | 0.25771 | 0.18277 | 0.18180 | 0.53% |
| 80.99 | 1.67 × 105 | 7.07 × 102 | 1.04 × 105 | 6.54 × 102 | 0.23569 | 0.16716 | 0.16690 | 0.15% | |
| 121.78 | 1.71 × 105 | 7.17 × 102 | 1.12 × 105 | 5.79 × 102 | 0.21264 | 0.15081 | 0.15040 | 0.27% | |
| 244.69 | 1.52 × 105 | 6.76 × 102 | 1.07 × 105 | 5.68 × 102 | 0.17199 | 0.12198 | 0.12180 | 0.14% | |
| 344.30 | 1.19 × 105 | 5.98 × 102 | 8.75 × 104 | 5.70 × 102 | 0.15292 | 0.10845 | 0.10760 | 0.78% | |
| 661.66 | 5.98 × 104 | 4.24 × 102 | 4.74 × 104 | 4.12 × 102 | 0.11603 | 0.08229 | 0.08222 | 0.08% | |
| 778.90 | 5.08 × 104 | 3.91 × 102 | 4.09 × 104 | 3.67 × 102 | 0.10849 | 0.07694 | 0.07636 | 0.76% | |
| 964.13 | 4.09 × 104 | 3.51 × 102 | 3.37 × 104 | 3.18 × 102 | 0.09693 | 0.06875 | 0.06903 | −0.41% | |
| 1173.23 | 3.33 × 104 | 3.17 × 102 | 2.80 × 104 | 2.90 × 102 | 0.08779 | 0.06226 | 0.06266 | −0.64% | |
| 1332.50 | 3.02 × 104 | 3.01 × 102 | 2.56 × 104 | 2.97 × 102 | 0.08290 | 0.05879 | 0.05871 | 0.14% | |
| 1408.01 | 2.78 × 104 | 2.89 × 102 | 2.37 × 104 | 2.67 × 102 | 0.08084 | 0.05733 | 0.05706 | 0.47% | |
| PVDF | 59.53 | 1.50 × 105 | 6.71 × 102 | 8.01 × 104 | 5.55 × 102 | 0.31363 | 0.17620 | 0.17600 | 0.11% |
| 80.99 | 1.67 × 105 | 7.07 × 102 | 9.44 × 104 | 5.33 × 102 | 0.28375 | 0.15941 | 0.15830 | 0.70% | |
| 121.78 | 1.71 × 105 | 7.17 × 102 | 1.03 × 105 | 5.57 × 102 | 0.25233 | 0.14176 | 0.14150 | 0.18% | |
| 244.69 | 1.52 × 105 | 6.76 × 102 | 1.01 × 105 | 5.81 × 102 | 0.20345 | 0.11430 | 0.11420 | 0.09% | |
| 344.30 | 1.19 × 105 | 5.98 × 102 | 8.27 × 104 | 5.80 × 102 | 0.18075 | 0.10155 | 0.10090 | 0.64% | |
| 661.66 | 5.98 × 104 | 4.24 × 102 | 4.55 × 104 | 4.21 × 102 | 0.13717 | 0.07706 | 0.07710 | −0.05% | |
| 778.90 | 5.08 × 104 | 3.91 × 102 | 3.93 × 104 | 3.43 × 102 | 0.12829 | 0.07207 | 0.07161 | 0.64% | |
| 964.13 | 4.09 × 104 | 3.51 × 102 | 3.24 × 104 | 3.36 × 102 | 0.11622 | 0.06529 | 0.06473 | 0.86% | |
| 1173.23 | 3.33 × 104 | 3.17 × 102 | 2.71 × 104 | 2.85 × 102 | 0.10403 | 0.05844 | 0.05877 | −0.56% | |
| 1332.50 | 3.02 × 104 | 3.01 × 102 | 2.48 × 104 | 2.73 × 102 | 0.09828 | 0.05522 | 0.05507 | 0.26% | |
| 1408.01 | 2.78 × 104 | 2.89 × 102 | 2.30 × 104 | 2.96 × 102 | 0.09495 | 0.05334 | 0.05353 | −0.35% | |
| PCTFE | 59.53 | 1.50 × 105 | 6.71 × 102 | 5.46 × 104 | 4.44 × 102 | 0.50455 | 0.24026 | 0.23990 | 0.15% |
| 80.99 | 1.67 × 105 | 7.07 × 102 | 7.85 × 104 | 5.47 × 102 | 0.37610 | 0.17910 | 0.17830 | 0.44% | |
| 121.78 | 1.71 × 105 | 7.17 × 102 | 9.40 × 104 | 5.31 × 102 | 0.29980 | 0.14276 | 0.14280 | −0.03% | |
| 244.69 | 1.52 × 105 | 6.76 × 102 | 9.51 × 104 | 5.34 × 102 | 0.23285 | 0.11088 | 0.11050 | 0.34% | |
| 344.30 | 1.19 × 105 | 5.98 × 102 | 7.89 × 104 | 5.16 × 102 | 0.20456 | 0.09741 | 0.09729 | 0.12% | |
| 661.66 | 5.98 × 104 | 4.24 × 102 | 4.38 × 104 | 3.88 × 102 | 0.15624 | 0.07440 | 0.07420 | 0.27% | |
| 778.90 | 5.08 × 104 | 3.91 × 102 | 3.80 × 104 | 3.38 × 102 | 0.14501 | 0.06905 | 0.06891 | 0.21% | |
| 964.13 | 4.09 × 104 | 3.51 × 102 | 3.15 × 104 | 3.23 × 102 | 0.13135 | 0.06255 | 0.06229 | 0.41% | |
| 1173.23 | 3.33 × 104 | 3.17 × 102 | 2.63 × 104 | 3.04 × 102 | 0.11807 | 0.05622 | 0.05655 | −0.58% | |
| 1332.50 | 3.02 × 104 | 3.01 × 102 | 2.42 × 104 | 2.90 × 102 | 0.11104 | 0.05288 | 0.05301 | −0.25% | |
| 1408.01 | 2.78 × 104 | 2.89 × 102 | 2.24 × 104 | 2.99 × 102 | 0.10836 | 0.05160 | 0.05154 | 0.12% | |
3. Results and Discussion
The Geant4 MC code was utilized to estimate the mass attenuation coefficients (μ/ρ) of the five polymer samples at energies between 0.05 and 1.4 MeV. Table 2 lists the results from Geant4 and the XCOM program and the corresponding relative differences. It is evident from Table 2 that under the selected γ-ray energy, the simulated μ/ρ results of the polymer samples were quite close to the theoretical results of the XCOM code at all energy regions. Therefore, the estimated μ/ρ value of the polymer showed the same dependence on γ-ray energy. The relative deviation RD (%) between XCOM and Geant4 values was computed using Equation (13):
| (13) |
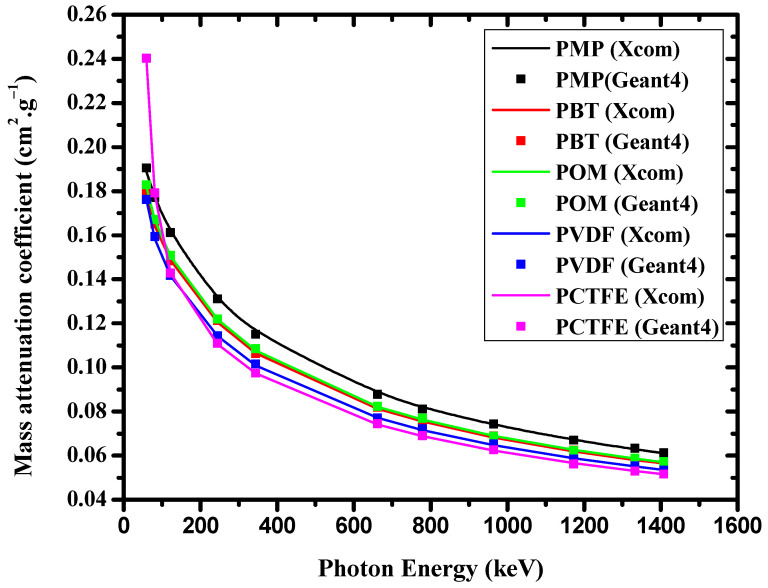
The μ/ρ values obtained using the XCOM online database of photon interaction cross-sections are plotted in Figure 3 relative to the Geant4 data with γ-ray energy in the range of 0.059–1.408 MeV. This figure clarifies that PCTFE’s value of μ/ρ was the highest at low energies and the lowest at high energies. In addition, it can be seen that among all the polymer types, the maximum μ/ρ value occurred at low energies, while the lowest μ/ρ occurred at high energies.
Figure 3.
Mass attenuation coefficients of PMP, PBT, POM, PVDF, and PCTFE polymers as a function of photon energy from XCOM and Geant4.
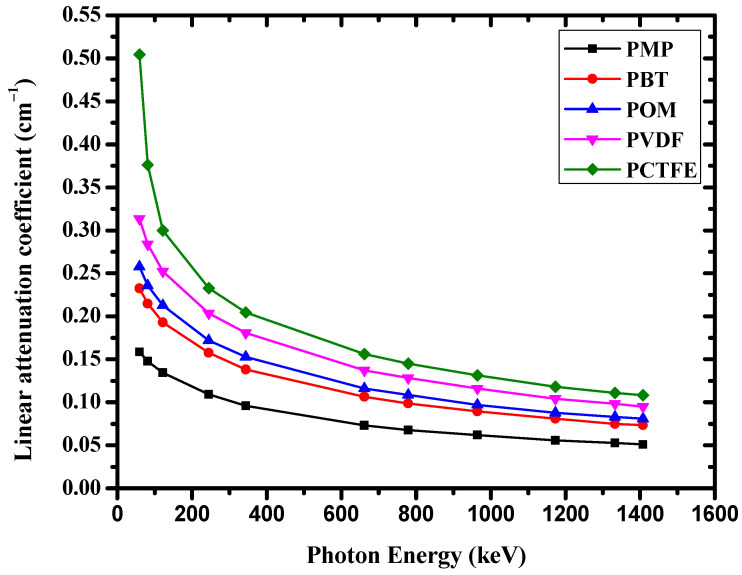
It is obvious from Figure 4 that as the photon energy increased, the μ value dropped sharply. This behavior can be attributed to the probability of interaction at low energy, where the predominant interaction is the photoelectric effect and its cross-section approximately increasing with E−3.5. The dominant phenomenon at the medium γ-ray energy region is known Compton scattering and its cross-section changes with E−1 and Z. While, in the high-energy, Compton scattering and the pair production process have a mixed effect.
Figure 4.
Geant4 linear attenuation coefficients of the present polymers as a function of photon energy.
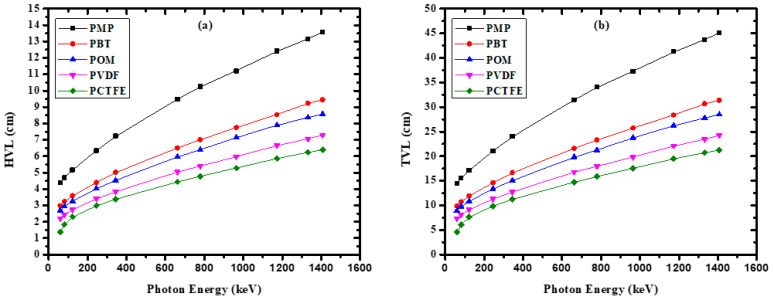
The variation of HVL and TVL values of the present polymers as a function of photon energies is depicted in Figure 5. According to Figure 5, PCTFE had the lowest HVL value, ranging from 2 to 6 cm, while PMP had the highest HVL value, ranging from 4.5 to 13.55 cm. These results imply that the higher the polymer density, the lower the HVL value, which enhances the shielding ability of the chosen polymer. Figure 5 also demonstrates that all the polymer samples had the lowest HVL results at low γ-ray energies. This trend may be due to the advantage of the photoelectric effect in this energy region. As the photon energy increased to the medium-energy region, the HVL value could be observed to gradually increase. This increase occurred because of the dominance of Compton scattering in this region. The little increase in HVL results at higher energy could be attributed to the dominance of the pair production process at these energies.
Figure 5.
The variation of (a) half-value layer and (b) tenth-value layer with photon energy for the investigated polymers.
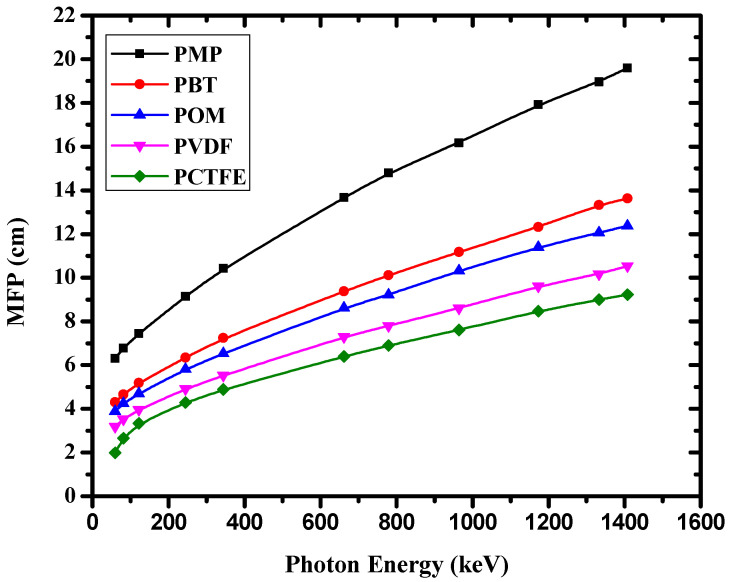
Figure 6 shows that the MFP values of the investigated polymer varied with γ-ray energy in the range of 0.059–1.408 MeV. From Figure 6, the γ-ray energy dependence of the MFP value was similar to the HVL trend, so the same discussion about photon interactions applies. The MFP values decreased from POM to PCTFE, which indicates that compared to other polymers, photons in this energy range could penetrate POM to the greatest extent.
Figure 6.
The variation of mean-free path with increasing photon energy for the investigated polymers.
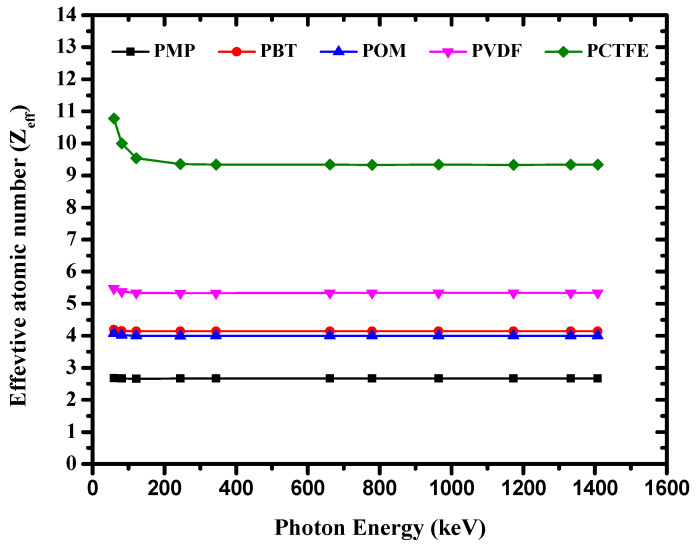
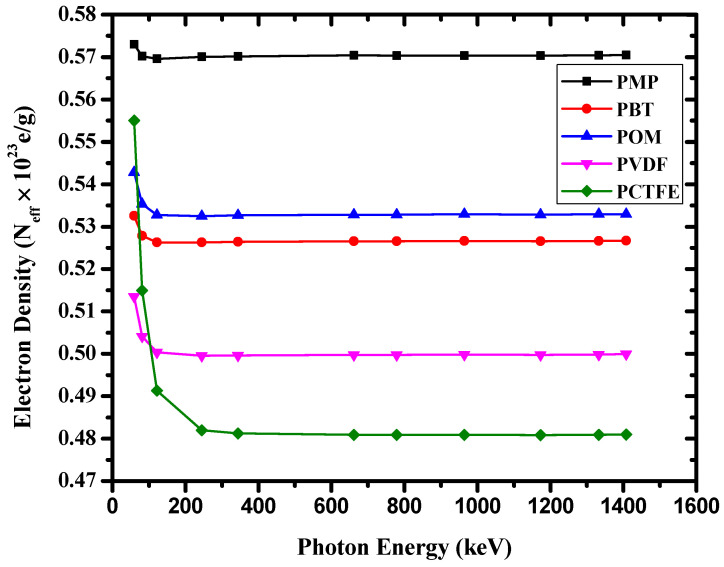
The Zeff of the studied materials was evaluated from the calculated (μ/ρ). The results were obtained and are shown in Figure 7. Figure 7 shows that the Zeff of PCTFE was greater than that of other discussed polymers. This high value was mainly due to the contents of fluorine (F) and chlorine (Cl) in PCTFE, besides the hydrogen content, which was negligible. Similarly, Figure 7 shows that Zeff of PBT and POM were nearly the same, but relatively lower than that of PVDF. Among the studied polymers, POM had the lowest Zeff value because of the high hydrogen content in this polymer. It is obvious from Figure 7 that Zeff values for all polymers remained almost constant. The Zeff trend of these five polymers was occurring because the present polymers were composed of elements very close in atomic numbers (such as H, C, O, and N). The changes of Zeff and Neff with photon energy are shown in Figure 7 and Figure 8, respectively.
Figure 7.
The variation of Zeff with photon energy for the investigated polymers.
Figure 8.
The variation of Neff with γ-ray energy for the investigated polymers.
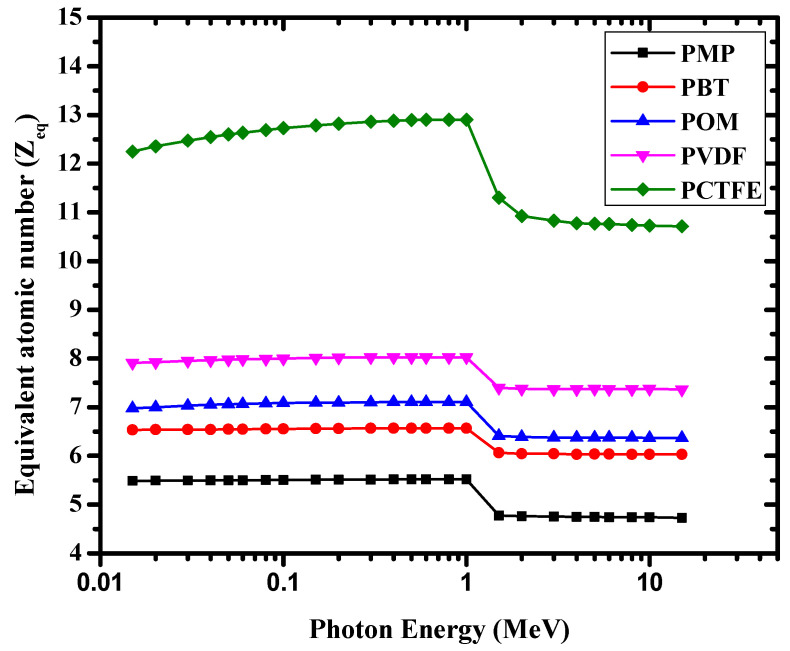
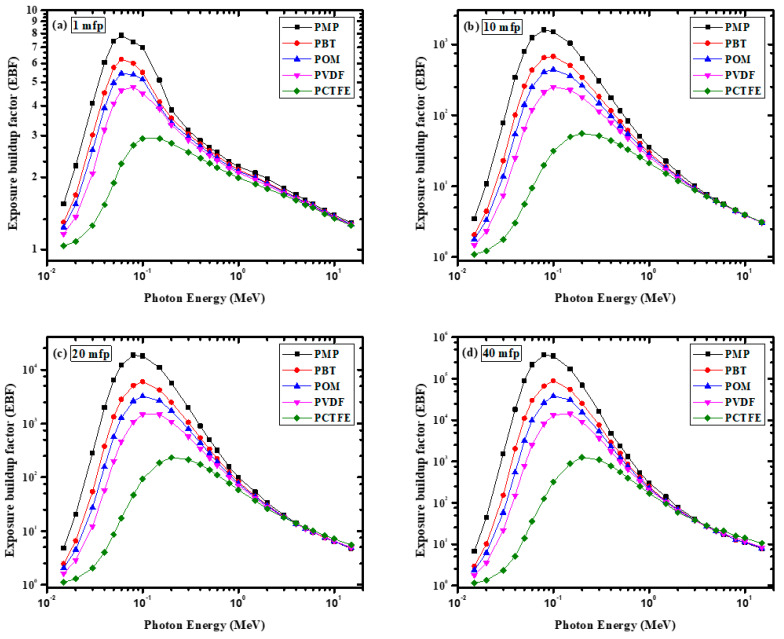
Figure 9 shows the calculated Zeq values for these polymers. The GP fitting parameters of PCTFE are tabulated in Table 1. The EBF of a given polymer varied between 0.015 and 15 MeV with photon energy. Additionally, Figure 10 illustrates the EBF of the samples at a fixed penetration depth. A similar trend has been studied for different samples reported in the reference [33]. The EBF values in the form demonstrate that as the energy increased, the values increased up to the medium-energy area. In addition, in the medium-energy region, at 10 and 40 mfp, the EBF value appeared to be very large. This result was due to the Compton scattering process at this energy. In this region, the γ-ray photons are not completely extracted, but their energies are reduced. These photons existed in the sample for a long time, causing multiple Compton scattering interactions, which raised the EBF to a higher value between 0.08 and 0.2 MeV.
Figure 9.
Zeq variation with different energy of photons for the investigated polymers.
Figure 10.
The variation of EBF with γ-ray energy for the investigated polymers at (a) 1 mfp, (b) 10 mfp, (c) 20 mfp, and (d) 40 mfp.
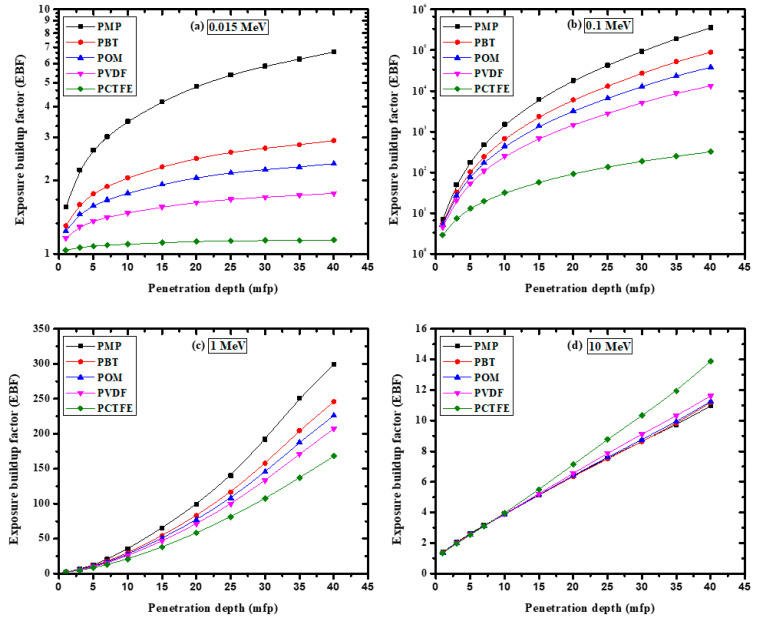
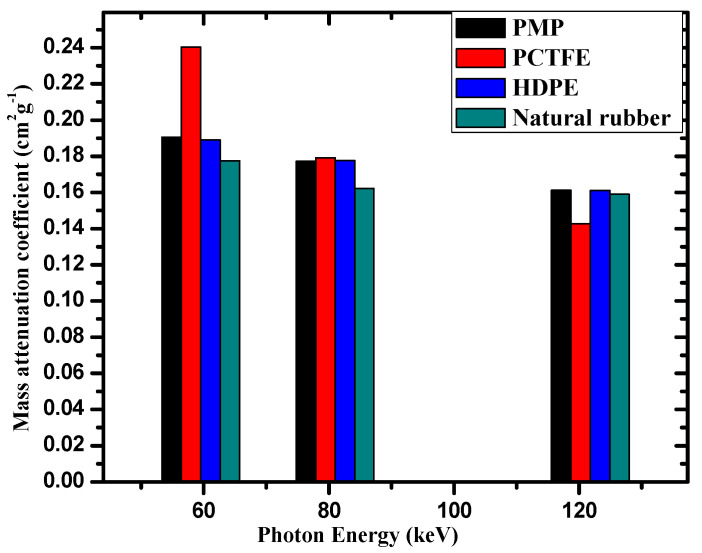
The EBF results for all the studied polymer samples had approximately the same value between 4 and 15 MeV, indicating that EBF had no relationship with the composition of the discussed samples in this region. The EBF trend between 4 and 15 MeV was due to the pair production process, a very important photon interaction phenomenon at these high energies. Additionally, among the selected polymers, POM had the highest EBF value. Likewise, PCTFE had the lowest EBF value. The lower EBF values for PCTFE could be attributed to the higher Zeq of this polymer. Moreover, it was found from Figure 10 that the EBF value of the polymer increased with increasing penetration depth. The lowest EBF value for all the samples was found at 1 mfp (Figure 10a), while the highest EBF value at 40 mfp (Figure 10d). This result can be attributed to multiple dispersions at a large penetration depth. In other words, an increase in the depth of penetration led to an increase in the photon interaction with the sample (see Figure 11), which led to the generation of low-energy photons. Finally, the mass attenuation coefficients of the present polymers were compared to those from some recent reports on HDPE [3] and natural rubber [34]. The comparison is shown in Figure 12 and shows a difference between them in the low energies, while the results are similar in the high energies.
Figure 11.
The variation of the exposure buildup factor with penetration depth for the tested polymers at (a) 0.015 MeV, (b) 0.1 MeV, (c) 1 MeV, and (d) 10 MeV.
Figure 12.
Mass attenuation coefficients of PMP and PCTFE polymers compared to other discussed experimental values of HDPE and natural rubbers.
4. Conclusions
The photon attenuation characteristics of various studied polymers (such as PMP, PBT, POM, PVDF, and PCTFE) were studied using factors such as HVL, MFP, Zeff, and EBF. A Geant4 simulation was used to determine these parameters at energies between 59 and 1408 keV. The maximum linear attenuation coefficient was determined for the PCTFE polymer. PCTFE’s Zeff was found to be relatively higher than that of other polymers. The HVL and MFP value of PCTFE were also lower than the value for other polymers, which indicates that this polymer attenuated gamma-rays more effectively. The results demonstrated that out of the present polymers, PMP’s EBF values tended to be high while PCTFE’s EBF tended to be low. The EBF values of the present polymers increased with penetration depth, being highest for 40 mfp and lowest for 1 mfp. This paper concludes that the current polymers can be used alone in low-energy or in combination with other high-Z materials for high-energy gamma-ray shielding.
Author Contributions
Conceptualization, M.E. and M.T.A.; methodology, M.E.; software, J.S.A.; validation, M.T.A., M.I.A., and D.I.T.; formal analysis, M.E.; investigation, M.I.A.; resources, M.I.S.; data curation, J.S.A.; writing original draft preparation, M.E.; writing—review and editing, M.E. and M.T.A.; visualization, M.I.A.; supervision, A.M.E.-K.; project administration, M.E.; funding acquisition, J.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
Not applicable.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are available in the manuscript.
Conflicts of Interest
The authors declare no conflict of interests.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Dong M., Zhou S., Xue X., Feng X., Sayyed M.I., Khandaker M.U., Bradley D.A. The potential use of boron containing resources for protection against nuclear radiation. Radiat. Phys. Chem. 2021;188:109601. doi: 10.1016/j.radphyschem.2021.109601. [DOI] [Google Scholar]
- 2.Dong M., Xue X., Yang H., Li Z. Highly cost-effective shielding composite made from vanadium slag and boron-rich slag and its properties. Radiat. Phys. Chem. 2017;141:239–244. doi: 10.1016/j.radphyschem.2017.07.023. [DOI] [Google Scholar]
- 3.El-Khatib A.M., Abbas M.I., Elzaher M.A., Badawi M.S., Alabsy M.T., Alharshan G.A., Aloraini D.A. Gamma Attenuation Coefficients of Nano Cadmium Oxide/High density Polyethylene Composites. Sci. Rep. 2019;9:16012. doi: 10.1038/s41598-019-52220-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Elbashir B.O., Dong M.G., Sayyed M.I., Issa S.A.M., Matori K.A., Zaid M.H.M. Comparison of Monte Carlo simulation of gamma ray attenuation coefficients of amino acids with XCOM program and experimental data. Results Phys. 2018;9:6–11. doi: 10.1016/j.rinp.2018.01.075. [DOI] [Google Scholar]
- 5.Sayyed M.I. Investigation of shielding parameters for smart polymers. Chin. J. Phys. 2016;54:408–415. doi: 10.1016/j.cjph.2016.05.002. [DOI] [Google Scholar]
- 6.Gurler O., Tarim U.A. Determination of radiation shielding properties of some polymer and plastic materials against gamma-rays. Acta Phys. Pol. A. 2016;130:236–238. doi: 10.12693/APhysPolA.130.236. [DOI] [Google Scholar]
- 7.Manjunatha H.C. A study of gamma attenuation parameters in poly methyl methacrylate and Kapton. Radiat. Phys. Chem. 2017;137:254–259. doi: 10.1016/j.radphyschem.2016.01.024. [DOI] [Google Scholar]
- 8.Mirji R., Lobo B. Computation of the mass attenuation coefficient of polymeric materials at specific gamma photon energies. Radiat. Phys. Chem. 2017;135:32–44. doi: 10.1016/j.radphyschem.2017.03.001. [DOI] [Google Scholar]
- 9.Mann K.S., Rani A., Heer M.S. Shielding behaviors of some polymer and plastic materials for gamma-rays. Radiat. Phys. Chem. 2015;106:247–254. doi: 10.1016/j.radphyschem.2014.08.005. [DOI] [Google Scholar]
- 10.Polymer Property Predictor and Database. [(accessed on 12 June 2021)]; Available online: https://www.nist.gov/programs-projects/polymer-property-predictor-and-database.
- 11.Polymer Properties Database. [(accessed on 30 May 2021)]; Available online: https://polymerdatabase.com/home.html.
- 12.Agostinelli S., Allison J., Amako K.A., Apostolakis J., Araujo H., Arce P., Asai M., Axen D., Banerjee S., Barrand G.J., et al. GEANT4: A simulation toolkit. Nucl. Instrum. Meth. A. 2003;506:250. doi: 10.1016/S0168-9002(03)01368-8. [DOI] [Google Scholar]
- 13.Berger M.J., Hubbell J.H. XCOM: Photon cross Sections on a Personal Computer. National Bureau of Standards; Washington, DC, USA: 1987. pp. 87–3597. [Google Scholar]
- 14.Nafee S.S., Abbas M.I. A theoretical approach to calibrate radiation portal monitor (RPM) systems. Appl. Radiat. Isot. 2008;66:1474–1477. doi: 10.1016/j.apradiso.2008.03.013. [DOI] [PubMed] [Google Scholar]
- 15.Abbas M.I. A new analytical method to calibrate cylindrical phoswich and LaBr 3(Ce) scintillation detectors. Nucl. Instrum. Methods Phys. Res. Sect. A. 2010;621:413–418. doi: 10.1016/j.nima.2010.05.025. [DOI] [Google Scholar]
- 16.Abbas M.I. Validation of analytical formulae for the efficiency calibration of gamma detectors used in laboratory and in-situ measurements. Appl. Radiat. Isot. 2006;64:1661–1664. doi: 10.1016/j.apradiso.2006.05.017. [DOI] [PubMed] [Google Scholar]
- 17.Rammah Y.S., Ali A.A., El-Mallawany R., El-Agawany F.I. Fabrication, physical, optical characteristics and gamma-ray competence of novel bismo-borate glasses doped with Yb2O3 rare earth. Phys. B Condens. Matter. 2020;583:412055. doi: 10.1016/j.physb.2020.412055. [DOI] [Google Scholar]
- 18.Mariyappan M., Marimuthu K., Sayyed M.I., Dong M.G., Kara U. Effect Bi2O3 on the physical, structural and radiation shielding properties of Er3+ ions doped bismuth sodiumfluoroborate glasses. J. Non-Cryst. Solids. 2018;499:75–85. doi: 10.1016/j.jnoncrysol.2018.07.025. [DOI] [Google Scholar]
- 19.Manohara S.R., Hanagodimath S.M., Thind K.S., Gerward L. On the effective atomic number and electron density: A comprehensive set of formulas for all types of materials and energies above 1 keV, Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms. 2008;266:3906–3912. [Google Scholar]
- 20.Kurudirek M. Photon buildup factors in some dosimetric materials for heterogeneous radiation sources. Radiat. Environ. Biophys. 2014;53:175–185. doi: 10.1007/s00411-013-0502-9. [DOI] [PubMed] [Google Scholar]
- 21.Harima Y. An approximation of gamma-ray buildup factors by modified geometrical progression. Nucl. Sci. Eng. 1983;83:299–309. doi: 10.13182/NSE83-A18222. [DOI] [Google Scholar]
- 22.Elsafi M., Alrashedi M.F., Sayyed M.I., Al-Hamarneh I.F., El-Nahal M.A., El-Khatib M., Khandaker M.U., Osman H., Askary A.E. The Potentials of Egyptian and Indian Granites for Protection of Ionizing Radiation. Materials. 2021;14:3928. doi: 10.3390/ma14143928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Elsafi M., El-Nahal M.A., Alrashedi M.F., Olarinoye O.I., Sayyed M.I., Khandaker M.U., Osman H., Alamri S., Abbas M.I. Shielding Properties of Some Marble Types: A Comprehensive Study of Experimental and XCOM Results. Materials. 2021;14:4194. doi: 10.3390/ma14154194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sayyed M.I., Albarzan B., Almuqrin A.H., El-Khatib A.M., Kumar A., Tishkevich D.I., Trukhanov A.V., Elsafi M. Experimental and Theoretical Study of Radiation Shielding Features of CaO-K2O-Na2O-P2O5 Glass Systems. Materials. 2021;14:3772. doi: 10.3390/ma14143772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kurudirek M., Özdemir Y. Energy absorption and exposure buildup factors for some polymers and tissue substitute materials: Photon energy, penetration depth and chemical composition dependence. J. Radiol. Prot. 2011;31:117. doi: 10.1088/0952-4746/31/1/008. [DOI] [PubMed] [Google Scholar]
- 26.Briesmeister J.F. MCNPTM—A General Monte Carlo N-Particle Transport Code. Los Alamos National Laboratory (LANL); Los Alamos, NM, USA: 2000. Version 4C, LA-13709-M. [Google Scholar]
- 27.Badawi M.S., Noureddine S., Kopatch Y.N., Abbas M.I., Ruskov I.N., Grozdanov D.N., Thabet A.A., Fedorov N.A., Gouda M.M., Hramco C., et al. Characterization of the efficiency of a cubic NaI detector with rectangular cavity for axially positioned sources. J. Instrum. 2020;15:P02013. doi: 10.1088/1748-0221/15/02/P02013. [DOI] [PubMed] [Google Scholar]
- 28.Abbas M.I., Badawi M.S., Thabet A.A., Kopatch Y.N., Ruskov I.N., Grozdanov D.N., Noureddine S., Fedorov N.A., Gouda M.M., Hramco C., et al. Efficiency of a cubic NaI (Tl) detector with rectangular cavity using standard radioactive point sources placed at non-axial position. Appl. Radiat. Isot. 2020;163:109139. doi: 10.1016/j.apradiso.2020.109139. [DOI] [PubMed] [Google Scholar]
- 29.Hurtado S., Garcia-León M., Garcia-Tenorio R. GEANT4 code for simulation of a germanium gamma-ray detector and its application to efficiency calibration. Nucl. Instrum. Methods Phys. Res. Sect. A. 2004;518:764–774. doi: 10.1016/j.nima.2003.09.057. [DOI] [Google Scholar]
- 30.Brun R., Rademakers F. ROOT—An object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res. Sect. A. 1997;389:81–86. doi: 10.1016/S0168-9002(97)00048-X. [DOI] [Google Scholar]
- 31.Genie™ 2000 Spectroscopy Software. Canberra Industries; Zellik, Belgium: 2006. [Google Scholar]
- 32.XCOM: Element/Compound/Mixture Selection. [(accessed on 11 July 2021)]; Available online: https://physics.nist.gov/PhysRefData/Xcom/html/xcom1.html.
- 33.Singh T., Kumar N., Singh P.S. Chemical composition dependence of exposure buildup factors for some polymers. Ann. Nucl. Energy. 2009;36:114–120. doi: 10.1016/j.anucene.2008.09.013. [DOI] [Google Scholar]
- 34.El-Khatib A.M., Doma A.S., Badawi M.S., Abu-Rayan A.E., Aly N.S., Alzahrani J.S., Abbas M.I. Conductive natural and waste rubbers composites-loaded with lead powder as environmental flexible gamma radiation shielding material. Mater. Res. Express. 2020;7:105309. doi: 10.1088/2053-1591/abbf9f. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data are available in the manuscript.