Quantitative analysis of mitochondrial ATP synthesis

Abstract

We present a computational framework for analyzing and simulating mitochondrial ATP synthesis using basic thermodynamic and kinetic principles. The framework invokes detailed descriptions of the thermodynamic driving forces associated with the processes of the electron transport chain, mitochondrial ATP synthetase, and phosphate and adenine nucleotide transporters. Assembling models of these discrete processes into an integrated model of mitochondrial ATP synthesis, we illustrate how to analyze and simulate in vitro respirometry experiments and how models identified from in vitro experimental data effectively explain cardiac respiratory control in vivo. Computer codes for these analyses are embedded as Python scripts in a Jupyter Book to facilitate easy adoption and modification of the concepts developed here. This accessible framework may also prove useful in supporting educational applications. All source codes are available on at https://beards-lab.github.io/QAMAS_book/.

1. Introduction

Acquired in the initiating event in the origin of eukaryotes, mitochondria are a defining feature of eukaryotic organisms [6]. They serve as a central hub for eukaryotic energy metabolism, oxidizing carbohydrates, fats, and ketones, producing the reducing equivalents to drive the proton pumps of the respiratory complexes, and synthesizing the majority of adenosine triphosphate (ATP) needed to drive essential cell functions in high metabolic demand tissues (e.g., heart, brain, kidney). Since oxygen (O₂) is the final electron acceptor of the respiratory chain, mitochondrial respiration is the primary reason why vertebrate animals need a heart and vascular system to deliver oxygen to within diffusional distances of nearly every cell in the body. In other words, mitochondria are, in large part, the reason why the mammalian heart must beat continuously throughout the life of the organism. Mitochondria are also the source of the ATP hydrolysis potential that drives the mechanical pumping of the heart. Thus, at a basic level, mitochondria are both the ends and the means of cardiovascular physiology.

In oxidizing primary substrates and synthesizing ATP, mitochondria transduce free energy through a multi-step process: (i) reduced cofactors nicotinamide adenine dinucleotide (NADH) and flavin adenine dinucleotide (FADH₂) are synthesized via the oxidation of fuels such as pyruvate and fatty acids; (ii) oxidation of NADH and FADH₂ drives the proton pumps of the respiratory chain, generating an electrostatic potential across the inner mitochondrial membrane (IMM); and (iii) that electrostatic potential, in turn, drives the phosphorylation of adenosine diphosphate (ADP) to ATP and the electrogenic exchange of a mitochondrial matrix ATP⁴⁻ for a cytosolic ADP³⁻. Thus, substrate oxidation drives the transduction of free energy of chemical reactions to free energy in an electrochemical transport gradient, and the electrochemical gradient is transduced back to chemical reaction free energy in the form of the ATP hydrolysis potential. The idea that chemical synthesis of ATP is thermodynamically coupled to the movement of ions across the electrochemical gradient of the mitochondrial membrane was introduced by Peter Mitchell, for which he was awarded the Nobel Prize in 1978 [13].

We aim to develop a computational framework to help understand how these electrochemical processes operate. Kinetic models of mitochondrial ATP synthesis date back to Chance and Williams [5], who observed a Michaelis-Menten type dependence of ATP synthesis on ADP concentration, yielding a phenomenological approach that is able to effectively describe mitochondrial ATP synthesis in human skeletal muscle in vivo [4]. While our approach is to analyze the component processes of oxidative phosphorylation with more mechanistic and thermodynamic fidelity, ultimately our models are in agreement with the overall dependence of ATP synthesis on the concentration of the products of ATP hydrolysis, namely ADP and inorganic phosphate (Pi). Ultimately, we follow the approach of Chance et al. [4] of first using in vitro data to identify a mitochondrial model, and then using the identified model to predict and analyze in vivo energetics.

2. Basic chemical, electrical, and thermodynamic principles

To develop a quantitative understanding of how these processes work, we start with a set of definitions of the some quantities and concepts with which we are concerned. Specifically, this section reviews basic biochemical, thermodynamic, and related concepts that are particularly relevant to the quantitative analysis of mitochondrial ATP synthesis.

2.1. Mitochondrial anatomy

The mitochondrion is a membrane-bound, rod-shaped organelle that is responsible for generating most of the chemical energy needed to power the cell’s biochemical reactions by respiration [14]. Mitochondria are comprised of an outer and inner membrane that are separated by the intermembrane space (IMS) (1). The outer mitochondrial membrane is freely permeable to small molecules and ions. The IMM folds inward to make cristae that extend into the matrix. Transmembrane channels called porins and the respiratory complexes involved in oxidative phosphorylation and ATP synthesis allow for more selective IMM permeability. The IMM encloses the mitochondrial matrix, which contains mitochondrial deoxyribonucleic acid (DNA), the majority of mitochondrial proteins, soluble metabolic inter-mediates including ATP, ADP, and Pi, and the enzymes catalyzing the tricarboxylic acid (TCA) cycle and β-oxidation.

2.2. IMM capacitance

The IMM acts as an electrical capacitor to store energy in an electrostatic potential difference between the milieu on each side. Electrical capacitance of a membrane (C_m) is the proportionality between the rate of charge transport across the membrane, i.e. current (I), to the rate of membrane potential (ΔΨ) change, that is,

$$C_m\frac{\text{d}\Delta \mathrm{\Psi }}{\text{d}t}=I.$$

In the model and associated calculations presented below, we express fluxes in units of moles per unit time per unit volume of mitochondria. Thus, it is convenient to obtain an estimate of Cm in units of mole per volt per volume of mitochondria. Mitochondria take on a roughly ellipsoid shape in vivo, and a more spherical morphometry in suspension of purified mitochondria [16]. To estimate the mitochondrial surface area-to-volume ratio, we take a representative mitochondrion as a sphere with radius r = 1 μm and obtain a surface area-to-volume ratio of 3 μm⁻¹. Furthermore, we estimate that the IMM has ten-fold greater surface area than the outer membrane, yielding a surface area to volume ratio of 30 μm⁻¹ for the IMM. Since the capacitance density of biological membranes ranges from 0.5–1.0μF cm⁻², or 0.5–1.0 × 10⁻⁸ μF μm⁻² [14], C_m is approximately 30 × 10⁻⁸ μF μm⁻³ = 300 F (L mito)⁻¹. To convert to the units used in the calculations below, we have

$$C_m=300\frac{\text{F}}{\text{L}\text{mito}}=300\frac{\text{C}}{\text{V}\cdot \text{L}\text{mito}}\cdot \frac{1}{F}\frac{\text{mol}}{\text{C}}=3.1\times {10}^{-3}\frac{\text{mol}}{\text{V}\cdot \text{Lmito}},$$

where F = 96,485 C mol⁻¹ is Faraday’s constant.

2.3. Gibbs free energy

A free energy is a thermodynamic quantity that relates a change in the thermodynamic state of a system to an associated change in total entropy of the system plus its environment. Chemical reaction processes necessarily proceed in the direction associated with a reduction in free energy [14]. When free energy of a system is reduced, total entropy (of the universe) is increased. The form of free energy that is operative in constant-temperature and constant-pressure systems (most relevant for biochemistry) is the Gibbs free energy, or simply the Gibbs energy.

For a chemical reaction of reactants Ai and products Bj,

$$\sum _{i=1}^M{m}_i{A}_i\rightleftharpoons \sum _{j=1}^N{n}_j{B}_j$$

where M and N are the total number of reactants and products, respectively, and m_i and nj are the coefficients of reactant i and product j, respectively, the Gibbs energy can be expressed as

$${\Delta }_{r}G={\Delta }_r{G}^{\circ }+R\text{T}\ln \left(\frac{{\prod }_{i=1}^N{\left[{\text{B}}_j\right]}^{n_i}}{{\prod }_{i=1}^M{\left[{\text{A}}_i\right]}^{m_i}}\right),$$ (1)

where Δ_rG° is the reference Gibbs energy for the reaction (a constant at given constant chemical conditions of temperature, pressure, ionic conditions, etc.), R = 8.314 J mol⁻¹ K⁻¹ is the gas constant, and T = 310.15 K is the temperature. The second term on the right hand side of Equation (1) governs how changes in concentrations of species affects ΔrG. Applications of Equation (1) to reactions in aqueous solution usually adopt the convention that all solute concentrations are measured relative to 1 Molar, ensuring that the argument of the logarithm is unitless regardless of the stoichiometry of the reaction.

A system is in chemical equilibrium when there is no thermodynamic driving force, that is, Δ_rG = 0. Thus, for this chemical reaction the reference Gibbs energy is related to the equilibrium constant as

$$K_{eq}={\left(\frac{{\prod }_{i=1}^N{\left[{\text{B}}_j\right]}^{n_i}}{{\prod }_{i=1}^M{\left[{\text{A}}_i\right]}^{m_i}}\right)}_{eq}=\exp \left\{-\frac{{\Delta }_r{G}^{\circ }}{R\text{T}}\right\}.$$

2.4. Membrane potential and proton motive force

Free energy associated with the oxidation of primary fuels is transduced to generate the chemical potential across the IMM known as the proton motive force, which is used to synthesize ATP in the matrix and transport ATP out of the matrix to the cytosol [14]. The thermodynamic driving force for translocation of hydrogen ions (H⁺) across the IMM has two components: the difference in electrostatic potential across the memlrane, ΔΨ (V), and the difference in H⁺ concentration (or activity) between the media on either side of the membrane, ΔpH, that is

$$\begin{gathered} \Delta G_{\text{H}}=-F\Delta \mathrm{\Psi }+R\text{T}\ln \left({\left[{\text{H}}^{+}\right]}_x/{\left[{\text{H}}^{+}\right]}_c\right) \\ =-F\Delta \mathrm{\Psi }-2.3R\text{T}\Delta \text{pH}, \end{gathered}$$ (2)

where the subscripts x and c indicate matrix and external (cytosol) spaces. ΔΨ is defined as the cytosolic potential minus matrix potential, yielding a negative change in free energy for a positive potential. Membrane potential in respiring mitochondria is approximately 150–200 mV, yielding a contribution to ΔG_h on the order of 15–20 kJ mol⁻¹ [1]. Under in vitro conditions, ΔpH between the matrix and external buffer is on the order of 0.1 pH units [1]. Thus, the contribution to proton motive force from a pH difference is less than 1 kJ mol⁻¹ and substantially smaller than that from ΔΨ.

2.5. Thermodynamics of ATP synthesis/hydrolysis

Under physiological conditions the ATP hydrolysis reaction

$${\text{ATP}}^{4-}+{\text{H}}_2\text{O}\rightleftharpoons {\text{ADP}}^{3-}+{\text{HPO}}_4^{2-}+{\text{H}}^{+}$$ (3)

is thermodynamically favored to proceed from the left-to-right direction. The Gibbs energy associated with turnover of this reaction is

$${\Delta }_r{G}_{\text{ATP}}={\Delta }_r{G}_{\text{ATP}}^o+R\text{T}\ln \left(\frac{\left[{\text{ADP}}^{3-}\right]\left[{\text{HPO}}_4^{2-}\right]\left[{\text{H}}^{+}\right]}{\left[{\text{ATP}}^{4-}\right]}\right),$$ (4)

where the Gibbs energy for ATP hydrolysis under physiological conditions is approximately ${\Delta }_r{G}_{\text{ATP}}^o=4.99\text{kJ}{\text{mol}}^{-1}$ [9]. Using the convention that all concentrations are formally defined as measured relative to 1 Molar, the argument of the logarithm in Equation (4) is unitless.

2.5.1. Calculation of the ATP hydrolysis potential

Equation (4) expresses the Gibbs energy of chemical Equation (3) in terms of its chemical species. In practice, biochemistry typically deals with biochemical reactants, which are comprised of sums of rapidly interconverting chemical species. We calculate the total ATP concentration, [ΣATP], in terms of its bound and unbound species, that is,

$$\begin{gathered} \left[\Sigma \text{ATP}\right]=\left[{\text{ATP}}^{4-}\right]+\left[{\text{MgATP}}^{2-}\right]+\left[{\text{HATP}}^{3-}\right]+\left[{\text{KATP}}^{3-}\right] \\ =\left[{\text{ATP}}^{4-}\right]+\frac{\left[{\text{Mg}}^{2+}\right]\left[{\text{ATP}}^{4-}\right]}{K_{\text{MgATP}}}+\frac{\left[{\text{H}}^{+}\right]\left[{\text{ATP}}^{4-}\right]}{K_{\text{HATP}}}+\frac{\left[{\text{K}}^{+}\right]\left[{\text{ATP}}^{4-}\right]}{K_{\text{KATP}}} \\ =\left[{\text{ATP}}^{4-}\right]\left(1+\frac{\left[{\text{Mg}}^{2+}\right]}{K_{\text{MgATP}}}+\frac{\left[{\text{H}}^{+}\right]}{K_{\text{HATP}}}+\frac{\left[{\text{K}}^{+}\right]}{K_{\text{KATP}}}\right) \\ =\left[{\text{ATP}}^{4-}\right]P_{\text{ATP}}, \end{gathered}$$ (5)

where P_ATP is a binding polynomial. Here, we we account for only the single cation-bound species. (Free H⁺ in solution associates with water to form H₃O⁺. Here we use [H⁺] to indicate hydrogen ion activity which is equal to 10^−pH.) 1 lists the dissociation constants used in this study from [9]. Similarly, total ADP, [ΣADP], and inorganic phosphate, [ΣPi], concentrations are

$$\begin{gathered} \left[\Sigma \text{ADP}\right]=\left[{\text{ADP}}^{3-}\right]\left(1+\frac{\left[{\text{Mg}}^{2+}\right]}{K_{\text{MgADP}}}+\frac{\left[{\text{H}}^{+}\right]}{K_{\text{HADP}}}+\frac{\left[{\text{K}}^{+}\right]}{K_{\text{KADP}}}\right) \\ =\left[{\text{ADP}}^{3-}\right]P_{\text{ADP}} \end{gathered}$$ (6)

and

$$\begin{gathered} \left[\Sigma \text{Pi}\right]=\left[{\text{HPO}}_4^{2-}\right]\left(1+\frac{\left[{\text{Mg}}^{2+}\right]}{K_{\text{MgPi}}}+\frac{\left[{\text{H}}^{+}\right]}{K_{\text{HPi}}}+\frac{\left[{\text{K}}^{+}\right]}{K_{\text{KPi}}}\right) \\ =\left[{\text{HPO}}_4^{2-}\right]P_{\text{Pi}}, \end{gathered}$$ (7)

for binding polynomials P_ADP and P_Pi.

Expressing the Gibbs energy of ATP hydrolysis in Equation (3) in terms of biochemical reactant concentrations, we obtain

$$\begin{gathered} {\Delta }_r{G}_{\text{ATP}}={\Delta }_r{G}_{\text{ATP}}^o+R\text{T}\ln \left(\frac{\left[\sum \text{ADP}\right]\left[\Sigma \text{Pi}\right]}{\left[\Sigma \text{ATP}\right]}\cdot \frac{\left[{\text{H}}^{+}\right]P_{\text{ATP}}}{P_{\text{ADP}}{P}_{\text{Pi}}}\right) \\ ={\Delta }_r{G}_{\text{ATP}}^o+R\text{T}\ln \left(\frac{\left[{\text{H}}^{+}\right]P_{\text{ATP}}}{P_{\text{ADP}}{P}_{\text{Pi}}}\right)+R\text{T}\ln \left(\frac{\left[\Sigma \text{ADP}\right]\left[\Sigma \text{Pi}\right]}{\left[\Sigma \text{ATP}\right]}\right) \\ ={\Delta }_r{G}_{\text{ATP}}^{\prime °}+R\text{T}\ln \left(\frac{\left[\Sigma \text{ADP}\right]\left[\Sigma \text{Pi}\right]}{\left[\Sigma \text{ATP}\right]}\right) \end{gathered}$$ (8)

where ${\Delta }_r{G}_{\text{ATP}}^{\prime °}$ is a transformed, or apparent, reference Gibbs energy for the reaction.

The following code computes the apparent Gibbs energy with pH = 7, [K⁺] = 150 mM, and [Mg²⁺] = 1 mM. Biochemical reactant concentrations are set such that the total adenine nucleotide (TAN) pool inside the mitochondrion is 10 mM, [ΣATP] = 0.5 mM, [ΣADP] = 9.5 mM, and [ΣPi] = 1 mM. Here, we obtain a value of approximately −45 kJ mol⁻¹.

Code for calculating Gibbs energy of ATP hydrolysis here.

The reactant concentrations used in the above calculation represent reasonable values for concentrations in the mitochondrial matrix. In the cytosol, the ATP/ADP ratio is on the order of 100:1, yielding a Δ_rG_ATP of approximately −64 kJ mol⁻¹.

Note the large difference in magnitude of the estimated Gibbs energy of ATP hydrolysis inside (−45 kJ mol⁻¹) versus outside (−64 kJ mol⁻¹) of the mitochondrial matrix. Light will be shed on the mechanisms underlying this difference via the calculations and analyses presented below.

2.5.2. ATP synthesis in the mitochondrial matrix

The F₀F₁ ATP synthase catalyzes the synthesis of ATP from ADP and Pi by coupling to the translocation of n_F = 8/3 protons from the cytosol to the matrix via the combined reaction

$${\left({\text{ADP}}^{3-}\right)}_x+{\left({\text{HPO}}_4^{2-}\right)}_x+{\left({\text{H}}^{+}\right)}_x+n_{\text{F}}{\left({\text{H}}^{+}\right)}_c\rightleftharpoons {\left(\text{ATP}\right)}_x^{4-}+{\text{H}}_2\text{O}+n_{\text{F}}{\left({\text{H}}^{+}\right)}_x.$$ (9)

Using the Gibbs energy of the reaction of Equation (8) and the proton motive force in Equation (2), the overall Gibbs energy for the coupled process of ATP synthesis and proton transport via the F₀F1 ATP synthase is

$$\begin{gathered} \Delta G_{\text{F}}=-{\Delta }_r{G}_{\text{ATP}}+n_{\text{F}}\Delta G_{\text{H}} \\ =-{\Delta }_r{G}_{\text{ATP}}^{\prime o}-R\text{T}\ln \left(\frac{{\left[\Sigma \text{ADP}\right]}_x{\left[\Sigma \text{Pi}\right]}_x}{{\left[\Sigma \text{ATP}\right]}_x}\right)-n_{\text{F}}F\Delta \mathrm{\Psi }+R\text{T}\ln {\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{\text{F}}}. \end{gathered}$$ (10)

Note that the negative before Δ_rG_ATP indicates that the reaction of Equation (3) is reversed in Equation (9). The equilibrium concentration ratio occurs when ΔG_F = 0. Solving for the second term in Equation (10), we calculate the apparent equilibrium constant for ATP synthesis as

$$K_{eq,\text{F}}^{\prime }={\left(\frac{{\left[\Sigma \text{ATP}\right]}_x}{{\left[\Sigma \text{ADP}\right]}_x{\left[\Sigma \text{Pi}\right]}_x}\right)}_{eq}=\exp \left\{\frac{{\Delta }_r{G}_{\text{ATP}}^{\prime o}+n_{\text{F}}F\Delta \mathrm{\Psi }}{R\text{T}}\right\}{\left(\frac{{\left[{\text{H}}^{+}\right]}_c}{{\left[{\text{H}}^{+}\right]}_x}\right)}^{n_{\text{F}}}.$$ (11)

2.5.3. Mathematical modeling ATP synthesis

A simple model of ATP synthesis kinetics can be constructed using the apparent equilibrium constant and mass- action kinetics in the form

$$J_{\text{F}}=X_{\text{F}}\left(K_{eq,\text{F}}^{\prime }{\left[\sum \text{ADP}\right]}_x{\left[\Sigma \text{Pi}\right]}_x-{\left[\Sigma \text{ATP}\right]}_x\right),$$ (12)

where X_F = 1000 mol s⁻¹ (L mito) ⁻¹ is a rate constant set to an arbitrarily high value that maintains the reaction in equilibrium in model simulations. To simulate ATP synthesis at a given membrane potential, matriX pH, cytosolic pH, and cation concentrations, we have

$$\{\begin{array}{l}\frac{\text{d}{\left[\Sigma \text{ATP}\right]}_x}{\text{d}t}=J_{\text{F}}/W_x\\ \frac{\text{d}{\left[\Sigma \text{ADP}\right]}_x}{\text{d}t}=-J_{\text{F}}/W_x\\ \frac{\text{d}{\left[\Sigma \text{Pi}\right]}_x}{\text{d}t}=-J_{\text{F}}/W_x,\end{array}$$ (13)

where W_x ((L matrix water) (L mito) ⁻¹) is the fraction of water volume in the mitochondrial matrix to total volume of the mitochondrion. Dissociation constants are listed in 1 and all other parameters are listed in 2.

The following code simulates steady state ATP, ADP, and Pi concentrations for ΔΨ = 175 mV. Here, a pH gradient is fixed across the IMM such that the pH in the matrix is slightly more basic than the cytosol, pH_x = 7.4 and pH_c = 7.2. All other conditions remain unchanged.

Code for model from Equation (13) here

The above simulation shows that under the clamped pH and ΔΨconditions simulated here, the model quickly approaches an equilibrium steady state. (Even though all reaction fluxes go to zero in the final steady state, the ATP hydrolysis potential attains a finite nonzero value because of the energy supplied by the clamped proton motive force.) Most of the adenine nucleotide remains in the form of ADP and the final ATP/ADP ratio in the matrix is approximately 1:20, with the inorganic phosphate concentration of approximately 1 mM.

To explore how the equilibrium changes with membrane potential, the following code computes the predicted equilibrium steady-state over a ranges of ΔΨ from 100 to 250 mV.

Code simulating concentration versus ΔΨ for Equation (13)

The above simulations show that under physiological levels of ΔpH, matrix ATP concentrations become essentially zero for values of the membrane potential less than approximately 150 mV. At higher levels of ΔΨ, all of the available phosphate is used to phosphorylate ADP to ATP. Since the initial [Pi] and [ATP] are 1 mM and 0.5 mM, respectively, the maximum ATP obtains’ at the maximal ΔΨ is 1.5 mM.

3. Building a model of oxidative ATP synthesis from energetic components

Simulations in the preceding section illustrate how matrix ATP and ADP concentrations are governed by the contributors to the proton motive force. They also show how the matrix ATP/ADP ratio must typically be less than 1, in contrast to the cytosolic ATP/ADP ratio, which is on the order of 100. To understand me dependence of ATP synthesis and transport on the proton motive force, the kinetics of the processes that generate it, and the interplay of these processes, we can assemble models of the F₀F₁ ATP synthase, adenine nucleotide translocase (ANT), mitochondrial phosphate transport, and complexes I, III, and IV of the electron transport chain (ETC) to generate a core model of mitochondrial oxidative ATP synthesis.

3.1. Adenine nucleotide translocase

Following synthesis of ATP from ADP and Pi in the matrix, the final step in delivering ATP to the cytosol at physiological free energy levels is the electrically driven exchange of a maf’ix ATP⁴⁻ for a cytosolic ADP³⁻. This exchange process,

$${\left({\text{ATP}}^{4-}\right)}_x+{\left({\text{ADP}}^{3-}\right)}_c\rightleftharpoons {\left({\text{ATP}}^{4-}\right)}_c+{\left({\text{ADP}}^{3-}\right)}_x,$$

is catalyzed by the ANT. Here, we assume rapid transport of species between the cytosol and the IMS, and therefore, equate IMS and cytosol species concentrations.

To simulate the kinetics of this process, we use the Metelkin et al. model [12], which accounts for pH and electrochemical dependencies. (Kinetic parameter value estimates for this model were updated by Wu et al. [23].) The steady-state flux of ANT is expressed

$$J_{\text{ANT}}=E_{\text{ANT}}\frac{\frac{k_2^{\text{ANT}}q}{K_o^D}{\left[{\text{ATP}}^{4-}\right]}_x{\left[{\text{ADP}}^{3-}\right]}_c-\frac{k_3^{\text{ANT}}}{K_o^T}{\left[{\text{ADP}}^{3-}\right]}_x{\left[{\text{ATP}}^{4-}\right]}_c}{\left(1+\frac{{\left[{\text{ATP}}^{4-}\right]}_c}{K_o^T}+\frac{{\left[{\text{ADP}}^{3-}\right]}_c}{K_o^D}\right)\left({\left[{\text{ADP}}^{3-}\right]}_x+{\left[{\text{ATP}}^{4-}\right]}_{x}q\right)},$$ (14)

where E_ANT (mol (L mito)⁻¹ ) is the total ANT content of the mitochondria and

$$\begin{gathered} k_2^{\text{ANT}}=k_{2,o}^{\text{ANT}}{e}^{(-3A-4B+C)\varphi }, \\ {k}_3^{\text{ANT}}=k_{3,o}^{\text{ANT}}{e}^{(-4A-3B+C)\varphi }, \\ {K}_o^D=K_o^{D,0}{e}^{3{\delta }_D\varphi }, \\ {K}_o^T=K_o^{T,0}{e}^{4{\delta }_T\varphi }, \\ q=\frac{k_3^{\text{ANT}}{K}_o^D}{k_2^{\text{ANT}}{K}_o^T}{e}^{\varphi },\text{and} \\ \varphi =F\Delta \mathrm{\Psi }/R\text{T}. \end{gathered}$$ (15)

All parameter values and units can be found in 3, reproduced from [1].

To simulate ANT and F₀F₁ ATP synthase activity simultaneously, we extend the system of Equation (13) by adding states for cytosolic species [ΣATP]_c and [ΣADP]_c, yielding

$$\{\begin{array}{l}\frac{\text{d}{\left[\Sigma \text{ATP}\right]}_x}{\text{d}t}=\left(J_{\text{F}}-J_{\text{ANT}}\right)/W_x,\frac{\text{d}{\left[\Sigma \text{ATP}\right]}_c}{\text{d}t}=\left(V_{m2c}{J}_{\text{ANT}}\right)/W_c,\\ \frac{\text{d}{\left[\Sigma \text{ADP}\right]}_x}{\text{d}t}=\left(-J_{\text{F}}+J_{\text{ANT}}\right)/W_x,\frac{\text{d}{\left[\Sigma \text{ADP}\right]}_c}{\text{d}t}=\left(-V_{m2c}{J}_{\text{ANT}}\right)/W_c,\\ \frac{\text{d}{\left[\Sigma \text{Pi}\right]}_x}{\text{d}t}=0\end{array}$$ (16)

where V_m2c (L mito) (L cyto)⁻¹ is the fraction of the volume of mitochondria per volume cytosol and W_c (L cyto water) (L cyto)⁻¹ is the fraction of water volume in the cytoplasm to the total volume of the cytoplasm (2).

Here, we clamp the matrix phosphate concentration at a constant value since the system of equations in Equation (16) does not account for phosphate transport between the matrix and the cytosol.

Code for model from Equation (16) here

The above simulations of the system of Equation (16) show how the electrogenic nature of the ANT transport results in the markedly different ATP/ADP ratios in the cytosol compared to the matrix. As we saw in the previous chapter, the ATP hydrolysis potential in the matrix is approximately −45 kJ mol⁻¹. The roughly 100:1 ratio of ATP to ADP in the cytosol is associated with a hydrolysis potential of approximately −65 kJ mol⁻¹. The difference of 20 kJ mol⁻¹ between the matrix and the cytosolic space is driven primarily by the membrane potential, which is roughly equivalent to 20 kJ mol⁻¹.

3.2. Inorganic phosphate transport

During active ATP synthesis, mitochondrial Pi is replenished via the activity of the phosphate-proton cotransporter (PiC), catalyzing the electroneutral cotransport of protonated inorganic phosphate, H₂PO₄⁻, and H⁺ across the membrane. Again, we assume rapid transport between the cytoplasm and intermembrane space, and hence, we have

$${\left({\text{H}}_2{\text{PO}}_4^{-}\right)}_c+{\left({\text{H}}^{+}\right)}_c\rightleftharpoons {\left({\text{H}}_2{\text{PO}}_4^{-}\right)}_x+{\left({\text{H}}^{+}\right)}_x.$$

Adopting the flux equation from Bazil et al. [1], we have

$$J_{\text{PiC}}=E_{\text{PiC}}\frac{{\left[{\text{H}}^{+}\right]}_c{\left[{\text{H}}_2{\text{PO}}_4^{-}\right]}_c-{\left[{\text{H}}^{+}\right]}_x{\left[{\text{H}}_2{\text{PO}}_4^{-}\right]}_x}{{\left[{\text{H}}_2{\text{PO}}_4^{-}\right]}_c+k_{\text{PiC}}},$$ (17)

where E_PiC (L matrix water) s⁻¹ (L mito)⁻¹ is the PiC activity rate and k_PiC = 1.61 mM is an effective Michaelis-Menten constant. The ${\text{H}}_2{\text{PO}}_4^{-}$ concentrations in the matrix and cytosol are computed via the relationship

$$\left[{\text{H}}_2{\text{PO}}_4^{-}\right]=\left[\Sigma \text{Pi}\right]\left(\left[{\text{H}}^{+}\right]/K_{\text{HPi}}\right)/P_{\text{Pi}}$$

from Equation (7).

To incorporate PiC into Equation (16), we add a new state [ΣPi]_c such that at given membrane potential, matrix and cytosolic pH, and cation concentrations, we obtain

$$\{\begin{array}{cc}\frac{\text{d}{\left[\Sigma \text{ATP}\right]}_x}{\text{d}t}=\left(J_{\text{F}}-J_{\text{ANT}}\right)/W_x,& \frac{\text{d}{\left[\Sigma \text{ATP}\right]}_c}{\text{d}t}=\left(V_{m2c}{J}_{\text{ANT}}\right)/W_c\\ \frac{\text{d}{\left[\Sigma \text{ADP}\right]}_x}{\text{d}t}=\left(-J_{\text{F}}+J_{\text{ANT}}\right)/W_x,& \frac{\text{d}{\left[\Sigma \text{ADP}\right]}_c}{\text{d}t}=\left(-V_{m2c}{J}_{\text{ANT}}\right)/W_c,\\ \frac{\text{d}{\left[\Sigma \text{Pi}\right]}_x}{\text{d}t}=\left(-J_{\text{F}}+J_{\text{PiC}}\right)/W_x,& \frac{\text{d}{\left[\Sigma \text{Pi}\right]}_c}{\text{d}t}=\left(-V_{m2c}{J}_{\text{PiC}}\right)/W_c,\end{array}$$ (18)

The following code simulates the synthesis of ATP from ADP and Pi and their translocation across the IMM under physiological conditions.

Code for model from Equation (18) here

For the above simulations, cytosolic inorganic phosphate is set to 10 mM initially, and all other initial conditions remain unchanged. Driven by ΔpH, a gradient in phosphate concentration is established, with a steady-state ratio of matrix-to-cytosol concentration of approximately 2.2. As seen in the previous section, with a constant membrane potential of 175 mV, the ATP/ADP ratio is maintained at a much higher level in the cytosol than in the matrix.

The final matrix and cytosol ATP and ADP concentrations depend not only on the membrane potential, but also on the total amount of exchangeable phosphate in the system. Here these simulations start with [Pi]_c = 10 mM and [Pi]_x = 1 mM. The initial 10 mM of ADP in the cytosol becomes almost entirely phosphorylated to ATP, leaving 0.32 mM of inorganic phosphate in the cytosol in the final steady state. To explore how these steady states depend on ΔΨ, the following code simulates the steady-state behavior of this system for a range of ΔΨ from 100 to 200 mV. These simulations, based on a simple, thermodynamically constrained model, show that it is not possible to synthesize ATP at physiological free energy levels for values of ΔΨ of lower than approximately 160 mV.

Code simulating concentration versus ΔΨ for Equation (18).

Simulation of this system reinforces the fact that ATP cannot be synthesized at physiological free energy levels for mitochondrial membrane potential of less than approximately 150 mV.

3.3. Respiratory complexes and NADH synthesis

The previous sections have assumed a constant membrane potential. To account for the processes that generate the membrane potential, we model proton pumping associated with the respiratory complexes I, III, and IV of the ETC (1).

3.3.1. ETC complex I

Coupled with the translocation of n_C1 = 4 protons across the IMM against the electrochemical gradient, electrons are transferred from NADH to ubiquinone (Q) at complex I of the ETC via the reaction

$${\left({\text{NADH}}^{2-}\right)}_x+{\left({\text{H}}^{+}\right)}_x+{\left(\text{Q}\right)}_x+n_{\text{C}1}{\left({\text{H}}^{+}\right)}_x\rightleftharpoons {\left({\text{NAD}}^{-}\right)}_x+{\left({\text{QH}}_2\right)}_x+{\text{H}}_2\text{O}+n_{\text{C}1}{\left({\text{H}}^{+}\right)}_c.$$ (19)

Since protons move against the gradient when the reaction proceeds in the left-to-right direction, the overall Gibbs energy for the reaction of Equation (19) is

$$\begin{gathered} \Delta G_{\text{C}1}={\Delta }_r{G}_{\text{C}1}-n_{\text{C}1}\Delta G_{\text{H}} \\ ={\Delta }_r{G}_{\text{Cl}}^{°}+R\text{T}\ln \left(\frac{{\left[{\text{NAD}}^{-}\right]}_x{\left[{\text{QH}}_2\right]}_x}{{\left[{\text{NADH}}^{2-}\right]}_x{\left[\text{Q}\right]}_x}\cdot \frac{1}{{\left[{\text{H}}^{+}\right]}_x}\right)+n_{\text{C}1}F\Delta \mathrm{\Psi }-R\text{T}\ln {\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{\text{C}1}} \\ ={\Delta }_r{G}_{\text{C}1}^{\prime °}+R\text{T}\ln \left(\frac{{\left[{\text{NAD}}^{-}\right]}_x{\left[{\text{QH}}_2\right]}_x}{{\left[{\text{NADH}}^{2-}\right]}_x{\left[\text{Q}\right]}_x}\right)+n_{\text{C}1}F\Delta \mathrm{\Psi }-R\text{T}\ln {\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{\text{C}1}}, \end{gathered}$$

where

$${\Delta }_r{G}_{\text{C}1}^{\prime °}={\Delta }_r{G}_{\text{C}1}^{°}-R\text{T}\ln \left({\left[{\text{H}}^{+}\right]}_x\right)$$

is the apparent Gibbs energy for the reaction in Equation (19). The apparent equilibrium constant is

$$K_{eq,\text{C}1}^{\prime }={\left(\frac{{\left[{\text{NAD}}^{-}\right]}_x{\left[{\text{QH}}_2\right]}_x}{{\left[{\text{NADH}}^{2-}\right]}_x{\left[\text{Q}\right]}_x}\right)}_{eq}=\exp \left\{\frac{-\left({\Delta }_r{G}_{\text{C}1}^{\prime °}+n_{\text{C}1}F\Delta \mathrm{\Psi }\right)}{R\text{T}}\right\}{\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{\text{C}1}}.$$ (20)

To simulate the flux of complex I, J_C1 (mol s⁻¹ (L mito)⁻¹), across the IMM by mass-action kinetics, we have

$$J_{\text{C}1}=X_{\text{C}1}\left(K_{eq,\text{C}1}^{\prime }{\left[{\text{NADH}}^{2-}\right]}_x{\left[\text{Q}\right]}_x-{\left[{\text{NAD}}^{-}\right]}_x{\left[{\text{QH}}_2\right]}_x\right),$$ (21)

for X_C1 (mol s⁻¹ (L mito)⁻¹) the a rate constant. 4 lists the constants for complex I.

3.3.2. ETC complex III

The reaction catalyzed by complex III reduces two cytochrome c proteins for every QH₂ oxidized

$${\left({\text{QH}}_2\right)}_x+2{\left({\text{c}}_{ox}^{3+}\right)}_i+n_{\text{C}3}{\left({\text{H}}^{+}\right)}_x\rightleftharpoons {\left(\text{Q}\right)}_x+2{\left({\text{c}}_{red}^{2+}\right)}_i+2{\left({\text{H}}^{+}\right)}_c+n_{\text{C}3}{\left({\text{H}}^{+}\right)}_c,$$ (22)

where ${\text{c}}_{ox}^{3+}$ and ${\text{c}}_{red}^{2+}$ are the oxidized and reduced cytochrome c species and the subscript i indicates that cytochrome c is confined to the IMS. This reaction is coupled with the transport of n_C3 = 2 protons from the matrix to the cytosol against the electrochemical gradient. Thus, the Gibbs energy for the overall reaction given in Equation (22) is

$$\begin{array}{l}\Delta G_{\text{C}3}={\Delta }_r{G}_{\text{C}3}-n_{\text{C}3}\Delta G_{\text{H}}\\ ={\Delta }_r{G}_{\text{C}3}^{°}+R\text{T}\ln \left(\frac{{\left[\text{Q}\right]}_x{\left[{\text{c}}_{\text{red}}^{2+}\right]}_i^2}{{\left[{\text{QH}}_2\right]}_x{\left[{\text{c}}_{ox}^{3+}\right]}_i^2}\cdot {\left[{\text{H}}^{+}\right]}_c^2\right)+n_{\text{C}3}F\Delta \mathrm{\Psi }-R\text{T}\ln {\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{\text{Cs}}}\\ ={\Delta }_r{G}_{\text{C}3}^{\prime °}+R\text{T}\ln \left(\frac{{\left[\text{Q}\right]}_x{\left[{\text{c}}_{red}^{2+}\right]}_i^2}{{\left[{\text{QH}}_2\right]}_x{\left[{\text{c}}_{ox}^{3+}\right]}_i^2}\right)+n_{\text{C}3}F\Delta \mathrm{\Psi }-R\text{T}\ln {\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{\text{C}3}},\end{array}$$

where

$${\Delta }_r{G}_{\text{C}3}^{\prime °}={\Delta }_r{G}_{\text{C}3}^{°}+2R\text{T}\ln \left({\left[{\text{H}}^{+}\right]}_c\right)$$

is the apparent Gibbs energy for complex III. The apparent equilibrium constant is

$$K_{eq,\text{C}3}^{\prime }={\left(\frac{{\left[\text{Q}\right]}_x{\left[{\text{c}}_{\text{red}}^{2+}\right]}_i^2}{{\left[{\text{QH}}_2\right]}_x{\left[{\text{c}}_{ox}^{3+}\right]}_i^2}\right)}_{eq}=\exp \left\{\frac{-\left({\Delta }_r{G}_{\text{C}3}^{\prime °}+n_{\text{C}3}F\Delta \mathrm{\Psi }\right)}{R\text{T}}\right\}{\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{\text{C}3}}.$$ (23)

To simulate the flux of complex III, J_C3 (mol s⁻¹ (L mito) ⁻¹), by mass-action kinetics, we have

$$J_{\text{C}3}=X_{\text{C}3}\left(K_{eq,\text{C}3}^{\prime }{\left[{\text{QH}}_2\right]}_x{\left[{\text{c}}_{ox}^{3+}\right]}_i^2-{\left[\text{Q}\right]}_x{\left[{\text{c}}_{red}^{2+}\right]}_i^2\right),$$ (24)

where X_C3 (mol s⁻¹ (L mito) ⁻¹) is the rate constant.

3.3.3. ETC complex IV

In the final step of the ETC catalyzed by complex IV, elecrtons are transferred from cytochrome c to oxygen, forming water

$$2{\left({\text{c}}_{\text{red}}^{2+}\right)}_i+\frac{1}{2}{\left({\text{O}}_2\right)}_x+2{\left({\text{H}}^{+}\right)}_c+n_{\text{C}4}{\left(\left[{\text{H}}^{+}\right]\right)}_x\rightleftharpoons 2{\left({\text{c}}_{ox}^{3+}\right)}_i+{\text{H}}_2\text{O}+n_{\text{C}4}{\left(\left[{\text{H}}^{+}\right]\right)}_c,$$ (25)

coupled with the translocation of n_C4 = 4 protons across the IMM against against the electrochemical gradient. The Gibbs energy of the reaction in Equation (25) is

$$\begin{gathered} \Delta G_{\text{C}4}={\Delta }_r{G}_{\text{C}4}-n_{\text{C}4}\Delta G_{\text{H}} \\ ={\Delta }_r{G}_{\text{C}4}^o+R\text{T}\ln \left(\frac{{\left[{\text{c}}_{ox}^{3+}\right]}_i^2}{{\left[{\text{c}}_{red}^{2+}\right]}_i^2{\left[{\text{O}}_2\right]}_x^{1/2}}\cdot \frac{1}{{\left[{\text{H}}^{+}\right]}_c^2}\right)+n_{\text{C}4}F\Delta \mathrm{\Psi }-R\text{T}\ln {\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{C4}} \\ ={\Delta }_r{G}_{\text{ATP}}^{\prime °}+R\text{T}\ln \left(\frac{{\left[{\text{c}}_{ox}^3\right]}_i^2}{{\left[{\text{c}}_{\text{red}}^{2+}\right]}_i^2{\left[{\text{O}}_2\right]}_x^{1/2}}\right)+n_{\text{C}4}F\Delta \mathrm{\Psi }-R\text{T}\ln {\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{\text{C}4}}, \end{gathered}$$

where

$${\Delta }_r{G}_{\text{C}4}^{\prime °}={\Delta }_r{G}_{\text{C}4}^{°}-2R\text{T}\ln \left({\left[{\text{H}}^{+}\right]}_c\right)$$

is the apparent Gibbs energy for complex IV. The apparent equilibrium constant is

$$K_{eq,\text{C}4}^{\prime }={\left(\frac{{\left[{\text{c}}_{ox}^{3+}\right]}_i^2}{{\left[{\text{c}}_{red}^{2+}\right]}_i^2{\left[{\text{O}}_2\right]}_x^{1/2}}\right)}_{eq}=\exp \left\{\frac{-\left({\Delta }_r{G}_{\text{C}4}^{\prime °}+n_{\text{C}4}F\Delta \mathrm{\Psi }\right)}{R\text{T}}\right\}{\left(\frac{{\left[{\text{H}}^{+}\right]}_x}{{\left[{\text{H}}^{+}\right]}_c}\right)}^{n_{C4}}.$$ (26)

To simulate the flux of complex IV, J_C4 (mol s⁻¹ (L mito)⁻¹), we use mass-action kinetics and account for binding of oxygen to complex IV as

$$J_{\text{C}4}=X_{\text{C}4}\left(\frac{1}{1+\frac{k_{{\text{O}}_2}}{\left[{\text{O}}_2\right]}}\right)\left({\left(K_{eq,\text{C}4}^{\prime }\right)}^{1/2}{\left[{\text{c}}_{red}^{2+}\right]}_i{\left[{\text{O}}_2\right]}_x^{1/4}-{\left[{\text{c}}_{ox}^{3+}\right]}_i\right),$$ (27)

where X_C4 (mol s⁻¹ (L mito) ⁻¹) is the rate constant and k_O2 is the O₂ binding constant (4). For this study, we assume a partial pressure of O₂ at 25 mmHg.

The apparent equilibrium constants for the F₀F₁ ATPase (Equation (11)), complex I (Equation (20)), complex III (Equation (23)), and complex IV (Equation (26)) depend on ΔΨ. In the model developed in this section, since ΔΨ is a variable, these apparent equilibrium constants are also variables. Thus, the flux expressions in Equations (12), (21), (24), and (27) depend on ΔΨ. These expressions may be compared to a generalized formulation of rate laws for reversible enzyme-catalyzed reactions [15], where in this case the saturating dependence of flux on substrate concentrations is not accounted for. These expressions may also be compared to the more detailed representations of the underlying catalytic mechanisms used by Bazil et al. [1]. The Bazil et al. model also accounts for side reactions generating reactive oxygen species that are not accounted for here.

3.3.4. Dehydrogenase activity

In this model, we do not explicitly simulate the reactions of the TCA cycle or beta oxidation, but rather the combined action of NADH-producing reactions, that is,

$${\left({\text{NAD}}^{-}\right)}_x\rightleftharpoons {\left({\text{NADH}}^{2-}\right)}_x+{\left({\text{H}}^{+}\right)}_x$$

From Beard [2], we represent a Pi dependence of NADH production using the following phenomenological expression

$$J_{\text{DH}}=X_{\text{DH}}\left(r\left[{\text{NAD}}^{-}\right]-\left[{\text{NADH}}^{2-}\right]\right)\left(\frac{1+{\left[\Sigma \text{Pi}\right]}_x/k_{\text{Pi},1}}{1+{\left[\Sigma \text{Pi}\right]}_x/k_{\text{Pi},2}}\right),$$ (28)

where X_DH (mol s⁻¹ (L mito)⁻¹) is the dehydrogenase activity and r (dimensionless), k_Pi,1 (mol (Lmatrix water)⁻¹), and k_Pi,₂ (mol (L matrix water)⁻¹) are constants. Parameter values are listed in Table 4. The dependence of NADH production on Pi reflects the Pi-dependence of the substrate-level phosphorylation step of the TCA cycle (the succinyl coenzyme-A synthetase reaction) and the fact that Pi drives substrate oxidation via the dicarboxylate carrier.

Table 4:

Respiratory complex and inorganic phosphate transport parameters.

Parameter	Units	Description	Value	Source
n C1		Protons translocated by complex I	4	[14]
n C3		Protons translocated by complex III	2	[14]
n C4		Protons translocated by complex IV	4	[14]
X C1	mol s−1 (L mito)−1	Complex I rate constant	1e4
X C3	mol s−1 (L mito)−1	Complex III rate constant	1e6
X C4	mol s−1 (L mito)−1	Complex IV rate constant	0.0125
X DH	mol s−1 (L mito)−1	NADH dehydrogenase rate constant	0.1732
X H	mol s−1 (L mito)−1	Proton leak activity	1e3
r		Dehydrogenase parameter	6.8385
k Pi,1	mmol (L matrix water)−1	Dehydrogenase parameter	0.466
k Pi,2	mmol (L matrix water)−1	Dehydrogenase parameter	0.658
k PiC	mmol (L cell)−1	PiC constant	1.61	[1]
k O2	μmol (L matrix water)−1	O2 binding constant	120	[22]
${\Delta }_r{G}_{\text{Cl}}^o$	kJ mol−1	Gibbs energy of reaction for complex I	−109.7	[9]
${\Delta }_r{G}_{\text{C}3}^o$	kJ mol−1	Gibbs energy of reaction for complex III	46.7	[9]
${\Delta }_r{G}_{\text{C}4}^o$	kJ mol−1	Gibbs energy of reaction for complex IV	−202.2	[9]
[NAD]tot	mmol (L matrix water)−1	Total NAD pool in the matrix	2.97	[22]
[Q]tot	mmol (L matrix water)−1	Total Q pool in the matrix	1.35	[22]
[c]tot	mmol (L IM water)−1	Total cytochrome c pool in the IMS	2.70	[22]

3.3.5. Proton leak

To simulate proton leak across the IMM, we adopt the Goldman-Hodgkins-Katz formulation from Wu et al. [23],

$$J_{\text{H}}=X_{\text{H}}\left({\left[{\text{H}}^{+}\right]}_c{e}^{\varphi /2}-{\left[{\text{H}}^{+}\right]}_x{e}^{-\varphi /2}\right)$$ (29)

where X_H = 1000 mol s⁻¹ (L mito)⁻¹ is the proton leak activity and ϕ is given in Equation (15). Even though the kinetic constants X_F and X_H attain equal values here, under the ATP-producing conditions the proton flux through the F₀F₁ ATPase (J_F, Equation (12)) is an order of magnitude greater than the proton leak flux (J_H, Equation (29)).

3.4. Simulating ATP synthesis in vitro

The flux expressions developed above may be used to simulate mitochondrial ATP synthesis in vitro, governed by the system of equations

$$\{\begin{array}{l}\underset{\_}{\frac{\text{d}\Delta \mathrm{\Psi }}{\text{d}t}=\left(n_{\text{Cl}}{J}_{\text{Cl}}+n_{\text{C}3}{J}_{\text{C}3}+n_{\text{C}4}{J}_{\text{C}4}-n_{\text{F}}{J}_{\text{F}}-J_{\text{ANT}}-J_{\text{H}}\right)/C_m}\\ \frac{\text{d}{\left[\Sigma \text{ATP}\right]}_x}{\text{d}t}=\left(J_{\text{F}}-J_{\text{ANT}}\right)/W_x\\ \frac{\text{d}{\left[\Sigma \text{ADP}\right]}_x}{\text{d}t}=\left(-J_{\text{F}}+J_{\text{ANT}}\right)/W_x\\ \frac{\text{d}{\left[\Sigma \text{Pi}\right]}_x}{\text{d}t}=\left(-J_{\text{F}}+J_{\text{PiC}}\right)/W_x\text{matrix}\text{species}\\ \frac{\text{d}{\left[{\text{NADH}}^{2-}\right]}_x}{\text{d}t}=\left(J_{\text{DH}}-J_{\text{Cl}}\right)/W_x\\ \underset{\_}{\frac{\text{d}{\left[{\text{QH}}_2\right]}_x}{\text{d}t}=\left(J_{\text{Cl}}-J_{\text{C}3}\right)/W_x}\\ \underset{\_}{\frac{\text{d}{\left[{\text{c}}_{\text{red}}^{2+}\right]}_i}{\text{d}t}=2\left(J_{\text{C}3}-J_{\text{C}4}\right)/W_i\text{intermembrane}\text{space}\text{species}}\\ \frac{\text{d}{\left[\Sigma \text{ATP}\right]}_c}{\text{d}t}=\left(V_{m2c}{J}_{\text{ANT}}-J_{\text{AtC}}\right)/W_c\\ \frac{\text{d}{\left[\Sigma \text{ADP}\right]}_c}{\text{d}t}=\left(-V_{m2c}{J}_{\text{ANT}}+J_{\text{AtC}}\right)/W_c\text{cytosol}\text{species}\\ \frac{\text{d}{\left[\Sigma \text{Pi}\right]}_c}{\text{d}t}=\left(-V_{m2c}{J}_{\text{PiC}}+J_{\text{AtC}}\right)/W_c,\end{array}$$ (30)

where the fluxes J_F (Equation (12)), J_ANT (Equation (14)), J_PiC (Equation (17)), J_C1 (Equation (21)), J_C3 (Equation (24)), J_C4 (Equation (27)), J_DH (Equation (28)), and J_H (Equation (29)) are given above and the constants are listed in Tables 2 and 4. Here, we incorporate a constant ATP consumption flux, J_AtC (mol s⁻¹ (L cyto) ⁻¹), that is

$$J_{\text{AtC}}=X_{\text{AtC}}/V_c$$

where V_c is the ratio of the volume of cytosol per L cell. X_AtC is the ATP consumption rate expressed in units of mmol s⁻¹ (L cell)⁻¹. Equation (30) does not explicitly treat matrix or external pH, K⁺, Mg²⁺, or O₂ as variables. Reasonable clamped concentrations for these variables are pH_x = 7.4, pH_c = 7.2, [Mg²+]_x = 1 mmol (L matrix water)⁻¹, [Mg²⁺]_c = 1 mmol (L cyto water)⁻¹, [K⁺]_x = 100 mmol (L matrix water)⁻¹, and [K⁺]_c = 140 mmol (L cyto water)⁻¹, and O₂ partial pressure of 25 mmHg. Respiratory chain reactants are determined from a total concentration of metabolites within the mitochondrion, that is, the total pools for NAD, cytochrome c, and Q species are

$${\left[\text{NAD}\right]}_{tot}={\left[{\text{NAD}}^{-}\right]}_x+{\left[{\text{NADH}}^{2-}\right]}_x$$

$${\left[\text{c}\right]}_{tot}={\left[{\text{c}}_{red}^{2+}\right]}_i+{\left[{\text{c}}_{ox}^{3+}\right]}_i,\text{and}$$

$${\left[\text{Q}\right]}_{tot}={\left[\text{Q}\right]}_x+{\left[{\text{QH}}_2\right]}_x.$$

The pools are [NAD]_tot = 2.97 mmol (L matrix water) ⁻¹, [c]_tot = 2.7 mmol (L IMS water) ⁻¹, and [Q]_tot = 1.35 mmol (L matrix water) ⁻¹. The finite nature of these metabolite pools constrains the maximal concentrations of substrates available for complexes I, III, and IV. Thus, although the simple mass-action models for these complexes do not account for saturable enzyme kinetics, the fluxes are limited by the availability of substrates. Initial conditions are set under the assumption that the TAN for both the matrix and cytosol is 10 mM, but the ATP/ADP ratio is <1 in the matrix and ~100 in the cytosol. The following code simulates in vitro mitochondrial function without ATP consumption in the external (cytosolic space).

Table 2:

Parameters for ATP synthesis in vitro.

Symbol	Units	Description	Value	Source
F 0 F 1 ATP synthase constants
n F		Protons translocated	8/3	[14]
X F	mol s−1 (L mito)−1	Rate constant	1000
${\Delta }_r{G}_{\text{ATP}}^{°}$	kJ mol−1	Reference Gibbs energy	4.99	[9]
Biophysical constants
R	J mol−1 K−1	Gas constant	8.314
T	K	Temperature	310.15
F	C mol−1	Faraday’s constant	96485
Cm	mol V−1 (L mito)−1	MM capacitance	3.1e-3	[2]
Volume ratios
Vc	(L cyto) (L cell)−1	Cyto to cell ratio	0.6601	[1]
Vm	(L mito) (L cell)−1	Mito to cell ratio	0.2882	[1]
V m2c	(L mito) (L cyto)−1	Mito to cyto ratio	Vm/Vc
Wc	(L cyto water) (L cyto)−1	Cyto water space ratio	0.8425	[1]
Wm	(L mito water) (L mito)−1	Mito water space ratio	0.7238	[1]
Wx	(L matrix water) (L mito)−1	Mito matrix water space ratio	0.9 Wm	[1]
Wi	(L IM water) (L mito)−1	IMS water space ratio	0.1 Wm	[1]

Code for model from Equation (30) here

The above simulations reach a final steady state where the phosphate metabolite concentrations are [ATP]_x = 0.9 mM, [ADP]_x =9.1 mM, [Pi]_x = 0.4 mM, [ATP]_c = 9.9 mM, [ADP]_c = 0.1 mM, [Pi]_c = 0.2 mM, and the membrane potential is 186 mV. This state represents a resting energetic state with no ATP hydrolysis in the cytosol. The Gibbs energy of ATP hydrolysis associated with this predicted state is ΔG_ATP = −70 kJ mol⁻¹,, as calculated below.

Code calculating the Gibbs energy in vitro here

4. Simulation of respiratory control in vitro

The integrated model developed in the previous section can be adapted to simulate in vitro experiments performed using suspensions of mitochondria purified from primary tissues. To simulate in vitro experiments, the major change that we make to the model is to replace the cytosolic components of the model with variables and associated volumes of distribution representing experimental buffers used in specific experiments. Here, we set V_c = 1, V_m = 5e-4, and W_c = 1 to represent mitochondria suspended in a buffer solution, i.e., in this virtual experiment, the mitochondria take up 0.05% of the volume of the experimental media.

The following code simulates an experiment in which the non-energized mitochondrial state (state 1), is followed by a leak state (state 2), followed by oxidative phosphorylation state (state 3), followed by another leak state (state 4) [8]. The virtual experiment represents a real experiment in which a purified suspension of mitochondria is introduced to a buffer containing no fuel substrates at time t = 0. This non-energized state is simulated by setting the dehydrogenase activity in the model to X_DH = 0 for 0 ≤ t < 25 s. State 2 is achieved by setting X_DH to 0.1732 for 25 ≤ t < 75 s to represent the addition of substrates (such as pyruvate and malate) to fuel NADH production. At time t = 75 s, 0.375 μM of ADP is introduced into the respiration buffer to initiate the active oxidative phosphorylation state, or state 3. State 4 occurs when the ADP is nearly fully phosphorylated at approximately t = 170 s, and the system returns to a leak state. Note that this experiment is conducted under high external inorganic phosphate conditions (i.e., initial [Pi]_c = 5 mM).

Code simulating respiratory control in vitro here

The first panel in the above figures shows oxygen consumption rate (OCR), which represents the oxidative flux necessary to balance proton leak across the IMM. In this study, we quantify OCR in units nmol O₂ min⁻¹ U CS⁻¹ proportional to the flux of complex IV, that is,

$$J_{\text{O}2}=\left(J_{\text{C}4}\frac{\text{mol}}{\text{s}\left(\text{L}\text{mito}\right)}\right)\left(60\frac{\text{s}}{\min }\right)\left(\text{le}9\frac{\text{nmol}}{\text{mol}}\right)\left(1.22\text{e}-6\frac{\text{L}\text{mito}}{\text{UCS}}\right)\text{.}$$

The factor 1.22e-6 (L mito) (U CS) ⁻¹ corresponds to roughly 740 (U CS) (mL mito) ⁻¹, reported by Vinnakota et al. [18]. Note that this approximation for J_O2 is valid for constant partial pressure of O₂, and hence, we do not model hypoxic or hyperoxic conditions. During the leak states, NADH and ΔΨ are maintained at a maximal values. During state 3 (oxidative phosphorylation), the OCR markedly increases while the magnitudes of NADH and ΔΨ are temporarily decreased. This simple model overestimates the degree to which the NADH becomes depleted during state 3.

Predictions of the in vitro model may also be compared to quasi-steady state data on OCRs, phosphate metabolite levels, ΔΨ, NADH, and cytochrome c redox state, analyzed by Bazil et al. [1]. In their experiments, several steady state ATP demand levels were achieved by titrating ATP hydrolyzing enzymes into the respiration buffer. We simulate this experiment with our model by varying the rate of the external ATP consuming process, J_AtC. We vary J_AtC by adjusting the ATP consumption rate X_AtC from 0 to 60 mol s⁻¹ (L cell) ⁻¹. Experiments were conducted under conditions of two different approximately constant external phosphate concentrations (1 and 5 mM) and with external TAN = 5 mM. The following code computes the steady state of the in vitro model at different levels of J_AtC and compares the measured data on OCR, ΔΨ, NADH, cytochrome c redox state, and buffer ADP concentration to data.

Code comparing OCR simulations to data here

The match to the data is remarkably good considering how much simpler the model developed here is compared to the model of Bazil et al. [1]. The Bazil et al. model accounts for the mechanisms underlying oxidative phosphorylation and associated side reactions at a deerper level of detail, and thus, finds broader applications. Yet the basic frameworks of our models are equivalent.

5. Simulation of cardiac energetics in vivo

In this final section we apply the developed model, which is shown to match data on the relationships between ATP synthesis and phosphate metabolite levels in vitro, to predict the nature of those relationships in vivo.

5.1. Creatine kinase

To use the mitochondrial model developed above to simulate energetics in muscle in vivo, we must account for the cytosolic creatine kinase reaction

$${\left({\text{ADP}}^{3-}\right)}_c+{\left({\text{CrP}}^{2-}\right)}_c+{\left({\text{H}}^{+}\right)}_c\rightleftharpoons {\left({\text{ATP}}^{4-}\right)}_c+{\left(\text{Cr}\right)}_c,$$ (31)

where Cr denotes creatine and CrP creatine phosphate. The total cytosolic creatine pool, [Cr]_tot, is conserved, that is,

$${\left[\text{Cr}\right]}_{tot}={\left[\text{Cr}\right]}_c+{\left[\text{CrP}\right]}_c.$$

To determine the effective Gibbs energy of the creatine kinase reaction in terms of measurable biochemical reactants, we substitute Equations (5) and (6) obtaining

$$\begin{gathered} {\Delta }_r{G}_{\text{CK}}={\Delta }_r{G}_{\text{CK}}^{°}+R\text{T}\ln \left(\frac{{\left[\text{EATP}\right]}_c{\left[\text{Cr}\right]}_c}{{\left[\Sigma \text{ADP}\right]}_c{\left[{\text{CrP}}^{2-}\right]}_c}\cdot \frac{P_{\text{ADP}}}{P_{\text{ATP}}{\left[{\text{H}}^{+}\right]}_c}\right) \\ ={\Delta }_r{G}_{\text{CK}}^{\prime °}+R\text{T}\ln \left(\frac{{\left[\Sigma \text{ATP}\right]}_c{\left[\text{Cr}\right]}_c}{{\left[\Sigma \text{ADP}\right]}_c{\left[{\text{CrP}}^{2-}\right]}_c}\right). \end{gathered}$$

where

$${\Delta }_r{G}_{\text{CK}}^{\prime °}={\Delta }_r{G}_{\text{CK}}^{°}+R\text{T}\ln \left(\frac{P_{\text{ADP}}}{P_{\text{ATP}}{\left[{\text{H}}^{+}\right]}_c}\right).$$

Here, ${\Delta }_r{G}_{\text{CK}}^{°}=-R\text{T}\ln \left(K_{eq,\text{CK}}\right)$ for experimental equilibrium constant K_eq,CK = 3.5×10⁸ [3]. The apparent equilibrium of the reaction in Equation (31) is

$$K_{eq,\text{CK}}^{\prime }={\left(\frac{{\left[\Sigma \text{ATP}\right]}_c{\left[\text{Cr}\right]}_c}{{\left[\Sigma \text{ADP}\right]}_c{\left[{\text{CrP}}^{2-}\right]}_c}\right)}_{eq}=\exp \left\{\frac{-{\Delta }_r{G}_{\text{CK}}^{\prime }}{R\text{T}}\right\}.$$

We simulate creatine kinase flux, J_CK (mol s⁻¹ (L mito) ⁻¹), via mass-action kinetics as

$$J_{\text{CK}}=X_{\text{CK}}\left(K_{eq,\text{CK}}^{\prime }{\left[\Sigma \text{ADP}\right]}_c{\left[\text{CrP}\right]}_C-{\left[\text{ATP}\right]}_c{\left[\text{Cr}\right]}_c\right)$$ (32)

where X_CK (mol s⁻¹ (L cyto) ⁻¹) is the creatine kinase activity.

To simulate cardiac energetics and in vivo experiments, we incorporate the creatine kinase module and obtain the following system:

$$\{\begin{array}{l}\underset{\_}{\frac{\text{d}\Delta \mathrm{\Psi }}{\text{d}t}=\left(n_{\text{Cl}}{J}_{\text{Cl}}+n_{\text{C}3}{J}_{\text{C}3}+n_{\text{C}4}{J}_{\text{C}4}-n_{\text{F}}{J}_{\text{F}}-J_{\text{ANT}}-J_{\text{H}}\right)/C_m}\\ \frac{\text{d}{\left[\Sigma \text{ATP}\right]}_x}{\text{d}t}=\left(J_{\text{F}}-J_{\text{ANT}}\right)/W_x\\ \frac{\text{d}{\left[\Sigma \text{ADP}\right]}_x}{\text{d}t}=\left(-J_{\text{F}}+J_{\text{ANT}}\right)/W_x\\ \frac{\text{d}{\left[\Sigma \text{Pi}\right]}_x}{\text{d}t}=\left(-J_{\text{F}}+J_{\text{PiC}}\right)/W_x\text{matrix}\text{species}\\ \frac{\text{d}{\left[{\text{NADH}}^{2-}\right]}_x}{\text{d}t}=\left(J_{\text{DH}}-J_{\text{Cl}}\right)/W_x\\ \underset{\_}{\frac{\text{d}{\left[{\text{QH}}_2\right]}_x}{\text{d}t}=\left(J_{\text{Cl}}-J_{\text{C}3}\right)/W_x}\\ \underset{\_}{\frac{\text{d}{\left[{\text{c}}_{\text{red}}^{2+}\right]}_i}{\text{d}t}=2\left(J_{\text{C}3}-J_{\text{C}4}\right)/W_i\text{intermembrane}\text{space}\text{species}}\\ \frac{\text{d}{\left[\Sigma \text{ATP}\right]}_c}{\text{d}t}=(V_{m2c}{J}_{\text{ANT}}-J_{\text{AtC}}+J_{\text{CK}})/W_c\\ \frac{\text{d}{\left[\Sigma \text{ADP}\right]}_c}{\text{d}t}=\left(-V_{m2c}{J}_{\text{ANT}}+J_{\text{AtC}}-J_{\text{CK}}\right)/W_c\text{cytoplasm}\text{species}\\ \frac{\text{d}{\left[\Sigma \text{Pi}\right]}_c}{\text{d}t}=\left(-V_{m2c}{J}_{\text{PiC}}+J_{\text{AtC}}\right)/W_c\\ \frac{\text{d}\left[\text{CrP}\right]}{\text{d}t}=-J_{\text{CK}}/W_c\end{array}$$ (33)

where the flux J_CK is given in Equation (32). In addition to the incorporation of the creatine kinase reaction, the in vivo model is adapted from the in vitro model by adjusting the mitochondrial volume. In the in vitro model, the volume fraction of the experimental system taken up by mitochondria is 0.0005 corresponding to a dilute suspension of purified mitochondria (2). In the in vivo model, the volume fraction of a cardiomyocyte taken up by mitochondria is 0.2882 (7).

5.2. Simulation of respiratory control in vivo

Previous investigations ([10, 11, 24]) have revealed that the certain cytosolic metabolite pools influence the phosphate metabolite levels in the myocardium in vivo. These metabolite pools are the total adenine nucleotide (TAN, mmol (L cell)⁻¹), total exchangeable phosphate (TEP, mmol (L cell) ⁻¹), and total creatine ([Cr]_tot, mmol (L cell) ⁻¹) pool, which may be computed from our model variables via

$$\text{TAN}=\left(V_c{W}_c+V_m{W}_i\right)\left({\left[\text{ATP}\right]}_c+{\left[\text{ADP}\right]}_c\right)+V_m{W}_x\left({\left[\text{ATP}\right]}_x+{\left[\text{ADP}\right]}_x\right),$$

$$\text{TEP}=\left(V_c{W}_c+V_m{W}_i\right)\left(2{\left[\text{ATP}\right]}_c+{\left[\text{ADP}\right]}_c+{\left[\text{Pi}\right]}_c+{\left[\text{CrP}\right]}_c\right)+V_m{W}_x\left({\left[\text{ATP}\right]}_x+{\left[\text{ADP}\right]}_x+{\left[\text{Pi}\right]}_x\right),\text{and}$$

$${\text{Cr}}_{tot}=V_c{W}_c\left({\left[\text{Cr}\right]}_c+{\left[\text{CrP}\right]}_c\right).$$

To simulate healthy normal conditions, these pools are set as TAN = 7.6, TEP = 27.5, and [Cr]_tot = 40 mM (L cell)⁻¹. The levels of these metabolite pools have been shown to decrease in heart failure compared to normal physiological conditions. In the simulations below we explore the predicted effects of altering these metabolite pool levels.

The code below computes the steady-state behavior of the in vivo model over a range of ATP consumption rates, representing myocardial ATP demand levels associated with resting and exercise conditions. The resting state is associated with a myocardial ATP consumption rate of approximately 0.4 mmol s⁻¹ (L cell) ⁻¹ while under vigorous exercise conditions the ATP consumption rate is approximately 1.2 mmol s⁻¹ (L cell) ⁻¹ [7]. Here, the myocardial ATP consumption rate is varied over the range of 0.4 to 1.2 mmol s⁻¹ (L cell) ⁻¹, corresponding to a range of myocardial oxygen consumption rate of approximately 4 to 12 μmol O₂ min⁻¹ (g tissue) ⁻¹.

Code simulating respiratory control in vivo here

Simulations of the normal case (blue lines) show that over the physiological range of ATP demand and oxygen consumption, the CrP/ATP ratio in the myocardium decreases from a value of 2.2 at rest to 2.0 in exercise, while the cytosolic phosphate concentration increases from approximately 0.75 mM at rest to 2.3 mM in exercise. These model predictions are remarkably close to experimem observations, given the relative simplicity of this model. Consistent with previous analyses, when the metabolite pool levels are changed to represent heart failure conditions (red lines), the CrP/ATP ratio decreases compared and the inorganic phosphate concentration is predicted to increase compared to physiological levels.

6. Summary and conclusions

The collection of calculations and simulations presented here represents a framework for analyzing and simulating mitochondrial function using basic thermodynamic and kinetic principles. This framework largely uses simple mass- action representations of kinetic processes, rather than models accounting for detailed catalytic mechanisms. It is perhaps remarkable that this simple approach is able effectively capture the systems-level function of ATP synthesis and respiratory control both in vitro and in vivo. Since these models and simulations are grounded in a rigorous treatment of the thermodynamics, we conclude that–with respect to the phenomena addressed in the simulations presented here–the thermodynamics of many of the underlying chemical processes is more important than the kinetics. However, in contrast to that general conclusion, the adenine nucleotide translocase, in particular, is represented with a model to account for the kinetics of its catalytic mechanism. Since the adenine nucleotide translocase catalyzes the final step in oxidative ATP synthesis, its kinetic mechanism is predicted to have the most direct influence of all the steps in governing cellular energetics and respiratory control in vivo. Moreover, the conclusion, for example, that the kinetics of complex I is effectively represented by the simple mass-action model of Equation (21), is dependent on context. While the model works for the purposes used here, it does not provide insights into phenomena that depend on a more detailed representation of a catalytic mechanism, as may be investigated using more complex models [1].

By embedding all of the computer codes for the calculations and simulations that we have presented, our intention is to facilitate an easy adoption and modification of the concepts developed here. The codes for these simulations are in Python in this Jupyter book, as well as in MATLAB and Tellurium [17]. Armed with these concepts and codes, it is hoped that readers will reuse, repurpose, update, modify, test, and extend these models. For example, this model can be used to investigate the effects of acidosis/alkalosis on mitochondrial function indirectly by the adjusting cytosolic pH.

This model may also be used to probe and simulate the mechanisms of respiratory control. Chance and Williams proposed in the 1950’s that respiratory control in vivo is achieved by the dependence of oxidative phosphorylation on concentration of ADP [5]. This idea has proved extremely powerful and largely correct, particularly for skeletal muscle. In vitro experiments on purified mitochondria [18, 19, 20] and model-based analysis of myocardial respiratory control in vivo [22, 23, 24] support the related hypothesis that in the myocardium Pi is the important feedback controller in respiratory control. According to this hypothesis, a key difference between skeletal muscle and the myocardium is that in skeletal muscle [ADP] tends to vary over a range comparable to the apparent Michaelis constant of ADP for oxidative ATP synthesis (approximately 30 μM), whereas Pi is several fold higher than its apparent Michaelis constant (approximately 1 mM) [21]. In the myocardium, the situation is reversed, with Pi varying around its apparent Michaelis constant and ADP several fold higher than its apparent Michaelis constant. This key difference may be explored in the models developed here by varying the sizes of the conserved cytoplasmic metabolite pools.

Finally, we hope that users and developers of these concepts will adopt publication vehicles such as this one, for sharing data, codes, and associated calculations with the community.

Figure 1:

Diagram of a mitochondrion with the cytosol, intermembrane space (IMS), and matrix indicated. *Inset from left to right:* Protein channels and complexes associated with oxidative phosphorylation in the cristae of the mitochondrion. Complex I (C1) catalyzes the oxidation of NADH²⁻ to NAD⁻ and reduction of ubiquinone (Q) to QH₂. Complex II (C2) catalyzes the oxidation of FADH₂ to FAD coupled to the reduction of Q. Complex III (C3) catalyzes the oxidation of QH₂ coupled to the reduction of cytochrome c (Cyt c). Complex IV (C4) catalyzes the oxidation of Cyt c coupled to the reduction of oxygen to water. These redox transfers drive pumping of H⁺ ions out of the matrix, establishing the proton motive force across the inner mitochondrial membrane (IMM) that drives ATP synthesis at complex V, or the F₀F₁-ATPase (F₀F₁). The adenine nucleotide translocase (ANT) exchanges matrix ATP for IMS ADP. The inorganic phosphate cotransporter (PiC) brings protons and Pi from the IMS to the matrix. Lastly, there is a passive H⁺ leak across the IMM.

Figure 2:

Steady state solution from Equation (13) for ΔΨ = 175 mV, pH_x = 7.4, and pH_c = 7.2.

Figure 3:

Simulation of concentration versus ΔΨ for Equation (13) for ΔΨ from 100 to 250 mV.

Figure 4:

Steady state solution from Equation (16) for the (a) matrix and (b) cytosol species with ΔΨ= 175 mV, pH_x = 7.4, and pH_c = 7.2.

Figure 5:

Steady state solution from Equation (18) for the (a) matrix and (b) cytosol species with ΔΨ = 175 mV, pH_x = 7.4, and pH_c = 7.2.

Figure 6:

Simulation of concentration versus ΔΨ for Equation (18) for the (a) matrix and (b) cytosol species with ΔΨ from 100 to 250 mV.

Figure 7:

Steady state solution from Equation (30) for the (a) matrix and (b) cytosol species with pH_x = 7.4 and pHc = 2.

Figure 8:

Simulation of respiratory control for (a) the oxygen consumption rate (OCR), (b) matrix NADH concentration ([NADH]_X), and (c) membrane potential (ΔΨ) using the conditions listed in Table 5.

Figure 9:

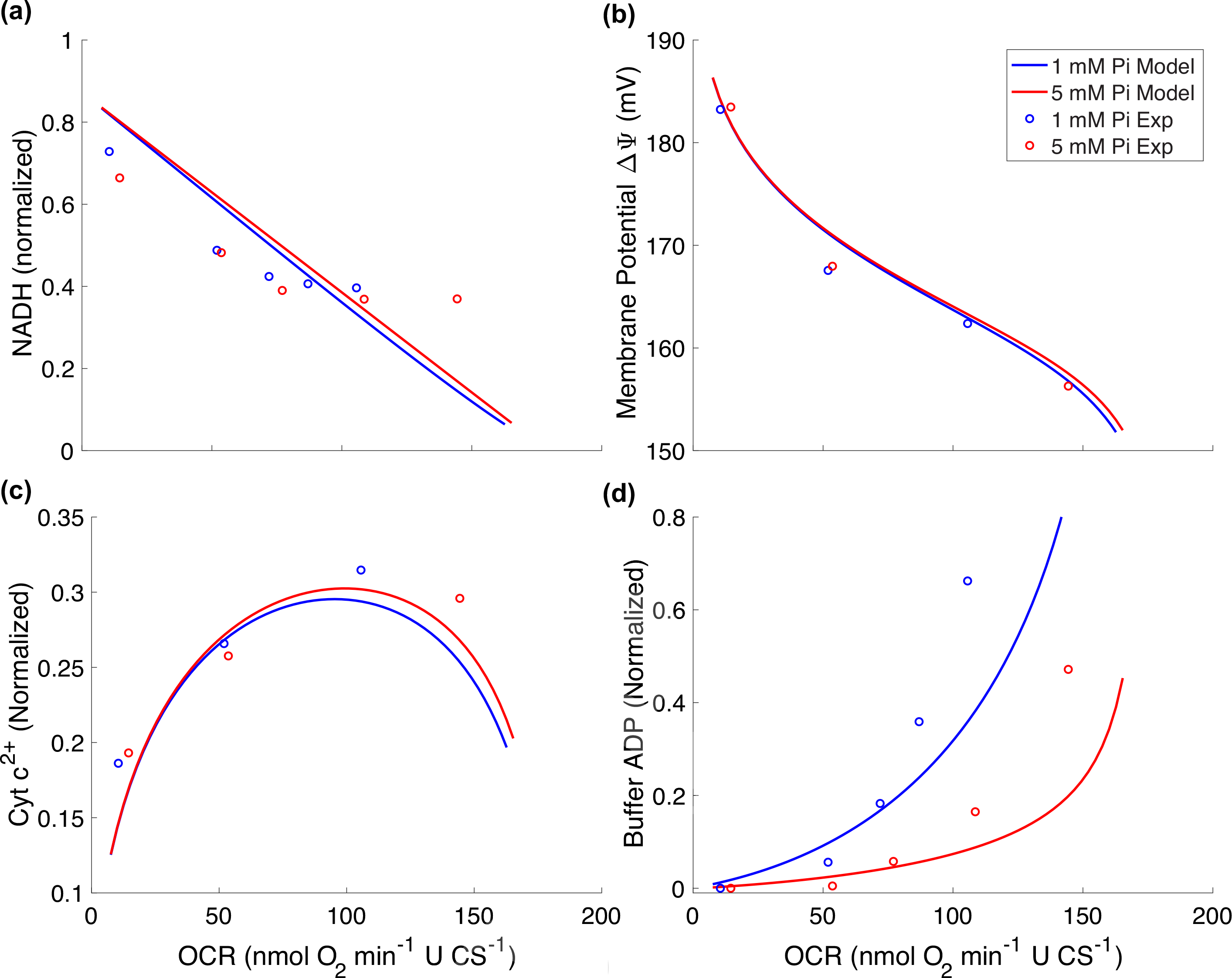
Comparison of oxygen consumption rate (OCR) simulations to data from [1].

Figure 10:

Simulation of respiratory control in vivo using the system in Equation (33) for (a) the creatine phosphate to ATP ratio ([CrP]_c/[ATP]_c) and (b) cytosolic Pi concentration ([Pi]_c).

Table 1:

Dissociation constants given as 10^−pK_a.

	Ligand
	Mg2+	H+	K+
K L–ATP	10−3.88	10−6.33	10−1.02
K L–ADP	10−3.00	10−6.26	10−0.89
K L–Pi	10−1.66	10−6.62	10−0.42

Table 3:

Adenine nucleotide translocase (ANT) parameters.

Parameter	Units	Description	Value
E ANT	mol (L mito)−1	ANT activity	0.325
δD		ADP displacement binding constant	0.0167
δT		ATP displacement binding constant	0.0699
$k_{2,o}^{\text{ANT}}$	s−1	Forward translocation rate	0.159
$k_{3,o}^{\text{ANT}}$	s−1	Reverse translocation rate	0.501
$K_o^{D,0}$	μmol (L cyto water)−1	ADP binding constant	38.89
$K_o^{T,0}$	μmol (L cyto water)−1	ATP binding constant	56.05
A		Translocation displacement constant	0.2829
B		Translocation displacement constant	−0.2086
C		Translocation displacement constant	0.2372

Table 5:

Isolated mitochondria in silico experiment.

Parameter or Condition	State 1	State 2	State 3 and 4
X DH	0	0.1732	–
[NADH]x	0	–	–
[ATP]c	0	–	–
[ADP]c	0	–	+375 μM
[Pi]c	5 mM	–	–

Table 6:

Parameters for ATP synthesis in vivo.

Symbol	Units	Description	Value	Source
X CK	mol s−1 (L cyto)−1	Creatine kinase activity	107	[1]
[Cr]tot	mmol (L cell)−1	Total creatine pool in the cell	40	[10]

Table 7:

In vivo metabolite pool concentrations.

Symbol	Units	Description	Healthy	Heart failure [10]
TAN	mmol (L cell)−1	Total adenine nucleotide	7.6	6.98
TEP	mmol (L cell)−1	Total exchangeable phosphate	27.5	24.11
[Crtot]	mmol (L cell)−1	Total creatine	40	23.03

Highlights.

• A kinetic and thermodynamic framework for mitochondrial energetics is developed.

• The framework is applied to simulate ATP synthesis and respiratory control.

• We illustrate how respiratory control in vitro translates to energetics in vivo.

• Computer codes are available at DOI: 10.5281/zenodo.4919564

Abbreviations

ADP

Adenosine diphosphate

ATP

Adenosine triphosphate

DNA

Deoxyribonucleic acid

FAD

Flavin adenine dinucleotide (oxidized)

FADH₂

Flavin adenine dinucleotide (reduced)

IMM

Inner mitochondrial membrane

Pi

Inorganic phosphate

IMS

Intermembrane space

NAD⁻

Nicotinamide adenine dinucleotide (oxidized)

NADH²⁻

Nicotinamide adenine dinucleotide (reduced)

OCR

Oxygen consumption rate

TAN

Total adenine nucleotide

TEP

Total enchangeable phosphate

TCA

Tricarboxylic acid