Abstract
Cell migration is a fundamental characteristic of vital processes such as tissue morphogenesis, wound healing and immune cell homing to lymph nodes and inflamed or infected sites. Therefore, various brain defect diseases, chronic inflammatory diseases as well as tumor formation and metastasis are associated with aberrant or absent cell migration. We embedded multicellular brain cancer spheroids in Matrigel™ and utilized single-particle tracking to extract the paths of cells migrating away from the spheroids. We found that – in contrast to local invasion – single cell migration is independent of Matrigel™ concentration and is characterized by high directionality and persistence. Furthermore, we identified a subpopulation of super-spreading cells with >200-fold longer persistence times than the majority of cells. These results highlight yet another aspect of cell heterogeneity in tumors.
Keywords: Invasion assay, Glioblastoma, Single-cell tracking, Diffusion models
Highlights
-
•
Multi-cellular brain cancer spheroids invasion is slowed down by matrix stiffening.
-
•
Single-cell invasion is not affected by Matrigel™ concentration.
-
•
Single-cells shows high persistence and dependence of matrix organization.
-
•
Identification of a distinct sub-population of super-spreaders.
1. Introduction
Tumor cell migration is a hallmark of cancer and is typically divided into three major types: amoeboid-, mesenchymal-, or collective migration [1]. Amoeboid and mesenchymal migration is the movement of single cells. Although cancers tend to exhibit one specific kind of migration – such as amoeboid migration by lymphoma cells – migrating cancer cells are known for their high plasticity and ability to interconvert between different modes of migration in response to environmental cues [2], [3]. In contrast, collective migration i.e. invasion involves the cooperative transport of whole groups of cells and describes the local expansion of tumor cells into the extracellular matrix (ECM).
A common system used to model tumors in 3D is that of tumor spheroids. Spheroids are dense multicellular structures that form due to most cells’ natural tendency to aggregate under certain environmental conditions [4]. The advantages of spheroids as tumor models include tighter cell–cell adhesion than cells cultured in 2D and that cells are not equally exposed to the local environment; instead there is an innermost and an outermost region emerging. This gives rise to nutrient, oxygen and cell proliferation gradients from the surface to the core [5], [6]. Cells in spheroids therefore exhibit different phenotypes depending on their proximity to the surface much like cancer cells in solid tumors which are e.g. dormant or necrotic at the core [6], [7]. For studies of metastasis, spheroids are embedded in a collagen, hydrogel or Matrigel™ matrix to mimic the natural cancer environment [8], [9], [10], [11]. Thus, this model system allows true three-dimensional migration/invasion of the cancer cells into the surrounding matrix.
Migration of tumor cells is a multistep process initiated by the epithelial to mesenchymal transition (EMT) where cells lose their apical–basal polarity and change their expression of e.g. surface adhesion molecules to allow a more migratory phenotype [12]. This transition is in itself a multistep process with multiple semi-stable intermediate states [7], [13], [14]. In order to migrate, mesenchymal cells have to develop pseudopods which protrude from their body and form focal contacts with the ECM. Proteases expressed on the cell surface then up-concentrate at these contacts to degrade the ECM locally and carve tunnels for the cell as it moves. The actual motion is driven by actomyosin contraction within the cell followed by detachment of the trailing edge by disassembly of focal contacts [2]. Due in part to the plasticity of cancer cells, the exact integrins, proteases and signaling molecules involved in this cascade of events depend not only on the cancer type but also on the microenvironment and the homogeneity among individual cells [2], [7].
A number of different random walk models have been used to describe cell migration in various species [15], [16]. Specifically, persistent random walk (PRW) models derived from the Ornstein–Uhlenbeck process have been very useful for describing the motility of various species from Dictyostelium and mouse fibroblasts to human endothelial cells [17], [18], [19], [20], [21]. However, there are several examples of motile cell types that are not exhaustively modeled as simple persistent random walkers [22], [23], [24], [25], [26]. In the specific case of glioblastoma invasion and migration, a sigmoidal Gompertzian model has been used to describe the growth of glioblastoma spheroids in vitro [27], while a cellular automaton model was used to highlight the importance of cell–cell adhesion/attraction during glioma cell migration [28]. Further, the PRW model has been used to describe both the growth and diffusion of cells away from glioblastoma spheroids [29]. While this work separated the proliferation and migration into two distinct populations, it has been shown that the combined growth and migration can be described by a density-dependency i.e. cell migration is inversely proportional to cell density, which is highest in the proliferating zone [30], [31], [32]. A number of studies have also modeled glioblastoma behavior regarding morphology, metabolism, vasculature, and medical treatment [33], for instance the targeting of chemotherapeutic peptides [34]. However, studies on the dynamics of glioblastoma cell migration are still limited and there seems to be no consensus on the subject.
We therefore set out to further characterize the invasion and migration of brain glioblastoma cells (U87-MG) from multicellular tumor spheroids, a cell type forming particularly tight spheroids [35]. We developed a brightfield live-cell imaging setup to follow the invasion of Matrigel™-embedded spheroids as well as subsequent migration of individual cells away from it. We found that the ability to invade the extracellular matrix is compromised by matrix stiffening. However, our analysis – based on machine learning algorithms [36] – also yielded insights into the migration behavior of individual cells and we found this to be highly ECM density independent. Surprisingly, we identified a subpopulation of fast migrating cancer cells. We found that these super-spreaders are not moving significantly faster along their trajectory, but with much more persistence.
2. Results
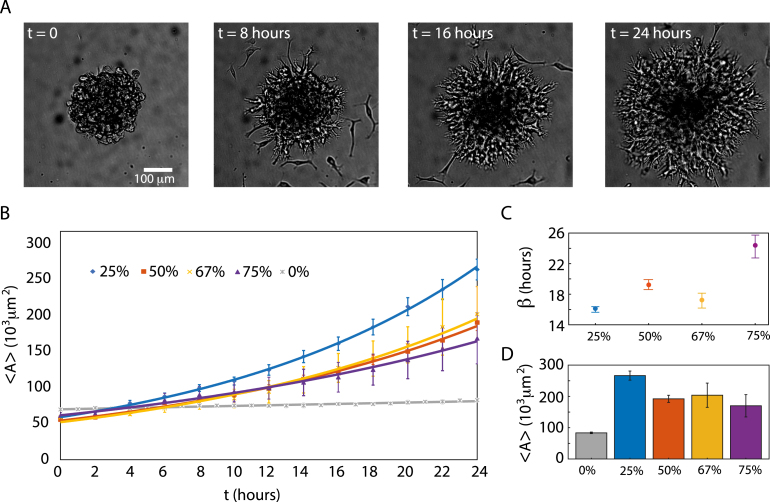
We cultured gravitation-assisted brain cancer spheroids by seeding U87-MG cells in 200 µL low-attachment U-formed wells. The spheroids were harvested after 4 days of incubation. At this point, they had an average diameter of µm (mean SD, ), an average aspect ratio of (mean SD, ), and a density of cells/µm3 [37]. To kick-start invasion, we interchanged growth medium with the ECM formulation Matrigel™ which consists of laminin, collagen IV, fibronectin, and various growth factors and, thus, mimics basement tissue membranes [38]. We used a range of concentrations of Matrigel™ in medium (v/v) from 25% to 75%, thus subjecting spheroids to various mechanical loads [39], [40] and imaged the spheroids for more than 24 h (maximum 31 h) with a frame rate of 1 every 5 min. All our data was obtained with simple wide-field microscopy, which limits sources of potential phototoxicity but complicates image segmentation. Examples of frames from the resulting time-lapse movies are shown in Fig. 1A for a spheroid in 50% ECM at time hours. Here it is obvious that there are two types of motility in play: (i) branch-like pattern of cells moving collectively through the ECM as well as (ii) individual cells leaving the spheroid body. These different motility modi are well-known [35], [41], [42] and correspond to invasion and migration, respectively.
Fig. 1.
Invasion of brain cancer cells in ECM. (A) Examples of migration/invasion of cells right after the transfer to ECM (50%) at time and then after 8 h, 16 h and 24 h, respectively. The star-shaped invasion pattern as well as individual migrating cells are clearly visible when . (B–C) Spheroid averaged invaded areas, , vs. for 25% (blue diamonds, ), 50% (red squares, ), 67% (yellow crosses, ), 75% (purple triangles, ), and 0% (gray asterisks, ). Error bars are one SEM and the full lines are exponential fit to the data with the growth exponents, , as in Eq. (1) and given in (C) together with 95% CI. (D) at hours, which corresponds to the last data points in (B) and error bars are one SEM.
2.1. Extracellular matrix stiffening slows down invasion
We measured the time-dependent average invaded cross sectional area, , as given by Eq. (3) and showed in Fig. 1B for various ECM concentrations ranging from 0% to 75% Matrigel™ concentration in medium (v/v). Here a concentration of 0% corresponds to growth in medium only (gray asterisks) with an average growth rate of 23 [21-26] µm/day (). Hence, we confirm that the cross sectional area of the tumor spheroid grows linearly with time in fresh culture medium [43], [44], [45]. In contrast, for the invading spheroids, we found an exponential dependence between cross-sectional area and with the characteristic growth exponent, ,
| (1) |
as shown in Fig. 1C. To the best of our knowledge, an exponential growth of the spheroids’ cross-sectional area in ECM has not been reported before. It should be noted, however, that our findings of such fast expansion and invasion of the brain cancer spheroids for the first 24 h after ECM addition are in agreement with previous reports of various cell lines invading type I collagen [46], [47]. The exponential exponent appears to correlate with ECM concentration, such that the higher the ECM concentration, the slower the spheroids invade. However, for 67% ECM, we detect an abrupt decrease in compared to the slightly lower and higher ECM concentrations of 50% and 75%.
However, for all cases of non-zero ECM concentration, the spheroids’ final average areas, , are significantly larger than the 8.4 µm2 spheroids in 0% ECM (gray bar) in Fig. 1D. This signifies that the resulting volume of an invading spheroid is larger than that of a non-invading – yet still proliferating – spheroid. The most pronounced difference is found for spheroids in 0% vs. 25% ECM () while further increases in ECM concentration slows down invasion. For instance, for spheroids in 75% compared to 25% ECM, the invaded drops by 1/3. Nevertheless, stiffening of ECM does hinder invasion but does not give rise to a full arrest. While at slower pace, spheroids still invade and remodel the surrounding matrix. This is in accordance with findings for breast cancer cells in type I collagen [46], [48].
2.2. Tumor cells migrate individually
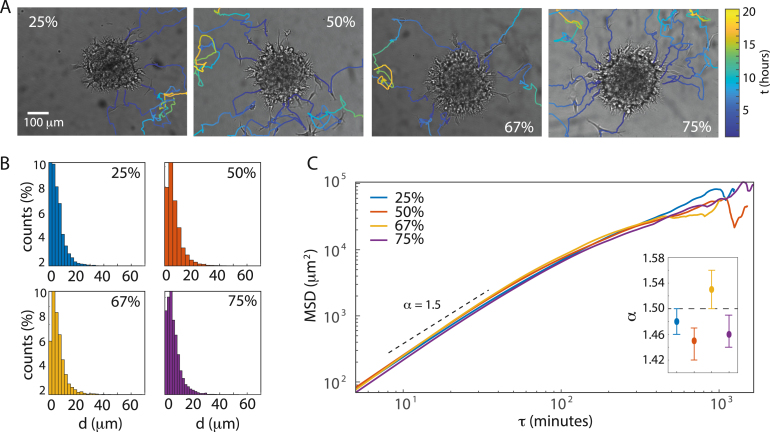
After analyzing the collective invasive motility of the investigated brain cancer tumor spheroids, we tracked the cells that succeeded in detaching from the spheroid or invading cell collections. We followed migration through the ECM for several hours over hundreds of microns and with an algorithm that tracked the center-of-mass of the cells, we distinguished translocation from membrane dynamics. With this large number of data points, even low-probability events are captured.
In Fig. 2A, still images of spheroids are overlaid with examples of cell trajectories (colored lines) for the various ECM concentrations. Cell trajectories are highly diffusive, but in contrast to the invading cell collections, the migrating cells seem indifferent to ECM density at a first glance. This indifference is confirmed by the distributions of displacements, , between two consecutive frames (5 min) as given by Eq. (5) and shown in Fig. 2B. Because of the heavy tails at longer , these bar plots cannot be described by a Gaussian distribution as we would expect for random walk models [23].
Fig. 2.
Cancer cell migration in various ECM concentrations. (A) Examples of migrating cells’ trajectories from spheroids in various ECM concentrations. The color bar converts color to time, . (B) The distributions of displacements or steps, , as given in Eq. (5). (C) MSDs vs. the time delay, , for ECM concentrations of 25% (), 50% (), 67% (), and 75% (). The first 25% of each MSDs were fitted to Eq. (2) to obtain the anomalous exponents, , which are given in the inset where error bars corresponds to 95% CI. As a guide to the eye, a dashed line with has been inserted.
2.2.1. Super-diffusive migration
To further rectify this, we found the ensemble-averaged mean-squared displacement (MSD) as calculated in Eq. (6) and shown for the cell ensembles in 25% (blue), 50% (red), 67% (yellow), and 75% (purple) ECM concentrations in Fig. 2C. For completeness, mean-squared displacements of the individual cell trajectories for all ECM concentrations can be found in Supplementary figure S1.
The MSDs show anomalous diffusion of the migrating cells characterized by a power law dependence of the time delay, :
| (2) |
where is the corresponding anomalous exponent. For normal diffusive motion . In contrast, anomalous diffusion is either sub-diffusive (), super-diffusive () or ballistic (). As for all concentrations (inset of Fig. 2C), the migrating cells are super-diffusing which is a sign of active motility and in agreement with prior findings e.g. [49], [50]. Thus, the investigated cells appear to overcome the steric hindrances, i.e. the added strength of the physical barrier from increased protein density and decreased pore sizes, imposed by the increasing concentration of ECM. This is very different from what has been found for lung and bladder cells in collagen [51], [52], where concentration increases in collagen caused the cell motility to drop from super- to sub-diffusive motion.
Moreover, the MSDs are almost indistinguishable up until 200 min. For the exponent of spheroids growing in 25%, 50%, and 75% ECM, the 95% CI’s overlap, meaning that the anomalous coefficients are indistinguishable (inset of Fig. 2C). In contrast, the 67% is significantly larger than for the other ECM concentrations, hence, cells migrate even more super-diffusively with this mechanical load and level of growth factors etc. Therefore, evolves non-linearly with ECM concentration. For even longer lag times, min, the MSDs exhibit erratic and erroneous behavior due to sparse data.
2.2.2. Migration speeds are independent of extra-cellular matrix stiffness
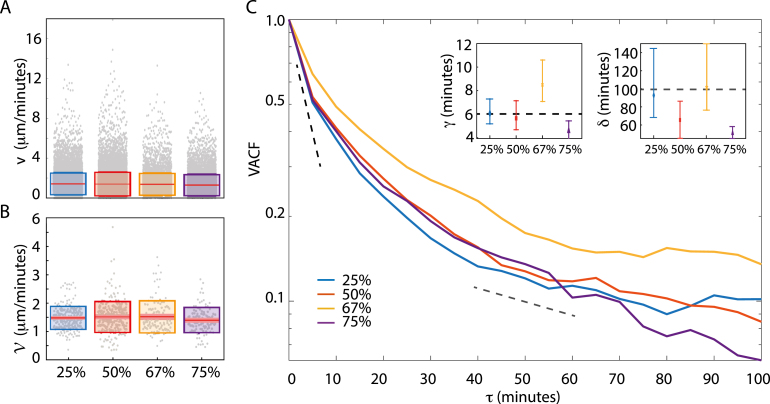
We then investigated how modulating matrix stiffness affects the instantaneous speeds, , of the individual steps along the migration trajectories; as given in Eq. (8). Box plots of the distributions of for the various ECM concentrations are given in Fig. 3A. From these results we concluded that the increased ECM stiffness has no considerable effect on for the migrating brain cancer cells. As is linearly proportional to the displacements, , we find the same heavy-tailed distributions as in Fig. 2B, which signifies that cells most often migrate in small steps but once in a while in large leaps. Similar bursts of motion have been observed before [53], [54] and, hence, both the frequency and the amplitude contribute to the overall migration speed of the cells.
Fig. 3.
Effect of matrix stiffness on instantaneous speeds. (A) Box plot of instantaneous velocities, , as defined in Eq. (8) for 25% (), 50% (), 67% (), and 75% () ECM, where the red line signifies the mean value, the pink box represents the 95% CI, and the edges of the colored boxes are one 1 SD. (B) Box plot of the average migration speed, , as defined in Eq. (9) for 25% (), 50% (), 67% (), and 75% () ECM. Again, the distributions are indistinguishable despite the increasing stiffness of the matrix. As in (A) the red line is the mean value, the pink box represents the 95% CI, and the edges of the colored boxes are one 1 SD. (C) Velocity auto-correlation functions, VACF, as defined in Eq. (10) for all ECM concentrations on a semi-log scale: 25% (), 50% (), 67% (), and 75% (). Each VACF were fitted to a double exponential to obtain the characteristic decay times and for fast and slow decay, respectively. Insets show and , for all ECM concentrations, where error bars represent 95% CI. As a guide to the eye, a dashed black line corresponding to and a gray dashed line for has been inserted. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
We also looked into the distributions of the migration speeds, , i.e., the average speed over the contour length of the trajectory, as defined in Eq. (9) and box plots of the distributions are shown in Fig. 3B. In contrast to the instantaneous speeds, the migration speeds are normally distributed with the following mean values: µm/min (mean SD, ), µm/min (), µm/min (), and µm/min () in the ECM concentration range from 25% to 75%, respectively. Thus, as verified by a Student’s -test there are no significant differences between the speed distributions. Hence, the increased ECM concentrations cause no reductions of neither nor , indicating a mechanism that allows for overcoming the increased tension of the surrounding matrix. As increasing ECM concentration does not only augment stiffness but also adhesion ligand density and decreases matrix porosity, the migration speed of cells in 3D ECMs is a result of the balance between stiffness, ligand density, proteolysis of the matrix and steric hindrances [39]. For instance, in response to increasing ECM concentration pancreatic cancer has been shown to upregulate the activity of matrix metalloproteinases [55], which are enzymes known to amplify cancer cell migration [56]. Our results are in favor of a similar behavior where migrating brain cancer cells boost their proteolytic activity to overcome the effects of increased matrix rigidity and cell–ECM adhesion as well as reduced pore sizes.
2.2.3. Velocity auto-correlation is a double exponential
To further investigate the nature of the motility, we found the velocity auto-correlation function (VACF) from Eq. (10) as presented in Fig. 3C. In general, the mean VACF is – strictly speaking – positive for all ECM concentrations, even at longer time scales. This behavior is consistent with a super-diffusive regime of motion where cells actively project forward in a direction dependent on the previous step. Ergo, the direction of motion is conserved in most cases. Although the correlation decays with time, the cells do not forget in which direction they were heading, i.e., for lag times of min, velocities stay correlated. This memory effect is most pronounced for spheroids in 67% ECM and the least for those in 75% ECM which indicates that the increased matrix stiffness weakens the cells’ ability to keep a consistent direction of motion.
Mammalian cells’ motility has been studied for decades and most classic models are based on the Langevin equation and paths are described as Ornstein–Uhlenbeck processes of the persistent random walk (PRW). Here the MSD depends on diffusion, dimensionality, and the so-called persistence time, , i.e. the time that the cell moves persistently in one direction [57], as given in Eq. (12). This model has been found to describe motions of e.g. fibroblasts [18], [19], lung epithelial cells [58], and neutrophils [59]. The Ornstein–Uhlenbeck process from Eq. (12) predicts a fast exponential relaxation [17]. In contrast, we found a slower decrease of the VACF for long . The decays of the experimentally observed VACFs are, therefore, characterized by two characteristic relaxation times, and , shown in the insets of Fig. 3C. As expected from the fast decay of 75% ECM (purple line), the is in this case significantly smaller than for 25% and 67% ECM. Such density-dependent decay suggests that augmented ECM density dampens cell motility. Similar double-exponential decay has been found previously in e.g. human fibrosarcoma cell migration in 2D and 3D [26], and in 2D migration of amoebas [49] as well as normal human dermal fibroblasts and human keratinocytes [22], while a gradual transition from exponential to power-law decay was found in mammalian kidney cells [23].
2.2.4. Cells migrate both with directionality and persistence
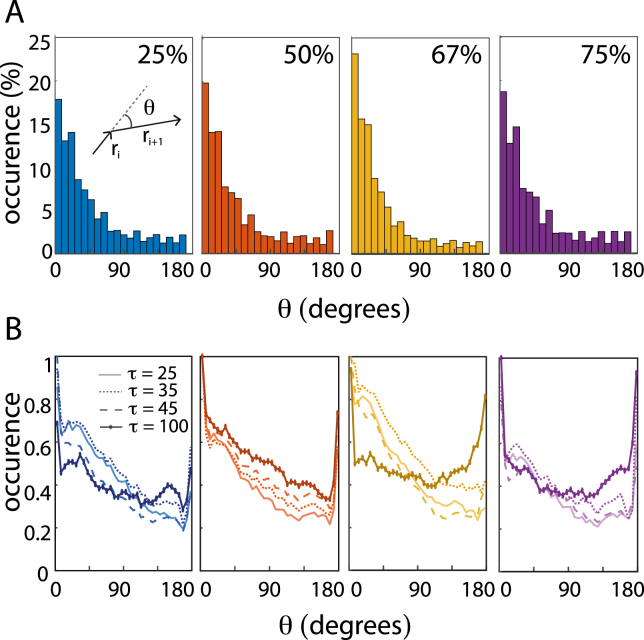
To further investigate the directionality revealed from the VACFs, we studied the angular change between successive steps, , as defined in Eq. (11). For a randomly walking cell, we would expect a flat distribution of values, as the cell orients randomly in all directions. However, Fig. 4A shows that the distributions are skewed towards small angles ( min). Therefore, the migrating brain cancer cells exhibit high directional persistence in all ECM concentrations. Fig. 4B shows the distribution of s for s in the range from 25 to 100 min. The high occurrence of small angles does not flatten with time, even at min. Instead, the motile cells show persistence, which goes directly against the predictions of the PRW model. Furthermore, the probability of observing large angles between two steps increases with increasing time lag. This is indicative of the tendency of the migrating cells to do ° turns and backtrack; a behavior that is more pronounced in the higher ECM concentrations (67% and 75%), which is in accordance with other observations [26], [60], [61]. A possible explanation for this is that cells – due to high adhesion and small ECM pore sizes – turn around and follow the beaten micro-tracks in the ECM back towards the spheroid. This asymmetric motility is described by the anisotropic persistence random walk (APRW) model, which encompasses both the high degree of heterogeneity between cells and the anisotropic movements [61].
Fig. 4.
Directionality in increased ECM stiffness. (A) Distributions of angles, , between two consecutive ( min) steps, and , as illustrated in the inset and defined by Eq. (11). The distributions for 25% (), 50% (), 67% (), and 75% () ECM all show that the majority of s fall within °. (B) Angle distributions, , for different time delays, , from 25 to 100 min, see legend. As the counts vary for different ’s, occurrences were normalized with respect to the counts for .
2.2.5. Identifying super-spreaders
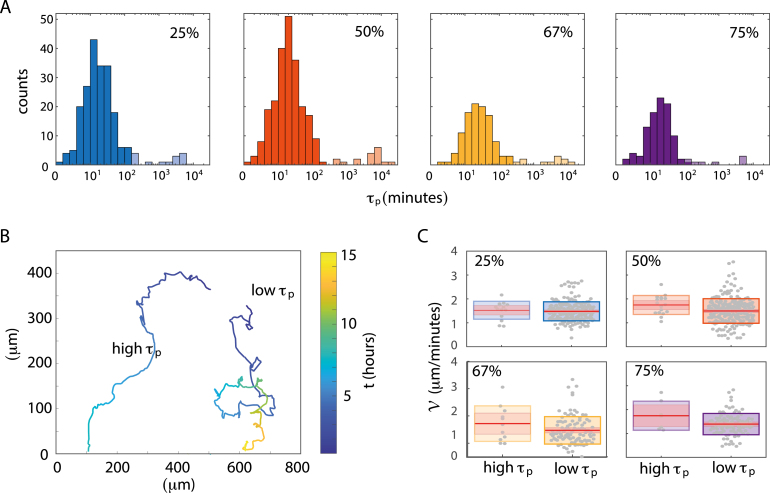
Based on these indications, we followed the train of thoughts of Wu et al. [61] to fit the MSDs of individual migrating cells along their trajectory eigenvectors, primary () and non-primary (), with the APRW model from Eq. (14). For each of the migrating cells’ trajectories, this model estimates the persistence time, , along the primary axis of migration, . The distributions of shown in Fig. 5A signify stochastic spreading dynamics with long ranged displacements [62]. It has previously been reported that metastatic cancer cells do not only move in a super-diffusive fashion, but also display movement patterns consistent with Lévy walks [15], [50]. We, thus, considered both power law (Lévy), exponential (Brownian) as well as log-normal models, which have been found to fit the motion of T-cells within lymph nodes [63]. We found that followed a log-normal distribution for all investigated ECM concentrations. Even more surprising is the revelation of two distinct populations. Using -means clustering we identified populations that are log-normal distributed around a lower (lighter color) and another with higher (full color). These two distinct log-normal distributions are characterized by their mean values and the SD of log(). Hence, we find the mean to be the exponential of the log-normal mean and the so-called multiplicative-SD relates to the SD as . Based on this, we find for the low populations (full color) average values of (15.7 ) min (mean , ), (18.32.7) min (), (23.92.4) min (), (17.72.2) min () for ECM concentrations of 25%, 50%, 67% and 75%, respectively. All means of for these populations are around a quarter of an hour. In contrast, for the populations with higher (light color), we find averages of (1,3293.9) min (), (4,1912.9) min (), (2,8423.3) min (), and (7122.2) min () for ECM concentrations of 25%, 50%, 67% and 75%, respectively. Hence, these cells spread faster with long ; actually much longer than the total observation time (2,000 min). Therefore, we termed this population of highly persistent cells super-spreaders.
Fig. 5.
Identifying a distinct subpopulation of super-spreaders. (A) Log-normal distributions of persistence times, , for the various ECM concentrations. Using -means clustering, we identified two distinct populations; one that is log-normal distributed around a lower (full color) and one around a higher (lighter color). (B) Example trajectories from the majority population with low and the minority population with high . Both examples are drawn from 75% ECM concentration and the color bar provides the conversion from color to time, . (C) Box plot of the average migration speed, , from Fig. 3B redistributed with respect to high (lighter color) vs. low (full color) for all investigated ECM concentrations: 25% (, ) for (high, low), 50% (, ), 67% (, ), and 75% (, ). The red line signifies the mean value, the pink box represents the 95% CI, and the edges of the colored boxes are one 1 SD. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
An example trajectory drawn from the majority population of migrating cancer cells is given in Fig. 5B together with an example of a super-spreader cell’s trajectory. For completeness, we redistributed all tracks on the basis of high and low (Supplementary figure S2). It is obvious from these traces that the super-spreading cells very seldom stay within the field of view more than 10 h after detachment from the spheroid body. As expected, this higher persistence of the super-spreaders is also reflected in the angle distributions. This is apparent from the sub-population medians which become significantly different for all tested ECM concentrations between 25% to 67% when evaluated with a Wilcoxon rank-sum test (). For 25% ECM the median is 23° and 33° for high and low , respectively. Likewise for 50%, we found 18° vs. 30° and for 67% 15° vs. 26°. In contrast, for 75% ECM we found a less significant difference between the median s, 27° vs. 32° (), suggesting that the super-spreader motions are damped at very high ECM concentrations.
Following the surprising revelation of super-spreaders, we investigated whether this minority population was only characterized by more persistence overcoming the diffusive motion, or whether cells also moved faster along their path. Hence, we re-distributed the migration speeds, , as shown in Fig. 5C. However, the slight differences we found in average migration speeds, , were non-significant (). This is also apparent from -means clustering of the versus scatter plots in Supplementary figure S3. So in conclusion, super-spreaders do not move faster — but more persistently.
3. Discussion
Spheroids are known to be very heterogeneous with an outer proliferating zone, an intermediate quiescent region with limited oxygen, nutrients, and metabolites [64], [65] as well as a necrotic core [35]; similar to solid in vivo tumors. Furthermore, when suspended in growth medium spheroids grow from the outer proliferating zone. However, the growth cannot be described by a logistic model, rather rates depend on population size [66], [67], [68], [69]. When moved from serum-containing growth medium to ECM, our brain cancer spheroids invaded the surrounding matrix by long finger-like protrusions. This is a sign of collective migratory behavior where multicellular groups infiltrate the ECM through gained motility and retained cell–cell adhesion [70]. These findings are paralleling earlier findings for similar spheroids (U87-MG) [35], [47] as well as for other glioblastoma spheroids (KNS42) [35], glioma spheroids (U-251-MG) [71], and breast carcinoma spheroids [35], [72]. This infiltrative nature makes it impossible to eliminate all cells in a host by surgery, thus leading to tumor recurrence.
From the acquired time-lapse sequences of invading spheroids, we found that the cross sectional area of the invading spheroid grows exponentially with time with no slowing of the growth rate within 24 h. Nevertheless, a gradual augmentation of the ECM (Matrigel™ ) concentration slows down invasion. Thus, the collective motility of cells in the finger-like protrusions responds to the polymer concentration in the matrix. However, increased ECM concentration will necessarily also increase the concentration of individual ECM components such as growth factors (IGF, EGF, PDGF etc.) which activate and sustain cancer proliferation and growth [73], [74]. Naively, one could therefore think that increased Matrigel™ concentration would augment the invasive capabilities of the spheroid. However, this augmentation is only observed when comparing ECM-embedded spheroids to spheroids in growth medium alone (0% ECM). In contrast, increasing the ECM concentration from 25% to 75% decreased spheroid invasion. One possible explanation is mechanosensing as several studies have shown that increased matrix stiffness triggers mechanosensitive transcriptional activators such as YAP and TAZ, which in turn activate e.g. proliferation, differentiation and metastasis in the tumor [75], [76], [77], [78]. However, increased matrix stiffness is accompanied by a decrease in matrix porosity which limits the ability of cell collections to move through the matrix [11]. Like so many other functions in the tumor [79], these mechanical cues might also be conveyed through YAP/TAZ and favor the full transformation into individual migrating cells rather than invasive cell collections. Consequently, the mechanical stiffness of the tumor microenvironment not only triggers spheroid invasion, but also regulates it effectively through mechanical feedback [80].
We further detected how individual cells detached from the spheroid – or the neighboring cells in the protrusion – to start individual migration through the ECM. This is indicative of a complete epithelial to mesenchymal transition, EMT, of the cells associated with weakening of the intercellular adhesion, loss of polarity, and increased motility [81], [82]. The cells were observed to first extend their pseudopodia, then displace the cell body followed by parallel retraction of pseudopodia. This behavior has been observed before in migrating glioblastoma cells [54] and in the highly invasive human breast carcinoma cells (MDA-MB-231) [53]. Particularly, bursts of speed were pronounced when cells escaped from areas crowded by non-transformed breast epithelium cells (MCF10 A). Moreover it was suggested that such fast movements contribute to the overall migration speed of each cell and they are the reason for their effective migration [54].
Surprisingly, we found that glioblastoma cells exhibit similar migratory behaviors in all tested ECM concentrations. In contrast, if mechanosensing causes a shift from invasion towards migration as hypothesized above, we would expect an increase in the overall migration speeds or diffusion constants with ECM concentration. The notion that increased stiffness increases cancer cell migration due to YAP/TAZ activation supports this argument. However, Matrigel™ has been found to play a dual role: While the presence of Matrigel™ in collagen gels promoted migration of lung cancer cells (H1299) at low concentration, it hindered migration at higher concentrations, probably due to increased adhesion-ligand concentration [11] and increased elastic modulus [40]. Thus, our hypothesis – that increased ECM concentration favors increased single cell migration – might be counteracted by increased adhesion-ligand concentration and result in no apparent ECM concentration dependence [60]. Moreover, earlier studies suggest that proteolysis serves as an important additional mechanism for migration of cancer cells, allowing them to move through the matrix — no matter how dense it is [39], [56], [83]. Further, it has been established that during collective cell invasion, the leading edge cells carve paths for the remaining cells by proteolytic remodeling of the ECM [84], [85]. For example for fibrosarcoma cells (HT-1080) invading 3D collagen, leader cells utilize proteolysis by a membrane-bound collagenase (MT1-MMP) to generate tracks [86]. Our detection of two different migrating populations is indicative of a similar leader/follower relationship for migrating cells: leader cells that proteolytically generate paths for subsequent cells to follow. However, we could not detect such a relationship between super spreaders and other migrating cells.
Additionally, tumor cells can switch between mesenchymal and amoeboid migration modes and thereby increase invasive capabilities [87]. Amoeboid migration is characterized by e.g. fast speeds and high levels of actomyosin contractility [88] and have also been reported for U87-MG in 3D hydrogels [89]. To decide whether the super spreading population found in this study is amoeboid will demand further investigations, e.g., of membrane flows [90].
Further, it has been shown that collagenase activity in pancreatic cancer cells (Panc-1) increases with matrix stiffness [55]. This indicates that the cells have mechanosensing abilities that cause them to increase proteolytic activity in order to overcome increased matrix stiffness, thus apparently rendering migration of U87-MG glioblastoma cells ECM-concentration independent. Nevertheless, we did observe slight concentration dependencies, such as decreased VACF decay times and increased probability of backtracking at long time scales in high ECM concentrations.
Any Brownian random walk model of cell migration would predict a uniform distribution of turning angles between successive steps, while the PRW model predicts a peaked distribution that flattens for time lags longer than the persistence time. In contrast to both these random walk models, we found that the probability of complete 180° turnarounds in the 3D matrix increased with time. This result indicates that the probability of observing cells backtracking through the tunnels – formed by the cells during their initial exploration – increases at longer time scales. Given such anisotropic persistence, we fitted our results to the APRW model and extracted the according persistence time distributions for the primary directions of migration. We found long-range displacement dynamics interspersed between long periods of short-range steps, which is characteristic of Lévy walks. Furthermore, a recent study proved that the motion of metastatic cancer cell lines performed Lévy walks, while their non-metastatic counterparts did not [50]. As Lévy walks also have uniformly distributed turning angles, the arguments for describing the motion of migrating glioblastoma cells as a Lévy walk were, hence, very compelling. However, our persistence time distributions did not follow a power-law. Instead we – unexpectedly – found the persistence time distributions to be log-normal and bimodal. This is suggestive of the existence of two subpopulations of which one is a population of super-spreaders with boosted persistence. Such contradictory observations have been done previously, e.g., for immune T-cell motion, which has been identified as either log-normal [63] or a Lévy walk [91] depending on the tissue they migrated in. Moreover, evidence that individual persistent random walkers exhibit Lévy walk movement patterns at the ensemble level has been published in the case of single bacteria vs. swarms [92], [93]. Evidently, the distinction between variants of PRWs and Lévy walks warrants further investigation [94], [95].
Glioblastoma is a particular fast-spreading form of brain cancer [96], due to its high plasticity, heterogeneity and therapy resistance [97]. Understanding metastasis and migration in these malignant cells is a critical step towards better prognoses. As the focus of this study is to compare uniform spheroids under different conditions, we used an immortalized human tumor-derived cell line. However, often long-term cultivation of tumor cell lines results in loss of genetic heterogeneity of the original tumor. In particular, the cell line used in this study (U87-MG) was recently found to be genetically different from its tumor of origin [98]. Therefore to extend the validity, a follow-up study should include the use of spheroids that are either derived from human glioma xenografts [99] or built as multi-cell type glioma spheroids [100].
In summary, we analyzed cell migration from glioblastoma spheroids embedded in varying concentrations of ECM-like Matrigel™. While collective migration was partially inhibited by high-density gels, single cell migration was not. However, migration of single cells did become more anisotropic with increasing ECM density. Modeling the migration as an APRW, we identified a subpopulation of super-spreading cells with extraordinary directional persistence. Development of a model that captures all the behaviors we have observed – namely double-exponential decay of the VACF, highly directional and persistent migration, anisotropic behavior at high ECM density and the existence of super-spreading cells – would allow prediction of the motility mode of the migrating cells further from the spheroid. This would be an important step en route to a unifying model of cancer metastasis. Moreover, although the concept of intra-tumoral heterogeneity has been established years ago, it is still an area of research that receives much attention. Our work presents yet another aspect of between-cell tumor heterogeneity with high clinical relevance since targeting the population of super-spreading cells would be the most efficient methodology for prevention of metastasis and relapse after surgery. Future studies will have to uncover whether our observations represent actual differences between cells within the tumor spheroids or whether they arise in response to different local environments.
4. Materials and methods
4.1. Cell culture
The glioblastoma multiforme cell line U87-MG was cultured under standard conditions (37 °C, 5% CO2, 95% humidity) in Dulbecco’s Modified Eagle Medium (DMEM) supplemented with 10% Fetal Bovine Serum (FBS) and 1% penicillin–streptomycin; all provided from Gibco (Gibco, Life Technologies Ltd. Paysley, UK).
4.1.1. Gravitation-assisted tumor spheroid formation
For the formation of spheroids, 650 cells (3250 cells/mL) were seeded in ultra-low attachment round-bottomed 96-well plates (Corning B.V. Life Sciences, Amsterdam, The Netherlands) with 200 µL DMEM and incubated for 4 days [37].
4.1.2. Spheroid invasion/migration
Our invasion assay was based on classic protocols described by Vinci et al. [35] and Richards et al. [101]. Matrigel™ (Corning B.V. Life Sciences, Amsterdam, Netherlands) was thawed on ice overnight at 4 °C. On the day of experimentation, the round-bottomed well plates with fully-formed spheroids were placed on ice to avoid untimely Matrigel™ solidification. For experimentation, we varied the concentration of Matrigel™ in medium (v/v) between 0%, 25%, 50%, 67%, and 75%. For this aim, medium was removed from the wells and replaced with ice-cold Matrigel™ (using pipette tips kept at °C) to the desired final concentration. When interchanging medium with Matrigel™ we took care to keep the spheroids centered in the bottom of the well and to remove all bubbles. Afterwards, plates were incubated for 1 h for solidification of the Matrigel™ and lastly 100 µL DMEM was added on top of each well to a final volume of 300 µL.
4.2. Time-lapse imaging
96-well plates were mounted on an inverted Juli Stage Real-Time cell history recorder (NanoEntek, Guro-gu, Seoul, Korea) with bright-field (10 objective) placed inside a cell incubator (37 °C, 5% CO2, 95% humidity). The focus of the microscope was set manually for each well and we used the built-in software to acquire time-lapses with a frame rate of 1 every 5 min, exposure time of 170 ms, and field of view of approximately (640) µm2 with a resolution of 440 nm/pixel. For 24 or 31 h of imaging, 50 µL of DMEM was added to the wells during experimentation to prevent dehydration of wells. Please, note that our imaging modality results in a 2D approximation of the 3D migration as discussed in detail by Wu et al. [26].
4.3. Image analysis
4.3.1. Spheroid invasion
To quantify spheroid invasion we used the Fiji - ImageJ [102] macro tool Analyze Spheroid Cell Invasion In 3D Matrix to obtain the projected area of the main spheroid body [103]. From the resulting cross sectional area, , we found the average area of all spheroids to be:
| (3) |
where is the area of the th tumor spheroid at time and is the total number of spheroids.
4.3.2. Image pre-processing
We used the open-source software ilastik, which enables automated – albeit supervised by the user – segmentation of spheroids and individual cells [36]. For training of the algorithm, we used a representative stack of 50 consecutive images from 0 to 250 min to minimize computation time. Please note that some manual track-editing was needed for our data because of over-segmentation, i.e., one cell is detected as two, and under-segmentation (vice versa). We also had to remove data points from objects (of size similar to cells) that mistakenly had been detected as cells. All these errors were filtered manually to ensure meaningful results.
4.3.3. Single cell migration
For automated single particle tracking we used the TrackMate plugin for Fiji - ImageJ, which consists of a spot detection followed by a particle tracking procedure. Since our cells expand over a rather large area in the segmented image (20 pixels 9 µm), we used the Downsample LoG detector [104] with the down sample factor set to 4, the estimated blob diameter to 50 µm, and a cell/background threshold value of 1 appropriate for our binary images. With these settings, the spot detection algorithm detected all centers of mass of migrating cells as well as cells on the spheroid surface. Once spot detection is completed, cells were tracked in every frame of the image stack using the The Simple Linear Assignment Problem algorithm since – upon visual inspection of the images – mitosis events were rare within our time frame. For post-processing, we used the TrackScheme module to edit the cell trajectories and we ended a track in the following cases: (i) if a cell moved out of the field of view (even if it returned later), (ii) if part of the cell left the field of view for more than 15 min, (iii) if cells never really detached from the spheroid before returning, (iv) after cell division [105].
4.4. Data analysis
4.4.1. Displacement analysis
An ensemble of particles undergoing Brownian motion is distributed as [106]:
| (4) |
where is the diffusion coefficient and is the time step. In the th cell trajectory we define a position vector in the projected plane as: . The length of the vector is the displacement, :
| (5) |
4.4.2. Mean squared displacement analysis
The mean squared displacement (MSD) describes the displacement of cells by determining the ensemble-averaged distance that the ensemble of cells move in a given time interval, , which is designated as the lag or delay time [107]:
| (6) |
where is the total number of trajectories for all measured spheroids, vector is the starting position of the th cell trajectory, and vector is the position of the th cell after time lag .
The MSD of a random walk, i.e., normal diffusion, of cells in 3D scales linearly with time:
| (7) |
4.4.3. Instantaneous speed distributions and migration speed
We defined the instantaneous speed, , at the th step of a cell as the displacement in the projected , -plane per time step:
| (8) |
and the migration speed of a cell, , as the mean over the entire contour length of the trajectory from to the total number of steps, :
| (9) |
4.4.4. Motion persistence and directionality
We also investigated the velocity auto-correlation function (VACF) of the ensemble average of cell trajectories which is:
| (10) |
where the velocity at time is of the th cell trajectory and the initial velocity is . In general, the VACF diminishes with increased , as the cells’ velocities become uncorrelated due to interactions with the surrounding environment. Furthermore, the angle between the position vectors between two successive steps and fulfill the relation:
| (11) |
4.4.5. The Ornstein–Uhlenbeck process
The Ornstein–Uhlenbeck process describes a random walk model but with an added persistence (PRW) [22]. This model of cell motility is derived from a stochastic differential equation describing the motion of a self-propelled cell. By introducing persistence, the MSD in 3D as given in Eq. (7) for a simple random walk is described by Fürth’s formula [24]:
| (12) |
where is the persistence time of the motion, i.e., the time for which a certain velocity is retained by the system [17]. Therefore, is the time before a cell changes direction. Eq. (12) can be rewritten as:
| (13) |
if we assume an exponential distribution of persistence times [108]. Furthermore, the Ornstein–Uhlenbeck velocity auto-correlation function, VACF, which can be derived by differentiating equation (12), is predicted to be a single-exponential decay.
4.4.6. Anisotropic persistent random walk model
We have adopted the anisotropic persistent random walk model (APRW) for the migration of cells in a 3D matrix [26], [61]. In the APRW, the velocity of the migrating cells is assumed to be spatially anisotropic and display different persistence times on two orthogonal axes, namely the primary migration axis and the non-primary migration axis; these are found through singular vector decomposition of cell velocities.
The migration of the cells in the APRW model is described by the same parameters as in the PRW model, the persistent time and cell speed , however they are different for each individual axis of motion. Therefore, for the primary axis they are denoted as () and for the non-primary they are (). The MSDs in the primary direction, , are given by:
| (14) |
and in the non-primary orthogonal direction :
| (15) |
where is the error in the position of the cell and the total MSD for each cell is given by:
| (16) |
4.5. Statistical analysis
When examining migration characteristics for different Matrigel™ concentrations, more than 100 cell trajectories originating from at least 4 different spheroids were evaluated for each condition (corresponding to >6,000 steps).
4.5.1. MSD curve fitting
For all MSD analysis of trajectories, the small time delays, ’s, are weighted more in the average MSD than longer delays. For example, if a trajectory has points, the delay, , that is equal to 1 time step will have points in the average, whereas the delay that corresponds to time units will have only 1 point in the average [109]. Therefore, the accuracy of the MSD becomes increasingly worse with as the variance depends on the number of trajectories available. Moreover, the curvature of the MSD is important when investigating whether there is active transport in the system under study. In the ensemble-averaged MSD, there are contributions from different kinds of motion which makes the curvature change over time thus increasing statistical uncertainty. Therefore, to limit the relative errors of the MSD, the plots should not be analyzed and fitted to any model further than 25% of the longest time lag. Furthermore, when fitting an MSD to a model, one should use proper weights, such as the inverse of the variance or standard deviation for each time lag, in order to give more weight to the parts of the MSD with the highest certainty [16], [110]. Both suggestions were adopted in this study.
From curve fitting of the various models to the MSD or VACF, the coefficients , , , and are obtained and given (in Figs. 1, 2, and 3) with error bars, which corresponds to the 95% confidence intervals (CI).
Furthermore, when analyzing MSD data, there are two possible approaches: (i) to truncate all trajectories to the same length (number of time steps) or (ii) to truncate all trajectories to the same distance from the spheroid (cut of by field of view). The advantage of the first approach is that there is no oversampling of the slow trajectories, which stay longer in the field of view. The strength of the second approach, is better statistics. For this analysis we used (ii) but we found that when using (i), the second populations of Fig. 5A grow substantially [111]. Specifically for the this analysis, we only registered the ’s for fits with the coefficient of determination .
4.5.2. Confidence and accuracy
Throughout the present study we state data as mean standard deviation (SD). However, for the investigation of spheroid invasion (Fig. 1) we presented the mean standard error of the mean (SEM) and for the persistence analysis (Fig. 5) we used the multiplicative standard deviation (SD); as detailed in the text.
For the box plots in Fig. 3, Fig. 5 the red line signifies the ensemble average, the pink box represents the 95% confidence interval (CI), and the edges of the colored boxes are one standard deviation (SD).
CRediT authorship contribution statement
Aimilia Nousi: Spheroid imaging and single-particle tracking. Maria Tangen Søgaard: Supportive experiments. Mélanie Audoin: Supportive data analysis. Liselotte Jauffred: Supervised the project.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
LJ acknowledges funding from the Danish National Research Council (DNRF116) Independent Research Fund Denmark (0165-00032B) and (0165-00103B). The authors thank Kristoffer Laugesen, Younes Farhangibarooji, Guillermo S. Moreno Pescador, Mads Kasper von Borries and Ioannis Koutsoukidis for fruitful discussions. All authors discussed the results and contributed to the final manuscript and all authors read and approved the final manuscript.
Footnotes
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.bbrep.2021.101120.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
The supplementary material includes 3 complimentary figures that provide additional information to the reader.
Data availability statements
All cell trajectories – as spatial coordinates and time – presented in this study are openly available in FigShare at doi:10.6084/m9.figshare.14229515.
References
- 1.Hanahan D., Weinberg R.A. Hallmarks of cancer: the next generation. Cell. 2011;144:646–674. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 2.Friedl P., Wolf K. Tumour-cell invasion and migration: Diversity and escape mechanisms. Nat. Rev. Cancer. 2003;3:362–374. doi: 10.1038/nrc1075. [DOI] [PubMed] [Google Scholar]
- 3.Friedl P., Sahai E., Weiss S., Yamada K.M. New dimensions in cell migration. Nature Rev. Mol. Cell Biol. 2012;13:743–747. doi: 10.1038/nrm3459. [DOI] [PubMed] [Google Scholar]
- 4.Anton D., Burckel H., Josset E., Noel G. Three-dimensional cell culture: A breakthrough in vivo. Int. J. Mol. Sci. 2015;16:5517–5527. doi: 10.3390/ijms16035517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Phung Y.T., Barbone D., Broaddus V.C., Ho M. Rapid generation of in vitro multicellular spheroids for the study of monoclonal antibody therapy. J. Cancer. 2011;2:507. doi: 10.7150/jca.2.507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yamada K.M., Cukierman E. Modeling tissue morphogenesis and cancer in 3D. Cell. 2007;130:601–610. doi: 10.1016/j.cell.2007.08.006. [DOI] [PubMed] [Google Scholar]
- 7.Nieto M.A., Huang R.Y.-J., Jackson R.A., Thiery J.P. EMT: 2016. Cell. 2016;166:21–45. doi: 10.1016/j.cell.2016.06.028. [DOI] [PubMed] [Google Scholar]
- 8.Correa de Sampaio P., Auslaender D., Krubasik D., Failla A.V., Skepper J.N., Murphy G., English W.R. A heterogeneous in vitro three dimensional model of tumour-stroma interactions regulating sprouting angiogenesis. PLoS One. 2012;7 doi: 10.1371/journal.pone.0030753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Smart C.E., Morrison B.J., Saunus J.M., Vargas A.C., Keith P., Reid L., Wockner L., Amiri M.A., Sarkar D., Simpson P.T., Clarke C., Schmidt C.W., Reynolds B.A., Lakhani S.R., Lopez J.A. In vitro analysis of breast cancer cell line tumourspheres and primary human breast epithelia mammospheres demonstrates inter- and intrasphere heterogeneity. PLoS One. 2013;8 doi: 10.1371/journal.pone.0064388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Goodman T.T., Olive P.L., Pun S.H. Increased nanoparticle penetration in collagenase-treated multicellular spheroids. Int. J. Nanomedicine. 2007;2:265–274. [PMC free article] [PubMed] [Google Scholar]
- 11.Anguiano M.M., Castilla C., Maška M., Ederra C., Peláez R., Morales X., Muñoz Arrieta G., Mujika M., Kozubek M., Muñoz Barrutia A., Rouzaut A., Arana S., Garcia-Aznar J.M., Ortiz-de Solorzano C. Characterization of three-dimensional cancer cell migration in mixed collagen-matrigel scaffolds using microfluidics and image analysis. PLoS One. 2017;12 doi: 10.1371/journal.pone.0171417. https://dx.plos.org/10.1371/journal.pone.0171417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huber M.A., Kraut N., Beug H. Molecular requirements for epithelial-mesenchymal transition during tumor progression. Curr. Opin. Cell Biol. 2005;17:548–558. doi: 10.1016/j.ceb.2005.08.001. [DOI] [PubMed] [Google Scholar]
- 13.Bidarra S.J., Oliveira P., Rocha S., Saraiva D.P., Oliveira C., Barrias C.C. A 3D in vitro model to explore the inter-conversion between epithelial and mesenchymal states during EMT and its reversion. Sci. Rep. 2016;6:1–14. doi: 10.1038/srep27072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jolly M.K., Tripathi S.C., Jia D., Mooney S.M., Celiktas M., Hanash S.M., Mani S.A., Pienta K.J., Ben-Jacob E., Levine H. Stability of the hybrid epithelial/mesenchymal phenotype. Oncotarget. 2016;7:27067–27084. doi: 10.18632/oncotarget.8166. http://www.oncotarget.com/fulltext/8166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Codling E.A., Plank M.J., Benhamou S. Random walk models in biology. J. R. Soc. Interface. 2008;5:813–834. doi: 10.1098/rsif.2008.0014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Saxton M.J. In: Methods in Membrane Lipids. Dopico A.M., editor. Humana Press; Totowa, NJ: 2007. Modeling 2D and 3D diffusion; pp. 295–321. [Google Scholar]
- 17.Selmeczi D., Li L., Pedersen L.I., Nørrelykke S.F., Hagedorn P.H., Mosler S., Larsen N.B., Cox E.C., Flyvbjerg H. Cell motility as random motion: A review. Eur. Phys. J.: Spec. Top. 2008;157:1–15. [Google Scholar]
- 18.Dunn G.A., Brown A.F. A unified approach to analysing cell motility. J. Cell Sci. 1987;102:81–102. doi: 10.1242/jcs.1987.supplement_8.5. [DOI] [PubMed] [Google Scholar]
- 19.Gail M.H., Boone C.W. The locomotion of mouse fibroblasts in tissue culture. Biophys. J. 1970;10:980–993. doi: 10.1016/S0006-3495(70)86347-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Guisoni N., Mazzitello K.I., Diambra L. Modeling active cell movement with the potts model. Front. Phys. 2018;6 [Google Scholar]
- 21.Stokes C.L., Lauffenburger D.A., Williams S.K. Migration of individual microvessel endothelial cells: stochastic model and parameter measurement. J. Cell Sci. 1991;99:419–430. doi: 10.1242/jcs.99.2.419. [DOI] [PubMed] [Google Scholar]
- 22.Selmeczi D., Mosler S., Hagedorn P.H., Larsen N.B., Flyvbjerg H. Cell motility as persistent random motion: theories from experiments. Biophys. J. 2005;89:912–931. doi: 10.1529/biophysj.105.061150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dieterich P., Klages R., Preuss R., Schwab A. Anomalous dynamics of cell migration. Proc. Natl. Acad. Sci. 2008;105:459–463. doi: 10.1073/pnas.0707603105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Campos D., Méndez V., Llopis I. Persistent random motion: Uncovering cell migration dynamics. J. Theoret. Biol. 2010;267:526–534. doi: 10.1016/j.jtbi.2010.09.022. [DOI] [PubMed] [Google Scholar]
- 25.Upadhyaya A., Rieu J.-P., Glazier J.A., Sawada Y. Anomalous diffusion and non-Gaussian velocity distribution of Hydra cells in cellular aggregates. Physica A. 2001;293:549–558. [Google Scholar]
- 26.Wu P.-H., Giri A., Sun S.X., Wirtz D. Three-dimensional cell migration does not follow a random walk. Proc. Natl. Acad. Sci. 2014;111:3949–3954. doi: 10.1073/pnas.1318967111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chignola R., Schenetti A., Andrighetto G., Chiesa E., Foroni R., Sartoris S., Tridente G., Liberati D. Forecasting the growth of multicell tumour spheroids: Implications for the dynamic growth of solid tumours. Cell Prolif. 2000;33:219–229. doi: 10.1046/j.1365-2184.2000.00174.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Aubert M., Badoual M., Féreol S., Christov C., Grammaticos B. A cellular automaton model for the migration of glioma cells. Phys. Biol. 2006;3:93–100. doi: 10.1088/1478-3975/3/2/001. [DOI] [PubMed] [Google Scholar]
- 29.Stein A.M., Vader D.A., Sander L.M., Weitz D.A. In: Mathematical Modeling of Biological Systems, Volume I: Cellular Biophysics, Regulatory Networks, Development, Biomedicine, and Data Analysis. Deutsch A., Brusch L., Byrne H., de Vries G., Herzel H., editors. Birkhäuser Boston; Boston, MA: 2007. A stochastic model of glioblastoma invasion; pp. 217–224. (Chapter 19) [Google Scholar]
- 30.Khain E., Sander L.M., Stein A.M. A model for glioma growth. Complexity. 2005 [Google Scholar]
- 31.Stepien T.L., Rutter E.M., Kuang Y. A data-motivated density-dependent diffusion model of in vitro glioblastoma growth. Math. Biosci. Eng. 2015 doi: 10.3934/mbe.2015.12.1157. [DOI] [PubMed] [Google Scholar]
- 32.Rutter E.M. Arizona State University; 2016. A Mathematical Journey of Cancer Growth. (Ph.D. thesis) https://repository.asu.edu/items/40193. [Google Scholar]
- 33.Martirosyan N.L., Rutter E.M., Ramey W.L., Kostelich E.J., Kuang Y., Preul M.C. Mathematically modeling the biological properties of gliomas: A review. Math. Biosci. Eng. 2015;12:879–905. doi: 10.3934/mbe.2015.12.879. [DOI] [PubMed] [Google Scholar]
- 34.Arcangeli C., Lico C., Baschieri S., Mancuso M. Characterization of blood–brain barrier crossing and tumor homing peptides by molecular dynamics simulations. Int. J. Nanomedicine. 2019;14:10123–10136. doi: 10.2147/IJN.S225793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vinci M., Gowan S., Boxall F., Patterson L., Zimmermann M., Court W., Lomas C., Mendiola M., Hardisson D., Eccles S.A. Advances in establishment and analysis of three-dimensional tumor spheroid-based functional assays for target validation and drug evaluation. BMC Biol. 2012;10:29. doi: 10.1186/1741-7007-10-29. http://bmcbiol.biomedcentral.com/articles/10.1186/1741-7007-10-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.C. Sommer, C. Straehle, U. Köthe, F.A. Hamprecht, U. Kothe, F.A. Hamprecht, Ilastik: Interactive learning and segmentation toolkit, in: Proceedings - International Symposium on Biomedical Imaging, 2011, pp. 230–233.
- 37.Niora M., Pedersbæk D., Münter R., Weywadt M.F.d.V., Farhangibarooji Y., Andresen T.L., Simonsen J.B., Jauffred L. Head-to-head comparison of the penetration efficiency of lipid-based nanoparticles into tumor spheroids. ACS Omega. 2020;5:21162–21171. doi: 10.1021/acsomega.0c02879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Engbring J.A., Kleinman H.K. The basement membrane matrix in malignancy. J. Pathol. 2003;200:465–470. doi: 10.1002/path.1396. [DOI] [PubMed] [Google Scholar]
- 39.Zaman M.H., Trapani A.L., MacKellar D., Gong H., Kamm R.D., Wells A., Lauffenburger D.A., Matsudaira P. Migration of tumor cells in 3D matrices is governed by matrix stiffness along with cell–matrix adhesion and proteolysis. Proc. Natl. Acad. Sci. 2006;103:10889–10894. doi: 10.1073/pnas.0604460103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Borries M., Barooji Y.F., Yennek S., Grapin-Botton A., Berg-Sørensen K., Oddershede L.B. Quantification of visco-elastic properties of a matrigel for organoid development as a function of polymer concentration. Front. Phys. 2020;8:1–9. [Google Scholar]
- 41.Berens E.B., Holy J.M., Riegel A.T., Wellstein A. A cancer cell spheroid assay to assess invasion in a 3D setting. JoVE J. Vis. Exp. 2015 doi: 10.3791/53409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Motaln H., Koren A., Gruden K., Ramšak Ž., Schichor C., Lah T.T. Heterogeneous glioblastoma cell cross-talk promotes phenotype alterations and enhanced drug resistance. Oncotarget. 2015;6 doi: 10.18632/oncotarget.5701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Blumlein A., Williams N., McManus J.J. The mechanical properties of individual cell spheroids. Sci. Rep. 2017;7:7346. doi: 10.1038/s41598-017-07813-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Thorsen F., Visted T., Lehtolainen P., Ylä-Herttuala S., Bjerkvig R. Release of replication-deficient retroviruses from a packaging cell line: Interaction with glioma tumor spheroids in vitro. Int. J. Cancer. 1997;71:874–880. doi: 10.1002/(sici)1097-0215(19970529)71:5<874::aid-ijc28>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- 45.Amaral R.L.F., Miranda M., Marcato P.D., Swiech K. Comparative analysis of 3D bladder tumor spheroids obtained by forced floating and hanging drop methods for drug screening. Front. Phys. 2017;8:605. doi: 10.3389/fphys.2017.00605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kuo C.-T., Wang J.-Y., Lin Y.-F., Wo A.M., Chen B.P.C., Lee H. Three-dimensional spheroid culture targeting versatile tissue bioassays using a PDMS-based hanging drop array. Sci. Rep. 2017;7:4363. doi: 10.1038/s41598-017-04718-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Oraiopoulou M.-E., Tzamali E., Tzedakis G., Liapis E., Zacharakis G., Vakis A., Papamatheakis J., Sakkalis V. Integrating in vitro experiments with in silico approaches for glioblastoma invasion: the role of cell-to-cell adhesion heterogeneity. Sci. Rep. 2018;8:16200. doi: 10.1038/s41598-018-34521-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gkretsi V., Stylianou A., Louca M., Stylianopoulos T. Identification of Ras suppressor-1 (RSU-1) as a potential breast cancer metastasis biomarker using a three-dimensional in vitro approach. Oncotarget. 2017;8:27364. doi: 10.18632/oncotarget.16062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Takagi H., Sato M.J., Yanagida T., Ueda M. Functional analysis of spontaneous cell movement under different physiological conditions. PLoS One. 2008;3:1–7. doi: 10.1371/journal.pone.0002648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Huda S., Weigelin B., Wolf K., Tretiakov K.V., Polev K., Wilk G., Iwasa M., Emami F.S., Narojczyk J.W., Banaszak M., Soh S., Pilans D., Vahid A., Makurath M., Friedl P., Borisy G.G., Kandere-Grzybowska K., Grzybowski B.A. Lévy-like movement patterns of metastatic cancer cells revealed in microfabricated systems and implicated in vivo. Nature Commun. 2018;9:1–11. doi: 10.1038/s41467-018-06563-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Laforgue L., Laurent V.M., Duperray A., Verdier C. 3D cancer cell migration in collagen matrices. Comput. Methods Biomech. Biomed. Eng. 2015;18:1968–1969. doi: 10.1080/10255842.2015.1069628. [DOI] [PubMed] [Google Scholar]
- 52.Plou J., Juste-Lanas Y., Olivares V., Del Amo C., Borau C., García-Aznar J.M. From individual to collective 3D cancer dissemination: roles of collagen concentration and TGF-$$ Sci. Rep. 2018;8:12723. doi: 10.1038/s41598-018-30683-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lee M.-H., Wu P.-H., Staunton J.R., Ros R., Longmore G.D., Wirtz D. Mismatch in mechanical and adhesive properties induces pulsating cancer cell migration in epithelial monolayer. Biophys. J. 2012;102:2731–2741. doi: 10.1016/j.bpj.2012.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Parker J.J., Canoll P., Niswander L., Kleinschmidt-DeMasters B.K., Foshay K., Waziri A. Intratumoral heterogeneity of endogenous tumor cell invasive behavior in human glioblastoma. Sci. Rep. 2018;8:18002. doi: 10.1038/s41598-018-36280-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Haage A., Schneider I.C. Cellular contractility and extracellular matrix stiffness regulate matrix metalloproteinase activity in pancreatic cancer cells. FASEB J. 2014;28:3589–3599. doi: 10.1096/fj.13-245613. [DOI] [PubMed] [Google Scholar]
- 56.Valastyan S., Weinberg R.A. Tumor metastasis: Molecular insights and evolving paradigms. Cell. 2011;147:275–292. doi: 10.1016/j.cell.2011.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Metzler R., Klafter J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000;339:1–77. [Google Scholar]
- 58.Wright A., Li Y.H., Zhu C. The differential effect of endothelial cell factors on in vitro motility of malignant and non-malignant cells. Ann. Biomed. Eng. 2008;36:958–969. doi: 10.1007/s10439-008-9489-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Parkhurst M.R., Saltzman W.M. Quantification of human neutrophil motility in three-dimensional collagen gels. Effect of collagen concentration. Biophys. J. 1992;61:306–315. doi: 10.1016/S0006-3495(92)81838-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Geiger F., Rüdiger D., Zahler S., Engelke H. Fiber stiffness, pore size and adhesion control migratory phenotype of MDA-MB-231 cells in collagen gels. PLoS One. 2019;14 doi: 10.1371/journal.pone.0225215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wu P.-H., Giri A., Wirtz D. Statistical analysis of cell migration in 3D using the anisotropic persistent random walk model. Nat. Protoc. 2015;10:517. doi: 10.1038/nprot.2015.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hallatschek O., Fisher D.S. Acceleration of evolutionary spread by long-range dispersal. Proc. Natl. Acad. Sci. USA. 2014;111:E4911–E4919. doi: 10.1073/pnas.1404663111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Fricke G.M., Letendre K.A., Moses M.E., Cannon J.L. Persistence and adaptation in immunity: T cells balance the extent and thoroughness of search. PLoS Comput. Biol. 2016;12:1–23. doi: 10.1371/journal.pcbi.1004818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Gole B., Beatriz M., Alonso D., Dolenc V., Lah T. Post-translational regulation of cathepsin b, but not of other cysteine cathepsins, contributes to increased glioblastoma cell invasiveness in vitro. Pathol. Oncol. Res. 2009;15:711. doi: 10.1007/s12253-009-9175-8. [DOI] [PubMed] [Google Scholar]
- 65.Weiswald L.-B., Guinebretière J.-M., Richon S., Bellet D., Saubaméa B., Dangles-Marie V. In situ protein expression in tumour spheres: development of an immunostaining protocol for confocal microscopy. BMC Cancer. 2010;10:106. doi: 10.1186/1471-2407-10-106. http://bmccancer.biomedcentral.com/articles/10.1186/1471-2407-10-106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ben-Jacob E., Coffey D.S., Levine H. Bacterial survival strategies suggest rethinking cancer cooperativity. TIM. 2012;20:403–410. doi: 10.1016/j.tim.2012.06.001. [DOI] [PubMed] [Google Scholar]
- 67.Korolev K.S., Xavier J.B., Gore J. Turning ecology and evolution against cancer. Nat. Rev. Cancer. 2014;14:371–380. doi: 10.1038/nrc3712. http://www.ncbi.nlm.nih.gov/pubmed/24739582. [DOI] [PubMed] [Google Scholar]
- 68.Ron I.G., Golding I., Lifsitz-Mercer B. Bursts of sectors in expanding bacterial colonies as a possible model for tumor growth and metastases. Physica A. 2003;320:485–496. [Google Scholar]
- 69.Wallace D.I., Guo X. Properties of tumor spheroid growth exhibited by simple mathematical models. Front. Oncol. 2013;3:1–9. doi: 10.3389/fonc.2013.00051. http://journal.frontiersin.org/article/10.3389/fonc.2013.00051/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Jolly M.K., Boareto M., Huang B., Jia D., Lu M., Ben-Jacob E., Onuchic J.N., Levine H. Implications of the hybrid epithelial/mesenchymal phenotype in metastasis. Front. Oncol. 2015;5:155. doi: 10.3389/fonc.2015.00155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Merz C., Strecker A., Sykora J., Hill O., Fricke H., Angel P., Gieffers C., Peterziel H. Neutralization of the CD95 ligand by APG101 inhibits invasion of glioma cells in vitro. Anti-Cancer Drugs. 2015;26:716. doi: 10.1097/CAD.0000000000000237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Daubriac J., Han S., Grahovac J., Smith E., Hosein A., Buchanan M., Basik M., Boucher Y. The crosstalk between breast carcinoma-associated fibroblasts and cancer cells promotes RhoA-dependent invasion via IGF-1 and PAI-1. Oncotarget. 2018;9:10375. doi: 10.18632/oncotarget.23735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Vukicevic S., Kleinman H.K., Luyten F.P., Roberts A.B., Roche N.S., Reddi A.H. Identification of multiple active growth factors in basement membrane matrigel suggests caution in interpretation of cellular activity related to extracellular matrix components. Exp. Cell Res. 1992;202:1–8. doi: 10.1016/0014-4827(92)90397-q. [DOI] [PubMed] [Google Scholar]
- 74.Kleinman H.K., Martin G.R. Matrigel: Basement membrane matrix with biological activity. Sem. Cancer Biol. 2005;15:378–386. doi: 10.1016/j.semcancer.2005.05.004. [DOI] [PubMed] [Google Scholar]
- 75.Jaalouk D.E., Lammerding J. Mechanotransduction gone awry. Nature Rev. Mol. Cell Biol. 2009;10:63–73. doi: 10.1038/nrm2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Dupont S., Morsut L., Aragona M., Enzo E., Giulitti S., Cordenonsi M., Zanconato F., Le Digabel J., Forcato M., Bicciato S., Elvassore N., Piccolo S. Role of YAP/TAZ in mechanotransduction. Nature. 2011;474:179–184. doi: 10.1038/nature10137. [DOI] [PubMed] [Google Scholar]
- 77.Park J.S., Kim D.H., Shah S.R., Kim H.N., Kim P., Quiñones Hinojosa A. Switch-like enhancement of epithelial-mesenchymal transition by YAP through feedback regulation of WT1 and Rho-family GTPases. Nature Commun. 2019;10:1–15. doi: 10.1038/s41467-019-10729-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Rice A.J., Cortes E., Lachowski D., Cheung B.C., Karim S.A., Morton J.P., Del Río Hernández A. Matrix stiffness induces epithelial-mesenchymal transition and promotes chemoresistance in pancreatic cancer cells. Oncogenesis. 2017;6:1–9. doi: 10.1038/oncsis.2017.54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Zanconato F., Cordenonsi M., Piccolo S. YAP And TAZ: a signalling hub of the tumour microenvironment. Nat. Rev. Cancer. 2019;19:454–464. doi: 10.1038/s41568-019-0168-y. [DOI] [PubMed] [Google Scholar]
- 80.Mark C., Grundy T.J., Strissel P.L., Böhringer D., Grummel N., Gerum R., Steinwachs J., Hack C.C., Beckmann M.W., Eckstein M., Strick R., O’Neill G.M., Fabry B. Collective forces of tumor spheroids in three-dimensional biopolymer networks. ELife. 2020;9:1–22. doi: 10.7554/eLife.51912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Hu B., Wang Q., . Wang Y.A, Hua S., Sauvé C.-E.G., Ong D., Lan Z.D., Chang Q., Ho Y.W., Monasterio M.M., Lu X., Zhong Y., Zhang J., Deng P., Tan Z., Wang G., Liao W.-T., Corley L.J., Yan H., Zhang J., You Y., Liu N., Cai L., Finocchiaro G., Phillips J.J., Berger M.S., Spring D.J., Hu J., Sulman E.P., Fuller G.N., Chin L., Verhaak R.G., DePinho R.A. Epigenetic activation of WNT5a drives glioblastoma stem cell differentiation and invasive growth. Cell. 2016;167:1281–1295. doi: 10.1016/j.cell.2016.10.039. http://linkinghub.elsevier.com/retrieve/pii/S009286741631460X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Iwadate Y. Epithelial-mesenchymal transition in glioblastoma progression. Oncol. Lett. 2016;11:1615–1620. doi: 10.3892/ol.2016.4113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Koh I., Cha J., Park J., Kang S.G., Kim P. The mode and dynamics of glioblastoma cell invasion into a decellularized tissue-derived extracellular matrix-based three-dimensional tumor model. Sci. Rep. 2018;8:1–12. doi: 10.1038/s41598-018-22681-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Khalil A.A., Friedl P. Determinants of leader cells in collective cell migration. Integr. Biol. 2010;2:568–574. doi: 10.1039/c0ib00052c. [DOI] [PubMed] [Google Scholar]
- 85.Trepat X., Wasserman M.R., Angelini T.E., Millet E., Weitz D.A., Butler J.P., Fredberg J.J. Physical forces during collective cell migration. Nat. Phys. 2009;5:426–430. [Google Scholar]
- 86.Wolf K., Wu Y.I., Liu Y., Geiger J., Tam E., Overall C., Stack M.S., Friedl P. Multi-step pericellular proteolysis controls the transition from individual to collective cancer cell invasion. Nature Cell Biol. 2007;9:893. doi: 10.1038/ncb1616. [DOI] [PubMed] [Google Scholar]
- 87.Wolf K., Mazo I., Leung H., Engelke K., Von Andrian U.H., Deryugina E.I., Strongin A.Y., Bröcker E.B., Friedl P. Compensation mechanism in tumor cell migration: Mesenchymal-amoeboid transition after blocking of pericellular proteolysis. J. Cell Biol. 2003;160:267–277. doi: 10.1083/jcb.200209006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Paluch E.K., Aspalter I.M., Sixt M. Focal adhesion-independent cell migration. Annu. Rev. Cell Dev. Biol. 2016;32:469–490. doi: 10.1146/annurev-cellbio-111315-125341. [DOI] [PubMed] [Google Scholar]
- 89.Huang Y., Tong L., Yi L., Zhang C., Hai L., Li T., Yu S., Wang W., Tao Z., Ma H., Liu P., Xie X. Three-dimensional hydrogel is suitable for targeted investigation of amoeboid migration of glioma cells. Mol. Med. Rep. 2018;17:250–256. doi: 10.3892/mmr.2017.7888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.O’Neill P.R., Castillo-Badillo J.A., Meshik X., Kalyanaraman V., Melgarejo K., Gautam N. Membrane flow drives an adhesion-independent amoeboid cell migration mode. Dev. Cell. 2018;46:9–22. doi: 10.1016/j.devcel.2018.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Harris T.H., Banigan E.J., Christian D.A., Konradt C., Wojno E.D.T., Norose K., Wilson E.H., John B., Weninger W., Luster A.D. Generalized Lévy walks and the role of chemokines in migration of effector CD8+ T cells. Nature. 2012;486:545. doi: 10.1038/nature11098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Ariel G., Rabani A., Benisty S., Partridge J.D., Harshey R.M., Be’Er A. Swarming bacteria migrate by Lévy Walk. Nature Commun. 2015;6 doi: 10.1038/ncomms9396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Reynolds A.M., Ouellette N.T. Swarm dynamics may give rise to Lévy flights. Sci. Rep. 2016;6:1–8. doi: 10.1038/srep30515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Auger-Méthé M., Derocher A.E., Plank M.J., Codling E.A., Lewis M.A. Differentiating the Lévy walk from a composite correlated random walk. Methods Ecol. Evol. 2015;6:1179–1189. [Google Scholar]
- 95.Svensson C.M., Medyukhina A., Belyaev I., Al-Zaben N., Figge M.T. Untangling cell tracks: Quantifying cell migration by time lapse image data analysis. Cytometry A. 2018;93:357–370. doi: 10.1002/cyto.a.23249. [DOI] [PubMed] [Google Scholar]
- 96.Vigneswaran K., Neill S., Hadjipanayis C.G. Beyond the World Health Organization Grading of Infiltrating Gliomas: Advances in the Molecular Genetics of Glioma Classification. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Friedmann-Morvinski D. Glioblastoma heterogeneity and cancer cell plasticity. Crit. Rev. Oncog. 2014;19:327–336. doi: 10.1615/critrevoncog.2014011777. [DOI] [PubMed] [Google Scholar]
- 98.Allen M., Bjerke M., Edlund H., Nelander S., Westermark B. Origin of the U87MG glioma cell line: Good news and bad news. Sci. Transl. Med. 2016;8 doi: 10.1126/scitranslmed.aaf6853. www.ScienceTranslationalMedicine.org. [DOI] [PubMed] [Google Scholar]
- 99.Hamerlik P., Lathia J.D., Rasmussen R., Wu Q., Bartkova J., Lee M., Moudry P., Bartek J., Fischer W., Lukas J., Rich J.N. Autocrine VEGF-VEGFR2-Neuropilin-1 signaling promotes glioma stem-like cell viability and tumor growth. J. Exp. Med. 2012;209:507–520. doi: 10.1084/jem.20111424. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3302235&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Sivakumar H., Devarasetty M., Kram D.E., Strowd R.E., Skardal A. Multi-cell type glioblastoma tumor spheroids for evaluating sub-population-specific drug response. Front. Bioeng. Biotechnol. 2020;8:1–9. doi: 10.3389/fbioe.2020.538663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Richards R., Mason D., Levy R., Bearon R., See V. D imaging and analysis of multicellular tumour spheroid cell migration and invasion. BioRxiv. 2018 https://www.biorxiv.org/content/early/2018/10/15/443648. [Google Scholar]
- 102.Schindelin J., Arganda-Carreras I., Frise E., Kaynig V., Longair M., Pietzsch T., Preibisch S., Rueden C., Saalfeld S., Schmid B. Fiji: an open-source platform for biological-image analysis. Nature Methods. 2012;9:676. doi: 10.1038/nmeth.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.V. Baecker, ImageJ macro tool sets for biological image analysis, in: Proceedings of the ImageJ User and Developer Conference, Luxembourg, 2012, pp. 24–26.
- 104.Tinevez J.-Y., Perry N., Schindelin J., Hoopes G.M., Reynolds G.D., Laplantine E., Bednarek S.Y., Shorte S.L., Eliceiri K.W. TrackMate: An open and extensible platform for single-particle tracking. Methods. 2017;115:80–90. doi: 10.1016/j.ymeth.2016.09.016. [DOI] [PubMed] [Google Scholar]
- 105.Mitchell S., Roy K., Zangle T.A., Hoffmann A. Nongenetic origins of cell-to-cell variability in B lymphocyte proliferation. Proc. Natl. Acad. Sci. 2018;115:E2888–E2897. doi: 10.1073/pnas.1715639115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Bian X., Kim C., Karniadakis G.E. 111 years of Brownian motion. Soft Matter. 2016;12:6331–6346. doi: 10.1039/c6sm01153e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Tarantino N., Tinevez J.-Y., Crowell E.F., Boisson B., Henriques R., Mhlanga M., Agou F., Israël A., Laplantine E. TNF And IL-1 exhibit distinct ubiquitin requirements for inducing NEMO IKK supramolecular structures. J. Cell Biol. 2014;204:231–245. doi: 10.1083/jcb.201307172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Potel M.J., Mackay S.A. Preaggregative cell motion in dictyostelium. J. Cell Sci. 1979;36:281–309. doi: 10.1242/jcs.36.1.281. [DOI] [PubMed] [Google Scholar]
- 109.Miura K., Sladoje N. Bioimage data analysis workflows. Learn. Mater. Biosci. 2019 [Google Scholar]
- 110.Diaspro A. CRC Press; 2010. Nanoscopy and Multidimensional Optical Fluorescence Microscopy. [Google Scholar]
- 111.Nousi A., Søgaard M.T., Jauffred L. Single-cell tracking reveals super-spreading cells with high persistence in invasive brain cancer. BioRxiv. 2020 doi: 10.1016/j.bbrep.2021.101120. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The supplementary material includes 3 complimentary figures that provide additional information to the reader.
Data Availability Statement
All cell trajectories – as spatial coordinates and time – presented in this study are openly available in FigShare at doi:10.6084/m9.figshare.14229515.